Evidential statistics as a statistical modern synthesis to support 21st century science

Abstract

During the 20th century, population ecology and science in general relied on two very different statistical paradigms to solve its inferential problems: error statistics (also referred to as classical statistics and frequentist statistics) and Bayesian statistics. A great deal of good science was done using these tools, but both schools suffer from technical and philosophical difficulties. At the turning of the 21st century (Royall in Statistical evidence: a likelihood paradigm. Chapman & Hall, London, 1997; Lele in The nature of scientific evidence: statistical, philosophical and empirical considerations. The University of Chicago Press, Chicago, pp 191–216, 2004a), evidential statistics emerged as a seriously contending paradigm. Drawing on and refining elements from error statistics, likelihoodism, Bayesian statistics, information criteria, and robust methods, evidential statistics is a statistical modern synthesis that smoothly incorporates model identification, model uncertainty, model comparison, parameter estimation, parameter uncertainty, pre-data control of error, and post-data strength of evidence into a single coherent framework. We argue that evidential statistics is currently the most effective statistical paradigm to support 21st century science. Despite the power of the evidential paradigm, we think that there is no substitute for learning how to clarify scientific arguments with statistical arguments. In this paper we sketch and relate the conceptual bases of error statistics, Bayesian statistics and evidential statistics. We also discuss a number of misconceptions about the paradigms that have hindered practitioners, as well as some real problems with the error and Bayesian statistical paradigms solved by evidential statistics.

Introduction

The use of statistics in science is a topic dear to our hearts. We were humbled and frightened by the request to give an overview introducing not only our field of Evidential Statistics, but also Error Statistics, and Bayesian Statistics. We are aware of the hubris of trying to define essentially all of statistics in a single essay, but we ask the readers’ indulgence for our following instructions.

The understandings of statistics expressed in this article are our ideas that we have come to through decades of struggling to make sense of ecology through statistics. It will be clear from the other papers in this special feature of Population Ecology that there are other viewpoints on the use of statistics in ecology. We offer these ideas in the hope that they may help readers with their own struggle to support their scientific endeavors through statistics.

Technological tools have historically expanded the horizons of science. The telescope gave us the skies. The microscope gave us the world’s fine structure. The cyclotron gave us the structure of matter. Perhaps the ultimate technological tool helping scientists see nature is statistics. It is not an exaggeration to state that statistics gives us all of science. Although mathematics has been recognized as a fundamental tool ecologists can use to learn from the natural world (Underwood 1997; Cohen 2004), our central tenet is that effective use of this tool requires learning to filter scientific arguments through the sieve of statistical argumentation.

There is confusion about statistics among ecologists, philosophers and even statisticians. This confusion is terminological, methodological, and philosophical. As the statistician Royall (2004) has said: “Statistics today is in a conceptual and theoretical mess.” That does not mean that statistics is not helpful, nor does it mean that scientific progress is not being made. Scientists have a phenomenal ability to “muddle through” (Lindblom 1959) with whatever tools they have. Our goal is to help working scientists understand statistics, and thereby help them muddle through more effectively.

More concretely our goals are: (1) to sketch the 3 major statistical paradigms that can be used by researchers, and in so doing introduce to many readers evidential statistics as a formal inferential paradigm that integrates control of error, model identification, model uncertainty, parameter estimation and parameter uncertainty. (2) To clarify some of the major confusions infesting arguments among paradigm adherents. (3) To discuss a few real problems arising in the error statistical and Bayesian approaches. And, (4) to raise some ideas about statistics and science which may help scientists use statistics well.

For more than a century a scientist wanting to make inference from experimental or observational data was stepping onto a battlefield strongly contested by two warring factions. These camps are generally referred to as frequentist and Bayesian statistics. In order to understand these factions, and given that statistics’ foundation lies in probability theory, one must be aware that the two camps have their roots in two widely different definitions of probability (Lindley 2000). Already confusion starts because the labels “frequentist” and “Bayesian” confound two related but distinct arguments: one on definitions of probability and another on styles of inference.

Evidential statistics has arisen as a natural response to this tension, and has been constructed, more or less consciously, from both paradigms by appropriating good features and jettisoning problematic features (Lele 2004a, b; Royall 2004). With three choices the debate can shift from a winner take all struggle to a discussion of what is most useful when dealing with particular problems. Given the scope, our discussion will be largely conceptual, with indicators into the scientific, statistical, and philosophical literatures for more technical treatment.

Interpretations of probability

The idea of probability, chance or randomness is very old and rooted in the analysis of gambling games. In mathematics, a random experiment is a process whose outcome is not known in advance. One simple example of a random experiment consists of (you guessed it) flipping a coin once. From the coin flip, we go onwards defining the sample space, Ω, of an experiment as the set of all possible outcomes in the sample (which in the coin flipping experiment is the set {Head, Tail}, and an event as a realized outcome or set of outcomes). These definitions set the stage for defining what models derived from probability theory.

However, we caution that even the most apparently simple of these definitions and concepts have subtle and hidden complexities. What we call “random”, like a coin flip, can be quite non-random. What we call and model as randomness comes from at least 4 different sources (Guttorp 1995): (1) uncertainty about initial conditions, (2) sensitivity to initial conditions, (3) incomplete process description, and (4) fundamental physical randomness.

Kolmogorov’s axioms and measure theory give the tools to work with many kinds of probabilities. These axioms state that a probability is a number between 0 and 1 associated with a particular event in the sample space of a random experiment. This number is a measure of the chance that the event will occur. If A is an event, then Pr(A) measures the chance that the event will occur. Furthermore, if Ω is the sample space of our random experiment, $\Pr (\Omega ) = 1$. Finally, if two or more events are disjoint (i.e., do not have any outcomes in common), the probability of at least one of these events occurring is equal to the sum of the individual probabilities.

Any system that satisfies the requirements of the preceding paragraph is a probability and can be manipulated according to the rules of probability theory. However, what these manipulations mean will depend on how probability is interpreted. There are 5 major schools of interpretation of probability: classical (or Laplacian), logical, frequentist, subjective, and propensity. All of them can be and have been critiqued (see Hájek 2012). When we think about science we use a combination of the frequentist, propensity, and subjective interpretations so for the purposes of this essay, we will give a brief introduction to only these three interpretations of probability. Laplacian probability is discussed by Yamamura (2015).

The frequency interpretation of probability itself has two flavors. The finite frequency interpretation of probability states that the probability of an event is just the proportion of times that event occurs in some finite number of trials (Venn 1876). The countable frequency interpretation of probability states: if the random process is hypothetically repeated, then the long-run proportion of times an event occurs is the probability of the event (von Mises 1951).

Propensity probability (Peirce 1878; Popper 1959) is simply the innate or natural tendency of an event to occur in an experimental or observational setting. If you flip a coin, there is an innate tendency for it land showing heads. Similarly, a radioactive atom has an innate tendency to decay in a given time period.

In our opinion, combining these two frequency definitions of probability with the propensity definition of probability creates an effective framework for learning from nature. While we cannot know this propensity fully, we can approximate it using finite frequencies. On the other hand, if one has a model or models of the workings of nature, one can calculate the long run frequency probabilities of events under the model. It is the matching of finite frequency approximations of event propensities with model based long run frequency calculations of event probabilities that form the bases of inference.

The subjective interpretation of probability involves personal statements of belief regarding the chance of a given event, with beliefs being constrained to vary between 0 and 1. Subjective probabilities for the same event vary among individuals.

The different interpretations of probability constitute fundamentally different approaches to representing the world. Consequently they lead to intrinsically different ways of carrying a statistical analysis in science.

Fisher’s foundational contribution to statistics science

Fisher’s likelihood function

Fisher’s likelihood function lies at the very foundation of statistics (Edwards 1992; Pawitan 2001). To introduce likelihood, consider experiments in which a series of success/failure trials are carried and their results recorded. Real examples are medical drug trials or wildlife mark-recapture studies. How do we write a probability model for these experiments? Can we build a statistical model to explain how the data arose?

The data being the number of successes recorded in a given experiment, it is natural to try to model these counts as the outcome of a binomial random variable X. By so doing, the set of all possible outcomes, or sample space, is formally associated with a set of probabilities. These sample space probabilities naturally add up to one. Let n be the number of (independent) trials carried out (set a priori) and x the number of successes actually observed in one realization of the experiment. Assume that the probability of success p in each trial remains unchanged. Hence, the probability of a particular sequence of x successes and n − x failures is $p^{x} (1 - p)^{n - x}$ and it follows that

$$\Pr (X = x;p) = \left( {\begin{array}{*{20}c} n \\ x \\ \end{array} } \right)p^{x} (1 - p)^{n - x}$$

The probabilities depend on the parameter p. Thus this model is useless for prediction and understanding the nature of the trials in question if the value of p is not estimated from real data. Once estimation is achieved, we may seek to answer questions such as: can the success probability be assumed to be constant over a given array of experimental settings? Using the same example, Fisher (1922) argued that, given an outcome x, graphing $\left( {\begin{array}{*{20}c} n \\ x \\ \end{array} } \right)p^{x} (1 - p)^{n - x}$ as a function of the unknown p, would reveal how likely the different values of p are in the face of the evidence. This is a switch in focus from the descriptive inference about the data common at the time to inference about the process generating the data. Noting that the word ‘probability’ implies a ratio of frequencies of the values of p and that “about the frequencies of such values we can know nothing whatever”, Fisher spoke instead of the likelihood of one value of the unknown parameter p being a number of times bigger than the likelihood of another value. He then defined the likelihood of any parameter as being proportional to the probability of observing the data at hand given the parameter. Thus, the likelihood function of p is:

$$\ell(p;x) = {c} \cdot \left( {\begin{array}{*{20}c} n \\ x \\ \end{array} } \right)p^{x} (1 - p)^{n - x} .$$

where ‘c’ is a constant that does not depend on the parameter of interest as (see Kalbfleisch 1985). This function uses the relative frequencies (probabilities) that the values of the hypothetical quantity p would yield the observed data as support for those hypothetical values (Fisher 1922). The distinction between likelihood and probability is critical, because as a function of p, ${\ell}$(p) is not a probability measure (i.e., it does not integrate to 1).

The value $\hat{p}$ that maximizes this function is called the Maximum Likelihood (ML) estimate of the parameter p. The graphing of the likelihood function supplies a natural order of preference among the possibilities under consideration (Fisher 1922). Such order of preference agrees with the inferential optimality concept that prefers a given probability model if it renders the observed sample more probable that other tentative explanations (i.e., models) do. Thus, by maximizing the likelihood function derived from multiple probability models (in this case values of p) as hypotheses of how the data arises, one is in fact seeking to quantify the evidential support in favor of one probabilistic model (value of p) over the others (see Fisher 1922; Kalbfleisch 1985; Sprott 2000; Pawitan 2001; Royall 2004).

Because likelihood ratios are ratios of frequencies, they have an objective frequency interpretation. Stating that the relative likelihood of one value p ₁ over another value p ₂, written as $\ell(p_{1};x)/\ell(p_{2};x)$, is equal to a constant k means that the observed data, x, will occur k times more frequently in repeated samples from the population defined by the value p ₁ than from the population defined by p ₂ (Sprott 2000). Because of this meaningful frequentist interpretation of likelihood ratios, authors like Barnard (1967), or Sprott (2000) stated that the best way to express the order of preference among the different values of the parameter of interest using likelihood is by working with the relative likelihood function:

$$R\text{(}p;x\text{)} = \frac{\ell(p;x)}{{\begin{array}{*{20}c} {\hbox{max} } \\ p \\ \end{array} \ell(p;x)}} = \frac{\ell(p;x)}{\ell(\hat{p};x)}$$

This frequency interpretation of likelihood ratios is the basis for likelihood inference and model selection.

It is useful to expand on our understandings of the terms “model”, “parameter”, and “hypothesis”. For us, a model is a conceptual device that explicitly specifies the distribution of data. To say for instance that the data are “gamma distributed” is only a vague model, inasmuch the values of the shape and rate parameters of this mathematical formulation of a hypothesis are not specified. Formally, biological hypotheses are not fully specified as a mathematical model until the parameter values of the probabilistic model are themselves explicitly defined. Different parameter values, or sets of values, actually index different families of models. Hypotheses then, become posited statements about features of the mathematical models that best describe data. We term a model that is described up to functional form, but not including specific parameter values, a model form.¹

Fisher’s principles of experimentation and testing

In Fisher’s (1971) experimental design book there is an account of an experiment famously known as “Fisher’s lady tasting tea experiment”. This account tells the story of a lady that claimed to be able to distinguish between a tea cup which was prepared by pouring the tea first and then the milk and another tea cup where the milk was poured first. Fisher then wonders if there is there a good experiment that could be devised in order to formally test the lady’s claim using logical and mathematical argumentation. Although seemingly trivial, this setting where a scientist, and in particular, an ecologist claims to be able to distinguish between two types of experimental units is a daily reality.

Decades ago, in the late 1980s, one of us was faced with a similar experimental problem. While in Japan doing research on seed-beetles, MLT taught himself to visually distinguish the eggs of Callosobruchus chinensis and C. maculatus to the point where he asserted that he could indeed make such distinction. Doubting himself (as he should have), MLT recruited the help of prof. Toquenaga to set up tea-lady like blind trials to test his assertion (except there was no beverage involved and the subject certainly is not a lady, and perhaps not even a gentleman). In this case, testing the researcher’s claim involved giving the facts—the data—a chance of disproving a skeptic’s view (say, prof. Toquenaga’s position) that the researcher had no ability whatsoever to distinguish between the eggs of these two beetle species.

This tentative explanation of the data is what is generally called “the null hypothesis”. To Fisher, the opposite hypothesis that some discrimination was possible was too vague and ambiguous in nature to be subject to exact testing and stated that the only testable expectations were “those which flow from the null hypothesis” (Fisher 1956). For him it was only natural to seek to formalize the skeptic’s view with an exact probabilistic model of how the data arose and then ponder how tenable such model would be in the face of the evidence. By so doing, he was adopting one of the logic tricks that mathematicians use while writing proofs: contradiction of an initial premise. Applied to this case, and given that MLT had correctly classified 44 out 48 eggs, the trick goes as follows: first we suppose that the skeptic is correct and that the researcher has no discrimination ability whatsoever, and that his choices are done purely at random, independently of each other. Then, because the seed-beetle experimental data is a series of classification trials with one of two outcomes (success or failure), we naturally model the skeptic’s hypothesis using a binomial distribution X counting the number of successfully classified eggs, with a probability of success p = 0.50. Next we ask, under this model, what are the chances of the researcher being correct as often as 44 times out of 48 (the observed count) or even more? According to the binomial model, that probability is about 8 × 10⁻¹⁰. That is, if the skeptic is correct, a result as good as or better than the one actually recorded would be observed only about 0.000008 % of the time under the same circumstances. Hence, either the null hypothesis is false, or an extremely improbable event has occurred.

The proximity to 0 of the number 0.000008 % (the P value) is commonly taken as a measure of the strength of the evidence against the null hypothesis. Such an interpretation is fraught with difficulty, and we would advise against it.

A sketch of error statistics

Error statistics (Mayo 1996) is the branch of statistics most familiar to ecologists. All of the methods in this category share the organizing principle that control of error is a paramount inferential goal. These procedures are designed so that an analyst using them will make an error in inference no more often than a pre specified proportion of the time.

Instead of focusing on testing a single assertion like Fisher, Neyman and Pearson (1933) showed that it was possible to assess one statistical model (called the null hypothesis) against another statistical model (called the “alternative hypothesis”). A function of potential data, T(X), is devised as a test statistic to indicate parameter similarity to either the null hypothesis or the alternate. A critical value or threshold for T is calculated so that if the null is true, the alternate will be indicated by T no more than a pre-designated a proportion of the time α. The Neyman and Pearson hypothesis test (NP-test) is designed so that the null hypothesis will be incorrectly rejected no more than a proportion α of the time. The NP-test appears to be a straight ahead model comparison.

Fisher, however, unraveled the NP-test unexpected connections with the Fisherian P value. Neyman and Pearson’s model-choice strategy could indeed deal with vague hypotheses (both alternative and null), such as “the researcher has indeed some discrimination ability”. Neyman and Pearson termed these “composite hypotheses”, as opposed to fully defined “simple” statistical models.

In Neyman and Pearson’s approach the researcher concedes that the null hypothesis could be true. In that case, the probability distribution of the test statistic is computable because the test statistic, being a function of the potential outcomes, inherits randomness from sample space probabilities. The difference between Neyman and Pearson and Fisher resides in what questions they would seek to answer with this distribution.

Fisher would ask here: if the null hypothesis is true, what is the probability of observing a value of the test statistic as extreme or more extreme than the test statistic actually observed? Fisher maintained that if such probability (the P value) is very small, then the null model should be deemed untenable.

Neyman and Pearson would ask what is the probability under the null of observing a value of the test statistic as extreme as or more extreme than the observed statistic in the direction of the alternative? If a skeptic is willing to assume a fixed threshold for such probability, then a decision between a null and as alternative hypotheses can be made. If, say, the probability of observing a value of the test statistic as large or larger than the one recorded is smaller than 1 %, then that would be enough to convince the skeptic to decide against her/his model.

Adopting such threshold comes with the recognition that whichever decision is made, two possible errors arise: first, the null hypothesis could be true, but it is rejected. The probability of such rejection is controlled by the value of the threshold. That error, for lack of a better name, was called an “error of the first type”, or “Type I error”, and the probability of this kind of error is denoted as α. Second, it may be possible that we fail to reject the null, even if it is false. This type of error is called “Type II” error. The probability of this error is usually denoted by β and can be computed from the probabilistic definition of the alternative hypothesis via its complement, 1 − β. This is the probability of rejecting the null when it is indeed false. Thus, by considering these two errors, Neyman and Pearson tied the testing of the tenability of a null hypothesis to an alternative hypothesis.

Returning to our seed-beetle egg classification problem, the null hypothesis is that the counts X, are binomially distributed with an n = 48 and p = 0.5. Suppose that before starting the test, professor Toquenaga (our skeptic) would have stated that he would only have conceded if MLT correctly classified 85 % or more of the eggs. That is, a number of successful classification events greater or equal to 41/48 would represent a rejection of the null. Under such null the skeptic’s threshold $\upalpha$ is

$$\upalpha = \Pr (X \ge 41) = \sum\limits_{x = 41}^{x = 48} {\left( {\begin{array}{*{20}c} {48} \\ x \\ \end{array} } \right)0.5^{x} (1 - 0.5)^{48 - x} = 3.12 \times 10^{ - 07} } .$$

If in fact, MLT’s probability of success is, say, p = 0.90, then the power of the test is computed by calculating the probability that the observed count will be greater than or equal to 41/48 under the true model is

$$1 -\upbeta = \Pr (X \ge 41) = \sum\limits_{x = 41}^{x = 48} {\left( {\begin{array}{*{20}c} {48} \\ x \\ \end{array} } \right)0.9^{x} (1 - 0.9)^{48 - x} \approx 0.89.}$$

In closing this account, note that an ideal test would of course have a pre-defined α = β = 0 but this cannot be achieved in practical cases. Because of the way these error probability calculations are set up, decreasing the probability of one type of error entails increasing the probability of the other. In practice, before the experiment starts, the researcher fixes the value of α in advance and then changes the sampling space probabilities by increasing the sample size and thus adjusts β to a desired level. Although Neyman and Pearson require setting the Type I error in advance, the magnitude of acceptable Type I error is left to the researcher.

Thus, Neyman and Pearson took Fisher’s logic to test assertions and formalized the scenario where a data-driven choice between two tentative explanations of the data needed to be made. Neyman and Pearson’s approach resulted in a well-defined rule of action that quickly became the workhorse of scientific inquiry. But, as Fisher quickly pointed out the Neyman and Pearson paradigm had lost track of the strength of the evidence and also, that the possibility existed that such evidence would, with further experimentation, very well become stronger or even weaker.

The NP-test requires a prespecification of hypotheses (i.e., parameter values). However, data are often collected before knowledge of parameter values is in hand. An error statistical approach to inference is still feasible. Confidence intervals, do not prespecify the hypotheses, data are collected, a parameter value estimated, and an interval constructed around the estimate to represent plausible values of the parameter in such a fashion that under repeated sampling, the true parameter will be outside of the interval no more than a pre-specified α proportion of the time. Despite the lack of prespecification, the connection between hypothesis tests and confidence intervals is very close. Confidence intervals can be conceived of, and calculated as, inverted hypothesis tests.

Fisher’s P value wears many hats in statistics. But, one of its interpretations lands it squarely in the Error Statistics category. The Fisherian significance test does not compare multiple models as do the NP-test and confidence intervals. A single null hypothesis is assumed, and a test statistic is devised to be sensitive to deviations from the hypothesis. If data are observed and the calculated test statistic is more dissimilar to the null hypothesis than a prespecified P value proportion of data randomly generated from the null, then the null hypothesis is rejected, otherwise one fails to reject it. However, if the P value is not pre-specified, but only observed post-sampling then it does not control error in the same fashion the NP-test and confidence interval do. Nevertheless, it is regarded by many as a quantitative measure of the evidence for or against the null hypothesis.

Mathematical theory concerning the distribution of likelihood ratios connected likelihood with hypotheses tests. Sample space probabilities pass on randomness not only to the test statistic, but also, to the likelihood profile and of course, likelihood ratios, and thus give rise to many of the tests that are nowadays the workhorse of statistical testing in science (Rice 1995). The idea of evaluating the likelihood of one set of parameters vis-à-vis the maximum likelihood gave rise not only to confidence intervals, but to relative profile likelihoods where the likelihood of every value of the parameter of interest is divided by the maximum of this curve. This idea, in turn, motivated the use of likelihood ratio tests for model selection.

A sketch of Bayesian statistics

Formally, Bayesian probabilities are measures of belief by an agent in a model or parameter value. The agent learns by adjusting her beliefs. Personal beliefs are adjusted by mixing belief in the model with the probability of the data under the model. This is done with an application of a formula from conditional probability known as Bayes’ rule: if A and C are two events and their joint probability is defined, then

$$\Pr (A |C) = \frac{{\Pr (A\,{\text{and}}\,C)}}{\Pr (C)} = \frac{\Pr (C |A)\Pr (A)}{\Pr (C)}$$

The application of Bayes’ rule in Bayesian statistics runs as follows. Given the conditional probability of observing the data x under the model M _i written as $f(x|M_{i} )$,² and if our prior opinion about such model is quantified with a prior probability distribution, f _prior (M _i ), then the updated, conditional probability of a model given the observed data becomes:

$$f_{post} (M_{i} |x) = \frac{{f(x|M_{i} )f_{prior} (M_{i} )}}{{\sum {f(x|M_{j} )f_{prior} (M_{j} )} }}$$

In English this equation reads that your belief in a model M _i after you have collected data x (that is your posterior probability) is a conditional probability, given by the product of the probability of the data under the model of interest and the prior probability of the model of interest, normalized so that the resulting ratios (posterior probabilities) of all of the models under consideration sum to one. This is a pretty important constraint. If they do not sum to one, then they are not probabilities and you cannot employ Bayes’ rule. If the models lie in a continuum, that is the models are indexed by a continuous parameter, then the sum in the denominator is replaced by an integral.

While the notation in Bayes’ rule treats all the probabilities as the same, they are not the same. The prior distribution, f _prior (M _i ), quantifies the degree of belief, a personal opinion, in model i. The model or parameter of interest is then seen as a random variable. By so doing, a key inferential change has been introduced: probability has been defined as a measure of beliefs. Let’s call, for the time being, these probabilities “b-probabilities”. Now the term $f(x|M_{i} )$ is taken as a conditional measure of the frequency with which data like the observed data x would be generated by the model M _i should M _i occur. It is taken to be equal to the likelihood function (aside from the constant ‘c’, which cancels out with the same constant appearing in the denominator of the posterior probability). This is not a belief based probability, it is the same probability used to define likelihood ratios and carry out frequentist inference. Let’s call it an “f-probability” to distinguish it from the beliefs-derived probabilities. In the application of Bayes formula above, probability of the data appears as multiplying the prior beliefs in the numerator. The resulting product, after proper normalization becomes the posterior probability of the model at hand, given the observations. It is true that both, f-probabilities and b-probabilities are true probabilities because they both satisfy Kolmogorov’s axioms (Kolmogorov 1933), but to think that they are the same is to think that cats and dogs are the same because they are both mammals: one is a sample space probability whereas the other one is beliefs probability. It is important to note that when you mix an f-probability with a b-probability using Bayes Theorem, one ends up with an updated b-probability.

We return to our binomial classification problem using Bayesian statistics. Our model of how the data arises is given by the binomial formula with n trials, x successes and a probability p of success. Changing p in such formula changes the hypothesized model of how the data arises. Because binomial formula accepts for p any value between 0 and 1, changing p amounts to changing models along a continuum. Let our prior beliefs about this parameter be quantified with the prior probability distribution g(p). The beta distribution with parameters a and b is a convenient distribution for g(p). The posterior distribution of p given the data x is proportional to:

$$f_{post} (p|x) \propto f(x|p)g(p) = \left( {\begin{array}{*{20}c} n \\ x \\ \end{array} } \right)p^{x} (1 - p)^{n - x} p^{a - 1} (1 - p)^{b - 1} \propto p^{a + x - 1} (1 - p)^{n + b - x - 1}$$

Note that the resulting posterior distribution is, after proper normalization, another beta distribution with parameters a + x and b + n−x. Because the mean of a beta distribution is a/(a + b), the mean of the posterior distribution is:

$$\frac{a + x}{(a + x) + b + n - x} = \frac{a + b}{a + b + n}\left( {\frac{a}{a + b}} \right) + \frac{n}{a + b + n}\bar{x},$$

where $\bar{x} = x/n$ is the sample mean. Therefore, the posterior mean is seen to be a weighted average of the prior mean and the sample mean. In a very real sense, the posterior mean is a mixture of the data and the prior beliefs. As the sample size gets large, however, the weight of the first term in this sum goes to 0 while the weight of the second one converges to 1. In that case, the influence of the prior beliefs gets “swamped” by the information in the data. Dorazio (2015) claims that the Bayesian posterior is valid at any sample size, but he also recognizes that does not necessarily mean that anything useful has been learned from the data. The Bayesian posterior may well be dominated by the prior at low sample sizes.

The posterior distribution becomes the instrument for inference: if the parameter of interest is assumed to be a random variable, then the posterior distribution instantly gives the b-probability that such value lies between any two limits, say p _low and p _high . Although either the posterior mean or mode is generally given as an estimate of the unknown parameter, the entire distribution can be used for statistical inference.

The Bayes factor (Kass and Raftery 1995; Raftery 1995) is used Bayesian statistics to measure the evidence in the data for one model over another. Written as

$$\Pr (D|M_{1} )/\Pr (D|M_{2} )$$

where D denotes the data and M _i the ith model, the Bayes factor looks very similar to the ratio of likelihoods evaluated under the two different models, and in fact serves a similar function. For models with specified parameter values, the two are the same. But, for the more common situation where the parameter values are to be determined by the analysis, the likelihood ratio and the Bayes factor are not the same. In this latter case, the Bayes factor is computed as the ratio of two averaged likelihoods, each averaged (integrated) over the prior b-probability of the parameters, whereas the likelihood ratio is calculated as the ratio of the two likelihood functions evaluated at the ML estimates (Raftery 1995). Consequently, the Bayes factor is not a measure of evidence independent of prior belief.

The above paragraphs in this section perhaps give the impression that Bayesianism is a monolithic school. It is not. For brevity we will speak of only three Bayesian schools that each focus on different interpretation of the prior. In subjective Bayesianism the prior is a quantitative representation of your personal beliefs. This makes sense as a statistics of personal learning. Although the subjectivity involved has made many scientists uncomfortable, subjective Bayesians posit that it is the prior distribution that conveys initial information and thus provides the starting point for Bayesian learning, which occurs when this process is iterated making the posterior the prior for the analysis of new data. (Lindley 2000; Rannala 2002). One justification for the Bayesian approach is the ability to bring into the analysis external, prior information concerning the parameters of interest (Rannala 2002).

Objective Bayesianism responded to the discomfort introduced by subjective priors by making the prior distribution a quantitative representation of a declaration of ignorance about the parameters of interest. Prior probabilities are assigned to alternative models/parameter values so as to favor one individual model over another as little as possible given mathematical constraints, either by making the priors uniform or by making them diffuse. These priors are called non-informative. Royle and Dorazio (2008) present an ecologically oriented introduction to statistical analysis emphasizing objective priors.

Empirical Bayesians estimate the prior from external empirical information. Clearly this is a different beast from either form of belief based Bayesianism described above. Although not always made clear, empirical Bayes is just a computational device for conducting likelihood based inference in hierarchical models. The critiques of Bayesianism found below are not directed at empirical Bayes. An excellent introduction to empirical Bayes can be found in Efron (2010).

A sketch of evidential statistics

Richard Royall (1997) begins his book Statistical Evidence: A likelihood paradigm with 3 questions:

• 1. What do I believe, now that I have this observation?

• 2. What should I do, now that I have this observation?

• 3. What does this observation tell me about model/hypothesis A versus B? (How should I interpret this observation as evidence regarding A versus B?).

This third question is not clearly addressed by error statistics. Nor is it addressed by Bayesian statistics, because belief and confirmation are actually quite distinct from evidence (Bandyopadhyay et al. 2016).

Following Hacking (1965) and Edwards (1992), Royall axiomatically took the likelihood ratio as his measure of evidence and proceeded to develop a very powerful inferential framework. Royall divided the result space of an experiment differently than the Neyman–Pearson paradigm. The NP-test has two regions: one where you accept A, and another region where you accept B. For Royall, there are 3 regions (Fig. 1): one where evidence is strong for A over B, another where evidence is strong for B over A, and a region between where evidence is weak (whether leaning towards A or towards B). The advantages of this in the actual interpretation of scientific results are obvious. First, no decision is made pro forma, only the strength of evidence is determined. Second, there is a region of indeterminacy, where the primary conclusion is that not enough data have been obtained.

Fig. 1

A graphical representation of evidence in the likelihood ratio for one model over another. The numbers reflect Royall’s treatment of evidence as a ratio, while the actual scale of the figure reflects our preference for representing evidence by a log of the likelihood ratio

Neyman–Pearson hypothesis tests have two important error rates, the probability of type I error, α, and the probability of type II error, β. With evidential statistics you never actually make an error, because you are not making a decision, only determining the strength of evidence. Nevertheless, evidence even properly interpreted can be misleading—one may find strong evidence for one model when in fact the data was generated by the other. This allows for two interesting probabilities reminiscent (but superior) to α and β. These are: the probability of misleading evidence, M, and the probability of weak evidence, W. This distinction will be discussed further later.

This approach combines strengths from NP-tests, and from Fisherian pure significance tests. Requiring evidence to pass an a priori threshold gives control of error. Royall (1997) shows that if the threshold for strong evidence is k, the probability of misleading evidence is M ≤ 1/k. The basis for such conclusion stems from the frequency interpretation of Royall’s measure of evidence: the likelihood ratio between any two models. This ratio can be interpreted as a random variable, which on average (over hypothetical repeated sampling) equals 1 if the two models (parameter values in our example) explain the data equally well. If we deem there is strong evidence for the first model only when the likelihood ratio exceeds a value k, then, a direct application of Markov’s Theorem allows us to write that

$$\Pr \left( {\frac{{\ell}(p_{1} )}{{\ell(p_{2} \text{)}}} \ge {\text{k}}} \right)$$

Therefore, the chance of observing a misleading likelihood ratio greater than the cut-off for strong evidence k, is less than or equal to 1/k.

The strong evidence threshold is a pre-data control of error, very much like Neyman and Pearson’s Type I error rate. Post data the actually observed evidence (likelihood ratio for Royall) is a fine grained measure. Thus, evidential statistics allows researchers to simultaneously make pre and post data inferences in a coherent framework, as so long craved by practitioners (see Taper and Lele 2011).

The mathematical treatment in Royall (1997) makes a true model assumption (i.e., one of the models in the evidential comparison is true). For the most honest and effective inference, the true model assumption needs to be relaxed. Lele (2004a) eliminates this assumption when he generalizes the likelihood ratio to evidence functions which are conceptualized as the relative generalized discrepancy between two models and reality. Relaxing the true model assumption creates a great philosophical advantage for the evidential approach, but because the focus of this essay is practical, we direct interested readers to Bandyopadhyay et al. (2016) for a fuller discussion.

Desiderata for evidence

Rather than presenting a single monolithic evidence function, Lele sets out a structure for constructing evidence functions. Lele (2004a) and Taper and Lele (2011) discuss desirable features for evidence functions. These desiderata include:

• D1. Evidence should be a data based estimate of the relative distance between two models and reality.

• D2. Evidence should be a continuous function of data. This means that there is no threshold that must be passed before something is counted as evidence.

• D3. The reliability of evidential statements should be quantifiable.

• D4. Evidence should be public not private or personal.

• D5. Evidence should be portable, that is it should be transferable from person to person.

• D6. Evidence should be accumulable: If two data sets relate the same pair of models, then the evidence should be combinable in some fashion, and any evidence collected should bear on any future inferences regarding the models in question.

• D7. Evidence should not depend on the personal idiosyncrasies of model formulation. By this we mean that evidence functions should be both scale and transformation invariant.

• D8. Consistency, that is as M + W → 0 as n → ∞. Or stated verbally, evidence for the true model/parameter is maximized at the true value only if the true model is in the model set, or at the best projection into the model set if it is not.

Likelihood ratios and information criteria as evidence functions

Although the formal structure of evidence functions is relatively new, a number of evidence functions have long been proving their utility. Likelihood ratio and log likelihood ratios, for instance, are evidence functions. Other evidence functions include order consistent information criteria, such as Schwarz’s (1978) Information Criterion, SIC also known as the BIC (Bayesian Information Criterion), the consistent AIC, CAIC, (see Bozdogan 1987), and the Information Criterion of Hannan and Quinn (1979), ICHQ. These information criteria are all functions of the log-likelihood maximized under the model at hand plus a penalty term. As a result, the difference in the values of a given information criteria between two models is always a function of the likelihood ratio. A basic introduction to information criteria can be found in Burnham and Anderson (2002) and a more technical treatment in Konishi and Kitagawa (2008).

Because the likelihood ratio is an evidence function, maximum likelihood parameter estimation is an evidential procedure. Furthermore, likelihood ratio based confidence intervals can also be interpreted as evidential support intervals.

Not all information criteria are sensu stricto evidence functions (Lele 2004a). There is a class of information criteria, strongly advocated by Burnham and Anderson (2002) that are not. These forms can be designated Minimum Total Discrepancy (MTD) forms (Taper 2004). They meet desiderata D1)-D7), but not D8). The very commonly employed Akaike (1974) information criterion, the biased corrected AIC (AIC_c, Hurvich and Tsai 1989) are MTD criteria. That these forms are not strict evidence functions is not to say that these forms are wrong per se, or that they should not be used evidentially, but that these criteria are evaluating models with a slightly different goal than are evidence functions. The design goal of these forms is to select models so as to minimize prediction error, while the design goal for evidence functions is to understand underlying causal structure (Bozdogan 1987; Taper 2004; and Aho et al. 2014). The consequence of this is that asymptotically, all MTD forms will over fit the data by tending to include variables with no real association with the response. But at smaller sample sizes the differences between the classes is not clear cut. The AIC tends to over fit at all sample sizes, while the AIC_c can actually have a stronger complexity penalty than the order consistent forms.

A small conceptual leap that needs to be made to recognize information criteria as evidence functions is the change of scale involved. Royall uses the likelihood ratio as his evidence measure while the difference of information criterion values can be thought of as a log likelihood ratio with bias corrections. Take for instance the difference in the score given by an Information Criterion (IC)³ between a model deemed as best among a set of models and any other model i within that set, and denote it as ΔIC _i  = IC _i  − IC _best . Note that because the IC of the best model is the smallest, by necessity this difference is positive. Because all information criteria can be written as twice the negative log-likelihood maximized under the model at hand plus a complexity penalty that can be a function of both, the sample size and the number of parameters in the model, we can write a general equation for the difference in any IC score. Denote the complexity penalty for model i as cp(d _i , n), where d _i is the dimension (number of estimated parameters) under model i and n is the sample size. For example, in the case of AIC, cp(d _i , n) = 2d _i whereas for SIC, cp(d _i , n) = d _i ln(n). Accordingly,

$$\begin{aligned} \Delta IC_{i} & = - 2\ln {\hat{\ell}}_{i} \text{ + }cp(d_{i} ,n) - \left( { - 2\ln {\hat{\ell}}_{best} \text{ + }cp(d_{best} ,n)} \right) \\ & = - 2\ln \left( {\frac{{{\hat{\ell}}_{i} }}{{{\hat{\ell}}_{best} }}} \right)\text{ + }\Delta cp, \\ \end{aligned}$$

where $\frac{{\hat{\ell }_{i} }}{{\hat{\ell }_{best} }}$ is the ratio of maximized likelihoods under each model, and Δcp = cp(d _i , n) − cp(d _best , n) denotes the difference in the complexity penalties from model i and the best model. For instance, in the case of the SIC, Δcp = ln(n)(d _i  − d _best ), and in the case of the AIC, Δcp = 2(d _i  − d _best ). Writing the difference in this fashion makes it clear that a ΔIC is indeed a log-likelihood ratio plus a bias correction constant that depends on the sample size and the difference in the number of parameters between the two models.

A priori control of error in evidential statistics

If the two models explain the data equally well, finding the probability of misleading evidence given a strong evidence threshold k amounts to finding Pr(ΔIC _i  ≥ k), which is equal to 1 − Pr(ΔIC _i  ≤ k). This quantity is readily recognized as one minus the cumulative density function (cdf) of the ΔIC _i evaluated at k. And yes, talking about the difference in IC having an associated cdf implies that one should be able to say something about the long-run distribution of such difference. Indeed, because ΔIC _i is written as the log likelihood ratio plus a constant, we can use the frequency interpretation of likelihood ratios, We can find the probability distribution of $\varLambda = - 2{ \ln }\left( {\frac{{\hat{\ell }_{\text{i}} }}{{\hat{\ell }_{\text{best}} }}} \right)$ under hypothetical repeated sampling and then express the distribution of the ΔIC _i as that of Λ shifted by the constant Δcp. The pre-data control of error is achieved by fixing first the size of the probability of misleading evidence, M, and then solving for the value of the threshold k that leads to Pr(ΔIC _i  ≥ k) = M. Upon substituting the expression for ΔIC _i in this equation we get that

$$\Pr (\varLambda + \Delta cp \ge {\text{k}}) = M \Leftrightarrow \Pr (\varLambda \ge {\text{k}} - \Delta cp) = M$$

or $1 - \Pr (\varLambda \le {\text{k}} - \Delta cp) = M$. From this calculation, it is readily seen that the pre-data control of the probability of misleading evidence strongly depends on the form of the complexity penalty.

We now turn to an example, one where we give a closer look to the assumptions behind the now ubiquitous cut-off of two points in ΔIC _i . The cut-off of two points of difference in IC is readily derived from the calculations above, yet it implies that the user is facing a rather stringent model selection scenario. To see why, it is important to know first that the long-run distribution of the log-likelihood ratio is in general very difficult to approximate analytically. Wilks (1938) provided for the first time the approximate distribution of Λ for various statistical models. If model i is true, as it is assumed when testing a null hypothesis vs. an alternative, and if the model deemed as best is the most parameter rich, then Wilks found that Λ has an approximate Chi square distribution with degrees of freedom equal to d _best  − d _i . In this case, the expression $1 - \Pr (\varLambda \le {\text{k}} - \Delta cp) = M$ can be readily computed. In the case of AIC, this expression becomes $1 - \Pr (\varLambda \le {\text{k}} - 2(d_{i} - d_{best} ))$ and in the case of the SIC, it is $1 - \Pr (\varLambda \le {\text{k}} - \ln (n)(d_{i} - d_{best} ))$. Using the now “classic” k = 2, d _i  − d _best  = −1 gives $1 - \Pr (\varLambda \le {\text{k}} - 2(d_{i} - d_{best} )) = 0.0455$ for the AIC. In the case of the SIC, assuming a sample size of n = 7 we get $1 - \Pr (\varLambda \le {\text{k}} - \ln (n)(d_{i} - d_{best} )) = 0.0470$. This example shows that under Wilks model setting (where the two models are nested and the simple model is the truth) a cut off of 2 does give an error control of about the conventional 0.05 size. Also, note that for the AIC and the SIC (unless sample size is tiny) an increase in difference in the number of parameters between the models results in an even stronger control of error. Finally, note that the strength of the error control does not vary when sample size is increased in the AIC but does so in the SIC. For the SIC, M decrease as sample size increases. This decrease is what makes the SIC an order consistent form.

Exact values of M will vary with criterion, sample size, functional form of the models, nestedness of models, and the nearness of the best model to the generating process. If you are acting in a regulatory setting, or in an experimental design setting, then the precise value of M may matter. In these cases M should be explicitly calculated a priori. But, in the general prosecution of science, it really matters very little whether M is bounded at 0.07 or 0.03; both give moderately strong control of error. Adopting an a priori cut off of say 2 for moderately strong control of error or of 4 for strong control of error gives the scientist and the scientific community the protection from wishful thinking that it needs without the fiction that control of error is known more precisely than it is.

Increasingly, ecological statistics has shifted its focus from point and interval estimation for parameters in models that magically seemed to appear from nowhere and whose connection to hypotheses of real scientific interest were often somewhat tenuous, to trying to incorporate theories of ecological processes directly in models to be statistically probed.

Evidential statistics as a statistical modern synthesis

Chatfield (1995) asserted that the major source of error in all statistical analysis is due to using the wrong model, and traditional statistics did not adequately address model uncertainty. Since then, Royall’s (1997) reconstruction of traditional statistics, and Lele’s (2004a) extension of the likelihood ratio to evidence functions have allowed a statistical modern synthesis that smoothly incorporates model identification, model uncertainty, parameter estimation, parameter uncertainty, pre-data error control, and post-data strength of evidence into a single coherent framework. We believe that that evidential statistics is currently the most effective statistical paradigm for promoting progress in science.

For completeness, we need to draw attention to another recent statistical paradigm called “severe testing” (e.g., Mayo and Cox 2006; Mayo and Spanos 2006). Similar to evidential statistics, severe testing combines pre-data control of error with a post data measure of the strength of inference. Despite very different surface presentations, there is considerable similarity in the underlying mathematics between evidence and severe testing. We find the evidential approach more useful for us for several reasons: first, in evidence the primary object of inference is the model, while the primary object of inference in severe testing is the parameter value. Second, we find the direct comparison involved in evidence clearer than the counterfactual arguments required for testing.

An example evidential application using information criteria

To illustrate the evidential use of information criteria, we revisit an example from Lele and Taper (2012). That is the single-species population growth data from Gause’s (1934) laboratory experiments with Paramecium aurelia with interest in the scientific questions of: (1) Does the population exhibit density dependent population growth? And, (2) If so what is the form of density dependence?

The observed growth rate for a population is calculated as r _t  = ln(N _t+1/N _t ). By definition the growth rate of a population with density dependence is a function of population size, N _t (Fig. 2). Consequently, we model the population’s dynamics by $r_{t} = g(N_{t} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } ) + v_{t} (\sigma )$, where g is a deterministic growth function, $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }$ is a vector of parameters, v _t (σ) is an independent random normally distributed environmental shock to the growth rate with mean 0 and standard deviation σ representing the effects of unpredictable fluctuations in the quality of the environment.

Fig. 2

Observed population growth rate plotted population size. The lines are expected growth rates for five fitted growth models. The data are the first of 3 replicate time series for Paramecium aurelia given in The Struggle for Existence (Figure after Fig. 1 Lele and Taper 2012)

We use a suite of common population growth models: Ricker, $(g(N_{t} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } ) = r_{i} (1 - N_{t} /K))$, generalized Ricker, $(g(N_{t} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } ) = r_{i} (1 - (N_{t} /K)^{\gamma } ))$, Beverton–Holt, $(g(N_{t} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } ) = r_{i} K/K + r_{i} N_{t} - N_{t} )$, Gompertz, $(g(N_{t} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } ) = a (1 - \ln (N_{t} /K)))$, and the density independent exponential growth model $(g(N_{t} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } ) = r_{i} )$. These models have been parameterized in as similar a fashion as possible. K represents the equilibrium population size, and r _i is the intrinsic growth rate, or limit to growth rate as N _t approaches 0. In the Gompertz model the parameter ‘a’ also scales growth rate, but is not quite the same thing as r _i because in this model growth rate is mathematically undefined at 0.

The log-likelihood function for all of these models is:

$$\ln \ell(r_{t} ,N_{t} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } ,\sigma ) = \frac{{\sum\nolimits_{t = 0}^{T - 2} {(g(N_{t} ,\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta }) - r_{t})} }}{{2\sigma^{2} }} - \frac{{(T - 1)\ln (2\pi \sigma^{2} )}}{2},$$

where T is the total number of population sizes observed. For the construction of information criteria, the number of parameters, p, is the length of the vector $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\theta } + 1$; the addition of 1 for the parameter σ.

Table 1 is typical of the tables produced in information criteria analysis. It contains the log-likelihoods, the number of parameters, and for several common criteria, the IC and ΔIC values. To have a priori control of error, we need to specify a threshold for strong evidence. As with α, the size of the NP-test, this threshold depends on the researchers needs. To match with scientific conventions, we set this threshold at a ΔIC value of 2. This translates roughly to a bound on misleading evidence of M < 0.05. From Table 1, one can make a number of observations that are very useful in framing our thinking about our driving questions. (1) For the exponential model, the ΔIC values for all criteria are all >14, confirming quantitatively what is visually obvious from the figure that it is essentially impossible that P. aurelia is growing in a density independent fashion under the conditions of Gause’s experiment. (2) All of the information criteria give strong evidence against the Gompertz as a potential best model given our threshold for strong evidence. (3) Because the Ricker model is nested within the generalized Ricker, and the exponential within the Ricker, the generalized Ricker has the highest log-likelihood among these three models, as dictated by theory, but it is not the best model according to the information criteria. (4) Different information criteria favor different models with different degrees of strength. Both the SIC and the AIC_c indicate moderately strong evidence that the generalized Ricker is not the best model. The evidence from the AIC is more equivocal. This may be an example of the tendency of the AIC to over fit. Although not the case in this example, the rank order for some models can change between different criteria. (5) The Ricker model has the lowest IC value, indicating that it is the “best model,” but the difference with the Beverton–Holt model is small, thus the evidence that the Ricker model is superior to the Beverton–Holt is very weak, and both models should be considered for prediction and interpretation, as should the generalized Ricker and Gompertz to considerably lesser degrees. (6) There are three classes of non-nestable models in this problem. Classical likelihood ratio tests do not compare across model families, thus an information criterion based analysis allows a richer probing of nature. In this case we see that the Beverton–Holt model is essentially indistinguishable in merit from the Ricker, at least for this population on the basis of this data. We also see that there is strong evidence that the Gompetz is not the best model.

Table 1 Population dynamic model identification for Gause’s P. aurelia using information criteria

Common confusions about the three paradigms

What is the frequency in frequentism?

Frequentism is an overloaded term within the field of statistics referring both to a definition of probability and to a style of inference. Sensu stricto, a frequentist is someone who adheres to a frequency definition of probability, under which an event’s probability is the long run limit of the event’s relative frequency in a series of trials. Another common use of the term frequentist is to describe a person who uses the frequency of error in a decision rule as their principle warrant for inference. Sometimes this branch of statistics is called “Classical Statistics”. We have followed Deborah Mayo (e.g., Mayo 1996) in referring to this style of inference as “error statistics”.

Do hierarchical models require a Bayesian analysis?

Hierarchical models are not Bayesian per se. Hierarchical models are probabilistic models including two or more layers of uncertainty in the statistical model of how the data arises. This includes latent variable and missing data problems (Dennis et al. 2006; Dennis and Ponciano 2014). Inference on hierarchical models can in principle be made under all three approaches. However, maximum likelihood estimation of hierarchical models can be very difficult. Generally accessible computer implementations of Markov Chain Monte Carlo (MCMC) algorithms made Bayesian estimation and inference broadly accessible in the 1990s. The ease with which Bayesian methods yielded inferential conclusions to difficult problems of interest to managers and practitioners quickly triggered a “Bayesian revolution” (Beaumont and Rannala 2004). Topics of inference, such as stochastic population dynamics modeling, once deemed inaccessible for practitioners, have experienced marked growth (Newman et al. 2014).

The drive to improve inference using Bayesian statistics has generated a plethora of technical novelties to sample from posterior distributions (like Approximate Bayesian Computation, see https://approximatebayesiancomputational.wordpress.com/), and even motivated novel approaches to ML estimation.

Data Cloning (Lele et al. 2007, 2010) for instance, is a recent algorithmic device inspired by Bayesian statistics that allows likelihood estimation by a simple algorithmic trick. It has long been known (Walker 1969) that in Bayesian analysis as the amount of data increases the posterior distribution converges to a normal distribution with the same mean and variance as the sampling distribution of the maximum likelihood estimate. Lele et al. (2007, 2010) show that this same effect can be achieved simply by creating large data sets from multiple (say k) copies of an original data set (preserving data dependencies). The mean of the resulting posterior distribution approximates the maximum likelihood estimate, but the variance is too low. An estimate of the asymptotic variance is recovered by multiplying the variance of the posterior by k. These estimates can be made arbitrarily accurate by increasing k and the MCMC run length.

As presented above, inference is available through t tests and Wald intervals, Ponciano et al. (2009) extend the data cloning inference tools to include information criterion based model selection, likelihood ratio tests and profile likelihood computations for hierarchical models relevant in Ecology. Using data cloning a full likelihood solution can be achieved for any hierarchical model.

The R package dclone (Solymos 2010) provides easy access to data cloning to anyone who can write a Bayesian model in WinBUGS, OpenBUGS, or JAGS. Gimenez et al. (2014) attribute the rise of Bayesian applications in ecology to the ease of software applications, and wonder what will be the consequence of readily available data cloning software. We would like to point out that Yamamura (2015) in this symposium introduces “empirical Jeffreys’ priors”, another computational device for achieving maximum likelihood inference for complex hierarchical models.

Are likelihood and probability the same thing?

This is a point that often confuses students making their first foray into mathematical statistics. The difficulty arises from omitting the proportionality constant and defining likelihood as ${\ell}$(M _i ; x) = f(x; M _i ). The left hand side of this equality is the likelihood while the right hand side is the probability, so they must be the same thing. Not at all, the likelihood is to be understood as a function of the model (parameter) given the data, while probability is a function of the data given the model. This probability can be thought of as the long run frequency with which a mechanism would generate all the possible observable events, while the likelihood, or rather the relative likelihood, is the support in the data for certain value(s) of the parameter(s) of interest vis-à-vis other values.

The examples shown in this paper deal mostly with discrete probability models (the binomial distribution). In the case of continuous probability models, writing the likelihood function as the joint probability density function of the data evaluated at the observations at hand is not the exact likelihood function (i.e., it is not the joint probability of the observations evaluated at the data at hand). The joint probability density function is only an approximation introduced for mathematical convenience (Barnard 1967; Sprott 2000; Montoya 2008; Montoya et al. 2009), one that works most of the time and hence advocated as the true likelihood function of continuous models in standard mathematical statistics books (e.g., Rice 1995). This approximation sometimes leads to strange behavior and singularities. However, the likelihood is proportional to probabilities and thus cannot have singularities. When these issues arise, Montoya et al. (2009) show how returning to the original definition of the likelihood function, not the approximation, solves the problems.

Are confidence intervals and credible intervals really the same thing?

The error statistical confidence interval is constructed so that under repeated sampling of data confidence intervals constructed with the same method will contain the true value a specified f-probability of the time. The Bayesian credible interval is constructed so that in this instance the true value is believed to be within the interval with a specified b-probability. Thus, confidence intervals are really about the reliability of the method, while credible intervals are about the distribution of belief given the current instance.

However, a confidence interval do also inform about the instance. A measurement made by a reliable method should be reliable. The width of a confidence interval is a function of the variance of the ML estimator of the parameter of interest (Rice 1995). If the data-gathering process is reliable and generates observations with high information content, then repeated instances of this sampling process will result in very similar estimators of the parameter of interest. In other words, the variance of this estimator over hypothetical repeated sampling will be small and the confidence interval will be narrow. The “confidence” then would stem from the reliability and repeatability of the conclusions.

A confidence interval informs that there is evidence that the instance is within the confidence interval (see Bandyopadhyay et al. 2016 appendix chapter 2). Many flavors of confidence intervals exist, but one most relevant to scientists is the one derived from profile likelihoods, or relative profile likelihoods (Royall 2000; Sprott 2004). Profile likelihoods allow one to evaluate the verisimilitude of a set of values of the parameter of interest vis-à-vis the likelihood of the ML estimate. Intuitively, there is no reason why parameter values to the left or right of the ML estimate that are say, 85 % as likely as the ML estimate should not be considered. The evidential support built in the profile likelihood interval gives a continuous measure of the likelihood of nearness to the central value, which serves much of the function of a credible interval without crossing the philosophical divide between frequentist and Bayesian definitions of probability.

A common criticism of the confidence interval relative to the credible interval is that they can include impossible values such as population sizes below the number of observed values. But these problems only occur in approximate confidence intervals. It is important to realize that this criticism does not apply to confidence intervals based on relative likelihoods or relative profile likelihoods (see Sprott 2000 page 16).

Is Bayesianism the only paradigm that can use expert opinion?

The ability to incorporate expert opinion into the statistical analysis of ecological problems is often cited as one of strengths of the Bayesian approach (Kuhnert et al. 2010). Lele (2004b) and Lele and Allen (2006) show how to elicit pseudo data not priors from experts and to treat these as measurements with observation error. This approach is easier for experts than supplying priors. Further, the reliability of the experts can be probed in ways not available with elicited priors.

Is Bayesianism the only paradigm that allows updating?

The ability to “update” on the basis of new data has been stated (e.g., Ellison 2004) as a major advantage of Bayesian analysis. However, as pointed out by van der Tweel (2005) all three paradigms allow updating. What is updated differs, but in each case relates to the paradigms core inferential process. A sequential Bayesian analysis updates belief, a sequential evidential analysis updates evidence, and a sequential error statistical analysis updates both the test statistic and critical values. Desiderata 6 in the sketch of evidential statistics given above indicates that updating is one of the defining characteristics of the evidential approach.

Does model choice inherently make frequentist statistics subjective?

There is some truth, but little sting to this criticism of frequentist statistics often raised by Bayesian scientists. Certainly, if we understand the world through the use of models; the models we actually use limit our understanding. Thus model choice does add a subjective element to science, which can influence the rate of gain of knowledge. However, what knowledge is gained is objective. For the evidential statistician, this is most clear. The evidential statistician makes no claim to the truth of any of the models that investigated. This statistician only claims that given the data in hand one model is estimated to be closer to truth than another. This claim is entirely objective. Further, the subjective choice of models act as a challenge to other scientists to subjectively choose other models that may themselves objectively prove closer to truth. We return to these important points in our conclusions.

Error statistics also maintains objectivity, although in a more cumbersome fashion. The carefully wrought and strict definitions of NP-test and significance testing make it clear both that the evidence is conditional on the models considered, and that the tests make no claims as to the truth of any hypotheses. Neyman and Pearson (1933) thought that operational and temporary decisions should be made between models based on the data and objective criteria “[w]ithout hoping to know whether each separate hypothesis is true or false”. Similarly, Fisher’s significance tests only indicate when a model is inadequate and make no exhortation to belief in the model when it is not rejected. However, the claim to objectivity for error statistics is slightly weaker than that of evidential statistics because error probabilities are the primary evidential measure, and error probabilities are calculated assuming one of the models is true.

Problems in the use of the paradigms

Difficulties in the relationships among P values, error probabilities and evidence

The bulk of science has been done using as statistical tools NP-tests and Fisherian significance tests of P values. Much of this science has been solid, which is amazing because both methods are seldom used the way they were intended. The NP-test does not present output which can be interpreted as evidence. Neyman and Pearson were clear on this in labeling it a decision procedure. The size of the test, α, which is an a priori error rate, could be taken as a crude measure of evidence under the rubric of realiablism, but it is almost never reported. What is reported as a “P value” is the minimum α that would have led to rejection with the observed data. This value is not the size of the test, it is not really evidence, and it is not a post hoc type I error rate (Blume and Peipert 2003). The persistence of this treatment of the NP-test in the face of all statistical education and literature is informative. Scientists very much want to be able to design experiments and studies with modest a priori control of error rates, and they want a post hoc interpretation of evidence which is something more than accept/reject. The NP-test does not give them both but evidential statistics does.

Another problem with the dominant error statistical procedures is that the evidence for or against a single model, H₀, represented by a Fisherian significance test is not commensurate with the evidence for or against that hypothesis when it is contrasted with an alternative model, H₁. This is known as the Lindley paradox. Lindley (1957) originally contrasted a significance test with a Bayesian comparison of two models. As might be expected, how often the contradiction occurs depends on the priors placed on the models.

The Lindley paradox is not restricted to Bayesian analysis. The problem can be reconstructed comparing a P value with a Neyman–Pearson test. The problem is that the significance test may indicate a rejection of H₀ when a comparison of the two models indicates that there is more evidence for H₀ than for H₁. The converse can also be true, a significance test can fail to reject H₀ whereas a model comparison indicates that there is more evidence for H₁ than there is for H₀. For the general prosecution of science, this is a flaw, although in certain contexts, such as drug trials, which require a conservative “first do no harm” attitude, it is a design feature.

Having discarded the “true model” assumption, an evidentialist statistician has trouble thinking in terms of evidence for a single model. For the evidentialist, these attempts are better described as model adequacy measures (Lindsay 2004). Basu et al. (2011) have recently published a technical treatment on the development and use of generalized distance measures for statistical inference. As pointed out by Taper and Lele (2004) evidence functions are the difference (or possibly ratio) of 2 model adequacies. Thus, the Basu et al. book can provide rich material for the construction of future evidence functions. Further, the model adequacy of the best model in a model set represents a limit on how much better a perfect model could do in representing the data.

Problems with error statistical inference and sample size

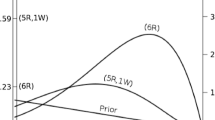
It is a long standing joke that a frequentist, (really an error statistician) is someone happy to be wrong 5 % of the time. This is more than just a joke—it is a reality. The way the control of error is built into error statistical tests implies that while the type I error does not increase when sample increase, it also does not decrease. Under the evidential paradigm, both error probabilities, the probability of strong misleading evidence, M, and the probability of weak evidence, W, go to zero as sample size increases (see Royall 1997, 2000). To illustrate this fact, in Fig. 3 we present Royall’s example where the setting was as follows: the null hypothesis (model 1) was that the data is normally distributed with mean θ ₁ and variance σ ². The alternative is that the data is normally distributed, with the same variance but with mean θ ₂ > θ ₁. If the null hypothesis is true, then the sample mean is $\bar{X}\sim{\text{N}}(\theta_{1} ,\sigma^{2} /n)$ and the critical threshold at a level α = 0.05 for the observed mean above which we would reject the null is given by $\bar{x}_{crit} = \frac{\sigma }{\sqrt n }z_{\alpha } + \theta_{1} = \frac{\sigma }{\sqrt n }1.645 + \theta_{1}$, where z _α is the percentile of a standard normal distribution so that (1 − α)100 % of the area under the Gaussian curve lies to the left of it. In that case, the Type II error, or probability of observing a sample mean that happens to fall within the “failing to reject” region given that the true probability model is $\bar{X}\sim{\text{N}}(\theta_{2} ,\sigma^{2} /n)$ is computed as $\Pr (\bar{X} \le \bar{x}_{crit} )$. On the other hand, the probabilities of misleading evidence and of weak evidence as a function of n in this case are computed respectively as

$$\begin{aligned} M(n) &= \Pr_{1} (\ell_{2} /\ell_{1} > {\text{k}}) = \Pr_{2} (\ell_{1} /\ell_{2} > {\text{k}}), \hfill \\ W(n) &= \Pr_{1(2)} (1/{\text{k}} < \ell_{2} /\ell_{1} < {\text{k}}). \hfill \\ \end{aligned}$$

These probabilities can be readily computed for various sample sizes, and a given cut-off k for the strength of evidence (see Royall 2000 and Fig. 3).

Fig. 3

A comparison of the behavior with increasing sample size of Neyman–Pearson error rates (Type I and Type II) with evidential error rates (M and W). The critical distinction is that Neyman and Pearson type I error remains constant regardless of sample size while both evidential error rates go to zero as sample size increases (Figure re-drawn after Royall (2000) Fig. 2 using $\left| {\theta_{2} - \theta_{1} } \right| =\upsigma = 15;\,\theta_{1} = 100;\,{\text{k}} = 8;\,\upalpha = 0.05.$)

Fisherian significance also has sample size difficulties. In this case, it is with the interpretation of a P value as the strength of evidence against a model. The common practice of science implicitly assumes that a P value from one study implies more or less the same degree of evidence against the null hypothesis that the same P value from another study would even if the two studies have different sample sizes. Unfortunately this is not true. But, how the evidence varies with sample depends on subtleties of the scientist’s interpretation of the procedure. If you impose a significance level and treat every P value greater than the level simply as exceeding the level then there is greater evidence against the null in small samples than in large. If on the other hand, the scientist is directly comparing P values without an a priori cut off, then there is greater evidence in large samples than small samples for a given P values. In either case the evidence depends on sample size making a hash of interpretation of published work (see Royall 1986 for further details).

Bayesian difficulties with detecting non-identifiability

A model is said to be non-estimable if the maximum value of the likelihood function evaluated at the data occurs for more than one set of parameters. That is to say that the data can not be used to distinguish between multiple possible estimates. If this failure is not due to a quirk of sampling, but is instead determined by the way the model is configured, then a model is said to non-identifiable if it is non-estimable for all possible data sets (Ponciano et al. 2012).

Non-estimability may cause programs that calculate maximum likelihood estimates through numerical optimization to return an error. This is an important indication that something is wrong with the way you are modeling your data.

A Bayesian estimation on the other hand will be completely oblivious to the non-estimability. Bayesian estimates are a combination of information from the data and information from the prior beliefs. The hope is that information from the data will swamp that in the prior:

Specification of the prior distribution can be viewed as the ‘price’ paid for the exactness of inferences computed using Bayes Theorem. When the sample size is low, the price of an exact inference may be high. As the size of a sample increases the price of an exact inference declines because the information in the data eventually exceeds the information in the prior (Royle and Dorazio 2008, Hierarchical Modeling and Inference in Ecology. Page 55)

However, this is not always true. In the case of non-estimability/non-identifiability there is no information in the data to distinguish between alternative estimates, and the decision is made entirely on the basis of the prior. Often with complex hierarchical models where non-estimability/non-identifiability might occur is not obvious.

As mentioned above, data-cloning is a method of transforming a Bayesian analysis into a likelihood analysis. In situations where non-estimability/non-identifiability is suspected, this is particularly useful. A data cloned estimation will return estimates of estimable parameters and diagnostics indicating that non-identifiability exists in the remainder (Lele et al. 2010; Ponciano et al. 2012).

Informative, non-informative or mis-informative priors?

As our sketch of Bayesian inference indicates, a specified prior is mandatory for Bayesian calculations. To avoid “subjectivity” many Bayesian scientists prefer to employ “non-informative” priors.

To compute the posterior distribution, the Bayesian has to prescribe a prior distribution for θ, and this is a model choice. Fortunately, in practice, this is usually not so difficult to do in a reasonably objective fashion. As such, we view this as a minor cost for being able to exploit probability calculus to yield a coherent framework for modeling and inference in any situation.

(Royle and Dorazio 2008, Hierarchical Modeling and Inference in Ecology. Page 21)

The problem, is that what constitutes a non-informative prior depends on how the model is parameterized (Fisher 1922; see also Dorazio 2015). Lele (2015) analyses 2 important ecological problems with simulated and real data sets. Each problem has multiple equivalent and commonly used parameterizations. Lele analyses population persistence projections for the San Joaquin kit fox using a Ricker equation parameterized in terms of growth rate and density dependence (a, b) or in terms of growth rate and carrying capacity (a, K).⁴ The two forms are mathematically equivalent. However, Bayesian estimation using “non-informative” priors yield very different parameters estimates and very different predictions of population persistence. Similarly occupancy models for the American toad can be parameterized either in terms of probabilities of occupancy and detection, or in terms of the logits of those quantities. Both formulizations are commonly used in studying occupancy. Again parameter estimates and posterior distributions from Bayesian estimates using non-informative priors are substantially different. Lele (2015) further demonstrates that the maximum likelihood estimates for these problems achieved through data cloning are transformation invariant.

While many statistical ecologists (e.g., Clark, 2005) agree with Royle and Dorazio (2008) that non-informative priors are benign, other eminent statisticians are much more cautious. Bradley Efron, a major proponent of empirical Bayes, closes a recent article (Efron 2013) with the statement: “be cautious when invoking uninformative priors. In the last case, Bayesian calculations cannot be uncritically accepted and should be checked by other methods, which usually means frequentistically.” Gelman and Shalizi (2013) also strongly argue for frequentist/falsificationist checking of Bayesian solutions, and go as far as saying that

the idea of Bayesian inference as inductive, culminating in the computation of the posterior probability…has had malign effects on statistical practice. At best, the inductivist view has encouraged researchers to fit and compare models without checking them; at worst, theorists have actively discouraged practitioners from performing model checking because it does not fit into their framework

(Gelman and Shalizi 2013).

We recommend that, while doing Bayesian statistics, practitioners should run frequentist checks on the validity of the inferences, despite the computational cost of so doing. By frequentist checks here we mean running a large number of simulations under the model (i.e., a parametric bootstrap) or a more complex setting where truth is known (i.e., a model structure adequacy analysis sensu Taper et al. 2008) so that the reliability of the inferences with the posterior distribution can be assessed (see also Dorazio 2015).

The true model assumption and the difficulty of using probability as a measure of evidence

A cryptic but fundamental assumption of Bayesian analysis is that the true model is in the model set. This is obvious because probabilities sum to 1. But, this flies in the face of our experience as scientists, modelers and statisticians. To quote George Box (1976) “All models are wrong.” If all models are wrong, what sense does it make to believe in any of them? If you do not believe in models, what sense does it make to depend on a statistical system predicated on belief in models? However, doubt about belief is not shared uniformly by scientists as evidenced by this quote from an unpublished manuscript by an ecologist.

Frequentists never explicitly state how their metrics such as P values and confidence intervals should be translated into belief about the strength of evidence, although such translation is clearly being done (otherwise data analysis is pointless if it is not informing belief). This is why I view the frequentist approach as subjective; there is no theory for how frequentist metrics should be translated into belief, so clearly the interpretation of frequentist metrics in terms of strength of evidence and belief must be subjective. (Anonymous, personal communication)

This ecologist believes in belief so strongly as to essentially accuse frequentists of lying when they say they do not.

Interestingly, some Bayesian statisticians concur with us. Gelman and Shalizi (2013) state: “It is hard to claim that the prior distributions used in applied work represent statisticians’ states of knowledge and belief before examining their data, if only because most statisticians do not believe their models are true, so their prior degree of belief in all of Θ is not 1 but 0.” Clearly, for these statisticians Bayesian statistics simply represents a very convenient calculation engine.

G.A. Barnard made a more psychological point when he said:

To speak of the probability of a hypothesis implies the possibility of an exhaustive enumeration of all possible hypotheses, which implies a degree of rigidity foreign to the true scientific spirit. We should always admit the possibility that our experimental results may be best accounted for by a hypothesis which never entered our own heads.

(Barnard 1949)

What does it do to us as scientists to continually condition ourselves to believe that our little systems comprehend reality?

Bayesian aspects of Akaike weights

Akaike weights are very important in so called frequentist model averaging (Burnham and Anderson 2002). They are the weights used in averaging models. However, as pointed out by Burnham and Anderson (2004) Akaike weights are posterior probabilities based on subjective priors of the form

$$q_{i} = C \cdot \exp \left( {\frac{1}{2}K_{i} \ln (n) - K_{i} } \right)$$

where q _i is the prior for model i, C is a normalization constant, K _i is the number of parameters in the model, and n is the number of observations. This prior is a b-probability, and as consequence so are Akaike weights. Thus, Burnham and Anderson’s model averaging depends on a subjectively chosen prior, and as such inherits all of the justified criticism of such priors.

Burnham and Anderson like this prior, calling it a savvy prior (their emphasis). The prior captures the Burnham and Anderson world-view very well. If you have more than 8 observations this is an “anti-parsimony” prior, where models of more parameters are being favored a priori over models with fewer.

It is important to note that multi-model inference can be carried out in an evidential framework (Taper and Ponciano 2016). Further, this framework uses the information from multiple models more effectively than does model averaging by computing projections in model space. Such projections are an extension of Akaike’s (1973) original AIC definition.

Priors as practical regularization devices

A class of intractable estimation problems using likelihood inference can be rendered tractable using subjective Bayesian statistics. Suppose we were wishing to estimate both, the probability of success p in a binomial trial whose total number of trials is unknown. In such cases, and depending on the values of p, the profile likelihood for the total number of trials N may not be well behaved and result in confidence limits with an infinite upper bound (Montoya 2008). In that case, as in similar species richness estimation problems, subjective prior elicitation results in reliable inferences that have found applications in planning of biodiversity studies (Christen and Nakamura 2000).

This is not to say the only way to control a badly behaving likelihood is through a prior. Moreno and Lele (2010) were able to greatly improve the performance of site occupancy estimation using penalized likelihood. Some statisticians claim that penalized likelihood is equivalent to using some prior (Wang and Lindsay 2005). In Moreno and Lele’s (2010) case, they penalized to an alternative estimator based on the same data so no belief or prior information was involved.

Using the paradigms

Statistics as a means to clarify arguments

There is a strong impulse among ecologists to seek a statistical paradigm that is true and exact and will make all their analyses beautiful. No such paradigm exists. No paradigm is bullet proof, and no paradigm applies to all situations. Science works by making demonstrations through evidence based arguments (Gelman and Hennig 2015). Statistics functions in science to quantify and clarify those arguments. Different statistical paradigms can be applied to different scientific arguments.

Scientists are not used to thinking about the merits of statistical paradigms usefully. Scientists judge scientific theories by how well they match an external reality. But, all statistical methods exist in the mind only, there is no external reality against which to judge them. Statistical methodologies are to be judged as tools. Are they useful in the construction of sound scientific arguments or are they not?

The central task of science

We hold the view that models carry the meaning in science (Frigg 2006; Giere 2004, 2008). Less radical views, of models such as that they represent reality (Giere 1988, 2004; Hughes 1997; Suppe 1989; van Fraassen 2002) or serve as tools for learning about reality (Giere 1999; Morgan 1999) all still give a very central place to models in science.

Consequently, the job of scientists is to replace old (possibly good) models with new better models. When we have taught courses in both ecological modeling and statistical modeling our primary instruction is always: “Never fall in love with your model—it should not be a long relationship.” Even if a scientist’s interest is primarily in parameter values, model identification is paramount. Without a good model, parameter estimation will be faulty.

Evidential statistics gives the scientist tools to choose among the models he has and motivation to formulate new ones. Evidential statistics is a complete framework. It encompasses: the design of experiments and surveys, pre-data control of error, post data assessment of the strength of inference, model identification, comparison of models, assessment of model uncertainty, parameter estimation, and assessment of estimate uncertainty.

Communicating about models: public versus personal epistemology

Science knows much more than any individual scientist. This knowledge has accumulated over thousands of years through a complex web of transmission, colleague to colleague and teacher to student. Science is a public epistemology.

Belief is personal and difficult to transfer. Belief also depends strongly on such individual things as cultural background and present mood. Evidence, on the other hand, is independent of the individual, transferable, and can accumulate. As such it is much better suited to form the basis of a public epistemology than is belief. Personal belief, although critically important for conducting first-person epistemology, needs to be strengthened with incorporation of data and information gathered from objectively grounded research to meet the demand of ever-growing science. Scientific epistemology, on the other hand is public, and is based on the transferrable and the accumulation of information from many people and over great periods of time (See Strevens 2010). However, the growth of scientific knowledge is not divorced from personal beliefs. Scientists are people, and create their research programs informed by their personal beliefs.

The character and contributions of statistical paradigms

Each of the statistical paradigms discussed has its own character and can make contributions to science. Error statistics, for instance, has been the backbone of science for a hundred years. Undoubtedly, it will continue to make major contributions in the 21st century. There are inherent conservative biases in error statistics generated by the focus on the null hypotheses and the pre-specification of error rates. This conservative bias makes error statistics well suited for application in regulatory situations, medical science, and legal testimony, all fields that ethically mandate a similar bias.

Evidential statistics, while still retaining control of error, places all models on equal footing. These properties and its focus on models make us feel that the evidential paradigm is best suited for the prosecution of general science. Nevertheless, when we are consulting for people answering to regulatory agencies, all of our evidential statistics get packed away, and out comes an error statistical tool kit.

Although we personally find the belief based philosophical foundations of Bayesian statistics unsound to support science as a public epistemology (this includes both subjective and objective Bayesian approaches), a lot of good work has been done with Bayesian statistics. A Bayesian analysis unchecked by frequentist methods runs the risk of undetected catastrophic failure, but in practice, much of the time it will be fine. Even if one seeks to avoid the use of a belief-based probability definition, an understanding of Bayesian methods in the analysis of hierarchical models is absolutely necessary. Most of the alternative methods for solving complex problems in science, empirical Bayes, data cloning, and empirical Jeffreys’ priors all require a solid grounding in Bayesian methods.

It is our opinion that the epistemological high ground is now held by evidential statistics. We look forward to developments that will further evidential statistics, and someday lead to something that supplants it. Currently, most of the purported advantages of both error statistics and Bayesian statistics are now held by evidential statistics. This is by design; the framers of evidential statistics have ruthlessly borrowed what was good and rejected what was faulty. Many of the key ideas in evidential statistics were pioneered by its predecessors.

The central theme of this essay is that there is no magic wand for scientists in statistics. If one wants to use statistics effectively in science, then one needs to learn how to clarify scientific arguments with statistical arguments. To do that one needs to understand how the statistical arguments work. In many ways, this is a much harder task than mastering statistical methods. There are a number of excellent sources to help with this task. As a beginning, we suggest: Royall (1997), Barnett (1999), Sprott (2000), Taper and Lele (2004), Thompson (2007), Bandyopadhyay et al. (2016).