Abstract
This paper discusses group decision-making (GDM) with interval multiplicative preference relations (IMPRs) based on the geometric consistency. We propose a logarithmically geometric compatibility degree between two IMPRs and then define a geometrically logarithmic consistency index of IMPRs. The new consistency index of IMPRs is invariant under permutation of alternatives and transpose of IMPRs. By the statistics theory, the thresholds of the geometrically logarithmic consistency index are provided. For an unacceptably consistent IMPR, an interactive iterative algorithm is designed to improve its consistency level. Using the relationship between an interval weight vector (IWV) and an IMPR, a fuzzy programming model is established to derive an IWV. This model is converted into a linear programming model for resolution. Subsequently, a new individual decision-making (IDM) method with an IMPR is put forward. By minimizing the logarithmically geometric compatibility degree between each individual IMPR and the collective one, a convex programming model is built to determine experts’ weights. Consequently, a novel GDM method with IMPRs is presented. Numerical examples and simulation experiments are conducted to reveal the superiority of the proposed IDM method and GDM method.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The preference relation [1,2,3,4] is one of the most important tools in decision science by pairwise comparisons. Along with the eruptible increasing of economic and social development, group decision-making (GDM) [5,6,7] can fully utilize experts’ opinions to deal with more and more complex decision-making problems. Generally, the experts’ opinions are measured by the 1–9 scale [8], the 0.1–0.9 scale [9], the verbal scale [10], and so on. In fact, it is a common phenomenon that much imprecise or uncertain information is involved in decision-making problems. To help experts to express their ambiguous and uncertain judgments, it is more faithful to measure the preference information by using intervals than crisp numbers, which results in the appearance of interval multiplicative preference relations (MPRs) [11].
The consistency of interval MPRs (IMPRs) is the essential problem in the application of IMPRs. To measure the inconsistency level of preference relations, Brunelli & Fedrizzi [12] proposed five axiomatic properties to scientifically describe the performances of seven existing consistency indices of MPRs. Using the hypothesis test, Vargas [13] provided a statistical test to judge the statistical consistency of MPRs. Lin, Kou & Ergu [14] resorted to a statistical approach to measuring the consistency level of MPRs. Amenta, Lucadamo & Marcarelli [15] discussed the approximated consistency thresholds for Salo–Hämäläinen index of MPRs [16]. At present, several consistency definitions of IMPRs have been studied in [17,18,19,20,21,22]. However, previous research shows that an agreement on the consistency definition of IMPRs has not yet reached, which increases the complexity of consistency index of IMPRs. Based on the consistency definition of IMPRs in [20], Zhang [23] defined a consistency level of IMPRs with the help of the logarithmic distance between two IMPRs. Combining the consistency definition of IMPRs in [20] with the geometric consistency index (GCI) [24], Liu et al. [25] proposed a GCI-based consistency index of IMPRs. Li et al. [19] pointed out that the consistency definition of IMPRs in [20] does not satisfy the invariance under the permutation of alternatives. To solve this problem, Li et al. [19] proposed a geometrical consistency definition of IMPRs. Later, Wang, Lin & Liu [17] pointed out that the geometrical consistency definition of IMPRs [19] satisfies the three properties: invariance, sensitivity, and inevitability. Using the consistency definition of IMPRs in [21], Conde & Paz Rivera Pérez [26] built a linear optimization problem to define the consistency index of IMPRs, which is a little complex and inconvenient. Using the deviation degree of two MPRs involved in an IMPR, Dong et al. [27] defined a consistency index of IMPRs.
To obtain more believable results of decision-making problems, it is necessary to construct a scientific model for deriving the weight vector of alternatives. For decision-making problems with IMPRs, the methods for deriving the prioritization of alternatives are generally divided into two classes. One is to extend some existing prioritization techniques of MPRs [23, 25, 28, 29], such as the eigenvector method [8] and the row geometric mean method (RGMM) [30]. Considering the continuous ordered weighted geometric averaging operator of intervals, Zhou et al. [29] transformed an IMPR into an expected MPR from which the ranking order is induced by RGMM [15]. The other is to use optimization theory to induce the weight vector of alternatives based on different forms of objective functions [19, 31]. Considering the indeterminacy ratio of intervals, a nonlinear programming model [19] was built to derive the interval weights of alternatives.
For GDM problems, experts’ weights play a crucial role in aggregating all individual IMPRs into a collective one. It is very important to quantify experts’ weights in that different experts generally have different abilities, skills, experience, and expertise. The values of similarity degree [32] and support degree [33] were generally used to compute experts’ weights. By minimizing the group continuous logarithm compatibility between the synthetic IMPR and its corresponding continuous characteristic preference relation, Zhou et al. [29] built a group continuous compatibility model to quantify experts’ weights and discussed an induced continuous ordered weighted geometric (ICOWG) operator for proposing an ICOWG-based GDM procedure by extending the continuous ordered weighted geometric averaging operator (COWGA) [34]. Combining the consistency index of MPRs with the induced continuous ordered weighted geometric operator, Wu et al. [28] put forward an approach to computing experts’ weights based upon the reliability of information sources. Of course, the programming model is a good way of determining experts’ weights [23, 35]. Minimizing the deviation degree between the opinions of each expert and the group [35], a maximum consensus-based goal programming model is established to determine the experts’ weights. Zhang [23] build an optimization model to determine experts’ weights for GDM problems with IMPRs by maximizing the consistency level of the collective IMPR.
Although the aforementioned literature reveals that a great progress has been made on GDM with IMPRs, there are still several limitations as follows:
(1) For measuring the inconsistency level of IMPRs, several inconsistency indices of IMPRs [23, 25,26,27, 36] were proposed. The consistency index of IMPRs in [23] is based on the consistency definition of IMPRs in [20]. However, the consistency definition in [20] is sensitive to the labels of compared objects [18, 19, 22]. That is to say, the consistency indices of IMPRs in [25, 36] are sensitive to the labels of alternatives [37, 38].
(2) It is undesirable to ignore the adjustment of a highly inconsistent IMPR. Moreover, the thresholds of consistency index have a direct impact on the final ranking order. However, the existing studies [23, 25,26,27] regarded the thresholds for those consistency indices of IMPRs.
(3) For GDM problems, different experts’ weight vectors generally gave rise to different ranking orders [32]. However, the approaches of allocating experts’ weight vectors in [25, 36] are sensitive to the labels of alternatives [37, 38]. By the basic unit monotonic (BUM) function [39], Wu et al. [28] defined an expected MPR of an IMPR. It should be noted that the expected MPR derived from the upper triangle elements of an IMPR is different from that derived from the lower triangle elements of the same IMPR, which results in different weight vectors of experts and ranking orders obtained by method in [28] (see Example 3).
To overcome the above problems, this paper investigates the GDM method with IMPRs based on the geometric consistency. The motivations of this paper are summarized as follows:
-
(1)
Proposing a more logical consistency index of IMPRs is an important issue during the application of IMPRs in decision science. It is necessary to provide the scientific thresholds of consistency index for IMPRs. This is the most important motivation of this paper.
-
(2)
The most existing method of improving the consistency degree of inconsistent IMPRs is based on programming models, which can be solved only by the specialized software. Hence, it is urgent to design an interactive algorithm to enhance the consistency level of IMPRs. This is the second motivation of this paper.
-
(3)
In GDM problems with IMPRs, it is inevitable to deal with the weights of experts. There is an imperative for putting forward a more scientific method to derive reasonable interval weight vectors (IWVs) and the weights of experts from GDM problems with IMPRs. This motivates us to propose a comprehensive GDM method with IMPRs.
Based on the above motivations, this paper mainly focuses on developing a new GDM method based on geometric consistency of IMPRs. The main innovations are summarized below:
-
(1)
This paper proposes the logarithmically geometric compatibility degree between two IMPRs. A geometrically logarithmical consistency index of IMPRs is defined, which is invariant under permutation of alternatives and transpose of an IMPR. Based on the hypothesis test, the thresholds of the new consistency index of IMPRs are determined. Then, an interactive iterative algorithm is proposed to enhance the consistency level of inconsistent IMPRs.
-
(2)
Based on the relationship between IWVs and IMPRs, a fuzzy programming model is constructed to determine an IWV by maximizing the degree of experts’ satisfaction with the IWV. The constructed fuzzy programming model is then turned into a linear programming model that is easily solved. Consequently, a new individual decision-making (IDM) method is summarized.
-
(3)
To minimize the logarithmically geometric compatibility degree of each individual IMPR and the collective one, a convex programming model is built to determine the objective weights of experts. Then, a novel GDM method with IMPRs is put forward. Moreover, the ranking order obtained from the upper triangle entries of an IMPR is the same as that obtained from the lower triangle entries of the IMPR.
-
(4)
Simulation experiments are conducted to reveal the validity and superiority of the proposed IDM method from three comparison criteria, i.e., average total deviation, difference index, and difference ratio.
The reminder of this paper is organized as follows. Section 2 presents some related concepts. Section 3 proposes the concept of logarithmically geometric compatibility degree between two IMPRs and the geometrically logarithmic consistency index of IMPRs. Section 4 discusses the thresholds for the geometrically logarithmic consistency index of IMPRs and proposes an interactive algorithm for improving the consistency of IMPRs. Section 5 builds a fuzzy linear programming model to derive an IWV and proposes a new IDM method with an IMPR. Then, simulation experiments are conducted to reveal the advantages of the proposed IDM method. Section 6 formulates a convex programming model to determine experts’ weights and proposes a novel GDM method with IMPRs. Numerical examples and comparative analyses are conducted in Sect. 7. Section 8 summarizes some concluding remarks.
2 Preliminaries
In this section, basic notions about intervals, preference relations, and interval multiplicative preference relations are reviewed.
Definition 1
[40]. An interval is defined as the form \(\tilde{a} = [a_{l} ,a_{u} ] = \{ x|a_{l} \le x \le a_{u} \}\). If \(a_{l} > 0\), \(\tilde{a}\) is called positive interval. Specially, an interval \(\tilde{a} = [a_{l} ,a_{u} ]\) degenerates into a real number a in case of \(a_{l} = a_{u} = a\).
For two intervals \(\tilde{a} = [a_{l} ,a_{u} ]\) and \(\tilde{b} = [b_{l} ,b_{u} ]\), \(\tilde{a}\) equals to \(\tilde{b}\) if and only if (iff) \(a_{l} = b_{l}\) and \(a_{u} = b_{u}\), denoted by \(\tilde{a} = \tilde{b}\).
Definition 2
[40, 41]. For two positive intervals \(\tilde{a} = [a_{l} ,a_{u} ]\) and \(\tilde{b} = [b_{l} ,b_{u} ]\), the arithmetic operations of intervals are defined as follows: (i) \(\tilde{a} \otimes \tilde{b} = [a_{l} b_{l} ,a_{u} b_{u} ]\); (ii) \((\tilde{a})^{\lambda } = [(a_{l} )^{\lambda } ,(a_{u} )^{\lambda } ]\) \((\lambda > 0)\); (iii) \(\lambda \tilde{a} = [\lambda a_{l} ,\lambda a_{u} ]\) \((\lambda > 0)\); (iv) \(\tfrac{{\tilde{a}}}{{\tilde{b}}} = [\tfrac{{a_{l} }}{{b_{u} }},\tfrac{{a_{u} }}{{b_{l} }}]\); (v) \(\ln \tilde{a} = [\ln a_{l} ,\ln a_{u} ]\).
Definition 3
[8]. Let \(N = \{ 1,2, \cdots ,n\}\). If an n-order matrix \({\varvec{P}} = (p_{ij} )_{n \times n}\) meets \(p_{ij} > 0\), \(p_{ij} p_{ji} = 1\) and \(p_{ii} = 1\) \((i,j \in N)\), then it is called an MPR. If \(C(\tilde{\user2{P}},\tilde{\user2{Q}}) = 0\) further satisfies \(p_{ij} = p_{ik} p_{kj}\) \((i,j,k \in N)\), then it is a consistent MPR. Otherwise, \({\varvec{P}}\) is inconsistent.
Let \(\mathcal{P}_{n \times n}^{*} {\text{ = \{ }}{\varvec{P}} = (p_{ij} )_{n \times n} {|}\;p_{ij} = p_{ik} p_{kj} ,\;i,j,k \in N{\text{\} }}\). Definition 3 is called Saaty consistency in this paper.
Definition 4
[27]. The consistency index \(CI({\varvec{P}})\) of an MPR \({\varvec{P}}\) is \(CI({\varvec{P}}) = \min \{ d({\varvec{P}},{\varvec{C}}{)|}{\varvec{C}} \in \mathcal{P}_{n \times n}^{*} \}\), where \(d({\varvec{P}},{\varvec{C}}{)}\) is the distance between two MPRs \({\varvec{P}} = (p_{ij} )_{n \times n}\) and \({\varvec{C}} = (c_{ij} )_{n \times n}\) and computed by
By the definition of an MPR, the diagonal element of an MPR always equals to one. Thus, it holds that \(\ln p_{ii} = 0\), \(\ln c_{ii} = 0\), and \(\ln p_{ij} - \ln c_{ij} = - (\ln c_{ji} - \ln p_{ji} )\) \((i,j \in N)\). Thus, Eq. (1) can be rewritten as:
\(d({\varvec{P}},{\varvec{C}}{)} = \frac{{2\sum\nolimits_{i = 1}^{n - 1} {\sum\nolimits_{j = i + 1}^{n} {\left( {\ln p_{ij} - \ln c_{ij} } \right)^{2} } } }}{{n^{2} }}\,{\text{or}}\,d({\varvec{P}},{\varvec{C}}{)} = \frac{{2\sum\nolimits_{i = 1}^{n - 1} {\sum\nolimits_{j = i + 1}^{n} {|\ln p_{ij} - \ln c_{ij} |} } }}{{n^{2} }}\).
Definition 5
[30] A metric of two MPRs \({\varvec{P}} = (p_{ij} )_{n \times n}\) and \({\varvec{Q}} = (q_{ij} )_{n \times n}\), denoted by \(m({\varvec{P}},{\varvec{Q}})\), is defined as:
For an MPR \({\varvec{P}} = (p_{ij} )_{n \times n}\), let \({\varvec{P}}^{*} = (p_{ij}^{*} )_{n \times n}\) be generated by
Obviously, \({\varvec{P}}^{*}\) is a consistent MPR, i.e., \({\varvec{P}}^{*} \in \mathcal{P}_{n \times n}^{*}\). In addition, \({\varvec{P}}^{*} = {\varvec{P}}\) is true if \(\tilde{\user2{P}}^{*}\) is consistent.
Theorem 1
[30]. Let \({\varvec{P}}^{*}\) be constructed from an MPR \(\tilde{\user2{P}}^{*}\) by Eq. (3). Then,
Remark 1
Let \({\varvec{P}}^{*} = (p_{ij}^{*} )_{n \times n}\) be constructed from an MPR \(\user2{P = }(p_{ij} )_{n \times n}\) by Eq. (3). Theorem 1 demonstrates \({\varvec{P}}^{*}\) is a consistent MPR which is the closest to the MPR \(\tilde{\user2{P}}\). If RGMM is used as the prioritization procedure, the GCI of MPRs is defined as follows [24, 42]:
Definition 6
[29]. A matrix \(\tilde{\user2{P}} = (\tilde{p}_{ij} )_{n \times n}\) with \(\tilde{p}_{ij} = [l_{ij} ,u_{ij} ]\) is called an IMPR if it meets
Definition 7
[19]. For an interval vector \(\tilde{\user2{\omega }} = (\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \cdots ,\tilde{\omega }_{n} )^{{\text{T}}}\) with \(\tilde{\omega }_{i} = [\omega_{i}^{l} ,\omega_{i}^{u} ]\), \(\tilde{\user2{\omega }}\) is called a multiplicative normalized interval weight vector (IWV) if it satisfies
Definition 8
[19, 37]. An IMPR \(\tilde{\user2{P}} = (\tilde{p}_{ij} )_{n \times n}\) with \(\tilde{p}_{ij} = [l_{ij} ,u_{ij} ]\) is geometrically consistent if it fulfills:
Let \(\tilde{\mathcal{P}}_{n \times n}^{*}\) be the set of all geometrically consistent n-order IMPRs. Clearly, Eq. (7) can be rewritten as
Remark 2
For an IMPR \(\tilde{\user2{P}} = ([l_{ij} ,u_{ij} ])_{n \times n}\), let \({\varvec{P}}_{(gm)} = (p_{ij}^{(gm)} )_{n \times n}\) with \(p_{ij}^{(gm)} = \sqrt {l_{ij} u_{ij} }\). Clearly, \({\varvec{P}}_{(gm)}\) is an MPR. For simplicity, \({\varvec{P}}_{(gm)}\) is called the geometric mean MPR of \(\tilde{\user2{P}}\) in this paper. Definition 8 illustrates that an IMPR is consistent iff its geometric mean MPR owns Saaty consistency. Moreover, if \(\tilde{\user2{P}}\) is reduced to an MPR P, then Definition 8 is reduced to Saaty’s consistency. In this case, Eq. (8) is reduced to Eq. (1). Therefore, geometric consistency of IMPRs is a generalization of Saaty consistency.
Theorem 2
[19]. Let \(\tilde{\user2{\omega }} = (\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \cdots ,\tilde{\omega }_{n} )^{{\text{T}}}\) be an IWV, where \(\tilde{\omega }_{i} = [\omega_{i}^{l} ,\omega_{i}^{u} ]\). Then, \(\tilde{\user2{W}} = (\tilde{\omega }_{ij} )_{n \times n}\) is a geometrically consistent IMPR, where
3 A new consistency index of IMPRs
This section develops a new logarithmic geometric compatibility degree between two IMPRs. Then, a new consistency index of IMPRs is defined to measure the consistency degree of IMPRs.
3.1 A new logarithmically geometric compatibility degree
Definition 9
For two IMPRs \(\tilde{\user2{P}} = (\tilde{p}_{ij} )_{n \times n}\) with \(\tilde{p}_{ij} = [l_{ij} ,u_{ij} ]\) and \(\user2{\tilde{P}^{\prime} = }(\tilde{p}^{\prime}_{ij} )_{n \times n}\) with \(\tilde{p}^{\prime}_{ij} = [l^{\prime}_{ij} ,u^{\prime}_{ij} ]\), the logarithmically geometric compatibility degree between \(\tilde{\user2{P}}\) and \(\user2{\tilde{P}^{\prime}}\), denoted by \(C(\tilde{\user2{P}},\user2{\tilde{P}^{\prime}})\), is defined as:
Remark 3
Based on Eq. (2), Eq. (10) can be rewritten as \(C(\tilde{\user2{P}},\user2{\tilde{P}^{\prime}}) = \tfrac{{2}}{n(n - 1)}(m({\varvec{P}}_{(gm)} ,\user2{P^{\prime}}_{(gm)} ))^{2}\), where \({\varvec{P}}_{(gm)}\) is the geometric mean MPR of \(\tilde{\user2{P}}\) and \(\user2{P^{\prime}}_{(gm)}\) is that of \(\user2{\tilde{P}^{\prime}}\).
Let \(\tilde{\user2{P}}_{(\sigma )} = (\tilde{p}_{\sigma (i)\sigma (j)} )_{n \times n}\) be an IMPR which is obtained from \(\tilde{\user2{P}}\) under a permutation function \(\sigma\) on N, where \(\sigma :\;i \to i_{p}\) \((i,\;i_{p} \in N)\) with \(\sigma (i) \ne \sigma (j)\) for \(i \ne j\) \((i,j \in N)\).
Theorem 3
For two IMPRs \(\tilde{\user2{P}}\) and \(\user2{\tilde{P}^{\prime}}\), the logarithmically geometric compatibility degree \(C(\tilde{\user2{P}},\user2{\tilde{P}^{\prime}})\) meets the following properties:
(i) \(C(\tilde{\user2{P}},\user2{\tilde{P}^{\prime}}) = C(\user2{\tilde{P}^{\prime}},\tilde{\user2{P}})\); (ii) \(0 \le C(\tilde{\user2{P}},\user2{\tilde{P}^{\prime}}) < + \infty\);
(iii) \(C(\tilde{\user2{P}},\user2{\tilde{P}^{\prime}}) = 0 \Leftrightarrow {\varvec{P}}_{(gm)} = \user2{P^{\prime}}_{(gm)}\); (iv) \(C(\tilde{\user2{P}}_{(\sigma )} ,\user2{\tilde{P}^{\prime}}_{(\sigma )} ) = C(\tilde{\user2{P}},\user2{\tilde{P}^{\prime}})\).
Proof
By Eq. (10), it is straightforward that (i) and (ii) are true.
(iii) Let \(\tilde{\user2{P}} = (\tilde{p}_{ij} )_{n \times n} = ([l_{ij} ,u_{ij} ])_{n \times n}\) and \(\user2{\tilde{P}^{\prime}} = (\tilde{p}^{\prime}_{ij} )_{n \times n} = ([l^{\prime}_{ij} ,u^{\prime}_{ij} ])_{n \times n}\). By Definition 9, \(C(\tilde{\user2{P}},\user2{\tilde{P}^{\prime}}) = 0\) is true iff \(lnl_{ij} + lnu_{ij} - \ln l^{\prime}_{ij} - \ln u^{\prime}_{ij} = 0\), i.e., \(\sqrt {l_{ij} u_{ij} } = \sqrt {l^{\prime}_{ij} u^{\prime}_{ij} }\) \((i,j \in N)\). Therefore, \(C(\tilde{\user2{P}},\user2{\tilde{P}^{\prime}}) = 0\) is equivalent to \({\varvec{P}}_{(gm)} = \user2{\tilde{P}^{\prime}}_{(gm)}\).
(iv) Let \(\tilde{\user2{P}}_{(\sigma )} = ([l_{\sigma (i)\sigma (j)} ,u_{\sigma (i)\sigma (j)} ])_{n \times n}\) and \(\user2{\tilde{P}^{\prime}}_{(\sigma )} = ([l^{\prime}_{\sigma (i)\sigma (j)} ,u^{\prime}_{\sigma (i)\sigma (j)} ])_{n \times n}\). By Eqs. (10–11), it yields that
\(= \tfrac{1}{2n(n - 1)}\sum\nolimits_{{i_{p} = 1}}^{n} {\sum\nolimits_{{j_{p} > i_{p} }} {(\ln l_{{i_{p} j_{p} }} + \ln u_{{i_{p} j_{p} }} - \ln l^{\prime}_{{i_{p} j_{p} }} - \ln u^{\prime}_{{i_{p} j_{p} }} )^{2} } } = C(\tilde{\user2{P}},\user2{\tilde{P}^{\prime}})\).
3.2 A new consistency index of IMPRs
This subsection proposes an approach to constructing a geometrically consistent IMPR from any given IMPR. Then, a new consistency index of IMPRs is defined.
Theorem 4
Let \(\tilde{\user2{P}} = (\tilde{p}_{ij} )_{n \times n}\) with \(\tilde{p}_{ij} = [l_{ij} ,u_{ij} ]\) be an IMPR. If \(\tilde{\user2{P}}^{*} = (\tilde{p}_{ij}^{*} )_{n \times n} = {(}[l_{ij}^{*} ,u_{ij}^{*} ]{)}_{n \times n}\) is generated by
Then, (i) \(\tilde{\user2{P}}^{*}\) is a geometrically consistent IMPR; (ii) If \(\tilde{\user2{P}} = \tilde{\user2{P}}^{*}\), then \(\tilde{\user2{P}}\) is geometrically consistent.
Proof
(i) By Eq. (11), one has \(l_{ii}^{*} = u_{ii}^{*} = 1\) and \(0 < l_{ij}^{*} \le u_{ij}^{*}\) \((i,j \in N)\). On the other hand, it holds for \(l_{ij}^{*} u_{ji}^{*} = (\prod\nolimits_{t = 1}^{n} {l_{it} l_{tj} } )^{1/n} (\prod\nolimits_{t = 1}^{n} {u_{it} u_{tj} } )^{1/n} = 1\) \((i \ne j;\;i,j \in N)\). Therefore, \(\tilde{\user2{P}}^{*}\) is an IMPR. Moreover, it yields that:
which indicates that \(\tilde{\user2{P}}^{*}\) fulfills Eq. (8). By Definition 8, \(\tilde{\user2{P}}\) is geometrically consistent.
(ii) It is straightforward from item (i).
Theorem 4 guarantees the existence of a geometrically consistent IMPR for anyone IMPR. Moreover, if \(\tilde{\user2{P}}\) is reduced to an MPR, then \(\tilde{\user2{P}}^{*}\) computed by Eq. (11) is degenerated into a consistent MPR.
Based on Definition 5 and Theorem 4, a new consistency index of IMPRs is proposed as follows.
Definition 10
The consistency index of an IMPR \(\tilde{\user2{P}}\) is defined as \(CI(\tilde{\user2{P}}) = \min \{ C(\tilde{\user2{P}},\tilde{\user2{R}}{)|}\tilde{\user2{R}} \in \tilde{\mathcal{P}}_{n \times n}^{*} \}\).
By Definition 10, the consistency index of an IMPR \(\tilde{\user2{P}}\) reflects the minimum deviation degree (in the sense of distance) between \(\tilde{\user2{P}}\) and a geometrically consistent IMPR. Apparently, the smaller the value of \(CI\left( {\tilde{\user2{P}}} \right)\), the higher the consistency degree of \(\tilde{\user2{P}}\).
Theorem 5
For an IMPR \(\tilde{\user2{P}}\), let \(\tilde{\user2{P}}^{*}\) be constructed by Eq. (11). Then, (i) \(CI(\tilde{\user2{P}}) = C(\tilde{\user2{P}},\tilde{\user2{P}}^{*} {)}\); (ii)\(CI(\tilde{\user2{P}}) = {{\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{n} {(\mu_{ij} )^{2} } } } \mathord{\left/ {\vphantom {{\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{n} {(\mu_{ij} )^{2} } } } {{4}n(n - 1)}}} \right. \kern-0pt} {{4}n(n - 1)}}\), where
Proof
(i) Let \(\tilde{\user2{P}} = (\tilde{p}_{ij} )_{n \times n} = ([l_{ij} ,u_{ij} ])_{n \times n}\) and \(\tilde{\user2{P}}^{*} = (\tilde{p}_{ij}^{*} )_{n \times n} = ([l_{ij}^{*} ,u_{ij}^{*} ])_{n \times n}\). Assume that \({\varvec{P}}_{(gm)}\) is the geometric mean MPR of \(\tilde{\user2{P}}\) and \({\varvec{P}}_{(gm)}^{*}\) is that of \(\tilde{\user2{P}}^{*}\). Based on Theorem 4 and Remark 2, \(\tilde{\user2{P}}^{*}\) is a geometrically consistent IMPR and \({\varvec{P}}_{(gm)}^{*}\) is a consistent MPR. By Theorem 1, it yields that:
Using Eq. (10) and Remark 3, it yields that
On the basis of Remark 3 and Eq. (13), the value of \(p_{ij}^{\prime - } \,p_{ji}^{\prime + } = 1\) can be computed by:
(ii) Using Eq. (10), the value of \(C(\tilde{\user2{P}},\tilde{\user2{P}}^{*} {)}\) is calculated by
Clearly, it is true for \(\mu_{ii} = 0\) and \(\mu_{ji} = - \mu_{ij}\) \((i,j \in N)\). Thus, \(CI(\tilde{\user2{P}}) = {{\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{n} {(\mu_{ij} )^{2} } } } \mathord{\left/ {\vphantom {{\sum\nolimits_{i = 1}^{n} {\sum\nolimits_{j = 1}^{n} {(\mu_{ij} )^{2} } } } {{4}n(n - 1)}}} \right. \kern-0pt} {{4}n(n - 1)}}\).
The consistency index of MPRs should be invariant under the labels of compared objects and the transpose of MPRs which is pointed out in [12] and [43]. The IMPR is a fuzzy extension of the MPR; it is natural and logical that the consistency index of IMPRs is invariant under the labels of compared objects and the transpose of IMPRs. For an IMPR \(\tilde{\user2{P}}\), let \(\tilde{\user2{P}}^{{\text{T}}}\) and \(F\) be the transpose of \(\tilde{\user2{P}}\) and a permutation matrix, respectively. A reasonable consistency index of IMPRs \(CI(\tilde{\user2{P}})\) should meet \(CI(\tilde{\user2{P}}) = CI(F^{{\text{T}}} \tilde{\user2{P}}F)\) and \(CI(\tilde{\user2{P}}) = CI(\tilde{\user2{P}}^{{\text{T}}} )\). Based on item (ii) of Theorem 5, it is trivial that the proposed consistency index of IMPRs is invariant under the labels of compared objects and the transpose of IMPRs.
Remark 4
Let \(\tilde{\user2{P}}^{*}\) be constructed from an IMPR \(\tilde{\user2{P}} = ([l_{ij} ,u_{ij} ]){}_{n \times n}\) by Eq. (11) and \({\varvec{P}}^{*} = {(}p_{ij}^{*} {)}_{n \times n}\) be constructed from an MPR \(\tilde{\user2{P}}^{*}\) by Eq. (3). If \(\tilde{\user2{P}}\) is reduced to the MPR \({\varvec{P}} = (p_{ij} ){}_{n \times n}\), then
(i) \(\tilde{\user2{P}}^{*}\) is reduced to the MPR \({\varvec{P}}^{*}\);
(ii) The consistency index of \({\varvec{P}}\) computed by Eq. (16) is \(CI({\varvec{P}}) = \frac{{2(m({\varvec{P}},{\varvec{P}}^{*} ))^{2} }}{n(n - 1)} = \frac{{(n - 2)GCI({\varvec{P}})}}{n}\);
(iii) If \(CI({\varvec{P}}) = 0\), then \(\tilde{\user2{P}}^{*}\) is consistent, and vice versa.
Theorem 6
An IMPR \(\beta_{ij}^{ + }\) is geometrically consistent iff \(CI(\tilde{\user2{P}}) = 0\).
Proof
Necessity. If an IMPR \(\tilde{\user2{P}} = ([l_{ij} ,u_{ij} ])_{n \times n}\) is geometrically consistent, it holds for \(\sqrt {l_{ij} u_{ij} } = \left( {\prod\limits_{t = 1}^{n} {\left( {\sqrt {l_{it} l_{tj} } \sqrt {u_{it} u_{tj} } } \right)} } \right)^{{\tfrac{1}{n}}}\) \((i,j \in N)\) which can be rewritten as
Obviously, Eq. (17) implies \(\mu_{ij} = 0\). Hence, \(CI(\tilde{\user2{P}}) = 0\) is true if \(\tilde{\user2{P}}\) is geometrically consistent.
Sufficiency. If \(CI(\tilde{\user2{P}}) = 0\), then \(\ln l_{ij} + \ln u_{ij} - \tfrac{1}{n}\sum\nolimits_{t = 1}^{n} {(\ln l_{it} { + }\ln l_{tj} } + \ln u_{it} { + }\ln u_{tj} ) = {0}\) \((i,j \in N)\). As a result, one has:
Therefore, \(\tilde{\user2{P}}\) is geometrically consistent.
4 A new method of improving consistency of IMPRs
From the perspective of statistics, this section mainly discusses the thresholds of the new consistency index of IMPRs. Then, an iterative algorithm is designed to improve the consistency level of an IMPR.
4.1 Thresholds of the new consistency index of IMPRs
For an IMPR \(\tilde{\user2{P}} = ([l_{ij} ,u_{ij} ])_{n \times n}\), let \(\mu_{ij}\) \((i < j;\;i,j \in N)\) be calculated by Eq. (12). Apparently, the closer the value of \(\mu_{ij}\) is to zero, the smaller the value of \(CI(\tilde{\user2{P}})\). Motivated by the idea in [30, 44], it is assumed that the variables \(\mu_{ij}\) \((i < j;\;i,j \in N)\) with the same normal distribution \(N(0,\sigma^{2} )\) are independent each other. Then, Theorem 7 is proposed as follows.
Theorem 7.
For an IMPR \(\tilde{\user2{P}} = ([l_{ij} ,u_{ij} ])_{n \times n}\), let \(\mu_{ij}\) \((i < j;\;i,j \in N)\) be calculated by Eq. (12). Assume that the variables \(\mu_{ij}\) \((i < j;\;i,j \in N)\) meet: (i) \(\mu_{ij}\) \((i < j;\;i,j \in N)\) are independent random variables; (ii) \(\mu_{ij}\) \((i < j;\;i,j \in N)\) are normally distributed with the same mean zero and variance \(\sigma^{2}\), i.e., \(\mu_{ij} \,N(0,\sigma^{2} )\). Then, \(\tfrac{{{2}n(n - 1)}}{{\sigma^{2} }}CI(\tilde{\user2{P}}) \sim\chi^{2} (\tfrac{n(n - 1)}{2})\), where \(\chi^{2} (\tfrac{n(n - 1)}{2}) \) is the chi-square distribution with \(\tfrac{n(n - 1)}{2}\) freedom degree.
Proof
It is true for \(\tfrac{{\mu_{ij} }}{\sigma }N(0,{1})\) if \(\mu_{ij} N(0,\sigma^{2} )\) \((i < j;\;i,j \in N)\). By Eq. (16), it holds that \(\sum\nolimits_{i = 1}^{n - 1} {\sum\nolimits_{j = i + 1}^{n} {\left( {\tfrac{{\mu_{ij} }}{\sigma }} \right)^{2} } } = \tfrac{{{2}n(n - 1)}}{{\sigma^{2} }}CI(\tilde{\user2{P}})\). Based on the statistics theory, if \(\mu_{ij}\) \((i < j;\;i,j \in N)\) are independent random variables, then \(\sum\nolimits_{i = 1}^{{n{ - 1}}} {\sum\nolimits_{j = i + 1}^{n} {\left( {\tfrac{{\mu_{ij} }}{\sigma }} \right)^{2} } } \sim\chi^{2} \left( {\tfrac{n(n - 1)}{2}} \right)\). Thus, \(\tfrac{{{2}n(n - 1)}}{{\sigma^{2} }}CI(\tilde{\user2{P}})\sim\chi^{2} \left( {\tfrac{n(n - 1)}{2}} \right)\).
Let \(\sigma^{2} = \overline{\sigma }_{n}^{2}\), i.e., \(\mu_{ij} N(0,\overline{\sigma }_{n}^{2} )\) \((i < j;\;i,j \in N)\). The consistency test of IMPRs can be transformed into the testing problem: \(H_{0}\): \(\sigma^{2} \le \overline{\sigma }_{n}^{2}\), \(H_{{1}}\): \(\sigma^{2} > \overline{\sigma }_{n}^{2}\), which is a one-side right-tailed test. Thus, the consistency threshold of n-order IMPRs, denoted by \(\overline{CI}_{n}\), is determined by
where \(\chi_{\alpha }^{{2}} (\tfrac{n(n - 1)}{2}) \) is the α-quantile of chi-square distribution with \(\tfrac{n(n - 1)}{2}\) freedom degree at the significant level α \((\alpha \in (0,1)) \). In practice, the significant level α in Eq. (19) is generally taken as 0.05 or 0.1. For a lot of randomly generated n-order IMPRs, the variables \(\mu_{ij}\) \((i < j;\;i,j \in N)\) can be viewed as random variables with the same distribution. Take \(\mu_{{{12}}}\) for example, Fig. 1 graphically depicts its frequency histograms when randomly generating one hundred thousand n-order IMPRs \((n = 3,4, \ldots ,10)\).
By Fig. 1, it is reasonable that the variables \(\mu_{ij}\) \((i < j;\;i,j \in N)\) are regarded as normally distributed random variables. The second assumption of Theorem 7 is just verified to be reasonable and scientific. It is well known that the standard deviation is a statistic which measures the dispersion of a dataset. In practice, the standard deviation \(\overline{\sigma }_{n}\) in Eq. (19) usually varies with the dimension of IMPRs. To obtain the more believable values of \(\overline{\sigma }_{n}\) and \(\overline{CI}_{n}\), the reference values of \(\overline{\sigma }_{n}\) and \(\overline{CI}_{n}\) \((n = 3,4, \ldots ,10)\) corresponding to different values of α are listed in Table 1 when randomly generating one hundred thousand IMPRs.
Definition 11
Let \(CI(\tilde{\user2{P}})\) be the consistency index of an n-order IMPR \(\tilde{\user2{P}}\) calculated by Eq. (16). Let \(\overline{CI}_{n}\) be the value of consistency threshold of any n-order IMPR. If \(CI(\tilde{\user2{P}}) \le \overline{CI}_{n}\), then \(\tilde{\user2{P}}\) is called an acceptably consistent IMPR. Otherwise, the IMPR \(\tilde{\user2{P}}\) is unacceptably consistent.
Example 1
Compute the consistency index of \( \user2{\tilde{P}} = \user2{ }\left( {\begin{array}{*{20}c} {[1,1]} & {[2,{\text{5}}]} & {[{\text{2}},{\text{4}}]} & {[{\text{1}},{\text{3}}]} \\ {[\tfrac{1}{{\text{5}}},\tfrac{1}{2}]} & {[1,1]} & {[{\text{1}},3]} & {[{\text{1}},{\text{2}}]} \\ {[\tfrac{1}{{\text{4}}},\tfrac{1}{2}]} & {[\tfrac{1}{3},{\text{1}}]} & {[1,1]} & {[\tfrac{1}{2},{\text{1}}]} \\ {[\tfrac{1}{3},{\text{1}}]} & {[\tfrac{1}{2},{\text{1}}]} & {[{\text{1}},{\text{2}}]} & {[1,1]} \\ \end{array} } \right) \)
Based on Eq. (12), the geometrically consistent IMPR \(\tilde{\user2{P}}^{ * }\) is derived from \(\tilde{\user2{P}}\) as follows:
\(\tilde{\user2{P}}^{*} = \left( {\begin{array}{*{20}c} {[1.0000,1.0000]} & {[1.0746,{4}{\text{.1618}}]} & {[1.6818,{6}{\text{.1601}}]} & {[{1}{\text{.1892}},4.3559]} \\ {[0.2403,0.9306]} & {[1.0000,1.0000]} & {[{0}{\text{.7953}},2.9130]} & {[{0}{\text{.5623}},{2}{\text{.5980}}]} \\ {[0.1623,0.5946]} & {[0.3433,{1}{\text{.2574}}]} & {[1.0000,1.0000]} & {[0.3799,{1}{\text{.3161}}]} \\ {[0.2296,0.8409]} & {[0.4855,{1}{\text{.7783}}]} & {[{0}{\text{.7598}},{26321}]} & {[1.0000,1.0000]} \\ \end{array} } \right)\).
By Eq. (16), one has \(CI(\tilde{\user2{P}}) = 0.{0574}\). If the significant level \(\alpha\) equals to 0.05, the consistency threshold of 4-order IMPRs is taken as \(\overline{CI}_{{4}} = 0.{0635}\) by Table 1. Obviously, \(CI(\tilde{\user2{P}}) < \overline{CI}_{{4}}\). Therefore, \(\tilde{\user2{P}}\) is acceptably consistent.
4.2 An algorithm of improving the consistency level of an IMPR
In many practical decision-making problems, it is unavoidable to deal with highly inconsistent IMPRs especially for the large number of alternatives. Naturally, it is necessary to improve the consistency of an unacceptably consistent IMPR. From an unacceptably consistent IMPR, the most common method of coping with an unacceptably consistent IMPR is to derive an acceptably consistent IMPR from the original IMPR. On the basis of Theorem 4, Theorem 8 is proposed to improve the consistency level of IMPRs.
Theorem 8
For an IMPR \(\tilde{\user2{P}} = (\tilde{p}_{ij} )_{n \times n}\), \(\tilde{\user2{P}}^{*} = (\tilde{p}_{ij}^{*} )_{n \times n}\) is obtained by Eq. (11). For a control parameter \(0 \le \beta \le 1\), a matrix \(\user2{\tilde{P^{\prime}}} = (\tilde{p^{\prime}}_{ij} )_{n \times n}\) is constructed by combining \(\tilde{\user2{P}} = (\tilde{p}_{ij} )_{n \times n}\) and \(\tilde{\user2{P}}^{*} = (\tilde{p}_{ij}^{*} )_{n \times n}\), where
Then, (i) \(\user2{\tilde{P^{\prime}}}\) is an IMPR; (ii) \(CI(\user2{\tilde{P^{\prime}}}) \le CI(\tilde{\user2{P}})\).
Proof
(i) Let \(\tilde{p}_{ij} = [l_{ij} ,u_{ij} ]\), \(\tilde{p}_{ij}^{*} = [l_{ij}^{*} ,u_{ij}^{*} ]\) and \(\tilde{p}^{\prime}_{ij} = [l^{\prime}_{ij} ,u^{\prime}_{ij} ]\). By Definition 2, it holds that:
\([l^{\prime}_{ij} ,u^{\prime}_{ij} ] = [(l_{ij} )^{\beta } (u_{ij} )^{1 - \beta } ,(l_{ij}^{*} )^{\beta } (u_{ij}^{*} )^{1 - \beta } ]\) \((i,j \in N)\).
Apparently, it is true for \(\tilde{p}^{\prime}_{ii} = [1,1]\) \((i \in N)\) and
Thus, \(\user2{\tilde{P^{\prime}}}\) is an IMPR by Definition 6.
(ii) For simplicity, for all \(i < j\) and \(i,j \in N\), let \(\mu_{ij} = \ln l_{ij} + \ln u_{ij} - \tfrac{1}{n}\sum\nolimits_{t = 1}^{n} {(\ln l_{it} { + }\ln l_{tj} } + \ln u_{it} { + }\ln u_{tj} )\),\(\mu_{ij}^{*} = \ln l_{ij}^{*} + \ln u_{ij}^{*} - \tfrac{1}{n}\sum\nolimits_{t = 1}^{n} {(\ln l_{it}^{*} { + }\ln l_{tj}^{*} } + \ln u_{it}^{*} { + }\ln u_{tj}^{*} )\), and \(\mu^{\prime}_{ij} = \ln l^{\prime}_{ij} + \ln u^{\prime}_{ij} - \tfrac{1}{n}\sum\nolimits_{t = 1}^{n} {(\ln l^{\prime}_{it} { + }\ln l^{\prime}_{tj} } + \ln u^{\prime}_{it} { + }\ln u^{\prime}_{tj} )\). Using Eq. (20), one has \(\mu^{\prime}_{ij} = \beta \mu_{ij} + (1 - \beta )\mu_{ij}^{*}\) \((i < j;\;i,j \in N)\). As a result, the consistency level of \(\user2{\tilde{P^{\prime}}}\) is computed by \(CI(\user2{\tilde{P^{\prime}}}) = \tfrac{1}{2n(n - 1)}\sum\nolimits_{i = 1}^{n - 1} {\sum\nolimits_{j = i + 1}^{n} {(\beta \mu_{ij} + (1 - \beta )\mu_{ij}^{*} )^{2} } }\). By Theorem 4, \(\mu_{ij}^{*} = 0\) \((i < j;\;i,j \in N)\) are induced in that \(\tilde{\user2{P}}^{*}\) is geometrically consistent. Therefore, one has
Obviously, Eq. (22) demonstrates that \(CI(\user2{\tilde{P^{\prime}}}) \le CI(\tilde{\user2{P}})\) is true in case of \(0 \le \beta \le 1\).
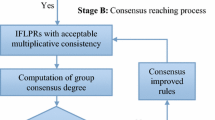
For an IMPR \(\tilde{\user2{P}}\), let \(\user2{\tilde{P^{\prime}}}\) be generated by Eq. (20). Item (ii) of Theorem 8 reveals the consistent degree of \(\user2{\tilde{P^{\prime}}}\) is greater than that of \(\tilde{\user2{P}}\). An interactive algorithm named by Algorithm 1 is designed to improve the consistency level of inconsistent IMPRs. Based on Theorem 8, Algorithm 1 is iterative and convergent.

To more intuitively display the flowchart of Algorithm 1, the concrete process of Algorithm 1 is graphically depicted in Fig. 2.
5 A new IDM method with an IMPR
To derive the multiplicative normalized IWV from an IMPR, a fuzzy programming model is built and concerted into a linear programming model for resolution. Then, an IDM method with an IMPR is proposed.
5.1 Determination of IWVs from IMPRs
Let \(\Omega = \{ \user2{\tilde{\omega } = }(\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \cdots ,\tilde{\omega }_{n} )^{{\text{T}}} {|}0 < \omega_{i}^{l} \le \omega_{i}^{u} ,\;\omega_{i}^{u} \prod\nolimits_{j = 1,j \ne i}^{n} {\omega_{j}^{l} } \le 1,\;\omega_{i}^{l} \prod\nolimits_{j = 1,j \ne i}^{n} {\omega_{j}^{u} } \ge 1,\;i \in N\}\) and \(\tilde{\omega }_{i} = [\omega_{i}^{l} ,\omega_{i}^{u} ]\) is the interval weight of the alternative \(x_{i}\) \((i \in N)\). If an IMPR \(\tilde{\user2{P}} = ([l_{ij} ,u_{ij} ])_{n \times n}\) is constructed by
then \(\tilde{\user2{P}}\) is geometrically consistent by Theorem 2.
By Definitions 2 and 6, Eq. (23) is equivalent to
For simplicity, some notations are introduced as follows:
To simplify the notations, the variables \(d_{ij}^{l} (\tilde{\user2{\omega }})\) and \(d_{ij}^{u} (\tilde{\user2{\omega }})\) are unified into \(d_{ij}^{\theta } (\tilde{\user2{\omega }})\) \((\theta = l,u;\;i < j;\;i,j \in N)\). If there are some contradictions in an IMPR, then there is no multiplicative normalized IWV that satisfies Eq. (24). In practice, it is reasonable to find a good enough multiplicative normalized IWV that satisfies Eq. (24) as well as possible. That is to say, a good enough multiplicative normalized IWV approximately satisfies Eq. (24) as much as possible, i.e.,
where the symbol \(a\) denotes the statement “fuzzy equal to”. Equation (26) is called the fuzzy equation.
Based on the fuzzy programming method [45], a fuzzy set on the universe \(\Omega\) is employed to describe the fuzzy equation \(d_{ij}^{\theta } (\tilde{\user2{\omega }}) \cong {0}\) whose membership function \(\phi_{ij}^{\theta } (\tilde{\user2{\omega }})\) decreases with increasing \(|d_{ij}^{\theta } (\tilde{\user2{\omega }})|\) \((\tilde{\user2{\omega }} \in \Omega ;\;\theta = l,u;\;i < j;\;i,j \in N)\). The value of \(\phi_{ij}^{\theta } (\tilde{\user2{\omega }})\) is generally regarded as the degree of the expert’s satisfaction with the fuzzy equation \(d_{ij}^{\theta } (\tilde{\user2{\omega }}) \cong {0}\) \((\theta = l,u;\;i < j;\;i,j \in N)\). In fact, the degree of experts’ satisfaction with \(\tilde{\user2{\omega }}\) can be represented as the following linear piecewise function:
where the parameters \(\delta_{ij,\theta }^{ + }\) and \(\delta_{ij,\theta }^{ - }\) are the tolerance parameters and nonnegative. If there is no additional information, it is generally assumed that \(\delta_{ij,\theta }^{ + } = \delta_{ij,\theta }^{ - } = \delta_{ij}\) \((\theta = l,u;\;i < j;\;i,j \in N)\). In what follows, the meaning of \(\phi_{ij}^{\theta } (\tilde{\user2{\omega }})\) is intuitively drawn in Fig. 3.
Obviously, \(\phi_{ij}^{\theta } (\tilde{\user2{\omega }}) \in [0,1]\) \((\theta = l,u;\;i < j;\;i,j \in N)\). By Fig. 3, three statements are drawn as follows:
(i) If \(d_{ij}^{\theta } (\tilde{\user2{\omega }}) = {0}\), then \(\phi_{ij}^{\theta } (\tilde{\user2{\omega }}) = 1\). In this situation, \(\tilde{\user2{\omega }}\) is completely satisfied;
(ii) If \(d_{ij}^{\theta } (\tilde{\user2{\omega }}) \in ( - \delta_{ij,\theta }^{ - } ,\delta_{ij,\theta }^{ + } ) - \{ 0\}\), then \(\phi_{ij}^{\theta } (\tilde{\user2{\omega }}) \in (0,1)\). In this situation, \(\tilde{\user2{\omega }}\) is partially satisfied;
(iii) If \(d_{ij}^{\theta } (\tilde{\user2{\omega }}) \notin ( - \delta_{ij,\theta }^{ - } ,\delta_{ij,\theta }^{ + } )\), then \(\phi_{ij}^{\theta } (\tilde{\user2{\omega }}) = {0}\). In this situation, \(\tilde{\user2{\omega }}\) is fully dissatisfied.
Let \(\tilde{\user2{\omega }} \in \Omega\) be derived from an IMPR \(\tilde{\user2{P}}\). Similar to the decision-making problems with fuzzy goals and fuzzy constraints in [45], the overall satisfaction degree of \(\tilde{\user2{\omega }}\), denoted by \(\phi_{{\tilde{\user2{P}}}} (\tilde{\user2{\omega }})\), is defined as:
According to Fig. 3, it is obvious that \(\phi_{{\tilde{\user2{P}}}} (\tilde{\user2{\omega }}) \in [0,1]\). To obtain the optimal multiplicative normalized IWV, the following programming model is built by maximizing the overall satisfaction degree:
where \(\tilde{\user2{\omega }}\) is the decision variable. Obviously, the model (M-1) is a maximin optimization problem which can be converted into the following programming model:
where \(\tilde{\user2{\omega }}\) and ε are decision variables. The variable ε denotes the degree of the minimally overall satisfaction with \(\tilde{\user2{\omega }}\). By Eq. (6) and Eq. (27), the model (M-2) is converted into the following model:
where \(\tilde{\omega }_{i} = [\omega_{i}^{l} ,\omega_{i}^{u} ]\) and ε are decision variables. The first two constraints are inferred from Eq. (27). The last constraint is equivalent to \(\phi_{{\tilde{\user2{P}}}} (\tilde{\user2{\omega }}) \in [0,1]\). The other constraints are obtained by Definition 7.
Let \(\omega_{i}^{\prime l} = \ln \omega_{i}^{l}\) and \(\omega_{i}^{\prime u} = \ln \omega_{i}^{u}\) \((i \in N)\). Then, the model (M-3) can be further expressed and simplified as the following linear programming model:
where \(\tilde{\omega }_{i}^{\prime } = [\tilde{\omega }_{i}^{\prime l} ,\tilde{\omega }_{i}^{\prime u} ]\) and ε are decision variables. The constraints are the same as those of model (M-3).
In the model (M-4), the tolerance parameters of should be large enough to guarantee the existence of a nonempty feasible area. By the model (M-4), the optimal solution \(\left( {\tilde{\omega }_{1}^{\prime *} ,\tilde{\omega }_{2}^{\prime *} , \cdots \tilde{\omega }_{n}^{\prime *} ,\varepsilon^{*} } \right)\) is obtained, where \(\tilde{\omega }_{i}^{\prime *} = [\tilde{\omega }_{i}^{\prime l} ,\tilde{\omega }_{i}^{\prime u} ]\). Let \(\tilde{\omega }_{i}^{*} = [\exp (\tilde{\omega }_{i}^{\prime l} ),\exp (\tilde{\omega }_{i}^{\prime u} )]\) \((i \in N)\). Then, \(\tilde{\user2{\omega }}_{i}^{*} = \left( {\tilde{\omega }_{1}^{*} ,\tilde{\omega }_{2}^{ * } , \cdots ,\tilde{\omega }_{n}^{*} } \right)\) is a multiplicative normalized IWV. The optimal objective value \(\varepsilon^{*}\) measures the degree of overall satisfaction with the optimal multiplicative normalized IWV \(\tilde{\user2{\omega }}^{*}\). If \(\varepsilon^{*} = 1\), then \(\user2{\tilde{P} = }(\tilde{p}_{ij} )_{n \times n}\) is geometrically consistent. By Theorem 2, a geometrically consistent IMPR \(\user2{\tilde{W} = }(\tilde{\omega }_{ij} )_{n \times n}\) is obtained by the following formula:
Remark 5
In this subsection, an optimal multiplicative normalized IWV is derived from an IMPR with the help of a fuzzy model. The advantages of the proposed fuzzy model are summarized as follows:
(i) The experts’ satisfaction (membership or acceptance) degree of an IWV is considered in the proposed fuzzy model (M-4), which is a linear programming method. Based on the optimization theory, the globally optimal solution of the model (M-4) can be obtained.
(ii) By Definition 6, the first two constraints of the model (M-4) are equivalent to \((\varepsilon - 1)\delta_{ij,l}^{ + } \; \le \ln u_{ji} + \omega_{i}^{\prime l} - \omega_{j}^{\prime u} \le (1 - \varepsilon )\delta_{ij,l}^{ - }\) and \((\varepsilon - 1)\delta_{ij,u}^{ + } \; \le \ln l_{ji} + \omega_{i}^{\prime u} - \omega_{j}^{\prime l} \le (1 - \varepsilon )\delta_{ij,u}^{ - }\) \((i < j;\;i,j \in N)\), respectively. Thus, if the tolerance parameters of the model (M-4) equal to each other, i.e.,\(\delta_{ij,l}^{ - } = \delta_{ij,l}^{ + } = \delta_{ij,u}^{ - } = \delta_{ij,u}^{ + }\), the multiplicative normalized IWV obtained from the lower triangle entries of IMPRs is the same as that obtained from the upper triangle entries of IMPR.
(iii) In the model (M-4), only the upper triangle entries of IMPRs are used to derive the optimal multiplicative normalized IWV from an IMPR.
5.2 A novel IDM method with an IMPR
Let \(X\user2{ = }(x_{1} ,x_{2} , \cdots ,x_{n} )^{{\text{T}}}\) be a set of alternatives. Let \(\tilde{\user2{P}}\) be an IMPR provided by an expert. On the basis of the aforesaid analyses, a novel IDM method with an IMPR is summarized as follows:
Step 1 Set the values of tolerance parameters \(\delta_{ij,\theta }^{ + }\), \(\delta_{ij,\theta }^{ - }\) \((\theta = l,u;\;i < j;\;i,j \in N)\), and the consistency threshold of n-order IMPRs \(\overline{CI}_{n}\) by Table 1.
Step 2 By Eq. (16) to compute the consistency index \(CI(\tilde{\user2{P}})\) of \(\tilde{\user2{P}}\).
(i) If \(CI(\tilde{\user2{P}}) \le \overline{CI}_{n}\), then \(\tilde{\user2{P}}\) is acceptably consistent. Set \(\user2{\tilde{P}^{\prime} = \tilde{P}}\) and go to Step 4;
(ii) Otherwise, \(\tilde{\user2{P}}\) is unacceptably consistent and go to Step 3.
Step 3 By Algorithm 1, an acceptably consistent IMPR \(\user2{\tilde{P}^{\prime}}\) is obtained from \(\tilde{\user2{P}}\).
Step 4 Obtain the multiplicative normalized IWV \(\tilde{\user2{\omega }} = (\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \cdots ,\tilde{\omega }_{n} )^{{\text{T}}}\) with \(\tilde{\omega }_{i} = [\omega_{i}^{l} ,\omega_{i}^{u} ]\) from \(\user2{\tilde{P}^{\prime}}\) by the model (M-4).
Step 5 By using the formula of possibility degree in [19], the possibility degree matrix \({\varvec{P}} = (p_{ij} )_{n \times n}\) is constructed, where \(p_{ij} = p(\tilde{\omega }_{i} \succ \tilde{\omega }_{j} ) = max\{ 1 - max\{ \tfrac{{\ln \omega_{j}^{u} - \ln \omega_{i}^{l} }}{{\ln \omega_{j}^{u} - \ln \omega_{j}^{l} + \ln \omega_{i}^{u} - \ln \omega_{i}^{l} }},0\} ,0\}\) \((i,j \in N)\). The larger the ranking value \(o_{i} = \sum\nolimits_{j = 1}^{n} {o_{ij} }\), the better the alternative \(x_{i}\) \((i \in N)\), where \(o_{ij}\) is computed by
The above process of the proposed IDM method with an IMPR is graphically depicted in Fig. 4.
6 A novel GDM method with IMPRs
This section devotes to developing a new method for GDM with IMPRs. Based on the concept of logarithmically geometrical compatibility degree between two IMPRs, a convex programming model is built to determine the weights of experts. Then, a GDM method with IMPRs is brought forward.
Let \(M = \{ 1,2, \cdots ,m\}\). Suppose that a GDM problem is composed of n alternatives \(x_{i}\) \((i \in N)\) and m experts \({\varvec{e}}_{k}\) \((k \in M)\). Let \(\lambda {}_{k}\) denote the weight of the expert \({\varvec{e}}_{k}\) and satisfies \(\sum\nolimits_{k = 1}^{m} {\lambda_{k} } = 1\) and \(\lambda_{k} > 0\) \((k \in M)\). Let \(\tilde{\user2{P}}_{k} = (\tilde{p}_{ijk} )_{n \times n}\) be an individual IMPR provided by the expert \({\varvec{e}}_{k}\) \((k \in M)\). Then, a collective IMPR \(\tilde{\user2{P}}_{G} = (\tilde{p}_{ij,G} )_{n \times n}\) is obtained by [29]:
6.1 Properties of GDM with IMPRs
For simplicity, let \(GC(\tilde{\user2{P}})\) denote the geometrically consistent IMPR of an IMPR \(\tilde{\user2{P}}\) generated by Eq. (11) hereafter in this paper.
Theorem 9.
For IMPRs \(\tilde{\user2{P}}_{k}\) \((k \in M)\), let \(\tilde{\user2{P}}_{G}\) and \(GC(\tilde{\user2{P}}_{k} )\) be computed by Eq. (31) and Eq. (11), respectively. Then,
(i) \(\tilde{\user2{P}}_{G}\) is geometrically consistent if \(\tilde{\user2{P}}_{k}\) \((k \in M)\) are geometrically consistent;
(ii) \(GC(\tilde{\user2{P}}_{G} )\) is a geometrically consistent IMPR;
(iii) \(GC(\tilde{\user2{P}}_{G} )\) is obtained by aggregating \(GC(\tilde{\user2{P}}_{k} )\) \((k \in M)\) by Eq. (31).
Proof
(i) Let \(\lambda {}_{k}\) \((k \in M)\) satisfy \(\sum\nolimits_{k = 1}^{m} {\lambda_{k} } = 1\) and \(\lambda_{k} > 0\).
Let \(\tilde{\user2{P}}_{k} = ([l_{ijk} ,u_{ijk} ])_{n \times n}\) and \(\tilde{\user2{P}}_{G} = ([l_{ij,G} ,u_{ij,G} ])_{n \times n}\) \((i,j \in N;\;k \in M)\). Using Eq. (31), it is obvious that
If \(\tilde{\user2{P}}_{k}\) \((k \in M)\) are geometrically consistent, then one has
Equations (33–34) imply \(l_{it,G} u_{it,G} l_{tj,G} u_{tj,G} = \prod\nolimits_{k = 1}^{m} {(l_{ijk} u_{ijk} )^{{\lambda_{k} }} } = l_{ij,G} u_{ij,G}\) \((i,j \in N)\) which means that \(\tilde{\user2{P}}_{G}\) is geometrically consistent.
(ii) It is straightforward from Theorem 4.
(iii) Let \(GC(\tilde{\user2{P}}_{G} ) = ([l_{ij,G}^{*} ,u_{ij,G}^{*} ])_{n \times n}\) and \(GC(\tilde{\user2{P}}_{k} ) = ([l_{ijk}^{*} ,u_{ijk}^{*} ])_{n \times n}\). According to Eq. (12), it holds that:
\(l_{ij,G}^{*} = \prod\nolimits_{t = 1}^{n} {(l_{it,G} l_{tj,G} )}^{1/n}\)\(= \prod\nolimits_{t = 1}^{n} {(\prod\nolimits_{k = 1}^{m} {(l_{itk} )^{{\lambda_{k} }} } \prod\nolimits_{k = 1}^{m} {(l_{tjk} )^{{\lambda_{k} }} } )}^{1/n}\)\(= \prod\nolimits_{k = 1}^{m} {(\prod\nolimits_{t = 1}^{n} {(l_{itk} l_{tjk} )}^{1/n} )}^{{\lambda_{k} }}\)\(= \prod\nolimits_{k = 1}^{m} {(l_{ijk}^{*} )}^{{\lambda_{k} }}\). (35).
In a similar way, we have
By Eqs. (35–36), it is true for \([l_{ij,G}^{*} ,u_{ij,G}^{*} ] = \prod\nolimits_{k = 1}^{m} {([l_{ijk}^{*} ,u_{ijk}^{*} ])^{{\lambda_{k} }} }\) \((i,j \in N)\). Therefore, \(GC(\tilde{\user2{P}}_{G} )\) is aggregated from \(GC(\tilde{\user2{P}}_{k} )\) \((k \in M)\) by Eq. (31).
Theorem 10
Let an IMPR \(\tilde{\user2{P}}_{G} = ([l_{ij,G} ,u_{ij,G} ])_{n \times n}\) be generated from IMPRs \(\tilde{\user2{P}}_{k} = ([l_{ijk} ,u_{ijk} ])_{n \times n}\) \((i,j \in N;\;k \in M)\) by Eq. (31) and \(\mu_{ijk}\) \((i < j;\;i,j \in N;\;k \in M)\) be calculated by:
Then, \(CI(\tilde{\user2{P}}_{G} )\) is computed by
where \(\sum\nolimits_{k = 1}^{m} {\lambda_{k} } = 1\) with \(\lambda_{k} > 0\).
Proof
Let \(\mu_{ij,G} = \ln l_{ij,G} + \ln u_{ij,G} - \tfrac{1}{n}\sum\nolimits_{t = 1}^{n} {(\ln l_{it,G} { + }\ln l_{tj,G} } + \ln u_{it,G} { + }\ln u_{tj,G} )\) \((i,j \in N)\). By Eq. (19), one has \(CI(\tilde{\user2{P}}_{G} ) = \tfrac{1}{{{2}n(n - 1)}}\sum\nolimits_{i = 1}^{{n{ - 1}}} {\sum\nolimits_{j = i + 1}^{n} {(\mu_{ij,G} )^{2} } }\). Using Eq. (32), \(\mu_{ij,G}\) can be computed by \(\mu_{ij,G} = \sum\nolimits_{k = 1}^{m} {\lambda_{k} \mu_{ijk} }\). Then, it yields that \(CI(\tilde{\user2{P}}_{G} ) = \tfrac{{1}}{{{2}n(n - 1)}}\sum\nolimits_{i = 1}^{{n{ - 1}}} {\sum\nolimits_{j = i + 1}^{n} {(\sum\nolimits_{k = 1}^{m} {\lambda_{k} \mu_{ijk} } )^{2} } }\).
Theorem 11
Let \(\tilde{\user2{P}}_{G}\) be generated by IMPRs \(\tilde{\user2{P}}_{k}\) \((k \in M)\) by Eq. (30). Then,
(i) \(CI(\tilde{\user2{P}}_{G} ) \le (\sum\nolimits_{k = 1}^{m} {\lambda_{k}^{2} )} (\sum\nolimits_{k = 1}^{m} {CI(\tilde{\user2{P}}_{k} )} )\);
(ii) If \(\lambda_{k} = 1{/}m\) \((k \in M)\), then \(CI(\tilde{\user2{P}}_{G} ) \le \tfrac{{1}}{m}\sum\nolimits_{k = 1}^{m} {CI(\tilde{\user2{P}}_{k} )}\);
(iii) If \(\lambda_{k} = 1{/}m\) \((k \in M)\), then \(CI(\tilde{\user2{P}}_{G} ) \le \mathop {\max }\limits_{k = 1,2, \cdots ,m} \{ CI(\tilde{\user2{P}}_{k} )\}\);
(iv) Let \(\lambda_{k} = 1{/}m\) \((k \in M)\). If all IMPRs \(\tilde{\user2{P}}_{k}\) \((k \in M)\) are acceptably consistent, then \(\tilde{\user2{P}}_{G}\) is acceptably consistent.
Proof
(i) Let \(\tilde{\user2{P}}_{k} = ([l_{ijk} ,u_{ijk} ])_{n \times n}\). Taking Cauchy–Schwarz inequality on Eq. (38) and Theorem 5, it yields that \(CI(\tilde{\user2{P}}_{G} ) \le (\sum\nolimits_{k = 1}^{m} {\lambda_{k}^{2} )} (\tfrac{{1}}{{{2}n(n - 1)}}\sum\nolimits_{i = 1}^{{n{ - 1}}} {\sum\nolimits_{j = i + 1}^{n} {\sum\nolimits_{k = 1}^{m} {\mu_{ijk}^{2} )} } } = (\sum\nolimits_{k = 1}^{m} {\lambda_{k}^{2} )} (\sum\nolimits_{k = 1}^{m} {CI(\tilde{\user2{P}}_{k} )} )\).
(ii) If \(\lambda_{k} = 1{/}m\) \((k \in M)\), then the equality \(CI(\tilde{\user2{P}}_{G} ) = \tfrac{1}{{m^{2} }}\tfrac{{1}}{{{2}n(n - 1)}}\sum\nolimits_{i = 1}^{{n{ - 1}}} {\sum\nolimits_{j = i + 1}^{n} {(\sum\nolimits_{k = 1}^{m} {\mu_{ijk} } )^{2} } }\) is true by Eq. (38). Based on the Cauchy–Schwarz inequality, it is clear that \((\sum\nolimits_{k = 1}^{m} {\mu_{ijk} } )^{2} \le m(\sum\nolimits_{k = 1}^{m} {\mu_{ijk}^{2} } )\). Thus, it holds that
(iii) It is straightforward from item (ii) of Theorem 11.
(iv) If \(\tilde{\user2{P}}_{k}\) is acceptably consistent, then \(CI(\tilde{\user2{P}}_{k} ) \le \overline{CI}_{n}\) \((k \in M)\). According to (iii) of Theorem 11, it is obvious that \(CI(\tilde{\user2{P}}_{G} ) \le \mathop {\max }\limits_{k = 1,2, \cdots ,m} \{ CI(\tilde{\user2{P}}_{k} )\} \le \overline{CI}_{n}\). Item (iv) is proved.
Remark 6
Theorem 11 explains the relationship between the consistency level of the collective IMPR and those of all individual IMPRs. For a GDM problem, Theorem 11 reveals that the consistency level of the collective IMPR is not worse than that of each individual IMPR with the largest consistency index if experts have the equal weight.
6.2 Determination of experts’ weights
During the aggregation process of GDM with IMPRs, the collective IMPR which is generated from all individual IMPRs has a dramatic effect on the final priority vector. If the experts’ weights are completely unknown, it is crucial to allocate an appropriate weight for each expert based on his/her provided IMPR. Based on the proposed logarithmic compatibility degree between two IMPRs, the following programming model is built to determine the experts’ weights:
where \(\lambda {}_{k}\) \((k = 1,2, \cdots ,m)\) are decision variables. The objective function is to minimize the logarithmic compatibility degree between the collective IMPR \(\tilde{\user2{P}}_{G}\) and each individual IMPR \(\tilde{\user2{P}}_{k}\). The constraints of model (M-5) are the conditions of the priority vector.
Let \(\rho_{ijk} = \ln l_{ijk} + \ln u_{ijk}\) \((i < j;\;i,j \in N;\;k = 1,2, \cdots ,m)\). Using Eqs. (10) and (31), it yields that
The model (M-5) is multiple objectives programming model. By means of min–max method, the model (M-5) is transformed into the following model:
where \(\lambda {}_{k}\) \((k = 1,2, \cdots ,m)\) and \(\xi\) are decision variables.
Theorem 12
The model (M-6) is a convex programming model.
Proof
Let \({\varvec{\lambda}} = (\lambda_{1} ,\lambda_{2} , \cdots \lambda_{m} )^{{\text{T}}}\). For sake of simplicity, some notations are introduced as follows:
\(f({\varvec{\lambda}},\xi ) = \xi\), \(g_{k} ({\varvec{\lambda}},\xi ) = \tfrac{{1}}{{{2}n(n - 1)}}\sum\nolimits_{i = 1}^{n - 1} {\sum\nolimits_{j = i + 1}^{n} {(\sum\nolimits_{s = 1}^{m} {\lambda_{s} \rho_{ijs} - \rho_{ijk} } )^{2} - \;} } \xi\) \((k = 1,2, \cdots ,m)\),
\(h_{k} ({\varvec{\lambda}},\xi ) = - \lambda_{k}\) \((k = 1,2, \cdots ,m)\), \(h_{0} ({\varvec{\lambda}},\xi ) = \lambda_{1} + \lambda_{2} + \cdots { + }\lambda_{m} - 1\).
Obviously, \(f({\varvec{\lambda}},\xi )\) and \(h_{k} ({\varvec{\lambda}},\xi )\) \((k = 0,1, \cdots ,m)\) are linear functions. To prove this theorem, the functions \(g_{k} ({\varvec{\lambda}},\xi )\) \((k = 1,2, \cdots ,m)\) are proved to be convex functions. The Hessian matrixes of \(g_{k} ({\varvec{\lambda}},\xi )\) \((k = 1,2, \cdots ,m)\) are computed as follows:
Let \({\varvec{\rho}}_{k} = (\rho_{12k} ,\rho_{13k} , \cdots ,\rho_{1nk} ,\rho_{23k} , \cdots ,\rho_{n - 1,n,k} )^{{\text{T}}}\) \((k = 1,2, \cdots ,m)\) and \({\mathbf{0}}\) be a \(0.5n(n - 1)\)-dimensional zero vector. Then, Eq. (41) is rewritten as:
Based on the theory of matrix analysis, \(\nabla^{{2}} g_{k}\) \((k = 1,2, \cdots ,m)\) are positive semi-definite. Therefore, model (M-6) is a convex programming model.
Remark 7
It is worth pointing out the locally optimal solution of a convex programming problem is also a globally optimal solution. Thus, by solving the model (M-6), we can obtain the globally optimal solution for the experts’ weights. Item (iv) of Theorem 3 illustrates that the logarithmically geometric compatibility degree is invariable for the labels of compared objects. The objective function of the model (M-5) is to minimize the logarithmic compatibility degree between the collective IMPR \(\tilde{\user2{P}}_{G}\) and each individual IMPR \(\tilde{\user2{P}}_{k}\) \((k = 1,2, \cdots ,m)\). The above analyses illustrate that the model (M-5) is equivalent to the model (M-6). Thus, the proposed method of allocating experts’ weights is not sensitive to the labels of compared objects.
6.3 GDM method with IMPRs
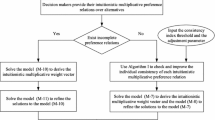
Based on the above analyses, a novel method of GDM with IMPRs is summarized as follows:
Step 1 Expert \(\tilde{\omega } = [\omega_{i}^{ - } ,\omega_{i}^{ + } ]\) provides individual IMPR \(\tilde{\user2{P}}_{k} = (\tilde{p}_{ijk} )_{n \times n}\)\((k = 1,2, \cdots ,m)\).
Step 2 Determine the values of tolerance parameters \(\delta_{ij,\theta }^{ + }\), \(\delta_{ij,\theta }^{ - }\) \((\theta = l,u;\;i < j;\;i,j \in N)\), and the consistency threshold of n-order IMPRs \(\overline{CI}_{n}\) by Table 1.
Step 3 By model (M-6), the weights of experts \(\lambda_{k}\) \((k = 1,2, \cdots ,m)\) are determined.
Step 4 Compute the collective IMPR \(\tilde{\user2{P}}_{G} = (\tilde{p}_{ij,G} )_{n \times n}\) by Eq. (31).
Step 5 If \(\lambda_{k} { = 1/}m\) \((k = 1,2, \cdots ,m)\), then compute \(CI(\tilde{\user2{P}}_{k} )\) of \(\tilde{\user2{P}}_{k}\) \((k = 1,2, \cdots ,m)\) by Eq. (16) and go to the next step. Otherwise, go to Step 7.
Step 6 If \(CI(\tilde{\user2{P}}_{k} ) \le \overline{CI}_{n}\), then \(\user2{\tilde{P}^{\prime}}_{G} = \tilde{\user2{P}}_{G}\) and go to Step 8. Otherwise, go to Step 7.
Step 7 By Algorithm 1, derive an acceptably consistent IMPR \(\user2{\tilde{P}^{\prime}}_{G}\) from \(\tilde{\user2{P}}_{G}\).
Step 8 After plugging \(\user2{\tilde{P}^{\prime}}_{G}\) into the model (M-4), the group multiplicative normalized IWV \(\tilde{\user2{\omega }} = (\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \cdots ,\tilde{\omega }_{n} )^{{\text{T}}}\) is derived.
Step 9 See Step 5 of the proposed IDM method with an IMPR in Sect. 5.2.
The above process of the proposed GDM method with IMPRs is graphically depicted in Fig. 5.
7 Numerical examples and comparative analyses
This section presents three examples to illustrate the application of IDM with an IMPR and GDM with IMPRs. Additionally, simulation-based comparison analyses are performed to reveal the superiority of the proposed IDM method with an IMPR and GDM method with IMPRs.
7.1 Application of IDM with an IMPR and comparative analyses
Firstly, a numerical example is given to illustrate the concrete steps of the proposed IDM method with an IMPR. Then, comparison analyses with methods in [19, 21, 31, 46] and simulation experiments are conducted to reveal the advantages of the proposed IDM method.
7.1.1 Application of IDM with an IMPR
Example 2
Consider the IMPR
which has been examined by Wang et al. [21] and Zhang [31].
(1) Detailed steps of the proposed IDM method with an IMPR.
Obviously, it holds that \(\sqrt {p_{12}^{ - } p_{12}^{ + } } \sqrt {p_{23}^{ - } p_{23}^{ + } } \ne \sqrt {p_{13}^{ - } p_{13}^{ + } }\). Therefore, the IMPR \(\tilde{\user2{P}}\) is not geometrically consistent by Definition 8. By Sect. 5.2, the concrete solving process of this example is given as follows:
Step 1 Set \(\delta_{ij,\theta }^{ - } = \delta_{ij,\theta }^{ + } = 0.{5}\) \((\theta = l,u;\;i < j;\;i,j = 1,2, \cdots ,{4})\). By Table 1, the threshold of 4-order IMPRs is taken as \(\overline{CI}_{{4}} = 0.{0635}\).
Step 2 Using Eq. (16), one has \(CI(\tilde{\user2{P}}) = 0.{3277} > \overline{CI}_{{4}}\). Hence, \(\tilde{\user2{P}}\) is unacceptably consistent by Definition 11.
Step 3 Algorithm 1 is used to improve the consistency level of an IMPR. Assumed that the control parameters \(\beta_{t}\) \((t = 0,\;1,\;2, \cdots )\) in each iteration are always taken as the same parameter \(\beta = 0.8\). The detailed process of deriving an acceptably consistent IMPR \(\user2{\tilde{P}^{\prime}}\) from \(\tilde{\user2{P}}\) is shown as follows:
Let \(k = 0\) and \(\tilde{\user2{P}}^{{(0)}} = (\tilde{p}_{{ij,{0}}}^{{}} )_{{{4} \times {4}}} = \tilde{\user2{P}}\). By Eq. (11), a geometrically consistent IMPR \(\tilde{\user2{P}}^{{*(0)}} = (\tilde{p}_{ij,0}^{*} )_{{{4} \times {4}}}\) derived from \(\tilde{\user2{P}}^{(0)}\) is obtained as follows:
\(\tilde{\user2{P}}^{{*(0)}} = \left( {\begin{array}{*{20}c} {[1.0000,1.0000]} & {{[0}{\text{.5318,1}}{.1892]}} & {[0.9306,2.1147]} & {[3.1302,6.1601]} \\ {[0.8409,1.8803]} & {[1.0000,1.0000]} & {[1.2247,2.5407]} & {[4.1195,7.4008]} \\ {[0.4729,1.0746]} & {[0.3936,0.8165]} & {[1.0000,1.0000]} & {[2.3166,4.2295]} \\ {[0.1623,0.3195]} & {[0.1351,0.2427]} & {[0.2364,0.4317]} & {[1.0000,1.0000]} \\ \end{array} } \right)\).
Then, \(\tilde{\user2{P}}^{(1)} = (\tilde{p}_{ij,1} )_{4 \times 4} = ((\tilde{p}_{{ij,{0}}} )^{\beta } (\tilde{p}_{{ij,{0}}}^{*} )^{{{1} - \beta }} )_{4 \times 4}\) is obtained as follows:
\(\tilde{\user2{P}}^{{(1)}} = \left( {\begin{array}{*{20}c} {[1.0000,1.0000]} & {{[0}{\text{.8814,1}}{.8025]}} & {[0.9857,2.0224]} & {[2.1874,3.4643]} \\ {[0.5548,1.1346]} & {[1.0000,1.0000]} & {[2.5079,4.3668]} & {[4.0239,5.4079]} \\ {[0.4945,1.0145]} & {[0.2290,0.3987]} & {[1.0000,1.0000]} & {[4.9601,7.0425]} \\ {[0.2287,0.4572]} & {[0.1849,0.2485]} & {[0.1420,0.2016]} & {[1.0000,1.0000]} \\ \end{array} } \right)\).
Using Eq. (16), it holds that \(CI(\tilde{\user2{P}}^{(1)} ) = 0.{2097} > \overline{CI}_{4}\). Thus, \(\tilde{\user2{P}}^{(1)}\) is not geometrically consistent by Definition 8. Let \(\tilde{\user2{P}}^{{*(1)}} = (\tilde{p}_{ij,1}^{*} )_{{{4} \times {4}}}\). Then,
\(\tilde{\user2{P}}^{{*(1)}} = \left( {\begin{array}{*{20}c} {[1.0000,1.0000]} & {{[0}{\text{.5161,1}}{.2255]}} & {[0.9{037},2.1{776}]} & {[3.{0180},6.{3890}]} \\ {[0.8{160},1.{9378}]} & {[1.0000,1.0000]} & {[1.{1840},2.{6281}]} & {[{3}{\text{.9539}},7.{7109}]} \\ {[0.4{592},1.{1065}]} & {[0.3{805},0.8{446}]} & {[1.0000,1.0000]} & {[2.{2252},4.{4031}]} \\ {[0.1{565},0.3{313}]} & {[0.1{292},0.2{529}]} & {[0.2{271},0.4{494}]} & {[1.0000,1.0000]} \\ \end{array} } \right)\).
By \(\tilde{\user2{P}}^{{({2})}} = (\tilde{p}_{{ij,{2}}} )_{{{4} \times {4}}} = ((\tilde{p}_{{ij,{1}}} )^{\beta } (\tilde{p}_{{ij,{1}}}^{*} )^{1 - \beta } )_{{{4} \times {4}}}\), \(\tilde{\user2{P}}^{{({2})}}\) is computed as follows:
\(\tilde{\user2{P}}^{{(2)}} = \left( {\begin{array}{*{20}c} {[1.0000,1.0000]} & {{[0}{\text{.7919,1}}{.6687]}} & {[0.9{68}7,2.0{526}]} & {[2.{3329},3.{9154}]} \\ {[0.5{993},1.{2628}]} & {[1.0000,1.0000]} & {[2.{1583},{3}{\text{.9451}}]} & {[4.0{096},5.{8056}]} \\ {[0.4{872},1.0{323}]} & {[0.2{535},0.{4633}]} & {[1.0000,1.0000]} & {[4.{2254},{6}{\text{.4112}}]} \\ {[0.2{554},0.4{287}]} & {[0.1{722},0.24{94}]} & {[0.1{560},0.2{367}]} & {[1.0000,1.0000]} \\ \end{array} } \right)\).
Using Eq. (16), it holds that \(CI(\tilde{\user2{P}}^{(2)} ) = 0.{1342} > \overline{CI}_{{4}}\). Thus, \(\tilde{\user2{P}}^{(2)}\) is not geometrically consistent by Definition 8. In the similar way, \(\tilde{\user2{P}}^{(3)} = (\tilde{p}_{ij,3} )_{{{4} \times {4}}}\) is calculated as follows:
\(\tilde{\user2{P}}^{{(3)}} = \left( {\begin{array}{*{20}c} {[1.0000,1.0000]} & {{[0}{\text{.7220,1}}{.5795]}} & {[0.9{490},2.0{909}]} & {[2.{4367},{4}{\text{.3528}}]} \\ {[0.{6331},1.{3851}]} & {[1.0000,1.0000]} & {[{1}{\text{.8998}},{3}{\text{.6647}}]} & {[{3}{\text{.9634}},{6}{\text{.1989}}]} \\ {[0.4{783},1.0{537}]} & {[0.2{729},0.{5264}]} & {[1.0000,1.0000]} & {[{3}{\text{.6848}},{5}{\text{.9987}}]} \\ {[0.2{297},0.4{104}]} & {[0.1{613},0.2{523}]} & {[0.1{667},0.2{714}]} & {[1.0000,1.0000]} \\ \end{array} } \right)\).
By Eq. (16), \(CI(\tilde{\user2{P}}^{(3)} ) = 0.{0859}\). Then, \(CI(\tilde{\user2{P}}^{(3)} ) > \overline{CI}_{{4}}\). Analogously, \(\tilde{\user2{P}}^{{({4})}} = (\tilde{p}_{{ij,{4}}} )_{{{4} \times {4}}}\) is obtained:
\(\tilde{\user2{P}}^{{(4)}} = \left( {\begin{array}{*{20}c} {[1.0000,1.0000]} & {{[0}{\text{.6653,1}}{.5233]}} & {[0.9{265},2.{1382}]} & {[2.{5011},{4}{\text{.7792}}]} \\ {[0.{6565},1.{5030}]} & {[1.0000,1.0000]} & {[{1}{\text{.7013}},{3}{\text{.4835}}]} & {[{3}{\text{.8898}},{6}{\text{.5948}}]} \\ {[0.4{677},1.0{793}]} & {[0.2{871},0.{5878}]} & {[1.0000,1.0000]} & {[{3}{\text{.2719}},{5}{\text{.7413}}]} \\ {[0.2{092},0.{3998}]} & {[0.1{516},0.2{571}]} & {[0.1{742},0.{3056}]} & {[1.0000,1.0000]} \\ \end{array} } \right)\).
Using Eq. (16), the consistency index of \(\tilde{\user2{P}}^{{(4)}}\) is \(CI(\tilde{\user2{P}}^{(4)} ) = 0.{0550}\). It is obvious that \(CI(\tilde{\user2{P}}^{(4)} ){ < }\overline{CI}_{{4}}\). Thus, \(\tilde{\user2{P}}^{{(4)}}\) is geometrical consistent by Definition 8.
Let \(\user2{\tilde{P}^{\prime}} = \tilde{\user2{P}}^{{(4)}}\). Then, \(\user2{\tilde{P}^{\prime}}\) is the acceptably consistent IMPR derived from the original IMPR \(\tilde{\user2{P}}\).
Step 4. Plugging \(\user2{\tilde{P}^{\prime}}\) into model (M-5), the IWV is generated as follows:
\(\tilde{\user2{\omega }} = ([1.{1634},{1}{\text{.7950}}],[1.{5652},{2}{\text{.3146}}],[{0}{\text{.8730}},1.{2221}],[0.{282}8,0.{3511}])^{{\text{T}}}\).
Step 5 According to the possibility degree of intervals in [19] and Eq. (30), the possibility degree matrix \({\varvec{P}}\) is \({\varvec{P}} = \left( {\begin{array}{*{20}c} {{0}{\text{.5000}}} & {{0}{\text{.1661}}} & {{0}{\text{.9361}}} & {{1}{\text{.0000}}} \\ {{0}{\text{.8339}}} & {{0}{\text{.5000}}} & {{1}{\text{.0000}}} & {{1}{\text{.0000}}} \\ {{0}{\text{.0639}}} & {{0}{\text{.0000}}} & {{0}{\text{.5000}}} & {{1}{\text{.0000}}} \\ {{0}{\text{.0000}}} & {{0}{\text{.0000}}} & {{0}{\text{.0000}}} & {{0}{\text{.5000}}} \\ \end{array} } \right)\). Then, the ranking values are obtained as \(o_{{1}} = {3}\), \(o_{{2}} = {4}\), \(o_{{3}} = {2}\) and \(o_{{4}} = {1}\). Thus, the ranking order of alternatives is \(x_{2} \mathop \succ \limits^{83.39\% } x_{1} \mathop \succ \limits^{93.61\% } x_{3} \mathop \succ \limits^{100\% } x_{4}\).
(2) Comparison analyses with existing methods in [19, 21, 31, 46]
To reveal the superiority of IDM methods, three comparison criteria are shown as follows:
(i) Average total deviation (ATD)
Using Eq. (9), an geometrically consistent IMPR \(\tilde{\user2{W}} = (\tilde{\omega }_{ij} )_{n \times n}\) with \(\tilde{\omega }_{ij} = [\omega_{ij}^{l} ,\omega_{ij}^{u} ]\) is generated by an IWV \(\tilde{\user2{\omega }}\), where \(\tilde{\user2{\omega }}\) is obtained from \(\tilde{\user2{P}} = ([l_{ij} ,u_{ij} ])_{n \times n}\). Generally, \(\tilde{\user2{W}}\) does not equal to the original IMPR \(\tilde{\user2{P}}\). Inspired by the concept of logarithm compatibility degree of IMPRs [41], the value of ATD is computed by \(ATD(\tilde{\user2{P}},\tilde{\user2{W}}) = \tfrac{2}{n(n - 1)}\sum\nolimits_{i = 1}^{n - 1} {\sum\nolimits_{j = i + 1}^{n} {(|\ln l_{ij} - \ln \omega_{ij}^{l} | + |\ln u_{ij} - \ln \omega_{ij}^{u} |)} }\).
(ii) Difference index (DI).
Based on the geometric mean, Wang [47] defined the concept of difference index (DI) to measure the difference level of two triangular fuzzy PRs. Accordingly, the difference index between two IMPRs \(\tilde{\user2{W}}\) and \(\tilde{\user2{P}}\) is defined as \(DI(\tilde{\user2{P}},\tilde{\user2{W}}) = 1 - \left( {\prod\limits_{i \ne j} {\left( {\tfrac{{\min \{ l_{ij} ,\omega_{ij}^{l} \} }}{{\max \{ l_{ij} ,\omega_{ij}^{l} \} }}} \right)\left( {\tfrac{{\min \{ u_{ij} ,\omega_{ij}^{u} \} }}{{\max \{ u_{ij} ,\omega_{ij}^{u} \} }}} \right)} } \right)^{{\frac{1}{{{2}n(n - 1)}}}}\).
(iii) Difference ratio (DR)
Li et al. [19] defined the difference ratio of two IMPRs \(\tilde{\user2{W}}\) and \(\tilde{\user2{P}}\), denoted by \(DR(\tilde{\user2{P}},\tilde{\user2{W}})\), which is calculated by \(DR(\tilde{\user2{P}},\tilde{\user2{W}}) = \left( {\prod\limits_{i < j} {\left( {\tfrac{{\max \{ l_{ij} ,\omega_{ij}^{l} \} }}{{\min \{ l_{ij} ,\omega_{ij}^{l} \} }}} \right)\left( {\tfrac{{\max \{ u_{ij} ,\omega_{ij}^{u} \} }}{{\min \{ u_{ij} ,\omega_{ij}^{u} \} }}} \right)} } \right)^{{\frac{1}{n(n - 1)}}}\).
Clearly, the smaller the values of above two comparison criteria, the more effective the corresponding decision-making method. Using methods in [19, 21, 31, 46] and the proposed IDM method to solve this example, the results are obtained and shown in Table 2.
Let the IWV \(\tilde{\user2{\omega }}\) is obtained by the proposed IDM method. Let an IMPR \(\tilde{\user2{W}}\) be constructed by \(\tilde{\user2{\omega }}\) using Eq. (9). From Table 2, the following conclusions are drawn:
(1) For different values of the control parameter \(\beta\) in Step 5 of Algorithm 1, the ranking order obtained by the proposed IDM method is always \(x_{2} \succ x_{1} \succ x_{3} \succ x_{4}\), which is in accordance with that obtained by methods in [19, 21, 46] but different from that obtained by method in [31]. However, the values of the possibility degree \(p_{21}\) and \(p_{13}\) vary with the control parameter \(\beta\).
(2) The last two columns of Table 2 show that the values of DI and DR obtained by the proposed IDM method are correspondingly smaller than those obtained by methods in [19, 21, 31]. Thus, the geometrically consistent IMPR \(\tilde{\user2{W}}\) constructed by the proposed IDM method retains more the original preference information than those constructed by method in [19, 21, 31]. Although some values of DI and DF obtained by the proposed IDM method are larger than those obtained by method in [46], simulation experiments in SubSect. 7.1.2 reveal that the mean of DI (or DF) obtained by the proposed IDM method is smaller than that obtained by method in [46] in case of randomly generated 1000 IMPRs.
(3) The eighth to the last columns in Table 2 indicate that the value of ATD obtained by the proposed IDM method is smaller than those obtained by methods in [19, 21, 31, 46]. That is to say, the geometrically consistent IMPR \(\tilde{\user2{W}}\) is the IMPR which is the closest to the original IMPR \(\tilde{\user2{P}}\) from the perspective of the distance deviation. Thus, the proposed IDM method is superior to methods in [19, 21, 31, 46].
(4)The methods in [19, 31] and the proposed IDM method are based on the geometric consistency of IMPR proposed by [19]. Table 2 clearly shows that the values of three comparison criteria obtained by the proposed IDM method are smaller than those obtained by methods in [19, 31]. Thus, the proposed IDM method with an IMPR could avoid information loss and contain more original information within the original IMPR, which further verifies the effectiveness of the proposed IDM method with an IMPR.
7.1.2 Comparative analyses based on simulation experiments
In what follows, comparison analyses based on simulation experiments are conducted to further illustrate the superiority and effectiveness of the proposed IDM method. When using the proposed IDM method and methods in [19, 21, 31, 46] to derive interval weights from lots of randomly generated IMPRs, some specifications are stipulated as follows:
(1) For the method in [21], Eqs. (12–15) on page 258 in [21] are applied to generate the IWV;
(2) For the method in [19], the parameter in Eq. (5.18) on p. 635 in [19] is taken as \(t_{ur} = 2\);
(3) For the proposed IDM method, the control parameter in Step 5 of Algorithm 1 is taken as \(\beta = 0.8\). Additionally, the tolerance parameters of model (M-4) with the same value are stipulated as follows:
(i) If \(n = 4\) or \(n = {5}\), then \(\delta_{ij,l}^{ - } = \delta_{ij,l}^{ + } = \delta_{ij,u}^{ - } = \delta_{ij,u}^{ + } = 0.5\); (ii) If \(n = {6}\) or \(n = {7}\), then \(\delta_{ij,l}^{ - } = \delta_{ij,l}^{ + } = \delta_{ij,u}^{ - } = \delta_{ij,u}^{ + } = {1}{\text{.2}}\); (iii) If \(n = {8}\), then \(\delta_{ij,l}^{ - } = \delta_{ij,l}^{ + } = \delta_{ij,u}^{ - } = \delta_{ij,u}^{ + } = {1}.5\).
(4) Let AV-ATD, AV-DI and AV-DF denote the average values of above three comparison criteria under randomly generating a large number of different dimensions of IMPRs.
(5) For simplicity, let Wang, Li, Zhang, Liu, and ∗ denote method in [21], method in [19], method in [31], method in [46] and the proposed IDM method in this paper, respectively.
(6) Let \(per_{\vartheta }^{\gamma }\) \((\vartheta \ne \;\gamma ;\;\vartheta ,\;\gamma = {\text{Wang}},\;{\text{Li}},\,{\text{Zhang}},\;{\text{Liu}},)\) denote the percentage of the same ranking order obtained by \(\;\gamma\)-method and \(\vartheta\)-method.
For randomly generated 1000 IMPRs, the values of AV-ATD, AV-DI, and AV-DF corresponding to methods in [19, 21, 31, 46] and the proposed IDM method are calculated and shown in Tables 3–5, respectively. In the meanwhile, the percentages of the same ranking order obtained any two methods in [19, 21, 31, 46] and the proposed IDM method are computed and shown in Table 6. To visually demonstrate the advantages of the proposed IDM method, the values of AV-ATD, AV-DI and AV-DF obtained by methods in [19, 21, 31, 46] and the proposed IDM method are depicted in Fig. 5.
By scrutinizing Tables 3–6 and Fig. 6, two constructive conclusions are drawn as follows:
(1) The values of AV-ATD, AV-DI and AV-DF obtained by the proposed IDM method are smaller than those obtained by methods in [19, 21, 31, 46] for different dimensions of IMPR. Moreover, it is worth noting that methods in [19, 31] and the proposed IDM method are all based on the geometrical consistency of IMPR. Thus, the proposed IDM method is more efficient than methods in [19, 21, 31, 46] from the perspectives of ATD, DI and DR.
(2) As can be seen in Table 6, the maximum of \(per_{\vartheta }^{\gamma }\) \((\vartheta ,\;\gamma = {\text{Wang}},\;{\text{Li}},\,{\text{Zhang}},\;{\text{Liu}},)\) is 75.4% and the value of \(per_{\vartheta }^{\gamma }\) decreases with the increase in dimension of IMPRs from 4 to 8. In fact, different IDM methods are generally based on different consistency definitions of IMPRs or models of adjusting the consistency of IMPRs. Moreover, different IDM methods apply different models to derive the interval priority vectors. Therefore, it is natural and reasonable that different IDM methods may result in different ranking orders from the same IMPR. The maximum of \(per_{\vartheta }^{\gamma }\) cannot reach 100%, which verifies that no two methods can get exactly the same ranking order. Moreover, the higher the dimension of IMPR, the more difficult the same ranking order obtained by two methods, which is in accordance with our intuition. Therefore, simulation experiments not only validate the proposed IDM method but also illustrate that the proposed IDM method is more believable and effective than methods in [19, 21, 31, 46] from the perspectives of ATD, DI and DR.
7.2 Application of GDM method with IMPRs and comparative analyses
Example 3
Consider an example presented in [25, 48]. A GDM problem is composed of five feasible alternatives \(x_{i}\) \((i = 1,2, \cdots ,5)\) and three experts \(e_{k}\) (k = 1, 2, 3) with unknown weights. Three individual IMPRs \(\tilde{\user2{P}}_{k}\) (k = 1, 2, 3) are provided as follows:
\(\tilde{\user2{P}}_{{1}} \user2{ = }\left( {\begin{array}{*{20}c} {[1,1]} & {[{6},{7}]} & {[\tfrac{{1}}{{7}},\tfrac{{1}}{{5}}]} & {[{7},{8}]} & {[\tfrac{{1}}{{6}},\tfrac{{1}}{{5}}]} \\ {[\tfrac{1}{{7}},\tfrac{{1}}{{6}}]} & {[1,1]} & {[\tfrac{{1}}{{2}},{1}]} & {[{6},{7}]} & {[\tfrac{{1}}{{7}},\tfrac{{1}}{{5}}]} \\ {[{5},{7}]} & {[{1},{2}]} & {[1,1]} & {[{6},{7}]} & {[{7},{8}]} \\ {[\tfrac{1}{{8}},\tfrac{{1}}{{7}}]} & {[\tfrac{1}{{7}},\tfrac{{1}}{{6}}]} & {[\tfrac{1}{{7}},\tfrac{{1}}{{6}}]} & {[1,1]} & {[\tfrac{{1}}{{2}},{1}]} \\ {[{5},{6}]} & {[{5},{7}]} & {[\tfrac{1}{{8}},\tfrac{{1}}{{7}}]} & {[{1},{2}]} & {[1,1]} \\ \end{array} } \right)\), \(\tilde{\user2{P}}_{{2}} \user2{ = }\left( {\begin{array}{*{20}c} {[1,1]} & {[{6},{7}]} & {[\tfrac{{1}}{{2}},{1}]} & {[{7},{8}]} & {[\tfrac{{1}}{{2}},{1}]} \\ {[\tfrac{1}{{7}},\tfrac{{1}}{{6}}]} & {[1,1]} & {[\tfrac{{1}}{{2}},{1}]} & {[{6},{7}]} & {[\tfrac{{1}}{{7}},\tfrac{{1}}{{6}}]} \\ {[{1},{2}]} & {[{1},{2}]} & {[1,1]} & {[{5},{7}]} & {[{7},{8}]} \\ {[\tfrac{1}{{8}},\tfrac{{1}}{{7}}]} & {[\tfrac{1}{{7}},\tfrac{{1}}{{6}}]} & {[\tfrac{1}{{7}},\tfrac{{1}}{{5}}]} & {[1,1]} & {[\tfrac{{1}}{{2}},{1}]} \\ {[{1},{2}]} & {[{6},{7}]} & {[\tfrac{1}{{8}},\tfrac{{1}}{{7}}]} & {[{1},{2}]} & {[1,1]} \\ \end{array} } \right)\),
\(\tilde{\user2{P}}_{{3}} \user2{ = }\left( {\begin{array}{*{20}c} {[1,1]} & {[{6},{7}]} & {[\tfrac{{1}}{{2}},{1}]} & {[{5},{6}]} & {[\tfrac{{1}}{{8}},\tfrac{{1}}{{7}}]} \\ {[\tfrac{1}{{7}},\tfrac{{1}}{{6}}]} & {[1,1]} & {[\tfrac{{1}}{{2}},{1}]} & {[{6},{7}]} & {[\tfrac{{1}}{{7}},\tfrac{{1}}{{6}}]} \\ {[{1},{2}]} & {[{1},{2}]} & {[1,1]} & {[{7},{8}]} & {[{6},{7}]} \\ {[\tfrac{1}{{6}},\tfrac{{1}}{{5}}]} & {[\tfrac{1}{{7}},\tfrac{{1}}{{6}}]} & {[\tfrac{1}{{8}},\tfrac{{1}}{{7}}]} & {[1,1]} & {[\tfrac{{1}}{{2}},{1}]} \\ {[{7,8}]} & {[6,{7}]} & {[\tfrac{1}{7},\tfrac{{1}}{6}]} & {[{1},{2}]} & {[1,1]} \\ \end{array} } \right)\).
7.2.1 Application of GDM method with IMPRs
Using the proposed GDM method to solve this example, the solving process is shown as follows.
Step 1 Set \(\delta_{ij,\theta }^{ - } = \delta_{ij,\theta }^{ + } = 0.{5}\)\((\theta = l,u;\;i < j;\;i,j = 1,2, \cdots ,{5})\) and \(\overline{CI}_{{5}} = 0.{1187}\) by Table 1.
Step 2 Using model (M-6), the experts’ weight vector is obtained as \({\varvec{\lambda}} = ({0}{\text{.3788}},{0}{\text{.4137}},{0}{\text{.2075}})^{{\text{T}}}\).
Step 3 By Eq. (31), the collective IMPR \(\tilde{\user2{P}}_{G} = (\tilde{p}_{ij,G} )_{5 \times 5}\) is computed as follows:
Step 6 Using Eq. (17), one has \(CI(\tilde{\user2{P}}_{G} ) = 0.{9665} > \overline{CI}_{{5}}\). Thus, \(\tilde{\user2{P}}_{G}\) is unacceptably consistent by Definition 11. It is assumed that the control parameter of Step 5 in Algorithm 1 is taken as \(\beta = 0.8\) in each iteration. As per Algorithm 1, an acceptably consistent IMPR \(\user2{\tilde{P}^{\prime}}_{G}\) is obtained as follows:
\(\user2{\tilde{P}^{\prime}}_{G} \user2{ = }\left( {\begin{array}{*{20}c} {[1.0000,1.0000]} & {[2.1616,3.9007]} & {[{0}{\text{.3333}},0.6993]} & {[{3}{\text{.8985}},7.0091]} & {[{0}{\text{.5454}},{1}{\text{.0711}}]} \\ {[{0}{\text{.2564}},{0}{\text{.4626}}]} & {[1.0000,1.0000]} & {[{0}.2124,{0}{\text{.4608}}]} & {[2.1452,3.8610]} & {[{0}{\text{.2657}},{0}{\text{.4995}}]} \\ {[{1}{\text{.4301}},{3}{\text{.0001}}]} & {[{2}{\text{.1703}},{4}{\text{.7092}}]} & {[1.0000,1.0000]} & {[{6}{\text{.0548}},{11}.{6102}]} & {[{2}{\text{.0845}},{4}{\text{.0107}}]} \\ {[{0}{\text{.1427}},{0}{\text{.2565}}]} & {[{0}{\text{.2590}},{0}{\text{.4662}}]} & {[{0}{\text{.0861}},{0}{\text{.1652}}]} & {[1.0000,1.0000]} & {[{0}{\text{.2094}},{0}{\text{.4448}}]} \\ {[{0}{\text{.9336,1}}{.8335}]} & {[{2}{\text{.0021}},{3}{\text{.7635}}]} & {[{0}{\text{.2493}},0.{4793}]} & {[{2}{\text{.2484}},{4}{\text{.7762}}]} & {[1.0000,1.0000]} \\ \end{array} } \right)\).
Step 7 Solving the model (M-6), the group multiplicative normalized IWV is derived from \(\user2{\tilde{P}^{\prime}}_{G}\) as:
Step 8 According to the possibility degree of intervals in [19] and Eq. (30), the possibility degree matrix \({\varvec{P}}\) is obtained as follows:
\({\varvec{P}} = \left( {\begin{array}{*{20}c} {{0}{\text{.5000}}} & {{1}{\text{.0000}}} & {{0}{\text{.0000}}} & {{1}{\text{.0000}}} & {{0}{\text{.5837}}} \\ {{0}{\text{.0000}}} & {{0}{\text{.5000}}} & {{0}{\text{.0000}}} & {{1}{\text{.0000}}} & {{0}{\text{.0000}}} \\ {{1}{\text{.0000}}} & {{1}{\text{.0000}}} & {{0}{\text{.5000}}} & {{1}{\text{.0000}}} & {{1}{\text{.0000}}} \\ {{0}{\text{.0000}}} & {{0}{\text{.0000}}} & {{0}{\text{.0000}}} & {{0}{\text{.5000}}} & {{0}{\text{.0000}}} \\ {{0}{\text{.4163}}} & {{1}{\text{.0000}}} & {{0}{\text{.0000}}} & {{1}{\text{.0000}}} & {{0}{\text{.5000}}} \\ \end{array} } \right)\).
The ranking values are obtained as \(o_{{1}} = {4}\), \(o_{{2}} = {2}\), \(o_{{3}} = {5}\), \(o_{{4}} = {1}\) and \(o_{{5}} = {3}\). Thus, the ranking order of five feasible alternatives is \(x_{3} \succ x_{1} \succ x_{{5}} \succ x_{2} \succ x_{4}\).
Without loss of generality, let the value of the control parameter \(\beta_{t}\) \((t = 0,\;1,\;2, \cdots )\) of Step 5 in Algorithm 1 be a constant \(\beta\). Additionally, suppose that the values of all tolerance parameters in model (M-4) are the same and taken as a constant \(\delta\), i.e., \(\delta_{ij,l}^{ - } = \delta_{ij,l}^{ + } = \delta_{ij,u}^{ - } = \delta_{ij,u}^{ + } = \delta\) \((i < j;\;i,j = 1,2, \cdots ,{5})\). For different values of \(\beta\) and \(\delta\), the corresponding results are computed and shown in Table 7. As can be seen from Table 7, the ranking orders of alternatives are always \(x_{3} \succ x_{1} \succ x_{{5}} \succ x_{2} \succ x_{4}\).
7.2.2 Comparative analyses
Let \(\tilde{\user2{\omega }} = (\tilde{\omega }_{1} ,\tilde{\omega }_{2} , \cdots ,\tilde{\omega }_{n} )^{{\text{T}}}\) be the group multiplicative normalized IWV and \(\tilde{\user2{W}} = (\tilde{\omega }_{ij} )_{n \times n} = ([\omega_{ij}^{ - } ,\omega_{ij}^{ + } ])_{n \times n}\) be constructed by \(\tilde{\user2{\omega }}\). Clearly, \(\tilde{\user2{W}}\) is a geometrically consistent IMPR. By Definition 9, the logarithmically geometric compatibility degree between \(\tilde{\user2{W}}\) and each individual IMPR \(\tilde{\user2{P}}_{k}\) is computed by.
\(C(\tilde{\user2{P}}_{k} ,\tilde{\user2{W}}) = \tfrac{1}{{{2}n(n - 1)}}\sum\nolimits_{i = 1}^{n - 1} {\sum\nolimits_{j = i + 1}^{n} {(\ln l_{ijk} + \ln u_{ijk} - \ln \omega_{ij}^{ - } - \ln \omega_{ij}^{ + } )^{2} } }\) \((k = 1,2, \ldots ,m)\).
To illustrate the effectiveness of the results obtained by the proposed GDM method, we resort to the mean of all logarithmically geometric compatibility degrees between \(\tilde{\user2{W}}\) and each individual IMPR \(\tilde{\user2{P}}_{k}\) \((k = 1,2, \cdots ,m)\), which is defined as \(MC = \tfrac{1}{m}\sum\nolimits_{k = 1}^{m} {C(\tilde{\user2{P}}_{k} ,\tilde{\user2{W}})}\). Apparently, the smaller the value of MC, the more reliable the GDM method. Using GDM methods in [25, 28] and the proposed GDM method to solve Example 3 and the following five GDM subproblems, some notes are stipulated as follows:
(1) For the GDM method in [25], the experts’ weights are obtained by Eq. (14) (on page 188 in [25]) with the parameter \(a = 0.{5}\);
(2) For the GDM method in [28], the BUM function and the parameter of Eq. (19) are taken as \(Q(y) = y^{1/4}\) and \(\alpha = 1\), respectively;
(3) Using the proposed GDM method to solve five GDM subproblems, the tolerance parameters in model (M-4) are equal to the constant 0.4. Additionally, the control parameters \(\beta_{t}\) \((t = 0,\;1,\;2, \cdots )\) of Step 5 in Algorithm 1 are taken as the constant \(\beta = 0.5\).
Using GDM methods in [25, 28] to solve Example 3, the corresponding results are obtained and displayed in Table 7. As can be seen in Table 7, three interesting conclusions are summarized as follows:
(1) Table 7 shows that the last column of Table 7 reveals that the values of MC computed by the proposed GDM method for different values of parameters \(\beta\) and \(\delta\) are smaller than those computed by GDM methods in [25, 28]. Thus, the proposed GDM method retains more original information GDM methods in [25, 28] and can avoid the loss of information. Additionally, the ranking orders of alternatives are always \(x_{3} \succ x_{1} \succ x_{{5}} \succ x_{2} \succ x_{4}\) for different values of parameters \(\beta\) and \(\delta\). However, the value of the possibility degree \(p_{15}\) varies with the control parameter \(\beta\) and tolerance parameter \(\delta\).
(2) The ranking order obtained by the proposed GDM method is the same as those obtained from the upper triangle entries of IMPRs by GDM methods in [25, 28]. However, the ranking order obtained by the proposed GDM method is different from that obtained from the lower triangle entries of IMPRs by the GDM method in [28]. That is to say, different ranking orders may be obtained from the same IMPR by the GDM method in [28]. For the proposed GDM method, Remark 5 demonstrates that the ranking order obtained from the upper triangle entries of an IMPR is in accordance with that obtained from the lower triangle entries of the IMPR.
(3) In fact, the reciprocity of IMPRs illustrates that an IMPR is completely determined by its lower (or upper) triangular entries. Therefore, the result obtained from the upper triangle entries of an IMPR should be the same as that obtained from the lower triangle entries of the same IMPR. Using the GDM method in [28] to determine the experts’ weights, two different experts’ weight vectors \({\varvec{\lambda}}_{1} = \left( {0.2{935},0.{432}9,0.2{736}} \right)^{{\text{T}}}\) and \({\varvec{\lambda}}_{{2}} = \left( {0.2{897},0.{4227},0.2{876}} \right)^{{\text{T}}}\) are obtained, where \({\varvec{\lambda}}_{1}\) and \({\varvec{\lambda}}_{{2}}\) are obtained from the upper and lower triangle entries of \(\tilde{\user2{P}}_{k}\) (k = 1, 2, 3), respectively. However, this paper constructs a convex programming model to derive the unique experts’ weight vector \({\varvec{\lambda}} = ({0}{\text{.3788}},{0}{\text{.4137}},{0}{\text{.2075}})^{{\text{T}}}\), which effectively improves the objectivity of decision results.
The phenomena of rank reversal [49] often occur in decision science. When an alternative is added to (or removed from) a set of alternatives, the rank reversal means that the ranking order of any other two alternatives is changed. A reasonable decision-making method should avoid the rank reversal by adding or deleting of an alternative. To further verify the superiority of the proposed GDM method, rank reversal test is performed. To test the rank reversal of the proposed GDM method, the original problem (Example 3) is decomposed into the following five GDM subproblem, where the i-th GDM subproblem is obtained by deleting alternative \(x_{i}\) \((i = 1,2, \cdots ,5)\) from the original GDM problem. Using GDM methods in [25, 28] and the proposed GDM method to solve these five GDM subproblem, respectively, the corresponding results are generated and given in Tables 8–12.
From Tables 8–12, the following conclusions are drawn:
(1) From the perspective of logarithmically geometric compatibility degree of IMPRs, the last columns of Tables 8–12 reveal that MC obtained by the proposed GDM method is smaller than that obtained by the GDM method in [25].
(2) If the GDM method in [28] is used to solve the above five GDM subproblems, the ranking order (or the experts’ weight vector) obtained from the upper triangle entries is different from that obtained from the lower triangle entries. This phenomenon illustrates that the GDM method in [28] is defective in theory.
(3) A decision-making method should avoid the phenomena of rank reversal as much as possible. When using GDM methods in [25, 28] and the proposed GDM method to solve the 3-th and 4-th GDM subproblems, Tables 10–11 reveal that the ranking order of \(x_{1}\) and \(x_{{5}}\) is changed. When using methods in [28] to solve the 1-th GDM subproblem, the ranking order of \(x_{{2}}\) and \(x_{{5}}\) is changed. When using methods in [25, 28] to solve the 5-th GDM subproblem, the ranking order of \(x_{1}\) and \(x_{3}\) is also changed. However, there is no reversal phenomenon for any two alternatives by the deletion of alternative \(x_{i}\) \((i = 1,\;2,\;5)\) for the proposed GDM method. Thus, the proposed GDM method can better avoid the phenomena of rank reversal than GDM methods in [25, 28]. The examination of the rank reversal shows the validity and practicability of the proposed GDM method.
8 Conclusion
This paper mainly discusses the GDM method with IMPRs based on geometric consistency. First, a new individual decision-making method with an IMPR is put forward. Then, a novel GDM method with IMPRs is proposed. The main contributions and features s of this paper are outlined as follows:
-
(1)
A logarithmic compatibility degree between two IMPRs is introduced to define a new consistency index of IMPRs. This new consistency index is invariant under permutation of alternatives and transpose of IMPRs. In virtue of statistical approach, the thresholds of the proposed consistency index are presented.
-
(2)
To repair and improve the consistency level of IMPRs, an interactive algorithm is designed. Using the relationship between an interval weight vector (IWV) and an IMPR, a fuzzy programming model is established to derive an IWV. As a result, an IDM method is proposed.
-
(3)
By minimizing the logarithmically geometric compatibility degree between each individual IMPR and the collective one, a convex programming model is established to objectively derive the experts’ weights. This model can retain more original information within the original IMPR.
-
(4)
By combining experts’ weights and the proposed IDM method, a novel GDM method with IMPRs is put forward.
-
(5)
Several numerical examples and simulation experiments are conducted to further reveal the superiority of the proposed IDM method and GDM method.
However, current research on IMPRs in this paper reveals that there is more than one consistency definition of IMPRs. Which consistency definition of IMPRs is the most scientific and reliable one? It will be researched in near future. Additionally, a large-scale group decision-making is a very common pattern of decision science in the modern information and digital economy time [50, 51]. A large-scale group decision-making with IMPRs should be taken into account to further enrich the theory and application of GDM with IMPRs.
References
Meng F, Tang J, Xu Z (2019) Deriving priority weights from intuitionistic fuzzy multiplicative preference relations. Int J Intell Syst 34(11):2937–2969
Lin M, Zhan Q, Xu Z (2020) Decision making with probabilistic hesitant fuzzy information based on multiplicative consistency. Int J Intell Syst 35(8):1233–1261
Meng F et al (2019) A new procedure for hesitant multiplicative preference relations. Int J Intell Syst 34(5):819–857
Wang F (2021) Geometric consistency of triangular fuzzy multiplicative preference relation and its application to group decision making. Knowl Inf Syst 63:21–38
Rani D, Garg H (2021) Complex intuitionistic fuzzy preference relations and their applications in individual and group decision-making problems. Int J Intell Syst 36(4):1800–1830
Wan S-P, Jin Z, Dong J-Y (2017) Pythagorean fuzzy mathematical programming method for multi-attribute group decision making with Pythagorean fuzzy truth degrees. Knowl Inf Syst 55(2):437–466
Wan S-P, Jin Z, Dong J-Y (2020) A new order relation for Pythagorean fuzzy numbers and application to multi-attribute group decision making. Knowl Inf Syst 62(2):751–785
Saaty TL (1977) A scaling method for priorities in hierarchical structures. J Math Psychol 15(3):234–281
Xu Y, Gao P, Martínez L (2019) An interindividual iterative consensus model for fuzzy preference relations. Int J Intell Syst 34(8):1864–1888
Xu Y, Wen X, Zhang Z (2019) Missing values estimation for incomplete uncertain linguistic preference relations and its application in group decision making. J Intell Fuzzy Syst 36(2):1809–1822
Saaty TL, Vargas LG (1987) Uncertainty and rank order in the analytic hierarchy process. Eur J Oper Res 32(1):107–117
Brunelli M, Fedrizzi M (2015) Axiomatic properties of inconsistency indices for pairwise comparisons. J Oper Res Soc 66(1):1–15
Vargas LG (2008) The consistency index in reciprocal matrices: comparison of deterministic and statistical approaches. Eur J Oper Res 191(2):454–463
Lin C, Kou G, Ergu D (2014) A statistical approach to measure the consistency level of the pairwise comparison matrix. J Oper Res Soc 65(9):1380–1386
Amenta P, Lucadamo A, Marcarelli G (2020) On the transitivity and consistency approximated thresholds of some consistency indices for pairwise comparison matrices. Inf Sci 507:274–287
Salo AA, Hämäläinen RP (1997) On the measurement of preferences in the analytic hierarchy process. J Multi-criteria Decis Anal 6:309–319
Wang ZJ, Lin J, Liu F (2019) Axiomatic property based consistency analysis and decision making with interval multiplicative reciprocal preference relations. Inf Sci 491:109–137
Meng F, Tan C (2017) A new consistency concept for interval multiplicative preference relations. Appl Soft Comput 52:262–276
Li KW, Wang ZJ, Tong X (2016) Acceptability analysis and priority weight elicitation for interval multiplicative comparison matrices. Eur J Oper Res 250(2):628–638
Liu F (2009) Acceptable consistency analysis of interval reciprocal comparison matrices. Fuzzy Sets Syst 160(18):2686–2700
Wang Y-M, Yang J-B, Xu D-L (2005) Interval weight generation approaches based on consistency test and interval comparison matrices. Appl Math Comput 167(1):252–273
Krejčí J (2017) On multiplicative consistency of interval and fuzzy reciprocal preference relations. Comput Ind Eng 111:67–78
Zhang H (2015) A consistency model for group decision making problems with interval multiplicative preference relations. Appl Soft Comput 34:60–71
Aguarón J, Moreno-Jiménez JM (2003) The geometric consistency index: Approximated thresholds. Eur J Oper Res 147(1):137–145
Liu F, Zhang W-G, Shang Y-F (2016) A group decision-making model with interval multiplicative reciprocal matrices based on the geometric consistency index. Comput Ind Eng 101:184–193
Conde E, Pérez MDPR (2010) A linear optimization problem to derive relative weights using an interval judgement matrix. Eur J Oper Res 201(2):537–544
Dong YC et al (2015) Consistency issues of interval pairwise comparison matrices. Soft Comput 19(8):2321–2335
Wu J et al (2009) The induced continuous ordered weighted geometric operators and their application in group decision making. Comput Ind Eng 56(4):1545–1552
Zhou L et al (2016) The optimal group continuous logarithm compatibility measure for interval multiplicative preference relations based on the COWGA operator. Inf Sci 328:250–269
Crawford G, Williams C (1985) A note on the analysis of subjective judgment matrices. J Math Psychol 29(4):387–405
Zhang Z (2017) Logarithmic least squares approaches to deriving interval weights, rectifying inconsistency and estimating missing values for interval multiplicative preference relations. Soft Comput 21(14):3993–4004
Koksalmis E, Kabak Ö (2019) Deriving decision makers’ weights in group decision making: an overview of objective methods. Information Fusion 49:146–160
Wang B, Liang J, Qian Y (2014) Determining decision makers’ weights in group ranking: a granular computing method. Int J Mach Learn Cybern 6(3):511–521
Yager RR, Xu ZS (2006) The continuous ordered weighted geometric operator and its application to decision making. Fuzzy Sets Syst 157(10):1393–1402
Zhang Z, Pedrycz W (2019) A consistency and consensus-based goal programming method for group decision-making with interval-valued intuitionistic multiplicative preference relations. IEEE Trans Cybern 49(10):3640–3654
Liu F et al (2018) A group decision making model based on an inconsistency index of interval multiplicative reciprocal matrices. Knowl Based Syst 145:67–76
Wang Z-J (2018) Comments on “A group decision-making model with interval multiplicative reciprocal matrices based on the geometric consistency index.” Comput Ind Eng 117:131–137
Wang Z-J (2018) A note on a group decision making model based on a generalized ordered weighted geometric average operator with interval preference matrices. Fuzzy Sets Syst 341:145–153
Yager RR (1988) On ordered weighted averaging aggregation operators in multicriteria decisionmaking. IEEE Trans Syst Man Cyberen 18(1):183–190
Alefeld G, Herzberger J (1993) Introduction to interval computations. Academic Press, London
Wang YL, Chen HY, Zhou LG (2013) Logarithm compatibility of interval multiplicative preference relations with an application to determining the optimal weights of experts in the group decision making. Group Decis Negot 22(4):759–772
Escobar MT, Aguarón J, Moreno-Jiménez JM (2015) Some extensions of the precise consistency consensus matrix. Decis Support Syst 74:67–77
Brunelli M (2017) Studying a set of properties of inconsistency indices for pairwise comparisons. Ann Oper Res 248(1–2):143–161
Xu Y, Liu X, Wang H (2018) The additive consistency measure of fuzzy reciprocal preference relations. Int J Mach Learn Cybern 9(7):1141–1152
Bellman RE, Zadeh LA (1970) Decision-making in a fuzzy environment. Manage Sci 17(4):141–164
Liu F, Pedrycz W, Zhang W-G (2017) Limited rationality and its quantification through the interval number judgments with permutations. IEEE Trans Cybern 47(12):4025–4037
Wang Z-J (2015) Consistency analysis and priority derivation of triangular fuzzy preference relations based on modal value and geometric mean. Inf Sci 314:169–183
Xia M, Chen J (2015) Studies on interval multiplicative preference relations and their application to group decision making. Group Decis Negot 24(1):115–144
Al Salem AA, Awasthi A (2018) Investigating rank reversal in reciprocal fuzzy preference relation based on additive consistency: causes and solutions. Comput Ind Eng 2018(115):573–581
Yuan R, Wu Z, Tu J (2022) Large-scale group decision-making with incomplete fuzzy preference relations: The perspective of ordinal consistency. Fuzzy Sets Syst. https://doi.org/10.1016/j.fss.2022.04.021
Wan S-P, Yan J, Dong J-Y (2022) Personalized individual semantics based consensus reaching process for large-scale group decision making with probabilistic linguistic preference relations and application to COVID-19 surveillance. Expert Syst Appl 191:116328
Acknowledgements
This research was supported by the National Natural Science Foundation of China (Nos. 62263012, 62141302 and 11861034), the Humanities Social Science Programming Project of Ministry of Education of China (No. 20YJA630059), The Natural Science Foundation of Jiangxi Province of China (No.20212BAB201011), The Science and Technology Research Project of Hubei Education Department (No. D20211303), the Philosophy and Social Science Project of Hubei Education Department (No. 20Y035).
Author information
Authors and Affiliations
Contributions
Shuping Wan: Supervision, Writing- Reviewing and Editing Xianjuan Cheng: Conceptualization, Methodology, Writing- Original draft, Visualization Jiuying Dong: Software, Formal analysis.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Wan, S., Cheng, X. & Dong, J. Group decision-making with interval multiplicative preference relations. Knowl Inf Syst 65, 2305–2346 (2023). https://doi.org/10.1007/s10115-022-01816-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10115-022-01816-z