Abstract
Multi-aspect data appear frequently in web-related applications. For example, product reviews are quadruplets of the form (user, product, keyword, timestamp), and search-engine logs are quadruplets of the form (user, keyword, location, timestamp). How can we analyze such web-scale multi-aspect data on an off-the-shelf workstation with a limited amount of memory? Tucker decomposition has been used widely for discovering patterns in such multi-aspect data, which are naturally expressed as large but sparse tensors. However, existing Tucker decomposition algorithms have limited scalability, failing to decompose large-scale high-order (\(\ge \) 4) tensors, since they explicitly materialize intermediate data, whose size grows exponentially with the order. To address this problem, which we call “Materialization Bottleneck,” we propose S-HOT, a scalable algorithm for high-order Tucker decomposition. S-HOT minimizes materialized intermediate data by using an on-the-fly computation, and it is optimized for disk-resident tensors that are too large to fit in memory. We theoretically analyze the amount of memory and the number of data scans required by S-HOT. Moreover, we empirically show that S-HOT handles tensors with higher order, dimensionality, and rank than baselines. For example, S-HOT successfully decomposes a real-world tensor from the Microsoft Academic Graph on an off-the-shelf workstation, while all baselines fail. Especially, in terms of dimensionality, S-HOT decomposes 1000 \(\times \) larger tensors than baselines.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Tensor decomposition is a widely used technique for the analysis of multi-aspect data. Multi-aspect data, which are naturally modeled as high-order tensors, frequently appear in many applications [9, 28, 33, 34, 43, 49, 50], including the following examples:
Social media: 4-way tensor (sender, recipient, keyword, timestamp).
Web search: 4-way tensor (user, keyword, location, timestamp).
Internet security: 4-way tensor (source IP, destination IP, destination port, timestamp).
Product reviews: 5-way tensor (user, product, keyword, rating, timestamp).
Most of these web-scale tensors are sparse (i.e., most of their entries are zero). For example, since typical customers buy and review a small fraction of products available at e-commerce sites, intermittently, most entries of the aforementioned product-review tensors are zero. To analyze such multi-aspect data, several tensor decomposition methods have been proposed, and we refer interested readers to an excellent survey [26]. Tensor decompositions have provided meaningful results in various domains [1, 9, 20, 26, 28, 29, 34, 43, 51]. Especially, Tucker decomposition [58] has been successfully applied in many applications, including web search [55], network forensics [54], social network analysis [10], and scientific data compression [4].
Developing a scalable Tucker decomposition algorithm has been a challenge due to a huge amount of intermediate data generated during the computation. Briefly speaking, alternating least square (ALS), the most widely used Tucker decomposition algorithm, repeats two steps: (1) computing an intermediate tensor, denoted by \(\varvec{\mathscr {Y}}\), and (2) computing the SVD of the matricized \(\varvec{\mathscr {Y}}\) (see Sect. 2 or [26] for details). Previous studies [22, 27] pointed out that a huge amount of intermediate data are generated during the first step, and they proposed algorithms for reducing the intermediate data by carefully ordering computation.
S-HOT scales up. Every version of S-HOT successfully decomposes tensors with high order, dimensionality, and rank, while the baseline algorithms fail, running out of memory as those three factors increase. Especially, every version of S-HOT handles a tensor with 1000 times larger dimensionality. We use two baselines: (1) BaselineNaive (described in Sect. 3.1): naive algorithm for Tucker decomposition, and (2) BaselineOpt [27] (described in Sect. 3.2): the state-of-the-art memory-efficient algorithm for Tucker decomposition. Note that all the methods have the same convergence properties (see Observation 1 in Sect. 4)
Illustration of M-Bottleneck. For a high-order (\(\ge 4\)) sparse input tensor, the amount of space required for the intermediate tensor \(\varvec{\mathscr {Y}}\) can be much larger than that for the input tensor and the outputs. As in the figure, \(\varvec{\mathscr {Y}}\) is usually thinner but much denser than the input tensor. In such a case, materializing intermediate data becomes the scalability bottleneck of existing Tucker decomposition algorithms
However, existing algorithms still have limited scalability and easily run out of memory, particularly when dealing with high-order (\(\ge 4\)) tensors. This is because existing algorithms explicitly materialize\(\varvec{\mathscr {Y}}\), which is usually thinner but much denser than the input tensor, despite the fact that the amount of space required for storing \(\varvec{\mathscr {Y}}\) grows rapidly with respect to the order, dimensionality, and rank of the input tensor. For example, as illustrated in Fig. 2, the space required for \(\varvec{\mathscr {Y}}\) is about 400 Giga Bytes for a 5-way tensor with 10 million dimensionality when the rank of Tucker decomposition is set to 10. We call this problem Materialization Bottleneck (or M-Bottleneck in short). Due to M-Bottleneck, existing algorithms are not suitable for decomposing tensors with high order, dimensionality, and/or rank. As seen in Fig. 1, even state-of-the-art algorithms [27] easily run out of memory as these factors increase.
To avoid M-Bottleneck, in this work, we propose S-HOT, a scalable Tucker decomposition algorithm for large-scale, high-order, but sparse tensors. S-HOT is designed for decomposing high-order tensors on an off-the-shelf workstation. Our key idea is to compute \(\varvec{\mathscr {Y}}\)on the fly, without materialization, by combining both steps in ALS without changing its results. Specifically, we utilize the reverse communication interface of a recent scalable eigensolver called implicitly restart Arnoldi method (IRAM) [30], which enables SVD computation without materializing \(\varvec{\mathscr {Y}}\). Moreover, S-HOT performs Tucker decomposition by streaming nonzero tensor entries from the disk, which enables it to handle disk-resident tensors that are too large to fit in memory. We offer the following versions of S-HOT with distinct advantagesFootnote 1:
\(\textsc {S-HOT}_{\text {space}}\): the most space-efficient version that does not require additional copies the input tensor.
\(\textsc {S-HOT}_{\text {scan}}\): a faster version that requires multiple copies of the input tensor.
\(\textsc {S-HOT}_{\text {memo}}\): the fastest version that requires multiple copies of the input tensor and a buffer in main memory.
Our experimental results demonstrate that S-HOT outperforms baseline algorithms by providing significantly better scalability, as shown in Fig. 1. Specifically, all versions of S-HOT successfully decompose a 6-way tensor, while baselines fail to decompose even a 4-way tensor or a 5-way tensor due to their high memory requirements. The difference is more significant in terms of dimensionality. As seen in Fig. 1b, S-HOT decomposes a tensor with 1000\(\times \)larger dimensionality than baselines.
Our contributions are summarized as follows.
Bottleneck resolution We identify M-Bottleneck (Fig. 2), which limits the scalability of existing Tucker decomposition algorithms, and we avoid it by using an on-the-fly computation.
Scalable algorithm design We propose S-HOT, a scalable Tucker decomposition algorithm carefully designed for sparse high-order tensors that are too large to fit in memory. Compared to baselines, S-HOT scales up to 1000\(\times \)bigger tensors (Fig. 1) with identical convergence properties (Observation 1).
Theoretical analyses We provide theoretical analyses on the amount of memory space and the number of data scans that S-HOT requires.
Reproducibility: The source code of S-HOT and the datasets used in the paper are available at http://dm.postech.ac.kr/shot.
In Sect. 2, we give preliminaries on tensors and Tucker decomposition. In Sect. 3, we review related work and introduce M-Bottleneck, which past algorithms commonly suffer from. In Sect. 4, we propose S-HOT, a scalable algorithm for high-order tucker decomposition, to address M-Bottleneck. After presenting experimental results in Sect. 5, we make conclusions in Sect. 6.
2 Preliminaries
In this section, we give the preliminaries on tensors (Sect. 2.1), basic tensor operations (Sect. 2.2), Tucker decomposition (Sect. 2.3), and implicitly restarted Arnoldi method (Sect. 2.4).
2.1 Tensors and notations
A tensor is a multi-order array which generalizes a vector (an one-order tensor) and a matrix (a two-order tensor) to higher orders. Let \(\varvec{\mathscr {X}}\in \mathbb {R}^{{I_{1}}\times \dots \times {I_{N}}}\) be the input tensor, whose order is denoted by \(N\). Like rows and columns in a matrix, \(\varvec{\mathscr {X}}\) has \(N\) modes, whose lengths, also called dimensionality, are denoted by \({I_{1}}, \dots , {I_{N}}\in \mathbb {N}\), respectively. We assume that most entries of \(\varvec{\mathscr {X}}\) are zero (i.e., \(\varvec{\mathscr {X}}\) is sparse), as in many real-world tensors [38, 40, 47].
We denote general N-order tensors by boldface Euler script letters e.g., \(\varvec{\mathscr {X}}\), while matrices and vectors are denoted by boldface capitals, e.g.,  , and boldface lowercases, e.g.,
, and boldface lowercases, e.g.,  , respectively. We use the MATLAB-like notations to indicate the entries of tensors. For example, \(\varvec{\mathscr {X}}(i_{1},...,i_{N})\) (or
, respectively. We use the MATLAB-like notations to indicate the entries of tensors. For example, \(\varvec{\mathscr {X}}(i_{1},...,i_{N})\) (or  in short) indicates the \((i_{1},...,i_{N})\)th entry of \(\varvec{\mathscr {X}}\). Similar notations are used for matrices and vectors.
in short) indicates the \((i_{1},...,i_{N})\)th entry of \(\varvec{\mathscr {X}}\). Similar notations are used for matrices and vectors.  and
and  (or
(or  and
and  in short) indicate the ith row and the jth column of
in short) indicate the ith row and the jth column of  . The ith entry of a vector
. The ith entry of a vector  is denoted by
is denoted by  (or
(or  in short).
in short).
2.2 Basic tensor terminologies and operations
We review basic tensor terminologies and operations, which are the building blocks of Tucker decomposition. Table 1 lists the symbols frequently used in this paper.
Definition 1
(Fiber) A mode-n fiber is an one-order section of a tensor, obtained by fixing all indices except the nth index.
Definition 2
(Slice) A slice is a two-order section of a tensor, obtained by fixing all indices but two.
Definition 3
(Tensor unfolding/matricization) Unfolding, also known as matricization, is the process of re-ordering the entries of an N-order tensor into a matrix. The mode-n matricization of a tensor \(\varvec{\mathscr {X}}\in \mathbb {R}^{{I_{1}}\times \dots \times {I_{N}}}\) is a matrix  whose columns are the mode-n fibers.
whose columns are the mode-n fibers.
Definition 4
(N-order outer product) The N-order outer product of vectors  is denoted by
is denoted by  and is an N-order tensor in \(\mathbb {R}^{{I_{1}}\times {I_{2}}\times \dots \times {I_{N}}}\). Elementwise, we have
and is an N-order tensor in \(\mathbb {R}^{{I_{1}}\times {I_{2}}\times \dots \times {I_{N}}}\). Elementwise, we have

For brevity, we use the following shorthand notations for outer products:

Definition 5
(n-mode vector product) The n-mode vector product of a tensor \(\varvec{\mathscr {X}}\in \mathbb {R}^{{I_{1}}\times \dots \times {I_{N}}}\) and a vector  is denoted by
is denoted by  and is an (N-1)-order tensor in \(\mathbb {R}^{{I_{1}}\times \dots {I_{n-1}}}\)\({}^{\times {I_{n+1}}\times \dots \times {I_{N}}}\). Elementwise, we have
and is an (N-1)-order tensor in \(\mathbb {R}^{{I_{1}}\times \dots {I_{n-1}}}\)\({}^{\times {I_{n+1}}\times \dots \times {I_{N}}}\). Elementwise, we have

Definition 6
(n-mode matrix product) The n-mode matrix product of a tensor \(\varvec{\mathscr {X}}\in \mathbb {R}^{{I_{1}}\times \dots \times {I_{N}}}\) and a matrix  is denoted by
is denoted by  and is an N-order tensor in \(\mathbb {R}^{{I_{1}}\times \dots {I_{n-1}}\times {J_{n}}\times {I_{n+1}}\times \dots \times {I_{N}}}\). Elementwise, we have
and is an N-order tensor in \(\mathbb {R}^{{I_{1}}\times \dots {I_{n-1}}\times {J_{n}}\times {I_{n+1}}\times \dots \times {I_{N}}}\). Elementwise, we have

We adopt the shorthand notations in [27] for all-mode matrix product and matrix product in every mode but one:

2.3 Tucker decomposition
Tucker decomposition [58] decomposes a tensor into a core tensor and N factor matrices so that the original tensor is approximated best. Specifically, \(\varvec{\mathscr {X}}\in \mathbb {R}^{{I_{1}}\times \dots \times {I_{N}}}\) is approximated by

where (a) \(\varvec{\mathscr {G}}\in \mathbb {R}^{{J_{1}}\times \dots \times {J_{N}}}\), (b) \({J_{n}}\) denotes the rank of the nth mode and (c)  is the set of factor matrices
is the set of factor matrices  , each of which is in \(\mathbb {R}^{{I_{n}}\times {J_{n}}}\).
, each of which is in \(\mathbb {R}^{{I_{n}}\times {J_{n}}}\).
The most widely used way to solve Tucker decomposition is Tucker-ALS (Algorithm 1), also known as higher-order orthogonal iteration (HOOI) [18].Footnote 2 It finds factor matrices whose columns are orthonormal by alternating least squares (ALS). Since \(\varvec{\mathscr {G}}\) is uniquely computed by  once
once  is determined [27], the objective function is simplified as
is determined [27], the objective function is simplified as


2.4 Implicitly restarted Arnoldi method (IRAM)
Vector iteration (or power method) is one of the fundamental algorithms for solving large-scale eigenproblem [44]. For a given matrix  , vector iteration finds the leading eigenvector corresponding to the largest eigenvalue by repeating the following updating rule from a randomly initialized
, vector iteration finds the leading eigenvector corresponding to the largest eigenvalue by repeating the following updating rule from a randomly initialized  .
.

As k increases,  converges to the leading eigenvector [44].
converges to the leading eigenvector [44].
Arnoldi, which is a subspace iteration method, extends vector iteration to find k leading eigenvectors simultaneously. Implicitly restarted Arnoldi method (IRAM) is one of the most advanced techniques for Arnoldi [44]. Briefly speaking, IRAM only keeps k orthonormal vectors that are a basis of the Krylov space, updates the basis until it converges, and then computes the k leading eigenvectors from the basis. One virtue of IRAM is the reverse communication interface, which enables users to compute eigendecomposition by viewing Arnoldi as a black box. Specifically, the leading k eigenvectors of a square matrix  are obtained as follows:
are obtained as follows:
- (1)
User initializes an instance of IRAM.
- (2)
IRAM returns
 (initially
(initially  ).
). - (3)
User computes
 , and gives
, and gives 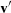 to IRAM.
to IRAM. - (4)
After an internal process, IRAM returns new vector
 .
. - (5)
Repeat steps (3)–(4) until the internal variables in IRAM converges.
- (6)
IRAM computes eigenvalues and eigenvectors from its internal variables, and it returns them.
For details of IRAM and the reverse communication interface, we refer interested readers to [30, 44].
3 Related work
We describe the major challenges in scaling Tucker decomposition in Sect. 3.1. Then, in Sect. 3.2, we briefly survey the literature on scalable Tucker decomposition to see how these challenges have been addressed. However, we notice that existing methods still commonly suffer from M-Bottleneck, which is described in Sect. 3.3. Lastly, we briefly introduce scalable methods for other tensor decomposition methods in Sect. 3.4.
3.1 Intermediate data explosion
The most important challenge in scaling Tucker decomposition is the intermediate data explosion problem which was first identified in [27] (Definition 7). It states that a naive implementation of Algorithm 1, especially the computation of  , can produce huge intermediate data that do not fit in memory or even on a disk. We shall refer to this naive method as BaselineNaive.
, can produce huge intermediate data that do not fit in memory or even on a disk. We shall refer to this naive method as BaselineNaive.
Definition 7
(Intermediate data explosion in BaselineNaive [27]) Let \(M\) be the number of nonzero entries in \(\varvec{\mathscr {X}}\). In Algorithm 1, naively computing  requires \(O(M\)\(\prod _{p\ne n} {J_{p}})\) space for intermediate data.Footnote 3
requires \(O(M\)\(\prod _{p\ne n} {J_{p}})\) space for intermediate data.Footnote 3
For example, if we assume a 5-order tensor with \(M=100\) millions and \({J_{n}}=10\) for all n, \(M\prod _{p\ne n} {J_{p}}=1\) trillions. Thus, if single-precision floating-point numbers are used, computing  requires about 4TB space, which exceeds the capacity of a typical hard disk as well as RAM.
requires about 4TB space, which exceeds the capacity of a typical hard disk as well as RAM.
3.2 Scalable tucker decomposition
Memory-efficient tucker (MET) [27]: MET carefully orders the computation of  in Algorithm 1 so that space required for intermediate data is reduced. Let
in Algorithm 1 so that space required for intermediate data is reduced. Let  . Instead of computing entire \(\varvec{\mathscr {Y}}\) at a time, MET computes a part of it at a time. Depending on the unit computed at a time, MET has various versions, and METfiber is the most space-efficient one.
. Instead of computing entire \(\varvec{\mathscr {Y}}\) at a time, MET computes a part of it at a time. Depending on the unit computed at a time, MET has various versions, and METfiber is the most space-efficient one.
In METfiber, each fiber (Definition 1) of \(\varvec{\mathscr {X}}\) is computed at a time. The specific equation when \(\varvec{\mathscr {X}}\) is a 3-way tensor is as follows:

The amount of intermediate data produced during the computation of a fiber in \(\varvec{\mathscr {Y}}\) by Eq. (2) is only \(O({I_{1}})\), and this amount is the same for general \(N\)-order tensors. However, since entire (matricized) \(\varvec{\mathscr {Y}}\) still needs to be materialized, METfiber suffers from M-Bottleneck, which is discussed in Sect. 3.3. METfiber is one of the most space-optimized tensor decomposition methods, and we shall refer to METfiber as BaselineOpt from now on.
Hadoop tensor method (HaTen2) [22]: HaTen2, in the same spirit as MET, carefully orders the computation of  in Algorithm 1 on MapReduce so that the amount of intermediate data and the number of MapReduce jobs are reduced. Specifically, HaTen2 first computes
in Algorithm 1 on MapReduce so that the amount of intermediate data and the number of MapReduce jobs are reduced. Specifically, HaTen2 first computes  for each \(p\ne n\) and then combines the results to obtain
for each \(p\ne n\) and then combines the results to obtain  . However, HaTen2 requires \(O(MN\sum _{p\ne n}{J_{p}})\) disk space for intermediate data, which is much larger than \(O({I_{n}})\) space, which BaselineOpt requires.
. However, HaTen2 requires \(O(MN\sum _{p\ne n}{J_{p}})\) disk space for intermediate data, which is much larger than \(O({I_{n}})\) space, which BaselineOpt requires.
Other work related to scalable tucker decomposition: Several algorithms were proposed for the case when the input tensor \(\varvec{\mathscr {X}}\) is dense so that it cannot fit in memory. Specifically, [57] uses random sampling of nonzero entries to sparsify \(\varvec{\mathscr {X}}\), and [4] distributes the entries of \(\varvec{\mathscr {X}}\) across multiple machines. However, in this chapter, we assume that \(\varvec{\mathscr {X}}\) is a large but sparse tensor, which is more common in real-world applications. Moreover, our method stores \(\varvec{\mathscr {X}}\) in disk, and thus, the memory requirement does not depend on the number of nonzero entries (i.e., M).
Another line of research focused on reducing redundant computations that occur during a tensor-times-matrix chain operation (TTMc) (i.e.,  in line 4 of Algorithm 2), which is the dominant computation in Tucker-ALS. It was observed in [6] that partial computations of TTMcs can be reused. For example,
in line 4 of Algorithm 2), which is the dominant computation in Tucker-ALS. It was observed in [6] that partial computations of TTMcs can be reused. For example,  , which is a partial computation of
, which is a partial computation of  , can be reused when computing
, can be reused when computing  . To exploit this, in [6], the \(N\) modes are partitioned into two groups: \(N_{1}:=\{1,...,\lceil N/2\rceil \}\) and \(N_{2}:=\{\lceil N/2\rceil +1,...,N\}\). Then,
. To exploit this, in [6], the \(N\) modes are partitioned into two groups: \(N_{1}:=\{1,...,\lceil N/2\rceil \}\) and \(N_{2}:=\{\lceil N/2\rceil +1,...,N\}\). Then,  is stored and used for computing
is stored and used for computing  for each \(n\in N_{2}\). Similarly,
for each \(n\in N_{2}\). Similarly,  is stored and used for computing
is stored and used for computing  for each \(n\in N_{1}\). In [25], partial computations of TTMcs are stored in the nodes of a binary tree and reused so that the number of n-mode products is limited to \(\log (N)\) per TTMc. It was shown in [47] that the partial computations can be reused “on the fly” and faster without having to be stored, while an additional amount of user-specified memory can be used for further reducing the number of n-mode products. To this end, the input tensor is stored in the compressed sparse fiber (CSF) format [46], where a tensor is stored as a forest of \({I_{n}}\) trees with \(N\) levels so that each path from a root to a leaf encodes a nonzero entry. All these algorithms are parallelized in shared-memory [6, 25, 47] and/or distributed-memory [25] environments, and a lightweight but near-optimal scheme for distributing the input tensor among processors was proposed in [15]. Note that these algorithms do not suffer from intermediate data explosion (see Definition 7), which may occur in TTMcs (line 4 of Algorithm 1), by computing
for each \(n\in N_{1}\). In [25], partial computations of TTMcs are stored in the nodes of a binary tree and reused so that the number of n-mode products is limited to \(\log (N)\) per TTMc. It was shown in [47] that the partial computations can be reused “on the fly” and faster without having to be stored, while an additional amount of user-specified memory can be used for further reducing the number of n-mode products. To this end, the input tensor is stored in the compressed sparse fiber (CSF) format [46], where a tensor is stored as a forest of \({I_{n}}\) trees with \(N\) levels so that each path from a root to a leaf encodes a nonzero entry. All these algorithms are parallelized in shared-memory [6, 25, 47] and/or distributed-memory [25] environments, and a lightweight but near-optimal scheme for distributing the input tensor among processors was proposed in [15]. Note that these algorithms do not suffer from intermediate data explosion (see Definition 7), which may occur in TTMcs (line 4 of Algorithm 1), by computing  row by row. However, they suffer from M-Bottleneck, which is described in the following subsection, since they compute (truncated) singular value decomposition (as in line 5 of Algorithm 1) on materialized
row by row. However, they suffer from M-Bottleneck, which is described in the following subsection, since they compute (truncated) singular value decomposition (as in line 5 of Algorithm 1) on materialized  .Footnote 4 To minimize memory requirements, our proposed methods, described in Sect. 4, store the input tensor on disk in the coordinate format and stream its nonzero entries one by one. Alternatively, the CSF format [46] can be used to reduce redundant computations that occur during TTMcs, as in [47], while it requires additional memory space.
.Footnote 4 To minimize memory requirements, our proposed methods, described in Sect. 4, store the input tensor on disk in the coordinate format and stream its nonzero entries one by one. Alternatively, the CSF format [46] can be used to reduce redundant computations that occur during TTMcs, as in [47], while it requires additional memory space.
In [11, 36], several algorithms were proposed for (coupled) Tucker decomposition when most entries of the input tensor are unobserved (or missing), and they were extended to heterogeneous platforms [37]. However, since they have time complexities proportional to the number of observed entries, they are inefficient for fully observable tensors (i.e., tensors without missing entries), which our algorithms assume. A fully observable tensor has \({I_{1}}\times ...\times {I_{N}}\) observed entries.
3.3 Limitation: M-bottleneck
Although BaselineOpt and HaTen2 successfully reduce the space required for intermediate data produced while  is computed, they have an important limitation. Both algorithms materialize
is computed, they have an important limitation. Both algorithms materialize  , but its size \(O({I_{n}}\prod _{p\ne n}{J_{p}})\) is usually huge, mainly due to \({I_{n}}\), and more seriously, it grows rapidly as N, \({I_{n}}\) or \(\{{J_{n}}\}_{n=1}^{N}\) increases. For example, as illustrated in Fig. 2 in Sect. 1, if we assume a 5-order tensor with \(I_{n}=10\) millions and \({J_{p}}=10\) for every \(p\ne n\), then \({I_{n}}\prod _{p\ne n}{J_{p}}=100\) billions. Thus, if single-precision floating-point numbers are used, materializing
, but its size \(O({I_{n}}\prod _{p\ne n}{J_{p}})\) is usually huge, mainly due to \({I_{n}}\), and more seriously, it grows rapidly as N, \({I_{n}}\) or \(\{{J_{n}}\}_{n=1}^{N}\) increases. For example, as illustrated in Fig. 2 in Sect. 1, if we assume a 5-order tensor with \(I_{n}=10\) millions and \({J_{p}}=10\) for every \(p\ne n\), then \({I_{n}}\prod _{p\ne n}{J_{p}}=100\) billions. Thus, if single-precision floating-point numbers are used, materializing  in a dense matrix format requires about 400GB space, which exceeds the capacity of typical RAM. Note that simply storing
in a dense matrix format requires about 400GB space, which exceeds the capacity of typical RAM. Note that simply storing  in a sparse matrix format does not solve the problem since
in a sparse matrix format does not solve the problem since  is usually dense.
is usually dense.
Considering this fact and the results in Sect. 3.2, we summarize the amount of intermediate data required during the whole process of tucker decomposition in each algorithm in Table 2. Our proposed S-HOT algorithms, which are discussed in detail in the following section, require several orders of magnitude less space for intermediate data.
3.4 Scalable algorithms for other tensor decomposition models
Comprehensive surveys on scalable algorithms for various tensor decomposition models can be found in [39, 45]. Among other models except Tucker decomposition, PARAFAC decomposition, which can be seen as a special case of Tucker decomposition where the core tensor has only super-diagonal entries, has been widely used. Below, we summarize previous approaches for scalable PARAFAC decomposition:
Parallelize standard approaches Standard optimization algorithms including ALS, (stochastic) gradient descent, and coordinate descent are optimized and parallelized in distributed-memory [12, 24] and MapReduce [8, 21,22,23, 51] settings.
Sampling or Subdivision Smaller subtensors of the input tensor are obtained by sampling [38] or subdivision [16, 17]. Then, each subtensor is factorized. After that, the factor matrices of the entire tensor are reconstructed from those of subtensors.
Compression In [14, 52], the input tensor is compressed before being factorized.
Concise representation: Several data structures, including compressed sparse fiber (CSF) [46], flagged coordinate (F-COO) [32], hierarchical coordinate (HiCOO) [32], have been developed for concisely representing tensors and accelerating tensor decomposition.
Memoization A sequence of matricized tensor times Khatri-Rao products (MTTKRPs) is the dominant computation in PARAFAC decomposition. In [31], partial computations of MTTKRPs are memoized and reused to reduce redundant computations that occur during MTTKRPs.
4 Proposed method: S-HOT
In this section, we develop a novel algorithm called S-HOT, which avoids M-Bottleneck caused by the materialization of \(\varvec{\mathscr {Y}}\). S-HOT enables high-order Tucker decomposition to be performed even in an off-the-shelf workstation. In Table 3, the different versions of S-HOT are compared with baseline algorithms in terms of objectives, update equations, and materialized data.
Specifically, we focus on the memory-efficient computation of the following two steps (lines 4 and 5 of Algorithm 1):

Our key idea is to tightly integrate the above two steps and compute the singular vectors through IRAM directly from \(\varvec{\mathscr {X}}\) without materializing the entire \(\varvec{\mathscr {Y}}\) at once. We also use the fact that top-\({J_{n}}\) left singular vectors of  are equivalent to the top-\({J_{n}}\) eigenvectors of
are equivalent to the top-\({J_{n}}\) eigenvectors of  .Footnote 5 Specifically, if we use the reverse communication interface of IRAM, the above two steps are computed by simply updating
.Footnote 5 Specifically, if we use the reverse communication interface of IRAM, the above two steps are computed by simply updating  repeatedly as follows:
repeatedly as follows:

where we do not need to materialize  (and thus, we can avoid M-Bottleneck) if we are able to update
(and thus, we can avoid M-Bottleneck) if we are able to update  directly from the \(\varvec{\mathscr {X}}\). Note that using IRAM does not change the result of the above two steps. Thus, final results of Tucker decomposition are also not changed, while space requirements are reduced drastically, as summarized in Table 3.
directly from the \(\varvec{\mathscr {X}}\). Note that using IRAM does not change the result of the above two steps. Thus, final results of Tucker decomposition are also not changed, while space requirements are reduced drastically, as summarized in Table 3.
The remaining problem is how to update  directly from \(\varvec{\mathscr {X}}\), which is stored in disk, without materializing
directly from \(\varvec{\mathscr {X}}\), which is stored in disk, without materializing  . To address this problem, we first examine a naive method extending BaselineOpt and then eventually propose \(\textsc {S-HOT}_{\text {space}}\), \(\textsc {S-HOT}_{\text {scan}}\), and \(\textsc {S-HOT}_{\text {memo}}\), which are the three versions of S-HOT with distinct advantages.
. To address this problem, we first examine a naive method extending BaselineOpt and then eventually propose \(\textsc {S-HOT}_{\text {space}}\), \(\textsc {S-HOT}_{\text {scan}}\), and \(\textsc {S-HOT}_{\text {memo}}\), which are the three versions of S-HOT with distinct advantages.
Note that all our ideas described in this section do not change the outputs of BaselineNaive and BaselineOpt. Thus, all versions of S-HOT have the same convergence properties of BaselineNaive and BaselineOpt, as described in Observation 1.
Observation 1
(Convergence property of S-HOT ) When all initial conditions are identical, \(\textsc {S-HOT}_{\text {space}}\), \(\textsc {S-HOT}_{\text {scan}}\), and \(\textsc {S-HOT}_{\text {memo}}\) give the same result of BaselineNaive and BaselineOpt after the same number of iterations.
4.1 First step: “Naive S-HOT”
How can we avoid M-Bottleneck? In other words, how can we compute Eq. (3) without materializing the entire \(\varvec{\mathscr {Y}}\)? We describe Naive S-HOT, which computes \(\varvec{\mathscr {Y}}\) fiber by fiber, for computing Eq. (3). Thus, Naive S-HOT computes  progressively on the basis of each column vector of
progressively on the basis of each column vector of  , which corresponds to a fiber in \(\varvec{\mathscr {Y}}\), as follows:
, which corresponds to a fiber in \(\varvec{\mathscr {Y}}\), as follows:

where  is a column vector of
is a column vector of  .
.
This equation can be reformulated by \(\varvec{\mathscr {X}}\) and  . For ease of explanation, let \(\varvec{\mathscr {X}}\) be a 3-order tensor. For each column vector
. For ease of explanation, let \(\varvec{\mathscr {X}}\) be a 3-order tensor. For each column vector  , there exists a fiber \(\varvec{\mathscr {Y}}(:,j_2,j_3)\) corresponding to
, there exists a fiber \(\varvec{\mathscr {Y}}(:,j_2,j_3)\) corresponding to  . By plugging Eq. (2) into Eq. (4), we obtain
. By plugging Eq. (2) into Eq. (4), we obtain

As clarified in Eq. (2),  is computed within \(O({I_{1}})\) space, which is significantly smaller than space required for
is computed within \(O({I_{1}})\) space, which is significantly smaller than space required for  .
.
However, Naive S-HOT is impractical because the number of scans of \(\varvec{\mathscr {X}}\) increases explosively, as stated in Lemmas 1 and 2.
Lemma 1
(Scan cost of computing a fiber) Computing a fiber on the fly requires a complete scan of \(\varvec{\mathscr {X}}\).
Proof
Computing a fiber consists of multiple n-mode vector products. Each n-mode vector product is considered as a weighted sum of \((N-1)\)-order section of \(\varvec{\mathscr {X}}\) as follows:

Thus, a complete scan of \(\varvec{\mathscr {X}}\) is required to compute a fiber. \(\square \)
Lemma 2
(Minimum scan cost of Naive S-HOT ) Let B be the memory budget, i.e., the number of floating-point numbers that can be stored in memory at once. Then, Naive S-HOT requires at least \(\frac{{I_{n}}}{B}\prod _{p\ne n}{J_{p}}\) scans of \(\varvec{\mathscr {X}}\) for computing Eq. (4).
Proof
Since we compute  ,
,  should be stored in memory requiring \({I_{n}}\) space, until the computation of
should be stored in memory requiring \({I_{n}}\) space, until the computation of  finishes. Thus, we can compute at most \(\frac{B}{{I_{n}}}\) fibers at the same time within one scan of \(\varvec{\mathscr {X}}\). Therefore, Naive S-HOT requires at least \(\frac{{I_{n}}}{B}\prod _{p\ne n}{J_{p}}\) scans of \(\varvec{\mathscr {X}}\) to compute Eq. (4). \(\square \)
finishes. Thus, we can compute at most \(\frac{B}{{I_{n}}}\) fibers at the same time within one scan of \(\varvec{\mathscr {X}}\). Therefore, Naive S-HOT requires at least \(\frac{{I_{n}}}{B}\prod _{p\ne n}{J_{p}}\) scans of \(\varvec{\mathscr {X}}\) to compute Eq. (4). \(\square \)
4.2 Proposed: “\(\textsc {S-HOT}_{\text {space}}\) ”
How can we avoid the explosion in the number of scans of the input tensor required in Naive S-HOT? We propose \(\textsc {S-HOT}_{\text {space}}\), which computes Eq. (3) within two scans of \(\varvec{\mathscr {X}}\). \(\textsc {S-HOT}_{\text {space}}\) progressively computes  from each row vector of
from each row vector of  . Specifically,
. Specifically,  is computed by:
is computed by:

where  is the ith row vector of
is the ith row vector of  , which corresponds to an \((N-1)\)-order segment of \(\varvec{\mathscr {Y}}\) where the nth mode index is fixed to i. When entire \(\varvec{\mathscr {Y}}\) does not fit in memory, Eq. (6) should be computed in the following two steps:
, which corresponds to an \((N-1)\)-order segment of \(\varvec{\mathscr {Y}}\) where the nth mode index is fixed to i. When entire \(\varvec{\mathscr {Y}}\) does not fit in memory, Eq. (6) should be computed in the following two steps:


This is since we cannot store all  in memory until the computation of
in memory until the computation of  finishes.
finishes.
Illustration of the two steps of \(\textsc {S-HOT}_{\text {space}}\) for computing Eq. (6). Note that we scan the nonzero entries of \(\varvec{\mathscr {X}}\) once during each step. a First step for Eq. (7): For each nonzero element, we add its contribution to  . To compute the contribution to
. To compute the contribution to  , we first compute the contribution to the corresponding row of
, we first compute the contribution to the corresponding row of  (i.e.,
(i.e.,  where i is the nth mode index of the element) by outer products and then multiply it and the corresponding element of
where i is the nth mode index of the element) by outer products and then multiply it and the corresponding element of  (i.e.,
(i.e.,  ). b Second step for Eq. (8): For each nonzero element, we add its contribution to the corresponding entry of
). b Second step for Eq. (8): For each nonzero element, we add its contribution to the corresponding entry of  (i.e.,
(i.e.,  where i is the nth mode index of the element). To compute the contribution to
where i is the nth mode index of the element). To compute the contribution to  , we first compute the contribution to the corresponding row of
, we first compute the contribution to the corresponding row of  (i.e.,
(i.e.,  ) by outer products and then multiply it and
) by outer products and then multiply it and  , which is obtained in the first step
, which is obtained in the first step
A pictorial description and a formal description of \(\textsc {S-HOT}_{\text {space}}\) are provided in Fig. 3 and Algorithm 2, respectively. As shown in Lemma 3, \(\textsc {S-HOT}_{\text {space}}\) requires two scans of \(\varvec{\mathscr {X}}\) for computing Eq. (3).
Lemma 3
(Scan Cost of \(\textsc {S-HOT}_{\text {space}}\) ) \(\textsc {S-HOT}_{\text {space}}\) requires two scans of \(\varvec{\mathscr {X}}\) for computing Eq. (3).
Proof
Each  can be computed as follows.
can be computed as follows.

where p is a tuple \((i_1, \dots , i_N)\) whose nth mode index is fixed to i; \(\varvec{\mathscr {X}}(p)\) is an entry specified by p. Based on each  , Eq. (7) can be computed progressively as follows:
, Eq. (7) can be computed progressively as follows:

Thus, computing Eq. (7) requires only one scan of \(\varvec{\mathscr {X}}\). Similarly, Eq. (8) also can be computed within one scan of \(\varvec{\mathscr {X}}\). Therefore, Eq. (6), which consists of Eqs. (7) and (8), can be computed within two scans of \(\varvec{\mathscr {X}}\). \(\square \)

In Lemma 4, we prove the amount of space required by \(\textsc {S-HOT}_{\text {scan}}\) for intermediate data.
Lemma 4
(Space complexity in \(\textsc {S-HOT}_{\text {space}}\) ) The update step of \(\textsc {S-HOT}_{\text {space}}\) lines (16–22 of Algorithm 2) requires
memory space for intermediate data.
Proof
\(\textsc {S-HOT}_{\text {space}}\) maintains  ,
,  , and
, and  in its update step. When each factor matrix
in its update step. When each factor matrix  is updated,
is updated,  and
and  are \({I_{n}}\) by 1 vectors and
are \({I_{n}}\) by 1 vectors and  is a \(\prod _{p=1}^{N}{J_{p}}/{J_{n}}\) by 1 vector. Thus, \(O({I_{n}}+\prod _{p=1}^{N}{J_{p}}/{J_{n}})\) space is required in the update step for each factor matrix
is a \(\prod _{p=1}^{N}{J_{p}}/{J_{n}}\) by 1 vector. Thus, \(O({I_{n}}+\prod _{p=1}^{N}{J_{p}}/{J_{n}})\) space is required in the update step for each factor matrix  . Since the factor matrices are update one by one, \(O(\max _{1\le n\le N}({I_{n}}+\prod _{p=1}^{N}{J_{p}}/{J_{n}}))\) space is required at a time. \(\square \)
. Since the factor matrices are update one by one, \(O(\max _{1\le n\le N}({I_{n}}+\prod _{p=1}^{N}{J_{p}}/{J_{n}}))\) space is required at a time. \(\square \)
4.3 Faster: “S-HOT\(_{scan}\)”
How can we further reduce the number of required scans of the input tensor? We propose \(\textsc {S-HOT}_{\text {scan}}\), which halves the number of scans of \(\varvec{\mathscr {X}}\) at the expense of requiring multiple (disk-resident) copies of \(\varvec{\mathscr {X}}\) sorted by different mode indices. In effect, \(\textsc {S-HOT}_{\text {scan}}\) trades off disk space for speed.
Our key idea for the further optimization is to compute \({J_{n}}\) right leading singular vectors of  , which are eigenvectors of
, which are eigenvectors of  , and use the result to compute the left singular vectors. Let
, and use the result to compute the left singular vectors. Let  be the SVD of
be the SVD of  . Then,
. Then,

Thus, left singular vectors are obtained from right singular vectors.
\(\textsc {S-HOT}_{\text {scan}}\) computes top-\({J_{n}}\) right singular vectors of  by updating the vector
by updating the vector  as follows:
as follows:

The virtue of \(\textsc {S-HOT}_{\text {scan}}\) is that it requires only one scan of \(\varvec{\mathscr {X}}\) for calculating Eq. (12), as stated in Lemma 6.
Lemma 5
(Scan cost for computing  )
)  can be computed by scanning only the entries of \(\varvec{\mathscr {X}}\) whose n-mode index is i.
can be computed by scanning only the entries of \(\varvec{\mathscr {X}}\) whose n-mode index is i.
Proof
Proven by Eq. (9). \(\square \)
Lemma 6
(Scan cost of \(\textsc {S-HOT}_{\text {scan}}\) ) \(\textsc {S-HOT}_{\text {scan}}\) computes Eq. (12) within one scan of \(\varvec{\mathscr {X}}\) when \(\varvec{\mathscr {X}}\) is sorted by the n-mode index.
Proof
By Lemma 5, only a section of tensor whose n-mode index is i is required for computing  . If \(\varvec{\mathscr {X}}\) is sorted by the nth mode index, we can sequentially compute each
. If \(\varvec{\mathscr {X}}\) is sorted by the nth mode index, we can sequentially compute each  on the fly. Moreover, once
on the fly. Moreover, once  is computed, we can immediately compute
is computed, we can immediately compute  . After that, we do not need
. After that, we do not need  anymore and can discard it. Thus, Eq. (12) can be computed on the fly within only a single scan of \(\varvec{\mathscr {X}}\). \(\square \)
anymore and can discard it. Thus, Eq. (12) can be computed on the fly within only a single scan of \(\varvec{\mathscr {X}}\). \(\square \)
In this paper, we satisfy the sort constraint for all modes by simply keeping N copies of \(\varvec{\mathscr {X}}\) sorted by each mode index.
A formal description for \(\textsc {S-HOT}_{\text {scan}}\) is in Algorithm 2. It is assumed that  is initialized by passing (\(\prod _{p\ne n} {J_{p}}\), \({J_{n}}\)) instead of (\({I_{n}}\), \({J_{n}}\)) at Line 4. Although one additional scan of \(\varvec{\mathscr {X}}\) is required for computing left singular vectors from the obtained right singular vectors (Eq. (11)), \(\textsc {S-HOT}_{\text {scan}}\) still requires fewer scans of \(\varvec{\mathscr {X}}\) than \(\textsc {S-HOT}_{\text {space}}\) since it saves one scan during
is initialized by passing (\(\prod _{p\ne n} {J_{p}}\), \({J_{n}}\)) instead of (\({I_{n}}\), \({J_{n}}\)) at Line 4. Although one additional scan of \(\varvec{\mathscr {X}}\) is required for computing left singular vectors from the obtained right singular vectors (Eq. (11)), \(\textsc {S-HOT}_{\text {scan}}\) still requires fewer scans of \(\varvec{\mathscr {X}}\) than \(\textsc {S-HOT}_{\text {space}}\) since it saves one scan during  computation, which is repeated more frequently.
computation, which is repeated more frequently.
In Lemma 7, we prove the amount of space required by \(\textsc {S-HOT}_{\text {scan}}\) for intermediate data.
Lemma 7
(Space complexity of \(\textsc {S-HOT}_{\text {scan}}\) ) The update step of \(\textsc {S-HOT}_{\text {scan}}\) ( lines 23–29 of Algorithm 2) requires
memory space for intermediate data.
Proof
In its update step for each factor matrix  , \(\textsc {S-HOT}_{\text {scan}}\) maintains
, \(\textsc {S-HOT}_{\text {scan}}\) maintains  ,
,  , and
, and  at a time. All of them are \(\prod _{p=1}^{N}{J_{p}}/{J_{n}}\) by 1 vectors. Thus, \(O(\prod _{p=1}^{N}{J_{p}}/{J_{n}})\) space is required in the update step for each factor matrix
at a time. All of them are \(\prod _{p=1}^{N}{J_{p}}/{J_{n}}\) by 1 vectors. Thus, \(O(\prod _{p=1}^{N}{J_{p}}/{J_{n}})\) space is required in the update step for each factor matrix  . Since the factor matrices are updated one by one, \(O(\max _{1\le n\le N}(\prod _{p=1}^{N}{J_{p}}/{J_{n}}))\) space is required at a time. \(\square \)
. Since the factor matrices are updated one by one, \(O(\max _{1\le n\le N}(\prod _{p=1}^{N}{J_{p}}/{J_{n}}))\) space is required at a time. \(\square \)
Power-law degree distributions in the Microsoft Academic Graph dataset (see Sect. 5.3 for a description of the dataset). a, b show the skewed degree distributions in the author and keyword modes, which are exploited by \(\textsc {S-HOT}_{\text {memo}}\) for speed-up. c, d show that \(\textsc {S-HOT}_{\text {memo}}\) can avoid accessing many (e.g., 50–75%) nonzero entries by memoizing a small percentage (e.g., 10%) of rows

4.4 Even faster: “S-HOT\(_{memo}\)”
How can we make good use of remaining memory when memory is underutilized by \(\textsc {S-HOT}_{\text {scan}}\), which requires little space for intermediate data (see Table 2)? We propose \(\textsc {S-HOT}_{\text {memo}}\), which improves \(\textsc {S-HOT}_{\text {scan}}\) in terms of speed by introducing the memoization technique. The memoization technique leverages the spare memory space, which we call memo, to store a part of intermediate data (i.e., some rows of  ) in memory instead of computing all of them on the fly. Especially, within a given memory budget, \(\textsc {S-HOT}_{\text {memo}}\) carefully decides the rows of
) in memory instead of computing all of them on the fly. Especially, within a given memory budget, \(\textsc {S-HOT}_{\text {memo}}\) carefully decides the rows of  to be memoized so that the speed gain is maximized. A formal description of \(\textsc {S-HOT}_{\text {memo}}\) is given in Algorithm 3, where the steps added for memoization (i.e., lines 5, 14–19, 23–24) are in red.
to be memoized so that the speed gain is maximized. A formal description of \(\textsc {S-HOT}_{\text {memo}}\) is given in Algorithm 3, where the steps added for memoization (i.e., lines 5, 14–19, 23–24) are in red.
Given a memory budget \(B\), let \({k_{n}}\) be the maximum number of rows of  that can be memoized within \(B\). When updating each factor matrix
that can be memoized within \(B\). When updating each factor matrix  , \(\textsc {S-HOT}_{\text {memo}}\) memoizes the \({k_{n}}\) rows that are most expensive to compute. Such rows can be found by comparing the degrees of the nth mode indices (see Definition 8 for the definition of degree), as described in lines 14-19.
, \(\textsc {S-HOT}_{\text {memo}}\) memoizes the \({k_{n}}\) rows that are most expensive to compute. Such rows can be found by comparing the degrees of the nth mode indices (see Definition 8 for the definition of degree), as described in lines 14-19.
Definition 8
(Degree of mode indices) The degree of each nth mode index i is defined as \(|\Theta _{i}^{(n)}(\varvec{\mathscr {X}})|\), i.e., the number of nonzero entries whose nth mode index is i.
This is because computing each row  of
of  takes time proportional the degree of nth mode index i (i.e., \(|\Theta _{i}^{(n)}(\varvec{\mathscr {X}})|\)), as shown in Eq. (9). The remaining steps for updating
takes time proportional the degree of nth mode index i (i.e., \(|\Theta _{i}^{(n)}(\varvec{\mathscr {X}})|\)), as shown in Eq. (9). The remaining steps for updating  are the same as those of \(\textsc {S-HOT}_{\text {scan}}\) except for that the memoized rows are used, as described in lines 20-29.
are the same as those of \(\textsc {S-HOT}_{\text {scan}}\) except for that the memoized rows are used, as described in lines 20-29.
This careful choice of the rows of  to be memoized in memory is crucial to speed up the algorithm. This is because, in real-world tensors, the degree of mode indices often follows a power-law distribution [13], and thus, there exist indices with extremely high degree (see Figs. 4a, b for example). By memoizing the rows of
to be memoized in memory is crucial to speed up the algorithm. This is because, in real-world tensors, the degree of mode indices often follows a power-law distribution [13], and thus, there exist indices with extremely high degree (see Figs. 4a, b for example). By memoizing the rows of  corresponding to such high-degree indices, \(\textsc {S-HOT}_{\text {memo}}\) avoids accessing many nonzero entries (see Fig. 4c, d for example) and thus saves considerable computation time, as shown empirically in Sect. 5.5.
corresponding to such high-degree indices, \(\textsc {S-HOT}_{\text {memo}}\) avoids accessing many nonzero entries (see Fig. 4c, d for example) and thus saves considerable computation time, as shown empirically in Sect. 5.5.
We prove the scan cost of \(\textsc {S-HOT}_{\text {memo}}\) in Lemma 8 and the space complexity of \(\textsc {S-HOT}_{\text {memo}}\) in Lemma 9.
Lemma 8
(Scan cost of \(\textsc {S-HOT}_{\text {memo}}\) ) \(\textsc {S-HOT}_{\text {memo}}\) computes Eq. (12) within one scan of \(\varvec{\mathscr {X}}\) when \(\varvec{\mathscr {X}}\) is sorted by the n-mode index.
Proof
Given memoized rows, \(\textsc {S-HOT}_{\text {memo}}\) computes Eq. (12) in the same way as does \(\textsc {S-HOT}_{\text {scan}}\) only except for that \(\textsc {S-HOT}_{\text {memo}}\) uses the memoized rows. Thus, \(\textsc {S-HOT}_{\text {memo}}\) and \(\textsc {S-HOT}_{\text {scan}}\) require the same number of scans of \(\varvec{\mathscr {X}}\), which is one, as shown in Lemma 6. We do not need an additional scan of \(\varvec{\mathscr {X}}\) for the memoization step if it is done while Eq. (12) is first computed. \(\square \)
Lemma 9
(Space complexity of \(\textsc {S-HOT}_{\text {memo}}\) ) The update step of \(\textsc {S-HOT}_{\text {memo}}\) (lines 20-29 of Algorithm 3) requires
memory space for intermediate data.
Proof
In addition to those maintained in \(\textsc {S-HOT}_{\text {scan}}\), which require \(O\Big (\max \limits _{1\le n\le N}\)\((\prod _{p=1}^{N}{J_{p}}/{J_{n}})\Big )\) space at a time (see Lemma 7), \(\textsc {S-HOT}_{\text {memo}}\) maintains the memoized rows, whose size is within the given budget B. Thus, \(O(B+\max _{1\le n\le N}(\prod _{p=1}^{N}{J_{p}}/{J_{n}}))\) space is required at a time. \(\square \)
Table 3 summarizes the key differences of BaselineOpt, S-HOT, \(\textsc {S-HOT}_{\text {scan}}\), \(\textsc {S-HOT}_{\text {memo}}\) in terms of objective, update equations, and materialized data of methods. The table also presents the figures illustrating how the methods work.
5 Experiments
In this section, we present experimental results supporting our claim that S-HOT outperforms state-of-the-art baselines. Specifically, our experiments are designed to answer the following two questions:
Q1. How scalable is S-HOT compared to the state-of-the-art competitors with respect to the dimensionality, the rank, the order, and the number of nonzero entries?
Q2. Can S-HOT decompose real-world tensors that are both large-scale and high-order?
Q3. How does the memory budget affect the speed of \(\textsc {S-HOT}_{\text {memo}}\)?
Q4. How does the degree distribution of the input tensor affect the speed of \(\textsc {S-HOT}_{\text {memo}}\)?
5.1 Experimental setting
Competitors: Throughout all experiments, we use two baseline methods and three versions of our proposed method:
- (1)
BaselineNaive: a naive method computing
 in a straightforward way.
in a straightforward way. - (2)
BaselineOpt [27]: the state-of-the-art memory-efficient Tucker decomposition which computes \(\varvec{\mathscr {Y}}\) fiber by fiber.
- (3)
\(\textsc {S-HOT}_{\text {space}}\) (Sect. 4.2): the most space-efficient version of S-HOT.
- (4)
\(\textsc {S-HOT}_{\text {scan}}\) (Sect. 4.3): a faster version of S-HOT.
- (5)
\(\textsc {S-HOT}_{\text {memo}}\) (Sect. 4.4): the fastest version of S-HOT with the memoization technique. We set the size of memo so that we can memoize up to 30 rows of
 for each nth mode unless otherwise stated.Footnote 6
for each nth mode unless otherwise stated.Footnote 6
For BaselineOpt and BaselineNaive, we use the implementation in Matlab Tensor Toolbox 2.6 [5]. We exclude HaTen2 because HaTen2 is designed for Hadoop, and thus, it takes too much time in a single machine. For example, in order to decompose a synthetic tensor with default parameters, HaTen2 takes 10,700 seconds for an iteration, which is almost 100\(\times \)slower than \(\textsc {S-HOT}_{\text {scan}}\).
Real-world datasets: We use the following high-order real-world tensors, whose statistics are given in Table 4:
LBNL [48]: This dataset, which was collected during the Traces project [41], contains information on internal network traffics from LBNL/ICSI. It is modeled as a 5-order tensor whose modes are sender IPs, sender ports, destination IPs, destination ports, and timestamps.
MS Academic Graph [53]: This dataset is a snapshot of the Microsoft Academic Graph on Feb 5, 2016. It contains 42 million papers; 1,283 conferences and 23,404 journals; 115 million authors; and 53,834 keywords used to annotate the topics of the papers. It is modeled as a 4-order tensor whose modes are authors, venues, years, and keywords. Since the papers with missing attributes are ignored, the final tensor is of size \(9{,}380{,}418\times 18{,}894\times 2016\times 37{,}000\).
Enron [48]: This dataset, which was collected for an investigation by the federal energy regulatory commission, contains information on emails from or to the employees of Enron Corporation [56]. It is modeled as a 4-order tensor whose modes are senders, receivers, words, and dates, respectively.
Note that both BaselineNaive and BaselineOpt methods fail to run on the three real-life tensors due to “out-of-memory” errors, while our S-HOT family successfully decompose them.
Synthetic datasets We also use synthetic tensors mainly to evaluate the scalability of methods with respect to various factors (i.e., the dimensionality, rank, order, and the number of nonzero entries) by controlling each factor while fixing the others. We generate synthetic tensors where the degree of their mode indices follows a Zipf distribution, which is common in real-world data [2, 42]. Specifically, to create an N-order tensor, we sample M entries where each nth mode index is sampled from the following probability density function:
where \(\alpha \) is a parameter determining the skewness of the distribution. We set the value of each entry to 1.Footnote 7 As default parameter values, we use \(N=4\), \(M=10^5\), \({I_{n}} = 10^3\) for every n, \({J_{n}} =8\) for every n, and \(\alpha =1.5\). These default values are chosen to effectively compare the scalability of competitors. We show that baselines (i.e., BaselineNaive and BaselineOpt) run out of memory if we increase these values. All experiments using synthetic datasets are repeated nine times (three times for each of three randomly generated tensors), and reported values are the average of the multiple trials.
Equipment All experiments are conducted on a machine with Intel Core i7 4700@3.4GHz (4 cores), 32GB RAM, and Ubuntu 14.04 trusty. Every version of S-HOT is implemented in C++ with OpenMP library and AVX instruction set, and the source code is available at http://dm.postech.ac.kr/shot. We used Arpack [30], which implements IRAM supporting reverse communication interface. It is worth noting that Arpack is an underlying package for a built-in function called eigs(), which is provided in many popular numerical computing environments including SciPy, GNU Octave, and Matlab. Therefore, S-HOT is numerically stable and has the similar reconstruction error with eigs() function in the above-mentioned numerical computing environments.
For fairness, we must note that a fully optimized C++ implementation could potentially be faster than that of Matlab (although that is unlikely, since Matlab is extremely well optimized for matrix operations). But in any case, our main contribution still holds: regardless of programming languages, S-HOT scales to much larger settings, thanks to our proposed “on-the-fly” computation (Eqs. (6) and (12)).
5.2 Q1: Scalability of S-HOT
We evaluate the scalability of the competing methods with respect to various factors: (1) the order, (2) the dimensionality, (3) the number of nonzero entries, and (4) the rank. Specifically, we measure the wall-clock time of a single iteration of each algorithm on synthetic tensors. Note that all the methods have the same convergence properties, as described in Observation 1 in Sect. 4.
Order First, we investigate the scalability of the considered methods with respect to the order by controlling the order of the input tensor from 3 to 6 while fixing the other factors to their default values. As shown in Fig. 1a, S-HOT outperforms baselines. BaselineNaive fails to decompose the 4-order tensor because it suffers from the intermediate explosion problem. BaselineOpt, which avoids the problem, is more memory efficient than BaselineNaive. However, it fails to decompose a tensor whose order is higher than 4 due to M-Bottleneck. On the contrary, every version of S-HOT successfully decomposes even the 6-order tensor. Especially, \(\textsc {S-HOT}_{\text {memo}}\) is up to \(50\times \) faster than \(\textsc {S-HOT}_{\text {space}}\) and \(\textsc {S-HOT}_{\text {scan}}\).
Dimensionality Second, we investigate the scalability of the considered methods with respect to the dimensionality. Specifically, we increase the dimensionality \({I_{n}}\) of every n from \(10^3\) to \(10^7\). That is, since the default order is 4, we increase the tensor from \(10^3\times 10^3\times 10^3\times 10^3\) to \(10^7\times 10^7\times 10^7\times 10^7\). As shown in Fig. 1b, S-HOT is several orders of magnitude scalable than the baselines. Specifically, BaselineNaive fails to decompose any 4-order tensor, and thus, it does not appear in the plot. BaselineOpt fails to decompose tensors with dimensionality larger than \(10^4\) since the space for storing \(\varvec{\mathscr {Y}}\) increases rapidly with respect to the size of dimensionality (M-Bottleneck). On the contrary, every version of S-HOT successfully decomposes the largest tensor of size \(10^7\times 10^7\times 10^7\times 10^7\). Moreover, the running times of \(\textsc {S-HOT}_{\text {scan}}\) and \(\textsc {S-HOT}_{\text {memo}}\) are almost constant since they solve the transposed problem, whose size is independent of the dimensionality. Between them, \(\textsc {S-HOT}_{\text {memo}}\) is up to \(6\times \) faster than \(\textsc {S-HOT}_{\text {scan}}\). On the other hand, the running time of \(\textsc {S-HOT}_{\text {space}}\) depends on dimensionality and increases as the dimensionality becomes greater than \(10^6\). For smaller dimensionalities, however, the effect of dimensionality on its running time is negligible because the outer products (i.e., lines 19 and 21 of Algorithm 2) are the major bottleneck.
Rank Third, we investigate the scalability of the considered methods with respect to the rank. To show the difference between the competitors clearly, we set the dimensionality of the input tensor to 20,000 in this experiment. However, the overall trends do not depend on the parameter values. As shown in Fig. 1c, the S-HOT has better scalability than baselines. Specifically, BaselineNaive fails to decompose any tensor and does not appear in this plot. BaselineOpt fails to decompose the tensors with rank larger than 6. On the contrary, every version of S-HOT successfully decomposes the tensors with larger ranks. Among them, \(\textsc {S-HOT}_{\text {memo}}\) is up to \(7\times \) faster than \(\textsc {S-HOT}_{\text {scan}}\) and \(\textsc {S-HOT}_{\text {space}}\). \(\textsc {S-HOT}_{\text {scan}}\) is faster than \(\textsc {S-HOT}_{\text {space}}\), but the difference between them decreases as the rank increases. This is because, as the rank increases, the outer products (i.e., lines 19 and 21 of Algorithm 2) become the major bottleneck, which are common in \(\textsc {S-HOT}_{\text {space}}\) and \(\textsc {S-HOT}_{\text {scan}}\).
Nonzero entries Lastly, we investigate the scalability of the considered methods with respect to the number of nonzero entries. We increase the number of nonzero entries in the input tensor from \(10^4\) to \(10^7\). As shown in Fig. 1d, every version of S-HOT scales near linearly with respect to the number of nonzero entries. This is because the S-HOT family scans most nonzero entries (especially, \(\textsc {S-HOT}_{\text {space}}\) and \(\textsc {S-HOT}_{\text {scan}}\) scan all the nonzero entries), and processing each nonzero entry takes almost the same time. Among them, \(\textsc {S-HOT}_{\text {memo}}\) is \(4\times \) faster than \(\textsc {S-HOT}_{\text {scan}}\) and \(\textsc {S-HOT}_{\text {space}}\). With respect to the number of nonzero entries, BaselineOpt shows better scalability than S-HOT since it explicitly materializes\(\varvec{\mathscr {Y}}\). Once \(\varvec{\mathscr {Y}}\) is materialized, since its size does not depend on the number of nonzero entries, the remaining tasks of BaselineOpt are not affected by the number of nonzero entries.
5.3 Q2: S-HOT at work
We test the scalability of S-HOT on the MS Academic Graphdataset. We note that since this tensor is high-order and large, both baseline algorithms fail to handle it running out of memory. However, every version of S-HOT successfully decomposes the tensor.
To better interpret the result of Tucker decomposition, we runs k-means clustering [3] where we treat each factor matrix as the low-rank embedding of the entities in the corresponding mode, as suggested in [27]. Specifically, for Tucker decomposition, we set the rank of each mode to 8 and run 30 iterations. For k-means clustering, we set the number of clusters to 400 and run 100 iterations.
Table 5 shows sample clusters in the venue mode. The first cluster contains many venues related to Computer Science. The second cluster contains many nanotechnology-related venues such as Nature Nanotechnology, Journal of Experimental Nanoscience. The third one have many venues related to Medical Science and Diseases. This result indicates that Tucker decomposition discovers meaningful concepts and groups entities related to each other. However, there is a vast array of methods for multi-aspect data analysis, and we leave a comparative study as to which one performs the best for future work.
5.4 Q3: Effect of the memory budget on the speed of \(\textsc {S-HOT}_{\text {memo}}\)
We measure the effect of memory budget B for memoization on the speed of \(\textsc {S-HOT}_{\text {memo}}\) using synthetic and real-world tensors. We use three 4-order tensors with dimensionality 20,000 for each mode. All the tensors have \(10^6\) nonzero entries, while they have different degree distributions characterized by the skewness \(\alpha \) of the Zipf distribution. We also use the real-world datasets listed in Table 4.
Figure 5a shows the result with the synthetic tensors where we set the rank of each mode to 6. \(\textsc {S-HOT}_{\text {memo}}\) tends to be faster as we use more memory for memoization. However, the speed-up slows down because we prioritize rows to be memoized by the degree of the corresponding mode indices, as described in Sect. 4.4. As the memory budget increases, \(\textsc {S-HOT}_{\text {memo}}\) memoizes rows corresponding to mode indices with smaller degree, which saves less computation. Notice that with only the 10KB memory budget, \(\textsc {S-HOT}_{\text {memo}}\) becomes over \(3.5\times \) faster than \(\textsc {S-HOT}_{\text {scan}}\), which does not use memoization.
As shown in Fig. 5b–d, we obtain the same trend with the real-world tensors. Notice that, in the MS Academic Graphdataset, \(\textsc {S-HOT}_{\text {memo}}\) becomes over \(2\times \) faster than \(\textsc {S-HOT}_{\text {scan}}\), which does not use memoization, with only a 4MB memory budget. \(\textsc {S-HOT}_{\text {scan}}\) saves much computation by memoization a small number of rows due to the power-law degree distributions, shown in Fig. 4.
\(\textsc {S-HOT}_{\text {memo}}\) significantly reduces computational cost on both synthetic and real-world tensors. In the synthetic tensors, \(\textsc {S-HOT}_{\text {memo}}\) achieves over \(3.5\times \) speed-up by memoizing less than 0.05% of rows with a 10 KB memory budget. In the MS Academic Graphdataset, \(\textsc {S-HOT}_{\text {memo}}\) achieves over \(2\times \) speed-up by memoizing less than 0.05% of the rows with a 5 MB memory budget. In e–h the y-axis represents the number of floating-point operations (FLOPs) for recomputing “unmemoized” rows of 
Additionally, Fig. 5e–h shows how the normalized number of floating-point operations (FLOPs) required for recomputing the “unmemoized” rows of  changes depending on the memory budget B for memoization. The computation costs are significantly reduced even when a small fraction of rows are memoized, due to our prioritization scheme.
changes depending on the memory budget B for memoization. The computation costs are significantly reduced even when a small fraction of rows are memoized, due to our prioritization scheme.
5.5 Q5: Effect of the skewness of data on the speed of \(\textsc {S-HOT}_{\text {memo}}\)
We measure the effect of the skewness of degree distribution on the speed of \(\textsc {S-HOT}_{\text {memo}}\). To this end, we use three 4-order tensors with different degree distributions characterized by the skewness \(\alpha \) of the Zipf distribution. All of them have \(10^6\) nonzero entries, and their dimensionality for each mode is 20,000.
Figure 5a shows how rapidly the speed-up of \(\textsc {S-HOT}_{\text {memo}}\) increases depending on the skewness \(\alpha \). In tensors with larger \(\alpha \), the speed-up of \(\textsc {S-HOT}_{\text {memo}}\) tends to increase faster. For example, with a 2KB memory budget, \(\textsc {S-HOT}_{\text {memo}}\) achieves over \(2.5\times \) speed-up in the tensor with \(\alpha =2.5\), while it achieves less than \(1.5\times \) speed-up in the tensor with \(\alpha =1.5\). This is because, with larger \(\alpha \), more nonzero entries are concentrated in few mode indices.
For every realistic degree distribution with \(\alpha >1\), \(\textsc {S-HOT}_{\text {memo}}\) achieves over \(3.5\times \) speed-up with a 10 KB memory budget. \(\textsc {S-HOT}_{\text {memo}}\) reverts to \(\textsc {S-HOT}_{\text {scan}}\) if the input tensor has an unrealistic uniform degree distribution with \(\alpha =0\).
6 Conclusions
In this paper, we propose S-HOT, a scalable algorithm for high-order Tucker decomposition. S-HOT solves M-bottleneck, which existing algorithms suffer from, by using an on-the-fly computation. We provide three versions of S-HOT: \(\textsc {S-HOT}_{\text {space}}\), \(\textsc {S-HOT}_{\text {scan}}\), and \(\textsc {S-HOT}_{\text {memo}}\), which provide an interesting trade-off between time and space. We theoretically and empirically show that all versions of S-HOT have better scalability than baselines.
In summary, our contributions are as follows.
Bottleneck resolution We identify M-Bottleneck (Fig. 2), the scalability bottleneck of existing Tucker decomposition algorithms, and avoid it by a novel approach based on an on-the-fly computation.
Scalable algorithm design We propose S-HOT, a Tucker decomposition algorithm that is carefully optimized for large-scale high-order tensors. S-HOT successfully decomposes 1000\(\times \) larger tensors than baselines algorithms (Fig. 1) with identical convergence properties (Observation 1).
Theoretical analyses We prove the amount of memory space and the number of data scans that the different versions of S-HOT require (Table 2 and Lemmas 3–9).
Future work includes reducing redundant computations that occur during TTMcs, which is a subroutine of S-HOT, using advanced data structures (e.g., compressed sparse fiber [46]), as suggested in [47]. For reproducibility and extensibility of our work, we make the source code of S-HOT publicly available at http://dm.postech.ac.kr/shot.
Notes
\(\textsc {S-HOT}_{\text {space}}\) and \(\textsc {S-HOT}_{\text {scan}}\) appeared in the conference version of this paper [35]. This work extends [35] with \(\textsc {S-HOT}_{\text {memo}}\), which is significantly faster than \(\textsc {S-HOT}_{\text {space}}\) and \(\textsc {S-HOT}_{\text {scan}}\), space complexity analyses, and additional experimental results.
When the input tensor is sparse, a straightforward way of computing
 is to (1) compute
is to (1) compute  for each nonzero element \(\varvec{\mathscr {X}}(i_{1},\dots ,i_{N})\) and (2) combine the results together. The result of
for each nonzero element \(\varvec{\mathscr {X}}(i_{1},\dots ,i_{N})\) and (2) combine the results together. The result of  takes \(O(\prod _{p\ne n}J_p)\) space. Since there are M nonzero elements, \(O(M \prod _{p\ne n}J_p)\) space is required in total.
takes \(O(\prod _{p\ne n}J_p)\) space. Since there are M nonzero elements, \(O(M \prod _{p\ne n}J_p)\) space is required in total.For example, see line 13 of Algorithm 4 in [25].
Instead of computing the eigenvectors of
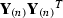 , we can use directly obtain the singular vectors of
, we can use directly obtain the singular vectors of  using, for example, Lanczos bidiagonalization [7]. We leave exploration of such variation for future work.
using, for example, Lanczos bidiagonalization [7]. We leave exploration of such variation for future work.The size of the memo never exceeds 200KB unless otherwise stated.
However, this does not mean that S-HOT is limited to binary tensors nor our implementation is optimized for binary tensors. We choose binary tensors for simplicity. Generating realistic values, while we control each factor, is not a trivial task.
References
Acar E, Çamtepe SA, Krishnamoorthy MS, Yener B (2005) Modeling and multiway analysis of chatroom tensors. In: ISI
Adamic LA, Huberman BA (2002) Zipf’s law and the Internet. Glottometrics 3(1):143–150
Arthur D, Vassilvitskii S (2007) k-means++: the advantages of careful seeding. In: SODA
Austin W, Ballard G, Kolda TG (2016) Parallel tensor compression for large-scale scientific data. In: IPDPS
Bader BW, Kolda TG. Matlab tensor toolbox version 2.6. http://www.sandia.gov/~tgkolda/TensorToolbox/
Baskaran M, Meister B, Vasilache N, Lethin R (2012) Efficient and scalable computations with sparse tensors. In: HPEC
Berry MW (1992) Large-scale sparse singular value computations. Int J Supercomput Appl 6(1):13–49
Beutel A, Kumar A, Papalexakis EE, Talukdar PP, Faloutsos C, Xing EP (2014) Flexifact: scalable flexible factorization of coupled tensors on hadoop. In: SDM
Cai Y, Zhang M, Luo D, Ding C, Chakravarthy S (2011) Low-order tensor decompositions for social tagging recommendation. In: WSDM
Chi Y, Tseng BL, Tatemura J (2006) Eigen-trend: trend analysis in the blogosphere based on singular value decompositions. In: CIKM
Choi D, Jang JG, Kang U (2017) Fast, accurate, and scalable method for sparse coupled matrix-tensor factorization. arXiv preprint arXiv:1708.08640
Choi JH, Vishwanathan S (2014) Dfacto: distributed factorization of tensors. In: NIPS
Clauset A, Shalizi CR, Newman ME (2009) Power-law distributions in empirical data. SIAM Rev 51(4):661–703
Cohen JE, Farias RC, Comon P (2015) Fast decomposition of large nonnegative tensors. IEEE Signal Process Lett 22(7):862–866
Chakaravarthy V-T, Choi J-W, Joseph D-J, Murali P, Pandian S-S, Sabharwal Y, Sreedhar D (2018) On optimizing distributed tucker decomposition for sparse tensors. IEEE Signal Process Mag
de Almeida AL, Kibangou AY (2013) Distributed computation of tensor decompositions in collaborative networks. In: CAMSAP, pp 232–235
de Almeida AL, Kibangou AY (2014) Distributed large-scale tensor decomposition. In: ICASSP
De Lathauwer L, De Moor B, Vandewalle J (2000) On the best rank-1 and rank-(R1, R2,., Rn) approximation of higher-order tensors. SIAM J Matrix Anal Appl 21(4):1324–1342
De Lathauwer L, De Moor B, Vandewalle J (2000) A multilinear singular value decomposition. SIAM J Matrix Anal Appl 21(4):1253–1278
Franz T, Schultz A, Sizov S, Staab S (2009) Triplerank: ranking semantic web data by tensor decomposition. In: ISWC
Jeon B, Jeon I, Sael L, Kang U (2016) Scout: Scalable coupled matrix-tensor factorization—algorithm and discoveries. In: ICDE
Jeon I, Papalexakis EE, Kang U, Faloutsos C (2015) Haten2: billion-scale tensor decompositions. In: ICDE
Kang U, Papalexakis E, Harpale A, Faloutsos C (2012) Gigatensor: scaling tensor analysis up by 100 times-algorithms and discoveries.e In: KDD
Kaya O, Uçar B (2015) Scalable sparse tensor decompositions in distributed memory systems. In: SC
Kaya O, Uçar B (2016) High performance parallel algorithms for the tucker decomposition of sparse tensors. In: ICCP
Kolda TG, Bader BW (2009) Tensor decompositions and applications. SIAM Rev 51(3):455–500
Kolda TG, Sun J (2008) Scalable tensor decompositions for multi-aspect data mining. In: ICDM
Kolda TG, Bader BW, Kenny JP (2005) Higher-order web link analysis using multilinear algebra. In: ICDM
Lamba H, Nagarajan V, Shin K, Shajarisales N (2016) Incorporating side information in tensor completion. In: WWW companion
Lehoucq RB, Sorensen DC, Yang C (1998) ARPACK users’ guide: solution of large-scale eigenvalue problems with implicitly restarted Arnoldi methods, vol 6. Siam
Li J, Choi J, Perros I, Sun J, Vuduc R (2017) Model-driven sparse CP decomposition for higher-order tensors. In: IPDPS
Li J, Sun J, Vuduc R (2018) HiCOO: hierarchical storage of sparse tensors. In: SC
Maruhashi K, Guo F, Faloutsos C (2011) Multiaspectforensics: pattern mining on large-scale heterogeneous networks with tensor analysis. In: ASONAM
Moghaddam S, Jamali M, Ester M (2012) ETF: extended tensor factorization model for personalizing prediction of review helpfulness. In: WSDM
Oh J, Shin K, Papalexakis EE, Faloutsos C, Yu H (2017) S-hot: scalable high-order tucker decomposition In: WSDM
Oh S, Park N, Sael L, Kang U (2018) Scalable tucker factorization for sparse tensors—algorithms and discoveries. In: ICDE, pp 1120–1131
Oh S, Park N, Sael L, Kang U (2019) High-performance tucker factorization on heterogeneous platforms. IEEE Trans Parallel Distrib Syst
Papalexakis EE, Faloutsos C, Sidiropoulos ND (2015) Parcube: sparse parallelizable candecomp-parafac tensor decomposition. TKDD 10(1):3
Papalexakis EE, Faloutsos C, Sidiropoulos ND (2016) Tensors for data mining and data fusion: models, applications, and scalable algorithms. TIST 8(2):16
Perros I, Chen R, Vuduc R, Sun J (2015) Sparse hierarchical tucker factorization and its application to healthcare. In: ICDM
Pang R, Allman M, Paxson V, Lee J (2014) The devil and packet trace anonymization. ACM SIGCOMM Comput Commun Rev 36(1):29–38
Powers DM (1998) Applications and explanations of Zipf’s law. In: NeMLaP/CoNLL
Rendle S, Schmidt-Thieme L (210) Pairwise interaction tensor factorization for personalized tag recommendation. In: WSDM
Saad Y (2011) Numerical methods for large eigenvalue problems. Society for Industrial and Applied Mathematics, Philadelphia
Sael L, Jeon I, Kang U (2015) Scalable tensor mining. Big Data Res 2(2):82–86
Smith S, Karypis G (2015) Tensor-matrix products with a compressed sparse tensor. In: IA3
Smith S, Karypis G (2017) Accelerating the tucker decomposition with compressed sparse tensors. In: Euro-Par
Smith S, Choi JW, Li J, Vuduc R, Park J, Liu X, Karypis G. FROSTT: the formidable repository of open sparse tensors and tools. http://frostt.io/
Shin K, Hooi B, Faloutsos C (2018) Fast, accurate, and flexible algorithms for dense subtensor mining. TKDD 12(3):28:1–28:30
Shin K, Hooi B, Kim J, Faloutsos C (2017) DenseAlert: incremental dense-subtensor detection in tensor streams. In: KDD
Shin K, Lee S, Kang U (2017) Fully scalable methods for distributed tensor factorization. TKDE 29(1):100–113
Sidiropoulos ND, Kyrillidis A (2012) Multi-way compressed sensing for sparse low-rank tensors. IEEE Signal Process Lett 19(11):757–760
Sinha A, Shen Z, Song Y, Ma H, Eide D, Hsu B-JP, Wang K (2015) An overview of microsoft academic service (MAS) and applications. In: WWW companion
Sun J, Tao D, Faloutsos C (2006) Beyond streams and graphs: dynamic tensor analysis. In: KDD
Sun J-T, Zeng H-J, Liu H, Lu Y, Chen Z (2005) Cubesvd: a novel approach to personalized web search. In: WWW
Shetty J, Adibi J. The Enron email dataset database schema and brief statistical report. Information sciences institute technical report. University of Southern California
Tsourakakis CE (2010) Mach: fast randomized tensor decompositions. In: SDM, SIAM
Tucker LR (1966) Some mathematical notes on three-mode factor analysis. Psychometrika 31(3):279–311
Vannieuwenhoven N, Vandebril R, Meerbergen K (2012) A new truncation strategy for the higher-order singular value decomposition. SIAM J Sci Comput 34(2):A1027–A1052
Acknowledgements
This research was supported by Disaster-Safety Platform Technology Development Program of the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (Grant Number: 2019M3D7A1094364) and the National Research Foundation of Korea (NRF) Grant funded by the Korea government (MSIP) (No. 2016R1E1A1A01942642).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Zhang, J., Oh, J., Shin, K. et al. Fast and memory-efficient algorithms for high-order Tucker decomposition. Knowl Inf Syst 62, 2765–2794 (2020). https://doi.org/10.1007/s10115-019-01435-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10115-019-01435-1







 (initially
(initially  ).
). , and gives
, and gives  to
to  .
.

 in a straightforward way.
in a straightforward way. for each nth mode unless otherwise stated.
for each nth mode unless otherwise stated.
 is to (1) compute
is to (1) compute  for each nonzero element
for each nonzero element  takes
takes  , we can use directly obtain the singular vectors of
, we can use directly obtain the singular vectors of  using, for example, Lanczos bidiagonalization [
using, for example, Lanczos bidiagonalization [