Leveraging external information in topic modelling

Abstract

Besides the text content, documents usually come with rich sets of meta-information, such as categories of documents and semantic/syntactic features of words, like those encoded in word embeddings. Incorporating such meta-information directly into the generative process of topic models can improve modelling accuracy and topic quality, especially in the case where the word-occurrence information in the training data is insufficient. In this article, we present a topic model called MetaLDA, which is able to leverage either document or word meta-information, or both of them jointly, in the generative process. With two data augmentation techniques, we can derive an efficient Gibbs sampling algorithm, which benefits from the fully local conjugacy of the model. Moreover, the algorithm is favoured by the sparsity of the meta-information. Extensive experiments on several real-world datasets demonstrate that our model achieves superior performance in terms of both perplexity and topic quality, particularly in handling sparse texts. In addition, our model runs significantly faster than other models using meta-information.

1 Introduction

With the rapid growth of the internet, huge amounts of text data are generated in social networks, online shopping and news websites, etc. These data are generally short but may contain rich and complex kinds of information that can be difficult to find in traditional information sources [44], therefore create demand for both effective and efficient machine learning techniques. Probabilistic topic models such as Latent Dirichlet Allocation (LDA) [4] are among the popular approaches for this task. In topic modelling, a document is assumed to be generated from a mixture of topics, where each topic is a probability distribution over a vocabulary. However, most existing topic models discover topics purely based on the word-occurrences, ignoring the meta-information (a.k.a., side information) associated with the content, which often results in degraded performance. We argue that meta-information associated with diverse texts can play the role of background knowledge in human text comprehension. When we humans read text, it is natural for us to leverage metadata, such as categories, authors, timestamps, words’ semantic/syntactic information, to improve our understanding of the text. Therefore, it is reasonable to expect topic models can also benefit from the meta-information and yield improved modelling accuracy and topic quality.

Fig. 1

Meta-information associated with a tweet

In practice, various kinds of meta-information are associated to tweets, product reviews, blogs, etc. They are often available at both the document level and the word level. At the document level, labels of documents can be used to guide topic learning so that more meaningful topics can be discovered. It is likely that documents with common labels should discuss similar topics, which can be modelled by similar distributions over topics. In the case of tweets, as shown in Fig. 1, they can have an author, hashtag, timestamp, etc. Previous work on tweet pooling [12, 19] has shown that aggregating tweets according to their authors or hashtags can significantly improve topic modelling. Furthermore, if we use authors as labels for scientific papers, the research topics of the papers published by the same researcher can be closely related, and authors having similar research topics are more likely to collaborate [34].

At the word level, different semantic/syntactic features are also accessible. For example, there are features regarding word relationships, such as synonyms obtained from WordNet [22], word co-occurrence patterns obtained from a large corpus, and linked concepts from knowledge graphs. It is preferable that words having similar meaning but different morphological forms, like “dog” and “puppy”, are likely to be assigned to the same topic, even if they barely co-occur in the modelled corpus. Recently, word embeddings generated by GloVe [27] and word2vec [20, 21] have attracted a lot of attention in natural language processing and related fields. It has been shown that the word embeddings can capture both the semantic and syntactic features of words so that similar words are close to each other in the embedding space. It is reasonable to expect that these word embeddings will improve topic modelling [8, 26]. Figure 1 also shows some word-level meta-information associated with the tweet.

It is known that most conventional topic models can suffer from a large performance degradation on short texts (e.g., tweets and news headlines) due to insufficient word co-occurrence information. In such cases, meta-information of documents and words can play the role of auxiliary information in analysing short texts, which can compensate for the lost information in word co-occurrences. At the document level, we can leverage the hashtags, users, locations, and timestamps of tweets so that the data sparsity problem can be alleviated. At the word level, word semantic similarity and embeddings obtained or trained on large external corpus (e.g., Google News or Wikipedia) can also be built into the generative process of topic models [17, 26, 36].

Recently, significant research effort has been devoted to handle short texts in topic modelling. Models along this line often take classical topic models, like LDA, as a building block, and manipulate the graphical structure to incorporate meta-information into the generative process [23, 26, 30]. However, what we found is that those models make use of either the document level or the word level meta-information, rather than both. The limitation is often caused by their complicated model structures, which lose conjugacy favoured by sampling methods, and further result in inefficient inference algorithms.

In this article, we propose MetaLDA,¹ a new topic model that can effectively and efficiently make use of arbitrary document and word meta-information encoded in binary form. Specifically, the labels of a document in MetaLDA are incorporated in the prior of the per-document topic distributions. If two documents have similar labels, their topic distributions should be generated with similar Dirichlet priors. Analogously, at the word level, the features of a word are incorporated in the prior of the per-topic word distributions, which encourages words with similar features to have similar proportions across topics. Therefore, both document and word meta-information, if and when they are available, can be flexibly and simultaneously incorporated in the generative process. MetaLDA has the following key properties:

• 1. MetaLDA jointly incorporates various kinds of document and word meta-information for both regular and short texts, yielding better modelling accuracy and topic quality.

• 2. With data augmentation techniques, the inference of MetaLDA can be done by an efficient and closed-form Gibbs sampling algorithm that benefits from the full local conjugacy of the model.

• 3. The simple structure of incorporating meta-information and the efficient inference algorithm give MetaLDA advantage in terms of running speed over other models with meta-information.

• 4. MetaLDA has an improved interpretability. For example, the inclusion of the document labels directly in the generative process gives the ability of both explaining each label with topics and assigning labels to each topic.

We conduct extensive experiments with several real datasets including regular and short texts in various domains. The experimental results demonstrate that MetaLDA outperforms all the competitors we considered in terms of perplexity, topic coherence and running time. The rest of the article, which extends our earlier contribution [42], is organised as follows. We first briefly discuss the related work in Sect. 2. Then, we elaborate on MetaLDA and derive its sampling algorithm in Sects. 3 and 4, respectively. The experimental results derived on several real-world datasets are reported in Sect. 5. We conclude the article in Sect. 6.

2 Related work

In this section, we review three lines of related work: models with document meta-information, models with word meta-information, and models for short texts.

At the document level, Supervised LDA (sLDA) [18] models document labels by learning a generalised linear model with an appropriate link function and exponential family dispersion function. But the restriction for sLDA is that one document can only have one label. Labelled LDA (LLDA) [29] assumes that each label has a corresponding topic and a document is generated by a mixture of the topics. Although multiple labels are allowed in LLDA, it requires that the number of topics must equal to the number of labels, i.e., exactly one topic per label. As an extension to LLDA, Partially Labelled LDA (PLLDA) [30] relaxes this requirement by assigning multiple topics to a label. The Dirichlet Multinomial Regression (DMR) model [23] incorporates document labels on the prior of the topic distributions like our MetaLDA but with the logistic-normal transformation. As full conjugacy does not exist in DMR, a part of the inference has to be done by numerical optimisation, which is slow for large sets of labels and topics. Similarly, in the Hierarchical Dirichlet Scaling Process (HDSP) [14], conjugacy is broken as well since the topic distributions have to be renormalised. A Poisson factorisation model with hierarchical document labels is introduced in [13], but the technique cannot be applied to regular topic models as the topic proportion vectors are also unnormalised.

There has been growing interest in incorporating word features in topic models. For example, DF-LDA [2] incorporates word must-links and cannot-links using a Dirichlet forest prior in LDA; MRF-LDA [35] encodes word semantic similarity in LDA with a Markov random field; WF-LDA [28] extends LDA to model word features with the logistic-normal transform; LF-LDA [26] integrates word embeddings into LDA by replacing the topic-word Dirichlet multinomial component with a mixture of a Dirichlet multinomial component and a word embedding component; Instead of generating word types (tokens), Gaussian LDA (GLDA) [8] directly generates word embeddings with the Gaussian distribution. Despite the exciting applications of the above models, their inference is usually less efficient due to the non-conjugacy and/or complicated model structures.

Analysis of short text with topic models has been an active area with the development of social networks. Generally, there are two ways to deal with the sparsity problem in short texts, either using the intrinsic properties of short texts or leveraging meta-information. For the first way, one popular approach is to aggregate short texts into pseudo-documents, for example, [12] introduces a model that aggregates tweets containing the same word; Recently, PTM [46] aggregates short texts into latent pseudo-documents. Another approach is to assume one topic per short document, known as mixture of unigrams or Dirichlet Multinomial Mixture (DMM) such as [36, 39]. For the second way, document meta-information can be used to aggregate short texts, for example, [12] aggregates tweets by the corresponding authors and [19] shows that aggregating tweets by their hashtags yields superior performance over other aggregation methods. Closely related work to ours are models that use word features for short texts. For example, [36] introduces an extension of GLDA on short texts which samples an indicator variable that chooses to generate either the type of a word or the embedding of a word and GPU-DMM [17] extends DMM with word semantic similarity obtained from embeddings for short texts. Although with improved performance, there still exist challenges for existing models:

• for aggregation-based models, it is usually hard to choose which meta-information to use for aggregation;

• the “single topic” assumption makes DMM models lose the flexibility to capture different topic ingredients of a document;

• the incorporation of meta-information in the existing models is usually less efficient.

To our knowledge, the attempts that jointly leverage document and word meta-information are relatively rare. For example, meta-information can be incorporated by first-order logic in Logit-LDA [3] and score functions in SC-LDA [37]. However, the first-order logic and score functions need to be defined for different kinds of meta-information and the definition can be infeasible for incorporating both document and word meta-information simultaneously.

3 The MetaLDA model

Given a corpus, LDA uses the same Dirichlet prior for all the per-document topic distributions and the same prior for all the per-topic word distributions [33]. While in MetaLDA, each document has a specific Dirichlet prior on its topic distribution, which is computed from the meta-information of the document, and the parameters of the prior are estimated during training. Similarly, each topic has a specific Dirichlet prior computed from the word meta-information. In this section we elaborate on our MetaLDA, in particular on how the meta-information is incorporated. Hereafter, we will use labels as document meta-information, unless otherwise stated. Table 1 summarises the notations used in this section.

Table 1 List of notations

Fig. 2

The graphical model of MetaLDA

The basic formulation mirrors that of standard LDA. Given a collection of D documents ${\mathcal {D}}$, MetaLDA generates document $d \in \{1,\ldots ,D\}$ with a mixture of K topics and each topic $k \in \{1,\ldots ,K\}$ is a distribution over the vocabulary with V tokens, denoted by ${\varvec{\phi }}_{k} \in {\mathbb {R}}^{V}_{+}$. For document d with $N_d$ words, to generate the ith ($i \in \{1,\ldots ,N_d\}$) word $w_{d,i}$, we first sample a topic $z_{d,i} \in \{1,\ldots ,K\}$ from the document’s topic distribution $\varvec{\theta _d} \in {\mathbb {R}}^{K}_{+}$, and then sample $w_{d,i}$ from ${\varvec{\phi }}_{z_{d,i}}$. Now this is extended with meta-information. Assume the labels of document d are encoded in a binary vector $\varvec{f_d} \in \{0,1\}^{L_\mathrm{doc}}$ where $L_\mathrm{doc}$ is the total number of unique labels. $f_{d,l}=1$ indicates label l is active in document d and vice versa. MetaLDA allows each document to have multiple labels. Similarly, the $L_\mathrm{word}$ features of token v are stored in a binary vector ${\varvec{g}}_v \in \{0,1\}^{L_\mathrm{word}}$. Therefore, the document and word meta-information associated with ${\mathcal {D}}$ are stored in the matrix $\mathbf {F} \in \{0,1\}^{D \times L_\mathrm{doc}}$ and $\mathbf {G} \in \{0,1\}^{V \times L_\mathrm{word}}$, respectively. Although MetaLDA incorporates binary features, categorical features and real-valued features can be converted into binary values with proper transformations such as discretisation and binarisation [10].

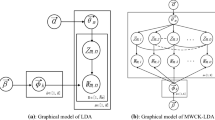
Figure 2 shows the graphical model of MetaLDA and the generative process is as follows:

• 1. For each topic k:

  • (a) For each doc-label l: Draw $\lambda _{l,k} \sim \mathrm {Ga}(\mu _0,\mu _0)$

  • (b) For each word-feature $l'$: Draw $\delta _{l',k} \sim \mathrm {Ga}(\nu _0,\nu _0)$

  • (c) For each token v: Compute $\beta _{k,v} = \prod _{l'=1}^{L_\mathrm{word}} \delta _{l',k}^{g_{v,l'}}$

  • (d) Draw ${\varvec{\phi }}_k \sim \text {Dir}_V({\varvec{\beta }}_{k})$

• 2. For each document d:

  • (a) For each topic k: Compute $\alpha _{d,k} = \prod _{l=1}^{L_\mathrm{doc}} \lambda _{l,k}^{f_{d,l}}$

  • (b) Draw ${\varvec{\theta }}_d \sim \text {Dir}_K({\varvec{\alpha }}_d)$

  • (c) For each word in document d:

    • (i) Draw topic $z_{d,i} \sim \text {Cat}_K(\varvec{\theta }_d)$

    • (ii) Draw word $w_{d,i} \sim \text {Cat}_V(\varvec{\phi }_{z_{d,i}})$

where $\text {Ga}(\cdot ,\cdot )$, $\text {Dir}(\cdot )$, $\text {Cat}(\cdot )$ are the gamma distribution with shape and rate parameters, the Dirichlet distribution, and the categorical distribution, respectively. K, $\mu _0$, and $\nu _0$ are the hyper-parameters.

To incorporate document labels, MetaLDA learns a specific Dirichlet prior over the topics for each document by using the label information. Specifically, the information of document d’s labels is incorporated in $\varvec{\alpha }_d$, the parameter of Dirichlet prior on $\varvec{\theta }_d$. As shown in Step 2a, $\alpha _{d,k}$ is computed as a log linear combination of the labels $f_{d,l}$. Since $f_{d,l}$ is binary, $\alpha _{d,k}$ is indeed the multiplication of $\lambda _{l,k}$ over all the active labels of document d, i.e., $\{l \mid f_{d, l}=1\}$. Drawn from the gamma distribution with mean 1, $\lambda _{l,k}$ controls the impact of label l on topic k. If label l has no or less impact on topic k, $\lambda _{l,k}$ is expected to be 1 or close to 1, and then $\lambda _{l,k}$ will have no or little influence on $\alpha _{d,k}$ and vice versa. The hyper-parameter $\mu _0$ controls the variation of $\lambda _{l,k}$. The incorporation of word features is analogous but in the parameter of the Dirichlet prior on the per-topic word distributions as shown in Step 1c.

The intuition of our way of incorporating meta-information is as follows. At the document level, if two documents have more labels in common, their Dirichlet parameter $\varvec{\alpha }_d$ will be more similar, resulting in more similar topic distributions $\varvec{\theta }_d$; At the word level, if two words have similar features, their $\beta _{k,v}$ in topic k will be similar and then we can expect that their $\phi _{k,v}$ could be more or less the same. Finally, the two words will have similar probabilities of showing up in topic k. In other words, if a topic “prefers” a certain word, we expect that it will also prefer other words with similar features to that word. Moreover, at both the document and the word level, different labels/features may have different impact on the topics ($\lambda$/$\delta$), which can be automatically learnt in MetaLDA from the data.

4 Inference

Unlike most existing methods, our way of incorporating the meta-information facilitates the derivation of an efficient Gibbs sampling algorithm. With two data augmentation techniques (i.e., the introduction of auxiliary variables), MetaLDA admits the local conjugacy that further gives us a close-form Gibbs sampling algorithm. Note that MetaLDA incorporates the meta-information on the Dirichlet priors, so we can still use LDA’s collapsed Gibbs sampling algorithm for the topic assignment $z_{d,i}$. Thus, there is no need to use a hybrid learning algorithm (i.e., optimisation + sampling), such as those in [23, 26]. Moreover, as shown in Step 2a and 1c, we only need to consider nonzero entries of $\mathbf {F}$ and $\mathbf {G}$ in computing the full conditionals, which further reduces the inference complexity, particularly when the feature space is sparse. This is often the case in real-world scenarios. In the rest of this section, we will focus on the derivation of the full conditionals for sampling the two Gamma random variables, $\varvec{\lambda }$ and $\varvec{\delta }$, used to modelling the influence of document labels and word features on topics. Table 2 shows the statistics that we need while running the inference.

Table 2 Summary of statistics

Given $\varvec{\phi }_{1:K}$ and $\varvec{\theta }_{1:D}$, the complete model likelihood (i.e., joint distribution) of MetaLDA is exactly the same as LDA’s likelihood, which is as follows:

$$\begin{aligned} \text{ Pr }({\varvec{w}}_{1:D}, {\varvec{z}}_{1:D} | \varvec{\theta }_{1:D}, \varvec{\phi }_{1:K}) = \prod _{d=1}^{D} \prod _{i=1}^{N_d}\theta _{d,z_{d,i}}\phi _{z_{d,i},v} = \prod _{d=1}^{D} \prod _{k=1}^{K} \theta _{d,k}^{m_{d,k}} \prod _{k=1}^{K} \prod _{v=1}^{V} \phi _{k,v}^{n_{k,v}} \end{aligned}$$

(1)

where $n_{k,v} = \sum _{d}^{D} \sum _{i=1}^{N_d} \varvec{1}_{(w_{d,i} = v, z_{d,i} = k)}$ counts the number of words v assigned to topic k, $m_{d,k} = \sum _{i=1}^{N_d} \varvec{1}_{(z_{d,i} = k)}$ counts the number of words in document d assigned to topic k, and $\varvec{1}_{(\cdot )}$ is the indicator function. In the standard LDA model, we can marginalise out $\varvec{\phi }$ and $\varvec{\theta }$ using the Dirichlet multinomial conjugacy, and then yield

$$\begin{aligned}&\text{ Pr }({\varvec{z}}_{1:D}, {\varvec{w}}_{1:D}; {\varvec{\alpha }}_{1:D}, \varvec{\beta }_{1:K}) \nonumber \\&\quad = \int _{\varvec{\theta }} \prod _{d=1}^{D} \frac{\varGamma \left( \sum _{k=1}^{K}\alpha _{d, k}\right) }{\prod _{k=1}^{K}\varGamma (\alpha _{d,k})}\prod _{k=1}^{K} \theta _{d,k}^{m_{d,k} + \alpha _{d,k} -1} \int _{\varvec{\phi }} \prod _{k=1}^{K} \frac{\varGamma \left( \sum _{v=1}^{V}\beta _{k,v}\right) }{\prod _{v=1}^{V}\varGamma (\beta _{k,v})} \prod _{v=1}^{V} \phi _{k,v}^{n_{k,v} + \beta _{k,v} -1} \cdot \nonumber \\&\quad = \prod _{d=1}^{D}\frac{\text{ Beta }_K({\varvec{\alpha }}_d + \varvec{m}_d)}{\text{ Beta }_K({\varvec{\alpha }}_d)} \prod _{k=1}^{K}\frac{\text{ Beta }_V(\varvec{\beta }_k + \varvec{n}_k)}{\text{ Beta }_V(\varvec{\beta }_k)} \end{aligned}$$

(2)

where $\varGamma (\cdot )$ is the Gamma function, $\text{ Beta }_N(\cdot )$ is a N-dimensional beta function as

$$\begin{aligned} \text{ Beta }_N(\varvec{x}) = \frac{\prod _{n}\varGamma (x_n)}{\varGamma \left( \sum _n x_n\right) } \end{aligned}$$

and here we assume that the Dirichlet priors are document and topic specific. Given $\varvec{\beta }_k$ and ${\varvec{\alpha }}_d$, it is straightforward to compute the full conditional for sampling topic assignment $z_{d,i}$, i.e.,

(3)

In MetaLDA, we have replaced ${\varvec{\alpha }}_d$ and $\varvec{\beta }_k$ with a log linear model in order to build informative priors from various side information associated with both documents and words. They are deterministically computed from a set of Gamma random variables, as shown in Step 2a and 1c in the generative process. Equation (3) can still be used in MetaLDA to sample the topic assignments. However, the major challenge is to sample the Gamma random variables, $\varvec{\lambda }$ and $\varvec{\delta }$ without significantly complicating the inference procedure.

4.1 Sampling Gamma random variable $\lambda _{l,k}$

$\lambda _{l,k}$ is involved in computing the Dirichlet prior over $\varvec{\theta }_{1:D}$ via the parameter ${\varvec{\alpha }}_{1:D}$. To sample $\lambda _{l,k}$, we expand the first Beta ratio in Eq. (2) with Gamma functions as follows:

$$\begin{aligned} \prod _{d=1}^{D}\frac{\text{ Beta }_K({\varvec{\alpha }}_d + \varvec{m}_d)}{\text{ Beta }_K({\varvec{\alpha }}_d)} =\prod _{d=1}^{D} \underbrace{\frac{\varGamma (\alpha _{d,\cdot })}{\varGamma (\alpha _{d,\cdot } + m_{d,\cdot })}}_{\text {Gamma ratio 1}} \prod _{k=1}^{K} \underbrace{\frac{\varGamma (\alpha _{d,k} + m_{d,k})}{\varGamma (\alpha _{d,k})}}_{\text {Gamma ratio 2}} \end{aligned}$$

(4)

where $\alpha _{d,\cdot } = \sum _{k=1}^{K} \alpha _{d,k}$, and $m_{d,\cdot } = \sum _{k=1}^{K} m_{d,k}$. It is not easy to directly work with these Gamma functions, while we replace $\alpha _k$ with $\prod _{l=1}^{L_\mathrm{doc}} \lambda _{l,k}^{f_{d,l}}$. In order to retain the sampling efficiency of the standard LDA model, we appeal to data augmentation.

Gamma ratio 1 in Eq. (4) can be seen to be the marginalisation of a set of Beta random variables, therefore can be augmented as (similar to the sampling of the Pitman–Yor concentration parameter in [9]):

$$\begin{aligned} \underbrace{\frac{\varGamma (\alpha _{d,\cdot })}{\varGamma (\alpha _{d,\cdot } + m_{d,\cdot })}}_{\text {Gamma ratio 1}}\propto & {} \int _{q_d} q_d^{\alpha _{d,\cdot }-1} (1-q_d)^{m_{d,\cdot }-1} \end{aligned}$$

(5)

where for each document d, $q_d \sim \text {Beta}(\alpha _{d,\cdot }, m_{d,\cdot })$. Given a set of $q_{1:D}$ for all the documents, Gamma ratio 1 can be approximated by the product of $q_{1:D}$, i.e., $\prod _{d=1}^{D} q_d^{\alpha _{d, \cdot }}$.

Gamma ratio 2 in Eq. (4) is the Pochhammer symbol for a rising factorial, which can be augmented with an auxiliary variable $t_{d,k}$ [7, 31, 40, 45] as follows:

$$\begin{aligned} \underbrace{\frac{\varGamma (\alpha _{d,k} + m_{d,k})}{\varGamma (\alpha _{d,k})}}_{\text {Gamma ratio 2}}= & {} \sum _{t_{d,k}=0}^{m_{d,k}} S^{m_{d,k}}_{t_{d,k}} \alpha _{d,k}^{t_{d,k}} \end{aligned}$$

(6)

where $S^{m}_{t}$ indicates an unsigned Stirling number of the first kind. Gamma ratio 2 is indeed a normalising constant for the probability of the number of tables in the Chinese Restaurant Process (CRP) [5], $t_{d,k}$ can be sampled by a CRP with $\alpha _{d,k}$ as the concentration and $m_{d,k}$ as the number of customers:

$$\begin{aligned} t_{d,k}= & {} \sum _{i=1}^{m_{d,k}} \text {Bern}\left( \frac{\alpha _{d,k}}{\alpha _{d,k}+i}\right) \end{aligned}$$

(7)

where $\text {Bern}(\cdot )$ samples a sequence of binary variables from the Bernoulli distribution. The complexity of sampling $t_{d,k}$ by Eq. (7) is ${\mathcal {O}}(m_{d,k})$. For large $m_{d,k}$, as the standard deviation of $t_{d,k}$ is ${\mathcal {O}}(\sqrt{\log m_{d,k}})$ [5], one can sample $t_{d,k}$ in a small window around the current value in complexity ${\mathcal {O}}(\sqrt{\log m_{d,k}})$.

By ignoring the terms unrelated to $\alpha$, the augmentation of Eq. (6) can be simplified to a single term $\alpha _{d,k}^{t_{d,k}}$. With those auxiliary variables, we can simplify Eq. (4) as:

$$\begin{aligned} \prod _{d=1}^{D} q_d^{\alpha _{d,.}}\prod _{k=1}^{K} \alpha _{d,k}^{t_{d,k}} = \prod _{d=1}^{D} \prod _{k=1}^{K} q_d^{\alpha _{d,k}} \alpha _{d,k}^{t_{d,k}} \end{aligned}$$

(8)

Now, replacing $\alpha _{d,k}$ with $\lambda _{l,k}$ (i.e., $\alpha _{d,k} = \prod _{l=1}^{L_\mathrm{doc}} \lambda _{l,k}^{f_{d,l}}$ ), we get:

$$\begin{aligned}&\left( \prod _{d=1}^{D} \prod _{k=1}^{K} e^{\alpha _{d,k} \log {q_d}}\right) \left( \prod _{d=1}^{D} \prod _{k=1}^{K}\left( \prod _{l=1}^{L_\mathrm{doc}} \lambda _{l,k}^{f_{d,l}}\right) ^{t_{d,k}} \right) \nonumber \\&\quad = \left( \prod _{d=1}^{D} \prod _{k=1}^{K} e^{- \alpha _{d,k} \log {\frac{1}{q_d}}}\right) \left( \prod _{l=1}^{L_\mathrm{doc}} \prod _{k=1}^{K} \lambda _{l,k}^{\sum _{d=1}^{D} f_{d,l} t_{d,k} } \right) \nonumber \\&\quad = \left( \prod _{k=1}^{K} e^{- \sum _{d=1}^{D}\alpha _{d,k} \log {\frac{1}{q_d}}} \right) \left( \prod _{l=1}^{L_\mathrm{doc}} \prod _{k=1}^{K} \lambda _{l,k}^{\sum _{d=1}^{D} f_{d,l} t_{d,k} } \right) \end{aligned}$$

(9)

Recall that all the document labels are binary and $\lambda _{l,k}$ is involved in computing $\alpha _{d,k}$ if and only if $f_{d,l}=1$. Extracting all the terms related to $\lambda _{l,k}$ in Eq. (9), we get the posterior likelihood of $\lambda _{l,k}$:

$$\begin{aligned} e^{- \lambda _{l,k} \left( \sum _{d=1:f_{d,l}=1}^{D} \frac{\alpha _{d,k}}{\lambda _{l,k}}\log \frac{1}{q_d} \right) } \lambda _{l,k} ^{\sum _{d=1}^{D} f_{d,l} t_{d,k}} \end{aligned}$$

where $\frac{\alpha _{d,k}}{\lambda _{l,k}}$ is the value of $\alpha _{d,k}$ with $\lambda _{l,k}$ removed when $f_{d,l}=1$. With these data augmentation techniques, the likelihood is transformed into a form that is conjugate to the gamma prior of $\lambda _{l,k}$.

Therefore, it is straightforward to yield the following sampling strategy for $\lambda _{l,k}$:

$$\begin{aligned} \lambda _{l,k}\sim & {} \mathrm {Ga}( \mu ', \mu '') \end{aligned}$$

(10)

$$\begin{aligned} \mu '= & {} \mu _0 + \sum _{d=1: f_{d,l} = 1}^{D} t_{d,k} \end{aligned}$$

(11)

$$\begin{aligned} \mu ''= & {} \mu _0 - \sum _{d=1:f_{d,l}=1}^{D} \frac{\alpha _{d,k}}{\lambda _{l,k}} \log q_d \end{aligned}$$

(12)

Before $\lambda _{l,k}$ is sampled, the value of $\alpha _{d,k}$ can be computed and cached. After a new value of $\lambda _{l,k}$ is sampled, $\alpha _{d,k}$ is updated by:

$$\begin{aligned} \alpha _{d,k} \leftarrow \frac{\alpha _{d,k} \lambda '_{l,k}}{\lambda _{l,k}}, ~\forall ~1 \le d \le D : f_{d,l} = 1 \end{aligned}$$

(13)

where $\lambda '_{i,k}$ is the newly sampled value of $\lambda _{i,k}$.

To sample/compute Eqs. (10)–(13), one only iterates over the documents where label l is active (i.e., $f_{d,l}=1$). Thus, the sampling for all $\lambda$ takes ${\mathcal {O}}(D'KL_\mathrm{doc})$ where $D'$ is the average number of documents where a label is active (i.e., the column-wise sparsity of $\mathbf {F}$). It is usually that $D' \ll D$ because if a label exists in nearly all the documents, it provides little discriminative information and can then be neglected. This demonstrates how the sparsity of document meta-information is leveraged. Moreover, sampling all the tables t takes ${\mathcal {O}}(\tilde{N})$ ($\tilde{N}$ is the total number of words in ${\mathcal {D}}$) which can be accelerated with the window sampling technique explained above.

4.2 Sampling Gamma random variable $\delta _{l',k}$

The derivation of sampling $\delta _{l',k}$ is analogous to $\lambda _{l,k}$. Here, we use the same data augmentation methods for re-parameterising the second Beta ratio in Eq. (2), i.e.,

$$\begin{aligned} \prod _{k=1}^{K}\frac{\text{ Beta }_V(\varvec{\beta }_k + \varvec{n}_k)}{\text{ Beta }_V(\varvec{\beta }_k)} =\prod _{k} \frac{\varGamma (\beta _{k,\cdot })}{\varGamma (\beta _{k,\cdot } + n_{k,\cdot })} \prod _{v} \frac{\varGamma (\beta _{k,v} + n_{k,v})}{\varGamma (\beta _{k,v})} \end{aligned}$$

(14)

as

$$\begin{aligned} \prod _{k=1}^{K} \prod _{v=1}^{V} \hat{q}_k^{\beta _{k,v}} \beta _{k,v}^{t'_{k,v}} \end{aligned}$$

(15)

where $\hat{q}_k \sim \text {Be}(\beta _{k,.}, n_{k,.})$ and $t'_{k,v} = \sum _{i=1}^{n_{k,v}} \text {Bern}\left( \frac{\beta _{k,v}}{\beta _{k,v}+i}\right)$. Now, we replace $\beta _{k,v}$ with $\prod _{l'=1}^{L_\mathrm{word}} \delta _{l',k}^{g_{v,l'}}$,

$$\begin{aligned}&\left( \prod _{k=1}^{K} \prod _{v=1}^{V} e^{ -\delta _{l', k} \frac{\beta _{k,v}}{\delta _{l',k}} \log {\frac{1}{\hat{q}_k}}} \right) \left( \prod _{k=1}^{K} \prod _{v=1}^{V} \left( \prod _{l' =1}^{L_\mathrm{word} } \delta _{l',k}^{g_{v,l'}} \right) ^{t'_{k,v}} \right) \\&\quad = \prod _{k=1}^{K} e^{ -\delta _{l', k} \left( \sum _{v=1}^V \frac{\beta _{k,v}}{\delta _{l',k}} \right) \log {\frac{1}{\hat{q}_k}}} \left( \prod _{k=1}^{K} \prod _{l' =1}^{L_\mathrm{word} } \delta _{l',k}^{\sum _{v=1}^{V} g_{v,l'}{t'_{k,v}}} \right) \end{aligned}$$

and then extract all the terms related to $\delta _{l',k}$ in Eq. (15), and add the Gamma prior, we derive the posterior of $\delta _{l',k}$:

We can then sample $\delta _{l',k}$ from a Gamma distribution parameterised with

$$\begin{aligned} \delta _{l',k}\sim & {} \mathrm {Ga}( \nu ', \nu '') \end{aligned}$$

(16)

$$\begin{aligned} \nu '= & {} \nu _0 + \sum _{v=1: g_{v,l'} = 1}^{V} t'_{k,v} \end{aligned}$$

(17)

$$\begin{aligned} \nu ''= & {} \nu _0 - \log \hat{q}_k \sum _{v=1:g_{v,l'}=1}^{V} \frac{\beta _{k,v}}{\delta _{l',k}} \end{aligned}$$

(18)

$\beta _{k,v}$ can be updated in a similar way to $\alpha _{d,k}$, i,e,

$$\begin{aligned} \beta _{k,v} \leftarrow \frac{\beta '_{k,v}\delta '_{l',k}}{\delta _{l',k}}, ~\forall ~1 \le k \le K : g_{v,l'} = 1 \end{aligned}$$

(19)

where $\delta '_{l',k}$ is newly sampled value of $\delta _{l',k}$. Sampling all $\delta$ takes ${\mathcal {O}}(V'KL_\mathrm{word})$ where $V'$ is the average number of tokens where a feature is active (i.e., the column-wise sparsity of $\mathbf {G}$ and usually $V' \ll V$) and sampling all the tables $t'$ takes ${\mathcal {O}}(\tilde{N})$. Figure 3 illustrates the full sampling algorithm.

Fig. 3

Collapsed Gibbs sampling algorithm for MetaLDA

4.3 MetaLDA as a hyper-parameter sampling approach

Besides the observed labels/features associated with the datasets, a default label/feature for each document/word is introduced in MetaLDA, which is always equal to 1. The default can be interpreted as the bias term in $\alpha$/$\beta$, which is supposed to capture the information unrelated to the labels/features. When working without document labels with the default, MetaLDA samples the Dirichlet parameters (i.e., Hyper-parameters of LDA) of the document-topic distributions, $\alpha$, according to the statistics in the target corpus. Similarly, without word features, the Dirichlet parameters of the topic-word distributions, $\beta$, are sampled. We demonstrate this by taking the document-topic distributions as an example.

Now assume each document only has a default label that is always equal to 1, i.e., $f_{d, 0} = 1$ and $f_{d, l} = 0$ for all $l > 0$. According to our construction (Step 1 and 2a), $a_{d, k} = \lambda _{0,k}$ for all the document. In other words, all the documents share the same asymmetric Dirichlet prior on the document-topic distributions ($\varvec{\theta }_d$) which is constructed as follows:

$$\begin{aligned} \alpha _{k}\sim & {} \text {Ga}(\mu _0,\nu _0) \end{aligned}$$

(20)

$$\begin{aligned} \varvec{\theta }_d\sim & {} \text {Dir}_K(\varvec{\alpha }) \end{aligned}$$

(21)

In this case, we can sample $\alpha _k$ as follows:

$$\begin{aligned} \alpha _k\sim & {} \text {Ga}\left( \mu _0 + t_{\cdot ,k}, \mu _0 - \sum _{d=1}^{D} \log q_d\right) \end{aligned}$$

(22)

Alternatively, we can vary MetaLDA to have a symmetric Dirichlet prior:

$$\begin{aligned} \alpha\sim & {} \text {Ga}(\mu _0,\mu _0) \end{aligned}$$

(23)

$$\begin{aligned} \varvec{\theta }_d\sim & {} \text {Dir}_K(\alpha ,\ldots ,\alpha ) \end{aligned}$$

(24)

In this case, we can sample $\alpha$ as follows:

$$\begin{aligned} \alpha\sim & {} \text {Ga}\left( \mu _0 + t_{\cdot ,\cdot }, \mu _0 - \sum _{d=1}^{D} \log q_d\right) \end{aligned}$$

(25)

Discussed in [6, 33], sampling the Dirichlet priors can gain significant performance improvement in topic models. In the case where document labels/word features are not used, MetaLDA offers an alternative hyper-parameter sampling approach to the methods such as fixed-point iterations [24] and Newton–Raphson [32]. These methods use MAP to optimise the hyper-parameters while ours uses MCMC sampling. We would like to point out that MetaLDA’s sampling of symmetric Dirichlet prior is similar to the approach introduced in [31]. However the sampling of asymmetric prior was not considered in [31]. Compared with the built-in hyper-parameter sampling methods in Mallet² which are based on histograms of the statistics, our approach is more robust in the case where the statistics are not sufficient (e.g., short texts). This is further discussed with experiments in Sect. 5.4.3.

5 Experiments

In this section, we evaluate the proposed MetaLDA against several recent alternatives that also incorporate meta-information, using 6 real datasets including both regular and short texts. We will focus on the evaluation of

• the modelling accuracy of MetaLDA in terms of perplexity, a standard measure used in topic modelling. The goal is to study how the meta-information contributes to the predictive likelihood of unseen documents.

• the quality of topics learned by MetaLDA. It is interesting to see whether or not the meta-information will positively affect the topic coherence. We will report both quantitative and qualitative analyses.

• the running time of MetaLDA. The introduction of meta-information increases the modelling complexity to some extend. However, as we discussed in previous sections, MetaLDA can benefit from the local conjugacy given by the data augmentation methods, and also be parallelised using the same distributed framework [25] in Mallet. Therefore, we will empirically study the efficiency of MetaLDA.

Besides, we will also study how word embeddings learnt by different techniques affect both perplexity and topic coherence.

5.1 Datasets

In the experiments, we used three regular and three short text datasets, which are as follows:

• Reuters is a widely used corpus extracted from the Reuters-21578 dataset where documents without any labels are removed.³ There are 11,367 documents and 120 labels. Each document is associated with multiple labels. The vocabulary size is 8817, and the average document length is 73.

• 20NG 20 Newsgroups is a widely used dataset consists of 18,846 news articles with 20 categories. The vocabulary size is 22,636 and the average document length is 108.

• NYT New York Times is extracted from the documents in the category “Top/News/Health” in the New York Times Annotated Corpus.⁴ There are 52,521 documents and 545 unique labels. Each document is with multiple labels. The vocabulary contains 21,421 tokens, and there are 442 words in a document on average.

• WS Web Snippets, used in [17], contains 12,237 web search snippets and each snippet belongs to one of 8 categories. The vocabulary contains 10,052 tokens, and there are 15 words in one snippet on average.

• TMN Tag My News, used in [26], consists of 32,597 English RSS news snippets from Tag My News. With a title and a short description, each snippet belongs to one of 7 categories. There are 13,370 tokens in the vocabulary, and the average length of a snippet is 18.

• AN ABC News, is a collection of 12,495 short news descriptions and each one is in multiple of 194 categories. There are 4255 tokens in the vocabulary, and the average length of a description is 13.

All the datasets were tokenised by Mallet (see footnote 2) and we removed the words that exist in less than 5 documents and more than 95% of the documents.

5.2 Meta-information settings

At the document level, the labels associated with documents in each dataset were used as the meta-information. At the word level, we used a set of binarised word embeddings as word features (see footnote 3), which are obtained from real-valued word embeddings such as GloVe or word2vec. To binarise word embeddings, we first adopted the following method similar to [11]:

$$\begin{aligned} g'_{v,j} = {\left\{ \begin{array}{ll} 1, &{} \text {if}\ g''_{v,j} > \text {Mean}_{+}(\varvec{g}''_{v}) \\ -\,1, &{} \text {if}\ g''_{v,j} < \text {Mean}_{-}(\varvec{g}''_{v}) \\ 0, &{} \text {otherwise} \end{array}\right. } \end{aligned}$$

(26)

where $\varvec{g}''_{v}$ is the original embedding vector for word v, $g'_{v,j}$ is the binarised value for jth element of $\varvec{g''_{v}}$, and $\text {Mean}_{+}(\cdot )$ and $\text {Mean}_{-}(\cdot )$ are the average value of all the positive elements and negative elements, respectively.

The insight is that we only consider features with strong opinions (i.e., large positive or negative value) on each dimension. To transform $g' \in \{-\,1,1\}$ to the final $g \in \{0,1\}$, we use two binary bits to encode one dimension of $g'_{v,j}$: the first bit is on if $g'_{v,j} = 1$ and the second is on if $g'_{v,j} = -\,1$. This means that if the original embeddings are 100-dimensional, the binarised embeddings will be with 200 dimensions. In our experiments, we also tried some other word embedding binarisation methods including the one in [10]. However, the performance with those binarisation methods is not comparable with the one we proposed above. Therefore, the experimental results with different binarisation methods will not be reported.

In the perplexity and topic coherence evaluation, i.e., Sects. 5.4 and 5.5, we will use the 50-dimensional GloVe word embeddings pre-trained on Wikipedia⁵ as the source of word features. We then study how different word embedding sources influence the performance of our model in Sect. 5.6. It is noteworthy that MetaLDA can also work with other word features such as semantic similarity.

5.3 Compared models and parameter settings

We evaluate the performance of the following models:

• MetaLDA and its variants: the proposed model and its variants. Here we use MetaLDA to indicate the model considering both document labels and word features. Several variants of MetaLDA with document labels and word features separately were also studied, which are shown in Table 3. These variants differ in the method of estimating ${\varvec{\alpha }}$ and $\varvec{\beta }$. All the models listed in Table 3 were implemented on top of Mallet. The hyper-parameters $\mu _0$ and $\nu _0$ were set to 1.0.

• LDA [4]: the baseline model. The Mallet implementation of SparseLDA [38] is used.

• LLDA, Labelled LDA [29] and PLLDA, Partially Labelled LDA [30]: two models that make use of multiple document labels. The original implementation⁶ is used.

• DMR, LDA with Dirichlet Multinomial Regression [23]: a model that can use multiple document labels. The Mallet implementation of DMR based on SparseLDA was used. Following Mallet, we set the mean of $\lambda$ to 0.0 and set the variances of $\lambda$ for the default label and the document labels to 100.0 and 1.0, respectively.

• WF-LDA, Word Feature LDA [28]: a model with word features. We implemented it on top of Mallet and used the default settings in Mallet for the optimisation.

• LF-LDA, Latent Feature LDA [26]: a model that incorporates word embeddings. The original implementation⁷ was used. Following the original paper, we used 1500 and 500 MCMC iterations for initialisation and sampling, respectively, and set $\lambda$ to 0.6, and used the original 50-dimensional GloVe word embeddings as word features.

• GPU-DMM, Generalized Pólya Urn DMM [17]: a model that incorporates word semantic similarity. The original implementation⁸ was used. The word similarity was generated from the distances of the word embeddings. Following the original paper, we set the hyper-parameters $\mu$ and $\epsilon$ to 0.1 and 0.7, respectively, and the symmetric document Dirichlet prior to 50 / K.

• PTM, Pseudo document based Topic Model [46]: a model for short text analysis. The original implementation⁹ was used. Following the paper, we set the number of pseudo-documents to 1000 and $\lambda$ to 0.1.

Table 3 MetaLDA and its variants

Table 4 Summary of the compared models

All the models, except where noted, the symmetric parameters of the document and the topic Dirichlet priors were set to 0.1 and 0.01, respectively, and 2000 MCMC iterations are used to train the models. We summarise the compared models in terms of their usage of meta-information in Table 4.

5.4 Perplexity evaluation

Perplexity is a measure that is widely used [33] to evaluate the modelling accuracy of topic models. The lower the score, the higher the modelling accuracy. To compute perplexity, we randomly selected some documents in a dataset as the training set and the remaining as the test set. We first trained a topic model on the training set to get the word distributions of each topic k ($\varvec{\phi }_k^\mathrm{train}$). Each test document d was split into two halves containing every first and every second word, respectively. We then fixed the topics and trained the models on the first half to get the topic proportions ($\varvec{\theta }_d^\mathrm{test}$) of test document d and compute perplexity for predicting the second half. With regard to MetaLDA, we fixed the matrices $\mathbf {\Phi }^\mathrm{train}$ and $\mathbf {\Lambda }^\mathrm{train}$ output from the training procedure. On the first half of test document d, we computed the Dirichlet prior $\varvec{\alpha }_d^\mathrm{test}$ with $\mathbf {\Lambda }^\mathrm{train}$ and the labels $\varvec{f}_d^\mathrm{test}$ of test document d (See Step 2a), and then point-estimated $\varvec{\theta }_d^\mathrm{test}$. We ran all the models 5 times with different random number seeds and report the average scores and the standard deviations.

In testing, we may encounter words that never occur in the training documents (a.k.a., unseen words or out-of-vocabulary words). There are two strategies for handling unseen words for calculating perplexity on test documents: ignoring them or keeping them in computing the perplexity. Here we investigate both strategies:

5.4.1 Perplexity computed without unseen words

In this experiment, the perplexity is computed only on the words that appear in the training vocabulary. Here we used 80% documents in each dataset as the training set and the remaining 20% as the test set.

Table 5 Perplexity comparison on the regular text datasets

Table 6 Perplexity comparison without unseen words on the short text datasets. The best results are highlighted in boldface

Tables 5 and 6 show¹⁰ the average perplexity scores with standard deviations for all the models. Note that: (1) The scores on AN with 150 and 200 topics are not reported due to overfitting observed in all the compared models. (2) Given the size of NYT, the scores of 200 and 500 topics are reported. (3) The number of latent topics in LLDA must equal to the number of document labels. (4) For PLLDA, we varied the number of topics per label from 5 to 50 (2 and 5 topics on NYT). The total number of topics used by PPLDA is the product of the number of labels and the number of topics per label.

The results show that the proposed MetaLDA outperformed all the competitors in terms of perplexity on nearly all the datasets, showing the benefit of using both document and word meta-information. Specifically, we have the following remarks:

• By looking at the models using only the document-level meta-information, we can see the significant improvement of these models over LDA, which indicates that document labels can play an important role in guiding topic modelling. Although the performance of the two variants of MetaLDA with document labels and DMR is comparable, our models run much faster than DMR, which will be studied later in Sect. 5.8.

• It is interesting that PLLDA with 50 topics for each label has better perplexity than MetaLDA with 200 topics in the 20NG dataset. With the 20 unique labels, the actual number of topics in PLLDA is 1000. However, if 10 topics for each label in PLLDA are used, which is equivalent to 200 topics in MetaLDA, PLLDA is outperformed by MetaLDA significantly.

• At the word level, MetaLDA-def-wf performed the best among the models with word features only. Moreover, our model has a clear advantage in running speed (see Table 13). Furthermore, comparing MetaLDA-def-wf with MetaLDA-def-def and MetaLDA-0.1-wf with LDA, we can see using the word features indeed improved perplexity.

• The scores show that the improvement gained by MetaLDA over LDA on the short text datasets is larger than that on the regular text datasets. This is expected because meta-information serves as complementary information in MetaLDA and can have significant impact when the data is sparse.

• It can be observed that models usually gained improved perplexity, if the Dirichlet parameter $\alpha$ is sampled/optimised, in line with [33]. We further study this in Sect. 5.4.3.

• On the AN dataset, there is no statistically significant difference between MetaLDA and DMR. On NYT, a similar trend is observed: the improvement in the models with the document labels over LDA is obvious but not in the models with the word features. Given the number of the document labels (194 of AN and 545 of NYT), it is possible that the document labels already offer enough information and the word embeddings have little contribution in the two datasets.

5.4.2 Perplexity computed with unseen words

To test the hypothesis that the incorporation of meta-information in MetaLDA can significantly improve the modelling accuracy in the cases where the corpus is sparse, we varied the proportion of documents used in training from 20 to 80% and used the remaining for testing. It is natural that when the proportion is small, the number of unseen words in testing documents will be large. Instead of simply excluding the unseen words in the previous experiments, here we compute the perplexity with unseen words for LDA, DMR, WF-LDA and the proposed MetaLDA. For perplexity calculation, $\phi ^\mathrm{test}_{k,v}$ for each topic k and each token v in the test documents is needed. If v occurs in the training documents, $\phi ^\mathrm{test}_{k,v}$ can be directly obtained. While if v is unseen, $\phi ^\mathrm{unseen}_{k,v}$ can be estimated by the prior:

$$\begin{aligned} \frac{\beta ^\mathrm{unseen}_{k,v}}{n^\mathrm{train}_{k,\cdot } + \beta ^\mathrm{train}_{k,\cdot } + \beta ^\mathrm{unseen}_{k,\cdot }}\,. \end{aligned}$$

For LDA and DMR which do not use word features, $\beta ^\mathrm{unseen}_{k,v} = \beta ^\mathrm{train}_{k,v}$; For WF-LDA and MetaLDA which are with word features, $\beta ^\mathrm{unseen}_{k,v}$ is computed with the features of the unseen token. Following Step 1c, for MetaLDA, $\beta ^\mathrm{unseen}_{k,v} = \prod _{l'}^{L_\mathrm{word}} \delta _{l',k}^{g^\mathrm{unseen}_{v,l}}$.

Figure 4 shows the perplexity scores on Reuters, 20NG, TMN and WS with 200, 200, 100 and 50 topics, respectively. MetaLDA outperformed the other models significantly with a lower proportion of training documents and relatively higher proportion of unseen words. The gap between MetaLDA and the other three models increases while the training proportion decreases. It indicates that the meta-information helps MetaLDA to achieve better modelling accuracy on predicting unseen words.

Fig. 4

Perplexity comparison with unseen words in different proportions of the training documents. Each pair of the numbers on the horizontal axis are the proportion of the training documents and the proportion of unseen tokens in the vocabulary of the test documents, respectively. For each setting, the four coloured bars from left to right correspond to LDA, WF-LDA, DMR and MetaLDA. The error bars are the standard deviations over 5 runs. a Reuters with 200 topics, b 20NG with 200 topics, c TMN with 100 topics, d WS with 50 topics

5.4.3 Perplexity evaluation for using MetaLDA as a hyper-parameter sampling approach

We further study how MetaLDA performs in terms of perplexity when used as a hyper-parameter sampling approach without meta-information. The experimental settings are the same as the ones used in Sect. 5.4.1. Table 7 shows the results of different variants of MetaLDA on hyper-parameter sampling. We would like to point out that MetaLDA-0.1-asym is equivalent to MetaLDA-0.1-def, MetaLDA-asym-0.01 is equivalent to MetaLDA-def-0.01, and MetaLDA-asym-asym is equivalent to MetaLDA-def-def in Table 3. Here we use the former to make the comparison clear. We have the following observations:

• In general, the best perplexity score is derived with the use of both asymmetric $\alpha$ and asymmetric $\beta$.

• If we fix the setting for the topic side and vary the setting for the document side (for example, compare MetaLDA-0.1-0.01, MetaLDA-sym-0.01 and MetaLDA-asym-0.01), we can derive that 1) the use of sampled priors (either symmetric or asymmetric) can significantly lower the perplexity scores, This is in line with the findings in [33]; 2) using asymmetric prior can further decrease perplexity.

• Similarly, fixing the setting for the document side and varying the setting for the topic side (for example, comparing MetaLDA-sym-0.01, MetaLDA-sym-sym and MetaLDA-sym-asym), we found that sampling either symmetric or asymmetric prior on per-topic word distributions does not significantly affect the perplexity scores, which also complies with [33]. However, there is a subtle difference: for our method an asymmetric prior on per-topic word distributions is marginally better, whereas it is often worse in [33].

• Now comparing the last row in Table 7 with the corresponding results in Tables 5 and 6 shows that constructing the priors with meta-information can further decrease the perplexity scores, which further proves our assumption that it is beneficial to use meta-information in topic modelling.

Table 7 Perplexity on 20NG with 200 topics, Reuters with 200 topics, WS with 100 topics

Table 8 Topic coherence (NPMI) on the short text datasets

5.5 Topic coherence evaluation

We further evaluate the semantic coherence of the words in a topic learnt by LDA, PTM, DMR, LF-LDA, WF-LDA, GPU-DMM and MetaLDA. Here we use the normalised point-wise mutual information (NPMI) [1, 16] to calculate topic coherence score for topic k with top T words:

$$\begin{aligned} \text {NPMI}(k) = \sum _{j=2}^{T} \sum _{i = 1}^{j-1} \log \frac{p(w_{j},w_{i})}{p(w_j)p(w_i)}/-\log p(w_j, w_i), \end{aligned}$$

where $p(w_i)$ is the probability of word i, and $p(w_i,w_j)$ is the joint probability of words i and j that co-occur together within a sliding window. Those probabilities were computed on an external large corpus, i.e., a 5.48 GB Wikipedia dump in our experiments. The NPMI score of each topic in the experiments is calculated with top 10 words ($T=10$) by the Palmetto package.¹¹ Again, we report the average scores and the standard deviations over 5 random runs.

It is known that conventional topic models directly applied to short texts suffer from low quality topics, caused by the insufficient word co-occurrence information. Here we study whether or not the meta-information helps MetaLDA improve topic quality, compared with other topic models that can also handle short texts. Table 8 shows the NPMI scores on the three short text datasets. Higher scores indicate better topic coherence. All the models were trained with 100 topics. Besides the NPMI scores averaged over all the 100 topics, we also show the scores averaged over top 20 topics with highest NPMI, where “rubbish” topics are eliminated, following [37]. It is clear that MetaLDA performed significantly better than all the other models in WS and AN dataset in terms of NPMI, which indicates that MetaLDA can discover more meaningful topics with the document and word meta-information. We would like to point out that on the TMN dataset, even though the average score of MetaLDA is still the best, the score of MetaLDA overlaps with the others’ when allowing for standard deviation, which indicates the difference is not statistically significant.

5.6 Changing word embeddings

In the above experiments, we used the binarised 50-dimensional GloVe embeddings as word features to demonstrate the superiority of MetaLDA over all the other competitors. It is also interesting to study how the performance of MetaLDA changes while we use different word embeddings. In this set of experiments, we varied the sources (i.e., the methods used to train the word embeddings) as well as the dimensions of those word embeddings. Here we used the embeddings pre-trained by three methods: GloVe, SkipGram¹² and CBOW [20].$^{12}$ For each word embedding method, 50 and 100 dimensional embeddings were used.

Tables 9 and 10 show the perplexity and topic coherence performance of MetaLDA, respectively, on the WS and TMN datasets. We followed the experiment settings used in the previous sections, except for the word features. MetaLDA work marginally better with GloVe embeddings than with word2vec embeddings. However, the difference is not significant, given the standard errors. The reasons might be:

• 1. The binarisation could water down the differences between word embeddings. Therefore, minor differences in word embedding might not significantly influence the performance. But it is interesting to develop a model that can directly utilise the real-valued word embeddings.

• 2. Using the embeddings as the prior information could make MetaLDA insensitive to the quality of binarised word embeddings.

Table 9 Perplexity comparison for MetaLDA with different word embeddings on WS and TMN

Table 10 Topic coherence (NPMI) comparison for MetaLDA with different word embeddings on WS and TMN

Table 11 Top 5 related topics of the document labels in the WS dataset with 100 topics

Table 12 Top 3 related labels of the topics in the WS dataset with 100 topics

5.7 Qualitative analysis

Now we show that besides better quantitative performance, MetaLDA with meta-information also allows more informative and interesting interpretation of the discovered topics.

As discussed in Sect. 3, the latent variable $\lambda _{l,k}$ is the weight measuring the association between document label l and topic k. Each label can be interpreted as an unnormalised mixture of topics, represented by a K-dimensional vector $\varvec{\lambda }_{l}$. Therefore, similar to finding the top words for each topic, ranking $\lambda _{l,k}$ can give us the most related topics for each label. Table 11 shows the top 5 related topics among 100 discovered by MetaLDA for the 9 document labels in the WS dataset. For each topic, the top 5 words (ranked with $\phi _{k,v}$) are listed. The results show that the topics are closely related to the labels. For example, the top 5 topics for the “Computers” category describe hardware, software, internet, and system, which are different aspects of computers. The “Sports” category broadly covers football, rugby, tennis, golf, cricket, etc. The major topics discussed in the “Health” related documents include diet, infectious diseases, lung cancer and its causes, and so on.

Furthermore, MetaLDA can also automatically assign the labels to the latent topics, which is known as automatic topic labelling [15]. The method proposed in [15] generates label from the top-ranked topic terms and the titles of Wikipedia articles containing these terms. It is an ad hoc process. In contrast, MetaLDA automatically learns the association between the document labels and the latent topics via the association matrix $\varvec{\lambda }$. Specifically, for each topic k, we rank the labels according the weight $\lambda _{l,k}$, and then retrieve the most likely labels for each topic. Table 12 shows some examples derived one the WS dataset. For instance, topic 46 is about web programming. The most probable label for this topic assigned by MetaLDA is “Computers”. The second and third probable labels are also very related to this topic. Topic 17 is about movies, and the most probable label found by MetaLDA is “Culture&Arts&Entertainment”. It is clear that topics and their most probable labels are well correlated. All these findings demonstrate that MetaLDA is able to discover meaningful topics and label the topics automatically.

Table 13 Running time (seconds per iteration) on 80% documents of each dataset

5.8 Running time

In this section, we empirically study the efficiency of the models in term of per-iteration running time. The implementation details of our MetaLDA are as follows:

• The SparseLDA framework [38] reduces the complexity of LDA to be sub-linear by breaking the conditional of LDA into three “buckets”, where the “smoothing only” bucket is cached for all the documents and the “document only” bucket is cached for all the tokens in a document. We adopted a similar strategy when implementing MetaLDA. When only the document meta-information is used, the Dirichlet parameters $\alpha$ for different documents in MetaLDA are different and asymmetric. Therefore, the “smoothing only” bucket has to be computed for each document, but we can cache it for all the tokens, which still gives us a considerable reduction in computing complexity. However, when the word meta-information is used, the SparseLDA framework no longer works in MetaLDA as the $\beta$ parameters for each topic and each token are different.

• By adapting the Distributed framework in [25], our MetaLDA implementation runs in parallel with multiple threads, which makes MetaLDA able to handle larger document collections. The parallel implementation was tested on the NYT dataset.

Fig. 5

MetaLDA’s running time (seconds per iteration) on the NYT dataset with 500 topics with different proportions of training documents and different number of threads

The per-iteration running time of all the models is shown in Table 13. Note that:

• On the Reuters and WS datasets, all the models ran with a single thread on a desktop PC with a 3.40 GHz CPU and 16 GB RAM.

• Due to the size of NYT, we report the running time for the models that are able to run in parallel. All the parallelised models ran with 10 threads on a cluster with a 14-core 2.6 GHz CPU and 128 GB RAM.

• All the models were implemented in JAVA.

• As the models with meta-information add extra complexity to LDA, the per-iteration running time of LDA can be treated as the lower bound.

At the document level, both MetaLDA-df-0.01 and DMR use priors to incorporate the document meta-information and both of them were implemented in the SparseLDA framework. However, our variant is about 6 to 8 times faster than DMR on the Reuters dataset and more than 10 times faster on the WS dataset. Moreover, it can be seen that the larger the number of topics, the faster our variant is over DMR. At the word level, similar patterns can be observed: our MetaLDA-0.1-wf ran significantly faster than WF-LDA and LF-LDA especially when more topics are used (20–30 times faster on WS). It is not surprising that GPU-DMM has comparable running speed with our variant, because only one topic is allowed for each document in GPU-DMM. With both document and word meta-information, MetaLDA still ran several times faster than DMR, LF-LDA, and WF-LDA. On NYT with the parallel settings, MetaLDA maintains its efficiency advantage as well.

To further examine our model’s scalability, we report the per-iteration running time of MetaLDA on NYT with 500 topics in Fig. 5. For this, we varied the proportion of training documents from 20 to 80% as well as the number of threads from 1 to 8. For the single thread version, when the training proportions change from 40 to 80% the per-iteration running time becomes 4 times slower. However, with multi-threading, our model scales much better. The per-iteration running time is only doubled while the training proportions quadruple. In terms of speed-up, the per-iteration running time increases nearly linearly with the number of threads. For example, given 60% training data, the per-iteration running time is reduced to half while the number of thread doubles.

6 Conclusion

In this article, we have presented a topic modelling framework named MetaLDA that can efficiently incorporate document and word meta-information. This results in a significant improvement over other models in terms of perplexity and topic quality. With two data augmentation techniques, MetaLDA enjoys full local conjugacy, allowing efficient Gibbs sampling, demonstrated by superiority in the per-iteration running time. MetaLDA$^{1}$ has been implemented within Mallet using the DistributedLDA framework, and works efficiently in a multicore context. Furthermore, without losing generality, MetaLDA can work with both regular texts and short texts. The improvement of MetaLDA over other models that also use meta-information is remarkable, particularly when the word-occurrence information is insufficient. Moreover, MetaLDA efficiently demonstrates that asymmetric-asymmetric LDA does beat regular symmetric LDA.

MetaLDA takes a particular approach for incorporating meta-information on topic models. However, the approach is general enough to be applied to other Bayesian probabilistic models that go beyond topics modelling, such as multi-label learning with sparse features [43]. Moreover, it would be interesting to extend our method to use real-valued meta-information directly without binarisation [41], which is the subject of future work.