Community-preserving anonymization of graphs

Abstract

In this paper, we propose a novel edge modification technique that better preserves the communities of a graph while anonymizing it. By maintaining the core number sequence of a graph, its coreness, we retain most of the information contained in the network while allowing changes in the degree sequence, i. e. obfuscating the visible data an attacker has access to. We reach a better trade-off between data privacy and data utility than with existing methods by capitalizing on the slack between apparent degree (node degree) and true degree (node core number). Our extensive experiments on six diverse standard network datasets support this claim. Our framework compares our method to other that are used as proxies for privacy protection in the relevant literature. We demonstrate that our method leads to higher data utility preservation, especially in clustering, for the same levels of randomization and k-anonymity.

1 Introduction

Data mining relies on a great set of tools and techniques to mine the vast amount of data that is available today to extract actionable patterns and gain insights on somebody’s records. However, these data often contain personal and private information about users and individuals. Privacy, particularly in the social web, is not just a nice to have but a requirement, particularly in the context of new laws of the European Union [26]. Data anonymization can be seen as a proxy for privacy protection and this is the assumption we also made in our work. For relational data, basic anonymization procedures such as removing names or other key identifiers are not sufficient to prevent an attacker from re-identifying users, leaving the resulting anonymized information still too sensitive to be released. For example, consider a company that wishes to share its social network with the research community for further analysis while preserving the privacy its users are entitled to. Releasing the network in the form of a graph with anonymized node labels would not be sufficient since it would still be possible to re-identify some nodes very quickly and from them most of the network [3, 28, 41], i. e. celebrities with a high and unique node degree in the case of Twitter for instance.

In order to overcome this issue, methods that add noise to the original data have been developed to hinder the re-identification processes. But the noise introduced by the anonymization steps may also affect the data, reducing its utility for subsequent data mining processes. Usually, the larger the data modification, the harder the re-identification but also the less the data utility. Therefore, it is necessary to preserve the integrity of the data (in the sense of retaining the information that we want to mine) to ensure that the data mining step is not altered by the anonymization step. Among other things, for the anonymization step to be considered any useful and thus valid, the analysis performed on the obfuscated data should produce results as close as possible to the ones the original data would have led to. A trade-off between data privacy and data utility must be reached and it is in this spirit that we developed our proposed edge modification technique.

In the rest of the paper, we only consider the case of graph anonymization. Graphs are ubiquitous and more and more data are in that form or can be represented as such. Therefore, the restriction is only partial and it allows us to focus the literature review and the datasets used in the experiments. Graph modification approaches anonymize a network by modifying (adding and/or deleting) edges or nodes. There exist two main approaches in the literature [33]: Firstly, random perturbation of the graph structure by randomly adding/removing/switching edges (often referred to as edge randomization). Secondly, constrained perturbation of the graph structure via sequential edge modifications in order to fulfill some desired constraints. For instance, k-degree anonymity-based approaches modify the graph structure so that every node is in the end indistinguishable from $k-1$ other nodes (in terms of node degree).

1.1 Highlights

In this work,¹ we explore the idea of coreness-preserving edge modification. Modifying edges is the building block of graph anonymization. And here, instead of doing it at random, we propose to only modify an edge when it does not change the core numbers of both its endpoints and, by extension, the whole core number sequence of a graph. By doing so, we preserve better the underlying graph structure, retaining more data utility than in the random case while still altering the node degrees, hindering the re-identification process and thus achieving a certain level of privacy. Here are the highlights of our work:

• We propose a novel edge modification technique that better preserves the communities of a graph while anonymizing it.

• We specify coreness-preserving algorithms for all four standard edge modification operations: deletion, addition, rotation and switch. We also discuss their time complexity.

• We empirically show that our methods achieve a better trade-off between data utility and data privacy than existing edge modification operations in terms of generic graph properties and real clustering applications.

• We empirically show that our edge modification technique is still able to deal with very large networks with thousands and millions of vertices and edges.

• We conduct a theoretical and empirical analysis of re-identification and risk assessment on our proposed coreness-preserving methods.

1.2 Outline

The rest of the paper is organized as follows. Section 2 provides a review of the related work. Section 3 defines the preliminary concepts our work is based upon. Section 4 introduces the proposed approach that randomly anonymizes a graph while preserving its coreness. Section 5 presents the experimental results we obtained on several network datasets considering both random and constrained graph perturbations. Section 6 discusses re-identification and risk assessment. Finally, Sect. 7 concludes our paper and mentions future work directions.

2 Related work

In this section, we present the related work published in the areas of graph anonymization and graph degeneracy. Our coreness-preserving edge modification operations are based on graph degeneracy principles and can be applied on any edge modification algorithm, based on random or constrained perturbation.

2.1 Graph anonymization

To preserve the privacy of the data contained in a graph, the most common way to do so is through anonymization, process that can be fully random or subject to constraints.

Randomization methods are based on introducing random noise in the original data. For graphs, there are two main approaches: (a) Rand Add/Del that randomly adds and deletes edges from the original graph (this strategy keeps the number of edges) and (b) Rand Switch that exchanges edges between pairs of nodes (this strategy keeps the degree of all nodes and a fortiori the number of edges). Naturally, edge randomization can also be considered as an additive-noise perturbation. Hay et al. [21] proposed a method to anonymize unlabeled graphs called Random Perturbation, which is based on removing p edges from the graph and then adding p false edges, all at random. Ying and Wu [38] proposed variants that preserve the spectral properties of the original graph. Ying et al. [37] suggested a variant of Rand Add/Del that divides the graph into blocks according to the degree sequence and performs modifications at random per block and not over the entire set of nodes. Nevertheless, it involves higher risk of re-identification.

Another widely adopted strategy for graph modification approaches consists of edge addition and deletion to meet desired constraints, usually to achieve a certain level of privacy. For instance, take the k-anonymity concept that was introduced by Sweeney [32] for the privacy preservation on relational data. It states that an attacker cannot distinguish among k different records although he managed to find a group of quasi-identifiers. Consequently, the attacker cannot re-identify an individual with a probability greater than 1 / k. The k-anonymity model can be applied using different concepts when dealing with networks rather than relational data like in our case. A widely used option is to consider the node degree as a quasi-identifier, which corresponds to k-degree anonymity. It is based on modifying the network structure (by adding and removing edges) to ensure that all nodes satisfy this condition. In other words, the main objective is that for every node in the graph, there are at least $k-1$ other nodes with the same degree. Liu and Terzi [25] developed a method which, given a network ${\mathcal {G}} = ({\mathcal {V}}, {\mathcal {E }})$ and an integer k, finds a k-degree anonymous network $\widetilde{{\mathcal {G}}} = ({\mathcal {V}}, \widetilde{{\mathcal {E }}})$ where ${\mathcal {E }} \cap \widetilde{{\mathcal {E }}} \approx {\mathcal {E }}$, trying to minimize the number of changes on edges. Other authors considered the 1-neighborhood subgraph of the objective nodes as quasi-identifiers (k-neighborhood anonymity) [41], all structural information about a target node (k-automorphism) [42] or generic queries (k-candidate anonymity) [20].

2.2 Graph degeneracy

The idea of a k-degenerate graph comes from the work of Bollobs [7, p. 222] that was further extended by Seidman [31] into the notion of a k-core, which explains the use of degeneracy as an alternative denomination for k-core in the literature. Henceforth, we will be using the two terms interchangeably. Baur et al. [5] proposed the first graph generator with predefined k-core structure. In a sense, their idea is similar to ours since their generator tries to maintain the k-core decomposition of an original graph while perturbing it. However, the edge modification operations considered are too restrictive for anonymization and actually flawed as we will see in Sect. 4.6. In a previous work [14], we capitalized on graph degeneracy for generalization of social networks, another type of anonymization with different applications. Alternatively, Assam et al. [2] proposed to use the concept from an attacker’s perspective in the context of structural anonymization of networks.

3 Preliminary concepts

In this section, we define the preliminary concepts upon which our work is built: the notion of graph, degeneracy and edge modification.

3.1 Graph

Let ${\mathcal {G}} = ({\mathcal {V}}, {\mathcal {E }})$ be a graph (also known as a network), ${\mathcal {V}}$ its set of vertices (also known as nodes) and ${\mathcal {E }}$ its set of edges (also known as arcs or links). By abusing the notation, when considering nodes from a graph, we will write $v \in {\mathcal {G}}$ rather than $v \in {\mathcal {V}}$. We denote by n the number of vertices ($n = |{\mathcal {V}}|$) and m the number of edges ($m = |{\mathcal {E }}|$).

3.1.1 Apparent degree

In our work, we considered undirected and unweighted edges, which represent relationships between entities that are bidirectional and independent of their strength (e.g., being friend on Facebook). In this context, we can define the degree of a vertex v in a graph ${\mathcal {G}}$ as the number of adjacent nodes and denoted by $deg_{{\mathcal {G}}}(v)$. Hereinafter, we will refer to it as the apparent degree because it represents the total number of neighbors a node has in a network but is usually an overestimation of the number of true relations. In the case of a social network, not all of someone’s connections are truly his friends but sometimes just acquaintances and intuitively, we might be more interested in mining information about his friends rather than all his connections.

3.2 Degeneracy

The concept of degeneracy for a graph was first introduced by Seidman [31] along with a description of its use as a graph decomposition technique.

3.2.1 k-core and main core

Let k be an integer. A subgraph ${\mathcal {H}}_k = ({\mathcal {V}}', {\mathcal {E }}')$, induced by the subset of vertices ${\mathcal {V}}' \subseteq {\mathcal {V}}$ (and a fortiori by the subset of edges ${\mathcal {E }}' \subseteq {\mathcal {E }}$), is called a k-core or a core of order k iff $\forall v \in {\mathcal {V}}',\ deg_{{\mathcal {H}}_k}(v) \ge k$ and ${\mathcal {H}}_k$ is the maximal subgraph with this property, i. e. it cannot be augmented without losing this property. In other words, the k-core of a graph corresponds to the maximal subgraph whose vertices are at least of degree k within the subgraph. The core of maximum order, i. e. the largest k such that the remaining subgraph is non-empty, is called the main core.

3.2.2 k-shell

From the k-core, we can then define the notion of k-shell [9], denoted by ${\mathcal {S}}_k$, which corresponds to the subset of vertices that belong to the k-core but not the $(k+1)$-core such that ${\mathcal {S}}_k = \{v \in {\mathcal {G}}\ |\ v \in {\mathcal {H}}_k \wedge v \notin {\mathcal {H}}_{k+1}\}$.

3.2.3 Core number, shell index and true degree

The core number of a vertex v is the highest order of a core that contains this vertex and denoted by core(v). It is also referred as the shell index since the k-shell is exactly the part of the k-core that will not survive in the $(k+1)$-core. We claim that it represents the true degree of a node as opposed to its apparent degree. Basically, its value corresponds to how cohesive one’s neighborhood is and is a measure of user engagement in a network [27]. Indeed, to belong to a k-core, a node needs at least k neighbors also meeting the same requirements, thus forming a community of “close” nodes. Again, in the case of a social network, the core number of a node would correspond to the number of close friends the user has, his inner circle that would collapse if he were to leave (through the cascading effect implied by the k-core condition—see the impact of the removal of node D in the black 3-shell of Fig. 1 for instance).

Fig. 1

Illustration of a graph ${\mathcal {G}}$ and its decomposition in k-shells. Node color indicates the set a vertex belongs to: white for the 0-shell, light gray for the 1-shell, dark gray for the 2-shell and black for the 3-shell. Node shape indicates whether the vertex belongs to a k-corona (square) or a k-lamina (disk)

3.2.4 k-corona, k-lamina and effective degree

Goltsev et al. [18] defined the k-corona as the subset of vertices from the k-shell with exactly k neighbors, denoted by ${\mathcal {C}}_k$ hereinafter. For our work, we introduce two novel notions: (1) the k-lamina ² defined as the subset of vertices from the k-shell with more than k neighbors and denoted by ${\mathcal {L}}_k$ ($= {\mathcal {S}}_k {\setminus } {\mathcal {C}}_k$); and (2) the effective degree defined as the degree of a node v in the last core it belongs to, denoted by $ef\_deg_{{\mathcal {G}}}(v)$ such that $\forall v \in {\mathcal {S}}_k,\ ef\_deg_{{\mathcal {G}}}(v) = deg_{{\mathcal {H}}_k}(v)$. It follows that ${\mathcal {C}}_k = \{v \in {\mathcal {S}}_k\ |\ core(v) = ef\_deg_{{\mathcal {G}}}(v)\}$ and ${\mathcal {L}}_k = \{v \in {\mathcal {S}}_k\ |\ core(v) < ef\_deg_{{\mathcal {G}}}(v)\}$.

3.2.5 Coreness

The coreness is defined³ as the set of vertices and their associated core numbers. By analogy with the degree sequence, it is also referred as the core number sequence even though in both cases there are no specific ordering over the vertices. Hence, a coreness-preserving graph modification approach means a technique that alters the network without changing the core number of any node of the graph.

3.2.6 Illustration

Figure 1 illustrates the decomposition of a given graph ${\mathcal {G}}$ of 36 vertices and 39 edges into disjoints shells and nested cores of order 0, 1, 2 and 3. In this example, $core(A) = ef\_deg_{{\mathcal {G}}}(A) = deg_{{\mathcal {G}}}(A) = 0$, $core(B) = 1$, $ef\_deg_{{\mathcal {G}}}(B) = deg_{{\mathcal {G}}}(B)=2$, $core(D) = ef\_deg_{{\mathcal {G}}}(D) = 3$, $deg_{{\mathcal {G}}}(D)=6$ and $core({\mathcal {G}})=3$.

3.2.7 Basic algorithm and complexity

The brute force approach for computing the coreness of a graph follows immediately from the procedural definition. Each k-core, from the 0-core to the $k_{max}$-core (the main core), can be obtained by iteratively removing all the nodes of degree less than k. Basically, for a given k, while there are nodes that can be removed because they have less than k neighbors then we do so and re-check their neighbors until no remaining node has less than k neighbors. Therefore, we may need to visit all n nodes for every k, but we only visit each edge once, whenever we delete one of its endpoints. This leads to an algorithm with complexity ${\mathcal {O}}(k_{max}\cdot n + m)$ in time and ${\mathcal {O}}(n)$ space.

3.2.8 Optimal linear algorithm

Thanks to Batagelj and Zaveršnik [4], the coreness of an unweighted graph can be more efficiently computed in linear time (${\mathcal {O}}(n + m)$) and space (${\mathcal {O}}(n)$). It immediately follows that the effective degree sequence can also be computed in linear time since for each node, when computing the degree, you only need to consider edges with nodes of equal or higher core number.

Fig. 2

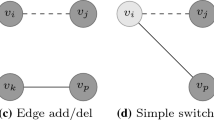
Illustration of the basic edge modification operations. Solid lines represent existing edges to be deleted and dashed lines new edges to be added. Node color indicates whether a node changes its degree (gray) or not (white) after the operation has been carried out. a Edge addition, b edge deletion, c edge rotation, d edge switch

3.3 Edge modification

Several privacy-preserving methods are based on edge modifications (i. e. adding or removing edges) such as randomization and k-anonymity methods. There exist four basic edge modification operations illustrated in Fig. 2:

• Edge Addition: It is simply defined as adding a new edge $(v, w) \not \in {\mathcal {E }}$.

• Edge Deletion: It is simply defined as deleting an existing edge $(v, w) \in {\mathcal {E }}$.

• Edge Rotation: This occurs between three nodes $(v, w, x) \in {\mathcal {V}}^3$ such that $(x, v) \in {\mathcal {E }}$ and $(x, w) \not \in {\mathcal {E }}$. It is defined as deleting edge (x, v) and creating a new edge (x, w) as Fig. 2c illustrates. Note that edge switch would have been more appropriate but it had already been defined in the relevant literature in the context of a “double switch”.

• Edge Switch: This occurs between four nodes $(v, w, x, y) \in {\mathcal {V}}^4$ where $\left( (v, w),\ (x, y)\right) \in {\mathcal {E }}^2$, $(v, y) \not \in {\mathcal {E }}$, $(x, w) \not \in {\mathcal {E }}$. It is defined as deleting edges (v, w) and (x, y) and adding new edges (v, y) and (x, w) as Fig. 2d illustrates.

Because in practice we usually want the number of edges to remain the same throughout the perturbation (to preserve some data utility), edge addition and edge deletion are usually performed simultaneously in a meta-operation referred to as Edge Add/Del. Edge rotation and edge switch can then be seen as special cases of Edge Add/Del. Note that edge switch preserves not only the number of edges but also the degree of each vertex, which has an impact in terms of privacy preservation.

These basic operations are applied as many times as necessary (for instance until 25% of the total number of edges has been modified). At each step, edges are selected at random from the original edge sets (${\mathcal {E }}$ for deletion and ${\mathcal {E }}^\complement$ for addition) and the operation is carried out. It will be the same with our methods, only that the basic operations will be different.

3.3.1 Terminology for anonymization

When all edges to add/delete are selected at random over the entire edge set, the corresponding anonymization method is referred to as Rand Add/Del and has served as building block for most random-based anonymization methods. Under additional constraints such as spectral properties preservation or blockwise modifications, it is, respectively, referred to as Spctr Add/Del [38] and Rand Add/Del-B [37], Rand Switch and Spctr Switch [38] when edges are switched.

Most k-anonymity methods can be also modeled through the Edge Add/Del concept [20, 41, 42]. More specifically, the UMGA algorithm [11] relies on edge rotation while the work of Liu and Terzi [25] relies on edge switch to anonymize the graph according to the k-degree anonymity concept.

4 Our approach

In this section, we present our approach that preserves the coreness of a graph while anonymizing it through various edge modification operations.

4.1 Idea and brute force algorithm

Our idea came from the observation that there is some space left between the two extremal edge modification techniques that are Rand Add/Del and Rand Switch. The former ensures privacy by randomly modifying the structure of the graph at the cost of rapidly increasing the information loss, as demonstrated in Casas-Roma et al. [12]. The latter maintains the apparent degree of every node to preserve some data utility but allowing an attacker to quickly re-identify nodes, i.e., Rand Switch does not preserve the privacy under knowledge-based degree attacks.

Preserving the coreness of the graph seems like a good trade-off. Instead of maintaining the apparent degree, we allow for some slack, increasing the level of randomization (privacy), but in the meantime preserving the true degree of every node that supposedly holds the information to mine (utility). Indeed, graph degeneracy has been used for community detection [16] and the core number has been shown to be a more robust version of the apparent degree [5]. Again, in the case of a social network, it seems legit to add/remove random relations as long as it preserves the community a node belongs to. Removing “satellite connections” while preserving “close friends” seems like an intuitive way to achieve our goal and empirical results on various networks support our claim.

The most straightforward way to apply our idea would be to randomly select an edge to add/delete, perform the operation and re-compute the coreness of the graph to check for any difference. There exists an optimal linear algorithm for degeneracy. However, it seems too expensive to do it for each edge modification, especially since the core number sequence should only change locally around the edge if anything. We present in the next subsections the algorithms we developed to perform faster edge modifications.

4.2 Coreness-preserving edge modification

Let $e = (v, w)$ be an undirected edge between vertices v and w. The goal is to check whether we can add/delete e without changing the graph’s coreness (and by extension safely rotate or switch edges). Actually, because the edge modification directly impacts v and w, it is sufficient to check whether the core numbers of v and w are preserved since it is not possible for the coreness to change without core(v) or core(w) changing.

Since the graph is undirected, we can always choose v and w such that $core(v) \le core(w)$. In the next subsections, we consider $core(v) = k$ and we will refer to the k-shell that v belongs to as the lower shell (${\mathcal {S}}_{k}$). It is also the k-shell w belongs to iff $core(v) = core(w)$, otherwise we will refer to the other subgraph as the upper core (${\mathcal {H}}_{k+1}$). In both cases (add/delete), it is important to note that if $core(v) < core(w)$ then we only need to check whether the edge modification preserves core(v). Indeed, by the time we reach the upper core (in the basic algorithm set up from Sect. 3.2.7), the edge will no longer exist since node v will have been removed and thus it will have no incidence on core(w).

Additionally, for the subsequent Algorithms, we assume two tables core and $ef\_deg$ indexed by vertex that have been pre-computed in linear time.

4.3 Coreness-preserving edge deletion: Crnss Deletion

Lemma 1

An edge can be removed from a graph without changing its coreness if none of its two endpoints belong to the k-corona of the lower shell.

Proof

For the node(s) in the lower shell, deleting an edge means decreasing its effective degree by one. Thus, for a node to remain in its k-shell after losing one connection, it needs at least $k+1$ neighbors in the first place—in other words, it cannot belong to the k-corona.

4.3.1 Algorithm

We present the detailed pseudocode in Algorithm 1. First, we place ourselves in the case where $core(v) \le core(w)$, swapping v and w if needed (line 2). Then, in the case where $core(v) < core(w)$, we only need to check that $v \notin {\mathcal {C}}_k$ (line 3) while in the case where $core(v) = core(w)$, we also need to check that $w \notin {\mathcal {C}}_k$ (line 4). In any case, assuming the coreness and the effective degree sequence have been pre-computed (in linear time), the check can be done in constant time. If the edge were to be removed, we would only need to decrease the effective degree of the node(s) from the lower shell (line 5). Therefore, the overall operation can be done in constant time.

4.3.2 Illustration

Figure 3a illustrates this procedure. We drew a couple of points from the 3-shell (${\mathcal {S}}_3$) and 4-core (${\mathcal {H}}_4$) of a graph. White nodes belong to the 3-corona (${\mathcal {C}}_3$), gray nodes to the 3-lamina (${\mathcal {L}}_3 = {\mathcal {S}}_3 {\setminus } {\mathcal {C}}_3$) and black nodes to ${\mathcal {H}}_4$. The dashed edges can be safely removed (but not both of them, the check being only valid for one edge at a time) because none of their endpoints belong to the k-corona of the lower shell (here the 3-shell). The dotted edges cannot be deleted because at least one of the two endpoints belong to the 3-corona. The solid edges indicate links with nodes from lower shells and not displayed for space constraints.

Fig. 3

Illustration of coreness-preserving edge modification. In subfigure a (resp. b), dashed edges can be safely removed (resp. added), dotted edges cannot without altering the coreness. a Coreness-preserving edge deletion, b Coreness-preserving edge addition

4.4 Coreness-preserving edge addition: Crnss Addition

Checking whether an edge can be added to a graph without changing its core number sequence appears to be less trivial than for deleting one. Nevertheless, we came up with an efficient alternative to the brute force approach mentioned in Sect. 4.1. Instead of recomputing the core number for every node in the graph, we estimate as early as possible if the core number of v will remain unchanged after adding the new edge—in other words, if v will move from ${\mathcal {S}}_{k}$ to ${\mathcal {H}}_{k+1}$ or not.

4.4.1 Algorithm

We present the detailed pseudocode in Algorithm 2. First, we add the new edge to the graph and we update the effective degree(s) (line 6). Then, we traverse the lower shell (${\mathcal {S}}_k$) starting from node v (line 14). For v to be in ${\mathcal {H}}_{k+1}$, it needs at least $k+1$ neighbors also in ${\mathcal {H}}_{k+1}$. There are four kinds of neighbors: (a) nodes with a lower core number, (b) nodes with an equal core number and in the k-corona (${\mathcal {C}}_k$), (c) nodes with an equal core number and in the k-lamina (${\mathcal {L}}_k$) and (d) nodes with a higher core number. Neighbors of type (a) and (b) cannot be by definition in ${\mathcal {H}}_{k+1}$ (lines 23 and 24). Neighbors of type (c) could be in ${\mathcal {H}}_{k+1}$ thanks to the new added edge (lines 29–31). Neighbors of type (d) are by definition in ${\mathcal {H}}_{k+1}$ (line 25). So, for a given node v, its effective degree in ${\mathcal {H}}_{k+1}$ is lower-bounded by the number of neighbors of type (d) and upper-bounded by the number of neighbors of type (c) and (d). The goal of the algorithm is to estimate as early as possible this effective degree to see if it is greater than k or not (function ${\texttt {|could\_be\_in\_next\_core|}}$, line 37).

From the bounds, it follows that if the lower bound is strictly greater than k then the node is definitely in ${\mathcal {H}}_{k+1}$ and thus the edge cannot be added (otherwise v would move up to the next core)—this happens when a node has already k connections with nodes in ${\mathcal {H}}_{k+1}$. Conversely, if the upper bound is strictly less than $k+1$ then the node is definitely not in ${\mathcal {H}}_{k+1}$ and thus the edge can be safely added (line 33). In-between, we need to visit the neighbors of type (c) (line 31) and apply on them the same procedure (line 14). It all comes down to the nodes from ${\mathcal {L}}_k$: even though they have enough neighbors to be in ${\mathcal {H}}_{k+1}$, these neighbors were not connected enough to be in ${\mathcal {H}}_{k+1}$ but the new added edge could make the difference. This leads to a recursive definition of the problem, i.e., depth-first-search (DFS) traversal of ${\mathcal {L}}_k$. Then, whenever we visit a node from the k-lamina that cannot move to the next core, we discard it (line 40) and we back propagate this information to lower the estimate on the degree we have for its visited neighbors (line 42). If at any point the degree estimate of the source node v drops below $k+1$ then we know the edge can be safely added (line 15). Otherwise, we keep visiting new neighbors of type (c) until we run out. At that point, we have basically found a set of nodes of type (c), including v, ready to move up altogether in ${\mathcal {H}}_{k+1}$, thus preventing the edge addition (line 17). Even in the case of $core(v) = core(w)$, we only need to do the traversal once, from v, since w will be visited anyway. It is not possible for v to move to the next core without w and vice-versa since the new added edge has to survive in the next core. Hence, contrary to edge deletion, we only need to run the check on v.

4.4.2 Illustration

Figure 3b illustrates this procedure using the same set up as Fig. 3a. The dashed edges can be safely added while the dotted edges cannot. We note that we cannot assert whether an edge can be added just by checking if its endpoint(s) belong to the k-corona (like $v_1$ or $v_3$) or not ($v_2$). It appears to depend on the structure of the neighborhood, hence the proposed algorithm.

4.4.3 Worst case complexity

In the worst case scenario (corresponding to a large k-lamina), we may need to visit all the nodes in ${\mathcal {L}}_k$ so an overall complexity of ${\mathcal {O}}(m)$ time and ${\mathcal {O}}(n)$ space. But in practice, we only visit the nodes from ${\mathcal {L}}_k$ that have at least $k+1$ neighbors in ${\mathcal {L}}_k \cup {\mathcal {H}}_{k+1}$, reducing very rapidly the number of candidates as observed experimentally. Moreover, we implemented a breadth-first-search (BFS) traversal with a FIFO queue Q to take advantage of the back propagation as soon as possible to prune nodes that cannot move to ${\mathcal {H}}_{k+1}$ anyway. Note that at the cost of some privacy (false negatives for edge addition), it is possible to limit the depth of the BFS traversal and cap the number of visited vertices. We did not need it in our experiments but for some particular graph structures with tight giant cores, it might help and ensure constant time edge addition.

4.4.4 Nodes from the 0-shell

Similar to Rand Switch, our method cannot add edges to nodes from the 0-shell since they would immediately move to the 1-shell. We see two options to deal with this particularity: (a) artificially allow them to move to the 1-shell under the assumption that the impact on the data utility is limited; or (b) consider that an attacker cannot learn anything from a node without neighbors (except if ${\mathcal {S}}_0$ is a singleton, in which case he can re-identify the node but this one only). In our experiments, we did not encounter this scenario.

4.4.5 Crnss Add/Del

Similar to Rand Add/Del, in order to maintain the total number of edges, Crnss Add and Crnss Deletion are performed simultaneously in a meta-operation referred to as Crnss Add/Del. This is called as many times as necessary (for instance until 25% of the total number of edges has been modified) considering again random edges from the original edge sets at each step.

4.5 Coreness-preserving edge rotation: Crnss Rotation

Considering three nodes (v, w, x) like in Fig. 2b, this operation modifies the apparent degrees of v and w as wanted while not changing any core number. We can combine the two previous approaches to perform the check. We present the detailed pseudocode in Algorithm 3. We first need to check that the edge $e = (x, v)$ can be safely deleted (lines 2–5) and then that the edge $e' = (x, w)$ can be safely added (line 7).

Note that we cannot directly reuse the function ${\texttt {|}}{\texttt {delete}}{\texttt {\_}}{\texttt {edge}}{\texttt {\_}}{\texttt {if}}{\texttt {\_}}{\texttt {possible}}{\texttt {|}}$ because of a particular case: when w belongs to a higher core than x and x belongs to the k-corona of the lower shell between v and x, it is safe to delete e because $e'$ compensates for the loss of v as a neighbor.

4.6 Coreness-preserving edge switch: Crnss Switch

Baur et al. [5, Lemma 2] proposed an edge modification operation called swapping that supposedly preserved the coreness but restricted anyway to pairs of edges with all their nodes belonging to the same k-shell. The lemma basically stated that considering four nodes of same core number and only two edges between these nodes, it is safe to switch the edges like in Fig. 2c. However, we discovered a flaw in the lemma when some of the endpoints belong to the k-lamina and not the k-corona as illustrated in Fig. 4.

Fig. 4

Illustration of a case where the edge swapping operation proposed by Baur et al. [5] does not preserve the coreness; bold edges are the ones being swapped. a Original graph, b after swapping

In any case, we believe that the edge switch operation should not be restricted to nodes of same core number. Considering four nodes (v, w, x, y) like in Fig. 2c, this operation has for effects to modify the connections while not changing any apparent degree nor any core number. We present the detailed pseudocode in Algorithm 4. Similar to edge rotation, we cannot directly reuse ${\texttt {|delete\_edge\_if\_possible|}}$ because the added edges can sometimes offset the deleted edges in terms of core number. Therefore, we define a new function ${\texttt {|can\_delete\_edge|}}$ that takes that into account: an edge cannot be deleted if the endpoint(s) belonging to the k-corona of the lower shell will be connected with a node of lower core number (i. e. not making up for the loss of a neighbor in the last k-core it belongs to). Otherwise, we can delete the edges (lines 4–5) and then check if the edge additions preserve the coreness (lines 6–8), adding back the deleted edges if not (lines 9–10).

5 Experiments

In this section, we present the experimental set up and the empirical results of our work. Section 5.1 introduces our experimental framework. Section 5.2 presents the experiments for randomization while Sect. 5.3 the ones related to k-anonymity. Finally, Sect. 5.4 explores the scalability of our proposed methods.

5.1 Experimental framework

In our experiments, we evaluated the various approaches on several datasets using two types of information loss: generic graph properties and clustering-specific graph metrics.

5.1.1 Datasets

We used 6 standard real networks to test our approach: (1) Zachary’s karate club [39], a network widely used in the literature that presents the relationships among 34 members of a karate club; (2) Jazz [17], a collaboration graph of 198 jazz musicians; (3) URV email [19], the email communication network of the University Rovira i Virgili in Tarragona, Spain; (4) Polblogs [1], a network of hyperlinks between weblogs on US politics; (5) Caida [24], a network of autonomous systems of the Internet connected with each other from the CAIDA project; and (6) DBLP [35], a co-authorship network where computer scientists are connected if they co-authored at least one paper together. We have selected these datasets because they have diverse statistics and properties as shown in Table 1.

Table 1 Network properties—number of vertices (n), number of edges (m), average degree ($\overline{deg}$), average distance ($\overline{dist}$) and diameter (d)

5.1.2 Generic graph properties

In order to quantify the noise introduced in the data, we used several structural and spectral graph properties. Some of them are at the graph level: average distance ($\overline{dist}$), diameter (d), transitivity (t) largest eigenvalue of the adjacency matrix ($\lambda _{1}$) and second smallest eigenvalue of the Laplacian matrix ($\mu _{2}$) and are thus a scalar value. Other metrics evaluate the graph at the node level: betweenness centrality ($C_B$) and closeness centrality ($C_C$) and are thus a vector of length n.

Given such a metric $\nu$, a graph ${\mathcal {G}}$ and $\widetilde{{\mathcal {G}}}_p$ the p-percent perturbed graph in the randomization case ($p \in \llbracket 0, 25 \rrbracket$) and the p-anonymous graph in the k-anonymity case ($p \in \llbracket 1, 10 \rrbracket$), we computed the information loss between the two networks as follows:

$$\begin{aligned} \epsilon _{\nu }({\mathcal {G}}, \widetilde{{\mathcal {G}}}_p) = ||\nu ({\mathcal {G}}) - \nu (\widetilde{{\mathcal {G}}}_p) ||_2. \end{aligned}$$

(1)

Variations in the generic graph properties are a good way to assess the information loss but they have their limitations because they are just a proxy to the changes in data utility we actually want to measure. What we are truly interested in is, given a data mining task at hand, quantify the disparity in the results between performing the task on the original network and on the anonymized one. We chose clustering because it is an active field of research, which provides interesting and useful information in community detection for instance. Therefore, the extracted clusters/communities of nodes are the data utility we want to preserve.

5.1.3 Clustering-specific graph metrics

We ran 4 graph clustering algorithms to evaluate the edge modifications techniques using the implementations from the ${\texttt {|igraph|}}$ library. All of them are unsupervised algorithms based on different concepts and developed for different applications and scopes. An extended revision and comparison of them can be found in Lancichinetti and Fortunato [22] and Zhang et al. [40]. The selected clustering algorithms are: Fastgreedy (FG) [15] , Walktrap (WT) [29] , Infomap (IM) [30] and (4) Multilevel (ML) [6]. Although some algorithms permit overlapping among different clusters, we did not allow it in our experiments by setting the corresponding parameter to zero, mainly for ease of evaluation.

We considered the following approach to evaluate the clustering assignment made by a given clustering method c using a particular graph perturbation method a: (1) apply a to the original data ${\mathcal {G}}$ and obtain $\widetilde{{\mathcal {G}}} = a({\mathcal {G}})$; (2) apply c to ${\mathcal {G}}$ and $\widetilde{{\mathcal {G}}}$ to obtain the cluster assignments $c({\mathcal {G}})$ and $c(\widetilde{{\mathcal {G}}})$; and (3) compare $c({\mathcal {G}})$ to $c(\widetilde{{\mathcal {G}}})$. In terms of information loss, it is clear that the more similar $c(\widetilde{{\mathcal {G}}})$ is to $c({\mathcal {G}})$, the less the information loss is. Thus, clustering-specific information loss metrics should measure the divergence between both cluster assignments $c({\mathcal {G}})$ and $c(\widetilde{{\mathcal {G}}})$. Ideally, if the anonymization step was lossless in terms of data utility, we should have the same number of clusters with the same elements in each cluster. When the clusters do not match, we need to quantify the divergence.

For this purpose, we used the precision index [8]. Assuming we know the true communities of a graph, the precision index can be directly used to evaluate the similarity between two cluster assignments. Given a graph of n nodes and q true communities, we assigned to nodes the same labels $l_{tc}(\cdot )$ as the community they belong to. In our case, the true communities are the ones assigned on the original dataset (i.e., $c({\mathcal {G}})$) since we want to obtain communities as close as the ones we would get on non-anonymized data. Assuming the perturbed graph has been divided into clusters (i.e., $c(\widetilde{{\mathcal {G}}})$), then for every cluster, we examine all the nodes within it and assign to them as predicted label $l_{pc}(\cdot )$ the most frequent true label in that cluster (basically the mode). Then, the precision index can be defined as follows:

$$\begin{aligned} precision\_index({\mathcal {G}},\widetilde{{\mathcal {G}}}) = \frac{1}{n} \sum _{v \in {\mathcal {G}}} {\mathbbm {1}}_{l_{tc}(v) = l_{pc}(v)} \end{aligned}$$

(2)

where $\mathbbm {1}$ is the indicator function such that $\mathbbm {1}_{x=y}$ equals 1 if $x=y$ and 0 otherwise. Note that the precision index is a value in the range [0, 1], which takes the value 0 when there is no overlap between the sets and the value 1 when the overlap between the sets is complete. To be consistent with the notion of error for the generic graph properties, we report $1 - precision\_index$ in the results tables so that the lower, the better.

Table 2 Average error over 10 independent runs and 25 levels of anonymization for Crnss Add/Del (C-A/D), Crnss Switch (C-Sw), Rand Add/Del (R-A/D) and Rand Switch (R-Sw) edge modification processes on 7 generic information loss metrics

5.2 Randomization experiments

Our framework generates perturbed (i. e. anonymized) networks from the original one by applying different edge modification methods. For each method, we considered 10 independent executions with a randomization ranging from 0% to 25% of the total number of edges. We quantified the noise introduced on the perturbed data using some generic information loss metrics and clustering-specific information loss metrics, as previously described.

5.2.1 Perturbation methods

We propose two coreness-preserving edge modification methods using the basic operations described in Sect. 4: coreness-preserving edge addition and deletion denoted by “Crnss Add/Del” (or C-A/D for short) following the terminology of Ying and Wu [38] that is based on coreness-preserving edge addition and deletion, and coreness-preserving edge switch denoted by “Crnss Switch” (C-Sw). We use as baselines “Rand Add/Del” (R-A/D) and “Rand Switch” (R-Sw).

5.2.2 Results

We present in Table 2 the average errors over 10 independent runs and 25 levels of randomization for Crnss Add/Del, Crnss Switch, Rand Add/Del and Rand Switch for all the information loss metrics aforementioned. Note that we do not include the biggest network DBLP because several results (e.g., betweenness centrality and the spectral measures) could not be computed in a reasonable time for reasons unrelated to our approach but due to the metrics in themselves, especially for the 250 versions of a network that each method produces (so overall 1000 computations per metric).

Our edge modification methods that preserve the coreness (Crnss Add/Del and Crnss Switch) perform better than the other methods on all generic metrics, specifically the Crnss Switch which achieves the best result, i. e. lowest information loss, on 29 out of 35 results. For instance, Fig. 5a illustrates the detailed results for average distance on Jazz network. The 0% perturbation point in the upper left corner represents the value of this metric on the original graph. Thus, values close to this point indicate low noise on perturbed data. As we can see, Crnss Switch remains closer to the original value than the other methods obtaining the lowest average error value (0.093), but we also note that Crnss Add/Del method gets results close to these ones, achieving a low average error value (0.1). Rand Add/Del and Rand Switch yield to the best results on Karate network, which is the smallest network with only 34 vertices and 78 edges. Thus, the total number of modified edges is very low compared to other datasets, which can be more sensitive to addition, deletion and switch operations.

We want to underline, as we have commented previously, that both methods using edge switch (Crnss Switch and Rand Switch) achieve pretty good results since they do not change the vertices’ degree. Therefore, they keep metrics related to paths (average distance, diameter, betweenness and closeness centrality) closer to the original ones. The first eigenvalue of the adjacency matrix is related to the maximum degree, clique number and chromatic number, which also be more stable when applying edge switch, as can be seen in Fig. 5b. On the contrary, using edge switch implies a strong drawback in terms of privacy, since the degree sequence remains the same and an attacker can use degree-based knowledge to re-identify users on anonymous data [3, 28, 41].

Fig. 5

Perturbation methods results for some generic and clustering-specific information loss measures for an anonymization varying from 0 to 25%. a $\overline{dist}$ on Jazz, b $\lambda _1$ on URV email, c precision index on Karate (Walktrap), d precision index on Polblogs (Fastgreedy)

Table 3 Average error over 10 independent runs and 25 levels of anonymization for Crnss Add/Del (C-A/D), Crnss Switch (C-Sw), Rand Add/Del (R-A/D) and Rand Switch (R-Sw) edge modification processes on 4 clustering-specific information loss metrics (IM – Infomap, ML – Multilevel, FG – Fastgreedy and WT – Walktrap)

Table 3 shows the error on precision index computed using the four clustering algorithms described in Sect. 5.1.3. The coreness-preserving approaches outperform the others in all datasets and all clustering methods hence the claim of a community-preserving graph anonymization technique. It is interesting to underline that, although our Crnss Add/Del approach does not get the best results on generic metrics for the Karate network, it achieves the best results on all clustering methods as Fig. 5c illustrates for the Walktrap method. Therefore, even if the generic metrics could indicate that Rand Switch introduces less noise on perturbed data, the clustering processes show the opposite. Figure 5d presents similar behavior on Polblogs using Fastgreedy algorithm. We think that Crnss Add/Del achieves better clusters preservation than Crnss Switch because the edge addition/deletion operation is less likely to “break” communities like edge switch could.

5.3 k-Anonymity experiments

In this section, we provide the results of a real k-degree anonymity application. We underline the impossibility of evaluating the methods based on edge switch (i. e. Crnss Switch and Rand Switch here) due to the fact that they are unable to change the vertices’ degree and therefore they cannot be applied in order to achieve k-degree anonymity. As we have claimed, these methods are good in terms of information loss but they have critical drawbacks in terms of anonymity.

In the following, we provide the results of a real application focusing on our Crnss Add/Del approach and the baseline Rand Add/Del. We have selected a k-degree anonymous algorithm based on Edge Add/Del and Edge Rotation to anonymize a network and we have adapted it to be coreness-preserving, decreasing the data utility loss while achieving the same level of privacy (the k in k-degree anonymity).

5.3.1 k-Anonymity algorithm

We used a recently developed algorithm that can easily be implemented and adapted: Univariate Micro-aggregation for Graph Anonymization (UMGA) [11, 13]. It relies on a two-step process: (1) degree sequence anonymization and (2) graph perturbation by successive edge modifications to reach the desired k-degree anonymous sequence. Basically, in order to smooth the degree sequence, it rotates some edges to increase/decrease some apparent degrees. Initially, Edge Add/Del and Edge Rotation operations are used by the algorithm to select the edges that will change during the second step. We compare its data utility loss to the same algorithm but using Crnss Add/Del and Crnss Rotation (as described in Sect. 4.5) as building blocks. In both cases, the level of privacy achieved is the same (the k in k-anonymity) so what matters is the data utility loss only.

5.3.2 Results

Table 4 discloses the results of our experimental tests on the four biggest networks, focusing on clustering-specific information loss metrics since they are a better estimate for quantifying the data utility loss on real graph mining processes.

Similarly to previous experiments, UMGA algorithm based on Crnss Add/Del (UMGA-Crnss) outperforms on 12 of 16 tests the same algorithm based on Rand Add/Del and Rand Rotation (UMGA-Rand). UMGA-Crnss gets the best results on all datasets using Multilevel clustering algorithm. For instance, Fig. 6a presents the results on URV email network. As we can see, the precision index values are reduced considerably for a $k \ge 2$ value, but they remain between 0.7 and 0.8 for UMGA-Crnss while ranging from 0.6 to 0.7 for UMGA-Rand. For instance, if this network is publicly released with a k-anonymity value equal to 4, researchers and third-parties who perform clustering or community detection analysis will obtain 80% of vertices in the same cluster or community as the original data using our coreness-preserving techniques, while with the same privacy level will decrease to 65% using standard edge addition and deletion. On the contrary, the precision index values keep close to 0.98 for both algorithms on Polblogs using Fastgreedy, as we can see in Fig. 6b. Caida being the second largest tested network, we expect to introduce less noise since the privacy level is the same ($1 \le k \le 10$) and the network is larger than others. Precision index values remain above 0.93 for UMGA-Crnss but decrease for UMGA-Rand from $k \ge 7$ as shown in Fig. 6c. Finally, Fig. 6d presents similar behavior on our largest network, DBLP.

Table 4 Average error over 10 levels of k-anonymity for UMGA-Crnss and UMGA-Rand algorithms on 4 clustering-specific information loss metrics (IM – Infomap, ML – Multilevel, FG – Fastgreedy and WT – Walktrap)

Fig. 6

Precision index for UMGA-Crnss and UMGA-Rand for an anonymization varying from $k=1$ to 10. a URV email (Multilevel), b Polblogs (Frastgreedy), c Caida (Infomap), d DBLP (Walktrap)

5.4 Scalability analysis

After randomization and k-anonymity information loss analysis we have performed in previous sections, we want to test our edge modification technique with large and very large networks. Our main goal is to prove that it is able to deal with large networks of thousands and millions of vertices and edges. We cannot perform the previous analysis with these networks due to the high complexity of some measures, which cannot be computed in reasonable time for any methods—baselines or ours. For instance, betweenness centrality, diameter or average distance involve the computation of the shortest paths between all vertices in the network, which is infeasible for large or very large networks. All tests in this section are made on a 4 CPU Intel Xeon X3430 at 2.40 GHz with 32 GB RAM running Debian GNU/Linux.

5.4.1 Tested networks

We have tested our algorithm with three real and large networks. All these networks are undirected and unlabeled. Table 5 shows a summary of the networks’ main features including number of vertices (n), edges (m), average degree ($\overline{deg}$) and k-degree anonymity value. Amazon [23] is based on “customers who bought X also bought Y” feature of the Amazon website. Yahoo! Instant Messenger friends connectivity graph (version 1.0) [34] contains a non-random sample of the Yahoo! Messenger friends network from 2003. LiveJournal [36] is a free online blogging community where users declare friendship with each other.

Table 5 General properties of our tested large networks

Table 6 Computation time (in hh:mm:ss) over 10 levels of anonymization (from 1% to 10% of total number of edges) for Crnss Add/Del (C-A/D), Rand Add/Del (R-A/D) and Rand Switch (R-Sw) edge modification processes on our tested large datasets

5.4.2 Performance of our technique

Table 6 shows the results of scalability experiments in our selected networks. The framework computes the time to generate perturbed (i. e. anonymized) networks from the original one by applying different edge modification methods. Specifically, we considered coreness-preserving edge addition and deletion (“Crnss Add/Del” or C-A/D for short) and our baselines “Rand Add/Del” (R-A/D) and “Rand Switch” (R-Sw). For each method, we considered a range from 1 to 10% of the total number of edges.

Rand Add/Del is faster than any other method in all datasets since it is the simplest edge modification technique. However, as we have seen in aforementioned sections, it introduces more noise in the anonymized data than our coreness-preserving method. Rand Switch produces similar results, though some verifications need to be done to check edge switch. Our proposed method, Crnss Add/Del is slower than others in all experiments. Nevertheless, it is able to anonymize large and very large networks in reasonable time, as demonstrated in Table 6.

Additionally, Fig. 7a presents the computation time on Yahoo! dataset. Horizontal axis represents the perturbation percentage, ranging from 0% (original graph) to 10% of the total number of edges. Vertical axis indicates the computation time (in seconds) for each method to reach the perturbation level. Rand Add/Dell and Rand Switch present similar computation time, which are both lower than Crnss Add/Del.

Table 7 shows the results of our scalability experiments in large networks based on a real k-degree anonymity application. Details of this algorithm and its implementation can be found in Sect. 5.3. As in the previous section, we used UMGA algorithm based on Crnss Add/Del (UMGA-Crnss) and Rand Add/Del and Rand Rotation (UMGA-Rand). We test both methods for values of $k \in \{ 10,20,50,100 \}$ in each network and show the computation time of each method.

Fig. 7

Computation time for random-based perturbation and k-degree anonymity experiments on Yahoo! dataset. a Randomization, b k-degree anonymity

Table 7 Computation time (in hh:mm:ss) of k-degree anonymity ($k \in (10, 20, 50 , 100)$) for UMGA-Crnss and UMGA-Rand algorithms on our tested large datasets

UMGA-Rand (based on Edge Add/Del and Edge Rotation operations) consumes less time than our proposed method based on Crnss Add/Del and Crnss Rotation operations. However, computation time stays in a similar range due to the fact that degree sequence anonymization is a time-consuming process and it is the same for both methods. Figure 7b shows the computation time evolution on Yahoo! dataset.

Summarizing, we claim that our proposed methods achieve higher data utility (i. e. lower information loss) at a certain cost of higher computation time. However, anonymization process is done once while many graph mining tasks can be performed on anonymous data. We believe that investing more time anonymizing the data is worth of getting lower information loss. Finally, we want to underline that our experiments in a real k-degree anonymity algorithm presented quite similar computation time but much better data preservation.

6 Re-identification and risk assessment

In this section, we evaluate empirically the impact of external information on the adversary’s ability to re-identify individuals. For each dataset, we consider each node in turn as a target. Firstly (6.1), we consider the set of possible worlds and our analysis focuses on the differences between Rand Add/Del and Crnss Add/Del. Secondly (6.2), we assume the adversary has degree-based knowledge. And finally (6.3), that he has 1-neighborhood knowledge.

6.1 The set of possible worlds

Assuming that the randomization method and the number w of fake edges are public, the adversary must consider the set of possible worlds implied by $\widetilde{G}$ and w. Informally, the set of possible worlds consists of all graphs that could result in $\widetilde{G}$ under w perturbations.

Using $E^c$ to refer to all edges not present in E, the set of possible worlds of $\widetilde{G}$ under w randomly edge perturbations, denoted by ${\mathcal {W}}_{Rand}^{w}(\widetilde{E})$, corresponds to:

$$\begin{aligned} {\mathcal {W}}_{Rand}^{w}(\widetilde{E}) = \left( {\begin{array}{c}\vert E \vert \\ w\end{array}}\right) \left( {\begin{array}{c}\vert E^c \vert \\ w\end{array}}\right) \end{aligned}$$

(3)

where $\vert E \vert = m$ is the number of edges, $\vert E^c \vert = \frac{n (n-1)}{2} - m$ is the number of edges of the graph’s complement.

The set of possible worlds under w coreness-preserving edge perturbations corresponds to:

$$\begin{aligned} {\mathcal {W}}_{Crnss}^{w}(\widetilde{E})&= \prod _{i=0}^{w-1} \left( {\begin{array}{c}\alpha (\vert E \vert - i)\\ 1\end{array}}\right) \left( {\begin{array}{c}\beta (\vert E^c \vert - i)\\ 1\end{array}}\right) \end{aligned}$$

(4)

$$\begin{aligned}&\simeq \alpha ^w \beta ^w \left( {\begin{array}{c}\vert E \vert \\ w\end{array}}\right) \left( {\begin{array}{c}\vert E^c \vert \\ w\end{array}}\right) \end{aligned}$$

(5)

where $\alpha$ and $\beta$ are parameters to denote, respectively, the percentage of edges that can be removed from E and added to $E^c$. As discussed previously, some edges cannot be removed or added in order to maintain the coreness of the network. Due to the fact that it is very hard to compute this values theoretically, we compute them empirically on all our tested networks and present the results in Table 8, where $\alpha$ indicates the values for Crnss Deletion and $\beta$ for Crnss Addition. Therefore, these values depend on the network properties and structure, but typically half of the edges can be removed and between 20–40% of nonexistent edges can be added to the network while preserving the coreness, which is a very large number given how sparse real networks are.

Table 8 $\alpha$ and $\beta$ experimental values for the datasets used in our experiments

Fig. 8

Re-identification (a, d) and risk assessment (b, c). The gray scale on b and c indicates the candidate set size, from 1 (black) to [21, $\infty$] (white). (a) Node degree on URV email, b $Cand_{{\mathcal {H}}_1}$ on Jazz, c $Cand_{{\mathcal {H}}_1}$ on Polblogs, d 1-Neighborhood on Jazz

6.2 Degree-based attacks

In this section, we consider an attacker with degree-based knowledge. First, we computed the number of vertices that changed their degree during the perturbation or anonymization process. It is clear that the higher the proportion of vertices that changed their degree, the harder the re-identification process will be. Figure 8a presents these values for URV email dataset. As we can see, Rand Add/Del achieves the highest values, followed by Crnss Add/Del. The former gets 30% of vertices that changed their degree at 10% of anonymization, while the latter achieves 20% at the same anonymization percentage. As previously stated, Rand Switch and Crnss Switch do not change the vertices’ degree during perturbation process. Thus, these methods do not protect users against an attacker with degree-based knowledge. Similar values are observed for the rest of our tested networks, ranging between 30-40% for Rand Add/Del and 20-30% for Crnss Add/Del.

Second, we assume the adversary computes a vertex refinement query on each node, and then computes the corresponding candidate set for each node. We report the distribution of candidate set sizes across the population of nodes to characterize how many nodes are protected and how many are identifiable. According to Hay et al. [20], the candidate set of a target vertex $v_i$ includes all vertices $v_j \in \widetilde{G}$ such that $v_j$ is a candidate is some possible world. We compute the candidate set of the target vertex $v_i$ based on vertex refinement queries of level 1 (${\mathcal {H}}_1$) (see Hay et al. [20] for further details) as shown in Eq. 6.

$$\begin{aligned}&Cand_{{\mathcal {H}}_1}(v_i) = \{v_j : deg^{-}(v_j) \le deg(v_i) \le deg^{+}(v_j) \} \end{aligned}$$

(6)

$$\begin{aligned}&deg^{-}(v_j) = \Big \Vert deg(v_j) \Big (1 - \frac{w}{\vert E \vert }\Big ) \Big \Vert \end{aligned}$$

(7)

$$\begin{aligned}&deg^{+}(v_j) = \Big \Vert deg(v_j) + (n-1-deg(v_j)) \Big ( \frac{w}{\vert E^c \vert } \Big ) \Big \Vert \end{aligned}$$

(8)

where $deg^{-}(v_j)$ is the minimum expected degree of $v_j$ and $deg^{+}(v_j)$ is the maximum expected degree after w edge deletion/addition process, and described by the following equations. We claim that the minimum and maximum expected degree is the same under Rand Add/Del and Crnss Add/Del, since an attacker cannot identity a fake edge on anonymous network even if this edge changes the coreness of the network because other true edges could be deleted after adding this one. It is important to underline that under this knowledge model, Rand Switch and Crnss Switch do not improve the privacy level and the candidate set size remains the same for all anonymization values.

Figure 8b, c shows the candidate set size ($Cand_{{\mathcal {H}}_1}$) evaluation on Jazz and Polblogs datasets. Perturbation varies along the horizontal axis from 0% (original graph) to 25% and vertex proportion is represented on the vertical axis. The trend lines show the proportions of vertices whose equivalent candidate set size falls into each of the following groups: [1] (black), [2, 4], [5, 10], [11, 20], [21, $\infty$] (white). As we can see, candidate set sizes shrink while perturbation increases in all datasets. The number of nodes at high risk of re-identification (the black area) decreases quickly up to 5–10% of anonymization. Nevertheless, well-protected vertices present different behavior on our tested networks. For instance, Jazz dataset does not achieve a significant percentage of strong protected users up to 15% of anonymization, but this set is empty on the original network. On the contrary, Polblogs dataset has more than 50% of well-protected nodes without any kind of anonymization or perturbation. This property is related to the power-law of real networks, where several users share degree’s value. Even so, anonymization produces significant improvement in terms of user’s privacy at 5-10% of perturbation.

6.3 1-Neighborhood-based attacks

Finally, we consider an adversary with 1-neighborhood-based knowledge [41], i.e., an adversary who knows the friends’ set of some target vertices. Similarly to the previous experiment, we computed the proportions of vertices that change their set of neighbors at distance one during the perturbation process. In this knowledge model, Rand Switch and Crnss Switch are also able to preserve users’ privacy, since they modify the relationships among users. Figure 8d presents results on the Jazz dataset, where we can see that all methods achieve more than 80% of vertices that changed their 1-neighborhood at 10% of anonymization and Rand Add/Del gets the highest number.

7 Conclusions and future work

In this paper, we proposed a novel edge modification technique that better preserves the communities of a graph while anonymizing it. By maintaining the core number sequence of a graph, its coreness, our methods Crnss Add/Del and Crnss Switch achieve a better trade-off between data utility and data privacy than existing edge modification operations. In particular, they outperform Rand Add/Del in terms of data utility and Rand Switch in terms of data privacy as empirical results have shown, both on generic graph properties and real applications, such as clustering.

Several anonymization methods are based on edge modification techniques, i.e., they use edge addition, edge deletion, edge rotation and edge switch as basic operations to construct more complex operations. It is true that some of them do not apply edge modification over the entire edge set but this behavior is specific and different for each anonymization method. We believe that this covers the basic behavior of edge modification-based methods for graph anonymization, even though each method has its specific peculiarities. Thus, we claim that using our coreness-preserving operations all these methods and algorithms can get the same privacy level while achieving higher data utility. A k-degree anonymous algorithm was used to prove our claim, demonstrating that it achieves the same privacy level and higher data utility when it comes to preserve the communities. Furthermore, we demonstrated that our edge modification technique is able to deal with large and very large networks with thousands and millions of vertices and edges.

Future work might involve the reuse of our edge modification operations in other contexts that rely on the impact of edge/node departure/arrival such as graph generators with predefined community structures or the study of engagement dynamics in social networks.