A primal nonsmooth reformulation for bilevel optimization problems

Abstract

The solution of bilevel optimization problems with possibly nondifferentiable upper objective functions and with smooth and convex lower-level problems is discussed. A new approximate one-level reformulation for the original problem is introduced. An algorithm based on this reformulation is developed that is proven to converge to a solution of the bilevel problem. Each iteration of the algorithm depends on the solution of a nonsmooth optimization problem and its implementation leverages recent advances on nonsmooth optimization algorithms, which are fundamental to obtain a practical method. Experimental work is performed in order to demonstrate some characteristics of the algorithm in practice.

1 Introduction

This work focuses on a special class of minimization problems that are commonly known as bilevel optimization [3, 10, 14]. The main feature of these problems is the hierarchical nature, in which decisions must be taken in two different levels – an upper and a lower one. Usually, both levels of decision are associated with two distinct agents: the upper-level one (also known as the leader) having exclusive control over a set of variables $\varvec{x}\in \mathbb {R}^n$, and the lower-level agent (the follower) with influence over another set of variables $\varvec{y}\in \mathbb {R}^m$, directly related with the choice taken in the upper level. Frequently, the agents have conflicting goals, which generate a dynamic interplay between them that only ceases by reaching an equilibrium point.

Hierarchical optimization problems usually emerge when one is trying to model an interaction between two or more individuals and, as a consequence, these problems appear in many real-world applications from a vast range of fields. For instance, bilevel problems can be seen in the energy sector [4], network design [11], revenue management [12], game theory [21, 32], and even in tomography [27] and image denoising [30]. Therefore, such problems are not only interesting (and challenging) from the theoretical perspective, but they also present a strong practical appeal.

The first main contribution of this paper is the proposal of a novel reformulation of bilevel optimization problems that does not rely on dual variables of the lower-level optimization. The resulting one-level problem is a nonsmooth optimization problem with an explicit description of the feasible region – without any implicit value function constraint. The second contribution is the presentation of a new algorithm for solving bilevel optimization problems that can be implemented in practice. Finally, our last main contribution relates to advancing the techniques for solving nonsmooth bilevel problems. Methods for solving those kind of problems do exist [7, 27, 28, 30, 35, 37, 39, 40], but many of these methods are restricted to the case in which there is no distinction between the decision variable of the leader and of the lower-level agent, the so-called simple bilevel optimization problem. As shown in [39], a general bilevel optimization problem can be rewritten in the form of a simple bilevel optimization problem and thus some methods developed for the simple problem might be applicable to the general problem this way.

One of the most commonly applied strategies for solving bilevel optimization problems is reformulating them into a one-level problem. Often, this can be done in two ways: use the so called optimal value reformulation [16, 36]; trade the lower-level optimization problem by its respective first-order necessary conditions, which is known as the KKT reformulation – see, for example, the recent references [2, 18]; or even making a combination of both [43]. Because the former approach leads to a nonsmooth problem even for simple bilevel optimizations, the latter technique has, in general, been preferred. However, the difficulties that arise when one chooses the KKT reformulation are far from being negligible either.

The resulting problem that comes from the KKT reformulation is an instance of a problem known as Mathematical Program with Equilibrium Constraints (MPEC). Such optimization problems are highly degenerated, in the sense that common Constraint Qualifications (CQs) do not hold at their optimal solutions [44]. Because of its importance, relatively efficient methods have been developed for the MPEC [22, 23, 42]. Interestingly, [23] takes an approach that directly tackles the degenerate geometry of the problem by rewriting the complementarity constraints as a discontinuous system of equations and using appropriate methods for the resulting problem. Besides, even in the scenario that one has successfully solved the reformulated problem, one is likely not to have reached an optimal point of the original problem. The original bilevel optimization and its MPEC reformulation can only be equivalent when global solutions are analyzed [15] and, since MPECs are not convex problems, an optimal candidate obtained by practical methods for solving MPECs, in general, will not be a (local) solution for the bilevel problem.

The reason why local solutions of the KKT reformulation are not necessarily local optimal points for the bilevel problem is that the one-level problem involves the dual variables of the lower-level optimization, and not only the primal ones. By enlarging the original space, the sense of locality cannot be carried over. This can be intuitively understood when one looks at Fig. 1a. In this illustrative example, we suppose that the lower-level agent defines a parametric optimization problem. Because the considered vicinity of $\varvec{y}(\varvec{x}^*)$ does not involve all the possible associated Lagrange multipliers, we can see that the respective neighborhood in the primal space does not have $\varvec{x}^*$ as an interior point. Consequently, local solutions for the KKT formulation can be valuable only if all the Lagrange multipliers associated with a primal point are considered – see Fig.1b and [15, Theorem 3.2].

Fig. 1

Illustrative representation of a parametric optimization in the lower-level problem. The red color stands for the points that satisfy the KKT conditions, the green curve stands for the values of the leader’s objective function, and the blue color represents the considered neighborhood of the solution in the primal$\times$dual space (plots in the first row), and its respective neighborhood only in the primal counterpart (plots in the second row). In the plots of column (a), one can see that the notion of locality is compromised, and consequently, in the degenerated vicinity of $\varvec{y}(\varvec{x}^*)$, the point is wrongly classified as a local minimizer of the original problem; however, in the plots of column (b), the notion of locality is preserved due to an enlargement in the considered neighborhood

Following the strategy of converting a bilevel problem into a one-level optimization, we propose a new primal nonsmooth reformulation of the lower-level problem. By avoiding the inclusion of dual variables, we were able to maintain an equivalence to the original bilevel optimization even when one is interested only in local solutions. In addition, although our strategy results in a nonsmooth optimization problem, we argue that our approach can potentially be more workable than some optimal value reformulations, specially with some of the most recent advances in the nonsmooth optimization field. We must notice, however, that recent works, unknown to us when elaborating the manuscript, bring advances in the theoretical [20] and in the numerical [45] properties of the optimal value reformulation. Particularly interesting, in [20], the calmness condition is smartly explored in order to shift the value-function constraint to the upper-level objective function and the non-differentiability of the optimal value function is approached by the use of upper estimates of its subdifferential.

For our analysis, we consider a bilevel optimization problem that is convex in the lower-level variables. The functions that describe the lower-level problem must be differentiable, whereas for the upper-level part we only suppose that the functions are locally Lipschitz continuous, i.e., the upper-level problem may admit nondifferentiable constraints and a nonsmooth objective function. All results are obtained under mild assumptions, with the exception perhaps being the assumption of the uniqueness of the follower’s response to each leader’s choice, i.e. each feasible $\varvec{x}$ determines a single solution $\varvec{y}(\varvec{x})$ for the lower-level agent.

The uniqueness of the follower’s response may considerably simplify the theoretical study of bilevel problems, since one can easily convert the bilevel problem into a one-level problem dependent only on the variable $\varvec{x}$. However, this simplification in the theoretical analysis is not extrapolated to the practical realm, since obtaining efficient algorithms for this special class of bilevel problems is not a simple task. In general, the computation of the response $\varvec{y}(\varvec{x})$ may require solving a constrained optimization problem, which greatly hinders the development of practical methods. For example, one of the algorithms that explore this implicit definition of $\varvec{y}(\cdot )$ is the descent method for bilevel problems [38]. Because every evaluation of $\varvec{y}(\cdot )$ in order to verify a sufficient descent criterion demands a solution of the lower-level problem, if we want descent methods to be practical, the follower’s problem must be sufficiently simple – e.g. a strictly convex quadratic minimization [41]. Additionally, it is important to mention that assumptions to simplify the lower-level problem are usually made in the literature in order to obtain a practical algorithm – for instance, the full-convexity assumption is another common request [16, 33].

Unlike the descent method (or the optimal value reformulation), our proposed algorithm does not rely on any implicit function, which gives us freedom to cope with more general convex problems in the lower level. Because of the explicit description of our reformulation, it has some resemblance with the technique known as double penalty method [3, 29], as we also use a penalty approach to approximate the follower’s problem. Yet, there are significant differences concerning each formulation and the respective convergence analysis.

Besides the presentation of a theoretical analysis, this study also contains a small but elucidative set of numerical experiments showing that the proposed method is able to practically solve bilevel optimization problems. Moreover, aiming at illustrating the importance of our main assumptions, optimization instances that violate such hypotheses are also considered.

ROADMAP   In Sect. 2, the assumptions needed to obtain our convergence analysis are presented, together with some new ideas that appear in our nonsmooth reformulation. Section 3 is reserved for all the theoretical analyses in the paper, including the convergence results of the proposed algorithm. In Sect. 4, numerical experiments are presented. Finally, the last section contains the concluding remarks of this study.

NOTATION   Throughout the text, $\Vert \cdot \Vert$ denotes the Euclidean norm, $\mathbb {R}_+$ stands for the nonnegative real numbers, whereas $\mathbb {R}_+^*$ refers to the strictly positive real numbers. The notation $v_+$ is defined as the real number $\max \{v, 0\}$ and, in case of a vector, this maximum is taken componentwise. Finally, for a function $f: \mathbb {R}^n\times \mathbb {R}^m\rightarrow \mathbb {R}$ dependent on the variables $\varvec{x}\in \mathbb {R}^n$ and $\varvec{y}\in \mathbb {R}^m$, the notation $\nabla _{\varvec{y}} f$ refers to the derivative of f solely with respect to $\varvec{y}$.

2 Preliminaries

Since there are many kinds of bilevel problems – each with its own distinct set of assumptions – we start by presenting the problem of our interest. Along the entire study, we refer to minimization problems that can be written as

where both objective $F:\mathbb {R}^n\times \mathbb {R}^m\rightarrow \mathbb {R}$ and constraint functions $\varvec{C}:\mathbb {R}^n\rightarrow \mathbb {R}^p$ are locally Lipschitz continuous (not necessarily smooth functions) and

$$\begin{aligned} \mathcal R(\varvec{x}):= {{\,\mathrm{\arg min}\,}}_{\varvec{y}\in \varOmega (\varvec{x})} f(\varvec{x},\varvec{y}),\quad \varOmega (\varvec{x}):= \left\{ \varvec{y}\in \mathbb {R}^m:\varvec{c^\text {in}}(\varvec{x},\varvec{y})\le \varvec{0},\varvec{c^\text {eq}}(\varvec{x},\varvec{y}) = \varvec{0} \right\} , \end{aligned}$$

with $f:\mathbb {R}^n\times \mathbb {R}^m\rightarrow \mathbb {R}$ and the constraint functions $\varvec{c^\text {in}}:\mathbb {R}^n\times \mathbb {R}^m\rightarrow \mathbb {R}^q$ and $\varvec{c^\text {eq}}:\mathbb {R}^n\times \mathbb {R}^m\rightarrow \mathbb {R}^s$ being of class $C^2$. Additionally, we suppose that, for each $\varvec{x}\in \mathbb {R}^n$ satisfying $\varvec{C}(\varvec{x})\le \varvec{0}$, the set $\varOmega (\varvec{x})$ is not empty, i.e., for each feasible leader’s choice, the follower can always find a feasible response. It should be noticed that we do not add equality constraints to the upper-level problem in order to simplify the presentation, but all the results can be easily obtained if equality constraints are considered as well. However, this simplification cannot be extended to the follower’s problem and, in order to encompass equality constraints into the model, we have to explicitly handle these constraints in the proof. The proofs are still valid in case the problem has no equality constraints.

We ask that the lower-level problem

must be a convex parametric optimization, i.e., for each fixed $\varvec{x}\in \mathbb {R}^n$ satisfying $\varvec{C}(\varvec{x})\le \varvec{0}$, the functions $f(\varvec{x},\cdot )$ and $c^\text {in}_i(\varvec{x},\cdot )$, $i\in \{1,\ldots ,q\}$, are convex and the functions $c^\text {eq}_j(\varvec{x},\cdot )$, $j\in \{1,\ldots ,s\}$, are affine-linear. We also assume throughout the text that (P-bilevel) always has a solution, and that the set

$$\begin{aligned} \mathcal S:= \{ (\varvec{x}, \varvec{y}) \in \mathbb {R}^n\times \mathbb {R}^m : \varvec{C}(\varvec{x})\le \varvec{0},~\varvec{y} \in \varOmega (\varvec{x})\} \end{aligned}$$

(1)

is compact. In addition, it is assumed that the rational react map $\mathcal R(\cdot )$ is upper-semicontinuous [14, Definition 4.2] for any $\varvec{x}\in \mathbb {R}^n$ such that $\varvec{C}(\varvec{x}) \le \varvec{0}$ – as argued by Dutta and Dempe in [19], this last assumption is not a strong requirement. Finally, when needed, we will also suppose that $\mathcal R(\varvec{x})$ is a singleton for every $\varvec{x}\in \mathbb {R}^n$ satisfying $\varvec{C}(\varvec{x}) \le \varvec{0}$, i.e., for each feasible leader’s choice, the follower has a unique optimal response. This last hypothesis guarantees that the bilevel problem is well-posed [17], although some KKT and optimal value reformulations do not, in theory, require this.

Recently, in order to approximate a nonsmooth constrained optimization problem by an unconstrained problem, a new penalization function has been proposed [26]. The smooth version of such a function will prove helpful in our context. Let us consider, for any $\tau \in \mathbb {R}_+^*$ and $\rho \in \mathbb {R}$, the function $\varTheta _{\tau ,\rho }: \mathbb {R}^n\times \mathbb {R}^m\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} \begin{aligned} \varTheta _{\tau ,\rho }(\varvec{x},\varvec{y}):= {}&\max \left\{ 1 - \frac{\Vert \varvec{c^\text {in}}(\varvec{x},\varvec{y})_+ \Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x},\varvec{y})\Vert ^2}{\tau ^2} , 0 \right\} ^2 [f(\varvec{x},\varvec{y})-\rho ] \\ {}&+ \Vert \varvec{c^\text {in}}(\varvec{x},\varvec{y})_+ \Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x},\varvec{y})\Vert ^2. \end{aligned} \end{aligned}$$

(2)

Although the function above becomes very sharp for small values of $\tau$, it should be said that this feature of $\varTheta _{\tau ,\rho }$ can be numerically handled by recent advances on optimization methods – e.g., Gradient Sampling [5, 6, 24, 25] and methods based on BFGS techniques [13, 34]. Looking carefully at the definition of $\varTheta _{\tau ,\rho }$, one can see that, for $\tau \approx 0$ and $\rho$ sufficiently large, minimizers for this function in relation to $\varvec{y}$ are good approximations to points in $\mathcal R(\varvec{x})$. Indeed, when $\Vert \varvec{c^\text {in}}(\varvec{x},\varvec{y})_+ \Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x},\varvec{y})\Vert ^2 \ge \tau ^2 > 0$, the function $\varTheta _{\tau ,\rho }$ is strictly positive and indifferent to the value of f, since the expression that multiplies f is null in that case. However, if $\rho$ is large enough, the term $f(\varvec{x},\varvec{y})-\rho$ is negative at feasible points of (P-lower), implying that minimizers for $\varTheta _{\tau ,\rho }$ will prioritize points satisfying $\Vert \varvec{c^\text {in}}(\varvec{x},\varvec{y})_+ \Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x},\varvec{y})\Vert ^2 < \tau ^2$ with small values of $f(\varvec{x},\varvec{y})$.

Roughly speaking, and for the sake of providing a preliminary motivation, we argue that the following approximation can be established for small values of $\tau >0$:

$$\begin{aligned} \mathcal R(\varvec{x}) \approx \{ (\varvec{x}, \varvec{y}) \in \mathbb {R}^n\times \mathbb {R}^m : \nabla _{\varvec{y}} \varTheta _{\tau ,\rho }(\varvec{x},\varvec{y}) = \varvec{0} \}. \end{aligned}$$

Therefore, the original bilevel problem admits a one-level reformulation of the type:

$$\begin{aligned} \begin{aligned} \min _{(\varvec{x},\varvec{y})\in \mathbb {R}^n\times \mathbb {R}^m} {}&\quad ~F(\varvec{x},\varvec{y}) \\ \text {s.t. }{}&\quad ~\varvec{C}(\varvec{x}) \le 0 \\ {}&\quad ~\nabla _{\varvec{y}} \varTheta _{\tau ,\rho }(\varvec{x},\varvec{y}) = \varvec{0}. \end{aligned} \end{aligned}$$

In the next section, we give, in a formal mathematical sense, how well the above minimization problem approximates the original problem (P-bilevel).

3 An algorithm and its theoretical analysis

Supported by the discussion in the previous section, we propose a method for solving (P-bilevel) that we call Nonsmooth Bilevel Optimization Algorithm – NoBOA for short –, and it is summarized in Algorithm 1. Before going into the details of Algorithm 1, it is important to say that, although in Step 1 we assume that problem ($\tilde{P}_k$) is globally solved, we show in Theorem 3 that this request can be weakened to a local solution. Moreover, the expected exactness of the solution $(\varvec{x}^k, \varvec{y}^k)$ given in Step 1 may initially concern the reader regarding the practice of such a method. This matter will be properly addressed at the end of this section.

Relying on the assumption that ($\tilde{P}_k$) approximates well the problem (P-bilevel), we perform Step 1 in order to obtain an approximation $(\varvec{x}^k,\varvec{y}^k)$ for a local solution of the original problem, with Step 2 being a stopping criteria. Moreover, since this approximation only makes sense when $\tau _k\approx 0$, Step 3 performs an update for the value of $\tau _k$ at each iteration driven by the term $\Vert \varvec{c^\text {in}}(\varvec{x}^k,\varvec{y}^k)_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x}^k,\varvec{y}^k)\Vert ^2$. The parameter $\tau _k$ plays the role of a target value for the infeasibility of the point $(\varvec{x}^k, \varvec{y}^k)$ in relation to the feasible set of the lower-level optimization. Therefore, when this target value is reached (i.e., $\Vert \varvec{c^\text {in}}(\varvec{x}^k,\varvec{y}^k)_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x}^k,\varvec{y}^k)\Vert ^2 < \tau ^2$), then a reduction on the parameter can be done – see Fig. 2; otherwise, we set $\tau _{k+1} = \tau _k$. Finally, Step 4 sets an adjustment on the value of $\rho _{k+1}$ in order to predict a sufficiently negative value for the difference $f(\varvec{x}^{k+1},\varvec{y}^{k+1}) - \rho _{k+1}$.

Fig. 2

An illustration of the update that appears inside Step 3 of Algorithm 1 whenever $\Vert \varvec{c^\text {in}}(\varvec{x}^k,\varvec{y}^k)_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x}^k,\varvec{y}^k)\Vert ^2 < \tau _k^2$

The subsequent results aim at proving that the NoBOA method is capable of converging to a local optimal solution of (P-bilevel). First, we need to establish a relation between the function $\varTheta _{\tau ,\rho }$ and problem (P-lower). For that, we need some preliminary results.

Lemma 1

Under the assumptions that the set $\mathcal S$ – defined in (1) – is nonempty and compact, and that, for every $\varvec{x}\in \mathbb {R}^n$ satisfying $\varvec{C}(\varvec{x})\le \varvec{0}$, the set $\varOmega (\varvec{x})$ is nonempty, it follows that

$$\begin{aligned} \mathcal S_{\alpha }:= \{ (\varvec{x},\varvec{y})\in \mathbb {R}^n\times \mathbb {R}^m: \varvec{C}(\varvec{x})\le \varvec{0},~\Vert \varvec{c^\text {in}}(\varvec{x},\varvec{y})_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x},\varvec{y})\Vert ^2 \le \alpha \} \end{aligned}$$

is also a nonempty and compact set for any $\alpha \in \mathbb {R}_+$. In particular, for any chosen $\alpha \in \mathbb {R}_+$, it follows that the set

$$\begin{aligned} \varOmega _\alpha (\bar{\varvec{x}}):= \left\{ \varvec{y}\in \mathbb {R}^m: \Vert \varvec{c^\text {in}}(\bar{\varvec{x}},\varvec{y})_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\bar{\varvec{x}},\varvec{y})\Vert ^2 \le \alpha \right\} \end{aligned}$$

is nonempty and compact for any $\bar{\varvec{x}}\in \mathbb {R}^n$ satisfying $\varvec{C}(\bar{\varvec{x}})\le \varvec{0}$.

Proof

Since $\mathcal S$ is nonempty, it is straightforward to see that $\mathcal S_{\alpha }$ is also a nonempty set. Moreover, because the functions $\varvec{c^\text {eq}}$, $\varvec{c^\text {in}}$ and $\varvec{C}$ are continuous, it also follows that $\mathcal S_{\alpha }$ is a closed set for any $\alpha > 0$. Therefore, it remains for us to prove that $\mathcal S_{\alpha }$ is bounded for any arbitrary $\alpha \in \mathbb {R}_+$. So, by contradiction, let us suppose that $\mathcal S_{\alpha }$ is not bounded for some $\alpha \in \mathbb {R}_+$. Therefore, there exists a sequence $\{(\varvec{x}^k, \varvec{y}^k)\} \subset \mathcal S_{\alpha }$ such that $\Vert (\varvec{x}^k, \varvec{y}^k) \Vert \rightarrow \infty$. Notice however that, because of our hypotheses, it follows that the set $\{ \varvec{x} \in \mathbb {R}^n : \varvec{C}(\varvec{x}) \le \varvec{0} \}$ is compact. Therefore, the sequence $\{\varvec{y}^k\}\subset \mathbb {R}^m$ must be unbounded. So, without loss of generality, we may suppose that

$$\begin{aligned} \varvec{x}^k \rightarrow \bar{\varvec{x}},\quad \varvec{y}^k\in \varOmega _\alpha (\varvec{x}^k)\quad \text {and}\quad \Vert \varvec{y}^k\Vert \ge k\text {, for all }k\in \mathbb {N}, \end{aligned}$$

for some $\bar{\varvec{x}}\in \mathbb {R}^n$ satisfying $\varvec{C}(\bar{\varvec{x}})\le \varvec{0}$. By hypothesis, $\varOmega (\bar{\varvec{x}})$ is nonempty. Additionally, $\varOmega (\bar{\varvec{x}})$ is also compact, otherwise the set $\mathcal S$ would not be compact. So, there must exist a sufficiently large ${\hat{k}}\in \mathbb {N}$ and $\bar{\varvec{y}} \in \varOmega (\bar{\varvec{x}})$ such that $\Vert \varvec{y}-\bar{\varvec{y}}\Vert \ge {\hat{k}}\Rightarrow \varvec{y}\notin \varOmega (\bar{\varvec{x}})$. We then define

$$\begin{aligned} \lambda _k = \frac{{\hat{k}}}{\Vert \varvec{y}^k-\bar{\varvec{y}}\Vert }. \end{aligned}$$

Since $\Vert \varvec{y}^k\Vert \rightarrow \infty$, we must have that $\lambda _k\in [0,1]$, for any large $k\in \mathbb {N}$. So, without loss of generality, we assume that $\lambda _k\in [0,1]$, for all $k\in \mathbb {N}$. Additionally, defining $\varvec{z}^k := (1-\lambda _k)\bar{\varvec{y}} + \lambda _k \varvec{y}^k$, we see that

$$\begin{aligned} \Vert \varvec{z}^k - \bar{\varvec{y}}\Vert = \lambda _k\Vert \varvec{y}^k - \bar{\varvec{y}} \Vert = \frac{{\hat{k}}}{\Vert \varvec{y}^k-\bar{\varvec{y}}\Vert }\Vert \varvec{y}^k - \bar{\varvec{y}}\Vert = {\hat{k}}. \end{aligned}$$

Consequently, $\{\varvec{z}^k\}$ is bounded. Hence, we may suppose without loss of generality that $\varvec{z}^k\rightarrow \bar{\varvec{z}}$, for some $\bar{\varvec{z}}\in \mathbb {R}^m$. By the definition of ${\hat{k}}$, it yields $\bar{\varvec{z}}\notin \varOmega (\bar{\varvec{x}})$.

Let us fix $i\in \{1,\ldots ,q\}$ and $j\in \{1,\ldots ,s\}$. Since, for each $k\in \mathbb {N}$, the function $c^\text {in}_i(\varvec{x}^k,\cdot )$ is convex, $c^\text {eq}_j(\varvec{x}^k,\cdot )$ is affine-linear, and $\varvec{y}^k \in \varOmega _{\alpha }(\varvec{x}^k)$, we must have

$$\begin{aligned} c^\text {in}_i\left( \varvec{x}^k, (1-\lambda _k)\bar{\varvec{y}} + \lambda _k \varvec{y}^k \right) _+\le & {} (1-\lambda _k)c^\text {in}_i(\varvec{x}^k, \bar{\varvec{y}})_+ + \lambda _k c^\text {in}_i(\varvec{x}^k, \varvec{y}^k)_{+} \nonumber \\\le & {} (1-\lambda _k)c^\text {in}_i(\varvec{x}^k, \bar{\varvec{y}})_+ + \lambda _k \sqrt{\alpha }, \end{aligned}$$

(3)

and

$$\begin{aligned} \begin{aligned} \left| c^\text {eq}_j\left( \varvec{x}^k, (1-\lambda _k)\bar{\varvec{y}} + \lambda _k \varvec{y}^k \right) \right| \le {}&(1-\lambda _k)|c^\text {eq}_j(\varvec{x}^k, \bar{\varvec{y}})| + \lambda _k |c^\text {eq}_j(\varvec{x}^k, \varvec{y}^k)| \\ \le {}&(1-\lambda _k)|c^\text {eq}_j(\varvec{x}^k, \bar{\varvec{y}})| + \lambda _k \sqrt{\alpha }. \end{aligned} \end{aligned}$$

(4)

Recalling that $c^\text {in}_i(\bar{\varvec{x}}, \bar{\varvec{y}})_+ = 0$ and $|c^\text {eq}_j(\bar{\varvec{x}}, \bar{\varvec{y}})| = 0$ – because $\bar{\varvec{y}}\in \varOmega (\bar{\varvec{x}})$ –, and noticing that $\lambda _k\rightarrow 0$, we see, by considering the limit $k\rightarrow \infty$ in inequalities (3) and (4), that $c^\text {in}_i(\bar{\varvec{x}}, \bar{\varvec{z}})_+ = 0$ and $|c^\text {eq}_j(\bar{\varvec{x}}, \bar{\varvec{z}})| = 0$. Since i and j are arbitrary, this is a contradiction with $\bar{\varvec{z}}\notin \varOmega (\bar{\varvec{x}})$. So, the statement must be true. $\square$

We proceed with our analysis by proving, under mild assumptions, that a global minimizer of $\varTheta _{\tau ,\rho }(\varvec{x},\cdot )$ can always be found.

Lemma 2

Let $\tau$ be any strictly positive real number and $\rho \in \mathbb {R}$. If $\bar{\varvec{x}}\in \mathbb {R}^n$ satisfies $\varvec{C}(\bar{\varvec{x}})\le \varvec{0}$, and $\varOmega (\bar{\varvec{x}})$ is nonempty and compact, then one can always find a global minimizer of $\varTheta _{\tau ,\rho }(\bar{\varvec{x}},\cdot )$.

Proof

We first show that $\varTheta _{\tau ,\rho }(\bar{\varvec{x}},\cdot )$ is bounded from below. Notice that for any $\varvec{y}\in \mathbb {R}^m$ satisfying $\Vert \varvec{c^\text {in}}(\bar{\varvec{x}},\varvec{y})_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\bar{\varvec{x}},\varvec{y})\Vert ^2\le \tau ^2$, there exists $L\in \mathbb {R}$ such that $L \le \varTheta _{\tau ,\rho }(\bar{\varvec{x}},\varvec{y})$, since, by Lemma 1, the set $\varOmega _\alpha (\bar{\varvec{x}})$ is compact for any $\alpha \in \mathbb {R}_+$. Moreover, for the case that $\varvec{y}\in \mathbb {R}^m$ satisfies $\Vert \varvec{c^\text {in}}(\bar{\varvec{x}},\varvec{y})_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\bar{\varvec{x}},\varvec{y})\Vert ^2 > \tau ^2$, we have

$$\begin{aligned} \varTheta _{\tau ,\rho }(\bar{\varvec{x}},\varvec{y}) = \Vert \varvec{c^\text {in}}(\bar{\varvec{x}},\varvec{y})_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\bar{\varvec{x}},\varvec{y})\Vert ^2 \ge 0. \end{aligned}$$

So, one can see that

$$\begin{aligned} \varTheta _{\tau ,\rho }(\bar{\varvec{x}},\varvec{y}) \ge \min \{L,0\}\text {, for any }\varvec{y}\in \mathbb {R}^m, \end{aligned}$$

which implies that $\displaystyle \inf _{\varvec{y}\in \mathbb {R}^m} \varTheta _{\tau ,\rho }(\bar{\varvec{x}},\varvec{y})$ exists. Therefore, let $\{ \varvec{y}^k \}\subset \mathbb {R}^m$ be a sequence such that

$$\begin{aligned} N:=\lim _{k\rightarrow \infty }\varTheta _{\tau ,\rho }(\bar{\varvec{x}},\varvec{y}^k) = \inf _{\varvec{y}\in \mathbb {R}^m} \varTheta _{\tau ,\rho }(\bar{\varvec{x}},\varvec{y}). \end{aligned}$$

We now split the proof in two complementary cases:

• i) there exists a sufficiently large ${\hat{k}}\in \mathbb {N}$ such that $k\ge {\hat{k}}$ implies the inequality $\Vert \varvec{c^\text {in}}(\bar{\varvec{x}},\varvec{y}^k)_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\bar{\varvec{x}},\varvec{y}^k)\Vert ^2\ge \tau ^2$;

• ii) there exists an infinite index set $\mathcal K\subset \mathbb {N}$ such that we obtain the strict inequality $\Vert \varvec{c^\text {in}}(\bar{\varvec{x}},\varvec{y}^k)_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\bar{\varvec{x}},\varvec{y}^k)\Vert ^2 < \tau ^2$, for all $k\in \mathcal K$.

Suppose case i) holds. Then, by the very definition of $\varTheta _{\tau ,\rho }$, we get

$$\begin{aligned} \varTheta _{\tau ,\rho }(\bar{\varvec{x}},\varvec{y}^k) = \Vert \varvec{c^\text {in}}(\bar{\varvec{x}},\varvec{y}^k)_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\bar{\varvec{x}},\varvec{y}^k)\Vert ^2\text {, for all }k\ge {\hat{k}}. \end{aligned}$$

Therefore, $N\ge \tau ^2$. However, since we assume that $\varOmega (\bar{\varvec{x}})$ is not empty, there must exist $\bar{\varvec{y}}\in \mathbb {R}^m$ such that $\varvec{c^\text {in}}(\bar{\varvec{x}},\bar{\varvec{y}})\le \varvec{0}$ and $\varvec{c^\text {eq}}(\bar{\varvec{x}},\bar{\varvec{y}}) = \varvec{0}$. Now, due to the continuity of the functions $\varvec{c^\text {in}}$ and $\varvec{c^\text {eq}}$, and because $\Vert \varvec{c^\text {in}}(\bar{\varvec{x}},\varvec{y}^{{\hat{k}}})_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\bar{\varvec{x}},\varvec{y}^{{\hat{k}}})\Vert ^2\ge \tau ^2$, it follows that there must exist $\tilde{\varvec{y}}\in \mathbb {R}^m$ such that

$$\begin{aligned} \Vert \varvec{c^\text {in}}(\bar{\varvec{x}},\tilde{\varvec{y}})_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\bar{\varvec{x}},\tilde{\varvec{y}})\Vert ^2 = \tau ^2. \end{aligned}$$

This implies that $N = \tau ^2$ and that the infimum is attained at $\tilde{\varvec{y}}$, which guarantees a global minimizer for $\varTheta _{\tau ,\rho }(\bar{\varvec{x}},\cdot )$.

If ii) is the case, then, because $\varOmega _\alpha (\bar{\varvec{x}})$ is a nonempty and compact set for any $\alpha \in \mathbb {R}_+$ (again, see Lemma 1), we see that the sequence $\{\varvec{y}^k\}_{k\in \mathcal K}$ belongs to a compact set of $\mathbb {R}^m$. Therefore, there must exist a subsequence of $\{\varvec{y}^k\}_{k\in \mathcal K}$ converging to some point $\bar{\varvec{y}}\in \mathbb {R}^m$ and attaining the infimum value of $\varTheta _{\tau ,\rho }(\bar{\varvec{x}},\cdot )$. This implies that $\bar{\varvec{y}}$ is a global minimizer of $\varTheta _{\tau ,\rho }(\bar{\varvec{x}},\cdot )$, which ends our proof. $\square$

The result above is of great importance, because it tells us that the feasible set of problem ($\tilde{P}_k$) is never empty, since a global minimizer of $\varTheta _{\tau ,\rho }$ is, in particular, a stationary point for the same function. We now exhibit the statement that presents a relation between $\varTheta _{\tau _k,\rho }$ and the minimizers of problem (P-lower).

Proposition 1

Let $\bar{\varvec{x}}\in \mathbb {R}^n$ be any point satisfying $\varvec{C}(\bar{\varvec{x}})\le \varvec{0}$, and suppose that $\varOmega (\bar{\varvec{x}})$ is a nonempty and compact set, and $\mathcal R(\bar{\varvec{x}}) = \{{ \bar{\varvec{y}}}\}$. Then, given any $\{\tau _k\}\subset \mathbb {R}^*_+$, with $\tau _k\rightarrow 0$, and any $\rho > f(\bar{\varvec{x}}, { \bar{\varvec{y}}})$, there must exist $\{\varvec{y}^k\}\subset \mathbb {R}^m$ such that $\varvec{y}^k\rightarrow { \bar{\varvec{y}}}$ and

$$\begin{aligned} \nabla _{\varvec{y}} \varTheta _{\tau _k,\rho }(\bar{\varvec{x}},\varvec{y}^k)= \varvec{0}\text{, }\quad \text {for all }k\in \mathbb {N}. \end{aligned}$$

Proof

Let $\{\varvec{y}^k\}\subset \mathbb {R}^m$ be a sequence such that each element is given by

$$\begin{aligned} \varvec{y}^k\in {{\,\mathrm{\arg min}\,}}_{\varvec{y}\in \mathbb {R}^m} \varTheta _{\tau _k,\rho }(\bar{\varvec{x}},\varvec{y}). \end{aligned}$$

(5)

Notice that Lemma 2 guarantees that the sequence above is well defined. As a consequence, we must have $\varTheta _{\tau _k,\rho }(\bar{\varvec{x}},\varvec{y}^k) \le \varTheta _{\tau _k,\rho }(\bar{\varvec{x}},{ \bar{\varvec{y}}}) = f(\bar{\varvec{x}},{ \bar{\varvec{y}}}) - \rho < 0$. But $\varTheta _{\tau _k,\rho }(\bar{\varvec{x}},\varvec{y}^k)$ can only be negative if

$$\begin{aligned} \Vert \varvec{c^\text {in}}(\bar{\varvec{x}},\varvec{y}^k)_+ \Vert ^2 + \Vert \varvec{c^\text {eq}}(\bar{\varvec{x}},\varvec{y}^k)\Vert ^2 < \tau _k^2. \end{aligned}$$

(6)

Hence, due to Lemma 1, $\{\varvec{y}^k\}$ must be a bounded sequence.

We claim that $\varvec{y}^k\rightarrow { \bar{\varvec{y}}}$. By contradiction, we assume that this convergence does not hold. So, there must exist an infinite index set $\mathcal K\subset \mathbb {N}$ and $\delta > 0$ such that $\Vert \varvec{y}^k-{ \bar{\varvec{y}}}\Vert \ge \delta$, for all $k\in \mathcal K$. Because $\{\varvec{y}^k\}$ is bounded, we can suppose without loss of generality that $\mathcal K$ was chosen in a way that $\varvec{y}^k\underset{k\in \mathcal K}{\rightarrow } \hat{\varvec{y}}$, for some $\hat{\varvec{y}}\ne { \bar{\varvec{y}}}$. Also, notice that

$$\begin{aligned} 0\le \mu _k:= \max \left\{ 1 - \frac{\Vert \varvec{c^\text {in}}(\bar{\varvec{x}},\varvec{y}^k)_+ \Vert ^2 + \Vert \varvec{c^\text {eq}}(\bar{\varvec{x}},\varvec{y}^k)\Vert ^2}{\tau _k^2} , 0 \right\} ^2 \le 1. \end{aligned}$$

Therefore, one may also assume without loss of generality that $\mathcal K$ was chosen to satisfy $\mu _k\underset{k\in \mathcal K}{\rightarrow } {\hat{\mu }}$, for some ${\hat{\mu \in }} [0,1]$. Then, recalling relation (6) and $\tau _k\rightarrow 0$, we see that $\hat{\varvec{y}}\in \varOmega (\bar{\varvec{x}})$. Moreover, since $\varvec{y}^k$ solves the problem in (5), the following holds

$$\begin{aligned} \lim _{k\in \mathcal K} \varTheta _{\tau _k,\rho }(\bar{\varvec{x}},\varvec{y}^k) \le \lim _{k\in \mathcal K} \varTheta _{\tau _k,\rho }(\bar{\varvec{x}},{ \bar{\varvec{y}}}) \Rightarrow {\hat{\mu [f}}(\bar{\varvec{x}}, \hat{\varvec{y}}) - \rho ]\le f(\bar{\varvec{x}},{ \bar{\varvec{y}}}) - \rho . \end{aligned}$$

Because $f(\bar{\varvec{x}},{ \bar{\varvec{y}}}) - \rho$ is negative, we see that ${\hat{\mu [f}}(\bar{\varvec{x}}, \hat{\varvec{y}})-\rho ]$ must also be negative. Additionally, since ${\hat{\mu \in }} [0,1]$, the right-hand side of the last implication above gives us $f(\bar{\varvec{x}}, \hat{\varvec{y}})\le f(\bar{\varvec{x}},{ \bar{\varvec{y}}})$. But $\hat{\varvec{y}}\in \varOmega (\bar{\varvec{x}})$, and $\mathcal R(\bar{\varvec{x}})$ was assumed to be a singleton, which yields $\hat{\varvec{y}} = { \bar{\varvec{y}}}$. However, this is a contradiction with the fact that $\hat{\varvec{y}} \ne { \bar{\varvec{y}}}$. Hence, $\varvec{y}^k\rightarrow { \bar{\varvec{y}}}$ and the statement is proven. $\square$

The next condition shows a relation between the function $\varTheta _{\tau ,\rho }$ and the Fritz John optimality conditions associated with the optimization problem that appears in $\mathcal R(\bar{\varvec{x}})$.

Lemma 3

Let $\bar{\varvec{x}}$ be any fixed vector in $\mathbb {R}^n$ satisfying $\varvec{C}(\bar{\varvec{x}})\le \varvec{0}$, and with $\varOmega (\bar{\varvec{x}})$ being nonempty and compact. Additionally, let $\bar{\varvec{y}}\in \varOmega (\bar{\varvec{x}})$. Assume also that $\{\rho _k\}\subset \mathbb {R}$ is a sequence such that each element satisfies $\rho _k\ge f(\bar{\varvec{x}},\bar{\varvec{y}}) + M$, for some $M>0$. If there exist sequences $\{(\varvec{x}^k, \varvec{y}^k)\}\subset \mathbb {R}^n\times \mathbb {R}^m$ and $\{\tau _k\}\subset \mathbb {R}_+^*$ satisfying $\tau _k\rightarrow 0$, $(\varvec{x}^k, \varvec{y}^k)\rightarrow (\bar{\varvec{x}},\bar{\varvec{y}})$ and

$$\begin{aligned} \Vert \nabla _{\varvec{y}}\varTheta _{\tau _k,\rho _k}({\varvec{x}^k}, {\varvec{y}^k})\Vert = o(\tau _k)\quad \text {for all }k\in \mathbb {N}, \end{aligned}$$

(7)

then the Fritz John optimality conditions associated with the optimization problem related to $\mathcal R(\bar{\varvec{x}})$ are satisfied at $\bar{\varvec{y}}$.

Proof

For fixed values $\tau \in \mathbb {R}_+^*$ and $\rho \in \mathbb {R}$, notice that

$$\begin{aligned} \begin{aligned} \nabla _{\varvec{y}}\varTheta _{\tau ,\rho }(\varvec{x},\varvec{y}) = {}&\sigma _{\tau ,\rho }(\varvec{x},\varvec{y})\left[ \sum _{i=1}^q [c^\text {in}_i(\varvec{x},\varvec{y})_+]\nabla _{\varvec{y}}c^\text {in}_i(\varvec{x},\varvec{y}) + \sum _{j=1}^s c^\text {eq}_j(\varvec{x},\varvec{y})\nabla _{\varvec{y}}c^\text {eq}_j(\varvec{x},\varvec{y}) \right] \\ {}&+ \zeta _{\tau }(\varvec{x},\varvec{y})\nabla _{\varvec{y}} f(\varvec{x}, \varvec{y}), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \sigma _{\tau ,\rho }(\varvec{x},\varvec{y}):= 1+\frac{2}{\tau ^2}[\rho - f(\varvec{x},\varvec{y})]\max \left\{ 1 - \frac{\Vert \varvec{c^\text {in}}(\varvec{x},\varvec{y})_+ \Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x},\varvec{y})\Vert ^2}{\tau ^2} , 0 \right\} \end{aligned}$$

and

$$\begin{aligned} \zeta _{\tau }(\varvec{x},\varvec{y}):= \max \left\{ 1 - \frac{\Vert \varvec{c^\text {in}}(\varvec{x},\varvec{y})_+ \Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x},\varvec{y})\Vert ^2}{\tau ^2} , 0 \right\} ^2. \end{aligned}$$

Additionally, we define, for all $(\varvec{x},\varvec{y})\in \mathbb {R}^n\times \mathbb {R}^m$,

$$\begin{aligned} \beta _{\tau , \rho }(\varvec{x},\varvec{y}):= \max _{1\le i\le q,1\le j\le s}\left\{ \sigma _{\tau ,\rho }(\varvec{x},\varvec{y})c^\text {in}_i(\varvec{x},\varvec{y})_+,\sigma _{\tau ,\rho }(\varvec{x},\varvec{y})|c^\text {eq}_j(\varvec{x},\varvec{y})|, \zeta _{\tau }(\varvec{x},\varvec{y}) \right\} . \end{aligned}$$

Now, without loss of generality, we can suppose that $f(\varvec{x}^k, \varvec{y}^k) - \rho _k < 0$, for all $k\in \mathbb {N}$, since we have by hypothesis that $\rho _k\ge f(\bar{\varvec{x}}, \bar{\varvec{y}}) + M$ and $(\varvec{x}^k, \varvec{y}^k)\rightarrow (\bar{\varvec{x}}, \bar{\varvec{y}})$. Then, $\beta _{\tau _k, \rho _k}(\varvec{x}^k, \varvec{y}^k)>0$ and, since $\Vert \nabla _{\varvec{y}}\varTheta _{\tau _k,\rho _k}(\varvec{x}^k, \varvec{y}^k)\Vert = o(\tau _k)$, it follows that

$$\begin{aligned} \lambda _{k}^f\nabla _{\varvec{y}} f(\varvec{x}^k, \varvec{y}^k) + \sum _{i=1}^q \lambda _{k}^{c^\text {in}_i}\nabla _{\varvec{y}}c^\text {in}_i(\varvec{x}^k, \varvec{y}^k) + \sum _{j=1}^s \lambda _{k}^{c^\text {eq}_j}\nabla _{\varvec{y}}c^\text {eq}_j(\varvec{x}^k, \varvec{y}^k) = \frac{o(\tau _k)}{\beta _{\tau _k, \rho _k}(\varvec{x}^k, \varvec{y}^k)}, \end{aligned}$$

where

$$\begin{aligned} \lambda _{k}^{c^\text {in}_i} := \frac{\sigma _{\tau _k,\rho _k}(\varvec{x}^k, \varvec{y}^k)c^\text {in}_i(\varvec{x}^k, \varvec{y}^k)_+}{\beta _{\tau _k, \rho _k}(\varvec{x}^k, \varvec{y}^k)}\text{, }\quad \lambda _{k}^{c^\text {eq}_j}:= \frac{\sigma _{\tau _k,\rho _k}(\varvec{x}^k, \varvec{y}^k)c^\text {eq}_j(\varvec{x}^k, \varvec{y}^k)}{\beta _{\tau _k, \rho _k}(\varvec{x}^k, \varvec{y}^k)} \end{aligned}$$

and

$$\begin{aligned} \lambda _{k}^f:= \frac{\zeta _{\tau _k}(\varvec{x}^k, \varvec{y}^k)}{\beta _{\tau _k, \rho _k}(\varvec{x}^k, \varvec{y}^k)}. \end{aligned}$$

We claim that $o(\tau _k)/\beta _{\tau _k, \rho _k}(\varvec{x}^k, \varvec{y}^k)\rightarrow 0$. To prove such a statement, we have two cases:

• i) there is an infinite index set $\mathcal K_1\subset \mathbb {N}$ such that $\zeta _{\tau _k}(\varvec{x}^k, \varvec{y}^k) > 0.5^2$ for all $k\in \mathcal K_1$;

• ii) there is an infinite index set $\mathcal K_2\subset \mathbb {N}$ such that $\zeta _{\tau _k}(\varvec{x}^k, \varvec{y}^k) \le 0.5^2$ for all $k\in \mathcal K_2$.

If case i) happens, then by the way $\beta _{\tau , \rho }(\varvec{x}, \varvec{y})$ was defined, it follows immediately that $o(\tau _k)/\beta _{\tau _k, \rho _k}(\varvec{x}^k, \varvec{y}^k)\underset{k\in \mathcal K_1}{\rightarrow } 0$. Moreover, if case ii) holds, then we must have, for all $k\in \mathcal K_2$,

$$\begin{aligned} 0.5\tau _k^2 \le \Vert \varvec{c^\text {in}}(\varvec{x}^k, \varvec{y}^k)_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x}^k, \varvec{y}^k)\Vert ^2. \end{aligned}$$

(8)

Recalling the definition of $\beta _{\tau , \rho }(\varvec{x}, \varvec{y})$, one can see that there exists $\alpha > 0$ such that $\alpha \tau _k\le \beta _{\tau _k, \rho _k}(\varvec{x}^k, \varvec{y}^k)$ for all $k\in \mathcal K_2$, since the inequality (8) guarantees that at least one constraint must be of order $\tau _k$. This ensures that $o(\tau _k)/\beta _{\tau _k, \rho _k}(\varvec{x}^k, \varvec{y}^k)\underset{k\in \mathcal K_2}{\rightarrow } 0$. So, putting together the cases i) and ii), we obtain $o(\tau _k)/\beta _{\tau _k, \rho _k}(\varvec{x}^k, \varvec{y}^k)\rightarrow 0$ as desired. Therefore, due to (7), it follows that

$$\begin{aligned} \lambda _{k}^f\nabla _{\varvec{y}} f(\varvec{x}^k, \varvec{y}^k) + \sum _{i=1}^q \lambda _{k}^{c^\text {in}_i}\nabla _{\varvec{y}}c^\text {in}_i(\varvec{x}^k, \varvec{y}^k) + \sum _{j=1}^s \lambda _{k}^{c^\text {eq}_j}\nabla _{\varvec{y}}c^\text {eq}_j(\varvec{x}^k, \varvec{y}^k) \rightarrow \varvec{0}. \end{aligned}$$

In addition, notice that $\lambda _{k}^{f},\lambda _{k}^{c^\text {in}_i}\in [0,1]$ and $\lambda _{k}^{c^\text {eq}_j}\in [-1,1]$, which yields that there must exist an infinite index set $\mathcal K\subset \mathbb {N}$ and values $\lambda ^f,\lambda ^{c^\text {in}_i}\in [0,1]$ and $\lambda ^{c^\text {eq}_j}\in [-1,1]$ such that

$$\begin{aligned} \lambda _{k}^f\underset{k\in \mathcal K}{\rightarrow } \lambda ^f,\quad \lambda _{k}^{c^\text {in}_i}\underset{k\in \mathcal K}{\rightarrow } \lambda ^{c^\text {in}_i}\quad \text {and}\quad \lambda _{k}^{c^\text {eq}_j}\underset{k\in \mathcal K}{\rightarrow } \lambda ^{c^\text {eq}_j}\text {, for all } i \in \{1,\ldots , q\},~j \in \{1,\ldots , s\}. \end{aligned}$$

Consequently, recalling $(\varvec{x}^k, \varvec{y}^k)\rightarrow (\bar{\varvec{x}},\bar{\varvec{y}})$ and that the underlying functions of the lower-level problems are of class $C^2$, we have

$$\begin{aligned} \lambda ^f\nabla _{\varvec{y}} f(\bar{\varvec{x}}, \bar{\varvec{y}}) + \sum _{i=1}^q \lambda ^{c^\text {in}_i}\nabla _{\varvec{y}}c^\text {in}_i(\bar{\varvec{x}},\bar{\varvec{y}}) + \sum _{j=1}^s \lambda ^{c^\text {eq}_j}\nabla _{\varvec{y}}c^\text {eq}_j(\bar{\varvec{x}},\bar{\varvec{y}}) = \varvec{0}. \end{aligned}$$

By the definition of the values $\lambda _{k}^{f}$, $\lambda _{k}^{c^\text {in}_i}$ and $\lambda _{k}^{c^\text {eq}_j}$, one can see that

$$\begin{aligned} \max _{1\le i\le q,1\le j\le s}\left\{ \lambda _{k}^{f},\lambda _{k}^{c^\text {in}_i},\left| \lambda _{k}^{c^\text {eq}_j}\right| \right\} = 1\text {, for all }k\in \mathbb {N}. \end{aligned}$$

This implies that $\lambda ^f$, $\lambda ^{c^\text {in}_i}$ and $\lambda ^{c^\text {eq}_j}$ cannot be all simultaneously zero, which completes the proof. $\square$

Our analysis proceeds with another technical lemma.

Lemma 4

Let $\tau \in \mathbb {R}_+$, $\rho \in \mathbb {R}$ and $(\tilde{\varvec{x}},\tilde{\varvec{y}})$ be any point in $\mathbb {R}^n\times \mathbb {R}^m$ satisfying $\varvec{C}(\tilde{\varvec{x}})\le \varvec{0}$ and $\nabla _{\varvec{y}}\varTheta _{\tau ,\rho }(\tilde{\varvec{x}},\tilde{\varvec{y}}) = \varvec{0}$. Additionally, suppose that $\varOmega (\tilde{\varvec{x}})$ is not empty. Then, $\Vert \varvec{c^\text {in}}(\tilde{\varvec{x}},\tilde{\varvec{y}})_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\tilde{\varvec{x}},\tilde{\varvec{y}})\Vert ^2 \le \tau ^2$.

Proof

By contradiction, suppose that the statement is false, i.e., $\Vert \varvec{c^\text {in}}(\tilde{\varvec{x}},\tilde{\varvec{y}})_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\tilde{\varvec{x}},\tilde{\varvec{y}})\Vert ^2 > \tau ^2$. Therefore, this ensures that

$$\begin{aligned} \nabla _{\varvec{y}}\varTheta _{\tau ,\rho }(\tilde{\varvec{x}},\tilde{\varvec{y}}) = \nabla _{\varvec{y}}\left( \Vert \varvec{c^\text {in}}(\tilde{\varvec{x}},\tilde{\varvec{y}})_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\tilde{\varvec{x}},\tilde{\varvec{y}})\Vert ^2\right) . \end{aligned}$$

Since $c^\text {in}_i(\tilde{\varvec{x}},\cdot )$ is convex for any $i\in \{1,\ldots ,q\}$, $c^\text {eq}_j(\tilde{\varvec{x}},\cdot )$ is affine-linear for any $j\in \{1,\ldots ,s\}$ and $\nabla _{\varvec{y}}\varTheta _{\tau ,\rho }(\tilde{\varvec{x}},\tilde{\varvec{y}}) = \varvec{0}$, it follows that $\tilde{\varvec{y}}$ is a global minimizer of $\Vert \varvec{c^\text {in}}(\tilde{\varvec{x}},\cdot )_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\tilde{\varvec{x}},\cdot )\Vert ^2$. But this contradicts our assumption that $\varOmega (\tilde{\varvec{x}})$ is nonempty. Therefore, the statement must be true. $\square$

In possession of these results, we are now able to make statements regarding the NoBOA method. For the remaining results, all hypotheses made in Sect. 2 for problem (P-bilevel) are assumed to hold true. First, we claim that Step 1 of Algorithm 1 is well defined.

Lemma 5

The procedure in Step 1 of Algorithm 1 is well defined, i.e., a solution of ($\tilde{P}_k$) can always be found for any $k\in \mathbb {N}$.

Proof

By Lemma 2, we know that the feasible region of ($\tilde{P}_k$) is never empty for any $k\in \mathbb {N}$. So, let us show that this feasible region is also compact for any fixed $k\in \mathbb {N}$. Lemma 4 tells us that any feasible point $(\tilde{\varvec{x}},\tilde{\varvec{y}})$ for ($\tilde{P}_k$) at iteration k belongs to the set

$$\begin{aligned} \mathcal S_{\tau ^2_k} = \{ (\varvec{x},\varvec{y})\in \mathbb {R}^n\times \mathbb {R}^m: \varvec{C}(\varvec{x})\le \varvec{0}, \Vert \varvec{c^\text {in}}(\varvec{x},\varvec{y})_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x},\varvec{y})\Vert ^2 \le \tau _k^2 \}. \end{aligned}$$

Additionally, Lemma 1 guarantees that $\mathcal S_{\tau ^2_k}$ is a compact set. Therefore, the feasible set of ($\tilde{P}_k$) must be bounded. Moreover, it is straightforward to see that such a set is also closed, which ensures that the feasible set is compact. Since $F(\varvec{x},\varvec{y})$ is a continuous function, the statement follows. $\square$

The following lemma guarantees that the value $\tau _k$ will monotonically decrease to zero, a result that is crucial to ensure that ($\tilde{P}_k$) approximates the original bilevel problem.

Lemma 6

Suppose that $\tau _\text {opt} = 0$, and let $\{\tau _k\}\subset \mathbb {R}^*_+$ be the sequence generated by Algorithm 1. Then, $\{\tau _k\}$ is a monotone decreasing sequence converging to zero.

Proof

The fact that $\{\tau _k\}$ is a monotone decreasing sequence follows immediately from Step 3. Therefore, since $\tau _k>0$, for all $k\in \mathbb {N}$, it follows that $\tau _k\rightarrow \bar{\tau }$, for some $\bar{\tau }\in \mathbb {R}_+$. By contradiction, suppose that $\bar{\tau }> 0$. From Step 3, it follows

$$\begin{aligned} \tau _{k}^2 - \tau _{k+1}^2 = (1-\theta _{\tau _k})^2\left[ \tau _k^2 - \left( \Vert \varvec{c^\text {in}}(\varvec{x}^k,\varvec{y}^k)_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x}^k,\varvec{y}^k)\Vert ^2\right) \right] _+. \end{aligned}$$

Taking the limit of the above equation, one obtains

$$\begin{aligned} \lim _{k\rightarrow \infty }\left[ \tau _k^2 - \left( \Vert \varvec{c^\text {in}}(\varvec{x}^k,\varvec{y}^k)_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x}^k,\varvec{y}^k)\Vert ^2\right) \right] _+=0 . \end{aligned}$$

Therefore, there exists a sequence $\{\delta _k\}\subset \mathbb {R}_+$ converging to zero such that

$$\begin{aligned} \tau _k^2 - \left( \Vert \varvec{c^\text {in}}(\varvec{x}^k,\varvec{y}^k)_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x}^k,\varvec{y}^k)\Vert ^2\right) \le \delta _k, \end{aligned}$$

which implies

$$\begin{aligned} 1 - \frac{\Vert \varvec{c^\text {in}}(\varvec{x}^k,\varvec{y}^k)_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x}^k,\varvec{y}^k)\Vert ^2}{\tau _k^2}\le \frac{\delta _k}{\tau _k^2}. \end{aligned}$$

Now, because we suppose $\bar{\tau }> 0$, it follows that

$$\begin{aligned} \max \left\{ 1 - \frac{\Vert \varvec{c^\text {in}}(\varvec{x}^k,\varvec{y}^k)_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x}^k,\varvec{y}^k)\Vert ^2}{\tau _k^2} , 0 \right\} \rightarrow 0. \end{aligned}$$

(9)

Furthermore, notice that the gradient of the function $\varTheta _{\tau ,\rho }(\varvec{x},\cdot )$ can be written as

$$\begin{aligned} \sigma _{\tau ,\rho }(\varvec{x},\varvec{y})\nabla _{\varvec{y}}\left( \Vert \varvec{c^\text {in}}(\varvec{x},\varvec{y})_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x},\varvec{y})\Vert ^2 \right) + \zeta _{\tau }(\varvec{x},\varvec{y})\nabla _{\varvec{y}} f(\varvec{x}, \varvec{y}), \end{aligned}$$

(10)

where

$$\begin{aligned} \sigma _{\tau ,\rho }(\varvec{x},\varvec{y}):= 1+\frac{2}{\tau ^2}[\rho - f(\varvec{x},\varvec{y})]\max \left\{ 1 - \frac{\Vert \varvec{c^\text {in}}(\varvec{x},\varvec{y})_+ \Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x},\varvec{y})\Vert ^2}{\tau ^2} , 0 \right\} \end{aligned}$$

and

$$\begin{aligned} \zeta _{\tau }(\varvec{x},\varvec{y}):= \max \left\{ 1 - \frac{\Vert \varvec{c^\text {in}}(\varvec{x},\varvec{y})_+ \Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x},\varvec{y})\Vert ^2}{\tau ^2} , 0 \right\} ^2. \end{aligned}$$

Additionally, because of Lemma 4 and from the fact that $\{\tau _k\}$ is a monotone decreasing sequence, it follows that the iterates $(\varvec{x}^k,\varvec{y}^k)$ must all satisfy

$$\begin{aligned} \Vert \varvec{c^\text {in}}(\varvec{x}^k,\varvec{y}^k)_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\varvec{x}^k,\varvec{y}^k)\Vert ^2 \le \tau _1^2\text {, for all }k\in \mathbb {N}. \end{aligned}$$

By Lemma 1, this yields that $\{(\varvec{x}^k,\varvec{y}^k)\}$ is a bounded sequence. Hence, one can find an infinite index set $\mathcal K\subset \mathbb {N}$ such that $(\varvec{x}^k,\varvec{y}^k)\underset{k\in \mathcal K}{\rightarrow } (\bar{\varvec{x}}, \bar{\varvec{y}})$, for some $(\bar{\varvec{x}}, \bar{\varvec{y}})\in \mathbb {R}^n\times \mathbb {R}^m$. So, because (9) and (10) hold and $\nabla _{\varvec{y}}\varTheta _{\tau _k,\rho _k}(\varvec{x}^k,\varvec{y}^k) = \varvec{0}$, for all $k\in \mathbb {N}$, we see that

$$\begin{aligned} \nabla _{\varvec{y}}\left( \Vert \varvec{c^\text {in}}(\bar{\varvec{x}},\bar{\varvec{y}})_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\bar{\varvec{x}},\bar{\varvec{y}})\Vert ^2\right) = \varvec{0}. \end{aligned}$$

Hence, $\bar{\varvec{y}}$ is a global minimizer of $\left\| \varvec{c^\text {in}}\left( \bar{\varvec{x}},\cdot \right) _+\right\| ^2 + \left\| \varvec{c^\text {eq}}\left( \bar{\varvec{x}},\cdot \right) \right\| ^2$. But since $\bar{\tau }>0$, we have $\Vert \varvec{c^\text {in}}(\bar{\varvec{x}},\bar{\varvec{y}})_+\Vert ^2 + \Vert \varvec{c^\text {eq}}(\bar{\varvec{x}},\bar{\varvec{y}})\Vert ^2 > 0$, and therefore, $\varOmega (\bar{\varvec{x}}) = \emptyset$. However,

$$\begin{aligned} \lim _{k\in \mathcal K}\varvec{C}(\varvec{x}^k)\le \varvec{0}\Rightarrow \varvec{C}(\bar{\varvec{x}})\le \varvec{0}, \end{aligned}$$

which implies that $\varOmega (\bar{\varvec{x}})$ cannot be empty by our initial assumptions on problem (P-bilevel). This contradiction arose due to our assertion that $\bar{\tau }> 0$. Therefore, one must have $\bar{\tau }= 0$. $\square$

We are now ready to present a fundamental result related to the convergence of the NoBOA method. The theorem below together with a suitable constraint qualification will guarantee the desired convergence to a solution of the original problem.

Theorem 1

Suppose that $\tau _\text {opt} = 0$ and the lower-level problem has a unique solution for every upper-level variable $\varvec{x}$. Then, for any limit point $(\varvec{x}^*,\varvec{y}^*)\in \mathbb {R}^n\times \mathbb {R}^m$ of the iterate sequence $\{({\varvec{x}^k},{\varvec{y}^k})\}$ generated by Algorithm 1, the following statements hold: $\varvec{C}(\varvec{x}^*)\le \varvec{0}$; the Fritz John optimality conditions associated with the optimization problem presented in $\mathcal R(\varvec{x}^*)$ are satisfied at $\varvec{y}^*$; and

$$\begin{aligned} F(\varvec{x}^*,\varvec{y}^*)\le F(\varvec{x},\varvec{y}), \end{aligned}$$

for any $(\varvec{x},\varvec{y})\in \mathbb {R}^n\times \mathbb {R}^m$ being a feasible point for the original problem (P-bilevel). Moreover, there must exist ${\hat{k}}\in \mathbb {N}$ and $\bar{\rho }\in \mathbb {R}$ such that $\rho _k = \bar{\rho }$, for all $k\ge {\hat{k}}$.

Proof

Notice that, since $\tau _\text {opt} = 0$, Algorithm 1 generates an infinite sequence of iterates. So, we start the proof showing that $\varvec{C}(\varvec{x}^*)\le \varvec{0}$. Let $\mathcal K\subset \mathbb {N}$ be any infinite index set such that $({\varvec{x}^k},{\varvec{y}^k})\underset{k\in \mathcal K}{\rightarrow } (\varvec{x}^*,\varvec{y}^*)$. Then, since every ${\varvec{x}^k}$ must satisfy $\varvec{C}({\varvec{x}^k})\le \varvec{0}$, we have

$$\begin{aligned} \lim _{k\rightarrow \infty } \varvec{C}({\varvec{x}^k})\le \varvec{0} \Rightarrow \varvec{C}(\varvec{x}^*)\le \varvec{0}. \end{aligned}$$

Let us now show that there must exist ${\hat{k}}\in \mathbb {N}$ and $\bar{\rho }\in \mathbb {R}$ such that $\rho _k = \bar{\rho }$, for all $k\ge {\hat{k}}$. Indeed, because of Lemmas 1, 4 and 6, one can see that the sequence $\{({\varvec{x}^k},{\varvec{y}^k})\}$ is bounded. Therefore, since f is a continuous function, it follows that $\{f({\varvec{x}^k},{\varvec{y}^k})\}$ is also a bounded sequence. Due to such a boundness, Step 3 assures that eventually $\rho _{k} \ge f({\varvec{x}^k},{\varvec{y}^k}) + M$ for all $k\in \mathbb {N}$ sufficiently large, implying that there must exist ${\hat{k}}\in \mathbb {N}$ and $\bar{\rho }\in \mathbb {R}$ such that $\rho _k = \bar{\rho }$, for all $k\ge {\hat{k}}$. Therefore, to simplify the presentation, we may suppose without loss of generality that $\rho _k$ remains fixed for all iterations, as a consequence of $f({\varvec{x}^k},{\varvec{y}^k}) - \rho _k< -M < 0$, for all $k\in \mathbb {N}$.

Now, let us choose any $(\varvec{x},\varvec{y})\in \mathbb {R}^n\times \mathbb {R}^m$ that is feasible for the original problem (P-bilevel). Then, Proposition 1 gives us a sequence $\{\tilde{\varvec{y}}^k\}\subset \mathbb {R}^m$ such that $(\varvec{x},\tilde{\varvec{y}}^k)$ is always feasible for ($\tilde{P}_k$) and $\tilde{\varvec{y}}^k\rightarrow \varvec{y}$. Therefore, because $({\varvec{x}^k},{\varvec{y}^k})$ solves ($\tilde{P}_k$), we obtain

$$\begin{aligned} F({\varvec{x}^k},{\varvec{y}^k}) \le F(\varvec{x},\tilde{\varvec{y}}^k)\Rightarrow \lim _{k\in \mathcal K} F({\varvec{x}^k},{\varvec{y}^k}) \le \lim _{k\in \mathcal K} F(\varvec{x},\tilde{\varvec{y}}^k) \Rightarrow F(\varvec{x}^*,\varvec{y}^*) \le F(\varvec{x},\varvec{y}), \end{aligned}$$

where $\mathcal K$ is any infinite index set such that $({\varvec{x}^k},{\varvec{y}^k})\underset{k\in \mathcal K}{\rightarrow } (\varvec{x}^*,\varvec{y}^*)$. To see that the Fritz John optimality conditions associated with the optimization problem presented in $\mathcal R(\varvec{x}^*)$ are satisfied at $\varvec{y}^*$, just notice that $\nabla _{\varvec{y}} \varTheta _{\tau _k,\rho _k}({\varvec{x}^k},{\varvec{y}^k}) = \varvec{0}$ for all $k\in \mathbb {N}$, and $\tau _k\rightarrow 0$ – because of Lemma 6 –, which together with Lemma 3, completes the proof. $\square$

In order to establish a strong connection between the original problem (P-bilevel) and the one-level approximation ($\tilde{P}_k$), we need to assume the following constraint qualification for the follower’s optimization problem [8, Section 6.3].

Definition 1

(Mangasarian-Fromovitz constraint qualification) For any fixed $\bar{\varvec{x}}\in \mathbb {R}^n$ satisfying $\varvec{C}(\bar{\varvec{x}}) \le 0$, we say that the Mangasarian-Fromovitz constraint qualification (MFCQ) is satisfied at $\bar{\varvec{y}}\in \varOmega (\bar{\varvec{x}})$ for the follower’s optimization problem if, for all i, the gradients $\nabla _{\varvec{y}} c^\text {eq}_i(\bar{\varvec{x}}, \bar{\varvec{y}})$ are linearly independent, and there exists a vector $\varvec{d}\in \mathbb {R}^m$ such that, for $\mathcal I_\text {in}:=\{i:c^\text {in}_i(\bar{\varvec{x}}, \bar{\varvec{y}}) = 0\}$,

$$\begin{aligned} \nabla _{\varvec{y}}c^\text {in}_i(\bar{\varvec{x}}, \bar{\varvec{y}})^T \varvec{d}<0~(i\in \mathcal I_\text {in})\text { and } \nabla _{\varvec{y}} c^\text {eq}_j(\bar{\varvec{x}}, \bar{\varvec{y}})^T \varvec{d} = 0~(j \in \{1, \ldots , s\}). \end{aligned}$$

The following result is a direct implication of the previous theorem and could be seen as its corollary, but due to its relevance, we have stated it as a theorem as well.

Theorem 2

Let $(\varvec{x}^*, \varvec{y}^*)$ be a limit point of the sequence $\{(\varvec{x}^k,\varvec{y}^k)\} \subset \mathbb {R}^n\times \mathbb {R}^m$ generated by Algorithm 1 with $\tau _\text {opt} = 0$ and assume that the lower-level problem has a unique solution for every upper-level variable $\varvec{x}$. If MFCQ is valid at $\varvec{y}^*$ for the optimization problem presented in $\mathcal R(\varvec{x}^*)$, then $(\varvec{x}^*,\varvec{y}^*)$ solves the original problem (P-bilevel).

Proof

Just notice that the Mangasarian-Fromovitz constraint qualification assures that the Fritz John optimality conditions that appear in the conclusion of Theorem 1 can be changed to the Karush-Kuhn-Tucker optimality conditions [8, Section 6.3]. Consequently, since the optimization problem related to $\mathcal R(\varvec{x}^*)$ is convex, the Karush-Kuhn-Tucker optimality conditions are sufficient to assure that $\varvec{y}^*\in \mathcal R(\varvec{x}^*)$. This information together with Theorem 1 guarantees the result. $\square$

Although the previous result is strong and assures, in the limit, a correspondence between the solutions of (P-bilevel) and ($\tilde{P}_k$), we needed to assume that ($\tilde{P}_k$) is globally solved. The following theorem is much more revealing since it ensures that, under mild assumptions, a relation between the local minimizers of the problems (P-bilevel) and ($\tilde{P}_k$) can be established.

Theorem 3

Let $\tau _\text {opt} = 0$, assume that the lower-level problem has a unique solution for every upper-level variable $\varvec{x}$, and suppose that the iterates $(\varvec{x}^k,\varvec{y}^k)$ are feasible for ($\tilde{P}_k$) and there exists $\delta > 0$ such that, for all $k\in \mathbb {N}$, we have

$$\begin{aligned} F(\varvec{x}^k,\varvec{y}^k)\le F(\varvec{x},\varvec{y})\text {, for all }(\varvec{x},\varvec{y})\in \mathcal B\left( (\varvec{x}^k,\varvec{y}^k),\delta \right) \text { that is feasible for }(\tilde{P}_k).\nonumber \\ \end{aligned}$$

(11)

Additionally, assume that $(\varvec{x}^*,\varvec{y}^*)\in \mathbb {R}^n\times \mathbb {R}^m$ is a limit point for $\{(\varvec{x}^k,\varvec{y}^k)\}$, and that MFCQ is valid at any $\varvec{y}\in \varOmega (\varvec{x}^*)$ for the optimization problem presented in $\mathcal R(\varvec{x}^*)$. Then, $(\varvec{x}^*,\varvec{y}^*)$ is a local solution for the original bilevel problem (P-bilevel).

Proof

Using the same reasoning of the beginning of the proof of Theorem 1, one can see that there exist ${\hat{k}}\in \mathbb {N}$ and $\bar{\rho }\in \mathbb {R}$ such that $\rho _k = \bar{\rho }$, for all $k\ge {\hat{k}}$, and moreover, $\varvec{C}(\varvec{x}^*)\le \varvec{0}$. Similarly, one can also guarantee that $\varvec{y}^*\in \mathcal R(\varvec{x}^*)$ by recalling that MFCQ is assumed to be valid at any $\varvec{y}\in \varOmega (\varvec{x}^*)$, and by proceeding in the same way that was done in the proof of Theorem 1 to see that the Fritz John optimality conditions associated with the optimization problem presented in $\mathcal R(\varvec{x}^*)$ are satisfied at $\varvec{y}^*$. So, since $\varvec{C}(\varvec{x}^*)\le \varvec{0}$ and $\varvec{y}^*\in \mathcal R(\varvec{x}^*)$, we conclude that $(\varvec{x}^*,\varvec{y}^*)$ is a feasible point for (P-bilevel). Therefore, it is sufficient to show that $(\varvec{x}^*,\varvec{y}^*)$ is also a local minimizer for the bilevel problem.

The fact that $\mathcal R(\cdot )$ is an upper-semicontinuous function and $\mathcal R(\varvec{x})$ is a singleton for any $\varvec{x}\in \mathbb {R}^n$ satisfying $\varvec{C}(\varvec{x})\le \varvec{0}$ reveals that $\mathcal R(\cdot )$ is a continuous function at $\varvec{x}^*$ [1, Lemma 16.6]. Therefore, there must exist ${\tilde{\delta }} \le \delta /4$ – where $\delta$ comes from (11) – such that

$$\begin{aligned} \Vert \varvec{x} - \varvec{x}^*\Vert \le {\tilde{\delta }}\quad \text {and}\quad \varvec{C}(\varvec{x})\le \varvec{0} \quad \Rightarrow \quad \Vert \mathcal R(\varvec{x}) - \mathcal R(\varvec{x}^*)\Vert \le \frac{\delta }{4}. \end{aligned}$$

Let $(\varvec{x},\varvec{y})\in \mathbb {R}^n\times \mathbb {R}^m$ be any point such that $\Vert \varvec{x} - \varvec{x}^*\Vert \le {\tilde{\delta }}$, $\varvec{C}(\varvec{x})\le \varvec{0}$ and $\varvec{y}\in \mathcal R(\varvec{x})$. Then, Proposition 1 gives us a sequence $\{\tilde{\varvec{y}}^k\}\subset \mathbb {R}^m$ such that $(\varvec{x},\tilde{\varvec{y}}^k)$ is always feasible for ($\tilde{P}_k$) and $\tilde{\varvec{y}}^k\rightarrow \varvec{y}$. Therefore, for any $k\in \mathbb {N}$ sufficiently large, we have $(\varvec{x},\tilde{\varvec{y}}^k)\in \mathcal B\left( (\varvec{x}^k,\varvec{y}^k),\delta \right)$, which implies $F(\varvec{x}^k,\varvec{y}^k) \le F(\varvec{x},\tilde{\varvec{y}}^k)$ – because $(\varvec{x}^k,\varvec{y}^k)$ satisfies (11). Hence,

$$\begin{aligned} \lim _{k\in \mathcal K} F(\varvec{x}^k,\varvec{y}^k) \le \lim _{k\in \mathcal K} F(\varvec{x},\tilde{\varvec{y}}^k) \Rightarrow F(\varvec{x}^*,\varvec{y}^*) \le F(\varvec{x},\varvec{y}), \end{aligned}$$

where $\mathcal K$ is any infinite index set such that $(\varvec{x}^k,\varvec{y}^k)\underset{k\in \mathcal K}{\rightarrow } (\varvec{x}^*,\varvec{y}^*)$. Consequently, since $(\varvec{x},\varvec{y})\in \mathbb {R}^n\times \mathbb {R}^m$ is any arbitrary point satisfying $\Vert \varvec{x} - \varvec{x}^*\Vert \le {\tilde{\delta }}$, $\varvec{C}(\varvec{x})\le 0$ and $\varvec{y}\in \mathcal R(\varvec{x})$, it follows that $F(\varvec{x}^*,\varvec{y}^*) \le F(\varvec{x},\varvec{y})$, for any $\varvec{x} \in \mathcal B(\varvec{x}^*,{\tilde{\delta }})$ such that $\varvec{C}(\varvec{x}) \le \varvec{0}$ and $\varvec{y} \in \mathcal R(\varvec{x})$. Since we have already shown that $(\varvec{x}^*,\varvec{y}^*)$ is a feasible point for (P-bilevel), the statement is proven. $\square$

With this last theoretical result, we ensure that, in the limit, any local optimal solution obtained in ($\tilde{P}_k$) is, in fact, a local minimizer for the original bilevel problem. Therefore, in opposition to the KKT formulation, our new one-level optimization problem does present a correspondence between local solutions. Additionally, this was done avoiding any kind of implicit description of the follower’s feasible set.

Exactness of solution in Step 1. The only matter that was not addressed yet is the fact that, at each iteration $k\in \mathbb {N}$, we request for the exactness of a solution $(\varvec{x}^k, \varvec{y}^k)$ in Step 1. Practical algorithms are not able, in general, to find the exact solution of an optimization problem, but only a good approximation can be expected. Therefore, if the errors of those approximations accumulate along the iterations, the convergence theory developed may not hold. We advocate, however, that this should not be a concern for our proposed algorithm.

It should be noticed that the convergence theory developed here would still hold if the sequence $\{\tau _k\}$ did not depend on $(\varvec{x}^k, \varvec{y}^k)$, but was a priori sequence given at Step 0 of NoBOA – as long as $\tau _k \downarrow 0$. Moreover, $\{\rho _k\}$ could also be given at Step 0 as a constant sequence such that $\rho _k \equiv \bar{\rho }$, for a sufficiently large $\bar{\rho }$ – resembling exact penalization strategies that, as long as a sufficiently large penalty parameter is given, the solution for the original constrained optimization problem is recovered. In this configuration, each iteration of NoBOA would not depend on the previous one, and therefore, $(\varvec{x}^{k-1}, \varvec{y}^{k-1})$ would just be a warm start for the optimization problem in Step 1 at iteration k. On these circumstances, accumulation errors cannot occur.

In its initial version, the NoBOA algorithm was tailored to function exactly as the description given in the previous paragraph. Although this approach works fine in the theoretical realm, the practicality of this preliminary method suffers by not considering the information obtained in the previous iterations to update the parameters $\tau _k$ and $\rho _k$. Hence, the aspects of the method that might be of practical concern were defined by exactly taking the practicality of the algorithm into consideration.

That said, it should be stressed that even in the present configuration of the NoBOA algorithm, accumulation errors cannot occur. Indeed, as explained, as long as $\tau _k\downarrow 0$ and $\rho _k$ is sufficiently large, the convergence theory still holds. So, the dependence of $(\varvec{x}^{k}, \varvec{y}^{k})$ on $(\varvec{x}^{k-1}, \varvec{y}^{k-1})$ does not exist from the theoretical perspective – although, in practice, this plays an important role. As such, accumulation errors that prevent the NoBOA method to converge cannot occur – under the assumption that $\tau _k\downarrow 0$ and $\rho _k$ is sufficiently large. Now, notice that $\rho _k$ will be sufficiently large even when one solves Step 1 inexactly. Indeed, suppose $(\varvec{x}^{k}, \varvec{y}^{k})$ has a convergent subsequence, then the reasoning used in the proof of Theorem 1 to ensure that $\rho _k$ is sufficiently large would still hold true in the vicinity of the limit point. Hence, the perfect accuracy of the solution obtained in Step 1 is not crucial to have a proper value for $\rho _k$. Finally, by simply looking at Step 3, one can see that $\tau _k$ will not converge to zero only if the feasibility of the lower-level problem is not being reached. Although the lower-level problem is assumed to be convex, it is possible that its feasible region is not attained due to the consideration of the functions that describe the upper-level problem – which are not necessarily convex –, i.e., the iterates $(\varvec{x}^{k}, \varvec{y}^{k})$ might be a stationary point of the measure of infeasibility associated with the method used to solve Step 1. Hence, the only possibility in which $\tau _k$ does not converge to zero coincides with the case that most methods designed for constrained optimization might also have drawbacks. As a result, we believe the difficulties that emerge from not solving Step 1 with exact precision are not greater than the difficulties faced by well-established optimization methods.

4 Numerical results

With the aim of illustrating the performance of the proposed reformulation, Algorithm 1 (NoBOA) has been implemented and used for solving three families of test problems, namely: (i) two examples of Bard’s book [3]; (ii) three instances of toll-setting problems from [9]; (ii) three examples of [15] for which some of the required hypotheses fail to hold. The specific details are described next, together with the achieved results. All the experiments were run in a DELL Latitude 7490 notebook, Intel Core i7-8650U processor clocked at 2.11GHz, 16GB RAM (64-bit), using Matlab R2018a.

The algorithmic parameters were chosen as follows: $\rho _1=500$, $\tau _1 = 10$, $\tau _{\text {opt}} = 10^{-4}$, $M=25$, $\theta _{\tau }=0.9$. The subproblems of Step 1 were solved using PACNO, the penalized algorithm for constrained nonsmooth optimization proposed in [26], with the gradient sampling (GS) algorithm [6] as the inner solver. Hence, to achieve statistically significant results, for each problem, 100 initial points $(\varvec{x}^0, \varvec{y}^0) \in {\mathbb {R}}^n \times {\mathbb {R}}^m$ were randomly and uniformly sampled in a box $[x_{\text {low}}, x_{\text {upp}}]^n \times [y_{\text {low}}, y_{\text {upp}}]^m$. The specific values for the bounds are reported together with the problem features.

The parameters of PACNO were defined adaptively, with a slow policy of adjustment, to provide enough room to progress while avoiding abrupt variations of the iterates: $\theta _{\xi } =0.9$, $\theta _{\epsilon } =0.9^2$, $\theta _{\nu } =0.75$. Loose tolerances were chosen in the beginning, to prevent premature stopping, thus at the first call, we set , $\xi _1 = \tau _1/2$, $\epsilon _1 = 0.5$, $\nu _1 =0.5$, $\xi _{\text {opt}} = \xi _1/2$, $\epsilon _{\text {opt}} = \epsilon _1/5$, $\nu _{\text {opt}} = \nu _1/5$. The remanining parameters were set as $\rho _1^{\text {PACNO}} = 100$, $M^{\text {PACNO}} = 10$ and $\omega = 0.99$. Additionally, for each call of GS at the j-th iteration of PACNO, the sampling radii were set first as $\min \{1, 10 \epsilon _j\}$, with optimality tolerance $\min \{1, 10 \nu _j\}$, and subsequently, the final sampling radius was defined as $\min \{1, \epsilon _j\}$, with optimality tolerance $\min \{1, \nu _j\}$, allowing a maximum of 10,000 iterations.

Along the iterations of NoBOA, as the threshold parameter $\tau _k$ decreases, the tolerances of PACNO are also diminished accordingly, starting with $\xi _1 = \min \{\tau _k/2, \tau _k^{1.5}\}$, $\epsilon _1 = \nu _1= \min \{10^{-1},\xi _1/2\}$, and setting the targets as follows

$$\begin{aligned} \xi _{\text {opt}}&= \max \left\{ \min \{ \tau _k, \xi _1/(k+1) \}, \tau _{\text {opt}}^{1.1} \right\} ,\\ \epsilon _{\text {opt}}&= \max \left\{ \min \{ \tau _k^{1.5}, \epsilon _1/(k+1)^{1.1} \}, \tau _{\text {opt}}^{1.5}\right\} ,\\ \nu _{\text {opt}}&= \max \left\{ \min \{\tau _k^2, \nu _1/(k+1)^{1.2}\}, \tau _{\text {opt}}^2\right\} . \end{aligned}$$

In preparation for each call of PACNO, within a continuation philosophy with respect to the set of constraints $\nabla _{\varvec{y}} \varTheta _{\tau , \rho } (\varvec{x}, \varvec{y}) = \varvec{0}$, the following strategy has been adopted to provide a hot start for the lower-level variables. Kepping fixed the upper-level variables, and taking the current value for the lower-level variables as the initial point, the smooth unconstrained problem $\min _{\varvec{y}} \varTheta _{\tau _k, \rho _k} (\varvec{x}^k, \varvec{y})$ was solved using the Matlab routine fminunc, with the default choices, except for the option ‘SpecifyObjectiveGradient’, that was activated.

As it happens for many practical implementations of numerical methods, safeguards are important for avoiding undesirable behavior. Therefore, specially because we are dealing with nonsmooth functions, an alternative termination criterion due to lack of progress (LOP) had to be devised and implemented. Taking into account either the whole set of variables, or just the upper-level ones, we have tracked the relative variation

$$\begin{aligned} \left\| \left( \varvec{x}^k, \varvec{y}^k \right) -\left( \varvec{x}^{k-1}, \varvec{y}^{k-1}\right) \right\| /\left\| \left( \varvec{x}^{k-1}, \varvec{y}^{k-1}\right) \right\| \end{aligned}$$

or $\Vert \varvec{x}^k -\varvec{x}^{k-1} \Vert / \Vert \varvec{x}^{k-1} \Vert$, stopping whenever the corresponding ratio remains below $\varepsilon _{\text {LOP}}= 10^{-3}$ along 5 consecutive iterations. Another reason for stopping was due to failure of PACNO, in case the inner solver exits with an infeasible iterate. Besides that, NoBOA was allowed to perform at most 2,000 iterations, but such a budget was never reached in our experiments.

4.1 Problems from Bard’s book

The double penalty function method [29], which was briefly discussed in the introduction, was adopted for solving two examples in Bard’s book [3, Tables 8.5 and 8.6]. Both examples possess a constraint in the upper-level problem depending on the lower-level variable(s), which does not fit into our hypotheses. In each case, such a constraint has been handled by adding an exact penalty term to the upper-level objective function.

The Example 8.3.1 of [3] is stated next, for the reader’s convenience

$$\begin{aligned}&\displaystyle \min _{x, y} x^2 + (y(x)-10)^2 \nonumber \\&\quad \text {s.t.} - x +y(x) \le 0, \; 0 \le x \le 15 \nonumber \\&\quad y(x) \in {{\,\mathrm{\arg min}\,}}_y (x+2y-30)^2 \, \text { s.t. } \, x+y \le 20, \, 0 \le y \le 20. \end{aligned}$$

(12)

Geometrical aspects for this problem are depicted in Fig. 3. Its global solution, $x^* = 10$, $y(x^*) = 10$, has been achieved in 74% of the runs (LOP termination), with the exact penalty parameter set as $\gamma = 20$, and bounds for the random initial points defined as $x_{\text {low}}=0$, $x_{\text {upp}}=15$, $y_{\text {low}}=0$, and $y_{\text {upp}}=20$. The remaining 26% of the runs stopped prematurely, with infeasible outputs for PACNO.

Fig. 3

Elements of the first example of Bard’s book, here presented in (12). Parameterized feasible region (shaded) with optimal value function (red) for the lower-level problem (a); ingredients of upper-level problem, with optimal solution $x^* = 10$ and enhanced feasible region in green (b); graph of the upper-level cost function plus penalty term $z=F(x,y(x)) + \gamma \max \{ -x +y(x),0\}$, with a few different choices for the penalty parameter $\gamma$ (c)

The main features of Example 8.3.2 of [3] are illustrated in Fig. 4, and its formulation is given by

$$\begin{aligned}&\displaystyle \min _{\varvec{x}, \varvec{y}} 2x_1+2x_2-3 y_1(\varvec{x}) - 3 y_2(\varvec{x}) -60 \nonumber \\&\quad \text {s.t.} x_1+x_2 + y_1(\varvec{x}) - 2 y_2(\varvec{x}) \le 40, \; 0 \le x_1 \le 50, \; 0 \le x_2 \le 50\nonumber \\&\quad \varvec{y}(\varvec{x}) \in {{\,\mathrm{\arg min}\,}}_{\varvec{y}} (y_1-x_1+20)^2 + (y_2-x_2+20)^2 \nonumber \\&\qquad \qquad \quad \text { s.t. } \quad 2y_1-x_1 +10\le 0, \; 2y_2-x_2+10 \le 0, \nonumber \\&\qquad \qquad \quad -10 \le y_1 \le 20, \; -10 \le y_2 \le 20. \end{aligned}$$

(13)

Setting the exact penalty parameter as $\gamma = 10$, and the bounds for generating the initial points as $x_{\text {low}} = 0$, $x_{\text {upp}} = 50$, $y_{\text {low}}=-10$, and $y_{\text {upp}}=20$, NoBOA stopped in 99% of the runs due to LOP, and 1% due to failure of PACNO. The reached points were $A \approx (25,30,5,10) ^T$ for 63% of the runs (the reported minimizer); $B \approx (20,0,0,-10) ^T$ for 21%; $C \approx (0,30,-10,10) ^T$ for 13%; $D \approx (0,0,-10,-10)^T$ for 1%, and $E \approx (25,50,5,20)^T$ for 1% of the runs. As can be seen in Fig. 5, the points B, C and D are local minimizers of the bilevel problem.

Fig. 4

Elements of the second example of Bard’s book, here presented in (13). Level sets (a) and graph (b) of parameterized lower-level cost, with a plateau in the region $[10,30]\times [10,30]$; level sets (c) and graph (d) of upper-level objective function, computed with the optimal lower-level variables

Fig. 5

Ingredients of upper-level problem of Example 8.3.2, with highlighted feasible region and level sets of original objective function with optimal lower- level variables $\varvec{y}^*(\varvec{x})$ (left); level sets of upper-level objective function plus penalty term to encompass the constraint that depends on $\varvec{y}^*(\varvec{x})$, with penalty parameter $\gamma = 10$ (right)

4.2 Toll-setting problems

Establishing a toll policy for a transportation network in which an authority sets tolls on a predefined subset of arcs, and the users travel on shortest routes between the origins and destinations, constitutes a class of models usually formulated as bilevel programs. The toll-setting instances Toll1, Toll4 and Toll5 from [9] have been considered here, expressed as the problem (TOP) of [31], a bilevel program with bilinear objectives and linear constraints. The features of the three networks are shown in Fig. 6.

Fig. 6

Transportation networks with (boldfaced) toll arcs, with a unique origin-destination (OD) pair (left) and two OD pairs (center and right). The costs and variables are indicated separately in each network, with the corresponding optimal solutions

For these problems, just the variation of the upper-level variables was considered for the LOP stopping criterion. Additionally, to conclude the run, a post-processing was adopted as follows: given the reached values for the tolls, the binary flows along the arcs were determined using the routine linprog of Matlab applied to the lower-level problem, with a discount of 1% for the toll fare, to favour an optimistic solution, since toll-setting problems have the feature of allowing multiple optimal solutions for the follower agent. Hence, although in theory our approach cannot solve these kind of bilevel instances, these examples show that the proposed algorithm is still useful for these more general degenerate problems. Nevertheless, it is worth mentioning that the continuous results achieved by NoBOA for the flows presented the expected patterns, within the prescribed tolerances.

The bounds for randomly selecting the initial upper-level variables were $x_{\text {low}}=0$, $x_{\text {upp}}=10$, for problem Toll1, and $x_{\text {low}}=-10$, $x_{\text {upp}}=10$, for problems Toll4 and Toll5. For the three instances, the initial flows were set to zero, prior to the hot-start preliminary strategy.

The achieved results for the toll values were as follows. Concerning problem Toll1, 35% of the runs stopped with LOP around $(7,4,6)^T$, 48% finished nearby $(5.9, 3.0, 4.4)^T$, with $\varvec{y} = (0,0,1,1,0,1,0,0)^T$, and 17% stopped prematurely. When it comes to problem Toll4, 93% of the runs stopped with LOP close to $(5,-2)^T$, whereas the remaining 7% did not manage to stabilize within the prescribed tolerance, thus diverging. Regarding problem Toll5, the level of sucess was even better, with 8% of the runs reaching the global solution ($x_1^*=5$) and 90% achieving the local solution ($x_1^*=2$). For this instance, 1% stopped prematurely, and 1% diverged.

4.3 Further instances

This section is devoted to explore further instances for which some of our theoretical hypotheses are not valid. In the article [15], examples enlight significant aspects of the theoretical analysis, mainly concerned with the prospective correspondence of solutions of the KKT reformulation of the lower-level problem with local and global solutions of the bilevel problem. Each example has a particular appeal, and we have investigated the performance of NoBOA to compute the solutions of three of them, namely Examples 2.2, 3.1 and 3.4. Due to the intrinsic difficulties of such instances, a tighter value for the initial threshold parameter produced better results, so we have used $\tau _1=5$, and all the remaining parameters as previously reported.

We start with Example 2.2 of [15], stated as

$$\begin{aligned}&\displaystyle \min _{x, \varvec{y}} x \\&\quad \text {s.t.} x \ge 0, \, \varvec{y}(x) \in {{\,\mathrm{\arg min}\,}}_{\varvec{y}} \, y_1 \, \text { s.t. } \, y_1^2 - y_2 \le x, \, y_1^2 + y_2\le 0. \end{aligned}$$

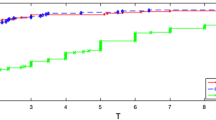
Its global solution ($x^*=0$, $\varvec{y}^* = \varvec{0}$) does not satisfy the Slater condition. Nevertheless, with initial points randomly generated in the box $[-5,5]^3$, 86% of the runs stopped close enough to the origin, at $(a,b,c)^T$, with |a| and |c| between 1e−8 and 1e−3, and |b| between 1e−2 and 1e−1. The remaining 14% stopped due to failure of PACNO. A general picture of the attained values is shown in Fig. 7.

Fig. 7

Values of the variables obtained with NoBOA for Example 2.2 of [15] at the top, and a zoomed view upon the range at the bottom

Our second test problem is Example 3.4 of [15], given next

$$\begin{aligned}&\displaystyle \min _{x, y} (x-1)^2 + (y(x)-1)^2 \\&\quad \text {s.t.} y(x) \in {{\,\mathrm{\arg min}\,}}_{y} \, - y \, \text { s.t. } \, x+ y \le 1, \, -x+y \le 1. \end{aligned}$$

Even though the feasible set ${\mathcal {S}}$ given in (1) of this problem is not compact, starting from points randomly generated in the box $[-5,5]^2$, 100% of the runs of NoBOA stopped due to LOP, close enough to its global solution, at $(0.5,0.5)^T$.

Finally, Example 3.1 of [15] is an instance for which not only the MFCQ fails at the global solution, but also the compacteness assumption of the set ${\mathcal {S}}$ given in (1) does not hold. Its original formulation is provided below

$$\begin{aligned}&\displaystyle \min _{\varvec{x}, \varvec{y}} - y_2(\varvec{x}) \\&\quad \text {s.t.} y_1(\varvec{x}) y_2(\varvec{x}) = 0, \; \varvec{x} \ge 0\\&\quad \varvec{y}(\varvec{x}) \in {{\,\mathrm{\arg min}\,}}_{\varvec{y}} y_1^2 + (y_2+1)^2 \\&\quad \text { s.t. } \quad (y_1-x_1)^2 +(y_2-1-x_1)^2 \le 1 \\&\quad (y_1+x_2)^2 +(y_2-1-x_2)^2 \le 1, \end{aligned}$$

where one can observe, in the upper-level problem, the presence of an equality constraint involving the lower-level variables, which imposes additional difficulties. Such a constraint was handled by adding the following exact penalty term to the upper-level objective function:

$$\begin{aligned} \gamma \max \left\{ \min \{ \max \{ y_1, -y_1\}, \max \{ y_2, -y_2\} \}, 0 \right\} , \end{aligned}$$

with $\gamma = 100$. By sampling initial points in the box with bounds $x_{\text {low}}=0$, $x_{\text {upp}}=2$, $y_{\text {low}}=-1$, $y_{\text {upp}}=1$, 100% of the runs stopped due to LOP, 26% of which nearby the global solution $(1,1,0,2)^T$, 67% remained close to the origin, and 7% around $(2,2,0,3)^T$.

4.4 Discussion

The theoretical features of the proposed reformulation have been corroborated with practical perspectives. In the first set of instances, the possibility of a nondifferentiable upper-level objective was exploited to handle constraints that do not fit within the expected format by means of an exact penalty approach. The two examples of Bard’s book were successfully solved with such a strategy. Three toll-setting problems, usually addressed in the literature by either enumerative techniques or mixed-integer programming, were solved by our continuous approach with satisfactory results. Last, but not least, three examples for which our theoretical assumptions fail to hold were analyzed, with not negligible achievements.

As revealed by the reported numerical results, our approach was strenghtened by recent advances in algorithms for nonconvex, nonsmooth optimization. The obtained outcomes are fruit of the robust performance of PACNO with the gradient sampling as the inner solver. It is worth mentioning that preliminary experimentation with GRANSO [13] instead of the gradient sampling within PACNO, as well as GRANSO directly applied to the subproblems of Step 1 of NoBOA, did not produce results as effective as the aforementioned ones.

Additionally, concerning the subproblems generated by our strategy, since different nonsmooth optimization algorithms lead to different degrees of success, an extensive benchmarking was not the focus of our numerical section, as this task would be a research subject in itself.

5 Final remarks

A new approximate primal reformulation for a large class of bilevel problems was introduced and an algorithm based on this formulation was presented, mathematically analysed and numerically tested with synthetic instances. The new reformulation is straightforward, with an explicit description of the feasible set, and requires no estimation of Lagrange multipliers, but leads to a nonsmooth model to be solved. Under mild assumptions, including MFCQ upon the lower-level problem, a relationship between local minimizers of the reformulation and local solutions of the bilevel problem has been established. As numerical experimentation shows, NoBOA, the proposed algorithm, can be made to be reliable when appropriate methods for one-level nonsmooth optimization are used to handle the subproblems. The gradient sampling technique was shown to work well for this application because of its robustness.

To conclude, the idea of approaching the ill-conditioning of bilevel problems from a nonsmooth perspective may lead to good results in practice, being worth further investigation. Also, more thorough experimentation with subproblem solvers might deliver useful insights. The BOLIB library [46] provides a useful basis of test-problems for these tasks.