Abstract
We investigate an inertial algorithm of gradient type in connection with the minimization of a non-convex differentiable function. The algorithm is formulated in the spirit of Nesterov’s accelerated convex gradient method. We prove some abstract convergence results which applied to our numerical scheme allow us to show that the generated sequences converge to a critical point of the objective function, provided a regularization of the objective function satisfies the Kurdyka–Łojasiewicz property. Further, we obtain convergence rates for the generated sequences and the objective function values formulated in terms of the Łojasiewicz exponent of a regularization of the objective function. Finally, some numerical experiments are presented in order to compare our numerical scheme and some algorithms well known in the literature.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Inertial optimization algorithms deserve special attention in both convex and non-convex optimization due to their better convergence rates compared to non-inertial ones, as well as due to their ability to detect multiple critical points of non-convex functions via an appropriate control of the inertial parameter [1, 8, 14, 24, 29, 32, 36, 39, 42, 43, 47, 51]. Non-inertial methods lack the latter property [25].
With the growing use of non-convex objective functions in some applied fields, such as image processing or machine learning, the need for non-convex numerical methods increased significantly. However, the literature of non-convex optimization methods is still very poor, we refer to [46] (see also [45]), [26, 52] for some algorithms that can be seen as extensions of Polyak’s heavy ball method [47] to the non-convex case and the papers [4, 5] for some abstract non-convex methods.
In this paper we investigate an algorithm, with a possibly non-convex objective function, which has a form similar to Nesterov’s accelerated convex gradient method [29, 43].
Let \(g:{\mathbb {R}}^m\longrightarrow {\mathbb {R}}\) be a (not necessarily convex) Fréchet differentiable function with \(L_g\)-Lipschitz continuous gradient, that is, there exists \(L_g\ge 0\) such that \(\Vert {\nabla }g(x)-{\nabla }g(y)\Vert \le L_g\Vert x-y\Vert \) for all \(x,y\in {\mathbb {R}}^m.\) We deal with the optimization problem
Of course regarding this possibly non-convex optimization problem, in contrast to the convex case where every local minimum is also a global one, we are interested to approximate the critical points of the objective function g. To this end we associate to the optimization problem (1) the following inertial algorithm of gradient type. Consider the starting points \(x_0,x_{-1}\in {\mathbb {R}}^m\) and for all \(n\in {\mathbb {N}}\) let
where \(\alpha >0,\,\beta \in (0,1)\) and \(0<s<\frac{2(1-\beta )}{L_g}.\)
We underline that the main difference between Algorithm (2) and the already mentioned non-convex versions of the heavy ball method studied in [26, 46] is the same as the difference between the methods of Polyak [47] and Nesterov [43], that is, meanwhile the first one evaluates the gradient in \(x_n\) the second one evaluates the gradient in \(y_n.\) One can observe at once the similarity between the formulation of Algorithm (2) and the algorithm considered by Chambolle and Dossal [29] (see also [2, 6, 12]) in order to prove the convergence of the iterates of the modified FISTA algorithm [14]. Indeed, the algorithm studied by Chambolle and Dossal in the context of a convex optimization problem can be obtained from Algorithm (2) by violating its assumptions and allowing the case \(\beta =1\) and \(s\le \frac{1}{L_g}.\)
Unfortunately, due to the form of the stepsize s, we cannot allow the case \(\beta =1\) in Algorithm (2), but what is lost at the inertial parameter it is gained at the stepsize, since in the case \(\beta <\frac{1}{2}\) one may allow a better stepsize than \(\frac{1}{L_g}\), more precisely the stepsize in Algorithm (2) satisfies \(s\in \left( \frac{1}{L_g},\frac{2}{L_g}\right) \).
Let us mention that to our knowledge Algorithm (2) is the first attempt in the literature to extend the Nesterov accelerated convex gradient method to the case when the objective function g is possibly non-convex.
Another interesting fact about Algorithm (2) which enlightens the relation with Nesterov’s accelerated convex gradient method is that both methods are modeled by the same differential equation that governs the so called continuous heavy ball system with vanishing damping, that is,
We recall that (3) (with \(\alpha =3\)) has been introduced by Su, Boyd and Candès [50] as the continuous counterpart of Nesterov’s accelerated gradient method and from then it was the subject of an intensive research. Attouch and his co-authors [6, 10] proved that if \(\alpha >3\) in (3) then a generated trajectory x(t) converges to a minimizer of the convex objective function g as \(t\longrightarrow +\infty \), meanwhile the convergence rate of the objective function along the trajectory is \(o(1/t^2)\). Further, in [7] some results concerning the convergence rate of the convex objective function g along the trajectory generated by (3) in the subcritical case \(\alpha \le 3\) have been obtained.
In one hand, in order to obtain optimal convergence rates of the trajectories generated by (3), Aujol, Dossal and Rondepierre [11] assumed that beside convexity the objective function g satisfies also some geometrical conditions, such as the Łojasiewicz property.
On the other hand, Aujol and Dossal obtained in [12] some general convergence rates and also the convergence of the trajectories generated by (3) to a minimizer of the objective function g by dropping the convexity assumption on g but assuming that the function \((g(x(t))-g(x^*))^\beta \) is convex, where \(\beta \) is strongly related to the damping parameter \(\alpha \) and \(x^*\) is a global minimizer of g. In case \(\beta =1\) they results reduce to the results obtained in [6, 7, 10].
However, the convergence of the trajectories generated by the continuous heavy ball system with vanishing damping in the general case when the objective function g is possibly non-convex is still an open question. Some important steps in this direction have been made in [27] (see also [25]), where convergence of the trajectories of a system, that can be viewed as a perturbation of (3), have been obtained in a non-convex setting. More precisely, in [27] is considered the continuous dynamical system
where \(t_0>0,\,u_0,\,v_0\in {\mathbb {R}}^m,\,\gamma >0\) and \(\alpha \in {\mathbb {R}}.\) Note that here \(\alpha \) can take nonpositive values. For \(\alpha =0\) we recover the dynamical system studied in [15]. According to [27] the trajectory generated by the dynamical system (4) converges to a critical point of g if a regularization of g satisfies the Kurdyka–Łojasiewicz property.
The connection between the continuous dynamical system (4) and Algorithm (2) is that the latter one can be obtained via discretization from (4), as it is shown in “Appendix”. Further, following the same approach as Su et al. [50] (see also [27]), we show in “Appendix” that by choosing appropriate values of \(\beta \) the numerical scheme (2) has the exact limit the continuous second order dynamical system governed by (3) and also the continuous dynamical system (4). Consequently, our numerical scheme (2) can be seen as the discrete counterpart of the continuous dynamical systems (3) and (4) in a full non-convex setting.
The paper is organized as follows. In the next section we prove an abstract convergence result that may become useful in the future in the context of related researches. Our result is formulated in the spirit of the abstract convergence result from [5], however it can also be used in the case when we evaluate the gradient of the objective function in iterations that contain inertial terms. Further, we apply the abstract convergence result obtained to (2) by showing that its assumptions are satisfied by the sequences generated by the numerical scheme (2), see also [5, 16, 26]. In sect. 3 we obtain several convergence rates both for the sequences \((x_n)_{n\in {\mathbb {N}}}\) and \((y_n)_{n\in {\mathbb {N}}}\) generated by the numerical scheme (2), as well as for the function values \(g(x_n)\) and \(g(y_n)\) in the terms of the Łojasiewicz exponent of the objective function g and a regularization of g, respectively (for some general results see [34, 35]). As an immediate consequence we obtain linear convergence rates in the case when the objective function is strongly convex. Further, in Sect. 4 via some numerical experiments we show that Algorithm (2) has a very good behavior compared with some well known algorithms from the literature. Finally, we conclude our paper with some future research plans. In “Appendix” we show that Algorithm (2) and the second order differential equations (3) and (4) are strongly connected.
2 Convergence analysis
The central question that we are concerned in this section regards the convergence of the sequences generated by the numerical method (2) to a critical point of the objective function g, which in the non-convex case critically depends on the Kurdyka–Łojasiewicz property [38, 41] of an appropriate regularization of the objective function. The Kurdyka–Łojasiewicz property is a key tool in non-convex optimization (see [3,4,5, 16, 17, 21,22,23, 25,26,27, 31, 34, 37, 46, 49]), and might look restrictive, but from a practical point of view in problems appearing in image processing, computer vision or machine learning this property is always satisfied.
We prove at first an abstract convergence result which applied to Algorithm (2) ensures the convergence of the generated sequences. The main result of this section is the following.
Theorem 1
In the settings of problem (1), for some starting points \(x_0,x_{-1}\in {\mathbb {R}}^m,\) consider the sequence \((x_n)_{n\in {\mathbb {N}}}\) generated by Algorithm (2). Assume that g is bounded from below and consider the function
Let \(x^*\) be a cluster point of the sequence \((x_n)_{n\in {\mathbb {N}}}\) and assume that H has the Kurdyka–Łojasiewicz property at a \(z^*=(x^*,x^*).\)
Then, the sequence \((x_n)_{n\in {\mathbb {N}}}\) converges to \(x^*\) and \(x^*\) is a critical point of the objective function g.
2.1 An abstract convergence result
In what follows, by using some similar techniques as in [5], we prove an abstract convergence result. For other works where these techniques were used we refer to [34, 46].
Let us denote by \(\omega ((x_n)_{n\in {\mathbb {N}}})\) the set of cluster points of the sequence \((x_n)_{n\in {\mathbb {N}}}\subseteq {\mathbb {R}}^m,\) that is,
Further, we denote by \({{\,\mathrm{crit}\,}}(g)\) the set of critical points of a smooth function \(g:{\mathbb {R}}^m\longrightarrow {\mathbb {R}}\), that is,
In order to continue our analysis we need the concept of a KL function. For \(\eta \in (0,+\infty ]\), we denote by \(\Theta _{\eta }\) the class of concave and continuous functions \(\varphi :[0,\eta )\longrightarrow [0,+\infty )\) such that \(\varphi (0)=0\), \(\varphi \) is continuously differentiable on \((0,\eta )\), continuous at 0 and \(\varphi '(s)>0\) for all \(s\in (0, \eta )\).
Definition 1
(Kurdyka–Łojasiewicz property) Let \(g:{\mathbb {R}}^m\longrightarrow {\mathbb {R}}\) be a differentiable function. We say that g satisfies the Kurdyka–Łojasiewicz (KL) property at \({{\overline{x}}}\in {\mathbb {R}}^m\) if there exist \(\eta \in (0,+\infty ]\), a neighborhood U of \({{\overline{x}}}\) and a function \(\varphi \in \Theta _{\eta }\) such that for all x in the intersection
the following, so called KL inequality, holds
If g satisfies the KL property at each point in \({\mathbb {R}}^m\), then g is called a KL function.
Of course, if \(g({{\overline{x}}})=0\) then the previous inequality can be written as
The origins of this notion go back to the pioneering work of Łojasiewicz [41], where it is proved that for a real-analytic function \(g:{\mathbb {R}}^m\longrightarrow {\mathbb {R}}\) and a critical point \(\overline{x}\in {\mathbb {R}}^m\) there exists \(\theta \in [1/2,1)\) such that the function \(x\rightarrowtail |g(x)-g({{\overline{x}}})|^{\theta }\Vert \nabla g(x)\Vert ^{-1}\) is bounded around \({{\overline{x}}}\). This corresponds to the situation when the function \(\varphi (s)=C(1-\theta )^{-1}s^{1-\theta }\). The result of Łojasiewicz allows the interpretation of the KL property as a re-parametrization of the function values in order to avoid flatness around the critical points, therefore \(\varphi \) is called a desingularizing function [15]. Kurdyka [38] extended this property to differentiable functions definable in an o-minimal structure. Further extensions to the nonsmooth setting can be found in [4, 18,19,20, 33].
A simple example of a KL function is a Morse function [4], that is, a function of class \(C^2({\mathbb {R}}^m)\) for which the Hessian has full rank in each critical point and in two different critical points the function values are different. In this case the desingularizing function has the form \(\varphi (s)=C\sqrt{s},\) for some \(C>0.\)
Probably the most important KL functions are the semi-algebraic functions, that is, the functions \(g:{\mathbb {R}}^m\longrightarrow {\mathbb {R}}\) whose graph are semi-algebraic sets in \({\mathbb {R}}^{m+1}.\) Recall that a subset of \({\mathbb {R}}^{m+1}\) is called semi-algebraic, if it can be written as a finite union of sets of the form
where \(P_i\) and \(Q_i,\, i=1,\dots ,p,\,p\in {\mathbb {N}}\) are real polynomial functions. The desingularizing function of a semi-algebraic function has the form \(\varphi (s)=Cs^{1-\theta },\) for some \(\theta \in [0,1)\cap {\mathbb {Q}}\) and \(C>0,\) [18, 19].
Further, to the class of KL functions belong real sub-analytic, semi-convex, uniformly convex and convex functions satisfying a growth condition. We refer the reader to [3,4,5, 15, 16, 18,19,20] and the references therein for more details regarding all the classes mentioned above and illustrating examples.
In what follows we formulate some conditions that beside the KL property at a point of a continuously differentiable function lead to a convergence result. Consider a sequence \((x_n)_{n\in {\mathbb {N}}}\subseteq {\mathbb {R}}^m\) and fix the positive constants \(a,b> 0,\,c_1,c_2\ge 0,\,c_1^2+c_2^2\ne 0.\) Let \(F : {\mathbb {R}}^m\times {\mathbb {R}}^m\longrightarrow {\mathbb {R}}\) be a continuously Fréchet differentiable function. Consider further a sequence \((z_n)_{n\in {\mathbb {N}}} := (v_n,w_n)_{n\in {\mathbb {N}}}\subseteq {\mathbb {R}}^m\times {\mathbb {R}}^m\) which is related to the sequence \((x_n)_{n\in {\mathbb {N}}}\) via the conditions (H1)-(H3) below.
-
(H1)
For each \(n\in {\mathbb {N}}\) it holds
$$\begin{aligned} a\Vert x_{n+1}-x_{n}\Vert ^2\le F(z_{n})-F(z_{n+1}). \end{aligned}$$ -
(H2)
For each \(n \in {\mathbb {N}},\,n\ge 1\) one has
$$\begin{aligned} \Vert {\nabla }F(z_n)\Vert \le b(\Vert x_{n+1}-x_{n}\Vert +\Vert x_n-x_{n-1}\Vert ). \end{aligned}$$ -
(H3)
For each \(n \in {\mathbb {N}}\,,\,n\ge 1\) and every \(z=(x,x)\in {\mathbb {R}}^m\times {\mathbb {R}}^m\) one has
$$\begin{aligned} \Vert z_n-z\Vert \le c_1\Vert x_n-x\Vert +c_2\Vert x_{n-1}-x\Vert . \end{aligned}$$
Remark 2
One can observe that the conditions (H1) and (H2) are very similar to those in [5, 34, 46], however there are some major differences. First of all observe that the conditions in [5] or [34] can be rewritten into our setting by considering that the sequence \((z_n)_{n\in {\mathbb {N}}}\) has the form \(z_n=(x_n,x_{n})\) for all \(n\in {\mathbb {N}}\) and the lower semicontinuous function f considered in [5] satisfies \(f(x_n)=F(z_n)\) for all \(n\in {\mathbb {N}}.\)
Further, in [46] the sequence \((z_n)_{n\in {\mathbb {N}}}\) has the special form \(z_n=(x_n,x_{n-1})\) for all \(n\in {\mathbb {N}}.\)
-
Our condition (H3) is automatically satisfied for the sequence considered in [5] that is \(z_n=(x_n,x_n)\) with \(c_1=\sqrt{2},\,c_2=0\) and also for the sequence considered in [46] \(z_n=(x_n,x_{n-1})\) with \(c_1=c_2=1.\)
-
In [5] and [34] the condition (H1) reads as
$$\begin{aligned} a_n\Vert x_{n+1}-x_{n}\Vert ^2\le F(z_n)-F(z_{n+1}), \end{aligned}$$where \(a_n=a>0\) in [5] and \(a_n>0\) in [34], which are formally identical to our assumption but our sequence \(z_n\) has a more general form, meanwhile in [46] (H1) is
$$\begin{aligned} a\Vert x_n-x_{n-1}\Vert ^2\le F(z_n)-F(z_{n+1}). \end{aligned}$$ -
The corresponding relative error (H2) in [5] is
$$\begin{aligned} \Vert {\nabla }F(z_{n+1})\Vert \le b\Vert x_{n+1}-x_{n}\Vert \end{aligned}$$consequently, in some sense, our condition may have a larger relative error. In [34] the condition (H2) has the form
$$\begin{aligned} \Vert {\nabla }F(z_{n+1})\Vert \le b_n\Vert x_{n+1}-x_{n}\Vert +c_n, \text{ where } b_n>0,\,c_n\ge 0. \end{aligned}$$Moreover, in [46] is considered \((z_n)_{n\in {\mathbb {N}}}=(x_n,x_{n-1})_{n\in {\mathbb {N}}}\), hence their condition (H2) has the form
$$\begin{aligned} \Vert {\nabla }F(x_{n+1},x_n)\Vert \le b(\Vert x_{n+1}-x_{n}\Vert +\Vert x_n-x_{n-1}\Vert ). \end{aligned}$$ -
Further, since in [5, 46] F is assumed to be lower semicontinuous only, their condition (H3) has the form: there exists a subsequence \((z_{n_j} )_{j\in {\mathbb {N}}}\) of \((z_n)_{n\in {\mathbb {N}}}\) such that \(z_{n_j}\longrightarrow z^*\) and \(F(z_{n_j})\longrightarrow F(z^*),\) as \(j\longrightarrow +\infty .\) Of course in our case this condition holds whenever \(\omega ((z_n)_{n\in {\mathbb {N}}})\) is nonempty since F is continuous. In [34] condition (H3) refers to some properties of the sequences \((a_{n\in {\mathbb {N}}}),(b_{n\in {\mathbb {N}}})\) and \((c_n)_{n\in {\mathbb {N}}}.\)
Consequently, at least in the smooth setting, our abstract convergence result stated in Lemma 3 below is an extension of the corresponding result in [5, 34, 46].
Lemma 3
Let \(F : {\mathbb {R}}^m\times {\mathbb {R}}^m\longrightarrow {\mathbb {R}}\) be a continuously Fréchet differentiable function which satisfies the Kurdyka–Łojasiewicz property at some point \(z^*=(x^*,x^*)\in {\mathbb {R}}^m\times {\mathbb {R}}^m.\)
Let us denote by U, \(\eta \) and \(\varphi : [0, \eta )\longrightarrow {\mathbb {R}}_+\) the objects appearing in the definition of the KL property at \(z^*.\) Let \(\sigma>\rho > 0\) be such that \(B(z^*,\sigma )\subseteq U.\) Furthermore, consider the sequences \((x_n)_{n\in {\mathbb {N}}},(v_n)_{n\in {\mathbb {N}}},(w_n)_{n\in {\mathbb {N}}}\) and let \((z_n)_{n\in {\mathbb {N}}}=(v_n,w_n)_{n\in {\mathbb {N}}}\subseteq {\mathbb {R}}^m\times {\mathbb {R}}^m\) be a sequence that satisfies the conditions (H1), (H2), and (H3).
Assume further that
Moreover, the initial point \(z_0\) is such that \(z_0\in B(z^*,\rho ),\) \(F(z^*)\le F(z_0)<F(z^*)+\eta \) and
Then, the following statements hold.
One has that \( z_n\in B(z^*,\rho )\) for all \(n \in \ N.\) Further, \(\sum _{n=1}^{+\infty }\Vert x_n-x_{n-1}\Vert <+\infty \) and the sequence \((x_n)_{n\in {\mathbb {N}}}\) converges to a point \({{\overline{x}}}\in {\mathbb {R}}^m.\) The sequence \((z_n)_{n\in {\mathbb {N}}}\) converges to \({{\overline{z}}}= (\overline{x},{{\overline{x}}}),\) moreover, we have \({{\overline{z}}}\in B(z^*,\sigma )\cap {{\,\mathrm{crit}\,}}(F)\) and \(F(z_n)\longrightarrow F({{\overline{z}}})=F(z^*),\, n \longrightarrow +\infty .\)
Due to the technical details of the proof of Lemma 3, we will first present a sketch of it in order to give a better insight.
1. At first, our aim is to show by classical induction that \(z_k\in B(z^*,\rho ),\,F(z_k)<F(z^*)+\eta \) and the inequality
holds, for every \(k\ge 1.\)
To this end we show that the assumptions in the hypotheses of Lemma 3 assures that \(z_1\in B(z^*,\rho )\) and \(F(z_1)<F(z^*)+\eta .\)
Further, we show that if \(z_k\in B(z^*,\rho ),\,F(z_k)<F(z^*)+\eta \) for some \(k\ge 1,\) then
which combined with the previous step assures that the base case, \(k=1\), in our induction process holds.
Next, we take the inductive step and show that the previous statement holds for every \(k\ge 1.\)
2. By summing up the inequality obtained at 1. from \(k=1\) to \(k=n\) and letting \(n\longrightarrow +\infty \) we obtain that the sequence \((x_n)_{n\in {\mathbb {N}}}\) is convergent and from here the conclusion of the Lemma easily follows.
We now pass to a detailed presentation of this proof.
Proof
We divide the proof into the following steps.
Step I. We show that \(z_1\in B(z^*,\rho )\) and \(F(z_1)< F(z^*)+\eta .\)
Indeed, \(z_0\in B(z^*,\rho )\) and (6) assures that \(F(z_1)\ge F(z^*).\) Further, (H1) assures that \(\Vert x_1-x_0\Vert \le \sqrt{\frac{F(z_0)-F(z_1)}{a}}\) and since \(\Vert x_1-x^*\Vert =\Vert (x_1-x_0)+(x_0-x^*)\Vert \le \Vert x_1-x_0\Vert +\Vert x_0-x^*\Vert \) and \(F(z_1)\ge F(z^*)\) the condition (7) leads to
Now, from (H3) we have \(\Vert z_1-z^*\Vert \le c_1\Vert x_1-x^*\Vert +c_2\Vert x_{0}-x^*\Vert \) hence
Thus, \(z_1\in B(z^*,\rho ),\) moreover (6) and (H1) provide that \(F(z^*)\le F(z_2)\le F(z_1)\le F(z_0)< F(z^*)+\eta .\)
Step II. Next we show that whenever for a \(k\ge 1\) one has \(z_k\in B(z^*,\rho ),\,F(z_k)<F(z^*)+\eta \) then it holds that
Hence, let \(k\ge 1\) and assume that \(z_k\in B(z^*,\rho ),\,F(z_k)<F(z^*)+\eta \). Note that from (H1) and (6) one has \(F(z^*)\le F(z_{k+1})\le F(z_k)<F(z^*)+\eta ,\) hence
thus (8) is well stated. Now, if \(x_k=x_{k+1}\) then (8) trivially holds.
Otherwise, from (H1) and (6) one has
Consequently, \(z_k\in B(z^*,\rho )\cap \{z\in {\mathbb {R}}^m: F(z^*)<F(z)<F(z^*)+\eta \}\) and by using the KL inequality we get
Since \(\varphi \) is concave, and (9) assures that \(F(z_{k+1})-F(z^*)\in [0,\eta ),\) one has
consequently,
Now, by using (H1) and (H2) we get that
Consequently,
and by arithmetical-geometrical mean inequality we have
which leads to (8), that is
Step III. Now we show by induction that (8) holds for every \(k\ge 1.\) Indeed, Step II. can be applied for \(k=1\) since according to Step I. \(z_1\in B(z^*,\rho )\) and \(F(z_1)< F(z^*)+\eta .\) Consequently, for \(k=1\) the inequality (8) holds.
Assume that (8) holds for every \(k\in \{1,2,\ldots ,n\}\) and we show also that (8) holds for \(k=n+1.\) Arguing as at Step II., the condition (H1) and (6) assure that \(F(z^*)\le F(z_{n+1})\le F(z_n)<F(z^*)+\eta ,\) hence it remains to show that \(z_{n+1}\in B(z^*,\rho ).\) By using the triangle inequality and (H3) one has
By summing up (8) from \(k=1\) to \(k=n\) we obtain
Combining (10) and (11) and neglecting the negative terms we get
But \(\varphi \) is strictly increasing and \(F(z_1)-F(z^*)\le F(z_0)-F(z^*)\), hence
According to (H1) one has
hence, from (7) we get
Hence, we have shown so far that \(z_n\in B(z^*,\rho )\) for all \(n\in {\mathbb {N}}.\)
Step IV. According to Step III. the relation (8) holds for every \(k\ge 1.\) But this implies that (11) holds for every \(n\ge 1.\) By using (12) and neglecting the nonpositive terms, (11) becomes
Now letting \(n\longrightarrow +\infty \) in (13) we obtain that
Obviously the sequence \(S_n=\sum _{k=1}^n\Vert x_k-x_{k-1}\Vert \) is Cauchy, hence, for all \(\epsilon >0\) there exists \(N_{\epsilon }\in {\mathbb {N}}\) such that for all \(n\ge N_\epsilon \) and for all \(p\in {\mathbb {N}}\) one has
But
hence the sequence \((x_n)_{n\in {\mathbb {N}}}\) is Cauchy, consequently is convergent. Let
Let \({{\overline{z}}}=({{\overline{x}}},{{\overline{x}}}).\) Now, from (H3) we have
consequently \((z_n)_{n\in {\mathbb {N}}}\) converges to \({{\overline{z}}}.\)
Further, \((z_n)_{n\in {\mathbb {N}}}\subseteq B(z^*,\rho )\) and \(\rho <\sigma \), hence \({{\overline{z}}}\in B(z^*,\sigma ).\) Moreover, from (H2) we have
which shows that \({{\overline{z}}}\in {{\,\mathrm{crit}\,}}(F).\) Consequently, \(\overline{z}\in B(z^*,\sigma )\cap {{\,\mathrm{crit}\,}}(F)\).
Finally, since \(z_n\longrightarrow {{\overline{z}}},\, n\longrightarrow +\infty \) an F is continuous it is obvious that \(\lim _{n\longrightarrow +\infty } F(z_n)=F(\overline{z}).\) Further, since \(F(z^*)\le F(z_n)<F(z^*)+\eta \) for all \(n\ge 1\) and the sequence \((F(z_n))_{n\ge 1}\) is decreasing, obviously \(F(z^*)\le F({{\overline{z}}})<F(z^*)+\eta .\) Assume that \(F(z^*)< F({{\overline{z}}}).\) Then, one has
and by using the KL inequality we get
impossible since \(\Vert {\nabla }F({{\overline{z}}})\Vert =0.\) Consequently \(F({{\overline{z}}})=F(z^*).\) \(\square \)
Remark 4
One can observe that our conditions in Lemma 3 are slightly different to those in [5, 46]. Indeed, we must assume that \(z_0\in B(z^*,\rho )\) and in the right hand side of (7) we have \(\frac{\rho }{c_1+c_2}.\)
Though does not fit into the framework of this paper, we are confident that Lemma 3 can be extended to the case when we do not assume that F is continuously Fréchet differentiable but only that F is proper and lower semicontinuous. Then, the gradient of F can be replaced by the limiting subdifferential of F. These assumptions will imply some slight modifications in the conclusion of Lemma 3 and only the lines of proof at Step IV. must be substantially modified.
Corollary 5
Assume that the sequences from the definition of \((z_n)_{n\in N}\) satisfy \(v_n=x_n+\alpha _n(x_n-x_{n-1})\) and \(w_n=x_n+\beta _n(x_n-x_{n-1})\) for all \(n\ge 1\), where \((\alpha _n)_{n\in {\mathbb {N}}},(\beta _n)_{n\in {\mathbb {N}}}\) are bounded sequences. Let \(c=sup_{n\in {\mathbb {N}}}(|\alpha _n|+|\beta _n|).\) Then (H3) holds with \(c_1=2+c\) and \(c_2=c\). Further, Lemma 3 holds true if we replace (6) in its hypotheses by
Proof
The claim that (H3) holds with \(c_1=2+c\) and \(c_2=c\) is an easy verification. We have to show that (6) holds, that is, \(z_n\in B(z^*,\rho )\) implies \(z_{n+1}\in B(z^*,\sigma )\) for all \(n\in {\mathbb {N}}.\)
According to (H1), the assumption that \(F(z_n)\ge F(z^*)\) for all \(n\ge 1\) and the hypotheses of Lemma 3, we have
and
for all \(n\ge 1\).
Assume now that \(n\ge 1\) and \(z_n\in B(z^*,\rho ).\) Then, by using the triangle inequality we get
Further,
where \(c=\sup _{n\in {\mathbb {N}}}(|\alpha _{n}|+|\beta _{n}|).\)
Consequently, we have
which is exactly \(z_{n+1}\in B(z^*,\sigma ).\) Further, arguing analogously as at Step I. in the proof of Lemma 3, we obtain that \(z_{1}\in B(z^*,\rho )\subseteq B(z^*,\sigma )\) and this concludes the proof. \(\square \)
Now we are ready to formulate the following result.
Theorem 6
(Convergence to a critical point). Let \(F : {\mathbb {R}}^m\times {\mathbb {R}}^m\longrightarrow {\mathbb {R}}\) be a continuously Fréchet differentiable function and let \((z_n)_{n\in N}=(x_n+\alpha _n(x_n-x_{n-1}),x_n+\beta _n(x_n-x_{n-1}))_{n\in {\mathbb {N}}}\) be a sequence that satisfies (H1) and (H2), (with the convention \(x_{-1}\in {\mathbb {R}}^m\)), where \((\alpha _n)_{n\in {\mathbb {N}}},(\beta _n)_{n\in {\mathbb {N}}}\) are bounded sequences. Moreover, assume that \(\omega ((z_n)_{n\in {\mathbb {N}}})\) is nonempty and that F has the Kurdyka–Łojasiewicz property at a point \(z^*=(x^*,x^*)\in \omega ((z_n)_{n\in {\mathbb {N}}}).\) Then, the sequence \((x_n)_{n\in {\mathbb {N}}}\) converges to \(x^*\), \((z_n)_{n\in {\mathbb {N}}}\) converges to \(z^*\) and \(z^*\in {{\,\mathrm{crit}\,}}(F).\)
Proof
We will apply Corollary 5. Since \(z^*=(x^*,x^*)\in \omega ((z_n)_{n\in {\mathbb {N}}})\) there exists a subsequence \((z_{n_k})_{k\in {\mathbb {N}}}\) such that
From (H1) we get that the sequence \((F(z_n))_{n\in {\mathbb {N}}}\) is decreasing and obviously \(F(z_{n_k})\longrightarrow F(z^*),\, k\longrightarrow +\infty ,\) which implies that
We show next that \(x_{n_k}\longrightarrow x^*,\, k\longrightarrow +\infty .\) Indeed, from (H1) one has
and obviously the right side of the above inequality goes to 0 as \(k\longrightarrow +\infty .\) Hence,
Further, since the sequences \((\alpha _n)_{n\in {\mathbb {N}}},(\beta _n)_{n\in {\mathbb {N}}}\) are bounded we get
and
Finally, \(z_{n_k}\longrightarrow z^*,\, k\longrightarrow +\infty \) is equivalent to
and
which lead to the desired conclusion, that is
The KL property around \(z^*\) states the existence of quantities \(\varphi \), U, and \(\eta \) as in Definition 1. Let \(\sigma > 0 \) be such that \( B(z^*, \sigma )\subseteq U\) and \(\rho \in (0,\sigma ).\) If necessary we shrink \(\eta \) such that \(\eta < \frac{a(\sigma -\rho )^2}{4(1+c)^2},\) where \(c=\sup _{n\in {\mathbb {N}}}(|\alpha _n|+|\beta _n|).\)
Now, since the functions F and \(\varphi \) are continuous and \(F(z_n)\longrightarrow F(z^*),\,n\longrightarrow +\infty \), further \(\varphi (0)=0\) and \(z_{n_k}\longrightarrow z^*,\,x_{n_k}\longrightarrow x^*,\, k\longrightarrow +\infty \) we conclude that there exists \(n_0\in {\mathbb {N}},\,n_0\ge 1\) such that \(z_{n_0}\in B(z^*,\rho )\) and \(F(z^*)\le F(z_{n_0})<F(z^*)+\eta ,\) moreover
Hence, Corollary 5 and consequently Lemma 3 can be applied to the sequence \((u_n)_{n\in {\mathbb {N}}},\, u_n=z_{n_0+n}.\)
Thus, according to Lemma 3, \((u_n)_{n\in {\mathbb {N}}}\) converges to a point \(({{\overline{x}}},{{\overline{x}}})\in {{\,\mathrm{crit}\,}}(F),\) consequently \((z_n)_{n\in {\mathbb {N}}}\) converges to \(({{\overline{x}}},{{\overline{x}}}).\) But then, since \(\omega ((z_n)_{n\in {\mathbb {N}}})=\{({{\overline{x}}},{{\overline{x}}})\}\) one has \(x^*={{\overline{x}}}.\) Hence, \((x_n)_{n\in {\mathbb {N}}}\) converges to \(x^*\), \((z_n)_{n\in {\mathbb {N}}}\) converges to \(z^*\) and \(z^*\in {{\,\mathrm{crit}\,}}(F).\) \(\square \)
Remark 7
We emphasize that the main advantage of the abstract convergence results from this section is that can be applied also for algorithms where the the gradient of the objective is evaluated in iterations that contain the inertial therm. This is due to the fact that the sequence \((z_n)_{n\in {\mathbb {N}}}\) may have the form proposed in Corollary 5 and Theorem 6.
2.2 The convergence of the numerical method (2)
Based on the abstract convergence results obtained in the previous section, in this section we show the convergence of the sequences generated by Algorithm (2). The main tool in our forthcoming analysis is the so called descent lemma, see [44], which in our setting reads as
Now we are able to obtain a decrease property for the iterates generated by (2).
Lemma 8
In the settings of problem (1), for some starting points \(x_0,x_{-1}\in {\mathbb {R}}^m,\) let \((x_n)_{n\in {\mathbb {N}}},\,(y_n)_{n\in {\mathbb {N}}}\) be the sequences generated by the numerical scheme (2). Consider the sequences
and
for all \(n\in {\mathbb {N}},\,n\ge 1\).
Then, there exists \(N\in {\mathbb {N}}\) such that
-
(i)
The sequence \( \left( g(y_{n})+\delta _{n}\Vert x_{n}-x_{n-1}\Vert ^2\right) _{n\ge N}\) is nonincreasing and \(\delta _n>0\) for all \(n\ge N\).
Assume that g is bounded from below. Then, the following statements hold.
-
(ii)
The sequence \(\left( g(y_{n})+\delta _{n}\Vert x_{n}-x_{n-1}\Vert ^2\right) _{n\in {\mathbb {N}}}\) is convergent;
-
(iii)
\(\sum _{n\ge 1}\Vert x_n-x_{n-1}\Vert ^2<+\infty .\)
Due to the technical details of the proof of Lemma 8, we will first present a sketch of it in order to give a better insight.
1. We start from (2) and (16) to obtain
From here, by using equalities only, we obtain the key inequality
for all \(n\in {\mathbb {N}},\,n\ge 1,\) where \(\Delta _n=A_{n-1}-C_{n-1}+B_n-C_n.\) Further, we show that \(C_n,\Delta _n\) and \(\delta _n\) are positive after an index N.
2. Now, the key inequality emphasized at 1. implies at once (i), and if we assume that g is bounded from below also (ii) and (iii) follows in a straightforward way.
We now pass to a detailed presentation of this proof.
Proof
From (2) we have \({\nabla }g(y_n)=\frac{1}{s}(y_n-x_{n+1})\), hence
Now, from (16) we obtain
consequently we have
Further, for all \(n\in {\mathbb {N}}\) one has
and
hence,
Since
we have,
and
for all \(n\in {\mathbb {N}}.\)
Replacing the above equalities in (18), we obtain
for all \(n\in {\mathbb {N}}.\)
Hence, for every \(n\in {\mathbb {N}},\,n\ge 1\), we have
By using the equality
we obtain
for all \(n\in {\mathbb {N}},\,n\ge 1.\)
Note that \(\delta _n=\frac{1}{2}(A_{n-1}-C_{n-1}-B_n+C_n)\), hence we have
for all \(n\in {\mathbb {N}},\, n\ge 1.\)
Let us denote \(\Delta _n=A_{n-1}-C_{n-1}+B_{n}-C_{n}\) for all \(n\ge 1.\) Then,
and
for all \(n\ge 1,\) consequently the following inequality holds.
for all \(n\in {\mathbb {N}},\, n\ge 1.\)
Since \(0<\beta <1\) and \(s<\frac{2(1-\beta )}{L_g}\) we have
Hence, there exists \(N\in {\mathbb {N}},\,N\ge 1\) and \(C>0,\,D>0\) such that for all \(n\ge N\) one has
which, in the view of (20), shows (i), that is, the sequence \(g(y_n)+\delta _n\Vert x_n-x_{n-1}\Vert ^2\) is nonincreasing for \(n\ge N.\)
By using (20) again, we obtain
for all \(n\ge N,\) or more convenient, that
for all \(n\ge N.\) Let \(r>N.\) By summing up the latter relation from \(n=N\) to \(n=r\) we get
which leads to
Now, if we assume that g is bounded from below, by letting \(r\longrightarrow +\infty \) we obtain
which proves (iii).
The latter relation also shows that
hence
But then, by using the assumption that the function g is bounded from below we obtain that the sequence \((g(y_n)+\delta _n\Vert x_n-x_{n-1}\Vert ^2)_{n\in {\mathbb {N}}}\) is bounded from below. On the other hand, from (i) we have that the sequence \((g(y_n)+\delta _n\Vert x_n-x_{n-1}\Vert ^2)_{n\ge N}\) is nonincreasing, hence there exists
\(\square \)
Remark 9
Observe that conclusion (iii) in Lemma 8 assures that the sequence \((x_n-x_{n-1})_{n\in {\mathbb {N}}}\in l^2,\) in particular that
Note that according the proof of Lemma 8, one has \(\delta _n\Vert x_n-x_{n-1}\Vert ^2\longrightarrow 0,\,n\longrightarrow +\infty .\) Thus, (ii) assures that there exists the limit \(\lim _{n\longrightarrow +\infty } g(y_n)\in {\mathbb {R}}.\)
In what follows, in order to apply our abstract convergence result obtained at Theorem 6, we introduce a function and a sequence that will play the role of the function F and the sequence \((z_n)\) studied in the previous section. Consider the sequence
and the sequence \(z_n=(y_{n+N},u_{n+N})\) for all \(n\in {\mathbb {N}},\) where N and \(\delta _n\) were defined in Lemma 8. Let us introduce the following notations:
for all \(n\in {\mathbb {N}}.\) Then obviously the sequences \((\alpha _n)_{n\in {\mathbb {N}}}\) and \((\beta _n)_{n\in {\mathbb {N}}}\) are bounded, (actually they are convergent), and for each \(n\in {\mathbb {N}}\), the sequence \(z_n\) has the form
Consider further the following regularization of g
Then, for every \(n\in {\mathbb {N}}\) one has
Now, (22) becomes
which is exactly our condition (H1) applied to the function H and the sequences \(({\tilde{x}}_n)_{n\in {\mathbb {N}}}\) and \((z_n)_{n\in {\mathbb {N}}}.\)
Remark 10
We emphasize that H is strongly related to the total energy of the continuous dynamical systems (3) and (4), (for other works where a similar regularization has been used we refer to [25, 26, 46]). Indeed, the total energy of the systems (3) and (4) (see [6, 9]), is given by \(E:[t_0,+\infty )\rightarrow {\mathbb {R}},\,E(t)=g(x(t))+\frac{1}{2}\Vert {\dot{x}}(t)\Vert ^2.\) Then, the explicit discretization of E (see [9]), leads to \(E_n=g(x_n)+\frac{1}{2}\Vert x_n-x_{n-1}\Vert ^2=H(x_n,x_{n-1})\) and this fact was thoroughly exploited in [46]. However, observe that \(H(z_n)\) cannot be obtained via the usual implicit/explicit discretization of E. Nevertheless, \(H(z_n)\) can be obtained from a discretization of E by using the method presented in [6] which suggest to discretize E in the form
where \(\mu _n\) and \(\eta _n\) are linear combinations of \(x_n\) and \(x_{n-1}.\) In our case we take \(\mu _n={\tilde{y}}_n\) and \(\eta _n=\sqrt{2\delta _{n+N}}({\tilde{x}}_n-{\tilde{x}}_{n-1})\) and we obtain
The fact that H and the sequences \(({\tilde{x}}_n)_{n\in {\mathbb {N}}}\) and \((z_n)_{n\in {\mathbb {N}}}\) are satisfying also condition (H2) is underlined in Lemma 11 (ii).
Lemma 11
Consider the function H and the sequences \(({\tilde{x}}_n)_{n\in {\mathbb {N}}}\) and \((z_n)_{n\in {\mathbb {N}}}\) defined above. Then, the following statements hold true.
-
(i)
\({{\,\mathrm{crit}\,}}(H)=\{(x,x)\in {\mathbb {R}}^m\times {\mathbb {R}}^m:x\in {{\,\mathrm{crit}\,}}(g)\}\);
-
(ii)
There exists \(b>0\) such that \(\Vert {\nabla }H(z_n)\Vert \le b(\Vert {\tilde{x}}_{n+1}-{\tilde{x}}_n\Vert +\Vert {\tilde{x}}_{n}-{\tilde{x}}_{n-1}\Vert ),\) for all \(n\in {\mathbb {N}}\).
Proof
For (i) observe that \({\nabla }H(x,y)=({\nabla }g(x)+x-y,y-x)\), hence, \({\nabla }H(x,y)=(0,0)\) leads to \(x=y\) and \({\nabla }g(x)=0.\) Consequently
(ii) By using (2), for every \(n\in {\mathbb {N}},\,n\ge N\) we have
Let \(b=\max \left\{ \frac{\sqrt{2}}{s},\sup _{n\ge N}\left( \frac{\sqrt{2}\beta n}{s(n+\alpha )}+\sqrt{6\delta _n}\right) \right\} .\) Then, obviously \(b>0\) and for all \(n\in {\mathbb {N}}\) it holds
\(\square \)
Remark 12
Till now we did not take any advantage from the conclusions (ii) and (iii) of Lemma 8. In the next result we show that under the assumption that g is bounded from below, the limit sets \(\omega ((x_n)_{n\in {\mathbb {N}}})\) and \(\omega ((z_n)_{n\in {\mathbb {N}}})\) are strongly connected. This connection is due to the fact that in case g is bounded from below then (24) holds, that is, one has \(\lim _{n\longrightarrow +\infty }(x_n-x_{n-1})=0\).
Moreover, we emphasize some useful properties of the regularization H which occur when we assume that g is bounded from below.
In the following result we use the distance function to a set, defined for \(A\subseteq {\mathbb {R}}^m\) as
Lemma 13
In the settings of problem (1), for some starting points \(x_0=x_{-1}\in {\mathbb {R}}^m,\) consider the sequences \((x_n)_{n\in {\mathbb {N}}},\,(y_n)_{n\in {\mathbb {N}}}\) generated by Algorithm (2). Assume that g is bounded from below. Then, the following statements hold true.
-
(i)
\(\omega ((u_n)_{n\in {\mathbb {N}}})=\omega ((y_n)_{n\in {\mathbb {N}}})=\omega ((x_n)_{n\in {\mathbb {N}}})\subseteq {{\,\mathrm{crit}\,}}(g)\), further \(\omega ((z_n)_{n\in {\mathbb {N}}})\subseteq {{\,\mathrm{crit}\,}}(H)\) and \(\omega ((z_n)_{n\in {\mathbb {N}}})=\{({{\overline{x}}},\overline{x})\in {\mathbb {R}}^m\times {\mathbb {R}}^m: {{\overline{x}}}\in \omega ((x_n)_{n\in {\mathbb {N}}})\}\);
-
(ii)
\((H(z_n))_{n\in {\mathbb {N}}}\) is convergent and H is constant on \(\omega ((z_n)_{n\in {\mathbb {N}}})\);
-
(iii)
\(\Vert {\nabla }H(y_n,u_n)\Vert ^2\le \frac{2}{s^2}\Vert x_{n+1}-x_n\Vert ^2+2\left( \left( \frac{\beta n}{s(n+\alpha )}-\sqrt{2\delta _n}\right) ^2+\delta _n\right) \Vert x_{n}-x_{n-1}\Vert ^2\) for all \(n\in {\mathbb {N}},\,n\ge N\).
Assume that \((x_n)_{n\in {\mathbb {N}}}\) is bounded. Then,
-
(iv)
\(\omega ((z_n)_{n\in {\mathbb {N}}})\) is nonempty and compact;
-
(v)
\(\lim _{n\longrightarrow +\infty } {{\,\mathrm{dist}\,}}(z_n,\omega ((z_n)_{n\in {\mathbb {N}}}))=0.\)
Proof
(i) Let \({{\overline{x}}}\in \omega ((x_n)_{n\in {\mathbb {N}}}).\) Then, there exists a subsequence \((x_{n_k})_{k\in {\mathbb {N}}}\) of \((x_n)_{n\in {\mathbb {N}}}\) such that
Since by (24) \(\lim _{n\longrightarrow +\infty }(x_n-x_{n-1})=0\) and the sequences \((\sqrt{2\delta _n})_{n\in {\mathbb {N}}},\,\left( \frac{\beta n}{n+\alpha }\right) _{n\in {\mathbb {N}}}\) converge, we obtain that
which shows that
Further, from (2), the continuity of \({\nabla }g\) and (24), we obtain that
Hence, \(\omega ((x_n)_{n\in {\mathbb {N}}})\subseteq {{\,\mathrm{crit}\,}}(g).\) Conversely, if \({{\overline{y}}}\in \omega ((y_n)_{n\in {\mathbb {N}}})\) then, from (24) results that \({{\overline{y}}}\in \omega ((x_n)_{n\in {\mathbb {N}}}).\) Further, if \({{\overline{u}}}\in \omega ((u_n)_{n\in {\mathbb {N}}})\) then by using (24) again we obtain that \({{\overline{u}}}\in \omega ((y_n)_{n\in {\mathbb {N}}}).\) Hence,
Obviously \(\omega (({\tilde{x}}_n)_{n\in {\mathbb {N}}})=\omega ((x_n)_{n\in {\mathbb {N}}})\) and since the sequences \((\alpha _n)_{n\in {\mathbb {N}}},\,(\beta _n)_{n\in {\mathbb {N}}}\) are bounded, (convergent), from (24) one gets
Let \(({{\overline{x}}},{{\overline{y}}})\in \omega ((z_n)_{n\in {\mathbb {N}}}).\) Then, there exists a subsequence \((z_{n_k})_{k\in {\mathbb {N}}}\) such that \(z_{n_k}\longrightarrow ({{\overline{x}}},{{\overline{y}}}),\,k\longrightarrow +\infty .\) But we have \(z_n=\left( {\tilde{x}}_{n}+\alpha _n({\tilde{x}}_{n}-{\tilde{x}}_{n-1}),{\tilde{x}}_{n}+\beta _n({\tilde{x}}_{n}-{\tilde{x}}_{n-1})\right) ,\) for all \(n\in {\mathbb {N}}\), consequently from (27) we obtain
Hence, \({{\overline{x}}}={{\overline{y}}}\) and \({{\overline{x}}}\in \omega ((x_n)_{n\in {\mathbb {N}}})\) which shows that
Conversely, if \({{\overline{x}}} \in \omega (({\tilde{x}}_n)_{n\in {\mathbb {N}}})\) then there exists a subsequence \(({\tilde{x}}_{n_k})_{k\in {\mathbb {N}}}\) such that \(\lim _{k\rightarrow +\infty }{\tilde{x}}_{n_k}={{\overline{x}}}.\) But then, by using (27) we obtain at once that \(z_{n_k}\longrightarrow (\overline{x},{{\overline{x}}}),\,k\longrightarrow +\infty ,\) hence by using the fact that \(\omega (({\tilde{x}}_n)_{n\in {\mathbb {N}}})=\omega ((x_n)_{n\in {\mathbb {N}}})\) we obtain
Finally, from Lemma 11 (i) and since \(\omega ((x_n)_{n\in {\mathbb {N}}})\subseteq {{\,\mathrm{crit}\,}}(g)\) we have
(ii) Follows directly by (ii) in Lemma 8.
(iii) We have:
for all \(n\in {\mathbb {N}},\,n\ge N.\)
Assume now that \((x_n)_{n\in {\mathbb {N}}}\) is bounded and let us prove (iv), (see also [27]). Obviously it follows that \((z_n)_{n\in {\mathbb {N}}}\) is also bounded, hence according to Weierstrass Theorem \(\omega ((z_n)_{n\in {\mathbb {N}}}),\) (and also \(\omega ((x_n)_{n\in {\mathbb {N}}})\)), is nonempty. It remains to show that \(\omega ((z_n)_{n\in {\mathbb {N}}})\) is closed. From (i) we have
hence it is enough to show that \(\omega ((x_n)_{n\in {\mathbb {N}}})\) is closed.
Let be \(({{\overline{x}}}_p)_{p\in {\mathbb {N}}}\subseteq \omega ((x_n)_{n\in {\mathbb {N}}})\) and assume that \(\lim _{p\longrightarrow +\infty }{{\overline{x}}}_p=x^*.\) We show that \(x^*\in \omega ((x_n)_{n\in {\mathbb {N}}}).\) Obviously, for every \(p\in {\mathbb {N}}\) there exists a sequence of natural numbers \(n_k^p\longrightarrow +\infty ,\,k\longrightarrow +\infty \), such that
Let be \(\epsilon >0\). Since \(\lim _{p\longrightarrow +\infty }{{\overline{x}}}_p=x^*,\) there exists \(P(\epsilon ) \in {\mathbb {N}}\) such that for every \(p\ge P(\epsilon )\) it holds
Let \(p\in {\mathbb {N}}\) be fixed. Since \(\lim _{k\longrightarrow +\infty }x_{n_k^p}=\overline{x}_p,\) there exists \(k(p,\epsilon )\in {\mathbb {N}}\) such that for every \(k\ge k(p,\epsilon )\) it holds
Let be \(k_p \ge k(p,\varepsilon )\) such that \(n_{k_p}^p >p\). Obviously \(n_{k_p}^p \longrightarrow \infty \) as \(p \longrightarrow +\infty \) and for every \(p \ge P(\epsilon )\)
Hence \(\lim _{p\longrightarrow +\infty }x_{n_{k_p}^p}=x^*,\) thus \(x^*\in \omega ((x_n)_{n\in {\mathbb {N}}}).\)
(v) By using (28) we have
Since there exists the subsequence \((z_{n_k})_{k\in {\mathbb {N}}}\) such that \(\lim _{k\longrightarrow \infty }z_{n_k}=({{\overline{x}}}_0,{{\overline{x}}}_0)\in \omega ((z_n)_{n\in {\mathbb {N}}})\) it is straightforward that
\(\square \)
Now we are ready to prove Theorem 1 concerning the convergence of the sequences generated by the numerical scheme (2).
Proof
(Proof of Theorem 1) Let \((z_n)_{n\in {\mathbb {N}}}\) be the sequence defined by (25). Since \(x^*\in \omega ((x_n)_{n\in {\mathbb {N}}})\) according to Lemma 13 (i) one has \(x^*\in {{\,\mathrm{crit}\,}}(g)\) and \(z^*=(x^*,x^*)\in \omega ((z_n)_{n\in {\mathbb {N}}}).\)
It can easily be checked that the assumptions of Theorem 6 are satisfied with the continuously Fréchet differentiable function H, the sequences \((z_n)_{n\in {\mathbb {N}}}\) and \(({\tilde{x}}_n)_{n\in {\mathbb {N}}}.\) Indeed, according to (26) and Lemma 11 (ii) the conditions (H1) and (H2) from the hypotheses of Theorem 6 are satisfied. Hence, the sequence \(({\tilde{x}}_n)_{n\in {\mathbb {N}}}\) converges to \(x^*\) as \(n\longrightarrow +\infty \). But then obviously the sequence \(({x}_n)_{n\in {\mathbb {N}}}\) converges to \(x^*\) as \(n\longrightarrow +\infty \). \(\square \)
Remark 14
Note that under the assumptions of Theorem 1 we also have that
Corollary 15
In the settings of problem (1), for some starting points \(x_0,x_{-1}\in {\mathbb {R}}^m,\) consider the sequence \((x_n)_{n\in {\mathbb {N}}}\) generated by Algorithm (2). Assume that g semi-algebraic and bounded from below. Assume further that \(\omega ((x_n)_{n\in {\mathbb {N}}})\ne \emptyset .\)
Then, the sequence \((x_n)_{n\in {\mathbb {N}}}\) converges to a critical point of the objective function g.
Proof
Since the class of semi-algebraic functions is closed under addition (see for example [16]) and \((x,y) \mapsto \frac{1}{2}\Vert x-y\Vert ^2\) is semi-algebraic, we obtain that the the function
is semi-algebraic. Consequently H is a KL function. In particular H has the Kurdyka–Łojasiewicz property at a point \(z^*=(x^*,x^*),\) where \(x^*\in \omega ((x_n)_{n\in {\mathbb {N}}}).\) The conclusion follows from Theorem 1. \(\square \)
Remark 16
In order to apply Theorem 1 or Corollary 15 we need to assume that \(\omega ((x_n)_{n\in {\mathbb {N}}})\) is nonempty. Obviously, this condition is satisfied whenever the sequence \((x_n)_{n\in {\mathbb {N}}}\) is bounded. Next we show that the boundedness of \((x_n)_{n\in {\mathbb {N}}}\) is guaranteed if we assume that the objective function g is coercive, that is, \(\lim _{\Vert x\Vert \rightarrow +\infty } g(x)=+\infty .\)
Proposition 17
In the settings of problem (1), for some starting points \(x_0,x_{-1}\in {\mathbb {R}}^m,\) consider the sequence \((x_n)_{n\in {\mathbb {N}}}\) generated by Algorithm (2). Assume that the objective function g is coercive.
Then, g is bounded from below, and the sequence \((x_n)_{n\in {\mathbb {N}}}\) is bounded.
Proof
Indeed, g is bounded from below, being a continuous and coercive function (see [48]). Note that according to (23) the sequence \(D\sum _{n=N}^r\Vert x_{n+1}-x_{n}\Vert ^2\) is bounded. Consequently, from (23) it follows that \(y_{r+1}\) is contained in a lower level set of g, for every \(r\ge N,\) (N was defined in the hypothesis of Lemma 8). But the lower level sets of g are bounded since g is coercive. Hence, \((y_n)_{n\in {\mathbb {N}}}\) is bounded and taking into account (24), it follows that \((x_n)_{n\in {\mathbb {N}}}\) is also bounded. \(\square \)
An immediate consequence of Theorem 1 and Proposition 17 is the following result.
Corollary 18
Assume that g is a coercive function. In the settings of problem (1), for some starting points \(x_0,x_{-1}\in {\mathbb {R}}^m,\) consider the sequence \((x_n)_{n\in {\mathbb {N}}}\) generated by Algorithm (2). Assume further that
is a KL function.
Then, the sequence \((x_n)_{n\in {\mathbb {N}}}\) converges to a critical point of the objective function g.
3 Convergence rates via the Łojasiewicz exponent
In this section we will assume that the regularization function H, introduced in the previous section, satisfies the Łojasiewicz property, which corresponds to a particular choice of the desingularizing function \(\varphi \) (see [3, 4, 18, 20, 30, 41]).
Definition 2
Let \(g:{\mathbb {R}}^m\longrightarrow {\mathbb {R}}\) be a differentiable function. The function g is said to fulfill the Łojasiewicz property at a point \(\overline{x}\in {{\,\mathrm{crit}\,}}(g)\) if there exist \(K,\epsilon >0\) and \(\theta \in [0,1)\) such that
The number K is called the Łojasiewicz constant, meanwhile the number \(\theta \) is called the Łojasiewicz exponent of g at the critical point \({{\overline{x}}}.\)
Note that the above definition corresponds to the case when in the KL property the desingularizing function \(\varphi \) has the form \(\varphi (t)=\frac{K}{1-\theta } t^{1-\theta }.\) For \(\theta =0\) we adopt the convention \(0^0=0\), such that if \(|g(x)-g({\overline{x}})|^0=0\) then \(g(x)=g({\overline{x}}),\) (see [3]).
In the following theorem we provide convergence rates for the sequences generated by (2), but also for the objective function values in these sequences, in terms of the Łojasiewicz exponent of the regularization H (see also [3, 4, 11, 18, 35]).
More precisely we obtain finite convergence rates if the Łojasiewicz exponent of H is 0, linear convergence rates if the Łojasiewicz exponent of H belongs to \(\left( 0,\frac{1}{2}\right] \) and sublinear convergence rates if the Łojasiewicz exponent of H belongs to \(\left( \frac{1}{2},1\right) .\)
Theorem 19
In the settings of problem (1), for some starting points \(x_0,x_{-1}\in {\mathbb {R}}^m,\) consider the sequences \((x_n)_{n\in {\mathbb {N}}},\,(y_n)_{n\in {\mathbb {N}}}\) generated by Algorithm (2). Assume that g is bounded from below and consider the function
Let \((z_n)_{n\in {\mathbb {N}}}\) be the sequence defined by (25) and assume that \(\omega ((z_n)_{n\in {\mathbb {N}}})\) is nonempty and that H fulfills the Łojasiewicz property with Łojasiewicz constant K and Łojasiewicz exponent \(\theta \in \left[ 0,1\right) \) at a point \(z^*=(x^*,x^*)\in \omega ((z_n)_{n\in {\mathbb {N}}}).\) Then \(\lim _{n\longrightarrow +\infty }x_n=x^*\in {{\,\mathrm{crit}\,}}(g)\) and the following statements hold true:
If \(\theta =0\) then
- \((\mathrm{a}_0)\):
-
\((g(y_n))_{n\in {\mathbb {N}}},(g(x_n))_{n\in {\mathbb {N}}},(y_n)_{n\in {\mathbb {N}}}\) and \((x_n)_{n\in {\mathbb {N}}}\) converge in a finite number of steps;
If \(\theta \in \left( 0,\frac{1}{2}\right] \) then there exist \(Q\in [0,1),\) \(a_1,a_2,a_3,a_4>0\) and \({{\overline{k}}}\in {\mathbb {N}}\) such that
- \((\mathrm{a}_1)\):
-
\(g(y_{n})-g(x^* )\le a_1 Q^n\) for every \(n\ge {{\overline{k}}}\),
- \((\mathrm{a}_2)\):
-
\(g(x_{n})-g(x^* )\le a_2 Q^n\) for every \(n\ge {{\overline{k}}}\),
- \((\mathrm{a}_3)\):
-
\(\Vert x_n-x^* \Vert \le a_3 Q^{\frac{n}{2}}\) for every \(n\ge {{\overline{k}}}\),
- \((\mathrm{a}_4)\):
-
\(\Vert y_n-x^* \Vert \le a_4 Q^{\frac{n}{2}}\) for all \(n\ge {{\overline{k}}}\);
If \(\theta \in \left( \frac{1}{2},1\right) \) then there exist \(b_1,b_2,b_3,b_4>0\) and \({{\overline{k}}}\in {\mathbb {N}}\) such that
- \((\mathrm{b}_1)\):
-
\(g(y_n)-g(x^* )\le b_1 {n^{-\frac{1}{2\theta -1}}}, \text{ for } \text{ all } n\ge {{\overline{k}}}\),
- \((\mathrm{b}_2)\):
-
\(g(x_n)-g(x^* )\le b_2 {n^{-\frac{1}{2\theta -1}}}, \text{ for } \text{ all } n\ge {{\overline{k}}}\),
- \((\mathrm{b}_3)\):
-
\(\Vert x_{n}-x^* \Vert \le b_3 {n^{\frac{\theta -1}{2\theta -1}}}, \text{ for } \text{ all } n\ge {{\overline{k}}}\),
- \((\mathrm{b}_4)\):
-
\(\Vert y_n-x^* \Vert \le b_4 {n^{\frac{\theta -1}{2\theta -1}}}, \text{ for } \text{ all } n\ge {{\overline{k}}}\).
Due to the technical details of the proof of Theorem 19, we will first present a sketch of it in order to give a better insight.
-
1.
After discussing a straightforward case, we introduce the discrete energy \({\mathcal {E}}_n=H(z_n)-H(z^*)\) where \({\mathcal {E}}_n>0\) for all \(n\in {\mathbb {N}}\), and we show that Lemma 15 from [28] (see also [3]), can be applied to \({\mathcal {E}}_n.\)
-
2.
This immediately gives the desired convergence rates (\(\hbox {a}_0\)), (\(\hbox {a}_1\)) and (\(\hbox {b}_1\)).
-
3.
For proving (\(\hbox {a}_2\)) and (\(\hbox {b}_2\)) we use the identity \(g(x_n)-g(x^* )=(g(x_n)-g(y_n))+(g(y_n)-g(x^* ))\) and we derive an inequality between \(g(x_n)-g(y_n)\) and \({\mathcal {E}}_n.\)
-
4.
For (\(\hbox {a}_3\)) and (\(\hbox {b}_3\)) we use the Eq. (8) and the form of the desingularizing function \(\varphi \).
-
5.
Finally, for proving (\(\hbox {a}_4\)) and (\(\hbox {b}_4\)) we use the results already obtained at (\(\hbox {a}_3\)) and (\(\hbox {b}_3\)) and the form of the sequence \((y_n)_{n\in {\mathbb {N}}}.\)
We now pass to a detailed presentation of this proof.
Proof
Obviously, according to Theorem 1 one has \(\lim _{n\longrightarrow +\infty }x_n=x^*\in {{\,\mathrm{crit}\,}}(g)\), which combined with Lemma 13 (i) furnishes \(\lim _{n\longrightarrow +\infty }z_n=z^*\in {{\,\mathrm{crit}\,}}(H).\) We divide the proof into two cases.
Case I. Assume that there exists \({{\overline{n}}}\in {\mathbb {N}},\) such that \(H(z_{{{\overline{n}}}})=H(z^*).\) Then, since \(H(z_n)\) is decreasing for all \(n\in {\mathbb {N}}\) and \(\lim _{n\longrightarrow +\infty }H(z_n)=H(z^*)\) we obtain that
The latter relation combined with (26) leads to
for all \(n\ge {{\overline{n}}}.\)
Hence \(({\tilde{x}}_n)_{n\ge {{\overline{n}}}}\) is constant, in other words \(x_n=x^*\) for all \({n\ge {{\overline{n}}}+N}\). Consequently \(y_n=x^*\) for all \({n\ge {{\overline{n}}}+N+1}\) and the conclusion of the theorem is straightforward.
Case II. In what follows we assume that \(H(z_{n})>H(z^*),\) for all \(n\in {\mathbb {N}}.\)
For simplicity let us denote \({\mathcal {E}}_n=H(z_n)-H(z^*)\) and observe that \({\mathcal {E}}_n>0\) for all \(n\in {\mathbb {N}}.\) From (21) we have that the sequence \(({\mathcal {E}}_n)_{n\in {\mathbb {N}}}\) is nonincreasing, that is, there exists \(D>0\) such that
Further, since \(\lim _{n\longrightarrow +\infty }z_n=z^*, \) one has
From Lemma 13 (iii) we have
for all \(n\in {\mathbb {N}}\). Let \(S_n=2\left( \frac{\beta (n+N)}{s(n+N+\alpha )}-\sqrt{2\delta _{n+N}}\right) ^2+\delta _{n+N},\) for all \(n\in {\mathbb {N}}.\)
Combining (29) and (31) it follows that, for all \(n\in {\mathbb {N}}\) one has
Now by using the Łojasiewicz property of H at \(z^*\in {{\,\mathrm{crit}\,}}(H)\), and the fact that \(\lim _{n\longrightarrow +\infty }z_n=z^*\), we obtain that there exists \(\epsilon >0\) and \({{\overline{N}}}_1\in {\mathbb {N}},\) such that for all \(n\ge {{\overline{N}}}_1\) one has
and
Consequently (29), (32) and (33) leads to
for all \(n\ge {{\overline{N}}}_1,\) where \(a_n= \frac{D}{K^2 S_n} \text{ and } b_n=\frac{2}{s^2S_n}.\)
Since the sequence \(({\mathcal {E}}_n)_{n\in {\mathbb {N}}}\) is nonincreasing, one has
and
thus, (34) becomes
for all \(n\ge \overline{N_1}.\)
It is obvious that the sequences \((a_n)_{n\ge {{\overline{N}}}_1}\) and \((b_n)_{n\ge {{\overline{N}}}_1}\) are positive and convergent, further
hence, there exists \({{\overline{N}}}_2\in {\mathbb {N}},\, {{\overline{N}}}_2\ge {{\overline{N}}}_1,\) and \(C_0>0\) such that
Consequently, (35) leads to
for all \(n\ge \overline{N_2}.\)
Now we can apply Lemma 15 [28] with \(e_n={\mathcal {E}}_{n+2},\,l_0=2\) and \(n_0={{\overline{N}}}_2.\) Hence, by taking into account that \({\mathcal {E}}_n>0\) for all \(n\in {\mathbb {N}}\), that is, in the conclusion of Lemma 15 (ii) from [28] one has \(Q\ne 0\), we have:
-
(K0)
if \(\theta =0,\) then \(({\mathcal {E}}_n)_{n\ge N}\) converges in finite time;
-
(K1)
if \(\theta \in \left( 0,\frac{1}{2}\right] \), then there exists \(C_1>0\) and \(Q\in (0,1)\), such that for every \(n\ge {{\overline{N}}}_2+2\)
$$\begin{aligned} {\mathcal {E}}_n\le C_1 Q^n; \end{aligned}$$ -
(K2)
if \(\theta \in \left[ \frac{1}{2},1\right) \), then there exists \(C_2>0\), such that for every \(n\ge {{\overline{N}}}_2+4\)
$$\begin{aligned} {\mathcal {E}}_n\le C_2(n-3)^{-\frac{1}{2\theta -1}}. \end{aligned}$$
The case \(\theta =0.\)
For proving (\(\hbox {a}_0\)) we use (K0). Since in this case \(({\mathcal {E}}_n)_{n\ge N}\) converges in finite time after an index \(N_0\in {\mathbb {N}}\) we have \({\mathcal {E}}_n-{\mathcal {E}}_{n+1}=0\) for all \(n\ge N_0\), hence (29) implies that \({\tilde{x}}_n={\tilde{x}}_{n-1}\) for all \(n\ge N_0\). Consequently, \(x_n=x_{n-1}\) and \(y_n=x_n\) for all \(n\ge N_0+N\), thus \((x_n)_{n\in {\mathbb {N}}},\, (y_n)_{n\in {\mathbb {N}}}\) converge in finite time which obviously implies that \(\left( g(x_n)\right) _{n\in {\mathbb {N}}},\,\left( g(y_n)\right) _{n\in {\mathbb {N}}}\) converge in finite time.
The case \(\theta \in \left( 0,\frac{1}{2}\right] .\)
We apply (K1) and we obtain that there exists \(C_1>0\) and \(Q\in (0,1)\), such that for every \(n\ge {{\overline{N}}}_2+2\), one has \({\mathcal {E}}_n\le C_1 Q^n.\) But, \({\mathcal {E}}_n=g({\tilde{y}}_n) - g(x^*) + \delta _{n+N} \Vert {\tilde{x}}_n - {\tilde{x}}_{n-1} \Vert ^2\) for all \(n\in {\mathbb {N}},\) consequently \(g(y_{n+N}) - g(x^*)\le C_1 Q^n,\) for all \(n\ge {{\overline{N}}}_2+2.\) Thus, by denoting \(\frac{C_1}{Q^N}=a_1\) we get
For (\(\hbox {a}_2\)) we start from (16) and Algorithm (2) and for all \(n\in {\mathbb {N}}\) we have
By using the inequality \(\langle X,Y\rangle \le \frac{1}{2}\left( a^2\Vert X\Vert ^2+\frac{1}{a^2}\Vert Y\Vert ^2\right) \) for all \(X,Y\in {\mathbb {R}}^m, a\in {\mathbb {R}}\setminus \{0\}\), we obtain
consequently
Taking into account that \({\mathcal {E}}_n>0\) for all \(n\in {\mathbb {N}},\) from (29) we have
Hence, for all \(n\ge N-1\) one has
Now, the identity \(g(x_n)-g(x^* )=(g(x_n)-g(y_n))+(g(y_n)-g(x^* ))\) and (37) lead to
for every \(n\ge {{\overline{N}}}_2+N+2\), which combined with (K1) gives
for every \(n\ge {{\overline{N}}}_2+N+2\), where \(a_2=\frac{C_1}{2sD(2-sL_g)Q^{N-1}}+a_1.\)
For (\(\hbox {a}_3\)) we will use (8). Since \(z_n\in B(z^*,\epsilon )\) for all \(n\ge {{\overline{N}}}_2\) and \(z_n\longrightarrow z^*,\, n\longrightarrow +\infty \), we get that there exists \({{\overline{N}}}_3\in {\mathbb {N}},\,{{\overline{N}}}_3\ge \overline{N}_2\) such that (8) holds for every \(n\ge {{\overline{N}}}_3.\) In this setting, by taking into account that the desingularizing function is \(\varphi (t)=\frac{K}{1-\theta }t^{1-\theta },\) the inequality (8) has the form
where D was defined at (26) and b was defined at Lemma 11 (ii). Observe that by summing up (42) from \(k=n\ge {{\overline{N}}}_3\) to \(k=P>n\) and using the triangle inequality we obtain
By letting \(P\longrightarrow +\infty \) and taking into account that \({\tilde{x}}_P\longrightarrow x^*,\, {\mathcal {E}}_{P+1}\longrightarrow 0,\,P\longrightarrow +\infty ,\) further using (39) we get
where \(M_0=\frac{9bK}{4D(1-\theta )}.\)
But \(({\mathcal {E}}_n)_{n\in {\mathbb {N}}}\) is a decreasing sequence and according to (30) \(({\mathcal {E}}_n)_{n\in {\mathbb {N}}}\) converges to 0, hence there exists \({{\overline{N}}}_4\ge \max \{\overline{N}_3,{{\overline{N}}}_2+2\}\) such that \(0\le {\mathcal {E}}_{n}\le 1,\) for all \(n\ge {{\overline{N}}}_4\). The latter relation combined with the fact that \(\theta \in \left( 0,\frac{1}{2}\right] \) leads to \({\mathcal {E}}_{n}^{1-\theta }\le \sqrt{{\mathcal {E}}_{n}}, \text{ for } \text{ all } n\ge {{\overline{N}}}_4.\) Consequently we have \(\Vert {\tilde{x}}_{n}-x^* \Vert \le M_1\sqrt{{\mathcal {E}}_{n}},\) for all \(n\ge {{\overline{N}}}_4,\) where \(M_1=\frac{1}{\sqrt{D}}+M_0.\) The conclusion follows via (K1) since we have
and consequently
for all \(n\ge {{\overline{N}}}_4+N,\) where \(a_3=M_1\sqrt{\frac{C_1}{Q^{N}}}.\)
Finally, for \(n\ge {{\overline{N}}}_4+N+1\) we have
Let \(a_4=\left( 1+\beta +\frac{\beta }{\sqrt{Q}}\right) a_3.\) Then, for all \(n\ge {{\overline{N}}}_4+N+1\) one has
Now, if we take \({{\overline{k}}}= {{\overline{N}}}_4+N+1\) then (37), (41), (44) and (45) lead to the conclusions (\(\hbox {a}_1)\)–(\(\hbox {a}_4)\).
The case \(\theta \in \left( \frac{1}{2},1\right) .\)
According to (K2) there exists \(C_2>0\), such that for every \(n\ge {{\overline{N}}}_2+4\) one has
Let \(M_2=C_2\sup _{n\ge \overline{N}_2+4}\left( \frac{n}{n-3}\right) ^{\frac{1}{2\theta -1}}=C_2\left( \frac{\overline{N}_2+4}{{{\overline{N}}}_2+1}\right) ^{\frac{1}{2\theta -1}}.\) Then, \({\mathcal {E}}_n\le M_2 n^{-\frac{1}{2\theta -1}},\) for all \(n\ge {{\overline{N}}}_2+4.\) But \({\mathcal {E}}_n=g({\tilde{y}}_n) - g(x^*) + \delta _{n+N} \Vert {\tilde{x}}_n - {\tilde{x}}_{n-1} \Vert ^2\), hence \(g({\tilde{y}}_n) - g(x^*)\le M_2 n^{-\frac{1}{2\theta -1}},\) for every \(n\ge {{\overline{N}}}_2+4.\) Consequently, for every \(n\ge \overline{N}_2+4\) we have
Let \(b_1=M_2\left( \frac{N_2+4+N}{N_2+4}\right) ^{\frac{1}{2\theta -1}}=C_2\left( \frac{\overline{N}_2+4}{\overline{N}_2+1}\right) ^{\frac{1}{2\theta -1}}\left( \frac{N_2+4+N}{N_2+4}\right) ^{\frac{1}{2\theta -1}}=C_2\left( \frac{N_2+4+N}{\overline{N}_2+1}\right) ^{\frac{1}{2\theta -1}}.\) Then,
For (\(\hbox {b}_2\)) note that (40) holds for every \(n\ge \overline{N}_2+4,\) hence
Further,
for all \(n\ge {{\overline{N}}}_2+N+3.\) Consequently, \(g(x_n)-g(y_n)\le M_3n^{-\frac{1}{2\theta -1}},\) for all \(n\ge {{\overline{N}}}_2+N+3,\) where \(M_3=\frac{1}{2sD(2-sL_g)}C_2\left( \frac{\overline{N}_2+N+3}{{{\overline{N}}}_2+1}\right) ^{\frac{1}{2\theta -1}}.\) Therefore, by using the latter inequality and (46) one has
Let \(b_2=M_3+b_1.\) Then,
For (\(\hbox {b}_3\)) we use (43) again. Arguing as at (\(\hbox {a}_3\)) we obtain that \(0\le {\mathcal {E}}_{n}\le 1,\) for all \(n\ge \overline{N}_5,\) where \({{\overline{N}}}_5= \max \{{{\overline{N}}}_4,{{\overline{N}}}_2+4\}\).
Now, by using the fact that \(\theta \in \left( \frac{1}{2},1\right) ,\) we get that \({\mathcal {E}}_{n}^{1-\theta }\ge \sqrt{{\mathcal {E}}_{n}}, \text{ for } \text{ all } n\ge {{\overline{N}}}_5.\) Consequently, from (43) we get \(\Vert {\tilde{x}}_{n}-x^* \Vert \le M_1{{\mathcal {E}}_{n}^{1-\theta }},\) for all \(n\ge {{\overline{N}}}_5.\)
Since \( {\mathcal {E}}_{n}^{1-\theta }\le (M_2 n^{\frac{-1}{2\theta -1}})^{1-\theta },\) for all \(n\ge {{\overline{N}}}_5\) we get
Let \(b_3=M_1 M_2^{\frac{\theta -1}{2\theta -1}}\left( \frac{\overline{N}_5}{{{\overline{N}}}_5+N}\right) ^{\frac{\theta -1}{2\theta -1}}.\) Then,
For the final estimate observe that for all \(n\ge {{\overline{N}}}_5+N+1\) one has
Let \(b_4 =b_3\sup _{n\ge {{\overline{N}}}_5+N+1}\left( 1+ 2\frac{\beta n}{n+\alpha } \right) (\frac{n}{n-1})^{\frac{1-\theta }{2\theta -1}}> 0\). Then,
Now, if we take \({{\overline{k}}}={{\overline{N}}}_5+N+1\) then (46), (47), (48) and (49) lead to the conclusions (\(\hbox {b}_1)\)-(\(\hbox {b}_4)\). \(\square \)
Remark 20
According to [40] (see also [15]), there are situations when it is enough to assume that the objective function g has the Łojasiewicz property instead of considering this assumption for the regularization function H. More precisely in [40] it was obtained the following result, reformulated to our setting.
Proposition 21
(Theorem 3.6. [40]) Suppose that g has the Łojasiewicz property with Łojasiewicz exponent \(\theta \in \left[ \frac{1}{2},1\right) \) at \({{\overline{x}}}\in {\mathbb {R}}^m.\) Then the function \(H:{\mathbb {R}}^m\times {\mathbb {R}}^m\longrightarrow {\mathbb {R}},\,H(x,y)=g(x)+\frac{1}{2}\Vert y-x\Vert ^2\) has the Łojasiewicz property at \(({{\overline{x}}},\overline{x})\in {\mathbb {R}}^m\times {\mathbb {R}}^m\) with the same Łojasiewicz exponent \(\theta .\)
Corollary 22
In the settings of problem (1), for some starting points \(x_0,x_{-1}\in {\mathbb {R}}^m,\) consider the sequences \((x_n)_{n\in {\mathbb {N}}},\,(y_n)_{n\in {\mathbb {N}}}\) generated by Algorithm (2). Assume that g is bounded from below and g has the Łojasiewicz property at \(x^*\in \omega ((x_n)_{n\in {\mathbb {N}}})\), (which obviously must be assumed nonempty), with Łojasiewicz exponent \(\theta \in \left[ \frac{1}{2},1\right) \). If \(\theta =\frac{1}{2}\) then the convergence rates (\(\hbox {a}_1)\)–(\(\hbox {a}_4)\), if \(\theta \in \left( \frac{1}{2},1\right) \) then the convergence rates (\(\hbox {b}_1)\)-(\(\hbox {b}_4)\) stated in the conclusion of Theorem 19 hold.
Proof
Indeed, from Lemma 13 (i) one has \(z^*=(x^*,x^*)\in \omega ((z_n)_{n\in {\mathbb {N}}})\) and according to Proposition 21H has the Łojasiewicz property at \(z^*\) with Łojasiewicz exponent \(\theta .\) Hence, Theorem 19 can be applied. \(\square \)
As an easy consequence of Theorem 19 we obtain linear convergence rates for the sequences generated by Algorithm (2) in the case when the objective function g is strongly convex. For similar results concerning Polyak’s algorithm and ergodic convergence rates we refer to [36, 51].
Theorem 23
In the settings of problem (1), for some starting points \(x_0,x_{-1}\in {\mathbb {R}}^m,\) consider the sequences \((x_n)_{n\in {\mathbb {N}}},\,(y_n)_{n\in {\mathbb {N}}}\) generated by Algorithm (2). Assume that g is strongly convex and let \(x^*\) be the unique minimizer of g. Then, there exists \(Q\in [0,1)\) and there exist \(a_1,a_2,a_3,a_4>0\) and \({{\overline{k}}}\in {\mathbb {N}}\) such that the following statements hold true:
- \((\mathrm{a}_1)\):
-
\(g(y_{n})-g(x^* )\le a_1 {Q^n}\) for every \(n\ge {{\overline{k}}}\),
- \((\mathrm{a}_2)\):
-
\(g(x_{n})-g(x^* )\le a_2{Q^n}\) for every \(n\ge {{\overline{k}}}\),
- \((\mathrm{a}_3)\):
-
\(\Vert x_n-x^* \Vert \le a_3 {Q^{\frac{n}{2}}}\) for every \(n\ge {{\overline{k}}}\),
- \((\mathrm{a}_4)\):
-
\(\Vert y_n-x^* \Vert \le a_4 {Q^{\frac{n}{2}}}\) for all \(n\ge {{\overline{k}}}\).
Proof
We emphasize that a strongly convex function is coercive, see [13]. According to Proposition 17 the function g is bounded from bellow. According to [3], g satisfies the Łojasiewicz property at \(x^*\) with the Łojasiewicz exponent \(\theta =\frac{1}{2}.\) Then, according to Proposition 21, H satisfies the Łojasiewicz property at \((x^*,x^*)\) with the Łojasiewicz exponent \(\theta =\frac{1}{2}.\) The conclusion now follows from Theorem 19. \(\square \)
4 Numerical experiments
The aim of this section is to highlight via numerical experiments some interesting features of the generic Algorithm (2). To this purpose we implement Algorithm (2) and several other known algorithms from literature in MATLAB R2016b. We underline that, though in the following numerical experiments we use some simple objective functions since our scope is to show the excellent behaviour of Algorithm (2), our numerical scheme is meant for a very large-scale of problems.
In order to give a better perspective on the advantages and disadvantages of Algorithm (2) for different choices of stepsizes and inertial coefficients, in our numerical experiments we consider the following algorithms, all associated to the minimization problem (1).
-
(a)
A particular form of Nesterov’s algorithm (see [29]), that is,
$$\begin{aligned} x_{n+1}=x_n+\frac{ n}{n+3}(x_n-x_{n-1})-s{\nabla }g\left( x_n+\frac{n}{n+3}(x_n-x_{n-1})\right) , \end{aligned}$$(50)where \(s=\frac{1}{L_g}.\) According to [29, 43], for optimization problems with convex objective function, Algorithm (50) provides convergence rates of order \({\mathcal {O}}\left( \frac{1}{n^2}\right) \) for the energy error \(g(x_n)-\min g.\)
-
(b)
Nesterov’s algorithm associated to optimization problems with a \(\mu -\)strongly convex function (see [44]), that is,
$$\begin{aligned} x_{n+1}=x_n+\frac{ \sqrt{L_g}-\sqrt{\mu }}{\sqrt{L_g}+\sqrt{\mu }}(x_n-x_{n-1})-s{\nabla }g\left( x_n+\frac{n}{n+3}(x_n-x_{n-1})\right) , \end{aligned}$$(51)where \(s=\frac{1}{L_g}.\) According to [44] Algorithm (51) provides linear convergence rates.
-
(c)
The gradient descent algorithm with a \(\mu -\)strongly convex objective function, that is,
$$\begin{aligned} x_{n+1}=x_n-s{\nabla }g\left( x_n\right) , \end{aligned}$$(52)where the maximal admissible stepsize is \(s=\frac{2}{L_g+\mu }.\) According to some recent results [11] depending by the geometrical properties of the objective function the gradient descent method may have a better convergence rate than Algorithm (50).
-
(d)
A particular form of Polyak’s algorithm (see [26, 46]), that is,
$$\begin{aligned} x_{n+1}=x_n+\frac{\beta n}{n+3}(x_n-x_{n-1})-s{\nabla }g\left( x_n\right) , \end{aligned}$$(53)with \(\beta \in (0,1)\) and \(0<s<\frac{2(1-\beta )}{L_g}.\) For a strongly convex objective function this algorithm provides linear convergence rates [45].
-
(e)
Algorithm (2) studied in this paper, with \(\alpha =3\), which in the view of Theorem 23 assures linear convergence rates whenever the objective function is strongly convex.
1. In our first numerical experiment we consider as an objective function the strongly convex function
Since \({\nabla }g(x,y)=(16x,100y)\), we infer that the Lipschitz constant of its gradient is \(L_g =100\) and the strong convexity parameter \(\mu =16\). Observe that the global minimum of g is attained at (0, 0), further \(g(0,0)=0.\)
Obviously, for this choice of the objective function g, the stepsize will become \(s=\frac{1}{L_g}=0.01\) in Algorithm (50) and Algorithm (51), meanwhile in Algorithm (52) the stepsize is \(s=\frac{2}{L_g+\mu }\approx 0.0172\).
In Algorithm (53) and Algorithm (2) we consider the instances
Obviously for these values we have \(\beta \in (0,1)\) and \(0<s<\frac{2(1-\beta )}{L_g}.\)
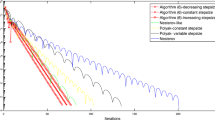
We run the simulations, by considering the same starting points \(x_0=x_{-1}=(1,-1)\in {\mathbb {R}}^2\) until the energy error \(|g(x_{n})-\min g|\) attains the value \(10^{-150}\). The results are shown in Fig. 1, where the horizontal axis measures the number of iterations and the vertical axis shows the error \(|g(x_{n})-\min g|\).
Comparing the energy error \(|g(x_n)-\min g|\) for Algorithm (50) (magenta), Algorithm (51) (blue), Algorithm (52) (green), Algorithm (53) (black) and Algorithm (2) (red), in the framework of the minimization of the strongly convex function \(g(x,y)=8x^2+50y^2\), by considering different stepsizes and different inertial coefficients (colour figure online)
Further, we are also interested in the behaviour of the generated sequences \(x_n\). To this end, we run the algorithms until the absolute error \(\Vert x_n-x^*\Vert \) attains the value \(10^{-150}\), where \(x^*=(0,0)\) is the unique minimizer of the strongly convex function g. The results are shown in Fig. 2, where the horizontal axis measures the number of iterations and the vertical axis shows the error \(\Vert x_{n}-x^*\Vert \).
Comparing the iteration error \(\Vert x_n-x^*\Vert \) for Algorithm (50) (magenta), Algorithm (51) (blue), Algorithm (52) (green), Algorithm (53) (black) and Algorithm (2) (red), in the framework of the minimization of the strongly convex function \(g(x,y)=8x^2+50y^2\), by considering different stepsizes and different inertial coefficients (colour figure online)
The experiments, depicted in Figs. 1 and 2, show that Algorithm (2) has a good behaviour since may outperform Algorithm (50), Algorithm (52) and also Algorithm (53). However Algorithm (51) seems to have in all these cases a better behaviour.
Remark 24
Nevertheless, for an appropriate choice of the parameters \(\alpha \) and \(\beta \) Algorithm (2) outperforms Algorithm (51). In order to sustain our claim observe that the inertial parameter in Algorithm (2) is \(\frac{\beta n}{n+\alpha }\approx \beta \) when n is big enough, (or \(\alpha \) is very small). Consequently, if one takes \(\beta \approx \frac{\sqrt{L_g}-\sqrt{\mu }}{\sqrt{L_g}+\sqrt{\mu }}\), then for n big enough the inertial parameters in Algorithm (2) and Algorithm (51) are very close. However if \(\beta <\frac{1}{2}\) then the stepsize in Algorithm (2) is clearly better then the stepsize in Algorithm (51). This happens whenever \(\frac{\sqrt{L_g}-\sqrt{\mu }}{\sqrt{L_g}+\sqrt{\mu }}<\frac{1}{2},\) that is \(L_g< 9\mu .\)
In the case of the strongly convex function g considered before, one has \(\frac{\sqrt{L_g}-\sqrt{\mu }}{\sqrt{L_g}+\sqrt{\mu }}=\frac{3}{7}\approx 0.428.\) Therefore, in the following numerical experiment we consider Algorithm (53) and Algorithm (2) with \(\beta = 0.4\) and optimal admissible constant stepsize \(s=0.0119< \frac{2(1-0.6)}{L_g}=0.012\), and all the other instances we let unchanged. We run the simulations until the energy error \(|g(x_{n})-\min g|\) and the absolute error \(\Vert x_n-x^*\Vert \) attains the value \(10^{-150},\) Fig. 3a, b. Observe that in this case Algorithm (2) clearly outperforms Algorithm (51).
2. In our second numerical experiment we consider a non-convex objective function
Then, \({\nabla }g(x,y)=(2x-y^2,2y(1-x))\), which is obviously not Lipschitz continuous on \({\mathbb {R}}^2\), but the restriction of \({\nabla }g\) on \([-1,1]\times [-1,1]\) is Lipschitz continuous. Indeed, for \((x_1,y_1),(x_2,y_2)\in [-1,1]\times [-1,1]\) one has
and
consequently,
Hence, one can consider that the Lipschitz constant of g on \([-1,1]\times [-1,1]\) is \(L_g=\sqrt{40}.\)
It is easy to see that the critical point of g on \([-1,1]\times [-1,1]\) is \(x^*=(0,0).\) Further, the Hessian of g is
which is indefinite on \([-1,1]\times [-1,1]\), hence g is neither convex nor concave on \([-1,1]\times [-1,1].\)
Since \(\det {\nabla }^2 g(x^*)=4>0\) and \(g_{xx}(x^*)=2>0\), we obtain that \(x^*\) is a local minimum of g and actually is the unique minimum of g on \([-1,1]\times [-1,1]\). However, \(x^*\) is not a global minimum of g since for instance \(g(2,3)=-9<0=g(x^*).\)
In our following numerical experiments we will use different inertial parameters in order to compare Algorithm (2), Algorithm (50) and Algorithm (53). In these experiments we run the algorithms until the energy error \(|g(x_{n})-g(x^*)|\) attains the value \(10^{-50}\) and the iterate error \(\Vert x_n-x^*\Vert \) attains the value \(10^{-50}\).
Since \(L_g=\sqrt{40}\) we take in Algorithm (50) the stepsize \(s=0.158\approx \frac{1}{\sqrt{40}}\). In Algorithm (53) and Algorithm (2) we consider the instances
Obviously for these values we have \(\beta \in (0,1)\) and \(0<s<\frac{2(1-\beta )}{L_g}.\) Further, we consider the same starting points \(x_0=x_{-1}=(0.5,-0.5)\) from \([-1,1]\times [-1,1]\).
The results are shown in Figs. 4a–c and 5a–c, where the horizontal axes measure the number of iterations and the vertical axes show the error \(|g(x_{n})- g(x^*)|\) and the error \(\Vert x_n-x^*\Vert \), respectively.
Consequently, also for this non-convex function, Algorithm (2) outperforms both Algorithm (53) and Algorithm (50).
5 Conclusions
In this paper we show the convergence of a Nesterov type algorithm in a full non-convex setting by assuming that a regularization of the objective function satisfies the Kurdyka–Łojasiewicz property. For this purpose we prove some abstract convergence results and we show that the sequences generated by our algorithm satisfy the conditions assumed in these abstract convergence results. More precisely, as a starting point we show a sufficient decrease property for the iterates generated by our algorithm and then via the KL property of a regularization of the objective in a cluster point of the generated sequence, we obtain the convergence of this sequence to this cluster point. Though our algorithm is asymptotically equivalent to Nesterov’s accelerated gradient method, we cannot obtain full equivalence due to the fact that in order to obtain the above mentioned decrease property we cannot allow the inertial parameter, more precisely the parameter \(\beta \), to attain the value 1. Nevertheless, we obtain finite, linear and sublinear convergence rates for the sequences generated by our numerical scheme but also for the function values in these sequences, provided the objective function, or a regularization of the objective function, satisfies the Łojasiewicz property with Łojasiewicz exponent \(\theta \in \left[ 0,1\right) .\)
A related future research is the study of a modified FISTA algorithm in a non-convex setting. Indeed, let \(f:{\mathbb {R}}^m\longrightarrow {{\overline{{\mathbb {R}}}}}\) be a proper convex and lower semicontinuous function and let \(g:{\mathbb {R}}^m\longrightarrow {\mathbb {R}}\) be a (possibly non-convex) smooth function with \(L_g\) Lipschitz continuous gradient. Consider the optimization problem
We associate to this optimization problem the following proximal-gradient algorithm. For \(x_0,x_{-1}\in {\mathbb {R}}^m\) consider
where \(\alpha >0,\,\beta \in (0,1)\) and \(0<s<\frac{2(1-\beta )}{L_g}.\)
Here
denotes the proximal point operator of the convex function sf.
Obviously, when \(f\equiv 0\) then (54) becomes the numerical scheme (2) studied in the present paper.
We emphasize that (54) has a similar formulation as the modified FISTA algorithm studied by Chambolle and Dossal [29] and the convergence of the generated sequences to a critical point of the objective function \(f+g\) would open the gate for the study of FISTA type algorithms in a non-convex setting.
References
Alvarez, F., Attouch, H.: An inertial proximal method for maximal monotone operators via discretization of a nonlinear oscillator with damping. Set Valued Anal. 9, 3–11 (2001)
Apidopoulos, V., Aujol, J.F., Dossal, Ch.: Convergence rate of inertial Forward–Backward algorithm beyond Nesterov’s rule. Math. Program. 180, 137–156 (2020)
Attouch, H., Bolte, J.: On the convergence of the proximal algorithm for nonsmooth functions involving analytic features. Math. Program. Ser. B 116(1–2), 5–16 (2009)
Attouch, H., Bolte, J., Redont, P., Soubeyran, A.: Proximal alternating minimization and projection methods for non-convex problems: an approach based on the Kurdyka–Łojasiewicz inequality. Math. Oper. Res. 35(2), 438–457 (2010)
Attouch, H., Bolte, J., Svaiter, B.F.: Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward–backward splitting, and regularized Gauss–Seidel methods. Math. Program. 137(1–2), 91–129 (2013)
Attouch, H., Chbani, Z., Peypouquet, J., Redont, P.: Fast convergence of inertial dynamics and algorithms with asymptotic vanishing viscosity. Math. Program. Ser. B 168(1–2), 123–175 (2018)
Attouch, H., Chbani, Z., Riahi, H.: Rate of convergence of the Nesterov accelerated gradient method in the subcritical case \(\alpha \le 3\), ESAIM: COCV, 25, Article number 2 (2019)
Attouch, H., Goudou, X., Redont, P.: The heavy ball with friction method, I. The continuous dynamical system: global exploration of the local minima of real-valued function by asymptotic analysis of a dissipative dynamical system. Commun. Contemp. Math. 2(1), 1–34 (2000)
Attouch, H., Peypouquet, J., Redont, P.: A dynamical approach to an inertial forward–backward algorithm for convex minimization. SIAM J. Optim. 24(1), 232–256 (2014)
Attouch, H., Peypouquet, J., Redont, P.: Fast convex optimization via inertial dynamics with Hessian driven damping. J. Differ. Equ. 261(10), 5734–5783 (2016)
Aujol, J.F., Dossal, Ch., Rondepierre, A.: Optimal convergence rates for Nesterov acceleration. SIAM J. Optim. 29(4), 3131–3153 (2019)
Aujol, J.F., Dossal, C.: Optimal rate of convergence of an ODE associated to the Fast Gradient Descent schemes for \(b > 0\). HAL preprint https://hal.inria.fr/hal-01547251v2/document
Bauschke, H.H., Combettes, P.L.: Convex Analysis and Monotone Operator Theory in Hilbert Spaces. Springer, New York (2011)
Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2(1), 183–202 (2009)
Bégout, P., Bolte, J., Jendoubi, M.A.: On damped second-order gradient systems. J. Differ. Equ. 259, 3115–3143 (2015)
Bolte, J., Sabach, S., Teboulle, M.: Proximal alternating linearized minimization for non-convex and nonsmooth problems. Math. Program. 146(1–2), 459–494 (2014)
Bolte, J., Nguyen, T.P., Peypouquet, J., Suter, B.W.: From error bounds to the complexity of first-order descent methods for convex functions. Math. Program. 165(2), 471–507 (2017)
Bolte, J., Daniilidis, A., Lewis, A.: The Łojasiewicz inequality for nonsmooth subanalytic functions with applications to subgradient dynamical systems. SIAM J. Optim. 17(4), 1205–1223 (2006)
Bolte, J., Daniilidis, A., Lewis, A., Shiota, M.: Clarke subgradients of stratifiable functions. SIAM J. Optim. 18(2), 556–572 (2007)
Bolte, J., Daniilidis, A., Ley, O., Mazet, L.: Characterizations of Łojasiewicz inequalities: subgradient flows, talweg, convexity. Trans. Am. Math. Soc. 362(6), 3319–3363 (2010)
Boţ, R.I., Csetnek, E.R.: Approaching nonsmooth non-convex optimization problems through first order dynamical systems with hidden acceleration and Hessian driven damping terms. Set Valued Var. Anal. 26, 227–245 (2018)
Boţ, R.I., Csetnek, E.R.: A forward-backward dynamical approach to the minimization of the sum of a nonsmooth convex with a smooth non-convex function. ESAIM COCV 24(2), 463–477 (2018)
Boţ, R.I., Csetnek, E.R.: Newton-like dynamics associated to non-convex optimization problems. In: Hosseini, S., Mordukhovich, B., Uschmajew, A. (eds.) Nonsmooth Optimization and Its Applications, International Series of Numerical Mathematics, vol. 170, pp. 131–149. Birkhäuser, Cham (2019)
Boţ, R.I., Csetnek, E.R., Hendrich, C.: Inertial Douglas–Rachford splitting for monotone inclusion problems. Appl. Math. Comput. 256, 472–487 (2015)
Boţ, R.I., Csetnek, E.R., László, S.C.: Approaching nonsmooth non-convex minimization through second-order proximal-gradient dynamical systems. J. Evol. Equ. 18(3), 1291–1318 (2018)
Boţ, R.I., Csetnek, E.R., László, S.C.: An inertial forward–backward algorithm for minimizing the sum of two non-convex functions. EURO J. Comput. Optim. 4(1), 3–25 (2016)
Boţ, R.I., Csetnek, E.R., László, S.C.: A second order dynamical approach with variable damping to non-convex smooth minimization. Appl. Anal. 99(3), 361–378 (2020)
Boţ, R.I., Nguyen, D.K.: The proximal alternating direction method of multipliers in the non-convex setting: convergence analysis and rates. arXiv:1801.01994
Chambolle, A., Dossal, Ch.: On the convergence of the iterates of the “fast iterative shrinkage/thresholding algorithm”. J. Optim. Theory Appl. 166(3), 968–982 (2015)
Chill, R.: On the Łojasiewicz–Simon gradient inequality. J. Funct. Anal. 201, 572–601 (2003)
Chouzenoux, E., Pesquet, J.C., Repetti, A.: Variable metric forward–backward algorithm for minimizing the sum of a differentiable function and a convex function. J. Optim. Theory Appl. 162(1), 107–132 (2014)
Combettes, P.L., Glaudin, L.E.: Quasinonexpansive iterations on the affine hull of orbits: from Mann’s mean value algorithm to inertial methods. SIAM J. Optim. 27(4), 2356–2380 (2017)
van den Dries, L., Miller, C.: Geometric categories and o-minimal structures. Duke Math. J. 84(2), 497–540 (1996)
Frankel, P., Garrigos, G., Peypouquet, J.: Splitting methods with variable metric for Kurdyka–Łojasiewicz functions and general convergence rates. J. Optim. Theory Appl. 165(3), 874–900 (2015)
Garrigos, G., Rosasco, L., Villa, S.: Convergence of the Forward-Backward algorithm: beyond the worst-case with the help of geometry, https://arxiv.org/pdf/1703.09477.pdf
Ghadimi, E., Feyzmahdavian, H.R., Johansson, M.: Global convergence of the heavy-ball method for convex optimization. In: 2015 European Control Conference (ECC). IEEE, pp. 310–315 (2015)
Haraux, A., Jendoubi, M.: Convergence of solutions of second-order gradient-like systems with analytic nonlinearities. J. Differ. Equ. 144(2), 313–320 (1998)
Kurdyka, K.: On gradients of functions definable in o-minimal structures. Annales de l’institut Fourier (Grenoble) 48(3), 769–783 (1998)
Lessard, L., Recht, B., Packard, A.: Analysis and design of optimization algorithms via integral quadratic constraints. SIAM J. Optim. 26, 57–95 (2016)
Li, G., Pong, T.K.: Calculus of the exponent of Kurdyka–Łojasiewicz inequality and its applications to linear convergence of first-order methods. Found. Comput. Math. 18(5), 1–34 (2018)
Łojasiewicz, S.: Une propriété topologique des sous-ensembles analytiques réels, Les Équations aux Dérivées Partielles, Éditions du Centre National de la Recherche Scientifique Paris, pp. 87–89 (1963)
Lorenz, D.A., Pock, T.: An inertial forward–backward algorithm for monotone inclusions. J. Math. Imaging Vis. 51(2), 311–325 (2015)
Nesterov, Y.: A method for solving the convex programming problem with convergence rate \(O(1/k^2)\). Dokl. Akad. Nauk SSSR 269(3), 543–547 (1983). (Russian)
Nesterov, Y.: Introductory Lectures on Convex Optimization: A Basic Course. Kluwer, Dordrecht (2004)
Ochs, P.: Local convergence of the heavy-ball method and ipiano for non-convex optimization. J. Optim. Theory Appl. 177(1), 153–180 (2018)
Ochs, P., Chen, Y., Brox, T., Pock, T.: iPiano: inertial proximal algorithm for non-convex optimization. SIAM J. Imaging Sci. 7(2), 1388–1419 (2014)
Polyak, B.T.: Some methods of speeding up the convergence of iteration methods. U.S.S.R. Comput. Math. Math. Phys. 4(5), 1–17 (1964)
Rockafellar, R.T., Wets, R.J.-B.: Variational Analysis, Fundamental Principles of Mathematical Sciences, vol. 317. Springe, Berlin (1998)
Simon, L.: Asymptotics for a class of nonlinear evolution equations, with applications to geometric problems. Ann. Math. 118(3), 525–571 (1983)
Su, W., Boyd, S., Candès, E.J.: A differential equation for modeling Nesterov’s accelerated gradient method: theory and insights. J. Mach. Learn. Res. 17, 1–43 (2016)
Sun, T., Yin, P., Li, D., Huang, C., Guan, L., Jiang, H.: Non-ergodic convergence analysis of heavy-ball algorithms. In: The Thirty-Third AAAI Conference on Artificial Intelligence (2019)
Zavriev, S.K., Kostyuk, F.V.: Heavy-ball method in non-convex optimization problems. Comput. Math. Model. 4, 336–341 (1993)
Acknowledgements
The author is thankful to two anonymous referees for their valuable remarks and suggestions which led to the improvement of the quality of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work was supported by a grant of Ministry of Research and Innovation, CNCS—UEFISCDI, Project Number PN-III-P1-1.1-TE-2016-0266, and by a grant of Ministry of Research and Innovation, CNCS—UEFISCDI, Project Number PN-III-P4-ID-PCE-2016-0190, within PNCDI III.
Appendix
Appendix
1.1 Second order continuous dynamical systems that are modelling Algorithm (2)
In what follows we emphasize the connections between Algorithm (2) and the continuous dynamical systems (3) and (4).
Consider (4) with the initial conditions \(x(t_0)=u_0,\,{\dot{x}}(t_0)=v_0,\,u_0,v_0\in {\mathbb {R}}^m\) and the governing second order differential equation
We will use the time discretization presented in [6], that is, we take the fixed stepsize \(h> 0,\) and consider \(\beta =1-\gamma h>0\), \(t_n = \frac{1}{\beta } nh\) and \(x_n = x(t_n).\) Then the implicit/explicit discretization of (3) leads to
where \(y_n\) is a linear combination of \(x_n\) and \(x_{n-1}\) and will be defined below.
Now, (55) can be rewritten as
which suggest to choose \(y_n\) in the form
However, for practical purposes, it is convenient to work with the re-indexation \(n\rightarrowtail n+\alpha \) and we obtain the following equivalent formulation
Hence, by taking \(h^2=s\) we get
which is exactly Algorithm (2).
Remark 25
Obviously, already the form \(\beta =1-\gamma h>0\) shows that \(\beta \in (0,1).\) We could not obtain Algorithm (2) via some similar discretization of the continuous dynamical system (3) as the discretization method presented above. Nevertheless, we can show that (3) is the exact limit of Algorithm (2) in the sense of Su, Boyd and Candès [50].
In what follows we show that by choosing appropriate values of \(\beta \), both the continuous second order dynamical systems (3) and the continuous dynamical system (4) are the exact limit of the numerical scheme (2).
To this end we take in (2) small step sizes and follow the same approach as Su, Boyd and Candès in [50], (see also [27] for similar approaches). For this purpose we rewrite (2) in the form
and introduce the Ansatz \(x_n\approx x(n\sqrt{s})\) for some twice continuously differentiable function \(x : [0,+\infty ) \rightarrow {\mathbb {R}}^m\). We let \(n=\frac{t}{\sqrt{s}}\) and get \(x(t)\approx x_n,\,x(t+\sqrt{s})\approx x_{n+1},\,x(t-\sqrt{s})\approx x_{n-1}.\) Then, as the step size s goes to zero, from the Taylor expansion of x we obtain
and
Further, since
it follows \(\sqrt{s} {\nabla }g(y_n)=\sqrt{s}{\nabla }g(x_n)+ o(\sqrt{s})\). Consequently, (56) can be written as
or, equivalently
Hence,
Now, if we take \(\beta =1-\gamma {s}<1\) in (57) for some \(\frac{1}{{s}}>\gamma >0\), we obtain
After dividing by \(\sqrt{s}\) and letting \(s\rightarrow 0\), we obtain
which after division by t gives (3), that is,
Similarly, by taking \(\beta =1-\gamma \sqrt{s}<1\) in (57), for some \(\frac{1}{\sqrt{s}}>\gamma >0\), we obtain
After dividing by \(\sqrt{s}\) and letting \(s\rightarrow 0\), we get
which after division by t gives (4), that is,
Rights and permissions
About this article
Cite this article
László, S.C. Convergence rates for an inertial algorithm of gradient type associated to a smooth non-convex minimization. Math. Program. 190, 285–329 (2021). https://doi.org/10.1007/s10107-020-01534-w
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10107-020-01534-w
Keywords
- inertial algorithm
- Non-convex optimization
- Kurdyka–Łojasiewicz inequality
- Convergence rate
- Łojasiewicz exponent