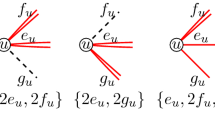Shorter tours and longer detours: uniform covers and a bit beyond

Abstract

Motivated by the well known “four-thirds conjecture” for the traveling salesman problem (TSP), we study the problem of uniform covers. A graph $G=(V,E)$ has an $\alpha$-uniform cover for TSP (2EC, respectively) if the everywhere $\alpha$ vector (i.e., $\{\alpha \}^{E}$) dominates a convex combination of incidence vectors of tours (2-edge-connected spanning multigraphs, respectively). The polyhedral analysis of Christofides’ algorithm directly implies that a 3-edge-connected, cubic graph has a 1-uniform cover for TSP. Sebő asked if such graphs have $(1-\epsilon )$-uniform covers for TSP for some $\epsilon > 0$. Indeed, the four-thirds conjecture implies that such graphs have $\frac{8}{9}$-uniform covers. We show that these graphs have $\frac{18}{19}$-uniform covers for TSP. We also study uniform covers for 2EC and show that the everywhere $\frac{15}{17}$ vector can be efficiently written as a convex combination of 2-edge-connected spanning multigraphs. For a weighted, 3-edge-connected, cubic graph, our results show that if the everywhere $\frac{2}{3}$ vector is an optimal solution for the subtour elimination linear programming relaxation for TSP, then a tour with weight at most $\frac{27}{19}$ times that of an optimal tour can be found efficiently. Node-weighted, 3-edge-connected, cubic graphs fall into this category. In this special case, we can apply our tools to obtain an even better approximation guarantee. An essential ingredient in our proofs is decompositions of graphs (e.g., cycle covers) that cover small-cardinality cuts an even (nonzero) number of times. Another essential tool we use is half-integral tree augmentation, which is known to have a small integrality gap. To extend our approach to input graphs that are 2-edge-connected, we present a procedure to decompose a point in the subtour elimination polytope into spanning, connected subgraphs that cover each 2-edge cut an even number of times. Using this decomposition, we obtain a $\frac{17}{12}$-approximation algorithm for minimum weight 2-edge-connected spanning subgraphs on subcubic, node-weighted graphs.

1 Introduction

The traveling salesman problem (TSP) and the minimum-weight 2-edge-connected spanning multigraph problem (2EC) are two fundamental and well-studied problems in combinatorial optimization. A folklore conjecture sometimes tersely called the “four-thirds conjecture” (see, e.g., [11, 18]) states that the optimal (integral) solution for the metric TSP is no more than $\frac{4}{3}$ times the value of the subtour elimination linear programming relaxation. However, the best known approximation ratio for both TSP and 2EC currently stands at $\frac{3}{2}$ [7, 14, 30, 31]. A recent spate of work has focused on the special case of graph-TSP when the underlying weights arise from hop distances in an undirected graph [6, 24,25,26]. The current best ratio for this problem is $\frac{7}{5}$ [29]. A parallel line of work has improved the ratio for 2EC in the unweighted case (commonly referred to as the 2-edge-connected spanning subgraph problem or 2ECSS for short) and resulted in a $\frac{4}{3}$-approximation for this problem [2, 29]. So far, these new techniques have not been extended to more general metrics.

One approach to general metrics is via convex combinations of incidence vectors of tours that can be derived from solutions to the well-known subtour elimination linear programming relaxation, which we will refer to as Subtour$^{=}(G)$. It is by now quite standard, but we invite the unfamiliar reader to visit Sect. 2.1 for the formal definition. For a solution $x\in \;$ Subtour$^{=}(G)$, we use $G_x=(V,E_x)$ to denote the graph $G=(V,E)$ with edge set $E_x \subseteq E$ restricted to the support of x. Goemans and Carr and Vempala showed that the four-thirds conjecture is equivalent to the following conjecture [11, 18].

Conjecture 1

If $x\in$ Subtour$^{=}(G)$, the vector $\frac{4}{3}x$ dominates a convex combination of tours in $G_x$.

Based on a polyhedral analysis of Christofides’ algorithm, we know that $\frac{3}{2}x$ dominates a convex combination of tours in $G_x$ [30, 31]; so far we cannot replace $\frac{3}{2}$ with any smaller constant. Following the terminology of Boyd and Sebő [5], for a graph $G=(V,E)$ on n vertices, let the everywhere r vector for G, be the vector in ${\mathbb {R}}^{V\atopwithdelims ()2}$ that is r in all coordinates corresponding to edges of G and 0 in all other coordinates. Conjecture 1 is closely related to the problem of uniform covers, which we now formally define.

Definition 1

A graph G has an $\alpha$-uniform cover for TSP (2EC) if the everywhere $\alpha$ vector for G dominates a convex combination of incidence vectors of tours (2-edge-connected spanning multigraphs).

This close connection is described in Proposition 1. Proposition 1 was observed by Carr and Vempala [11] but for completeness we provide a (quite straightforward) proof in Sect. 3.

Proposition 1

The following statements are equivalent.

• (a) If $x\in$ Subtour$^{=}(G)$, the vector $\frac{4}{3}x$ dominates a convex combination of tours in $G_x$.

• (b) For any positive integer k and an arbitrary k-edge-connected k-regular graph G, the everywhere $\frac{8}{3k}$ vector for G dominates a convex combination of tours in G.

The first interesting case is when $k=3$ (i.e., the case of 3-edge-connected, cubic graphs). Since the everywhere $\frac{2}{3}$ vector for a 3-edge-connected, cubic graph G is in Subtour$^{=}(G)$, Sebő pointed out that the four-thirds conjecture implies that for a 3-edge-connected, cubic graph, the everywhere $\frac{8}{9}$ vector dominates a convex combination of tours [27]. The following is therefore a relaxed version of Conjecture 1 [5, 27].

Conjecture 2

Let $G=(V,E)$ be a 3-edge-connected, cubic graph. The everywhere $\frac{8}{9}$ vector for G dominates a convex combination of tours of G.

For such graphs, the everywhere 1 vector does indeed dominate a convex combination of tours, which can be shown via the aforementioned polyhedral proof of Christofides’ algorithm by Wolsey [30, 31]. In other words, a 3-edge-connected, cubic graph has a 1-uniform cover. Sebő [27] asked if this bound can be improved: Does a 3-edge-connected, cubic graph have a $(1-\epsilon )$-uniform cover (for some small constant $\epsilon$)? For the special class of 3-edge-connected, cubic graphs that are also Hamiltonian, Boyd and Sebő show that the everywhere $\frac{6}{7}$ vector for G dominates a convex combination of tours [5]. We give an affirmative answer to Sebő’s question and improve this factor from 1 to $\frac{18}{19}$ for all 3-edge-connected, cubic graphs.¹

Theorem 1

Let $G=(V,E)$ be a 3-edge-connected, cubic graph. The everywhere $\frac{18}{19}$ vector for G dominates a convex combination of tours of G and this convex combination can be found in polynomial time.

The same question can be posed replacing tours with 2-edge-connected spanning multigraphs: for an arbitrary positive integer k and an arbitrary k-edge-connected k-regular graph G, can the everywhere $\alpha _k$ vector be decomposed into a convex combination of 2-edge-connected spanning multigraphs? For general k, the best-known factor for this question (as in the case for tours) is $\alpha _k=\frac{3}{k}$, which can be obtained via the polyhedral proof of Christofides’ algorithm [31]. For special cases, however, better factors are known. For $k=4$, Carr and Ravi showed that the everywhere $\frac{2}{3}$ vector can be decomposed into a convex combination of 2-edge-connected spanning multigraphs [10]. Their proof is constructive but is not guaranteed to run in polynomial time.

For a 3-edge-connected, cubic graph (i.e., the case $k=3$), Boyd and Legault showed that the everywhere $\frac{4}{5}$ vector can be written as a convex combination of 2-edge-connected spanning multigraphs [4]. This factor was subsequently improved to $\frac{7}{9}$ by Legault [22]. These convex combinations are a key ingredient for a related result on half-triangle graphs [4]. Both the factors $\frac{4}{5}$ and $\frac{7}{9}$ are obtained via constructive procedures that are not shown to run in polynomial time. In this paper, we show that for a 3-edge-connected, cubic graph, there is a polynomial-time algorithm to write the everywhere $\frac{15}{17}$ vector as a convex combination of 2-edge-connected spanning multigraphs.

Theorem 2

Let $G=(V,E)$ be a 3-edge-connected, cubic graph. The everywhere $\frac{15}{17}$ vector for G dominates a convex combination of 2-edge-connected spanning multigraphs of G and this convex combination can be found in polynomial time.

One implication of Theorem 1 is that for a weighted, 3-edge-connected, cubic graph for which the everywhere $\frac{2}{3}$ vector is an optimal solution for Subtour$^{=}(G)$, we can achieve an approximation ratio of $\frac{27}{19}$ for TSP, which improves over the approximation factor of Christofides’ algorithm for these graphs.² A natural class of such graphs are 3-edge-connected, cubic, node-weighted graphs. In the node-weight metric, each vertex of an undirected graph is assigned a positive integer weight; the weight of an edge is the sum of the weights of its two endpoints. (The node-weight metric is an intermediate class between weighted and unweighted graphs for studying the TSP and has been previously studied by Frank [15].) In fact, we show that using some of the same tools applied to the uniform cover problems, we can prove the following improved approximation ratio for such graphs.

Theorem 3

There is a $\frac{7}{5}$-approximation algorithm for TSP on node-weighted, 3-edge-connected, cubic graphs.

Similarly, Theorem 2 implies that for a weighted, 3-edge-connected, cubic graph for which the everywhere $\frac{2}{3}$ vector is an optimal solution for Subtour$^{=}(G)$, we can obtain an approximation ratio of $\frac{45}{34}$ for 2EC, which improves upon the best-known approximation factor for such graphs derived from Christofides’ algorithm. We explore this problem further when the input graph is no longer 3-edge-connected and prove the following theorem for subcubic, node-weighted graphs.

Theorem 4

If G is a node-weighted, subcubic graph, then there exists a $\frac{17}{12}$-approximation for 2EC on G.

1.1 Outline and organization

In Sect. 2, after stating some basic notation, we formally present the tools we use to prove our main theorems. The first tool, presented in Sect. 2.2, is an efficient algorithm by Boyd, Iwata and Takazawa to find a cycle cover that covers all 3- and 4-edge cuts in a bridgeless, cubic graph [3]. This is an essential tool in the proofs of Theorems 1, 2 and 3.

In Sect. 2.3, we present a key tool for proving Theorems 2 and 4, which is a theorem by Cheriyan, Jordán and Ravi proving a small integrality gap for the half-integral 1-cover problem [8]. The 1-cover problem generalizes the tree augmentation problem: given a connected subgraph S, the goal is to find an additional subset of edges (from the edges not in the subgraph S) to make S 2-edge-connected. The best-known approximation factor for this problem is 2 [13], but when the solution is half-integral, there is a $\frac{4}{3}$-approximation [8]. This latter result has been generalized by Iglesias and Ravi [19].

In Sect. 3, we show how to apply these tools to prove our main theorems on uniform covers, which we introduced and motivated in the introduction. In Sect. 4, we show how to apply these tools to go beyond the approximation guarantee obtained via uniform covers and present several applications to connectivity problems on node-weighted, 3-edge-connected, cubic graphs. In addition to Theorem 3, we present a $\frac{13}{10}$-approximation algorithm for 2EC in cubic, 3-edge-connected graphs. This improves the approximation ratio of $\frac{3}{2}$ for this problem that follows from Christofides’ algorithm. A natural question is if we can extend these results to graphs that are 2-edge-connected and either cubic or subcubic.

Extending our approach to input graphs that are 2-edge-connected necessitates finding methods for covering 2-edge cuts. In Sect. 4.2, we present a procedure to decompose a solution for the subtour elimination linear program into spanning, connected sub(multi)graphs that cover each 2-edge cut an even (nonzero) number of times. In Sect. 4.3.1, we demonstrate an application of this decomposition theorem for TSP on node-weighted, cubic graphs; we show that an algorithm similar to that of Christofides has an approximation factor better than $\frac{3}{2}$ when the weight of an optimal subtour solution is strictly larger than twice the sum of the node weights. In Sect. 4.3.2, we give another application of our decomposition theorem, which allows us to (again) apply the aforementioned theorem of Cheriyan, Jordán and Ravi and augment these spanning multigraphs with half-integral tree augmentations. Combining this with ideas from Sect. 4.3.1, we prove Theorem 4.

2 Preliminaries and tools

In the remainder of this paper, $G=(V,E)$ denotes a weighted graph and w(e) denotes the weight of edge $e \in E$. We can assume that G is 2-vertex-connected (e.g., applying Lemma 2.1 from [24]). Graph G is node-weighted if there is a function $f:V\rightarrow {\mathbb {R}}^+$ such that for each $e=uv\in E$, we have $w(e)=f(v)+f(u)$. In this case, we say G is node-weighted with node-weight function f. Denote by w(E) the total edge weight: $\sum _{e\in E}w(e)$. For ease of notation let $n = |V|$. For vectors $a,b\in {\mathbb {R}}^m$ we say a dominates b if $a_i\ge b_i$ in each coordinate $i \in \{1,\dots , m\}$.

We will work with multisets of edges of G. For a multisubset F of E, the submultigraph induced by F (henceforth referred to simply as a multigraph) is a graph that has the same number of copies of each edge as in F. For a positive integer t, the multiset $t\cdot F$ is the multiset that contains t copies of each element in F. For multisets F and $F'$, we denote by $F\cup F'$ the multiset that contains as many copies of each edge as those in F plus those in $F'$. For a multiset F and edge $e \in F$, we denote by $F - e$ the multiset that results from removing a single copy of e from F. By $F + e$, we denote the multiset that results from adding a single copy of e to F. For a multiset of edges (or a multigraph) F the summand $\sum _{e\in F} w(e)$ counts each edge $e\in F$ as many times as it appears in the multiset F.

A multigraph F of G is a tour if the vertex set of F spans V, F is connected, and every vertex in F has even degree. For the sake of brevity, we henceforth use the term 2-edge-connected multigraph of G to refer to a 2-edge-connected spanning multigraph (i.e., a multigraph that spans all the vertices of G). For a subset of edges $S\subseteq E$, the graph G / S is the graph obtained from G by contracting the edges in S (and deleting self-loops). For a subset S of vertices of G let $\delta (S) \subset E$ denote the edges crossing the cut $(S, V{\setminus }{S})$.

2.1 Subtour elimination linear program

Consider a (not necessarily complete) weighted graph $G=(V,E)$ with edge weights w(e) for $e\in E$. The output of TSP and 2EC on input graph G is a minimum weight tour and a minimum weight 2-edge connected multigraph of G, respectively. The following relaxation provides a lower bound on the weight of an optimal solution for both problems.

The metric completion of G is the complete graph $G^{met}$ on the vertex set of G such that for $u,v\in V$ the weight of the uv edge in $G^{met}$ is the weight of the shortest path between u and v in G. Clearly, these weights obey the triangle inequality. TSP on G is equivalent to finding a minimum weight tour in $G^{met}$. Since $G^{met}$ contains a minimum weight tour that is a Hamilton cycle, the following degree constraints are valid and yield the following seemingly stronger lower bound for TSP.

Note that in the above formulation, edges uv and vu are the same, so $x_{uv}$ and $x_{vu}$ represent the same variable. Cunningham showed that the bounds $z_G$ and $z_{G^{met}}$ are in fact equal [16, 23]. For a solution $x\in \;$ Subtour$^{=}(G)$ let $G_x=(V,E_x)$, where $E_x=\{uv : u,v \in V \text { and } x_{uv}>0\}$.

We will frequently use the following well-known fact [17].

Fact 1

Any point $x \in$ Subtour(G) dominates a convex combination of spanning trees, which can be found efficiently.

2.2 Cycle covers covering all 3- and 4-edge cuts

We now present one of our main tools for proving Theorems 1 and 2. Given a graph $G=(V,E)$, a cycle cover (also known as a 2-factor) of G is a collection of vertex disjoint cycles whose vertex sets partition V. Cycle covers have been extensively studied in the area of matching theory and have been also used to obtain approximation algorithms for TSP.

Kaiser and Škrekovski [21] proved that every bridgeless, cubic graph has a cycle cover that covers all 3-edge and 4-edge cuts of the graph. Their proof is not algorithmic and an efficient, constructive version was given by Boyd, Iwata and Takazawa [3].

Theorem 5

(Boyd et al. [3]) Let G be a bridgeless, cubic graph. Then there is an algorithm whose running time is polynomial in the size of G that finds a cycle cover of G covering every 3-edge and 4-edge cut of G.

A straightforward observation is the following.

Observation 1

Let G be a 3-edge-connected, cubic graph. Let C be a cycle cover that covers 3-edge cuts and 4-edge cuts in the graph. Then G / C is a 5-edge-connected multigraph.

Cubic, bipartite graphs exhibit even more structure, allowing for a stronger corollary.

Observation 2

Let G be a cubic, bipartite graph. Let C be a cycle cover of G. Then the graph G / C is Eulerian.

Proof

Each vertex in G / C corresponds to a cycle in C and the degree of this vertex has the same parity as the number of edges in the cycle. Since G is bipartite, every cycle in C is an even cycle. Therefore, each vertex in G / C has even degree, since it is obtained by contracting a cycle in C. We can conclude that G / C is an Eulerian graph. $\square$

Observation 3

Let G be a 3-edge-connected, cubic, bipartite graph. Let C be a cycle cover that covers 3-edge cuts and 4-edge cuts in the graph. Then G / C is a 6-edge-connected graph.

Proof

Graph G / C is 5-edge-connected by Observation 1. By Lemma 2, G / C is Eulerian. Therefore, G / C does not contain any cuts crossed by an odd number of edges. In particular, G / C contains no 5-edge cuts. $\square$

2.3 Tree augmentation

We next present one of our main tools for proving Theorem 2. We first state the 1-cover problem on a laminar family of sets. A family of sets ${\mathcal {S}}$ is called laminar if for any S and $S'$ in ${\mathcal {S}}$, the set $S\cap S'$ is equal to either S, $S'$ or $\emptyset$. For a graph $G=(V,E)$, we are given a laminar family of sets, ${\mathcal {S}}$, where each set in ${\mathcal {S}}$ consists of a subset of vertices. Additionally, we are given a set of edges E with nonnegative edge weights w(e) for $e\in E$. The 1-cover problem on family ${\mathcal {S}}$ asks for a 1-cover of ${\mathcal {S}}$: a minimum weight subset of edges $C \subseteq E$ such that $|C\cap \delta (S)|\ge 1$ for all $S \in {\mathcal {S}}$. Indeed, we are interested in a special case of the 1-cover problem on a laminar family of sets. Let F be a spanning, connected multigraph of a given graph G, and let ${\mathcal {S}}$ be the family of 1-edge cuts of F: ${\mathcal {S}} = \{S:~|\delta (S)\cap F|=1\}$. In this case, we refer to a 1-cover of ${\mathcal {S}}$ as a 1-cover of F. Define a block to be a maximal 2-edge-connected induced subgraph of F. Consider the tree obtained from contracting the blocks of F. Rooting this tree at an arbitrary vertex, we can find a laminar family ${\mathcal {S}}_F$ of sets in ${\mathcal {S}}$ such that the 1-covers of ${\mathcal {S}}$ are exactly the 1-covers of ${\mathcal {S}}_F$. Hence, the natural linear programming relaxation for the 1-cover problem for a graph $G = (V,E)$ and multigraph F of G is:

Let us denote the feasible region of the above linear program by Cover(G, F). By contracting the blocks of F, we get a tree on these contracted components and the 1-cover problem on ${\mathcal {S}}_F$ is equivalent to the tree augmentation problem [13]. Its integrality gap is known to be between $\frac{3}{2}$ and 2 [9, 13, 20]. However, in the special case of half-integral points, the integrality gap is much smaller. Cheriyan, Jordan and Ravi [8] proved that if $y\in$ Cover(G, F) and $y_e\in \{0,\frac{1}{2},1\}$ for all $e\in E$, then there is an algorithm, whose running time is polynomial in the size of G, that writes the vector $\frac{4}{3}\cdot y$ as a convex combination of 1-covers $C_1,\ldots ,C_h$ of F. Iglesias and Ravi generalized this result [19].

Theorem 6

(Iglesias and Ravi [19]) If $y\in$ Cover(G, F) and $y_e\ge \alpha$ or $y_e=0$ for all $e\in E$, then there is an algorithm, whose running time is polynomial in the size of G, that writes the vector $\frac{2}{1+\alpha }\cdot y$ as a convex combination of 1-covers $C_1,\ldots ,C_h$ of F.

3 Uniform covers

First, we recall Proposition 1, stated in the introduction. This observation is due to Carr and Vempala [11], but we prove the proposition for completeness.

Proposition 1

The following statements are equivalent.

• (a) If $x\in$ Subtour$^{=}(G)$, the vector $\frac{4}{3}x$ dominates a convex combination of tours in $G_x$.

• (b) For any positive integer k and an arbitrary k-edge-connected k-regular graph G, the everywhere $\frac{8}{3k}$ vector for G dominates a convex combination of tours in G.

Proof

(a)$\implies$(b): If G is k-edge-connected and k-regular, then y, defined to be the everywhere $\frac{2}{k}$ vector for G, is in Subtour$^{=}(G)$. Therefore $\frac{4}{3}y$, which is the everywhere $\frac{8}{3k}$ vector for G, is dominated by a convex combination of tours of $G_y$. Notice that $G_y=G$.

(b)$\implies$(a): Let $x\in$ Subtour$^{=}(G)$ for graph $G=(V,E)$. Let k be the smallest integer such that $x_e$ is a multiple of $\frac{1}{k}$ for every edge $e \in E_x$. Let $G'=(V,E')$ be such that $E'$ has $kx_e$ copies of each $e\in E_x$. It is easy to observe that $G'$ is 2k-edge-connected and 2k-regular. Let y be the everywhere $\frac{8}{6k}$ vector for $G'$. So by (b), y dominates a convex combination of tours in $G'$: $y\ge \sum _{i=1}^{\ell }\lambda _i \chi ^{F_i}$, where $\sum _{i=1}^{\ell }\lambda _i=1$, $\lambda _i>0$, and $F_i$ is a tour of $G'$ for $i=\{1,\ldots ,\ell \}$. Since $G'= k \cdot G_x$, each $F_i$ also corresponds to a tour in $G_x$, and $\sum _{i=1}^{\ell }\lambda _i \chi ^{F_i}(e)=\frac{8}{6k}kx_e = \frac{4}{3}x_e.$ $\square$

3.1 Algorithms for uniform covers

Recall that the polyhedral proof of Christofides’ algorithm can be used to prove statement (b) in Proposition 1 when the factor $\frac{8}{3k}$ is replaced by $\frac{3}{k}$. The problem of reducing this factor to anything less than $\frac{3}{k}$ has been open for decades. In the case where $k=3$, we can improve this result.

Theorem 1

Let $G=(V,E)$ be a 3-edge-connected, cubic graph. The everywhere $\frac{18}{19}$ vector for G dominates a convex combination of tours of G and this convex combination can be found in polynomial time.

Proof

By Theorem 5, graph G has a cycle cover C such that C covers every 3-edge and 4-edge cut of G. Let G / C be the graph obtained by contracting each cycle of C in G. By Observation 1, G / C is 5-edge-connected. Define vector $y\in {\mathbb {R}}^{E(G / C)}$ as follows: $y_e = \frac{2}{5}$ for $e\in E(G/C)$. Observe that $y\in$ Subtour(G / C). Thus, y dominates a convex combination of spanning trees of G / C, which can be computed in polynomial time (see Fact 1). More precisely, we can write $y \ge \sum _{i=1}^{\ell } \lambda _i \chi ^{T_i}$, where $T_i$ is a spanning tree of G / C, $\sum _{i=1}^{\ell } \lambda _i =1$, and $\lambda _i>0$ for $i \in \{1,\ldots ,\ell \}$. Consequently, we have $2 y \ge \sum _{i=1}^{\ell } \lambda _i \chi ^{2 T_i}$ (i.e., the vector 2y dominates a convex combination of doubled spanning trees of G / C).

Let M be the set of edges in $E{\setminus } C$ that are not in G / C; these are the edges that connect two vertices of the same cycle in C. Define vector $v\in {\mathbb {R}}^{V\atopwithdelims ()2}$ as follows: $v_e = 1$ for $e\in C$, $v_e = \frac{4}{5}$ for $e\in E{\setminus } (M\cup C)$, and $v_e=0$ otherwise. Note that $v \ge \sum _{i=1}^{\ell } \lambda _i \chi ^{C\cup 2 T_i}$. For $i\in \{1,\ldots ,\ell \}$, the graph induced by $C\cup 2 T_i$ is a tour.

Now we define $u\in {\mathbb {R}}^{V\atopwithdelims ()2}$ as follows: $u_e= \frac{1}{2}$ for $e\in C$ and $u_e=1$ for $e\in E{\setminus } C$, and $u_e=0$ otherwise. We have $u\in$ Subtour$^{=}(G)$ : for each cut D of G, if $|D|\ge 4$, clearly $\sum _{e \in D} u_e \ge 2$. If $|D|=3$, then $|C\cap D|= 2$, so $\sum _{e \in D}u_e = 2\cdot \frac{1}{2} + 1 = 2$. We can write $\frac{3}{2} u$ as a convex combination of tours [31].

Now vector $\frac{15}{19}v + \frac{4}{19}(\frac{3}{2}u)$ can be written as convex combination of tours of G. For edge $e\in C$ we have $\frac{15}{19}v_e+\frac{4}{19}(\frac{3}{2}u_e) = \frac{15}{19}+\frac{4}{19}(\frac{3}{2}\cdot \frac{1}{2})=\frac{18}{19}$. For $e\in E(G/C)$ we have $\frac{15}{19}v_e+\frac{4}{19}(\frac{3}{2}u_e) = \frac{15}{19}\cdot \frac{4}{5}+\frac{4}{19}(\frac{3}{2})=\frac{18}{19}$. For $e\in M$, we have $\frac{15}{19}v_e+\frac{4}{19}(\frac{3}{2}u_e) = 0 +\frac{4}{19}(\frac{3}{2})=\frac{6}{19}$. Therefore $\frac{15}{19}v + \frac{4}{19}(\frac{3}{2}u)$ is dominated by the everywhere $\frac{18}{19}$ vector for G. $\square$

If G is also bipartite, then by Observation 3, the graph G / C in the proof of Theorem 1 is 6-edge connected. We can therefore improve Theorem 1 in this case.

Theorem 7

Let $G=(V,E)$ be a 3-edge-connected, cubic, bipartite graph. The everywhere $\frac{12}{13}$ vector for G dominates a convex combination of tours of G and this convex combination can be found in polynomial time.

Proof

Let C be the cycle cover in G that covers 3-edge and 4-edge cuts of G. By Observation 3, G / C is 6-edge-connected. Let M be the set of edges that have both endpoints in the same cycle in the cycle cover C. Similar to the proof of Theorem 1, define vector $v \in {\mathbb {R}}^{V\atopwithdelims ()2}$ as follows: $v_e=1$ for $e\in C$, $v_e=\frac{2}{3}$ for $e\in E(G/C)$, and $v_e=0$ otherwise. The vector v can be written as a convex combination of tours of G.

Now define $u \in {\mathbb {R}}^{V \atopwithdelims ()2}$ as follows: $u_e=\frac{1}{2}$ for $e\in C$, $u_e=1$ for $e\in E{\setminus } C$, and $u_e=0$ otherwise. Since $u\in \;$ Subtour$^{=}(G)$, this implies that $\frac{3}{2}u$ can be written as a a convex combination of tours of G.

Finally, vector $\frac{9}{13}v + \frac{4}{13}(\frac{3}{2}u)$ can be written as a convex combination of tours of G. For $e\in C$, $\frac{9}{13}v_e + \frac{4}{13}u_e= \frac{9}{13}+\frac{4}{13}(\frac{3}{4})= \frac{12}{13}$. For $e\in E(G/C)$ we have $\frac{9}{13}v_e + \frac{4}{13}u_e= \frac{9}{13}\cdot \frac{2}{3}+\frac{4}{13}(\frac{3}{2})= \frac{12}{13}$. Finally, if $e\in M$, $\frac{9}{13}v_e + \frac{4}{13}u_e= \frac{4}{13}(\frac{3}{2})= \frac{6}{13}$. This proves the result. $\square$

We can further relax Conjecture 2 and ask whether or not the everywhere $\frac{8}{9}$ vector for a 3-edge-connected, cubic graph G can be written as a convex combination of 2-edge-connected multigraphs of G. The answer to this question is yes, and is a direct corollary of a decomposition theorem due to Carr and Ravi [10]. In fact, in Lemma 1, we show that for a 3-edge-connected, cubic graph G, the problem of determining if G has an $\alpha$-uniform cover can be reduced to bounding the integrality gap of half-integer solutions for Subtour$^=(G)$.

Lemma 1

Let $G=(V,E)$ a 3-edge-connected, cubic graph. Suppose for any $x\in$ Subtour$^=(G)$ such that $x\in \{0,\frac{1}{2},1\}^{{V}\atopwithdelims ()2}$, the vector $\alpha x$ dominates a convex combination of tours (2-edge-connected multigraphs) of $G_x$. Then the everywhere $\frac{2}{3}\alpha$ vector for G dominates a convex combination of tours (2-edge-connected multigraphs) of G.

Proof

Let $y\in {\mathbb {R}}^{E}$ be such that $y_e=\frac{2}{3}$ for $e\in E$. By Corollary 30.8a in [28], y is in the convex hull of cycle covers of G. Thus, there are cycle covers $C_1,\ldots ,C_\ell$ and positive multipliers $\lambda _1,\ldots ,\lambda _\ell$ such that $\sum _{i=1}^{\ell }\lambda _i=1$ and $y= \sum _{i=1}^{\ell }\lambda _i C_i$. For $i \in \{1,\ldots ,\ell \}$, define vector $y^i\in {\mathbb {R}}^{V\atopwithdelims ()2}$ as follows: $y^i_e=\frac{1}{2}$ for $e\in C_i$, $y^i_e=1$ for $e\in E{\setminus } C_i$, and $y^i_e=0$ otherwise. Observe that $y^i\in$ Subtour$^=(G)$ for $i \in \{1,\ldots ,\ell \}$. Furthermore, $v=\sum _{i=1}^{\ell }\lambda _i y^i$ is the everywhere $\frac{2}{3}$ vector for G; for $e\in E$ we have $\sum _{i:e \in C_i} \lambda _i=\frac{2}{3}$ and $\sum _{i:e \notin C_i}\lambda _i=\frac{1}{3}$, and so $\sum _{i=1}^\ell \lambda _i y_e^i = \sum _{i: e\in C_i}\lambda _i \cdot \frac{1}{2}+\sum _{i: e\notin C_i}\lambda _i = \frac{2}{3}$.

Since the vector $y^i \in \{0,\frac{1}{2},1\}^{{V}\atopwithdelims ()2}$, the vector $\alpha y^i$ dominates a convex combination of tours (2-edge-connected multigraphs) of $G_{y^i}=G$ for $i \in \{1,\ldots ,\ell \}$. Therefore, the everywhere $\frac{2}{3}\alpha$ vector for G dominates a convex combination of tours (2-edge-connected multigraphs) of G. $\square$

Theorem 8

(Carr and Ravi [10]) If $x\in$ Subtour$^{=}(G)$ and $x\in \{0,\frac{1}{2},1\}^{V \atopwithdelims ()2}$, then the vector $\frac{4}{3} x$ dominates a convex combination of 2-edge-connected multigraphs of $G_x$.

Corollary 8.1

Let $G=(V,E)$ be a 3-edge-connected, cubic graph. The everywhere $\frac{8}{9}$ vector for G dominates a convex combination of 2-edge-connected multigraphs of G.

Proof

Follows directly from Lemma 1 and Theorem 8. $\square$

However, this proof does not yield a polynomial-time decomposition since the number of multigraphs in the convex combination output via Theorem 8 is not guaranteed to be polynomial in the size of G. In fact, Legault proved a result that is stronger than Lemma 1: the everywhere $\frac{7}{9}$ vector for G can be written as a convex combination of 2-edge-connected subgraphs [22]. Notice that the result of Legault is stronger not only because the $\frac{7}{9}$ is smaller than $\frac{8}{9}$, but also in the sense that it restricts the multigraphs to subgraphs, i.e. no edge in G is doubled. However, the proof in [22] also does not guarantee that the number of subgraphs in the decomposition is polynomial in the size of G.

We now present a stronger version of Corollary 8.1. For the rest of this section we will do all computations on the edges of the graph $G=(V,E)$ so all the vectors are in dimension of E. Thus, henceforth we slightly abuse the everywhere vector notation to make the presentation simpler. Indeed, we can extend all the vectors to dimension $V\atopwithdelims ()2$ by adding zeros.

Theorem 9

Let $G=(V,E)$ be a 3-edge-connected, cubic graph. The everywhere $\frac{8}{9}$ vector for G dominates a convex combination of 2-edge-connected subgraphs of G and this convex combination can be found in polynomial time.

Proof

Let $y\in {\mathbb {R}}^E$ be such that $y_e=\frac{2}{3}$ for $e\in E$. Since $y\in$ Subtour(G), we can find in polynomial time spanning trees $T_1,\ldots ,T_\ell$ of G and positive multipliers $\lambda _1,\ldots ,\lambda _\ell$ such that $\sum _{i=1}^{\ell }\lambda _i =1$ and $y\ge \sum _{i=1}^{\ell } \lambda _i \chi ^{T_i}$. For $i \in \{1,\ldots ,\ell \}$ define vector $y^i\in {\mathbb {R}}^E$ as follows: $y^i_e= 0$ for $e\in T_i$ and $y^i_e=\frac{1}{2}$ for $e\notin T_i$. Since G is 3-edge-connected, we have $y^i\in$ Cover$(G,T_i)$ for $i \in \{1,\ldots ,\ell \}$. By Theorem 6, there is a polynomial-time algorithm that finds 1-covers $C^i_1,\ldots ,C^i_{\ell _i}$ of $T_i$ for $i \in \{1,\ldots ,\ell \}$ and positive multipliers $\lambda ^i_1,\ldots ,\lambda ^i_{\ell _i}$ such that $\sum _{j=1}^{\ell _i}\lambda ^i_j = 1$ and $\frac{4}{3} y^i = \sum _{j=1}^{\ell _i} \lambda ^i_j \chi ^{C^i_j}$ for $i \in \{1,\ldots ,\ell \}$. Note that $T_i+C^i_j$ is a 2-edge-connected subgraph of G for $i\in \{1,\ldots ,\ell \}$ and $j\in \{1,\ldots ,\ell _i\}$. Hence,

$$\begin{aligned} u=\sum _{i\in \{1,\ldots ,\ell \}} \sum _{j\in \{1,\ldots ,\ell _i\}} \lambda _i \lambda ^i_j \chi ^{T_i\cup C^i_j}, \quad \text {where }\sum _{i\in \{1,\ldots ,\ell \}} \sum _{j\in \{1,\ldots ,\ell _i\}} \lambda _i \lambda ^i_j =1 \end{aligned}$$

is a convex combination of 2-edge-connected multigraphs of G. By construction, an edge cannot belong both to a tree $T_i$ and to a 1-cover $C^i_j$. Thus, there are no doubled edges in any solution. Vector u is the everywhere $\frac{8}{9}$ vector for G: for $e\in E$, we have

$$\begin{aligned} u_e = \sum _{i: e\in T_i} \sum _{j=1}^{\ell _i}\lambda _i\lambda ^i_j + \sum _{i: e\notin T_i} \sum _{j: e\in C^i_j}\lambda _i\lambda ^i_j \le \frac{2}{3} + \frac{1}{3}\cdot \frac{2}{3} = \frac{8}{9}. \end{aligned}$$

$\square$

Observe that in the proof of Lemma 9, we never double any edge in any of the 2-edge-connected subgraphs. (Hence, the statement of lemma uses subgraph rather than multigraph.) If we relax this and allow doubled edges, we can indeed improve the factor by combining the ideas from Theorem 1 and Theorem 9 to improve the bound in Theorem 9 from $\frac{8}{9}$ to $\frac{15}{17}$.

Theorem 2

Let $G=(V,E)$ be a 3-edge-connected, cubic graph. The everywhere $\frac{15}{17}$ vector for G dominates a convex combination of 2-edge-connected spanning multigraphs of G and this convex combination can be found in polynomial time.

Proof

Let C be a cycle cover of G that covers every 3-edge and 4-edge cut of G. By Observation 1, the graph G / C is 5-edge-connected. Let $M=E{\setminus } (C\cup E(G/C))$. Define $r \in {\mathbb {R}}^{E(G/C)}$ as follows: $r_e = \frac{2}{5}$ for $e\in E(G/C)$. We have $r\in$ Subtour(G / C), so $\frac{3}{2} r$ dominates a convex combination of tours of G / C: namely $R_1,\ldots , R_\ell$. Observe that the graph induced by $C\cup R_i$ is a 2-edge-connected multigraph of G for $i \in \{1,\ldots ,\ell \}$. So, the vector $v\in {\mathbb {R}}^E$ where $v_e = 1$ for $e\in C$, $v_e = \frac{3}{5}$ for $e\in E(G/C)$, and $v_e = 0$ for $e\in M$ dominates a convex combination of 2-edge-connected multigraphs of G.

Now define $y\in {\mathbb {R}}^{E}$ as follows: $y_e = \frac{1}{2}$ for $e\in C$ and $y_e=1$ for $e\in E{\setminus } C$. Since $y\in$ Subtour(G), we can efficiently find spanning trees $T_1,\ldots ,T_\ell$ of G and convex multipliers $\lambda _1,\ldots ,\lambda _{\ell }$ such that $y\ge \sum _{i=1}^{\ell } \lambda _i\chi ^{T_i}$. For $i \in \{1,\ldots ,\ell \}$ define $y^i\in {\mathbb {R}}^E$ as follows: $y^i_e=\frac{1}{2}$ for $e\notin T_i$ and $y^i_e=0$ otherwise. Notice, that $y^i\in$ Cover$(G,T_i)$, hence by Theorem 6, there is a polynomial-time algorithm that finds 1-covers $C^i_1,\ldots ,C^i_{\ell _i}$ of $T_i$ for $i \in \{1,\ldots ,\ell \}$ and positive multipliers $\lambda ^i_1,\ldots ,\lambda ^i_{\ell _i}$ such that $\sum _{j=1}^{\ell _i}\lambda ^i_j = 1$ and $\frac{4}{3} y^i = \sum _{j=1}^{\ell _i} \lambda ^i_j \chi ^{C^i_j}$ for $i \in \{1,\ldots ,\ell \}$. Note that $T_i+C^i_j$ is a 2-edge-connected subgraph of G for $i\in \{1,\ldots ,\ell \}$ and $j\in \{1,\ldots ,\ell _i\}$. Hence,

$$\begin{aligned} u=\sum _{i\in \{1,\ldots ,\ell \}} \sum _{j\in \{1,\ldots ,\ell _i\}} \lambda _i \lambda ^i_j \chi ^{T_i\cup C^i_j}, \quad \text {where }\sum _{i\in \{1,\ldots ,\ell \}} \sum _{j\in \{1,\ldots ,\ell _i\}} \lambda _i \lambda ^i_j =1 \end{aligned}$$

is a convex combination of 2-edge-connected multigraphs of G. For $e\in C$, we have

$$\begin{aligned} u_e = \sum _{i: e\in T_i} \sum _{j=1}^{\ell _i}\lambda _i\lambda ^i_j + \sum _{i: e\notin T_i} \sum _{j: e\in C^i_j}\lambda _i\lambda ^i_j \le \frac{1}{2} + \frac{1}{2}\cdot \frac{2}{3}= \frac{5}{6}. \end{aligned}$$

For $e\notin C$, we have

$$\begin{aligned} u_e = \sum _{i: e\in T_i} \sum _{j=1}^{\ell _i}\lambda _i\lambda ^i_j + \sum _{i: e\notin T_i} \sum _{j: e\in C^i_j}\lambda _i\lambda ^i_j \le 1+0 =1. \end{aligned}$$

Finally we conclude that the vector $\frac{5}{17} v+\frac{12}{17}u$ can be efficiently written as convex combination of 2-edge-connected multigraphs of G. For $e\in C$ we have $\frac{5}{17} v_e+\frac{12}{17}u_e = \frac{5}{17}+ \frac{12}{17}\cdot \frac{5}{6}= \frac{15}{17}$. For $e\in G/C$ we have $\frac{5}{17} v_e+\frac{12}{17}u_e = \frac{5}{17}\cdot \frac{3}{5}+ \frac{12}{17}= \frac{15}{17}$. For $e\in M$ we have $\frac{5}{17} v_e+\frac{12}{17}u_e = \frac{5}{17}\cdot 0+ \frac{12}{17}= \frac{12}{17}$. Therefore $\frac{5}{17} v+\frac{12}{17}u$ is dominated by the everywhere $\frac{15}{17}$ vector for G. $\square$

We note that in the proof of Theorem 2, since the vector y is half-integral, we can apply Theorem 8 to conclude that $\frac{4}{3}y$ dominates a convex combination of 2-edge-connected multigraphs of G. This shows that the everywhere $\frac{7}{8}$ vector for G dominates a convex combination of 2-edge-connected multigraphs. (Specifically, $\frac{3}{8}(\frac{4}{3}y) + \frac{5}{8}v$ is dominated by the everywhere $\frac{7}{8}$ vector for G.) But this approach does not produce a convex combination in polynomial-time. We can improve Theorem 2 slightly when the graph G is also bipartite.

Theorem 10

Let $G=(V,E)$ be a 3-edge-connected, cubic, bipartite graph. The everywhere $\frac{7}{8}$ vector for G dominates a convex combination of 2-edge-connected multigraphs of G and this convex combination can be found in polynomial time.

Proof

Let C be the cycle cover in G that covers 3-edge and 4-edge cuts of G. Let M be the set of edges in G that have both endpoints in the same cycle of C. Since G / C is 6-edge-connected, the vector r with $r_e=\frac{1}{3}$ for $e\in E(G/C)$ is in Subtour(G / C). Therefore, we can show, similarly as in the proof of Theorem 2, that the vector v such that $v_e=1$ for $e\in C$ and $v_e = \frac{3}{2}\cdot \frac{1}{3}=\frac{1}{2}$ for $e\in E(G/C)$ and $v_e=0$ for $e\in M$ can be written as a convex combination of 2-edge-connected multigraphs of G in polynomial time. Furthermore, as in the proof of Theorem 2, the vector u, where $u_e=\frac{5}{6}$ for $e\in C$, $u_e=1$ for $e\in E {\setminus } C$, can be written as a convex combination of 2-edge-connected subgraphs of G in polynomial time. Note that the vector $\frac{1}{4}v+\frac{3}{4}u$ is dominated by the everywhere $\frac{7}{8}$ vector for G. $\square$

For the case where $k=4$ in Proposition 1, Carr and Ravi [10] showed that the everywhere $\frac{2}{3}$ vector can be written as a convex combination of 2-edge-connected subgraphs.³ But as we mentioned earlier, their proof is constructive but might require exponential time. The only known result on this problem before this work is applying Wolsey [31]’s decomposition which implies that the everywhere $\frac{3}{4}$ vector for a 4-edge-connected 4-regular graph can be decomposed into a convex combination of 2-edge-connected spanning multigraphs in polynomial time. However, this is weaker in terms of both the factor and the fact that we now allow doubled edges. By applying Theorem 6 we can slightly improve this. The proof of the following theorem is very similar to the proof of Theorem 9.

Theorem 11

Let $G = (V,E)$ be a 4-edge-connected, 4-regular graph. The everywhere $\frac{3}{4}$ vector for G dominates a convex combination of 2-edge-connected subgraphs of G and this convex combination can be found in polynomial time.

Proof

Since G is a 4-edge-connected 4-regular graph the everywhere $\frac{1}{2}$ vector for G, call it v, is in Subtour(G). Therefore, v can be written as convex combination of spanning trees of G: $v\ge \sum _{i=1}^{\ell } \lambda _i \chi ^{T_i}$, where $\lambda _1,\ldots ,\lambda _{\ell }$ are convex multipliers and $T_1,\ldots ,T_\ell$ are spanning trees of G. For $i\in \{1,\ldots ,\ell \}$, define a vector $y^i$, where $y^i_e=0$ if $e\in T_i$ and $y^i_e=\frac{1}{3}$ if $e\notin T_i$. Since G is 4-edge-connected we have $y^i\in$ Cover$(G,T_i)$. By Theorem 6, we can find 1-covers $C^i_1,\ldots ,C^i_{\ell _i}$ of $T_i$ for $i\in \{1,\ldots ,\ell \}$ with convex multipliers $\lambda ^i_1,\ldots ,\lambda ^i_{\ell _i}$ such that $\frac{3}{2}y^i = \sum _{j=1}^{\ell _i}\lambda ^i_j \chi ^{C^i_j}$ for $i\in \{1,\ldots ,\ell \}$. Now $T_i+C^i_j$ is a 2-edge-connected subgraph of G for $i\in \{1,\ldots ,\ell \}$ and $j\in \{1,\ldots ,\ell _i\}$. Let

$$\begin{aligned} u=\sum _{i\in \{1,\ldots ,\ell \}} \sum _{j\in \{1,\ldots ,\ell _i\}} \lambda _i \lambda ^i_j \chi ^{T_i\cup C^i_j}, \quad \text {where }\sum _{i\in \{1,\ldots ,\ell \}} \sum _{j\in \{1,\ldots ,\ell _i\}} \lambda _i \lambda ^i_j =1. \end{aligned}$$

We can write u as a convex combination of 2-edge-connected subgraphs of G. Also,

$$\begin{aligned} u_e = \sum _{i: e\in T_i} \sum _{j=1}^{\ell _i}\lambda _i\lambda ^i_j + \sum _{i: e\notin T_i} \sum _{j: e\in C^i_j}\lambda _i\lambda ^i_j = \frac{1}{2} + \frac{1}{2} \cdot \frac{1}{3}\cdot \frac{3}{2}= \frac{3}{4}. \end{aligned}$$

$\square$

4 A bit beyond uniform covers: node-weight metrics

Theorems 1 and 2, which we proved in Sect. 3, imply that when G is a 3-edge-connected, cubic graph and the everywhere $\frac{2}{3}$ vector is an optimal solution for Subtour$^{=}(G)$, we can efficiently find a tour and a 2-edge-connected spanning multigraph whose costs are at most $\frac{27}{19}$ and $\frac{45}{34}$, respectively, times that of an optimal solution. A 3-edge-connected, cubic graph with node-weight function $f:V\rightarrow {\mathbb {R}}^+$ falls into this category, as we will show later on. However, for such graphs we can obtain approximation guarantees better than $\frac{27}{19}$ and $\frac{45}{34}$ for the respective problems. The techniques we use to show this are similar to those used in Sect. 3. However, these techniques do not generalize to cubic graphs that have 2-edge cuts. In order to obtain improved approximation algorithms for this more general class of graphs, we introduce a connector decomposition theorem. We use this decomposition theorem to design algorithms for 2EC and TSP on node-weighted, subcubic graphs.

4.1 3-Edge-connected cubic graphs

First we show that the everywhere $\frac{2}{3}$ vector is in fact an optimal solution for Subtour(G) when G is a cubic, 3-edge-connected graph.

Lemma 2

Let $G=(V,E)$ be a 3-edge-connected, cubic graph with node-weight function $f:V \rightarrow {\mathbb {R}}^+$. Then $z_G=2\cdot \sum _{v\in V}f_v$.

Proof

For any $x\in$ Subtour(G), we have $x(\delta (v))\ge 2$. So,

$$\begin{aligned} \sum _{e\in E}w(e) x_e ~=~ \sum _{v\in V} x(\delta (v))\cdot f_v ~\ge ~ 2 \cdot \sum _{v\in V}f_v. \end{aligned}$$

Thus, $z_G\ge 2\cdot \sum _{v\in V}f_v$. On the other hand, let $x'_e$ denote the everywhere $\frac{2}{3}$ vector for G. Note that $x'\in$ Subtour(G), since G is 3-edge-connected. Moreover, $\sum _{e\in E}w(e)x'_e = 2\cdot \sum _{v\in V}f_v$. Hence $z_G\le 2\cdot \sum _{v\in V}f_v$. $\square$

Thus, we see that we can achieve a $\frac{27}{19}$-approximation for TSP on node-weighted, cubic, 3-edge-connected graphs. We now show in fact this approximation ratio can be improved in this special case. We start with the following observations.

Fact 2

Let C be a cycle cover of G. Then $\sum _{e\in C}w(e)= 2\cdot \sum _{v\in V}f_v = z_G.$

Fact 3

Let M be a perfect matching of G. Then $\sum _{e\in M}w(e) = \sum _{v\in V}f_v=\frac{z_G}{2}.$

Theorem 3

There is a $\frac{7}{5}$-approximation algorithm for TSP on node-weighted, 3-edge-connected, cubic graphs.

Proof

Let C be a cycle cover of G that covers all 3-edge and 4-edge cuts of G. By Observation 1, the graph G / C is 5-edge-connected. Let $y_e = \frac{2}{5}$ if $e\in E(G/C)$, and $y_e=0$ otherwise. Notice that $y\in$ Subtour(G / C), since for every $S \subset V(G/C)$, we have $y(\delta (S))\ge \frac{2}{5}\cdot 5\ge 2$. By Fact 1, y dominates a convex combination of spanning trees of G / C. Let T be a minimum spanning tree of G / C.

$$\begin{aligned} \sum _{e\in T}w(e)&\le \sum _{e\in E(G/C)}w(e) y_e \\&\le \sum _{e \in E{\setminus }{C}} w(e) y_e&(E(G/C)\subseteq E{\setminus } C)\\&\le \sum _{e \in E{\setminus }{C}} w(e) \cdot \frac{2}{5}&\left( y_e\le \frac{2}{5} \text{ for } e\in E{\setminus } C\right) \\&= \frac{z_G}{2} \cdot \frac{2}{5} ~ = ~ \frac{z_G}{5}&(\text{ By } \text{ Fact } 3; ~E{\setminus } C \text{ is } \text{ a } \text{ perfect } \text{ matching } \text{ of } G). \end{aligned}$$

Finally, note that $C\cup 2T$ is a tour of G and

$$\begin{aligned} \sum _{e\in C\cup 2T}w(e)\le \sum _{e\in C}w(e)+2\cdot \sum _{e\in T}w(e)\le z_G+\frac{2}{5}z_G=\frac{7}{5}z_G. \end{aligned}$$

$\square$

Next we show that we can use a very similar approach to 2EC on node-weighted, 3-edge-connected, cubic graphs.

Theorem 12

There is a $\frac{13}{10}$-approximation algorithm for 2EC on node-weighted, 3-edge-connected, cubic graphs.

Proof

Let C be a cycle cover of G that covers all 3-edge and 4-edge cuts of G. By Observation 1 graph G / C is 5-edge-connected. For $e\in E(G/C)$ let $y_e = \frac{2}{5}$, and $y_e=0$ otherwise. Notice that $y\in$ Subtour(G / C). By Christofides’ algorithm, one can find a 2-edge-connected multigraph F on G / C, such that $\sum _{e\in F}w(e)\le \frac{3}{2} \sum _{e\in E(G/C)}w(e) y_e$. In particular,

$$\begin{aligned} \sum _{e\in F}w(e)&\le \frac{3}{2} \sum _{e\in E(G/C)} w(e) y_e \\&\le \frac{3}{2} \sum _{e\in E{\setminus } C} w(e) y_e&(E(G/C)\subseteq E{\setminus } C)\\&\le \frac{3}{5} \sum _{e\in E{\setminus } C}w(e)&\left( y_e\le \frac{2}{5} \text{ for } e\in E{\setminus } C\right) \\&= \frac{3}{10} z_G&(\text{ By } \text{ Fact } 3; ~E{\setminus } C \text{ is } \text{ a } \text{ perfect } \text{ matching } \text{ of } G). \end{aligned}$$

Note that $C\cup F$ is a 2-edge-connected multigraph of G and

$$\begin{aligned} \sum _{e\in C\cup F}w(e)\le \sum _{e\in C}w(e)+\sum _{e\in F}w(e)\le z_G+\frac{3}{10}z_G=\frac{13}{10}z_G. \end{aligned}$$

$\square$

We note that for the 2EC problem on 3-edge-connected cubic graphs, there are better (i.e., smaller) bounds on the integrality gap than those implied by Theorem 12. In particular, Boyd and Legault [4] and Legault [22] gave bounds of $\frac{6}{5}$ and $\frac{7}{6}$, respectively, on the integrality gap. While their procedures are constructive, they do not run in polynomial time. Thus, the best previously known approximation factor for this problem is $\frac{3}{2}$ via Christofides algorithm. Finally one can easily obtain the following theorem using the ideas in the above theorems together with Observation 3.

Theorem 13

There is a $\frac{4}{3}$-approximation (respectively, $\frac{5}{4}$-approximation) algorithm for TSP (respectively, 2EC) on node-weighted, 3-edge-connected, cubic, bipartite graphs.

4.2 A tool for covering 2-edge cuts

The results in Theorems 3 and 12 do not apply to bridgeless, cubic graphs. In this section, we give an alternative tool to the BIT cycle cover (from Theorem 5) for graphs that are not 3-edge-connected (i.e., graphs that contain 2-edge cuts). In particular, we find a decomposition of a point $x^*$ in Subtour(G) such that this decomposition has certain properties. Many approaches for TSP decompose $x^*$ into a convex combination of spanning trees, whose average weight does not exceed $z_G$. In this section, we propose an alternate way of decomposing $x^*$ into connectors.

Definition 1

A connector F of graph G is a (multi) subset of edges of G such that F is connected and spanning and contains at most two copies of each edge in G.

It is known that a vector $x^* \in$ Subtour(G) dominates a convex combination of spanning trees (and hence connectors) of G. We now show that $x^*$ can be decomposed into connectors with the additional property that every 2-edge cut is covered an even number of times. These connectors can be augmented to obtain a tour or a 2-edge-connected multigraph of G, and under certain conditions, this property can be exploited to bound the weight of an augmentation.

Theorem 14

Let $x^*\in$ Subtour(G). We can find a family of connectors ${{{\mathcal {F}}}}=\{F_1, \ldots , F_{\ell }\}$ and multipliers $\lambda _1,\ldots ,\lambda _{\ell }$, in polynomial-time in the size of the graph G, such that

• (a) $x^* \ge \sum _{i=1}^{\ell } \lambda _i F_i$, where $\sum \lambda _i = 1$ and $\lambda _i > 0$, and

• (b) every $F_i$ has an even number of edges crossing each 2-edge cut in G.

We note that G can be assumed to be the support of $x^*$, so every $F_i$ will actually have an even number of edges crossing each 2-edge cut in the support of G on $x^*$.

4.2.1 Proof of Theorem 14

To prove Theorem 14, we need to understand the structure of 2-edge cuts in a 2-edge connected graph. Assume $G=(V,E)$ is a 2-edge-connected graph. For $S\subseteq V$, let G[S] denote the subgraph induced by vertex set S (i.e., the graph on the vertex set S containing edges from E with both endpoints in S).

Lemma 3

If $S\subseteq V$ and $|\delta (S)|=2$, then G[S] is connected.

Proof

Suppose not, then S can be partitioned into $S_1$ and $S_2$, such that there is no edge in G between $S_1$ and $S_2$. Hence, $|\delta (S_1)|+|\delta (S_2)|=2$. However, since G is 2-edge-connected we have $|\delta (S_1)|+|\delta (S_2)|\ge 4$, which is a contradiction. $\square$

Lemma 4

Let e, f and g be distinct edges of G. If $\{e,f\}$ and $\{f,g\}$ are each 2-edge cuts in G, then $\{e,g\}$ is also a 2-edge cut in G.

Proof

Let $S,T\subset V$ be such that $\delta (S)=\{e,f\}$ and $\delta (T)=\{f,g\}$. Without loss of generality, we can assume that neither endpoint of e belongs to T. (If both endpoints of e belong to T, we set T equal to its complement.) Moreover, we can assume that $S \cap T \ne \emptyset$ (since otherwise we can set S equal to its complement). We can also assume that $S{\setminus } T\ne \emptyset$ (since one endpoint of e belongs to S but not to T). Suppose $T{\setminus } S$ is not empty. By Lemma 3, G[T] is connected. Hence there exists an edge h from $S\cap T$ to $T{\setminus } S$. Notice $h\in \delta (S)$, and $h\notin \delta (T)$. Therefore, $h=e$. However, since both endpoints of h are in T, this is a contradiction. So we can assume that $T {\setminus } S = \emptyset$. In other words, $T \subset S$.

Now we show that $\delta (S{\setminus } T)= \{e,g\}$. Since $T \subset S$ and neither endpoint of e belongs to T, it follows that $e \in \delta (S {\setminus } T)$. Moreover, since only one endpoint of g belongs to T (and therefore to S) and $g \notin \delta (S)$, it follows that $g \in \delta (S {\setminus } T)$. So we have $\{e,g\}\subseteq \delta (S{\setminus } T)$. Suppose there is another edge $h\in \delta (S{\setminus } T)$ with endpoints $v\in S{\setminus } T$ and $u\notin S{\setminus } T$. Note that $h \ne f$, because neither endpoint of f belongs to $S {\setminus } T$. If $u\in T$, then $h\in \delta (T)$ which is a contradiction to T being a 2-edge cut. Otherwise if $u\in V{\setminus } S$, then $h\in \delta (S)$ which is again a contradiction to S being a 2-edge cut. $\square$

We will later use these properties when building a family of connectors to delete and replace edges along the 2-edge cuts of the graph. Next, we need a decomposition lemma for $x^*$.

Lemma 5

A vector $x^*\in$ Subtour(G) can be represented as a convex combination of connectors of G, and the number of connectors in this convex combination is polynomial in the number of vertices of G.

Proof

By Corollary 50.8a in [28] the following polytope is the convex hull of connectors of G.

$$\begin{aligned} x(\delta ({\mathcal {P}}))&\ge |{\mathcal {P}}|-1&\text{ for }&{\mathcal {P}}\in \Pi _{n}\\ 0&\le x_e \le 2&\text{ for }&e\in E \end{aligned}$$

Here, $\Pi _n$ is the collection of partitions of V. For ${\mathcal {P}}\in \Pi _n$, we denote by $\delta ({\mathcal {P}})$ the set of edges with endpoint in different parts of partition ${\mathcal {P}}$, and $|{\mathcal {P}}|$ is the number of parts in partition ${\mathcal {P}}$. Notice that for any partition ${\mathcal {P}}$ of V with parts $P_1,\ldots ,P_{|{\mathcal {P}}|}$ we have

$$\begin{aligned} x^*(\delta ({\mathcal {P}})) = \frac{1}{2} \sum _{i=1}^{|{\mathcal {P}}|} x^*(\delta (P_i)) \ge |{\mathcal {P}}|. \end{aligned}$$

Therefore, $x^*$ can be written as a convex combination of connectors of G. The fact that the number of connectors in the convex combination is polynomial follows from the fact that the polytope above is separable, and hence we can apply the constructive version of Carathéodory’s theorem to get the result [17, 28]. $\square$

By Lemma 5, there exists positive reals $\lambda _1,\ldots ,\lambda _{\ell }$, such that $\sum _{i=1}^{\ell }\lambda _i=1$, and connectors $F_1,\dots ,F_{\ell }$ such that

$$\begin{aligned} x^*=\sum _{i=1}^{\ell } \lambda _i \chi ^{F_i}, \end{aligned}$$

(1)

where $\chi ^{F_i}$ is the characteristic vector of $F_i$ for $i \in \{1,\ldots ,\ell \}$. Furthermore, we can find this decomposition in time polynomial in the size of G. Notice $F_1,\dots ,F_{\ell }$ satisfy (a) in the statement of Theorem 14. We will now show that given $F_1, \ldots , F_{\ell }$, we can obtain a new family of connectors satisfying both (a) and (b) from Theorem 14.

Lemma 6

Given a family of connectors $F_1,\ldots ,F_{\ell }$ of G such that $x^*= \sum _{i=1}^{\ell } \lambda _i \chi ^{F_i}$, $\lambda _i>0$ for $i \in \{1,\ldots ,\ell \}$, and $\sum _{i=1}^{\ell }\lambda _i=1$, there is a polynomial-time algorithm that outputs connectors $F'_1,\ldots ,F'_{\ell }$ such that

• (1) $x^*= \sum _{i=1}^{\ell } \lambda _i \chi ^{F'_i}$.

• (2) If $x^*_e\ge 1$, then $\chi ^{F'_i}(e)\ge 1$ for all $i\in \{1,\ldots ,\ell \}$.

• (3) If $x^*_e<1$, then there is no $i\in \{1,\ldots ,\ell \}$ such that $\chi ^{F'_i}(e) = 2$.

Proof

Call a tuple (e, i, j) where $e\in E$, $i,j\in \{1,\dots ,\ell \}$ bad if

$$\begin{aligned} \chi ^{F_i}(e)=2 \text{ and } \chi ^{F_j}(e)=0. \end{aligned}$$

Let m be the number of bad tuples and let (e, i, j) be a bad tuple. Then

$$\begin{aligned} F'_i=F_i - e, \; F'_j=F_j + e, \text{ and } F'_p = F_p \text{ for } p \in \{1,\dots ,\ell \}{\setminus } \{i,j\} \end{aligned}$$

satisfies property (1). Notice that now $F'_1,\ldots ,F'_{\ell }$ has at most $m-1$ bad tuples; no new bad tuples are created by the above procedure. Thus, after at most m iterations, we have that for each $e\in E$, there is no $i,j\in \{1,\dots ,\ell \}$ such that $\chi ^{F'_i}(e)=2$ and $\chi ^{F'_j}(e)= 0$. This implies properties (2) and (3) in the statement of the lemma. Finally, it is also easy to see that fixing each tuple can be done in polynomial time, and that the number of tuples is polynomial in the size of G. $\square$

We now proceed to the proof of Theorem 14. By Lemma 4, the relation “is in a 2-edge cut with” is transitive. So, we can partition the edges in 2-edge cuts of G into equivalence classes via this relation. Let ${\mathcal {D}}$ be the collection of disjoint subsets of edges of G such that for all $D\in {\mathcal {D}}$: (i) $|D|\ge 2$, and (ii) for each pair of edges $\{e,f\} \subseteq D$, edges e and f form a 2-edge cut of G. Note that for $D\in {\mathcal {D}}$ and any distinct edges $e, f \in D$, it cannot be the case that both $x^*_e<1$ and $x^*_f<1$, since $\{e,f\}$ is a 2-edge cut and $x^*\in$ Subtour(G). We classify the subsets in ${\mathcal {D}}$ into two types:

$$\begin{aligned} {\mathcal {D}}_1&= \{D\in {\mathcal {D}}: \text { for all } e\in D, ~x^*_e\ge 1 \},\\ {\mathcal {D}}_2&= \{D\in {\mathcal {D}}: \text { there is exactly one edge } e\in D \text { such that }x^*_e<1 \}. \end{aligned}$$

Let $F_1, \dots , F_{\ell }$ be a family of connectors satisfying properties (1), (2) and (3) in Lemma 6. We propose a procedure to modify these connectors and output $F'_1, \dots , F'_{\ell }$ such that for each $D\in {\mathcal {D}}$, property (b) in Theorem 14 is satisfied while property (a) is preserved. In particular, by property (1) from Lemma 6, we have

$$\begin{aligned} \sum _{i=1}^{\ell } \chi ^{F_i}(e)= x^*_e\quad \text{ for } e\in E. \end{aligned}$$

Our specific procedure depends on whether $D\in {\mathcal {D}}_1$ or $D\in {\mathcal {D}}_2$.

Case 1 ($D\in {\mathcal {D}}_1$): In this case, we have $\chi ^{F_i}(e)\ge 1$ for all $e\in D$ and $i\in \{1,\dots ,\ell \}$, by property (2) in Lemma 6. For $i \in \{1,\ldots ,\ell \}$ let $F'_i$ be such that

$$\begin{aligned} \chi ^{F'_i}(e)=1 \text{ for } e\in D \hbox { and } \chi ^{F'_i}(e)=\chi ^{F_i}(e) \quad \text{ for } e\in E{\setminus } D. \end{aligned}$$

Now we reset $F_1, \dots , F_{\ell } := F'_1, \ldots , F'_{\ell }$, and proceed to the next $D \in {\mathcal {D}}_1$.

It is easy to see that we can apply this procedure iteratively for $D\in {\mathcal {D}}_1$. This is because after applying this operation on $D\in {\mathcal {D}}_1$, properties (2) and (3) in Lemma 6 are preserved. Moreover, property (1) in Lemma 6 is also preserved for every edge not in D, i.e.

$$\begin{aligned} \sum _{i=1}^{\ell }\lambda _i \chi ^{F'_i}(e) = x^*_e \quad \text{ for } \text{ all } e\in E{\setminus } D \quad \quad \left( \text{ and } \sum \nolimits _{i=1}^{\ell }\lambda _i \chi ^{F'_i}(e) \le x^*_e \text{ for } \text{ all } e\in D\right) . \end{aligned}$$

In addition, given any 2-edge cut $\{e,f\}$ such that $\{e,f\} \subseteq D$ for $D\in {\mathcal {D}}_1$, we have $\chi ^{F'_i}(e)+\chi ^{F'_i}(f)=1+1=2$ for all $i\in \{1,\dots ,\ell \}$.

Case 2 ($D\in {\mathcal {D}}_2$): Let e be the unique edge in D with $x^*_e<1$. By property (3) in Lemma 6, we have $\chi ^{F_i}(e)\le 1$ for all $i\in \{1,\ldots ,\ell \}$. Without loss of generality, assume for $\chi ^{F_i}(e)=1$ for $i \in \{1,\ldots ,p\}$ and $\chi ^{F_i}(e)=0$ for $i \in \{p+1,\ldots ,\ell \}$. For $i\in \{1,\ldots ,p\}$, let $F'_i$ be such that

$$\begin{aligned} \chi ^{F'_i}(f)=1 \text{ for } f\in D \text{ and } \chi ^{F'_i}(f)=\chi ^{F_i}(f) \text{ for } f\in E{\setminus } D. \end{aligned}$$

For $i \in \{p+1,\ldots ,\ell \}$, let $F'_i$ be such that

$$\begin{aligned} \chi ^{F'_i}(e)=0,\; \chi ^{F'_i}(f)=2 \text{ for } f\in D{\setminus } \{e\} \text { and } \chi ^{F'_i}(f)=\chi ^{F_i}(f) \text{ for } f\in E{\setminus } D. \end{aligned}$$

Now we reset $F_1, \dots , F_{\ell } := F'_1, \ldots , F'_{\ell }$, and proceed to the next $D \in {\mathcal {D}}_2$. After each iteration, we observe that

$$\begin{aligned} \sum _{i=1}^{\ell }\lambda _i \chi ^{F'_i}(e)&= \sum _{i=1}^{p}\lambda _i \chi ^{F'_i}(e)+ \sum _{i=p+1}^{\ell }\lambda _i \chi ^{F'_i}(e) \nonumber \\&=\sum _{i=1}^{p}\lambda _i =x^*_e. \end{aligned}$$

(2)

For $f\in D{\setminus } \{e\}$, we have

$$\begin{aligned} \sum _{i=1}^{\ell }\lambda _i \chi ^{F'_i}(f)&= \sum _{i=1}^{p}\lambda _i \chi ^{F'_i}(f)+ \sum _{i=p+1}^{\ell }\lambda _i \chi ^{F'_i}(f)\\&=\sum _{i=1}^{p} \lambda _i +2\sum _{i=p+1}^{\ell }\lambda _i \\&= x^*_e+ 2(1-x^*_e)&(\text{ From } 2)\\&=2-x^*_e&\\&\le x^*_f&(\text{ Since } x^*\in \textsc {Subtour}(G)). \end{aligned}$$

This also clearly holds for any $f\in E{\setminus } D$ as we do not touch these edges. Note that after the final iteration, $F_1,\ldots ,F_{\ell }$ are connected, spanning multigraphs of G, because we began with connected, spanning multigraphs and we only remove an edge f from $F_i$ if it contained at least two copies of f.

Finally, note that given any 2-edge cut $\{e,f\} \in D$ for $D \in {\mathcal {D}}_2$, we have $\chi ^{F_i}(e)+ \chi ^{F_i}(f)=1+1=2$, $\chi ^{F_i}(e)+ \chi ^{F_i}(f)=0+2=2$ or $\chi ^{F_i}(e)+ \chi ^{F_i}(f)=2+2=4$ for all $i \in \{1,\ldots ,\ell \}$. This concludes the proof of Theorem 14.

4.3 Subcubic graphs

We now present two applications of Theorem 14. In the first application, we show that for a node-weighted, subcubic graph, Christofides’ algorithm has an approximation factor better than $\frac{3}{2}$ when the weight of an optimal subtour solution is strictly larger than twice the sum of the node weights. In the second application, we show that there is a set of edges that can be added to a connector to yield a 2-edge-connected graph, and this addition can be found via an application of the tree augmentation problem, which we introduced in Sect. 2.3. This resembles methods used in the proof of Theorem 9. We then show that combining the approaches in these applications, we can beat the approximation ratio of Christofides’ algorithm for 2EC on node-weighted, subcubic graphs.

A useful fact about node-weighted, subcubic graphs is that the total edge weight cannot be too much larger than $z_G$.

Fact 4

Let $G=(V,E)$ be a node-weighted, subcubic graph. Then $w(E) \le \frac{3}{2} z_G$.

Proof

Observe that $w(E) \le 3 \cdot \sum _{v \in V} f_v$, where $f: V \rightarrow {\mathbb {R}}^+$ is the node-weight function. Also, notice that $z_G \ge 2 \cdot \sum _{v \in V} f_v$. $\square$

Since all graphs are assumed to be 2-vertex-connected (i.e., bridgeless), we can show the following fact.

Fact 5

Let $G=(V,E)$ be a node-weighted, subcubic graph. Then $z_G \le 3 \cdot \sum _{v \in V} f_v$.

Proof

This follows from the fact that $x_e=1$ for all $e \in E$ is a feasible solution for Subtour(G) when G is a 2-vertex-connected subcubic graph. $\square$

For the remainder of this section, let $x^*$ be an optimal solution for Subtour(G). By Theorem 14, we have $x^*\ge \sum _{i=1}^{\ell }\lambda _i\chi ^{F_i}$ where $F_i$ is a connector satisfying (a) and (b) in the statement of Theorem 14 for $i \in \{1,\ldots ,\ell \}$. Let $x'=\sum _{i=1}^{\ell }\lambda _i\chi ^{F_i}$. Clearly $\sum _{e \in E}w(e)x'_e \le z_G$. Define ${\bar{x}}\in {\mathbb {R}}^E$ as follows: ${\bar{x}}_e=\min \{1,x'_e\}$.

4.3.1 An algorithm for TSP à la Christofides with simple deletions

In the graph metric, every (minimum) spanning tree has weight at most n. It follows that in the case where $z_G \ge (1+\epsilon )n$, Christofides’ algorithm has an approximation guarantee strictly better than $\frac{3}{2}$ (in fact, at most $(\frac{3}{2}-\frac{\epsilon }{1+\epsilon })$). This implies that, in some sense, the most difficult case for graph-TSP is when $z_G = n$. It seems that it should also be the case for node-weighted graphs: the most difficult case should be when $z_G = 2\cdot \sum _{v\in V}f_v$, and when $z_G \ge (1+\epsilon ) \cdot 2 \cdot \sum _{v \in V} f_v$, Christofides’ algorithm should give an approximation guarantee strictly better than $\frac{3}{2}$.

However, in the case of node-weighted graphs (even for subcubic graphs), a minimum spanning tree of G may have weight exceeding $2\cdot \sum _{v\in V}f_v$ when $z_G >2\cdot \sum _{v\in V}f_v$. See Fig. 1 for an example. Thus, proving an approximation factor strictly better than $\frac{3}{2}$ for node-weighted graphs in this scenario does not follow the same argument as in the graph metric. Nevertheless, we can use connectors to prove that we can beat Christofides’ algorithm when G is a subcubic node-weighted graph and $z_G$ is much larger than $2 \cdot \sum _{v \in V} f_v$.

Fig. 1

The graph in b has a total of 10t (here $t = 5$) vertices: each circular vertex corresponds to the gadget in a. The weight of each square vertex in b is 1, and all other vertices have weight zero. A minimum spanning tree (denoted by the thick, blue edges) has weight $5t-2$ while sum of the node weights is 2t. In this case, Theorem 15 yields a tour of weight $7t-2$, providing a $\frac{7}{5}$-approximation for this instance (color figure online)

Lemma 7

Let $G=(V,E)$ be a graph with nonnegative edge weights. There is an efficient algorithm to find a tour in G with weight at most $z_G + \frac{w(E)}{3}$.

In fact, we prove something slightly stronger that will be useful later in the paper.

Lemma 8

Let $G=(V,E)$ be a graph with nonnegative edge weights. There is an efficient algorithm to find a tour in G with weight at most $\frac{w(E)}{3} + \frac{1}{3} \cdot \sum _{e\in E}w(e) x'_e + \frac{2}{3} \cdot \sum _{e \in E} w(e){\bar{x}}_e$.

For a subset T of vertices in V, where |T| is even, a T-join of G is a subgraph J of G in which the set of odd-degree vertices of J are exactly T. Edmonds and Johnson [12] proved that the inequalities below describe the convex hull of T-joins of G.

In Christofides’ algorithm, one can write an optimal solution $x^*$ for Subtour(G) as a convex combination of spanning trees (see Fact 1). Each of these spanning trees is then augmented with a T-join, where $T \subseteq V$ is the set of odd-degree vertices in the spanning tree. In particular, for a spanning tree F of G, let T be the set of odd-degree vertices of F. Then, $\frac{x^*}{2}$ dominates a point in the T-join polytope. This mean the vector $x^*+\frac{x^*}{2}=\frac{3}{2}x^*$ dominates a convex combination of tours of G.

If we decompose the optimal solution for Subtour(G) into a family of connectors according to Theorem 14, then we can augment each connector by a T-join that is obtained from writing the vector $\{\frac{1}{3}\}^{E}$ as a convex combination of T-joins.

Lemma 9

Let ${\mathcal {F}}$ be a family of connectors for $G=(V,E)$ satisfying properties (a) and (b) from Theorem 14. For an $F_i \in {\mathcal {F}}$, let T denote the odd-degree vertices in $F_i$. Then the vector $\{\frac{1}{3}\}^{E}$ belongs to T -Join(G).

Proof

Let F be a connector of G and let $T \subseteq V$ denote the vertices with odd degree in F. Since all edges have value $\frac{1}{3}$, we only need to check that

$$\begin{aligned} \frac{|\delta (U)|}{3} + \frac{|W|}{3} \ge 1&\quad \text { for } U \subseteq V, W \subseteq \delta (U), |U \cap T| + |W| \text { odd}. \end{aligned}$$

(3)

Consider $U \subset V$ such that $|\delta (U)| = 2$. Note that $\sum _{e \in \delta (U)}\chi ^F_e$ is even by the properties of a connector. This implies that $|U \cap T|$ is even. So we need to check the case where $|W| = 1$. In this case, we see that Inequality (3) is satisfied. Now consider case in which $|\delta (U)| \ge 3$. In this case,

$$\begin{aligned} \frac{|\delta (U)|}{3} + \frac{|W|}{3} \ge \frac{|\delta (U)|}{3} \ge 1. \end{aligned}$$

Hence, $\{\frac{1}{3}\}^E \in$ T -Join(G). $\square$

Observe that Lemma 9 is sufficient to prove Lemma 7. To prove (the potentially stronger) Lemma 8, we modify Christofides’ algorithm further by adding the following deletion step. Suppose an edge e occurs in a connector F as a doubled edge. If this edge e also belongs to the T-join J, we remove two copies of e from the multigraph $F \cup J$. We observe that the resulting multigraph remains a tour.

Observation 4

Let F be a connector for $G=(V,E)$ and let J be a T-join, where T is the set of vertices with odd degree in F. Let $E' \subset E$ denote the set of edges that occur doubled in F and also belong to J. Then the multigraph $F \cup J {\setminus }{\{2E'\}}$ is a tour.

We are now ready to prove Lemma 8 via an analysis of the modified Christofides’ algorithm we have just described.

Proof of Lemma 8

We have $x'=\sum _{i=1}^{\ell }\lambda _i\chi ^{F_i}$ where $F_i$ is a connector satisfying (a) and (b) in the statement of Theorem 14 for $i \in \{1,\ldots ,\ell \}$. Choose $i\in \{1,\ldots ,\ell \}$ uniformly at random according to the probability distribution defined by $\lambda _1,\ldots ,\lambda _{\ell }$. Let $T_i$ be the set of odd-degree vertices of $F_i$. By Lemma 9, we have $\{\frac{1}{3}\}^E = \sum _{j=1}^{\ell _i}\lambda ^i_j\chi ^{J^i_j}$, where ${J^i_j}$ is a $T_i$-join of G. Choose $j\in \{1,\ldots ,\ell _i\}$ at random according to probability distribution defined by $\lambda _1^i, \dots , \lambda ^i_{\ell _i}$. Let $E' \subset E$ denote the edges that occur doubled in $F_i$ and also belong to $J^i_j$. By Observation 4, $H = F_i \cup J^i_j {\setminus }{\{2E'\}}$ is a tour of G. We have

$$\begin{aligned} \mathop {{\mathbb {E}}}[w(H)]&= \mathop {{\mathbb {E}}}[w(F_i)] + \mathop {{\mathbb {E}}}[w(J^i_j)] - 2\cdot \mathop {{\mathbb {E}}}[w(E')]\\&= \sum _{e \in E}w(e)x'_e + \frac{w(E)}{3} - 2 \cdot \sum _{e \in E: x'_e> 1} w(e) \cdot \Pr [\chi _e^{F_i} = 2] \cdot \Pr [e \in J^i_j]\\&= \sum _{e \in E}w(e)x'_e+ \frac{w(E)}{3} - 2 \cdot \sum _{e \in E: x'_e> 1} w(e) (x'_e -1) \cdot \frac{1}{3}\\&= \sum _{e \in E}w(e)x'_e+ \frac{w(E)}{3} - \frac{2}{3} \left( \sum _{e \in E: x'_e> 1} w(e) x'_e -\sum _{e \in E: x'_e > 1} w(e)\right) \\&= \sum _{e \in E}w(e)x'_e+ \frac{w(E)}{3} - \frac{2}{3} \left( \sum _{e \in E} w(e) x'_e -\sum _{e \in E} w(e){\bar{x}}_e\right) \\&= \frac{\sum _{e\in E}w(e)x'_e}{3} + \frac{w(E)}{3} + \frac{2}{3} \cdot \sum _{e \in E} w(e){\bar{x}}_e. \end{aligned}$$

$\square$

Theorem 15

Let G be a node-weighted, subcubic graph. If $z_G \ge 2\cdot (1+\epsilon )\cdot \sum _{v\in V}f_v$, then there is an $(\frac{3}{2}-\frac{\epsilon }{3})$-approximation algorithm for TSP on G.

Proof

For a node-weighted, subcubic graph, we have

$$\begin{aligned} w(E)\le & {} 3 \cdot \sum _{v \in V} f_v. \end{aligned}$$

(4)

By the assumption of the theorem and (4), we have $z_G\ge 2(1+\epsilon )\sum _{v \in V} f_v \ge \frac{2(1+\epsilon )}{3}w(E)$. Applying Lemma 7, we get a tour of weight at most

$$\begin{aligned} z_G+\frac{w(E)}{3}\le & {} \left( \frac{3+2\epsilon }{2 + 2\epsilon }\right) \cdot z_G\\= & {} \left( \frac{3}{2} - \frac{\epsilon }{2 + 2\epsilon }\right) \cdot z_G\\\le & {} \left( \frac{3}{2} -\frac{\epsilon }{3}\right) \cdot z_G. \end{aligned}$$

The last inequality comes from the fact that $\epsilon \le \frac{1}{2}$ since $z_G\le 3\cdot \sum _{v\in V}f_v$, which follows from Fact 5. $\square$

4.3.2 An algorithm for 2EC

Recall the set-up for 2EC. We are given a graph $G=(V,E)$ with nonnegative weights w(e) for $e\in E$. Our goal is to find a minimum weight 2-edge-connected multigraph of G. We now prove the following lemma.

Lemma 10

Let $G=(V,E)$ be a graph with nonnegative edge weights. We can find a 2-edge-connected multigraph of G with weight at most $\sum _{e \in E} w(e)x'_e + \frac{2}{3}w(E) - \frac{2}{3}\cdot \sum _{e\in E}w(e){\bar{x}}_e$.

Proof

Recall that we have $x'=\sum _{i=1}^{\ell }\lambda _i\chi ^{F_i}$ where $F_i$ is a connector satisfying (a) and (b) in the statement of Theorem 14 for $i \in \{1,\ldots ,\ell \}$. For $i \in \{1,\ldots ,\ell \}$, let ${\mathcal {S}}_i$ be the family of 1-edge cuts of $F_i$. As discussed in Sect. 2.3, there is a laminar family ${\mathcal {S}}^*_i\subseteq {\mathcal {S}}_i$ that is enough to describe Cover$(G,F_i)$ for all $i\in \{1,\ldots ,\ell \}$. Define vector $y^i\in {\mathbb {R}}^E$ as follows: $y^i_e=0$ for $e\in F_i$ and $y^i_e=\frac{1}{2}$ for $e\in E{\setminus } F_i$.

Claim 1

For $i \in \{i, \dots , \ell \}$, we have $y^i \in$ Cover$(G,F_i)$.

Proof

Let S be a 1-edge cut of $F_i$. Then $\delta (S)\cap F_i$ contains exactly one edge e. Note that it cannot be the case that $|\delta (S)|=2$. This is because if $\delta (S)$ were a 2-edge cut of G, then by property (b) in Theorem 14, there would be an even number of edges in $F_i$ that are also in $\delta (S)$. Hence, $|\delta (S)|\ge 3$. So we have

$$\begin{aligned} \sum _{e \in \delta (S)}y_e ~ = \sum _{e \in \delta (S){\setminus } F_i} \frac{1}{2} ~ = \sum _{e \in \delta (S){\setminus } \{e\}} \frac{1}{2} ~ = ~\frac{|\delta (S){\setminus } \{e\}|}{2} ~ \ge ~1. \end{aligned}$$

This concludes the proof of the claim. $\square$

For $i\in \{1,\ldots ,\ell \}$, define vector $r^i$ as follows: $r^i_e=0$ for $e\in F_i$ and $r^i_e=\frac{2}{3}$ for $e\in E{\setminus } F_i$.

Claim 2

For $i \in \{1,\ldots ,\ell \}$, the vector $r^i$ can be written as a convex combination of 1-covers of $F_i$.

Proof

By Claim 1 and Theorem 6, vector $\frac{4}{3}y^i$ can be written as a convex combination of 1-covers of $F_i$, and $\frac{4}{3}y^i=r^i$. $\square$

By Claim 2, for $i \in \{1,\ldots ,\ell \}$ we can write $r^i$ as $\sum _{j=1}^{\ell _i}\lambda ^i_j C^i_j$, where for $j \in \{1,\ldots ,\ell _i\}$, $C^i_j$ is a 1-cover for $F_i$. Let $R^i_j = F_i \cup C^i_j$. Notice, for all choices of i and j, $R_i^j$ is a 2-edge-connected multigraph of G. To argue that there exists a low-weight, 2-edge-connected multigraph, we show the following claim.

Claim 3

There exists $i \in \{1,\ldots ,\ell \}$ and $j\in \{1,\ldots ,\ell _i\}$ such that $R^i_j\le \sum _{e \in E} w(e)x'_e + \frac{2}{3}w(E) - \frac{2}{3}\cdot \sum _{e\in E}w(e){\bar{x}}_e$.

Proof

Pick $i\in \{1,\ldots ,\ell \}$ at random according to the probability distribution defined by $\lambda _1,\ldots ,\lambda _{\ell }$. Now, pick $j\in \{1,\ldots ,\ell _i\}$ at random according to the probability distribution defined by $\lambda ^i_1,\ldots ,\lambda ^i_{\ell _i}$. We have

$$\begin{aligned} \mathop {{\mathbb {E}}}[w(R^i_j)]&= \mathop {{\mathbb {E}}}[w(F_i)] + \mathop {{\mathbb {E}}}[w(C^i_j)]\\&= \sum _{e \in E}\left( 2 w(e)\cdot \Pr [\chi ^{F_i}(e)=2]+ w(e)\cdot \Pr [\chi ^{F_i}(e)=1]\right) +\sum _{e\in E}w(e)\cdot \Pr [e\in C^i_j]\\&= \sum _{e \in E}\left( 2 w(e)\cdot \Pr [\chi ^{F_i}(e)=2]+ w(e)\cdot \Pr [\chi ^{F_i}(e)=1]\right) +\sum _{e\in E} \frac{2}{3} w(e) \cdot \Pr [\chi ^{F_i}(e)=0]\\&= \sum _{e \in E: x'_e>1}\left( 2 w(e)\cdot \underbrace{\Pr [\chi ^{F_i}(e)=2]}_{=(x'_e-1)}+ w(e)\cdot \underbrace{\Pr [\chi ^{F_i}(e)=1]}_{=(2-x'_e)}+ \frac{2}{3} w(e) \cdot \underbrace{\Pr [\chi ^{F_i}(e)=0]}_{=0}\right) \\&\quad + \sum _{e \in E: x'_e\le 1}\left( 2 w(e)\cdot \underbrace{\Pr [\chi ^{F_i}(e)=2]}_{=0}+ w(e)\cdot \underbrace{\Pr [\chi ^{F_i}(e)=1]}_{=x'_e}+ \frac{2}{3} w(e) \cdot \underbrace{\Pr [\chi ^{F_i}(e)=0]}_{=(1-x'_e)}\right) \\&=\sum _{e\in E: x'_e>1}\left( 2 w(e)x'_e - 2 w(e) + 2 w(e) -w(e) x'_e \right) + \sum _{e\in E: x'_e\le 1} \left( w(e)x'_e +\frac{2}{3} w(e)- \frac{2}{3} w(e)x'_e \right) \\&=\sum _{e\in E: x'_e>1} w(e)x'_e + \sum _{e\in E: x'_e\le 1} \left( \frac{1}{3} w(e)x'_e +\frac{2}{3} w(e)\right) \\&= \sum _{e\in E: x'_e>1}w(e)(x'_e - 1) + \sum _{e\in E} \left( \frac{1}{3}w(e){\bar{x}}_e +\frac{2}{3} w(e)\right) \\&= \sum _{e \in E} w(e)x'_e - \sum _{e\in E}w(e){\bar{x}}_e+ \sum _{e\in E} \frac{1}{3}w(e){\bar{x}}_e +\sum _{e\in E}\frac{2}{3} w(e)\\&= \sum _{e \in E} w(e)x'_e + \frac{2}{3}w(E) - \frac{2}{3}\cdot \sum _{e\in E}w(e){\bar{x}}_e. \end{aligned}$$

$\square$

This concludes the proof of Lemma 10. $\square$

Assume $w(E)\le \frac{3}{2} z_G$. In this case, Lemma 10 finds a 2-edge-connected multigraph of weight at most $2z_G- \frac{2}{3} \cdot \sum _{e\in E}w(e){\bar{x}}_e$. If $\sum _{e\in E}w(e){\bar{x}}_e=z_G$, then this implies a $\frac{4}{3}$-approximation for 2EC. (Note that this is the case if $x^*\le 1$.) However, there are instances for which this does not happen. Figure 2 illustrates an example where the algorithm in Lemma 10 does not improve the bound of Christofides’ algorithm.

Fig. 2

Let $G=(V,E)$ be the node-weighted $K_4$ shown above. For $e\in E$, $w_e$ is defined as the sum of the node-weights of the two endpoints (e.g., $w_{v_1v_2}= 2 + 1= 3$). The edge labels represents solution $x^*\in$ Subtour(G). Here we have $x'=x^*$. We have $w(E)= 12$, $\sum _{e \in E}w(e)x'_e = 8$, $\sum _{e \in E}w(e){\bar{x}}_e = 6+4\epsilon$. For this $x^*$, Lemma 10 yields a $(\frac{3-\epsilon }{2})$-approximation, which does not outperform Christofides’ algorithm by any constant factor. However, Lemma 8 provides a $(\frac{4+\epsilon }{3})$-approximation for 2EC on the graph G

Lemma 11

Let $G=(V,E)$ be a graph such that $w(E)\le \beta \cdot z_G$, then there is a $(\frac{2}{3}+\frac{\beta }{2})$-approximation for 2EC on graph G.

Proof

Taking the best of the guarantees from Lemmas 8 and 10,we have an algorithm that outputs a 2-edge-connected multigraph of weight at most

$$\begin{aligned}&\frac{1}{2}\left( \frac{4}{3}\sum _{e \in E}w(e)x'_e + w(E)) \right) \le \frac{1}{2} \left( \frac{4}{3}z_G + w(E) \right) = \left( \frac{2}{3}+\frac{\beta }{2}\right) \cdot z_G. \end{aligned}$$

Note that the above bound is obtained by taking the average of the two guarantees. $\square$

Theorem 4

If G is a node-weighted, subcubic graph, then there exists a $\frac{17}{12}$-approximation for 2EC on G.

Proof

For a node-weighted, subcubic graph, we have $w(E) \le \frac{3}{2}z_G$ (by Fact 4). By Lemma 11, we get a $\frac{17}{12}$-approximation for 2EC on graph G. $\square$

5 Concluding remarks

Carr and Ravi [10] proved that for any 4-regular 4-edge-connected graph G, the everywhere $\frac{2}{3}$ vector can be decomposed into a convex combination of 2-edge-connected subgraphs of G. This implies an upper bound of $\frac{4}{3}$ on the integrality gap of half-integer points for the 2EC problem with metric weights. Their proof however does not lead to a polynomial-time algorithm for such instances. In Theorem 11, we gave an alternate way (as opposed to that of Wolsey [31]) to obtain such a convex combination for the everywhere $\frac{3}{4}$ vector. It is an interesting open problem to determine if the everywhere $\frac{3}{4}-\epsilon$ vector for G can be decomposed into convex combination tours of G in polynomial time. Another open problem is stated in Conjecture 2, which is implied by the four-thirds conjecture. Finally, for node-weighted metrics, it would be interesting to find a $\frac{4}{3}$-approximation algorithm for TSP in bridgeless, cubic graphs to match the corresponding bound for graph metrics [6].