Geometric random edge

Abstract

We show that a variant of the random-edge pivoting rule results in a strongly polynomial time simplex algorithm for linear programs $\max \{c^Tx :x \in \mathbb R^n, \, Ax\leqslant b\}$, whose constraint matrix A satisfies a geometric property introduced by Brunsch and Röglin: The sine of the angle of a row of A to a hyperplane spanned by $n-1$ other rows of A is at least $\delta$. This property is a geometric generalization of A being integral and each sub-determinant of A being bounded by $\Delta$ in absolute value. In this case $\delta \geqslant 1/(\Delta ^2 n)$. In particular, linear programs defined by totally unimodular matrices are captured in this framework. Here $\delta \geqslant 1/ n$ and Dyer and Frieze previously described a strongly polynomial-time randomized simplex algorithm for linear programs with A totally unimodular. The expected number of pivots of the simplex algorithm is polynomial in the dimension and $1/\delta$ and independent of the number of constraints of the linear program. Our main result can be viewed as an algorithmic realization of the proof of small diameter for such polytopes by Bonifas et al., using the ideas of Dyer and Frieze.

1 Introduction

Our goal is to solve a linear program

$$\begin{aligned} \begin{array}{c} \max c^Tx \\ Ax \leqslant b \end{array} \end{aligned}$$

(1)

where $A \in \mathbb R^{m\times n}$ is of full column rank, $b \in \mathbb R^m$ and $c \in \mathbb R^n$. The rows of A are denoted by $a_i, \, 1 \leqslant i \leqslant m$. We assume without loss of generality that the rows have Euclidean length one, i.e., that $\Vert a_i\Vert =1$ holds for $i=1,\ldots ,m$. The rows shall have the following $\delta$ -distance property (we use $\langle . \rangle$ to denote linear span):

For any $I \subseteq [m]$, and $j \in [m]$, if $a_j \notin {\langle } a_i :i \in I {\rangle }$ then $d(a_j, {\langle } a_i :i \in I {\rangle }) \geqslant \delta$. In other words, if $a_j$ is not in the span of the $a_i, i \in I$, then the distance of $a_j$ to the subspace that is generated by the $a_i, \, i \in I$ is at least $\delta$.

In this paper, we analyze the simplex algorithm [8] to solve (1) with a variant of the random edge pivoting rule. Our main result is a strongly polynomial running time bound for linear programs satisfying the $\delta$-distance property.

Theorem 1

There is a random edge pivot rule that solves a linear program using $\hbox {poly}(n, 1/\delta )$ pivots in expectation. The expected running time of this variant of the simplex algorithm is polynomial in n, m and $1/\delta$.

The $\delta$-distance property is a geometric generalization of the algebraic property of an integer matrix having small sub-determinants in absolute value. (Recall that a $k\times k$ sub-determinant of A is the determinant of a sub-matrix that is induced by a choice of k rows and k columns of A.) To see this, let $A \in \mathbb {Z}^{m\times n}$ with each of its sub-determinants bounded by $\Delta$ in absolute value. Let $B \subseteq \{1,\dots ,m\}$ be a basis of A, i.e., an index set satisfying $|B| = n$ and $\langle a_i :i \in B \rangle = \mathbb R^n$. Let $A_B$ be the sub-matrix of A that is induced by the rows indexed by B and let $w \in \mathbb {Q}^n$ be the column of $A_B^{-1}$ with $a_i^T w =1$. The distance of $a_i$ to $\langle a_j :j \in B - i \rangle$ is the absolute value of

$$\begin{aligned} \frac{a_i^T w }{ \Vert w \Vert }. \end{aligned}$$

(2)

By Cramer’s rule, each entry of w is a $(n-1) \times (n-1)$ sub-determinant of $A_B$ divided by $\det (A_B)$. The division by $\det (A_B)$ cancels out in (2). After this cancellation, the numerator is an integer and the denominator is at most $\sqrt{n} \cdot \Delta$. This shows that the absolute value of (2) is at least $1/(\sqrt{n} \cdot \Delta )$. To bound $\delta$ from below, this distance needs to be divided by $\Vert a_i \Vert \leqslant \sqrt{n} \cdot \Delta$ since the rows of the matrix should be scaled to length one when we measure the distance. Thus an integer matrix satisfies the $\delta$-distance property with $\delta \geqslant 1/(n \cdot \Delta ^2)$.

This shows that our result is an extension of a randomized simplex-type algorithm of Dyer and Frieze [9] that solves linear programs (1) for totally unimodular ($\Delta = 1$) $A \in \{0,\pm 1\}^{m\times n}$ and arbitrary b and c. In this case, $\delta \geqslant 1/n$.

1.1 Related work

General linear programming problems can be solved in weakly polynomial time [16, 17]. This means that the number of basic arithmetic operations performed by the algorithm is bounded by a polynomial in the binary encoding length of the input. It is a longstanding open problem whether there exists a strongly polynomial time algorithm for linear programming. Such an algorithm would run in time polynomial in the dimension and the number of inequalities on a RAM machine. For general linear programming, the simplex method is sub-exponential [15, 21].

The $\delta$-distance property is a geometric property and not an algebraic one. In fact, the matrix A can be irrational even. This is in contrast to a result of Tardos [26], who gave a strongly polynomial time algorithm for linear programs whose constraint matrix has integer entries that are bounded by a constant. The algorithm of Tardos is not a simplex-type algorithm.

Spielman and Teng [25] have shown that the simplex algorithm with the shadow-edge pivoting rule runs in expected polynomial time if the input is randomly perturbed. This smoothed analysis paradigm was subsequently applied to many other algorithmic problems. Brunsch and Röglin [5] have shown that, given two vertices of a linear program satisfying the $\delta$-distance property, one can compute in expected polynomial time a path joining these two vertices with $O(m n^2 / \delta ^2)$ edges in expectation with the shadow-edge rule. However, the two vertices need to be known in advance. The authors state the problem of finding an optimal vertex w.r.t. a given objective function vector c in polynomial time as an open problem. We solve this problem and obtain a path whose length is independent of the number m of inequalities.

Klee and Minty [18] have shown that the simplex method is exponential if Dantzig’s original pivoting rule is applied. More recently, Friedmann et al. [11] have shown that the random edge pivot rule results in a superpolynomial number of pivoting operations. Here, random edge means to choose an improving edge uniformly at random. The authors also show such a lower bound for random facet. Friedmann [10] also recently showed a superpolynomial lower bound for Zadeh’s pivoting rule. Nontrivial, but exponential upper bounds for random edge are given in [12, 14].

Bonifas et al. [3] have shown that the diameter of a polytope defined by an integral constraint matrix A whose sub-determinants are bounded by $\Delta$ is polynomial in n and $\Delta$ and independent of the number of facets. In the setting of the $\delta$-distance property, their proof yields a polynomial bound in $1/\delta$ and the dimension n on the diameter that is independent of m. Our result is an extension of this result in the setting of linear programming. We show that there is a variant of the simplex algorithm that uses a number of pivots that is polynomial in $1/\delta$ and the dimension n.

1.2 Assumptions

Throughout we assume that c and the rows of A, denoted by $a_i, \, 1\leqslant i \leqslant m$, have Euclidean norm $\Vert \cdot \Vert _2$ one. We also assume that the linear program is non-degenerate, meaning that for each feasible point $x^*$, there are at most n constraints that are satisfied by $x^*$ with equality. It is well known that this assumption can be made without loss of generality [23]. Furthermore, we assume that $n \geqslant 4$, i.e., that the number of variables is at least 4.

2 Identifying an element of the optimal basis

Before we describe our variant of the random-edge simplex algorithm, we explain the primary goal, which is to identify one inequality of the optimal basis. Then, we can continue with the search for other basis elements by running the simplex algorithm in one dimension lower.

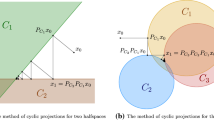
Let $K = \{x \in \mathbb R^n :Ax \leqslant b \}$ be the polyhedron of feasible solutions of (1). Without loss of generality, see Sect. 1, we can assume that K is a polytope, i.e., that K is bounded. Let $v \in K$ be a vertex. The normal cone $C_v$ of v is the set of vectors $w \in \mathbb R^n$ such that, if $c^Tx$ is replaced by $w^Tx$ in (1), then v is an optimal solution of that linear program. Equivalently, let $B \subseteq \{1,\dots ,m\}$ be the n row-indices with $a_i^T v = b_i, \, i \in B$, then the normal cone of v is the set $\mathrm {cone}\{a_i :i \in B\}=\{ \sum _{i \in B} \lambda _i a_i :\lambda _i \geqslant 0, \, i \in B\}$. The cones $C_u$ and $C_v$ of two vertices $u\ne v$ intersect if and only if u and v are neighboring vertices of K. In this case, they intersect in the common facet $\mathrm {cone}\{ a_i :i \in B_u \cap B_v\}$, where $B_u$ and $B_v$ are the indices of tight inequalities of u and v respectively, see Fig. 1.

Fig. 1

Two neighboring vertices u and v and their normal-cones $C_u$ and $C_v$

Suppose that we found a point $c' \in \mathbb R^n$ together with a vertex v of K whose normal cone $C_v$ contains $c'$ such that:

$$\begin{aligned} \Vert c - c'\Vert < \delta /(2 \cdot n). \end{aligned}$$

(3)

The following variant of a lemma proved by Cook et al. [6] shows that we then can identify at least one index of the optimal basis of (1). We provide a proof of the lemma in the appendix.

Lemma 2

Let $c' \in \mathbb R^n$ and let $B \subseteq \{1,\dots ,m\}$ be the optimal basis of the linear program (1) and let $B'$ be an optimal basis of the linear program (1) with c being replaced by $c'$. Consider the conic combination

$$\begin{aligned} c' = \sum _{j \in B'} \mu _j a_j. \end{aligned}$$

(4)

For $k \in B' {\setminus } B$, one has

$$\begin{aligned} \Vert c - c' \Vert \geqslant \delta \cdot \mu _k. \end{aligned}$$

Following the notation of the lemma, let $B'$ be the optimal basis of the linear program with objective function $c'x$. Since (3) holds and since $\Vert c\Vert =1$ we have $\Vert c'\Vert > 1 - \delta / (2\cdot n)$. This means that there exists a $\mu _k$ with $\mu _k > 1/n \cdot \left( 1 - \delta / (2\cdot n) \right)$. But then k must be in B since $\delta \cdot \mu _k > \delta /n \left( 1 - \delta / (2\cdot n) \right) \geqslant \delta /(2\cdot n)$.

Once we have identified an index k of the optimal basis B of (1) we set this inequality to equality and let the simplex algorithm search for the next element of the basis on the induced face of K. This is in fact a $n-1$-dimensional linear program with the $\delta$-distance property. We explain now why this is the case.

Suppose that the element from the optimal basis is $a_1$. Let $U \in \mathbb R^{n \times n}$ be a non-singular orthonormal matrix that rotates $a_1$ into the first unit vector, i.e.

$$\begin{aligned} a_1^T \cdot U = e_1^T. \end{aligned}$$

The linear program $\max \{c^Tx :x \in \mathbb R^n, \, Ax\leqslant b\}$ is equivalent to the linear program $\max \{c^T U\cdot x :x \in \mathbb R^n, \, A \cdot U \cdot x \leqslant b\}$. Notice that this transformation preserves the $\delta$-distance property. Therefore we can assume that $a_1$ is the first unit vector.

Now we can set the constraint $x_1 \leqslant b_1$ to equality and subtract this equation from the other constraints such that they do not involve the first variable anymore. The $a_i$ are in this way projected into the orthogonal complement of $e_1$. We scale the vectors and right-hand-sides with a scalar $\geqslant 1$ such that they lie on the unit sphere and are now left with a linear program with $n-1$ variables that satisfies the $\delta$-distance property as we show now.¹

Lemma 3

Suppose that the vectors $a_1,\ldots ,a_m$ satisfy the $\delta$-distance property, then $a_2^*,\ldots ,a_m^*$, after being scaled to unit length, satisfy the $\delta$-distance property as well, where $a_i^*$ is the projection of $a_i$ onto the orthogonal complement of $a_1$.

Proof

Let $I \subseteq \left\{ 2,\dots ,m\right\}$ and $j \in \left\{ 2, \dots , m\right\}$ such that $a_j^*$ is not in the span of the $a_i^*, \, i \in I$. Let $d(a^*_j, {\langle } a^*_i :i \in I {\rangle }) = \gamma$. Clearly, $d(a_j^*, {\langle } a_i :i \in I \cup \{1\} {\rangle } \leqslant \gamma$ and since $a_j^*$ stems from $a_j$ by subtracting a suitable scalar multiple of $a_1$, we have $d(a_j, {\langle } a_i :i \in I \cup \{1\} {\rangle } \leqslant \gamma$ and consequently $\gamma \geqslant \delta$.$\square$

This shows that we can solve the linear programming problem efficiently if we can efficiently solve the following algorithmic problem.

3 A random walk controls the simplex pivot operations

Next we show how to solve Problem 1 with the simplex algorithm wherein the pivoting is carried out by a random walk. Consider the function

$$\begin{aligned} f(x) = \exp ( - \Vert x - \alpha \cdot c \Vert _1 ), \end{aligned}$$

(5)

where $\alpha \geqslant 1$ is a constant whose value will be determined later. Imagine that we could sample a point $x^*$ from the distribution with density proportional to (5) and that, at the same time, we are provided with a vertex v that is an optimal solution of the linear program (1) where c has been replaced by $x^*$. We are interested in the probability that $c' = x^* / \alpha$ together with v is not a solution of Problem 1. This happens if $\Vert x^* -\alpha \cdot c \Vert _2 \geqslant \alpha \cdot \delta / 2n$ and since $\Vert \cdot \Vert _1 \geqslant \Vert \cdot \Vert _2$ one has

$$\begin{aligned} \Vert x^* -\alpha \cdot c \Vert _1 \geqslant \alpha \cdot \delta / 2n \end{aligned}$$

(6)

in this case. The probability of the event (6) is equal to the probability that a random $y^*$ chosen with a density proportional to $\exp (-\Vert y\Vert _1)$ has $\ell _1$ norm at least $\alpha \cdot \delta / 2n$. Since at least one component of y needs to have absolute value at least $\alpha \cdot \delta / 2n^2$ to satisfy (6), this probability is upper bounded by

$$\begin{aligned} n \int _{\alpha \cdot \delta / 2n^2}^\infty \exp (-x)\, dx = n / \exp (\alpha \cdot \delta / 2n^2) \end{aligned}$$

(7)

by applying the union bound. Thus if $\alpha \geqslant 2n^3 / \delta$, this probability is exponentially small in n.

Approximate sampling for log-concave distributions can be dealt with by random-walk techniques [1]. As in the paper of Dyer and Frieze [9] we combine these techniques with the simplex algorithm to keep track of the optimal vertex of the current point of the random walk.

Remember that the normal cones $C_v$ of the vertices v partition the space $\mathbb R^n$. Each of these cones is now again partitioned into countably infinitely many parallelepipeds whose axes are parallel to the unit vectors defining the cone of length $1/n^2$ see Fig. 2. More precisely, a given cone $C_v = \{ \sum _{i \in B} \lambda _i a_i :\lambda _i \geqslant 0, \, i \in B\}$ is partitioned into translates of the parallelepiped

$$\begin{aligned} \left\{ \sum _{i \in B} \lambda _i \cdot a_i :0 \le \lambda _i \le 1/n^2, \, i \in B \right\} . \end{aligned}$$

The volume of such a parallelepiped P is $\mathrm {vol}(P) =(1/n^2)^n |\det (A_B)|$ where $A_B$ is the sub-matrix of A consisting of the rows indexed by the basis B. For a parallelepiped P, we define

$$\begin{aligned} f(P) = f(z_P)\mathrm {vol}(P) \end{aligned}$$

where $z_P$ is the center of P. The state space of the random walk will be all parallelepipeds used to partition all cones, a countably infinite collection. One iteration is as follows.

Fig. 2

The partitioning of $\mathbb R^2$ into parallelepipeds for the polytope in Fig. 1 together with the illustration of a parallelepiped (blue) and its neighbors (green) (color figure online)

Notice that $P'$ can be a parallelepiped that is contained in a different cone. If we then make the transition to $P'$ we perform a simplex pivot. In this way we can always keep track of the normal cone containing the current parallelepiped. We assume that we are given some vertex of the polytope, $x^0$ and its associated basis $B_0 \subseteq \{1,\dots ,m\}$ to start with. We explain in the appendix how this assumption can be removed. We start the random walk at the parallelepiped of the cone $C_{x_0}$ that has vertex 0. The algorithm is completely described below.

Before we analyze the convergence of the random walk, we first explain the reason behind our choice for $1/n^2$ for the length of the edges of the parallelepipeds. In short, this is because the value of the function $f(x) = \exp (-\Vert x -\alpha \cdot c\Vert _1)$ does not vary too much for points in neighboring parallelepipeds. More precisely, we can state the following lemma.

Lemma 4

Let $P_1$ and $P_2$ be two parallelepipeds that share a common facet and let $x_1, x_2 \in P_1 \cup P_2$. If $n \geqslant 4$ then

$$\begin{aligned} f(x_1) / f(x_2) \leqslant e. \end{aligned}$$

Proof

The Euclidean distance between any two points in one of the two parallelepipeds is at most 1 / n and thus $\Vert x_1 - x_2\Vert \leqslant 2/n$. This implies $\Vert x_1-x_2\Vert _1 \leqslant 2/\sqrt{n}\leqslant 1$ since $n \geqslant 4$. Consequently

$$\begin{aligned} f(x_1) / f(x_2)= & {} \exp (- \Vert x_1 - \alpha \cdot c\Vert _1 + \Vert x_2 - \alpha \cdot c\Vert _1 ) \\\leqslant & {} \exp ( \Vert x_1 - x_2\Vert _1 ) \\\leqslant & {} \exp (1). \end{aligned}$$

In the second line of the above equation, we have applied the triangle inequality. $\square$

4 Analysis of the walk

We assume that the reader is familiar with basics of Markov chains (see e.g., [20]). The random walk above with its transition probabilities is in fact a Markov chain $\mathcal {M} = (\mathscr {P}, p)$ with a countably infinite state space $\mathscr {P}$ which is the set of parallelepipeds and transition probabilities $p:\mathscr {P} \times \mathscr {P} \longrightarrow \mathbb R_{\geqslant 0}$. Let $Q:\mathscr {P} \longrightarrow \mathbb R_{\geqslant 0}$ be a probability distribution on $\mathscr {P}$. The distribution Q is called stationary if for each $P \in \mathscr {P}$ one has

$$\begin{aligned} Q(P) = \sum _{P' \in \mathscr {P}} p(P',P) \cdot Q(P'). \end{aligned}$$

Our Markov chain is lazy since, at each step, with probability $\geqslant 1/2$ it does nothing. The rejection sampling step where we step from P to $P'$ with probability $1/2 \cdot \min \{1, f(P')/f(P)\}$ is called a Metropolis filter. Laziness and the Metropolis filter ensure that $\mathcal {M}= (\mathscr {P},p)$ has the unique stationary distribution (see e.g., Section 1, Thm 1.4 of [19] or Thm 2.1 of [27]):

$$\begin{aligned} Q(P) = f(P) {\Bigg /}\!\!\sum _{P' \in \mathscr {P}} f(P') \end{aligned}$$

which is a discretization of the continuous distribution with density $2^{-n} \exp (\Vert x - \alpha c \Vert _1)$ from (5).

Performing $\ell$ steps of the walk induces a distribution $Q^{\ell }$ on $\mathscr {P}$ where $Q^\ell (P)$ is the probability that the walk is in the parallelepiped P in the end. In the limit, when $\ell$ tends to infinity, $Q^\ell$ converges to Q. We now show that, due to the $\delta$-distance property of the matrix A, the walk quickly converges to Q. More precisely, we only need to run it for a polynomial number (in n and $1/\delta$) iterations. Then $Q^\ell$ will be sufficiently close to Q which shows that Algorithm 1 solves Problem 1 with high probability.

To prove convergence of the walk, we bound the conductance of the underlying Markov chain [24]. The conductance of $\mathcal {M}$ is

$$\begin{aligned} \phi = \min _{ \begin{array}{c} S \subseteq \mathscr {P} :\\ 0 <Q(S)\leqslant 1/2 \end{array}}\frac{\sum _{P \in S, P' \in \mathscr {P}{\setminus } S} Q(P) \cdot p(P,P')}{ Q(S)}. \end{aligned}$$

(8)

Jerrum and Sinclair [24] related the conductance to the convergence of a finite Markov chain to its stationary distribution. Lovász and Simonovits [19] extended their result to general Markov chains and in particular to Markov chains with a countably infinite set of states like our chain $\mathcal {M} = (\mathscr {P},p)$. We state their theorem in our setting.

Theorem 5

[19, Corollary 1.5] Let $Q^{\ell }$ be the distribution obtained after $\ell$ steps of the Markov chain $\mathcal {M} = (\mathscr {P},p)$ started at the initial parallelepiped $P_0$ and let $\phi$ be the conductance as in (8). Then for any $T \subseteq \mathscr {P}$ one has

$$\begin{aligned} |Q^{\ell }(T)-Q(T)| \le Q(P_0)^{-1/2} \left( 1-\frac{\phi ^2}{2}\right) ^{\ell }. \end{aligned}$$

The rate of convergence is thus $O(1/\phi ^2)$. Our goal is now to bound $\phi$ from below.

4.1 Bounding the conductance

Inspecting (8), we first note that the transition probability $p(P,P')$ is zero, unless the parallelepiped $P'$ is a neighbor of P, i.e., shares a facet with P. In this case one has

$$\begin{aligned} p(P,P') = \frac{1}{4n} \min \{1, f(P') / f(P)\}. \end{aligned}$$

The ratio $f(P') / f(P)$ can be bounded from below by $\delta / e$. This is because $f(z_{P'})/f(z_P) \geqslant 1/e$ by Lemma 4 and since $\mathrm {vol}(P') / \mathrm {vol}(P) \geqslant \delta$. The latter inequality is a consequence of the $\delta$-distance property, as the ratio $\mathrm {vol}(P') / \mathrm {vol}(P)$ is equal to the ratio of the height of $P'$ and the height of P measured from the common facet that they share respectively. This ratio is at least $\delta$. Consequently we have for neighboring parallelepipeds P and $P'$,

$$\begin{aligned} p(P,P') \geqslant \delta / (4 e n). \end{aligned}$$

Clearly $Q(P) \cdot p(P,P') = Q(P') \cdot p(P',P)$ which implies that the conductance can be bounded by

$$\begin{aligned} \phi \geqslant \min _{ \begin{array}{c} S \subseteq \mathscr {P} :\\ 0 <Q(S)\leqslant 1/2 \end{array}}({\displaystyle \delta }/{4en}) \, \frac{Q(N(S))}{Q(S)}. \end{aligned}$$

(9)

where $N(S) \subseteq \mathscr {P} {\setminus } S$ denotes the neighborhood of S, which is the set of parallelepipeds $P' \notin S$ for which there exists a neighboring $P \in S$.

We next make use of the following isoperimetric inequality that was shown by Bobkov and Houdre [2] for more general product probability measures. For our function $f(x) = \exp (-\Vert x - \alpha \cdot c\Vert _1)$ it reads as follows, where $\partial (A)$ denotes the boundary of A.

Theorem 6

[2] Let $f(x) = \exp (-\Vert x - \alpha \cdot c\Vert _1)$. For any measurable set $A \subset \mathbb R^n$ with $0<2^{-n} \int _A f(x) \, dx <1/2$ one has

$$\begin{aligned} \int _{\partial A} f(x)\, dx \ge \frac{1}{2 \sqrt{6}} \int _A f(x)\, dx. \end{aligned}$$

Theorem 6 together with the $\delta$-distance property yields a lower bound on Q(N(S)) / Q(S) as follows. Each parallelepiped $P' \in N(S)$ has at least one facet F at the boundary $\partial (\cup _{P \in S} P)$, see Fig. 3. Lemma 4 implies that $\int _F f(x) \, dx \leqslant e \cdot {\mathrm {Area}}(F) \cdot f(z_{P'})$ and since the height of $P'$ w.r.t. F is at least $\delta$ one has ${\mathrm {Area}}(F) \cdot \delta \leqslant \mathrm {vol}(P')$ which implies

$$\begin{aligned} \int _F f(x) \, dx \leqslant e/\delta \cdot f(z_{P'}) \mathrm {vol}(P') = e / \delta \cdot f(P'). \end{aligned}$$

Since each $P' \in N(S)$ has 2n facets, this implies

$$\begin{aligned} 2n\,e / \delta \cdot \sum _{P' \in N(S)} f(P') \geqslant \frac{1}{2 \sqrt{6}} \displaystyle \int _{\cup _{P \in S} P} f(x)\, dx \geqslant \frac{1}{2\, e\, \sqrt{6}} \sum _{P \in S} f(P) \end{aligned}$$

(10)

where we used Lemma 4 again in the last inequality. Thus $Q(N(S))/Q(S) \geqslant \delta / (4 e^2 \sqrt{6} n)$ which implies a bound of $\Omega (\delta ^2/n^2)$ on the conductance.

Fig. 3

An illustration of Theorem 6 in our setting. The gray parallelepipeds are the set S and the boundary $\partial S$ is in blue. The green parallelepipeds are N(S) (color figure online)

Lemma 7

The conductance of the random walk on the parallelepipeds is $\Omega (\delta ^2 / n^2)$.

4.2 Bounding the failure probability of the algorithm

Algorithm 1 does not return an element of the optimal basis if

$$\begin{aligned} \Vert z_P - \alpha \cdot c\Vert _2 \geqslant \delta / 2n. \end{aligned}$$

What is the probability of this event if P is sampled according to Q, the stationary distribution of the walk? If this happens, then the final parallelepiped is contained in the set

$$\begin{aligned} \{x \in \mathbb R^n :\Vert x - \alpha \cdot c\Vert _2 \geqslant \alpha \delta / 2n - 1/n\} \end{aligned}$$

(11)

since the diameter of a parallelepiped is at most 1 / n. Let $T \subseteq \mathscr {P}$ be the set of parallelepipeds that are contained in the set (11). To estimate Q(T) we use the notation $\widetilde{T}$ to denote the set of points in the union of the parallelepipeds, i.e., $\widetilde{T} = \cup _{P \in T}P$. Using Lemma 4, we see that

$$\begin{aligned} Q(T) = \sum _{P \in T} f(P) \bigg / \sum _{P \in \mathscr {P}} f(P) \leqslant e^2 \cdot 2^{-n} \cdot \int _{\widetilde{T}}f(x) \, dx. \end{aligned}$$

Clearly $2^{-n} \cdot \int _{\widetilde{T}}f(x) \, dx$ is at most the probability that a random point $x^* \in \mathbb R^n$ sampled from the distribution with density $2^{-n}\cdot \exp (-\Vert x \Vert _1)$ has $\ell _2$-norm at least $\alpha \cdot \delta / 2n - 1/n \geqslant \alpha \cdot \delta / 4n$ where we assume that $\alpha \geqslant 2 n^3 / \delta$ in the last inequality. Arguing as in (7) we conclude that

$$\begin{aligned} Q(T) \leqslant e^2 \cdot n / \exp ( \alpha \cdot \delta / 4n^2). \end{aligned}$$

Thus is $\alpha = 4n^3 / \delta$, then

$$\begin{aligned} Q(T) \leqslant e^2\cdot n / \exp (n) \end{aligned}$$

(12)

which is exponentially small in n.

How many steps $\ell$ of the walk are necessary until

$$\begin{aligned} |Q^\ell (T) - Q(T)| \leqslant \exp (-n) \end{aligned}$$

(13)

holds? Remember that the conductance $\phi \geqslant \xi \cdot (\delta /n)^2$ for some constant $\xi >0$. Thus (13) holds if

$$\begin{aligned} \sqrt{e^2 2^{n} / f(P_0)} \left( 1 - \xi \cdot (\delta /n)^2\right) ^\ell < \exp (-n). \end{aligned}$$

(14)

Now $f(P_0) = f(z_{P_0}) \mathrm {vol}(P_0) \geqslant \exp (-\Vert 2 \alpha c \Vert _1) n^{-n} \delta ^n \geqslant \exp (-8 \cdot n^{3.5}/\delta ) (\delta /n)^n$. Thus (14) holds if

$$\begin{aligned} \left( 1 - \xi \cdot (\delta /n)^2\right) ^\ell < \exp (- \nu n^{3.5}/\delta ) (\delta / n)^{n}, \end{aligned}$$

where $\nu >0$ is an appropriate constant. Using the inequality $(1+x) \leqslant \exp (x)$ and taking logarithms on both sides, this holds if

$$\begin{aligned} - \ell \cdot \xi \cdot (\delta /n)^2 < -\nu n^{3.5}/\delta + n \ln \delta / n \end{aligned}$$

(15)

and thus $\ell = \Omega (n^{5.5} / \delta ^3)$ is a polynomial lower bound on $\ell$ such that (13) holds. With the union bound we thus have our main result.

Theorem 8

If Algorithm 1 performs $\Omega (n^{5.5} / \delta ^3)$ steps of the random walk, then the probability of failure is bounded by $e^2 \cdot n \exp (-n) + \exp (-n)$. Consequently, there exists a randomized simplex-type algorithm for linear programming with an expected running time that is polynomial in $n/\delta$.

4.3 Remarks

Remark 1

The $\delta$-distance property is a global property of the matrix A. However, we used it only for the feasible bases of the linear program when we showed rapid mixing of the random walk. In the first submission of our paper, we asked whether an analog of Lemma 2 also holds for linear programs where a local $\delta$-distance property holds. This was answered positively by Dadush and Hähnle [7]. Thus our random walk can be used to solve linear programs whose basis matrices $A_B$, for each feasible basis B, satisfy the $\delta$-distance property in expected polynomial time in $n/ \delta$. The paper of Dadush and Hähnle shows this as well via a variant of the shadow-vertex pivoting rule. Their algorithm is much faster than ours. Also Brunsch et. al [4] could recently show that the shadow-vertex pivoting rule results in a polynomial-time algorithm for linear programs with the $\delta$-distance property. Their number of pivot-operations however also depends on the number m of constraints.

Remark 2

Our random walk, and especially the partitioning scheme, is similar to Dyer and Frieze [9] and is directly inspired by their paper. The main differences are the following. Dyer and Frieze rely on a finite partitioning of a bounded subset of $\mathbb R^n$, adapting a technique of Applegate and Kannan [1]. Our walk, however, is on a countably infinite set of states. For this, we rely on the paper of Lovàsz and Simonovits [19] which extends the relation of the conductance and rapid mixing to more general Markov chains, in particular countably infinite Markow chains. We also choose the $\ell _1$-norm, i.e., the function $\exp (-\Vert x - \alpha \cdot c\Vert _1)$, whereas Dyer and Frieze used the Euclidean norm. With this choice, the isoperimetric inequality of Bobkov and Houdré [2] makes the conductance analysis much simpler. Finally, we analyze the walk in terms of the $\delta$-distance in a satisfactory way. We feel that this geometric property is better suited for linear programming algorithms, as it is more general.

Appendix

Proof of Lemma 2

We denote the normal cones of B and $B'$ by

$$\begin{aligned} {C} = \left\{ \sum _{i\in B} \lambda _i a_i:\lambda _i\geqslant 0 \right\} \quad \text {and} \quad {C}' = \left\{ \sum _{j \in B'} \mu _j a_j :\mu _j \geqslant 0\right\} . \end{aligned}$$

By a gift-wrapping technique, we construct a hyperplane $(h^T x = 0)$, $h \in \mathbb R^n {\setminus } \{0\}$ such that the following conditions hold.

• (i) The hyperplane separates the interiors of C and $C'$.

• (ii) The row $a_k$ does not lie on the hyperplane.

• (iii) The hyperplane is spanned by $n-1$ rows of A.

Once we construct $(h^Tx = 0)$ we can argue as follows. The distance of $\mu _k \cdot a_k$ to the hyperplane $(h^Tx = 0)$ is at least $\mu _k\cdot \delta$. Since $c'$ is the sum of $\mu _k \cdot a_k$ and a vector that is on the same side of the hyperplane as $a_k$ it follows that the distance of $c'$ to this hyperplane is also at least $\mu _k \cdot \delta$. Since c lies on the opposite side of the hyperplane, the distance of c and $c'$ is at least $\mu _k \cdot \delta$.

We start with a hyperplane $(h^Tx = 0)$ strictly separating the interiors of C and $C'$. The conditions (i, ii) are satisfied. Suppose that (iii) is not satisfied and let $\ell < n-1$ be the maximum number of linearly independent rows of A that are contained in $(h^Tx = 0)$.

We tilt the hyperplane by moving its normal vector h along a chosen equator of the ball of radius $\Vert h\Vert$ to augment this number. Since $\ell < n-1$ there exists an equator leaving the rows of A that are in contained in $(h^T = 0)$ invariant under each rotation.

However, as soon as the hyperplane contains a new row of A we stop. If this new row of A is not $a_k$ then still, conditions (i, ii) hold and the hyperplane now contains $\ell +1$ linearly independent rows of A.

If this new row is $a_k$, then we redo the tilting operation but this time by moving h in the opposite direction on the chosen equator. Since there are n linearly independent rows of A without the row $a_k$ this tilting will stop at a new row of A which is not $a_k$ and we end the first tilting operation.

This tilting operation has to be repeated at most $n-1 - |B \cap B'|$ times to obtain the desired hyperplane. $\square$

1.1 Phase 1

We now describe an approach to determine an initial basic feasible solution or to assert that the linear program (1) is infeasible. Furthermore, we justify the assumption that the set of feasible solutions is a bounded polytope. This phase 1 is different from the usual textbook method since the linear programs that we need to solve have to comply with the $\delta$ -distance property.

To find an initial basic feasible solution, we start by identifying n linearly independent linear inequalities $\widetilde{a}_1^Tx \leqslant \widetilde{b}_1, \dots ,\widetilde{a}_n^Tx \leqslant \widetilde{b}_n$ of $Ax \leqslant b$. Then we determine a ball that contains all feasible solutions. This standard technique is for example described in [13]. Using the normal-vectors $\widetilde{a}_1,\dots ,\widetilde{a}_n$ we next determine values $\beta _i, \gamma _i \in \mathbb R$, $i=1,\dots ,n$ such that this ball is contained in the parallelepiped $Z = \{ x \in \mathbb R^n :\beta _i \leqslant \widetilde{a}_i^Tx \leqslant \gamma _i, \, i=1,\dots ,n\}$. We start with a basic feasible solution $x_0^*$ of this parallelepiped and then proceed in m iterations. In iteration i, we determine a basic feasible solution $x^*_i$ of the polytope

$$\begin{aligned} P_i = Z \cap \left\{ x \in \mathbb R^n :a_j^Tx \leqslant b_j, \,1 \leqslant j \leqslant i \right\} \end{aligned}$$

using the basic feasible solution $x^*_{i-1}$ from the previous iteration by solving the linear program

$$\begin{aligned} \min \left\{ a_i^Tx :x \in P_{i-1} \right\} . \end{aligned}$$

If the optimum value of this linear program is larger than $b_i$, we assert that the linear program (1) is infeasible. Otherwise $x^*_i$ is the basic feasible solution from this iteration.

Finally, we justify the assumption that $P = \{x \in \mathbb R^n :Ax \leqslant b\}$ is bounded as follows. Instead of solving the linear program (1), we solve the linear program $\max \{ c^Tx :x \in P \cap Z\}$ with the initial basic feasible solution $x^*_m$. If the optimum solution is not feasible for (1) then we assert that (1) is unbounded.