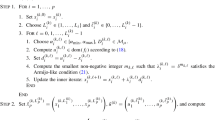1 Introduction

Consider the problem of minimizing a nonsmooth convex function f(x):

$$\begin{aligned} \begin{array}{ll} \text{ minimize } &{} \displaystyle f(x):=g\left( x_1,\ldots , x_K\right) +\sum _{k=1}^{K}h_k(x_k)\\ \text{ subject } \text{ to } &{} x_k\in X_k,\quad k=1,\ldots ,K, \end{array} \end{aligned}$$
(1.1)

where \(g(\cdot )\) is a smooth convex function; \(h_k\) is a closed nonsmooth convex function (possibly with extended values); \(x=(x_1^T,\ldots ,x_K^T)^T\in \mathbb {R}^n\) is a partition of the optimization variable x, with \(x_k\in X_k\subseteq \mathbb {R}^{n_k}\). Let \(X:=\prod _{k=1}^{K}X_k\) denote the feasible set for x.

A well known family of algorithms for solving (1.1) is the block coordinate descent (BCD) type method whereby, at every iteration a single block of variables is optimized while the remaining blocks are held fixed. One of the best known algorithms in the BCD family is the block coordinate minimization (BCM) algorithm, where at iteration r, the blocks are updated by solving the following problem exactly [3]

$$\begin{aligned} x_k^r \in \arg \min _{x_k\in X_k} \quad&g\left( x_1^{r},\ldots ,x_{k-1}^{r},x_k,x_{k+1}^{r-1},\ldots , x_K^{r-1}\right) +h_k(x_k), \ \forall ~k. \end{aligned}$$
(1.2)

When problem (1.2) is not easily solvable, a popular variant is to solve an approximate version of problem (1.2), yielding the block coordinate gradient descent (BCGD) algorithm, or the block coordinate proximal gradient (BCPG) algorithm in the presence of a nonsmooth function [2, 28, 32, 36]. In particular, at a given iteration r, the following problem is solved for each block k:

$$\begin{aligned} x_k^r= & {} \arg \min _{x_k\in X_k}\; \left\langle \nabla _k g\left( x_1^{r},\ldots ,x_{k-1}^{r},x_{k}^{r-1},\ldots , x_K^{r-1}\right) , x_k-x^{r-1}_k\right\rangle \\&+\frac{L_k}{2}\Vert x_k-x^{r-1}_k\Vert ^2+h_k(x_k), \end{aligned}$$

where \(L_k>0\) is some appropriately chosen constant. Other variants of the BCD-type algorithm include those that solve different subproblems [24], or those with different block selection rules, such as the Gauss–Seidel (G–S) rule, the Gauss–Southwell (G–So) rule [31], the randomized rule [22], the essentially cyclic (E-C) rule [29], or the maximum block improvement (MBI) rule [6].

In all the above mentioned variants of BCD method, each step involves solving a simple subproblem of small size, therefore the BCD method can be quite effective for solving large-scale problems; see e.g., [10, 22, 24, 26, 28] and the references therein. The existing analysis of the BCD method [4, 5, 23, 29] requires the uniqueness of the minimizer for each subproblem (1.2), or the pseudo-convexity of f [11]. Recently, a unified BCD-type framework, termed the block successive upper-bound minimization (BSUM) method, was proposed in [24]. At each iteration of the BSUM method, certain approximate function of the per-block subproblem (1.2) is constructed and optimized. Due to the flexibility in choosing the approximate function, the BSUM includes many BCD-type algorithms as special cases. It is shown in [24] that the method converges to stationary solutions for nonconvex problems and to global optimal solutions for convex problems, as long as certain regularity conditions are satisfied for the per-block subproblems.

The global rate of convergence for BCD-type algorithm has been studied extensively. When the objective function is strongly convex, the BCM algorithm converges globally linearly [18]. When the objective function is smooth and not strongly convex, Luo and Tseng have shown that the BCD method with the classic G–S/G–So update rules converges linearly, provided that a certain local error bound is satisfied around the solution set [16–19]. In addition, such linear rate is global when the feasible set is compact. This line of analysis has recently been extended to allow certain class of nonsmooth functions in the objective [30, 36]. For more general problems where the objective is not strongly convex and the error bound condition does not hold, several recent studies have established the \({\mathcal {O}}(1/r)\) iteration complexity for various BCD-type algorithms including the randomized BCGD algorithm [22], and for more general settings with nonsmooth objective as well [15, 25, 28]. When the coordinates are updated according to the traditional G–S/G–So/E-C rule, however, the literature on the iteration complexity for the BCD-type algorithm is scarce. In [26], Saha and Tewari have proven the \({\mathcal {O}}(1/r)\) rate for the G–S BCPG algorithm when applied to certain special \(\ell _1\) minimization problem. In [2], Beck and Tetruashvili have shown the \({\mathcal {O}}(1/r)\) sublinear convergence for the G–S BCGD algorithm for constrained smooth problems. In [1], Beck has shown the sublinear convergence for the G–S BCM algorithm (termed Alternating Minimization method therein) when the number of blocks is two. Although the BCD-type algorithm with G–S rule sometimes has been found to perform better than its randomized counterpart (see, e.g., [26]), establishing its iteration complexity in a general multi-block nonsmooth setting is challenging [22]. To the best of our knowledge, the iteration complexity of the BCD-type algorithm with the classic G–S update rule has not yet been characterized for multi-block nonsmooth problems, not to mention other types of deterministic coordinate selection rules such as G–So, E-C or MBI. Further, there has been no iteration complexity analysis for the classic BCM iteration (1.2) when the number of variable blocks is more than two (i.e., \(K\ge 3\)).

In this paper, we provide a unified iteration complexity analysis for K-block BCD-type algorithm by utilizing the BSUM framework [24]. Our result covers many different BCD-type algorithms such as BCM, BCPG, and BCGD under a number of deterministic coordinate update rules. First, for a broad class of nonsmooth convex problems, we show that the BSUM algorithm achieves a global sublinear convergence rate of \(\mathcal{{O}}({1}/{r})\), provided that each subproblem is strongly convex. Second, for the BCM algorithm (1.2), we show the global convergence rate of \(\mathcal{{O}}({1}/{r})\) without the per-block strong convexity assumption. The main results of this paper are summarized in the following Table 1.Footnote 1

Table 1 Summary of the Results
Full size table

Notations: For a given matrix A, we use A[i, j] to denote its (i, j)th element. For a symmetric matrix A use \(\rho _{\max }(A)\) to denote its spectral norm. For a given vector x, we use x[j] to denote its jth component; use \(\Vert x\Vert \) to denote its \(\ell _2\) norm. We use \(I_{X}(\cdot )\) to denote the indicator function for a given set X, i.e., \(I_{X}(y)=1\) if \(y\in X\), and \(I_{X}(y)=\infty \) if \(y\notin X\). Let \(x_{-k}\) denote the vector x with \(x_k\) removed. For a given function \(f(x_1,\ldots ,x_K)\) which contains K block variables, we use \(\nabla _k f(x_1,\ldots , x_K)\) to denote the partial gradient with respect to its kth block variable. We use \(\partial f\) to denote the subdifferential set of a function f. For a given convex nonsmooth closed function \(\ell (\cdot )\), we define the proximity operator \(\text{ prox }_{\ell }(\cdot ):\mathbb {R}^n\mapsto \mathbb {R}^n\) as

$$\begin{aligned} \text{ prox }^{\beta }_{\ell }(x)={{{\mathrm{argmin}}}_{u\in \mathbb {R}^n}}\;\;\ell (u)+\frac{\beta }{2}\Vert x-u\Vert ^2. \end{aligned}$$

Similarly, for a given closed convex set X, the projection operator \(\mathrm{proj}_{X}(\cdot ):\mathbb {R}^n\mapsto X\) is defined as

$$\begin{aligned} \hbox {proj}_{X}(x)={{{\mathrm{argmin}}}_{u\in X}}\;\;\frac{1}{2}\Vert x-u\Vert ^2. \end{aligned}$$

2 The BSUM algorithm and preliminaries

2.1 The BSUM algorithm

In this paper, we consider a family of block coordinate descent methods (BCD) for solving problem (1.1). The family of the algorithms we consider falls in the general category of block successive upper-bound minimization (BSUM) method, in which certain approximate version of the objective function is optimized one block variable at a time, while fixing the rest of the block variables [24]. In particular, at iteration \(r+1\), we first pick an index set \({{\mathcal {C}}}^{r+1}\subseteq \{1,\ldots ,K\}\). Then the kth block variable is updated by

$$\begin{aligned} x^{r+1}_k \left\{ \begin{array}{ll}\in \arg \min _{x_k\in X_k}\; u_k\left( x_k; x^{r+1}_{1},\ldots , x^{r+1}_{k-1}, x^{r}_{k},\ldots , x^r_{K}\right) +h_k(x_k), &{} \text{ if }\; k\in {{\mathcal {C}}}^{r+1};\\ =x^{r}_k, &{}\text{ if }\; k\notin {{\mathcal {C}}}^{r+1}, \end{array}\right. \end{aligned}$$
(2.1)

where \(u_k(\cdot ; x^{r+1}_{1},\ldots , x^{r+1}_{k-1}, x^{r}_{k},\ldots , x^r_{K})\) is an approximation of g(x) at a given iterate \((x^{r+1}_{1},\ldots , x^{r+1}_{k-1}, x^{r}_{k},\ldots , x^r_{K})\). We will see shortly that by properly specifying the approximation function \(u_k(\cdot )\) as well as the index set \({{\mathcal {C}}}^{r+1}\), we can recover many popular BCD-type algorithms such as the BCM, the BCGD, the BCPG methods and so on.

To simplify notations, let us define a set of auxiliary variables

$$\begin{aligned} w^r_k&:=\left[ x^{r}_1,\ldots , x^{r}_{k-1}, x^{r-1}_{k}, x^{r-1}_{k+1}, \ldots , x^{r-1}_K\right] ,&\ k=1,\ldots , K, \\ w^r_{-k}&:=\left[ x^{r}_1,\ldots , x^{r}_{k-1}, x^{r-1}_{k+1}, \ldots , x^{r-1}_K\right] ,&\ k=1,\ldots , K, \\ x_{-k}&:=\left[ x_1,\ldots , x_{k-1}, x_{k+1}, \ldots , x_K\right] ,&\ k=1,\ldots , K. \end{aligned}$$

Clearly we have \(w^{r}_{K+1}:=x^r, \; w^{r}_1:=x^{r-1}\). Moreover, at each iteration \(r+1\), define a set of new variables \(\{\hat{x}_k^{r+1}\}_{k=1}^{K}\) as follows

$$\begin{aligned} \hat{x}^{r+1}_k\in \arg \min _{x_k\in X_k}\; u_k\left( x_k; x^{r}\right) +h_k(x_k), \; k=1,\ldots , K. \end{aligned}$$
(2.2)

Clearly \(\{\hat{x}^{r+1}_k\}_{k=1}^{K}\) represents a “virtual” update where all variables are optimized in a Jacobi manner based on \(x^r\).

The BSUM algorithm is described formally in the following table.

figure a

In this paper, we consider the following well-known block selection rules:

  1. 1.

    Gauss–Seidel (G–S) rule At each iteration \(r+1\) all the indices are chosen, i.e., \({{\mathcal {C}}}^{r+1}=\{1,\ldots ,K\}\). Using this rule, the blocks are updated cyclically with fixed order.

  2. 2.

    Essentially cyclic (E-C) rule There exists a given period \(T\ge 1\) during which each index is updated at least once, i.e.,

    $$\begin{aligned} \bigcup _{i=1}^{T}{{\mathcal {C}}}^{r+i}=\{1,\ldots ,K\}, \; \forall ~r. \end{aligned}$$
    (2.3)

    We call this update rule a period-T essentially cyclic update rule. Clearly when \(T=1\) we recover the G–S rule.

  3. 3.

    Gauss–Southwell (G–So) rule At each iteration \(r+1\), \({{\mathcal {C}}}^{r+1}\) contains a single index \(k^*\) that satisfies:

    $$\begin{aligned} k^*\in \left\{ k \;\bigg | \; \Vert \hat{x}^{r+1}_{k}-x^{r}_{k}\Vert \ge q \max _{j}\Vert \hat{x}^{r+1}_j-x^{r}_j\Vert \right\} , \end{aligned}$$
    (2.4)

    for some constant \(q\in (0,\; 1]\).

  4. 4.

    Maximum block improvement (MBI) rule At each iteration \(r+1\), \({{\mathcal {C}}}^{r+1}\) contains a single index \(k^*\) that satisfies:

    $$\begin{aligned} k^*\in \arg \max _{k}-f\left( x^{r}_{-k}, \hat{x}^{r+1}_k\right) , \end{aligned}$$
    (2.5)

    where \(f(x^{r}_{-k}, \hat{x}^{r+1}_k)\) means the function \(f(\cdot )\) evaluated at the vector \([x^{r}_{-k}, \hat{x}^{r+1}_k]\).

2.2 Main assumptions

Suppose f is a closed proper convex function in \(\mathbb {R}^n\). Let \(\mathrm{dom}\ f\) denote the effective domain of f and let \(\hbox {int}({\hbox {dom}\,} f)\) denote the interior of \(\mathrm{dom} f\). We make the following standing assumptions regarding problem (1.1):

Assumption A

  1. (a)

    Problem (1.1) is a convex problem, and its global minimum is attained. The intersection \(X\cap \hbox {int}(\hbox {dom } f)\) is nonempty. Each \(h_k\) is a proper closed and convex function (not necessarily smooth), and its subdifferential set is nonempty at the relative boundary point of \(X_k\).

  1. (b)

    The gradient \(\nabla g(\cdot )\) is block-wise uniformly Lipschitz continuous

    $$\begin{aligned}&\Vert \nabla _k g\left( \left[ x_{-k}, x_k\right] \right) -\nabla _k g\left( \left[ x_{-k},{x}'_k\right] \right) \Vert \nonumber \\&\quad \le M_k \Vert x_k-{x}'_k\Vert ,~\forall ~x_k,x_k'\in X_k, ~ \forall ~x \in X, \ \forall \ k \end{aligned}$$
    (2.6)

    where \(M_k>0\) is a constant. Define \(M_{\max }=\max _k M_k\). The gradient of \(g(\cdot ) \) is also uniformly Lipschitz continuous

    $$\begin{aligned}&\Vert \nabla g(x)-\nabla g(x')\Vert \le M\Vert x-x'\Vert ,~\quad \quad \forall ~x,x'\in X \end{aligned}$$
    (2.7)

    where \(M>0\) is a constant.

Next we make the following assumptions regarding the approximation function \(u_k(\cdot ;\cdot )\) in (2.1).

Assumption B

  1. (a)

    \(u_k(x_k; x)= g(x), \; \forall \; x\in {X}, \ \forall \; k.\)

  1. (b)

    \(u_k(v_k; x) \ge g(v_k,x_{-k}),\; \forall \; v_k \in {X}_k, \ \forall \; x \in {X}, \ \forall \; k.\)

  2. (c)

    \(\nabla u_k(x_k;x)= \nabla _{k}g(x), \; \forall \; x\in X, \; \forall \; k\), where the notation \(\nabla u_k(x_k;x)\) represents the partial derivative with respect to \(x_k\).

  3. (d)

    \(u_k(v_k; x)\) is continuous in \(v_k\) and x. Further, for any given \(x\in X\), it is a proper, closed and strongly convex function of \(v_k\), satisfying

    $$\begin{aligned} u_k(v_k; x)\ge u_k(\hat{v}_k; x)+\left\langle \nabla u_k(\hat{v}_k; x),v_k-\hat{v}_k\right\rangle +\frac{\gamma _k}{2}\Vert v_k-\hat{v}_k\Vert ^2,\ \forall ~v_k, \ \hat{v}_k\in X_k, \end{aligned}$$

    where \(\gamma _k>0\) is independent of the choice of x.

  4. (e)

    For any given \(x\in X\), \(u_k(v_k; x)\) has Lipschitz continuous gradient, that is

    $$\begin{aligned} \Vert \nabla u_k(v_k; x)-\nabla u_k(\hat{v}_k; x)\Vert \le L_k\Vert v_k-\hat{v}_k\Vert ,\ \forall \ \hat{v}_k,\ v_k\in X_k, \ \forall \ k, \end{aligned}$$
    (2.8)

    where \(L_k>0\) is some constant. Further, we have

    $$\begin{aligned} \Vert \nabla u_k(v_k; x)-\nabla u_k({v}_k; y)\Vert \le G_k\Vert x-y\Vert ,\ \forall \ v_k\in X_k, \ \forall \ k, \ \forall ~x, y\in X. \end{aligned}$$
    (2.9)

    Define \(L_\mathrm{max}:=\max _{k}L_k\); \(G_\mathrm{max}:=\max _{k}G_k\).

We refer to the \(u_k\)’s that satisfy Assumption B as a valid upper-bound.

A few remarks are in order regarding to the assumptions made above.

First of all, Assumption B indicates that for any given x, each \(u_k(\cdot ; x)\) is a locally tight upper bound for g(x). When the approximation function is chosen as the original function g(x), then we recover the classic BCM algorithm; cf. (1.2). In many practical applications especially nonsmooth problems, minimizing the approximation functions often leads to much simpler subproblems than directly minimizing the original function; see e.g., [12, 14, 33, 34, 37]. For example, if \(h_k(\cdot )=0\) for all k, and \(u_k\) takes the following form

$$\begin{aligned} u_k\left( x_k; w_k^{r+1}\right) =g\left( w_k^{r+1}\right) +\left\langle \nabla _k g\left( w_k^{r+1}\right) , x_k-x^r_k \right\rangle +\frac{M_k}{2}\Vert x_k-x^r_k\Vert ^2, \end{aligned}$$
(2.10)

then we recover the well known BCGD method [2, 18, 22], in which \(x_k\) is updated by

$$\begin{aligned} x^{r+1}_k=\text{ proj }_{X_k}\left[ x^{r}_k-\frac{1}{M_k}\nabla _k g\left( w_k^{r+1}\right) \right] . \end{aligned}$$
(2.11)

When the nonsmooth components \(h_k\)’s are present, the above choice of \(u_k(\cdot ;\cdot )\) in (2.10) leads to the so-called BCPG method [7, 24, 36], in which \(x_k\) is updated by

$$\begin{aligned} x^{r+1}_k=\text{ prox }^{M_k}_{h_k+I_{X_k}}\left[ x^{r}_k-\frac{1}{M_k}\nabla _k g\left( w_k^{r+1}\right) \right] . \end{aligned}$$
(2.12)

For other possible choices of the approximation function, we refer the readers to [20, 24].

Secondly, the strong convexity requirement on \(u_k(\cdot ;x)\) in Assumption B(d) is quite mild, and is satisfied for the BCPG and BCGD algorithms; see the discussion in the previous remark. When \(u_k\) is chosen as the original function g(x), this requirement says that g(x) must be block-wise strongly convex (BSC). The BSC condition is in fact satisfied in many practical engineering problems. The following are two interesting examples.

Example 1

Consider the rate maximization problem in an uplink wireless communication network, where K users transmit to a single base station (BS) in the network. Suppose each user has \(n_t\) transmit antennas, and the BS has \(n_r\) receive antennas. Let \(C_k\in \mathbb {R}^{n_t\times n_t}\) denote user k’s transmit covariance matrix, \(P_k\) denote the maximum transmit power for user k, and \(H_k\in \mathbb {R}^{n_r\times n_t}\) denote the channel matrix between user k and the BS. Then the uplink channel capacity optimization problem is given by the following convex program [8, 35]

$$\begin{aligned} \min _{\{C_k\}_{k=1}^{K}} -\log \det \left| \sum _{k=1}^{K}{H_k C_k H^T_k} +I_{n_r}\right| , \; \mathrm{s.t.}\; C_k\succeq 0,\; {\text{ Tr }}{[C_k]}\le P_k, \ \forall ~k, \end{aligned}$$
(2.13)

where \(I_{n_r}\) is the \(n_r\times n_r\) identity matrix. The celebrated iterative water-filling algorithm (IWFA) [35] for solving this problem is simply the BSUM algorithm with exact block minimization (i.e. the BCM algorithm) and G–S update rule. It is easy to verify that when \(n_t\le n_r\) (i.e., the number of transmit antenna is smaller than that of the receive antenna), and when the channels are generated randomly, then with probability one \(H^T_k H_k\) is of full rank, implying that the BSC condition is satisfied. We note that there has been no iteration complexity analysis of the IWFA algorithm for any type of block selection rules.

Example 2

Consider the following LASSO problem:

$$\begin{aligned} \min _{x}\Vert Ax-b\Vert ^2+\lambda \Vert x\Vert _1, \end{aligned}$$

where \(A\in \mathbb {R}^{M\times K}, \; b\in \mathbb {R}^{M}\), and \(x=[x_1,\ldots , x_K]^T\), with \(x_k\in \mathbb {R}\) for all k. That is, each block consists of a single scalar variable. In this case, as long as none of A’s columns are zero (in which case we simply remove that column and the corresponding block variable), the problem satisfies the BSC property. Prior to our work, there is no iteration complexity analysis for applying BCD with deterministic block selection rules such as G–S and E-C for LASSO (with general data matrix A).

Note that the BSC property, or more generally the strong convexity assumption on the approximate function \(u_k\), is reasonable as it ensures that each step of the BSUM algorithm is well-defined and has a unique solution. In the ensuing analysis of the BSUM algorithm, we assume that either the BSC property holds true, or \(u_k\) is a valid upper-bound. Later in Sects. 4–6, we will consider the case where the BSC assumption is absent.

3 Convergence analysis for BSUM

In this section, we show that under assumptions A and B, the BSUM algorithm with flexible update rules achieves global sublinear rate of convergence.

Let us define \(X^*\) as the optimal solution set, and let \({x}^*\in X^*\) be one of the optimal solutions. For the BSUM algorithm, define the optimality gap as

$$\begin{aligned} \varDelta ^r:&=f(x^{r})-f({x}^*). \end{aligned}$$
(3.1)

Despite the generality of the BSUM algorithm, our analysis of BSUM only consists of three simple steps: (S1) estimate the amount of successive decrease of the optimality gaps; (S2) estimate the cost yet to be minimized (i.e., the cost-to-go) after each iteration; (S3) estimate the rate of convergence.

We first characterize the successive difference of the optimality gaps before and after one iteration of the BSUM algorithm, with different update rules.

Lemma 1

(Sufficient Descent) Suppose Assumption A–B hold. Then

  1. 1.

    For BSUM with either G–S rule or the E-C rule, the following is true

    $$\begin{aligned} \varDelta ^{r}-\varDelta ^{r+1}\ge \sum _{k=1}^{K}\frac{\gamma _k}{2}\Vert x_k^{r} - x_k^{r+1}\Vert ^2\ge {\gamma }\Vert x^{r} - x^{r+1}\Vert ^2,\quad \forall ~r\ge 1, \end{aligned}$$
    (3.2)

    where the constant \(\gamma :=\frac{1}{2}\min _k\gamma _k>0\).

  2. 2.

    For BSUM with G–So rule and MBI rule, the following is true

    $$\begin{aligned} \varDelta ^{r}-\varDelta ^{r+1}\ge \frac{c_1}{K} {\gamma }\Vert x^r - \hat{x}^{r+1}\Vert ^2, \quad \forall ~r\ge 1, \end{aligned}$$
    (3.3)

    where the constant \(\gamma :=\frac{1}{2}\min _k\gamma _k>0\); For G–So rule, \(c_1=q\), and for MBI rule, \(c_1=1\).

Proof

We first show part (1) of the proof. Suppose that \(k\notin {{\mathcal {C}}}^{r+1}\), then we have the following trivial inequality

$$\begin{aligned} f\left( w^{r+1}_k\right) - f\left( w^{r+1}_{k+1}\right) \ge \frac{\gamma _k}{2}\Vert x^{r+1}_k-x^r_k\Vert ^2, \end{aligned}$$
(3.4)

as both sides of the inequality are zero.

Suppose \(k\in {{\mathcal {C}}}^{r+1}\). Then using Assumption B, we have that

$$\begin{aligned}&f\left( w^{r+1}_k\right) - f\left( w^{r+1}_{k+1}\right) \nonumber \\&\quad \ge u_k\left( x^{r}_{k} ; w^{r+1}_k\right) +h_k\left( x^r_k\right) -\left( u_k\left( x^{r+1}_{k} ; w^{r+1}_k\right) +h_k\left( x^{r+1}_k\right) \right) \nonumber \\&\quad \ge \left\langle \nabla u_k\left( x^{r+1}_{k} ; w^{r+1}_k\right) , x^r_k-x^{r+1}_k\right\rangle +h_k\left( x^r_k\right) -h_k\left( x^{r+1}_k\right) +\frac{\gamma _k}{2}\Vert x^{r+1}_k-x^r_k\Vert ^2\nonumber \\&\quad \ge \left\langle \nabla u_k\left( x^{r+1}_{k} ; w^{r+1}_k\right) +\zeta _k^{r+1}, x^r_k-x^{r+1}_k\right\rangle +\frac{\gamma _k}{2}\Vert x^{r+1}_k-x^r_k\Vert ^2\nonumber \\&\quad \ge \frac{\gamma _k}{2}\Vert x^{r+1}_k-x^r_k\Vert ^2 \end{aligned}$$
(3.5)

where the first inequality is due to Assumption B(a)–B(b); the second inequality is due to Assumption B(d); in the third inequality we have defined \(\zeta _k^{r+1}\in \partial h_k(x^{r+1}_{k})\) as any subgradient vector in the subdifferential \(\partial h_k(x^{r+1}_{k})\); in the last inequality we have used the fact that \(x_k^{r+1}\) is the optimal solution for the strongly convex problem

$$\begin{aligned} \hbox {arg} \!\min _{x_k\in X_k}u_k\left( x_k; w^{r+1}_k\right) +h_k(x_k), \end{aligned}$$

and we have specialized \(\zeta _k^{r+1}\) to the subgradient that satisfying the optimality condition of the problem above. Summing over k, we have

$$\begin{aligned} f(x^r)- f(x^{r+1})\ge \gamma \Vert x^r - x^{r+1}\Vert ^2, \end{aligned}$$
(3.6)

where \(\gamma :=\frac{1}{2}\min _{k}\gamma _k\).

We now show part (2) of the claim. Suppose \(k\in {{\mathcal {C}}}^{r+1}\), then we have the following series of inequalities for the G–So rule

$$\begin{aligned} f(x^r)- f\left( x^{r+1}\right)&=f(x^r)-f\left( x^r_{-k},\hat{x}^{r+1}_k\right) \nonumber \\&\ge u_k\left( x^r_k; x^r\right) +h_k\left( x^r_k\right) -u_k\left( \hat{x}^{r+1}_k; x^r\right) -h_k\left( \hat{x}^{r+1}_k\right) \nonumber \\&\ge \frac{1}{2}\gamma _k\Vert x^r_k-\hat{x}^{r+1}_k\Vert ^2\nonumber \\&\ge \frac{q\min _{j}\gamma _j}{2K}\sum _{j=1}^{K}\Vert x^r_j-\hat{x}^{r+1}_j\Vert ^2= \frac{q}{K}{\gamma }\Vert x^r - \hat{x}^{r+1}\Vert ^2. \end{aligned}$$
(3.7)

Similar steps lead to the result for the MBI rule. \(\square \)

Next we show the second step of the proof, which estimates the gap yet to be minimized after each iteration. Let us define the following constants:

$$\begin{aligned}&R:=\max _{x\in X}\max _{x^*\in X^*}\left\{ \Vert x-x^*\Vert \ : \ f(x)\le f(x^1) \right\} ,\nonumber \\&Q:=\max _{x\in X}\left\{ \Vert \nabla g(x)\Vert :\ f(x)\le f(x^1)\right\} . \end{aligned}$$
(3.8)

When assuming that the level set \(\{x: f(x)\le f(x^1)\}\) is compact, then all the above constants are finite. Clearly we have

$$\begin{aligned} \Vert x^r-x^*\Vert \le R,\quad \Vert \nabla g(x^r)\Vert \le Q, \ \forall \ r=1,\ldots . \end{aligned}$$
(3.9)

Occasionally we need to further make the assumption that the nonsmooth part h(x) is Lipschitz continuous:

$$\begin{aligned} \Vert h(x)-h(y)\Vert \le L_h\Vert x-y\Vert ,\ \forall \ x, y\in X, \end{aligned}$$
(3.10)

with some \(L_h>0\). Note that such assumption is satisfied by most of the popular nonsmooth regularizers such as the \(\ell _1\) norm, the \(\ell _2\) norm and so on. Also note that even with this assumption, our considered problem is still a constrained one, as the convex constraints \(x_k\in X_k\) have not been moved to the objective as nonsmooth indicator functions.

Lemma 2

(Cost-to-go estimate) Suppose Assumptions A–B hold. Then

  1. 1.

    For the BSUM with G–S update rule, we have

    $$\begin{aligned} (\varDelta ^{r+1})^2\le R^2 K G^2_{\max }\Vert x^{r+1}-x^{r}\Vert ^2,\ \forall \ x^*\in X^*. \end{aligned}$$
  2. 2.

    For the BSUM with period-T E-C update rule, we have

    $$\begin{aligned} (\varDelta ^{r+T})^2\le T R^2 K G^2_{\max }\sum _{t=1}^{T}\Vert x^{r+t}-x^{r+t-1}\Vert ^2,\ \forall \ x^*\in X^*. \end{aligned}$$
  3. 3.

    For the BSUM with G–So and MBI rules, further assume that \(h(\cdot )\) is Lipschitz continuous (cf. (3.10)). Then we have

    $$\begin{aligned} (\varDelta ^{r})^2&=\left( f(x^{r})-f(x^*)\right) ^2\\&\le 2\left( \left( Q+L_h\right) ^2+L^2_{\max } {K} R^2\right) \Vert \hat{x}^{r+1}-x^{r}\Vert ^2,\ \forall \ x^*\in X^*. \end{aligned}$$

Proof

We first show part (1). We have the following sequence of inequalities

$$\begin{aligned} f(x^{r+1})-f(x^*)= & {} g(x^{r+1})-g(x^*)+h(x^{r+1})-h(x^*)\nonumber \\\le & {} \left\langle \nabla g(x^{r+1}), x^{r+1}-x^*\right\rangle +h(x^{r+1})-h(x^*)\nonumber \\= & {} \sum _{k=1}^{K}\left\langle \nabla _k g(x^{r+1})-\nabla u_k\left( x_k^{r+1};w^{r+1}_k\right) , x^{r+1}_k-x^{*}_k\right\rangle \nonumber \\&\quad +\sum _{k=1}^{K}\left\langle \nabla u_k\left( x_k^{r+1};w^{r+1}_k\right) , x^{r+1}_k-x^{*}_k\right\rangle +h(x^{r+1})-h(x^*).\nonumber \\ \end{aligned}$$
(3.11)

Notice that \(x^{r+1}_k\) is the optimal solution for problem: \({{\mathrm{argmin}}}_{x_k\in X_k}u_k(x_k; w^{r+1}_k)+h_k(x_k)\). It follows from the optimality condition of this problem that there exists some \(\zeta _k^{r+1}\in \partial (h_k(x^{r+1}_k))\) such that

$$\begin{aligned} 0&\ge \left\langle \nabla u_k\left( x^{r+1}_k; w^{r+1}_k\right) + \zeta _k^{r+1}, x^{r+1}_k-x^*_k\right\rangle \nonumber \\&\ge \left\langle \nabla u_k\left( x^{r+1}_k; w^{r+1}_k\right) , x^{r+1}_k-x^*_k\right\rangle +h_k\left( x^{r+1}_k\right) -h_k\left( x^*_k\right) , \end{aligned}$$
(3.12)

where in the last inequality we have used the definition of subgradient

$$\begin{aligned} h_k\left( x^{r+1}_k\right) -h_k\left( x_k^*\right) \le \left\langle \zeta _k^{r+1}, x^{r+1}_k-x_k^*\right\rangle ,\;\forall \ x^{r+1}_k, x_k^*\in X_k. \end{aligned}$$
(3.13)

Combining (3.11) and (3.12), we obtain

$$\begin{aligned} \left( f(x^{r+1})-f(x^*)\right) ^2&\mathop {\le }\limits ^\mathrm{(i)}\left( \sum _{k=1}^{K}\Vert \nabla _k g(x^{r+1})-\nabla u_k\left( x^{r+1}_k; w^{r+1}_k\right) \Vert \Vert x^{r+1}_k-x^{*}_k\Vert \right) ^2 \\&\mathop {\le }\limits ^\mathrm{(ii)}\left( \sum _{k=1}^{K}G_k\Vert x^{r+1}-w^{r+1}_k\Vert \Vert x^{r+1}_k-x^{*}_k\Vert \right) ^2 \\&\le R^2 K G^2_{\max }\Vert x^{r+1}-x^r\Vert ^2, \end{aligned}$$

where in \(\text{(i) }\) we have used the Cauchy–Schwarz inequality and the Lipschitz continuity of \(u_k(\cdot ;\cdot )\) in (2.8); in \(\text{(ii) }\) we have used the Lipschitz continuity of \(\nabla g(\cdot )\) in (2.7), and that \(\nabla _k g(x^{r+1})=\nabla u_k(x_k^{r+1}; x^{r+1})\) (cf. Assumption B(c)).

Next we show part (2) of the claim. Let us define an index set \(\{r_k\}\) as:

$$\begin{aligned} r_k:=\arg \max _t \{ x_k^{t}\ne x_k^{r+T} \}+1, \; k=1,\ldots , K. \end{aligned}$$
(3.14)

That is, \(r_k\) is the latest iteration index (up until \(r+T\)) in which the kth variable has been updated. From this definition we have \(x^{r_k}_k=x^{r+T}_k\), for all k. We have the following sequence of inequalities

where in \(\mathrm (i)\) we have used the fact that \(x^{r+T}_k=x_k^{r_k}\), for all k; in \(\mathrm (ii)\) we have used the optimality of \(x^{r_k}_k\). Taking the square on both sides, we obtain

$$\begin{aligned} (f(x^{r+T})-f(x^*))^2&\le \left( \sum _{k=1}^{K}\Vert \nabla _k g(x^{r+T})-\nabla u_k\left( x^{r_k}_k; w^{r_k}_{k}\right) \Vert \Vert x_k^{r+T}-x_k^*\Vert \right) ^2\\&\le \left( \sum _{k=1}^{K}G_k \Vert x^{r+T}-w^{r_k}_{k}\Vert \Vert x_k^{r+T}-x_k^*\Vert \right) ^2\\&\le \left( \sum _{k=1}^{K}G_k \left( \Vert x^{r+T}-x^{r_k}\Vert +\Vert x^{r_k}-w^{r_k}_{k}\Vert \right) \Vert x_k^{r+T}-x_k^*\Vert \right) ^2\\&\le T K G^2_{\max } R^2 \sum _{t=1}^{T}\Vert x^{r+t-1}-x^{r+t}\Vert ^2. \end{aligned}$$

Finally we show part (3). We have the following sequence of inequalities

(3.15)

where step \(\mathrm (i)\) follows from the Lipschitz continuity assumption (3.10) and the convexity of \(g(\cdot )\). Similar to the proof of (3.12) in part (1), we can show that

$$\begin{aligned} \sum _{k=1}^{K}\;\left\langle \nabla u_k\left( \hat{x}^{r+1}_k;x^r\right) , \hat{x}_k^{r+1}-x_k^*\right\rangle +h\left( \hat{x}^{r+1}\right) -h\left( x^*\right) \le 0. \end{aligned}$$
(3.16)

Moreover, it follows from Assumption B(c) and B(e) that

$$\begin{aligned}&\left( \sum _{k=1}^{K}\;\left\langle \nabla _k g(x^r)-\nabla u_k\left( \hat{x}^{r+1}_k;x^r\right) , x_k^{r+1}-x_k^*\right\rangle \right) ^2\nonumber \\&=\left( \sum _{k=1}^{K}\;\left\langle \nabla u_k\left( x^r_k; x^r\right) -\nabla u_k\left( \hat{x}^{r+1}_k;x^r\right) , x_k^{r+1}-x_k^*\right\rangle \right) ^2\nonumber \\&\le K\sum _{k=1}^{K}L^2_k\Vert x^r_k-\hat{x}^{r+1}_k\Vert ^2\Vert x_k^{r+1}-x_k^*\Vert ^2\nonumber \\&\le K L^2_{\max }\Vert x^r-\hat{x}^{r+1}\Vert ^2R^2. \end{aligned}$$
(3.17)

Putting the above three inequalities together, we have

$$\begin{aligned} (f(x^{r})-f(x^*))^2\le 2\left( \left( Q+L_h\right) ^2+KL^2_{\max }R^2\right) \Vert x^r-\hat{x}^{r+1}\Vert ^2. \end{aligned}$$
(3.18)

This completes the proof. \(\square \)

We are now ready to prove the \({\mathcal {O}}({1}/{r})\) iteration complexity for the BSUM algorithm when applied to problem (1.1). Our results below are more general than the recent analysis on the iteration complexity for BCD-type algorithms. The generality of our results can be seen from several fronts: (1) The family of algorithms we analyze is broad; it includes the classic BCM (with the additional BSC condition), the BCGD method, the BCPG methods as well as their variants based on different coordinate selection rules as special cases, while the existing works only focus on one particular algorithm; (2) When the coordinates are updated in a G–S fashion, our result covers the general multi-block nonsmooth case, where \(h_k(x)\) can take any proper closed convex nonsmooth function, while existing works only cover some special cases [1, 2, 26]; (3) When the coordinates are updated using other update rules such as G–So, MBI, E-C fashion, our convergence results appear to be new.

Theorem 1

Suppose Assumption A(a), B hold true. We have the following.

  1. 1.

    Let \(\{x^r\}\) be the sequence generated by the BSUM algorithm with G–S rule. Then we have

    $$\begin{aligned} \varDelta ^r=f(x^r)-f^*\le \frac{c_1}{\sigma _1}\frac{1}{r}, \; \forall ~r\ge 1, \end{aligned}$$
    (3.19)

    where the constants are given below

    $$\begin{aligned} {c}_1&=\max \{4\sigma _1-2, f(x^1)-f^*,2\}, \quad \sigma _1=\frac{\gamma }{KG^2_{\max }R^2}.\quad \end{aligned}$$
    (3.20)
  2. 2.

    Let \(\{x^r\}\) be the sequence generated by the BSUM algorithm with E-C rule. Then we have

    $$\begin{aligned} \varDelta ^r=f(x^r)-f^*\le \frac{c_2}{\sigma _2}\frac{1}{r-T}, \; \forall ~r>T, \end{aligned}$$
    (3.21)

    where the constants are given below

    $$\begin{aligned} {c}_2&=\max \{4\sigma _2-2, f(x^1)-f^*,2\}, \quad \sigma _2=\frac{\gamma }{ K {T} R^2 G^2_\mathrm{max}}. \end{aligned}$$
    (3.22)
  3. 3.

    Suppose the Lipschitz continuity assumption (3.10) holds true. Let \(\{\mathbf {x}^r\}\) be the sequence generated by BSUM with G–So and MBI rule. Then we have

    $$\begin{aligned} \varDelta ^r=f(x^r)-f^*\le \frac{1}{{\sigma }_3 r}, \end{aligned}$$
    (3.23)

    where

    $$\begin{aligned} {\sigma }_3=\left\{ \begin{array}{ll} \frac{{\gamma }q}{2K\left( \left( Q+L_h\right) ^2+L^2_\mathrm{max}KR^2\right) },\quad &{} \text{(G--So } \text{ rule) }\\ \frac{{\gamma }}{2K\left( \left( Q+L_h\right) ^2+L^2_\mathrm{max}KR^2\right) },\quad &{} \text{(MBI } \text{ rule) } \end{array}\right. . \end{aligned}$$
    (3.24)

Proof

We first show part (1) of the claim by mathematical induction on r. From Lemmas 1 and 2, we have that for the G–S rule, we have

$$\begin{aligned} \varDelta ^r-\varDelta ^{r+1}\ge \frac{\gamma }{K G^2_{\max }R^2}(\varDelta ^{r+1})^2:=\sigma _1 (\varDelta ^{r+1})^2, \; \forall ~r\ge 1, \end{aligned}$$
(3.25)

or equivalently

$$\begin{aligned} \sigma _1 (\varDelta ^{r+1})^2+\varDelta ^{r+1}\le \varDelta ^r, \ \forall \ r\ge 1. \end{aligned}$$
(3.26)

By definition, we have \(\varDelta ^1=f(x^1)-f^*\). We first argue that

$$\begin{aligned} \varDelta ^2\le \frac{{c}_1}{2\sigma _1},\ \text{ with }\; {c}_1:=\max \{4\sigma _1-2, f(\mathbf {x}^1)-f^*,2\}. \end{aligned}$$
(3.27)

From (3.26) and the fact that \(\varDelta ^1\le {c}_1\), we have

$$\begin{aligned} \varDelta ^2 \le \frac{-1+\sqrt{1+4\sigma _1 {c}_1}}{2\sigma _1}=\frac{2 {c}_1}{1+\sqrt{1+4\sigma _1 {c}_1}}\le \frac{2 {c}_1}{1+|4\sigma _1-1|}, \end{aligned}$$

where in the last inequality we have used the fact that \({c}_1\ge 4\sigma _1-2\). Suppose \(4\sigma _1-1\ge 0\), then we immediately have \(\varDelta ^2\le \frac{{c}_1}{2\sigma _1}\). Suppose \(4\sigma _1-1<0\), then

$$\begin{aligned} \varDelta ^2\le \frac{2{c}_1}{2-4\sigma _1}\le \frac{2{c}_1}{8\sigma _1-4\sigma _1}=\frac{{c}_1}{2\sigma _1}. \end{aligned}$$
(3.28)

Next we argue that if \(\varDelta ^r\le \frac{{c}_1}{r\sigma _1}\), then we must have

$$\begin{aligned} \varDelta ^{r+1}\le \frac{{c}_1}{(r+1)\sigma _1}. \end{aligned}$$
(3.29)

Using the condition (3.26) and the inductive hypothesis \(\varDelta ^r\le \frac{{c}_1}{r\sigma _1}\), we have

$$\begin{aligned} \varDelta ^{r+1}&\le \frac{-1+\sqrt{1+\frac{4{c}_1}{r}}}{2\sigma _1} =\frac{2{c}_1}{r\sigma _1\left( 1+\sqrt{1+\frac{4{c}_1}{r}}\right) }\nonumber \\&\le \frac{2{c}_1}{\sigma _1\left( r+\sqrt{r^2+4r+4}\right) }=\frac{{c}_1}{\sigma _1(r+1)}, \end{aligned}$$
(3.30)

where the last inequality is due to the fact that \({c}_1\ge 2\), and \(r\ge 2\). Consequently, we have shown that for all \(r\ge 1\)

$$\begin{aligned} \varDelta ^r=f(x^r)-f^*\le \frac{{c}_1}{\sigma _1}\frac{1}{r}. \end{aligned}$$
(3.31)

For the E-C rule, first note that from Lemma 1, we have

$$\begin{aligned} \varDelta ^r-\varDelta ^{r+T}\ge \frac{\gamma }{T K R^2 G^2_\mathrm{max}}(\varDelta ^{r+T})^2:=\sigma _2 (\varDelta ^{r+T})^2, \; \forall ~r\ge 1. \end{aligned}$$
(3.32)

Then using the similar argument as for the G–S rule, we can obtain the desired result.

Next we show part (3) of the claim. For the G–So rule, we have from Lemma 2, the second part of Lemma 1, that for all \(r\ge 1\)

$$\begin{aligned} \varDelta ^r-\varDelta ^{r+1}&\ge \frac{q}{K}{\gamma }\Vert \hat{x}^{r+1}-x^r\Vert ^2\ge \frac{{\gamma }q}{2K\left( \left( Q+L_h\right) ^2+L^2_\mathrm{max}KR^2\right) }(\varDelta ^{r})^2\nonumber \\&:={\sigma }_3 (\varDelta ^{r})^2. \end{aligned}$$
(3.33)

Similar relation can be shown for the MBI rule as well. The rest of the proof follows standard argument, see for example [22, Theorem 1]. \(\square \)

Below we provide further remarks on some special cases of BSUM.

  • One popular choice of the upper bound function \(u_k(\cdot ,\cdot )\) is [2, 12, 22, 33, 37]

    $$\begin{aligned} u_k(z_k; x):= g(x)+\left\langle \nabla _k g(x), z_k-x_k\right\rangle +\frac{L_k}{2}\Vert z_k-x_k\Vert ^2, \end{aligned}$$
    (3.34)

    where the constant \(L_k \ge \rho _{\max }(\nabla ^2 g(x))\), is often chosen to be largest eigenvalue of the Hessian of g(x). In this case, evidently we have \(\gamma _k=L_k=M_k\le M\), for all k, and \(G_{\max }\le M\). We can also verify that \(G_k\le 2M\) for all k. Using this choice of \(u_k(\cdot ;\cdot )\) and \(L_k\), the first result in Theorem 1 reduces to

    $$\begin{aligned} \varDelta ^r&\le 2\frac{{c}_1 KM^2R^2}{M_\mathrm{min}}\frac{1}{r}, \end{aligned}$$
    (3.35)

    where \(M_\mathrm{min}:=\min _{k}M_k\). Let us compare the order given in (3.35) with the one stated in [2, Theorem 6.1], which is the best known complexity bound for the G–S BCD algorithm for smooth problems (i.e., when \(h_k\) is not present). The bound derived in [2] for smooth constrained problem (resp. smooth unconstrained problem) is in the order of \(\frac{KM^2R^2}{M_{\min }}\frac{1}{r}\) (resp. \(\frac{M_{\max }K M^2 R^2}{M^2_{\min }}\frac{1}{r}\)). These orders are approximately the same as (3.35). However, our proof covers the general nonsmooth cases, and is simpler. Similarly, when \(u_k(\cdot ;\cdot )\) takes the form (3.34), the bounds for the BSUM with the E-C/G–So/MBI rules shown in Theorem 1 can also be simplified.

  • The results derived in Theorem 1 is equally applicable to the BCM scheme (1.2) with various block selection rules discussed above. In particular, we can specialize the upper-bound function \(u_k\) to be the original smooth function g. As long as \(g(x_1,\ldots ,x_K)\) satisfies the BSC property, Theorem 1 carries over. As mentioned in Sect. 2.2, the BSC property is fairly mild and is satisfied in many engineering applications. Nevertheless, we will further relax the BSC condition in the subsequent sections.

4 The BSUM for single block problems

4.1 The SUM algorithm

In this section, we consider the following single-block problem with \(K=1\):

$$\begin{aligned} \min&\quad f(x):=g(x)+h(x), \quad \mathrm{s.t.}\;\quad x\in X. \end{aligned}$$
(4.1)

In this case the BSUM algorithm reduces to to the so-called successive upper-bound minimization (SUM) algorithm [24], listed in the following table.

figure b

Let us make the following assumptions on the function u(v; x).

Assumption C

  1. (a)

    \(u(x; x)= g(x), \quad \forall \; x\in {X}.\)

  1. (b)

    \(u(v; x) \ge g(v),\quad \; \forall \; v \in {X}, \ \forall \; x \in {X}.\)

  2. (c)

    \(\nabla u(x;x)= \nabla g(x), \quad \; \forall \; x\in X\).

  3. (d)

    For any given x, u(v; x) is convex in v and satisfies the following

    $$\begin{aligned} \Vert \nabla u(v; x)-\nabla u(\hat{v}; x)\Vert \le L\Vert v-\hat{v}\Vert ,\ \forall \ \hat{v},\ v\in X, \forall ~x\in X, \end{aligned}$$
    (4.3)

    where \(L>0\) is some constant.

Compared to Assumptions B and C does not require u(v; x) to be strongly convex in v, nor \(\nabla u(v; x)\) to be Lipschitz continuous over x.

Proposition 1

Suppose g(x) is convex, and u(v; x) satisfies Assumption C. Then we must have

$$\begin{aligned} \Vert \nabla g(v)-\nabla g(x)\Vert \le L \Vert v-x\Vert ,\quad \forall ~x,v \in X. \end{aligned}$$
(4.4)

That is, \(\nabla g\) is Lipschitz continuous with the coefficient no larger than L.

Proof

Utilizing Assumption C, we must have

$$\begin{aligned} g(v)-g(x)&\le u(v; x) - u(x; x)\\&\le \langle \nabla u(x;x), v-x\rangle +\frac{L}{2}\Vert x-v\Vert ^2\\&= \langle \nabla g(x), v-x\rangle +\frac{L}{2}\Vert x-v\Vert ^2, \; \forall ~x, v\in X. \end{aligned}$$

Further, using the convexity of g we have

$$\begin{aligned} g(v)-g(x)\ge \langle \nabla g(x), v-x\rangle , \; \forall ~x, v\in X. \end{aligned}$$

Combining these two inequalities we obtain

$$\begin{aligned} 0\le g(v)-g(x)- \langle \nabla g(x), v-x\rangle \le \frac{L}{2}\Vert x-v\Vert ^2, \; \forall ~x, v\in X. \end{aligned}$$
(4.5)

Similar to [21, Theorem 2.1.5], we construct \(\phi (x) := g(x) - \langle \nabla g(v), x\rangle .\) Clearly \(v \in \arg \min \phi (x) \). We have

$$\begin{aligned} \phi (v)\le \phi \left( x-\frac{1}{L}\nabla \phi (x)\right) \le \phi (x)-\frac{1}{2L}\Vert \nabla \phi (x)\Vert ^2, \end{aligned}$$
(4.6)

where the first inequality is due to the optimality of v and the second inequality uses (4.5). Plugging in the definition of \(\phi (x)\) and \(\phi (v)\) we have

$$\begin{aligned} g(v)-\langle \nabla g(v), v\rangle \le g(x)-\langle \nabla g(v), x\rangle -\frac{1}{2L}\Vert \nabla g(v)-\nabla g(x)\Vert ^2. \end{aligned}$$

Since the above inequality is true for any \(x, v\in X\), we can interchange x and v and obtain

$$\begin{aligned} g(x)-\langle \nabla g(x), x\rangle \le g(v)-\langle \nabla g(x), v\rangle -\frac{1}{2L}\Vert \nabla g(v)-\nabla g(x)\Vert ^2. \end{aligned}$$

Adding these two inequalities we obtain

$$\begin{aligned} \frac{1}{L}\Vert \nabla g(x)-\nabla g(v)\Vert ^2\le \langle \nabla g(x)-\nabla g(v), x-v\rangle \le \Vert \nabla g(x)-\nabla g(v)\Vert \Vert x-v\Vert . \end{aligned}$$

Cancelling \(\Vert \nabla g(x)-\nabla g(v)\Vert \) we arrive at the desired results. \(\square \)

We remark that this result is only true when \(g(\cdot )\) is a convex function.

Our main result is that the SUM algorithm converges sublinearly under Assumption C, without the strong convexity of the upper-bound function u(v; x) in v. The proof of this claim is an extension of Theorem 1, therefore we will only provide its key steps. Observe that the following is true

$$\begin{aligned}&f(x^r) - f(x^{r+1})\mathop {\ge }\limits ^\mathrm{(i)}f(x^r) - \left( u(x^{r+1}; x^r)+h(x^{r+1})\right) \nonumber \\&\quad \mathop {\ge }\limits ^\mathrm{(ii)}f(x^r) - \left( u(\widetilde{x}^{r+1}; x^r)+h(\widetilde{x}^{r+1})\right) \mathop {\ge }\limits ^\mathrm{(iii)}\frac{\gamma }{2}\Vert x^r- \widetilde{x}^{r+1}\Vert ^2, \end{aligned}$$
(4.7)

where \(\widetilde{x}^{r+1}\) is obtained by solving the following problem for any \(\gamma >0\)

$$\begin{aligned} \widetilde{x}^{r+1}=\arg \min _{x\in X} u(x; x^r)+h(x)+\frac{\gamma }{2}\Vert x-x^r\Vert ^2. \end{aligned}$$
(4.8)

In (4.7), \(\mathrm {(i)}\) is true because u(x; y) is an upper-bound function for g(x) satisfying Assumption C(b); \(\mathrm {(ii)}\) is true because \(x^{r+1}\) is a minimizer of problem (4.2); \(\mathrm {(iii)}\) is true due to the fact that \(\widetilde{x}^{r+1}\) is the optimal solution of (4.8) while \(x^r\) is a feasible solution.

Then we bound \(f(x^{r+1})\) using \(f(\widetilde{x}^{r+1})\). We have

$$\begin{aligned} f(x^{r+1})&\le u(x^{r+1};x^r)+ h(x^{r+1})\mathop {\le }\limits ^\mathrm{(i)}u(\widetilde{x}^{r+1};x^r)+ h(\widetilde{x}^{r+1}) \\&\mathop {\le }\limits ^\mathrm{(ii)}u(x^{r};x^r)+\left\langle \nabla u(x^r; x^r), \widetilde{x}^{r+1}-x^r \right\rangle +\frac{L}{2}\Vert \widetilde{x}^{r+1}-x^r\Vert ^2 + h(\widetilde{x}^{r+1}) \\&\mathop {\le }\limits ^\mathrm{(iii)}g(\widetilde{x}^{r+1})+\left\langle \nabla u(x^r; x^r), \widetilde{x}^{r+1}-x^r \right\rangle +\left\langle \nabla g(\widetilde{x}^{r+1}), x^{r}-\widetilde{x}^{r+1} \right\rangle \\&\quad +{L}\Vert \widetilde{x}^{r+1}-x^r\Vert ^2 + h(\widetilde{x}^{r+1}) \\&\mathop {=}\limits ^\mathrm{(iv)} g(\widetilde{x}^{r+1})+\left\langle \nabla g(\widetilde{x}^{r+1})-\nabla g(x^r), x^{r}-\widetilde{x}^{r+1} \right\rangle \\&\quad +{L}\Vert \widetilde{x}^{r+1}-x^r\Vert ^2 + h(\widetilde{x}^{r+1}) \\&\mathop {\le }\limits ^\mathrm{(v)}f(\widetilde{x}^{r+1}) +{L}\Vert \widetilde{x}^{r+1}-x^r\Vert ^2, \end{aligned}$$

where \(\mathrm (i)\) is due to the optimality of \(x^{r+1}\) for problem (4.2); \(\mathrm (ii)\) uses the gradient Lipschitz continuity of \(u(\cdot ; x^r)\); \(\mathrm (iii)\) uses the fact that \(u(x^r;x^r) = g(x^r)\), the gradient Lipschitz continuity of \(g(\cdot )\) derived in Proposition 1; \(\mathrm {(iv)}\) uses the fact that \(\nabla u(x^r; x^r) = \nabla g(x^r)\) (cf. Assumption C(c)); \(\mathrm (v)\) uses the convexity of \(g(\cdot )\).

Utilizing this bound, we derive the estimate of the cost-to-go

$$\begin{aligned} f(x^{r+1})-f(x^*)&\le f(\widetilde{x}^{r+1})-f(x^*)+{L}\Vert \widetilde{x}^{r+1}-x^r\Vert ^2\\&\le \left\langle \nabla g(\widetilde{x}^{r+1}), \widetilde{x}^{r+1}-x^*\right\rangle +h(\widetilde{x}^{r+1})-h(x^*)+{L}\Vert \widetilde{x}^{r+1}-x^r\Vert ^2\\&= \left\langle \nabla g(\widetilde{x}^{r+1})- \nabla g(x^r), \widetilde{x}^{r+1}-x^*\right\rangle +{L}\Vert \widetilde{x}^{r+1}-x^r\Vert ^2 \\&\quad +\left\langle \nabla g(x^{r})- \nabla \left( u(\widetilde{x}^{r+1}; x^r)+\frac{\gamma }{2}\Vert \widetilde{x}^{r+1}-x^r\Vert ^2\right) , \widetilde{x}^{r+1}-x^*\right\rangle \\&\quad +h(\widetilde{x}^{r+1})-h(x^*)\\&\quad +\left\langle \nabla \left( u(\widetilde{x}^{r+1}; x^r)+\frac{\gamma }{2}\Vert \widetilde{x}^{r+1}-x^r\Vert ^2\right) , \widetilde{x}^{r+1}-x^*\right\rangle \\&\mathop {\le }\limits ^\mathrm{(i)}\left\langle \nabla g(\widetilde{x}^{r+1})- \nabla g(x^r), \widetilde{x}^{r+1}-x^*\right\rangle +{L}\Vert \widetilde{x}^{r+1}-x^r\Vert ^2\\&\quad +\left\langle \nabla u(x^{r}; x^{r})- \nabla u(\widetilde{x}^{r+1}; x^r), \widetilde{x}^{r+1}-x^*\right\rangle \\&\quad - \gamma \left\langle \widetilde{x}^{r+1}-x^r, \widetilde{x}^{r+1}-x^*\right\rangle \\&\mathop {\le }\limits ^\mathrm{(ii)}(2L+\gamma )\Vert \widetilde{x}^{r+1}-x^r\Vert R +{L}\Vert \widetilde{x}^{r+1}-x^r\Vert \Vert \widetilde{x}^{r+1}-x^*+x^*-x^r\Vert \\&\le (4L+\gamma )\Vert \widetilde{x}^{r+1}-x^r\Vert R . \end{aligned}$$

Here \(\mathrm {(i)}\) is due to the optimality of \(\widetilde{x}^{r+1}\) to the problem (4.8); in \(\mathrm {(ii)}\) we have used (4.4), Cauchy–Schwartz inequality and the definition of R (it is easy to show that \(f(\widetilde{x}^{r+1})\le f(x^r)\le f(x^0)\), hence \(\Vert \widetilde{x}^{r+1}-x^*\Vert \le R\) for all r).

Combining the above two inequalities, we obtain

$$\begin{aligned} \varDelta ^{r}-\varDelta ^{r+1}\ge \frac{\gamma }{2R^2 (4L+\gamma )^2}(\varDelta ^{r+1})^2,\quad \forall \gamma >0. \end{aligned}$$
(4.9)

Maximizing over \(\gamma \) (with \(\gamma =4L\)), we have

$$\begin{aligned} \varDelta ^{r}-\varDelta ^{r+1}\ge \frac{1}{32R^2 L}(\varDelta ^{r+1})^2:=\sigma _4(\varDelta ^{r+1})^2. \end{aligned}$$
(4.10)

Using the same derivation as in Theorem 1, we obtain

$$\begin{aligned} \varDelta ^{r+1}\le \frac{c_4}{\sigma _4}\frac{1}{r}, \quad \text{ with }\quad \sigma _4=\frac{1}{32R^2 L},\quad c_4:=\max \{4 \sigma _4-2, f(x^1)-f^*, 2\}. \end{aligned}$$
(4.11)

4.2 Application

To see the importance of the above result, consider the well-known method of iterative reweighted least squares (IRLS) [1, 9]. The IRLS is a popular algorithm used for solving problems such as sparse recovery and Fermat-Weber problem; see [1, Section 4] for applications. Consider the following problem

$$\begin{aligned} \min _{x}&\quad h(x) + \sum _{j=1}^{\ell }\Vert A_j x + b_j\Vert _2,\quad \mathrm{s.t.}\quad x\in X , \end{aligned}$$
(4.12)

where \(A_j\in \mathbb {R}^{k_i\times m}\), \(b_j\in \mathbb {R}^{k_i}\), \(X\subseteq \mathbb {R}^m\), and h(x) is some convex function not necessarily smooth. Let us introduce a constant \(\eta >0\) and consider a smooth approximation of problem (4.12):

$$\begin{aligned} \min _{x}&\quad h(x)+g(x): = h(x) + \sum _{j=1}^{\ell }\sqrt{\Vert A_j x + b_j\Vert ^2_2+\eta ^2},\quad \mathrm{s.t.}\quad x\in X . \end{aligned}$$
(4.13)

The IRLS algorithm generates the following iterates

$$\begin{aligned} x^{r+1}=\arg \min _{x\in X }\left\{ h(x)+\frac{1}{2}\sum _{j=1}^{\ell }\frac{\Vert A_j x+b_j\Vert ^2+\eta ^2}{\sqrt{\Vert A_j x^r+b_j\Vert ^2+\eta ^2}}\right\} . \end{aligned}$$
(4.14)

It is known that the IRLS is equivalent to a BCM method applied to the following two-block problem (i.e., the first block is x and the second is \(\{z_j\}_{j=1}^{\ell }\))

$$\begin{aligned} \min&\quad h(x)+\frac{1}{2}\sum _{j=1}^{\ell }\left( \frac{\Vert A_j x+b_j\Vert ^2+\eta ^2}{z_j}+z_j\right) \nonumber \\ \mathrm{s.t.}&\quad x\in X,\quad z_j\in [\eta /2,\infty ), \ \forall ~j. \end{aligned}$$
(4.15)

Utilizing such two-block BCM interpretation, the author of [1] shows that the IRLS converges sublinearly when h(x) has Lipschitz continuous gradient; see [1, Theorem 4.1].

Differently from [1], here we take a new perspective. We argue that the IRLS is in fact the SUM algorithm in disguise, therefore our simple iteration complexity analysis given in Sect. 4.1 for SUM can be directly applied.

Let us consider the following function:

$$\begin{aligned} u(x; x^r) = \frac{1}{2}\sum _{j=1}^{\ell }\left( \frac{\Vert A_j x+b_j\Vert ^2+\eta ^2}{\sqrt{\Vert A_j x^r+b_j\Vert ^2+\eta ^2}}+\sqrt{\Vert A_j x^r+b_j\Vert ^2+\eta ^2}\right) . \end{aligned}$$
(4.16)

It is clear that \(g(x^r) = u(x^r; x^r)\), so Assumption C(a) is satisfied. To verify Assumption C(b), we apply the arithmetic-geometric inequality, and have

$$\begin{aligned} u(x; x^r)&= \frac{1}{2}\sum _{j=1}^{\ell }\left( \frac{\Vert A_j x+b_j\Vert ^2+\eta ^2}{\sqrt{\Vert A_j x^r+b_j\Vert ^2+\eta ^2}}+\sqrt{\Vert A_j x^r+b_j\Vert ^2+\eta ^2}\right) \\&\ge \sum _{j=1}^{\ell }\sqrt{\Vert A_j x+b_j\Vert ^2+\eta ^2} = g(x), \; \forall ~x\in X. \end{aligned}$$

Assumptions C(c), (d) are also easy to verify. Note that the matrices \(A_j\)’s do not necessarily have full column rank, so \(u(x;x^r)\) may not be strongly convex over \(x\in X\). Nevertheless, \(u(x;x^r)\) defined in (4.16) is indeed an upper bound function for the smooth function g(x), and we have shown that it satisfies Assumptions C. It follows that the iteration (4.14) corresponds to a single-block BSUM algorithm. Our analysis leading to (4.11) suggests that this algorithm converges in a sublinear rate, even when h(x) is a nonsmooth function. To be more specific, for this problem we have

$$\begin{aligned} L=\frac{1}{\eta }\rho _{\max }\left( \sum _{j=1}^{\ell }A^T_j A_j\right) . \end{aligned}$$

Therefore the rate can be expressed as

$$\begin{aligned} \varDelta ^{r+1}\le \max \{4 \sigma _4-2, f(x^1)-f(x^*), 2\}\frac{ 32 R^2 \rho _{\max }\left( \sum _{j=1}^{\ell }A^T_j A_j\right) }{\eta r}. \end{aligned}$$
(4.17)

Note that compared with the result derived in [1, Theorem 4.1] which is based on transforming the IRLS algorithm to the two-block BCM problem (4.15), our analysis is based on the key insight of the equivalence between IRLS and the single block BSUM, and it is significantly simpler. Further we do not require h(x) to be smooth, while the result in [1, Theorem 4.1] additionally requires that the gradient of h(x) is Lipschitz continuous.Footnote 2

5 The BSUM for two block problems

5.1 Iteration complexity for 2-block BSUM

In this section, we consider the following two-block problem (\(K=2\)), which is a special case of problem (1.1):

$$\begin{aligned} \min&\quad f(x_1,x_2):=g(x_1,x_2)+h_1(x_1)+h_2(x_2)\nonumber \\ \mathrm{s.t.}&\quad x_1\in X_1, \ x_2\in X_2. \end{aligned}$$
(5.1)

This problem has many applications, such as the special case of Example 1 with two users, the two-block formulation of the IRLS algorithm (4.15) or the example presented in [1, Section 5]. Throughout this section, we assume that Assumption A(a) is true. We make the following additional assumptions about problem (5.1).

Assumption D

  1. (a)

    The problem \(\min _{x_2\in X_2} f(x_1, x_2)\) has a unique solution.

  2. (b)

    The gradient of \(g(x_1,x_2)\) with respect to \(x_1\) is Lipschitz continuous, i.e.,

    $$\begin{aligned} \Vert \nabla _1 g(x_1, x_2)-\nabla _1 g(v_1, x_2)\Vert \le M_1\Vert x_1-v_1\Vert . \end{aligned}$$

Note that here we do not require that the gradient of \(g(\cdot )\) with respect to the second block to be Lipschitz continuous.

We show that for this problem BSUM with G–S update rule is able to achieve sublinear rate without the BSC condition or the Lipschitz continuity of \(\nabla _2 g(x_1,x_2)\). In the table given below we list the two-block BSUM algorithm with G–S update rule.

figure c

Unfortunately for the problem of interest here the rate analysis provided in Theorem 1 is no longer applicable because \(\nabla _2 g(x_1,x_2)\) may not be Lipschitz continuous, and both subproblems may not be strongly convex. To analyze the convergence rate, let us consider the following special choices of the upper bound where \(u_1(x_1; x)\) satisfies Assumption B(a)–(c) and the Lipschtiz continuous gradient condition (2.8), restated below for convenience

$$\begin{aligned} \Vert \nabla u_1(x_1; x)-\nabla u_1(v_1; x)\Vert \le L_1\Vert x_1-v_1\Vert , \; \forall ~x_1, v_1\in X_1, \ \forall ~x\in X. \end{aligned}$$
(5.3)

By utilizing the argument in Proposition 1, we can show that \(L_1\ge M_1\), and therefore the following is true as well

$$\begin{aligned} \Vert \nabla _1 g(x_1, x_2)-\nabla _1 g(v_1, x_2)\Vert \le L_1\Vert x_1-v_1\Vert . \end{aligned}$$

Further we do not use any upper bound for the second block, i.e., we let

$$\begin{aligned} u_2(v_2; x)=g(v_2,x_1), \; \forall ~x_1\in X_1, \ v_2\in X_2. \end{aligned}$$

This suggests that the \(x_2\)-block is minimized exactly.

To analyze the algorithm, it is convenient to consider an equivalent single-block problem, which only takes \(x_1\) as its variable:

$$\begin{aligned} \min _{x_1\in X_1}&\quad \ell (x_1)+h_1(x_1):=\min _{x_1\in X_1}\min _{x_2\in {X}_2}{f}(x_1, x_2), \end{aligned}$$
(5.4)

where we have defined \(\ell (x_1):=\min _{x_2\in X_2} g(x_1,x_2)+h_2(x_2)\). Let us denote an optimal solution of the inner problem \(\min _{x_2\in {X}_2}{f}(x_1, x_2)\) by the mapping: \(x^*_2(x_1): X_1\rightarrow X_2\), which is a singleton for any \(x_1\in X_1\) by Assumption D(a). Next we analyze problem (5.4).

Let us define a new function

$$\begin{aligned} u(v_1; x_1):=u_1\left( v_1; x_1, x^*_2(x_1)\right) +h_2\left( x^*_2(x_1)\right) . \end{aligned}$$
(5.5)

First we argue that for all \(x_1,v_1\in X_1\), \(u(v_1;x_1)\) is an upper bound for \(\ell (v_1)\), and it satisfies Assumption C given in Sect. 4.1. Clearly Assumption C(a) is true because

$$\begin{aligned} \ell (x_1)&=g\left( x_1,x_2^*(x_1)\right) +h_2\left( x^*_2(x_1)\right) \nonumber \\&= u_1\left( x_1; x_1, x^*_2(x_1)\right) +h_2\left( x^*_2(x_1)\right) =u(x_1; x_1) \end{aligned}$$
(5.6)

where the second equality is due to the fact that \(u_1(x_1; x)\) is an upper bound function for \(g(\cdot , x_2)\). The last equality is from the definition of \(u(\cdot ;\cdot )\).

Assumption C(b) is true because

$$\begin{aligned} u(v_1 ;x_1)= & {} u_1\left( v_1; x_1, x^*_2(x_1)\right) +h_2\left( x^*_2(x_1)\right) \nonumber \\\ge & {} g\left( v_1, x^*_2(x_1)\right) +h_2\left( x^*_2(x_1)\right) \ge \min _{x_2}g(v_1,x_2)+h_2(x_2). \end{aligned}$$
(5.7)

To verify Assumption C(c), recall that by Assumption D, \(\min _{x_2\in {X}_2}{f}(x_1, x_2)\) has a unique solution, or equivalently for any given \(x_1\in X_1\), the mapping \(x^*_2(x_1)\) is a singleton. By applying [13, Corollary 4.5.2–4.5.3], we obtain

$$\begin{aligned} \nabla \ell (x_1)=\nabla _1 g\left( x_1, \widetilde{x}_2\right) , \; \forall ~x_1\in X_1, \end{aligned}$$
(5.8)

where \(\widetilde{x}_2=\arg \min _{x_2\in X_2} f(x_1,x_2)\). Therefore, we must have

$$\begin{aligned} \nabla \ell (x_1) = \nabla _1 g\left( x_1, \widetilde{x}_2\right) = \nabla u_1(x_1; x_1, \widetilde{x}_2)= \nabla u_1\left( x_1; x_1, x^*_2(x_1)\right) =\nabla u(x_1;x_1), \end{aligned}$$

where the second equality comes from the fact that \(u_1(\cdot ; \cdot )\) satisfies Assumption B(c); the third inequality is because \(\widetilde{x}_2=x^*_2(x_1)\) by definition; the last equality is from (5.9). This verifies Assumption C(c).

The Lipschitz continuous gradient condition (with constant \(L_1\)) in Assumption C(d) can be verified by combining (5.3) and the following equality

$$\begin{aligned} \nabla u_1\left( v_1; x_1, x^*_2(x_1)\right) =\nabla u(v_1;x_1),\; \forall ~v_1, x_1\in X_1. \end{aligned}$$
(5.9)

Now that we have verified that \(u(v_1; x_1)\) given in (5.5) satisfies Assumption C, then Proposition 1 implies \(\ell (\cdot )\) also has Lipschitz continuous gradient with constant \(L_1\), that is

$$\begin{aligned} \Vert \nabla \ell (x_1)-\nabla \ell (v_1)\Vert \le L_1\Vert x_1-v_1\Vert ,\; \forall ~v_1, x_1\in X. \end{aligned}$$

At this point it is clear that the 2-block BSUM algorithm with G–S update rule is in fact the SUM algorithm given in Sect. 4.1, where the iterates are generated by

$$\begin{aligned} x^{r+1}_1\in \arg \min u\left( x_1; x^r_1\right) . \end{aligned}$$
(5.10)

By applying the argument leading to (4.11), we conclude that the 2-block BSUM in which the second block performs an exact minimization converges sublinearly. Also note that neither subproblems in (5.1) is required to be strongly convex, which suggests that the BCM applied to problem (5.1) converges sublinearly without block strong convexity. The precise statement is given in the following corollary.

Corollary 1

Assume that Assumption A(a) and D hold for problem (5.1). Then we have the following.

  1. 1.

    Suppose that \(u_2(v_2; x)=g(x_1,v_2)\) for all \(v_2\in X_2, \ x\in X\) and that \(u_1(v_1; x)\) satisfies Assumption B(a)–(c) and the Lipschtiz continuous gradient condition (2.8). Then the 2-block BSUM algorithm with G–S rule is equivalent to the SUM algorithm and converges sublinearly, i.e.,

    $$\begin{aligned} \varDelta ^{r+1}\le \frac{c_4}{\sigma _4}\frac{1}{r}, \end{aligned}$$
    (5.11)

    where \(c_4\) and \(\sigma _4\) is given in (4.11), with L in (4.11) replaced by \(L_1\).

  2. 2.

    The BCM algorithm applied to (5.1) converges sublinearly with the same rate, again with L in (4.11) replaced by \(L_1\).

To conclude this section, we note that the schemes and analysis developed in this section are special in the sense that they heavily rely on the fact that \(K=2\), and the resulting transformation to the single block problem. At this point, it is unclear whether the same \({\mathcal {O}}(1/r)\) iteration complexity holds for a general K without the BSC condition. In the next section we will address the first issue and show that without BSC one can still achieve \({\mathcal {O}}(1/r)\) complexity.

6 Analysis of the BCM without per-block strong convexity

In this section, we consider the BCM algorithm below, which is the BSUM algorithm without using approximation for each block. We analyze its iteration complexity without the BSC assumption.

figure d

In the absence of the BSC property, there can be multiple optimal solutions for each subproblem. This makes it tricky to establish the convergence rate of BCM. Specifically, in the context of the three-step analysis framework presented herein, it is difficult to bound the sufficient descent of the objective using the size of of the successive iterates (as per Lemma 1). In this section, we overcome this obstacle by developing a variant of the sufficient descent estimate step. We will show that BCM with MBI, G–S and E-C rules has an iteration complexity of O(1 / r) for problem (1.1) without the BSC condition. Throughout this section we will impose Assumption A.

We first consider the MBI rule. We notice that the following is true

$$\begin{aligned} f(x^{r})-f(x^{r+1})\mathop {\ge }\limits ^\mathrm{(i)}f(x^r)-f(\bar{x}^{r+1})\mathop {\ge }\limits ^\mathrm{(ii)}\frac{\gamma }{K}\Vert x^r-\hat{x}^{r+1}\Vert ^2, \end{aligned}$$
(6.1)

where \(\bar{x}^{r+1}\) is the iterates obtained by any BSUM algorithm with MBI rule; \(\hat{x}^{r+1}\) is defined in (2.2). In the above expression \(\mathrm (ii)\) can be obtained using Lemma 1, while \(\mathrm (i)\) is true because we used the exact minimization in each step. Then it is straightforward to establish, using the additional assumption that h is Lipschitz continuous, the same rate stated in part (3) of Theorem 1.

Next we show that the BCM algorithm with the G–S and E-C rules also achieves an \({\mathcal {O}}(1/r)\) iteration complexity, without the BSC assumption. These are the key results of this section.

The main difficulty in analyzing the BCM without the BSC is that the size of the difference of the successive iterates is no longer a good measure of the “sufficient descent”. Indeed, due to the lack of per-block strong convexity, it is possible that a block variable travels a long distance without changing the objective value (e.g., it stays in the per-block optimal solution set).

Below we analyze the iteration complexity of BCM. We need to make use of the following key inequality due to Nesterov [21]; also see (4.5) for a proof. From Assumption A we know that g is convex and has Lipschitz continuous gradient with constant M, then we must have

$$\begin{aligned} g(x)-g(v)\ge \langle \nabla g(v), x-v \rangle +\frac{1}{2M}\Vert \nabla g(v)-\nabla g(x)\Vert ^2, \; \forall ~v,x\in X. \end{aligned}$$
(6.2)

Utilizing this inequality, the sufficient descent estimate is given by the following lemma.

Lemma 3

Suppose Assumption A holds. Then for BCM with either G–S rule or the E-C rule, we have that for all \(r\ge 1\)

$$\begin{aligned} \varDelta ^r - \varDelta ^{r+1} \ge \frac{1}{2M}\sum _{k=1}^K \Vert \nabla g\left( w_k^{r+1}\right) - \nabla g\left( w_{k+1}^{r+1}\right) \Vert ^2. \end{aligned}$$
(6.3)

Proof

Suppose that \(k\notin {{\mathcal {C}}}^{r+1}\), then we have the following trivial inequality

$$\begin{aligned} f\left( w_k^{r+1}\right) - f\left( w_{k+1}^{r+1}\right) \ge \frac{1}{2M} \Vert \nabla g\left( w^{r+1}_k\right) -\nabla g\left( w^{r+1}_{k+1}\right) \Vert ^2 \end{aligned}$$
(6.4)

as both sides of the inequality are zero.

Suppose \(k\in {{\mathcal {C}}}^{r+1}\). Then by (6.2), we have that

$$\begin{aligned}&f\left( w^{r+1}_{k}\right) -f\left( w^{r+1}_{k+1}\right) \nonumber \\&\quad \ge \left\langle \nabla g\left( w^{r+1}_{k+1}\right) , w^{r+1}_{k}- w^{r+1}_{k+1}\right\rangle +h_k\left( w_k^{r+1}\right) -h_k\left( w_{k+1}^{r+1}\right) \nonumber \\&\quad \quad +\frac{1}{2M}\Vert \nabla g\left( w^{r+1}_k\right) -\nabla g\left( w^{r+1}_{k+1}\right) \Vert ^2\nonumber \\&\quad \mathop {\ge }\limits ^\mathrm{(i)}\langle \nabla _k g\left( w^{r+1}_{k+1}\right) , x^{r}_{k}- x^{r+1}_k\rangle +h_k\left( x_k^{r}\right) -h_k\left( x_k^{r+1}\right) \nonumber \\&\qquad +\frac{1}{2M}\Vert \nabla g\left( w^{r+1}_k\right) -\nabla g\left( w^{r+1}_{k+1}\right) \Vert ^2\nonumber \\&\quad \mathop {\ge }\limits ^\mathrm{(ii)}\frac{1}{2M}\Vert \nabla g\left( w^{r+1}_k\right) -\nabla g\left( w^{r+1}_{k+1}\right) \Vert ^2, \end{aligned}$$
(6.5)

where \(\mathrm {(i)}\) is because \(w^{r+1}_{k+1}\) and \(w^{r+1}_k\) only differs by a single block; \(\mathrm {(ii)}\) is due to the optimality of \(x^{r+1}_{k}\). Summing over k, we have

$$\begin{aligned} f(x^r)-f(x^{r+1}) \ge \sum _{k=1}^K \frac{1}{2M}\Vert \nabla g\left( w_k^{r+1}\right) - \nabla g\left( w_{k+1}^{r+1}\right) \Vert ^2. \end{aligned}$$
(6.6)

This completes the proof of this lemma. \(\square \)

Lemma 4

Suppose Assumptions A is satisfied. Then

  1. 1.

    For the BCM with the G–S update rule, we have

    $$\begin{aligned} (\varDelta ^{r+1})^2 \le 2 K^2 R^2 \sum _{k=1}^{K}\Vert \nabla g\left( w_{k+1}^{r+1}\right) -\nabla g\left( w^{r+1}_{k}\right) \Vert ^2, \; \forall x^*\; \in X^*. \end{aligned}$$
  2. 2.

    For the BCM with the period-T E-C update rule, we have

    $$\begin{aligned} (\varDelta ^{r+T})^2 \le 2 T K^2 R^2 \sum _{k=1}^{K}\sum _{t=1}^{T}\Vert \nabla g\left( w_{k+1}^{r+t}\right) -\nabla g\left( w^{r+t}_{k}\right) \Vert ^2, \; \forall \; x^* \in X^*. \end{aligned}$$

Proof

We only show the second part of the claim, as the proof for the first part is simply a special case. Define a new index set \(\{r_k\}\) as in (3.14). Recall that we have \(x_k^{r_k} = x_k^{r+T}\), for all k. We have the following series of inequalities

where in \(\mathrm{(i)}\) we have used the optimality of \(x_k^{r_k}\) and \(x_k^{r_k} = x_k^{r+T}\), for all k. Then taking the square on both sides, we obtain

$$\begin{aligned}&\left( f(x^{r+T})-f(x^*) \right) ^2 {{\le T K^2 R^2 \sum _{t=1}^T \sum _{k=1}^K \Vert \nabla g\left( w_{k+1}^{r+t}\right) -\nabla g\left( w_k^{r+t}\right) \Vert ^2}}. \end{aligned}$$
(6.7)

The proof is complete. \(\square \)

Combining these two results, and utilizing the technique in Theorem 1, we readily have the following main result for BCM.

Theorem 2

Suppose Assumption A holds true. We have the following.

  1. 1.

    Let \(\{x^r\}\) be the sequence generated by BCM with G–S rule. Then we have

    $$\begin{aligned} \varDelta ^r=f(x^r)-f^*\le \frac{c_5}{\sigma _5}\frac{1}{r}, \; \forall ~r\ge 1, \end{aligned}$$
    (6.8)

    where the constants are given below

    $$\begin{aligned} {c}_5&=\max \{4\sigma _5-2, f(x^1)-f^*,2\}, \quad \sigma _5=\frac{1}{2MK^2R^2},\quad \end{aligned}$$
    (6.9)
  2. 2.

    Let \(\{x^r\}\) be the sequence generated by BCM with E-C rule. Then we have

    $$\begin{aligned} \varDelta ^r=f(x^r)-f^*\le \frac{c_6}{\sigma _6}\frac{1}{r-T}, \; \forall ~r>T, \end{aligned}$$
    (6.10)

    where the constants are given below

    $$\begin{aligned} {c}_6&=\max \{4\sigma _6-2, f(x^1)-f^*,2\}, \quad \sigma _6=\frac{1}{ 2 K^2 T R^2 M}. \end{aligned}$$
    (6.11)

Remark 1

Our analysis above implies that when using the BCM (or equivalently the IWFA algorithm [35]) to solve the rate optimization problem given in Example 1, a sublinear rate can be obtained regardless of the rank of the channel matrices \(\{H_k\}\). In fact, it is easy to check that Assumption A is satisfied for this problem; see for example a related discussion in [27, Section V-A]. Then Theorem 2 implies that IWFA converges in a rate O(1 / r), regardless of the rank of the channel matrices. Prior to our work, no convergence rate analysis has been done for the IWFA when solving problem (2.13).

7 Discussion and concluding remarks

In this paper we have analyzed the iteration complexity of a family of BCD-type algorithms for solving general convex nonsmooth problems of the form (1.1). Using a three-step argument, we show that the family of BCD-type algorithms, which includes BCM, BCGD, BCPG algorithms with G–S, E-C, G–So and MBI update rules, converges globally in a sublinear rate of \({\mathcal {O}}(1/r)\). It should be noted that in case of the classical BCM algorithm, the sublinear rate can be achieved even without the per-block strong convexity.

We note that the structure of the three-step approach, i.e., estimate the sufficient descent, estimate the cost-to-go and obtain the rate of convergence, is not new. For example Luo and Tseng in [18] has developed a three-step argument for proving linear convergence rate of certain descent method (including BCD) for certain non-strongly convex problems. Beck and Tetruashvili [2] has used such argument for showing sublinear convergence for using cyclic BCPG to solve smooth constrained problem. However it is important to note that these works differ significantly in how each step is proved. For example, the proof of cost-to-go in Lemma 2 differs from its counterpart in [2] and [18] because we have to take into consideration the nonsmooth function \(h_k\)’s, as well as various different update rules. The proof of both sufficient descent and cost-to-go steps in Lemmas 3–4 differ from those in [2, 18], because without per-block strong convexity a different measure is used to show sufficient descent, which to the best of our knowledge has not been used in any related analysis before.

As a future work, it will be interesting to see whether the three-step approach can be extended to establish the iteration complexity bounds for other first order methods. Also we will investigate whether the problem dependent constants in front of the 1 / r can be further reduced, or even be made independent of problem dimension K.