Exact augmented Lagrangian duality for mixed integer linear programming

Abstract

We investigate the augmented Lagrangian dual (ALD) for mixed integer linear programming (MIP) problems. ALD modifies the classical Lagrangian dual by appending a nonlinear penalty function on the violation of the dualized constraints in order to reduce the duality gap. We first provide a primal characterization for ALD for MIPs and prove that ALD is able to asymptotically achieve zero duality gap when the weight on the penalty function is allowed to go to infinity. This provides an alternative characterization and proof of a recent result in Boland and Eberhard (Math Program 150(2):491–509, 2015, Proposition 3). We further show that, under some mild conditions, ALD using any norm as the augmenting function is able to close the duality gap of an MIP with a finite penalty coefficient. This generalizes the result in Boland and Eberhard (2015, Corollary 1) from pure integer programming problems with bounded feasible region to general MIPs. We also present an example where ALD with a quadratic augmenting function is not able to close the duality gap for any finite penalty coefficient.

1 Introduction

We consider the general mixed integer (linear) programming (MIP) problem

$$\begin{aligned} z^\text {IP}:=\inf \{ \varvec{c}^\top \varvec{x} \; | \; \varvec{Ax}=\varvec{b}, \varvec{x}\in X\}, \end{aligned}$$

(1)

and its augmented Lagrangian dual (ALD)

$$\begin{aligned} z^\text {LD+}_\rho :=\sup \limits _{\varvec{\lambda }\in \mathbb {R}^n} \inf \limits _{\varvec{x}\in X} \{\varvec{c}^\top \varvec{x} + \varvec{ \lambda }^\top ( \varvec{b}-\varvec{Ax}) + \rho \psi (\varvec{b}-\varvec{Ax})\}, \end{aligned}$$

where X is a mixed integer linear set, $\rho$ is a given positive scalar, and $\psi (\cdot )$ is an augmenting function with $\psi (\varvec{0})=0$ and $\psi (\varvec{u})>0$ for all $\varvec{u}\ne \varvec{0}$. Here, $\varvec{Ax}=\varvec{b}$ are the complicating constraints, and relaxing these makes the remaining problem easier.

In contrast to the convex setting, for nonconvex optimization problems, a non-zero duality gap may exist when certain constraints are relaxed by using classical Lagrangian dual (LD). ALD modifies classical LD by appending a nonlinear penalty on the violation of the dualized constraints. The resulting ALD problem then involves dual functions which are not necessarily affine as in LD, and may be capable of penetrating possible ‘dents’ in the value function (or perturbation function) thereby reducing the duality gap [26]. Depending on the properties of the value function of the underlying optimization problem, various different forms of ALD approaches have been introduced (cf. [1, 9–12, 18, 19, 22, 23, 25–30, 32, 34]). Under certain conditions, a zero duality gap can be reached asymptotically by increasing the coefficient on penalty function to infinity [32]. In some cases, the duality gap can be closed with a large enough finite value of the penalty coefficient. In this case, we say that the corresponding ALD involves exact penalization or is exact. Rockafellar [25] and Bertsekas [2] used convex quadratic augmenting functions. Burke [13, 14] used norms as convex augmenting functions. For these cases, necessary and sufficient conditions for exact penalization are provided in [13, 14, 26] which we will review in Sect. 2. For some classes of non-convex optimization problems, the duality gap cannot be closed by using convex augmenting functions. For these problems, more general forms of ALD are needed. For example, level-bounded augmenting functions were used in [18] rather than convex ones. The works in [29] and [30] used a family of augmenting functions with the almost peak at zero property, which includes the augmenting functions in [18] as special cases. Note that the class of augmenting functions in [29] and [30] are generalizations of convex augmenting functions in [26]. A weaker peak at zero property was considered in [22]. A more general form of peak at zero property was investigated in [32] to provide a unified nonlinear ALD. Using abstract convexity, ALD was studied in [12] and [9] in Banach and Hausdorff topological spaces, respectively.

In this paper, we consider non-negative level bounded augmenting functions in ALD for solving MIPs. Because of the non-convexity in MIP (1), a non-zero duality gap may exist [33], that is $z^\text {IP}-z^\text {LD+}_\rho >0$. Recently, Boland and Eberhard [7] showed that in ALD for MIPs, with a specific class of nonnegative convex augmenting functions, $\lim \nolimits _{\rho \rightarrow \infty } z^\text {LD+}_\rho =z^\text {IP}$. They also proved that if X is a finite set (e.g. a bounded pure IP), then there exists a finite penalty coefficient which closes the duality gap. We significantly generalize the results of [7] . In particular, our contributions are as follows:

• 1. We first provide a primal characterization for the ALD of an MIP. This is an alternative characterization to the one provided in [7, Theorem 1]. Using this characterization, the ALD of an MIP can be viewed as a traditional LD in a lifted space.

• 2. We give an alternative proof for the asymptotic zero duality gap property of ALD for MIPs when the penalty coefficient is allowed to go to infinity. This was first proved in [7, Proposition 3].

• 3. We prove that ALD using any norm as the augmenting function with a sufficiently large but finite penalty coefficient closes the duality gap for general MIPs. This generalizes the result in [7, Corollary 1] from the case of pure integer programming with a bounded feasible region to general MIPs with unbounded feasible regions.

• 4. Using our primal characterization, we also present an example where ALD with a quadratic augmenting function is not able to close the duality gap for any finite penalty coefficient.

The paper is organized as follows. Section 2 provides definitions and surveys existing results on Lagrangian relaxation and augmented Lagrangian relaxation of general nonlinear optimization problems and specifically of MIPs. Section 3 presents a primal characterization of the ALD of a general MIP and the zero duality gap property when the penalty coefficient is allowed to go to infinity. Section 4 proves that under mild conditions the ALD achieves zero duality gap using any norm as the augmenting function with a finite penalty coefficient.

2 Preliminaries

Let $\mathbb {R}$, $\mathbb {Q}$, and $\mathbb {Z}$ denote the sets of real, rational, and integer numbers, respectively. For any vector $\varvec{a}$ and matrix $\varvec{A}$ with finite dimensions, denote their transpose by $\varvec{a}^\top$ and $\varvec{A}^\top$, respectively. For any set $S \subseteq \mathbb {R}^n$, let $\mathbf {conv}(S)$, $\mathbf {ri}(S)$ and $\mathbf {cl}(S)$ denote the convex hull, relative interior, and closure of the set S, respectively. Moreover, let $\mathbf {diam} (S) :=\sup \{ \Vert \varvec{u}-\varvec{v} \Vert _\infty : \varvec{u}\in S, \varvec{v}\in S\}$ denote the diameter of set S, where $\Vert \cdot \Vert _\infty$ is the $l_\infty$ norm.

Let $\varvec{x}\in \mathbb {Z}^{n_1} \times \mathbb {R}^{n_2}$ be the vector of decision variables, where $n_1$ and $n_2$ are numbers of integer and continuous variables, respectively, and $n:=n_1+n_2$. For given $\varvec{c}\in \mathbb {Q}^n$, $\varvec{b}\in \mathbb {Q}^m$, and $\varvec{A}\in \mathbb {Q}^{m\times n}$, consider the general MIP problem (1),

$$\begin{aligned} z^\text {IP}:=\inf \{ \varvec{c}^\top \varvec{x} | \varvec{Ax}=\varvec{b}, \varvec{x}\in X\}, \end{aligned}$$

where m is the number of complicating or coupling constraints, $\varvec{Ax}=\varvec{b}$. The case with $n_2=0$ is called a pure IP, while for a MIP we have $n_2\ge 1$ and $n_1\ge 1$. Denote the LP relaxation of $z^\text {IP}$ in problem (1) by $z^\text {LP}$. We consider MIP problems that satisfy the following assumption.

Assumption 1

For the MIP (1) we have the following:

• (a) X is a mixed integer linear set given by $X=\{ \varvec{x}\in \mathbb {Z}^{n_1} \times \mathbb {R}^{n_2}: \varvec{Ex}\le \varvec{f}\}$ for some $\varvec{E}\in \mathbb {Q}^{\bar{m}\times n}$ and $\varvec{f}\in \mathbb {Q}^{{\bar{m}}}$, where $\bar{m}$ is the number of the inequality constraints in the definition of X. The problem data $\varvec{A}$, $\varvec{b}$, $\varvec{c}$, $\varvec{E}$, and $\varvec{f}$ all have rational entries, and without loss of generality, we can assume that they are integral.

• (b) Problem (1) is feasible and its optimal value is bounded.

Usually problem (1) is taken to be structured so that X includes integrality constraints, simple bounds on variables, and other simple constraints.

Remark 1

Note that under Assumption 1-a, $\mathbf {conv}(X)$ and $\mathbf {conv}(\{\varvec{x}: \varvec{Ax}=\varvec{b}, \varvec{x}\in X\})$ are rational polyhedra by Meyer’s theorem [20]. By Assumption 1 (rationality of input data and boundedness of $z^\text {IP}$), the value of the LP relaxation of MIP (1) is bounded [5], i.e. $-\infty < z^\text {LP} \le z^\text {IP}< \infty$. Let $\bar{\varvec{\lambda }}_\text {LP}$ be a rational optimal vector of dual variables for $\varvec{Ax}=\varvec{b}$ in the LP relaxation of (1). Moreover, $z^\text {IP}$ is attainable and the $\inf$ in the objective function of (1) can be replaced by $\min$. That is, there exists an optimal solution $\varvec{x}^*$ of problem (1) such that $\varvec{x}^*\in X$, $\varvec{Ax}^*=\varvec{b}$ and $z^\text {IP}=\varvec{c}^\top \varvec{x}^*$.

It is worth mentioning that the equality relation in $\varvec{Ax}=\varvec{b}$ does not impose any restriction on the type of these constraints. Because any inequality can be replaced by an equality constraint with a new non-negative slack variable. The non-negativity of the introduced variable can be absorbed in X. Moreover, in the case of a pure IP, this slack variable will automatically be an integer variable following Assumption 1-a.

Definition 1

(Value function) The value function for problem (1) is defined as

$$\begin{aligned} p(\varvec{u}):=\inf \{ \varvec{c}^\top \varvec{x} | \varvec{Ax}=\varvec{b}+\varvec{u}, \varvec{x}\in X\}. \end{aligned}$$

(2)

Note that $p(\varvec{0})= z^\text {IP}$. The value function is a very important tool for the theoretical examination of constrained optimization problems [29]. The properties of the value functions for IPs and MIPs were studied in [4–6, 21, 24]. For an MIP problem with rational data, the value function is lower semicontinuous [21] and piecewise polyhedral with finitely many pieces in any bounded set [4].

Definition 2

(Lagrangian relaxation and dual) For a given Lagrange multiplier vector $\varvec{\lambda }\in \mathbb {R}^m$, the corresponding Lagrangian relaxation (LR) of (1) is given as

$$\begin{aligned} z^\text {LR}( \varvec{\lambda }):=\inf \limits _{\varvec{x}\in X} \left\{ \varvec{c}^\top \varvec{x} + \varvec{ \lambda }^\top ( \varvec{b}-\varvec{Ax})\right\} , \end{aligned}$$

(3)

and the associated Lagrangian dual (LD) is

$$\begin{aligned} z^\text {LD}:=\sup \limits _{\varvec{ \lambda } \in \mathbb {R}^m} ~z^\text {LR}(\varvec{\lambda }). \end{aligned}$$

(4)

A well known primal characterization of LD is given by [17] as

$$\begin{aligned} z^\text {LD}=\inf \limits _{\varvec{x}}\left\{ \varvec{c}^\top \varvec{x} \; |\; \varvec{Ax}=\varvec{b}, \varvec{x}\in \mathbf {conv}(X)\right\} . \end{aligned}$$

(5)

Remark 2

Note that by rationality of the input data in Assumption 1, $z^\text {LD}$ is attainable and $\inf$ in the objective function of (5) can be replaced by $\min$.

Definition 3

(Augmented Lagrangian relaxation and dual) The augmented Lagrangian relaxation (ALR) of (1) has the following form [26]:

$$\begin{aligned} z^\text {LR+}_\rho (\varvec{ \lambda }):=\inf \limits _{\varvec{x}\in X} ~ \{\varvec{c}^\top \varvec{x} + \varvec{ \lambda }^\top ( \varvec{b}-\varvec{Ax}) + \rho \psi (\varvec{b}-\varvec{Ax}) \}. \end{aligned}$$

(6)

Here, $\rho >0$ is a fixed given parameter called penalty coefficient and $\psi$ is an augmenting function. In this paper, unless explicitly mentioned, we assume that $\psi$ satisfies the following assumption.

Assumption 2

$\psi :\mathbb {R}^m\rightarrow \mathbb {R}_+$ is a proper, nonnegative, lower semicontinuous, and level-bounded augmenting function, that is $\psi (\varvec{0})=0$, $\psi (\varvec{u})>0$ for all $\varvec{u}\ne \varvec{0}$, $\mathbf {diam} \{\varvec{u}\;|\; \psi (\varvec{u})\le \delta \} <+\infty$ for all $\delta >0$. Moreover $\lim \nolimits _{\delta \downarrow 0} \mathbf {diam} \{\varvec{u}\;|\; \psi (\varvec{u})\le \delta \} =0$.

Note that non-negative convex augmenting functions satisfy Assumption 2. The augmented Lagrangian dual (ALD) is as follows.

$$\begin{aligned} z^\text {LD+}_\rho :=\sup \limits _{\varvec{\lambda } \in \mathbb {R}^m} ~z^\text {LR+}_\rho (\varvec{\lambda }). \end{aligned}$$

(7)

For all $\rho >0$, it is well known that

$$\begin{aligned} -\infty < z^\text {LP}\le z^\text {LD}\le z^\text {LD+}_\rho \le z^\text {IP}< +\infty , \end{aligned}$$

(8)

where the strict inequalities in the upper and lower bounds hold from Assumption 1.

2.1 Exact penalty representation

Definition 4

(Exact penalty representation [26, Definition 11.60]) For a given augmenting function $\psi (\cdot )$, a dual vector $\bar{\varvec{\lambda }}$ is said to support an exact penalty representation for problem (1) if, for all $\rho$ sufficiently large, $z^\text {IP}=z^\text {LR+}_\rho (\bar{\varvec{\lambda }})$ and

$$\begin{aligned} \mathop {\hbox {argmin}}\limits _{\varvec{x}\in X:\varvec{Ax}=\varvec{b}} ~ \varvec{c}^\top \varvec{x} =\mathop {\hbox {argmin}}\limits _{\varvec{x}\in X} \{\varvec{c}^\top \varvec{x} + \bar{\varvec{\lambda }}^\top ( \varvec{b}-\varvec{Ax}) + \rho \psi (\varvec{b}-\varvec{Ax})\}. \end{aligned}$$

A criterion for the exact penalty representation presented in [26].

If $z^\text {LD+}_\rho = z^\text {IP}$ for some $\rho >0$, then ALR (6) can recover a primal solution for the MIP problem (1).

Proposition 1

Suppose Assumption 1 holds and $z^\text {IP}=z^\text {LD+}_{\hat{\rho }}=z^\text {LR+}_{\hat{\rho }}(\bar{\varvec{\lambda }})$ for some finite $\hat{\rho }>0$ and $\bar{\varvec{\lambda }} \in \mathbb {R}^m$. Then, any optimal solution of ALR (6) with ${\varvec{\lambda }}=\bar{\varvec{\lambda }}$ and $\rho =\rho ^*>\hat{\rho }$ is an optimal solution of the MIP problem (1), and vice versa. That is, $\bar{\varvec{\lambda }}$ supports an exact penalty representation for the MIP problem (1).

Proof

Let $\rho ^*$ be any scalar such that $\rho ^*>\hat{\rho }$. Let $\bar{\varvec{x}}$ be an optimal solution of MIP problem (1) (the existence of an optimal solution for problem (1) is guaranteed under Assumption 1). Then, it holds that $\bar{\varvec{x}} \in X$, $\varvec{A}\bar{\varvec{x}}=\varvec{b}$, and $\varvec{c}^\top \bar{\varvec{x}}=z^\text {IP}$. Thus,

$$\begin{aligned} \varvec{c}^\top \bar{\varvec{x}}+ \bar{\varvec{\lambda }}^{\top } ( \varvec{b}-\varvec{A}\bar{\varvec{x}}) + \rho ^*\psi (\varvec{b}-\varvec{A}\bar{\varvec{x}})=\varvec{c}^\top \bar{\varvec{x}}=z^\text {IP}=z^\text {LR+}_{\rho ^*}(\bar{\varvec{\lambda }}), \end{aligned}$$

where the last equality follows from the facts that $z^\text {LR+}_{\hat{\rho }}(\bar{\varvec{\lambda }})\le z^\text {LR+}_{\rho ^*}(\bar{\varvec{\lambda }})\le z^\text {IP}$ and $z^\text {IP}=z^\text {LR+}_{\hat{\rho }}(\bar{\varvec{\lambda }})$. Therefore, $\bar{\varvec{x}}$ solves ALR (6) with $\rho ^*$ and $\bar{\varvec{\lambda }}$. Moreover, it shows that the optimality is achieved for this case of ALR (6).

To prove the other side, let $\varvec{x}^*\in X$ be any optimal solution of ALR (6) with $\rho ^*$ and $\bar{\varvec{\lambda }}$, i.e. $z^\text {LR+}_{\rho ^*}(\bar{\varvec{\lambda }})=\varvec{c}^\top \varvec{x}^*+ \bar{\varvec{\lambda }}^{\top } ( \varvec{b}-\varvec{Ax}^*) + \rho ^*\psi (\varvec{b}-\varvec{Ax}^*)$. We claim that $\varvec{x}^*$ solves problem (1), i.e. $\varvec{x}^*\in X$, $\varvec{Ax}^*=\varvec{b}$ and $\varvec{c}^\top \varvec{x}^*=z^\text {IP}$. Note that as a feasible solution of ALR (6), $\varvec{x}^*$ belongs to X. Assume by contradiction $\varvec{Ax}^*\ne \varvec{b}$. Then, $\psi (\varvec{b}-\varvec{Ax}^*)>0$ and therefore

$$\begin{aligned} \hat{\rho } \psi (\varvec{b}-\varvec{Ax}^*)< \rho ^*\psi (\varvec{b}-\varvec{Ax}^*). \end{aligned}$$

(9)

Moreover,

$$\begin{aligned} \begin{aligned} z^\text {IP}=z^\text {LD+}_{\hat{\rho }}=z^\text {LR+}_{\hat{\rho }}(\bar{\varvec{\lambda }})&\le \varvec{c}^\top \varvec{x}^*+ \bar{\varvec{\lambda }}^{\top } (\varvec{b}-\varvec{Ax}^*) + \hat{\rho } \psi (\varvec{b}-\varvec{Ax}^*) \\&< \varvec{c}^\top \varvec{x}^*+ \bar{\varvec{\lambda }}^{\top } ( \varvec{b}-\varvec{Ax}^*) + \rho ^*\psi (\varvec{b}-\varvec{Ax}^*)\\&=z^\text {LR+}_{\rho ^*}(\bar{\varvec{\lambda }}), \end{aligned} \end{aligned}$$

(10)

which contradicts $z^\text {LR+}_{\rho ^*}(\bar{\varvec{\lambda }})$ being a lower bound for $z^\text {IP}$. Therefore, $\varvec{Ax}^*=\varvec{b}$. Note that in (10) the equality relations hold by assumption, the first inequality holds by definition of $z^\text {LR+}_{\hat{\rho }}(\bar{\varvec{\lambda }})$, and the strict inequality follows from (9). Furthermore,

$$\begin{aligned} \begin{aligned} z^\text {IP}&=z^\text {LR+}_{\hat{\rho }}(\bar{\varvec{\lambda }}) \\&\le z^\text {LR+}_{\rho ^*}(\bar{\varvec{\lambda }})= \varvec{c}^\top \varvec{x}^*+ \bar{\varvec{\lambda }}^{\top } ( \varvec{b}-\varvec{Ax}^*) + \rho ^*\psi (\varvec{b}-\varvec{Ax}^*)=\varvec{c}^\top \varvec{x}^*\\&\le z^\text {IP}, \end{aligned} \end{aligned}$$

(11)

where the first two equalities hold by assumption and the third equality follows from $\varvec{Ax}^*=\varvec{b}$. Therefore, $\varvec{c}^\top \varvec{x}^*=z^\text {IP}$ which completes the proof. $\square$

Two important cases of ALR are the proximal and sharp Lagrangian. Next, we present their definitions, and necessary and sufficient conditions for supporting an exact penalty representation in these cases.

2.2 Proximal Lagrangian

Definition 5

(Proximal Lagrangian) An ALR generated with the augmenting function $\psi (\varvec{u})=\frac{1}{2}\Vert \varvec{u}\Vert _2^2$ is called a proximal Lagrangian.

Definition 6

(Proximal subgradient [26, Definition 8.45]) A vector $\varvec{\lambda }\in \mathbb {R}^m$ is called a proximal subgradient of a function $f : \mathbb {R}^m \rightarrow \overline{\mathbb {R}}$ at $\bar{\varvec{u}}$, a point where $f(\bar{\varvec{u}})$ is finite, if there exist $\rho > 0$ and $\delta > 0$ such that

$$\begin{aligned} f({\varvec{u}}) \ge f(\bar{\varvec{u}}) - \varvec{\lambda }^\top ( {\varvec{u}}-\bar{\varvec{u}}) - \frac{1}{2} \rho \Vert {\varvec{u}}-\bar{\varvec{u}} \Vert _2^2, ~ \forall {\varvec{u}} \text { s.t. } \Vert {\varvec{u}}-\bar{\varvec{u}} \Vert _2\le \delta . \end{aligned}$$

The existence of a proximal subgradient at $\bar{\varvec{u}}$ corresponds to the existence of a ‘local quadratic support’ to f at $\bar{\varvec{u}}$.

In a proximal Lagrangian, suppose that there exists $(\varvec{\lambda }, \rho ) \in \mathbb {R}^n \times (0,\infty )$ such that $z^\text {LR+}_\rho ({\varvec{\lambda }})>-\infty$ . Then, a necessary and sufficient condition for a vector $\bar{\varvec{\lambda }}$ to support an exact penalty representation is that $\bar{\varvec{\lambda }}$ is a proximal subgradient of the value function $p(\varvec{u})$ at $\varvec{u} =\varvec{0}$ [26].

2.3 Sharp Lagrangian

Definition 7

(Sharp Lagrangian) An ALR which uses a norm as an augmenting function, i.e. $\psi (\varvec{u})=\Vert \varvec{u}\Vert$, is called a sharp Lagrangian.

Definition 8

(Calmness [26, Ch. 8.F]) A function $f: \mathbb {R}^m\rightarrow \overline{\mathbb {R}}$ is calm at $\overline{\varvec{u}}$ from below with modulus $\kappa \in \mathbb {R}_+$ if $f(\overline{\varvec{u}})$ is finite and on some open neighborhood V of $\overline{\varvec{u}}$, one has

$$\begin{aligned} f(\varvec{u})\ge f(\overline{\varvec{u}})-\kappa \Vert \varvec{u}-\overline{\varvec{u}}\Vert ,~ \forall \varvec{u} \in V. \end{aligned}$$

Consider a function f which is not calm at $\overline{\varvec{u}}$ from below. Then, a small shift in ${\varvec{u}}$ can produce a proportionally unbounded downward shift in f. Calmness is a basic regularity condition under which we can study the sensitivity properties of certain variational systems [15].

In the sharp Lagrangian, suppose that $z^\text {LR+}_\rho ({\varvec{0}})>-\infty$ for some $\rho \in (0,\infty )$. Then, a necessary and sufficient condition for the vector $\bar{\varvec{\lambda }}=\varvec{0}$ to support an exact penalty representation is that the value function $p(\varvec{u})$ is calm from below at $\varvec{u} =\varvec{0}$ [13, 14, 26].

2.4 ALD for MIPs

For the MIP problem (1), under some technical assumptions, Boland and Eberhard [7] showed that the duality gap for ALD, $z^\text {LD+}_{\rho }-z^\text {IP}$, goes to zero as the penalty coefficient $\rho$ goes to infinity.

Proposition 2

[7, Proposition 3] Suppose $\psi$ is of the form $\psi (\varvec{u})=\phi (\Vert \varvec{u}\Vert )$ for some norm $\Vert \cdot \Vert$ in $\mathbb {R}^m$ where $\phi :\mathbb {R}_+ \rightarrow \mathbb {R}_+$ is a convex, monotonically increasing function for which $\phi (0)=0$ and there exists $\delta >0$ for which

$$\begin{aligned} \liminf \limits _{a\rightarrow +\infty } \frac{\phi (a)}{a}\ge \delta >0 \end{aligned}$$

with $\mathbf {diam} \{\varvec{a}|\phi (\varvec{a})\le \delta \} \downarrow 0$ as $\delta \downarrow 0$. Moreover, at least one of the following conditions holds: (1) the solution set of the LP relaxation of problem (1) does not contain a lineality space. (2) The matrices $\varvec{A}$ and $\varvec{D}$ have rational entries and the norm $\Vert .\Vert$ used in the definition of $\psi$ is the $l_\infty$ norm. (3) $\mathbf {conv}(X)$ is bounded. Then

$$\begin{aligned} z^\text {LD*}:=\sup \limits _{\rho >0} z^\text {LD+}_\rho =\lim \limits _{\rho \rightarrow \infty } z^\text {LD+}_\rho =z^\text {IP}. \end{aligned}$$

Boland and Eberhard [7] also showed that if X is a finite set of discrete elements then $\rho$ does not need to go to infinity to close duality gap.

Corollary 1

[7, Corollary 1] Suppose X is a finite set and assumptions in Proposition 2 hold. Then, there exists a $\rho ^*$ with $0<\rho ^*< \infty$ such that $z^\text {LD+}_{\rho ^*}=z^\text {IP}$.

3 Zero duality gap with ALD

In this section, we first present a primal characterization of the ALD for MIPs. Then, we prove that strong duality holds for ALD of general MIPs when the penalty coefficient is allowed to go to infinity. Our primal characterization and the strong duality result hold for a general, not necessarily convex augmenting function, satisfying Assumption 2. We also discuss the relation of our results to the recent results in [7].

3.1 A primal characterization of ALD

Similar to the equivalence of (4) and (5) for the LD, we can give a primal characterization for the ALD problem (7). The key observation is that (7) can be viewed as an LD of a problem in a lifted space. Then, the primal characterization follows from strong duality in convex optimization with usual regularity conditions.

Let us first find the primal problem for the ALD problem (7).

$$\begin{aligned} z^\text {LD+}_\rho&= \sup _{\lambda \in \mathbb {R}^m}\inf \limits _{\varvec{x}\in X} ~ \{\varvec{c}^\top \varvec{x} + \varvec{ \lambda }^\top ( \varvec{b}-\varvec{Ax}) + \rho \psi (\varvec{b}-\varvec{Ax}) \} \nonumber \\&= \sup _{\lambda \in \mathbb {R}^m}\inf \limits _{\varvec{x}\in X, \psi (\varvec{b}-\varvec{Ax})\le \omega } \{\varvec{c}^\top \varvec{x} + \rho \omega + \varvec{ \lambda }^\top ( \varvec{b}-\varvec{Ax}) \} \end{aligned}$$

(12)

$$\begin{aligned}&= \sup _{\lambda \in \mathbb {R}^m} \inf _{\varvec{x}, \omega } \{\varvec{c}^\top \varvec{x} + \rho \omega + \varvec{ \lambda }^\top ( \varvec{b}-\varvec{Ax}) \; : \; (\varvec{x},\omega ) \in \mathbf {conv}(S_{\psi })\}, \end{aligned}$$

(13)

where $S_{\psi }$ denotes the feasible region of the inf problem in (12), i.e.

$$\begin{aligned} S_{\psi } := \left\{ (\varvec{x}, \omega ) \in \mathbb {R}^{n+1} : \psi (\varvec{b}-\varvec{Ax}) \le \omega ,\; \varvec{x} \in X\right\} , \end{aligned}$$

(14)

and (13) holds because the objective function in (12) is linear. Now switching the sup and inf in (13), we have the dual problem of (13) given as

$$\begin{aligned} \hat{z}^\text {LD+}_\rho&:= \inf _{(\varvec{x},\omega )\in \mathbf {conv}(S_{\psi })}\sup _{\lambda \in \mathbb {R}^m}\{\varvec{c}^\top \varvec{x} + \rho \omega + \varvec{ \lambda }^\top ( \varvec{b}-\varvec{Ax})\} \nonumber \\&= \inf _{\varvec{x},\omega } \{ \varvec{c}^\top \varvec{x} + \rho \omega : \varvec{Ax} = \varvec{b} , (\varvec{x}, \omega ) \in \mathbf {conv}(S_{\psi }) \}. \end{aligned}$$

(15)

Theorem 1 below shows that, under a mild regularity condition, strong duality holds between (13) and (15), i.e. $z^\text {LD+}_\rho = \hat{z}^\text {LD+}_\rho$. Note that (15) only involves primal variables $\varvec{x}, \omega$. Therefore, this gives a primal characterization of the ALD problem (13). To prove this result, we need a few simple propositions and a nonlinear Farkas lemma.

Proposition 3

$\mathrm {Proj}_x(\mathbf {conv}(S_{\psi }))=\mathbf {conv}(X)$.

Proof

For any $(\varvec{x},\omega )\in \mathbf {conv}(S_{\psi })$, there exist $\varvec{x}^i\in X$ and $\psi (\varvec{b}-\varvec{Ax}^i)\le \omega ^i$ for $i=1,\dots , n+2$ so that $\varvec{x}=\sum _{i=1}^{n+2}\lambda _i \varvec{x}^i$, $\omega = \sum _{i=1}^{n+2} \lambda _i \omega ^i$, and $\sum _{i=1}^{n+2} \lambda _i = 1$ with $\lambda _i\ge 0$ for all $i=1,\dots ,n+2$ (by Caratheodory’s Theorem). Clearly, $\varvec{x}\in \mathbf {conv}(X)$, which shows $\mathrm {Proj}_x(\mathbf {conv}(S_{\psi }))\subseteq \mathbf {conv}(X)$.

For the other direction, take any $\varvec{x}\in \mathbf {conv}(X)$. Then $\varvec{x}$ can be written as $\varvec{x}=\sum _{i=1}^{n+1}\lambda _i \varvec{x}^i$ for each $\varvec{x}^i\in X$ and $\lambda _i$’s form a convex combination. Let $\omega _i:=\psi (\varvec{b}-\varvec{Ax}^i)$ and $\omega :=\sum _i\lambda _i \omega _i$. Then, for each i, $(\varvec{x}^i,\omega ^i)\in S_{\psi }$, and $(\varvec{x},\omega )=\sum _i \lambda _i (\varvec{x}^i, \omega ^i)$. Therefore, $(\varvec{x},\omega )\in \mathbf {conv}(S_{\psi })$, i.e. $\varvec{x}\in \mathrm {Proj}_x(\mathbf {conv}(S_{\psi }))$. This completes the proof. $\square$

Proposition 4

Let S be a nonempty convex set in $\mathbb {R}^{n+1}$. Then $\mathbf {ri}(\mathrm {Proj}_x(S))=\mathrm {Proj}_x(\mathbf {ri}(S))$.

This follows from the well-known fact $\mathbf {ri}(A(S))=A(\mathbf {ri}(S))$, where A is a linear transformation and S is a convex set. See e.g., [3].

Proposition 5

There exists $\varvec{x}\in \mathbf {ri}(\mathbf {conv}(X))$ and $\varvec{Ax}=\varvec{b}$ if and only if Problem (15) has a feasible point in $\mathbf {ri}(\mathbf {conv}(S_{\psi }))$.

Proof

If (15) has a feasible point $(\bar{\varvec{x}}, \bar{\omega })$ in $\mathbf {ri}(\mathbf {conv}(S_{\psi }))$, then $\varvec{A}\bar{\varvec{x}}=\varvec{b}$ and $\bar{\varvec{x}}\in \text {Proj}_x(\mathbf {ri}(\mathbf {conv}(S_\psi )))$. By Proposition 4, $\bar{\varvec{x}}\in \mathbf {ri}(\mathrm {Proj}_x(\mathbf {conv}(S_{\psi })))$. By Proposition 3, we have $\bar{\varvec{x}}\in \mathbf {ri}(\mathbf {conv}(X))$.

For the other direction, take any $\bar{\varvec{x}}\in \mathbf {ri}(\mathbf {conv}(X))$ and $\varvec{A}\bar{\varvec{x}}=\varvec{b}$. By Proposition 3, we have $\bar{\varvec{x}}\in \mathbf {ri}(\mathrm {Proj}_x(\mathbf {conv}(S_{\psi })))$. By Proposition 4, then we know that $\bar{\varvec{x}}\in \mathrm {Proj}_x(\mathbf {ri}(\mathbf {conv}(S_{\psi })))$, i.e. there exists $(\bar{\varvec{x}},\bar{\omega })\in \mathbf {ri}(\mathbf {conv}(S_{\psi }))$ and $\varvec{A}\bar{\varvec{x}}=\varvec{b}$. $\square$

Lemma 1

(Nonlinear Farkas’ Lemma (Prop. 3.5.4, [3])) Let C be a nonempty convex subset of $\mathbb {R}^n$, and let $f : C\rightarrow \mathbb {R}$ and $g_j : C\rightarrow \mathbb {R}$, for $j=1,\dots , r$ be convex functions. Consider the set F given by $F = \{ \varvec{x} \in C : g(\varvec{x})\le 0\}$, where $g(\varvec{x}) = (g_1(\varvec{x}), \dots , g_r(\varvec{x}))$, and assume that $f(\varvec{x})\ge 0$ for all $\varvec{x}\in F$. Consider the subset $Q^*$ of $\mathbb {R}^r$ given by

$$\begin{aligned} Q^* = \left\{ \varvec{\lambda }\in \mathbb {R}^r : \varvec{\lambda }\ge \varvec{0}, f(\varvec{x}) + \varvec{\lambda }^\top g(\varvec{x}) \ge 0, \forall \varvec{x}\in C\right\} . \end{aligned}$$

Then, $Q^*$ is nonempty if the functions $g_j$ for $j=1,\dots , r$ are affine, and F contains a relative interior point of C.

Next, we present the primal characterization of the ALD problem (7) as following theorem.

Theorem 1

If there exists $\varvec{x}\in \mathbf {ri}(\mathbf {conv}(X))$ such that $\varvec{Ax}=\varvec{b}$, and $z^{\text {LD+}}_\rho >-\infty$, then for all $\rho >0$,

$$\begin{aligned} z^{\text {LD+}}_{\rho } = \inf _{\varvec{x},\omega }&\quad \varvec{c}^\top \varvec{x} + \rho \omega \end{aligned}$$

(16a)

$$\begin{aligned} \text {s.t.}&\quad \varvec{Ax} = \varvec{b} \end{aligned}$$

(16b)

$$\begin{aligned}&\quad (\varvec{x}, \omega ) \in \mathbf {conv}(S_{\psi }). \end{aligned}$$

(16c)

Proof

Essentially, we want to show that strong duality holds between the primal and dual pair of convex programs (13) and (15), i.e. $\hat{z}_{\rho }^{LD+}={z}_{\rho }^{LD+}$ [recall that $\hat{z}_\rho ^{LD+}$ is defined in (15)]. By Proposition 5, if there exists $\varvec{x}\in \mathbf {ri}(\mathbf {conv}(X))$ and $\varvec{Ax}=\varvec{b}$, then (16) has a feasible point in $\mathbf {ri}(\mathbf {conv}(S_{\psi }))$. To apply the nonlinear Farkas’ lemma, we first rewrite the linear equality constraints in (16b) as linear inequalities $\tilde{\varvec{A}}\varvec{x}\le \tilde{\varvec{b}}$ with $\tilde{\varvec{A}}=[\varvec{A}^\top , -\varvec{A}^\top ]^\top$ and $\tilde{\varvec{b}}=[\varvec{b}^\top , -\varvec{b}^\top ]^\top$; we can also subtract $\hat{z}_{\rho }^{LD+}$ from the objective function of (16a) so the new optimal value is zero. Furthermore, denote the feasible region of (16) as

$$\begin{aligned} F := \left\{ (\varvec{x},\omega ) \in \mathbf {conv}(S_{\psi }) : \tilde{\varvec{A}}\varvec{x}\le \tilde{\varvec{b}}\right\} . \end{aligned}$$

Since F contains a point in the relative interior of $\mathbf {conv}(S_{\psi })$, by Lemma 1, we know that there exists a multiplier vector $\varvec{\lambda }^*\le \varvec{0}$ such that

$$\begin{aligned} \varvec{c}^\top \varvec{x} + \rho \omega - \hat{z}_\rho ^\text {LD+} + (\varvec{\lambda }^*)^\top (\tilde{\varvec{b}}-\tilde{\varvec{A}}\varvec{x}) \ge 0, \qquad \forall (\varvec{x},\omega )\in \mathbf {conv}(S_{\psi }). \end{aligned}$$

From this, we obtain

$$\begin{aligned}&\inf _{(\varvec{x},\omega )\in \mathbf {conv}(S_{\psi })} \varvec{c}^\top \varvec{x} + \rho \omega + (\varvec{\lambda }^*)^\top (\tilde{\varvec{b}}-\tilde{\varvec{A}}\varvec{x}) \ge \hat{z}_\rho ^{LD+} \\&\Rightarrow z_\rho ^{LD+}=\sup _{\varvec{\lambda }\le \varvec{0}}\inf _{(\varvec{x},\omega )\in \mathbf {conv}(S_{\psi })} \varvec{c}^\top \varvec{x} + \rho \omega + \varvec{\lambda }^\top (\tilde{\varvec{b}}-\tilde{\varvec{A}}\varvec{x}) \ge \hat{z}_\rho ^{LD+}. \end{aligned}$$

By the weak duality between (13) and (15), we already have $z_\rho ^{LD+}\le \hat{z}_\rho ^{LD+}$, therefore, this shows that $z^\text {LD+}_\rho = \hat{z}^\text {LD+}_\rho$ for all $\rho >0$. $\square$

Remark 3

A similar primal characterization of (7) is given in [7, Theorem 1]. In particular, the primal characterization in [7] has the following form

$$\begin{aligned} z^\text {LD+}_\rho = \min _{\hat{\omega }>0}\biggl \{\rho \hat{\omega } + \min _{\varvec{x}}\bigl \{\varvec{c}^\top \varvec{x} : \varvec{Ax}=\varvec{b}, \varvec{x}\in X_{\psi }(\hat{\omega })\bigr \} \biggr \}, \end{aligned}$$

(17)

where $X_{\psi }(\hat{\omega }):=\mathbf {conv}(\{\varvec{x}\in \mathbb {R}^n : \psi (\varvec{b}-\varvec{Ax})\le \hat{\omega },\; \varvec{x}\in X\})$. Note that (17) first minimizes over $\hat{\omega }$ then over $\varvec{x}$, whereas the primal characterization obtained in (16) minimizes $\varvec{x},\omega$ jointly. Of course, (16) can also be written in this order as

$$\begin{aligned} z^\text {LD+}_\rho = \min _{\hat{\omega }>0}\biggl \{\rho \hat{\omega } + \min _{\varvec{x}}\bigl \{\varvec{c}^\top \varvec{x} : \varvec{Ax}=\varvec{b}, \varvec{x}\in X'_{\psi }(\hat{\omega }) \bigr \} \biggr \}, \end{aligned}$$

(18)

where $X'_{\psi }(\hat{\omega }):=\{\varvec{x}\in \mathbb {R}^n : (\varvec{x},\hat{\omega })\in \mathbf {conv}(S_{\psi })\}$. The difference between (17) and (16) is more clear if we rewrite the sets $X_{\psi }(\hat{\omega })$ and $X'_{\psi }(\hat{\omega })$ as follows,

$$\begin{aligned} X_{\psi }(\hat{\omega })&=\text {Proj}_{{x}}\biggl (\mathbf {conv}\bigl (S_{\psi }\cap \{(\varvec{x},\omega ) : \omega =\hat{\omega }\}\bigr )\biggr ) \nonumber \\ X'_{\psi }(\hat{\omega })&=\text {Proj}_{{x}}\biggl (\mathbf {conv}\bigl (S_{\psi }\bigr )\cap \{(\varvec{x},\omega ) : \omega =\hat{\omega }\}\biggr ). \end{aligned}$$

(19)

From this, we can see $X_{\psi }(\hat{\omega })\subseteq X'_{\psi }(\hat{\omega })$. In this sense, (17) provides a stronger characterization than (18), when the joint minimization over $(\varvec{x},\omega )$ is split out in the order of $\omega$ and $\varvec{x}$. In fact, the proof in [7] that established (17) is quite involved. The difficulty exactly lies in characterizing the properties of the optimal objective value of the inner minimization in (17) as a single variable function in $\omega$. In comparison, our primal characterization (16) bypasses this difficulty by only looking at the joint minimization problem. It seems that this insight to view the ALD as a traditional LD problem in a lifted space is new, which makes the derivation of (16) quite simpler. Our primal characterization also requires less assumptions than (17). In particular, (17) requires that the augmenting function is convex in a particular form and at least one of the three assumptions stated in Proposition 2 hold, whereas our primal characterization works for both convex and non-convex augmenting functions, and the relative interior condition in Theorem 1 is a rather mild regularity condition. In addition, as we will show now, Assumptions 1 and 2 are enough to prove the zero duality gap result for ALD of general MIPs. A similar result is also proved in [7, Proposition 3] through their characterization (17), again under more restrictive conditions.

3.2 Zero duality gap for MIPs

From the primal characterization (16) we can see the $z^{\text {LD+}}_\rho$ is a non-decreasing function of $\rho$. Since $z^{\text {LD+}}_\rho$ is upper bounded by $z^{\text {IP}}$, therefore we have

$$\begin{aligned} -\infty < z^\text {LD*}:=\sup \limits _{\rho >0} z^\text {LD+}_\rho = \lim \limits _{\rho \rightarrow +\infty } z^\text {LD+}_\rho \le z^{\text {IP}}. \end{aligned}$$

We want to show that in fact $z^\text {LD*}=z^{\text {IP}}$. Recall that $\bar{\varvec{\lambda }}_\text {LP}$ is defined as a rational optimal vector of dual variables for $\varvec{Ax}=\varvec{b}$ in the LP relaxation of problem (1).

Proposition 6

Suppose Assumptions 1 and 2 hold. For given $\rho >0$ and $\epsilon >0$, define $\omega ^*_{\rho ,\epsilon }$ as

(20)

Then, the limit $\omega ^*_\rho :=\lim \nolimits _{\epsilon \downarrow 0} \omega ^*_{\rho ,\epsilon }$ exists and $\lim \nolimits _{\rho \rightarrow +\infty } \omega ^*_\rho =0$.

Proof

First, we show that problem (20) is feasible for all $\rho >0$ and $\epsilon >0$. By Assumption 1, $z^\text {LR+}_\rho (\bar{\varvec{\lambda }}_\text {LP})$ has a finite value in $[ z^\text {LP},z^\text {IP}]$. For any $\rho >0$ and $\epsilon >0$, by definition of $z^\text {LR+}_\rho (\bar{\varvec{\lambda }}_\text {LP})$, there exists a $\varvec{x}_{\rho ,\epsilon } \in X$ such that

$$\begin{aligned} \varvec{c}^\top \varvec{x}_{\rho ,\epsilon } + \bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax}_{\rho ,\epsilon } ) +\rho \psi (\varvec{b}- \varvec{Ax}_{\rho ,\epsilon } ) -z^\text {LR+}_\rho (\bar{\varvec{\lambda }}_\text {LP})\le \epsilon . \end{aligned}$$

Let $\omega _{\rho ,\epsilon }:= \psi (\varvec{b}- \varvec{Ax}_{\rho ,\epsilon } )$. Then, $(\varvec{x}_{\rho ,\epsilon },\omega _{\rho ,\epsilon })$ is a feasible solution of problem (20). For all $\rho >0$ and $\epsilon >0$, nonnegativity of $\psi$ implies $\omega ^*_{\rho ,\epsilon }\ge 0$. Moreover, the first and third constraints in (20) imply

$$\begin{aligned} \begin{aligned} \omega ^*_{\rho ,\epsilon }&\le \frac{1}{\rho } ( z^\text {LR+}_\rho (\bar{\varvec{\lambda }}_\text {LP})+\epsilon - \varvec{c}^\top \varvec{x} - \bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax} ) ), \text { for some } \varvec{x}\in X\\&\le \frac{1}{\rho } ( z^\text {IP} +\epsilon - z^\text {LP}), \end{aligned} \end{aligned}$$

(21)

where the second inequality follows from the facts that $z^\text {LR+}_\rho (\bar{\varvec{\lambda }}_\text {LP}) \le z^\text {IP}$ and $z^\text {LP} \le \varvec{c}^\top \varvec{x} + \bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax} )$, for all $\varvec{x}\in X$. By taking limits $\epsilon \downarrow 0$ on both sides of (21) we have

$$\begin{aligned} 0\le \omega ^*_\rho =\lim \limits _{\epsilon \downarrow 0} \omega ^*_{\rho ,\epsilon } \le \lim \limits _{\epsilon \downarrow 0} \frac{1}{\rho } ( z^\text {IP} +\epsilon - z^\text {LP})= \frac{1}{\rho } ( z^\text {IP} - z^\text {LP}) \end{aligned}$$

(22)

Note that $\omega ^*_{\rho ,\epsilon }$ is non-decreasing as $\epsilon \downarrow 0$. Moreover, $\omega ^*_{\rho ,\epsilon }$ is upper bounded. Then, $\lim \nolimits _{\epsilon \downarrow 0} \omega ^*_{\rho ,\epsilon }$ exists. By taking limits $\rho \rightarrow +\infty$ on both sides of (22) we have $\lim \nolimits _{\rho \rightarrow +\infty } \omega ^*_\rho =0$. $\square$

Lemma 2

Consider $\omega ^*_\rho$ as described in Proposition 6. Let us define $\tilde{z}^\text {LR+}_\rho (\bar{\varvec{\lambda }}_\text {LP})$ as follows:

$$\begin{aligned} \begin{aligned} \tilde{z}^\text {LR+}_\rho (\bar{\varvec{\lambda }}_\text {LP}) := \inf _{\varvec{x},\omega } ~~&\{ \varvec{c}^\top \varvec{x} + \bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax} ) +\rho \omega \}\\ \text {s.t. }&\varvec{x}\in X, \\&\psi (\varvec{b}- \varvec{Ax} ) \le \omega ,\\&(1-\delta ) \omega ^*_\rho \le \omega \le (1+\delta ) \omega ^*_\rho .\\ \end{aligned} \end{aligned}$$

(23)

Then,

$$\begin{aligned} \begin{aligned} z^\text {LR+}_\rho (\bar{\varvec{\lambda }}_\text {LP}) =&\tilde{z}^\text {LR+}_\rho (\bar{\varvec{\lambda }}_\text {LP}) \\ \ge&\inf _{\varvec{x}} ~ \{ \varvec{c}^\top \varvec{x} + \bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax} ) +\rho (1-\delta ) \omega ^*_\rho \}\\&~ \text {s.t. } \varvec{x}\in X, \\&~~~~~ \psi (\varvec{b}- \varvec{Ax} ) \le (1+\delta ) \omega ^*_\rho ,\\ \ge&\inf _{\varvec{x}} ~ \{ \varvec{c}^\top \varvec{x} + \bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax} )\}\\&~ \text {s.t. } \varvec{x}\in X, \\&~~~~~ \psi (\varvec{b}- \varvec{Ax} ) \le (1+\delta ) \omega ^*_\rho , \end{aligned} \end{aligned}$$

(24)

for any $0<\delta <1$.

Proof

Clearly, $z^\text {LR+}_\rho (\bar{\varvec{\lambda }}_\text {LP}) \le \tilde{z}^\text {LR+}_\rho (\bar{\varvec{\lambda }}_\text {LP})$, due to the last constraint in (23). Let $\alpha _\rho := \tilde{z}^\text {LR+}_\rho (\bar{\varvec{\lambda }}_\text {LP})-z^\text {LR+}_\rho (\bar{\varvec{\lambda }}_\text {LP})$. Assume by contradiction, $z^\text {LR+}_\rho (\bar{\varvec{\lambda }}_\text {LP}) < \tilde{z}^\text {LR+}_\rho (\bar{\varvec{\lambda }}_\text {LP})$ or equivalently $\alpha _\rho >0$. Then, for all $(\varvec{x},\omega )$ satisfying constraints of (23) it holds

$$\begin{aligned} \varvec{c}^\top \varvec{x} + \bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax} ) +\rho \omega \ge \tilde{z}^\text {LR+}_\rho (\bar{\varvec{\lambda }}_\text {LP})= z^\text {LR+}_\rho (\bar{\varvec{\lambda }}_\text {LP}) +\alpha _\rho , \end{aligned}$$

which implies $(\varvec{x},\omega )$ is infeasible for problem (20) if $0<\epsilon <\alpha _\rho$. Therefore, $\omega ^*_{\rho ,\epsilon } \notin ( (1-\delta ) \omega ^*_\rho , (1+\delta ) \omega ^*_\rho )$ for $0<\epsilon <\alpha _\rho$, which contradicts with $\omega ^*_\rho =\lim \limits _{\epsilon \downarrow 0} \omega ^*_{\rho ,\epsilon }$. Therefore, $z^\text {LR+}_\rho (\bar{\varvec{\lambda }}_\text {LP}) = \tilde{z}^\text {LR+}_\rho (\bar{\varvec{\lambda }}_\text {LP})$. Inequalities in (24) hold, because $\rho \omega \ge \rho (1-\delta ) \omega ^*_\rho \ge 0$ and $\psi (\varvec{b}- \varvec{Ax} ) \le (1+\delta ) \omega ^*_\rho$, for all $(\varvec{x},\omega )$ satisfying constraints of (23). $\square$

Theorem 2

Suppose Assumptions 1 and 2 hold. Then, $\sup \nolimits _{\rho >0} z^\text {LD+}_\rho =z^{\text {IP}}$.

Proof

Following (8), it is enough to show that $\sup \nolimits _{\rho >0} z^\text {LD+}_\rho \ge z^{\text {IP}}$. Let $\delta$ be a given positive scalar in (0, 1). By definition of ALD, we have

$$\begin{aligned} z^\text {LD+}_\rho&=\sup _{\varvec{\lambda }\in \mathbb {R}^m} \inf _{\varvec{x},\omega } \; \{ \varvec{c}^\top \varvec{x} + \varvec{\lambda }^\top (\varvec{b}-\varvec{Ax} ) +\rho \omega :\varvec{x}\in X, ~\psi (\varvec{b}- \varvec{Ax} ) \le \omega \} \nonumber \\&\ge \inf _{\varvec{x},\omega } \; \{ \varvec{c}^\top \varvec{x} + \bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax} ) +\rho \omega :\varvec{x}\in X, ~\psi (\varvec{b}- \varvec{Ax} ) \le \omega \} \nonumber \\&\ge \inf _{\varvec{x}} \; \{ \varvec{c}^\top \varvec{x} + \bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax} ) :\varvec{x}\in X, ~\psi (\varvec{b}- \varvec{Ax} ) \le (1+\delta )\omega ^*_\rho \} \end{aligned}$$

(25a)

$$\begin{aligned}&\ge \inf _{\varvec{x}} \; \{ \varvec{c}^\top \varvec{x} + \bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax} ) :\varvec{x}\in X, ~\Vert \varvec{b}- \varvec{Ax} \Vert _\infty \le \kappa _\rho \} \end{aligned}$$

(25b)

$$\begin{aligned}&= \min _{\varvec{x}} \; \{ \varvec{c}^\top \varvec{x} + \bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax} ) :\varvec{x}\in X, ~\Vert \varvec{b}- \varvec{Ax} \Vert _\infty \le \kappa _\rho \} \end{aligned}$$

(25c)

where $\kappa _\rho := \mathbf {diam} \{\varvec{u}\;|\; \psi (\varvec{u})\le (1+\delta )\omega ^*_\rho \} =\sup \{\Vert \varvec{u}\Vert _\infty \;|\; \psi (\varvec{u})\le (1+\delta )\omega ^*_\rho \}$. Inequality (25a) holds by Lemma 2, and (25b) follows from level boundedness of $\psi$. Equality (25c) is valid by Assumption 1. By taking limits on both sides of (25b) we have

$$\begin{aligned} \lim \limits _{\rho \rightarrow +\infty } z^\text {LD+}_\rho&\ge \lim \limits _{\rho \rightarrow +\infty } \min _{\varvec{x}} \{ \varvec{c}^\top \varvec{x} + \bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax} ) :\varvec{x}\in X, \Vert \varvec{b}- \varvec{Ax} \Vert _\infty \le \kappa _\rho \} \nonumber \\&\ge \min _{\varvec{x}} \{ \varvec{c}^\top \varvec{x} + \bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax} ) :\varvec{x}\in X, \Vert \varvec{b}- \varvec{Ax} \Vert _\infty \le \lim \limits _{\rho \rightarrow +\infty } \kappa _\rho \} \end{aligned}$$

(26a)

$$\begin{aligned}&= \min _{\varvec{x}} \{ \varvec{c}^\top \varvec{x} + \bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax} ) :\varvec{x}\in X, \Vert \varvec{b}- \varvec{Ax} \Vert _\infty \le 0 \} \nonumber \\&=\min _{\varvec{x}} \{ \varvec{c}^\top \varvec{x} + \bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax} ) :\varvec{x}\in X, \varvec{Ax}=\varvec{b} \} \nonumber \\&= \min _{\varvec{x}} \{ \varvec{c}^\top \varvec{x} :\varvec{x}\in X, \varvec{Ax}=\varvec{b}\} \nonumber \\&=z^\text {IP}. \end{aligned}$$

(26b)

where (26a) follows from lower semicontinuity of value functions for MIPs with rational data [21]. Equality (26b) holds by Assumption 2, i.e. $\lim \nolimits _{\rho \rightarrow +\infty } \kappa _\rho =0$. This completes the proof. $\square$

4 Exact penalty representation of ALD for MIPs

4.1 Pure IP case

A special case of problem (1) is the pure IP case, where all variables are integral, i.e. $n_2=0$. Zero duality gap and exact penalty representation using proximal Lagrangian for pure IPs were established in [5, Theorem 1.5]. Boland and Eberhard [7, Corollary 1] proved exact penalty representation for ALD of pure IPs with a bounded feasible region, i.e. X is finite, and the augmenting functions satisfying assumptions in Proposition 2. In this section, we extend this recent result to show exact penalty representation for pure IPs under weaker assumptions on the augmenting functions (e.g., the augmenting function does not have to be convex) and X may not be necessarily finite.

Theorem 3

Suppose problem (1) is a pure IP with potentially infinitely many feasible solutions, and Assumption 1 holds. If

$$\begin{aligned} \inf \{\psi (\varvec{b}-\varvec{Ax}): \varvec{x}\in X, \varvec{Ax}\ne \varvec{b} \}\ge \delta >0 \end{aligned}$$

(27)

for some strictly positive value of $\delta$, then there exists a finite $\rho ^*\in (0,+\infty )$ such that $z^\text {LD+}_{\rho ^*}=z^\text {IP}$.

Proof

Following (8), it suffices to find a finite $\rho ^*$ such that $z^\text {LD+}_{\rho ^*}\ge z^\text {IP}$. Let $\bar{\rho }>0$ be any positive penalty coefficient. By assumption, there exists a $\delta >0$ which satisfies (27). Furthermore, let $\varvec{x}^0$ be any arbitrary feasible solution of (1), i.e. $\varvec{x}^0\in X$ and $\varvec{Ax}^0=\varvec{b}$. Set $\rho ^*=\frac{\varvec{c}^\top \varvec{x}^0 - z^\text {LP} }{\delta }$. Note that $0<\rho ^*<+\infty$, because $\delta >0$ and $-\infty < z^\text {LP} \le \varvec{c}^\top \varvec{x}^0<+\infty$. We claim that $z^\text {LD+}_{\rho ^*}\ge z^\text {IP}$. Observe that we have

$$\begin{aligned} z_{\rho ^*}^{\text {LD+}} = \sup _{\varvec{\lambda }} z_{\rho ^*}^\text {LR+}(\varvec{\lambda })\ge z_{\rho ^*}^\text {LR+}(\bar{\varvec{\lambda }}_\text {LP}) = \inf _{\varvec{x}\in X}\bigl \{\varvec{c}^\top \varvec{x}+\bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax})+\rho ^*\psi (\varvec{b}-\varvec{Ax})\bigr \}. \end{aligned}$$

(28)

There are two cases.

• 1. For all $\varvec{x}\in X$ with $\varvec{Ax}=\varvec{b}$,

  $$\begin{aligned} \varvec{c}^\top \varvec{x} + \bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax})+\rho ^*\psi (\varvec{b}-\varvec{Ax}) = \varvec{c}^\top \varvec{x} \ge z^\text {IP}. \end{aligned}$$

  (29)

• 2. For all $\varvec{x}\in X$ with $\varvec{Ax}\ne \varvec{b}$,

  $$\begin{aligned} \varvec{c}^\top \varvec{x} +&\bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax})+\rho ^*\psi (\varvec{b}-\varvec{Ax}) \nonumber \\&= \varvec{c}^\top \varvec{x} + \bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax}) +\left( \frac{\varvec{c}^\top \varvec{x}^0 - z^\text {LP} }{\delta } \right) \psi (\varvec{b}-\varvec{Ax}) \nonumber \\&\ge \varvec{c}^\top \varvec{x} + \bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax}) +\left( \varvec{c}^\top \varvec{x}^0 - z^\text {LP} \right) \end{aligned}$$

  (30a)
  $$\begin{aligned}&\ge z^\text {LP}+\left( \varvec{c}^\top \varvec{x}^0 - z^\text {LP}\right) \nonumber \\&=\varvec{c}^\top \varvec{x}^0 \nonumber \\&\ge z^\text {IP}, \end{aligned}$$

  (30b)

  where (30a) holds because $-\infty <z^\text {LP} \le z^\text {IP} \le \varvec{c}^\top \varvec{x}^0$ and $\psi (\varvec{b}-\varvec{Ax}) \ge \delta >0$ for all $\varvec{x}\in X$ with $\varvec{Ax}\ne \varvec{b}$ by (27); (30b) follows by definition of $\bar{\varvec{\lambda }}_\text {LP}$.

Inequalities (29) and (30) imply

$$\begin{aligned} z_{\rho ^*}^\text {LR+}(\bar{\varvec{\lambda }}_\text {LP})=\inf _{\varvec{x}\in X}\biggl \{\varvec{c}^\top \varvec{x} + \bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}-\varvec{Ax})+\rho ^*\psi (\varvec{b}-\varvec{Ax})\biggr \} \ge z^\text {IP}. \end{aligned}$$

Together with (28), we have

$$\begin{aligned} z^\text {LD+}_{\rho ^*}\ge z^\text {IP}. \end{aligned}$$

(31)

This completes the proof. It is worth mentioning that the relations (8), (28) and (31) imply

$$\begin{aligned} z^\text {LD+}_{\rho ^*}= z_{\rho ^*}^\text {LR+}(\bar{\varvec{\lambda }}_\text {LP})=z^\text {IP}, \end{aligned}$$

which means the finite $\bar{\varvec{\lambda }}_\text {LP}$ solves $\sup \limits _{\varvec{\lambda }} z_{\rho ^*}^\text {LR+}(\varvec{\lambda })$. $\square$

Note that for the pure IP case of problem (1) under Assumption 1, any augmenting function defined in Proposition 2 satisfies (27). Even the index function $\mathbb {I}:\mathbb {R}^m \rightarrow \{0,1\}$ where

$$\begin{aligned} \mathbb {I}( \varvec{u})=\left\{ \begin{array}{cc} 0 &{}\quad \text { if } \varvec{u}= \varvec{0}, \\ 1 &{}\quad \text { otherwise } \end{array} \right. \end{aligned}$$

can be used as an augmenting function $\psi (\cdot )$ to satisfy (27). We can extend Theorem 3 to general MIPs, if Assumption 1 and inequality (27) hold.

4.2 MIP case

For a general MIP with both continuous and integer variables, we need more conditions on the augmenting function to have an exact penalty representation. For example, if $\psi (\cdot )=\Vert \cdot \Vert _2^2$, i.e. the proximal Lagrangian case, this augmenting function satisfies the assumptions in Proposition 2 as well as (27) when X is a pure integer set. However, for a general MIP, there may not exist a finite $0<\rho ^*<\infty$ such that $z^\text {LD+}_{\rho ^*}=z^\text {IP}$ under this augmenting function. In this section, we first give an example to show that proximal Lagrangian fails to have an exact penalty representation for a simple MIP in three variables. Then we prove that, when the augmenting function is any norm (but not the squared norm) i.e., for the sharp Lagrangians, the ALD always has an exact penalty representation for general MIPs. Finally, we extend this result to some classes of augmenting functions that are not convex.

4.2.1 Counterexample MIP for proximal Lagrangian

Proposition 7

There exists an MIP problem of the form (1) and an augmenting function satisfying assumptions in Proposition 2 such that $z^\text {LD+}_{\rho }<z^\text {IP}$ for all finite $\rho >0$.

Next, we verify this proposition with a simple example.

Example 1

Consider the following MIP problem, with one binary and two continuous variables.

$$\begin{aligned} \begin{aligned} z^{\text {IP}}=\min \limits _{x_1,x_2,x_3}&-x_1-x_2\\ \text {s.t. }&-x_1+x_2= 0\\&0\le x_1\le x_3\\&0\le x_2\le 1-x_3\\&x_3\in \{0,1\} \end{aligned} \end{aligned}$$

(32)

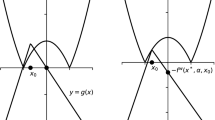
The only feasible points for (32) are $(x_1,x_2,x_3)=(0,0,0)$ and $(x_1,x_2,x_3)=(0,0,1)$ with objective value 0. Then, $z^{\text {IP}}=0$. Projection of the feasible region of (32) without the constraint $-x_1+x_2= 0$ into the space of $x_1$ and $x_2$ contains the blue lines in Fig. 1. The points satisfying $-x_1+x_2= 0$ are depicted by a red line in this space.

Fig. 1

Projection of the feasible region of Example 1 in the space of $x_1$ and $x_2$

We show that in Example 1, for ALD with $\psi (\cdot )=\Vert \cdot \Vert _2^2$, $z^\text {LD+}_\rho <0$ for all $\rho >0$. From Theorem 1, ALD (15) with $\psi (\cdot )=\Vert \cdot \Vert _2^2$ becomes

$$\begin{aligned} \begin{aligned} z^\text {LD+}_{\rho }=\inf ~&~ -x_1-x_2+\rho \omega \\ \text{ s.t. }&(x_1,x_2,x_3,\omega )\in \mathbf {conv}(S_2)\\&-x_1+x_2= 0. \end{aligned} \end{aligned}$$

(33)

where,

$$\begin{aligned} S_2:=\left\{ (x_1,x_2,x_3,\omega )\in \mathbb {R}^{4}: \begin{array}{l} \omega \ge ( -x_1+x_2 )^2 \\ 0\le x_1\le x_3\\ 0\le x_2\le 1-x_3\\ x_3\in \{0,1\} \end{array} \right\} . \end{aligned}$$

Consider $(\hat{x}_1,\hat{x}_2,\hat{x}_3,\hat{\omega })=(0,r,0,r^2)$ and $(\tilde{x}_1,\tilde{x}_2,\tilde{x}_3,\tilde{\omega })=(r,0,1, r^2)$ where $r(\rho )=\min \{1,\frac{1}{2\rho }\}$. Obviously, both $(\hat{x}_1,\hat{x}_2,\hat{x}_3,\hat{\omega })$ and $(\tilde{x}_1,\tilde{x}_2,\tilde{x}_3,\tilde{\omega })$ belong to $S_2$. Then, $(\bar{x}_1,\bar{x}_2, \bar{x}_3, \bar{\omega }):= \frac{1}{2}(\hat{x}_1,\hat{x}_2,\hat{x}_3,\hat{\omega })+\frac{1}{2}(\tilde{x}_1,\tilde{x}_2,\tilde{x}_3,\tilde{\omega })=(\frac{r}{2},\frac{r}{2},\frac{1}{2},r^2)$ belongs to $\text{ Conv } (S_2)$. Projection of the points $(\hat{x}_1,\hat{x}_2,\hat{x}_3,\hat{\omega })$, $(\tilde{x}_1,\tilde{x}_2,\tilde{x}_3,\tilde{\omega })$ and $(\bar{x}_1,\bar{x}_2,\bar{x}_3, \bar{\omega })$ in the space of $x_1$ and $x_2$ can be depicted as points A, B and C, respectively, in Fig. 1. Because $(\bar{x}_1,\bar{x}_2,\bar{x}_3, \bar{\omega })\in \mathbf {conv}(S_2)$ and $-\bar{x}_1+\bar{x}_2=0$, the point $(\bar{x}_1,\bar{x}_2,\bar{x}_3,\bar{\omega })$ is a feasible solution of (33). Therefore,

$$\begin{aligned} z^\text {LD+}_{\rho }\le -\bar{x}_1- \bar{x}_2 +\rho \bar{\omega }=-r+\rho r^2 \le \max \left\{ -\frac{1}{2}, -\frac{1}{4\rho } \right\} <0=z^{\text {IP}}, ~~ \forall \rho >0 \end{aligned}$$

(34)

which shows $z^\text {LD+}_{\rho }< z^{\text {IP}}$ for all $\rho >0$, i.e. there is no finite $\rho ^*$ such that $z^\text {LD+}_{\rho ^*}= z^{\text {IP}}$. Note that the second inequality in (34) follows from the fact that

$$\begin{aligned} -r+\rho r^2= \left\{ \begin{array}{ll} -1+\rho \times 1^2=-1+\rho \le -\frac{1}{2} , &{}\quad \text {if } 0<\rho <\frac{1}{2}\\ -\frac{1}{2\rho } +\rho \times \left( \frac{1}{2\rho }\right) ^2=-\frac{1}{4\rho }, &{}\quad \text {if } \frac{1}{2}\le \rho . \end{array} \right. \end{aligned}$$

Example 1 showed that, for $\psi (\cdot )=\Vert \cdot \Vert _2^2$, there may exist MIP problems such that $z^\text {LD+}_{\rho }<z^\text {IP}$, for any finite value of $\rho$.

4.2.2 Exact ALD with the sharp Lagrangian for MIPs

Next, we show that using any norm as an augmenting function with a sufficiently large penalty coefficient closes the duality gap for general MIPs. One approach is to verify the calmness condition in Sect. 2.3 for the value function of an MIP. In this section, we provide a self contained proof for this result.

Theorem 4

Consider problem (1) with both integer and continuous variables. Suppose Assumption 1 holds, and $\psi ( \cdot )=\Vert \cdot \Vert$, where $\Vert \cdot \Vert$ is any norm. Then there exists a finite $0<\rho ^*<+\infty$ such that $z^\text {LD+}_{\rho ^*}=z^\text {IP}$.

Proof

First, let us show the result for $\psi ( \cdot )=\Vert \cdot \Vert _\infty$. Then, we extend it to any norm by the equivalence of norms in a Euclidean space. Let $\psi ( \cdot )=\Vert \cdot \Vert _\infty$ and $\varvec{1}_m$ be the m dimensional vector with all entries equal to 1. Then $S_\psi {=S_{\Vert .\Vert _\infty }}$ is a polyhedron,

$$\begin{aligned} \begin{aligned} {S_{\Vert .\Vert _\infty }}&= \left\{ (\varvec{x}, \omega ) \in \mathbb {R}^{n+1} : \Vert \varvec{b}-\varvec{Ax}\Vert _\infty \le \omega ,\; \varvec{x} \in X\right\} \\&= \left\{ (\varvec{x}, \omega ) \in \mathbb {Z}^{n_1} \times \mathbb {R}^{n_2+1} : -\varvec{1}_m \omega \le \varvec{b}-\varvec{Ax} \le \varvec{1}_m \omega , ~ \varvec{Ex}\le \varvec{f} \right\} . \end{aligned} \end{aligned}$$

(35)

Then, by Assumption 1 and due to Meyer’s theorem [20], there is a rational polyhedral representation for the set $\mathbf {conv}(S_{\Vert .\Vert _\infty }) \cap \{(\varvec{x},\omega ) \in \mathbb {R}^{n+1}:\varvec{Ax}=\varvec{b}\}$. Denote this representation by $\varvec{H} \left[ \begin{array}{c} \varvec{x} \\ \omega \end{array} \right] \ge \varvec{h}$, where $\varvec{H}\in \mathbb {Q}^{\hat{m}\times (n+1)}$ and $\varvec{h}\in \mathbb {Q}^{\hat{m}}$, for some finite integer $\hat{m}$. Then, by the primal characterization of ALD in Theorem 1, the ALD problem (7) for a given $\rho >0$ can be written as follows,

$$\begin{aligned} \begin{aligned} z_\rho ^\text {LD+}=\inf \limits _{ \varvec{x}, \omega } ~&~\varvec{c}^\top \varvec{x}+\rho \omega \\ \text{ s.t. }&\varvec{H} \left[ \begin{array}{c} \varvec{x} \\ \omega \end{array} \right] \ge \varvec{h}. \end{aligned} \end{aligned}$$

(36)

Note that, for a given $\rho >0$, problem (36) is an LP and its dual can be written as follows.

$$\begin{aligned} \begin{aligned} z_\rho ^\text {DLD+}:=\sup \limits _{\varvec{y}} ~&~\varvec{h}^\top \varvec{y} \\ \text{ s.t. }&\varvec{H}^\top \varvec{y} = \left[ \begin{array}{c} \varvec{c} \\ \rho \end{array} \right] \\&\varvec{y}\ge \varvec{0}. \end{aligned} \end{aligned}$$

(37)

Note that $z_\rho ^\text {LD+}=z_\rho ^\text {DLD+}$, since $z_\rho ^\text {LD+}>-\infty$ and by strong duality for LPs. We are interested in a finite positive $\rho ^*$ such that $z^{\text {LD+}}_{\rho ^*}\ge \varvec{c}^\top \varvec{x}^*$, where $\varvec{x}^*$ is an optimal solution of (1). The existence of such a $\rho ^*$ is equivalent to the existence of $(\varvec{y}^*,\xi ^*, \rho ^*)$ with $\xi ^*=0$ for the following feasibility problem in $(\varvec{y},\xi , \rho )$,

$$\begin{aligned} \begin{aligned} \varvec{h}^\top \varvec{y} +\xi&\ge \varvec{c}^\top \varvec{x}^*\\ \varvec{H}^\top \varvec{y}&= \left[ \begin{array}{c} \varvec{c} \\ \rho \end{array} \right] \\&\varvec{y}\ge \varvec{0}\\&\rho \ge 1\\&\xi \ge 0. \end{aligned} \end{aligned}$$

(38)

Let $\varXi$ be the projection of the feasible set of (38) into the $\xi$ space. Note that by Fourier-Motzkin Elimination, $\varXi$ is itself a polyhedron. Then, $\varXi$ is a closed set.

Consider a sequence $\xi _k\downarrow 0$ as $k\rightarrow +\infty$. Since $z_\rho ^\text {DLD+}=z_\rho ^\text {LD+}\le z^\text {IP}$ for any $\rho \ge 0$, and $\psi (\cdot )=\Vert \cdot \Vert _\infty$ satisfies Assumption 2, by Theorem 2, $z^\text {LD+}_{\rho } \uparrow z^\text {IP}=\varvec{c}^\top \varvec{x}^*$ as $\rho \rightarrow \infty$. By closedness of $\Xi$, $0\in \Xi$ because $\xi ^*=0$ is a cluster point of $\Xi$. That is, there exists some $\varvec{y}^*$ and $\rho ^*$ such that $(\varvec{y}^*,0, \rho ^*)$ is a feasible solution of (38). Therefore, $z^\text {LD+}_{\rho ^*}\ge z^\text {IP}$, which along with $z^\text {LD+}_{\rho ^*}$ being a lower bound for $z^\text {IP}$, we conclude $z^\text {LD+}_{\rho ^*}= z^\text {IP}=\varvec{c}^\top \varvec{x}^*$. Note that

$$\begin{aligned} \begin{aligned} z^\text {IP}&=\sup \limits _{\varvec{\lambda }\in \mathbb {R}^m} \inf \limits _{\varvec{x}\in X} ~ ~\varvec{c}^\top \varvec{x} + {\varvec{ \lambda }}^\top ( \varvec{b}-\varvec{Ax}) + \rho ^*\Vert \varvec{b}-\varvec{Ax}\Vert _\infty \\&= \sup \limits _{\varvec{\lambda }\in \mathbb {R}^m} \inf \limits _{ (\varvec{x}, \omega ) \in S_{\Vert \cdot \Vert _\infty }} ~ ~\varvec{c}^\top \varvec{x} + {\varvec{ \lambda }}^\top ( \varvec{b}-\varvec{Ax}) + \rho ^*\omega \\&=\sup \limits _{\varvec{\lambda }\in \mathbb {R}^m} \inf \limits _{ (\varvec{x}, \omega ) \in \mathbf {conv}(S_{\Vert \cdot \Vert _\infty })} ~ ~\varvec{c}^\top \varvec{x} + {\varvec{ \lambda }}^\top ( \varvec{b}-\varvec{Ax}) + \rho ^*\omega \\&= \inf \limits _{ (\varvec{x}, \omega ) \in \mathbf {conv}(S_{\Vert \cdot \Vert _\infty })} ~ ~\varvec{c}^\top \varvec{x} + \bar{\varvec{ \lambda }}^\top ( \varvec{b}-\varvec{Ax}) + \rho ^*\omega \\&= \inf \limits _{ (\varvec{x}, \omega ) \in S_{\Vert \cdot \Vert _\infty }} ~ ~\varvec{c}^\top \varvec{x} + \bar{\varvec{ \lambda }}^\top ( \varvec{b}-\varvec{Ax}) + \rho ^*\omega \\&= \inf \limits _{ \varvec{x} \in X} ~ ~\varvec{c}^\top \varvec{x} + \bar{\varvec{ \lambda }}^\top ( \varvec{b}-\varvec{Ax}) + \rho ^*\Vert \varvec{b}-\varvec{Ax}\Vert _\infty \end{aligned} \end{aligned}$$

(39)

for some finite $\bar{\varvec{\lambda }}\in \mathbb {R}^m$, where the second equality follows from definition of $S_{\Vert \cdot \Vert _\infty }$ in (35). The third and fifth equations hold because minimizing a linear objective function on a set is equivalent to minimizing it on the convex hull of that set. The fourth equality is valid by strong duality for LPs, because under Assumption 1 and due to Meyer’s theorem [20], $\mathbf {conv}(S_{\Vert \cdot \Vert _\infty })$ is a rational polyhedron. Due to this fact, $\bar{\varvec{\lambda }}$ is a finite vector. The last equality follow from definition of $S_{\Vert \cdot \Vert _\infty }$ in (35). Then,

$$\begin{aligned} \varvec{c}^\top \varvec{x} +\bar{\varvec{ \lambda }}^\top ( \varvec{b}-\varvec{Ax}) + \rho ^*\Vert \varvec{b}-\varvec{Ax}\Vert _\infty \ge z^\text {IP}, ~\forall \varvec{x}\in X \end{aligned}$$

Recall that for any norm $\Vert \cdot \Vert$ in finite dimensions there exists $0 < \gamma < 1$ such that $\frac{1}{\gamma }\Vert \varvec{u}\Vert \ge \Vert \varvec{u}\Vert _\infty \ge \gamma \Vert \varvec{u}\Vert$, by the equivalence of norms. Take $\hat{\rho }=\frac{\rho ^*}{\gamma }$. Then,

$$\begin{aligned} \varvec{c}^\top \varvec{x} +\bar{\varvec{ \lambda }}^\top ( \varvec{b}-\varvec{Ax}) + {\hat{\rho }} \Vert \varvec{b}-\varvec{Ax}\Vert \ge \varvec{c}^\top \varvec{x} +\bar{\varvec{ \lambda }}^\top ( \varvec{b}-\varvec{Ax}) + \rho ^*\Vert \varvec{b}-\varvec{Ax}\Vert _\infty , ~\forall \varvec{x}\in X \end{aligned}$$

which implies

$$\begin{aligned} z^\text {LD+}_{\hat{\rho }} \ge z^\text {LR+}_{\hat{\rho }} (\bar{\varvec{ \lambda }})= \inf \limits _{\varvec{x}\in X} ~ ~\varvec{c}^\top \varvec{x} + \bar{\varvec{ \lambda }}^\top ( \varvec{b}-\varvec{Ax}) + {\hat{\rho }} \Vert \varvec{b}-\varvec{Ax}\Vert \ge z^\text {IP} \end{aligned}$$

(40)

On the other hand, $z^\text {LD+}_{\hat{\rho }}\le z^\text {IP}$ by (8). Therefore, $z^\text {LD+}_{\hat{\rho }}=z^\text {IP}$. $\square$

Remark 4

Note that $\hat{\rho }$ and $\bar{\varvec{ \lambda }}$ in the proof of Theorem 4 satisfy the assumptions in Proposition 1. Therefore, any optimal solution of ALR (6) with ${\varvec{\lambda }}=\bar{\varvec{\lambda }}$ and $\rho >\hat{\rho }$ solves the MIP problem (1).

Next, we show that the value of $\bar{\varvec{\lambda }}$ in the proof of Theorem 4 really does not matter.

Proposition 8

Consider problem (1) under Assumption 1. Suppose $\psi ( \cdot )=\Vert \cdot \Vert$, where $\Vert \cdot \Vert$ is any norm. For any $\tilde{\varvec{\lambda }}\in \mathbb {R}^m$, there exists a finite $\rho ^*(\tilde{\varvec{\lambda }})$ such that $z^\text {LR+}_{\rho ^*}(\tilde{\varvec{\lambda }})=z^\text {IP}$.

Proof

Let $\hat{\rho }$ and $\bar{\varvec{\lambda }}$ be as considered in (40). By the equivalence of norms, there exists $0 < \gamma < 1$ such that $\frac{1}{\gamma }\Vert \varvec{u}\Vert \ge \Vert \varvec{u}\Vert _2 \ge \gamma \Vert \varvec{u}\Vert$. From Cauchy–Schwarz inequality, for all ${\varvec{x}}\in X$, it holds

$$\begin{aligned}&\tilde{\varvec{\lambda }}^\top ( \varvec{b}-\varvec{Ax}) \ge - \Vert \tilde{\varvec{\lambda }}\Vert _2 \Vert \varvec{b}-\varvec{Ax}\Vert _2 \ge - \frac{1}{\gamma }\Vert \tilde{\varvec{\lambda }}\Vert _2 \Vert \varvec{b}-\varvec{Ax}\Vert , \\&\quad \bar{\varvec{\lambda }}^\top ( \varvec{b}-\varvec{Ax}) \le \Vert \bar{\varvec{\lambda }}\Vert _2 \Vert \varvec{b}-\varvec{Ax}\Vert _2 \le \gamma \Vert \bar{\varvec{\lambda }}\Vert _2 \Vert \varvec{b}-\varvec{Ax}\Vert , \end{aligned}$$

and consequently,

$$\begin{aligned} \tilde{\varvec{\lambda }}^\top ( \varvec{b}-\varvec{Ax}) \ge \bar{\varvec{\lambda }}^\top ( \varvec{b}-\varvec{Ax}) -\left( \frac{1}{\gamma }\Vert \tilde{\varvec{\lambda }}\Vert _2 +\gamma \Vert \bar{\varvec{\lambda }}\Vert _2 \right) \Vert \varvec{b}-\varvec{Ax}\Vert . \end{aligned}$$

(41)

Take $\rho ^*=\hat{\rho }+\left( \frac{1}{\gamma }\Vert \tilde{\varvec{\lambda }}\Vert _2 +\gamma \Vert \bar{\varvec{\lambda }}\Vert _2 \right)$. Then,

$$\begin{aligned} \begin{aligned} \varvec{c}^\top \varvec{x} + \tilde{\varvec{\lambda }}^\top ( \varvec{b}-\varvec{Ax}) + \rho ^*\Vert \varvec{b}-\varvec{Ax}\Vert \ge \varvec{c}^\top \varvec{x} + \bar{\varvec{\lambda }}^\top ( \varvec{b}-\varvec{Ax}) + \hat{\rho } \Vert \varvec{b}-\varvec{Ax}\Vert . \end{aligned} \end{aligned}$$

(42)

By taking $\inf \limits _{\varvec{x}\in X}$ from both sides of (42) and considering (40) it is implied that $z^\text {LR+}_{\rho ^*}(\tilde{\varvec{\lambda }})\ge z^\text {IP}$. This result along with $z^\text {LR+}_{\rho ^*}(\tilde{\varvec{\lambda }})$ being a lower bound for $z^\text {IP}$, concludes $z^\text {LR+}_{\rho ^*}(\tilde{\varvec{\lambda }})=z^\text {IP}$. $\square$

Next, we extend Theorem 4 to a more general class of augmenting functions than norms.

Theorem 5

Consider an MIP problem (1) satisfying Assumption 1. Then, there exists a finite $\hat{\rho }$ such that $z^\text {LD+}_{\hat{\rho }}=z^\text {LR+}_{\hat{\rho }}(\bar{\varvec{\lambda }}_\text {LP})=z^\text {IP}$ if $\psi$ is an augmenting function such that

• $\psi (\varvec{0})=0$,

• $\psi (\varvec{u})\ge \delta >0$, for all $\varvec{u}\notin V$,

• $\psi (\varvec{u})\ge \gamma \Vert \varvec{u}\Vert _\infty$, for all $\varvec{u}\in V$,

for some open neighborhood V of $\varvec{0}$, and positive scalars $\delta , \gamma >0$.

Proof

From Proposition 8, there exists a finite $\rho ^*$ such that $z^\text {LR+}_{\rho ^*}(\bar{\varvec{\lambda }}_\text {LP})=z^\text {IP}$ for $\psi (\cdot )=\Vert \cdot \Vert _\infty$. Now, consider the cases where $\psi$ is not a norm but it satisfies the conditions stated above. Take $\hat{\rho }=\max \left\{ \frac{z^\text {IP} -z^\text {LP}}{\delta }, \frac{\rho ^*}{\gamma } \right\}$. There are two cases.

• 1. For all $\varvec{x}\in X$ such that $(\varvec{b}- \varvec{A}\varvec{x} ) \notin V$, it holds

  $$\begin{aligned} \begin{aligned} \varvec{c}^\top \varvec{x} +\bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}- \varvec{A}\varvec{x}) +\hat{\rho } \psi (\varvec{b}- \varvec{A}\varvec{x} )&\ge z^\text {LP}+\hat{\rho } \psi (\varvec{b}- \varvec{A}\varvec{x} ) \\&\ge z^\text {LP}+\frac{z^\text {IP} -z^\text {LP}}{\delta } \psi (\varvec{b}- \varvec{A}\varvec{x} )\\&\ge z^\text {LP} +z^\text {IP} -z^\text {LP} \\&\ge z^\text {IP} \end{aligned} \end{aligned}$$

• 2. For all $\varvec{x}\in X$ such that $(\varvec{b}- \varvec{A}\varvec{x} ) \in V$, it holds

  $$\begin{aligned} \begin{aligned} \varvec{c}^\top \varvec{x} +\bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}- \varvec{A}\varvec{x}) +\hat{\rho } \psi (\varvec{b}- \varvec{A}\varvec{x} )&\ge \varvec{c}^\top \varvec{x} +\bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}- \varvec{A}\varvec{x}) + \frac{\rho ^*}{\gamma } \psi (\varvec{b}- \varvec{A}\varvec{x}) \\&\ge \varvec{c}^\top \varvec{x} +\bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}- \varvec{A}\varvec{x}) + \rho ^*\Vert \varvec{b}- \varvec{A}\varvec{x} \Vert _\infty \\&\ge z^\text {IP}. \end{aligned} \end{aligned}$$

Then,

$$\begin{aligned} \varvec{c}^\top \varvec{x} +\bar{\varvec{\lambda }}_\text {LP}^\top (\varvec{b}- \varvec{A}\varvec{x}) + \hat{\rho } \psi (\varvec{b}- \varvec{A}\varvec{x} )\ge z^\text {IP}, \; \forall \varvec{x}\in X, \end{aligned}$$

(43)

which implies $z^\text {LD+}_{\hat{\rho }}\ge z^\text {LR+}_{\hat{\rho }}(\bar{\varvec{\lambda }}_\text {LP})\ge z^\text {IP}$. This result along with $z^\text {LR+}_{\hat{\rho }}(\bar{\varvec{\lambda }}_\text {LP})$ being a lower bound for $z^\text {IP}$, concludes $z^\text {LR+}_{\hat{\rho }}(\tilde{\varvec{\lambda }})=z^\text {IP}$. $\square$

Remark 5

It is easy to check that for any norm $\Vert \cdot \Vert$ and scalar r with $0<r<1$, the non-convex function $\psi (\cdot )=\Vert \cdot \Vert ^r$ satisfies the conditions stated in Theorem 5.

5 Conclusions and final remarks

In this paper we studied ALD for general linear MIP problems. We presented a primal characterization of ALD for MIPs and showed the asymptotic zero duality gap property with non-negative level bounded and not necessarily convex augmenting functions. Moreover, we showed that under some mild assumptions, ALD achieves zero duality gap for general MIPs with a finite penalty coefficient and a general class of augmenting functions. We also showed that some augmenting functions such as the squared Euclidean norm are exact in the pure IP cases, but there exists MIP counterexamples for which these augmenting functions may result in a non-zero duality gap for any value of the penalty coefficient.

Solving IP and MIP problems by ALD may have computational advantages over the classical Lagrangian relaxation approaches, since ALD may produce better dual bounds and provide primal solutions. The main drawback of ALR and ALD methods is that the resulting subproblems are not separable because of the nonlinear augmenting functions. To overcome this issue, the alternating direction method of multipliers (ADMM) [8] and related schemes have been developed for convex optimization problems. However, it is not at all clear how to decompose ALD for MIP and more general nonconvex problems and utilize parallel computation. Based on ADMM, a heuristic decomposition method was developed in [16] to solve MIPs arising from electric power network unit commitment problems. In a continuous and non-convex setting, a decomposition approach using ADMM was developed for the AC optimal power flow problem in electric power grid optimization [31]. Further developing theories and algorithms to solve ALD for MIPs and general non-convex optimization problems with decomposition schemes is an important future research direction. Another interesting research topic would be to determine subclasses of MIPs where strong duality holds with a provably “small” value of $\rho$.