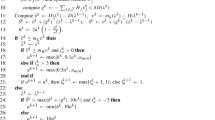1 Introduction

Stochastic mixed-integer programs (SMIPs) have long been recognized as an important class of models for many practical operational problems (see e.g. [26]). However, algorithmic advances to solve SMIP models have lagged behind other forms of stochastic programs. In addition to the standard difficulties associated with stochastic linear programming (e.g. designing scalable ways to approximate the expected recourse/value function), SMIP formulations with mixed-integer recourse decisions in the second stage encounter value functions that are possibly non-convex and discontinuous. Early work by Carøe and Tind [4] presented a decomposition algorithm based on mixed integer programming (MIP) duality, and while it is conceptually applicable to SMIPs with general mixed-integer recourse decisions, the algorithm is not easily realizable because it requires calculations involving exact MIP value functions. Such value functions are not only difficult to construct for the second stage, but also lead to discontinuous and non-convex first-stage approximations in general. Other decomposition algorithms, based on scenario decomposition, were proposed in [5, 14]. These algorithms essentially view the SMIP problem as a very large scale MIP using a deterministic equivalent formulation. The decomposition principles used by the above methods are dual to each other (price and resource directive decomposition respectively) and may be recommended for instances in which special structures associated with scenario subproblems can be exploited (as in unit-commitment models, lot-sizing models etc.). However, when the number of scenarios is very large, and special structures are either absent or difficult to exploit, such scenario decomposition methods are not particularly effective.

Subsequent to the work of Carøe and Tind [4], most authors addressed some sub-class of the two-stage SMIP problems. For instance, the global optimization algorithm of Ahmed et al. [1] assumed fixed tenders in the two-stage model. Others have addressed alternative sub-classes which either focus on mixed-binary recourse decisions, or pure integer recourse decisions. Decomposition-based cutting plane algorithms using disjunctive cuts (e.g. [15, 21, 24]), using Gomory cuts (e.g. [10, 28]), novel branch-and-bound methods [9], decomposition based branch-and-cut [23], as well as primal approaches using certain IP value function characterizations [12, 25] now offer a range of algorithms for alternative model characteristics. As a consequence of the sharper focus, there has been significant progress with SMIP algorithms for specialized cases of SMIP. In contrast to some of the earlier multi-stage SMIP algorithms, these methods are based on time-staged decomposition, very much in the spirit of Benders’ decomposition. We refer to surveys by Louveaux and Schultz [13] and Sen [20] for discussions related to these and other advances.

In this paper, we are interested in designing time-staged decomposition algorithms for solving two-stage SMIPs in which mixed-integer decisions appear in both stages. In other words, we return to the class of models addressed in [4]. Fortunately, due to significant algorithmic advances in the interim, we are able to draw upon new approximations which not only ensure finite convergence, but also avoid intractable operations in each iteration. The first thought which comes to mind for addressing problems with general integer variables is to replace the general integers by their binary expansion, thus, converting the general SMIP problem to one with mixed-binary variables. However, such transformations have already been discredited in the deterministic MIP literature where Owen and Mehrotra [18] have shown, mathematically and computationally, that branch-and-bound methods examine many more nodes for the transformed problem, than for the original instance with general integer variables. Consequently, the issue of devising decomposition algorithms using branch and cut methods for SMIP remains an open question which we address in this paper. Perhaps, the most critical result that helps us resolve this open question is the recent constructive characterization due to Chen et al. [7] that the feasible set of a mixed-integer linear program can be convexified using a hierarchy of multi-term disjunctions. This result helps us design the Ancestral Benders’ Cutting Plane (\(\mathbf {ABC}\)) algorithm presented in this paper.

In order to state the problem, let \(A \in {\mathbb {R}}^{m_1 \times n_1}, b \in {\mathbb {R}}^{m_1}\), and \(X_L = \{x \in {\mathbb {R}}^{n_1}: Ax \le b\}\). Then consider the SMIP as stated below.

$$\begin{aligned} \min _{x\in X \cap Q_1} c^\mathsf {T} x + \mathsf {E}\left[ f(x,\tilde{\omega })\right] \end{aligned}$$
(1)

where

$$\begin{aligned} X=&\left\{ x \in X_L \ | \ x_i \ \mathrm {is} \ \mathrm {integer}, \quad \forall i \in I_2 \subseteq I_1 =\{1,\ldots ,n_1\} \right\} \subseteq {\mathbb {R}}^{n_1},\\ \mathrm {and} \ Q_1=&\{x \ | \ l_1 \le x \le u_1\}. \end{aligned}$$

Also \(\tilde{\omega }\) denotes a discrete random variable, and for each scenario (realization) \(\omega \) of \(\tilde{\omega }\), we define the recourse function by

$$\begin{aligned} f(x,\omega )=\min&\quad g(\omega )^\top y\nonumber \\ \text {s.t.}&\quad W(\omega ) y\ge r(\omega )-T(\omega )x\nonumber \\&\quad y \in Y \cap Q_2, \end{aligned}$$
(2)

where,

$$\begin{aligned} Y&=\left\{ y \ | y_j \ \mathrm {is} \ \mathrm {integer}, \quad \forall j \in J_2 \subseteq J_1 =\{1,\ldots ,n_2\} \right\} \subseteq {\mathbb {R}}^{n_2},\\ \mathrm {and} \ Q_2&=\{y \ | l_2 \le y \le u_2\}. \end{aligned}$$

For subproblem (2), we let the decision variable \(y \in {\mathbb {R}}^{n_2}\), objective coefficient \(g(\omega ) \in {\mathbb {R}}^{n_2}\), constraint matrix \(W(\omega ) \in {\mathbb {R}}^{m_2 \times n_2}\), \(r(\omega ) \in {\mathbb {R}}^{m_2} \) and \(T(\omega ) \in {\mathbb {R}}^{m_2 \times n_1}\). In our notation, when \(I_2 (J_2)\) is a strict subset of \(I_1 (J_1)\), then stage 1 (stage 2) has both continuous as well as integer variables. We assume the random variable \(\tilde{\omega }\) is discrete with each scenario \(\omega \) having a non-zero probability \(p(\omega )\), for all \(\omega \in \Omega \).

The algorithms that we propose in this paper impose the following assumptions on the model.

A1 :

Both X and Y are assumed to be non-empty mixed-integer sets, and the integer variables in both stages are bounded.

A2 :

The random variable \(\tilde{\omega }\) in the problem is discrete, with a finite number of scenarios, \(\omega \in \Omega \), each with an associated non-zero probability of occurrence \(p(\omega ) , \forall \omega \in \Omega \).

A3 :

For any \(x \in X_L \cap Q_1\), the set defined by \(\{y \ | \ W(\omega )y \ge r(\omega ) - T(\omega ) x, y \in Y \cap Q_2\}\) is feasible for all \(\omega \in \Omega \).

Due to assumption A2, (1) can be rewritten as:

$$\begin{aligned} \min _{x\in X \cap Q_1} c^\mathsf {T} x + \sum _{\omega \in \Omega }p(\omega ) f(x,\omega ). \end{aligned}$$
(3)

For the rest of the paper, we begin by first introducing the overall architecture in which a branch-and-bound (B&B) algorithm in the first-stage controls how approximations are created and passed from one generation of nodes to another. Subsequently, we present two closely related convexification schemes for the second stage, one based on the cutting plane tree method [7], and the other referred to as a B&B-based convexification method. Both of these methods can be used to approximate the second-stage recourse function \(f(x,\omega )\). Finally, we illustrate our approach by using several variants of an SMIP example from the literature. In addition we present preliminary evidence that the decomposition framework promises to be more scalable than solving a deterministic equivalent problem (3) using a standard commercial MIP solver. We also present a new class of test instances which we refer to as Stochastic Server Location and Sizing. Computational experience with these instances demonstrates that under some restrictions on the growth of first-stage decisions, the algorithm provides a realistic approach to solving SMIP models with many scenarios. Overall, our framework provides the most comprehensive time-staged decomposition approach to date, allowing randomness in all data elements, while also allowing general mixed-integer variables as decision variables in both stages.

2 The Ancestral Benders’ cutting plane algorithm

If we denote decision variables y under scenario \(\omega \) as \(y(\omega )\), the deterministic equivalent formulation (DEF) for (3) is

$$\begin{aligned} \min _{x, y(\omega )}&\quad c^\top x + \sum _{\omega \in \Omega }p(\omega ) g(\omega ) ^\top y(\omega ) \end{aligned}$$
(4a)
$$\begin{aligned} \text {s.t.}&\quad T(\omega ) x + W(\omega ) y(\omega ) \ge r(\omega ), \quad \forall \omega \in \Omega \end{aligned}$$
(4b)
$$\begin{aligned}&\quad x \in X \cap Q_1, y(\omega ) \in Y \cap Q_2, \quad \forall \omega \in \Omega . \end{aligned}$$
(4c)

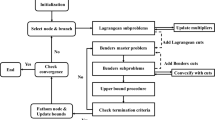
Figure 1 shows the basic building blocks of the \(\mathbf {ABC}\) algorithm.

Fig. 1
figure 1

Building blocks for the \(\mathbf {ABC}\) algorithm

Full size image

It uses a branch-and-bound process to search for first-stage decisions while carrying out a convexification process in the second stage (see the box on the bottom right hand side), followed by a successive approximation scheme to update approximations of the expected recourse function \(E[f(x,\tilde{\omega })]\) in the top box of Fig. 1. These ingredients provide a fully integrated algorithm which ties together all the pieces in a manner that is not only computationally realistic, but is also provably convergent. A brief description of the elements in Fig. 1 follows.

  1. (a)

    The B&B search in the first stage divides the range of first-stage integer variables into a partition consisting of disjoint subsets \(\{Q_1^t\}\) covering the entire set \(Q_1\). The partition is refined using a breadth-first search strategy.

  2. (b)

    For any subset \(Q_1^t\) of the first-stage decisions (x), we create polyhedral approximations of

    $$\begin{aligned} \mathcal {Z}(t,\omega ):= & {} \big \{(x,y(\omega )) \ | \ T(\omega ) x\nonumber \\&+\, W(\omega ) y(\omega ) \ge r(\omega ) , x \in X \cap Q^{t}_1, y(\omega ) \in Y \cap Q_2\big \}. \end{aligned}$$
    (5)

    The existence and construction of the polyhedral set follows the work of Chen et al. [6] on using multi-term disjunctions.

  3. (c)

    Using Benders’ decomposition for each box \(Q^t_1\), we then create lower bounding approximations. Using these bounds, one can proceed to partition the most promising node, and continue with the branch-and-bound search.

Clearly, the above ideas are fairly straightforward. As with most stochastic programming algorithms however, the effectiveness of any scheme depends on the ease with which approximations are updated and optimized, sequentially. In addition, implementing these processes requires us to assemble a variety of concepts, including disjunctive programming, L-shaped decomposition, and appropriate data structures. In this section, we provide a summary of these aspects of the \(\mathbf {ABC}\) algorithm. In the following section, we discuss multi-term disjunctions based on either the cutting plane tree (CPT) algorithm [6] or a branch-and-bound algorithm.

We use index k to denote an iteration. As in other Benders’ type algorithms, we let \(x^k\) denote the first stage decisions in iteration k. Let t(k) denote a node of the first-stage B&B tree such that \(x^k \in Q_1^{t(k)}\). A B&B tree for the first stage provides a partition \(\{Q^t_1\}\) of the box constraints \(Q_1.\) In addition to node t’s bounds \(Q_1^{t}\), \(\mathcal {Z}(t,\omega )\) covers all constraints for variables x and \(y(\omega )\). Next, we introduce a polyhedral approximation \({\mathcal {Z}_L}(t,\omega )\) such that

$$\begin{aligned} {\mathcal {Z}_L}(t,\omega ) \supseteq \mathbf {conv}\{\mathcal {Z}(t,\omega )\}. \end{aligned}$$
(6)

This approximation \(\mathcal {Z}_L(t,\omega )\), will be generated using a convexification procedure due to Chen et al. [6]. Since the approximations are in the space of variables \((x, y(\omega ))\), the polyhedron \({\mathcal {Z}_L(t, \omega )}\) includes valid inequalities appended to the linear inequalities already in (5). That is,

$$\begin{aligned} \mathcal {Z}_L (t, \omega ):= & {} \big \{(x, y(\omega )) \ | T(\omega ) x + W(\omega ) y(\omega ) \ge r(\omega ), x \in X_L \cap Q^{t}_1,y(\omega ) \in Q_2, \nonumber \\&\Pi _1(t, \omega ) x + \Pi _2(t, \omega ) y \ge \Pi _0 (t, \omega ) \big \}, \end{aligned}$$
(7)

where the additional constraints in (7) represent the valid inequalities. Note that because of assumption A3, the projection of this set for any \(x \in Q_1\) is non-empty. It is important to point out that the coefficients \(\Pi _1(t,\omega )\), and the first stage decision \(x^k\) will be used to create right-hand side parameters of second stage subproblems. As a result, such inequalities are referred to as parametric cuts, and are useful for “warm-starting” approximations as \(Q_1\) is successively refined in the B&B process.

Since the inequalities in (7) are valid for the entire set \(Q_1^{t}\), they can be re-used for any of its subsets. At iteration k, we can define a lower bounding approximation of the second-stage objective by an approximation \(f^{k,t}_L(x,\omega )\) as follows

$$\begin{aligned} f^{k,t}_L(x,\omega ) := \min \left\{ g(\omega )^\top y(\omega ) : \ (x,y(\omega )) \in \mathcal {Z}^k_L(t,\omega ) \right\} . \end{aligned}$$
(8)

where \(\mathcal {Z}^k_{L} (t, \omega )\) includes only a subset of the inequalities of (7) revealed in the first k iterations.

$$\begin{aligned} \mathcal {Z}^k_{L} (t, \omega )= & {} \left\{ (x, y(\omega )) \ | \ T(\omega ) x + W(\omega ) y(\omega ) \ge r(\omega ), x \in X_L \cap Q^{t}_1,\right. \end{aligned}$$
(9)
$$\begin{aligned}&\Pi ^k_1(t, \omega ) x + \Pi ^k_2(t, \omega ) y(\omega ) \ge \Pi ^k_0 (t, \omega ), \end{aligned}$$
(10)
$$\begin{aligned}&\left. l_2 \le y(\omega ) \le u_2 \right\} . \end{aligned}$$
(11)

The constraints in \(\mathcal {Z}^k_L (t, \omega )\) are best treated as constraints that evolve through the iterations, that is, let \(W^{k}(t, \omega )={\left[ \begin{array}{c} W(\omega )\\ \Pi ^{k}_2(t, \omega ) \end{array} \right] }\), and similarly, \(T^{k}(t, \omega )={\left[ \begin{array}{c} T(\omega )\\ \Pi ^{k}_1(t, \omega ) \end{array} \right] }\), \(r^{k}(t, \omega )={\left[ \begin{array}{c} r(\omega )\\ \Pi ^{k}_0(t, \omega ) \end{array} \right] }\). Then a relaxation of the integer recourse (or value) function can be obtained as in Benders’ decomposition by using the dual multipliers of the above cut-enhanced LP relaxation, for any choice of \(x \in Q^{t}_1\).

Unlike standard Benders’ decomposition (which is normally applied to the case where the second stage is a linear program), the subproblem (8) is a relaxation of the MIP subproblem. Let \(y^k(\omega )\) denote the optimal solution for (8) given \(x = x^k\). Let \(\Theta ^{k}(t,\omega )\) denote the optimal dual multipliers associated with (9) and (10) and \(\theta ^{k}_l(t,\omega )\), \(\theta ^{k}_u(t,\omega )\) denote the multipliers associated with constraints (11). Then the Benders’ approximation from (8) is given as

$$\begin{aligned} \eta (t, \omega )\ge & {} \Theta ^{k}(t, \omega )^\top r^{k}(t, \omega ) + \theta ^{k}_l(t, \omega )^\top l_2 \nonumber \\&\quad - \theta ^{k}_u(t, \omega )^\top u_2 -\Theta ^{k}(t, \omega )^\top T^{k}(t, \omega ) x, \quad \mathrm {for}\ x \in Q^{t}_1 \end{aligned}$$
(12)

where \(\eta (t,\omega )\) is the variable representing the recourse function for the pair \((t, \omega )\). Finally, the above cuts are aggregated using all \(\omega \in \Omega \) as in a Benders’ cut for node t. In other words, let

$$\begin{aligned} \xi ^{k, t}&=\sum _{\omega \in \Omega }p(\omega )\left( \Theta ^{k}(t, \omega )^\top r^{k}(t, \omega )+ \theta ^{k}_l(t, \omega )^\top l_2 - \theta ^{k}_u(t, \omega )^\top u_2\right) , \nonumber \\ \zeta ^{k, t}&= \left( \sum _{\omega \in \Omega }p(\omega )\Theta ^{k}(t, \omega )^\top T^{k}(t, \omega ) \right) ^\top . \end{aligned}$$
(13)

We define \(\eta _t\) as the value function cut variable for node t. Then the Benders’ cut at iteration k for node t is as follows,

$$\begin{aligned} \eta _t \ge \xi ^{k, t}-(\zeta ^{k, t})^\top x, \quad \mathrm {for}\ x \in Q^{t}_1. \end{aligned}$$
(14)

Recall that Benders’ cuts generated for \(Q^t_1\) can be used for all subsets \(Q'_1 \subseteq Q^t_1\). Similar inheritance also holds for the second-stage cuts in (10). In order to help record this inheritance we use index set \(\mathcal {G}_x(t)\) to record Benders’ cuts for node t and \(\mathcal {G}_z(t, \omega )\) as the index set for the second-stage cuts. Both \(\mathcal {G}_x(t)\) and \(\mathcal {G}_z(t, \omega )\) start as empty sets, and when a new valid cut is derived for node t, either \(\mathcal {G}_x(t)\) or \(\mathcal {G}_z(t, \omega )\) are enlarged depending on whether it is a Benders’ cut or a second stage (parametric) cut.

We now proceed to discuss the B&B method for the first stage. Suppose the set of active (unfathomed) nodes for the first stage is denoted as \(\mathcal {T}^k_1\) and let \(Q^t_1\) denote the bounding constraints for \(t \in \mathcal {T}_1\). Then the lower bounding master problem for node t at iteration k is as follows,

$$\begin{aligned} \min&\quad c^\top x+\eta _t \end{aligned}$$
(15a)
$$\begin{aligned} \text {s.t.}&\quad \eta _t \ge \xi _s-\zeta _s^\top x , \quad \text {for} \ \forall s \in \mathcal {G}_x(t) \end{aligned}$$
(15b)
$$\begin{aligned}&\quad \eta _t \ge -M , \end{aligned}$$
(15c)
$$\begin{aligned}&\quad x \in X_L \cap Q^t_1, \end{aligned}$$
(15d)

where \(-M\) is a valid lower bound on second-stage expected recourse function. In problem (15), \(Q^t_1\) will include ranges \([l_{1i}^t,u_{1i}^t]\) which denote the ranges for variable \(x_i\) at node t.

The entire algorithm starts from iteration \(k=1\) with \(\mathcal {T}^k _1=\{o\}\) where the root node o has bounding constraints \(Q^o_1\equiv Q_1\) and we initialize \(\mathcal {G}_x(t)\) as an empty set. Let the optimal objective value for (15) be \(v^t\) and let \(x^t\) denote an optimal first-stage solution. Thus, the global lower bound is \(v \equiv \min _{t \in \mathcal {T}^k_1} \{v^t \}\). Also denote the upper bound of optimal objective value for (1) by V. At iteration k, problem (15) is solved for node \(t(k-1)\) with updated (15b) from iteration \(k-1\) and for our breadth-first approach, we choose the node with the least lower bound as the node to branch on. Suppose this node is \(\bar{t}\) and its optimal first-stage solution is \(x^{\bar{t}}\). Having selected the node, one chooses the variable to be used for branching. We follow a common rule which uses the least relative fractional variable as follows. Let

$$\begin{aligned} \delta _i=\min \left\{ x^{\bar{t}}_i-l^{\bar{t}}_{1i}, u^{\bar{t}}_{1i}-x^{\bar{t}}_i\right\} , \end{aligned}$$
(16)
$$\begin{aligned} p\in \mathrm {argmax}_{i \in I_2, u^{\bar{t}}_{1i} \ne l^{\bar{t}}_{1i}, \delta _i >0}\left\{ \frac{\delta _i}{u^{\bar{t}}_{1i} -l^{\bar{t}}_{1i} }\right\} . \end{aligned}$$
(17)

Then we select variable \(x_p\) and split its bounding constraint \([l_{1p},u_{1p}]\) as shown in (18)

$$\begin{aligned}{}[l_{1p},\lfloor x_p \rfloor ] \ \text {and} \ [\lceil x_p \rceil ,u_{1p}]. \end{aligned}$$
(18)

The two newly created nodes are denoted as \(\bar{t}^1, \bar{t}^2\). Both \(\mathcal {G}_x(t)\) and \(\mathcal {G}_z(t, \omega ), \forall \omega \in \Omega \) are copied to initialize \(\mathcal {G}_x(\bar{t}^1)\), \(\mathcal {G}_x(\bar{t}^2)\) and \(\mathcal {G}_z(\bar{t}^1, \omega )\), \(\mathcal {G}_z(\bar{t}^2, \omega ) \forall \omega \in \Omega \). Then the tree is updated as follows,

$$\begin{aligned} \mathcal {T}^k_1 \leftarrow \left\{ \mathcal {T}^k_1 \setminus {\bar{t}}\right\} \cup \left\{ \bar{t}^1, \bar{t}^2\right\} . \end{aligned}$$
(19)

We then solve the LP relaxation associated with the two new nodes, update the upper bound (if possible), and choose the node with the least lower bound to explore further. This process continues until a mixed-integer optimum is found.

The B&B process for the first stage is flexible, allowing us to either do a few iterations, or solving the first stage approximation to optimality. When a solution (denoted as \(x^k\)) to the master problem is found, we identify the first-stage node to which it belongs, and refer to it as t(k) and its bounding constraints as \(Q_1^{t(k)}\). Given \(x^k\) and \(Q_1^{t(k)}\), we approximate the second-stage recourse function for all \(\omega \) as described in (14). With Benders’ cut indexed in \(\mathcal {G}_x(t)\) updated, the master problem continues to find new integer solutions and updating nodal value functions until the node is fathomed, or the algorithm stops. A summary of the prescribed process is shown in Algorithm 1, and we refer to it as the \(\mathbf {ABC}\) algorithm.

figure a

The sufficient conditions for convergence of the \(\mathbf {ABC}\) algorithm are provided in the following proposition, which is consistent with sufficient conditions for finiteness of B&B methods. The precise cutting planes to be used are postponed to the following section where we will demonstrate how multi-term disjunctions ensure that these conditions are satisfied.

Proposition 1

Let assumptions A1–A3 hold. In iteration k, let t(k) denote the index identifying the subset \(Q_1^{t(k)}\) for which a lower bound \(v^{t(k)}\) is evaluated in iteration k. Let \(V^k\) denote an upper bound on the optimum at iteration k. Suppose that for any subset \(Q_1^t\) created during the B&B process, there exists a finite iteration K(t) such that for \(k\ge K(t)\) with \(t(k)=t\), we either have \(v^{t}\ge V^k\) or \(f_L^{k,t} (x^k, \omega ) = f(x^k, \omega )\) for all \(\omega \in \Omega \). Then, the \( B \& B\) procedure produces an optimal solution \(x^*\), as well as its optimal value \(V^*\) in finitely many iterations.

Proof

Let \(K = K(t)\) be an iteration such that \(t(K) = t\) and either the lower bound for node t matches or exceeds the global upper bound (i.e. \(v^{t} := c^\top x^K + E[f_L^{K,t} (x^K, \omega )] \ge V^K \ge V^*\)), or the lower bound for node t matches the true second-stage cost at node t (i.e. \(f_L^{K,t} (x^K, \omega ) = f(x^K, \omega )\)) for all outcomes \(\omega \in \Omega \). In case the former holds true, node t is deleted from further consideration, while if the latter holds true, there are two possibilities: either \(x^K\) satisfies the mixed-integer requirements or not. In case of the former, the B&B process deletes the node \(Q_1^t\), and possibly updates the upper bound using the value \(V^K\). On the other hand (i.e. \(x^K\) does not satisfy the MIP requirements) the node \(Q_1^t\) is replaced by two other descendant nodes in the first stage. Thus the only case for which the number of B&B nodes increases in the first stage is when the node \(Q_1^t\) is replaced by two descendant nodes. Due to the finiteness of bounds defining \(Q_1\), this subdivision can happen only finitely many times. Therefore, after finitely many iterations, the nodal solution \(x^K\) cannot violate the mixed-integer restrictions. Hence one of the nodes of the B&B tree must reveal a mixed-integer solution \(x^K\) which becomes the incumbent and its optimal value \(V^K\) provides the value \(V^*\) in finitely many steps.

3 Approximations using multi-term disjunctions

This section presents two approaches for approximating the second-stage recourse function. Both methods convexify the set of feasible solutions of the second stage. However, one of these is based on a pure cutting plane approach, while the other performs a convexification prompted by a B&B tree.

3.1 Convexification using pure cutting planes

Until recently, the question of computing the convex hull of mixed-integer points which satisfy a system of rational linear inequalities was open. For example, Owen and Mehrotra [17] and Balas [2] have shown that for general MIP, traditional two-term disjunctive cuts [3] are inadequate to the task of satisfying the conditions of Proposition 1. The above question was resolved by Del Pia and Weismantel [8], although their characterization is not based on an algorithmic construction. For the case of bounded mixed-integer sets, Chen et al. [6] present two algorithms for constructing polyhedral approximations which provide the same solution as the original MIP in finitely many iterations. One of the algorithms, the convex hull tree algorithm, essentially provides a proof technique, and is not recommended as a solution methodology. The other algorithm, the cutting plane tree (CPT) algorithm, is a sequential cutting plane scheme which generates a finite sequence of cuts which, in the worst case, verifies that the polyhedral approximation provides an optimal solution which is the same as the MIP solution. This method may be summarized as one that generates cutting planes from a hierarchy of multi-term disjunctions which are recorded in the form of nodes of a search tree. So long as each visit to a node (i.e. a multi-term disjunction) generates one facet of the disjunction, and nodes can only be visited finitely many times, finiteness of the number of multi-term disjunctions implies that the CPT algorithm converges in finitely many iterations. We refer the reader to Chen et al. [6] for the details, and Chen et al. [7] for computational results for deterministic MIP problems. Another similar result has been proposed by Jörg [11], although its computability is not clear as of this writing. In any event, the method of Chen et al. [6] is able to deliver the property required by Proposition 1. Because these multi-term disjunctions are intimately tied to the CPT algorithm, we refer to the resulting cuts as “CPT cuts”.

Suppose that at the k-th iteration of \(\mathbf {ABC}\) algorithm, we have a fixed \(x^k \in X_L\cap Q_1^{t(k)}\) and are given an initial approximation \(f^{k,t(k)}_L(x, \omega )\) from previous iterations. We seek to approximate \(f(x, \omega )\) further using \(x^k\) and \(f^{k,t(k)}_L(x, \omega )\) by executing the CPT algorithm for a few iterations. Note that this approximation is only valid for \(x \in X \cap Q^{t(k)}_1\). To initialize a sequence of subproblem approximations of the CPT algorithm, we start by solving (8). Let d denote the iteration counter of the CPT algorithm (for the second stage), and let \(y^d(\omega )\) denote a solution with some fractional variable(s) at iteration d. Let \(\mathcal {T}^d_2(\omega )\) denote an index set of the sets that constitute a partition \(\{Q^\tau _2(\omega ), \tau \in \mathcal {T}^d_2(\omega )\}\) of \(Q_2\). For each \(\tau \in \mathcal {T}^d_2 (\omega )\), let \(Q^\tau _2(\omega )\) denote bounding constraints for the vectors y as shown in (20),

$$\begin{aligned} Q^\tau _2 (\omega )=\left\{ y \ | \ l^\tau _2 \le y \le u^\tau _2 \right\} , \quad \forall \tau \in \mathcal {T}^d_2 (\omega ). \end{aligned}$$
(20)

Given Y only imposes integer restrictions, the set \(\mathcal {T}^d_2 (\omega )\) can be used to index a disjunctive relaxation of \(Y \cap Q_2\) because

$$\begin{aligned} \bigcup _{\tau \in \mathcal {T}^d_2(\omega )} Q^\tau _2(\omega ) \supseteq Y \cap Q_2. \end{aligned}$$
(21)

Since \(y^d(\omega )\) is presumed to have some fractional values for integer variables, we separate the fractional point \((x^k, y^d(\omega ))\) from the convex hull of those points \((x,y(\omega ))\) which require \(y(\omega )\) to be integral. Thus, we construct a disjunctive set which satisfies the following,

$$\begin{aligned} (x^k,y^d(\omega )) \notin \bigcup _{\tau \in \mathcal {T}^d_2} \left\{ (x,y(\omega )) \ | \ x \in X_L \cap Q^{t(k)}_1, y(\omega ) \in Q^\tau _2(\omega )\right\} . \end{aligned}$$
(22)

We use the same rules as in the CPT algorithm [7] to construct the disjunctive set. Moreover, the hierarchy of disjunctions represented in \({\mathcal {T}^d_2(\omega )}\) is generated in the form of a tree structure (called cutting plane tree) and \({\mathcal {T}^d_2(\omega )}\) contains all nodes that do not have children nodes. The tree itself is initialized with one global node defining the constraints for \(Q_2\). If the solution \(y^d(\omega )\) does not satisfy the mixed-integer restrictions, then the algorithm walks through the cutting plane tree to locate the deepest node (from the root node) that contains \(y^d(\omega )\). Let us refer to this node as \(\tau ^d\). If \(\tau ^d \in {\mathcal {T}^d_2(\omega )}\) (implying it does not have any children node), two nodes are created as its children nodes and \(\tau ^d\) is removed from \({\mathcal {T}^d_2(\omega )}\). On the other hand, if \(\tau ^d \notin {\mathcal {T}^d_2(\omega )}\), no new node is created. In this way, \({\mathcal {T}^d_2(\omega )}\) is updated such that conditions (21) and (22) are satisfied.

By intersecting every subset of the partition (20) with \(Z^k_L(t,\omega )\), a cut generation linear program (CGLP) can then be formulated to derive multi-term disjunctive cuts as follows.

$$\begin{aligned} \max \quad&\pi _0(\omega )-\pi _1(\omega )^\top x^k- \pi _2(\omega )^\top y^d(\omega ) \end{aligned}$$
(23a)
$$\begin{aligned} \text {s.t.}\quad&\pi _1(\omega ) = {T^{k}(t,\omega )}^\top \lambda _{2\tau }- A^\top \lambda _{1}+\mu _1-\nu _1 \quad \forall \tau \in \mathcal {T}^d_2(\omega ) \end{aligned}$$
(23b)
$$\begin{aligned}&\pi _2(\omega ) = {W^{k}(t, \omega )}^\top \lambda _{2\tau }+\mu _{2\tau }-\nu _{2\tau } \quad \forall \tau \in \mathcal {T}^d_2 (\omega ) \end{aligned}$$
(23c)
$$\begin{aligned}&r^{k}(t, \omega )^\top \lambda _{2\tau } - b^\top \lambda _{1}+{(l^\tau _2)}^\top \mu _{2\tau } +{(l^{t}_1)}^\top \mu _1 -{(u^\tau _2)}^\top \nu _{2\tau } - {(u^{t}_1)}^\top \nu _1 \nonumber \\&\qquad \ge \pi _0(\omega ) \quad \tau \in \mathcal {T}^d_2 (\omega ) \end{aligned}$$
(23d)
$$\begin{aligned}&-\mathbf {1} \le \pi _1(\omega ) \le \mathbf {1}, \quad -\mathbf {1} \le \pi _2(\omega ) \le \mathbf {1},\end{aligned}$$
(23e)
$$\begin{aligned}&-1 \le \pi _0(\omega ) \le 1 \end{aligned}$$
(23f)
$$\begin{aligned}&\lambda _{1}, \lambda _{2\tau }\ge 0, \nu _{1},\nu _{2\tau }\ge 0, \mu _1, \mu _{2\tau }\ge 0, \quad \text {for } \forall \ \tau \in \mathcal {T}^d _2 (\omega ). \end{aligned}$$
(23g)

There is significant latitude in formulating the CGLP (23) when it comes to the treatment of the first stage variables x, because the search for the optimal value of these variables is carried out via a B&B process in stage 1. As with the use of disjunctive programming to explain intersection cuts, one may ignore one or more first stage constraints by using elements of \(\lambda _1\) to be 0. In formulating (23), we have opted to use \(\lambda _{1t} = \lambda _1, \mu _{1t} = \mu _1,\) and \(\nu _{1t} = \nu _1\) for all t. This reduces the size of the CGLP, while recognizing that the first stage variables x must satisfy \(x \in X_L \cap Q_1^t\). Note that such a restriction does not ensure access to facets of the convex hull of \(X \cap Q_1^t\). However, such facets are not necessary for convergence because the B&B process of the first stage is used to ensure convergence. Note also that in generating the cut coefficients of the second stage, we do index the multipliers \(\lambda _{2\tau }, \mu _{2,\tau }, \nu _{2,\tau }\) by the subsets in the disjunction. The critical aspect of these cuts is that they provide the correct second stage value function as required by Proposition 1. This result will be shown in Proposition 3. In any event, the solution to the above CGLP provides the following valid inequality.

$$\begin{aligned} \pi _1(\omega )^\top x+\pi _2(\omega )^\top y(\omega ) \ge \pi _0(\omega ). \end{aligned}$$
(24)

Note that (24) is associated with scenario \(\omega \), and we derive separate cuts for each \(\omega \in \Omega \). Since (22) includes inequalities that are valid for \(X\cap Q^{t}_1\), this CGLP combines the convexification in the space \((x,y(\omega ))\) where \(x \in Q^{t}_1\). As a result, the CGLP suggested in this paper is larger than that used for the original \(D^2\) algorithm [21]. However, the \(\mathbf {ABC}\) algorithm does not require the convexification using the epi-reverse polar used in [21]. In this sense, the cuts used in the \(\mathbf {ABC}\) algorithm are different from those in the \(D^2\) algorithm.

Proposition 2

Cutting plane (24) is valid for feasible set \(\{(x,y(\omega )) \ | \ T^k(t, \omega )x+ W^{k}(t,\omega ) y(\omega )\ge r^{k}(t,\omega ), x \in X \cap Q^{t}_1, y(\omega ) \in Y \cap Q_2 \}\).

Proof

For any \((x,y(\omega ))\) satisfying \(\{(x,y(\omega )) \ | \ T^k(t, \omega )x+ W^k(t,\omega ) y(\omega )\ge r^k(t, \omega ), x \in X \cap Q^{t}_1, y(\omega ) \in Y \cap Q_2 \}\), (23b, c, d, g) imply that

$$\begin{aligned}&\pi _1(\omega )^\top x+\pi _2(\omega )^\top y(\omega ) \end{aligned}$$
(25a)
$$\begin{aligned}&\quad = \left( \lambda _{2\tau }^\top T^{k}(t, \omega )x-\lambda _1^\top Ax+\mu _1^\top x-\nu _1^\top x\right) \nonumber \\&\qquad + \left( \lambda _{2\tau }^\top W^k (t,\omega )y(\omega )+\mu _{2\tau }^\top y(\omega )-\nu _{2\tau }^\top y(\omega )\right) \end{aligned}$$
(25b)
$$\begin{aligned}&\quad \ge r^k (t,\omega )^\top \lambda _{2\tau } - b^\top \lambda _{1}+{l^\tau _2}^\top \mu _{2\tau } +{l^t_1}^\top \mu _1 -{u^\tau _2}^\top \nu _{2\tau } - {u^t_1}^\top \nu _1 \end{aligned}$$
(25c)
$$\begin{aligned}&\quad \ge \pi _0(\omega ), \end{aligned}$$
(25d)

as required.

The cut (24) is included in the second-stage formulation, leading to a stronger approximation of the second-stage polyhedron, and consequently, a stronger approximation of the recourse function, which is denoted as \(f^{k,t,d}_L(x,\omega )\). In the following, a superscript \(k-\) denotes the most recent update of any particular data element (e.g. W, T, r). In general, after d iterations of the CPT algorithm for the subproblem, we have

$$\begin{aligned} f^{k,t,d}_L(x,\omega )=&\min \quad g(\omega )^\mathsf {T} y \end{aligned}$$
(26a)
$$\begin{aligned}&\text {s.t. } W^{k-}(t, \omega ) y\ge r^{k-}(t, \omega )-T^{k-}(t, \omega )x \end{aligned}$$
(26b)
$$\begin{aligned}&\qquad \Pi ^d_2(\omega )y \ge \Pi ^d_0(\omega )-\Pi ^d_1(\omega )x \end{aligned}$$
(26c)
$$\begin{aligned}&\qquad y \in Q_2 \end{aligned}$$
(26d)

where constraint (26b) denotes the approximation of subproblem for \(x \in Q_1^{t}\) before starting iteration k. In addition, (26c) includes all cuts generated during this round of iterations for solving/approximating the subproblem. There is another algorithmic point to be noted here; (26) is essentially the same as (8), but the left hand side of (26a) includes three superscripts (k, t, d) while the function in (8) has two superscripts. The reason for this distinction is to emphasize that there are “outer iterations” (first stage) indexed by k, whereas, the “inner iterations” (second stage) are indexed by d. Depending on the course of the CPT algorithm, (26c) needs to be included in the CGLP to ensure convergence of the algorithm [6]. After the approximation \(f^{k,t,d}_L(x,\omega )\) is obtained, the cut-enhanced LP is re-solved and new cuts are generated as long as the inner iteration generates \(y^d(\omega )\) that are fractional. At any outer iteration k, we allow at most D cuts to be added for the second-stage CPT (approximation) algorithm. Once the process of solving the subproblem stops, we form a Benders’ cut as in (14) and return to the master problem. As a reminder, recall that the cuts for the first stage are recorded via the index set \(\mathcal {G}_{x}(t)\), while cuts for the second stage are indexed by elements of \(\mathcal {G}_{z}(t, \omega )\). Since \(x^k\) is integer feasible, then \(x^k \in X_L \cap Q^{t(k)}_1\). An algorithm to approximately solve subproblems for each \(\omega \), with at most D cuts added, called cutting plane tree disjunction (CPT-D), is shown as Algorithm 2.

figure b

Proposition 3

Assume that the second-stage problems are all bounded, and moreover, suppose that the cuts coefficients (24) correspond to extreme point solutions of the CGLP (23). Then for fixed t(k) there exists a finite integer \(D < \infty \), such that algorithm CPT-D finds mixed integer optimal solutions for all subproblems (2) indexed by \(\omega \); that is, with \(x = x^k\) we have \(f^{k,t,D}_L(x^k,\omega )=f(x^k, \omega ) \ \text {for }\forall \omega \).

Proof

When D is large enough, algorithm CPT-D is the same as the CPT algorithm to solve each subproblem. Due to the finiteness of the CPT algorithm proved in [6], all we need to prove is that for fixed \(\mathcal {T}^d_2(\omega )\) and \(Q^{t(k)}_1\), only finitely many constraints can be generated from the CGLP (23) as \((x^k, y^d(\omega ))\) changes. To see this, note that the constraints in (23) depend on the disjunction that is violated, but not the specific vectors \((x^k, y^d(\omega ))\). With fixed \(\mathcal {T}^d_2(\omega )\), there are only finitely many disjunctions that can be violated. Thus, the number of extreme points of (23) is finite. Since with the generation of each cut, there is one less extreme point of the CGLP that can be generated. So in the worst case, all extreme points are generated which implies the finiteness of the number of potential cuts. This completes the proof.

Chen et al. [7] shows that a formulation which minimizes the 1-norm provides better numerical stability than the CGLP in (23). Therefore, our computational experiments use the following as the CGLP to generate disjunctive cuts.

$$\begin{aligned} \min \quad&\sum _{i \in I} |\pi _{1i}(\omega )| + \sum _{j \in J} |\pi _{2j}(\omega )| \end{aligned}$$
(27a)
$$\begin{aligned} \text {s.t.} \quad&\pi _1(\omega ) = {T^k(t,\omega )}^\top \lambda _{2\tau } - A^\top \lambda _1+\mu _1-\nu _1 \quad \forall \tau \in \mathcal {T}^d_2(\omega ) \end{aligned}$$
(27b)
$$\begin{aligned}&\pi _2(\omega ) = {W^k(t, \omega )}^\top \lambda _{2\tau }+\mu _{2\tau }-\nu _{2\tau } \quad \forall \tau \in \mathcal {T}^d_2(\omega ) \end{aligned}$$
(27c)
$$\begin{aligned}&{r^k(t, \omega )}^\top \lambda _{2\tau } - b^\top \lambda _1+{(l^\tau _2)}^\top \mu _{2\tau } +{(l^t_1)}^\top \mu _1 -{(u^\tau _2)}^\top \nu _{2\tau } - {(u^t_1)}^\top \nu _1 \nonumber \\&\qquad \ge \pi _1(\omega )^\top x^k+ \pi _2(\omega )^\top y^d(\omega )+ 1 \quad \tau \in \mathcal {T}^d_2 (\omega ) \end{aligned}$$
(27d)
$$\begin{aligned}&\lambda _{1}, \lambda _{2\tau }\ge 0, \nu _{1},\nu _{2\tau }\ge 0, \mu _1, \mu _{2\tau }\ge 0, \quad \text {for } \forall \ \tau \in \mathcal {T}^d _2 (\omega ). \end{aligned}$$
(27e)

If one wishes to implement (27) and still ensure finiteness of the algorithm, one has to ensure that the cuts from (27) can be mapped to an extreme point of (23). This can be accomplished in several algorithmic ways. One should observe that any cut obtained by using (27) has an equivalent cut in (23). If this mapping reveals an extreme point of (23), then, finiteness is ensured. However, if the solution from (27) is not equivalent to an extreme point of (23), then, one should identify the lowest dimensional face of (23) whose interior contains the equivalent cut coefficients. Then one could optimize (23) by restricting the LP solution to belong to that face. Since this process would identify an extreme point of (23), finiteness of the cut generation scheme would be ensured.

In our implementation, we gradually increase the number of cuts we generate during any outer iteration k. To do so, we initialize an integer \(D\leftarrow 2\) and at each outer iteration, we update \(D\leftarrow D+2\). This style of implementation is motivated by our prior experience (e.g. [27]) that seeking very accurate objective function estimates requires much more computational resources than what can be justified in early (outer) iterations of the algorithm; in later iterations however, seeking greater accuracy tends to pay off.

3.2 Convexification implied by branch-and-bound

Most deterministic MIP algorithms combine valid inequalities in the context of branch-and-bound methods, and as a result, branch-and-cut methods form the backbone for most state-of-the-art commercial solvers. The CPT algorithm used in the previous section is a pure cutting plane method. The fact that it also utilizes a tree structure to manage the disjunctive sets inspires a way that transforms the B&B tree obtained from an MILP solver to help create a polyhedral approximation which gives the same MIP optimal value as that obtained from the B&B method. In the remainder of this section, we describe such an algorithm and prove that this approximation can also be obtained in finitely many steps. It turns out that this combination (of B&B with valid inequalities) extends the branch-and-cut approaches of Sen and Sherali [23], and Yuan and Sen [27].

Suppose that for a fixed \(x^k \in X_L\cap Q^{t(k)}_1\), the subproblem (2) is either solved to optimality by a B&B method, or an approximate solution is obtained via a truncated B&B process. The latter is typically stopped when a node limit or a time limit is reached. Let the optimal/incumbent solution be denoted \(y^k(\omega )\). Due to the B&B (or truncated B&B) process, it is reasonable to assume that we have a set of leaf nodes of a B&B tree. Let \(\mathcal {T}^{\mathrm {remain}}_2\) denote the remaining leaf nodes in the B&B tree and \(\mathcal {T}^{\mathrm {fathom}}_2\) denote the leaf nodes that have been fathomed. Note that these nodes depend on \(\omega \), but we have dropped that dependence to ease the notational burden. However, we do define \(\mathcal {T}_2 (\omega ) =\mathcal {T}^{\mathrm {remain}}_2 \cup \mathcal {T}^{\mathrm {fathom}}_2\). Suppose the constraint set used in (7) is represented in the form

$$\begin{aligned} \mathcal {Z}^{k-}_L(t,\omega )= & {} \left\{ (x, y(\omega )) \ | \ T^{k-}(t,\omega )x + W^{k-}(t,\omega ) y(\omega )\right. \nonumber \\&\left. \ge r^{k-}(t, \omega ), x \in X_L \cap Q_1^{t}, y(\omega ) \in Q_2 \right\} , \end{aligned}$$
(28)

where similar to (26), a superscript \(k-\) denotes the most recent update of any data element (e.g. W, r) before iteration k. We also define

$$\begin{aligned} \mathcal {Z}^{k}_D(t, \omega ) = \bigcup _{\tau \in \mathcal {T}_2(\omega )} \left( \mathcal {Z}^{k-}_L(t,\omega )\bigcap \{(x,y(\omega )) \ | \ x \in {\mathbb {R}}^{n_1}, y \in Q^\tau _2\}\right) . \end{aligned}$$
(29)

Since \(Q^\tau _2, \ \forall \ \tau \in \mathcal {T}_2(\omega )\) are disjoint from each other, \(\mathcal {T}_2(\omega )\) provides a disjunctive relaxation in the space of \((x,y(\omega ))\). Thus, the same form of CGLP as in (23) can be used to derive multi-term disjunctive cuts using the partition \(\mathcal {T}_2(\omega )\). The rest of the algorithm is similar to CPT-D. There are two phases: the first phase is to use a B&B method to either solve the second-stage MIP, or obtain an approximate solution using a truncated B&B process. In either case, we have \(\mathcal {T}_2(\omega )\) which is used to obtain a disjunctive approximation. The second phase starts by seeking the value \(f^{k,t,d}_L(x^k,\omega )\) with \(d=1\). At iteration d, if the optimal solution of (26) is fractional (denoted \(y^d(\omega )\)), we formulate (23) based on \(\mathcal {T}_2(\omega )\) and \(Q^{t}_1\) to cut off \((x^k, y^d(\omega ))\). The index of the new cut is added into \(\mathcal {G}_{z}(t, \omega )\). Then, we re-solve (26), and this process continues until \((x^k,y^d(\omega ))\) belongs to \(\mathcal {Z}^{k}_D(t,\omega )\). The method is called Branch and Bound with Disjunction (BB-D) and is shown in Algorithm 3.

figure c

While the form of the BB-D process is similar to the CPT-D process presented in the previous section, the inclusion of B&B, especially its truncated version, makes this decomposition approach much more realistic for practical instances of MIP in the second stage. Nevertheless, the proof of convergence derives from the same concept that one can obtain a polyhedral approximation of a disjunctive set embodied by a B&B tree. This is summarized in the following proposition.

Proposition 4

Under the same assumptions as in Proposition 3, Algorithm 3 terminates in finitely many steps, provided D is sufficiently large so that the B&B process provides an optimal second-stage solution for any node indexed by t.

Proof

A B&B tree embodies a multi-term disjunction. Using such a disjunction to formulate the CGLP in (23) results in a polyhedral approximation which creates the convex hull of the partition provided by the B&B tree. Hence there exists a counter \(K < \infty \) such that for any subset \(Q_1^t\), we obtain the same solution as from B&B. Hence for a B&B algorithm such that there is \(D < \infty \) such that \(f(x^K, \omega ) = f_L^{K,t,D} (x^K,\omega )\), for all \(\omega \in \Omega \). Since this satisfies the requirements of Proposition 1, the result follows.

Both Algorithms 2 and 3 use multi-term disjunctive cuts which are added to the second stage MIP, and the resulting polyhedral approximation then allows us to update a piecewise linear approximation of the expected recourse function as in (14–13). The difference between the two algorithms is simply the manner in which the disjunctive sets are constructed: Algorithm 3 uses the B&B nodes to construct one disjunctive set, whereas, Algorithm 2 iteratively builds up a collection of cuts based on a sequence of disjunctions, which may vary depending on the second stage fractional points encountered during the CPT process.

4 Illustrative examples

This section illustrates the workings of the algorithm using four examples, all of which are variants of Example 1.0. This example, which originally appeared in [19], has been used to illustrate several algorithms whose structures are specialized to binary second stage problems in [22], and to problems with fixed tenders [1]. In our presentation, we will start with the binary instance, and then, make the example progressively more difficult, allowing general integers in the second stage (Example 1.1), general integers in both stages (Example 1.2), and finally allowing randomness in the T matrix (Example 1.3). Figures illustrating the progress of the first-stage search are provided in the “Appendix”.

Example 1.0

$$\begin{aligned}&\min \quad -1.5x_1 - 4x_2 + \sum _{\omega \in \Omega }p(\omega ) f(x,\omega ) \end{aligned}$$
(30a)
$$\begin{aligned}&\text {s.t.} \quad x_1,x_2 \ \mathrm {binary} \end{aligned}$$
(30b)

where

$$\begin{aligned} f(x,\omega )=&\min \quad - 16y_1 - 19y_2 - 23y_3 - 28y_4 + 100 R \end{aligned}$$
(31a)
$$\begin{aligned}&\text {s.t.} \quad \left[ \begin{array}{c} 2y_1 + 3y_2 + 4y_3 + 5y_4 -R \\ 6y_1 + 1y_2 + 3y_3 + 2y_4 -R \end{array} \right] \le r(\omega )-T(\omega )x \end{aligned}$$
(31b)
$$\begin{aligned}&\qquad \ y_i \ \mathrm {binary} \ i=1, \ldots ,4, R\ge 0 , \end{aligned}$$
(31c)

\(\Omega =\{\omega _1,\omega _2\}\), \(p(\omega _1)=p(\omega _2)=0.5\), \(r(\omega _1)={\left[ \begin{array}{c} 10\\ 3 \end{array} \right] }\), \(T(\omega _1)={\left[ \begin{array}{cc} 1&{} 0\\ 0 &{} 1 \end{array} \right] }\), \(r(\omega _2)={\left[ \begin{array}{c} 5\\ 2 \end{array} \right] }\), \(T(\omega _2)={\left[ \begin{array}{cc} 1&{} 0\\ 0 &{} 1 \end{array} \right] }\). We first apply the \(\mathbf {ABC}\) algorithm with CPT-D to solve this example.

At iteration \(k=1\), the algorithm starts by solving a relaxed LP master problem. We put a very low bound on \(\eta \).

$$\begin{aligned} \min \quad&-1.5x_1 - 4x_2 + \eta \end{aligned}$$
(32a)
$$\begin{aligned} \text {s.t.} \quad&0 \le x_1, x_2 \le 1 \end{aligned}$$
(32b)
$$\begin{aligned}&\eta \ge -M \end{aligned}$$
(32c)

We get a solution \((x_1,x_2, \eta )=(1,1,-M)\) with objective \(v=-M-5.5\). Here only the root node is in the \( B \& B\) tree. With \(x=(1,1)\) and \(Q^o_1=\{0 \le x_1 \le 1, 0 \le x_2 \le 1\}\) we solve the subproblems. We now invoke CPT-D (Algorithm 2) as explained next. For scenario \(\omega _1\), (8) is solved and we get \(y(\omega _1)=(0,1,0,0.5,0)\). Note that \(y_4\) is fractional and partitions are formed for that integer variable: \(\{y_4 \le 0\}\cap Q_2\) or \(\{y_4 \ge 1\} \cap Q_2\). The cut derived from CGLP (27) for \(x\in Q^o_1\) is

$$\begin{aligned} -2y_2-2y_4+2R \ge -4+2x_2. \end{aligned}$$
(33)

After including the cut, (8) is re-optimized and the solution is \(y(\omega _1)=(0,0,0,1,0)\). This satisfies the integer constraints. For scenario \(\omega _2\), (8) is solved and we get \(y(\omega _2)=(0,1,0,0,0)\). Again, this solution satisfies the integer constraints, and hence, no additional cuts are needed. Since all scenarios have integer solution, we update V: \(V=-29\) and, the Benders’ cut for \(x\in Q^o_1\) is

$$\begin{aligned} -16.5x_2+\eta \ge -40. \end{aligned}$$
(34)

At iteration \(k=2\), the master problem continues to be solved by a B&B method. We get a solution \((x_1,x_2, \eta )=(1,0,-40)\) with objective \(v=-41.5\). The first stage B&B tree still contains only the root node. With \(x=(1,0)\) and \(Q^o_1=\{0 \le x_1 \le 1, 0 \le x_2 \le 1\}\) we solve the subproblems. Again we invoke CPT-D. For scenario \(\omega _1\), (8) is initialized as follows:

$$\begin{aligned} f_L(x,\omega _1)=\min&\quad - 16y_1 - 19y_2 - 23y_3 - 28y_4 + 100 R \end{aligned}$$
(35a)
$$\begin{aligned} \text {s.t.}&\quad \ 2y_1 + 3y_2 + 4y_3 + 5y_4 -R \le 10 - x_1 \end{aligned}$$
(35b)
$$\begin{aligned}&\quad \ 6y_1 + 1y_2 + 3y_3 + 2y_4 -R \le 3 - x_2 \end{aligned}$$
(35c)
$$\begin{aligned}&\quad \ -2y_2-2y_4+2R \ge -4+2x_2 \end{aligned}$$
(35d)
$$\begin{aligned}&\quad \ 0 \le y_i \le 1 \ i=1, \ldots ,4, R\ge 0 \end{aligned}$$
(35e)

where constraint (35d) is from cut (33) generated in iteration 1. (35) is solved and we get \(y(\omega _1)=(0,1,0,1,0)\). The solution satisfies integer constraints. For scenario \(\omega _2\), (8) is solved and we get \(y(\omega _2)=(0.1154,1,0,0.1538,0)\). We now choose \(y_1\) as the variable to split. The partitions we form are: \(\{y_1 \le 0\} \cap Q_2\) or \(\{y_1 \ge 1\} \cap Q_2\). The cut derived from CGLP (27) for \(x\in Q^o_1\) is

$$\begin{aligned} -4.875y_2-6.5y_4+1.625R \ge -6.5+1.625x_1. \end{aligned}$$
(36)

After including the cut, (8) is re-optimized and the solution is

$$\begin{aligned} y(\omega _2)=(0.056,1,0.222,0,0). \end{aligned}$$
(37)

Following the CPT algorithm, we locate \(y(\omega _2)\) on the root node of CPT tree. There are no splits needed. We continue with the same partition: \(\{y_1 \le 0\} \cap Q_2\) or \(\{y_1 \ge 1\} \cap Q_2\). The cut derived from (27) for \(x\in Q^o_1\) is

$$\begin{aligned} -2.25y_2-4.5y_3+2.25R \ge -2.25. \end{aligned}$$
(38)

After including the cut, (8) is re-optimized and the new solution is \(y(\omega _2)=(0.06,0.68,0.16,0.24,0)\). Again, \(y(\omega _2)\) is located on the root node, and no more splits are needed. The same partition: \(\{y_1 \le 0\} \cap Q_2\) or \(\{y_1 \ge 1\} \cap Q_2\) is used to formulate (27). With only \(y(\omega _2)\) changed, another cut derived from (27) for \(x\in Q^o_1\) and that is

$$\begin{aligned} -2.5y_3-2.5y_4+2.5R \ge -2.5+2.5 x_1. \end{aligned}$$
(39)

After including the cut, (8) is re-optimized and the solution is \(y(\omega _2)=(0.1667,1,0,0,0)\). Since \(y(\omega _2)\) is located at the root node no more splits are necessary. We use the same partition: \(\{y_1 \le 0\} \cap Q_2\) or \(\{y_1 \ge 1\} \cap Q_2\) to formulate (27). The cut derived from (27) for \(x\in Q^o_1\) is

$$\begin{aligned} -6y_1+1.5R \ge 0. \end{aligned}$$
(40)

After including the cut, (8) is re-optimized and the solution is \(y(\omega _2)=(0,1,0,0,0)\). This solution satisfies the integer constraints. Since all scenarios have integer solutions, we update V: \(V=-34.5\) and, Benders’ optimality cut for \(x\in Q^o_1\) is

$$\begin{aligned} -7.55x_1-3.8333x_2+\eta \ge -40.55. \end{aligned}$$
(41)

At iteration \(k=3\), the master problem continues to be solved by the B&B method. We get \((x_1,x_2, \eta )=(0,0,-40)\) with objective \(v=-40\). The solution is on node 1 with \(Q^1_1=\{0 \le x_1 \le 0, 0 \le x_2 \le 1\}\). Hence, \(x=(0,0)\) and \(Q^1_1\) are treated as input parameters for CPT-D for each \(\omega \in \Omega \). For scenario \(\omega _1\), no cuts are needed. The solution is \(y(\omega _1)=(0,1,0,1,0)\). For scenario \(\omega _2\), one cut is needed and is shown below.

$$\begin{aligned} -3.6923y_2-2.4615y_3-3.6923y_4+1.2308R \ge -3.6923. \end{aligned}$$
(42)

The solution is \(y(\omega _2)=(0,0,0,1,0)\). We update V: \(V=-37.5\) and, the Benders’ optimality cut for \(Q^1_1\) is

$$\begin{aligned} -8.3333x_2+\eta \ge -37.5. \end{aligned}$$
(43)

At iteration \(k=4\), with updated Benders’ cut for node 1, the master problem continues to be solved by a B&B method. We get solution \((x_1,x_2, \eta )=(0,0,-37.5)\) with objective \(v=-37.5\). Since \(V-v\le \epsilon \), the algorithm stops. A short summary of using \(\mathbf {ABC}\) algorithm with CPT-D to solve this problem is shown in Table 1. Each row shows the information for one iteration. Column “Num Nodes” denotes the number of active nodes in the B&B tree. “Num Cuts” means the number of multi-term disjunctive cuts generated for that scenario.

Table 1 \(\mathbf {ABC}\) algorithm with CPT-D for Example 1.0
Full size table

We also apply the same \(\mathbf {ABC}\) algorithm but with BB-D to solve this example. The algorithm starts by solving a relaxed LP master problem. We put a very low bound on \(\eta \). At iteration \(k=1\), we get a solution \((x_1,x_2, \eta )=(1,1,-M)\) with objective \(v=-M-5.5\) from the B&B method. With \(x=(1,1)\) and \(Q^o_1=\{0 \le x_1 \le 1, 0 \le x_2 \le 1\}\), we invoke BB-D to solve the subproblems for each \(\omega \in \Omega \). For scenario \(\omega _1\), (8) is solved by the B&B method and we get 2 nodes in \(\mathcal {T}_2\) with bounds \(\{y_4 \le 0\} \cap Q_2\) and \(\{y_4 \ge 1\} \cap Q_2\). With one cut derived from (27) for \(x\in Q^o_1\), we get a new constraint

$$\begin{aligned} -2y_2-2y_4+2R \ge -4+2x_2, \end{aligned}$$
(44)

and upon solving the updated formulation, we get \(y(\omega _1) = (0,0,0,1,0)\), and no more cuts are necessary. For scenario \(\omega _2\), (8) is solved by a B&B method and we get only one node in \(\mathcal {T}_2\) with \(Q_2\) untouched. No cuts are needed, and \(y(\omega _2)=(0,1,0,0,0)\). Since all scenarios have integer solutions, we update V: \(V=-29\) and, the Benders’ cut for \(x\in Q^o_1\) is

$$\begin{aligned} -16.5x_2+\eta \ge -40. \end{aligned}$$
(45)

At iteration \(k=2\), the master problem continues to be solved by a B&B method. We get a solution \((x_1,x_2, \eta )=(1,0,-40)\) with objective \(v=-41.5\). Using \(x=(1,0)\) with \(Q^o_1=\{0 \le x_1 \le 1, 0 \le x_2 \le 1\}\) we now derive the subproblems. The BB-D is called for each \(\omega \in \Omega \). For scenario \(\omega _1\), (8) is initialized as follows:

$$\begin{aligned} f(x,\omega _1)=\min&\quad - 16y_1 - 19y_2 - 23y_3 - 28y_4 + 100 R \end{aligned}$$
(46a)
$$\begin{aligned} \text {s.t.}&\quad \ 2y_1 + 3y_2 + 4y_3 + 5y_4 -R \le 10 - x_1 \end{aligned}$$
(46b)
$$\begin{aligned}&\quad \ 6y_1 + 1y_2 + 3y_3 + 2y_4 -R \le 3 - x_2 \end{aligned}$$
(46c)
$$\begin{aligned}&\quad \ -2y_2-2y_4+2R \ge -4+2x_2 \end{aligned}$$
(46d)
$$\begin{aligned}&\quad \ y_i \ \mathrm {binary} \ i=1, \ldots ,4, R\ge 0 \end{aligned}$$
(46e)

where constraint (46d) is inherited from iteration 1 [see (44)]. We solve (46) by a B&B method and we get \(\mathcal {T}_2\) with one node. Its bound is \(Q_2\). We have \(y(\omega _1)=(0,1,0,1,0)\). For scenario \(\omega _2\), (8) is solved by a B&B method and we get \(\mathcal {T}_2\) with 4 nodes. Their bounds are \(\{y_1 = 1\} \cap Q_2\), \(\{y_1 = 1, y_3=1\} \cap Q_2\), \(\{y_1 = 0, y_3=0, y_4=0\} \cap Q_2\) and \(\{y_1 = 0, y_3=0, y_4=1\} \cap Q_2\). Here 4 cuts are derived from (27) for \(x\in Q^o_1\):

$$\begin{aligned} -8.6667y_1+2.1667R\ge & {} 0 \nonumber \\ -4y_3+4R\ge & {} 0 \nonumber \\ -3.75 y_2 -5 y_4+ 1.25 R\ge & {} -5 \nonumber \\ -x_1 - y_4 + R\ge & {} -1. \end{aligned}$$
(47)

With these 4 cuts added, the solution \(y(\omega _2)=(0,1,0,1,0)\). Since all scenarios have integer solutions, we update V: \(V=-34.5\) and, the Benders’ cut for \(x\in Q^o_1\) is

$$\begin{aligned} -4.5x_1-3.8333x_2+\eta \ge -37.5. \end{aligned}$$
(48)

At iteration \(k=3\), the master problem continues to be solved by the B&B method. We get a solution \((x_1,x_2, \eta )=(0,0,-37.5)\) with objective \(v=-37.5\). The solution belongs to node 2 with \(Q^2_1=\{0 \le x_1 \le 1, 0 \le x_2 \le 0\}\). Here the first stage solution \(x=(0,0)\) and the box \(Q^2_1\) are treated as input parameters for BB-D for each scenario \(\omega \in \Omega \). For scenario \(\omega _1\), the solution is \(y(\omega _1)=(0,1,0,1,0)\). For scenario \(\omega _2\), the solution is \(y(\omega _2)=(0,0,0,1,0)\). \(V=-37.5\) and, the Benders’ cut for \(Q^2_1\) is

$$\begin{aligned} -2.8333x_1-5.1667x_2+\eta \ge -37.5. \end{aligned}$$
(49)

At iteration \(k=4\), with updated Benders’ cut for node 2, the master problem continues to be solved by a B&B method. We obtain \((x_1,x_2, \eta )=(0,0,-37.5)\) with objective \(v=-37.5\). \(V-v\le \epsilon \) and, the algorithm stops. A short summary of the \(\mathbf {ABC}\) algorithm with BB-D is shown in Table 2. As one might notice, there is only a small difference between BB-D and CPT-D for Example 1.0. At iteration 2, because BB-D uses partitions with 4 terms to generate cuts, the quality of the Benders’ cut is better than CPT-D.

Table 2 \(\mathbf {ABC}\) algorithm with BB-D for Example 1.0
Full size table

Example 1.1

is an extension of Example 1.0, and is intended to illustrate the workings of the algorithm when we include general integer variables in the second stage.

$$\begin{aligned}&\min \quad -1.5x_1 - 4x_2 + \sum _{\omega \in \Omega }p(\omega ) f(x,\omega ) \end{aligned}$$
(50a)
$$\begin{aligned}&\text {s.t.} \quad x_1,x_2 \ \mathrm {binary} \end{aligned}$$
(50b)

where

$$\begin{aligned} f(x,\omega )=\min&- 16y_1 - 19y_2 - 23y_3 - 28y_4 + 100 R \end{aligned}$$
(51a)
$$\begin{aligned} \text {s.t.} \quad&\left[ \begin{array}{c} 2y_1 + 3y_2 + 4y_3 + 5y_4 -R \\ 6y_1 + 1y_2 + 3y_3 + 2y_4 -R \end{array} \right] \le r(\omega )-T(\omega )x \end{aligned}$$
(51b)
$$\begin{aligned}&y_i \in \{0,1 \ldots 5\}, i = 1, \ldots ,4; R\ge 0 , \end{aligned}$$
(51c)

\(\Omega =\{\omega _1,\omega _2\}\), \(p(\omega _1)=p(\omega _2)=0.5\), \(r(\omega _1)=\left[ \begin{array}{c} 10\\ 3 \end{array} \right] \), \(T(\omega _1)=\left[ \begin{array}{cc} 1&{} 0\\ 0 &{} 1 \end{array} \right] \), \(r(\omega _2)=\left[ \begin{array}{c} 5\\ 2 \end{array} \right] \), \(T(\omega _2)=\left[ \begin{array}{cc} 1&{} 0\\ 0 &{} 1 \end{array} \right] \).

The summaries of applying \(\mathbf {ABC}\) algorithm with CPT-D and BB-D on Example 1.1 are shown in Table 3 and Table 4.

Table 3 \(\mathbf {ABC}\) algorithm with CPT-D for Example 1.1
Full size table
Table 4 \(\mathbf {ABC}\) algorithm with BB-D for Example 1.1
Full size table

In Tables 3 and 4, the rows show the information generated in each successive iteration of the algorithm. The column header “Num Nodes” indicates the number of active nodes in the B&B tree and “Num Cuts” indicates the number of multi-term disjunctive cuts generated for that scenario. In the first iteration, \(v=-M-5.5\) where \(-M\) denotes the lower bound for \(\eta _t\) [see (15)] and in our experiment we set \(M =1000000\). From the Table 4, we can observe that both algorithms require one more iteration and generate more cuts in the subproblem than in Example 1.0 (Tables 1, 2), but the differences between the execution of BB-D and CPT-D for this example are minimal.

To better illustrate the algorithm, we also include two sets of figures (Figs. 2, 3 in “Appendix 2”) which show the master problem B&B tree at each iteration of the algorithm. The node with bold circle contains the solution \(x^k\) and gets the objective function approximation updated in the iteration. Similar to the results shown in the Tables 1 and 2, there are only minor differences for the master problem B&B tree between the two algorithms.

In connection with this illustration, we also present two figures (Figs. 4, 5 in “Appendix 2”) which show how one tracks the index sets of cuts associated with various nodes of the B&B trees. With all generated Benders’ cuts as one pool and all generated subproblem’ cuts as another pool, the sequence encodes the validity of the cuts from each pool for any given node of the master problem B&B tree. Again, there are only minor differences in the execution of the two algorithms for this example.

Example 1.2

This example extends Example 1.1 by requiring general integer variables in the first-stage as well. So instead of having \(x_1,x_2\) to be binary, they are now allowed to be integers and bounded by \(0 \le x_1,x_2 \le 5\). The summaries of applying two algorithms are shown in Tables 5 and 6. Compared to the previous example, Tables 5 and 6 demonstrate that due to a larger number of choices resulting from general integer variables in the first stage, the algorithms require more iterations to solve the problem. Note also that using BB-D requires more iterations than CPT-D for this instance, although the average number of cuts for BB-D is fewer than that used by CPT-D.

Table 5 \(\mathbf {ABC}\) algorithm with CPT-D for Example 1.2
Full size table
Table 6 \(\mathbf {ABC}\) algorithm with BB-D for Example 1.2
Full size table

Example 1.3

As with Example 1.2, we maintain the same range of integers in the range [0, 5], although we allow randomness in the T matrix, stated as follows.

$$\begin{aligned} T(\omega _1)=\left[ \begin{array}{c@{\quad }c} 0.1&{} 0\\ 0 &{} 0.5 \end{array} \right] , T(\omega _2)=\left[ \begin{array}{c@{\quad }c} 0.3&{} 0.2\\ 0 &{} 0.2 \end{array} \right] . \end{aligned}$$

The summary of applying the algorithms are shown in Tables 7 and 8. From Tables 7 and 8 we can conclude that BB-D requires fewer disjunctive cuts on average for solving subproblems than CPT-D. In addition, the total number of iterations and Benders’ cuts in the first stage are also fewer. Comparing Example 1.3 with Example 1.2, we also observe it takes more iterations to solve Example 1.3 (with random T) than to solve Example 1.2 (with fixed T). This is due the fact that T in Example 1.3 has higher density than in Example 1.2.

Table 7 \(\mathbf {ABC}\) algorithm with CPT-D for Example 1.3
Full size table
Table 8 \(\mathbf {ABC}\) algorithm with BB-D for Example 1.3
Full size table

5 Computational experiments

This section presents three computational experiments. In Sect. 5.1, we present computations using larger versions of the examples of Sect. 4. These examples are solved using a combination of MATLAB and CPLEX 12.3. The MATLAB code implements the first-stage B&B, whereas, the rest of the algorithm was coded in C++. The purpose of this combination was to study whether a deterministic equivalent formulation (DEF), solved using a commercial state-of-the-art solver provides any advantage over our decomposition methodology. One would expect that the DEF approach would win this race because of the advances in commercial solvers for deterministic MIPs. The results of Sect. 5.1 reveal that despite the strides made by commercial MIP solvers for DEF, they are not competitive with the decomposition approach for SMIP models.

There are two further sub-sections of computations in this section. In Sect. 5.2 we upgrade the first-stage branch-and-bound implementation from MATLAB to C++, and report whether the algorithm scales well with first-stage decisions. And finally in Sect. 5.3, we present computations with a new class of test instances which are generalizations of the SSLP instances [16]. The new test instances, which we refer to as Stochastic Server Location and Sizing (SSLS), allow general integer variables in both stages.

5.1 Comparisons between \(\mathbf {ABC}\) and DEF

In this subsection we compare the decomposition approach of ABC with solving a deterministic equivalent formulation (DEF) using state-of-the-art CPLEX MIP solvers with default setting through CPLEX 12.3 MATLAB API. We designed a MATLAB implementation of the \(\mathbf {ABC}\) algorithm which calls the CPLEX LP solver whenever an LP solution is required. For all other purposes (e.g. managing the B&B tree) the MATLAB script operates in the MATLAB environment.

Three sets of instances are generated based on Examples 1.1–ex1.3. For each example, we create 4, 9, 36, 121, 441, 1681, 10201 scenarios by generating the right hand sides \(r(\omega )\) from equidistant lattice points in \([5,15]\times [5,15]\) with equal probability assigned to each point. This methodology was borrowed from Schultz et al. [19] (see also [1]). For the seven instances based on Example 1.3, we use the same random right hand side \(r(\omega )=\left[ \begin{array}{c} r_1(\omega )\\ r_2(\omega )\end{array} \right] \) as in Example 1.2, but in addition \(T(\omega )\) is also random. The entries for these matrices were 0 or 1 with equal probability.

Table 9 compares the performance of three algorithms: two based on using the \(\mathbf {ABC}\) algorithm with CPT-D and BB-D whereas, the third algorithm used CPLEX 12.3 (with default setting) for the MILP formulation of the deterministic equivalent formulation (DEF). All approaches were run on a Windows 7 PC operating with Intel i7-3770K 3.5 GHz processors and 8 GB memory. Instances 1-3 in the table correspond to the variations based on Examples 1.1–ex1.3. The column heading Obj denotes the optimal objective value of the SMIP, Var and Constr denote the number of variables and constraints in the DEF. The entries in column \(\mathbf {ABC}\) \(\mathbf {(CPT-D)}\) and \(\mathbf {ABC}\) \(\mathbf {(BB-D)}\) denote Iterations (Master Nodes, Second-stage Leaf Nodes, Running Time) which correspond to the total number of iterations, the total number of nodes in the B&B tree in the master problem, the maximum leaf nodes encountered during solving the subproblem and the total running time. The DEF column shows the CPU time (in s) required to solve DEF using the default version CPLEX 12.3 MIP solver. The maximum CPU time allowed was 60 min.

Table 9 Comparison of \(\mathbf {ABC}\) with DEF
Full size table

The results reported in Table 9 clearly demonstrate that the approach of solving a DEF with a commercial solver does not scale well, failing to solve 9 instances for which the number of scenarios were somewhat large. In comparing the performance of \(\mathbf {ABC}\) \(\mathbf {(CPT-D)}\) and \(\mathbf {ABC}\) \(\mathbf {(BB-D)}\), we observe that the former also runs into numerical difficulties for 4 of the larger instances. In contrast, \(\mathbf {ABC}\) \(\mathbf {(BB-D)}\) produces optimal solutions for all the instances within very reasonable computational times. From the log-log plot in Fig. 6 (see “Appendix”), as number of scenarios increases, the running time also increases polynomially for \(\mathbf {ABC}\) \(\mathbf {(BB-D)}\). The slopes of each of the three graphs are slightly larger than one (with values 1.0048, 1.1245, 1.1677) which suggests that as the number of scenarios increases, the running time increases at a rate that is only slightly worse than “linear”. To sum up, based on the instances tested, algorithm \(\mathbf {ABC}\) shows very stable results and scales quite well with the number of scenarios. When CPLEX is able to solve an instance, it does so faster than our approach; however, when the number of scenarios increases, it does not find an optimal solution within an hour of CPU time, while the \(\mathbf {ABC}\) approach does.

5.2 Computations with larger first-stage instances

In this subsection we study how the ABC algorithm performs when the number of first-stage (search) variables increase. The larger instances are generated by including two more variables at a time to Examples 1.2 and 1.3. For the i-th time, the newly added pair of variables have objective coefficients given by \(-1.5*2^i\) and \(-4*2^i\). For the larger instance of Example 1.2, matrix \(T(\omega )\) is fixed. The fixed matrix is extended by a \(2 \times 2\) identity matrix with the newly pair of variables added. In the case of Example 1.3, \(T(\omega )\)’s elements are uniformly generated from set \(\{0.1, 0.2, 0.3, \ldots , 0.9\}\). The rest of the parameters are generated the same way as in instance 2 and instance 3.

We remind the reader that the objective function contours of this instance have been depicted in the case of 2 variables by Schultz et al. [19] and Ahmed et al. [1]. These papers also captured the challenges posed by the two variable instance. In comparison, the total number of first-stage feasible solutions in our extension increases the number of feasible first-stage solutions exponentially according to the sequence \(36^i\), \(i = 1,2\), etc. The largest instances we attempt have a total number of feasible first-stage solutions given by \(36^6\), implying a total of more than 2.1 billion feasible solutions. Of course, using MATLAB to search for optimal solutions of such instances would be untenable. So, the entire ABC algorithm is implemented in C++ including the first-stage B&B and second-stage decomposition. All linear programs were solved using CPLEX 12.6. Finally, we also note that our experiments were conducted for the most promising scheme among those compared in the previous section. Thus, the following reports our results using the BB-D version of the ABC algorithm.

The computational results of extending Example 1.2 are shown in Table 10. The column heading First-Stage Var Num denotes the number of first-stage variables, and the remaining information follows the same style as reported in Table 9. Comparing \(\mathbf First-Stage Var Num =2\) with instance 2 from Table 9, we can see the speed up of C++ implementation compared to using MATLAB. And as First-Stage Var Num grows each time by two, Iterations and Master Nodes required to solve the problem grow exponentially. We encounter some numerical difficulties for solving instances of 8 variables with 121 and 441 scenarios and 10 variables with 441 scenarios. Nevertheless, the algorithm did solve instances of 12 variables in reasonable time. Thus, as the number of first-stage variables grows, instances may not become harder, and such anomalies are also known to exist for deterministic MIPs as well.

The computational result of extending Example 1.3 (random T) is shown in Table 11. We can see the same speed up of C++ implementation compared to MATLAB as well as the exponential growth of Iterations and Master Nodes as First-Stage Var Num are added by two each time. There are numerical difficulties for solving instances of 8 and 10 variables with 121 and 441 scenarios and 12 variables with 441 scenarios. Because T is random and relatively dense, these instances become harder to solve.

Table 10 Computational results with \(\mathbf {ABC}\)/BB-D as first-stage variables increase for Example 1.2 (fixed T)
Full size table
Table 11 Computational results with \(\mathbf {ABC}\)/BB-D as first-stage variables increase Example 1.3 (random T)
Full size table
Table 12 SSLS-\((m \times u)\)-\((n \times v)\)-S
Full size table
Table 13 Computational results with \(\mathbf {ABC}\)/BB-D on SSLS instances
Full size table

5.3 Computational results with stochastic server location and sizing

One application of SMIP is in the network design and planning where servers need to be located in a least cost manner before demand from customers is known. This problem arises in a variety of domains such as telecommunication, electricity power, water distribution, internet service and anti-terrorism. One of the instances available in the literature, attributed to Ntaimo and Sen [16] is a stochastic server location problem (SSLP) in which demand uncertainty is limited to whether or not demand will occur at nodes of a graph. The goal of SSLP is to place servers at discrete locations in such a way that the expected cost of serving demand is minimized. That collection of instances have 0–1 variables in both stages. In order to test the ABC algorithm, we extend the above instances to a class of problems where in addition to location, we are interested in sizing the servers, where the size is measured in discrete units \([0,1,2,\ldots ,5]\). We refer to these test instances as the Stochastic Server Location and Sizing (SSLS) instances. The precise model formulation is given in “Appendix 1”.

The size of the model is captured by the name “SSLS-\((m \times u)\)-\((n \times v)\)-S”, where m is the number of potential server locations, u is the maximum number of servers allowed for each location, n is the number of potential client locations, v is the maximum number of possible clients for each location and S is the number of scenarios. We report results on problem instances with \(m \in \{2,3,4\}\), \(n \in \{5,10,15\}\), \(S \in \{50, 100, 500\}\), \(u=5\) and \(v=5\). A summary of the notations is shown in Table 12. We should note that while the number of potential server locations appear to be small, the fact that there are alternative sizes possible makes the combinatorial content significant, and more-or-less on par with the SSLP instances.

The computational environment is the same as in Section 5.2 and we used the C++ implementation for this experiment. Table 13 shows the results which are reported in a manner similar to Table 9, 10 etc. Again the number of variables (Var) and constraints (Constr) refer to numbers in the DEF formulation. The metrics reported in the column labeled ABC(BB-D) refer to the number of iterations and in parentheses, the numerical quantities refer to the number of master nodes, the number of second-stage leaf nodes, and the running time. The algorithm can handle most of the instances except the last two where the task of generating cuts for all outcomes slowed down the process. One should expect that problems with fixed recourse would be easier to handle. Among the runs completed, we can see that as m gets larger, Iterations and Master Nodes required to solve the problem grow dramatically as expected. On the other hand, as n gets larger while m,u,v and S stay the same, we find the Iterations and Master Nodes do not change in general, while the Second-stage Leaf Nodes and Running Time grow exponentially. We conclude this section by evaluating the potential of the ABC algorithm by comparing the run time and number of successfully solved problems. As for total run time in Table 13, the ABC algorithm requires about 3.18 h and successfully solved 25 instances. In comparison, CPLEX 12.6 requires 12.81 h and solved 15 instances successfully. Based on these comparisons, the ABC approach shows far greater potential for SMIP models.

6 Conclusion

As stated at the outset, our paper returns to the general class of two stage SMIP problems that was the focus of the paper by Carøe and Tind [4]. This class of problems involves mixed-integer variables in both stages, and randomness is also allowed in all data elements of the second-stage MIP. Despite the elegance of the work of Carøe and Tind [4], the chasm between first and second stage strategies has persisted over the ensuing decades. Using several building blocks that have been effective in the interim, we have developed a time-staged decomposition algorithm for very general SMIP models. Other effective ideas, such as allowing the second-stage problem to be solved inexactly are also permitted within the overall strategy. The key feature of this algorithm is a first-stage B&B process (i.e. the ABC algorithm) which simultaneously guides both the construction of approximations as well as the search for optimal first-stage decisions. Furthermore, the recourse function approximations remain piecewise linear and convex for each first-stage B&B node, and similarly, the second-stage relaxations (built using multi-term disjunctions) are also polyhedral. While these elements maintain convex building blocks, the overall search is facilitated by a B&B scheme which selectively chooses valid approximations of functions and sets in a manner that allows the algorithm to discover an optimal solution to the overall problem.

We have also presented the most comprehensive computational experiment to date for problems in which mixed-integer variables appear in both stages. Our computations reveal that as the number of scenarios grow, our MATLAB-guided implementation was faster and more stable than the commercial solver for an extensive form SMIP. We also reported computational results for larger instances which required a more sophisticated implementation than the MATLAB prototype. Both of those experiments (one with an extended test instance, and another with a new test problem) reveal that the ABC framework, especially in the BB-D setting, leads to a viable approach for realistic instances. We recommend at least two avenues in which the ABC/BB-D approach may be promising: (a) implementing these ideas on parallel machines should be fruitful, and (b) these concepts should be extended to multi-stage models. Our computational experiment shows that when the SMIP models have large number of first stage variables and large number of scenarios, our decomposition approach is preferable to using a state-of-the-art commercial solver for the DEF.