On integrality ratios for asymmetric TSP in the Sherali–Adams hierarchy

Abstract

We study the Asymmetric Traveling Salesman Problem (ATSP), and our focus is on negative results in the framework of the Sherali–Adams (SA) Lift and Project method. Our main result pertains to the standard linear programming (LP) relaxation of ATSP, due to Dantzig, Fulkerson, and Johnson. For any fixed integer $t\ge 0$ and small $\epsilon$, $0<\epsilon \ll {1}$, there exists a digraph G on $\nu =\nu (t,\epsilon )=O(t/\epsilon )$ vertices such that the integrality ratio for level t of the SA system starting with the standard LP on G is ${\ge } 1+\frac{1-\epsilon }{2t+3} \approx \frac{4}{3}, \frac{6}{5}, \frac{8}{7}, \ldots$. Thus, in terms of the input size, the result holds for any $t = 0,1,\ldots ,{\varTheta }(\nu )$ levels. Our key contribution is to identify a structural property of digraphs that allows us to construct fractional feasible solutions for any level t of the SA system starting from the standard LP. Our hard instances are simple and satisfy the structural property. There is a further relaxation of the standard LP called the balanced LP, and our methods simplify considerably when the starting LP for the SA system is the balanced LP; in particular, the relevant structural property (of digraphs) simplifies such that it is satisfied by the digraphs given by the well-known construction of Charikar, Goemans and Karloff (CGK). Consequently, the CGK digraphs serve as hard instances, and we obtain an integrality ratio of $1 +\frac{1-\epsilon }{t+1}$ for any level t of the SA system, where $0<\epsilon \ll {1}$ and the number of vertices is $\nu (t,\epsilon )=O((t/\epsilon )^{(t/\epsilon )})$. Also, our results for the standard LP extend to the path ATSP (find a min cost Hamiltonian dipath from a given source vertex to a given sink vertex).

1 Introduction

The Traveling Salesman Problem (TSP) is a celebrated problem in combinatorial optimization, with many connections to theory and practice. The problem is to find a minimum cost tour of a set of cities; the tour should visit each city exactly once. The most well known version of this probelm is the symmetric one (denoted TSP), where the distance (a.k.a. cost) from city i to city j is equal to the distance (cost) from city j to city i. The more general version is called the asymmetric TSP (denoted ATSP), and it does not have the symmetry restriction on the costs. Throughout, we assume that the costs satisfy the triangle inequalities, i.e., the costs are metric.

Linear programming (LP) relaxations play a central role in solving TSP or ATSP, both in practice and in the theoretical setting of approximation algorithms. Many LP relaxations are known for ATSP, see [19] for a recent survey. The most well-known relaxation (and the one that is most useful for theory and practice) is due to Dantzig, Fulkerson and Johnson; we call it the standard LP or the DFJ LP. It has a constraint for every nontrivial cut, and has an indegree and an outdegree constraint for each vertex; see Sect. 2.1. There is a further relaxation of the standard LP that is of interest; we call it the balanced LP (Bal LP); it is obtained from the standard LP by replacing the indegree and outdegree constraint at each vertex by a balance (equation) constraint. For metric costs, the optimal value of the standard LP is the same as the optimal value of the balanced LP; this is a well-known fact, see [19], [7, Footnote 3].

One key question in the area is the quality of the objective value computed by the standard LP. This is measured by the integrality ratio (a.k.a. integrality gap) of the relaxation, and is defined to be the supremum over all instances of the integrality ratio of the instance. The integrality ratio of an instance I is given by $\textit{opt}(I)/\textit{dfj}(I)$, where $\textit{opt}(I)$ denotes the optimum (minimum cost of a tour) of I, and $\textit{dfj}(I)$ denotes the optimal value of the standard LP relaxation of I; we assume that the optima exist and that $\textit{dfj}(I)\not =0$.¹

For both TSP and ATSP, significant research efforts have been devoted over several decades to prove bounds on the integrality ratio of the standard LP. For TSP, methods based on Christofides’ algorithm show that the integrality ratio is ${\le }\frac{3}{2}$, whereas the best lower bound known on the integrality ratio is $\frac{4}{3}$. Closing this gap is a major open problem in the area. For ATSP, a result of Asadpour et al. [3] showed that the integrality ratio is ${\le } O(\log {n}/\log \log {n})$. Recently, Anari et al. [1] improved the upper bound on the integrality ratio to polyloglog(n) for ATSP. On the other hand, Charikar, et al. [7] showed a lower bound of 2 on the integrality ratio, thereby refuting an earlier conjecture of Carr and Vempala [6] that the integrality ratio is ${\le }\frac{4}{3}$.

Lampis [14] and Papadimitriou and later Vempala [18], respectively, have proved hardness-of-approximation thresholds of $\frac{185}{184}$ for TSP and $\frac{117}{116}$ for ATSP; both results assume that $\mathbf {P}$ $\not =$ $\mathbf {NP}$. Recently, Karpinski et al. [13] have improved both hardness-of-approximation thresholds to 123/122 and 75/74, respectively, assuming that $\mathbf {P}$ $\not =$ $\mathbf {NP}$.

Our goal is to prove lower bounds on the integrality ratios for ATSP for the tighter LP relaxations obtained by applying the Sherali–Adams Lift-and-Project method. Before stating our results, we present an overview of Lift-and-Project methods.

1.1 Hierarchies of convex relaxations

Over the past 25 years, several methods have been developed in order to obtain tightenings of relaxations in a systematic manner. Assume that each variable $y_i$ is in the interval [0, 1], i.e., the integral solutions are zero/one, and let n denote the number of variables in the original relaxation. The goal is to start with a simple relaxation, and then iteratively obtain a sequence of stronger/tighter relaxations such that the associated polytopes form a nested family that contains (and converges to) the integral hull.²

These procedures, usually called Lift-and-Project hierarchies (or systems, or methods, or procedures), use polynomial reasonings together with the fact that in the 0/1 domain, general polynomials can be reduced to multilinear polynomials (utilizing the identity $y_i^2=y_i$), and then finally obtain a stronger relaxation by applying linearization (e.g., for subsets S of $\{1,\ldots ,n\}$, the term $\prod _{i \in S} y_i$ is replaced by a variable $y_S$). In this overview, we gloss over the Project step. In particular, Sherali and Adams [20] devised the Sherali–Adams (SA) system, Lovász and Schrijver [17] devised the Lovász–Schrijver (LS) system, and Lasserre [15] devised the Lasserre system. See Laurent [16] for a survey of these systems; several other Lift-and-Project systems are known, see [4, 10].

The index of each relaxation in the sequence of tightened relaxations is known as the level in the hierarchy; the level of the original relaxation is defined to be zero. The relaxation at level n is exact, i.e., the associated polytope is equal to the integral hull. For Lovász–Schrijver hierarchy and Sherali–Adams hierarchy, and for any $t=O(1)$, it is known that the relaxation at level t of the hierarchy can be solved to optimality in polynomial time, assuming that the original relaxation has a polynomial-time separation oracle, [21].

Over the last two decades, a number of important improvements on approximation guarantees have been achieved based on relaxations obtained from Lift-and-Project systems. See [10] for a recent survey of many such positive results.

Starting with the work of Arora et al. [2], substantial research efforts have been devoted to showing that tightened relaxations (for many levels) fail to reduce the integrality ratio for many combinatorial optimization problems (see [10] for a list of negative results). This task seems especially difficult for the SA system because it strengthens relaxations in a “global manner;” this enhances its algorithmic leverage for deriving positive results, but makes it more challenging to design instances with bad integrality ratios. Moreover, an integrality ratio for the SA system may be viewed as an unconditional inapproximability result for a restricted model of computation, whereas, hardness-of-approximation results are usually proved under some complexity assumptions, such as $\mathbf {P}$ $\,\not =\,\,$ $\mathbf {NP}$. The SA system is known to be more powerful than the LS system, while it is weaker than the Lasserre system; it is incomparable with the LS $_+$ system (the positive-semidefinite version of the Lovász–Schrijver system [17]).

A key paper by Fernández de la Vega and Kenyon-Mathieu [11] introduced a probabilistic interpretation of the SA system, and based on this, negative results (for the SA system) have been proved for a number of combinatorial problems; also see Charikar et al. [8] and Benabbas et al. [5]. At the moment, it is not clear that methods based on [11] could give negative results for TSP and its variants, because the natural LP relaxations (of TSP and related problems) have “global constraints.”

To the best of our knowledge, there are only two previous papers with negative results for Lift-and-Project methods applied to TSP and its variants. Cheung [9] proves an integrality ratio of $\frac{4}{3}$ for TSP, for O(1) levels of LS $_+$. For ATSP, Watson [22] proves an integrality ratio of $\frac{3}{2}$ for level 1 of the Lovász–Schrijver hieararchy, starting from the balanced LP (in fact, both the hierarchies LS and SA give the same relaxation at level one).

We mention that Cheung’s results [9] for TSP do not apply to ATSP, although at level 0, it is well known that any integrality ratio for the standard LP for TSP applies also to the standard LP for ATSP (this relationship does not hold for level 1 or higher).

1.2 Our results and their significance

Our main contribution is a generic construction of fractional feasible solutions for any level t of the SA system starting from the standard LP relaxation of ATSP. We have a similar but considerably simpler construction when the starting LP for the SA system is the balanced LP. Our results on integrality ratios are direct corollaries.

We have the following results pertaining to the balanced LP relaxation of ATSP: We formulate a property of digraphs that we call the good decomposition property, and given any digraph with this property, we construct a vector y on the edges such that y is a fractional feasible solution to the level t tightening of the balanced LP by the Sherali–Adams system. Charikar, Goemans, and Karloff (CGK) [7] constructed a family of digraphs for which the balanced LP has an integrality ratio of 2. We show that the digraphs in the CGK family have the good decomposition property, hence, we obtain an integrality ratio for level t of SA. In more detail, we prove that for any integer $t\ge 0$ and small enough $\epsilon >0$, there is a digraph G from the CGK family on $\nu =\nu (t,\epsilon )=O((t/\epsilon )^{t/\epsilon })$ vertices such that the integrality ratio of the level-t tightening of Bal LP is at least $1+\frac{1-\epsilon }{t+1} \approx 2, \frac{3}{2}, \frac{4}{3}, \frac{5}{4}, \ldots$ (where $t=0$ identifies the original relaxation).

Our main result pertains to the standard LP relaxation of ATSP. Our key contribution is to identify a structural property of digraphs that allows us to construct fractional feasible solutions for the level t tightening of the standard LP by the Sherali–Adams system. This construction is much more difficult than the construction for the balanced LP. We present a simple family of digraphs that satisfy the structural property, and this immediately gives our results on integrality ratios. We prove that for any integer $t\ge 0$ and small enough $\epsilon >0$, there are digraphs G on $\nu =\nu (t,\epsilon )=O(t/\epsilon )$ vertices such that the integrality ratio of the level t tightening of the standard LP on G is at least $1+\frac{1-\epsilon }{2t+3} \approx \frac{4}{3}, \frac{6}{5}, \frac{8}{7}, \frac{10}{9}, \ldots$. The rank of a starting relaxation (or polytope) is defined to be the minimum number of tightenings required to find the integral hull (in the worst case). An immediate corollary is that the SA-rank of the standard LP relaxation on a digraph $G=(V,E)$ is at least linear in |V|, whereas, the rank in terms of the number of edges is ${\varOmega }(\sqrt{|E|})$ (since the LP is on a complete digraph, namely, the metric completion).

Our results for the balanced LP and for the standard LP are incomparable, because the SA system starting from the standard LP is strictly stronger than the SA system starting from the balanced LP, although both the level zero LPs have the same optimal value, assuming metric costs. (In fact, there is an example on 5 vertices [12, Figure 4.4, p. 60] such that the optimal values of the level 1 tightenings are different: $9\frac{1}{3}$ for the balanced LP and 10 for the standard LP.)

Finally, we extend our main results to the natural relaxation of path ATSP (min cost Hamiltonian dipath from a given source vertex to a given sink vertex), and we obtain integrality ratios ${\ge } 1+\frac{2-\epsilon }{3t+4} \approx \frac{3}{2}, \frac{9}{7}, \frac{6}{5}, \frac{15}{13}, \ldots$ for the level-t SA tightenings. Our result on path ATSP is obtained by “reducing” from the result for ATSP; the idea behind this comes from an analogous result of Watson [22] in the symmetric setting; Watson gives a method for transforming Cheung’s [9] result on the integrality ratio for TSP to obtain a lower bound on the integrality ratio for path TSP.

The solutions given by our constructions are not positive semidefinite; thus, they do not apply to the LS $_+$ hierarchy nor to the Lasserre hierarchy.

Let us assess our results, and place them in context. Observe that our integrality ratios fade out as the level of the SA tightening increases, and for $t\ge 35$ (roughly) our integrality ratio falls below the hardness threshold of $\frac{75}{74}$ of [13]. Thus, our integrality ratios cannot be optimal, and it is possible that an integrality ratio of 2 can be proved for O(1) levels of the SA system.

On the other hand, our results are not restricted to $t=O(1)$. For example, parameterized with respect to the number of vertices in the input $\nu$, our lower bound for the standard LP holds even for level $t={\varOmega }(\nu )$, and our lower bound for the balanced LP (which improves on our lower bound for the standard LP) holds even for level $t={\varOmega }(\log \nu / \log \log \nu )$, thus giving unconditional inapproximability results for these restricted algorithms, even allowing super-polynomial running time.

Moreover, our results (and the fact that they are not optimal) should be contrasted with the known integrality ratio results for the level zero standard LP, a topic that has been studied for decades.

2 Preliminaries

When discussing a digraph (directed graph), we use the terms dicycle (directed cycle), etc., but we use the term edge rather than directed edge or arc. For a digraph $G=(V,E)$ and $U\subseteq {V}$, $\delta ^{out}(U)$ denotes $\{ (v,w)\in {E}: v\in U, w\not \in U\}$, the set of edges outgoing from U, and $\delta ^{in}(U)$ denotes $\{ (v,w)\in {E}: v\not \in U, w\in U\}$. For $x\in \mathbb {R}^{E}$ and $S\subseteq {E}$, x(S) denotes $\sum _{e\in {S}}x_e$.

By the metric completion of a digraph $G=(V,E)$ with nonnegative edge costs $c\in \mathbb {R}^E$, we mean the complete digraph $G'$ on V with the edge costs $c'$, where $c'(v,w)$ is taken to be the minimum cost (w.r.t. c) of a v, w dipath of G.

An Eulerian subdigraph of G is defined as follows: the vertex set is V and the edge set is a “multi-subset” of E (that is, each edge in E occurs zero or more times) such that (i) the indegree of every vertex equals its outdegree, and (ii) the subdigraph is weakly connected (i.e., the underlying undirected graph is connected). The ATSP on the metric completion $G'$ of G is equivalent to finding a minimum cost Eulerian subdigraph of G.

For a positive integer t and a ground set U, let $\mathcal {P}_{t}$ denote the family of subsets of U of size at most t, i.e., $\mathcal {P}_{t} = \{ S : S \subseteq U, |S| \le t\}$. We usually take the ground set to be the set of edges of a fixed digraph. Now, let G be a digraph, and let the ground set (for $\mathcal {P}_{t}$) be $E=E(G)$. Let $E'$ be a subset of E. Let $\mathbf{1}^{E',\,t}$ denote a vector indexed by elements of $\mathcal {P}_{t}$ such that for any $S \in \mathcal {P}_t$, $\mathbf{1}^{E',\,t}_S=1$ if $S\subseteq {E'}$, and $\mathbf{1}^{E',\,t}_S = 0$, otherwise. Note that $\mathbf{1}^{E',\,1}$ has the entry for $\emptyset$ at 1, and the other entries give the incidence vector of $E'$.

We denote set difference by $-$, and we denote the addition (removal) of a single item e to (from) a set S by $S+e$ (respectively, $S-e$), rather than by $S\cup \{e\}$ (respectively, $S-\{e\}$).

2.1 LP relaxations for asymmetric TSP

Let $G=(V,E)$ be a digraph with nonnegative edge costs c. Let $\widehat{\textsf {ATSP}}_{{DFJ}}(G)$ be the feasible region (polytope) of the following linear program that has a variable $x_e$ for each edge e of G:

$$\begin{aligned} \hbox {minimize}&\sum _{e} c_e x_e \\ \hbox {subject to} \quad&x\left( \delta ^{in}(S)\right) \ge 1,&\quad \forall S:~\emptyset \subset S \subset V \\&x\left( \delta ^{out}(S)\right) \ge 1,&\quad \forall S:~\emptyset \subset S \subset V \\&x\left( \delta ^{in}(\{v\})\right) = 1, \quad x\left( \delta ^{out}(\{v\})\right) = 1,&\quad \forall v \in V\\&\mathbf{0} \le \mathbf{x}\le \mathbf{1} \\ \end{aligned}$$

In particular, when G is a complete digraph with metric costs, the above linear program is the standard LP relaxation of ATSP (a.k.a. DFJ LP).

We obtain the balanced LP (Bal LP) from the standard LP by replacing the two constraints $x\left( \delta ^{in}(\{v\})\right) = 1,\; x\left( \delta ^{out}(\{v\})\right) = 1$ by the constraint $x\left( \delta ^{in}(\{v\})\right) = x\left( \delta ^{out}(\{v\})\right)$, for each vertex v. Let $\widehat{\textsf {ATSP}}_{BAL}(G)$ be the feasible region (polytope) of Bal LP.

$$\begin{aligned} \hbox {minimize}&\sum _{e} c_e x_e \\ \hbox {subject to} \\&x\left( \delta ^{in}(S)\right) \ge 1,&\quad \forall S:~\emptyset \subset S \subset V \\&x\left( \delta ^{out}(S)\right) \ge 1,&\quad \forall S:~\emptyset \subset S \subset V \\&x\left( \delta ^{out}(\{v\})\right) = x\left( \delta ^{in}(\{v\})\right) ,&\quad \forall v \in V \\&\mathbf{0} \le \mathbf{x}\le \mathbf{1} \\ \end{aligned}$$

In particular, when G is a complete digraph with metric costs, the above linear program is the balanced LP relaxation of ATSP.

Our construction of fractional feasible solutions exploits the structure of the original digraph. This is the reason for discussing the polytopes on the original digraph (and not only on the complete digraph). To justify this, we observe that any feasible solution for the original digraph can be extended to a feasible solution for the complete digraph by “padding with zeros.” (This argument is formalized in Sect. 2.2.1).

2.2 The Sherali–Adams system

Definition 1

(The Sherali–Adams it system) Consider a polytope $\widehat{P} \subseteq [0,1]^n$ over the variables $y_1,\ldots , y_n$, and its description by a system of linear constraints of the form $\sum _{i=1}^n a_i y_i \ge {b}$; note that the constraints $y_i\ge 0$ and $y_i\le {1}$ for all $i\in \{1,\ldots ,n\}$ are included in the system. The level-t Sherali–Adams tightened relaxation $\mathcal {SA}^t(\widehat{P})$ of $\widehat{P}$, is an LP over the variables $\{y_S{:}\; S\subseteq \{1,2,\ldots ,n\},\; |S|\le {t+1} \}$ (thus, $y\in \mathbb {R}^{\mathcal {P}_{t+1}}$ where $\mathcal {P}_{t+1}$ has ground set $\{1,2,\ldots ,n\}$); moreover, we have $y_{\emptyset } =1$. For every constraint $\sum _{i=1}^n a_i y_i\ge {b}$ of $\widehat{P}$ and for every disjoint $S,Q \subseteq \{1,\ldots , n\}$ with $|S|+|Q|\le t$, the following is a constraint of the level-t Sherali–Adams relaxation.

$$\begin{aligned} \sum _{i=1}^n a_i \sum _{\emptyset \subseteq T \subseteq Q} (-1)^{|T|} y_{S \cup T \cup \{i\} } \ge b \sum _{\emptyset \subseteq T \subseteq Q} (-1)^{|T|} y_{S \cup T }. \end{aligned}$$

(1)

We will use a convenient abbreviation:

$$\begin{aligned} z_{S,Q} := \sum _{\emptyset \subseteq T \subseteq Q} (-1)^{|T|} y_{S \cup T }, \end{aligned}$$

where $z_{S,Q}$ are auxiliary variables between 0 and 1.

Informally speaking, the level-t Sherali–Adams relaxation is derived by multiplying any constraint of the original relaxation by the high degree polynomial

$$\begin{aligned} \prod _{j \in S} y_i \prod _{j \in Q} (1-y_i), \end{aligned}$$

where S, Q are disjoint subsets of $\{1,\ldots , n\}$ with $|S|+|Q|\le t$. After expanding the products, we obtain a polynomial of degree at most $t+1$. Replacing any occurrences of $\prod _{i \in S} y_i$ by the corresponding variable $y_S$ for all $S\subseteq \{1,\ldots , n\}$ gives the constraint described in Inequality (1) (Definition 1).

There are a number of approaches for certifying that ${y}\in \mathcal {SA}^t(\widehat{P})$ for a given ${y}$. One popular approach is to give a probabilistic interpretation to the entries of ${y}$, satisfying certain conditions. We follow an alternative approach, that is standard, see [16], [21, Lemma 2.9], but has been rarely used in the context of integrality ratios.

First, we introduce some notation. Given a polytope $\widehat{P} \subseteq [0,1]^n$, consider the cone ${P}= \{ y_\emptyset (1, {y}){:}~ y_\emptyset \ge 0, {y}\in \widehat{P}\}$. (Throughout the paper, we use an accented symbol to denote a polytope, e.g., $\widehat{P}$, and the symbol (without accent) to denote the associated cone, e.g., P.) It is not difficult to see that the SA system can be applied to the cone P, so that the projection in the n original variables can be obtained by projecting any $y\in \mathcal {SA}^t({P})$ with $y_\emptyset = 1$ on the n original variables. Note that $\mathcal {SA}^t({P})$ is a cone, hence, we may have $y\in \mathcal {SA}^t({P})$ with $y_\emptyset \not = 1$; but if $y_\emptyset \not =0$, we can replace y by $\frac{1}{y_\emptyset } y$. Also, note that $\mathcal {SA}^t(\widehat{P})=\{y{:}~ y_\emptyset =1, y\in \mathcal {SA}^t({P})\}$ by Definition 1.

For a vector ${y}$ indexed by subsets of $\{1,\ldots ,n\}$ of size at most $t+1$, define a shift operator “$*$” as follows: for every $e \in \{1,\ldots ,n\}$, let $e*{y}$ to be a vector indexed by subsets of $\{1,\ldots ,n\}$ of size at most t, such that $(e*y)_S :=y_{S + e}$. We have the following folklore fact, [21, Lemma 2.9].

Fact 1

${y}\in \mathcal {SA}^t({P}) ~~\mathbf{if ~and ~only~ if}\, e*{y}\in \mathcal {SA}^{t-1}({P}), ~\mathbf{and}~ {y}- e*{y}\in \mathcal {SA}^{t-1}({P}), \forall e \in \{1,\ldots ,n\}$.

The reader familiar with the Lovász–Schrijver system may recognize the similarity of its definition with the characterization of the Sherali–Adams system of Fact 1. In fact, the SA system differs from the LS system only in that it imposes additional consistency conditions; namely, the moment vector ${y}$, indexed by subsets of size $t+1$, has to be fixed beforehand. This seemingly small detail gives the SA system enhanced power compared to the LS system.

2.2.1 Eliminating variables to 0

In our discussion of the standard LP and the balanced LP, it will be convenient to restrict the support to the edge set of a given digraph rather than the complete digraph. Thus, we assume that some of the variables are absent. Formally, this is equivalent to setting these variables in advance to zero. As long as the nonzero variables induce a feasible solution, we are justified in setting the other variables to zero. The following result formalizes the arguments.

Proposition 1

Let $\widehat{P}$ be the feasible region (polytope) of a linear program. Let C be a set of indices (of the variables) that does not contain the support of any “positive constraint” of $\widehat{P}$, where a constraint $\sum _{i=1}^n a_i y_i\ge {b}$ of $\widehat{P}$ is called positive if $b>0$. Let $\widehat{P}_C$ be the feasible region (polytope) of the linear program obtained by removing all variables with indices in C from the constraints of the linear program of $\widehat{P}$ (informally, the new LP fixes all variables with indices in C at zero). Then, for the SA system, for any feasible solution ${y}$ to the level-t tightening of $\widehat{P}_C$, there exists a feasible solution ${y}'$ to the level-t tightening of $\widehat{P}$; moreover, ${y}'$ is obtained from ${y}$ by fixing variables, indexed by subsets intersecting C, to zero.

Proof

For ${y}\in \mathcal {SA}^t(\widehat{P}_C)$, the “extension” ${y}'$ of ${y}$ is defined as follows:

$$\begin{aligned} {y}'_S = \left\{ \begin{array}{ll} {y}_S, &{} \,\text {if}\, S\cap C = \emptyset \\ 0, &{} \,\text {otherwise}\, \\ \end{array} \right. \end{aligned}$$

For the corresponding auxiliary variables ${z}$, this would imply that

$$\begin{aligned} {z}_{S,Q}' = \left\{ \begin{array}{ll} 0, &{} \,\text {if}\, S\cap C \not = \emptyset \\ {z}_{S,Q-C}, &{} \,\text {otherwise}\,. \\ \end{array} \right. \end{aligned}$$

In order to show that ${y}' \in \mathcal {SA}^t(\widehat{P})$, we need to verify that for every pair of sets S, Q as in Definition 1, we have $\sum _{i=1}^n a_i z_{S \cup \{i\},Q}' \ge b z_{S,Q}'$.

First we note that if $S \cap C \not = \emptyset$, then for every i we have ${z}'_{S \cup \{i\},Q} = {z}'_{S ,Q} = 0$, and hence the constraint is satisfied trivially.

For the remaining case $S \cap C = \emptyset$, we have

$$\begin{aligned} \sum _{i=1}^n a_i z_{S \cup \{i\},Q}'= & {} \sum _{i \in C} a_i z_{S \cup \{i\},Q}' + \sum _{i \not \in C} a_i z_{S \cup \{i\},Q}' \nonumber \\= & {} \sum _{i \not \in C} a_i z_{S \cup \{i\},Q}' \nonumber \\= & {} \sum _{i \not \in C} a_i z_{S \cup \{i\},Q-C} \nonumber \\\ge & {} b ~ z_{S,Q-C} \nonumber \\= & {} b ~ z_{S,Q-C}' \nonumber \\= & {} b ~ z_{S,Q}', \end{aligned}$$

(2)

where (2) follows from the validity of the corresponding constraint of $\widehat{P}_C$; here, we use the fact that C does not contain the support of any positive constraint—otherwise, the summation $\sum _{i\not \in {C}}(\dots )$ would be zero since the index set $\{i{:} i\not \in {C}\}$ would be empty, and hence, the inequality $0 = \sum _{i\not \in {C}}(\dots ) \ge b\; z_{S,Q-C}$ would fail to hold for $b>0$ and $z_{S,Q-C} > 0$.

3 SA applied to the balanced LP relaxation of ATSP

3.1 Certifying a feasible solution

Fig. 1

A digraph G with a good decomposition given by the dicycle with thick edges, and the length 2 dicycles $C_j$ formed by the anti-parallel pairs of thin edges; $G-E(C_j)$ is strongly connected for each dicycle $C_j$

A strongly connected digraph $G=(V,E)$ is said to have a good decomposition with witness set $\mathcal {F}$ if the following hold

• (i) E partitions into edge-disjoint dicycles $C_1,C_2,\ldots ,C_N$, that is, there exist edge-disjoint dicycles $C_1,C_2,\ldots ,C_N$ such that $E = \bigcup _{1\le j \le N} E(C_j)$; let $\mathcal {N}$ denote the set of indices of these dicycles, thus $\mathcal {N}=\{1,\dots ,N\}$;

• (ii) moreover, there exists a nonempty subset $\mathcal {F}$ of $\mathcal {N}$ such that for each $j\in \mathcal {F}$ the digraph $G-E(C_j)$ is strongly connected.

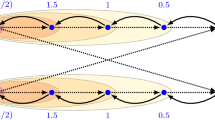
Let $\overline{\mathcal {F}}$ denote $\mathcal {N}-\mathcal {F}$. For an edge e, we use $\textit{index}(e)$ to denote the index j of the dicycle $C_j, j\in \mathcal {N}$ that contains e. In this section, by a dicycle $C_i, C_j,$ etc., we mean one of the dicycles $C_1,\dots ,C_N$, and we identify a dicycle $C_j$ with its edge set, $E(C_j)$. See Fig. 1 for an illustration of a good decomposition of a digraph.

Informally speaking, our plan is as follows: for digraph G that has a good decomposition with witness set $\mathcal {F}$, we construct a feasible solution to $\mathcal {SA}^t({\widehat{\textsf {ATSP}}_{BAL}(G)})$ by assigning the same fractional value to the edges of the dicycles $C_j$ with $j\in \mathcal {F}$, while assigning the value 1 to the edges of the dicycles $C_i$ with $i\in \overline{\mathcal {F}}$ (this is not completely correct; we will refine this plan). Let ${\textsf {ATSP}_{BAL}}(G)$ be the associated cone of $\widehat{\textsf {ATSP}}_{BAL}(G)$.

Definition 2

Let t be a nonnegative integer. For any set $S\subseteq E$ of size $\le t+1$, and any subset $\mathcal {I}$ of $\mathcal {F}$, let $F^{\mathcal {I}}(S)$ denote the set of indices $j\in \mathcal {F}-\mathcal {I}$ such that $E(C_j) \cap S \not =\emptyset$; moreover, let $f^{\mathcal {I}}(S)$ denote $|F^{\mathcal {I}}(S)|$, namely, the number of dicycles $C_j$ with indices in $\mathcal {F}-\mathcal {I}$ that intersect S.

Definition 3

For a nonnegative integer t and for any subset $\mathcal {I}$ of $\mathcal {F}$, let $y^{\mathcal {I},\,t}$ be a vector indexed by the elements of $\mathcal {P}_{t+1}$ and defined as follows:

$$\begin{aligned} y^{\mathcal {I},\,t}_S = \frac{t+2-f^{\mathcal {I}}(S)}{t+2}, \quad \forall S \in \mathcal {P}_{t+1} \end{aligned}$$

Theorem 2

Let $G=(V,E)$ be a strongly connected digraph that has a good decomposition, and let $\mathcal {F}$ be the witness set. Then

$$\begin{aligned} y^{\mathcal {I},\,t} \in \mathcal {SA}^t({\widehat{\textsf {ATSP}}_{BAL}(G)}), \quad \forall t\in \mathbb {Z}_+, \forall \mathcal {I}\subseteq \mathcal {F}. \end{aligned}$$

In order to prove our integrality ratio result for $\widehat{\textsf {ATSP}}_{BAL}$, we will invoke Theorem 2 for $\mathcal {I}=\emptyset$ (the more general setting of the theorem is essential for our induction proof; we give a high-level explanation in the last paragraph of the proof of Theorem 2 below). Since also only the values of $y^{\emptyset ,\,t}$ indexed at singleton edges affect the integrality ratio, it is worthwhile to summarize all relevant quantities in the next corollary.

Corollary 1

We have

$$\begin{aligned} y^{\emptyset ,\,t} \in \mathcal {SA}^t({\widehat{\textsf {ATSP}}_{BAL}(G)}), \quad \forall t\in \mathbb {Z}_+. \end{aligned}$$

Moreover, for each dicycle $C_j$, $j\in \mathcal {N}$, and each edge e of $C_j$ we have

$$\begin{aligned} y^{\emptyset ,\,t}_e = {\left\{ \begin{array}{ll} \frac{t+1}{t+2}, &{}\text {if } j \in \mathcal {F}\\ {1}, &{}\text {otherwise}. \end{array}\right. } \end{aligned}$$

(3)

Informally speaking, we assign the value 1 (rather than a fractional value) to the edges of the dicycles $C_j$ with $j\in \mathcal {I}\subseteq \mathcal {F}$. For the sake of exposition, we call the dicycles $C_j$ with $j\in \mathcal {F}-\mathcal {I}$ the fractional dicycles, and we call the remaining dicycles $C_i$ (thus $i\in \mathcal {I}\cup \overline{\mathcal {F}}$) the integral dicycles.

Proof

(Proof of Theorem 2): To prove Theorem 2, we need to prove

$$\begin{aligned} y^{\mathcal {I},\,t} \in \mathcal {SA}^{t}({{\textsf {ATSP}_{BAL}}(G)}). \end{aligned}$$

We prove this by induction on t.

Note that $y^{\mathcal {I},\,t}_\emptyset =1$ by Definition 3.

The induction basis is important, and it follows easily from the good decomposition property. In Lemma 1 (below) we show that $y^{\emptyset ,\,0} \in \mathcal {SA}^0({{\textsf {ATSP}_{BAL}}(G)})$. We conclude that $y^{\mathcal {I},\,0}$ satisfies the first two sets of constraints of ${\textsf {ATSP}_{BAL}}(G)$, since $y^{\mathcal {I},\,0} \ge y^{\emptyset ,\,0}$ (this follows from Definitions 2, 3, since $F^{\mathcal {I}}(S) \subseteq F^{\emptyset }(S)$). As for the balance constraints, it is enough to observe that every vertex of our instance (see Fig. 1) is incident to pairs of outgoing and ingoing edges, which due to Definition 3 are assigned the same value. Finally, again by Definition 3, and for all edges e, we have $0\le y^{\mathcal {I},\,0}_e \le 1$. All the above imply that $y^{\mathcal {I},\,0} \in \mathcal {SA}^0({{\textsf {ATSP}_{BAL}}(G)}),\;\forall \mathcal {I}\subseteq \mathcal {F}$, as wanted.

In the induction step, we assume that $y^{\mathcal {I},\,t} \in \mathcal {SA}^t({{\textsf {ATSP}_{BAL}}(G)})$ for some integer $t\ge 0$ (the induction hypothesis), and we apply the recursive definition based on the shift operator, namely, $y^{\mathcal {I},\,t+1} \in \mathcal {SA}^{t+1}({{\textsf {ATSP}_{BAL}}(G)})$ iff for each $e\in E$

$$\begin{aligned} e * y^{\mathcal {I},\,t+1} \in \mathcal {SA}^t({{\textsf {ATSP}_{BAL}}(G)}), \end{aligned}$$

(4)

$$\begin{aligned} y^{\mathcal {I},\,t+1} - e*y^{\mathcal {I},\,t+1} \in \mathcal {SA}^t({{\textsf {ATSP}_{BAL}}(G)}). \end{aligned}$$

(5)

Lemma 2 (below) proves (4) and Lemma 3 (below) proves (5).

We prove that $e*y^{\mathcal {I},\,t+1}$ is in $\mathcal {SA}^t({{\textsf {ATSP}_{BAL}}(G)})$ by showing that for some edges e, $e*y^{\mathcal {I},\,t+1}$ is a scalar multiple of $y^{\mathcal {I}',\,t}$, where $\mathcal {I}'\supsetneq \mathcal {I}$ (see Eq. 6 in Lemma 2); thus, the induction hinges on the use of $\mathcal {I}$.

Lemma 1

We have $\displaystyle y^{\emptyset ,\,0} \in \mathcal {SA}^{0}({{\textsf {ATSP}_{BAL}}(G)}).$

Proof

Observe that $y^{\emptyset ,\,0}$ has $|E|+1$ elements, and $y^{\emptyset ,\,0}_{\emptyset } =1$ (by Definition 3); the other |E| elements are indexed by the singleton sets of E. For notational convenience, let $y \in \mathbb {R}^{E}$ denote the restriction of $y^{\emptyset ,\,0}$ to indices that are singleton sets; thus, $y_e = y^{\emptyset ,\,0}_{\{e\}}, \forall e\in {E}$. By Definition 3, $y_e =1/2$ if $e\in E(C_j)$ where $j\in \mathcal {F}$, and $y_e=1$, otherwise. We claim that y is a feasible solution to $\widehat{\textsf {ATSP}}_{BAL}(G)$.

y is clearly in $[0, 1]^{E}$. Moreover, y satisfies the balance-constraint at each vertex because it assigns the same value (either 1 / 2 or 1) to every edge in a dicycle $C_j$, $\forall j\in \mathcal {N}$.

To show feasibility of the cut-constraints, consider any cut $\emptyset \ne U\subset V$. Since $\mathbf{1}^{E}$ is a feasible solution, there exists an edge $e\in E$ crossing from U to $V-U$. If $e\in E(C_j), j\in \overline{\mathcal {F}}$, then we have $y_e=1$, which implies $y(\delta ^{out}(U))=y(\delta ^{in}(U))\ge 1$ (from the balance-constraints at the vertices). Otherwise, we have $e\in E(C_j), j\in \mathcal {F}$. Applying the good-decomposition property of G, we see that there exists an edge $e^{\prime } (\ne e) \in E - E(C_{j})$ such that $e^{\prime }\in \delta ^{out}(U)$, i.e., $|\delta ^{out}(U)|\ge 2$. Since $y_e\ge \frac{1}{2}$ for each $e\in E$, the cut-constraints $y(\delta ^{in}(U))=y(\delta ^{out}(U))\ge 1$ are satisfied.

Before proving Lemmas 2, 3, we show that $y^{\mathcal {I},\,t+1}$, restricted to $\mathcal {P}_{t+1}$ (the family of subsets of E of size at most $t+1$), can be written as a convex combination of $y^{\mathcal {I},\,t}$ and the integral feasible solution $\mathbf{1}^{E,\,t+1}$. This is used in the proof of Lemma 2; for some of the edges $e\in E$, we show that $e * y^{\mathcal {I},\,t+1} = y^{\mathcal {I},\,t+1}$ (see Eq. 6), and then we have to show that the latter is in $\mathcal {SA}^t({{\textsf {ATSP}_{BAL}}(G)})$.

Fact 3

Let t be a nonnegative integer and let $\mathcal {I}$ be a subset of $\mathcal {F}$. Then for any $S\in \mathcal {P}_{t+1}$ we have       $\displaystyle y^{\mathcal {I},\,t+1}_S ~=~ \frac{t+2}{t+3} y^{\mathcal {I},\,t}_S + \frac{1}{t+3}\mathbf{1}^{E,\,t+1}_S.$

Proof

We have $S\subseteq E$, $|S|\le t+1$, and we get $\mathbf{1}^{E,\,t+1}_S=1$ from the definition. Thus,

$$\begin{aligned} y^{\mathcal {I},\,t+1}_S = \frac{t+3-f^{\mathcal {I}}(S)}{t+3} = \frac{t+2-f^{\mathcal {I}}(S)}{t+3}+\frac{1}{t+3} = \frac{t+2}{t+3} y^{\mathcal {I},\,t}_S+\frac{1}{t+3}\mathbf{1}^{E,\,t+1}_S. \end{aligned}$$

Lemma 2

Suppose that $y^{\mathcal {I},\,t} \in \mathcal {SA}^t({{\textsf {ATSP}_{BAL}}(G)})$, for each $\mathcal {I}\subseteq \mathcal {F}$. Then for all $e\in E$ and for all $\mathcal {I}\subseteq \mathcal {F}$ we have $\displaystyle e*y^{\mathcal {I},\,t+1} \in \mathcal {SA}^t({{\textsf {ATSP}_{BAL}}(G)})$

Proof

For any $S \in \mathcal {P}_{t+1}$, the definition of the shift operator gives $\displaystyle (e*y^{\mathcal {I},\,t+1})_S = y^{\mathcal {I},\,t+1}_{S+e}.$ Let C(e) denote the dicycle containing edge e, and recall that $\textit{index}(e)$ denotes the index of C(e).

We first show that

$$\begin{aligned} e*y^{\mathcal {I},\,t+1}_S = {\left\{ \begin{array}{ll} \frac{t+2}{t+3} y^{\mathcal {I}+\textit{index}(e),\,t}_S &{}\text {if}\, \textit{index}(e) \in \mathcal {F}- \mathcal {I}\\ y^{\mathcal {I},\,t+1}_S &{}\text {otherwise} \end{array}\right. } \end{aligned}$$

(6)

If $\textit{index}(e) \in \mathcal {I}\cup \overline{\mathcal {F}}$, that is, the dicycle C(e) is not “fractional,” then Definition 3 directly gives $y^{\mathcal {I},\,t+1}_{S+e} = y^{\mathcal {I},\,t+1}_S$. Otherwise, if $\textit{index}(e) \in \mathcal {F}-\mathcal {I}$, then from Definition 3 we see that if $C(e)\cap S\ne \emptyset$, then $F^{\mathcal {I}}(S+{e}) = F^{\mathcal {I}}(S)$, and otherwise, $f^{\mathcal {I}}(S+{e}) = f^{\mathcal {I}}(S) + 1$. Hence,

$$\begin{aligned} (e*y^{\mathcal {I},\,t+1})_S&= {\left\{ \begin{array}{ll} \frac{t+3 - f^{\mathcal {I}}(S)}{t+3} &{}\text {if}\, C(e)\cap S\ne \emptyset \\ \frac{t+2 - f^{\mathcal {I}}(S)}{t+3} &{}\text {if}\, C(e)\cap S=\emptyset \end{array}\right. } \end{aligned}$$

(7)

$$\begin{aligned} (e*y^{\mathcal {I},\,t+1})_S&= \frac{t+2}{t+3} y^{\mathcal {I}+\textit{index}(e),\,t}_S \end{aligned}$$

(8)

where in the last line we use Definition 3 to infer that $f^{\mathcal {I}+\textit{index}(e)}(S) = f^{\mathcal {I}}(S) - 1$, if $C(e)\cap S\ne \emptyset$, and $f^{\mathcal {I}+\textit{index}(e)}(S) = f^{\mathcal {I}}(S)$, otherwise.

Note that Fact 3 along with $y^{\mathcal {I},\,t} \in \mathcal {SA}^t({{\textsf {ATSP}_{BAL}}(G)})$ implies that $y^{\mathcal {I},\,t+1}$, restricted to $\mathcal {P}_{t+1}$, is in $\mathcal {SA}^t({{\textsf {ATSP}_{BAL}}(G)})$ because it can be written as a convex combination of $y^{\mathcal {I},\,t}$ and an integral feasible solution $\mathbf{1}^{E,\,t+1}$. Equation (6) proves Lemma 2 because both $y^{\mathcal {I}+\textit{index}(e),\,t}$ and $y^{\mathcal {I},\,t+1}$ (restricted to $\mathcal {P}_{t+1}$) are in $\mathcal {SA}^t({{\textsf {ATSP}_{BAL}}(G)})$.

Lemma 3

Suppose that $y^{\mathcal {I},\,t} \in \mathcal {SA}^t({{\textsf {ATSP}_{BAL}}(G)})$, for each $\mathcal {I}\subseteq \mathcal {F}$. Then for all $e \in E$ and for all $\mathcal {I}\subseteq \mathcal {F}$ we have $y^{\mathcal {I},\,t+1} - e*y^{\mathcal {I},\,t+1} \in \mathcal {SA}^t({{\textsf {ATSP}_{BAL}}(G)})$.

Proof

Let C(e) denote the dicycle containing edge e, and recall that $\textit{index}(e)$ denotes the index of C(e). If $\textit{index}(e)\in \mathcal {I}\cup \overline{\mathcal {F}}$, then we have $F^{\mathcal {I}}(S+e) = F^{\mathcal {I}}(S), \forall S\in \mathcal {P}_{t+1}$, hence, we have $y^{\mathcal {I},\,t+1} = e*y^{\mathcal {I},\,t+1}$, and the lemma follows.

Otherwise, we have $\textit{index}(e)\in \mathcal {F}-\mathcal {I}$. Then, for any $S\in \mathcal {P}_{t+1}$, Equation (7) gives

$$\begin{aligned} (y^{\mathcal {I},\,t+1} - e*y^{\mathcal {I},\,t+1})_S&= {\left\{ \begin{array}{ll} 0 &{}\text {if}\, C(e)\cap S\ne \emptyset \\ \frac{1}{t+3} &{}\text {if}\, C(e)\cap S=\emptyset \end{array}\right. }\end{aligned}$$

(9)

$$\begin{aligned}&= \frac{1}{t+3}\mathbf{1}^{E-C(e),\,t+1}_S \end{aligned}$$

(10)

The good-decomposition property of G implies that $\mathbf{1}^{E-C(e),\,t+1}$ is a feasible integral solution of $\mathcal {SA}^t({\textsf {ATSP}_{BAL}}(G))$.

The next result presents our first lower bound on the integrality ratio for the level t relaxation of the Sherali–Adams procedure starting with the balanced LP. The relevant instance is a simple digraph on ${\varTheta }(t)$ vertices; see Fig. 1. In the next subsection, we present better integrality ratios using the CGK construction, but the CGK digraph is not as simple and it has ${\varTheta }(t^t)$ vertices.

Theorem 4

Let t be a nonnegative integer, and let $\epsilon \in \mathbb {R}$ satisfy $0<\epsilon \ll {1}$. There exists a digraph on $\nu =\nu (t,\epsilon )={\varTheta }(t/\epsilon )$ vertices such that the integrality ratio for the level t tightening of the balanced LP (Bal LP) (by the Sherali–Adams system) is $\ge 1+\frac{1-\epsilon }{2t+3}$.

Proof

Let G be the digraph together with the good decomposition shown in Figure 1, and let the cost of each edge in G be 1. We call an edge of G a thin edge if it is contained in a dicycle of length 2; we call the other edges of G the thick edges; see the illustration in Fig. 1. Consider the metric completion H of G. It can be seen that the optimal value of an integral solution of ATSP on H (equivalent to the minimum cost Eulerian subdigraph of G) is ${\ge } 4\ell +2$, where $\ell$ is the length of the “middle path.” (This can be proved by induction on $\ell$, using similar arguments as in Cheung [9, Claim 3 of Theorem 11].)

Given t and $\epsilon$, we fix $\ell = 2(2t+3)/\epsilon$ to get a digraph G (and its edge costs) from the above family.

By Corollary 1 the fractional solution $y^{\emptyset ,\,t}$ (Definition 3) is in $\mathcal {SA}^t(\widehat{\textsf {ATSP}}_{BAL}(G))$: we have $y^{\emptyset ,\,t}_e=1$ for each thick edge e, and $y^{\emptyset ,\,t}_e=\frac{t+1}{t+2}$ for each thin edge e. By Sect. 2.2.1, we can extend $y^{\emptyset ,\,t}$ to a feasible solution of $\mathcal {SA}^t(\widehat{\textsf {ATSP}}_{BAL}(H))$.

Hence, the integrality ratio is

$$\begin{aligned} \ge \frac{4\ell + 2}{2\ell + 4 + 2\ell \frac{t+1}{t+2}} \ge \frac{2(t+2)}{2t+3} - \frac{2}{\ell } \ge 1+ \frac{1 - \epsilon }{2t+3}. \end{aligned}$$

3.2 Charikar–Goemans–Karloff (CGK) construction

We briefly explain the CGK [7] construction and show in Theorem 7 that the resulting digraph has a good decomposition. This theorem along with a lemma from [7] shows that the integrality ratio is $\ge 1+\frac{1-\epsilon }{t+1}$ for t rounds of the Sherali–Adams procedure starting with the Balanced LP, for any given $0<\epsilon \ll {1}$, see Theorem 8.

Let r be a fixed positive integer. Let $G_{0}$ be the digraph with a single vertex. Let $G_{1}$ consist of a bidirected path of $r+2$ vertices, starting at the “source” p and ending at the “sink” q, whose $2(r+1)$ edges have cost 1 (see Fig. 2). We call $E(G_1)$ the external edge set of $G_1$ (we use this in the proof of Lemma 4).

Fig. 2

$G_0$ and $G_{1}$ for $r=3$

Fig. 3

$G_{k}$ and $L_k$ for $k\ge 2$ and $r=3$

For each $k\ge 2$, we construct $G_k$ by taking r copies of $G_{k-1}$, additional source and sink vertices p and q, a dipath from p to q of $r+1$ edges visiting the sources of the r copies in the order $u_1, u_2, \ldots , u_r$, and another dipath from q to p of $r+1$ edges visiting the sinks of the r copies in the order $v_r, v_{r-1}, \ldots , v_1$ where $u_i, v_i$ denote the source and sink of the i-th copy of $G_{k-1}$ (see Fig. 3). All the new edges have cost $r^{k-1}$. Denote the i-th copy of $G_{k-1}$ by $G_{k-1}^{(i)}$. Let $E_k=E(G_{k})-\cup _{1\le i\le r} E(G_{k-1}^{(i)})$. Let $\{G_{k-2}^{(i, j)}\}_{1\le j\le r}$ be the r copies of $G_{k-2}$ in $G_{k-1}^{(i)}$. Let $E_{k-1}^{(i)}=E(G_{k-1}^{(i)})- \bigcup _{1\le j\le r} E(G_{k-2}^{(i,j)})$. Let $A^{(i)}$ be the dipath from $u_i$ to $v_i$ in $E_{k-1}^{(i)}$ and let $B^{(i)}$ be the dipath from $v_i$ to $u_i$ in $E_{k-1}^{(i)}$. Let $E^{[r]}_{k-1}=\cup _{1\le i\le r} E_{k-1}^{(i)}$. We call $E_{k}\cup E^{[r]}_{k-1}$ the external edge set of $G_k$. The other edges form the internal edge set of $G_k$.

For each $k\ge 2$, the digraph $L_k$ is constructed from $G_k$ by removing vertices p and q, and adding the edges $(u_r,u_1)$ and $(v_1,v_r)$, both of cost $r^{k-1}$. Let $E^{'}_k=(E_k\cup \{(u_r, u_1), (v_1, v_r)\})-\{ (p, u_1), (v_1, p), (u_r, q), (q, v_r)\}$. We call $E^{'}_k\cup E^{[r]}_{k-1}$ the external edge set of $L_k$. The other edges form the internal edge set of $L_k$. (Our description of the CGK construction is essentially the same as in [7], but they use s and t to denote the source and sink vertices, whereas we use p and q; this is to avoid conflict with our symbol t for the number of rounds of the SA procedure.)

Fact 5

Let $k\ge 2$ be a positive integer. The external edge set of $L_{k}$, i.e., $E_k^{'}\cup E^{[r]}_{k-1}$, can be partitioned into r dicycles $C_1', \ldots , C_{r}'$ such that

• $C_i'=\{(u_{i}, u_{i+1}), (v_{i+1}, v_{i})\}\cup B^{(i)}\cup A^{(i+1)}$, for $1\le i\le r-1$, and

• $C_{r}'=\{(u_{r}, u_1), (v_1, v_{r})\}\cup B^{(r)}\cup A^{(1)}$.

Moreover, for each dicycle $C_i'$, $i=1,\dots ,r$, $L_{k}-E(C_i')$ is strongly connected.

We denote the decomposition of the external edge set of $L_k$ by $\mathcal {C}_{L_k}(E_k^{'}\cup E^{[r]}_{k-1})=\{C_1', \ldots , C_{r}'\}$.

Fact 6

Let $k\ge 2$ be a positive integer. The external edge set of $G_{k}$, i.e., $E_k \cup E^{[r]}_{k-1}$, can be partitioned into $r+1$ dicycles $C_0, C_1, \ldots , C_{r}$ such that

• $C_i=\{(u_{i}, u_{i+1}), (v_{i+1}, v_{i})\}\cup B^{(i)}\cup A^{(i+1)}$,   for $1\le i\le r-1$,

• $C_0=\{(p, u_1), (v_1, p)\}\cup A^{(1)}$, and

• $C_{r}=\{(u_{r}, q), (q, v_{r})\}\cup B^{(r)}$.

Moreover, for each dicycle $C_i$, $i=0,1,\dots ,r$, $G_{k}-E(C_i)$ has two strongly-connected components, where one contains the source p and the other one contains the sink q.

We denote the decomposition of the external edge set of $G_k$ by $\mathcal {C}_{G_k}(E_k\cup {E^{[r]}_{k-1}})=\{C_0,C_1, \ldots , C_{r}\}$. Next we identify a structural property that will allow us to prove that $L_k$ has a good decomposition.

Definition 4

We say that $G_k$ has a (p, q)-good decomposition, if the edge set of $G_{k}$ can be partitioned into dicycles $C_1, C_2, \ldots , C_N$ such that for each $1\le i\le N$, either

• (1) $C_i$ consists of external edges, and moreover, $G_{k}-E(C_i)$ has two strongly connected components, one containing the source p and the other one containing the sink q.

• (2) $C_i$ consists of internal edges of $G_k$, and moreover, $G_{k}-E(C_i)$ is strongly connected.

Lemma 4

For all $k\ge 1$, $G_k$ has a (p, q)-good decomposition.

Proof

We prove the result by strong induction on k. For the base cases, consider $G_{1}$ and $G_{2}$. For $G_{1}$, we take the dicycles $C_1,\dots ,C_N$ to be the length 2 dicycles formed by two anti-parallel edges; thus, $N={r+1}$ (see Fig. 2). For $G_{2}$, we use the decomposition of the external edge set given by Fact 6.

For the induction step, we have $k\ge 3$; we assume that the statement holds for $1,2,\dots ,k-1$ and prove that it holds for k. By the induction hypothesis, for each $1\le {i,j}\le {r}$, we know that $G^{(i, j)}_{k-2}$ has a (p, q)-good decomposition $\mathcal {C}(E(G^{(i,j)}_{k-2}))=\{C^{(i,j)}_1, C^{(i,j)}_2, \ldots , C^{(i,j)}_{N_{(i,j)}}\}$. Consider the decomposition of $E(G_k)$ into edge-disjoint dicycles given by $\widehat{\mathcal {C}}=\mathcal {C}_{G_k}(E_k\cup {E^{[r]}_{k-1}})\cup \bigcup _{1\le {i,j}\le {r}} \mathcal {C}(E(G^{(i,j)}_{k-2}))$. We claim that $\widehat{\mathcal {C}}$ is a (p, q)-good decomposition of $G_k$. Clearly, for $C\in \widehat{\mathcal {C}}$ such that $E(C)\subseteq E_k\cup {E^{[r]}_{k-1}}$, we are done by Fact 6. Now, consider one of the other dicycles $C\in \widehat{\mathcal {C}}$; thus C consists of some internal edges of $G_k$. Then, there exists an i and j ($1\le {i,j}\le {r}$) such that $C\in \mathcal {C}(E(G^{(i,j)}_{k-2}))$. We have two cases, since either condition (1) or (2) of (p, q)-good decomposition of $G^{(i,j)}_{k-2}$ applies to C. In the first case, $G^{(i, j)}_{k-2}-E(C)$ has two strongly connected components, where one contains the source $p^{(i, j)}$ of $G^{(i, j)}_{k-2}$ and the other one contains the sink $q^{(i, j)}$ of $G^{(i, j)}_{k-2}$. Note that the external edge set of $G_k$ “strongly connects” $p^{(i, j)}$ and $q^{(i, j)}$, hence, $G_k-E(C)$ is strongly connected. In the second case, $G^{(i,j)}_{k-2}-E(C)$ is strongly connected; then clearly, $G_k-E(C)$ is strongly connected. Thus $\widehat{\mathcal {C}}$ is a (p, q)-good decomposition of $G_k$.

Theorem 7

For $k\ge 2$, $L_{k}$ has a good decomposition with witness set $\mathcal {F}$ such that $\mathcal {F}=\mathcal {N}$, i.e. every edge in any cycle in the decomposition can be assigned a fractional value.

Proof

Let $\mathcal {C}_{L_k}(E_k^{'}\cup E^{[r]}_{k-1})$ be the decomposition of the external edge set of $L_{k}$ given by Fact 5. If $k=2$, then we are done (we have a good decomposition of $L_{k}$ with $\mathcal {F}=\mathcal {N}$). Otherwise, we use the decomposition $\widehat{\mathcal {C}}=\mathcal {C}_{L_{k}}(E_k^{'}\cup {E^{[r]}_{k-1}}) \cup \bigcup _{1\le {i,j}\le {r}} \mathcal {C}(E(G^{(i,j)}_{k-2}))$, where $\mathcal {C}(E(G^{(i,j)}_{k-2}))$ is a (p, q)-good decomposition of $G^{(i,j)}_{k-2}$. Using similar arguments as in the proof of Lemma 4, it can be seen that $\widehat{\mathcal {C}}$ is a good decomposition with $\mathcal {F}=\mathcal {N}$.

Lemma 5

(Lemma 3.2 [7]) For $k\ge 2$ and $r\ge 3$, the minimum cost of the Eulerian subdigraph of $L_k$ is ${\ge } (2k-1)(r-1)r^{k-1}$.

Theorem 8

Let t be a nonnegative integer, and let $\epsilon \in \mathbb {R}$ satisfy $0<\epsilon \ll {1}$. There exists a digraph on $\nu =\nu (t,\epsilon )=O((t/\epsilon )^{(t/\epsilon )})$ vertices such that the integrality ratio for the level t tightening of the balanced LP for ATSP (Bal LP) (by the Sherali–Adams system) is ${\ge } 1+\frac{1-\epsilon }{t+1}$.

Proof

Given t and $\epsilon$, we apply the CGK construction with $k=r= 5(t+1)/\epsilon$ to get the digraph $L_k$ and its edge costs. Let $H_k$ be the metric completion of $L_k$.

We know from CGK [7] that the total cost of the edges in $L_k$ is $\le 2k(r+1)r^{k-1}$. By Theorem 7, $L_k$ has a good decomposition $C_1,\dots ,C_N$ such that each of the dicycles $C_j$ has its index in the witness set $\mathcal {F}$ (informally, each edge is assigned to a fractional dicycle). Hence, Corollary 1 implies that the fractional solution that assigns the value $\frac{t+1}{t+2}$ to (the variable of) each edge is feasible for $\mathcal {SA}^t({\widehat{\textsf {ATSP}}_{BAL}(L_k)})$. By Sect. 2.2.1, this feasible solution can be extended to a feasible solution in $\mathcal {SA}^t({\widehat{\textsf {ATSP}}_{BAL}(H_k)})$.

Then, using Lemma 5, we see that the integrality ratio of $\mathcal {SA}^t({\widehat{\textsf {ATSP}}_{BAL}(H_k)})$ is

$$\begin{aligned} {\ge }&\frac{(2k-1)(r-1)r^{k-1}}{(\frac{t+1}{t+2})2k(r+1)r^{k-1}} = 1+\frac{1}{t+1}-\frac{5r-1}{\frac{t+1}{t+2}(r+1)(2r)} {\ge } 1+\frac{1}{t+1}-\frac{5}{\frac{t+1}{t+2}}\frac{1}{(2r)} \\ {\ge }&1+ \frac{1-\epsilon }{t+1}. \end{aligned}$$

4 SA applied to the standard (DFJ LP) relaxation of ATSP

Let $G = (V,E)$ be a strongly connected digraph that has a good decomposition, and moreover, has both indegree and outdegree $\le 2$ for every vertex. We use the same notation as in Sect. 3.1, i.e., $C_1, C_2, \ldots , C_N$ denote the edge disjoint dicycles of the decomposition, and there exists $\mathcal {F}\subseteq \mathcal {N}=\{1,\dots ,N\}$ such that $\mathcal {F}$ is nonempty and $G-E(C_j)$ is strongly connected for all $j\in \mathcal {F}$. For an illustration of important notions introduced in this section, the reader may consult Figs. 4, 5, 6, 7.

We define a splitting operation that splits every vertex that has indegree 2 (and outdegree 2) into two vertices (along with some edges); our definition depends on the given good decomposition of the digraph. The purpose of the splitting operation will be clear from Fact 9.

Splitting Operation: Let $v\in V(G)$ whose indegree and outdegree is 2. Suppose $C_i, C_j$ are the dicycles in the good decomposition going through v. Let $e_{i1}=(v_{i1}, v), e_{j1}=(v_{j1}, v)$ and $e_{i2}=(v, v_{i2}), e_{j2}=(v, v_{j2})$ be the edges in $\delta ^{in}(v)$, $\delta ^{out}(v)$, respectively, where $e_{i1}, e_{i2}\in C_i$ and $e_{j1}, e_{j2}\in C_j$. We split v into $v^{u}, v^{b}$ as follows:

• Replace $e_{i1}, e_{j2}$ by $e_{i1}^{new}=(v_{i1},v^{u}), e_{j2}^{new}=(v^{u}, v_{j2})$ (the new edges are called solid edges)

• Replace $e_{i2}, e_{j1}$ by $e_{i2}^{new}=(v^{b},v_{i2}), e_{j1}^{new}=(v_{j1}, v^{b})$ (the new edges are called solid edges)

• Add the auxiliary edges (also called dashed edges) $e_{0}=(v^{b}, v^{u}), e'_{0}=(v^{u}, v^{b})$.

See Fig. 4 for an illustration.

Fig. 4

An illustration of the vertex splitting operation used for mapping G to $G^{new}$

We obtain $G^{new}=(V^{new}, E^{new})$ from G by applying the splitting operation to every vertex in G whose indegree and outdegree is 2. We map each dicycle $C_j$, $j\in \mathcal {N}$, of G to a set of edges of $G^{new}$ that we call a cycle and that we will (temporarily) denote by $C_j^{new}$. We define $C_j^{new}$ to be the following set of edges: for every edge of $C_j$, its image (in $G^{new}$) is in $C_j^{new}$; moreover, for every splitted vertex v of G incident to $C_j$, note that one of $v^{u}$ or $v^{b}$ (the two images of v) is the head of one of the two edges of $C_j^{new}$ incident to $\{v^{u},v^{b}\}$, and one of the two auxiliary edges $e_{0},e'_{0}$ has its head at the same vertex; we place this auxiliary edge also in $C_j^{new}$. Note that $C_j^{new}$ is not a directed cycle. For example, in Fig. 4, the cycle $C_i^{new}$ contains the edges $e_{i1}^{new}$ (image of $e_{i1}$), $e_{i2}^{new}$ (image of $e_{i2}$), and the auxiliary edge $e_{0}$, whereas the cycle $C_j^{new}$ contains the edges $e_{j1}^{new}$, $e_{j2}^{new}$, and the auxiliary edge $e'_{0}$.

In what follows, we simplify the notation for the cycles of $G^{new}$ to $C_j$ (rather than $C_j^{new}$); there is some danger of ambiguity, but the context will resolve this. We denote the set of auxiliary edges (also called the dashed edges) of a cycle $C_j=C_j^{new}$ by $D(C_j)$, and we denote the set of remaining edges of $C_j=C_j^{new}$ by $E(C_j)$. Note that $E^{new} = E(G^{new}) = \bigcup _{j\in \mathcal {N}} (E(C_j) \cup D(C_j))$. Clearly, there is a bijection between the edges of $E(C_j)=E(C_j^{new})$ in $G^{new}$ and the edges of $E(C_j)$ in G. Also, observe that in $G^{new}$, the dashed edges are partitioned among the cycles $C_j^{new},j\in \mathcal {N}$.

Fact 9

Consider a digraph $G=(V,E)$ that has a good decomposition, and consider $x\in \mathbb {R}^{E}$ such that (1) $0 \le x\le 1$, (2) for every dicycle $C_j$, $j\in \mathcal {N}$, $x_e$ is the same for all edges e of $C_j$, and    (3) for every vertex v with indegree = 1 = outdegree, $x(\delta ^{in}(v))=x(\delta ^{out}(v))=1$. Then, for the digraph $G^{new}=(V^{new},E^{new})$ obtained by applying the splitting operations, there exists $x^{new}\in \mathbb {R}^{E^{new}}$ such that $0 \le x^{new}\le 1$, and $x^{new}(\delta ^{in}(v))=x^{new}(\delta ^{out}(v))=1, \forall v\in V^{new}$.

Proof

For each $j\in \mathcal {N}$, we consider the dicycle $C_j$. Let $\alpha _j$ be the x-value associated with the dicycle $C_j$ of G, i.e., $x_e=\alpha _j, \forall e\in E(C_j)$. Then, in $x^{new}$ and $G^{new}$, we fix $x_e=\alpha _j, \forall e\in E(C_j)=E(C_j^{new})$, and we fix $x_e=(1-\alpha _j), \forall e\in D(C_j)=D(C_j^{new})$. It can be seen that $x^{new}$ satisfies the given conditions.

Definition 5

Consider the digraph $G^{new}$. For any $j\in \mathcal {F}$, let $\textit{tour}(j) := D(C_j) \cup \bigcup _{i\in (\mathcal {N}-j)} E(C_i)$.

Thus $\textit{tour}(j)$ consists of all the solid edges except those in $C_j$ together with all the dashed edges of $C_j$. Note that each vertex in $G^{new}$ has exactly one incoming edge and exactly one outgoing edge in $\textit{tour}(j)$. Thus $\textit{tour}(j)$ forms a set of vertex-disjoint dicycles that partition $V^{new}$.

Fig. 5

Digraph from Fig. 1 after the splitting operation

Fig. 6

Transforming a dicycle $C_j$ formed by an anti-parallel pair of thin edges in Fig. 1 to $C_j^{new}$ by the splitting operation

Fig. 7

tour(e)

Definition 6

Let G be a digraph with indegree and outdegree $\le 2$ at every vertex, and suppose that G has a good decomposition with witness set $\mathcal {F}$. Let $G^{new}$ be the digraph obtained by applying splitting operations to G and its good decomposition. Then G is said to have the good tours property if $\textit{tour}(j)$ is connected (i.e., $\textit{tour}(j)$ forms a Hamiltonian dicycle of $G^{new}$) for each $j\in \mathcal {F}$.

4.1 Certifying a feasible solution

In what follows, we assume that G is a digraph that satisfies the conditions stated in Definition 6. We focus on the digraph $G^{new}$ obtained by applying splitting operations to G; observe that $G^{new}$ depends on G as well as on the given good decomposition of G. Let ${\textsf {ATSP}_{DFJ}}(G^{new})$ be the associated cone of $\widehat{\textsf {ATSP}}_{{DFJ}}(G^{new})$.

Let E denote the set of images of the edges of G (the solid edges), and let D denote the set of auxiliary edges (the dashed edges). Given $S\subseteq E$ and $\mathcal {I}\subseteq \mathcal {F}$, let $F^{\mathcal {I}}(S)$ denote the set of indices $j\in \mathcal {F}- \mathcal {I}$ such that $E(C_j)$ intersects S, and let $f^{\mathcal {I}}(S)$ denote the size of this set; thus, $f^{\mathcal {I}}(S)$ denotes the number of “fractional cycles” that intersect S in the solid edges.

Note that each (solid or dashed) edge e is in a unique cycle C(e); let $\textit{index}(e)$ denote the index of C(e) in $\mathcal {N}$; if $\textit{index}(e)\in \mathcal {F}-\mathcal {I}$, then we use $\textit{tour}(e)$ to denote $\textit{tour}(\textit{index}(e))$.

Let t be a nonnegative integer. We define the feasible solution $y$ for the level t tightening of the DFJ-LP (of ATSP, by the SA system) as follows:

Definition 7

For a nonnegative integer t and for any subset $\mathcal {I}$ of $\mathcal {F}$, let $y^{\mathcal {I},\,t}$ be a vector indexed by the elements of $\mathcal {P}_{t+1}$ and defined as follows:

$$\begin{aligned} (y^{\mathcal {I},\,t})_S = {\left\{ \begin{array}{ll} \frac{t+2-f^{\mathcal {I}}(S)}{t+2} &{}\quad \hbox {if}\, S\cap D = \emptyset \qquad (S\, \hbox {has no dashed edges}) \\ \frac{1}{t+2} &{}\quad \hbox {if}\, S\cap D \not = \emptyset \,\hbox {and}\, \exists i\in \mathcal {F}- \mathcal {I}~:~ \textit{tour}(i) \supseteq S \\ &{} \qquad (S\, contains\, some\, dashed\, edges\, and\, is\, contained\, in\, a\, tour) \\ 0 &{}\quad \hbox {otherwise} \end{array}\right. } \end{aligned}$$

(11)

Observe that the second case applies when the set S has one or more dashed edges, and moreover, S is contained in a $\textit{tour}(i)$, $i\in \mathcal {F}- \mathcal {I}$; also, observe that there is at most one tour that contains S, because the dashed edges are partitioned among the cycles $C_j,j\in \mathcal {N}$, so each dashed edge in S belongs to a unique tour.

To show the feasibility of $y^{\mathcal {I},\,t}$ for the level t tightening of the DFJ-LP, we need the size of $\mathcal {F}$ to be large. In fact, we require $|\mathcal {F}|\ge |\mathcal {I}|+t+2$.

Theorem 10

Let $G=(V,E)$ be a strongly connected digraph that has a good decomposition with witness set $\mathcal {F}$, and moreover, has (i) both indegree and outdegree $\le 2$ for every vertex, and (ii) satisfies the “good tours” property. Then, for any nonnegative integer t, and any $\mathcal {I}\subseteq \mathcal {F}$ with $|\mathcal {I}|\le |\mathcal {F}| - (t+2)$, we have

$$\begin{aligned} y^{\mathcal {I},\,t} \in \mathcal {SA}^t({\widehat{\textsf {ATSP}}_{{DFJ}}(G^{new})}). \end{aligned}$$

Proof

Note that $y^{\mathcal {I},\,t}_\emptyset =1$ by Definition 7. Thus, we only need to prove $y^{\mathcal {I},\,t} \in \mathcal {SA}^t({{\textsf {ATSP}_{DFJ}}(G^{new})})$. The proof is by induction on t. The base case is important, and it follows easily from the good decomposition property and the “good tours” property of G. This is done in Lemma 6 below, where we show that $y^{\mathcal {I},\,0} \in \mathcal {SA}^0({\textsf {ATSP}_{DFJ}}(G^{new})), \;\forall \mathcal {I}\subseteq \mathcal {F}, |\mathcal {I}|\le |\mathcal {F}|-2$.

In the induction step, we assume that $y^{\mathcal {I},\,t} \in \mathcal {SA}^t({\textsf {ATSP}_{DFJ}}(G^{new}))$ for some integer $t\ge 0$ (the induction hypothesis), and we apply the recursive definition based on the shift operator, namely, $y^{\mathcal {I},\,t+1} \in \mathcal {SA}^{t+1}({\textsf {ATSP}_{DFJ}}(G^{new}))$ iff for each $e\in E^{new}$

$$\begin{aligned}&e * y^{\mathcal {I},\,t+1} \in \mathcal {SA}^{t}({\textsf {ATSP}_{DFJ}}(G^{new})), \end{aligned}$$

(12)

$$\begin{aligned}&y^{\mathcal {I},\,t+1} - e*y^{\mathcal {I},\,t+1} \in \mathcal {SA}^{t}({\textsf {ATSP}_{DFJ}}(G^{new})). \end{aligned}$$

(13)

Lemma 7 (below) proves (12) and Lemma 9 (below) proves (13).

The next lemma proves the base case for the induction; it follows from the “good tours” property of the digraph.

Lemma 6

$$\begin{aligned} y^{\mathcal {I},\,0} \in \mathcal {SA}^{0}({\textsf {ATSP}_{DFJ}}(G^{new})), \quad \forall \mathcal {I}\subseteq \mathcal {F}, |\mathcal {I}|\le |\mathcal {F}|-2 \end{aligned}$$

Proof

Note that $y^{\mathcal {I},\,0}_{\emptyset }=1$. Let z be the subvector of $y^{\mathcal {I},\,0}$ on the singleton sets $\{e_i\}$. We need to prove that z is a feasible solution of the DFJ LP. It can be seen that z is as follows: if $\textit{index}(e)\in \mathcal {F}-\mathcal {I}$, then $z_e=\frac{1}{2}$, otherwise, if $e\in E$ (e is a solid edge), then $z_e=1$, otherwise, if $e\in D$ (e is a dashed edge), then $z_e=0$. Clearly, z is in $[0, 1]^{E^{new}}$, and z satisfies the degree constraints (see the proof of Fact 9). Now, we need to verify that z satisfies the cut constraints in the digraph $G^{new}$. Consider any nonempty set of vertices $U\not =V$, and the cut $\delta ^{out}(U)$.

Observe that $|\mathcal {F}-\mathcal {I}| \ge 2$, hence, there are at least two indices i, j such that $i,j\in \mathcal {F}-\mathcal {I}$. Hence, both $\textit{tour}(i)$ and $\textit{tour}(j)$ exist; moreover, every edge e (either solid or dashed) in either $\textit{tour}(i)$ or $\textit{tour}(j)$ has $z_e\ge \frac{1}{2}$. Clearly, each of $\textit{tour}(i)$ and $\textit{tour}(j)$ has at least one edge in $\delta ^{out}(U)$. Let $e_j$ be an edge of $\textit{tour}(j)$ that is in $\delta ^{out}(U)$. If $z_{e_j}=1$, then we are done, since we have $z(\delta ^{out}(U))\ge z_{e_j}=1$. Thus, we may assume $z_{e_j}=\frac{1}{2}$. Now, we have two cases.

First, suppose that $e_j$ is a dashed edge. Then, note that the edge of $\textit{tour}(i)$ in $\delta ^{out}(U)$, call it $e_i$, is distinct from $e_j$ (since the tours are disjoint on the dashed edges), and again we are done, since $z(\delta ^{out}(U))\ge z_{e_i}+z_{e_j}\ge 1$.

In the remaining case, $e_j\in \textit{tour}(j)$ is a solid edge and $z_{e_j}=\frac{1}{2}$. Then, $\textit{index}(e_j)\in \mathcal {F}-\mathcal {I}$, and so $\textit{tour}(e_j)$ exists and it has at least one edge $e'$ in $\delta ^{out}(U)$; moreover, $e'\not =e_j$ because $\textit{tour}(e_j)$ contains none of the solid edges of the cycle $C_{\textit{index}(e_j)}$. Thus, we are done, since $z(\delta ^{out}(U))\ge z_{e_j}+z_{e'}\ge 1$. It follows that z staisfies all of the cut constraints.

The following fact summarizes some easy observations; this fact is used in the next lemma.

Fact 11

Let $\mathcal {I}$ be a subset of $\mathcal {F}$. Suppose that S is not contained in any $\textit{tour}(j)$, $j\in \mathcal {F}- \mathcal {I}$. (1) Then, for any edge e, $S+e$ is also not contained in any $\textit{tour}(j)$, $j\in \mathcal {F}- \mathcal {I}$. (2) Similary, for any index $h\in \mathcal {F}$, S is not contained in any $\textit{tour}(j)$, $j\in \mathcal {F}- (\mathcal {I}+ h)$.

Lemma 7

Suppose that for any nonnegative integer t and any $\mathcal {I}'\subseteq \mathcal {F}$ with $|\mathcal {I}'|\le |\mathcal {F}| - (t+2)$, we have $y^{\mathcal {I}',\,t} \in \mathcal {SA}^t({\textsf {ATSP}_{DFJ}}(G^{new}))$. Then for any $\mathcal {I}\subseteq \mathcal {F}$ with $|\mathcal {I}|\le |\mathcal {F}| - (t+3)$,

$$\begin{aligned} e*y^{\mathcal {I},\,t+1} \in \mathcal {SA}^t({\textsf {ATSP}_{DFJ}}(G^{new})), \quad \forall e\in E^{new}. \end{aligned}$$

Proof

For any edge e and any $S \in \mathcal {P}_{t+1}$, the definition of the shift operator gives

$$\begin{aligned} (e * y^{\mathcal {I},\,t+1})_S ~=~ y^{\mathcal {I},\,t+1}_{S+e} \end{aligned}$$

Let C(e) denote the cycle containing edge e, and let $\textit{index}(e)$ denote the index of C(e) in $\mathcal {N}$.

We will show that

$$\begin{aligned} (e * y^{\mathcal {I},\,t+1})_S = {\left\{ \begin{array}{ll} y^{\mathcal {I},\,t+1}_S &{} \hbox {if}\, e\in E(C_j) \,\hbox {where}\, j\in \mathcal {I}\cup \overline{\mathcal {F}}\\ &{} \qquad (e\, is\, a\, solid,\, integral\, edge) \\ 0 &{} \hbox {if}\, e\in D(C_j)\, \hbox {where}\, j\in \mathcal {I}\cup \overline{\mathcal {F}}\\ &{} \qquad (e\, is\, a\, dashed,\, integral\, edge) \\ \frac{t+2}{t+3}y^{\mathcal {I}+\textit{index}(e),\,t}_S &{} \hbox {if}\, e\in E(C_j) \,\hbox {where}\, j\in \mathcal {F}- \mathcal {I}\\ &{} \qquad (e\, is\, a\, solid,\, fractional\, edge) \\ \frac{1}{t+3}\mathbf{1}^{\textit{tour}(e),\,t+1}_S &{} \hbox {if}\, e\in D(C_j) \,\hbox {where}\, j\in \mathcal {F}- \mathcal {I}\\ &{} \qquad (e\, is\, a\, dashed,\, fractional\, edge) \\ \end{array}\right. } \end{aligned}$$

(14)

Lemma 8 (below) shows that

$$\begin{aligned} y^{\mathcal {I},\,t+1}_S=\frac{t+2}{t+3} y^{\mathcal {I}+h,\,t}_S + \frac{1}{t+3}\mathbf{1}^{\textit{tour}(h),\,t+1}_S, \qquad \forall h\in \mathcal {F}- \mathcal {I}. \end{aligned}$$

Hence, for every edge e (i.e., in every case), $e*y^{\mathcal {I},\,t+1}$ is in $\mathcal {SA}^t({\textsf {ATSP}_{DFJ}}(G^{new}))$.

Case 1.:

$e\in E(C_j) \,\hbox {where}\, j\in \mathcal {I}\cup \overline{\mathcal {F}}$ (e is a solid, integral edge). We apply Definition 11 (the definition of $y$), and consider the three cases in it:

Subcase 1.1.:

$S\cap D=\emptyset$. Then we have $(S+e)\cap D=\emptyset$, and moreover, we have $f^{\mathcal {I}}(S) = f^{\mathcal {I}}(S+e)$ (the number of “fractional cycles” intersecting $S\cap {E}$ and $(S+e)\cap {E}$ is the same, since e is a non-fractional edge). Hence, $y^{\mathcal {I},\,t+1}_{(S+e)} = y^{\mathcal {I},\,t+1}_{S}$.

Subcase 1.2.:

$S\cap D\not =\emptyset$ and $\exists i\in \mathcal {F}-\mathcal {I}:\textit{tour}(i)\supseteq {S}$. Then it is clear that $(S+e)\cap D\not =\emptyset$ and $\textit{tour}(i)\supseteq {S+e}$, because $\textit{tour}(i)$ contains every solid edge except those in the fractional cycle $C_i$. Hence, $y^{\mathcal {I},\,t+1}_{S+e} = \frac{1}{t+3} = y^{\mathcal {I},\,t+1}_{S}$.

Subcase 1.3.:

$S\cap D\not =\emptyset$ and $\forall j\in \mathcal {F}-\mathcal {I}:\textit{tour}(j)\not \supseteq {S}$. Then it is easily seen that both conditions apply to $S+e$ (rather than S). Hence, $y^{\mathcal {I},\,t+1}_{S+e} = 0 = y^{\mathcal {I},\,t+1}_{S}$.

Case 2.:

We have $e\in D(C_j) \,\hbox {where}\, j\in \mathcal {I}\cup \overline{\mathcal {F}}$ (e is a dashed, integral edge). We apply Definition 11, noting that $(S+e)\cap D\not =\emptyset$ and there exists no index $i\in \mathcal {F}-\mathcal {I}$ such that $\textit{tour}(i)\supseteq {S+e}$ (no “valid tour” contains a dashed, integral edge), hence, $y^{\mathcal {I},\,t+1}_{S+e} = 0$.

Case 3.:

We have $e\in E(C_j) \,\hbox {where}\, j\in \mathcal {F}-\mathcal {I}$ (e is a solid, fractional edge). We apply Definition 11. We have two subcases, either $S\cap D=\emptyset$, or not.

Subcase 3.1.:

If $S\cap D=\emptyset$, then $(S+e)\cap D=\emptyset$. Thus, the analysis is the same as in the previous section; in particular, see Eq. 6 in the proof of Lemma 2. Hence, we have $y^{\mathcal {I},\,t+1}_{S+e} = \frac{t+2}{t+3}y^{\mathcal {I}+\textit{index}(e),\,t}_S$.

Subcase 3.2.:

Otherwise, $S\cap D\not =\emptyset$. Then we have two further subcases: either there is an $i\in \mathcal {F}-\mathcal {I}$ with $\textit{tour}(i)\supseteq {S}$ or not.

Subcase 3.2.1.:

Consider the first subcase; thus, $S\subseteq \textit{tour}(i)$ where $i\in \mathcal {F}-\mathcal {I}$. Note that S is not contained in other tours since $S\cap D\not =\emptyset$. We have two further subcases, either $e\in E(C_i)$ or not.

Subcase 3.2.1.1.:

If $e\in E(C_i)$, then $\textit{tour}(i)\not \supseteq {(S+e)}$, hence, $y^{\mathcal {I},\,t+1}_{S+e} = 0$ (by the last case in the definition of $y$); moreover, note that $\textit{tour}(i)$ is the unique tour containing S but it is not a “valid tour” w.r.t. $\mathcal {I}+\textit{index}(e)$, hence, $y^{\mathcal {I}+\textit{index}(e),\,t}_S=0$ (by the last case in Definition 11).

Subcase 3.2.1.2.:

Otherwise, if $e\not \in E(C_i)$, then $\textit{tour}(i)\supseteq {(S+e)}$, and moreover, $\textit{tour}(i)$ is a “valid tour” w.r.t. $\mathcal {I}+\textit{index}(e)$ (since $i\not \in \mathcal {I}$ and $i\not =\textit{index}(e)$), hence, we have $y^{\mathcal {I},\,t+1}_{S+e} = \frac{1}{t+3} = \frac{t+2}{t+3} \frac{1}{t+2} = \frac{t+2}{t+3} y^{\mathcal {I}+\textit{index}(e),\,t}_S$ (by the second case in Definition 11, for both LHS and RHS).

Subcase 3.2.2.:

Consider the last subcase; thus, $S\not \subseteq \textit{tour}(i)$ for all $i\in \mathcal {F}-\mathcal {I}$. Then by Fact 11, the same assertion holds w.r.t. $(S+e)$ (rather than S), as well as w.r.t. $(\mathcal {I}+\textit{index}(e))$ (rather than $\mathcal {I}$). Hence, we have $y^{\mathcal {I},\,t+1}_{S+e} = 0 = \frac{t+2}{t+3} y^{\mathcal {I}+\textit{index}(e),\,t}_S$ (by the last case in Definition 11, for both LHS and RHS).

Case 4.:

We have $e\in D(C_j) \,\hbox {where}\, j\in \mathcal {F}-\mathcal {I}$ (e is a dashed, fractional edge). We apply Definition 11, noting that $(S+e)\cap D\not =\emptyset$. We have two subcases, either $\textit{tour}(e)\supseteq {S}$, or not. If $\textit{tour}(e)\supseteq {S}$, then the second case of Definition 11 together with the fourth case of Equation (14) (the definition of $e*y$) gives $y^{\mathcal {I},\,t+1}_{S+e} = \frac{1}{t+3} = \frac{1}{t+3} \mathbf{1}^{\textit{tour}(e),\,t+1}_S$. Otherwise, $\textit{tour}(e)\not \supseteq {S}$, and then we have $y^{\mathcal {I},\,t+1}_{S+e} = 0 = \frac{1}{t+3} \mathbf{1}^{\textit{tour}(e),\,t+1}_S$; note that the last case of Definition 11 applies because $\textit{tour}(e)$ is the unique “valid tour” that could contain e.

Lemma 8 shows that $y^{\mathcal {I},\,t+1}$, restricted to $\mathcal {P}_{t+1}$, is in $\mathcal {SA}^t({\textsf {ATSP}_{DFJ}}(G^{new}))$; this is used in Lemma 7 to show that $e * y^{\mathcal {I},\,t+1}$ is in $\mathcal {SA}^t({\textsf {ATSP}_{DFJ}}(G^{new}))$.

Lemma 8

For any nonnegative integer t, any $S\in \mathcal {P}_{t+1}$, any $\mathcal {I}\subseteq \mathcal {F}$ with $|\mathcal {I}|\le |\mathcal {F}| - (t+3)$, and any $h\in \mathcal {F}-\mathcal {I}$, we have

$$\begin{aligned} y^{\mathcal {I},\,t+1}_S ~=~ \frac{t+2}{t+3} y^{\mathcal {I}+h,\,t}_S + \frac{1}{t+3}\mathbf{1}^{\textit{tour}(h),\,t+1}_S \end{aligned}$$

(15)

Proof

We have $S\subseteq D\cup {E}, |S|\le {t+1}$.

We apply Definition 11 (the definition of $y$) to $y^{\mathcal {I},\,t+1}$, and we have three cases.

Case 1.:

$S\cap {D}=\emptyset$. Then $y^{\mathcal {I},\,t+1}_S = \frac{(t+3)-f^{\mathcal {I}}(S)}{t+3}$. For the RHS, we have two subcases, either $\textit{tour}(h)\supseteq {S}$ or not. In the first subcase, we have $S\cap E(C_{h})=\emptyset$ (since $\textit{tour}(h)$ contains none of the solid edges of $C_{h}$), hence, $f^{\mathcal {I}+h}(S) = f^{\mathcal {I}}(S)$, consequently, the RHS is $\frac{t+2}{t+3} \frac{(t+2)-f^{\mathcal {I}}(S)}{t+2} + \frac{1}{t+3}$, which is the same as the LHS. In the other subcase, $\textit{tour}(h)\not \supseteq {S}$. Then, we have $S\cap {E(C_{h})}\not =\emptyset$ (because $S\subseteq {E}$ and $\textit{tour}(h)$ contains all solid edges except those in $C_{h}$), hence, $f^{\mathcal {I}+h}(S) = f^{\mathcal {I}}(S) - 1$, and consequently, the RHS is $\frac{t+2}{t+3} \frac{(t+3)-f^{\mathcal {I}}(S)}{t+2} + 0 = \frac{(t+3)-f^{\mathcal {I}}(S)}{t+3}$, which is the same as the LHS.

Case 2.:

$S\cap {D}\not =\emptyset$ and there exists $j\in \mathcal {F}-\mathcal {I}$ such that $\textit{tour}(j)\supseteq {S}$. Then $y^{\mathcal {I},\,t+1}_S = \frac{1}{t+3}$, by Definition 11. For the RHS, we have two subcases, either $j=h$ or not. In the first subcase, we have $y^{\mathcal {I}+h,\,t}_S = 0$, because $\textit{tour}(h)$ is the unique tour containing S but it is not a “valid tour” w.r.t. $\mathcal {I}+h$, hence, the last case in Definition 11 applies. Thus, the RHS is $0 + \frac{1}{t+3} \mathbf{1}^{\textit{tour}(h),\,t+1}_S = \frac{1}{t+3}$, which is the same as the LHS. In the second subcase, $j\not =h$. Then, in the RHS, $y^{\mathcal {I}+h,\,t}_S = \frac{1}{t+2}$, because $j\in \mathcal {F}-(\mathcal {I}+h)$ and $\textit{tour}(j)\supseteq {S}$ so the second case in Definition 11 applies. Moreover, $\mathbf{1}^{\textit{tour}(h),\,t+1}_S = 0$, because $j\not =h$, and $\textit{tour}(j)$ is the unique tour containing S, so $\textit{tour}(h)\not \supseteq {S}$. Thus, the RHS is $\frac{t+2}{t+3} \frac{1}{t+2} + 0 = \frac{1}{t+3}$, which is the same as the LHS.

Case 3.:

$S\cap {D}\not =\emptyset$ and $\textit{tour}(j)\not \supseteq {S}$, $\forall j\in \mathcal {F}-\mathcal {I}$. Then $y^{\mathcal {I},\,t+1}_S = 0$. In the RHS, $y^{\mathcal {I}+h,\,t}_S = 0$, by the third case in Definition 11, since the relevant conditions hold (by Fact 11). Moreover, $\mathbf{1}^{\textit{tour}(h),\,t+1}_S = 0$, because $h\in \mathcal {F}-\mathcal {I}$ and $\textit{tour}(h)\not \supseteq {S}$. Thus, the RHS is 0, which is the same as the LHS.

This completes the proof of the lemma.

Lemma 9

Suppose that for any nonnegative integer t and any $\mathcal {I}'\subseteq \mathcal {F}$ with $|\mathcal {I}'|\le |\mathcal {F}| - (t+2)$, we have $y^{\mathcal {I}',\,t} \in \mathcal {SA}^t({\textsf {ATSP}_{DFJ}}(G^{new}))$. Then for any $\mathcal {I}\subseteq \mathcal {F}$ with $|\mathcal {I}|\le |\mathcal {F}| - (t+3)$,

$$\begin{aligned} y^{\mathcal {I},\,t+1}-e*y^{\mathcal {I},\,t+1} \in \mathcal {SA}^t({\textsf {ATSP}_{DFJ}}(G^{new})), \quad \forall e\in E^{new} \end{aligned}$$

Proof

By Lemmas 7, 8, we have for each $e\in E^{new}=E\cup {D}$ and any $S\in \mathcal {P}_{t+1}$,

$$\begin{aligned} ( y^{\mathcal {I},\,t+1} - e * y^{\mathcal {I},\,t+1} )_S ~=~ {\left\{ \begin{array}{ll} 0&{} \hbox {if}\, e\in E(C_j)\, \hbox {where}\, j\in \mathcal {I}\cup \overline{\mathcal {F}}\\ &{} \qquad (e\, is\, a\, solid,\, integral\, edge) \\ y^{\mathcal {I},\,t+1}_S &{} \hbox {if}\, e\in D(C_j) \,\hbox {where}\, j\in \mathcal {I}\cup \overline{\mathcal {F}}\\ &{} \qquad (e\, is\, a\, dashed,\, integral\, edge) \\ \frac{1}{t+3}\mathbf{1}^{\textit{tour}(e),\,t+1}_S &{} \hbox {if}\, e\in E(C_j) \,\hbox {where}\, j\in \mathcal {F}- \mathcal {I}\\ &{} \qquad (e\, is\, a\, solid,\, fractional\, edge) \\ \frac{t+2}{t+3}y^{\mathcal {I}+\textit{index}(e),\,t}_S &{} \hbox {if}\, e\in D(C_j) \,\hbox {where}\, j\in \mathcal {F}- \mathcal {I}\\ &{} \qquad (e\, is\, a\, dashed,\, fractional\, edge) \\ \end{array}\right. } \end{aligned}$$

(16)

Hence, in every case, $y^{\mathcal {I},\,t+1}-e*y^{\mathcal {I},\,t+1} \in \mathcal {SA}^t({\textsf {ATSP}_{DFJ}}(G^{new}))$

Theorem 12

Let t be a nonnegative integer, and let $\epsilon \in \mathbb {R}$ satisfy $0<\epsilon \ll {1}$. There exists a digraph on $\nu =\nu (t,\epsilon )={\varTheta }(t/\epsilon )$ vertices such that the integrality ratio for the level t tightening of the standard LP (DFJ LP) (for ATSP, by the Sherali–Adams procedure) is ${\ge } 1+\frac{1-\epsilon }{2t+3}$.

Proof

Given t and $\epsilon$, we fix $\ell = 2 (2t+3)/\epsilon$ to get a digraph G shown in Figure 1 where $\ell$ is the length of the “middle path”. Let the cost of each edge in G be 1. Then we construct $G^{new}$ from G. We keep the cost of edges in G to be 1 and fix the cost of new edges to be 0. See Fig. 5; each solid edge has cost 1 and each dashed edge has cost 0. In the proof of Theorem 4, we claimed that the minimum cost of an Eulerian subdigraph of G is ${\ge } 4\ell +2$. It can be seen that the minimum cost of an Eulerian subdigraph of $G^{new}$ is ${\ge } 4\ell +2$ (to see this, take an Eulerian subdigraph of $G^{new}$, then contract all dashed edges contained in it, to get an Eulerian subdigraph of G of the same cost). Let H be the metric completion of $G^{new}$. Then, the optimal value of the integral solution in $\mathcal {SA}^t(\widehat{\textsf {ATSP}}_{{DFJ}}(H))$ is ${\ge } 4\ell +2$.

Now we invoke Theorem 10, according to which the fractional solution $y^{\emptyset ,\,t}$ (Definition 7) is in $\mathcal {SA}^t(\widehat{\textsf {ATSP}}_{{DFJ}}(G^{new}))$; see Fig. 5; we have $y^{\emptyset ,\,t}_e=1$ for each solid, thick edge e (the solid edges of the outer cycle), $y^{\emptyset ,\,t}_e=\frac{t+1}{t+2}$ for each solid, thin edge e (the solid edges of the middle paths), while the value of the dashed edges do not contribute to the value of the objective. By Sect. 2.2.1, this feasible solution can be extended to a feasible solution in $\mathcal {SA}^t(\widehat{\textsf {ATSP}}_{{DFJ}}(H))$.

Hence, the integrality ratio of $\mathcal {SA}^t(\widehat{\textsf {ATSP}}_{{DFJ}}(H))$ is

$$\begin{aligned} \ge \frac{4\ell + 2}{2\ell + 4 + 2\ell \frac{t+1}{t+2}} \ge \frac{2(t+2)}{2t+3} - \frac{2}{\ell } \ge 1+ \frac{1 - \epsilon }{2t+3}. \end{aligned}$$

5 Path ATSP

Let $G=(V,E)$ be a digraph with nonnegative edge costs c, and let p and q be two distinguished vertices. We define $\widehat{\textsf {PATSP}}_{p,q}(G)$ to be the polytope of the following LP that has a variable $x_e$ for each edge e of G:

$$\begin{aligned} \hbox {minimize}&\sum _{e} c_e x_e \\ \hbox {subject to} \\&x\left( \delta ^{in}(S)\right) \ge 1,&\quad \forall S:~\emptyset \subset S \subseteq V-\{p\} \\&x\left( \delta ^{out}(S)\right) \ge 1,&\quad \forall S:~\emptyset \subset S \subseteq V-\{q\} \\&x\left( \delta ^{in}(\{v\})\right) = 1,&\quad \forall v \in V-\{p\} \\&x\left( \delta ^{out}(\{v\})\right) = 1,&\quad \forall v \in V-\{q\} \\&x\left( \delta ^{in}(\{p\})\right) = 0,\\&x\left( \delta ^{out}(\{q\})\right) = 0, \\&\mathbf{0} \le \mathbf{x}\le \mathbf{1} \\ \end{aligned}$$

In particular, when G is a complete digraph with metric costs, the above LP is the standard relaxation for the p-q path ATSP, which is to compute a Hamiltonian (or, spanning) dipath from p to q with minimum cost in the complete digraph with metric costs. For $\widehat{\textsf {PATSP}}_{p,q}(G)$, we denote the associated cone by $\textsf {PATSP}_{p, q}(G)$.

(In the literature, the notation for the two distinguished vertices is s, t, but we use p, q to avoid conflict with our symbol t for the number of rounds of the SA procedure.)

An (p, q)-Eulerian subdigraph $\overline{G}$ of G is V together with a collection of edges of G with multiplicities such that (i) for any $v\in V-\{p, q\}$, the indegree of v equals its outdegree and (ii) the outdegree of p is larger than its indegree by 1 and the indegree of q is larger than its outdegree by 1 and (iii) $\overline{G}$ is weakly connected (i.e., the underlying undirected graph is connected). The p-q path ATSP on the metric completion H of G is equivalent to finding a minimum cost (p, q)-Eulerian subdigraph of G.

For any subset $V^{\prime }$ of V, we use $G(V^{\prime })$ to denote the subdigraph of G induced by $V^{\prime }$. As before, we use $\mathcal {P}_t$ to denote $\mathcal {P}_t(E)$ (for the groundset E). Also, by the restriction of $y$ on $E^{\prime }\subseteq E$ we mean the vector $y|_{E^{\prime }}\in \mathbb {R}^{\mathcal {P}_{t+1}(E^{\prime })}$ that is given by $(y|_{E^{\prime }})_S=y_S$ for all $S \in \mathcal {P}_{t+1}(E^{\prime })$.

Lemma 10

Let t be a nonnegative integer. Let $y\in \mathcal {SA}^t({\widehat{\textsf {ATSP}}_{{DFJ}}(G)})$. Suppose that there exists a dipath $Q\subseteq E$ from some vertex q to another vertex p such that $y_e=1$ for each $e\in Q$. Let $V_Q$ denote the set of internal vertices of the dipath Q, and let $G^{\prime } = G(V - V_Q) = G - V_Q$. Then,

$$\begin{aligned} y|_{E(G^{\prime })}\in \mathcal {SA}^t({\widehat{\textsf {PATSP}}_{p,q}(G^{\prime })}). \end{aligned}$$

Proof

Let $V^{\prime }=V - V_Q$ and let $E^{\prime }=E(G^{\prime })$, i.e., $G^{\prime }=(V^{\prime }, E^{\prime })$. The proof is by induction on t. Denote $y|_{E^{\prime }}$ by $y^{\prime }$ for short. Clearly, $y^{\prime }_{\emptyset }=1$. Thus, we only need to prove $y^{\prime }\in \mathcal {SA}^t({\textsf {PATSP}_{p,q}(G^{\prime })})$.

Base case: $t=0$. Let z be the subvector of $y$ on the singleton sets $\{e_i\}$, and let $z^{\prime }$ be the subvector of $y^{\prime }$ on the singleton sets.

We have to prove that $z^{\prime }$ is a feasible solution of $\widehat{\textsf {PATSP}}_{p, q}(G^{\prime })$. It is easy to see that $z^{\prime }$ is in $[0, 1]^{E^{\prime }}$ and it satisfies the degree constraints. Thus, we are left with the verification of the cut constraints. Observe that each positive edge (on which z is positive) of G with its head (tail) in $V_Q$ has its tail (head) in $V_Q+q$ ($V_Q+p$). Let $\emptyset \ne U\subseteq V^{\prime }$. If $U\subseteq V^{\prime } - \{q\}$, then observe that every edge in $\delta ^{out}_{G}(U)$ has its head in $V - V_Q - U = V'-U$, hence, we have $z^{\prime }(\delta ^{out}_{G^{\prime }}(U)) = z(\delta ^{out}_{G}(U))\ge {1}$. Similarly, if $U\subseteq V^{\prime } - \{p\}$, then we have $z^{\prime }(\delta ^{in}_{G^{\prime }}(U)) = z(\delta ^{in}_{G}(U))\ge 1$; the equation holds because every edge in $\delta ^{in}_{G}(U)$ has its tail in $V - V_Q - U = V'-U$.

Induction step: For $t\ge 0$, we know $y^{\prime }\in \mathcal {SA}^{t+1}({\textsf {PATSP}_{p,q}(G^{\prime })})$ if and only if for any $e\in E^{\prime }$,

$$\begin{aligned} e*y^{\prime }&\in \mathcal {SA}^{t}({\textsf {PATSP}_{p,q}(G^{\prime })}) \nonumber \\ y^{\prime } - e*y^{\prime }&\in \mathcal {SA}^{t}({\textsf {PATSP}_{p,q}(G^{\prime })}) \end{aligned}$$

(17)

Since $y$ is a feasible solution in $\mathcal {SA}^{t+1}({{\textsf {ATSP}_{DFJ}}(G)})$, we have

$$\begin{aligned} e*y&\in \mathcal {SA}^{t}({{\textsf {ATSP}_{DFJ}}(G)}) \nonumber \\ y- e*y&\in \mathcal {SA}^{t}({{\textsf {ATSP}_{DFJ}}(G)}) \end{aligned}$$

(18)

Note that $e\in E^{\prime }$. For any $S\subseteq E^{\prime }$ such that $|S|\le t+1$, we have $(e*y^{\prime })_S=y^{\prime }_{S\cup \{e\}}=y_{S\cup \{e\}}=(e*y)_S$. Thus, $e*y^{\prime }=(e*y)|_{E^{\prime }}$. Similarly, we have $y^{\prime } - e*y^{\prime }=(y- e*y)|_{E^{\prime }}$. For any $e^{i}\in Q$, since $y_{e_i}=1$, we have $y_{\{e,e_i\}}=y_e$ (by the definition of the SA procedure), hence, we have

$$\begin{aligned} (e*y)_{\{e^{i}\}}=y_{\{e,e_i\}}=y_e=(e*y)_\emptyset . \end{aligned}$$

Similarly,

$$\begin{aligned} (y-e*y)_{\{e^{i}\}}=y_{e^i}-y_{\{e,e_i\}}=1-y_e=(y-e*y)_\emptyset . \end{aligned}$$

Case 1: $(e*y)_{\emptyset }=0$. In this case, all items in $e*y$ are zero. This implies $e*y^{\prime } \in \mathcal {SA}^{t}({\textsf {PATSP}_{p, q}(G^{\prime })})$.

Case 2: $(e*y)_\emptyset >0$. In this case, we consider $\frac{e*y}{(e*y)_\emptyset }$. Note that $(\frac{e*y}{(e*y)_\emptyset })_{\{e_i\}}=1$ for any $e_i\in Q$ and $\frac{e*y}{(e*y)_\emptyset }\in \mathcal {SA}^{t}({{\textsf {ATSP}_{DFJ}}(G)})$ with value 1 at the item indexed by $\emptyset$. By the inductive hypothesis, we have $\frac{e*y}{(e*y)_\emptyset }|_{E^{\prime }}\in \mathcal {SA}^{t}({\textsf {PATSP}_{p, q}(G^{\prime })})$, i.e., $\frac{e*y^{\prime }}{(e*y^{\prime })_\emptyset }\in \mathcal {SA}^{t}({\textsf {PATSP}_{p, q}(G^{\prime })})$. Thus, $e*y^{\prime } \in \mathcal {SA}^{t}({\textsf {PATSP}_{p, q}(G^{\prime })})$.

Similarly, we have $y^{\prime } - e*y^{\prime }\in \mathcal {SA}^{t}({\textsf {PATSP}_{p, q}(G^{\prime })})$. This completes the proof.

From the last section, we know that $y^{\emptyset ,\,t}$ (Definition 7) is in $\mathcal {SA}^{t}({{\textsf {ATSP}_{DFJ}}(G)})$, where G is defined in Figure 5; note that G is obtained from the digraph and the good decomposition given in Figure 1. The solid edges in G have cost 1 and the dashed edges in G have cost 0.

Let q be the right-most vertex in the second row (incident to two dashed edges), let p be the left-most vertex in the second row (incident to two dashed edges), and let Q be the dipath of solid edges from q to p. By the definition of $y^{\emptyset ,\,t}$, we have $y^{\emptyset ,\,t}_{e_i}=1$ for each $e_i\in Q$. Let $G^{\prime }=G(V^{\prime })$ where $V^{\prime }=V - V_Q$ where $V_Q$ is the set of internal vertices of the dipath Q. The next result is a direct corollary of Lemma 10.

Corollary 2

We have

$$\begin{aligned} y^{\emptyset ,\,t}|_{E(G^{\prime })}\in \mathcal {SA}^t({\widehat{\textsf {PATSP}}_{p, q}(G^{\prime })}), \quad \forall t \in \mathbb {Z}_+. \end{aligned}$$

The proof of the next lemma follows from arguments similar to those in the proof of Theorem 12.

Lemma 11

The minimum cost of a (p, q)-Eulerian subdigraph of $G^{\prime }$ is ${\ge } 3\ell$, where $\ell$ is the number of edges in the middle path in G.

Theorem 13

Let t be a nonnegative integer, and let $\epsilon \in \mathbb {R}$ satisfy $0<\epsilon \ll {1}$. There exists a digraph on $\nu =\nu (t,\epsilon )={\varTheta }(t/\epsilon )$ vertices such that the integrality ratio for the level t tightening of $\textsf {PATSP}$ by the Sherali–Adams procedure is $\ge 1 + \frac{2-\epsilon }{3t+4}$.

Proof

Given t and $\epsilon$, we fix $\ell = 2 (3t+4)/\epsilon$. Consider the metric completion H of $G^{\prime }$. By Sect. 2.2.1, we can extend the feasible solution from Corollary 2 to a feasible solution to $\mathcal {SA}^t({\widehat{\textsf {PATSP}}_{p, q}(H)})$. This gives an upper bound on the optimal value of a fractional feasible solution to $\mathcal {SA}^t({\widehat{\textsf {PATSP}}_{p,q}(H)})$. On the other hand, Lemma 11 gives a lower bound on the optimal value of an integral solution. Thus, the integrality ratio is at least

$$\begin{aligned} \frac{3\ell }{\frac{t+1}{t+2}2\ell + l + 2} \ge 1+\frac{2}{3t+4} - \frac{2}{\ell } \ge 1+ \frac{2 - \epsilon }{3t+4}. \end{aligned}$$