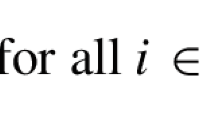1 Introduction

Binary knapsack programs are a common model for choosing between discrete alternatives. If the choice is continuous but limited; the resulting model is called a classical single node flow set, as studied in [17, 19]. If the choice is semi-continuous; we must consider mixed-binary knapsack programs. This problem is known as the semi-continuous knapsack problem (SCKP). If binary variables are subjected to independent clique constraints we have what we call a semi-continuous knapsack problem with generalized upper bound constraints (SCKPGUB). This kind of model is common for representing (possibly non-linear) functions (with only one GUB constraint), or for studying the combined non-linear output of several machines.

This is the case in production scheduling problems, such as in electricity generation [6, 9, 18, 26], where the cost function of each generating unit can be highly non-linear and even discontinuous. Furthermore, if the original problem has integer variables; these functions are usually approximated by a piece-wise linear function.

In this setting, sequential lifting is too limited in the sense that whenever we have a constraint \(y\le x\) for \(x\in \{0,1\}\) and \(y\in [0,1]\), lifting must be carried out first on the integer variable and then on the continuous variable. This precludes finding some facet-defining inequalities for the complete problem; making simultaneous lifting essential in this setting. For a basic reference on simultaneous lifting, see [13, 27], and see [8, 11, 15] for some experiments and results regarding sequential and simultaneous lifting.

In this paper, we use generalized flow cover (GFC) inequalities [21]; show that they are valid in our setting and, under mild assumptions, they induce facets or high dimensional faces of the original problem. We then propose a valid sequence-independent multidimensional lifting scheme to obtain valid inequalities for SCKPGUB. We show that the proposed lifting function is superadditive on a restricted set of feasible right-hand sides, and show that this condition is sufficient to obtain sequence-independent lifting. Finally, we also provide sufficient conditions for this lifting to be maximal.

The paper is organized as follows. Section 2 covers some known facts about semi-continuous knapsack problems; including a class of valid inequalities and basic results for the semi-continuous knapsack problem with GUB constraints. Section 3 deals with multidimensional lifting for SCKPGUB; specifically on how to obtain valid sequence-independent lifting functions for them. We also propose simple algorithms to solve the separation problem both for the seed inequality and for the selection of maximally violated lifted inequalities. In Sect. 4 we propose a heuristic separation algorithm that provides good numerical results and shows that the lifting step is crucial. We generate our test-instances from problems in electricity generation where some of the parameters are randomly perturbed. Finally, we present our conclusions and explore further research questions in Sect. 5.

2 Definitions and basic polyhedral results

In this section we introduce most of the notation used throughout the paper. This includes the precise definition of the polytope with which we will work. We also present some previously known results and state some basic polyhedral results. Finally, we prove that our seed inequality, under mild hypothesis, is also a facet.

2.1 The problem

We consider the semi-continuous knapsack problem with generalized upper bound constraints given by

$$\begin{aligned} X_G = \left\{ \begin{aligned} \textstyle (x,y) \in \left\{ \{0,1\}\times [0,1]\right\} ^M :\\ \textstyle \sum _{k\in M}\left( a_{k} x_{k} + m_{k} y_{k}\right)&\le b&\\ \textstyle y_{k}&\le x_{k}&\quad \forall k\in M\\ \textstyle \sum _{k \in M_g} x_k&\le 1&\quad \forall g \in G \end{aligned} \right\} , \end{aligned}$$
(1)

where \(G\) is the set of GUB constraints, for each \(g\in G, n_g\in \mathbb {N}\) is the number of elements in the GUB constraint indexed by \(g, n=\sum _{g\in G}n_g, M=\{(g,j):g\in G,j\in 1,\ldots ,n_g\}\), and \(M_g=\{(g',j')\in M:g'=g\}\). This implies that each \(k\in M\) is an ordered pair \((g,j)\); we will use both notations interchangeably. Also, to simplify notation, when we have a vector \(\mu \in \mathbb {R}^r\) (for some \(r\in \mathbb {N}\)) and \(R\subseteq \{1,\ldots ,r\}\), we will denote \(\mu (R):=\sum \mu _i:i\in R\). Note that \(a_{k}x_{k}+m_{k}y_{k}\) is a model for a semi-continuous variable with values in \(\{0\}\cup [a_{k},a_{k}+m_{k}]\). Although \(a_k\) and \(m_k\) could in general be negative, we will focus on the case where both quantities are non-negative, i.e., \(a_k,m_k\ge 0,\,\forall k\in M\). Note that unlike in the classical knapsack case, this assumption is restrictive, but we choose it nonetheless because it follows what happens in many applications. The first constraint is the semi-continuous knapsack constraint, the second constraint ensures semi-continuity, and the third constraint imposes a generalized upper bound condition among disjoint sets of binary variables.

2.2 Literature review

Several special subsets of this structure have been studied before. For example, the classical binary knapsack problem (KP) was studied by Balas and Jeroslow [4] in a theoretical study where canonical cuts on the unit hypercube were introduced. Based on this work, in 1975, Wolsey [24] and Balas [3] presented facet-defining inequalities for the KP by using the notion of cover for the first time. Hammer, Johnson and Peled [12] also studied facets of regular 0–1 polytopes, which include knapsack problems. This study also characterizes every non-trivial facet with 0–1 coefficients. In 1978, Balas and Zemel [5] extended previous work by applying lifting procedures to valid inequalities obtained from minimal covers. In 1980, Padberg [20] presented \((1,k)\)-configurations as a generalization of minimal cover inequalities. Johnson and Padberg [14] studied the inclusion of GUB constraints in the KP (KPGUB); they also showed how to transform a general instance of the problem into one with only non-negative coefficients. In 1988, Wolsey [23] defined some valid inequalities for the KPGUB and proved that they are facet-defining under certain conditions. Sherali and Lee [22] applied sequential and simultaneous lifting to valid inequalities for KPGUB deduced from minimal covers.

Another special case is when \(a_{k}=0\) and \(|M_g|=1\). This case is called single-node flow sets (SNFS), and their study has been extended from the work of Gu et al. [10] from lifting procedures applied to this set. In 2007, Louveaux and Wolsey [16] provided a survey of strong valid inequalities for knapsack and single-node flow sets.

As can be seen, the application of lifting procedures is a fundamental part of cut generation techniques for many specific sets. In 1977, Wolsey [25] presented the first work in this area and used the concept of superadditivity. In 2000, Gu et al. [11] generalized it and defined sequence-independent lifting of general mixed integer programs. In 2004, Atamtürk [2] presented similar results.

The above research can be seen as concerned with one-dimensional lifting, since all of these studies consider the perturbation of only one constraint. Applications of multidimensional lifting are scarce, with work by Zeng [28] and Zeng and Richard [29, 30] as the most relevant. They defined a general framework to derive multidimensional and superadditive lifting functions and applied it to the precedence-constrained knapsack problem and the single-node flow set. They showed that the traditional concept of superadditivity used by Gu et al. [11] can be restricted depending on the problem at hand. We provide a simple proof of this result in the context of SCKPGUB.

2.3 Polyhedral results

2.3.1 Basic results for SCKPGUB

We will henceforth assume that \(\bar{a}:=\max \{a_k:k\in M\}<b\). With this in place, Proposition 1 follows:

Proposition 1

  1. 1.

    \(X_G\) is full-dimensional.

  2. 2.

    Inequality \(y_{k}\ge 0\) is facet-defining for \(X_G, \forall k\in M\).

  3. 3.

    If \(a_k+m_k\le b\), the inequality \(y_{k}\le x_{k}\) is facet-defining for \(X_G, \forall k\in M\).

  4. 4.

    If \(\overline{a}_g:=\max \limits _{k\in M{\setminus } M_g}\{a_{k}\}+\min \limits _{k\in M_g}\{a_{k}\}<b\), then \(\sum _{k\in M_g}x_{k}\le 1\) is facet defining for \(X_G\), for \(g\in G\).

Proof

The basic idea of the proof is to find the appropriate number of feasible affinely-independent points satisfying each inequality at equality. For details see “Proof of Proposition 1”. \(\square \)

2.3.2 Generalized flow cover inequalities for SCKP

Consider the set

$$\begin{aligned} X = \left\{ \begin{aligned} \textstyle (x,y) \in \{0,1\}^{n} \times [0,1]^{n}:\\ \textstyle \sum _{j \in M}\left( a_{k} x_{k} + m_{k} y_{k}\right)&\le b&\\ y_{k}&\le x_{k}&\quad \forall k \in M \end{aligned} \right\} . \end{aligned}$$
(2)

Van Roy and Wolsey [21] studied (a generalization of) this polyhedron and proposed a family of valid inequalities that they called generalized flow cover (GFC) inequalities. In our setting, we restate this family of inequalities as follows:

Given \(X\) as defined in (2), we call a pair \((C,C_U)\), with \(C\subset M\) and \(C_U\subset C\), satisfying \({\varGamma }:=a(C)+m(C_U)-b>0\) and \(m(C_U)>0\), a generalized cover. Then the inequality

$$\begin{aligned} \sum \limits _{j\in C}\min \left\{ 1,\frac{\xi _j}{{\varGamma }}\right\} (x_j-1)+\sum \limits _{j\in C_U}\frac{m_j}{{\varGamma }}\left( y_j-x_j\right) \le -1, \end{aligned}$$
(3)

where \(\xi _j=a_j\) for \(j\in C{\setminus } C_U\) and \(\xi _j=a_j+m_j\) for \(j\in C_U\), is valid for \(X\).

Theorem 1 gives sufficient conditions for (3) to be facet-defining for \(X\).

Theorem 1

Let \((C,C_U)\) be a generalized flow cover satisfying \(\sum _{j\in C_U:\xi _j>{\varGamma }}m_j>{\varGamma }\). Then, inequality (3) is facet-defining for \(X_o:=X\cap \{x_i=0,\forall i\notin C\}\).

Proof

Van Roy and Wolsey [21] proved the validity of inequality (3). We prove that (3) is facet-defining for \(X_o:=X\cap \{x_i=0,i\notin C\}\) by constructing a set of \(2s\) affinely independent points in \(X_o\) satisfying it at equality. For details see “Proof of Theorem 1”. \(\square \)

Note that \(X\) is a face of \(X_G\) where we choose at most one element from every GUB constraint to be active. Given this, Theorem 1 ensures that whenever \(\sum _{j\in C_U:\xi _j>{\varGamma }}m_j>{\varGamma }\), the resulting flow cover inequality is facet-defining for this face of \(X_G\). Moreover, since \(X\) is also a relaxation of \(X_G\), (3) defines valid inequalities for \(X_G\).

3 Multidimensional lifting for SCKPGUB

In this section we deal with the problem of lifting our seed inequality, defined in (3). To achieve this, we first define what is a valid lifting function in a setting that allows simultaneous and multidimensional lifting in general, and apply it to our particular set. We also identify simple conditions under which optimal lifting coefficients are zero; and introduce a superadditive approximation for maximal lifting functions. Since the full separation of the seed inequality is \(\mathcal {N}\mathcal {P}\)-hard, we propose a heuristic algorithm to find seed inequalities, and describe a simple algorithm to apply our sequence-independent lifting function.

3.1 Valid lifting functions

In this section we study the following problem: given a polytope

$$\begin{aligned} P=\left\{ \begin{array} {l@{\quad }l} x\in \mathbb {R}^n:&{}Ax\le b,\\ {} &{}0\le x\le u,\\ &{}x_i\in \mathbb {Z},\,\forall i\in I\end{array}\right\} , \end{aligned}$$

where \(I\subseteq \{1,\ldots ,n\}\); a set \(N\subseteq \{1,\ldots ,n\}, N^c=\{1,\ldots ,n\}{\setminus } N\); and an inequality \(ax\le b_o\) valid for \(P\), satisfying \(a_i=0,\,\forall i\in N\); we want to find \(\alpha \in \mathbb {R}^n\) satisfying \(\alpha _i=0,\,\forall i\notin N\) such that \(ax + \alpha x \le b_o\) is a valid inequality (and hopefully tight) for \(P\), i.e.

$$\begin{aligned} ax+\alpha x \le b_o,\,\forall x\in P \end{aligned}$$

Taking advantage of the condition that \(a_i\cdot \alpha _i=0,\,\forall i\in \{1,\ldots ,n\}\), we can think that \(x\in \mathbb {R}^n\) has two independent components \(x=(x_{N^c},x_N)=(v,w)\) and that \(P=\{(v,w)\in \mathbb {R}^n:A_1v+A_2w\le \bar{b}, v\in V,\,w\in W\}\), where \(V,W\) describe the corresponding box-constraints, integrality requirements, and inequalities involving variables indexed by \(N^c\) and \(N\) respectively. Abusing notation, we can re-state our problem as finding \(\alpha \) such that

$$\begin{aligned} av+\alpha w \le b_o,\quad \forall A_1v\le \bar{b}-A_2w,\,v\in V,\,w\in W. \end{aligned}$$

Here, we can make a second observation; the interaction between \(v\) and \(w\) is only through the common inequalities \(A_1v \le \bar{b}- A_2w\); and there, the interaction is only through values of \(A_2w:w\in W\) for which there exists \(v\in V\) satisfying \(A_1v+A_2w\le \bar{b}\). Moreover, the problem of ensuring the condition for all feasible points in \(P\) is an optimization problem in a different space. Formally, we state this problem as follows:

$$\begin{aligned} \overbrace{\begin{matrix}\max &{}\alpha w\\ s.t.&{}A_2w=z\\ &{}w\in W\end{matrix}}^{h_\alpha (z)}\le \overbrace{\begin{matrix}\min &{}b_o-ax\\ s.t.&{}A_1v\le \bar{b}-z\\ {} &{}v\in V\end{matrix}}^{f(z)}\quad \forall z\in Z, \end{aligned}$$

where \(Z=\{z:\exists v\in V,\, w\in W,\,z=A_2w,\,A_1v+z\le \bar{b}\}\). With these definitions, our problem can be simply stated as finding \(\alpha \) such that

$$\begin{aligned} h_\alpha (z)\le f(z),\,\forall z\in Z. \end{aligned}$$

Note that in the literature, usually \(Z\subseteq \mathbb {R}\); however, in our set, \(Z\subseteq \mathbb {R}\times \{0,1\}^G\), and the elements in \(Z\) will have a continuous component \(z\) and a binary vector component \(\varvec{v}\in \{0,1\}^G\). In this sense, our lifting is multidimensional. Also, since at every step \(N\) will have two variables, we will be doing simultaneous lifting.

To apply these ideas iteratively, in this section, we re-write (3) as

$$\begin{aligned} \sum \limits _{i\in C}\gamma _jx_j+\sum \limits _{j\in C_U}\frac{m_j}{{\varGamma }}\left( y_j-x_j\right) \le \gamma (C)-1, \end{aligned}$$
(4)

where \(\gamma _j=\min \{1,\frac{\xi _j}{{\varGamma }}\}\). As noted before, given a generalized flow cover \(C,C_U\) in \(X_G\) satisfying \(|C\cap \{k:k\in M_g\}|\le 1, \forall g\in G\); (4) is valid for \(X_G\) and, if \(m(C_U^+)>{\varGamma }\), where \(C_U^+=\{k\in C_U:a_k+m_k>{\varGamma }\}\), (4) is a facet-defining inequality for \(X_G\cap \{x_i=0,\forall i\notin C\}\). Following Gu et al. [11], we consider the problem of sequentially lifting pairs of variables \((x_k,y_k),\,k\notin C\) to obtain

$$\begin{aligned} \sum \limits _{i\in C}\gamma _jx_j+\sum \limits _{j\in C_U}\frac{m_j}{{\varGamma }}\left( y_j-x_j\right) +\sum \limits _{k\notin C}\left( \alpha _kx_k+\beta _ky_k\right) \le \gamma (C)-1. \end{aligned}$$
(5)

For simplicity we index pairs \(\{k_i\}_{i=1}^{n-|C|}=\{(g_i,j_i)\}_{i=1}^{n-|C|}=M{\setminus } C\) and assume that the first \(i-1\) pairs of variables have been lifted. With this, the \(i\)-th lifting function reduces to

$$\begin{aligned} h_{k_i}(z,\varvec{v})= & {} \max \alpha _{k_i} x_{k_i} + \beta _{k_i} y_{k_i} \nonumber \\&\; \; s.t.\ a_{k_i} x_{k_i} + m_{k_i} y_{k_i}= z \nonumber \\&\; \; x_{k_i} = \varvec{v_{g_i}} \nonumber \\&\; \; 0 \le y_{k_i}\le x_{k_i} \nonumber \\&\; \; x_{k_i} \in \{0,1\}, \end{aligned}$$
(6)

and \(f_{k_i}(z,\varvec{v})\) reduces to

$$\begin{aligned} f_{k_i}(z,\varvec{v})= & {} \min \sum \limits _{i\in C}\gamma _j\left( 1-x_j\right) -\sum \limits _{j\in C_U}\frac{m_j}{{\varGamma }}\left( y_j-x_j\right) \nonumber \\&-\sum \limits _{k\in K^i}\left( \alpha _kx_k+\beta _ky_k\right) -1\nonumber \\&s.t. \sum \limits _{k \in C\cup K^i}\left( a_kx_k+m_ky_k\right) \le b-z \nonumber \\&\sum \limits _{k\in M_g(C\cup K^i)} x_{k} \le 1-\varvec{v}_g, \quad \forall g \in G \nonumber \\&0 \le y_k \le x_k,\,x_k\in \{0,1\}\quad \forall k \in C \cup K^i, \end{aligned}$$
(7)

where \(K^i=\{k_1,\ldots ,k_{i-1}\}, z\in [0,b]\), and \(\varvec{v}\) has the dimension of the right-hand sides of \(X_G\) for GUB constraints; and define \(\varvec{v_{g'}}=\delta _{g',g_i}\) for \(g\in G\); where \(\delta _{a,b}=1\) if \(a=b\), and zero otherwise, i.e., \(\varvec{v}=e_{g_i}\). Our objective is to find \(\alpha _{k_i},\beta _{k_i}\) that ensure that \(h_{k_i}(z,u{\varvec{v}})\le f_{k_i}(z,u{\varvec{v}})\) for all \((z,u)\in \{(0,0)\}\cup \{([a_{k_i},a_{k_i}+m_{k_i}],1)\}\) and \(\varvec{v}=e_{g_i}\). This implies that we are not interested in \(h_{k_i},f_{k_i}\) for all possible \((z,\varvec{v})\in \mathbb {R}\times \{0,1\}^{G\cup M}\), but only in the true domain of feasible points of \(X_G\).

Although the lifting is multidimensional, there are only two degrees of freedom at each step in the functions, namely \(z\) and \(u\in \{0,1\}\). The analysis of \(h_{k_i}\) is easy because for the case where \(m_{k_i}>0\) the optimal value of \(h_{k_i}(z,\varvec{v})\) is

$$\begin{aligned} h_{k_i}(z,\varvec{v}) = \left\{ \begin{array}{ll} 0 &{} \quad u=0, z=0 \\ \tilde{\alpha }+\tilde{\beta }z &{} \quad u=1, a_{k_i} \le z \le a_{k_i}+m_{k_i} \end{array} \right. \end{aligned}$$

where \(\tilde{\alpha }=\alpha _{k_i}-\frac{a_{k_i}}{m_{k_i}}\beta _{k_i}\) and \(\tilde{\beta }=\frac{1}{m_{k_i}}\beta _{k_i}\).

For the case where \(m_{k_i}=0\), the optimal value of the function is

$$\begin{aligned} h_{k_i}(z,\varvec{v}) = \left\{ \begin{array}{ll} 0 &{} \quad u=0, z=0 \\ \tilde{\alpha } &{} \quad u=1, z=a_{k_i} \end{array} \right. \end{aligned}$$

where \(\tilde{\alpha }=\alpha _{k_i}\) and \(\tilde{\beta }=\beta _{k_i}=0\). We call \(\tilde{\alpha }\) and \(\tilde{\beta }\) normalized lifting coefficients.

To study \(f_{k_i}\), we start with a simple case in the following proposition:

Proposition 2

Let \(D=\{(g,j)\in M{\setminus } C:\exists (g,j')\in C,\,\xi _{gj'}\ge {\varGamma },\,a_{gj}+m_{gj}\le \xi _{gj'}-{\varGamma }\}\). Then, for all \(k\in D\), the maximal lifting coefficients \((\alpha _k,\beta _k)\) are \((0,0)\).

Proof

Since \(f_{k_{i}}\le f_{k_{i+1}}\); we obtain the best possible lifting coefficients for these variables when we lift them first. We will prove that even in this best case these coefficients are zero. So, we assume that the first elements to lift from the seed inequality are from \(D\). Let \(k\) be an element in \(D\). It is known that \(f_{k}(z,\varvec{v})\ge 0\) is a monotonic, non-decreasing function, and that \(f(0,\varvec{0})=0\). This implies that it is enough to find a feasible point for \(z=a_{k}+m_{k}\) with an objective value equal to zero to prove our result. Let \(k_o\in C\) satisfying \(\xi _{k_o}>{\varGamma }\) and \(a_k+m_k\le \xi _{k_o}-{\varGamma }\). Then, setting \((x,y)=(\varvec{1}_C-e_{k_o},\varvec{1}_C-e_{k_o})\), we obtain \(f_{k}(z,{\varvec{v}})\le 0\) for \(z\in [a_k,a_k+m_k],{\varvec{v}}=e_{g_k}\).

\(\square \)

Note that Theorem 1 ensures that there is nothing to be gained from lifting \(x\) and/or \(y\) in \(C\); whereas Proposition 2 ensures the same for variables in \(D\). The following proposition will allow us to assume that it is enough to consider the case when \(D=\emptyset \) and where \(m(C_L)=0\), where \(C_L:=C{\setminus } C_U\).

Proposition 3

If \(k\in M{\setminus }(C\cup D)\), then for every optimal solution of the problem \(f_k(z,\varvec{v})\), it is always possible to find an optimal solution \(x^*,y^*\) satisfying \(y^*_k=0\) for \(k \in C_L\) and \(x^*_k=y^*_k=0\) for \(k \in D\).

Proof

Let \(y^*,x^*\) be an optimal solution to \(f_k(z,\varvec{v})\). Note that if \(x^*,y^*\) is valid for (7), then for any \(j\in M\), changing any \(x^*_j,y^*_j\) to zero maintain feasibility. Thus, we only need to prove that by making this change for \(j\in D\) and \(y_j^*,\,j\in C_L\), the objective function will not deteriorate.

For \(j\in D\), the optimal lifting coefficients \((\alpha _j,\beta _j)=(0,0)\). Then, any valid lifting coefficient pairs \(\alpha _jx^*_j+\beta _jy^*_j\le 0\). Replacing \(x^*_j,y^*_j\) with \((0,0)\) will then not deteriorate the objective function; thus proving that there exists an optimal solution with these variables set to zero.

For \(j\in C_L\) the argument is similar: if \(k=1\), note that the objective function has a zero coefficient for \(y_j\), from where \(\beta _j\le 0\). Using the fact that the lifting functions will be decreasing and that the coefficients in the objective function accompanying \(y_j\), for all \(j\in C_L\), are non-positive; we conclude that we can always find an optimal solution with \(y^*_j=0\) for \(j\in C_L\).\(\square \)

These two propositions allow us to work with the assumption that \(D=\emptyset \) and that \(m(C_L)=0\). This is because Proposition 2 ensures that the best possible lifting coefficients are zero; while Proposition 3 ensures that, if \(D\ne \emptyset \), there exists an optimal solution for \(f_{k_i}\) with \(x_i,y_i=0\) for all \(i\in D\).

3.2 A lower bound for lifting functions

Given \(\varvec{v}\in \{0,1\}^G\), and defining \(C_{\varvec{v}}=\{(g,j)\in C:{\varvec{v}}_g=1\}\), we can re-write the first lifting function \(f(z_1,\varvec{v})\) as

$$\begin{aligned} f_1(z,\varvec{v})= & {} \gamma (C)-1-\max \sum \limits _{k\in C{\setminus } C_{\varvec{v}}}\left( \gamma _kx_k+\frac{m_k}{{\varGamma }}(y_k-x_k)\right) \nonumber \\&s.t.\quad \sum \limits _{k \in C{\setminus } C_{\varvec{v}}}\left( \xi _kx_k+m_k(y_k-x_k)\right) \le b-z \nonumber \\&\qquad 0 \le y_k \le x_k,\,x_k\in \{0,1\}\, \forall k \in C{\setminus } C_{\varvec{v}}. \end{aligned}$$
(8)

In general, \(f_1(z,\varvec{v})\) is a complex function, and a simpler functional form \(\tilde{f}\) is needed satisfying \(\tilde{f}\le f_1\). We propose the following relaxation of \(f_1\): first note that \(b=\xi (C)-{\varGamma }\); replace \(x\) by \(1-x\) and \(y\) by \(x-y\); and we obtain the following equivalent form for \(f_1\):

$$\begin{aligned} f_1(z,\varvec{v})= & {} \gamma (C_v)-1+\min \sum \limits _{k\in C{\setminus } C_{\varvec{v}}}\left( \gamma _kx_k+\frac{m_k}{{\varGamma }}y_k\right) \\&s.t.\quad \sum \limits _{k \in C{\setminus } C_{\varvec{v}}}\left( \xi _kx_k+m_ky_k\right) \ge z+{\varGamma }-\xi (C_v) \\&\qquad 0 \le y_k \le x_k,\,x_k\in \{0,1\}\, \forall k \in C{\setminus } C_{\varvec{v}}. \end{aligned}$$

Now we define \(C^+=\{k\in C:\xi _k>{\varGamma }\}, s=\sum _{k\in \left( C{\setminus } C^+\right) {\setminus } C_{\varvec{v}}}\left( \xi _kx_k+m_ky_k\right) +\sum _{k\in C^+{\setminus } C_{\varvec{v}}}m_ky_k\), discard the inequality \(y_k\le x_k\) and the integrality condition of \(x_k\) for \(k\in \left( C{\setminus } C^+\right) {\setminus } C_{\varvec{v}}\) to obtain the following relaxation:

$$\begin{aligned} \tilde{f}(z,\varvec{v})= & {} \gamma (C_{\varvec{v}})-1+\min \sum \limits _{k\in C^+{\setminus } C_{\varvec{v}}}x_k+\frac{s}{{\varGamma }}\nonumber \\&s.t.\quad \sum \limits _{k\in C^+{\setminus } C_{\varvec{v}}}\xi _kx_k+s\ge z +{\varGamma }-\xi (C_{\varvec{v}})\nonumber \\&\qquad \; \; 0\le s,\,x_k\in \{0,1\},\,\forall k\in C^+{\setminus } C_{\varvec{v}}. \end{aligned}$$
(9)

Note that, under mild conditions,Footnote 1 \(f_1(z,\varvec{v})\) is equivalent to \(\tilde{f}\).

Now, we will prove that \(\tilde{f}\) has a closed form, and then we will prove that it is also superadditive in an appropriated domain.

Proposition 4

By renaming \(C^+{\setminus } C_{\varvec{v}}=\{1,\ldots ,r_{\varvec{v}}\}\) while ensuring that \(\xi ^{\varvec{v}}_h\ge \xi ^{\varvec{v}}_{h+1}\), defining \(\Lambda _{h}^{\varvec{v}}=\xi (C_{\varvec{v}})+\sum _{i< h}\xi ^{\varvec{v}}_i\), and defining \(H(z)=0\) if \(z\le 0\) and \(H(z)=1\) if \(z>0\), we have

$$\begin{aligned} \tilde{f}(z,\varvec{v})=\gamma (C_{\varvec{v}})-1+\frac{s^*}{{\varGamma }}+\sum \limits _{h=1}^{r_{\varvec{v}}}H\left( z-s^*-\Lambda _h^{\varvec{v}}+{\varGamma }\right) , \end{aligned}$$
(10)

where

$$\begin{aligned} s^*= & {} \left( z-\Lambda _{r_{\varvec{v}+1}}^{\varvec{v}}+{\varGamma }\right) H\left( z-\Lambda _{r_{\varvec{v}+1}}^{\varvec{v}}+{\varGamma }\right) \\&+\sum \limits _{h=1}^{r_{\varvec{v}}}\left( z-\Lambda _h^{\varvec{v}}\right) \left( H(z-\Lambda _h^{\varvec{v}})-H({\varGamma }+\Lambda _h^{\varvec{v}}-z)\right) . \end{aligned}$$

Moreover, the optimal solution for \(x\) is given by \(x^*_h=H(z-s^*-\Lambda _h^{\varvec{v}}+{\varGamma }),\,\forall h=1,\ldots ,r_{\varvec{v}}\).

Proof

Using the definition of \(\tilde{f}(z,\varvec{v})\) given in (9), if we consider \(z\ge \Lambda _{r_{\varvec{v}}+1}^{\varvec{v}}-{\varGamma }\); the solution of the continuous relaxation is also integer-feasible (with \(x^*_i=1\) for all \(i\in C^+{\setminus } C_{\varvec{v}}\)); from where we have that \(s^*=z-\Lambda _{r_{\varvec{v}}+1}^{\varvec{v}}+{\varGamma }\) and \(z-s^*-\Lambda _{h}^{\varvec{v}}+{\varGamma }=\Lambda _{r_{\varvec{v}}+1}^{\varvec{v}}-\Lambda _h^{\varvec{v}}>0\); thus proving our result for this case.

If we now consider \(z<\Lambda _{r_{\varvec{v}}+1}^{\varvec{v}}-{\varGamma }\) and restrict ourselves to solutions where \(s=0\); the resulting problem has an optimal solution given by

$$\begin{aligned} x_h=H(z+{\varGamma }- \Lambda _i^{\varvec{v}}),\quad \forall h=1,\ldots ,r_{\varvec{v}}, \end{aligned}$$

whence (10) is directly obtained.

To compute \(\tilde{f}(z,\varvec{v})\), consider first a simpler optimization problem:

$$\begin{aligned} q(z) = \min \limits _{s\ge 0} \left\{ g(z,s):=\frac{s}{b} + aH(z-s) \right\} \ge 0. \end{aligned}$$

Note that if \(s\ge ab\), then \(g(z,s)\ge g(z,0)=aH(z)\), thus proving that we can restrict ourselves to \(s\in [0,ab]\). We now compute \(q(z)\) by identifying three cases:

  • Case 1 If \(z\le 0\), we have

    $$\begin{aligned} \left. \frac{s}{b} + aH(z-s)\right| _{s=0}=0<\left. \frac{s}{b} + aH(z-s)\right| _{0<s\le ba} \quad \Rightarrow \quad q(z)=0,\quad s^*=0 \end{aligned}$$

  • Case 2 If \(z>ba\), we have

    $$\begin{aligned} \left. \frac{s}{b} + aH(z-s)\right| _{s=0}=a<\left. \frac{s}{b} + aH(z-s)\right| _{0<s\le ba} \quad \Rightarrow \quad q(z)=a,\quad s^*=0 \end{aligned}$$

    because \(z-s>0\).

  • Case 3 If \(0<z\le ba\), we can select \(s^*=z\) and we have

    $$\begin{aligned} \left. \frac{s}{b} + aH(z-s)\right| _{s=0}=a\ge \left. \frac{s}{b} + aH(z-s)\right| _{s=s^*} \quad \Rightarrow \quad q(z)=\frac{z}{b},\quad s^*=z. \end{aligned}$$

We can now write

$$\begin{aligned} \tilde{f}(z,{\varvec{v}})=\gamma (C_{\varvec{v}})-1+\min \limits _{s\ge 0}\left\{ \frac{s}{{\varGamma }}+\sum \limits _{h=1}^{r_{\varvec{v}}} H\left( z-s-\Lambda _h^{\varvec{v}}+{\varGamma }\right) \right\} , \end{aligned}$$
(11)

Note that

$$\begin{aligned} \tilde{f}(z,{\varvec{v}})\ge \gamma (C_{\varvec{v}})-1+ \min \limits _{h=1}^{r_{\varvec{v}}}\left\{ \min \limits _{s\ge 0} \left\{ \frac{s}{{\varGamma }}+H(z-s-\Lambda _h^{\varvec{v}}+ {\varGamma })\right\} \right\} . \end{aligned}$$
(12)

Using the optimal solution and values computed for \(q(z)\); we see that the optimal solution \(\{s^*_h\}_{h=1}^{r_{\varvec{v}}}\) for the lower bound (12) is either the all-zero vector, or it is the case that exactly one component, say \(h^*\), is non-zero and is in the range \(]0,{\varGamma }]\). In the first case, setting \(s=0\) in (11), we attain the lower bound, and thus solve the problem. In the second case, we have \(0\le s^*=z-\Lambda _{h^*}^{\varvec{v}}\le {\varGamma }\). Since \(\xi _h>{\varGamma }\), for \(h\ne h^*, H(z-\Lambda _h^{\varvec{v}}+{\varGamma })=H(z-s^*_{h^*}-\Lambda _h^{\varvec{v}}+{\varGamma })\), thus proving that setting \(s=s^*_h\) in (11) is a feasible solution that attains the lower bound. \(\square \)

Theorem 2

The function \(\tilde{f}(z,\varvec{v})\) is superadditive for \((z,\varvec{v})\in [0,+\infty )\times \{0,1\}^G\).

Proof

Note that \(\tilde{f}(z,\varvec{0})\) is exactly the superadditive function defined in [10]. Namely,

$$\begin{aligned} \tilde{f}(z,\varvec{0})=\left\{ \begin{array}{lll} -1&{}\quad z\le -{\varGamma }\\ \left( z-\Lambda _i\right) /{\varGamma }+i-1 &{}\quad \Lambda _i-{\varGamma }\le z\le \Lambda _i,\,&{}\quad \forall i=1,\ldots ,r-1\\ i-1&{}\quad \Lambda _i\le z\le \Lambda _{i+1}-{\varGamma },\,&{}\quad \forall i=1,\ldots ,r\\ \left( z-\Lambda _r\right) /{\varGamma }+r-1 &{}\quad \Lambda _r-{\varGamma }\le z\le b \end{array}\right. \end{aligned}$$

We propose a different proof for this more general case.

We start with \(\tilde{f}(z_1,\varvec{0})+\tilde{f}(z_2,\varvec{0})\le \tilde{f}(z_1+z_2,\varvec{0})\):

Let \(\{x^o_h\}_{h=1}^{r_{\varvec{v}}},s^o\) be the optimal solution of \(\tilde{f}(z_1+z_2,\varvec{0})\), defined as in Proposition 4, and \(\{x^1_h\}_{h=1}^{r_{\varvec{v}}},s^1\) be the optimal solution of \(\tilde{f}(z_1,\varvec{0})\). By construction, \(x^o\ge x^1\), and assume that \(h_o^*,h_1^*\in \{0,\ldots ,r_{\varvec{v}}\}\) are the last active elements in \(x^o,x^1\) respectively.

We prove this by analyzing two cases:

Case a \(\xi \cdot x^1+s^1={\varGamma }+z_1\):

Define \(x^2_h=x^o_{h+h^*_1}\) for \(h\le h^*_o-h^*_1, x^2_h=0\) for \(h>h^*_o-h^*_1\) and \(0\le s^2={\varGamma }+s^o-s^1\). By construction and Proposition 4, we have \(\tilde{f}(z_1+z_2,\varvec{0})=\tilde{f}(z_1,\varvec{0})+\mathbb {I}\cdot x^2+s^2/{\varGamma }-1\), where \(\mathbb {I}\) is the vector of all ones of the appropriate dimension. Thus, it is enough to prove that \((x^2,s^2)\) is feasible for (9). However, by hypothesis, we have \({\varGamma }+z_2\le \xi (x^o-x^1)+(s^o-s^1)+{\varGamma }\le \xi x^2+s^2\), thus proving our result.

Case b \(\xi \cdot x^1+s^1>{\varGamma }+z_1\):

In this case, by optimality, \(s^1=0\) and \(\xi x^1=\Lambda _{h^*_1+1}^0\). Define \(x^2_h=x^o_{h+h^*_1-1}\) for \(h\le 1+ h^*_o-h^*_1, x^2_h=0\) for \(h\ge 2+h^*_o-h^*_1\) and \(s^2=s^o\). By construction, we have \(\tilde{f}(z_1+z_2,\varvec{0})=\tilde{f}(z_1,\varvec{0})+\mathbb {I}\cdot x^2+s^2/{\varGamma }-1\). Thus, is enough to prove that \((x^2,s^2)\) is feasible for (9). However by hypothesis, we have \(z_1\ge \Lambda ^0_{h^*_1}-{\varGamma }\), whence \({\varGamma }+z_2\le \xi x^o+s^o-z_1\le \xi (x^o-x^1)+\xi _{h^*_1}+ s^2\le \xi x^2+s^2\), thus proving our result. This concludes Case 1.

The cases \(\tilde{f}(z_1+z_2,e_i)\) and \(\tilde{f}(z_1+z_2,e_i+e_j)\) are analogous. \(\square \)

Corollary 1

If, for each pair of variables \((x_{k},y_{k})\), where \(k=(g,j)\), we choose lifting coefficients \((\alpha _k,\beta _k)\) such that \(h_{k}(z,u)\le \tilde{f}(z,u\varvec{e_{g}})\) for \((z,u)\in \{([a_{k},a_{k}+m_{k}],1), (0,0)\}\); then the lifting process is sequence-independent.

Proof

We only need to prove validity at any intermediate step \(r\), and call \(L^r\) the set of variables (not in \(C\)) lifted at step \(r\). That is, we need to prove that

$$\begin{aligned} \begin{array}{lll} \max &{}\displaystyle \sum \limits _{k\in C}\left( \gamma _kx_k+\frac{m_k}{{\varGamma }}(y_k-x_k)\right) +\sum \limits _{k\in L^r}^r\left( \alpha _rx_r+\beta _ry_r\right) \\ s\displaystyle .t. &{} \sum \limits _{k\in C\cup L^r}\left( \xi _jx_j+m_j\left( y_j-x_j\right) \right) \le b\\ &{}\displaystyle \sum \limits _{k\in M_g^r}x_{k}\le 1&{}\forall g\in G\\ &{}\displaystyle 0\le y_k\le x_k,\,x_k\in \{0,1\}&{}\forall k\in C\cup L^r,\\ \end{array} \end{aligned}$$
(13)

where \(M_g^r=\{(g',j)\in C\cup L^r:g'=g\}\) is less than or equal to \(\gamma (C)-1\). Note that by hypothesis, \(\alpha _kx_k+\beta _ky_k\) \(=\) \(h(\xi _kx_k+m_k(y_k-x_k),x_k)\) \(\le \) \(\tilde{f}(\xi _kx_k+m_k(y_k-x_k),x_ke_{g(k)}), \forall k\in L^r\). Using this, Eq. (13) can be re-written as

$$\begin{aligned} \begin{array}{lll} \displaystyle \max &{}\displaystyle \sum \limits _{k\in C}\left( \gamma _kx_k+\frac{m_k}{{\varGamma }}(y_k-x_k)\right) \\ &{}\displaystyle +\sum \limits _{k\in L^r}^r\tilde{f}\left( \xi _kx_k+m_k(y_k-x_k),x_kg(k)\right) \\ s.t. &{}\displaystyle \sum \limits _{k\in C\cup L^r}\left( \xi _jx_j+m_j\left( y_j-x_j\right) \right) \le b\\ &{}\displaystyle \sum \limits _{k\in M_g^r}x_{k}\le 1&{}\forall g\in G\\ &{}\displaystyle 0\le y_k\le x_k,\,x_k\in \{0,1\}&{}\forall k\in C\cup L^r,\\ \end{array} \end{aligned}$$
(14)

where \(g((g',j'))=g'\) for \(k=(g'j')\). By defining \(z_g\!=\!\sum _{k\in L^r}\left( \xi _kx_k+m_k\left( y_k-x_k\right) \right) , \delta _g=\sum _{k\in L^r\cap M_g}x_k\), and \(M_g=\{(g',j')\in M:g'=g\}\), we bound (14) above by the following expression:

$$\begin{aligned} \begin{array}{lll} \max &{}\displaystyle \sum \limits _{k\in C}\left( \gamma _kx_k+\frac{m_k}{{\varGamma }}\left( y_k-x_k\right) \right) \\ &{}\displaystyle +\sum \limits _{g\in G}^r\tilde{f}\left( z_g,\delta _ge_g\right) \\ s.t. &{}\displaystyle \sum \limits _{k\in C}\left( \xi _jx_j+m_j\left( y_j-x_j\right) \right) +\sum \limits _{g\in G}z_g\le b\\ &{}\displaystyle \sum \limits _{k\in M_g\cap C}x_{k}\le 1-\delta _g&{}\forall g\in G\\ &{}\displaystyle 0\le z_g\le b\delta _g,\,\delta _g\in \{0,1\}&{}\forall g\in G\\ &{}\displaystyle 0\le y_k\le x_k,\,x_k\in \{0,1\}&{}\forall k\in C.\\ \end{array} \end{aligned}$$
(15)

Note that by the definition of \(C\), we have \(|C\cap M_g|\in \{0,1\}, \forall g\in G\). We set \(G^o=\{g\in G:|C\cap M_g|=0\}\), define \(z_o=\sum _{g\in G^o}z_g\), and identify \(C\) with \(G{\setminus } G^o\). With this, Eq. (15) is equivalent to

$$\begin{aligned} \begin{array}{lll} \max &{}\displaystyle \sum \limits _{g\in G{\setminus } G^o}\left( \gamma _gx_g+m_g\left( y_g-x_g\right) \right) \\ &{}\displaystyle +\tilde{f}(z_o,0)+\tilde{f}(z_g,\delta _ge_g)\\ s.t. &{}\displaystyle z_o+\sum \limits _{g\in G{\setminus } G^o}\left( \xi _gx_g+m_g\left( y_g-x_g\right) \right) +z_g\le b\\ &{}\displaystyle x_g\le 1 -\delta _g&{}\forall g\in G{\setminus } G^o\\ &{}\displaystyle 0\le z_g\le b\delta _g,\,\delta _g\in \{0,1\}&{}\forall g\in G{\setminus } G^o\\ &{}\displaystyle 0\le y_g\le x_g,\,x_g\in \{0,1\}&{}\forall g\in G{\setminus } G^o\\ &{} 0\le z_o\le b. \end{array} \end{aligned}$$
(16)

Using that \(\delta \in \{0,1\}^{G{\setminus } G^o}\) and the definition of \(\tilde{f}(z,\delta )\); we can bound (16) as

$$\begin{aligned} \begin{array}{lll} \max &{}\displaystyle \gamma (\delta )-1-\tilde{f}(\sum \limits _{g\in \{o\}\cup G{\setminus } G^o}z_g,\delta )\\ &{}\displaystyle +\,\tilde{f}(z_o,0)+\sum \limits _{g\in G{\setminus } G^o}\tilde{f}(z_g,\delta _g)\\ s.t. &{}\displaystyle \sum \limits _{g\in \{o\}\cup G{\setminus } G^o}z_g\le b\\ &{} 0\le z_g\le b\delta _g,\,\delta _g\in \{0,1\}&{}\forall g\in \{o\}\cup G{\setminus } G^o.\\ \end{array} \end{aligned}$$
(17)

Finally, by using the superadditivity of \(\tilde{f}\), we bound (17) by

$$\begin{aligned} \max \left\{ \gamma (\delta )-1:\delta \in \{0,1\}^{G{\setminus } G^o}\right\} ={\varGamma }(C)-1. \end{aligned}$$
(18)

which proves our result. \(\square \)

3.3 Algorithmic separation

The foregoing results show that we can use \(\tilde{f}(z,\varvec{v})\) to find valid lifting coefficients for GFC inequalities for SCKPGUB; and thus obtain strong inequalities for \(X_G\).

In this subsection we deal with the separation problem of such lifted inequalities. More precisely, given \(x^*\) as a fractional solution in the linear programming (LP) relaxation of (1), we try to find a violated lifted constraint. We address this problem in two stages: we first show how to lift a candidate inequality, and then propose a heuristic to identify a candidate seed inequality. Finally, we only keep strictly violated inequalities.

figure a

3.3.1 Lifting GUB-constrained flow cover inequalities

It is important to note that for each pair of lifted variables \(y_k,x_k, k\in M{\setminus } C\); there are several maximal pairs of coefficients \(\alpha _k,\beta _k\) satisfying \(h_k(z,x_k)\le \tilde{f}(z,x_ke_{g(k)})\). This implies that the number of possible lifted inequalities derived by this method can be exponential. Fortunately, Algorithm 1 provides a complete description of all pairs of maximal lifting coefficients; and its complexity is \(\mathcal {O}(|C|)\). Moreover, we perform this process once, before performing any lifting step. Figure 1 shows an example for \(\tilde{f}(z,\varvec{v})\) and its lower envelope (for a given range \([a,b]\)), which also shows how some key variables of the algorithm change from iteration to iteration.

Fig. 1
figure 1

Example \(\tilde{f}(z,\varvec{v})\), and a lower envelope for given \(a,b\)

Full size image

It follows that a proper method to choose the (set of) inequalities to be used is crucial and it should depend on the fractional values of the current fractional point \(x^{*},y^*\). If we want to maximize the resulting violation of the lifted inequality, a possible criterion is to choose \((\alpha ^{*},\beta ^{*})\in \hbox {argmax}\{x^{*}_k\alpha +y^{*}_k\beta :(\alpha ,\beta )\in \mathcal {H}\}\), where \(\mathcal {H}\) is the set of maximal lifting coefficients. In our implementation, we choose \(\alpha ^{*},\beta ^{*}\) as defined before, as long as \(x_k^{*}\alpha ^{*}+y_k^{*}\beta ^{*}>0\); otherwise, we take \((\alpha ^{*},\beta ^{*})\in \hbox {argmax}\{\alpha +\beta :(\alpha ,\beta )\in \mathcal {H}\}\).

3.3.2 Finding generalized flow cover inequalities in proper faces of \(X_G\)

Finding maximally violated cover inequalities is already \(\mathcal {N}\mathcal {P}\)-hard [10]. Although it is possible to formulate the separation problem of generalized flow cover inequalities as an IP; we propose a simple heuristic described in Algorithm 2, this heuristic is a simple extension of other classical heuristics [11] to find maximally violated cover inequalities.

In this heuristic, for each GUB constraint \(g\in G\), we compute the net contribution of the current fractional solution \(x^{*},y^*\) to the knapsack constraint \(a\cdot x^{*}+m\cdot y^{*}\le b\). We call this net contribution \(z_g\). If the current GUB constraint is inactive (\(z_g=0\)) we discard it from \(C\). Otherwise, we identify the segment (called \(\bar{k}_g\in M_g\)), whose boundary is closest to \(z_g\), and add it to \(C\). If the closest boundary is the upper limit of the segment we also add that segment to \(C_U\). This process can be seen as a greedy construction heuristic. The final step is a local search procedure [1] whose objective is to maximize the likelihood that the resulting inequality will be violated. In our implementation 1-OPT evaluate whether adding or deleting any element from \(C\) and/or \(C_U\) improves the value of \(\sum _{k\in C}\gamma _k(x^{*}_k-1)\) while maintaining the condition that \((C,C_U)\) is a GFC. If so, we perform the change; otherwise we evaluate the next element. We repeat this process until no further improvements are found.

figure b

4 Numerical experiments

In this section we provide partial evidence on the effect of using the resulting set of lifted inequalities. We test the effect of using only the seed inequality and other simple heuristic methods. We also show the effect of the heuristic separation of the seed inequality. For this, we first describe a wide range of instances; then the set of experiments; and also an analysis of closed gapFootnote 2 with respect to the size of the problem.

4.1 Instances

To evaluate the performance of the inequalities presented in this paper, we consider a set of 3000 random instances inspired by the unit commitment problem. We also assume that the GUB structure and semi-continuous variables are already identified. In these instances, \(|G|\in \{5,10,20,40,80\}\) and the number of elements in each GUB constraint were randomly chosen as \(|M_g|\sim \{\mathcal {U}[2,8],\mathcal {U}[7,13],\mathcal {U}[17,23]\}\). \(a_j\sim \mathcal {U}[10,150],m_j\sim \mathcal {U}[20,300], \forall j\in M, b\sim \mathcal {U}[0.25,0.95]b_{\max }\), where \(b_{\max }=\) is the maximum value of the left-hand side of the knapsack constraint. We chose the cost coefficients as \(c_k^x\sim 2500a_k-\mathcal {U}[370,1000]-\mathcal {U}[15,50]a_k, c_k^y\sim 2500m_k-\mathcal {U}[15,50]m_k, \forall k\in M\); which represent typical cost functions in unit commitment instances. To evaluate the effect of having \(m_k=0\); half of the instances contain GUB constraints where \(m_k=0\) for 40 % of the elements in each GUB constraint.

4.2 Quality measures

We use performance profiles (see [7]) on two quality measures: closed root gap (CG) and closed relative gap (CRG), which we define as

$$\begin{aligned} {\textit{CG}} = 100 \times \frac{z_{{{\textit{LP}}_n}}-z_{{{\textit{LP}}_o}}}{z_{\textit{MIP}}-z_{{{\textit{LP}}_o}}}, \quad {\textit{CRG}} = 100 \times \frac{z_{{{\textit{LP}}_n}}}{z_{\textit{MIP}}}, \end{aligned}$$

where \(z_{\textit{MIP}}\) is the optimal objective value of the mixed integer problem; \(z_{{{\textit{LP}}_o}}\) is the optimal objective value of the original linear relaxation; and \(z_{{{\textit{LP}}_n}}\) is that of the final LP relaxation. Note that for all our instances, \(z_{{\textit{LP}}_o}<z_{\textit{MIP}}\), and \(z_{\textit{MIP}}>0\). Thus, when computing CG, we never divide by zero. CRG is an approximation of the reported gap when using any commercial mixed-integer programming (MIP) solver (which might be more relevant for practitioners). CG is the actual improvement in the lower bound due to the given method (which is a proxy for the extent to which we improve the polyhedral representation of the given set for the given objective function).

We do not report running times because the separation process is quick in all instances and the number of calls of the separation heuristic is always less than fourteen. We do not evaluate branch and bound performance because our instances are exactly those of a single \(X_G\) problem and are always easy to solve; whereas unit commitment problems can have between 24 and 336 sub-structures of this sort in addition to other side constraints. This is why we chose to leave this study for a future work.

4.3 The experiments

4.3.1 The general cutting scheme

In each case, we apply the cutting scheme described in Algorithm 3.

figure c

This scheme can be seen as a basic cutting loop at the root node. We will evaluate the following variations of this scheme:

  • IP: Separation of GFC seed inequality by solving an integer program that maximizes the violation of the resulting GFC inequality (if any) without lifting.

  • IP+Lift: The same as before, except that we lift the resulting inequality as described in (5).

  • Heu: We execute Algorithm 2 without performing step 9 and use the resulting inequality (i.e., no lifting step is carried out).

  • Heu+1-opt: We execute Algorithm 2 and use the resulting inequality (i.e., no lifting step is performed).

  • Heu+1-opt+Lift: We execute Algorithm 3.

  • Heu+Lift: We execute Algorithm 2 without performing step 9 and lift the resulting inequality as described in (5).

4.3.2 Effectiveness of the separation heuristic

Figure 2a, b shows the performance profiles of CG and for CRG in 600 instances with five GUB constraints where we can solve the IP-separation of the base GFC inequality. Figure 3a, b shows the performance profiles of CG and CRG for all 3000 instances.Footnote 3 Table 1 lists a summary of these results.

Fig. 2
figure 2

Top CG performance profile; bottom CRG performance profile; for instances with \(|G|=5\)

Full size image
Fig. 3
figure 3

Top CG performance profile; bottom CRG performance profile; for all instances

Full size image
Table 1 Summary results of experiments of the average CG, CRG, and number of cuts, for small and all instances for all algorithm variations
Full size table

From these results it is clear that measured by either CRG or CG, Heu+1-opt performs very close to the IP separation of the base heuristic on the set of small instances while maintaining its edge over the basic heuristic for all instances. This, In addition to the excessive running time cost of an exact separation routine, justifies the use of the proposed method for evaluation purposes; however, any practical implementation should address this matter in much greater detail.

4.3.3 Robustness of the results

The robustness of the results given the size of the instances is an important consideration. For this, we categorize our instances according to the number of GUB constraints (\(|G|\)) and the number of elements in each GUB constraint (\(|M_g|\)), and calculate the average CG and CRG for Heu+1-opt+Lift. Figure 4 is a graphical representation of the variation in the average \(CR\) and CRG values given these two criteria. Although we expected that CG performance deteriorates as we increase the number of GUB constraints and the number of elements in each GUB; it is surprising that this tendency is reversed for CRG. This might be due to the special cost structure used in these instances. However, if this result holds at a larger scale as well, the fact that the final relative integrality gap decreases can be beneficial.

Fig. 4
figure 4

Left average CG for categorized instances; right average CRG for categorized instances

Full size image

4.3.4 The effect of lifting

As noted in Sect. 3, our seed inequality is already valid for \(X_G\). From this, a natural question is how much do we gain by performing the lifting process? Table 1 clearly represents this aspect. If we measure CG, the effect is a 15–20 % larger closed root gap, and 0.5–4 % more CRG. Moreover, in all variations of our cutting scheme where lifting was carried out, there were only two instances where we could not find a cut. For variations without lifting, we could not find cuts for 2167 instances using Heu and 174 instances when using Heu+1-opt. This shows a strong lifting effect.

4.3.5 Number of added cuts

A common problem with cutting schemes is that they may require too many cutting rounds to achieve the desired quality. Surprisingly, in our experiments, we added an average of 2.14 cuts to all instances; in 92.2 % of instances, we added up to three cuts; for 99.33 % of instances, we added up to six cuts. In the worst case, we added 14 cuts.

5 Final comments

In this paper, we studied sequence-independent multidimensional lifting of generalized flow cover inequalities to obtain strong inequalities for the so-called semi-continuous knapsack problem with GUB constraints. We also proved that under mild assumptions, the starting inequality is facet-defining on a face of our polyhedron. Moreover, with simple assumptions, we showed that the sequence-independent lifting function is indeed the optimal (maximal) lifting function which, together with the previous result, enabled us to obtain high-dimensional facets. Unlike one-dimensional lifting, in our setting, the superadditive lifting function defines a large class of valid inequalities. This introduces the problem of selecting the inequality to be added. In our study, we chose the inequality to be added by maximizing the resulting violation. We used a set of 3000 randomly generated instances of different sizes to conduct our experiments. These experiments show that although the separation problem is \(\mathcal {N}\mathcal {P}\)-hard, using simple heuristics and superadditive lifting function, it is possible to close, on average, 57.70 % of the root integrality gap and 97.70 % of the relative gap.

There remain several open issues, some of them are:

  • Can we take advantage of GUB-partitioned binary variables in other polyhedral sets to find tight valid inequalities?

  • In our setting, can we extend our analysis to the case where \(a_k\) might be negative?

  • Is it possible to efficiently detect the basic GUB and the semi-continuous structure in general problems?

  • Even if we are given the GUB constraints; can we use the proposed methodology in general problems?

  • Other relevant questions relate to the selection of the seed inequality, and whether we should simultaneously use several seed inequalities that can better complement each other when we add them to the current LP relaxation.

  • Can we prove that some class of seed inequalities are always dominated by others?

  • More precisely, should we take only a minimal GFC, or is it better to add small elements to the cover?

  • Are our results too specific for instances derived from the unit commitment problem?

We think that all these questions are relevant to the practical use of the proposed inequalities, and we hope to tackle them in the near future.