Thermal field and tissue damage analysis of moving laser in cancer thermal therapy

Abstract

In this paper, a closed-form analytical solution of hyperbolic Pennes bioheat equation is obtained for spatial evolution of temperature distributions during moving laser thermotherapy of the skin and kidney tissues. The three-dimensional cubic homogeneous perfused biological tissue is adopted as a media and the Gaussian distributed function in surface and exponentially distributed in depth is used for modeling of laser moving heat source. The solution procedure is Eigen value method which leads to a closed form solution. The effect of moving velocity, perfusion rate, laser intensity, absorption and scattering coefficients, and thermal relaxation time on temperature profiles and tissue thermal damage are investigated. Results are illustrated that the moving velocity and the perfusion rate of the tissues are the main important parameters in produced temperatures under moving heat source. The higher perfusion rate of kidney compared with skin may lead to lower induced temperature amplitude in moving path of laser due to the convective role of the perfusion term. Furthermore, the analytical solution can be a powerful tool for analysis and optimization of practical treatment in the clinical setting and laser procedure therapeutic applications and can be used for verification of other numerical heating models.

Introduction

The non-invasive thermal therapy has some advantages for reduction of physical, emotional, and financial impacts on the cancer patient, which main of them are low cost, minimal scarring, less pain, and shorter hospitalization time [1]. The thermal therapy method is chosen depending on cancer tumor location, stage, or whether it became resistant to the ongoing treatment. There are some challenges to select the heating power of cancer cells without damaging the surrounding tissue; therefore, obtaining appropriate temperature distribution is an important issue. Developing effective strategies to treat cancer has been an important task in the field of medical research. The mathematical models can play a vital role in providing significant information to the clinical practitioners about the possible outcomes and risks involved before the onset of thermotherapy cancer treatment. The applications of simple bioheat equation comprise simulations of hyperthermia [2], cryosurgery [3,4,5], thermal parameter estimation [6, 7], radiofrequency ablation [8, 9], laser thermotherapy [10,11,12,13,14,15,16,17], and microwave ablation [18, 19] for estimating temperature profiles and thermal parameters of perfused tissues. In these medical problems, heat transfer analysis needs to simultaneously deal with transient and spatial heating both on the biological tissues. Up to now, several bioheat transfer models have been suggested by researchers [20]. One of the most distinguished and earliest bioheat models is the Pennes bioheat equation, which is declared the parabolic natured bioheat transfer equation in 1948 [21]:

$$ \frac{\mathrm{\partial T}}{\mathrm{\partial t}}=\upalpha {\nabla}^2\mathrm{T}+\frac{\uprho_{\mathrm{b}}{\upvarpi}_{\mathrm{b}}{\mathrm{C}}_{\mathrm{b}}}{\uprho_{\mathrm{t}}{\mathrm{c}}_{\mathrm{t}}}\left({T}_{\mathrm{b}}-T\right)+\frac{Q}{\uprho_{\mathrm{t}}{\mathrm{c}}_{\mathrm{t}}} $$

(1)

Where, Q is the heat source term, ρ_t and C_t refer to density and specific heat of tissue, ρ_b, ϖ_b, and C_b are the density, the perfusion rate per unit volume of tissue, and the specific heat of blood, respectively, α is thermal diffusivity and T_b is the blood temperature. Heat transfer modeling must consider both of temperature changes and impact of blood flow which acts as a heat sink and influences the temperature field in the vicinity of the vessels. The main idea of the Pennes bioheat equation is to apply the effect of blood convective heating or cooling in live tissues as the perfusion term in conduction equation. Perfusion plays an important role in the local transport of oxygen, nutrients, pharmaceuticals, and heat through the body.

The Fourier heat conduction equation is acceptable for most engineering applications; however, it estimates the infinite speed of thermal propagation which is physically unrealistic. Hence, it has been modified and more complex models have been introduced. A relaxation time is considered between heat flux and temperature gradient in non-Fourier or hyperbolic heat transfer equation (HHTE) which leads to finite speed and wave behavior of heat propagation [22]. The relaxation time has an important influence on the transient temperature and temperature gradient. At first, the modified heat flux model is introduced in the following form by Cattaneo and Vernotte [23]:

$$ \mathrm{q}+{\uptau}_{\mathrm{q}}\frac{\partial \mathbf{q}}{\mathrm{\partial t}}=-\mathrm{k}\nabla \mathrm{T} $$

(2)

Where q is the heat flux vector, τ_q is the thermal relaxation time which shows the delay between heat flux and temperature gradient, and k is the material thermal conductivity. It is known that$\kern0.5em w=\sqrt{\upalpha_{\mathrm{t}}/{\uptau}_{\mathrm{q}}}$ denotes the propagation speed of temperature wave, where ${\upalpha}_{\mathrm{t}}=\frac{\mathrm{k}}{\uprho \mathrm{c}}$ is the material thermal diffusivity. Due to long-thermal relaxation time of biological tissue, the non-Fourier model becomes more reliable for depicting the propagation process and estimating the temperature distribution than the classical Fourier one. Thus, the hyperbolic Pennes bioheat equation is introduced and applied in the literature as follows [24, 25]:

$$ {\uptau}_{\mathrm{q}}\frac{\partial^2\mathrm{T}}{\partial {\mathrm{t}}^2}+\left(1+{\uptau}_{\mathrm{q}}\frac{\uprho_{\mathrm{b}}{\upvarpi}_{\mathrm{b}}{\mathrm{C}}_{\mathrm{b}}}{\uprho_{\mathrm{t}}{\mathrm{c}}_{\mathrm{t}}}\right)\frac{\mathrm{\partial T}}{\mathrm{\partial t}}={\upalpha}_{\mathrm{t}}{\nabla}^2\mathrm{T}+\frac{\uprho_{\mathrm{b}}{\upvarpi}_{\mathrm{b}}{\mathrm{C}}_{\mathrm{b}}}{\uprho_{\mathrm{t}}{\mathrm{c}}_{\mathrm{t}}}\left({T}_{\mathrm{b}}-T\right)+\frac{1}{\uprho_{\mathrm{t}}{\mathrm{c}}_{\mathrm{t}}}\left({\uptau}_{\mathrm{q}}\frac{\mathrm{\partial Q}}{\mathrm{\partial t}}+\mathrm{Q}\right) $$

(3)

Clearly, considering τ_q = 0 leads to the special case of above equation which corresponds to the Fourier or parabolic heat transfer. In recent years, the solutions of parabolic and hyperbolic Pennes bioheat Eqs. (1) and (3) are focused by researchers.

Thermal conduction and convection of tissues, blood perfusion, metabolism heat generation, and changing of the tissue properties are some of the features that make hard to obtain an accurate knowledge of heat transfer of living systems for all the thermal clinical therapies [26]. Hence, due to the complexity of the boundary conditions and irradiated flux, the most solutions of Eqs. (1) and (3) are numerical. For example, Xu et al. [27] surveyed previous researches on the parabolic, hyperbolic, and dual phase lag (DPL) models of bioheat transfer processes and developed a numerical solution for single layer one-dimensional skin tissue model under uniform heat source. Zhou et al. [28] considered DPL model on Pennes bioheat equation to investigate thermal damage of laser-irradiated biological tissues numerically. They found that hyperbolic model has a significant difference in estimation of temperature compared with Fourier one. Ströhers [29] used numerical methods to solve the parabolic and hyperbolic Pennes bioheat equation of the skin tissue transient temperature and burn injury distributions.

Since finite element method (FEM) is a domain-based numerical technique which requires discretizing the entire computational media, it has some disadvantages like that large computational costs (memory and CPU time) for complex bioheat problems. Consequently, a theoretical model is needed that not only has a good adaptability to complex tumor shapes but also is computationally efficient. Therefore, Askarizadeh and Ahmadikia [30] derived analytical solution of the parabolic and hyperbolic bioheat transfer equation for two-dimensional skin tissue under instantaneous surface heating boundary condition using Laplace transform and separation of variables. Lee et al. [31] studied the hyperbolic heat conduction equation of the skin tissue with an inverse algorithm to determine tissue temperature profiles under the unknown time-dependent surface heat flux based on the temperature measurements. Jaunich et al. [32] analyzed the temperature distributions and heat-affected zone of skin tissue during short-pulse laser beam exposure. They used hyperbolic and parabolic bioheat equations for modeling and verified the results of hyperbolic model by comparing them with experimental results of a multi-layer tissue. Talaee and Kabiri [33] solved the hyperbolic bioheat equation of radiofrequency heating (RFH) technique in spherical coordinates using Eigen value method and introduced closed-form solutions. Also, they [34] presented the analytical solution of parabolic Pennes bioheat equation under concentric moving heat source for one-dimensional non-homogeneous layer of biological tissue with blood perfusion term. Brix et al. [35] investigated thermal response of radiofrequency exposure during magnetic resonance (MR) procedures and introduced analytical solution for the parabolic Pennes bioheat equation using the Green’s function. Ahmadikia et al. [36] solved the one-dimensional Fourier and non-Fourier bioheat transfer equation under laser heating using the Laplace transform method. Liu [37] investigated the hyperbolic Pennes bioheat equation to study the thermal behavior of a living tissue subjected to constant, sinusoidal and step surface heating using combined Laplace and finite deference. Hooshmand et al. [38] derived a generalized DPL model based on the non-equilibrium heat transfer of biological tissues during laser irradiation and solved it by the separation of variables and Duhamel’s integral method. They found that the results of generalized DPL model are different from the classical DPL and Pennes bioheat transfer models.

Some of the analytical solutions of the biological tissues’ thermal transfer are done as non-perfused (i.e., without considering the blood perfusion term). For example, Trujillo et al. [39] solved hyperbolic heat transfer equation of the one-dimensional non-perfuse homogeneous biological tissue which is irradiated by laser beam. Manns et al. [40] presented a semi-analytical technique to calculate the heat transfer equation of homogeneous non-perfuse tissue during collimated laser beams with Gaussian intensity distributions and convective boundary conditions at the surface. Talaee et al. [41] derived an exact analytical solution for the three-dimensional hyperbolic heat conduction equation under pulsed surface heat flux using combined separation of variables and the Duhamel integral. Also, he [42] continued to obtain the exact solution for this problem with time-dependent and Gaussian distributed heat source using Eigen value procedure which is used for modeling laser heating of biological tissues.

Laser treatment has become an established clinical modality over the past decade [43]. Laser ablation is a non-invasive tumor treatment modality which utilizes photothermal interaction between lasers and tissues and produces minimal damage to healthy tissue compared with the most conventional therapies like surgery and chemotherapy [44]. High-speed startup, selective energy absorption, instantaneous electric control, non-pollution, high energy efficiency, and high product quality are several advantages of laser treatment [45]. Both continue wave (CW) and pulsed lasers have been employed for the ablation of subsurface tumors. Modeling laser-tissue interaction is a potent tool to help in analyzing and optimizing the parameters governing planned laser ablation procedures. Moreover, the lack of experimentation in this field makes bioheat models more significant. Conventional laser thermal modeling has included the following steps: calculation of the laser energy in tissue based on the absorption and scattering coefficients, calculation of the temperature increase using various bioheat transfer equations, and calculation of the thermal damage [45]. Up to our knowledge, there is not any analytical solution for three-dimensional hyperbolic Pennes bioheat equation (Eq. (3)) under moving heat source to obtain thermal field and damage of tissues. For the applicability of the solution, the Gaussian distributed in surface and exponentially distributed in depth function of moving heat source are used for modeling a sample laser scanning of tissue. The solution procedure is Eigen value method which leads to a closed-form solution and the effect of moving velocity, perfusion rate, and laser intensity, absorption, and scattering on temperature profiles are investigated. Also, Arrhenius equation is used for determining the spatial and temporal extent of tissue damage to minimize damage of surrounding healthy tissue in vital organs.

Mathematical model

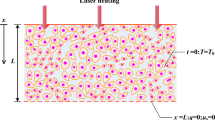
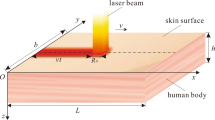
For modeling of biological tissue, a cubic with length of l on each side was considered as shown schematically in Fig. 1. The tissue was simulated under laser treatment moving in the x direction with Gaussian distribution in top surface and exponentially distribution in absorption depth.

Fig. 1

Schematic of cubic biological tissue under moving heat source in the x-direction with a constant velocity (v)

The tissue was assumed to be homogeneous such that tissue properties (mass density, thermal conductivity, and specific heat) were constant and independent of temperature. The wasting of energy from tissue was negligible, and neither phase change and nor chemical reactions occurred in the tissue. The distribution of blood vessels was considered isotropic and heat dissipation due to blood flow was modeled with a constant perfusion. Due to the relatively high magnitude of the laser energy source term compared with the metabolic heat generation, the metabolic heat generation rate was neglected [46]. The moving laser heat source term Q(x, y, z, t) was expressed in the following form [47]:

$$ Q\left(\mathrm{x},\mathrm{y},\mathrm{z},\mathrm{t}\right)=\frac{\mathrm{P}}{2\uppi {\upsigma}^2}{\mathrm{e}}^{-\left(\frac{{\left(\mathrm{x}-\mathrm{vt}\right)}^2+{\mathrm{y}}^2}{2{\upsigma}^2}\right)}\exp \left(-\upmu \mathrm{z}\right) $$

(4)

Where, P is a constant power, μ = (μ_a + μ_s) is the summation of absorption and scattering coefficients, v is the constant velocity along the positive direction of the x-axis, and σ is the spot radius which shows the concentration of laser point.

Here, it was focused on the simulation of treating kidney and skin tumor through one laser beam with Gaussian distribution. The heat source term is based on Beer’s Law, which identifies the exponential attenuation of light as it travels through a medium [46]. This approximation is less accurate than the mathematically rigorous Monte Carlo method; however, it is less computationally intensive and is frequently used in modeling light propagation of tissues. This method has been extensively used in the literature for the measurement of temperature rise during laser irradiation of tissues [48].

Due to the convenience of the results, the following dimensionless variables were introduced:

$$ X=\mathrm{wx}/2\upalpha $$

(5.a)

$$ Y=\mathrm{wy}/2\upalpha $$

(5.b)

$$ Z=w\mathrm{z}/2\upalpha $$

(5.c)

$$ V=\mathrm{v}/\mathrm{w} $$

(5.d)

$$ \tau =\mathrm{t}/2{\uptau}_{\mathrm{q}} $$

(5.e)

$$ \theta =\left(T-{T}_b\right)/\left({T}_m-{T}_b\right) $$

(5.f)

$$ \psi =Q{\tau}_q/\left[{\rho}_t{C}_t\left({T}_m-{T}_b\right)\right] $$

(5.g)

$$ \beta =2w{\tau}_q\mu $$

(5.h)

$$ \zeta ={\tau}_q{\rho}_b{\varpi}_b{C}_b/{\rho}_t{C}_t $$

(5.i)

where  T_m is an arbitrary reference temperature.

The governing Eq. (3) can be rewritten in terms of dimensionless variables as follows:

$$ \frac{\partial^2\uptheta}{\partial {\uptau}^2}+2\left(1+\upzeta \right)\frac{\mathrm{\partial \uptheta }}{\mathrm{\partial \uptau }}=\left(\frac{\partial^2\uptheta}{\partial {\mathrm{X}}^2}+\frac{\partial^2\uptheta}{\partial {\mathrm{Y}}^2}+\frac{\partial^2\uptheta}{\partial {\mathrm{Z}}^2}\right)-4\upzeta \uptheta +f\left(X,Y,Z,\tau \right) $$

(6)

where$f\left(X,Y,Z,\tau \right)=2\frac{\partial \psi }{\partial \tau }+4\psi$ is the non-dimensional moving distributed heat source function, which ψ is in the following non-dimensional form as follows:

$$ \psi ={\uppsi}_0{\mathrm{e}}^{-\left(2{\left(\frac{\upalpha}{\upsigma \mathrm{w}}\right)}^2\left({\left(X-\mathrm{V}\uptau \right)}^2+{\mathrm{Y}}^2\right)+\upbeta \mathrm{Z}\right)} $$

(7)

where${\psi}_0=\frac{P}{2\pi {\sigma}^2{P}_r}$ that P_r is the reference power.

The tissue initial temperature was considered at constant body temperature of (Tb = 37 ° C) and the the surroundings were kept at body temperature too. Due to the small value for thermal conductivity of tissue, the boundary conditions were considered adiabatic, except the upper surface. Thus, the boundary conditions can be written in the dimensionless form as follows:

$$ \frac{\partial }{\mathrm{\partial X}}\uptheta \left(0,Y,Z,\tau \right)=\frac{\partial }{\mathrm{\partial X}}\uptheta \left(L,Y,Z,\tau \right)=0 $$

(8.a)

$$ \frac{\partial }{\mathrm{\partial Y}}\uptheta \left(X,0,Z,\tau \right)=\frac{\partial }{\mathrm{\partial Y}}\uptheta \left(X,L,Z,\tau \right)=0 $$

(8.b)

$$ \frac{\partial }{\mathrm{\partial Z}}\uptheta \left(X,Y,0,\tau \right)=0,\kern1.25em \frac{\partial }{\mathrm{\partial Z}}\uptheta \left(X,Y,L,\tau \right)=h\uptheta \left(X,Y,L,\tau \right) $$

(8.c)

where h is the dimensionless number and denotes the convection cooling coefficient. It was assumed that the tissue was in equilibrium with the body and blood temperature at its initial state. Hence, the dimensionless initial conditions of the problem were assumed as follows:

$$ \theta \left(X,Y,Z,0\right)=0 $$

(9.a)

$$ \frac{\partial }{\partial \tau}\theta \left(X,Y,Z,0\right)=0 $$

(9.a)

The model was used to investigate the effects of surface temperature and treatment time on the depth of tissue injury. It is hoped that this model can contribute to improve the current operations and lead to more effective treatments and greater patient safety.

Analytical solution

The problem is the three-dimensional Poisson equation with homogeneous boundary conditions. Due to the homogeneous boundary, selection of Eigen function series solution which composed of harmonic functions with zeroes on the boundary can solve this problem. Extension of our procedure for solution of the Poisson equation with nonhomogeneous boundary condition is simply done with the help of super position principle. According to the super position principle, the Poisson equation with nonhomogeneous boundary conditions is divided to the summation of two problems of Steady (Dirichlet problem) with nonhomogeneous boundary conditions and transient (Poisson problem) with homogeneous boundary conditions and reformed initial conditions.

Due to boundary conditions (Eq. (8)), the below Eigen function was considered the solution of Eq. (6):

$$ \theta \left(X,Y,Z,\tau \right)=\sum \limits_{\mathrm{m}=0}^{\infty}\sum \limits_{\mathrm{n}=0}^{\infty}\sum \limits_{\mathrm{k}=1}^{\infty }{\mathrm{A}}_{\mathrm{m}\mathrm{nk}}\left(\uptau \right)\cos \left(\frac{\mathrm{m}\uppi \mathrm{X}}{\mathrm{L}}\right)\cos \left(\frac{\mathrm{n}\uppi \mathrm{Y}}{\mathrm{L}}\right)\cos \left({\upmu}_{\mathrm{k}}\mathrm{Z}\right) $$

(10)

where the Eigen values μ_k are positive zeroes of the characteristic equation of tan (μ_kL) + h/μ_k = 0, and A_mnk(τ) is time dependent constant which can be determined from application of the solution (Eq. (10)) into the Eq. (6). This leads to the following ordinary differential equation with the initial conditions (Eq. (9)):

$$ \left\{\begin{array}{c}{\ddot{A}}_{\mathrm{m}\mathrm{nk}}\left(\uptau \right)+2\left(1+\upzeta \right){\dot{A}}_{\mathrm{m}\mathrm{nk}}\left(\uptau \right)+\left({\left(\frac{\mathrm{m}\uppi}{\mathrm{L}}\right)}^2+{\left(\frac{\mathrm{n}\uppi}{\mathrm{L}}\right)}^2+{\left({\upmu}_{\mathrm{k}}\right)}^2+4\upzeta \right)\ {A}_{\mathrm{n}}\left(\uptau \right)={\mathrm{R}}_{\mathrm{m}\mathrm{nk}}\left(\uptau \right)\\ {}\mathrm{A}(0)=0,\kern0.5em \dot{\mathrm{A}}(0)=0\end{array}\right. $$

(11)

where R_mnk(τ) is the Fourier expansion coefficient of the source term function due to the below Eigen function:

$$ f\left(X,Y,Z,\tau \right)=\sum \limits_{\mathrm{m}=0}^{\infty}\sum \limits_{\mathrm{n}=0}^{\infty}\sum \limits_{\mathrm{k}=1}^{\infty }{\mathrm{R}}_{\mathrm{m}\mathrm{nk}}\left(\uptau \right)\cos \left(\frac{\mathrm{m}\uppi \mathrm{X}}{\mathrm{L}}\right)\cos \left(\frac{\mathrm{n}\uppi \mathrm{X}}{\mathrm{L}}\right)\cos \left({\upmu}_{\mathrm{k}}\mathrm{Z}\right) $$

(12)

Considering Fourier expansion relation, R_mnk(τ) is determined as below:

$$ {\mathrm{R}}_{\mathrm{m}\mathrm{nk}}\left(\uptau \right)=\frac{32{\uppsi}_0}{{\mathrm{L}}^3}\underset{0}{\overset{\mathrm{L}}{\iiint }}\left(\left(1+2{\left(\frac{\upalpha}{\upsigma \mathrm{w}}\right)}^2\mathrm{V}\left(\mathrm{X}-\mathrm{V}\uptau \right)\right){\mathrm{e}}^{-\left(2{\left(\frac{\upalpha}{\upsigma \mathrm{w}}\right)}^2\left({\left(\mathrm{X}-\mathrm{V}\uptau \right)}^2+{\mathrm{Y}}^2\right)+\upbeta \mathrm{Z}\right)}\right)\cos \left(\frac{\mathrm{m}\uppi \mathrm{X}}{\mathrm{L}}\right)\cos \left(\frac{\mathrm{n}\uppi \mathrm{X}}{\mathrm{L}}\right)\cos \left({\upmu}_{\mathrm{k}}\mathrm{Z}\right)\mathrm{dXdYdZ} $$

(13)

The above integration is solvable and the results are shown in appendix A. Equation (11) is an ordinary differential equation of second order, thus its solution consists of homogeneous ${A}_{\mathrm{mnk}}^{\mathrm{h}}\left(\tau \right)$ and particular solution ${A}_{\mathrm{mnk}}^{\mathrm{p}}\left(\tau \right)$ [49]:

$$ {A}_{mnk}\left(\tau \right)={A}_{mnk}^h\left(\tau \right)+{A}_{mnk}^p\left(\tau \right) $$

(14)

The homogeneous solution is expressed as follows:

$$ \left\{\begin{array}{c}{\mathrm{A}}_{\mathrm{mnk}}^{\mathrm{h}}\left(\uptau \right)={\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_1}+{\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_2}={\mathrm{e}}^{-\left(1+\upzeta \right)\uptau}\left({\mathrm{B}}_{\mathrm{mnk}}\cos \left({\upalpha}_{\mathrm{mnk}}\uptau \right)+{\mathrm{C}}_{\mathrm{mnk}}\sin \left({\upalpha}_{\mathrm{mnk}}\uptau \right)\right)\ {\upgamma}_{\mathrm{mnk}}>0\\ {}{\mathrm{A}}_{\mathrm{mnk}}^{\mathrm{h}}\left(\uptau \right)={\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_1}+{\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_2}={\mathrm{e}}^{-\left(1+\upzeta \right)\uptau}\left({\mathrm{B}}_{\mathrm{mnk}}+{\mathrm{C}}_{\mathrm{mnk}}\uptau \right)\kern1em {\upgamma}_{\mathrm{mnk}}=0\\ {}{\mathrm{A}}_{\mathrm{mnk}}^{\mathrm{h}}\left(\uptau \right)={\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_1}+{\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_2}={\mathrm{e}}^{-\left(1+\upzeta \right)\uptau}\left({\mathrm{B}}_{\mathrm{mnk}}\cosh \left({\upalpha}_{\mathrm{mnk}}\uptau \right)+{\mathrm{C}}_{\mathrm{mnk}}\sinh \left({\upalpha}_{\mathrm{mnk}}\uptau \right)\right){\upgamma}_{\mathrm{mnk}}<0\ \end{array}\right. $$

(15)

where${\alpha}_{\mathrm{mnk}}=\sqrt{{\left(1+\zeta \right)}^2-\left({\left(\frac{m\pi}{L}\right)}^2+{\left(\frac{n\pi}{L}\right)}^2+{\left({\mu}_k\right)}^2+4\zeta \right)}$ and ${\gamma}_{\mathrm{mnk}}={\left(1+\zeta \right)}^2-\left({\left(\frac{m\pi}{L}\right)}^2+{\left(\frac{n\pi}{L}\right)}^2+{\left({\mu}_k\right)}^2+4\zeta \right).$

The particular solution can be found based on homogeneous solution, by the method of variation of parameters as follows [50,51,52,53,54,55,56,57,58,59]:

$$ {\mathrm{A}}_{\mathrm{mnk}}^{\mathrm{p}}\left(\uptau \right)={\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_1}\int \left(-\frac{{\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_2}{\mathrm{R}}_{\mathrm{mnk}}\left(\uptau \right)}{\mathrm{W}\left({\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_1},{\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_2}\right)}\right)\mathrm{d}\uptau +{\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_2}\int \left(\frac{{\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_1}{\mathrm{R}}_{\mathrm{mnk}}\left(\uptau \right)}{\mathrm{W}\left({\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_1},{\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_2}\right)}\right)\mathrm{d}\uptau $$

(16)

where $W\left({\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_1},{\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_2}\right)$ is the Wronskian of the homogeneous solutions:

$$ \mathrm{W}\left({\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_1},{\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_2}\right)={\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_1}{{\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_2}}^{\prime }-{\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_2}{{\mathrm{A}}_{\mathrm{mnk}}^{{\mathrm{h}}_1}}^{\prime } $$

(17)

Thus, the particular solution can be expressed as follows:

$$ \left\{\begin{array}{c}{\mathrm{A}}_{\mathrm{mnk}}^{\mathrm{p}}\left(\uptau \right)=\frac{{\mathrm{e}}^{-\left(1+\upzeta \right)\uptau}}{\upalpha_{\mathrm{mnk}}}\left(\left(\sin \left({\upalpha}_{\mathrm{mnk}}\uptau \right)\underset{0}{\overset{\uptau}{\int }}{\mathrm{e}}^{\left(1+\upzeta \right)\uptau}\cos \left({\upalpha}_{\mathrm{mnk}}\uptau \right){\mathrm{R}}_{\mathrm{mnk}}\left(\uptau \right)\mathrm{d}\uptau \right)-\left(\cos \left({\upalpha}_{\mathrm{mnk}}\uptau \right)\underset{0}{\overset{\uptau}{\int }}{\mathrm{e}}^{\left(1+\upzeta \right)\uptau}\sin \left({\upalpha}_{\mathrm{mnk}}\uptau \right){\mathrm{R}}_{\mathrm{mnk}}\left(\uptau \right)\mathrm{d}\uptau \right)\right)\kern2.75em {\upgamma}_{\mathrm{n}}>0\\ {}\ {\mathrm{A}}_{\mathrm{mnk}}^{\mathrm{p}}\left(\uptau \right)={\mathrm{e}}^{-\left(1+\upzeta \right)\uptau}\left(\left(\uptau \underset{0}{\overset{\uptau}{\int }}{\mathrm{e}}^{\left(1+\upzeta \right)\uptau}{\mathrm{R}}_{\mathrm{mnk}}\left(\uptau \right)\mathrm{d}\uptau \right)-\left(\underset{0}{\overset{\uptau}{\int }}\uptau {\mathrm{e}}^{\left(1+\upzeta \right)\uptau}{\mathrm{R}}_{\mathrm{mnk}}\left(\uptau \right)\mathrm{d}\uptau \right)\right)\kern15.75em {\upgamma}_{\mathrm{n}}=0\\ {}{\mathrm{A}}_{\mathrm{mnk}}^{\mathrm{p}}\left(\uptau \right)=\frac{{\mathrm{e}}^{-\left(1+\upzeta \right)\uptau}}{\upalpha_{\mathrm{mnk}}}\left(\left(\sinh \left({\upalpha}_{\mathrm{mnk}}\uptau \right)\underset{0}{\overset{\uptau}{\int }}{\mathrm{e}}^{\left(1+\upzeta \right)\uptau}\cosh \left({\upalpha}_{\mathrm{mnk}}\uptau \right){\mathrm{R}}_{\mathrm{mnk}}\left(\uptau \right)\mathrm{d}\uptau \right)-\left(\cosh \left({\upalpha}_{\mathrm{mnk}}\uptau \right)\underset{0}{\overset{\uptau}{\int }}{\mathrm{e}}^{\left(1+\upzeta \right)\uptau}\sinh \left({\upalpha}_{\mathrm{mnk}}\uptau \right){\mathrm{R}}_{\mathrm{mnk}}\left(\uptau \right)\mathrm{d}\uptau \right)\right)\kern1.5em {\upgamma}_{\mathrm{n}}<0\end{array}\right. $$

(18)

Then, by applying the initial conditions, the time-dependent coefficient of A_mnk(τ) reduces to the particular solution Eq. (18). Hence, θ(X, Y, Z, τ) will obtain from Eq. (10) and a closed form analytical solution of hyperbolic Pennes bioheat (Eq. (6)) will achieve for spatial and the temporal evolution of temperature distributions during laser moving thermotherapy.

For demonstration of the solution, the kidney and skin tissues were modeled. The thermophysical properties and the optical properties for each tissue are summarized in the Table 1 which is based on the literature. For the convergence of the solution, 100 terms of the Eq. (10) solution series were calculated.

Table 1 Applied values of tissues and laser parameters [32, 35, 36, 38, 60,61,62]

Prediction of thermal damage

Estimation of tissue thermal damage is necessary to optimize laser treatment, increase the efficacy of each treatment sessions, and minimize the total number of required treatment sessions. Arrhenius equation for evaluating the thermal damage of biological tissues was used as follows [63]:

$$ \Omega \left(\mathrm{X},\mathrm{Y},\mathrm{Z},\uptau \right)=\underset{0}{\overset{\uptau}{\int }}{\mathrm{A}}_0\exp \left[-\frac{{\mathrm{E}}_{\mathrm{a}}}{\mathrm{RT}\left(\mathrm{X},\mathrm{Y},\mathrm{Z},\uptau \right)}\right]\mathrm{d}\uptau $$

(19)

where R = 8.314 J/(mol K) is the universal gas constant; T is the tissue absolute temperature. A₀ is the frequency factor and E_a is the activation energy of protein denaturation reaction. These parameters are dependent on the type of tissue. Due to the lack of available data on the properties of damaged tissue, similar material properties were assumed for the healthy and the thermally damaged tissue.

The damage function Ω(X, Y, Z, τ) was obtained by evaluating the right-hand side of Eq. (19) at any time and position in the tissue. The criteria for the thermal damage of tissue are assumed to be 40 ° C to represent comfort, 60 − 100 ° C for coagulation, 100 ° C for vaporization, and greater than 100 ° C for carbonization [64]. On the other hand, temperatures above 100 ° C can lead to tissue boiling and cavitation and can cause undefined and unpredictable lesion growth. Increase of Ω over the value of 1 leads to higher degree of burn and complete necrosis of the tissue [60].

Validation

Experimental validation was performed by irradiating excised pig skin tissue with a Gaussian-shaped spot size laser and calculation of the surface temperature results. Experimental results of Museux et al. [65] were used to validate the present mathematical model and analytical results. Figure 2 shows the temperature profiles of the hyperbolic bioheat model and experimental analysis. Good agreement (error less than 5%) between the analytical result and the obtained data from in vivo experiment is seen. Due to the natural convection, evaporative cooling and water vaporization heat loss, the difference of the predicted temperature and the measured one is observed.

Fig. 2

Comparison of hyperbolic bioheat model temperature history with experimental result

Results

In this study, the influences of five parameters such as laser moving velocity (v), laser intensity (σ), absorption and scattering coefficient (μ = μ_a + μ_s), tissue perfusion rate (${\overline{\omega}}_b\Big).$ and thermal relaxation time (τ_q) have been investigated. The laser beam was considered to impact on the top surface and moved on a path with beginning point of (l/6, l/2, 0) as shown in Fig. 1. The solution is depicted as temperature contours of kidney tissue surface plane at some steps of laser movement with velocity=0.01 (ms⁻¹) in Fig. 3. Also, the temperature contours of the vertical middle plane of kidney tissue beneath the moving path are shown in Fig. 4. The zones with the highest temperature value occurred in the laser beam concentrated hot spot. The maximum temperature of the tissue at the center of the spot zone reached to 110 °C.

Fig. 3

Temperature contours of surface plane (Z = 0) of kidney tissue under the moving laser with v = 0.01 (ms⁻¹)

Fig. 4

Temperature contours of vertical middle plane (Y = 0.5) of kidney tissue under the moving laser with v = 0.01 (ms⁻¹)

The most important objective of clinical thermal therapy is to achieve an efficient treatment outcome without damaging normal tissues. Hence, Figs. 5 and 6 illustrate the thermal damage contours of the surface plane and the vertical middle plane of kidney tissue.

Fig. 5

Thermal damage contours of surface plane (Z = 0) of kidney tissue under the moving laser with v = 0.01 (ms⁻¹)

Fig. 6

Thermal damage contours of vertical middle plane (Y = 0.5) of kidney tissue under the moving laser with v = 0.01 (ms⁻¹)

The behavior of the temperature profiles for some different treatment times at moving path on the surface plane of kidney tissue is shown in Fig. 7. The temperature increases eventually to a final distribution from the beginning of heating. However, as time passes, the temperature gradient becomes weaker. At higher treatment temperatures, the temperature profiles are much steeper.

Fig. 7

Temperature profiles of kidney tissue in various times; v = 0.01 (ms⁻¹)

The thermal interaction of laser irradiation with biological tissues is quantified by the thermal dose accumulated in the tissue, which can be identified from the time history of temperature during laser irradiation. Hence, the temperature time history of kidney tissue under the heating path is shown in Fig. 8. The time lag for reaching the temperature gradient to the upper point of the moving path, which is one of the characteristic properties of hyperbolic temperature profiles, is seen in Fig. 8.

Fig. 8

Temperature histories of kidney tissue in various points; v = 0.01 (ms⁻¹)

The effect of moving velocity of heat source on the temperature profiles is shown in Figs. 9 and 10. Due to the lower time of heat absorption of the moving source with higher velocity, increasing of laser moving velocity leads to decrease of tissue temperature amplitude. Also, Fig. 11 shows the influence of the heat source moving velocity on the thermal damage of kidney tissue. The thermal damage decreases with the increase of the velocity of moving heat source.

Fig. 9

Temperature profiles of kidney tissue in τ = 0.11 due to various moving heat source velocity

Fig. 10

Temperature histories of kidney tissue in X = 0.3 due to various moving heat source velocity

Fig. 11

Thermal damage histories of kidney tissue in X = 0.3 due to various moving heat source velocity

The spatial distribution of the tumor therapy laser beam is another important parameter for efficient delivery of thermal energy to targeted tissues. Hence, the effect of concentration factor of laser heating function (σ) on the temperature distribution and thermal damage is shown in Figs. 12 and 13. Increasing laser concentration due to smaller values of σ in the laser distribution function leads to focus of absorbed heat in the smaller point of the tissue and as a result, higher temperature is produced.

Fig. 12

Temperature contours of kidney tissue due to various spot radius (σ) of moving heat source at τ = 0.66 and v = 0.01 (ms⁻¹)

Fig. 13

Thermal damage contours of kidney tissue due to various spot radius (σ) of moving heat source at τ = 0.66 and v = 0.01 (ms⁻¹)

The laser must penetrate into the tissue and release the thermal energy at a specific target to achieve tissue coagulation. Hence, studying the effects of absorption and scattering parameters (μ) of laser function is conducted. The depth temperature profile in vertical path of tissue middle point is plotted in Fig. 14 under the same laser moving velocity and three (40, 200, 2000) values of μ.

Fig. 14

The effect of μ on kidney tissue temperature profile; τ = 0.16 and v = 0.01 (ms⁻¹)

Blood perfusion plays an important role in thermoregulation of living tissues, regulating and controlling tissues temperature in biological transmission. To investigate the effect of perfusion term on temperature distribution, the comparison of skin and kidney temperature and thermal damage time history are shown in Figs. 15 and 16 under the same heating conditions.

Fig. 15

Comparison of the kidney and skin tissue temperature history in X = 0.2 and v = 0.01 (ms⁻¹)

Fig. 16

Comparison of the kidney and skin tissue thermal damage history in X = 0.2 and v = 0.01 (ms⁻¹)

Since various values for relaxation time (8–16 (sec)) of biological tissues were reported in the literature [67,68,69], for showing the effect of the relaxation time (τ_q) on temperature profile, three values of 8, 10, and 16 are compared for Kidney tissue in Fig. 17. Due to the inertial effect of hyperbolic temperature profiles in balance of heat flux and temperature gradient, increase of τ_q may lead to increase of temperature amplitude and the cooling rate decreases drastically.

Fig. 17

Comparison of the temperature profiles due to various tissue relaxation times at τ = 0.66 and v = 0.01 (ms⁻¹)

Discussion

Kidney tissue temperature contours (Figs. 3 and 4) demonstrate that the heat transfer within the tissue is due to heat conduction, blood perfusion, and power absorption. Since the value of the tissue conductivity is low, the distribution of tissue temperature in the outside of the laser spot is very small. The movement of the laser source leads to stretching of the affected zone against the moving direction. The depth of affected zone and the wavy behavior of temperature profiles in depth, which are due to the hyperbolic modeling of bioheat equation, can be seen in contours of Fig. 4. Penetration of the temperature field into the tissue is obvious from the pattern of the isotherms which move into the interior of the tissue with time increasing.

Necrosis and ablation of tissues initiate at 45 ° C. Heat deposition of tissue causes it to swell, and extensive heating makes tissue dehydration, which can lead to tissue shrinkage and coagulation. Figures 5 and 6 illustrate that the thermal damage increases due to decrease of laser moving velocity. The damaged zone has an elliptical shape according to the laser distribution function. The iso-lines which are located closest to the surface, representing the highest damage and those that are located deeper into the tissue, representing lower damage value. The highest damage value (Ω = 2.2 × 10⁴) is reached at the end of treatment on the tissue surface.

To examine the treatment process, temperature profiles of different treatment times and temperature time history are shown in Figs. 7 and 8, respectively. They illustrate that the temperature increases rapidly in the early time of heating, reaches a peak value, and then decreases gradually toward steady state. This is because the laser power is absorbed within the kidney tissue and increases the tissue temperature, but the peak temperature is controlled by the internal convective role of tissue perfusion rate and convective boundary condition on the top surface of the tissue. The results of Fig. 8 demonstrate that the tissue maximum temperature value is over 45 ° C, which is capable of destroying kidney tissue tumor. Since the temperature greater than 100 °C is recorded in the tissue, the vaporization of water and mechanical destruction of tissue will occur very rapidly under laser ablation.

Laser intensity control is crucial to prevention of tissue damage (keeps normal tissue temperature surrounding the tumor below 45 ° C). It is interesting to observe that the hotspot zone which is produced under laser point in the tumor leads the higher temperature of tumor from nominal tissue. Figures 12 and 13 demonstrate that lower value of σ which means the more concentrated heating source leads to higher temperature amplitude and smaller radius of affected zone. The increase of σ leads to larger heated spot diameters and causes greater fragmentation, but also may lead to decrease of the maximum central temperature. Thus, the different values of σ could affect the treatment thermal damage. The thermal damage intensity with σ = 0.2 is much smaller than that of σ = 0.1. This showed that scenarios of efficient laser treatment should be controlled by all of parameters in different dose of treatment.

Another important parameter of laser treatment is the summation of absorption and scattering coefficients. Since this parameter presented in the decreasing exponential function as e−μz, increasing of μ leads to decrease of absorbed heat and the temperature amplitude decreases (Fig. 14). Increasing of μ to very high values may lead to very small calculated number and may produce oscillation in the temperature profiles. As the waves propagated through the tissue, their magnitude decreased. In other words, the temperature gradient is steep near the tissue surface but diminishes rapidly with increasing tissue depth.

As laser increases the temperature of tissue, blood vessels count as heat sinks by dissipating the heat to the surrounding tissue. Loss of heat through blood perfusion is proportional to the amount of blood perfusion [28]. The level of blood perfusion varies greatly from body types and physiological conditions [66]. Increasing of perfusion term leads to decrease of temperature variation (Figs. 15 and 16). Due to the convective role of the perfusion term in the Pennes bioheat equation, the blood perfusion term contributes strongly to temperature changes of the tissue. At first, temperature increases and then decreases due to cooling by blood perfusion. The temperature amplitude is higher for skin with lower perfusion term compared with kidney tissue. Lower blood perfusion leads to lower heat sink effect and in turn enhances the maximal thermal dosage required for necrosis Fig. 16).

Conclusion

The three-dimensional hyperbolic Pennes bioheat equation under moving laser irradiation was solved analytically based on the Eigen value method. Comparisons with results of in vivo experimental showed the good prediction of presented closed form solution. The parametric study illustrated that the amplitude, shape, and size of the temperature distribution and thermal damage could be controlled by appropriately selecting laser velocity, intensity, absorption, and scattering coefficients. The higher perfusion rate of kidneys compared with skin may lead to lower induced temperature amplitude in moving path of laser. Due to the convective role of the perfusion term in the Pennes bioheat equation, higher perfusion rate caused to decrease temperature variation and produce more uniform temperature profile in kidney tissue. Moreover, the increase in both blood perfusion rate at the periphery of coagulation region and thermal properties for rising in temperature reduced the thermal damage and its hysteresis. Furthermore, increase of laser moving velocity leads to decrease of tissue temperature amplitude and the thermal damage due to the lower chance of heat absorption for the moving source with higher velocity. Also, the effect of concentrated laser spot on the tissue which caused higher temperature amplitude and smaller radius of affected zone can be investigated by the presented model. The presented closed-form solution could be applied to measure laser parameters in real to provide a better insight of how to set the parameters to achieve better therapeutic outcomes resulting from clinical laser treatment. Finally, the exact analytical solution can be used as a validation for numerical solutions of biological tissues surgery under moving heat source such as laser cutting tools, bone drilling, and neurosurgery bone grinding in future works. However, it is important that the temperature dependence of the tissue optical and thermal properties should be incorporated in future studies.

Appendix

The simplified relation of R_mnk(τ) is as follows:

$$ {R}_{mnk}\left(\tau \right)=\left[\frac{\psi_0\pi \sigma w\left(\beta {e}^{\left[\beta L\right]}-\beta Cos\left[L{\mu}_k\right]+{\mu}_k Sin\left[L{\mu}_k\right]\right)}{2{\alpha}^2{L}^4\left({\beta}^2+{\mu_k}^2\right)}\right]\times {e}^{-\left[\beta L+\frac{im\pi \left(L-\tau v\right)}{L}+\frac{2{\alpha}^2\left({L}^2-2 L\tau v+2{\tau}^2{v}^2\right)}{\sigma^2{w}^2}+\frac{\left({m}^2+{n}^2\right){\pi}^2{\sigma}^2{w}^2}{8{\alpha}^2{L}^2}\right]} $$

$$ \left[2\alpha L v\sqrt{\frac{2}{\pi }}{e}^{\left[-\frac{im\pi \tau v}{L}+\frac{2{\alpha}^2\tau v\left(-2L+\tau v\right)}{\sigma^2{w}^2}+\frac{m^2{\pi}^2{\sigma}^2{w}^2}{8{\alpha}^2{L}^2}\right]}\left(2{e}^{\left[ im\pi +\frac{2{\alpha}^2{L}^2}{\sigma^2{w}^2}\right]}-{e}^{\left[\frac{4{\alpha}^2 L\tau v}{\sigma^2{w}^2}\right]}\left(1+{e}^{\left[2 im\pi \right]}\right)\right)+\sigma w{e}^{\left[\frac{im\pi \left(L-2\tau v\right)}{L}+\frac{2{\alpha}^2\left({L}^2-2 L\tau v+2{\tau}^2{v}^2\right)}{\sigma^2{w}^2}\right]}\left({e}^{\left[\frac{2 im\pi \tau v}{L}\right]}\left[2L+ im\pi v\right]\left(\mathit{\operatorname{erf}}\left[\frac{\sqrt{2}\alpha \left(L-\tau v\right)}{\sigma w}-\frac{im\pi \sigma w}{2\sqrt{2}\alpha L}\right]+\mathit{\operatorname{erf}}\left[\frac{\sqrt{2}\alpha \tau v}{\sigma w}+\frac{im\pi \sigma w}{2\sqrt{2}\alpha L}\right]\right)+\left[2L- im\pi v\right]\left(\mathit{\operatorname{erf}}\left[\frac{\sqrt{2}\alpha \tau v}{\sigma w}-\frac{im\pi \sigma w}{2\sqrt{2}\alpha L}\right]+\mathit{\operatorname{erf}}\left[\frac{\sqrt{2}\alpha \left(L-\tau v\right)}{\sigma w}+\frac{im\pi \sigma w}{2\sqrt{2}\alpha L}\right]\right)\right)\right]\left[\mathit{\operatorname{erf}}\left[\frac{\sqrt{2}\alpha L}{\sigma w}-\frac{in\pi \sigma w}{2\sqrt{2}\alpha L}\right]+\mathit{\operatorname{erf}}\left[\frac{\sqrt{2}\alpha L}{\sigma w}+\frac{in\pi \sigma w}{2\sqrt{2}\alpha L}\right]\right] $$