Various approaches to multiobjective linear programming problems with interval costs and interval weights

Abstract

Optimization problems are often subject to various kinds of inexactness or inaccuracy of input data. Here, we consider multiobjective linear programming problems, in which two kinds of input entries have the form of interval data. First, we suppose that the objectives entries are interval values, and, second, we suppose that we have an interval estimation of weights of the particular criteria. These two types of interval data naturally lead to various definitions of efficient solutions. We discuss six meaningful concepts of efficient solutions and compare them to each other. For each of them, we attempt to characterize the corresponding kind efficiency and investigate computational complexity of deciding whether a given solution is efficient.

1 Introduction

Consider a multiobjective linear programming problem

$$\begin{aligned} \max \ Cx {\ \ \text{ subject } \text{ to }\ \ }Ax\le b, \end{aligned}$$

(1)

where $A\in {\mathbb {R}}^{m\times n}$, $b\in {\mathbb {R}}^m$ and $C\in {\mathbb {R}}^{p\times n}$. We suppose that the feasible set is nonempty. Throughout the paper, inequalities $\le$ and < are understood entrywise.

Recall that a feasible solution $x^*$ is called efficient if there is no other feasible solution x such that $Cx\ge Cx^*$ and $Cx\not =Cx^*$. One of the basic methods to solve (1) is to employ a weighted sum scalarization, which has the form of a linear program

$$\begin{aligned} \max \ \lambda ^TCx {\ \ \text{ subject } \text{ to }\ \ }Ax\le b. \end{aligned}$$

(2)

It is known (Ehrgott 2005; The Luc 2016) that each efficient solution is an optimal solution of (2) for some $\lambda >0$, and conversely each optimal solution of (2) with $\lambda >0$ is efficient to (1). This means that scalarizations with positive weight completely characterize efficient solutions.

In this paper we suppose that the objective function coefficients are not exact, but we have deterministic lower and upper bounds for the exact values. That is, we know only an interval matrix ${{\varvec{C}}}$ comprising the exact value (for more general uncertainty sets see, e.g., Dranichak and Wiecek 2019). By definition, an interval matrix is the set of matrices

$$\begin{aligned} {{\varvec{C}}} =[{\underline{{{C}}}},{\overline{{{C}}}}] =\{C\in {\mathbb {R}}^{p\times n};\,{\underline{{{C}}}}\le C\le {\overline{{{C}}}}\}, \end{aligned}$$

where ${\underline{{{C}}}},{\overline{{{C}}}}\in {\mathbb {R}}^{p\times n}$, ${\underline{{{C}}}}\le {\overline{{{C}}}}$ are given matrices. We will also use the notion of the midpoint and the radius matrices, which are defined, respectively, as

$$\begin{aligned} C_{c} \,{:}{=}\,\frac{1}{2}({\underline{{{C}}}}+{\overline{{{C}}}}),\quad C_{\Delta } \,{:}{=}\,\frac{1}{2}({\overline{{{C}}}}-{\underline{{{C}}}}). \end{aligned}$$

Similar notation is used for interval vectors, considered as one-column interval matrices, and for interval numbers. Interval arithmetic is described, e.g., in the textbooks (Hansen and Walster 2004; Moore et al. 2009).

Interval-valued linear programming problems are well studied in the single-objective case (González-Gallardo et al. 2021; Garajová et al. 2019; Mohammadi and Gentili 2021; Mostafaee and Hladík 2020), but there are considerably less works in the multiple-objective case. We remind two basic concepts of efficiency studied in the context of interval multiobjective programming (Bitran 1980; Henriques et al. 2020; Ida 1996; Inuiguchi and Kume 1989; Inuiguchi and Sakawa 1996; Oliveira and Antunes 2007). A feasible solution $x^*$ is possibly efficient if it is efficient for at least one $C\in {{\varvec{C}}}$, and it is necessarily efficient if it is efficient for every $C\in {{\varvec{C}}}$. Necessarily efficient solutions are very robust, but the drawback is that it might happen that there is no such solution. It is also computationally demanding to check for necessarily efficiency (Hladík 2012) even though there are various sufficient conditions (Hladík 2008) that can be employed. The recent approaches utilize maximum regret techniques; see (Rivaz and Yaghoobi 2013, 2018; Rivaz et al. 2016). In contrast, possibly efficiency is polynomially decidable (both checking possibly efficiency of a given solution (Inuiguchi and Sakawa 1996) and checking if there is at least one possibly efficient solution (Hladík 2017)), and there are typically many of them.

It is often difficult for a user to give precise weights to objectives. It is more natural for the user to provide us with a range of possible weights. Thus we suppose that intervals for possible weights are given in addition, too. In particular, we consider weights $\lambda \in {{\varvec{\lambda }}}=[{\underline{{{\lambda }}}},{\overline{{{\lambda }}}}]$, where ${\underline{{{\lambda }}}}>0$. The interval vector of weights naturally introduces other solution concepts and gives a decision maker flexibility to choose the right degree of robustness and the model that fits the interpretation of the interval entries. We will discuss these concepts in the next section.

Various concepts of efficiency.

The goal of this paper is to discuss the possible definitions of robust efficiency for interval objectives ${{\varvec{C}}}$ and interval weights ${{\varvec{\lambda }}}$. A feasible solution $x^*$ is called:

• (I)-efficient if $\exists \lambda \in {{\varvec{\lambda }}}\ \exists C\in {{\varvec{C}}}$ such that $x^*$ is an optimal solution to (2);

• (II)-efficient if $\exists \lambda \in {{\varvec{\lambda }}}\ \forall C\in {{\varvec{C}}}$ such that $x^*$ is an optimal solution to (2);

• (III)-efficient if $\forall C\in {{\varvec{C}}}\ \exists \lambda \in {{\varvec{\lambda }}}$ such that $x^*$ is an optimal solution to (2);

• (IV)-efficient if $\forall \lambda \in {{\varvec{\lambda }}}\ \exists C\in {{\varvec{C}}}$ such that $x^*$ is an optimal solution to (2);

• (V)-efficient if $\exists C\in {{\varvec{C}}}\ \forall \lambda \in {{\varvec{\lambda }}}$ such that $x^*$ is an optimal solution to (2);

• (VI)-efficient if $\forall \lambda \in {{\varvec{\lambda }}}\ \forall C\in {{\varvec{C}}}$ we have that $x^*$ is an optimal solution to (2).

Based on the definition, we immediately get some relations between these concepts. Figure 1 shows which kind of efficiency implies the other and which are incomparable in general. Obviously, (I)-efficiency is the least robust concept, whereas (VI)-efficient solutions are the most robust solutions. On the other hand, those more robust solutions need not exist.

Fig. 1

Relations between various definitions of efficiency

Roadmap

In Sect. 2, we characterize the particular concepts of efficiency for a basic solution $x^*$. We also thoroughly investigate computational complexity of the problem. An illustration by examples is provided in Sect. 3. In Sect. 4, we discuss extensions to an arbitrary feasible solution, and we also touch the problem how to find a suitable $x^*$.

Notation.

$I_n$ denotes the identity matrix of size n, $0_{m,n}$ stands for the zero matrix of size $m\times n$, $A_{i*}$ denotes the ith row and $A_{*i}$ the ith column of a matrix A. We use $e=(1,\dots ,1)^T$ for the vector of ones of a convenient length. The diagonal matrix with entries $s=(s_1,\dots ,s_n)^T$ is denoted by ${{\,\mathrm{diag}\,}}(s)$.

2 Concepts of efficiency for a basic solution

In this section, we assume that $x^*$ is a basic feasible solution. We also suppose that $x^*$ is nondegenerate. If it is not the case, we restrict to a particular optimal basis only. All the results remain valid, however, the conditions need not be so strong (the basis stable region is smaller than the region of optimality of $x^*$ in general).

Suppose that $x^*$ corresponds to a basis B and denote by $A_B$ the restriction of matrix A to the basic rows. Then the tangent cone to the feasible set at $x^*$ is described by $A_Bx\le 0$. Denoting $D\,\,{:}{=}\,\, (A_B^{-1})^T$, then the normal cone to the feasible set at $x^*$ is characterized by $Dy\ge 0$; see (Nožička et al. 1988; Rockafellar and Wets 2004). Thus $x^*$ is efficient if and only if there is $\lambda$ such that

$$\begin{aligned} DC^T\lambda \ge 0,\ \ \lambda >0. \end{aligned}$$

(3)

Table 1 summarizes the concepts and their computational complexity.

Table 1 List of possibilities for a basic solution

2.1 Case (I): $\exists {\lambda }\in {{\varvec{\lambda }}}\ \exists {C}\in {{\varvec{C}}}$

This is the least robust concept and relates to possibly efficiency. Indeed, if ${\underline{{{\lambda }}}}$ is sufficiently close to zero, then each possibly efficient solution is (I)-efficient for some $\lambda$ and thus both notions coincide. Similarly to possibly efficiency, (I)-efficiency is polynomially decidable, too.

Proposition 1

(I)-efficiency of $x^*$ is characterized by feasibility of the linear system

$$\begin{aligned} Dy\ge 0,\ \ {\underline{{{C}}}}^T\lambda \le y\le {\overline{{{C}}}}^T\lambda ,\ \ {\overline{{{\lambda }}}}\ge \lambda \ge {\underline{{{\lambda }}}} \end{aligned}$$

(4)

with respect to variables $y\in {\mathbb {R}}^n$ and $\lambda \in {\mathbb {R}}^p$.

Proof

By (3), $x^*$ is (I)-efficient iff there is $C\in {{\varvec{C}}}$ such that the linear system

$$\begin{aligned} DC^T\lambda \ge 0,\ \ {\overline{{{\lambda }}}}\ge \lambda \ge {\underline{{{\lambda }}}} \end{aligned}$$

is feasible. Introducing an additional variable $y\in {\mathbb {R}}^n$ we have an equivalent system

$$\begin{aligned} Dy\ge 0,\ \ y=C^T\lambda ,\ \ {\overline{{{\lambda }}}}\ge \lambda \ge {\underline{{{\lambda }}}}. \end{aligned}$$

By the characterization of solvability of interval systems (Fiedler et al. 2006; Hladík 2013; Oettli and Prager 1964), (I)-efficiency of $x^*$ equivalently reads (4). $\square$

Let $y^*$, $\lambda ^*$ be a feasible solution to (4). By adapting the approach from Fiedler et al. (2006); Hladík (2013), we can construct matrix ${\tilde{C}}\in {{\varvec{C}}}$ such that $x^*$ is an optimal solution to (2) with respect to ${\tilde{C}}$ and $\lambda ^*$. For each $i=1,\dots ,n$ define

$$\begin{aligned} d_i\,\,{:}{=}\,\,y_i^*- (C_{c}^T)_{i*}\lambda ^* \end{aligned}$$

Then the ith column of ${\tilde{C}}$ is defined

$$\begin{aligned} {\tilde{C}}_{*i}\,{:}{=}\,{\left\{ \begin{array}{ll} (C_{c})_{*i} &{} \text{ if } (C_{\Delta }^T)_{i*}\lambda ^*=0,\\ (C_{c})_{*i}+\frac{d_i}{(C_{\Delta }^T)_{i*}\lambda ^*}(C_{\Delta })_{*i} &{} \text{ otherwise. } \end{array}\right. } \end{aligned}$$

It is easy to verify that ${\tilde{C}}^T\lambda ^*=y^*$, whence $D{\tilde{C}}^T\lambda ^*=Dy^*\ge 0$.

2.2 Case (II): $\exists {\lambda }\in {{\varvec{\lambda }}}\ \forall {C}\in {{\varvec{C}}}$

Proposition 2

(II)-efficiency of $x^*$ is characterized by feasibility of the linear system

$$\begin{aligned} \big (DC_{c}^T-|D|C_{\Delta }^T\big )\lambda \ge 0,\ {\underline{{\lambda }}}\le \lambda \le {\overline{{\lambda }}} \end{aligned}$$

(5)

with respect to variables $\lambda \in {\mathbb {R}}^p$.

Proof

Let $\lambda \in {{\varvec{\lambda }}}$. Then $x^*$ is optimal to (2) for each $C\in {{\varvec{C}}}$ iff

$$\begin{aligned} DC^T\lambda \ge 0\ \forall C\in {{\varvec{C}}}, \end{aligned}$$

or, in other words,

$$\begin{aligned} \min _{C\in {{\varvec{C}}}}DC^T\lambda \ge 0. \end{aligned}$$

(6)

For each $i\in {\{1, \ldots , {n}\}}$,

$$\begin{aligned} (DC^T\lambda )_i=\sum _{j=1}^n\sum _{k=1}^p D_{ij}C_{kj}\lambda _k, \end{aligned}$$

and by basic properties of interval analysis (Moore 1966; Moore et al. 2009; Neumaier 1990) we have that its minimum on $C\in {{\varvec{C}}}$ is

$$\begin{aligned} \min _{C\in {{\varvec{C}}}} (DC^T\lambda )_i =\sum _{j,k} \big (D_{ij}(C_{c})_{kj}\lambda _k-|D|_{ij}(C_{\Delta })_{kj}\lambda _k\big ) =\big (DC_{c}^T\lambda -|D|C_{\Delta }^T\lambda \big )_i. \end{aligned}$$

Therefore (6) equivalently reads

$$\begin{aligned} DC_{c}^T\lambda -|D|C_{\Delta }^T\lambda \ge 0. \end{aligned}$$

Since $\lambda$ can be chosen arbitrarily from ${{\varvec{\lambda }}}$, we get that $x^*$ is (II)-efficient iff (5) is feasible. $\square$

If system (5) is feasible, then each solution serves as a certificate of (II)-efficiency of $x^*$. More concretely, let $\lambda ^*$ be a feasible solution of (5). Then $\lambda ^*$ is that vector of weights such that $x^*$ is optimal with respect to each $C\in {{\varvec{C}}}$. We can verify it a posteriori by checking that ${\underline{{{v}}}}\ge 0$ for ${{\varvec{v}}}\,{:}{=}\,(D{{\varvec{C}}}^T)\lambda ^*$ evaluated by interval arithmetic.

2.3 Case (III): $\forall {C}\in {{\varvec{C}}}\ \exists {\lambda }\in {{\varvec{\lambda }}}$

For $s\in \{\pm 1\}^n$ we denote by $C_s\in {{\varvec{C}}}$ the matrix $C_s\,{:}{=}\,C_{c}+C_{\Delta }{{\,\mathrm{diag}\,}}(s)$. Then in each column of $C_s$, either all entries are the right-end points of the intervals, or all entries are the left-end points of the intervals.

Proposition 3

We have that $x^*$ is (III)-efficient if and only if for every $s\in \{\pm 1\}^n$ the linear system

$$\begin{aligned} D(C_s)^T\lambda \ge 0,\ \ {\underline{{\lambda }}}\le \lambda \le {\overline{{\lambda }}} \end{aligned}$$

(7)

is feasible with respect to variables $\lambda \in {\mathbb {R}}^p$.

Proof

Let $C\in {{\varvec{C}}}$. Then $x^*$ is an optimal solution to (2) for some $\lambda \in {{\varvec{\lambda }}}$ iff the linear system

$$\begin{aligned} D^{-1}y=C^T\lambda ,\ \ y\ge 0,\ \ {\underline{{\lambda }}}\le \lambda \le {\overline{{\lambda }}} \end{aligned}$$

is feasible. By the Farkas lemma, the dual system

$$\begin{aligned} D^{-T}u\ge 0,\ \ -Cu+v-w\ge 0,\ \ {\overline{{\lambda }}}^Tv-{\underline{{\lambda }}}^Tw\le -1,\ \ v,w\ge 0 \end{aligned}$$

(8)

should be infeasible. Thus $x^*$ is not (III)-efficient iff there is $C\in {{\varvec{C}}}$ such that (8) is feasible. By the characterization of weak solvability of interval linear inequalities (Fiedler et al. 2006; Gerlach 1981; Hladík 2013) it is true iff there is $s\in \{\pm 1\}^n$ such that

$$\begin{aligned} D^{-T}u\ge 0,\ \ -C_su+v-w\ge 0,\ \ {\overline{{\lambda }}}^Tv-{\underline{{\lambda }}}^Tw\le -1,\ \ v,w\ge 0 \end{aligned}$$

is feasible. By the Farkas lemma again, we arrive at (7). $\square$

In other words, the proposition states that instead of checking

$$\begin{aligned} \forall C\in {{\varvec{C}}}\ \exists \lambda \in {{\varvec{\lambda }}}: x^* \text{ is } \text{ optimal } \end{aligned}$$

it is sufficient to check

$$\begin{aligned} \forall C_s\ \exists \lambda \in {{\varvec{\lambda }}}: x^* \text{ is } \text{ optimal }. \end{aligned}$$

Thus we reduced infinitely many instances ${{\varvec{C}}}$ to only instances $C_s$, $s\in \{\pm 1\}^n$.

If $x^*$ is not (III)-efficient, then (7) is infeasible for some $s\in \{\pm 1\}^n$. The corresponding cost matrix $C_s$ is a certificate of (III)-inefficiency – there is no $\lambda \in {{\varvec{\lambda }}}$ for which $x^*$ would be optimal.

By Bitran (1980), solution $x^*$ is necessarily efficient if and only if it is efficient only with respect to matrices $C_s$, $s\in \{\pm 1\}^n$. This reduces the problem to $2^n$ instances. The above characterization of (III)-efficiency requires solving $2^n$ linear systems, too. It can hardly be better than exponential since the problem is provably intractable.

Proposition 4

(III)-efficiency of $x^*$ is co-NP-complete to check.

Proof

Let ${{\varvec{C}}}$ be given and construct ${{\varvec{\lambda }}}$ such that ${\overline{{{\lambda }}}}=e$ and ${\underline{{{\lambda }}}}$ is sufficiently close to zero. Then $x^*$ is (III)-efficient iff it is necessarily efficient since each efficient solution is an optimal solution to (2) for some $\lambda >0$. However, necessarily efficiency is known to be NP-hard even for basic nondegenerate solutions (Hladík 2012).

The statement that it is sufficient to consider ${\underline{{{\lambda }}}}$ small enough follows from the following reasoning. Solution $x^*$ is necessarily efficient iff it is efficient with respect to matrices $C_s$, $s\in \{\pm 1\}^n$. For each of these $2^n$ cases, there is a corresponding weighted sum scalarization, so we can consider ${\underline{{{\lambda }}}}$ to be the minimum of them. Moreover, it has a polynomial size, so we can set a lower bound in advance; cf (Schrijver 1998).

Proposition 3 then implies that $s\in \{\pm 1\}^n$ is a certificate of (III)-inefficiency of $x^*$, so the problem belongs to class co-NP. $\square$

2.4 Case (IV): $\forall {\lambda }\in {{\varvec{\lambda }}}\ \exists {C}\in {{\varvec{C}}}$

For $s\in \{\pm 1\}^p$ we denote by $\lambda _s\in {{\varvec{\lambda }}}$ the vector $\lambda _s\,{:}{=}\,\lambda _{c}+{{\,\mathrm{diag}\,}}(s)\lambda _{\Delta }$. Geometrically, $\lambda _s$ is a vertex of the box ${{\varvec{\lambda }}}$ in space ${\mathbb {R}}^p$.

Proposition 5

We have that $x^*$ is (IV)-efficient if and only if for every $s\in \{\pm 1\}^p$ the linear system

$$\begin{aligned} {\underline{{{C}}}}^T\lambda _s\le D^{-1}y\le {\overline{{{C}}}}^T\lambda _s,\ \ y\ge 0 \end{aligned}$$

(9)

is feasible with respect to variables $y\in {\mathbb {R}}^n$.

Proof

Let $\lambda \in {{\varvec{\lambda }}}$. Then $x^*$ is optimal to (2) for some $C\in {{\varvec{C}}}$ iff

$$\begin{aligned} C^T\lambda =D^{-1}y,\ \ y\ge 0,\ \ C\in {{\varvec{C}}} \end{aligned}$$

is feasible. Equivalently, by avoiding the interval matrix,

$$\begin{aligned} {\underline{{{C}}}}^T\lambda \le D^{-1}y\le {\overline{{{C}}}}^T\lambda ,\ \ y\ge 0. \end{aligned}$$

(10)

We need to check that this system is solvable for each $\lambda \in {{\varvec{\lambda }}}$. Let $\lambda ^1,\lambda ^2\in {{\varvec{\lambda }}}$ and suppose that the system has the corresponding solutions $y^1,y^2$. Then for any $\alpha \in [0,1]$ we have

$$\begin{aligned} {\underline{{{C}}}}^T(\alpha \lambda ^1+(1-\alpha )\lambda ^2) \le D^{-1}(\alpha y^1+(1-\alpha )y^2) \le {\overline{{{C}}}}^T(\alpha \lambda ^1+(1-\alpha )\lambda ^2), \end{aligned}$$

so $\alpha y^1+(1-\alpha )y^2\ge 0$ is a solution for $\alpha \lambda ^1+(1-\alpha )\lambda ^2\in {{\varvec{\lambda }}}$. This means that the set of $\lambda$’s for which (10) is feasible is a convex set. Therefore, it is sufficient that the system is feasible for vertices of the box ${{\varvec{\lambda }}}$ only. $\square$

The above characterization reduces the problem to solving $2^p$ linear systems. Thus it is exponential in p, but not in n. Therefore we can effectively solve even large problems provided the number of criteria is low. Biobjective linear programs in particular are easy to solve.

Corollary 6

Checking (IV)-efficiency of $x^*$ is a polynomial problem provided p is fixed.

If $x^*$ is not (IV)-efficient, then (9) is infeasible for some $s\in \{\pm 1\}^p$. The corresponding vector of weights $\lambda _s$ then serves as a certificate of (IV)-inefficiency – there is no $C\in {{\varvec{C}}}$ for which $x^*$ would be optimal.

Proposition 7

(IV)-efficiency of $x^*$ is co-NP-complete to check.

Proof

We will use a reduction from the NP-complete problem of checking feasibility of the system

$$\begin{aligned} |Mx|\le e,\ \ e^T|x|>1 \end{aligned}$$

on a set of non-negative positive definite rational matrices $M\in {\mathbb {R}}^{n\times n}$; see (Fiedler et al. 2006; Hladík 2012). Substituting $x'\,{:}{=}\,Mx$ leads to system

$$\begin{aligned} |x'|\le e,\ \ e^T|M^{-1}x'|>1. \end{aligned}$$

Next, we substitute $z\,{:}{=}\,\frac{1}{2}(x'+3e)$ to obtain

$$\begin{aligned} z\in [1,2]^n,\ \ e^T|M^{-1}(2z-3e)|>1. \end{aligned}$$

Its infeasibility says that for every $z\in [1,2]^n$ we have

$$\begin{aligned} e^T|M^{-1}(2z-3e)|\le 1. \end{aligned}$$

Now, we rewrite it as follows by using additional variables $u\in {\mathbb {R}}^n$

$$\begin{aligned} e^Tu\le 1,\ \ u\ge 0,\ \ M^{-1}(2z-3e)\le u,\ \ -u\le M^{-1}(2z-3e). \end{aligned}$$

(11)

We claim that its feasibility is equivalent to feasibility of

$$\begin{aligned} u,v,w&\ge 0, \end{aligned}$$

(12a)

$$\begin{aligned} M^{-1}(2z-3e)&\le u-v\le \alpha ee^T z+\alpha e,\end{aligned}$$

(12b)

$$\begin{aligned} -\alpha ee^T z-\alpha e&\le 2v-u\le M^{-1}(2z-3e),\end{aligned}$$

(12c)

$$\begin{aligned} 0&\le e^Tu+w\le 1 \end{aligned}$$

(12d)

with respect to variables $u,v\in {\mathbb {R}}^n$, $w\in {\mathbb {R}}$, where $\alpha >0$ is a sufficiently large constant of a polynomial size. If z, u solves (11), then z, u, v, w solves (12), where $v=0$ and $w=0$. Conversely, if z, u, v, w solves (12), then z, u solves (11).

Thus, we reduced the co-NP-complete problem of checking feasibility of (12) to the form of (10), where

$$\begin{aligned}&\lambda \,{:}{=}\,\begin{pmatrix}z\\ {1}\end{pmatrix} \in \begin{pmatrix}^n\\ {1}\end{pmatrix}\,{=}{:}\,{{\varvec{\lambda }}},\ \ y\,{:}{=}\,\begin{pmatrix}u\\ {v}\\ {w}\end{pmatrix},\ \ D^{-1}\,{:}{=}\,\begin{pmatrix} I_n&{}-I_n&{}0_{n,1}\\ -I_n&{}2I_n&{}0_{n,1}\\ e^T &{} 0_{1,n}&{}1 \end{pmatrix},\\&{\underline{{{C}}}}^T\,{:}{=}\,\begin{pmatrix} 2M^{-1} &{} -3M^{-1}e \\ -\alpha ee^T &{} -\alpha e \\ 0_{1,n} &{} 0 \end{pmatrix},\ \ {\overline{{{C}}}}^T\,{:}{=}\,\begin{pmatrix} \alpha ee^T &{} \alpha e \\ 2M^{-1} &{} -3M^{-1}e \\ 0_{1,n} &{} 1 \end{pmatrix}. \end{aligned}$$

Notice that indeed $D^{-1}$ is nonsingular and ${\underline{{{C}}}}\le {\overline{{{C}}}}$. Proposition 5 implies that the problem belongs to class co-NP because it gives a certificate of (IV)-inefficiency in the form of $s\in \{\pm 1\}^p$. $\square$

2.5 Case (V): $\exists {C}\in {{\varvec{C}}}\ \forall {\lambda }\in {{\varvec{\lambda }}}$

Proposition 8

(V)-efficiency of $x^*$ is characterized by feasibility of the linear system

$$\begin{aligned} F\lambda _{c}-M\lambda _{\Delta }\ge 0,\ \ M\ge F,\ \ M\ge -F,\ \ {\underline{{{C}}}}^T\le D^{-1}F\le {\overline{{{C}}}}^T \end{aligned}$$

(13)

with respect to variables $M,F\in {\mathbb {R}}^{n\times p}$.

Proof

Let $C\in {{\varvec{C}}}$. Then $DC^T\lambda \ge 0$ for every $\lambda \in {{\varvec{\lambda }}}$ iff

$$\begin{aligned} DC^T\lambda _{c}-|DC^T|\lambda _{\Delta }\ge 0. \end{aligned}$$

Substituting $M\,{:}{=}\,|DC^T|$, we can write it as

$$\begin{aligned} DC^T\lambda _{c}-M\lambda _{\Delta }\ge 0,\ \ M\ge \pm DC^T. \end{aligned}$$

Using yet another substitution $F\,{:}{=}\,DC^T$, we have $D^{-1}F=C^T$ and so the condition reads

$$\begin{aligned} F\lambda _{c}-M\lambda _{\Delta }\ge 0,\ \ M\ge \pm F,\ \ D^{-1}F=C^T. \end{aligned}$$

Therefore the problem of finding a suitable $C\in {{\varvec{C}}}$ can be formulated as (13). $\square$

Let $M^*,F^*$ be a feasible solution to (13). Then $x^*$ is (V)-efficient and $M^*,F^*$ give the following certificate of (V)-efficiency: $C^*\,{:}{=}\,(D^{-1}F)^T$. For this cost matrix, $x^*$ is an optimal solution to (2) for every $\lambda \in {{\varvec{\lambda }}}$. Moreover, we can a posteriori verify (V)-efficiency of $x^*$ by calculating ${{\varvec{v}}}\,{:}{=}\,(D(C^*)^T){{\varvec{\lambda }}}$ by interval arithmetic and checking whether ${\underline{{{v}}}}\ge 0$.

2.6 Case (VI): $\forall {\lambda }\in {{\varvec{\lambda }}}\ \forall {C}\in {{\varvec{C}}}$

Proposition 9

(VI)-efficiency of $x^*$ is characterized by the condition

$$\begin{aligned} {\underline{{{v}}}}\ge 0,\ \text{ where } \ {{\varvec{v}}} \,{:}{=}\,(D{{\varvec{C}}}^T){{\varvec{\lambda }}} \end{aligned}$$

(14)

is computed by interval arithmetic.

Proof

Due to the basic properties of interval arithmetic (Moore 1966; Moore et al. 2009; Neumaier 1990), ${{\varvec{v}}}=(D{{\varvec{C}}}^T){{\varvec{\lambda }}}$ gives the smallest interval vector (the so called interval hull) containing the set

$$\begin{aligned} \{DC^T\lambda ;\,\lambda \in {{\varvec{\lambda }}},\, C\in {{\varvec{C}}}\}. \end{aligned}$$

Therefore (14) follows. $\square$

Condition (14) is easy to verify. It takes only ${\mathcal {O}}(pn^2)$ number of arithmetic operations, so the complexity depends on the dimension, but not on the size of input data. Therefore the problem of checking (VI)-efficiency of $x^*$ is strongly polynomial.

If $x^*$ is not (VI)-efficient, then ${\underline{{{v}}}}_i<0$ for some $i\in {\{1, \ldots , {n}\}}$. We will show how to construct a particular instance $C\in {{\varvec{C}}}$ and $\lambda \in {{\varvec{\lambda }}}$, for which $x^*$ is not optimal. Let $s\in \{\pm 1\}^n$ be the sign vector of $D_{i*}$, that is, $s_j=1$ if $D_{ij}\ge 0$ and $s_j=-1$ otherwise. Then the smallest value of $D_{i*}C^T\lambda$ on $C\in {{\varvec{C}}}$ and $\lambda \in {{\varvec{\lambda }}}$ is attained for $C_{-s}=C_{c}-C_{\Delta }{{\,\mathrm{diag}\,}}(s)$. Similarly, let $s'\in \{\pm 1\}^p$ be the sign vector of $D_{i*}C_{-s}$. Then the smallest value of $D_{i*}C^T_{-s}\lambda$ is attained for $\lambda _{-s'}\,{:}{=}\,\lambda _{c}-{{\,\mathrm{diag}\,}}(s')\lambda _{\Delta }$. Moreover, $D_{i*}C^T_{-s}\lambda _{-s'}={\underline{{{v}}}}_i<0$. Therefore, $C_{-s}$ and $\lambda _{-s'}$ serve as a certificate of (VI)-inefficiency, and this certificate has a special form with the entries being endpoints of the interval entries of ${{\varvec{\lambda }}}$ and ${{\varvec{C}}}$.

2.7 Further results

For (VI)-efficiency we have a close form arithmetic formula to check it. We also observed that (I), (II) and (V)-efficiency can be checked by means of linear programming. Linear programming is, however, among the hardest polynomial problem (so called P-complete, see Greenlaw et al. 1995) and hard to parallelize. Thus it is a natural question whether these kinds of efficiency are P-complete, too. We show that this is the case, so a closed-form formula does not seem to exist.

Proposition 10

Let C be fixed. Checking whether there is $\lambda \in {{\varvec{\lambda }}}$ such that $x^*$ is an optimal solution to (2) is a P-complete problem.

Proof

Vector $x^*$ is an optimal solution to (2) for some $\lambda \in {{\varvec{\lambda }}}$ iff the linear system

$$\begin{aligned} DC^T\lambda \ge 0,\ \ {\underline{{{\lambda }}}}\le \lambda \le {\overline{{{\lambda }}}} \end{aligned}$$

(15)

is feasible. It is known (Dobkin et al. 1979) that it is a P-complete problem to check feasibility of the system

$$\begin{aligned} Ax\le b,\ \ 0\le x\le e, \end{aligned}$$

where $A\in \{0,1,-1\}^{k\times \ell }$ and $b\in {\mathbb {Z}}^k$. Substituting $x'\,{:}{=}\,x+e$, we obtain system

$$\begin{aligned} Ax'\le b+Ae,\ \ e\le x'\le 2e. \end{aligned}$$

Thus we put $D\,\,{:}{=}\,\, I_{k+1}$, $C\,\,{:}{=}\,\, (-A\mid b+Ae)^T$, ${\underline{{{\lambda }}}}\,{:}{=}\,(e^T,1)^T$ and ${\overline{{{\lambda }}}}\,\,{:}{=}\,\, (2e^T,1)^T$, and the problem is reduced to feasibility of (15). $\square$

As a consequence, checking (I), (II) and (III)-efficiency is P-complete, too, even for the problems with real C and $D=I_n$.

As a necessary condition, we can use the following simple (strongly polynomial) test: By interval arithmetic compute ${{\varvec{v}}}\,{:}{=}\,(DC^T){{\varvec{\lambda }}}$. If ${\overline{{v}}}_i<0$ for some $i\in {\{1, \ldots , {n}\}}$, then there cannot exist $\lambda \in {{\varvec{\lambda }}}$ for which $x^*$ is an optimal solution.

Proposition 11

Let $\lambda >0$ be fixed. Checking whether there is $C\in {{\varvec{C}}}$ such that $x^*$ is an optimal solution to (2) is a P-complete problem.

Proof

By (13), solution $x^*$ is an optimal solution to (2) for some $C\in {{\varvec{C}}}$ iff the linear system

$$\begin{aligned} F\lambda \ge 0,\ \ {\underline{{{C}}}}^T\le D^{-1}F \le {\overline{{{C}}}}^T \end{aligned}$$

(16)

is feasible in variable $F\in {\mathbb {R}}^{n\times p}$. Again we use the fact that it is a P-complete problem to check feasibility of the system

$$\begin{aligned} Ax\le b,\ \ 0\le x\le e, \end{aligned}$$

(17)

where $A\in \{0,1,-1\}^{k\times \ell }$ and $b\in {\mathbb {Z}}^k$. Each solution of this system satisfies $Ax\ge -\ell \cdot e$. Put

$$\begin{aligned} \lambda =1,\ \ F\,{:}{=}\,\begin{pmatrix}x\\ [-1pt]{y}\end{pmatrix},\ \ D^{-1}\,{:}{=}\,\begin{pmatrix}{A}&{}I_m\\ [-1pt]{I_n}&{}0_{n,m}\end{pmatrix},\ \ {\underline{{{C}}}}^T\,{:}{=}\,\begin{pmatrix}{-\ell \cdot e}\\ [-1pt]{0}\end{pmatrix},\ \ {\overline{{{C}}}}^T\,{:}{=}\,\begin{pmatrix}{b}\\ [-1pt]{e}\end{pmatrix}. \end{aligned}$$

Notice that matrix $D^{-1}$ is indeed nonsingular. Then (16) has the form

$$\begin{aligned} x,y\ge 0,\ \ -\ell \cdot e\le Ax+y\le b,\ \ 0\le x\le e. \end{aligned}$$

Variable y is redundant, so the system is equivalent to (17). Thus the problem is reduced to feasibility of (16). $\square$

As a consequence, checking (I), (IV) and (V)-efficiency is P-complete, too, even for the problems with real one criterion and $\lambda =1$.

Again, we can use a simple test as a necessary condition: By interval arithmetic compute ${{\varvec{v}}}\,{:}{=}\,(D{{\varvec{C}}}^T)\lambda$. If ${\overline{{v}}}_i<0$ for some $i\in {\{1, \ldots , {n}\}}$, then there cannot exist $C\in {{\varvec{C}}}$ for which $x^*$ is an optimal solution.

3 Examples

Example 1

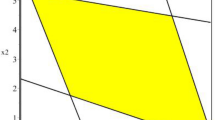
Consider the problem (1) with data

$$\begin{aligned} {{\varvec{C}}}=\begin{pmatrix}&{}[-1,1]\\ {}[0,1]&{}[7,8]\end{pmatrix},\ \ A=\begin{pmatrix}1&{}1\\ 0&{}1\\ {}-1&{}0\\ 0&{}-1\end{pmatrix},\ \ b=\begin{pmatrix}10\\ 5\\ 0\\ 0\end{pmatrix},\ \ {{\varvec{\lambda }}}=([1,2],[1,2])^T, \end{aligned}$$

(18)

and consider solution $x^*=(5,5)^T$; see Fig. 2. The basis associated to $x^*$ is $B=\{1,2\}$, and the corresponding matrix $D=(A_B^{-1})^T$ reads

$$\begin{aligned} D=\begin{pmatrix}1&{}0\\ {}-1&{}1\end{pmatrix}. \end{aligned}$$

It turns out that $x^*$ is (I), (II), (III), (IV) and (V)-efficient, but not (VI)-efficient. (II)-efficiency is certified by $\lambda =(1,2)^T$ computed from (5); for these weights, solution $x^*$ is an optimal solution to (2) for each $C\in {{\varvec{C}}}$. This is easily observed by calculating $(D{{\varvec{C}}}^T)\lambda =([5,8],[5,12])^T$, which is nonnegative. (V)-efficiency is certified by the objective matrix

$$\begin{aligned} C=\begin{pmatrix}5&{}1\\ 0&{}8\end{pmatrix} \end{aligned}$$

(19)

computed from (13) using $C\,{:}{=}\,(D^{-1}F)^T$, where F is a particular solution. Then $x^*$ is an optimal solution to (2) for each $\lambda \in {{\varvec{\lambda }}}$ since $(D{C}^T){{\varvec{\lambda }}}=([5,10],[0,12])^T$ is nonnegative. Weaker types of (I), (III) and (IV)-efficiency then follow automatically. Solution $x^*$ is not (VI)-efficient since $(D{{\varvec{C}}}^T){{\varvec{\lambda }}}=([5,14],[-8,12])^T$ is not nonnegative. A particular instance for which $x^*$ fails to be an optimal solution to (2) is constructed as follows. Since $D_{2*}=(-1,1)$, we set $s\,{:}{=}\,(-1,1)$ and

$$\begin{aligned} C_{-s}=\begin{pmatrix}6&{}-1\\ 1&{}7\end{pmatrix}. \end{aligned}$$

Since $D_{2*}C^T_{-s}=(-7,6)$, we put $s'\,{:}{=}\,(-1,1)$ and $\lambda _{-s'}=(2,1)^T$ is the corresponding vector of weights. One can verify that $(DC^T_{-s})\lambda _{-s'}=(13,-8)^T$.

Fig. 2

(Examples 1 and  3) The feasible set is in dark gray, the normal cone at $x^*$ in light gray, and the two interval objective vectors are depicted as boxes filled by lines

Example 2

Now, let us change the coefficient ${{\varvec{C}}}_{12}=[-1,1]$ to ${{\varvec{C}}}_{12}=[-1,0]$; see Fig. 3. Solution $x^*$ remains (I), (II) and (III)-efficient. (II)-efficiency is still certified by $\lambda =(1,2)^T$ and by checking the condition $(D{{\varvec{C}}}^T)\lambda =([5,8],[5,11])^T\ge 0$. In contrast to the previous example, $x^*$ is not (IV), (V) and (VI)-efficient. (IV)-inefficiency of $x^*$ is certified by $s=(1,-1)^T$ and the corresponding weights $\lambda _s=(2,1)^T$. We have $(D{{\varvec{C}}}^T)\lambda _s=([10,13],[-8,-2])^T$, so there cannot exist $C\in {{\varvec{C}}}$ for which $x^*$ is optimal. Notice, however, that this test is only a sufficient condition for (IV)-inefficiency; in view of Proposition 11 there can hardly be such a simple test, and we have to verify nonexistence of $C\in {{\varvec{C}}}$ by means of linear programming in general.

Fig. 3

(Example 2) The feasible set is in dark gray, the normal cone at $x^*$ in light gray, and the two interval objective vectors are depicted as boxes filled by lines

Example 3

Eventually, in the third example, consider the original interval matrix ${{\varvec{C}}}$ from (18), but we change the interval vector of weights to ${{\varvec{\lambda }}}=([3,4],[2,3])^T$. In this setting, $x^*$ is (I), (IV) and (V)-efficient, but not for the other types of efficiency. (V)-efficiency is certified by matrix C in the form (19) and the condition $(D{C}^T){{\varvec{\lambda }}}=([15,20],[0,12])^T\ge 0$. (III)-inefficiency is certified by the cost matrix

$$\begin{aligned} C=\begin{pmatrix}6&{}-1\\ 1&{}7\end{pmatrix}. \end{aligned}$$

To show that then there is no $\lambda \in {{\varvec{\lambda }}}$ for which $x^*$ is optimal can be checked by linear programming. In view of Proposition 10, there is probably no close-form expression, however, the following sufficient condition helps: $(D{C}^T){{\varvec{\lambda }}}=([20,27],[-16,-3])^T$, so it is nonnegative for no $\lambda \in {{\varvec{\lambda }}}$.

Example 4

Here, we apply the methodology to a classical transportation problem. Consider the bicriteria problem from Murad et al. (2010) (see also Hladík and Sitarz (2013)) with four main stores (suppliers) providing goods to six mill stones (warehouses). We have to transport goods from suppliers to warehouses. There are two criteria which have to be minimized: the transportation costs and the transportation deteriorations. The input data are displayed in Table 2. Notice that we have to add a dummy supplier to make the problem feasible.

Table 2 (Example 4) The input data for the transportation problem with two criteria

Suppose that the cost coefficients are not known precisely and the recored values have accuracy $5\%$. That is, we get the interval cost matrix ${{\varvec{C}}}$ such that $C_{c}=C$ is the cost matrix given in Table 2 and $C_{\Delta }=0.05|C|$. Next, suppose that the decision maker prefers the first objective function about 2 to 3 times more than the second one. This brings us the interval vector of weights ${{\varvec{\lambda }}}=([2,3],[1,1])^T$.

In this setting, it seems that the concept of (II)-efficiency is the most appropriate one. The reason is that the resulting efficient solution would be robust with respect to variations of the cost coefficients, while taking the advantage of choosing admissible weights. Moreover, in contrast to (III)-efficiency, this concept is polynomially solvable.

Consider an efficient solution

$$\begin{aligned} x^*= \begin{pmatrix} 2900&{} 1450&{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 1174&{} 3560 &{} 0 &{} 606 &{} 0\\ 0 &{} 0 &{} 0 &{} 4213 &{} 1107 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 6 &{} 4011\\ 0 &{} 0 &{} 0 &{} 0 &{} 2010 &{} 0 \end{pmatrix}, \end{aligned}$$

which is the optimal solution of the weighted sum scalarization with midpoint values, that is, with cost matrix C and weights $\lambda _{c}=(2.5,1)^T$.

By the calculations it turns out that $x^*$ is (II)-efficient. System (5) has a solution $\lambda =(2,1)^T$, for instance. Therefore, the decision maker can be sure that the point $x^*$ is efficient and optimal for the weighted sum scalarization with $\lambda =(2,1)^T$, and this is true even when any cost coefficient is subject to an arbitrary perturbation up to $5\%$ of the nominal value, simultaneously and independently of other coefficients.

Notice that provided the cost coefficients may vary up to $10\%$ of their nominal values, then $x^*$ is no more (II)-efficient. The break point is about $9.375\%$.

4 Extensions

4.1 General case of $x^*$

Let $x^*$ be a feasible solution and define the index set of active constraints

$$\begin{aligned} P \,{:}{=}\,\{i;\,(Ax^*)_i=b_i\}. \end{aligned}$$

Analogously as for the basic solution, we use $A_P$ to denote the restriction of matrix A to the rows indexed by P. By The Luc (2016) (or using optimality conditions in linear programming for (2)) we have that $x^*$ is efficient for a particular realization $C\in {{\varvec{C}}}$ if and only if the system

$$\begin{aligned} A^T_Py=C^T\lambda ,\ \ y\ge 0,\ \ \lambda >0 \end{aligned}$$

(20)

is feasible. If it is the case, then $\lambda$ is the corresponding vector of weights and y is an optimum of the dual problem.

In the following, we discuss the particular six concepts of efficiencies introduced at the beginning of the paper, but now for a general feasible solution $x^*$. Table 3 gives an overview of the computational complexity issues. We see that the situation is more pessimistic now.

Table 3 List of possibilities for a general solution

Case (I): $\exists \lambda \in {{\varvec{\lambda }}}\ \exists C\in {{\varvec{C}}}$ .

To characterize (I)-efficiency of $x^*$, we need to characterize solvability of (20) with respect to $C\in {{\varvec{C}}}$ and $\lambda \in {{\varvec{\lambda }}}$. Similarly as in the proof of Proposition 1 we obtain that (I)-efficiency of $x^*$ is equivalent to feasibility of the linear system

$$\begin{aligned} {\underline{{{C}}}}^T\lambda \le A^T_Py\le {\overline{{{C}}}}^T\lambda ,\ \ y\ge 0,\ \ {\overline{{{\lambda }}}}\ge \lambda \ge {\underline{{{\lambda }}}}. \end{aligned}$$

Case (II): $\exists \lambda \in {{\varvec{\lambda }}}\ \forall C\in {{\varvec{C}}}$ .

Here we need to find $\lambda \in {{\varvec{\lambda }}}$ such that the system (20) is solvable for each $C\in {{\varvec{C}}}$. Using the theory of interval systems (Fiedler et al. 2006; Hladík 2013) (and the so called strong solvability), the problem is reduced to solvability of (20) for matrices of type $C_s$, $s\in \{\pm 1\}^n$. Therefore, $x^*$ is (II)-efficient if and only if the system

$$\begin{aligned} A^T_Py_s=C^T_s\lambda , \ \ y_s\ge 0, \ s\in \{\pm 1\}^n, \ \ {\underline{{{\lambda }}}}\le \lambda \le {\overline{{{\lambda }}}} \end{aligned}$$

is feasible in variables $\lambda$ and $y_s$, $s\in \{\pm 1\}^n$. In contrast to the case of a basic solution $x^*$, we now encounter an exponentially large system. We can hardly make better since this kind of efficiency is intractable even for problems with one objective function (Hladík 2012).

Case (III): $\forall C\in {{\varvec{C}}}\ \exists \lambda \in {{\varvec{\lambda }}}$ .

In this case, we need to check that the system

$$\begin{aligned} A^T_Py=C^T\lambda ,\ \ y\ge 0,\ \ {\overline{{{\lambda }}}}\ge \lambda \ge {\underline{{{\lambda }}}} \end{aligned}$$

is solvable for each $C\in {{\varvec{C}}}$. Again, using the results on strong solvability of interval systems (Fiedler et al. 2006; Hladík 2013) we get that $x^*$ is (III)-efficient if and only if for each $s\in \{\pm 1\}^n$ the system

$$\begin{aligned} A^T_Py=C^T_s\lambda ,\ \ y\ge 0,\ \ {\underline{{{\lambda }}}}\le \lambda \le {\overline{{{\lambda }}}} \end{aligned}$$

is solvable. Notice the difference from the previous case – therein, we have one large system, whereas herein we have many small systems.

Case (IV): $\forall \lambda \in {{\varvec{\lambda }}}\ \exists C\in {{\varvec{C}}}$ .

Let $\lambda \in {{\varvec{\lambda }}}$. The point $x^*$ is optimal to (2) for some $C\in {{\varvec{C}}}$ if and only if the system

$$\begin{aligned} {\underline{{{C}}}}^T\lambda \le A^T_Py\le {\overline{{{C}}}}^T\lambda ,\ \ y\ge 0 \end{aligned}$$

(21)

is feasible. Thus we need to check feasibility of the above system for each $\lambda \in {{\varvec{\lambda }}}$. Since the system describes a convex polyhedral set, it is sufficient to check for feasibility of the vertices of ${{\varvec{\lambda }}}$ only. Therefore, $x^*$ is (IV)-efficient if and only if (21) is feasible for each $\lambda$ such that $\lambda _i\in \{{\underline{{\lambda }}}_i,{\overline{{\lambda }}}_i\}$, $i=1,\dots ,p$.

This characterization is exponential in p, but not in n. So the complexity is the same as for a basic solution $x^*$.

Case (V): $\exists C\in {{\varvec{C}}}\ \forall \lambda \in {{\varvec{\lambda }}}$ .

Let $C\in {{\varvec{C}}}$. How to check that (20) is solvable for each $\lambda \in {{\varvec{\lambda }}}$? Basically, we need to check $\{C^T\lambda ;\,\lambda \in {{\varvec{\lambda }}}\}\subseteq \{A^T_Py;\,y\ge 0\}.$ Since both sets are convex, it is sufficient to verify $C^T\lambda \in \{A^T_Py;\,y\ge 0\}$ for the vertices of ${{\varvec{\lambda }}}$ only. Denote $\lambda _s\,{:}{=}\,\lambda _{c}+{{\,\mathrm{diag}\,}}(s)\lambda _{\Delta }$. Now, $x^*$ is (V)-efficient if and only if the system

$$\begin{aligned} A^T_Py_s=C^T\lambda _s,\ \ y_s\ge 0,\ \ s\in \{\pm 1\}^p,\ \ {\underline{{{C}}}}\le C\le {\overline{{{C}}}} \end{aligned}$$

is solvable in variables C and $y_s$, $s\in \{\pm 1\}^p$.

This characterization is exponential in p, but not in n (in contrast to the case of a basic solution $x^*$, which is polynomially decidable). Again, we can hardly improve the complexity since the problem is co-NP-hard: Take ${{\varvec{C}}}\,{:}{=}\,I_n$ a real matrix and then (V)-efficiency reduces to necessary efficiency with respect to one objective function ${{\varvec{\lambda }}}^TCx={{\varvec{\lambda }}}^Tx$, which is an co-NP-hard problem (Hladík 2012).

Case (VI): $\forall \lambda \in {{\varvec{\lambda }}}\ \forall C\in {{\varvec{C}}}$ .

Since this case includes checking for necessary efficiency of a general feasible solution, it is again co-NP-hard (Hladík 2012). So in contrast to the case of a basic solution, complexity increased rapidly. This is also reflected in the exponential characterization that we present below.

Using a similar argument as for the previous case of (V)-efficiency, we need to check that for each $C\in {{\varvec{C}}}$ and each $s\in \{\pm 1\}^p$ the system

$$\begin{aligned} A^T_Py=C^T\lambda _s,\ \ y\ge 0 \end{aligned}$$

is solvable. Using similar ideas as for (III)-efficiency, we obtain that this system is solvable for each $C\in {{\varvec{C}}}$ if and only if it is solvable for each matrix of type $C_{s'}$, $s'\in \{\pm 1\}^n$. Therefore we arrive at the final characterization of (VI)-efficiency of $x^*$ that is equivalent to solvability of the system

$$\begin{aligned} A^T_Py=C^T_{s'}\lambda _s,\ \ y\ge 0 \end{aligned}$$

for each $s\in \{\pm 1\}^p$ and each $s'\in \{\pm 1\}^n$.

4.2 How to find $x^*$?

So far, we assumed that a feasible solution $x^*$ is given. This is a typical situation: A feasible solution is calculated and a decision maker needs to check for its robustness. If $x^*$ is not provided, we can compute it using a suitable heuristic—for example as an optimum of a weighted sum scalarization of the midpoint values of the interval coefficients. In general, however, determining $x^*$ is a hard problem. Even more, as we observed in the previous sections, such a solution need not exist if we choose too restrictive concept of robustness. The good news is that we can at least design a fail-safe method for (I)-efficiency.

(I)-efficiency.

Here, we present a method that computes a (I)-efficient solution or states there is no one. Basically, we need to find $\lambda \in {{\varvec{\lambda }}}$ and $C\in {{\varvec{C}}}$ such that the weighted sum scalarization

$$\begin{aligned} \max \ \lambda ^TCx {\ \ \text{ subject } \text{ to }\ \ }Ax\le b \end{aligned}$$

has an optimal solution. Optimality of the scalarization is equivalent to feasibility of the dual LP problem. That is, the system

$$\begin{aligned} C^T\lambda =A^Ty,\ \ y\ge 0 \end{aligned}$$

has a solution with respect to variable y. As C varies in ${{\varvec{C}}}$, the vector $C^T\lambda$ attains any value in the interval vector $[{\underline{{{C}}}}^T\lambda ,{\overline{{{C}}}}^T\lambda ]$. Thus we come to the system

$$\begin{aligned} {\underline{{{C}}}}^T\lambda \le A^Ty \le {\overline{{{C}}}}^T\lambda ,\ \ y\ge 0,\ \ {\underline{{{\lambda }}}}\le \lambda \le {\overline{{{\lambda }}}}. \end{aligned}$$

This is a linear system in $y,\lambda$ and any solution yields an appropriate weighted sum scalarization.

5 Conclusion

We introduced several concepts of efficient solutions in multiobjective linear programming with interval costs and interval vectors of weights. Choosing the right model depends on the decision maker and also on what kind of uncertainty is modelled by intervals. Sometimes, we need to take into account all possible values from interval data, and sometimes we can choose the most convenient scenario. This results in six meaningful combinations that were discussed in detail and characterized by appropriate conditions. We investigated computational complexity of testing the corresponding kinds of efficiency. It turned out that four of them are polynomially decidable by means of linear programming or interval arithmetic, and two of them are intractable.