1 Introduction

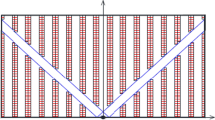
As global trade and e-commerce increases, warehousing becomes increasingly important for supply chain management due to increasing importance of responsiveness. Therefore, many companies get closer to their customer by opening new warehouses. However, many of them still goes with traditional storage blocks and arrangement of aisles that actually have greater impact on efficiency of warehouse operations such as receiving, put-away and especially order-picking (Scholz and Wäscher 2017). Two unspoken and hidden assumptions of traditional warehouse layouts were put forward by Gue and Meller (2009) such that (1) picking aisles are arranged parallel to each other while (2) cross aisles are placed perpendicular to the picking aisles as shown in Fig. 1. Gue and Meller (2009) then proposed two non-traditional warehouse layouts that offer reduction on average single-command distance (10–20%) over traditional layouts. The main principle behind of the new non-traditional layouts and the reduction on travel distance is to obtain the Euclidean distance, which is the shortest distance between given two points, between the pick-up and deposit (P&D) point and a storage location. Even though this phenomenon was first introduced by White (1972) in a warehouse layout problem, this became alive in Gue and Meller (2009)’s Flying-V and Fishbone designs.

Fig. 1
figure 1

Representation of traditional warehouse designs

Full size image

After Gue and Meller (2009)’s pioneering study, Pohl et al. (2009) and Pohl et al. (2011) showed that Fishbone designs also offer improvements in travel distance for the dual-command operations and turnover-based storage in unit-load warehouses. Öztürkoğlu et al. (2012) took non-traditional aisle studies further and provided optimal layouts with one, two and three angled cross aisles that minimize single-command travel distance. In addition, they showed that the Chevron, the optimal one-cross aisle design, provides the same amount of reduction on travel as the Fishbone. In the meantime, Öztürkoğlu et al. (2012) also shared one of the implications of non-traditional aisles in warehousing industry. Additionally, Cardona et al. (2012), Clark and Meller (2013), Bortolini et al. (2015), Venkitasubramony and Adil (2016), and Bortolini et al. (2019) studied on the Flying-V and Fishbone designs to show their effectiveness.

Cardona et al. (2012) identified the optimal angle for the diagonal cross aisles in the Fishbone design to demonstrate the robustness of original Fishbone design to varying warehouse dimensions. Clark and Meller (2013) embedded the vertical travel dimension into travel time models of Flying-V and Fishbone to investigate the robustness of their layout. Bortolini et al. (2015) reported that inserting one additional cross aisle into the Flying-V design reduced the single-command travel distance, although there was loss of storage space due to the inserted angled aisles. Venkitasubramony and Adil (2016) showed that the Fishbone layout reduces pick distance more when product demand is highly skewed rather than uniform demand. Bortolini et al. (2019) inserted angled cross aisles into traditional layouts and showed that the position of the angled aisles are insensitive to demand curve in class-based storage policy.

Different from the previously mentioned studies, Gue et al. (2012), Galvez and Ting (2012), Öztürkoğlu et al. (2014), Öztürkoğlu (2015, 2016), Mesa (2016) and Öztürkoğlu et al. (2018) considered multiple P&D points where a picker receives a pallet for put-away, an order list for picking, or a shrink-wrap machine is located for packaging. Gue et al. (2012) demonstrated that Flying-V designs still reduces single-command distances when multiple P&D points are located on the front of the warehouse, but not as much as with one centrally-located P&D point. Galvez and Ting (2012) presented several efficient locations for multiple P&D points in the Fishbone and rotated Fishbone designs for reducing the single- and dual-command travel distances. Öztürkoğlu et al. (2014) developed new non-traditional aisle designs that have multiple P&D points where they are located on the sides of the warehouses under four scenarios. Öztürkoğlu (2015, 2016) relaxed the limitations on the number of multiple P&D points on the designs proposed by Öztürkoğlu et al. (2014) to investigate how the number of P&D points affects the orientation of the angled aisles. Mesa (2016) proposed the diamond-shape layout with two P&D points for unit-load warehouses. Mesa (2016) showed that the diamond-shape layout has lower single-command distance than the equivalent traditional design and the design C1 which is developed by Öztürkoğlu et al. (2014). All of the abovementioned studies about multiple P&D points assumed uniform usage of the P&D points. Different from these studies, Öztürkoğlu et al. (2018) analyzed expected-single command travel distances under two different material flow policies in the Chevron design inserting multiple P&D points on the front. The authors showed that the Chevron presents decreasing savings on distance over equivalent traditional designs as the number of P&D points increases. Additionally, Chevron, as expected, performs better when flows are denser around the center than distributed.

Table 1 lists and categorizes the abovementioned studies according to some design, methodological and operational criteria. First, we categorized them according to the number of P&D points used in those studies. Second, the type of developed models to calculate travel distance in a layout is considered. Some studies developed analytical models to calculate distance and provided travel distance functions. However, some studies developed the network of the layouts and calculated distances on the network of nodes and edges. We also categorized them according to the types of layouts that they studied. Fixed layouts refer that the studied layouts do not change throughout the study. In the semi-fixed layout studies, only one type of aisle, either cross or picking, is assumed to be variable. If a study is categorized under variable layout, angles of all types of aisles are assumed to be variable. As seen in the table, there are a few non-traditional aisle studies with multiple P&D, although there are many with single P&D point. Additionally, the multiple P&D studies are either the lack of an analytical model or variable layouts. Therefore, this study aims to fill the these gaps in the warehousing literature (see the last row in Table 1 for the characteristics of this study.) The next section highlights the differences between the previous studies and this study, as well as its contribution to the literature.

Table 1 Characteristics of the selected non-traditional warehouse layout studies
Full size table

In addition to the above-mentioned studies on unit-load warehousing, there are several non-traditional aisle studies on order-picking warehouses such as Dukic and Opetuk (2008), Çelik and Süral (2014), Henn et al. (2013), Öztürkoğlu and Hoşer (2018, 2019) and Öztürkoğlu and Mağara (2019). Because these studies are out of scope of this manuscript, we leave their details to readers.

1.1 Scope and contribution of this study

As seen in Table 1, the majority of the previous non-traditional aisle studies assumed single P&D point. However, it is very common to have multiple P&D points in warehouses in practice, especially in larger ones to avoid congestion and facilitate flow through receiving and shipping docks. Therefore, this study focuses on non-traditional warehouse layouts with multiple P&D points.

Even though some studies considered multiple P&D points, they focused on fixed designs such as Flying-V in Gue et al. (2012), Diamond-shape in Mesa (2016) and Chevron in Öztürkoğlu et al. (2018). The other important limitations of multiple P&D-point studies are the lack of analytical models and the assumption of uniform usage of P&D points. Although Öztürkoğlu et al. (2014) and Öztürkoğlu (2015, 2016) looked for the optimal values of cross and picking aisles’ angles, they did not provide analytical distance models for general use. Additionally, except for the Öztürkoğlu et al. (2018), all of these studies supposed uniform usage of P&D points. Thus, there is no study in the literature that provide an analytical model of expected single-command distance in non-traditional aisle designs in which (1) aisles are not fixed, (2) any number of P&D points might be located on the front, (3) the P&D points might have any usage rate, and (4) the layout could be any size. Hence, this study aims to present optimal layouts for different warehouse design parameters. To make this study’s contribution clearer, the following discussions point out the similarities and differences from the closest relevant studies.

  1. (1)

    Although Öztürkoğlu et al. (2014) looked for optimal aisle designs with multiple P&D points; the main limitation of that study is the lack of analytical model. Öztürkoğlu et al. (2014) developed a constructive aisle model to design any non-traditional layout in a discrete space and evaluate its cost; however, it is not easy to use it for experiments because of the complexity of the model and the burdening computational time. Similarly, Öztürkoğlu (2015, 2016) also used Öztürkoğlu et al. (2014)’s model. They did not provide any analytical travel distance model. Hence, the main difference between those and this study is the modeling approach.

  2. (2)

    In this study, we develop analytical distance models in warehouses using continuous space approach similar to Öztürkoğlu et al. (2012, 2018). Öztürkoğlu et al. (2012) developed models for travels from only one centrally located P&D point. In those models, the starting point of the angled cross aisles are assumed to be fixed at the P&D point. However, we relax the assumption of fixed start point of the cross aisle in this study. Additionally, we develop travel distance models from each P&D point that can be located anywhere on the front of the warehouse, which makes the models more complicated. Even though Öztürkoğlu et al. (2018) developed travel models for multiple P&D points, the biggest limitation of this study is the fixed design, which is Chevron. Öztürkoğlu et al. (2018) analyzed the changes in expected single-command distance in Chevron with multiple P&D points that might have different usage. The biggest difference between that and our study is that we search for the optimal aisle configuration using the new travel distance functions from multiple P&D points. We introduce different material flow policies from Öztürkoğlu et al. (2018).

The rest of the paper is organized as the followings. In the next section, we first discuss the assumptions of our warehouse design problem. We then introduce our problem and develop its model step by step under the assumption of continuous space. After introducing sub problems we provided their travel distance functions. Next, we present our proposed solution algorithm, which is Particle Swarm Optimization, to solve our problem. In order to represent some practical aspects, we then introduce three different material flow policies that determine usage rates of P&D points. In Sect. 5, we solved our problem with varying number of P&D points, warehouse shape ratios and flow policies. After we presented our observations, we concluded the paper with several practical insights.

2 The continuous warehouse layout problem with multiple P&D points

Previous studies showed that continuous space models can be used as a good approximation of discrete space models. For example, Venkitasubramony and Adil (2016) reported that the gap between continuous and discrete models of single-command distance in the Fishbone design is within 2.5%. Öztürkoğlu et al. (2012) found that the gap between discrete and continuous models decreases as warehouse size increases. While the gap in the Chevron design is around 4% for small warehouses, it falls to around 2% for large warehouses. We therefore assume that the continuous warehouse space in our models allows us to derive analytical travel distance expressions because of its good approximation and strength to consider various travel paths in a flexible layout problem where aisles and racks can be arranged freely.

2.1 Assumptions

The generic warehouse layout we consider in this study is shown in Fig. 2 while Table 2 describes the model parameters and variables used to define the warehouse layout given in Fig. 2. We made the following design assumptions to develop the layout and its model.

Fig. 2
figure 2

The warehouse model in continuous space

Full size image
Table 2 Layout parameters and model variables
Full size table
  1. (i)

    The warehouse has a rectangular shape.

  2. (ii)

    There are cross aisles on both front and rear of the warehouse but no cross aisles on the right and left walls, in contrast to Öztürkoğlu et al. (2014), in order to accommodate racks against these walls. Therefore, travel is not allowed along the right and left sides of the warehouse (see Fig. 3a).

    Fig. 3
    figure 3

    Feasible and unfeasible travel routes (blue arrows) along the right and left sides of the warehouse (color figure online)

    Full size image
  3. (iii)

    There is one angled cross aisle to facilitate travel between picking aisles. It can emerge from anywhere on the front cross aisle where incoming and outgoing materials flow. It is also assumed to terminate on the rear cross aisle to prevent unfeasible travel paths along the sides of the warehouse with respect to the angles of the picking aisles.

  4. (iv)

    The angled cross aisle divides the storage area into right and left regions with respect to the position of the cross aisle. In each region, the picking aisles are arranged parallel to each other.

  5. (v)

    P&D points are equidistantly and symmetrically located with respect to the centrally-located P&D point on the front cross aisle. This assumption can be easily relaxed (see Sect. 5.2 for the details).

In Fig. 2, the bold red lines represent the fixed front, and rear cross aisles while the double red line represents the angled cross aisle. The dashed lines originating from m represent the diagonals on the right and left sides while the thin lines emerging from m are “central picking aisles” in the left and right regions. Thus, there is an infinite number of picking aisles parallel to the central picking aisles in the regions. Because of assumption (iii) above, the angle of the cross aisle can take any value between \( \gamma_{R} < \beta < \gamma_{L} \). Because m is not fixed, which will be explained later, \( \gamma_{R} \) and \( \gamma_{L} \) change depending on \( m \). P&D points can be located anywhere between \( 0\, \le \,p_{i} \le L \). Because of assumption (v) above, the location of the \( i{\text{th}} \) P&D point is defined by

$$ p_{i} = \frac{L}{2} - \frac{{a\left( {n - 1} \right)}}{2} + a\left( {i - 1} \right), \forall i = 1,2,3, \ldots ,n. $$

2.2 The problem and the model

The main goal of this study is to find the optimal angles of the angled cross aisle \( (\beta ) \) and picking aisles \( (\alpha_{R} \,{\text{and}}\,\alpha_{L} ) \), and the optimal location of the originating point of the cross aisle (\( m \)) to minimize the expected travel distance in a unit-load warehouse with multiple P&D points. Hence, the design can be represented by a vector of four continuous variables \( S = \left\{ {m, \beta , \alpha_{R} , \alpha_{L} } \right\} \), for a given set of \( n \) P&D points, \( L \), \( H, \) and \( a \). Since we assume that each storage location has equal probability of being visited due to the randomized storage policy, the generally expected single-command travel distance \( (E[D]) \) is the ratio of the total travel distance from all P&D points to every available storage location on the right and left regions in a continuous warehouse space, to its total storage area, as in Eq. 1.

$$ E\left[ D \right] = \frac{{\mathop \sum \nolimits_{i}^{n} U_{i} \left( {\mathop \int \nolimits_{{x \in A_{R} }}^{ } \mathop \int \nolimits_{{y \in A_{R} }}^{ } f\left( {x,y,p_{i} } \right) + \mathop \int \nolimits_{{x \in A_{L} }}^{ } \mathop \int \nolimits_{{y \in A_{L} }}^{ } f\left( {x,y,p_{i} } \right)} \right)}}{H \cdot L} $$
(1)

where \( \left( {x,y} \right) \) is the coordinate of a randomly chosen point in a region; \( A_{R} \) and \( A_{L} \) are the areas of the right and left regions, respectively; and \( f\left( {x,y,p_{i} } \right) \) is the one-way single-command travel distance to point \( \left( {x,y} \right) \) from \( p_{i} \).

As mentioned before, \( \beta \) can take any value between \( \gamma_{R} \) and \( \gamma_{L} \). However, to avoid duplication from symmetric designs and simplify the model, we let \( \beta \) take values between \( \gamma_{R} \le \beta \le \pi /2 \) because of Proposition 1 below. Additionally, because of assumption (ii) above, the angles of picking aisles on the right and left regions can take values between \( 0 < \alpha_{R} < \pi /2 \) and \( \pi /2 < \alpha_{L} < \pi \) (see Fig. 3a for an example of unfeasible travel when \( \alpha_{R} > \pi /2 \)).

Proposition 1

There are always symmetric cases of \( \beta \) when \( \gamma_{L} \ge \beta \ge \pi /2 \) on the interval of \( \pi /2 \ge \beta \ge \gamma_{R} \) when P&D points are symmetrically allocated around the central P&D point.

Proof

Suppose \( S \) and \( S^{{\prime }} \) are the respective two-solution vectors of \( S = \left( {\beta ,\alpha_{R} ,\alpha_{L} , m} \right) \) and \( S^{{\prime }} = \left( {\beta^{{\prime }} ,\alpha_{R}^{ '} ,\alpha_{L}^{ '} , m^{{\prime }} } \right), \) which result in expected travel distances \( E\left[ D \right] \) and \( E\left[ {D^{{\prime }} } \right] \) for the layouts given in Fig. 4a, b, respectively. Because we assume that P&D points are distributed evenly around the centrally-located P&D point, let us draw a vertical line through the central P&D point. Because of the mirror effect with respect to this vertical line, there are always symmetric cases of \( \beta^{\prime},\alpha_{R}^{ '} ,\alpha_{L}^{ '} \) and \( m^{{\prime }} \). Therefore, \( E\left[ {D '} \right] \) is equal to \( E\left[ D \right] \) when \( \beta^{\prime} = \pi - \beta ; \) \( \alpha_{R}^{ '} = \pi - \alpha_{L} ; \) \( \alpha_{L}^{ '} = \pi - \alpha_{R } ; \) \( m^{{\prime }} = L - m;\gamma_{R}^{ '} = \pi - \gamma_{L} ; \gamma_{L}^{ '} = \pi - \gamma_{R} . \)

Fig. 4
figure 4

Symmetric cases of the angled cross aisle

Full size image

Similar to Öztürkoğlu et al. (2012), we divide our model into sub cases based on possible aisle angles to derive cost (expected single-command distance) functions. However, there are six cases in our model because of the complexity of the problem. The respective cost fctions of each case, which are defined in Table 3, are described by \( E\left[ {D_{C1} } \right], E\left[ {D_{C2} } \right], E\left[ {D_{C3} } \right],E\left[ {D_{C4} } \right],E\left[ {D_{C5} } \right], \) and \( E\left[ {D_{C6} } \right] \) respectively. To find the optimal solution vector, we solve each of these cases separately before selecting the variables of the case that gives the minimum expected travel distance: \( E\left[ D \right] = min\left\{ {E\left[ {D_{C1} } \right], E\left[ {D_{C2} } \right],E\left[ {D_{C3} } \right],E\left[ {D_{C4} } \right],E\left[ {D_{C5} } \right],E\left[ {D_{C6} } \right]} \right\}. \)

Table 3 Definitions of the cases of the model
Full size table

To derive travel distance functions to a random point \( \left( {x,y} \right) \) in the warehouse storage area, it is divided into travel regions where the travel path to reach a location is the same. Figure 5 illustrates four travel regions in Case 1 along with the example travel paths. Region \( A \) is the area between the central picking aisle on the right and the front cross aisle. Region \( B \) is the area between the central picking aisle on the right and the angled cross aisle. Regions \( C \) and \( D \) are the counterpart regions of \( A \) and \( B \) on the left respectively. For space reasons, region definitions for other cases and their representations are given in the online appendix. In addition of these cases, the relative position of the P&D points according to the central P&D point should also be considered in developing travel distance functions because it causes different travel routes. For instance, as shown in Fig. 5, if a worker travels from a P&D point located on the right side of \( m\,(p_{i} > m) \) to any point \( \left( {x,y} \right) \) in region \( B \), the routing rule is (1) travel along the front cross aisle until \( m \); (2) travel along the angled cross aisle; (3) travel along the appropriate picking aisle with angle \( \alpha_{R} \). If a worker starts to travel from a P&D point on the left of \( m\,(p_{i } < m) \), then that worker travels towards the right rather than left along the front cross aisle. Even though the routes along the front cross aisle are different, the distance on the front cross aisle can be described by a similar function using absolute values for simplification.

Fig. 5
figure 5

Travel route regions in Case 1

Full size image

Table 4 shows the portions of the travel distance equation to any \( \left( {x,y} \right) \) point from any P&D point in each region. Finally, \( f_{A} \left( {x,y,p_{i} } \right), f_{B} \left( {x,y,p_{i} } \right), \) \( f_{C} \left( {x,y,p_{i} } \right) \), and \( f_{D} \left( {x,y,p_{i} } \right) \) are the travel distance functions from the \( i{\text{th}} \) P&D point to \( \left( {x,y} \right) \) point in regions \( A, B, C \) and \( D \) respectively, as defined in Table 4. For \( f_{B} \) and \( f_{D} \), specifically, the angles of lines going from \( m \) to (x, y) points in regions \( B \) and \( D \) are defined as \( \theta \), as shown in Fig. 5. \( \theta = Tan^{ - 1} \left( {\left( {x - m} \right),y} \right) \) is the angle defined by the front cross aisle and a line between \( m \) and any \( \left( {x,y} \right) \) point on the right of \( m \).

Table 4 Portions of the travel distance equations from a P&D point to a \( \left( {\varvec{x},\varvec{y}} \right) \) point
Full size table

To obtain each case’s cost function, we calculate the total travel distance by integrating the travel distance functions in Table 4 through the relevant sub regions under the assumption of continuous space. While integrating these cost functions, according to a travel region we use either the negative or the positive of the absolute functions given in Table 4. To integrate our cost functions in sub regions, we use the appropriate boundaries depicted in Fig. 6 with respect to the studied case. These boundaries are also described in Table 5 in details.

Fig. 6
figure 6

Main boundaries of cases

Full size image
Table 5 Boundary definitions of computed subregions
Full size table

Figure 7 shows the partitioned sub regions depicted in Fig. 5a that are used to integrate the travel distance functions for Case 1 when \( p_{i} \ge m \). Using these sub regions’ definitions, Eq. 2 shows the expected travel distance \( \left( {E\left[ {DR_{C1} } \right]} \right) \) for Case 1 when \( p_{i} \ge m \). Each integral of the travel distance functions in parenthesis shows the order of total travel distances in sub regions \( A_{1} \), \( A_{2} \), \( A_{3} \), \( B_{1} \), \( B_{2} \), \( C \), and \( D \).

Fig. 7
figure 7

Representation of lines indicating borders of regions for Case 1 if Pi ≥ m

Full size image
$$\begin{aligned} E\left[ {DR_{C1} } \right] & = \frac{1}{H \cdot L}\mathop \sum \limits_{i = 1}^{n} U_{i} \left( \mathop \int \limits_{{x = p_{i} }}^{L} \mathop \int \limits_{y = 0}^{{y_{i}^{R} }} f_{A} \left( {x,y,p_{i} } \right)dydx + \mathop \int \limits_{x = m}^{{p_{i} }} \mathop \int \limits_{y = 0}^{{y_{PR} }} f_{A} \left( {x,y,p_{i} } \right)dydx\right.\\ &\quad + \mathop \int \limits_{{x = p_{i} }}^{L} \mathop \int \limits_{{y = y_{i}^{R} }}^{{y_{PR} }} f_{A} \left( {x,y,p_{i} } \right)dydx \\ & \quad + \mathop \int \limits_{x = m}^{L} \mathop \int \limits_{{y = y_{PR} }}^{{y_{DR} }} f_{B} \left( {x,y,p_{i} } \right)dydx + \mathop \int \limits_{y = 0}^{H} \mathop \int \limits_{{x = x_{C} }}^{{x_{DR} }} f_{B} \left( {x,y,p_{i} } \right)dxdy\\ &\quad \left. + \mathop \int \limits_{y = 0}^{H} \mathop \int \limits_{x = 0}^{{y_{PL} }} f_{C} \left( {x,y,p_{i} } \right)dxdy + \mathop \int \limits_{y = 0}^{H} \mathop \int \limits_{{x = x_{PL} }}^{{x_{C} }} f_{D} \left( {x,y,p_{i} } \right)dxdy \right) \end{aligned}$$
(2)

Similarly, we also develop the cost function when \( p_{i} < m \) because of differences in several travel routes compared to routes where \( p_{i} \ge m \). This is necessary because the boundaries of travel region \( C \) change with respect to the relative position of a P&D point to \( q_{L} \) (see Table 5 for its definition) when \( \alpha_{L} < \gamma_{L} \). We divide Case 1 for \( p_{i} < m \) into two partitions: \( p_{i} \ge q_{L} \) and \( p_{i} < q_{L} \) (see Fig. 8).

Fig. 8
figure 8

Partitioning of the warehouses for Case 1 if Pi < m

Full size image

The cost functions for \( p_{i} \ge q_{L} \) and \( p_{i} < q_{L} \) are defined as \( E\left[ {DL1_{C1} } \right] \) and \( E\left[ {DL2_{C1} } \right] \), and given in Eqs. 3 and 4, respectively. In these equations, the first four terms are the same. These define total travel distances in region \( A \), sub regions \( B1 \) and \( B2 \), region \( D \) respectively. While the last term in Eq. 3 gives the total travel distance for sub regions \( C1 \) and \( C2 \) in Fig. 8a, the last three terms in Eq. 4 show the total travel distance in sub regions \( C1 \), \( C2 \), \( C3 \), and \( C4 \) in Fig. 8b, respectively.

$$\begin{aligned} E\left[ {DL1_{C1} } \right] & = \frac{1}{H \cdot L}\mathop \sum \limits_{i = 1}^{n} U_{i} \left( \mathop \int \limits_{x = m}^{L} \mathop \int \limits_{y = 0}^{{y_{PR} }} f_{A} \left( {x,y,p_{i} } \right)dydx + \mathop \int \limits_{x = m}^{L} \mathop \int \limits_{{y = y_{PR} }}^{{y_{DR} }} f_{B} \left( {x,y,p_{i} } \right)dydx\right.\\ &\quad + \mathop \int \limits_{y = 0}^{H} \mathop \int \limits_{{x = x_{C} }}^{{x_{DR} }} f_{B} \left( {x,y,p_{i} } \right)dxdy \\ & \quad \left. + \mathop \int \limits_{y = 0}^{H} \mathop \int \limits_{{x = x_{PL} }}^{{x_{C} }} f_{D} \left( {x,y,p_{i} } \right)dxdy + \mathop \int \limits_{y = 0}^{H} \mathop \int \limits_{x = 0}^{{x_{PL} }} f_{C} \left( {x,y,p_{i} } \right)dxdy \right) \end{aligned} $$
(3)
$$\begin{aligned} E\left[ {DL2_{C1} } \right] & = \frac{1}{H \cdot L} \mathop \sum \limits_{i = 1}^{n} U_{i} \left( \mathop \int \limits_{x = m}^{L} \mathop \int \limits_{y = 0}^{{y_{PR} }} f_{A} \left( {x,y,p_{i} } \right)dydx + \mathop \int \limits_{x = m}^{L} \mathop \int \limits_{{y = y_{PR} }}^{{y_{DR} }} f_{B} \left( {x,y,p_{i} } \right)dydx\right. \\ &\quad + \mathop \int \limits_{y = 0}^{H} \mathop \int \limits_{{x = x_{C} }}^{{x_{DR} }} f_{B} \left( {x,y,p_{i} } \right)dxdy \\ & \quad + \mathop \int \limits_{y = 0}^{H} \mathop \int \limits_{{x = x_{PL} }}^{{x_{C} }} f_{D} \left( {x,y,p_{i} } \right)dxdy\mathop \int \limits_{x = 0}^{{p_{i} }} \mathop \int \limits_{y = 0}^{{y_{qL} }} f_{C} \left( {x,y,p_{i} } \right)dydx\\ &\quad \left. + \mathop \int \limits_{{x = p_{i} }}^{{q_{L} }} \mathop \int \limits_{y = 0}^{{y_{qL} }} f_{C} \left( {x,y,p_{i} } \right)dydx + \mathop \int \limits_{y = 0}^{H} \mathop \int \limits_{{x = x_{qL} }}^{{x^{PL} }} f_{C} \left( {x,y,p_{i} } \right)dxdy \right) \end{aligned}$$
(4)

Finally, the expected travel distance in Case 1 is calculated using Eq. 5. For the sake of the manuscript’s flow, the other cases and their cost functions are presented in the online supplementary appendix.

$$ E\left[ {D_{C1} } \right] = \left\{ {\begin{array}{*{20}l} {E\left[ {DL1_{C1} } \right]; } \hfill & {p_{i} < m\;and\;p_{i} > q_{L} } \hfill \\ {E\left[ {DL2_{C1} } \right]; } \hfill & {p_{i} < m \;and\;p_{i} < q_{L} } \hfill \\ {E\left[ {DR_{C1} } \right]; } \hfill & {p_{i} > m } \hfill \\ \end{array} } \right\} $$
(5)

2.3 Cost in the traditional design

To provide an accurate comparison, we take the one-block warehouse design as a base because of its superiority for single-command operations (Roodbergen and De Koster 2001). We provide the continuous space model for the expected single-command distance in a one-block warehouse with multiple P&D points. Suppose that two random points \( \left( {{\text{x}}_{R} ,y_{R} } \right) \) and \( \left( {{\text{x}}_{L} ,y_{L} } \right) \) are generated on the right and left sides of a P&D point, respectively (see Fig. 9). Because of the rectilinear travel from the P&D point to these random points, the travel distance functions on the right and left sides of the P&D point are \( D_{R} = x_{R} - p_{i} + y_{R} \) and \( D_{L} = p_{i} - x_{L} + y_{L} \), respectively. Last, the expected travel distance \( \left( {E\left[ {TD} \right]} \right) \) from all P&D points in a one-block warehouse are given by Eq. 6:

Fig. 9
figure 9

One-block traditional aisle layout model

Full size image
$$ {E\left[ {TD} \right]} = \frac{1}{HL}\mathop \sum \limits_{i = 1}^{n} U_{i} \left( {\mathop \int \limits_{{x = p_{i} }}^{L} \mathop \int \limits_{y = 0}^{H} D_{R} \,dydx + \mathop \int \limits_{x = 0}^{{p_{i} }} \mathop \int \limits_{y = 0}^{H} D_{L} \,dydx} \right) $$
(6)
$$\kern35pt = \frac{1}{HL}\mathop \sum \limits_{i = 1}^{n} U_{i} \left( {\frac{1}{4}H\left( {L\left( {2H + L} \right) + a^{2} \left( { - 1 - 2i + n} \right)^{2} } \right)} \right) $$
(7)

3 Particle swarm optimization algorithm

To search for the optimal solution vector \( \left( {S = \left\{ {m, \beta , \alpha_{R} , \alpha_{L} } \right\}} \right) \), we use particle swarm optimization (PSO) algorithm because it was specifically developed for continuous and non-linear optimization by Kennedy and Eberhart (1995). Because our variables are continuous and the cost functions are non-linear, this algorithm is appropriate for our purpose.

The essence of the algorithm relies on observations of the social interactions of flock of birds and schools of fish. In PSO, a population is composed of members, called particles, and each particle is assumed to be connected to each other. Each particle represents a solution and searches the multi-dimensional, non-linear cost function’s space with a specific velocity. During the search, particles learn from both their own and the others’ experience. These two characteristics are described as individual learning as a cognitive factor and social learning as a social factor, referring to local and global search, respectively. While particles memorize their best previous position by individual learning, they also share their best positions found so far with each other in their neighborhood. Hence, the algorithm defines the previous best position of each particle as \( p_{best} \) while the best position of the population, which is the best among all particles, found so far is defined as \( g_{best} \). A particle moves from its current position to a new position by adjusting its velocity and direction using \( p_{best} \) and \( g_{best} \).

In our implementation, we rely on the PSO algorithm presented by Öztürkoğlu et al. (2014), who also applied it to a warehouse design problem. So, we adopted their notation to explain the proposed PSO algorithm. Let \( X_{i}^{t} \) include \( d \) dimensions (variables) and denote the position of the ith particle at iteration \( t \); \( X_{i}^{t} = \left\{ {x_{i1}^{t} , x_{i2}^{t} , \ldots ,x_{id}^{t} } \right\} \), where \( x_{id}^{t} \) is the position of the dth dimension of the ith particle. \( V_{i}^{t} \) is the set of \( d \) velocities of particle \( i \) at iteration \( t \), \( V_{i}^{t} = \left\{ {v_{i1}^{t} , v_{i2}^{t} , \ldots ,v_{id}^{t} } \right\} \). Each dimension of each particle moves with velocity \( v_{id}^{t} \) in the search space. \( P_{i} \) is the best previous location that gives the best fitness value of the ith particle and \( P_{i} = \left\{ {p_{i1 } ,p_{i2 } , \ldots ,p_{id} } \right\} \) where \( p_{id} \) is the best value of dimension \( d \) of the ith particle. \( G = \left\{ {g_{1, } g_{2, \ldots , } g_{d} } \right\} \) represents the best particle among all particles where \( g_{d } \) is the best value of dimension \( d \) in G. Additionally, learning coefficients \( c_{1} \) and \( c_{2} \) are used to control how much a particle is affected by its previous location and by the population, respectively. Shi and Eberhart (1998a, b) introduced another coefficient called inertia weight (\( w \)) to balance the particles’ global and local searches. This weight can be defined as a positive constant or a function of time if a user prefers to change the importance of the global or local search over iterations. A smaller \( w \) favors the local search whereas a larger \( w \) favors the global search. The velocity and particle update functions are defined in our implementation as in Eqs. 8 and 9:

$$ v_{id}^{t} = w^{t - 1} v_{id}^{t - 1} + c_{1} rnd_{1} \left( {p_{id} - x_{id}^{t - 1} } \right) + c_{2} rnd_{2} \left( {g_{d} - x_{id}^{t - 1} } \right) $$
(8)
$$ x_{id}^{t} = v_{id}^{t} + x_{id}^{t - 1} $$
(9)

where \( w^{t} = w_{u} - \frac{1}{N}t \) is defined as a linear function of the number of iterations in our implementation. In this equation, \( N \) is the maximum number of iterations that an algorithm can run first, \( w_{u} \) is the maximum value of the inertia weight, and \( w^{t} \) is the value of inertia weight at iteration \( t \). Hence, the inertia weight decreases as the algorithm runs over iterations to strengthen the local search. Additionally, \( rnd_{1 } \) and \( rnd_{2 } \) are uniformly distributed random numbers [0,1] that influence movement toward the individual or global best. In our implementation, there are 50 particles, which are all connected in a single neighborhood. The algorithm stops after are determined number of iterations \( \varepsilon \). When the algorithm reaches \( \varepsilon {\text{th}} \) iteration, it allows to search \( \overline{\varepsilon } \) more number of iterations. If the best solution is improved in the last \( \overline{\varepsilon } \) iterations, another \( \overline{\varepsilon } \) number of iteration is added to the search process. If the best solution cannot be improved in the last \( \overline{\varepsilon } \) iterations, the algorithm is terminated and the best solution is reported. In our algorithm, we take \( \varepsilon \) and \( \overline{\varepsilon } \) as 10,000 and 500 iterations. Because Clerk and Kennedy (2002) recommended that \( c_{1} + c_{2 } = 4.1 \), we select \( c_{1} = c_{2 } = 2.05 \) to give equal importance to cognitive and social learning. Because Shi et al. (1998a) mentioned that PSO has the best chance of finding the global optimum when \( 0.8 < w < 1.2 \), we select \( w_{u} = 1.3 \) to give more weight to global search in the initial iterations. The pseudo-code of the algorithm used in our study is presented in Table 6.

Table 6 The pseudocode for the developed PSO algorithm
Full size table

4 Material flow policies

As mentioned in Sect. 1, previous studies considering multiple P&D points (synonymously docks or input–output points) have assumed uniform usage of P&D points. This might be generally true during high-demand seasons when all available docks are busy almost all time. However, workers usually palletize and stretch-wrap the received loads before the put-away operation. Furthermore, even if a warehouse receives appropriately palletized loads, workers should inspect them before put-away. If there are fewer shrink-wrap machines than docks, stretch-wrap machines are distributed along the receiving docks and sometimes assigned to a group of docks. In their daily schedule, warehouses also assign specific docks for receiving and others for shipping. Some warehouses even reserve some docks for specific suppliers because they are the closest docks to the storage locations reserved for those suppliers. Thus, P&D points may have varying usage rates over time. Therefore, in this section we introduce two new material flow policies that are assumed to represent actual usage of P&D points in a warehouse, which we call “bell-shaped” and “inverted bell-shaped”. These two policies, and the uniform flow policy, are shown in Fig. 10. In the uniform flow policy, it is assumed that each P&D point is equally likely to be used. In the bell-shaped and inverted bell-shaped policies, we assume that P&D points located symmetrically in relation to the central P&D point have the same usage rate. Whereas the central P&D point is least likely to be used in a bell-shaped policy, it is most likely to be used in the inverted bell-shaped policy. Hence, the usage rates of P&D points decrease as they are located further away from the center in inverted bell-shaped policy whereas the furthest P&D points from the center are assumed to be the busiest points in a bell-shaped policy.

Fig. 10
figure 10

Material flow policies (line lengths indicate the density of usage rate)

Full size image

Because P&D points are symmetrically and equally-spaced in relation to the center of the warehouse, there should always be an odd number of P&D points that are evenly distributed around the central P&D point. We therefore refer to \( U_{0} \) as the usage rate of the central P&D point. Similarly, \( U_{i} \) refers the usage rate of the \( \left( {\frac{n + 1}{2} \mp i} \right)^{th} \). P&D point, represented by \( p_{{\frac{n + 1}{2} \mp i}} \), for all \( i = 1, \ldots ,\left( {n - 1} \right)/2 \). For instance, \( U_{1} \) refers the usage rate of \( p_{4} \) and \( p_{6} \) in a warehouse with nine P&D points (see Fig. 10).

In the uniform policy, \( U_{i} = \frac{1}{n}, \forall i = 0, \ldots ,\frac{n - 1}{2} \). To generate usage rates in the bell-shaped and inverted bell-shaped policies, we use Bender (1981)’s Pareto curve model, as used by several previous studies to calculate the probability of visiting storage locations in a warehouse under turnover-based storage (Pohl et al. 2011; Çelik and Süral 2014). In our implementation, Bender (1981)’s model shows the cumulative percentage of total material flows going through the P&D points. This cumulative activity level of a P&D point is represented by \( F\left( x \right) \), as shown in Eq. 10:

$$ F\left( x \right) = \frac{{\left( {1 + S} \right)x}}{S + x}\quad F\left( x \right) \ge 0 \,and \,x \le 1, S \ge 0 \,and\, S + x \ne 0; $$
(10)

x is the fraction of the total number of P&D points used, so \( F\left( x \right) \) is a cumulative distribution function defined for \( x \in \left[ {0,1} \right] \cdot S \) is the shape parameter that shows the skewness of the curve. Thus, we first calculate the activity level of each P&D point \( i\,(r_{i} ) \) for all \( n \) P&D points separately using Eq. 11. We then calculate the usage rate of P&D points using the equations in Table 7 for the respective material flow policy. For bell-shaped and inverted bell-shaped policies, except for the central P&D point, we take the arithmetic average of symmetric P&D points’ activity levels to calculate their usage rates:

Table 7 Usage rate of central and symmetric P&D points
Full size table
$$ r_{i} = F\left( {\frac{i}{n}} \right) - F\left( {\frac{i - 1}{n}} \right)\quad \forall i = 1,2, \ldots ,n\;{\text{where}}\;\mathop \sum \limits_{i = 1}^{n} r_{i} = 1. $$
(11)

5 Computational results

To determine the usage rates of the P&D points in both the bell-shaped and inverted bell-shaped policies, we assume that 50% of the incoming and outgoing materials pass through 20% of the P&D points. Thus, the shape parameter in Eq. 10 is 0.4. Table 8 shows the calculated usage rates for each P&D point in predetermined warehouse layouts for both bell-shaped and inverted bell-shaped policies. For instance, if there are 7 P&D points, the usage rate of the central P&D is 36.8% while the usage rates of the P&D points around the central one in both sides are 17.8%, 8.7%, and 5.1%, respectively.

Table 8 Usage rate of P&D points
Full size table

Although Francis (1967) showed that 2:1 is the optimal shape ratio for a one-block traditional warehouse to minimize the expected single-command distance from a centrally-located single P&D point, we also consider shape ratios of 1:1 and 3:1 to investigate their effects on both the warehouse layout and the expected single-command distance. To provide equal warehouse capacities, the warehouse sizes for the three shape ratios of 1:1, 2:1, and 3:1 are (70.71, 70.71), (100, 50), and (122.47, 40.82), respectively, using the notation of (L, H). We assume the gap between two adjacent P&D points (a) is 5 (pallet) units to enable several trucks or containers to park at the same time for loading or unloading. Therefore, a warehouse with shape ratios of 1:1, 2:1, and 3:1 can have a maximum of 13, 19, and 23 P&D points on the front cross aisle, respectively.

To provide an accurate comparison, we first solve the expected travel distance in a traditional one-block design for the predetermined warehouse sizes and material flow policies (see Table 12 in the appendix for its results). We then search for the optimal aisle angles and starting points of the single cross aisle in each problem using the PSO algorithm in the previous section. In order to test the robustness of the algorithm to randomness, we also conducted five replications.

The best solutions for each problem instance constructed by the number of P&D points, warehouse shape ratios, and material flow policies are shown in Table 12 in the appendix. According to the best solutions, the single cross aisle always originates from the middle of the front cross aisle, where \( m \) is 35.35, 50 and 61.2 at 1:1, 2:1 and 3:1 shape ratios, respectively, irrespective to the number of P&D points and material flow policies. Additionally, the cross aisle always takes an angle of \( \beta = \pi /2 \). This confirms to the Chevron design proposed by Öztürkoğlu et al. (2012). Moreover, the best solution for a single P&D point in a warehouse with a 2:1 shape ratio under each material flow policy is the Chevron design, which was previously found to be an optimal design for randomized storage by Öztürkoğlu et al. (2012). These results also validate our travel models and the optimization algorithm. That is the arrangement of the cross aisle simply divides the storage area into two equal regions. Additionally, the best angles for the picking aisles on the right and left sides of the cross aisle are approximately symmetric with respect to the angled cross aisle. We think that the following factors can explain these design characteristics in the best solutions: (1) the P&D point is located at the center of the front cross aisle; (2) other P&D points are symmetrically distributed around the first central P&D point; (3) usage rates of the P&D points are symmetric around the central P&D point. These design characteristics were also observed in previous studies with similar design and operational assumptions (Gue et al. 2012; Öztürkoğlu et al. 2014; Öztürkoğlu 2016). We can therefore easily analyze the similarities of the best designs for each shape ratio considering the angle of the picking aisles in the right region alone. Fig 11 presents changes in the angles of the picking aisles in the right region for each P&D problem for a given material flow policy and shape ratio. We also highlight the angle of the diagonal in the right region, which runs from \( m \) to the upper right-hand corner of the rectangle warehouse shape, as a base line to evaluate the obliquity of the picking aisles.

Fig. 11
figure 11

Angle of picking aisles and diagonal on the right side of the angled cross aisle

Full size image

Observation 1: The angles of picking aisles on the right increase as the number of P&D points increase for a given material flow policy and shape ratio.

As the number of P&D points increases, newly added P&D points move away from the center of the warehouse. Considering that the best angles of picking aisles are less than \( \pi /2 \), the travel distance from the P&D point leftwards in the right region is worse than the rectilinear distance (see example in Fig. 12a). Additionally, as new P&D points are inserted, the area of the travel region that is accessed by traveling rightwards from the P&D points decreases. Thus, the model increases the angle of picking aisles in the best designs to avoid leftwards travel as the number of P&D points increases. This is represented by the example in Fig. 12.

Fig. 12
figure 12

Effect of the angles of picking aisles on travel distance

Full size image

Let us consider two similar layouts where the angle of the picking aisles in Fig. 12a is smaller than that in Fig. 12b. It is clear that the travel distance from P&D point \( p_{i} \) to location (x,y) in region \( S \) is shorter in Fig. 12b than in Fig. 12a.

Observation 2: The angle of the picking aisles on the right becomes greater than the angle of the diagonal as the warehouse shape ratio increases.

While central picking aisles stay below the diagonal for a small number of P&D points in a warehouse with shape ratio 1:1, they move above the diagonal as both the shape ratio and the number of P&D points increase. As the shape ratio increases, the length of the front cross aisle increases while the length of the vertical cross aisle decreases. Hence, the model aims to increase the number of locations that can be reached from the longer cross aisle by locating the central picking aisle above the diagonal for higher shape ratios. Thus, the model gets more benefit from a longer cross aisle than a shorter one. Suppose that Fig. 13 represents two best solutions in equal-capacity warehouses with different shape ratios and single P&D points. It is easy to see that the model first locates the central picking aisle close to the shorter cross aisle so that the storage area (\( S \)) reachable from the longer cross aisle increases. It then facilitates travel to locations in region \( S \) by using the longer cross aisle more with an appropriate picking aisle angle. A similar observation was made and proved by Öztürkoğlu et al. (2012) for a centrally-located, single-P&D-point warehouses with various shape ratios.

Fig. 13
figure 13

Effect of shape ratio on the angle of picking aisles according to the angle of the diagonal

Full size image

Observation 3: Changes in the angles of picking aisles in the best designs increase less under the inverted bell-shaped policy than other policies.

As Fig. 11 shows, the slopes of the increment in angles of the picking aisles in the best designs increase over the flow policies in the order of bell-shaped, uniform, and inverted bell-shaped policies. This can also be shown by computing the average coefficient of variation of the picking aisle angles over the shape ratios: 0.06 for inverted bell-shaped; 0.08 for uniform; and 0.1 for bell-shaped. Thus, the best designs are more robust in terms of aisle orientations under an inverted bell-shaped policy than other policies.

We compare the best designs and the equivalent traditional one-block designs based on the improvement in the expected single-command distance, calculated by \( 100 \times {{\left( {E\left[ {D_{Traditional} } \right] - E\left[ {D_{Best - found} } \right]} \right)} \mathord{\left/ {\vphantom {{\left( {E\left[ {D_{Traditional} } \right] - E\left[ {D_{Best - found} } \right]} \right)} {E\left[ {D_{Traditional} } \right]}}} \right. \kern-0pt} {E\left[ {D_{Traditional} } \right]}} \). Figure 14 shows the percentage improvements of the best designs over the equivalent traditional design for each P&D problem under different material flow policies. As seen in Fig. 14, the improvement decreases as the number of P&D points increases, irrespective of the material flow policy. The reason for this is that travel patterns in the best designs are close to rectilinear as in the traditional design because the angle of the picking aisles in the right region increase with an increasing number of P&D points.

Fig. 14
figure 14

Improvement of the best found aisle designs over the equivalent traditional designs under varying material flow policies

Full size image

Observation 4: A warehouse with a 1:1 shape ratio and multiple P&D points has a longer single-command travel distance than warehouses with 2:1 and 3:1 shape ratios when there are symmetrically-distributed P&D points around the center of the front cross aisle.

As the length of a warehouse increases, the distance from all P&D points to locations close to the rear of the warehouse increases. Therefore, increasing width up to some point should reduce single-command distances when P&D points are solely located at the front of the warehouse. A similar observation was made and proved by Francis (1967) and Bassan et al. (1980). They showed that a warehouse that is twice as wide as its depth (2:1 shape ratio) is optimal for single-command operations when there is a single and centrally-located P&D point at the front. Additionally, Thomas and Meller (2014) showed that the optimal shape ratio is 2:1 for single-command travel in a traditional one-block warehouse with multiple P&D points. However, our results show that 2:1 warehouses do not always provide shorter single-command distances than 3:1 warehouses for multiple P&D points. The results in Fig. 14 show that the best warehouse designs with 3:1 shape ratios are slightly more efficient than the best designs for 2:1 warehouses if there are more than 7 P&D points at the front, irrespective to the material flow policy.

Observation 5: The inverted bell-shaped material flow policy provides shorter single-command travel distances than the uniform and bell-shaped policies if multiple P&D points are symmetrically distributed around the central P&D point at the front.

Fig 15 shows that the best designs under the inverted bell-shaped policy are always superior to the other best designs under the other flow policies, regardless of the number of P&D points and the warehouse shape ratio. Moreover, the best designs under the uniform policy are also superior to those under the bell-shaped policy.

Fig. 15
figure 15

Improvement of the best-found aisle designs according to the shape ratios

Full size image

These results show that increasing flow through P&D points close to the center of the warehouse reduces the expected single-command distance. This result might be expected because the central P&D point is the closest point to the centroid of a rectangular area, which lies at intersection of two diagonals and is equal to (\( H/2, L/2 \)).

In conclusion, the best designs under the inverted bell-shaped policy reduce expected single-command travel distances by 8 to 20% compared to the equivalent traditional design with a given shape ratio and P&D points. For example, Fig. 16 shows the best aisle designs developed under a 3:1 shape ratio and inverted bell-shaped policy for different numbers of P&D points.

Fig. 16
figure 16

The best found aisle designs for shape ratio 3:1 under inverted bell-shaped flow policy

Full size image

5.1 The performance of the PSO algorithm

The developed PSO algorithm was coded in Java environment and run on a computer with Intel® Core i7, 2.50 GHz and 8 GB RAM operating on MS Windows. In each replication we changed the random number generator’s seed and collected how long the algorithm run until it was terminated and the last iteration where the best solution was found, as well as the best solution. In total, the algorithm solved 435 problems: (5 replications x 3 flows)x(7 + 10 + 12 P&D point-cases). Table 9 demonstrates the summary of those results. As seen in the table, the PSO algorithm produces very similar solutions over replications (average Gap is 0.03% over all problems). The algorithm found the best solutions in average of about 6000 iterations. In some problems (17 out of 435), the algorithm is terminated around 11,000 iterations because they found their best solution around 10,500 iterations. This shows that our termination policy seems to work appropriately. As expected, the computational time to solve the problem increases as the number of P&D points increases. For instance, it takes 968 s (or 16.1 min) to solve the problem with 2:1 shape ratio and 19 P&D points. To solve a similar problem, which has two P&D points on the front and 2:1 shape ratio with a width of 19 aisles, took 1597.8 min by using the Öztürkoğlu et al. (2014)’s discrete constructive aisle model. When comparing the computational burdening of our model with Öztürkoğlu et al. (2014)’s model, we can easily confirm our discussion (number 1) in Sect. 1.1. Hence, these results show that our model and the algorithm provide good solutions in reasonable amount of time for the warehouse design problem with multiple P&D points.

Table 9 Computational performance of the PSO algorithm
Full size table

5.2 The designs with unsymmetrical P&D points and irregular material flow rates

According to the observations and discussions made in the previous section, we can simply say that the best designs with multiple P&D points under different material flow policies through them, the best designs seem to have similar characteristics with the Chevron. The main reason of this is that the P&D points are symmetrically distributed around the center, as well as their usage rates. However, some might ask whether the best designs have still the similar characteristics when P&D points are unsymmetrically-positioned and their usage rates are irregular. To answer that question and to show how our model could be applied to unsymmetrical P&D allocation with irregular flows, we generate one example problem instance with 3 P&D points. In this problem instance, the active P&D points are the second, fourth and the sixth nearest P&D points on the left side of the central P&D point. The usage rates of these P&D points are assumed to be 40%, 20% and 40%, respectively. We then solve this problem instance in the predefined three warehouse sizes.

The algorithm in Table 10 explains how to solve the new problem instance. This algorithm is required to solve the new problem because the aforementioned cases and the models were developed under the assumption of the symmetric P&D points and flows around the center (see proposition 1). Here, we show that how these assumptions could be easily relaxed and our models could be used for unsymmetrical P&D allocations with irregular flows.

Table 10 The algorithm for calculating expected single-command travel distance for unsymmetrically-located P&D points with irregular flows
Full size table

According to the predefined warehouse sizes, we generated three problems because each has different maximum number of P&D points. These problems are defined by the vector of \( U \) as given in Table 11.

Table 11 The new problems with unsymmetrical P&D points and irregular flows
Full size table

As seen in Fig. 17, the best solutions do not have similar characteristics with either the Chevron or the other best solutions found in previous section. Because the active P&D points are position on the left of the center and there is no flow through the central P&D point, the cross aisle originates from the rightmost active P&D point. The cross aisle is then positioned to rightwards to facilitate to travel to the right region with an angled picking aisle. It seems that the cross aisle moves away from the upper rightmost corner as the width of warehouse increases. The angles of picking aisles are not symmetric anymore. As the angle of picking aisles on the right is very close to the angle of its diagonal, the angles of picking aisles on the left is less than the angle of its diagonal to alleviate some portion of the inefficient travel (worse than rectilinear travel) from the P&D points to the left region. Similar to our previous observations, warehouse with 2:1 shape ratio also superiors than the others while the warehouse with 1:1 is still the worse. Last, these designs show that the locations of active P&D points and their usages may generate unsymmetrical designs. Therefore, practitioners should be aware of this and be careful when designing a warehouse.

Fig. 17
figure 17

The best solutions of the problems with unsymmetrical P&D points and irregular flows. The arrows show the active P&D points and their representative usage rates

Full size image

6 Summary and conclusion

In this study, we inserted a single cross aisle into a warehouse space to determine the best aisle designs for single-command operations with multiple P&D points. In contrast to Öztürkoğlu et al. (2012), who proposed a Chevron design, we relaxed the position of the single cross aisle. We divided the main design problem into six cases, where the variables were position and angle of the cross aisle, and the angles of the picking aisles, to efficiently develop the distance functions. The operational assumptions of our model were (i) randomized storage policy, (ii) single-command operation, and (iii) flow through multiple P&D points. We assumed that the P&D points, from where incoming and outgoing pallets of products move, are at the front of the warehouse and symmetrically distributed around the center. However, the proposed travel distance functions and the model can also be used for unsymmetrical P&D point configurations with irregular flows We presented an algorithm that shows how to solve the warehouse design problem with unsymmetrical P&D points using our proposed model. During the search for the best aisle designs, we also examined the effect of three warehouse shape ratios and three material flow policies, called uniform, bell-shaped, and inverted bell-shaped, that determine the usage rates of the P&D points.

First, the best designs in the present study showed that the Chevron is still the best for a warehouse with a 2:1 shape ratio and a single P&D point, irrespective of the material flow policy. As the number of P&D points increases, while the cross aisle still originates from the central P&D point at an angle of \( \pi /2 \) in the best designs, the angles of the picking aisles on the right and left sides of the cross aisle approach \( \pi /2 \), irrespective of the shape ratio and material flow policy. The best designs obtained under the inverted bell-shaped policy were more robust than those under other flow policies regarding changes in the angles of the picking aisles. While flow policies had no significant effect on aisle design, warehouse shape ratios affected both aisle design and distance savings compared to the equivalent traditional design. For instance, we showed that a warehouse with a 1:1 shape ratio always has a higher expected single-command distance than 2:1 and 3:1 shape ratios. Hence, this result suggests that warehouse managers should expand their warehouses horizontally as long as the P&D points are located on the front of the warehouse. Although the best designs with a 2:1 shape ratio provide short travel distances for few P&D points, those with a 3:1 shape ratio have slightly shorter single-command distances for more than 7 P&D points. For instance, the best designs with 7 P&D points for 2:1 and 3:1 shape ratios offered 12%, 10%, and 15% savings on the expected single-command distance over the equivalent traditional design under uniform, bell-shaped, and inverted bell-shaped policies, respectively.

The results also show that the inverted-bell shape policy leads shorter travel distances than the uniform and bell-shaped policies. Hence, this result suggests warehouse managers to concentrate their flows toward the center if there are symmetrically allocated multiple P&D points on one side of the warehouse. Additionally, the managers of the warehouses that implemented Fishbone-like designs highlighted several extra benefits of non-traditional aisle designs. They mentioned that forklift-drivers easily access to picking aisles from the P&D point because of the angled aisles, which provides 45-degree turn instead of 90-degree as in traditional layouts. The best proposed designs in this study could also provide similar benefits to workers in industry, hence it could increase productivity. Moreover, the proposed designs in this study has even more advantages than Fishbone-like designs such that Chevron-like designs allow direct access from any point on the front cross aisle to storage locations due to slanted aisles. As a result, this study provides both many observations and a model for designing pallet-in pallet-out warehouses, where single-command operation is fully utilized, to answer the most commonly asked questions about non-traditional designs by warehouse managers: “what if there are multiple P&D points?” (Meller and Gue 2009).

To extend this study, researchers could relax any of the abovementioned design and operational assumptions (see them in Sect. 2 in details). Thus, researchers could develop models to incorporate two angled cross aisles in warehouses, different storage policies such as turnover or class-based like Bortolini et al. (2019), or different locations of P&D points like Öztürkoğlu et al. (2014).