Performance comparison of feedforward neural network training algorithms in modeling for synthesis of polycaprolactone via biopolymerization

Abstract

This paper reports the biopolymerization of ε-caprolactone, using lipase Novozyme 435 catalyst at varied impeller speeds and reactor temperatures. A multilayer feedforward neural network (FFNN) model with 11 different training algorithms is developed for the multivariable nonlinear biopolymerization of polycaprolactone (PCL). In previous works, biopolymerization carried out in scaled-up bioreactors is modeled through FFNN. No review discussed the role of different training algorithms in artificial neural network on the estimation of biopolymerization performance. This paper compares mean absolute error, mean square error, and mean absolute percentage error (MAPE) in the PCL biopolymerization process for 11 different training algorithms that belong to six classes, namely (1) additive momentum, (2) self-adaptive learning rate, (3) resilient backpropagation, (4) conjugate gradient backpropagation, (5) quasi-Newton, and (6) Bayesian regulation propagation. This paper aims to identify the most effective training method for biopolymerization. Results show that the quasi-Newton-based and Levenberg–Marquardt algorithms have the best performance with MAPE values of 4.512, 5.31, and 3.21% for the number of average molecular weight, weight average molecular weight, and polydispersity index, respectively.

Introduction

Polycaprolactone (PCL), which is largely produced through chemical polymerization, is emerging as a preferred biodegradable plastic in the recent years. PCL has remarkable resistance to water, oil, solvent, and chlorine; hydrophobic; and relatively high biodegradability and biocompatibility, making it a highly potential biomaterial and environment-friendly thermoplastic (Bassi et al. 2011). Although the synthetic production of PCL has been established, it has a major drawback of having metallic catalyst residues, which can cause adverse effect, especially in biomaterial application (Labet and Thielemans 2009). As a result, green methods of producing PCL via biopolymerization are investigated widely. Biopolymerization using enzyme as catalysts is known as enzymatic polymerization. The enzymatic polymerization of PCL, as an alternative to the conventional chemical polymerization, addresses the issue of metallic residues on the final product. Biopolymers produced using biocatalyst show no signs of toxic residues (Varma et al. 2005).

Several enzymatic polymerization techniques, such as condensation, anionic, cationic, and ring opening polymerizations (ROP), are available. Among these techniques, ROP is the most preferred (Varma et al. 2005). In the past decade, PCL production via ROP has been extensively investigated, and different enzymes, such as lipase Candida antarctica (CA), lipase Candida cylindracea (CC), lipase Pseudomonas fluorescens (PF) (), lipase PP (PP porcine pancreas), lipase PC (Pseudomonas cepacia), and lipase RJ (Rhizopus japonicus) (Uyama et al. 1996; Varma et al. 2005; Torres et al. 2010) and non-lipase enzymes, such as Humicola Insolens Cutinase (HIC) (Hunsen et al. 2007), have been used. The scope and significance of enzymatic polymerization are wide, and its other aspects should be explored. The molecular weight of a polymer determines its quality and application. This paper addresses molecular weight prediction accuracy. The accuracy of molecular weight prediction in a polymer can be affected by the nonlinear relationship in the biopolymerization process parameters, such as reaction temperature, reactor impeller speed, polymerization time, and catalyst type (Kobayashi and Makino 2009).

The artificial neural network (ANN) is an emerging technique used for accurately predicting the molecular weight of PCL. ANN mimics the biological neural network in the human brain. Although ANNs are not smart, they can analyze and recognize the patterns of the input and target data inserted and create rules to solve complex problems (Lee-Cosio et al. 2012). Most research in this field has been conducted for the production of PCLs with desired molecular weights through the optimization of the main polymerization parameters. Arumugasamy and Ahmad (2010) modeled a feedforward neural network (FFNN) for the large-scale production of PCL to investigate the effect of temperature and impeller speed on PCL biopolymerization. Arumugasamy et al. (2012) conducted a modeling study on PCL production in a flask and reactor and used lipase Novozyme 435 as catalyst. Khatti et al. (2017) carried out a study on the analysis of ANN and response surface methodology to determine effective parameters, such as polymer concentration, voltage, and nozzle-to-collector distance, on the diameter of electrospun PCL (Khatti et al. 2017).

A remarkable drawback in using ANN is the long duration required for training a network and ensuring the convergence of a local minimum value. Different training algorithms that improve performance in different aspects have been proposed for this drawback. Xinxing et al. (2013) compared 12 different ANN training algorithms based on the mean absolute percentage error (MAPE) and training time for electricity load forecasting. Forouzanfar et al. (2010) compared the different training algorithms for oscillometric blood pressure estimation. Ghaffari et al. (2006) performed four different training algorithms in the modeling of bimodal drug delivery on predictive ability. The outcome of these studies determines the best training algorithm, which provides optimal training duration and accurate prediction that are suitable for their processes. The same approach is attempted for biopolymerization in this work.

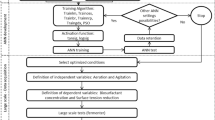
The objective of this work is to conduct experimental studies in a bioreactor setup in order to optimize the parameters, namely time, temperature, and impeller speed. We used the experimental data to develop an empirical model for the biopolymerization of ε-caprolactone (ε-CL) to PCL. FFNN was used. A total of 11 different training algorithms that belong to six classes, namely additive momentum, self-adaptive learning rate, resilient backpropagation, conjugate gradient, quasi-Newton, and Bayesian regulation propagation were evaluated. The dataset collected from 84 samples from the biopolymerization experiments was used for the evaluation. Number average molecular weight (M_n), weight average molecular weight (M_w), and polydispersity index (PDI) estimation from biopolymerization using different training algorithms are compared in term of estimation errors, which are mean absolute error (MAE), mean square error (MSE), and mean absolute percentage error (MAPE) with the experimental results.

Materials and methods

Preparation of PCL

Infors-HT Labfors bioreactor with an effective volume of 2 L was used for the scale-up production of PCL. Parameters, such as reactor temperature, reactor impeller speed, and polymerization time, were selected. The monomer used in this work was ε-CL, which was purchased from Merck Private Limited. Toluene was used as solvent. Toluene had undergone drying over calcium hydride and distillation under nitrogen atmosphere prior to its use as solvent. Candida antarctica lipase B (CALB) used was purchased from Science Technics Private Limited, Penang, Malaysia. The ratio of solvent to monomer to catalyst was fixed at 2:1:10 (v/v/wt) (Ajay and Gross 2000).

Biopolymerization process

The monomer, enzyme, and solvent were fed into the bioreactor. The desired bioreactor temperature was set, and a computer was connected to the bioreactor. When the desired temperature was attained, the stirrer was switched on at the preset speed. During polymerization, sampling was conducted every hour for 7 h. Polymerization was performed at 60, 70, and 80 °C. The temperatures were selected on the basis of the conclusion from the conical flask results obtained in a previous study (Arumugasamy and Ahmad 2010). The rotational speed of the impeller was varied (250, 500, 750, or 1000 rpm) (Chaibakhsh et al. 2012).

PCL analysis

Gel permeation chromatography (GPC) analysis was performed with Waters 2414 Refractive Index Detector, Waters 1525 Binary HPLC Pump, and three Waters GPC columns, two Styragel^® HR-4 columns, and one HR-5E column for the observation of molecular weights (particle size: 5 μm, Ø 4.6 mm × 300 mm). The analysis conditions were as follows: tetrahydrofuran as eluent, flow rate of 1.0 mL/min, column temperature of 40 °C, and analysis time of 45 min/cycle. The calibration curves for GPC analysis were obtained by using PCL standards.

We performed GPC analysis on three different PCL standards PCL with known molecular weights to plot the calibration curve. Table 1 shows the molecular weight of PCL standard provided by the supplier and the values of molecular weight from the GPC analysis. After calibration, the molecular weight of the samples obtained from the bioreactor experiments was analyzed (Figs. 1, 2).

Table 1 Commercial standard PCL molecular weight with GPC

Fig. 1

Schematic diagram of batch bio-reactor

Fig. 2

Schematic diagram of gel permeation chromatography (GPC) system

ANNs

ANN can learn a vast range of application and provide solution by training samples from a particular application. ANN can predict and generalize and has been used to solve complex problems in control, optimization, and classification. It is a data-driven nonlinear model that is formed through the use of artificial neurons and by mapping biological-inspired computational model. Similar to biological neurons, a neural network is composed of three common layers, namely input, hidden, and output. The neurons are connected via coefficients (weights), which are composed of neural structures. The connection among the neurons has a remarkable impact to the ANN. Generally, connection has two main types: feedback (recurrent) and feedforward connections. Feedback is a connection where the output of either the previous or the same layer returns to the input layer. In feedforward, the output does not return to the input neurons. FFNN is a popular and successful neural network architecture that suits extensive range of applications and is proven to be a universal approximator (Hornik et al. 1989).

Three inputs: polymerization time, reactor temperature, and impeller stirring speed and three outputs: M_n, M_w, and PDI were considered in this work. An FFNN with two-to-five hidden layers (depending on the training algorithm) is used.

Figure 3 presents a feedforward multilayer perception network trained with the Levenberg–Marquardt (LM) training algorithm. The network has an architecture structure of 3–4–3, which corresponds to the number of nodes in the input layer, hidden layer 1, hidden layer 2, and output layer, respectively. This indicates that there are three neurons in the input layer referring to time, temperature, and impeller speed, followed by four neurons in the hidden layer and three neurons in the output layer which are the M_n, M_w, and PDI. Figure 4 shows the schematic of fundamental building block for neural networks. First, the scalar input p represents time, impeller speed, or temperature. It is multiplied to a scalar connection weight w, which can be positive or negative, for the formation of a weighted input wp. The weighted input is combined with a scalar bias b, which has a constant input of 1, to form a net input. Finally, the net input is passed through a transfer function f to produce scalar output a for a selected neuron.

Fig. 3

Schematic representation of a multilayer perceptron feedforward network consisting of three inputs, one hidden layer with six neurons and three outputs

Fig. 4

Schematic representation of fundamental building block for neural networks

Data normalization

Data normalization is generally performed for reducing or eliminating the influence of the variations of attributes, such as large numeric ranges that dominate small numeric ranges and scaling of input variables performed prior to forecasting (Sulaiman and Wahab 2018). Min–max normalization is adopted in this research. The data are normalized in the range of [− 1,1], as shown in Eq. (1):

$$y = (y_{ \hbox{max} } - y_{ \hbox{min} } ) \frac{{x - x_{ \hbox{min} } }}{{x_{ \hbox{max} } - x_{ \hbox{min} } }} + y_{ \hbox{min} } ,$$

(1)

where x = original data, x_max = minimum value in the original data, x_min = maximum value in the original data, y = normalized data, y_max = maximum value in the normalized data (default is 1), y_min = minimum value in the normalized data (default is −1).

Hidden layer selection

The hidden layer is an intermediate layer between the input and output layers. Neurons in the hidden layer are activated by a function. Table 2 summarizes the capabilities of neural network architectures with various hidden layers (Heaton 2008). In general, one hidden layer is selected for most of the process. Two hidden layers are generally used for modeling data with discontinuities, such as the sawtooth wave pattern. The use of two hidden layers rarely improves the model and may introduce great risk of convergence in a local minima. Therefore, a process that requires two hidden layers is rarely encountered. The use of more than two hidden layers has no theoretical reason. In this work, an FFNN with one hidden layer is used. One hidden layer is sufficient to capture the intricacy of ring opening polymerization process, and the risk of converging to local minima becomes almost nil.

Table 2 Determining the number of hidden layers

Hidden neuron selection

Determining the number of neurons in a hidden layer is an important characteristic of an FFNN or perceptron network. Neuron collection determines the overall neural network architect and greatly influences the final output. If inadequate number of neurons are used, then the network is unable to model complex data, resulting in underfitting. If excessive unnecessary neurons are present in the network, then the training time may become excessively long and cause overfitting. When overfitting occurs, the network starts to model random noise in the data. The outcome may cause a model to fit the training data extremely well but generalizes poorly to new data. Usually, rule-of-thumb methods are used to determine a suitable number of neurons to be used in the hidden layers, such as the following (Karsoliya 2012):

• 1. The number of hidden neurons should be between the number of neurons in the input and output layers.

• 2. The number of hidden neurons should be 2/3 the number of neurons in the input layer. If the number is insufficient, then add the number of neurons in the output layer.

• 3. The number of hidden neurons should be less than twice the number of neurons in the input layer.

This work implemented a cross-validation technique where the value of hidden nodes for training and testing varied based on trial and error. The number of hidden nodes with the lowest mean sum squared error and high correlation coefficient “r” is selected.

Training algorithms

As mentioned previously, ANN is programmed rather than trained because of its capability of learning. ANN can self-adjust the weighted connection of the links found among neurons in the network to produce the desired output through algorithm training. Training is the core process that enables the network to learn from previous data. After sufficient training, the network can process and respond to the new set of inputs. Optimal weights are then determined. This process is normally performed by identifying the accuracy between the desired target and the network output and then minimizing them according to the weights. In this research, three different performance functions were used for the evaluation of target and output accuracy. These functions, namely (1) MAPE, (2) MAE, and (3) root MSE (RMSE), were used to evaluate the measure of accuracy.

$${\text{MAPE}} = \frac{1}{n}\mathop \sum \limits_{t = 1}^{n} \left| {\frac{{A_{t} - F_{t} }}{{A_{t} }}} \right| \times 100,$$

(2)

$${\text{MAE}} = \frac{1}{n}\mathop \sum \limits_{t = 1}^{n} \left| {F_{t} - A_{t} } \right|,$$

(3)

$${\text{RMSE}} = \frac{1}{n}\mathop \sum \limits_{t = 1}^{n} \left( {F_{t} - A_{t} } \right)^{0.5} ,$$

(4)

where F_t = forecasted value, A_t = actual value, n = number of samples.

Backpropagation is a technique used by calculating the gradient and minimizing the error through batch or incremental styles. In this research, the main consideration is that the training algorithms for backpropagation can be categorized into six different classes, namely (1) additive momentum (gradient descent with momentum); (2) self-adaptive learning rate (LR) (variable LR gradient descent and gradient descent with momentum and adaptive LR); (3) resilient backpropagation; (4) conjugate gradient backpropagation (scaled conjugate gradient (SCG), conjugate gradient with Powell–Beale restarts, Fletcher–Powell conjugate gradient, and Polak–Ribiére conjugate gradient); (5) quasi-Newton (Levenberg–Marquardt (LM), BFGS quasi-Newton, and one-step secant); and (6) Bayesian regulation propagation (Bayesian regularization). The ANN presented was conducted by using MATLAB™ R2014b, and the training algorithms used were as follows:

• (a) Additive momentum (training function: traingdm)

In this algorithm, the variation tendency of the error curve that tolerates small changes in the neural network and the error of the gradient are considered during the backpropagation of the network. This algorithm can prevent the network from falling into local minimum point in the training process. An additive value that is proportional to the value of the previous weights is added together with the thresholds of change to each change of the weight and threshold. Threshold is referring to $\frac{{\partial {\text{E}}}}{{\partial {\text{X}}}}$. Weight is initiated by the system. A new change of the weights and threshold is generated based on the backpropagation algorithm. The adjust function ∆X is as follows:

$$\Delta X\left( {t + 1} \right) = {\text{mc}} \times \Delta X\left( t \right) + {\text{Ir}} \times {\text{mc}} \times \frac{\partial E}{\partial X}$$

(5)

where t = training times, mc = momentum factor (normally 0.95), Ir = LR (a constant number that ranges from 0 < Ir ≤ 1), E = error function.

The downsides of this training algorithm are that it is time consuming and its parameters can only be determined through experiments.

• (b) Self-adaptive LR (training function: traingda, traingdx)

Slow speed for convergence during training is mainly caused by the improper selection of LR. An adaptive LR attempts to keep the learning step size as large as possible and ensures that the learning is stable. The function expression is the same as the additive momentum, but the LR, Ir, is not a constant variable:

$${\text{Ir}}\left( {t + 1} \right) = \left\{ {\begin{array}{*{20}c} {1.05{\text{Ir}}\left( t \right)} \\ {0.7{\text{Ir}}\left( t \right)} \\ {{\text{Ir}}\left( t \right)} \\ \end{array} } \right\},$$

(6)

$$\begin{aligned} {\text{MSE}}\left( {t + 1} \right) & < {\text{MSE}}\left( t \right) \\ {\text{MSE}}\left( {t + 1} \right) & > 1.04{\text{MSE}}\left( t \right) \\ \end{aligned}$$

• (c) Resilient backpropagation (training function: trainrp)

A sigmoid transfer function is usually used in the hidden layers of a multilayer network. Therefore, the slope of the transfer function must approach zero as the input increases. Sigmoid function may have a small magnitude of gradient. Therefore, when the weights and biases are far from its optimal values, only small changes in the weights and biases occur. Thus, this process becomes time consuming. Resilient backpropagation training algorithm is usually used for eliminating the harmful effects of partial derivate magnitudes, and only the plus or minus symbol of the derivative, $\Delta_{ij}^{\left( t \right)}$, is considered for the direction of updating the correct values. This approach is a clear and simple learning rule with rapid speed and reaches the best convergence without selecting parameters.

$$\Delta X_{ij}^{\left( t \right)} = \left\{ {\begin{array}{*{20}c} { - \Delta_{ij}^{\left( t \right)} ,\, {\text{if}} \frac{{\partial {\text{E}}}}{{\partial {\text{X}}}} > 0} \\ { + \Delta_{ij}^{\left( t \right)} , \,{\text{if}} \frac{{\partial {\text{E}}}}{{\partial {\text{X}}}} < 0} \\ {0, {\text{else}}} \\ \end{array} } \right.,$$

(7)

where $\frac{\partial E}{\partial X}$ = Sum of gradient information for all the patterns, t = at the time (t).

• (d) Conjugate gradient backpropagation (training function: traincgb, traincgp, trainscg)

Conjugate gradient backpropagation is an algorithm that combines conjugate gradient and line search strategies to converge faster and minimize the performance function. Most conjugate gradient backpropagations have processes for updating weight and threshold. The cost of calculation is low because second-order function method eliminates the calculation and storage of second-order derivatives. It starts by searching P_o in the steepest descent direction -g_o (negative of the gradient) on the first iteration.

$$P_{0} = - g_{0} .$$

(8)

Next, the weight and threshold value (X) are determined by using the line search method

$$X_{t + 1} = X_{t} + \alpha_{t} P_{t} ,$$

(9)

where P = search direction, $\alpha$ = parameter used to decrease the gradient.

• (e) Quasi-Newton (training function: trainbfg, trainlm, trainoss)

Newton’s method provides optimization. Newton’s method often converges faster than conjugate gradient method. However, the computation of Hessian matrix (second derivative) is complex and expensive for FFNN. An algorithm that does not compute the second derivative, known as quasi-Newton method, is proposed to overcome this issue. The basic step of Newton’s method is

$$X_{t + 1} = X_{t} + A_{t}^{ - 1} g_{t} ,$$

(10)

where A_t = Hessian matrix.

• (f) Bayesian regulation backpropagation (training function: trainbr)

In the Bayesian regulation framework, weights and biases are assumed to be random variables with specified distributions on the basis of LM optimization. The combination of squared errors and weights are minimized for the generalization of a remarkable network. The Bayesian regulation occurs within the LM algorithm. Jacobian performance, jX, is determined on the basis of the weight and bias of variable X through backpropagation. The variables are adjusted according to the LM algorithm.

$$\begin{aligned} jj & = jX*jX, \\ je & = jX*E, \\ dX & = - \left( {jj + I*mu} \right)/je, \\ \end{aligned}$$

(11)

where E = all errors, I = identity matrix.

Results and discussion

Effect of reactor impeller speed on PCL molecular weight

Figures 5, 6 and 7 explain the relationship between biopolymerization time and molecular weight at 60, 70, and 80 °C with a ε-CL-to-toluene ratio of 1:2 (v/v). Each plot exhibits the molecular weights of polymers obtained at varied impeller speeds, namely 250, 500, 750, and 1000 rpm. The trend of the plot is uniform at all impeller speeds.

Fig. 5

Effect of reactor impeller speed on molecular weight with reaction time at 60 °C

Fig. 6

Effect of reactor impeller speed on molecular weight with reaction time at 70 °C

Fig. 7

Effect of reactor impeller speed on molecular weight with reaction time at 80 °C

Figure 5 shows the behavior of the impeller at 60 °C. An M_n value of 2902 g/mol is obtained at the third hour at rotation speed of 250 rpm. An M_n value of 1677 g/mol is obtained at the first hour and at rotational speed of 500 rpm. Figure 6 shows the variation of molecular weight with reaction time at a temperature of 70 °C. Figure 6 indicates the trend for 70 °C at rotational speeds of 250, 500, 750, and 1000 rpm. An M_n value of 3095 g/mol is obtained at the second hour at rotational speed of 250 rpm. An M_n value of 1444 g/mol is obtained at the first hour at rotational speed of 500 rpm. Figure 7 shows the effect of 80 °C on the rotational speed of the impeller. An M_n values of 3091 and 2194 g/mol are obtained at rotational speed of 500 and 1000 rpm, respectively, in the third hour. This non-uniform behavior can be due to the mixing effect, which may have affected enzyme behavior, which in turn may have affected the polymer molecular weight. Possible explanations may lie in the differences among the heat transfer rates.

The overall conclusion based on Figs. 5, 6 and 7 is that the maximum molecular weight of PCL obtained is 3095 g/mol at 70 °C when 250 rpm for 2 h. Furthermore, at high impeller speed, the molecular weight produced by PCL is consistently varying. This instability can be due to the formation of vortices and dead zones in the reactor, leading to poor mixing effect. This phenomenon contributes to the collisions of radicals and the termination of polymerization. The increase in reaction temperature, from 70 to 80 °C, causes a slight reduction in the molecular weight of the sample (Fig. 7). At high temperatures, the propagation rate is enhanced. However, the increased movement of chains inside the reactor causes a thermal effect that resulted in the depletion of the monomer. The results obtained at low impeller speeds are better than those obtained at high values. The molecular weight obtained from this analysis clearly indicates that the molecular weight lies within the range of 1500–3000 g/mol. Therefore, uniformity in the molecular weight values is maintained.

Comparison of neural network algorithm results

The objective of this research is to compare different types of backpropagation training algorithms used in building FFNN models for predicting the M_n, M_w, and PDI at the end of PCL biopolymerization in a batch mode. The best training algorithm is selected on the basis of the fitting of the graphs with least MAPE, MAE, and RMSE values for the training of the model for PCL molecular weight prediction. The datasets used in the research are data collected in a scaled-up PCL production study. The data contain 84 samples that exhibit six features, namely polymerization time, reaction temperature, impeller speed, M_n, M_w, and PDI. A total of 58 samples are randomly selected as training dataset (70%). Another 13 samples are randomly selected as validation dataset (15%) used for the construction of neural network models using different training algorithms, and the last 13 samples are used as testing dataset (15%) to access the models. For this purpose, three different performance functions: MAE, MAPE and MSE, are adopted.

The parameters of the network are as follows: LR, 0.05; maximum amount of epoch, 1000; and level of error, 0.001. During the data processing, the number of neurons in the hidden layer is adjusted in numerous iterations, ranging from 1 to 20, and different weightages for training, testing, and validation are performed. The best performance for each algorithm is tabulated as follows:

Figures 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 and 18 show the comparison between the actual and predicted data, that is, M_n, M_w, and PDI for various training algorithms. The gradient decent with momentum backpropagation training algorithm has one hidden neuron as the optimal value because it provides the lowest MSE value (1.326; Table 3). Gradient descent with adaptive LR backpropagation training algorithm has five hidden neuron as optimum because the lowest MSE value is 0.395. Gradient descent with momentum and adaptive LR backpropagation training algorithm has 10 hidden neurons because the lowest MSE value is 0.333. Resilient backpropagation training algorithm has three hidden neuron because the lowest MSE value is 0.318. Conjugate gradient backpropagation with Powell–Beale restart training algorithm shows two hidden neuron because the lowest MSE value is 0.335. Conjugate gradient backpropagation with Polak–Ribiére updates 12 hidden neuron as optimum because the lowest MSE value is 0.315. SCG backpropagation training algorithm has 10 hidden neurons because the lowest MSE value is 0.206.

Fig. 8

Graph of actual data versus predicted data in series under gradient descent with momentum backpropagation training algorithm for combined data of training, testing and validation

Fig. 9

Graph of actual data versus predicted data in series under gradient descent with adaptive learning rate backpropagation training algorithm for combined data of training, testing and validation

Fig. 10

Graph of actual data versus predicted data in series under gradient descent with momentum and adaptive learning rate backpropagation training algorithm for combined data of training, testing and validation

Fig. 11

Graph of actual data versus predicted data in series under resilient backpropagation training algorithm for combined data of training, testing and validation

Fig. 12

Graph of actual data versus predicted data in series under conjugate gradient backpropagation with Powell–Beale restarts training algorithm for combined data of training, testing and validation

Fig. 13

Graph of actual data versus predicted data in series under conjugate gradient backpropagation with Polak–Ribiére updates training algorithm for combined data of training, testing and validation

Fig. 14

Graph of actual data versus predicted data in series under scaled conjugate gradient backpropagation training algorithm for combined data of training, testing and validation

Fig. 15

Graph of actual data versus predicted data in series under Levenberg–Marquardt backpropagation training algorithm for combined data of training, testing and validation

Fig. 16

Graph of actual data versus predicted data in series under one-step secant backpropagation training algorithm for combined data of training, testing and validation

Fig. 17

Graph of actual data versus predicted data in series under BFGS quasi-Newton backpropagation training algorithm for combined data of training, testing and validation

Fig. 18

Graph of actual data versus predicted data in series under Bayesian regulation backpropagation training algorithm for combined data of training, testing and validation

Table 3 Mean-squared error in test data for different number of hidden neuron in different training algorithms

Table 4 Comparison of NN-based approach using different training algorithms in terms of estimation error in training data (MAE, MAPE and MSE)

LM backpropagation has 10 hidden neurons as optimum because the lowest MSE value is 0.095. One-step secant backpropagation has seven hidden neurons as optimum because the lowest MSE value is 0.315. BFGS quasi-Newton backpropagation has eight hidden neurons as optimum because the lowest MSE value is 0.309. Bayesian regulation backpropagation has 11 hidden neurons as optimum because the lowest MSE value is 0.100.

The estimation errors in terms of MAPE, MAE and RMSE for the FFNN using different training algorithms are represented in Tables 4, 5 and 6 for training, testing, and validation data, respectively. The models with low MAPE, MAE, and MAPE values are considered remarkable fit models. Two differences are observed in each training algorithm, namely calculation method and convergence quality, which can also be known as the mathematical equation behind each training algorithm and prediction ability.

Table 5 Comparison of NN-based approach using different training algorithms in terms of estimation error in testing data (MAE, MAPE and MSE)

Table 6 Comparison of NN-based approach using different training algorithms in terms of estimation error in validation data (MAE, MAPE and MSE)

Figures  8, 9, 10, 11, 12, 13, 14, 15, 16, 17 and 18 show the comparison of the accuracy of all the different types of training algorithms using the predicted and real data. The X axis shows the biopolymer samples, whereas the Y axis shows the value for M_n, M_w, and PDI. Three subplots are provided for each training algorithm, one subplot for each modeled variable. Furthermore, training, testing, and validation data are distinguished in the plot. The plots show that the closer the value of the predicted value is to the real data, the more suitable the training algorithm is for the process, indicating higher accuracy of the model.

The results in Tables 4, 5 and 6 show that LM algorithm has the best training algorithm with minimum error in most of the cases. LM algorithm is an effective training algorithm with the fastest convergence. Additive momentum algorithm has the worst prediction for biopolymerization process because the errors are greatly higher than those of other training algorithms. Additive momentum algorithm can smoothen the training by considering previously executed weight changes. However, the momentum coefficient is held constant, and no concrete reason assumes that such a strategy is optimum. Thus, the wrong coefficient for additive momentum algorithm might have led to the worst performance among all training algorithms.

Among the self-adaptive LR training algorithms, the GDA has a large estimation error with the worst training performance. The GDX has slightly considerable training performance and estimation error. In GDA, the training algorithm adapts the LR that corresponds to the current error surface encountered during the training. However, the LR is not subject to specific process during training but it is increased or decreased by a constant factor, β_∆+, and β_∆ (Patricia et al. 2010). GDX, which combines momentum and adaptive LR and presents the advantages of GDA and GDX, is the latest training algorithm proposed.

As discussed earlier, resilient training algorithm is a remarkable training algorithm with relatively high accuracy, convergence speed, and robustness. Therefore, the performance of resilient algorithm is relatively better than that of other training algorithms. Among the conjugate gradient training algorithms, conjugate gradient with Powell–Beale restarts and Polak–Ribiére conjugate gradient provide similar results in error estimation and training performance, whereas SCG provides relatively poor results. The conjugate-based training algorithms have the same estimation errors as other training algorithms. Among the quasi-Newton training algorithms, LM has the least estimation errors and the best training performance. Bayesian regulation training algorithm can perform early stopping during training. However, this property is unsuitable for this application because biopolymerization is an extremely sensitive process and often results in large estimation errors.

Conclusion

Biopolymerization was investigated in a bioreactor setup. Polymerization temperature and impeller speed were optimized. An M_n of 3095 Da was obtained at 70 °C at impeller speed of 250 rpm and time of 2 h. A total of 11 different training algorithms in the neural network, including (1) additive momentum (gradient descent with momentum), (2) self-adaptive LR (variable LR gradient descent and gradient descent with momentum and adaptive LR), (3) resilient backpropagation, (4) conjugate gradient backpropagation (SCG, conjugate gradient with Powell–Beale restarts, Fletcher–Powell conjugate gradient and Polak–Ribiére conjugate gradient), and (5) quasi-Newton (LM, BFGS quasi-Newton, and one-step secant); and (6) Bayesian regulation propagation (Bayesian regularization) are tested. The network parameters include maximum epoch of 1000, LR of 0.05, and target error of 0.001. LM is the most suitable training algorithm for biopolymerization. The MAPE values for M_n, M_w, and PDI are 4.512, 5.31, and 3.21%, respectively.