1 Introduction

Divergence-free finite element finite element methods for incompressible flows intrinsically enjoy many advantages such as conservation of mass, improved accuracy, pressure-robustness (i.e., any modification to the source function by a gradient field only effects the discrete pressure solution) and so on. These desirable benefits have made the study of constructing stable, divergence-free methods an active area of research and many such schemes have been introduced, analyzed in the literature (e.g., [8, 9, 17, 18, 20]).

While the construction of divergence-free methods is a well-studied area of research, most of the existing methods in the literature are limited to polytopal domains, and as a result, have limited accuracy due to geometric error when applied on domain with curved boundary. However, there has been a recent trend to extend divergence-free methods to more complex settings, in particular, on non-polyhedral domains [3, 10, 12, 15].

In this paper, we add to these contributions by constructing and analyzing a stable, \(H^1\)-conforming and divergence-free method using isoparametric elements. As far as we are aware, this is the first isoparametric finite element scheme for the Stokes problem with all three of these properties. The construction is based on the lowest-order Scott–Vogelius method finite element pair defined on Clough-Tocher partitions. In the affine setting, this pair takes the discrete velocity space to consist of continuous, piecewise quadratic polynomials, whereas the discrete pressure space is the space of discontinuous, piecewise linear polynomials. A Clough-Tocher refinement of a triangulation is obtained by connecting the vertices of each triangle to its barycenter.

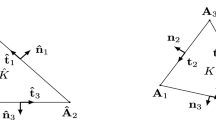
The construction in the present work is based on the recent paper [15], where a divergence-free scheme based on Scott-Vogelius isoparametric elements is also constructed and analyzed. The finite element spaces constructed in [15] centers on two main ideas. The first is to treat the Scott-Vogelius pair as finite element spaces defined on macro-elements rather than on a refined Clough-Tocher triangulation. In particular, local spaces are defined via quadratic mappings of a reference macro element, and therefore these mappings do not depend on the geometry of the Clough-Tocher partition (cf. Fig. 1). The second idea in [15] is to utilize the Piola (divergence-preserving) transform in the definition of the discrete velocity space rather than traditional composition. The end result is a stable, convergent, and divergence-free method for the Stokes problem. However, due to the use of the Piola transform, the discrete velocity space in [15] is only \({\varvec{H}}(\textrm{div})\)-conforming, namely, the discrete velocity functions are not continuous in an O(h) neighborhood of the boundary.

To explain our contributions and to differentiate our construction from [15], let us elaborate on the previous paragraph.

As is typically done in the isoparametric framework, the starting point is an \(O(h^2)\) polygonal approximation \({\tilde{\Omega }}_h\) of the physical domain and an affine simplicial triangulation \({{\tilde{\mathcal {T}}}}_h\) of \({\tilde{\Omega }}_h\). In the isoparametric regime, the computational domain, denoted by \(\Omega _h\), is a \(O(h^3)\) approximation to \(\Omega \), defined via a piecewise quadratic mapping \(G_h:{\tilde{\Omega }}_h \rightarrow \Omega _h\). This quadratic mapping induces a partition \(\mathcal {T}_{h} = \{G_h({\tilde{T}}): {\tilde{T}}\in {\tilde{\mathcal {T}}}_h\}\) consisting of triangles with curved edges.

On the polygon \({\tilde{\Omega }}_h\), the Scott-Vogelius velocity space, defined via macro elements, is given by

$$\begin{aligned} {\tilde{\varvec{V}}}_h = \{{\tilde{\varvec{v}}}\in \varvec{H}^1_0({\tilde{\Omega }}_h): {\tilde{\varvec{v}}}|_{{\tilde{T}}} \in \varvec{\mathcal {P}}^c_2({\tilde{T}}^{ct})\ \forall {\tilde{T}}\in {\tilde{\mathcal {T}}}_h\}, \end{aligned}$$

where \({\tilde{T}}^{ct}\) is the local Clough-Tocher triangulation of \({\tilde{T}}\), and \(\varvec{\mathcal {P}}^c_2({\tilde{T}}^{ct})\) is the vector-valued, quadratic Lagrange space on \({\tilde{T}}^{ct}\). From \({\tilde{\varvec{V}}}_h\), we build our isoparametric velocity space, given abstractly by

$$\begin{aligned} \varvec{V}_h = \{{\varvec{\Psi }}{\tilde{\varvec{v}}}:\ {\tilde{\varvec{v}}}\in {\tilde{\varvec{V}}}_h\} \end{aligned}$$

for some operator \({\varvec{\Psi }}\). Traditional isoparametric elements define \({\varvec{\Psi }}\) via composition, i.e., \({\varvec{\Psi }}{\tilde{\varvec{v}}}|_T = {\tilde{\varvec{v}}} \circ F_{{\tilde{T}}} \circ F_T^{-1}|_T\), where \(F_T:{\hat{T}}\rightarrow T\) and \(F_{{\tilde{T}}}:{\hat{T}}\rightarrow {\tilde{T}}\) are quadratic and affine diffeomorphisms, respectively. This assignment of \({\varvec{\Psi }}\) yields an \(\varvec{H}^1_0(\Omega _h)\) conforming finite element space that generally enjoys optimal-order approximation properties [1, 4, 11, 16]. However, this transformation is not divergence-preserving, and as consequence, its use on the Scott-Vogelius finite element pair mars the divergence-free and pressure robustness properties of the resulting scheme.

On the other hand, the construction in [15] uses the Piola transform in the definition of \({\varvec{\Psi }}\) in a manner that preserves values at the nodal Lagrange degrees of freedom. In symbols, this means \(({\varvec{\Psi }}{\tilde{\varvec{v}}})|_T(a_i) = {\tilde{\varvec{v}}}|_{{\tilde{T}}}({\tilde{a}}_i)\), where \(\{a_i\}\) and \(\{{\tilde{a}}_i\}\) are the locations of the canonical quadratic Lagrange degrees of freedom of T and \({\tilde{T}}\) respectively, with \(a_i = G_h(\tilde{a}_i)\). This construction, along with a pressure space defined through composition, yields a divergence-free and stable pair for the Stokes problem. However, while the definition of \({\varvec{\Psi }}\) yields a weakly continuous velocity space, the use of the Piola transform only preserves normal continuity across interelement boundaries, i.e., the resulting space is only \({\varvec{H}}(\textrm{div};\Omega _h)\)-conforming.

The key contribution of this paper is to construct a mapping \({\varvec{\Psi }}\) via the Piola transform with the additional property

$$\begin{aligned} {\varvec{\Psi }}{\tilde{\varvec{v}}}|_{e} = {\tilde{\varvec{v}}}|_e \end{aligned}$$

on all interior (affine) edges e. This property ensures that the resulting isoparametric space is \(H^1\)-conforming, which potentially leads to improved error estimates in finite element schemes due to improved consistency. Furthermore, the properties of divergence-preserving mapping yield a divergence-free and inf-sup stable pair for the Stokes problem.

Our construction is based on isoparametric \(C^1\) elements on Clough-Tocher splits in [13]. There, \(C^1\) elements on curved elements are constructed by considering an enriched local reference space. A subspace of this enriched space is extracted and mapped via composition to the computational domain in a way that preserves function and gradient values on interior edges. Likewise, we add divergence-free polynomials of higher degree to the reference macro element and extract and map a subspace via a Piola transform to defined \({\varvec{\Psi }}\). We emphasize that, while we consider an enriched space in our construction, the resulting spaces have the same dimensions as their affine counterparts.

The rest of the paper is organized as follows. In the next section, we state some properties of the isoparametric framework as well as the Piola transform and set the notation that is used throughout the following sections. In Sect. 3, we present several local spaces and state some of their properties. In this section, we also introduce the local mappings between the local spaces, which eventually leads to the definition of the local mapping that is used for the construction of the discrete velocity space (see Theorem 3.8). Here, we also study the behavior of this local mapping including its stability and approximation properties. In Sect. 4, we define the global mappings, the global spaces, and prove the inf-sup stability. In Sect. 5, we state the finite element method, prove the divergence-free property and that the method is of optimal order of convergence. Section 3 discusses the implementation of the method and presents numerical experiments which support the theoretical results.

2 Notation and preliminary results

In this section we set up the notation and state some preliminary results. Throughout the paper, the letter C (with or without subscripts) denotes a generic positive constant, independent of the mesh size and may change values at each occurrence. We also use the letter \(\varvec{n}\) to denote an outward unit normal with respect to a boundary that is understood from context.

2.1 Affine mesh

Let \(\Omega \subset \mathbb {R}^2\) be a bounded, sufficiently smooth, open domain and assume that the boundary of \(\Omega \), \(\partial \Omega \), is given by a finite number of local charts. Denote by \({\tilde{\mathcal {T}}}_h\) a shape regular, affine triangulation of \(\Omega \) such that the boundary vertices of \({\tilde{\mathcal {T}}}_h\) lies on \(\Omega \) and \({\tilde{\Omega }}_h:=\textrm{int}\Big (\cup _{{\tilde{T}}\in {\tilde{\mathcal {T}}}_h} \overline{{\tilde{T}}}\Big )\) is an \(\mathcal {O}(h^2)\) polygonal approximation to \(\Omega \), where \(h = \max _{{\tilde{T}}\in {\tilde{\mathcal {T}}}_h} {\textrm{diam}}({\tilde{T}})\). Furthermore, we assume that \({\tilde{\mathcal {T}}}_h\) has at most two vertices on \(\partial \Omega \).

2.2 Isoparametric mesh

We follow the well established isoparametric framework [1, 4, 5, 11, 21].

Let \(G:{\tilde{\Omega }}_h \rightarrow \Omega \) be a bijective map satisfying \(\Vert G\Vert _{W^{1,\infty }({\tilde{\Omega }}_h)}\le C\) with the additional properties that \(G|_{{\tilde{T}}}(x) = x\) at all vertices of \({\tilde{T}}\), and G reduces to the identity mapping on any triangle \({\tilde{T}}\in {\tilde{\mathcal {T}_h}}\) with no more than one vertex on the boundary. We then let \(G_h\) denote the piecewise quadratic nodal interpolant of G such that \(\Vert DG_h\Vert _{W^{1,\infty }({\tilde{T}})}\le C\) and \(\Vert DG_h^{-1}\Vert _{W^{1,\infty }({\tilde{T}})}\le C\) for all \({\tilde{T}}\in {\tilde{\mathcal {T}}}_h\).

We define the isoparametric triangulation and the computational domain, respectively, as follows:

$$\begin{aligned} \mathcal {T}_h= \{G_h({\tilde{T}}):\ {\tilde{T}}\in {\tilde{\mathcal {T}}}_h\},\qquad \Omega _h:=\textrm{int}\Big (\bigcup _{ T\in \mathcal {T}_h} {\overline{T}}\Big ). \end{aligned}$$

2.3 Local mappings

Denote by \({\hat{T}}\) the reference triangle with vertices \((0,0), (0,1)\ \text {and} \ (1,0)\), and for \({\tilde{T}}\in {\tilde{\mathcal {T}}}_h\), let \(F_{{\tilde{T}}}:{\hat{T}}\rightarrow {\tilde{T}}\) be an affine mapping. With the aid of the mappings \(G_h\) and \(F_{{\tilde{T}}}\), we introduce the quadratic mapping \(F_T:{\hat{T}}\rightarrow T\), defined by \(F_T:= G_h\circ F_{{\tilde{T}}}\), which satisfies [1, 4, 11]

$$\begin{aligned} \begin{aligned}&|F_T|_{W^{m,\infty }({\hat{T}})}\le C h_T^m\quad 0\le m\le 2,\qquad |F_T^{-1}|_{W^{m,\infty }(T)}\le C h_T^{-m}\quad 0\le m\le 3,\\&c_1 h_T^2 \le \det (DF_T)\le c_2 h_T^2, \end{aligned} \end{aligned}$$
(2.1)

with \(h_T = \textrm{diam}(G_h^{-1}(T))\). It is important to note that \(F_{T}=F_{{\tilde{T}}}\) at the vertices of \({\hat{T}}\), and indeed, \(F_{T}=F_{{\tilde{T}}}\) for all \({\tilde{T}} \in {\tilde{\mathcal {T}}}_h\) with no more than one boundary vertex.

The following scaling result is found in [1].

Lemma 2.1

For \(\varvec{v}\in \varvec{H}^m(T)\) \((m\ge 0)\), define \({\hat{\varvec{v}}}:{\hat{T}}\rightarrow \mathbb {R}^2\) such that \({\hat{\varvec{v}}}({\hat{x}}) = \varvec{v}(x)\) with \(x = F_T({\hat{x}})\). Then \({\hat{\varvec{v}}}\in \varvec{H}^m(T)\) and

$$\begin{aligned} |\varvec{v}|_{H^m(T)}&\le C h_T^{1-m} \sum _{r=0}^m h_T^{2(m-r)} |{\hat{\varvec{v}}}|_{H^r({\hat{T}})},\\ |{\hat{\varvec{v}}}|_{H^m({\hat{T}})}&\le Ch_T^{m-1} \sum _{r=0}^m | \varvec{v}|_{H^r({\hat{T}})}. \end{aligned}$$

Next, we introduce a matrix-valued function \(A_T\) which arises in the Piola transform. For reference, we state the well-known divergence and normal-preserving properties of this transform [14], and we also state bounds of \(A_T\) and its inverse [15, Lemma 2.3].

Lemma 2.2

For each \(T\in \mathcal {T}_h\), define the matrix-valued function \(A_T:{\hat{T}}\rightarrow \mathbb {R}^{2\times 2}\) as

$$\begin{aligned} A_T({\hat{x}}):= \frac{DF_T({\hat{x}})}{\det (DF_T({\hat{x}}))}. \end{aligned}$$
(2.2)

The Piola transform of a function \({\hat{\varvec{v}}}:{\hat{T}}\rightarrow \mathbb {R}^2\) is the function \(\varvec{v}:T\rightarrow \mathbb {R}^2\) given by

$$\begin{aligned} \varvec{v}(x) = A_T({\hat{x}}) {\hat{\varvec{v}}}({\hat{x}}),\qquad x = F_T({\hat{x}}). \end{aligned}$$
(2.3)

There holds

$$\begin{aligned} (\textrm{div}\,\varvec{v})(x) = \frac{1}{\det (DF_T({\hat{x}}))} ({\widehat{\textrm{div}\,}} {\hat{\varvec{v}}})({\hat{x}}), \end{aligned}$$
(2.4)

and

$$\begin{aligned} \varvec{v}\cdot \varvec{n}= \frac{{\hat{\varvec{v}}} \cdot {\hat{\varvec{n}}}}{\left| \det (DF_T) DF_T^{-T} {\hat{\varvec{n}}}\right| }. \end{aligned}$$

The matrix \(A_T\) and its inverse satisfy the following estimates:

$$\begin{aligned} |A_T|_{W^{m,\infty }({\hat{T}})}\le C h_T^{m-1},\qquad \text {and}\qquad |A_T^{-1}|_{W^{m,\infty }({\hat{T}})} \le \left\{ \begin{array}{ll} Ch_T^{1+m} &{} m=0,1\\ 0 &{} m\ge 2. \end{array} \right. \end{aligned}$$
(2.5)

In particular, \(A_T^{-1}\) is the adjugate matrix of \(DF_T\), and therefore the entries of \(A_T^{-1}\) are linear polynomials.

2.4 Clough-Tocher splits

We let \({\hat{T}}^{ct} = \{{\hat{K}}_i\}_{i=1}^3\) denote the Clough-Tocher triangulation of the reference triangle \({\hat{T}}\), which is obtained by connecting its vertices with its barycenter. We define the corresponding triangulations on \({\tilde{T}}\in {\tilde{\mathcal {T}}}_h\) and \(T\in \mathcal {T}_h\), respectively, as follows:

$$\begin{aligned} {\tilde{T}}^{ct}&= \{F_{{\tilde{T}}}({\hat{K}}): {\hat{K}}\in {\hat{T}}^{ct}\},\quad T^{ct} = \{F_T({\hat{K}}):\ {\hat{K}}\in {\hat{T}}^{ct}\}. \end{aligned}$$

The globally refined triangulations are then given by

$$\begin{aligned} {\tilde{\mathcal {T}}}_h^{ct}&= \{{\tilde{K}}:\ {\tilde{K}}\in {\tilde{T}}^{ct},\ \exists {\tilde{T}}\in {\tilde{\mathcal {T}}}_h\},\qquad \mathcal {T}_h^{ct} = \{ K:\ K\in T^{ct},\ \exists T\in \mathcal {T}_h\}. \end{aligned}$$

Remark 2.3

We emphasize that the isoparametric framework is applied to \({\tilde{\mathcal {T}}}_h\), not to \({\tilde{\mathcal {T}}}_h^{ct}\), i.e., the isoparametric Clough-Tocher mesh \(\mathcal {T}_h\) (or \({\tilde{\mathcal {T}}}_h\)) is constructed through the reference macroelement \({\hat{T}}^{ct}\) via the mapping \(F_T\) (or \(F_{{\tilde{T}}}\)). In other words, we first consider the isoparametric mesh induced by the mapping \(F_T\) (or \(F_{{\tilde{T}}}\)), and then consider its barycenter refinement.

We let \(\Delta _s({\hat{T}}^{ct})\) denote the set of s-dimensional simplices of the local reference mesh \({\hat{T}}^{ct}\). For example, \(\Delta _0({\hat{T}}^{ct})\) is the set of four vertices of \({\hat{T}}^{ct}\), and \(\Delta _1({\hat{T}}^{ct})\) is the set of six edges of \({\hat{T}}^{ct}\). Likewise, and with a slight abuse of notation, we denote by \(\Delta _s({\hat{T}})\) the set of s-dimensional simplices of \({\hat{T}}\).

2.5 Function spaces

For a non-negative integer k, and for an affine, regular, and simplicial triangulation \(\mathcal {S}_h\), we set

$$\begin{aligned} \mathcal {P}_k(\mathcal {S}_h) = \{q\in L^2(S):\ q|_K\in \mathcal {P}_k(K)\ \forall K\in \mathcal {S}_h\}, \end{aligned}$$

where \(S = \textrm{int}\big (\cup _{K\in \mathcal {S}_h} {\bar{K}}\big )\), and \(\mathcal {P}_k(K)\) denotes the space of polynomials of degree \(\le k\) with domain K. We further set

$$\begin{aligned} \mathcal {P}_k^c(\mathcal {S}_h) = \mathcal {P}_k(\mathcal {S}_h)\cap H^1(S),\qquad \mathcal {P}_k^{c1}(\mathcal {S}_h) = \mathcal {P}_k(\mathcal {S}_h)\cap H^2(S). \end{aligned}$$

For example, \(\mathcal {P}_k^c({\hat{T}}^{ct})\) is the local kth-degree Lagrange finite element space, and \(\mathcal {P}_k^{c1}({\hat{T}}^{ct})\) is the local kth-degree \(C^1\) finite element space, both defined on the reference Clough-Tocher split. Analogous vector-valued spaces are denoted in boldface. For example, \(\varvec{\mathcal {P}}_k^c({\hat{T}}^{ct}) = [\mathcal {P}_k^c({\hat{T}}^{ct})]^2\) and \(\varvec{\mathcal {P}}_k^c({\tilde{T}}^{ct}) = [\mathcal {P}_k^c({\tilde{T}}^{ct})]^2\).

3 Local spaces on macro elements

We define the following spaces on the reference macro element \({\hat{T}}^{ct}\):

$$\begin{aligned}&{\hat{P}}:=\mathcal {P}_3^{c1}({\hat{T}}^{ct}),\quad{} & {} {\hat{\varvec{V}}} := \varvec{\mathcal {P}}_2^c({\hat{T}}^{ct}),\quad {\hat{Q}} := \mathcal {P}_1({\hat{T}}^{ct}). \end{aligned}$$

That is, \({\hat{P}}\) is the local \(C^1\) Clough-Tocher element, \({\hat{\varvec{V}}}\) is the vector-valued, quadratic Lagrange finite element space, and \({\hat{Q}}\) is the space of piecewise linear polynomials without continuity constraints. A simple counting argument shows these spaces form the exact sequence

$$\begin{aligned} \mathbb {R}\overset{\subset }{\longrightarrow }\ {\hat{P}} \overset{\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}}{\longrightarrow } {\hat{\varvec{V}}} \overset{\widehat{\textrm{div}\,}}{\longrightarrow } {\hat{Q}} \longrightarrow 0, \end{aligned}$$

where \({\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}} = (\frac{{\partial }{\hat{z}}}{{\partial }{\hat{x}}_2},-\frac{{\partial }{\hat{z}}}{{\partial }{\hat{x}}_1})^\intercal \). In particular, (i) if \({\hat{\varvec{v}}}\in {\hat{\varvec{V}}}\) is divergence–free, then \(\varvec{v}= \widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}} {\hat{z}}\) for some \({\hat{z}}\in {\hat{P}}\) (unique up to a constant), and (ii) the mapping \(\widehat{\textrm{div}}:{\hat{\varvec{V}}} \rightarrow {\hat{Q}}\) is surjective. We also state well-known dimension formulas of these spaces (cf. [6] and Lemma 3.1 below):

$$\begin{aligned} \dim {\hat{P}} = 12,\qquad \dim {\hat{\varvec{V}}} = 20,\qquad \dim {\hat{Q}} = 9. \end{aligned}$$

Analogous spaces on the affine macro element \({\tilde{T}}^{ct}\) (with \({\tilde{T}}\in {\tilde{\mathcal {T}}}_h\)) are given by

$$\begin{aligned} \varvec{V}({\tilde{T}}) = \{{\tilde{\varvec{v}}}\in \varvec{\mathcal {P}}_2^c({\tilde{T}}^{ct}): {\tilde{\varvec{v}}}|_{{\partial }{\tilde{T}}\cap {\partial }{\tilde{\Omega }}_h}=0\},\qquad Q({\tilde{T}}) = \mathcal {P}_1({\tilde{T}}^{ct}). \end{aligned}$$

For \(T\in \mathcal {T}_h\), possibly with curved edge, we define \(\varvec{V}(T)\) to be the image of \({\hat{\varvec{V}}}\) by the Piola transform (2.3), and Q(T) the image of \({\hat{Q}}\) via composition i.e.,

$$\begin{aligned} \begin{aligned} \varvec{V}(T)&= \{\varvec{v}\in \varvec{H}^1(T):\ \varvec{v}(x) = A_T({\hat{x}}){\hat{\varvec{v}}}({\hat{x}}),\ \exists {\hat{\varvec{v}}}\in {\hat{\varvec{V}}},\text { and }\varvec{v}|_{{\partial }T\cap {\partial }\Omega _h} = 0\},\\ Q(T)&= \{q\in L^2(T):\ q(x) = {\hat{q}}({\hat{x}}),\ \exists {\hat{q}}\in {\hat{Q}}\}, \end{aligned} \end{aligned}$$
(3.1)

where \(x = F_T({\hat{x}})\). Note that if T is affine, then \(A_T\) is constant, and therefore \(\varvec{V}(T) = \varvec{V}({\tilde{T}})\) in this case.

Finally, variants of the above spaces with boundary conditions are given by

$$\begin{aligned}&{\hat{\varvec{V}}}_0= {\hat{\varvec{V}}} \cap \varvec{H}^1_0({\hat{T}}),\quad \ \ \ \ {}{} & {} {\hat{Q}}_0= {\hat{Q}} \cap L^2_0({\hat{T}}),\\&\varvec{V}_0({\tilde{T}}) = \varvec{V}({\tilde{T}})\cap \varvec{H}^1_0({\tilde{T}}),\qquad{} & {} Q_0({\tilde{T}}) = Q({\tilde{T}})\cap L^2_0({\tilde{T}}),\\&\varvec{V}_0(T) = \varvec{V}(T)\cap \varvec{H}^1_0(T),\quad{} & {} Q_0(T) = \{q\in L^2(T):\ q(x) = {\hat{q}}({\hat{x}}),\ \exists {\hat{q}}\in {\hat{Q}}_0\}, \end{aligned}$$

where \(L^2_0(S)\) is the space of \(L^2(S)\) functions with vanishing mean.

The main goal of this section to construct an injective divergence-preserving operator that maps functions in \(\varvec{V}({\tilde{T}})\) onto a space of functions with domain T (with \(T = G_h({\tilde{T}})\)) and preserves function values on the common affine edges. In addition, the range of the operator inherits the approximation properties of \(\varvec{V}({\tilde{T}})\). This construction is based on an enriching procedure used in the construction of isoparametric \(C^1\) elements which we describe next.

3.1 A local and enriched Clough-Tocher \(C^1\) element

Here we summarize and extend the results of the isoparametric Clough-Tocher element proposed by Mansfield in [13]. The essential idea of the construction is to consider an enriched local space of \({\hat{P}}\), and to extract and map via composition a 12-dimensional subspace in a way that preserves function and gradient values on affine edges.

The enriched space consists of \(C^1\) tricubic polynomials defined on the reference Clough-Tocher split, i.e., \(C^1\) piecewise quartic polynomials which are cubic along all six edges in the split [2]. Adopting the notation in the previous section, this space is given by

$$\begin{aligned} \hat{\mathbb {P}}:=\{{\hat{z}}\in \mathcal {P}_4^{c1}({\hat{T}}^\textrm{ct}):\ {\hat{z}}|_{{\hat{e}}}\in \mathcal {P}_3({\hat{e}})\ \forall {\hat{e}}\in \Delta _1({\hat{T}}^\textrm{ct})\}. \end{aligned}$$

The following two lemmas state the dimension counts and degrees of freedom for the spaces \({\hat{P}}\) and the enriched space \(\hat{\mathbb {P}}\). The first result is found in [6, Theorem  6.1.2] and [7, Theorem 1]. The proof of Lemma 3.2 is implicitly shown in [13, Theorem 1]; we provide a proof of this result in the appendix.

Lemma 3.1

The space \({\hat{P}}\) is 12-dimensional, and a function \({\hat{z}}\in {\hat{P}}\) is uniquely determined by the degrees of freedom (DOFs)

$$\begin{aligned}&{\hat{z}}({\hat{a}}),\ {\hat{\nabla }} {\hat{z}}({\hat{a}})\qquad \forall {\hat{a}}\in \Delta _0({\hat{T}}),\end{aligned}$$
(3.2a)
$$\begin{aligned}&\frac{{\partial }{\hat{z}}}{{\partial }{\hat{\varvec{n}}}_{{\hat{e}}}}({\hat{m}}_{{\hat{e}}}) \qquad \forall {\hat{e}}\in \Delta _1({\hat{T}}), \end{aligned}$$
(3.2b)

where \({\hat{m}}_{{\hat{e}}}\) denotes the edge midpoint of \({\hat{e}}\), and \({\hat{\varvec{n}}}_{{\hat{e}}}\) denotes the outward normal of \({\partial }{\hat{T}}\) restricted to \({\hat{e}}\).

Lemma 3.2

The space \(\hat{\mathbb {P}}\) is 15-dimensional, and a function \({\hat{z}}\in \hat{\mathbb {P}}\) is uniquely determined by the DOFs (3.2a)–(3.2b) and

$$\begin{aligned}&\frac{{\partial }^2 {\hat{z}}}{{\partial }{\hat{\varvec{t}}}_{{\hat{e}}} {\partial }{\hat{\varvec{n}}}_{{\hat{e}}}}({\hat{m}}_{{\hat{e}}})\qquad \forall {\hat{e}}\in \Delta _1({\hat{T}}), \end{aligned}$$
(3.2c)

where \({\hat{\varvec{t}}}_{{\hat{e}}}\) is the unit tangent of \({\hat{e}}\), obtained by rotating \({\hat{\varvec{n}}}_{{\hat{e}}}\) 90 degrees clockwise.

Consequently, the space

$$\begin{aligned} \hat{\mathbb {W}}:= \{{\hat{z}}\in \hat{\mathbb {P}}: {\hat{z}} \text {vanishes on} (3.2b)--2.2c\} \subset H^2(T)\cap H^1_0(T) \end{aligned}$$
(3.3)

is three-dimensional, a function \({\hat{z}}\in \hat{\mathbb {W}}\) is uniquely determined by its values (3.2c), and there holds \(\hat{\mathbb {P}} = \hat{P}\oplus \hat{\mathbb {W}}\).

Lemma 3.3

Let \({\hat{w}}\in \mathcal {P}_3({\hat{T}}^{ct})|_{\partial {\hat{T}}}\) such that \({\hat{w}}\) vanishes at the three vertices and the three edge midpoints of \({\hat{T}}\), i.e., \({\hat{w}}({\hat{a}}) =0\) and \({\hat{w}}({\hat{m}}_{{\hat{e}}})=0\) for all \({\hat{a}}\in \Delta _0({\hat{T}})\) and \({\hat{e}}\in \Delta _1({\hat{T}})\). Then, there exists a unique \({\hat{z}}\in \hat{\mathbb {W}}\) such that

$$\begin{aligned} \frac{{\partial }{\hat{z}}}{{\partial }{\hat{\varvec{n}}}}\big |_{{\partial }{\hat{T}}} = {\hat{w}}. \end{aligned}$$

Proof

Let \({\hat{w}}\in \mathcal {P}_3({\hat{T}}^{ct})|_{\partial {\hat{T}}}\) be a function that vanishes on \(\Delta _0({\hat{T}})\) and edge midpoints of \({\hat{T}}\). Using Lemma 3.2, we uniquely determine \({\hat{z}}\in \hat{\mathbb {W}}\) by the conditions

$$\begin{aligned}&\frac{{\partial }^2 {\hat{z}}}{{\partial }{\hat{\varvec{t}}}_{{\hat{e}}} {\partial }{\hat{\varvec{n}}}_{{\hat{e}}}}({\hat{m}}_{{\hat{e}}}) = \frac{{\partial }{\hat{w}}}{{\partial }{\hat{\varvec{t}}}_{{\hat{e}}}} ({\hat{m}}_{{\hat{e}}})\quad{} & {} \forall {\hat{e}}\in \Delta _1({\hat{T}}). \end{aligned}$$

For an edge \({\hat{e}}\in \Delta _1({\hat{T}})\), set \({\hat{r}}_{{\hat{e}}} = \big (\frac{{\partial }{\hat{z}}}{{\partial }{\hat{\varvec{n}}}_{{\hat{e}}}} - {\hat{w}}\big )|_{{\hat{e}}}\in \mathcal {P}_3({\hat{e}})\). Then by the properties of \({\hat{w}}\) and the definition of \({\hat{\mathbb {W}}}\), \({\hat{r}}_{{\hat{e}}}\) vanishes at three distinct points on \({\hat{e}}\). Furthermore, with an abuse of notation, \({\hat{r}}'_{{\hat{e}}}({\hat{m}}_{{\hat{e}}}) = 0\). These conditions imply \({\hat{r}}_{{\hat{e}}} =0\), and we conclude \(\frac{{\partial }{\hat{z}}}{{\partial }{\hat{\varvec{n}}}}|_{{\partial }{\hat{T}}} = {\hat{w}}|_{\hat{\partial }T}\). \(\square \)

3.2 A local and enriched Lagrange \(C^0\) element

Using the space \(\hat{\mathbb {W}}\) given by (3.3), we define the enriched (local) Lagrange space as

$$\begin{aligned} \hat{\mathbb {V}} = \hat{\varvec{V}}+{\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}}\,\hat{\mathbb {W}}. \end{aligned}$$
(3.4)

Proposition 3.4

The sum in (3.4) is direct, in particular, \(\hat{\varvec{V}}\cap {\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}}\,\hat{\mathbb {W}}=\{0\}\).

Proof

If \({\hat{\varvec{v}}}\in {\hat{\varvec{V}}}\cap {\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}}\,\hat{\mathbb {W}}\), then \({\hat{\varvec{v}}}\in {\hat{\varvec{V}}}\) and is divergence-free. Therefore \({\hat{\varvec{v}}} = {\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}}_1\) for some \({\hat{z}}_1\in \hat{P}\). On the other hand, because \({\hat{\varvec{v}}}\in {\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{\mathbb {W}}}\), we may write \({\hat{\varvec{v}}} = {\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}}_2\) for some \({\hat{z}}_2\in {\hat{\mathbb {W}}}\); thus, \({\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}}_1 = {\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}}_2\), implying that \({\hat{z}}_1 = {\hat{z}}_2+{\hat{c}}\) for some \({\hat{c}}\in \mathbb {R}\). Because \({\hat{c}}\in {\hat{P}}\) and \({\hat{z}}_1 = {\hat{c}}\) on the DOFs (3.2a)–(3.2b) (by the definition of \({\hat{\mathbb {W}}}\)), we conclude \({\hat{z}}_1 \equiv {\hat{c}}\) by Lemma 3.1. Therefore \({\hat{\varvec{v}}} \equiv 0\). \(\square \)

3.3 Local mappings

We denote by \(\{{\hat{a}}_i\}_{i=1}^{10}\) and \( {\tilde{a}}_i\}_{i=1}^{10}\) the sets of vertices and edge midpoints with respect to \({\hat{T}}^{ct}\) and \({\tilde{T}}^{ct}\), respectively, labeled such that \({\tilde{a}}_i = F_{{\tilde{T}}}({\hat{a}}_i)\). That is, \(\{{\hat{a}}_i\}_{i=1}^{10}\) and \(\{{\tilde{a}}_i\}_{i=1}^{10}\) are the locations of the Lagrange DOFs for \({\hat{\varvec{V}}}\) and \(\varvec{V}({\tilde{T}})\), respectively.

Using Lemma 3.3 and [15, Lemma 3.3], we introduce three mappings.

Definition 3.5

Let \({\tilde{T}}\in {\tilde{\mathcal {T}}}_h\) and \(T\in \mathcal {T}_h\) with \(T = G_h({\tilde{T}})\).

  1. (i)

    We define the bijection \({\varvec{\Psi }}_T:\varvec{V}({\tilde{T}})\rightarrow \varvec{V}(T)\) uniquely determined by the conditions

    $$\begin{aligned} ({\varvec{\Psi }}_T {\tilde{\varvec{v}}})(a_i) = {\tilde{\varvec{v}}}({\tilde{a}}_i)\quad i=1,2\ldots ,10, \end{aligned}$$
    (3.5)

    where \(a_i = G_h({\tilde{a}}_i) = F_T({\hat{a}}_i)\).

  2. (ii)

    We define the operator \({\hat{\Theta }}_{\tilde{T}}:\varvec{V}({\tilde{T}})\rightarrow {\hat{\mathbb {W}}}\) uniquely determined by the conditions

    $$\begin{aligned} \frac{{\partial }{\hat{\Theta }}_{{\tilde{T}}}{\tilde{\varvec{v}}}}{{\partial }{\hat{\varvec{n}}}}\big |_{{\partial }{\hat{T}}} = A_T^{-1}\big ({\varvec{\Psi }}_T {\tilde{\varvec{v}}} \circ F_T -{\tilde{\varvec{v}}} \circ F_{{\tilde{T}}}\big )\cdot {\hat{\varvec{t}}}\big |_{{\partial }{\hat{T}}}. \end{aligned}$$
    (3.6)
  3. (iii)

    We define the operator \(\Upsilon _T:{\tilde{Q}}({\tilde{T}})\rightarrow Q(T)\) as

    $$\begin{aligned} (\Upsilon _T {\tilde{q}})(x) = {\tilde{q}}(F_{{\tilde{T}}}({\hat{x}})). \end{aligned}$$

Remark 3.6

Recalling the definition of the space \(\varvec{V}(T)\) (3.1), we see from (3.5) that \({\varvec{\Psi }}_T {\tilde{\varvec{v}}}\) is of the form \(({\varvec{\Psi }}_T {\tilde{\varvec{v}}})(x) = (A_T{\hat{\varvec{v}}}_0)({\hat{x}})\), where \(x = F_T({\hat{x}})\) and \({\hat{\varvec{v}}}_0\in {\hat{\varvec{V}}}\) is the unique piecewise quadratic function satisfying \({\hat{\varvec{v}}}_0({\hat{a}}_i) = A_T^{-1}({\hat{a}}_i) {\tilde{\varvec{v}}}({\tilde{a}}_i)\ (i=1,2,\ldots ,10)\). We then immediately see that \(A_T^{-1} {\varvec{\Psi }}_T{\tilde{\varvec{v}}} \circ F_T = {\hat{\varvec{v}}}_0 \in {\hat{\varvec{V}}}\), and moreover, \(A_T^{-1} {\tilde{\varvec{v}}} \circ F_{{\tilde{T}}} \in \mathcal {P}_3^c({\hat{T}}^{ct})\) because the entries of \(A_T^{-1}\) are linear polynomials on \({\hat{T}}\). We conclude from properties of \({\varvec{\Psi }}_T\) that \({\hat{\Theta }}_{{\tilde{T}}}\) is well-defined by Lemma 3.3 with \({\hat{w}} = A_T^{-1}\big ({\varvec{\Psi }}_T {\tilde{\varvec{v}}} \circ F_T -{\tilde{\varvec{v}}} \circ F_{{\tilde{T}}}\big )\cdot {\hat{\varvec{t}}}\big |_{{\partial }{\hat{T}}}\).

Remark 3.7

From Lemmas 3.2–3.3, we see that (3.6) is satisfied if and only if

$$\begin{aligned} \frac{{\partial }^2 {\hat{\Theta }}_{{\tilde{T}}} {\tilde{\varvec{v}}}}{{\partial }{\hat{\varvec{n}}}_{{\hat{e}}}{\partial }{\hat{\varvec{t}}}_{{\hat{e}}}}({\hat{m}}_{{\hat{e}}})= \frac{{\partial }}{{\partial }{\hat{\varvec{t}}}_{{\hat{e}}}}\Big (A_T^{-1}({\varvec{\Psi }}_T {\tilde{\varvec{v}}} \circ F_T -{{\tilde{\varvec{v}}}} \circ F_{{\tilde{T}}})\cdot {\hat{\varvec{t}}}_{{\hat{e}}}\Big )({\hat{m}}_{{\hat{e}}})\quad \forall {\hat{e}}\in \Delta _1({\hat{T}}). \end{aligned}$$

The construction of a global continuous space using isoparametric Piola mappings is based on the following theorem.

Theorem 3.8

We define the operator \({\varvec{\Psi }}_T^C:\varvec{V}({\tilde{T}})\rightarrow \varvec{H}^1(T)\) as

$$\begin{aligned} {\varvec{\Psi }}_T^C{\tilde{\varvec{v}}}= {\varvec{\Psi }}_T {\tilde{\varvec{v}}} - (A_T {\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{\Theta }}_{{\tilde{T}}}{\tilde{\varvec{v}}})\circ F_{T}^{-1}\qquad \forall {\tilde{\varvec{v}}}\in \varvec{V}({\tilde{T}}). \end{aligned}$$

Then there holds

$$\begin{aligned} {\varvec{\Psi }}_T^C{\tilde{\varvec{v}}}|_e = {\tilde{\varvec{v}}}|_e\qquad \forall e\in \mathcal {E}^I_T,\quad \text {and}\quad {\varvec{\Psi }}_T^C{\tilde{\varvec{v}}}|_{{\partial }T\cap {\partial }\Omega _h} = 0, \end{aligned}$$

where \(\mathcal {E}^I_T\) is the set of (affine) interior edges of T.

Proof

Set \({\hat{z}} = {\hat{\Theta }}_{{\tilde{T}}} {\tilde{\varvec{v}}} \in {\hat{\mathbb {W}}}\), and write (cf. (3.6))

$$\begin{aligned} ({\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}})\cdot {\hat{\varvec{t}}}\big |_{{\partial }{\hat{T}}} = \frac{{\partial }{\hat{z}}}{{\partial }{\hat{\varvec{n}}}}\big |_{{\partial }{\hat{T}}}&= A_T^{-1}\big ({\varvec{\Psi }}_T {\tilde{\varvec{v}}} \circ F_T -{\tilde{\varvec{v}}} \circ F_{{\tilde{T}}}\big )\cdot {\hat{\varvec{t}}} \big |_{{\partial }{\hat{T}}}. \end{aligned}$$

By the definition of \({\varvec{\Psi }}_T\) and the properties of the Piola transform (cf. [15, Lemma 2.4]), there holds

$$\begin{aligned} A_T^{-1}\big ({\varvec{\Psi }}_T {\tilde{\varvec{v}}} \circ F_T -{\tilde{\varvec{v}}} \circ F_{{\tilde{T}}}\big )\cdot {\hat{\varvec{n}}}\big |_{{\hat{e}}} = 0\qquad \forall {\hat{e}}\in \mathcal {E}^I_{{\hat{T}}}:=\{F_T^{-1}(e):\ e\in \mathcal {E}^I_T\}. \end{aligned}$$

Consequently, because \({\hat{z}}|_{{\partial }{\hat{T}}}=0\) there holds \(({\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}})\cdot {\hat{\varvec{n}}}|_{{\partial }{\hat{T}}}=0\), and so

$$\begin{aligned} \widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}} {\hat{z}}|_{{\hat{e}}}&= A_T^{-1}\big ({\varvec{\Psi }}_T {\tilde{\varvec{v}}} \circ F_T -{\tilde{\varvec{v}}} \circ F_{{\tilde{T}}}\big ) \big |_{ {\hat{e}}}\qquad \forall {\hat{e}}\in \mathcal {E}_{{\hat{T}}}^I. \end{aligned}$$
(3.7)

We then have for \({\hat{x}}\in \mathcal {E}_{{\hat{T}}}^I\), with \(x = F_T({\hat{x}}) = F_{{\tilde{T}}}({\hat{x}})\),

$$\begin{aligned} {\varvec{\Psi }}_T^C{\tilde{\varvec{v}}}(x)&= {\varvec{\Psi }}_T {\tilde{\varvec{v}}}(x) - (A_T{\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}})({\hat{x}})\\&= {\varvec{\Psi }}_T {\tilde{\varvec{v}}}(x)-\big ({\varvec{\Psi }}_T {\tilde{\varvec{v}}} \circ F_T -{\tilde{\varvec{v}}} \circ F_{{\tilde{T}}}\big )({\hat{x}})\\&= {\tilde{\varvec{v}}}(x). \end{aligned}$$

Thus, \({\varvec{\Psi }}_T^C{\tilde{\varvec{v}}}|_e = {\tilde{\varvec{v}}}|_e\) for \(e\in \mathcal {E}_T^I\).

Finally, if \(e:= {\partial }T\cap {\partial }\Omega _h\) is a curved boundary edge, set \({\tilde{e}} = G_h^{-1}(e) = {\partial }{\tilde{T}}\cap {\partial }{\tilde{\Omega }}_h\) to be the corresponding affine boundary edge. Then \({\tilde{\varvec{v}}}|_{\tilde{e}} =0\) by definition of \(\varvec{V}({\tilde{T}})\), and consequently \({\varvec{\Psi }}_T {\tilde{\varvec{v}}}|_e = 0\). This implies \({\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}}|_{{\hat{e}}} = 0\), and therefore \({\varvec{\Psi }}_T^C {\tilde{\varvec{v}}} |_e = {\varvec{\Psi }}_T {\tilde{\varvec{v}}}|_e = 0\). \(\square \)

Next, we shall derive additional useful properties of the operator \({\varvec{\Psi }}^C_T\). As an intermediate step, we provide some estimates for the operator \({\varvec{\Psi }}_T\).

Lemma 3.9

Let \({\tilde{T}}\in {\tilde{\mathcal {T}}}_h\) and \(T\in \mathcal {T}_h\) such that \(T = G_h({\tilde{T}})\). There holds

$$\begin{aligned} \Vert {\varvec{\Psi }}_T {\tilde{\varvec{v}}}\Vert _{H^1(T)}\le C\Vert {\tilde{\varvec{v}}}\Vert _{H^1(\tilde{T})},\quad \text {and}\quad \Vert {\tilde{\varvec{v}}}\Vert _{H^1({\tilde{T}})}\le C \Vert {\varvec{\Psi }}_T {\tilde{\varvec{v}}}\Vert _{H^1(T)}. \end{aligned}$$
(3.8)

Moreover, if T is affine, so that \({\tilde{T}} = T\), then \({\varvec{\Psi }}_T {\tilde{\varvec{v}}} = {\tilde{\varvec{v}}}\).

Proof

The identity \({\varvec{\Psi }}_T {\tilde{\varvec{v}}} = {\tilde{\varvec{v}}}\) on affine elements and the first estimate in (3.8) is shown in [15, Theorem 3.7].

To prove the second estimate, we assume that T has a curved edge, for otherwise the proof is trivial. Write \(({\varvec{\Psi }}_T {\tilde{\varvec{v}}})(x) = (A_T {\hat{\varvec{v}}}_0)({\hat{x}})\), where \({\hat{\varvec{v}}}_0\in {\hat{\varvec{V}}}\) is uniquely determined by the conditions \({\hat{\varvec{v}}}_0({\hat{a}}_i) = A_T^{-1} ({\hat{a}}_i){\tilde{\varvec{v}}}({\tilde{a}}_i)\) for \(i=1,2,\ldots ,10\). Then a standard scaling argument, along with Lemmas 2.2, yield

$$\begin{aligned} \Vert {\tilde{\varvec{v}}}\Vert _{H^1({\tilde{T}})}^2&\le C \sum _{i=1}^{10} |{\tilde{\varvec{v}}}({\tilde{a}}_i)|^2 = C \sum _{i=1}^{10} |(A_T {\hat{\varvec{v}}}_0)({\hat{a}}_i)|^2\\&\le C h_T^{-2} \sum _{i=1}^{10} |{\hat{\varvec{v}}}_0({\hat{a}}_i)|^2\le C h_T^{-2} \Vert {\hat{\varvec{v}}}_0\Vert _{H^1({\hat{T}})}^2. \end{aligned}$$

We then apply Lemmas  2.1–2.2 and the Poincare inequality to conclude

$$\begin{aligned} \Vert {\tilde{\varvec{v}}}\Vert _{H^1({\tilde{T}})}&\le C h_T^{-2} \Vert A_T^{-1}\Vert _{W^{1,\infty }({\hat{T}})}^2 \Vert A_T{\hat{\varvec{v}}}_0\Vert _{H^1({\hat{T}})}^2\le C \Vert A_T {\hat{\varvec{v}}}_0\Vert _{H^1({\hat{T}})}^2\le C \Vert {\varvec{\Psi }}{\tilde{\varvec{v}}}\Vert _{H^1(T)}^2. \end{aligned}$$

\(\square \)

Lemma 3.10

Let \({\tilde{T}}\in {\tilde{\mathcal {T}}}_h\) and \(T\in \mathcal {T}_h\) such that \(T = G_h({\tilde{T}})\). There holds for all \({\tilde{\varvec{v}}} \in \varvec{V}({\tilde{T}})\),

  1. (i)

    \({\varvec{\Psi }}^C_T {\tilde{\varvec{v}}} = {\tilde{\varvec{v}}}\) if T is affine.

  2. (ii)

    \(\textrm{div}\,{\varvec{\Psi }}_T^C {\tilde{\varvec{v}}} = \textrm{div}\,{\varvec{\Psi }}_T{\tilde{\varvec{v}}}\).

  3. (iii)

    \(\Vert {\varvec{\Psi }}^C_T {\tilde{\varvec{v}}}\Vert _{H^1(T)} \le C \Vert {\tilde{\varvec{v}}}\Vert _{H^1({\tilde{T}})}\).

Proof

  1. (i)

    If T is an (interior) affine element, then \({\varvec{\Psi }}_T {\tilde{\varvec{v}}} = {\tilde{\varvec{v}}}\) by Lemma 3.9. Also, we conclude from (3.6) and Lemma 3.3 that \(\frac{{\partial }\hat{\Theta }_{{\tilde{T}}}{\tilde{\varvec{v}}}}{{\partial }{\hat{\varvec{n}}}}\big |_{{\partial }{\hat{T}}}=0\), which implies \( {\hat{\Theta }}_{{\tilde{T}}}{\tilde{\varvec{v}}} = 0\). Thus if T is affine, \({\varvec{\Psi }}^C_T {\tilde{\varvec{v}}} ={\varvec{\Psi }}_T {\tilde{\varvec{v}}} = {\tilde{\varvec{v}}}\).

  2. (ii)

    The divergence-preserving property of the Piola transform (2.4) shows

    $$\begin{aligned} \textrm{div}\,\Big ((A_T {\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{\Theta }}_{{\tilde{T}}} {\tilde{\varvec{v}}})\circ F_T^{-1}\Big ) = \Big (\frac{1}{\det (DF_T)} \widehat{\textrm{div}\,} \widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}({\hat{\Theta }}_{{\tilde{T}}} {\tilde{\varvec{v}}})\Big )\circ F_T^{-1} = 0. \end{aligned}$$

    This identity immediately yields \(\textrm{div}\,{\varvec{\Psi }}_T^C {\tilde{\varvec{v}}} = \textrm{div}\,{\varvec{\Psi }}_T{\tilde{\varvec{v}}}\).

  3. (iii)

    Assume that T is a boundary triangle with curved edge, for otherwise the result is trivial. Set \({\hat{z}} = \hat{\Theta }_{{\tilde{T}}} {\tilde{\varvec{v}}}\in {\hat{\mathbb {W}}}\) so that

    $$\begin{aligned} {\varvec{\Psi }}_T^C {\tilde{\varvec{v}}} = {\varvec{\Psi }}_T {\tilde{\varvec{v}}} - (A_T{\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}})\circ F_{T}^{-1}. \end{aligned}$$
    (3.9)

    In light of (3.8), it suffices to estimate \(\Vert {\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}}\Vert ^2_{H^1({\hat{T}})}\).

Using Lemma 3.2, equivalence of norms, and (3.6) we get

$$\begin{aligned} \Vert {\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}}\Vert _{H^1({\hat{T}})}^2 \le C \Big (\Vert \hat{\nabla }{\hat{z}}\Vert ^2_{L^2(\partial {\hat{T}})} + \Vert {\hat{z}}\Vert ^2_{L^2(\partial {\hat{T}})}\Big ) = C \big \Vert \frac{{\partial }{\hat{z}}}{{\partial }{\hat{\varvec{n}}}}\big \Vert ^2_{L^2(\partial {\hat{T}})} \\ \le C\Vert A_T^{-1}\Vert _{L^\infty ({\hat{T}})}^2 \Big (\Vert {\varvec{\Psi }}_T {\tilde{\varvec{v}}} \circ F_T\Vert ^2_{L^2({\hat{T}})} + \Vert {{\tilde{\varvec{v}}}} \circ F_{\tilde{T}}\Vert ^2_{L^2({\hat{T}})} \Big ). \end{aligned}$$

Thus, by Lemmas 2.1–2.2, (3.8), and the Poincare inequality

$$\begin{aligned} \Vert {\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}}\Vert _{H^1({\hat{T}})}^2&\le Ch_T^2 \Big (\Vert {\varvec{\Psi }}_T {\tilde{\varvec{v}}} \circ F_T\Vert ^2_{L^2({\hat{T}})} + \Vert {{\tilde{\varvec{v}}}} \circ F_{{\tilde{T}}}\Vert ^2_{L^2({\hat{T}})} \Big )\\&\le C \Big (\Vert {\varvec{\Psi }}_T {\tilde{\varvec{v}}} \Vert ^2_{L^2(T)} + \Vert {{\tilde{\varvec{v}}}} \Vert ^2_{L^2({\tilde{T}})} \Big )\le C h_T^2 \Vert {\tilde{\varvec{v}}}\Vert _{H^1(\tilde{T})}^2. \end{aligned}$$

Finally, we apply this estimate to (3.8)–(3.9) and again apply Lemmas 2.1–2.2:

$$\begin{aligned} \Vert {\varvec{\Psi }}_T^C {\tilde{\varvec{v}}}\Vert _{H^1(T)}&\le \Vert {\varvec{\Psi }}_T {\tilde{\varvec{v}}}\Vert _{H^1(T)} +C\Vert A_T{\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}}\Vert _{H^1({\hat{T}})}\\&\le C\big ( \Vert {\tilde{\varvec{v}}}\Vert _{H^1({\tilde{T}})} + \Vert A_T\Vert _{W^{1,\infty }({\hat{T}})} \Vert {\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}}\Vert _{H^1({\hat{T}})}\big )\\&\le C\big ( \Vert {\tilde{\varvec{v}}}\Vert _{H^1({\tilde{T}})} + h_T^{-1} \Vert {\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}}\Vert _{H^1({\hat{T}})}\big )\le C \Vert {\tilde{\varvec{v}}}\Vert _{H^1({\tilde{T}})}. \end{aligned}$$

\(\square \)

Lemma 3.11

For \(T \in \mathcal {T}_h\) and \(\varvec{u}\in \varvec{H}^3(T)\), let \({\tilde{\varvec{v}}} \in \varvec{V}({\tilde{T}})\) be the unique function satisfying \({\tilde{\varvec{v}}}({\tilde{a}}_i)=\varvec{u}(a_i)\) with \(G_h({\tilde{a}}_i)=a_i\) for \(i=1,2,...,10\). Then, there holds

$$\begin{aligned} \Vert \varvec{u}- {\varvec{\Psi }}^C_T {\tilde{\varvec{v}}}\Vert _{H^m(T)}\le h_{T}^{3-m}\Vert \varvec{u}\Vert _{H^3(T)}\qquad m=0,1. \end{aligned}$$
(3.10)

Proof

Write \({\varvec{\Psi }}^C_T {\tilde{\varvec{v}}} = {\varvec{\Psi }}_T {\tilde{\varvec{v}}} - (A_T \widehat{\varvec{{\mathop {\textrm{curl}\,}}}}{\hat{z}})\circ F_T^{-1}\) with \({\hat{z}} = \hat{\Theta }_{{\tilde{T}}} {\tilde{\varvec{v}}} \in {\hat{\mathbb {W}}}\). First, the result in [15, Lemma 3.5] yields

$$\begin{aligned} \Vert \varvec{u}- {\varvec{\Psi }}_T {\tilde{\varvec{v}}}\Vert _{H^m(T)}\le h_{T}^{3-m}\Vert \varvec{u}\Vert _{H^3(T)}\qquad m=0,1. \end{aligned}$$
(3.11)

We also have by equivalence of norms,

$$\begin{aligned} \begin{aligned} |{\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}}|_{H^m({\hat{T}})}&\le C \Vert {\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}}\Vert _{L^2(\partial {\hat{T}})}\\&\le C\Vert A_T^{-1} \big ({\varvec{\Psi }}_T {\tilde{\varvec{v}}} \circ F_T - {\tilde{\varvec{v}}}\circ F_{{\tilde{T}}}\big )\big \Vert _{L^2({\hat{T}})}^2\\&\le C h_T^2 \big (\Vert {\hat{\varvec{u}}} - {\varvec{\Psi }}_T {\tilde{\varvec{v}}}\circ F_T\Vert _{L^2({\hat{T}})}^2 + \Vert {\hat{\varvec{u}}}- {\tilde{\varvec{v}}}\circ F_{\tilde{T}}\Vert _{L^2({\hat{T}})}^2\big ), \end{aligned} \end{aligned}$$
(3.12)

where \({\hat{\varvec{u}}}\in \varvec{H}^3({\hat{T}})\) satisfies \({\hat{\varvec{u}}}({\hat{x}}) = \varvec{u}(x)\). By a change of variables (cf. Lemma 2.1) and (3.11),

$$\begin{aligned} \Vert {\hat{\varvec{u}}} - {\varvec{\Psi }}_T {\tilde{\varvec{v}}}\circ F_T\Vert _{L^2({\hat{T}})}^2\le C h_T^{-2} \Vert \varvec{u}- {\varvec{\Psi }}_T {\tilde{\varvec{v}}}\Vert _{L^2(T)}^2\le C h_T^{4} \Vert \varvec{u}\Vert _{H^3(T)}^2. \end{aligned}$$
(3.13)

By properties of \({\tilde{\varvec{v}}}\), standard approximation theory and Lemma 2.1,

$$\begin{aligned} \Vert {\hat{\varvec{u}}}- {\tilde{\varvec{v}}}\circ F_{{\tilde{T}}}\Vert _{L^2({\hat{T}})}^2\le C |{\hat{\varvec{u}}}|_{H^3({\hat{T}})}^2\le C h_T^4 \Vert \varvec{u}\Vert _{H^3(T)}^2. \end{aligned}$$
(3.14)

Combining (3.12)–(3.14) yields

$$\begin{aligned} |{\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}}|_{H^m({\hat{T}})} \le C h_T^6 \Vert \varvec{u}\Vert _{H^3(T)}^2, \end{aligned}$$

and therefore by (3.11) and Lemmas  2.1–2.2,

$$\begin{aligned} \Vert \varvec{u}- {\varvec{\Psi }}^C_T {\tilde{\varvec{v}}}\Vert _{H^m(T)}&\le \Vert \varvec{u}-{\varvec{\Psi }}_T {\tilde{\varvec{v}}}\Vert _{H^m(T)} + \Vert (A_T {\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}})\circ F_T^{-1}\Vert _{H^m(T)}\\&\le C \big ( h_T^{3-m} \Vert \varvec{u}\Vert _{H^3(T)} + h_T^{1-m} \Vert A_T {\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}}\Vert _{H^m({\hat{T}})}\big )\\&\le C \big ( h_T^{3-m} \Vert \varvec{u}\Vert _{H^3(T)} + h_T^{-m} \Vert {\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}}\Vert _{H^m({\hat{T}})}\big )\\&\le C h_T^{3-m}\Vert \varvec{u}\Vert _{H^3(T)}. \end{aligned}$$

\(\square \)

4 Global Spaces and Inf-Sup Stability

Using the local mappings \({\varvec{\Psi }}_T\), \({\varvec{\Psi }}_T^C\), and \(\Upsilon _T\), for \(T\in \mathcal {T}_h\), we define the analogous global mappings \({\varvec{\Psi }}\), \({\varvec{\Psi }}^C\), and \(\Upsilon \) piecewise as

$$\begin{aligned} {\varvec{\Psi }}|_{T}:=\varvec{\Psi }_T,\qquad {\varvec{\Psi }}^C|_{T}:=\varvec{\Psi }^C_T,\qquad \Upsilon |_{T}:=\Upsilon _T,\quad \forall T\in \mathcal {T}_h. \end{aligned}$$

The Scott-Vogelius pair on the affine triangulation \({\tilde{\mathcal {T}}}_h\) is defined as

$$\begin{aligned} {\tilde{\varvec{V}}}_h&= \{{\tilde{\varvec{v}}}\in \varvec{H}^1_0({\tilde{\Omega }}_h): {\tilde{\varvec{v}}}|_{{\tilde{T}}}\in \varvec{V}({\tilde{T}}),\ \forall {\tilde{T}}\in {\tilde{\mathcal {T}}}_h\},\\ {\tilde{Q}}_h&= \{{\tilde{q}}\in L^2_0({\tilde{\Omega }}_h):\ {\tilde{q}}|_{{\tilde{T}}}\in {\tilde{Q}}({\tilde{T}}),\ \forall {\tilde{T}}\in {\tilde{\mathcal {T}}}_h\}. \end{aligned}$$

Using this pair \({\tilde{\varvec{V}}}^h \times {\tilde{Q}}^h\) and the global mappings \({\varvec{\Psi }}^C\), \(\Upsilon \), we define the global velocity space and global pressure space, respectively, as follows:

$$\begin{aligned} \varvec{V}^C_h:=\{\varvec{v}:\ \varvec{v}={\varvec{\Psi }}^C {\tilde{\varvec{v}}},\ \exists {\tilde{\varvec{v}}}\in {\tilde{\varvec{V}}}_h\},\quad Q_h:= \{q:\ q = \Upsilon {\tilde{q}},\ \exists {\tilde{q}}\in {\tilde{Q}}_h\}. \end{aligned}$$

It follows from Theorem 3.8 that \(\varvec{V}^C_h \subset \varvec{H}^1_0(\Omega _h)\). We also define the \(\varvec{H}(\textrm{div};\Omega _h)\)-conforming space (cf. [15, Theorem 4.2])

$$\begin{aligned} \varvec{V}_h = \{\varvec{v}:\ \varvec{v}={\varvec{\Psi }}{\tilde{\varvec{v}}},\ \exists {\tilde{\varvec{v}}}\in {\tilde{\varvec{V}}}_h\}. \end{aligned}$$

The following theorem shows that that conforming Stokes pair \(\varvec{V}_h^C\times Q_h\) is inf-sup stable.

Theorem 4.1

There exists \(\beta >0\) independent of h such that

$$\begin{aligned} \sup _{\varvec{v}\in \varvec{V}_h^C\backslash \{0\}} \frac{\int _{\Omega _h} (\textrm{div}\,\varvec{v})q\, dx}{\Vert \nabla \varvec{v}\Vert _{L^2(\Omega _h)}} \ge \beta \Vert q\Vert _{L^2(\Omega _h)}\qquad \forall q\in Q_h. \end{aligned}$$
(4.1)

Proof

It is established in [15, Theorem 4.4] that the (nonconforming) pair \(\varvec{V}_h\times Q_h\) is inf-sup stable. In particular, there exists \(\gamma >0\) such that for a given \(q\in Q_h\), there exists \(\varvec{v}\in \varvec{V}_h\) such that

$$\begin{aligned} \frac{\int _{\Omega _h} (\textrm{div}\,\varvec{v})q\, dx}{\Vert \varvec{v}\Vert _{H^1(\Omega _h)}} \ge \gamma \Vert q\Vert _{L^2(\Omega _h)}. \end{aligned}$$
(4.2)

Let \({\tilde{\varvec{v}}} \in {\tilde{\varvec{V}}}_h\) be the unique function such that \(\varvec{v}= {\varvec{\Psi }}{\tilde{\varvec{v}}}\in \varvec{V}_h\), and set \(\varvec{v}^C = {\varvec{\Psi }}^C {\tilde{\varvec{v}}}\). By Lemma 3.9–3.10, we have

$$\begin{aligned} \textrm{div}\,\varvec{v}^C = \textrm{div}\,{\varvec{\Psi }}^C {\tilde{\varvec{v}}} = \textrm{div}\,{\varvec{\Psi }}{\tilde{\varvec{v}}} = \textrm{div}\,\varvec{v}, \end{aligned}$$

and

$$\begin{aligned} \Vert \varvec{v}^C\Vert _{H^1(\Omega _h)}\le C \Vert {\tilde{\varvec{v}}}\Vert _{H^1({\tilde{\Omega }}_h)}\le C \Vert \varvec{v}\Vert _{H^1(\Omega )}. \end{aligned}$$

Using these two identities in (4.2) yields

$$\begin{aligned} \gamma \Vert q\Vert _{L^2(\Omega _h)}\le \frac{\int _{\Omega _h} (\textrm{div}\,\varvec{v}^C )q\, dx}{\Vert \varvec{v}\Vert _{H^1(\Omega _h)}} \le C \frac{\int _{\Omega _h} (\textrm{div}\,\varvec{v}^C )q\, dx}{\Vert \varvec{v}^C\Vert _{H^1(\Omega _h)}}. \end{aligned}$$

This implies the desired result with \(\beta = \gamma /C\). \(\square \)

5 Finite element method for the Stokes problem and convergence analysis

We consider finite element approximations for the Stokes problem with no-slip boundary conditions

$$\begin{aligned} -\nu \Delta \varvec{u}+ \nabla p&= f \qquad \text {in }\Omega ,\\ \textrm{div}\,\varvec{u}&= 0 \qquad \text {in }\Omega ,\\ \varvec{u}&=0 \qquad \text {on }{\partial }\Omega , \end{aligned}$$

where we assume the viscosity \(\nu >0\) is constant for simplicity. We assume the data is sufficient regular, such that the exact solution satisfies \((\varvec{u},p)\in \varvec{H}^3(\Omega )\times H^2(\Omega )\). Because \({\partial }\Omega \) is assumed smooth, there exists extensions of the solution, still denoted by \((\varvec{u},p)\) such that \(\textrm{div}\,\varvec{u}= 0\) in \(\mathbb {R}^2\), and

$$\begin{aligned} \Vert \varvec{u}\Vert _{H^3(\mathbb {R}^2)}\le C \Vert \varvec{u}\Vert _{H^3(\Omega )},\qquad \Vert p\Vert _{H^2(\mathbb {R}^2)}\le C\Vert p\Vert _{H^2(\Omega )}. \end{aligned}$$

We extend the source function via \({\varvec{f}} = -\nu \Delta \varvec{u}+ \nabla p\) in \(\mathbb {R}^2\).

The proposed method seeks \((\varvec{u}_h,p_h)\in \varvec{V}_h^C\times Q_h\) such that

$$\begin{aligned} \int _{\Omega _h} \nu \nabla \varvec{u}_h:\nabla \varvec{v}\, dx - \int _{\Omega _h} (\textrm{div}\,\varvec{v}) p_h\, dx&= \int _{\Omega _h} {\varvec{f}}_h\cdot \varvec{v}\, dx \qquad{} & {} \forall \varvec{v}\in \varvec{V}_h^C,\end{aligned}$$
(5.1a)
$$\begin{aligned} \int _{\Omega _h} (\textrm{div}\,\varvec{u}_h)q\, dx&=0\qquad{} & {} \forall q\in Q_h, \end{aligned}$$
(5.1b)

where \({\varvec{f}}_h\in \varvec{L}^2(\Omega _h)\) is some computable approximation of \({\varvec{f}}|_{\Omega }\). It follows from the inf-sup stability result in Theorem 4.1 and standard arguments in mixed finite element theory that there exists a unique solution to (5.1). Moreover, the method yields a divergence-free velocity approximation as the following lemma shows.

Lemma 5.1

Suppose \(\varvec{u}_h\in \varvec{V}_h^C\) satisfies (5.1b). Then \(\textrm{div}\,\varvec{u}_h \equiv 0\) in \(\Omega _h\).

Proof

Write \(\varvec{u}_h = {\varvec{\Psi }}^C {\tilde{\varvec{v}}}\) for some \({\tilde{\varvec{v}}} \in {\tilde{\varvec{V}}}_h\). Then, by (5.1b) and Lemma 3.10 we have

$$\begin{aligned} \int _{\Omega _h} (\textrm{div}\,\varvec{u}_h)q\, dx&= \int _{\Omega _h} (\textrm{div}\,{\varvec{\Psi }}^C {\tilde{\varvec{v}}} )q\, dx = \int _{\Omega _h} (\textrm{div}\,{\varvec{\Psi }}{\tilde{\varvec{v}}} )q\, dx = 0,\qquad{} & {} \forall q\in Q_h. \end{aligned}$$

It is shown in [15, Lemma 5.2] that the right hand side of the above equation implies that \(\textrm{div}\,{\varvec{\Psi }}{\tilde{\varvec{v}}} = 0\) in \(\Omega _h\). Hence, \(\textrm{div}\,{\varvec{\Psi }}{\tilde{\varvec{v}}} = \textrm{div}\,{\varvec{\Psi }}^C {\tilde{\varvec{v}}} = \textrm{div}\,\varvec{u}_h = 0\) in \(\Omega _h\). \(\square \)

Next, we state that the method is well-posed and optimally convergent. In the light of Theorem 4.1, Lemma 3.9, the next two theorems follow from standard arguments of mixed finite element theory.

Theorem 5.2

There exists a unique solution \((\varvec{u}_h, p_h) \in \varvec{V}_h^C \times Q_h\) satisfying (5.1).

Theorem 5.3

There holds

$$\begin{aligned} \Vert \nabla (\varvec{u}- \varvec{u}_h)\Vert _{L^2(\Omega _h)}&\le C\big ( h^2 \Vert \varvec{u}\Vert _{H^3(\Omega )} + \nu ^{-1} |{\varvec{f}}-{\varvec{f}}_h|_{X_h^*}\big ), \end{aligned}$$
(5.2)

where

$$\begin{aligned} |{\varvec{f}}-{\varvec{f}}_h|_{X_h^*} = \sup _{\varvec{v}\in {\varvec{X}}^C_h\backslash \{0\}} \frac{\int _{\Omega _h} ({\varvec{f}}-{\varvec{f}}_h)\cdot \varvec{v}\,dx}{\Vert \nabla \varvec{v}\Vert _{L^2(\Omega _h)}}, \quad {\varvec{X}}_h^C:=\{\varvec{v}\in \varvec{V}_h^C:\ \textrm{div}\,\varvec{v}= 0\}. \end{aligned}$$

The pressure approximation satisfies

$$\begin{aligned} \Vert p-p_h\Vert _{L^2(\Omega _h)}\le C\big (\nu h^2 \Vert \varvec{u}\Vert _{H^3(\Omega )}+ \inf _{q\in Q_h} \Vert p-q\Vert _{L^2(\Omega _h)} + \Vert {\varvec{f}}-{\varvec{f}}_h\Vert _{L^2(\Omega _h)}\big ). \end{aligned}$$
(5.3)

6 Numerics

6.1 Implementation aspects

In this section, we discuss the implementation of the proposed method, in particular, the computation of a basis for the velocity space \(\varvec{V}_h^C\). Recall this space is defined as the image of the operator \({\varvec{\Psi }}^C\) acting on the affine quadratic Lagrange finite element space \({\tilde{\varvec{V}}}_h\). For any basis of \({\tilde{\varvec{V}}}_h\) restricted to some \({\tilde{T}}\in {\tilde{\mathcal {T}}}_h\), call \(\{{\tilde{\varvec{\varphi }}}_i^{(k)}\}\), the set \(\{{\varvec{\Psi }}_T^C {\tilde{\varvec{\varphi }}}^{(k)}_i\}\) represents a basis of \(\varvec{V}_h^C\) restricted to \(T = G_h({\tilde{T}})\in \mathcal {T}_h\). In the following discussion, we take \({\tilde{\varvec{\varphi }}}_i^{(k)}\) to be the canonical nodal basis, and discuss the computation in the case T has a curved edge; if T is affine, then \({\varvec{\Psi }}^C_T {\tilde{\varvec{\varphi }}}_i^{(k)} = {\tilde{\varvec{\varphi }}}_i^{(k)}|_T\), and so the computation is standard. We start with some notation and assumptions.

To ease presentation, we set \(B = A_T^{-1} = \textrm{adj}(DF_T):{\hat{T}}\rightarrow \mathbb {R}^{2\times 2}\). Because \(F_T:{\hat{T}}\rightarrow T\) is a quadratic mapping, we see that the entries of B are linear polynomials. We denote the kth column of B by \({\varvec{\beta }}^{(k)}\), i.e.,

$$\begin{aligned} {\varvec{\beta }}^{(k)}_i = B_{i,k}. \end{aligned}$$

Let \({\hat{e}}_1\) denote the edge of \({\hat{T}}\) connecting (0, 0) and (1, 0), \({\hat{e}}_2\) denote the edge of \({\hat{T}}\) connecting (0, 0) and (0, 1), and \({\hat{e}}_3\) denote the remaining edge. Without loss of generality and with an abuse of notation, we assume \(F_{ T}({\hat{e}}_3) \subset \partial \Omega _h\), i.e., \({\hat{e}}_3\) is the pre-image of the curved edge of T. Also, let \(\{{\hat{a}}_i\}_{i=1}^{10}\) denote the ten Lagrange DOFs of \({\hat{\varvec{V}}}\) where, in order to ease the presentation, we assume \({\hat{a}}_1= {\hat{m}}_{{\hat{e}}_1}\), \({\hat{a}}_2 = {\hat{m}}_{{\hat{e}}_2}\), and \({\hat{a}}_3 = (0,0)\); see Fig. 1. We also assume \({\hat{a}}_8,{\hat{a}}_9,{\hat{a}}_{10}\in \bar{{\hat{e}}}_3\), so that, due to the boundary conditions, these DOFs are not active. This labeling convention also implies that the unit tangent on \({\hat{e}}_k\) is \({\hat{\varvec{t}}}_{{\hat{e}}_k} = \pm \varvec{e}^{(k)}\) for \(k=1,2\), where \(\varvec{e}^{(k)}= (\delta _{k1}, \delta _{k2})^{\intercal }\). Furthermore, let \({\hat{K}}_i \in {\hat{T}}^{ct}\), \(i=1,2,3,\) be such that \({\hat{K}}_i\) does not contain \({\hat{a}}_i\).

Fig. 1
figure 1

Node labeling convention

Full size image

Let \({\hat{\varphi }}_j\) denote the nodal Lagrange basis function of \(\mathcal {P}_2^c({\hat{T}}^{ct})\) corresponding to the node \({\hat{a}}_i\), i.e., \({\hat{\varphi }}_j({\hat{a}}_i) = \delta _{i,j}\). Let \({\hat{\varvec{\varphi }}}_j^{(k)} = {\hat{\varphi }}_j \varvec{e}^{(k)}\) \((k=1,2)\), so that \(\{{\hat{\varvec{\varphi }}}_j^{(k)}\}\) is a nodal basis of \({\hat{\varvec{V}}}\). Likewise, we set \({\tilde{\varphi }}_j\in \mathcal {P}_2^c({\tilde{T}}^{ct})\) as \({\tilde{\varphi }}_j({\tilde{x}}) = {\hat{\varphi }}({\hat{x}})\) with \({\tilde{x}} = F_{{\tilde{T}}}({\hat{x}})\), and \({\tilde{\varvec{\varphi }}}_j^{(k)} = {\tilde{\varphi }}_j \varvec{e}^{(k)}\). Then \(\{{\tilde{\varvec{\varphi }}}_j^{(k)}\}\) is a nodal basis of \(\varvec{V}({\tilde{T}})\).

The construction of \(\varvec{\varphi }_j^{(k)}:={\varvec{\Psi }}_T^C {\tilde{\varvec{\varphi }}}_j^{(k)}\) is summarized in the following proposition.

Proposition 6.1

Let \(\{{\hat{\tau }}_1,{\hat{\tau }}_2\}\subset {\hat{\mathbb {W}}}\) be the nodal basis functions of \({\hat{\mathbb {W}}}\) satisfying (cf. Table 1)

$$\begin{aligned} \frac{{\partial }^2 {\hat{\tau }}_j}{{\partial }{\hat{\varvec{n}}}_{{\hat{e}}_i}{\partial }\varvec{t}_{{\hat{e}}_i}}({\hat{m}}_{{\hat{e}}_i}) = \delta _{i,j},\quad i,j=1,2,\qquad \frac{{\partial }^2 {\hat{\tau }}_j}{{\partial }{\hat{\varvec{n}}}_{{\hat{e}}_3}{\partial }\varvec{t}_{{\hat{e}}_3}}({\hat{m}}_{e_3})=0. \end{aligned}$$

Define the functions \({\hat{z}}_j^{(k)}\in {\hat{\mathbb {W}}}\) as

$$\begin{aligned} {\hat{z}}_j^{(k)} = -\frac{{\partial }B_{j,k}}{{\partial }{\hat{x}}_j} {\hat{\tau }}_j\ \ \text {for }j=1,2,\quad {\hat{z}}_3^{(k)} = -\frac{1}{2} ({\hat{z}}_1^{(k)} + {\hat{z}}_2^{(k)}),\quad {\hat{z}}_j^{(k)} = 0\ \ \text {for }4\le j\le 7. \end{aligned}$$

Then a nodal basis of \(\varvec{V}(T)\) is given by the formula

$$\begin{aligned} \varvec{\varphi }_j^{(k)} \circ F_T = A_T \big ({\varvec{\beta }}^{(k)}({\hat{a}}_j) \hat{\varphi }_j - {\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}}_j^{(k)}\big ). \end{aligned}$$
(6.1)

Proof

Set \({\hat{z}}_j^{(k)} = {\hat{\Theta }}_{{\tilde{T}}} {\tilde{\varvec{\varphi }}}_j^{(k)}\), so that, by definition of \({\varvec{\Psi }}_T^C\),

$$\begin{aligned} \varvec{\varphi }_j^{(k)}= {\varvec{\Psi }}_T {\tilde{\varvec{\varphi }}}_j^{(k)} - (A_T\widehat{\varvec{{\mathop {\textrm{curl}\,}}}}{\hat{z}}_j^{(k)})\circ F_T^{-1}, \end{aligned}$$
(6.2)

where we recall the function \({\varvec{\Psi }}_T{\tilde{\varvec{\varphi }}}_j^{(k)}\in \varvec{V}(T)\) is uniquely defined by the conditions

$$\begin{aligned} {\varvec{\Psi }}_T {\tilde{\varvec{\varphi }}}_j^{(k)}(a_i) = {\tilde{\varvec{\varphi }}}_j^{(k)}({\tilde{a}}_i) = \delta _{i,j}\varvec{e}^{(k)}\qquad i=1,2,\ldots ,10. \end{aligned}$$
(6.3)

By the definition of \(\varvec{V}(T)\), we can write \({\varvec{\Psi }}_T {\tilde{\varvec{\varphi }}}_j^{(k)}(x) = (A_T {\hat{\varvec{\psi }}}_j^{(k)})({\hat{x}})\), for some \({\hat{\varvec{\psi }}}_j^{(k)}\in {\hat{\varvec{V}}}\). In particular, from (6.3), we see that \({\hat{\varvec{\psi }}}^{(k)}_j = {\varvec{\beta }}^{(k)}({\hat{a}}_j) {\hat{\varphi }}_j.\) Combining this identity with (6.2) yields

$$\begin{aligned} {\varvec{\Psi }}_T {\tilde{\varvec{\varphi }}}_j^{(k)} \circ F_T&= A_T {\varvec{\beta }}^{(k)}({\hat{a}}_j) {\hat{\varphi }}_j, \end{aligned}$$
(6.4)
$$\begin{aligned} \varvec{\varphi }_j^{(k)} \circ F_T&= A_T\big ({\varvec{\beta }}^{(k)}({\hat{a}}_j) {\hat{\varphi }}_j- {\widehat{{\varvec{{\mathop {\textrm{curl}\,}}}}}} {\hat{z}}_j^{(k)} \big ). \end{aligned}$$
(6.5)

Notice that, due to the boundary conditions and labeling convention, there holds \({\tilde{\varvec{\varphi }}}_j^{(k)}|_{{\partial }{\tilde{T}}} = 0\) for \(j=4,5,6,7\) and \(k=1,2\). This implies \({\hat{z}}_j^{(k)}=0\) (cf. Remark 3.7), and thus we conclude

$$\begin{aligned} \varvec{\varphi }_j^{(k)} \circ F_T = A_T {\varvec{\beta }}^{(k)}({\hat{a}}_j) \hat{\varphi }_j\qquad \text {for }j=4,5,6,7,\ k=1,2. \end{aligned}$$

Hence, it remains to discuss the construction of \( {\hat{z}}^{(k)}_{j}\) for \(j=1,2,3\), \(k=1,2\).

Using Remark 3.7, the function \({\hat{z}}_j^{(k)}\) is uniquely determined by the conditions

$$\begin{aligned} c_{j,i}^{(k)}:= \frac{{\partial }^2 {\hat{z}}_j^{(k)}}{{\partial }{\hat{\varvec{n}}}_{{\hat{e}}_i}{\partial }\varvec{t}_{{\hat{e}}_i}}({\hat{m}}_{{\hat{e}}_i})&= \frac{{\partial }}{{\partial }{\hat{\varvec{t}}}_{{\hat{e}}_i}}\Big (B({\varvec{\Psi }}_T {\tilde{\varvec{\varphi }}}_j^{(k)} \circ F_T -{{\tilde{\varvec{\varphi }}}_j^{(k)}} \circ F_{{\tilde{T}}})\cdot {\hat{\varvec{t}}}_{{\hat{e}}_i}\Big )({\hat{m}}_{{\hat{e}}_i})\quad i=1,2,3. \end{aligned}$$

Due to the boundary conditions and labeling convention, the right-hand side expression is zero in the case \(i=3\). Thus, we have

$$\begin{aligned} {\hat{z}}_j^{(k)} = c_{j,1}^{(k)} {\hat{\tau }}_1 + c_{j,2}^{(k)} {\hat{\tau }}_2. \end{aligned}$$
(6.6)

Using the identity \({\hat{\varvec{t}}}_{{\hat{e}}_i} = \pm \varvec{e}^{(i)}\) for \(i=1,2\) and (6.4), we have

$$\begin{aligned} c_{j,i}^{(k)}&= \frac{{\partial }}{{\partial }{\hat{x}}_i}\Big (B(A_T{\varvec{\beta }}^{(k)}({\hat{a}}_j)\hat{\varphi }_j -{{\hat{\varvec{\varphi }}}_j^{(k)}} )\cdot \varvec{e}^{(i)}\Big )({\hat{a}}_{i})\\&= \frac{{\partial }}{{\partial }{\hat{x}}_i}\Big ( {\hat{\varphi }}_j \big ({\varvec{\beta }}^{(k)}({\hat{a}}_j) - B \varvec{e}^{(k)} \big )\cdot \varvec{e}^{(i)}\Big )({\hat{a}}_i)\\&= \frac{{\partial }}{{\partial }{\hat{x}}_i}\Big ( {\hat{\varphi }}_j \big (B_{i,k}({\hat{a}}_j) - B_{i,k}\big )\Big )({\hat{a}}_i)\qquad i=1,2. \end{aligned}$$

By the product rule and the property \({\hat{\varphi }}_j({\hat{a}}_i) = \delta _{i,j}\) yields

$$\begin{aligned} c_{j,i}^{(k)}&= \frac{{\partial }{\hat{\varphi }}_j}{{\partial }{\hat{x}}_i}({\hat{a}}_i) \big ( B_{i,k}({\hat{a}}_j) - B_{i,k}({\hat{a}}_i) \big ) - \delta _{i,j} \frac{{\partial }B_{i,k}}{{\partial }{\hat{x}}_i}. \end{aligned}$$

In particular, there holds

$$\begin{aligned} c_{j,i}^{(k)} = \frac{{\partial }^2 {\hat{z}}_j^{(k)}}{{\partial }{\hat{\varvec{n}}}_{{\hat{e}}_i}{\partial }\varvec{t}_{{\hat{e}}_i}}({\hat{a}}_i) = -\delta _{i,j} \frac{{\partial }B_{i,k}}{{\partial }{\hat{x}}_i}\quad \text {for }j=1,2. \end{aligned}$$
(6.7)

because \(\frac{{\partial }{\hat{\varphi }}_j}{{\partial }{\hat{x}}_i} ({\hat{a}}_i) = 0\) for \(i\ne j\). The case \(j=3\) reads

$$\begin{aligned} c_{3,i}^{(k)} = \frac{{\partial }^2 {\hat{z}}_3^{(k)}}{{\partial }{\hat{\varvec{n}}}_{{\hat{e}}_i}{\partial }\varvec{t}_{{\hat{e}}_i}}({\hat{a}}_i)&= \frac{{\partial }{\hat{\varphi }}_3}{{\partial }{\hat{x}}_i}({\hat{a}}_i) \big ( B_{i,k}({\hat{a}}_3) - B_{i,k}({\hat{a}}_i) \big ). \end{aligned}$$

A simple calculation yields \( \frac{{\partial }{\hat{\varphi }}_3}{{\partial }{\hat{x}}_i}({\hat{a}}_i) = -1\) for \(i=1,2\), and therefore,

$$\begin{aligned} c_{3,i}^{(k)}&= \big ( B_{i,k}({\hat{a}}_i) - B_{i,k}({\hat{a}}_3) \big ) = \frac{1}{2} \frac{{\partial }B_{i,k}}{{\partial }{\hat{x}}_i}. \end{aligned}$$
(6.8)

The statements (6.6)–(6.8) provide the formula for \(z_j^{(k)}\), which combined with (6.5), yields the desired result (6.1). \(\square \)

Table 1 Formulas for nodal basis functions of \({\hat{\mathbb {W}}}\)
Full size table

6.2 Numerical experiments

To support the theoretical results, we compute the finite element method (5.1) on the domain \(\Omega = B_1(0)\) and construct the source function such that the exact solution is

$$\begin{aligned} \varvec{u}= & {} {\varvec{{\mathop {\textrm{curl}\,}}}}\big ((1 - x_1^2 - x_2^2)^2\sin (5 x_1 + 2 x_2)\big ),\nonumber \\ p= & {} x_1^2 + x_2^2 + \sin (10\pi (x_1^2 + x_2^2)) -\frac{1}{2}. \end{aligned}$$
(6.9)

Table 2 lists the errors of the discrete solution on a sequence of refined quasi-uniform meshes with viscosity \(\nu =10^{-1}\). The numerical experiments indicate second-order convergence of the velocity and pressure in the \(H^1\) and \(L^2\)-norms, respectively, which is in agreement with the theoretical results given in Theorem 5.3. In addition, we observe third-order convergence of discrete velocity function in the \(L^2\)-norm.

Table 2 Errors of the finite element method (5.1) with \(\Omega =B_1(0)\), \(\nu =10^{-1}\), and exact solution (6.9)
Full size table