Abstract
We consider the numerical computation of finite-range singular integrals

that are defined in the sense of Hadamard Finite Part, assuming that \(g\in C^\infty [a,b]\) and \(f(x)\in C^\infty ({\mathbb {R}}_t)\) is T-periodic with \(f \in C^\infty ({\mathbb {R}}_t),\) \({\mathbb {R}}_t={\mathbb {R}}{\setminus }\{t+ kT\}^\infty _{k=-\infty }\), \(T=b-a\). Using a generalization of the Euler–Maclaurin expansion developed in [A. Sidi, Euler–Maclaurin expansions for integrals with arbitrary algebraic endpoint singularities. Math. Comp., 81:2159–2173, 2012], we unify the treatment of these integrals. For each m, we develop a number of numerical quadrature formulas \({\widehat{T}}^{(s)}_{m,n}[f]\) of trapezoidal type for I[f]. For example, three numerical quadrature formulas of trapezoidal type result from this approach for the case \(m=3\), and these are
For all m and s, we show that all of the numerical quadrature formulas \({\widehat{T}}^{(s)}_{m,n}[f]\) have spectral accuracy; that is,
We provide a numerical example involving a periodic integrand with \(m=3\) that confirms our convergence theory. We also show how the formulas \({\widehat{T}}{}^{(s)}_{3,n}[f]\) can be used in an efficient manner for solving supersingular integral equations whose kernels have a \((x-t)^{-3}\) singularity. A similar approach can be applied for all m.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and background
In this work, we consider the efficient numerical computation of

where
Clearly, the integrals \(\int ^b_af(x)\,dx\) are not defined in the regular sense, but they are defined in the sense of Hadamard Finite Part (HFP), the HFP of \(\int ^b_af(x)\,dx\) being commonly denoted by  .Footnote 1
.Footnote 1
By invoking a recent generalization of the Euler–Maclaurin (E–M) expansion developed in Sidi [23, Theorem 2.3] that also applies to both regular and HFP integrals, we unify the treatments of the HFP integrals in (1.1)–(1.2) and derive a number of very effective numerical quadrature formulas for I[f] for each \(m\ge 1\). In the process of derivation, we also obtain a result that shows that all the quadrature formulas derived here enjoy spectral convergence. As examples, we provide the different quadrature formulas for the cases \(m=1,2,3,4\) and illustrate the application of those formulas with \(m=3\) to a nontrivial numerical example.
We note that the case \(m=1\) was considered earlier in Sidi and Israeli [29] and Sidi [25], the technique used in [29] being different from that used in [25]. The case \(m=2\) was treated in [25]. In [25], we also gave a detailed study of the exactness and convergence properties of the numerical quadrature formulas for the cases with \(m=1,2.\) In Sidi [26], we considered further convergence properties of these formulas and, in Sidi [27], we analyzed the numerical stability issues related to the application of the Richardson extrapolation process to them. (For the Richardson extrapolation process, see Sidi [22, Chapters 1,2], for example.)
For the definition and properties of Hadamard Finite Part integrals, see the books by Davis and Rabinowitz [2], Evans [4], Krommer and Ueberhuber [9], and Kythe and Schäferkotter [10], for example. These integrals have most of the properties of regular integrals and some properties that are quite unusual. For example, they are invariant with respect to translation, but they are not necessarily invariant under a scaling of the variable of integration, which is linear; therefore, they are not necessarily invariant under a nonlinear variable transformation either. Finally,  when \(\phi (x)\) is integrable over [a, b] in the regular sense. For more recent developments, see the books by Lifanov, Poltavskii, and Vainikko [13] and Ladopoulos [13], for example. See also the papers by Kaya and Erdogan [7], Monegato [16, 17], and Monegato and Lyness [18]. For an interesting two-dimensional generalization, see Lyness and Monegato [15].
when \(\phi (x)\) is integrable over [a, b] in the regular sense. For more recent developments, see the books by Lifanov, Poltavskii, and Vainikko [13] and Ladopoulos [13], for example. See also the papers by Kaya and Erdogan [7], Monegato [16, 17], and Monegato and Lyness [18]. For an interesting two-dimensional generalization, see Lyness and Monegato [15].
Cauchy principal value, hypersingular, and supersingular integrals described in footnote\(^{1}\) arise in different branches of science and engineering, such as fracture mechanics, elasticity, electromagnetic scattering, acoustics, and fluid mechanics, for example. They appear naturally in boundary integral equation formulations of boundary value problems in these disciplines. Periodic singular integrals arise naturally from Cauchy transforms  , where \(\Gamma \) is an infinitely smooth closed contour in the complex z-plane and \(z\in \Gamma \); we discuss this briefly in Sect. 5.
, where \(\Gamma \) is an infinitely smooth closed contour in the complex z-plane and \(z\in \Gamma \); we discuss this briefly in Sect. 5.
Various numerical quadrature formulas for these integrals have been developed in many papers. Some of these papers make use of trapezoidal sums or composite Simpson and Newton Cotes rules with appropriate correction terms to account for the singularity at \(x=t\); see Li and Sun [11], Li, Zhang, and Yu [12], Zeng, Li, and Huang [33], and Zhang, Wu, and Yu [34], for example. The paper by Huang, Wang, and Zhu [6] approaches the problem of computing HFP integrals of the form  , (with the restriction \(1<\beta \le 2\)) by following Sidi and Israeli [29], which is based on the generalizations of the Euler–Maclaurin expansion by Navot [19, 20]. The papers by Wu, Dai, and Zhang [30] and by Wu and Sun [32] take similar approaches. The approach of [25] is based on the most recent developments in Euler–Maclaurin expansions of [23] that are valid for all HFP integrals even with possible arbitrary algebraic endpoint singularities. We also mention here the papers by Criscuolo [1], De Bonis and Occorsio [3], Filbir, Occorsio, and Themistoclakis [5], and Wu and Sun [31]. Of these, [5, 31] consider integrands that are not infinitely smooth over [a, b], [5] considers numerical quadrature formulas that are based on equally spaced points and use Bernstein polynomials and their generalizations, while [3] considers HFP integrals over the infinite interval \((0,+\infty )\) and uses polynomial approximations.
, (with the restriction \(1<\beta \le 2\)) by following Sidi and Israeli [29], which is based on the generalizations of the Euler–Maclaurin expansion by Navot [19, 20]. The papers by Wu, Dai, and Zhang [30] and by Wu and Sun [32] take similar approaches. The approach of [25] is based on the most recent developments in Euler–Maclaurin expansions of [23] that are valid for all HFP integrals even with possible arbitrary algebraic endpoint singularities. We also mention here the papers by Criscuolo [1], De Bonis and Occorsio [3], Filbir, Occorsio, and Themistoclakis [5], and Wu and Sun [31]. Of these, [5, 31] consider integrands that are not infinitely smooth over [a, b], [5] considers numerical quadrature formulas that are based on equally spaced points and use Bernstein polynomials and their generalizations, while [3] considers HFP integrals over the infinite interval \((0,+\infty )\) and uses polynomial approximations.
In the next section, we review the author’s generalization of the E–M expansion for integrals whose integrands are allowed to have arbitrary algebraic endpoint singularities. This generalization is given as Theorem 2.1. In Sect. 3, we apply Theorem 2.1 to construct the generalized E–M expansion for I[f] given in (1.1)–(1.2). In Sect. 4, we develop a number of numerical quadrature formulas of trapezoidal type for I[f] with arbitrary m and analyze their convergence properties. We also analyze their numerical stability in floating-point arithmetic.
When applied to the HFP integrals  in (1.1)–(1.2), all these quadrature formulas possess the following favorable properties, which transpire from the developments in Sects. 3 and 4:
in (1.1)–(1.2), all these quadrature formulas possess the following favorable properties, which transpire from the developments in Sects. 3 and 4:
-
1.
Unlike the quadrature formulas developed in the papers mentioned above, they are compact in that they consist of trapezoidal-like rules with very simple, yet sophisticated and unexpected, “correction” terms to account for the singularity at \(x=t\).
-
2.
They have a unified convergence theory that follows directly and very simply from the way they are derived.
-
3.
Unlike the methods developed in the papers mentioned above, which attain very limited accuracies, our methods enjoy spectral accuracy.
-
4.
Because they enjoy spectral accuracy, they are much more stable numerically than existing methods.
In Sect. 5, we apply the quadrature formulas for supersingular integrals (\(m=3\)) of Sect. 4 to a T-periodic f(x) in \(C^\infty ({\mathbb {R}}_t)\) and confirm numerically the convergence theory of Sect. 4. Finally, in Sect. 6, we show how two of these quadrature formulas, denoted \({\widehat{T}}^{(0)}_{3,n}[\cdot ]\) and \({\widehat{T}}^{(2)}_{3,n}[\cdot ]\), can be used in the solution of supersingular integral equations.
Before proceeding to the next sections, we would like to recall some of the properties of the Riemann Zeta function \(\zeta (z)\) and the Bernoulli numbers \(B_k\) and the connection between them for future reference:
For all these and much more, see Olver et al. [21, Chapters 24, 25] or Luke [14, Chapter 2], for example. See also Sidi [22, Appendices D, E].
2 Generalization of the Euler–Maclaurin expansion to integrals with arbitrary algebraic endpoint singularities
The following theorem concerning the generalization of the E–M expansion to integrals with arbitrary algebraic endpoint singularities was published recently by Sidi [23, Theorem 2.3]. It serves as the main analytical tool for all the developments in this paper.
Theorem 2.1
Let \(u\in C^{\infty }(a,b)\), and assume that u(x) has the asymptotic expansions
where the \(\gamma _s\) and \(\delta _s\) are distinct complex numbers that satisfy

Assume furthermore that, for each positive integer k, \(u^{(k)}(x)\) has asymptotic expansions as \(x\rightarrow a+\) and \(x\rightarrow b-\) that are obtained by differentiating those of u(x) term by term k times.Footnote 2 Let also \(h=(b-a)/n\) for \(n=1,2,\ldots \ .\) Then, as \(h\rightarrow 0\),

where \(C=0.577\cdots \) is Euler’s constant.Footnote 3
Remarks
-
1.
Note that if \(K=L=0\) and \(\text {Re}\gamma _0>-1\) and \(\text {Re}\delta _0>-1\), then \(\int ^b_a u(x)\,dx\) exists as a regular integral; otherwise, it does not, but its HFP does.
-
2.
When \(u\in C^\infty [a,b]\), the Taylor series of u(x) at \(x=a\) and at \(x=b\), whether convergent or divergent, are also (i) asymptotic expansions of u(x) as \(x\rightarrow a+\) and as \(x\rightarrow b-\), respectively, and (ii) can be differentiated term-by-term any number of times. Thus, Theorem 2.1 applies without further assumptions on u(x) when \(u\in C^\infty [a,b]\).
-
3.
When \(u\in C^\infty (a,b)\), the E–M expansion is completely determined by the asymptotic expansions of u(x) as \(x\rightarrow a+\) and as \(x\rightarrow b-\), nothing else being needed. What happens in (a, b) is immaterial.
-
4.
It is clear from (2.3) that the positive even integer powers of \((x-a)\) and \((b-x)\), if present in the asymptotic expansions of u(x) as \(x\rightarrow a+\) and \(x\rightarrow b-\), do not contribute to the asymptotic expansion of \(h\sum ^{n-1}_{j=1}u(a+jh)\) as \(h\rightarrow 0\), the reason being that \(\zeta (-2k)=0\) for \(k=1,2,\ldots ,\) by (1.3). We have included the “limitations” \(\gamma _s\not \in \{2,4,6,\ldots \}\) and \(\delta _s\not \in \{2,4,6,\ldots \}\) in the sums on the right-hand side of (2.3) only as “reminders.”
-
5.
Theorem 2.1 is only a special case of a more general theorem in [23] involving the so-called “offset trapezoidal rule” \(h\sum ^{n-1}_{i=0}f(a+jh+\theta h)\), with \(\theta \in [0,1]\) fixed,Footnote 4 that contains as special cases all previously known generalizations of the E–M expansions for integrals with algebraic endpoint singularities. For a further generalization pertaining to arbitrary algebraic-logarithmic endpoint singularities, see Sidi [24].
3 Generalized Euler–Maclaurin expansion for 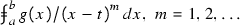
We now present the derivation of the generalized E–M expansion for the HFP integral I[f] in (1.1)–(1.2). As already mentioned, our starting point and main analytical tool is Theorem 2.1. Before we begin, we would like to mention that this has already been discussed in [25], separately for even m and odd m and using an indirect approach. Our approach here unifies the treatments for all m, is direct, and is much simpler than that in [25].
First, we claim that, because f(x) is T-periodic, with \(T=b-a\), we can express I[f] in (1.1) as

As we are dealing with HFP integrals that are not defined in the regular sense, this claim needs to be justified rigorously. For this, we need to recall some of the properties of HFP integrals we mentioned in Sect. 1. We begin by noting that

because HFP integrals are invariant with respect to the union of integration intervals. Next, we recall that HFP integrals are invariant under a translation of the interval of integration; therefore, under the variable transformation \(y=x+T\), which is only a translation of the interval [a, t] to \([b,t+T]\), there holds

Finally, by T-periodicity of f(x), we have \(f(x-T)=f(x)\), hence

The claim in (3.1) is now justified by combining (3.3) and (3.4) in (3.2), thus obtaining

With (3.1) justified, we now show that Theorem 2.1 can be applied as is to the integral  instead of the integral
instead of the integral  . Of course, for this, we need to show that (i) f(x) is infinitely differentiable on the interval \((t,t+T)\) and (ii) f(x), as \(x\rightarrow t+\) and as \(x\rightarrow (t+T)-\), has asymptotic expansions of the forms shown in Theorem 2.1. In doing so, we need to remember that neither g(x) nor \((x-t)^{-m}\) is T-periodic even though f(x) is. The details follow.
. Of course, for this, we need to show that (i) f(x) is infinitely differentiable on the interval \((t,t+T)\) and (ii) f(x), as \(x\rightarrow t+\) and as \(x\rightarrow (t+T)-\), has asymptotic expansions of the forms shown in Theorem 2.1. In doing so, we need to remember that neither g(x) nor \((x-t)^{-m}\) is T-periodic even though f(x) is. The details follow.
-
By the fact that \(f\in C^\infty ({\mathbb {R}}_t)\) and by T-periodicity of f(x), it is clear that \(f\in C^\infty (t,t+T)\), with singularities only at \(x=t\) and \(x=t+T\).
-
Asymptotic expansion of f(x) as \( x\rightarrow t+:\) Expanding g(x) in a Taylor series at \(x=t\), we obtain
$$\begin{aligned} f(x)\sim \sum ^\infty _{i=0}\frac{g^{(i)}(t)}{i\hbox \mathrm{!}}\, (x-t)^{i-m} \quad \text {as}\,{ x\rightarrow t}, \end{aligned}$$which we write in the form
$$\begin{aligned} f(x)\sim \frac{g^{(m-1)}(t)}{(m-1)\hbox \mathrm{!}}(x-t)^{-1} +\sum ^\infty _{\begin{array}{c} i=0\\ i\ne m-1 \end{array}}\frac{g^{(i)}(t)}{i\hbox \mathrm{!}}\, (x-t)^{i-m} \quad \text {as}\,{ x\rightarrow t+}.\nonumber \\ \end{aligned}$$(3.5) -
Asymptotic expansion of f(x) as \(x\rightarrow (t+T)-\): We first note that
$$\begin{aligned} f(x)=f(x-T)=\frac{g(x-T)}{(x-T-t)^m}\quad \text {by}\,\, T\text {-periodicity of}{ f(x)}. \end{aligned}$$Next, expanding \(g(x-T)\) in a Taylor series at \(x=t+T\), we obtain
$$\begin{aligned} f(x)\sim \sum ^\infty _{i=0}\frac{g^{(i)}(t)}{i\hbox \mathrm{!}}\, (x-t-T)^{i-m} \quad \text {as}\,{ x\rightarrow (t+T)}, \end{aligned}$$which we write in the form
$$\begin{aligned}&f(x)\sim -\frac{g^{(m-1)}(t)}{(m-1)\hbox \mathrm{!}}(t+T-x)^{-1}\nonumber \\&\quad +\sum ^\infty _{\begin{array}{c} i=0\\ i\ne m-1 \end{array}}(-1)^{i-m}\frac{g^{(i)}(t)}{i\hbox \mathrm{!}}\, (t+T-x)^{i-m} \quad \text {as}\, {x\rightarrow (t+T)-}. \end{aligned}$$(3.6)
Note that here we have recalled Remark 2 concerning Taylor series expansions following the statement of Theorem 2.1.
Clearly, Theorem 2.1 applies with \(a=t\) and \(b=t+T\), and
and
Letting \(h=T/n\), and noting that the terms \(K(x-t)^{-1}\) and \(L(t+T-x)^{-1}\) in the asymptotic expansions of f(x) given in (3.5) and (3.6) make contributions that cancel each other for all m, we thus have the asymptotic expansion
Now, this asymptotic expansion assumes different forms depending on whether m is even or odd. We actually have the following result:
Theorem 3.1
With f(x) as in (1.1)–(1.2) and
the following hold:
-
1.
For m even, \(m=2r\), \(r=1,2,\ldots ,\)
$$\begin{aligned} {\widetilde{T}}_{2r,n}[f]=I[f]+ & {} 2\sum ^r_{i=0}\frac{g^{(2i)}(t)}{(2i)\hbox \mathrm{!}}\,\zeta (2r-2i)\,h^{-2r+2i+1} +o(h^\mu ) \quad \nonumber \\&\text {as} \,{ n\rightarrow \infty }\quad \forall \mu >0.\end{aligned}$$(3.9) -
2.
For m odd, \(m=2r+1\), \(r=0,1,\ldots ,\)
$$\begin{aligned} {\widetilde{T}}_{2r+1,n}[f]=I[f]+ & {} 2\sum ^r_{i=0}\frac{g^{(2i+1)}(t)}{(2i+1)\hbox \mathrm{!}}\,\zeta (2r-2i)\,h^{-2r+2i+1} +o(h^\mu ) \quad \nonumber \\&\text {as}\,{ n\rightarrow \infty }\quad \forall \mu >0.\end{aligned}$$(3.10)
Proof
We consider the cases of even and odd m separately.
-
1.
For \(m=2r\), \(r=1,2,\ldots ,\) we have that only terms with even i contribute to the infinite sum \(\sum ^\infty _{\begin{array}{c} i=0\\ i\ne m-1 \end{array}}\) in (3.7), which reduces to
$$\begin{aligned} 2\sum ^\infty _{i=0}\frac{g^{(2i)}(t)}{(2i)\hbox \mathrm{!}}\,\zeta (2r-2i)\,h^{-2r+2i+1}. \end{aligned}$$(3.11) -
2.
For \(m=2r+1\), \(r=0,1,\ldots ,\) we have that only terms with odd i contribute to the infinite sum \(\sum ^\infty _{\begin{array}{c} i=0\\ i\ne m-1 \end{array}}\) in (3.7), which reduces to
$$\begin{aligned} 2\sum ^\infty _{i=0}\frac{g^{(2i+1)}(t)}{(2i+1)\hbox \mathrm{!}}\,\zeta (2r-2i)\,h^{-2r+2i+1}. \end{aligned}$$(3.12)
Recalling that \(\zeta (-2k)=0\) for \(k=1,2, \ldots ,\) we realize that all the terms with \(i>r\) in the two sums in (3.11) and (3.12) actually vanish. This, of course, does not necessarily mean that
Since there are no powers of h in addition to \(h^{-2r+1},h^{-2r+3},\ldots ,h^{-1},h^1\) that are already present, a remainder term of order \(o(h^\mu )\) for every \(\mu >0\) is present on the right-hand side of each of these “equalities.” This completes the proof. \(\square \)
As can be seen from (3.9) and (3.10), the finite sums involving g(t) and its derivatives are completely known provided g(x) and its derivatives are known or can be computed, since \(\zeta (0),\zeta (2),\ldots ,\zeta (2r)\) are known from (1.3). In the next section, we derive numerical quadrature formulas that rely on (i) all of the \(g^{(k)}(t)\), (ii) some of the \(g^{(k)}(t)\), and (iii) none of the \(g^{(k)}(t)\).
4 Compact numerical quadrature formulas
4.1 Development of numerical quadrature formulas
Theorem 3.1 can be used to design numerical quadrature formulas in different ways. The first ones are obtained directly from (3.9) and (3.10), and they read
Clearly, g(x) and derivatives of g(x) that are present in the asymptotic expansions of Theorem 3.1 are an essential part of the formulas \({\widehat{T}}^{(0)}_{m,n}[f]\). Numerical quadrature formulas that use less of this information can be developed by applying a number of steps of a “Richardson-like extrapolation” process to the sequence \({\widehat{T}}^{(0)}_{m,n}[f], {\widehat{T}}^{(0)}_{m,2n}[f], {\widehat{T}}^{(0)}_{m,4n}[f],\ldots ,\) thereby eliminating the powers of h in the order \(h^1,h^{-1},h^{-3},\ldots .\)Footnote 5 For \(m=1,2,3,4\), for example, we obtain the following quadrature formulas via this process:
-
1.
The case \(m=1\):
$$\begin{aligned} {\widehat{T}}^{(0)}_{1,n}[f]&=h\sum ^{n-1}_{j=1}f(t+jh)+g'(t)h \end{aligned}$$(4.3)$$\begin{aligned} {\widehat{T}}^{(1)}_{1,n}[f]&=h\sum ^{n}_{j=1}f(t+jh-h/2) \end{aligned}$$(4.4) -
2.
The case \(m=2\):
$$\begin{aligned} {\widehat{T}}^{(0)}_{2,n}[f]&=h\sum ^{n-1}_{j=1}f(t+jh)-\frac{\pi ^2}{3}g(t)h^{-1}+ \frac{1}{2}g''(t)h \end{aligned}$$(4.5)$$\begin{aligned} {\widehat{T}}^{(1)}_{2,n}[f]&=h\sum ^{n}_{j=1}f(t+jh-h/2)-{\pi ^2}g(t)h^{-1} \end{aligned}$$(4.6)$$\begin{aligned} {\widehat{T}}^{(2)}_{2,n}[f]&=2h\sum ^{n}_{j=1}f(t+jh-h/2) -\frac{h}{2}\sum ^{2n}_{j=1}f(t+jh/2-h/4) \end{aligned}$$(4.7) -
3.
The case \(m=3\):
$$\begin{aligned} {\widehat{T}}^{(0)}_{3,n}[f]&=h\sum ^{n-1}_{j=1}f(t+jh)-\frac{\pi ^2}{3}g'(t)h^{-1}+ \frac{1}{6}g'''(t)h \end{aligned}$$(4.8)$$\begin{aligned} {\widehat{T}}^{(1)}_{3,n}[f]&=h\sum ^{n}_{j=1}f(t+jh-h/2)-{\pi ^2}g'(t)h^{-1} \end{aligned}$$(4.9)$$\begin{aligned} {\widehat{T}}^{(2)}_{3,n}[f]&=2h\sum ^{n}_{j=1}f(t+jh-h/2) -\frac{h}{2}\sum ^{2n}_{j=1}f(t+jh/2-h/4) \end{aligned}$$(4.10) -
4.
The case \(m=4\):
$$\begin{aligned} {\widehat{T}}^{(0)}_{4,n}[f]&=h\sum ^{n-1}_{j=1}f(t+jh)-\frac{\pi ^4}{45}g(t)h^{-3} -\frac{\pi ^2}{6}g''(t)h^{-1}+\frac{1}{24}g^{(4)}(t)h \end{aligned}$$(4.11)$$\begin{aligned} {\widehat{T}}^{(1)}_{4,n}[f]&=h\sum ^{n}_{j=1}f(t+jh-h/2)-\frac{\pi ^4}{3}g(t)h^{-3} -\frac{\pi ^2}{2}g''(t)h^{-1} \end{aligned}$$(4.12)$$\begin{aligned} {\widehat{T}}^{(2)}_{4,n}[f]&=2h\sum ^{n}_{j=1}f(t+jh-h/2) -\frac{h}{2}\sum ^{2n}_{j=1}f(t+jh/2-h/4)+2\pi ^4g(t)h^{-3} \end{aligned}$$(4.13)$$\begin{aligned} {\widehat{T}}^{(3)}_{4,n}[f]&=\frac{16h}{7}\sum ^{n}_{j=1}f(t+jh-h/2) -\frac{5h}{7}\sum ^{2n}_{j=1}f(t+jh/2-h/4) \nonumber \\&\quad +\frac{h}{28}\sum ^{4n}_{j=1}f(t+jh/4-h/8) \end{aligned}$$(4.14)
Each of the quadrature formulas \({\widehat{T}}^{(s)}_{m,n}[f]\) above is obtained by performing s steps of “Richardson-like extrapolation” on the sequence \(\{{\widehat{T}}^{(0)}_{m,2^kn}[f]\}^s_{k=0}\). Indeed, for \(s=1\) (eliminating only the power \(h^1\)), for \(s=2\) (eliminating only the powers \(h^1,h^{-1}\)), and for \(s=3\) (eliminating only the powers \(h^1,h^{-1},h^{-3}\)), we have, respectively,
and
In general, eliminating only the powers \(h^1,h^{-1},h^{-3},\ldots , h^{-2s+3},\) we have
Remarks
-
1.
The quadrature formulas \({\widehat{T}}^{(1)}_{1,n}[f]\) and \({\widehat{T}}^{(1)}_{2,n}[f]\) were derived and studied in [29] and [25], respectively.
-
2.
In case \(g^{(k)}(t)\), \(k=1,2,\ldots ,\) are not known or cannot be computed exactly, we can replace them wherever they are present in (4.3)–(4.13) by suitable approximations based on the already computed (i) \(g(t+jh)\) in case of \({\widehat{T}}^{(0)}_{m,n}[f]\), and (ii) \(g(t+jh-h/2)\) in case of \({\widehat{T}}^{(1)}_{m,n}[f]\), for example. We can use differentiation formulas based on finite differences as approximations, for example. Of course, the error expansions of the quadrature formulas will now have additional powers of h that result from the differentiation formulas used. (For another approach that uses trigonometric interpolation and also preserves spectral accuracy, see Sect. 6.3.)
-
3.
In case g(x) is not known, which happens when f(x) is given as a black box, for example, or in case we do not wish to approximate the different \(g^{(k)}(x)\), quadrature formulas that do not involve g(x) become very useful. The formulas \({\widehat{T}}^{(1)}_{1,n}[f]\) in (4.4), \({\widehat{T}}^{(2)}_{2,n}[f]\) in (4.7), \({\widehat{T}}^{(2)}_{3,n}[f]\) in (4.10), and \({\widehat{T}}^{(3)}_{4,n}[f]\) in (4.14) do not involve g(x).
4.2 General convergence theorem
We now state a convergence theorem concerning all the quadrature formulas \({\widehat{T}}^{(s)}_{m,n}[f]\) defined in (4.15) in general, and those in (4.3)–(4.13) in particular. This theorem results from the developments above, especially from the fact that the asymptotic expansions of \({\widehat{T}}^{(0)}_{m,n}[f]-I[f]\) as \(h\rightarrow 0\) are all empty:
Theorem 4.1
Let f(x) be as in (1.1)–(1.2), and let the numerical quadrature formulas \({\widehat{T}}^{(s)}_{m,n}[f]\) be as defined above. Then \(\lim _{n\rightarrow \infty }{\widehat{T}}^{(s)}_{m,n}[f]=I[f]\), and we have
In words, the errors in the \({\widehat{T}}^{(s)}_{m,n}[f]\) tend to zero as \(n\rightarrow \infty \) faster than every negative power of n.
Proof
We begin by observing that, by (3.8), (3.9)–(3.10), and (4.1)–(4.2), there holds
that is, (4.16) is true for \(s=0\). Next by (4.15),
Letting \(n\rightarrow \infty \) and invoking (4.17), the result in (4.16) follows. \(\square \)
Remarks
-
1.
In the nomenclature of the common literature, the quadrature formulas \({\widehat{T}}^{(s)}_{m,n}[f]\) have spectral accuracy. Thus, \({\widehat{T}}^{(s)}_{m,n}[f]\) are excellent numerical quadrature formulas for computing I[f] when f(x) is infinitely differentiable and T-periodic on \({\mathbb {R}}_t\), with \({\mathbb {R}}_t\) as defined in (1.2). This should be compared with most existing quadrature formulas based on trapezoidal sums, which have errors that behave at best like \(O(n^{-\nu })\) for some low value of \(\nu >0\).
-
2.
In case f(z), the analytic continuation of f(x) to the complex z-plane, is analytic in the strip \(|\text {Im}z|<\sigma \), the result of Theorem 4.1 can be improved optimally at least for \(m=1,2,3.\) We now have that the errors \(({\widehat{T}}^{(s)}_{m,n}[f]-I[f])\), for every s, tend to zero as \(n\rightarrow \infty \) like \(e^{-2n\pi \sigma /T}\) for all practical purposes, as shown in [29] for \(m=1\), in [25] for \(m=2\), and in [28] for \(m=3\).
4.3 Analysis of the \({\widehat{T}}^{(s)}_{m,n}[f]\) in floating-point arithmetic
Due to the fact that the integrand f(x) tends to infinity as \(x\rightarrow t\), the quadrature formulas \({\widehat{T}}^{(s)}_{m,n}[f]\) are likely to present some stability issues when applied in floating-point (or finite-precision) arithmetic. Before proceeding further, we would like to address this issue in some detail. We will study \({\widehat{T}}^{(0)}_{3,n}[f]\) only; the studies of \({\widehat{T}}^{(s)}_{m,n}[f]\) with general m and s are similar and so are the conclusions derived from them.
Let us denote the numerically computed \({\widehat{T}}^{(0)}_{3,n}[f]\) by \({\overline{T}}^{(0)}_{3,n}[f]\). Then the true numerical error is \(({\overline{T}}^{(0)}_{3,n}[f]-I[f])\), and we can rewrite it as
and we can bound it as in
Clearly, the theoretical error \(({\widehat{T}}{}^{(0)}_{3,n}[f]-I[f])\) tends to zero faster than any negative power of n by Theorem 4.1. Therefore, we need to analyze \(({\overline{T}}^{(0)}_{3,n}[f]-{\widehat{T}}^{(0)}_{3,n}[f])\), which is the source of numerical instability.
For all practical purposes, it is clear from (4.8) that the stability issue arises as a result of errors committed in computing g(x) and its derivatives in the interval [a, b] because f(x) is given and computed on the interval [a, b] and \(f(x)=f(x-T)\) for \(x\in [b,b+T]\) since f(x) is T-periodic.Footnote 6 Thus, with the integer r being such that \(t+rh\le b<t+(r+1)h\), the sum \(\sum ^{n-1}_{j=1}f(t+jh)\) in (4.8) is actually computed as
We are assuming that the rest of the computations are being carried out with no errors.
Now, the computed g(x), which we shall denote by \({\overline{g}}(x)\), is given as \({\overline{g}}(x)=g(x)[1+\eta (x)]\), where \(\eta (x)\) is the relative error in \({\overline{g}}(x)\). Thus, letting \(y_j=t+jh\), we have
where we have denoted by \(\eta _1(t)\) and \(\eta _3(t)\) the relative errors in the computed \(g'(t)\) and \(g'''(t)\), respectively. Assuming that g(x), \(g'(x)\), and \(g'''(x)\) are being computed with maximum precision allowed by the floating-point arithmetic being used, we have \(\big |\eta (y_j)\big |\le \mathbf{u} \), \(\big |\eta _1(t)\big |\le \mathbf{u} \), and \(\big |\eta _3(t)\big |\le \mathbf{u} \), where \(\mathbf{u} \) is the roundoff unit of this arithmetic. Therefore,
Here \(\Vert w\Vert =\max _{a\le x\le b}\big |w(x)\big |\) and \(\zeta (3)=\sum ^\infty _{k=1}k^{-3}\).
The conclusion from this is that \(({\overline{T}}^{(0)}_{3,n}[f]-{\widehat{T}}^{(0)}_{3,n}[f])\) will dominate the true error \(({\overline{T}}^{(0)}_{3,n}[f]-I[f])\) for large n, depending on the size of u (equivalently, whether we are using single- or double- or quadruple-precision arithmetic). Fortunately, substantial accuracy will have been achieved by \({\overline{T}}^{(0)}_{3,n}[f]\) before n becomes large since \(({\widehat{T}}^{(0)}_{3,n}[f]-I[f])\) tends to zero faster than \(n^{-\mu }\) for every \(\mu >0\). Tables 1, 2 and 3 that result from the numerical example in the next section amply substantiate this conclusion.
Finally, we would like to note that the abscissas of the formulas \({\widehat{T}}^{(s)}_{3,n}[f]\) will never be arbitrarily close to the point of singularity \(x=t\); the smallest distance from this point is h, h/2, and h/4 for \(s=0,1,2,\) respectively. This is not the case for most known formulas.
5 A numerical example
We can apply the quadrature formulas \({\widehat{T}}^{(s)}_{m,n}[f]\) we have derived to supersingular integrals  , where f(x) is T-periodic, \(T=b-a\), and is of the form
, where f(x) is T-periodic, \(T=b-a\), and is of the form
Such integrals arise from Cauchy transforms on the unit circle

Actually, making the substitution \(\zeta =e^{\text {i}x}\), \(0\le x\le 2\pi \), so that \(T=2\pi \), and letting \(t\in [0,2\pi ]\) be such that \(z=e^{\text {i}t}\), \(J_m[w]\) becomes

After some manipulation, it can be shown that

For all \(m\ge 2\), we have

We have applied the quadrature formulas \({\widehat{T}}^{(s)}_{3,n}\) to supersingular integrals  , where f(x) is T-periodic and of the form
, where f(x) is T-periodic and of the form
In order to approximate such integrals via the formulas \({\widehat{T}}{}^{(0)}_{3,n}[f]\), \({\widehat{T}}{}^{(1)}_{3,n}[f]\), and \({\widehat{T}}{}^{(2)}_{3,n}[f]\), we need to determine the quantities \(g'(t)\) and \(g'''(t)\). Now, \(g(x)=(x-t)^3f(x)\) can be expressed as
Upon expanding in powers of z, we obtain
and, therefore,
Unfortunately, we are not aware of the existence of tables of supersingular periodic integrals when f(x) is given as in (5.1). Therefore, we need to construct a simple but nontrivial periodic u(x) for which I[f] is given analytically and can easily be computed. This is what we do next.
We apply the three quadrature formulas developed in Sect. 4, with \(T=2\pi \), to

with
which follows from
Clearly, u(x) is \(2\pi \)-periodic, and so is f(x). In addition, u(x) is analytic in the strip \(\big |\text {Im}\,z\big |<\sigma =\log \eta ^{-1}.\)
To obtain an analytical expression for I[f], we proceed as follows:
By the fact that \(u(x)=\tfrac{1}{2}\sum ^\infty _{m=0}\eta ^m(e^{\text {i}mx}+e^{-\text {i}mx})\) and by

which follows from Theorem 2.2 in Sidi [28], we have
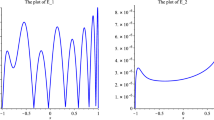
We have applied \({\widehat{T}}{}^{(s)}_{3,n}[f]\) with \(t=1\) and \(\eta =0.1(0.1)0.5.\) The results of this computation, using quadruple-precision arithmetic for which \(\mathbf{u} =1.93\times 10^{-34}\) (approximately 34 decimal digits), are given in Tables 1, 2 and 3.
Judging from Tables 1, 2 and 3, we may conclude that, all three quadrature formulas \({\widehat{T}}{}^{(s)}_{3,n}[f]\) produce approximately the same accuracies. Actually, as shown in Sidi [28, Theorem 5.2], \(E^{(s)}_n(\eta )=\big |{\widehat{T}}{}^{(s)}_{3,n}[f]-I[f]\big |=O(\eta ^n)\) as \(n\rightarrow \infty \) for all three formulas; that is, all three formulas converge at the same rate as \(n\rightarrow \infty \). The numerical results in Tables 1, 2 and 3 are in agreement with this theoretical result as can be checked easily.
In Sect. 4.3, we analyzed the true error in \({\overline{T}}^{(0)}_{3,n}[f]\), the computed \({\widehat{T}}{}^{(0)}_{3,n}[f]\), and concluded that
with K(n) bounded for all large n. That is, the accuracy of \({\overline{T}}^{(0)}_{3,n}[f]\) increases quickly (and exponentially) like \(\eta ^n\) up to a certain point where the term \(K(n)\mathbf{u} n^2\) increases to the point where it prevents \({\overline{T}}^{(0)}_{3,n}[f]\) from picking up more correct significant digits. This takes place after \({\overline{T}}^{(0)}_{3,n}[f]\) has achieved a very good accuracy in floating-point arithmetic, allowed by the size of \(\mathbf{u} \). The numerical results in Tables 1, 2 and 3 demonstrate the validity of this argument amply.
6 Application to numerical solution of periodic supersingular integral equations
6.1 Preliminaries
We now consider the application of the quadrature formulas \({\widehat{T}}^{(s)}_{3,n}\) to the numerical solution of supersingular integral equations of the form

such that, with T, \({\mathbb {R}}\), and \({\mathbb {R}}_t\) as in (1.2), and the following hold in addition:
-
1.
K(t, x) is T-periodic in both x and t, and is in \(C^\infty ({\mathbb {R}}_t)\) as a function of x, and is of the form
$$\begin{aligned} K(t,x)=\frac{U(t,x)}{(x-t)^3},\quad U\in C^\infty ([a,b]\times [a,b]).\end{aligned}$$(6.2)That is, as a function of x, K(t, x) has poles of order 3 at the points \(x=t+kT\), \(k=0,\pm 1,\pm 2,\ldots .\)
-
2.
w(t) is T-periodic in t and is in \(C^\infty ({\mathbb {R}})\).
-
3.
The solution \(\phi (x)\) is T-periodic in x and is in \(C^\infty ({\mathbb {R}})\). (That \(\phi \in C^\infty ({\mathbb {R}})\) under the conditions imposed on K(t, x) and w(t) can be argued heuristically, as was done in [29, Introduction].)
In some cases, additional conditions are imposed on the solution to ensure uniqueness, which we will skip below. We now turn to the development of numerical methods for solving (6.1).
6.2 The “simple” approach
Noting that the quadrature formula \({\widehat{T}}{}^{(2)}_{3,n}[f]\) uses only function values \(f(x_j)\), and no derivatives of g(x), it is clearly very convenient to use, and we try this quadrature formula first.
Since h, h/2, and h/4 all feature in \({\widehat{T}}{}^{(2)}_{3,n}\), we proceed as follows: For a given integer n, let \({\widehat{h}} = T/(4n)\), and \(x_j = a +j{\widehat{h}} \), \(j = 0,1,\ldots ,4n,\ldots .\) Then \(x_{4n}=b\) and \(h=4{\widehat{h}}\) in \({\widehat{T}}{}^{(2)}_{3,n}\). Let t be any one of the \(x_j\), say \(t=x_i\), \(i\in \{1,2,\ldots ,4n\}\), and approximate the integral  by the rule \({\widehat{T}}{}^{(2)}_{3,n}\), namely,
by the rule \({\widehat{T}}{}^{(2)}_{3,n}\), namely,
Finally, noting that, for \(k\le 4n\),
when f(x) is T-periodic, and replacing the \(\phi (x_j)\) by corresponding approximations \({\widehat{\phi }}_j\), and recalling that everything here is T-periodic, [for example, \(\phi (x_{j+4n})=\phi (x_j+T)=\phi (x_j)\) for all j, and the same holds true for K(t, x) and w(x)], we write down the following set of 4n equations for the 4n unknown \({\widehat{\phi }}_j\):
where
Note that \(\epsilon _{ii}=0\) for all i, which means that \(K(x_i,x_i)\) is avoided. The linear equations in (6.3) can be rewritten in the form
Here \(\delta _{ij}\) stands for the Kronecker delta.
Remark
Note that if we were to use either of the quadrature formulas \({\widehat{T}}{}^{(0)}_{3,n}[K(x_i,\cdot )\phi ]\) or \({\widehat{T}}{}^{(1)}_{3,n}[K(x_i,\cdot )\phi ]\) instead of \({\widehat{T}}{}^{(2)}_{3,n}[K(x_i,\cdot )\phi ]\), we would have to know the first and third derivatives (with respect to x) of \(U(x_i,x)\phi (x)\) at \(x=x_i\), which implies that we must have knowledge of \(\phi '(x)\), \(\phi ''(x)\), and \(\phi '''(x)\). Of course, one may think that this is problematic since \(\phi (x)\) is the unknown function that we are trying to determine. The quadrature formula \({\widehat{T}}{}^{(2)}_{3,n}[K(x_i,\cdot )\phi ]\) has no such problem since it relies only on integrand values. We take up this issue in our next (“advanced”) approach.
6.3 The “advanced” approach
In view of the fact that, for \(m=1,2,3,\) all approximations \({\widehat{T}}{}^{(s)}_{m,n}[f]\) converge to I[f] as \(n\rightarrow \infty \) at the same rate when f(z) is analytic and T-periodic in the strip \(|\text {Im}z|<\sigma \), we may want to keep the number of abscissas in \({\widehat{T}}{}^{(s)}_{m,n}[f]\) to a minimum. We can achieve this goal for \(m=3\), for example, by using \({\widehat{T}}{}^{(0)}_{3,n}[f]\), which requires only n abscissas, unlike the 4n abscissas required by \({\widehat{T}}{}^{(2)}_{3,n}[f]\). We apply this approach to  next.
next.
With \(f(t,x)=K(t,x)\phi (x)=U(t,x)\phi (x)/(x-t)^3\) and (6.2), we have
Letting
we have
where \(\phi ^{(k)}(x)\) is the kth derivative of \(\phi (x)\). Therefore, by (4.8), we have
which, after some simple manipulation, can be written in the form
where
The unknown quantities here are \(\phi ^{(j)}(x)\), \(j=0,1,2,3\). We can take care of \(\phi ^{(j)}(x)\), \(j=1,2,3,\) as follows: We first construct the trigonometric interpolation polynomial \(Q_n(x)\) for \(\phi (x)\) over the set of (equidistant) abscissas \(\{x_0,x_1,\ldots ,x_{n-1}\}\) already used for constructing \({\widehat{T}}^{(0)}_{3,n}[K(t,\cdot )\phi ]\); therefore, \(Q_n(x_j)=\phi (x_j)\), \(j=0,1,\ldots ,n-1\). Now, since \(\phi (x)\) is T-periodic and infinitely differentiable on \({\mathbb {R}}\), it is known that \(Q_n(x)\) converges to \(\phi (x)\) over [a, b] with spectral accuracy. Similarly, for each k, \(Q_n^{(k)}(x)\), the \(k^{\text {th}}\) derivative of \(Q_n(x)\), converges to \(\phi ^{(k)}(x)\) over [a, b] with spectral accuracy and at the same rate. Now, with \(x_j=a+jT/n,\) \(Q_n(x)\) is of the form
whereFootnote 7

Taking \(t\in \{x_0,x_1,\ldots ,x_{n-1}\}\), we thus have
Letting now \(t=x_i\) and \({\widehat{\phi }}_i\approx \phi (x_i)\), we can replace the integral equation in (6.1) by the following set of n equations for the n unknown \({\widehat{\phi }}_i\):
where we have used the fact that
when f(x) is T-periodic and \(k\le n-1\). Finally, these equations can be rewritten in the form
We note that the idea of using trigonometric interpolation was introduced originally by Kress [8] in connection with the numerical solution of hypersingular integral equations. Needless to say, it can be used for all the singular integral equations with kernels having singularities of the form \((x-t)^{-m}\) with arbitrary integers \(m\ge 1\).
Change history
19 June 2021
Factorial signs ‘!’ and ‘semicolons’ in equations have been updated.
01 June 2021
A Correction to this paper has been published: https://doi.org/10.1007/s10092-021-00422-9
Notes
When \(m=1\), the HFP of \(\int ^b_af(x)\,dx\) is also called its Cauchy Principal Value (CPV) and the accepted notation for it is
 When \(m=2\),
When \(m=2\),  is called a hypersingular integral, and when \(m=3\),
is called a hypersingular integral, and when \(m=3\),  is called a supersingular integral. We reserve the notation \(\int ^b_au(x)\,dx\) for integrals that exist in the regular sense.
is called a supersingular integral. We reserve the notation \(\int ^b_au(x)\,dx\) for integrals that exist in the regular sense.We express this briefly by saying that “the asymptotic expansions in (2.1) can be differentiated infinitely many times.”
Note that, with \(\theta =1/2\), the offset trapezoidal rule becomes the mid-point rule.
Recall that, when applying the Richardson extrapolation process, we would eliminate the powers of h in the order \(h^{-2r+1},h^{-2r+3},\ldots ,h^{-3},h^{-1},h^1\).
Note that even a small error committed when computing g(x) is magnified by the denominator \((x-t)^3\) when x is close to t.
There is a similar result for odd n, which we omit. What is important here is the main idea.
References
Criscuolo, G.: Numerical evaluation of certain strongly singular integrals. IMA J. Numer. Anal. 34, 651–674 (2014)
Davis, P.J., Rabinowitz, P.: Methods of Numerical Integration, 2nd edn. Academic Press, New York (1984)
De Bonis, M.C., Occorsio, D.: Appoximation of Hilbert and Hadamard transforms on \((0,+\infty )\). Appl. Numer. Math. 116, 184–194 (2017)
Evans, G.: Practical Numerical Integration. Wiley, New York (1993)
Filbir, F., Occorsio, D., Themistoclakis, W.: Appoximation of finite Hilbert and Hadamard transforms by using equally spaced nodes. Mathematics, 8. Article number 542 (2020)
Huang, J., Wang, Z., Zhu, R.: Asymptotic error expansions for hypersingular integrals. Adv. Comput. Math. 38, 257–279 (2013)
Kaya, A.C., Erdogan, F.: On the solution of integral equations with strongly singular kernels. Quart. Appl. Math. 45, 105–122 (1987)
Kress, R.: On the numerical solution of a hypersingular integral equation in scattering theory. J. Comput. Appl. Math. 61, 345–360 (1995)
Krommer, A.R., Ueberhuber, C.W.: Computational Integration. SIAM, Philadelphia (1998)
Kythe, P.K., Schäferkotter, M.R.: Handbook of Computational Methods for Integration. Chapman & Hall/CRC Press, New York (2005)
Li, B., Sun, W.: Newton-Cotes for Hadamard finite-part integrals on an interval. IMA J. Numer. Anal. 30, 1235–1255 (2010)
Li, J., Zhang, X., Yu, D.: Superconvergence and ultraconvergence of Newton-Cotes rules for supersingular integrals. J. Comput. Appl. Math. 233, 2841–2854 (2010)
Lifanov, I.K., Poltavskii, L.N., Vainikko, G.M.: Hypersingular Integral Equations and their Applications. CRC Press, New York (2004)
Luke, Y.L.: The Special Functions and Their Approximations, vol. I. Academic Press, New York (1969)
Lyness, J.N., Monegato, G.: Asymptotic expansions for two-dimensional hypersingular integrals. Numer. Math. 100, 293–329 (2005)
Monegato, G.: Numerical evaluation of hypersingular integrals. J. Comput. Appl. Math. 50, 9–31 (1994)
Monegato, G.: Definitions, properties and applications of finite-part integrals. J. Comput. Appl. Math. 229, 425–439 (2009)
Monegato, G., Lyness, J.N.: The Euler-Maclaurin expansion and finite-part integrals. Numer. Math. 81, 273–291 (1998)
Navot, I.: An extension of the Euler–Maclaurin summation formula to functions with a branch singularity. J. Math. Phys. 40, 271–276 (1961)
Navot, I.: A further extension of the Euler–Maclaurin summation formula. J. Math. Phys. 41, 155–163 (1962)
Olver, F.W.J., Lozier, D.W., Boisvert, R.F., Clark, C.W. (eds.): NIST Handbook of Mathematical Functions. Cambridge University Press, Cambridge (2010)
Sidi, A.: Practical Extrapolation Methods: Theory and Applications. Number 10 in Cambridge Monographs on Applied and Computational Mathematics. Cambridge University Press, Cambridge (2003)
Sidi, A.: Euler–Maclaurin expansions for integrals with arbitrary algebraic endpoint singularities. Math. Comput. 81, 2159–2173 (2012)
Sidi, A.: Euler–Maclaurin expansions for integrals with arbitrary algebraic-logarithmic endpoint singularities. Constr. Approx. 36, 331–352 (2012)
Sidi, A.: Compact numerical quadrature formulas for hypersingular integrals and integral equations. J. Sci. Comput. 54, 145–176 (2013)
Sidi, A.: Analysis of errors in some recent numerical quadrature formulas for periodic singular and hypersingular integrals via regularization. Appl. Numer. Math. 81, 30–39 (2014)
Sidi, A.: Richardson extrapolation on some recent numerical quadrature formulas for singular and hypersingular integrals and its study of stability. J. Sci. Comput. 60, 141–159 (2014)
Sidi, A.: Exactness and convergence properties of some recent numerical quadrature formulas for supersingular integrals of periodic functions. Calcolo, to appear (2021)
Sidi, A., Israeli, M.: Quadrature methods for periodic singular and weakly singular Fredholm integral equations. J. Sci. Comput., 3:201–231, 1988. Originally appeared as Technical Report No. 384, Computer Science Dept., Technion–Israel Institute of Technology, (1985), and also as ICASE Report No. 86-50 (1986)
Wu, J., Dai, Z., Zhang, X.: The superconvergence of the composite midpoint rule for the finite-part integral. J. Comput. Appl. Math. 233, 1954–1968 (2010)
Wu, J., Sun, W.: Interpolatory quadrature rules for Hadamard finite-part integrals and their superconvergence. IMA J. Numer. Anal. 28, 580–597 (2008)
Wu, J., Sun, W.: The superconvergence of Newton-Cotes rules for the Hadamard finite-part integral on an interval. Numer. Math. 109, 143–165 (2008)
Zeng, G., Lei, L., Huang, J.: A new construction of quadrature formulas for Cauchy singular integral. J. Comput. Anal. Appl. 17, 426–436 (2014)
Zhang, X., Wu, J., Yu, D.: Superconvergence of the composite Simpson’s rule for a certain finite-part integral and its applications. J. Comput. Appl. Math. 223, 598–613 (2009)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Factorial signs ! and semicolons in equations on pages 4, 5, 7, 8, 9, 10 and 12 have been updated as they were incorrect due to typesetting mistakes.
Rights and permissions
About this article
Cite this article
Sidi, A. Unified compact numerical quadrature formulas for Hadamard finite parts of singular integrals of periodic functions. Calcolo 58, 22 (2021). https://doi.org/10.1007/s10092-021-00407-8
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10092-021-00407-8
Keywords
- Hadamard finite part
- Singular integrals
- Hypersingular integrals
- Supersingular integrals
- Generalized Euler–Maclaurin expansions
- Asymptotic expansions
- Numerical quadrature
- Trapezoidal rule


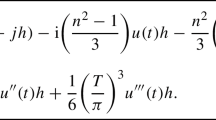

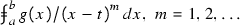
 When
When  is called a hypersingular integral, and when
is called a hypersingular integral, and when  is called a supersingular integral. We reserve the notation
is called a supersingular integral. We reserve the notation