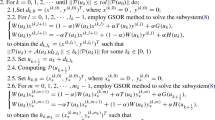Modified Newton-AGSOR method for solving nonlinear systems with block two-by-two complex symmetric Jacobian matrices

Abstract

In this paper, we modify the accelerated generalized successive overrelaxation (AGSOR) method for block two-by-two complex linear systems, and use the AGSOR method as an inner iteration for the modified Newton equations to solve the nonlinear system whose Jacobian matrix is a block two-by-two complex symmetric matrix. Our new method is named modified Newton AGSOR (MN-AGSOR) method. Because generalized successive overrelaxation (GSOR) method is a special form of the AGSOR method, the modified Newton GSOR (MN-GSOR) method is also analyzed in the discussion. Next, we use the Hölder continuous condition instead of the Lipschitz assumption to analyze and prove the local convergence properties of the MN-AGSOR method. At last, numerical experiments verify the efficiency of the MN-AGSOR method, and it can be seen from the comparison of various aspects that the MN-AGSOR method is superior to some other recently proposed methods.

1 Introduction

In this paper, we mainly consider the problem of solving a nonlinear system

$$\begin{aligned} F({x})=0, \end{aligned}$$

(1)

where $F:\mathbb {D}\subset \mathbb {C}^{2n}\rightarrow \mathbb {C}^{2n}$ is nonlinear and continuously differentiable. As studied in [6, 19], suppose that the Jacobian matrix of the above nonlinear system is a block two-by-two complex symmetric matrix in the form of

$$\begin{aligned} F'{({x})}= \left( \begin{array}{cc} W(x) &{} iT(x)\\ iT(x)&{} W(x)\\ \end{array}\right) . \end{aligned}$$

Here the matrices $W(x),T(x)\in \mathbb {R}^{n\times n}$ are symmetric, and at least one of them is positive definite. The symbol $i=\sqrt{-1}$ represents the imaginary unit, throughout the paper.

In general, the Newton method is widely used for solving the nonlinear system (1). By applying the Newton method, the solution of the nonlinear system is equivalently obtained by solving the corresponding Newton equation

$$\begin{aligned} F'({x}_k)s_k=-F({x}_k) \qquad k=0,1, \ldots ,\quad {x}_{k+1}=s_k+{x}_{k}, \end{aligned}$$

with $s_k$ being the unknown vector. In order to improve the convergence speed of the Newton method, the modified Newton method was proposed by Darvishi and Barati [7] in 2007

$$\begin{aligned} {\left\{ \begin{array}{ll} F'({x}_k)d_k&{}=-F({x}_k) \qquad k=0,1, \ldots ,\quad \hat{y}_{k}=d_k+{x}_{k};\\ F'({x}_k)h_k&{}=-F(\hat{y}_k) \qquad k=0,1, \ldots ,\quad {x}_{k+1}=h_k+\hat{y}_{k}.\\ \end{array}\right. } \end{aligned}$$

(2)

Unlike the Newton method, the modified Newton method needs only one more evaluation of F per step, but it has the order of convergence three at least. For the nonlinear system (1) mentioned above, the corresponding Newton equation can be written in the following form:

$$\begin{aligned} \left( \begin{array}{cc} W({x}) &{} iT({x})\\ iT({x})&{} W({x})\\ \end{array}\right) \left( \begin{array}{cc} d_{x1}\\ d_{x2} \end{array}\right) = \left( \begin{array}{cc} P({x}) \\ Q({x})\\ \end{array}\right) , \end{aligned}$$

(3)

where $d_{x1}$ and $d_{x2}$ are two unknown vectors with dimension n. As can be seen from the previous discussion, the main task of solving the nonlinear system (1) is to solve the linear system (3), so we pay our attention to solving the block two-by-two complex linear systems

$$\begin{aligned} \left( \begin{array}{cc} W &{} iT\\ iT&{} W\\ \end{array}\right) \left( \begin{array}{cc} z\\ y \end{array}\right) = \left( \begin{array}{cc} p \\ q\\ \end{array}\right) , \end{aligned}$$

(4)

where the matrices $W,T\in \mathbb {R}^{n\times n}$ are symmetric, and W is positive definite. This system is very common in many fields, especially in the finite element method discretization of elliptic PDE problems [1, 12, 14, 16, 17].

Since Bai and Golub proposed the Hermitian/skew-Hermitian splitting (HSS) method [4] in 2003, many novel and effective methods have been proposed for solving the linear system (4), such as the modified HSS (MHSS) [2], preconditioned MHSS (PMHSS)[3] and generalized PMHSS (GPMHSS) [8] methods. These methods are based on the Hermitian/skew-Hermitian splitting of the coefficient matrix. They can efficiently solve non-Hermitian positive definite system of linear equations. Recently, some single-step iterative methods based on the HSS method have been extensively studied, and they are also quite effective for complex symmetric linear systems [13, 20, 22].

In 2015, the generalized successive overrelaxation (GSOR) [18] method was proposed by Salkuyeh et al. to solve the linear system of equations. Its performance is quite excellent in terms of the convergence speed and accuracy of the solution. In the same year, Edalatpour et al. proposed an accelerated generalized successive overrelaxation (AGSOR) [9] method which is an extension of the GSOR method. Subsequently, the preconditioned GSOR [11] method and the shifted GSOR [10] method were successively proposed. Inspired by their ideas, we propose to apply the AGSOR method to the block two-by-two complex linear systems. By applying the AGSOR method as the inner iteration, and using the modified Newton method as the outer iteration, we present the modified Newton-AGSOR method for solving nonlinear systems with block two-by-two complex Jacobian matrices.

Finally, we give a brief introduction to the structure of this paper. In Sect. 2, we will make convergence analysis of the AGSOR method for block two-by-two complex linear systems. We use the AGSOR method introduced in Sect. 2 as the inner iteration of our new method, and elaborate on the modified Newton-AGSOR (MN-AGSOR) method, including its algorithm and iterative formula in Sect. 3. In Sect. 4, the local convergence of the MN-AGSOR method will be analyzed and proved under the Hölder continuous condition. The numerical results of the MN-AGSOR method are shown and comparisons with several recently proposed methods are made to confirm its effectiveness in Sect. 5. At the end of the paper, we summarize the results of the entire article.

2 The AGSOR method for block two-by-two complex linear systems

In this section, we apply the AGSOR method proposed by Edalatpour et al. in [9] to solve block two-by-two complex linear systems, although it is slightly different from the standard AGSOR.

Consider the linear system of equations whose coefficient matrix has complex block two-by-two form, i.e.

$$\begin{aligned} \left( \begin{array}{cc} W &{} iT\\ iT &{} W \end{array}\right) \left( \begin{array}{cc} z \\ y \end{array}\right) =\left( \begin{array}{cc} p \\ q \end{array}\right) , \end{aligned}$$

(5)

where $W,T \in \mathbb {R}^{n \times n}$ are symmetric positive definite, and symmetric matrices, respectively. The difference between this system of linear equations and the one solved by AGSOR method in [9] is that the matrix on the skew-diagonal is complex symmetric.

Inspired by the AGSOR method, we can easily establish the iteration algorithm for solving the system (5).

In fact, the iterative equation (6) can be changed to the following form:

$$\begin{aligned} \left( \begin{array}{cc} z_{k+1}\\ y_{k+1}\\ \end{array} \right) =\mathcal {G}_{\alpha ,\beta } \left( \begin{array}{cc} z_{k}\\ y_{k}\\ \end{array} \right) +\mathcal {R}_\alpha \left( \begin{array}{cc} p \\ q \\ \end{array} \right) , \end{aligned}$$

(7)

where

$$\begin{aligned} \mathcal {R}_{\alpha }=\left( \begin{array}{cc} W &{} 0 \\ \beta iT &{} W \\ \end{array} \right) ^{-1}\left( \begin{array}{cc} \alpha I &{} 0 \\ 0 &{} \beta I \\ \end{array} \right) , \end{aligned}$$

and

$$\begin{aligned} \mathcal {G}_{\alpha ,\beta }&=\left( \begin{array}{cc} W &{} 0 \\ \beta iT &{} W \\ \end{array} \right) ^{-1} \left( \begin{array}{cc} (1-\alpha )W &{} -\alpha iT \\ 0 &{} (1-\beta )W \\ \end{array} \right) \\&=\left( \begin{array}{cc} I &{} 0 \\ \beta iS &{} I \\ \end{array} \right) ^{-1} \left( \begin{array}{cc} (1-\alpha )I &{} -\alpha iS \\ 0 &{} (1-\beta )I \\ \end{array} \right) , \end{aligned}$$

with $S= W^{-1}T$ and $0\ne \alpha \beta \in \mathbb {R}$.

So far, we have completed the construction of the AGSOR method adapted to solve the block two-by-two complex linear systems.

Obviously, the GSOR method introduced in [18] is a special form of the AGSOR method [9], with the condition $\alpha =\beta$.

Lemma 1

Let$\alpha$and$\beta$be two real numbers with$\alpha \beta \ne 0$and$\mathcal {G}_{\alpha , \beta }$be the iteration matrix of the AGSOR method adapted to solve the block two-by-two complex linear systems (5). Then, for every eigenvalue$\lambda$of$\mathcal {G}_{\alpha ,\ \beta }$there is an eigenvalue$\gamma$of$S=W^{-1}T$which satisfies

$$\begin{aligned} (1-\alpha -\lambda )(1-\beta -\lambda )=-\lambda \alpha \beta \gamma ^{2}. \end{aligned}$$

Proof

Let $\alpha \ne \beta$ and $\lambda$ be an eigenvalue of $\mathcal {G}_{\alpha ,\beta }$ with $x=(z^{T},y^{T})^{T}$ being the eigenvector of $\lambda$. Then, we have

$$\begin{aligned} \left( \begin{array}{cc} I &{} 0 \\ \beta iS &{} I \\ \end{array} \right) ^{-1} \left( \begin{array}{cc} (1-\alpha )I &{} -\alpha iS \\ 0 &{} (1-\beta )I \\ \end{array} \right) \left( \begin{array}{cc} z\\ y\\ \end{array} \right) =\lambda \left( \begin{array}{cc} z\\ y\\ \end{array} \right) , \end{aligned}$$

which is equivalent to

$$\begin{aligned} \left( \begin{array}{cc} (1-\alpha )I &{} -\alpha iS \\ 0 &{} (1-\beta )I \\ \end{array} \right) \left( \begin{array}{cc} z\\ y\\ \end{array} \right) =\lambda \left( \begin{array}{cc} I &{} 0 \\ \beta iS &{} I \\ \end{array} \right) \left( \begin{array}{cc} z\\ y\\ \end{array} \right) . \end{aligned}$$

Therefore, we can obtain the following equations:

$$\begin{aligned} (1-\alpha -\lambda )z&=\alpha iSy,\nonumber \\ (1-\beta -\lambda )y&=\beta \lambda iSz. \end{aligned}$$

(8)

First we show $y\ne 0$ if $\lambda \ne 1 -\alpha$. In fact, when $\lambda \ne 1 -\alpha$, we assume $y=0$, then according to the first equation of (8), we have $z=y=0$, which contradicts with the fact that $x=(z^{T},y^{T})^{T}$ is an eigenvector.

Now, if $\lambda \ne 1 -\alpha$, then

$$\begin{aligned} (1-\alpha -\lambda )(1-\beta -\lambda )y=\lambda \alpha \beta (iS)^{2}y=-\lambda \alpha \beta S^{2}y, \end{aligned}$$

which means that for every eigenvalue $\lambda$ of $\mathcal {G}_{\alpha ,\beta }$, there is an eigenvalue $\gamma$ of S with its corresponding eigenvector y, i.e.

$$\begin{aligned} Sy = \gamma y, \end{aligned}$$

thus

$$\begin{aligned} (1-\alpha -\lambda )(1-\beta -\lambda )=-\lambda \alpha \beta \gamma ^{2}. \end{aligned}$$

If $\lambda = 1 -\alpha$, since $\alpha \ne \beta$ which implies $\lambda \ne 1 -\beta$, the conclusion is still correct. In addition, if $\alpha =\beta$, by the above process, we can get a simpler equation:

$$\begin{aligned} (1-\alpha -\lambda )^{2}=-\lambda \alpha ^{2}\gamma ^{2}. \end{aligned}$$

(9)

Now we prove the equation (9) only for $\lambda = 1 -\alpha =1-\beta$, which means that $Sy=0$ and $\lambda Sz=0$ according to (8). Therefore, S has an eigenvalue $\gamma =0$ or $\lambda =0$, and then (9) holds true. $\square$

Remark 1

We can see that the above Lemma 1 is consistent with the Lemma 2 in [9] and the conditions of the matrices W and T are the same as those given in [9]. Therefore, the AGOSR method for solving linear systems (5) has the same convergence condition as the AGOSR method for solving block two-by-two real linear system, i.e.

$$\begin{aligned} 0<\alpha \beta<\alpha +\beta <\alpha \beta \frac{1-\lambda _{max}^2 }{2}+2. \end{aligned}$$

Its proof can be found in Theorem 1 in [9]. And the selection of the optimal parameters $\alpha _\star$ and $\beta _\star$ of the AGSOR method is also given in Theorem 2 of [9]. We directly show the results as follows:

$$\begin{aligned} \alpha _\star = \frac{b_\star +\sqrt{b_{\star }^{2}-4c_\star }}{2} , \qquad \beta _\star = \frac{b_\star -\sqrt{b_{\star }^{2}-4c_\star }}{2}, \end{aligned}$$

where

$$\begin{aligned} b_\star =4\frac{1+\sqrt{(1+\lambda _{min}^2)(1+\lambda _{max}^2)}}{\sqrt{1+\lambda _{min}^2}+\sqrt{1+\lambda _{max}^2}},\qquad c_\star =4\frac{1}{\sqrt{1+\lambda _{min}^2}+\sqrt{1+\lambda _{max}^2}}. \end{aligned}$$

Here $\lambda _{max}$ and $\lambda _{min}$ are the largest and smallest eigenvalues of the modulus of the matrix $S=W^{-1}T$, respectively. Moreover, it has been mentioned in [9] that the optimal values of parameters $\alpha _\star$ and $\beta _\star$ of the AGSOR method are the optimal values of $\alpha$ and $\beta$ in the set

$$\begin{aligned} \varOmega _{b,c}= \left\{ b,c \in \mathbb {R} \,| \left. \begin{array}{l} 0<c<b<c\frac{1-\lambda _{max}^{2}}{2}+2,\\ b=-c\lambda _{max}^{2}+2\sqrt{c(1+\lambda _{max}^2)},\\ (\lambda _{max}^2+\lambda _{min}^2)c+2b-4\ge 0\\ \end{array} \right. \right\} \end{aligned}$$

where $b= \alpha + \beta$ and $c = \alpha \beta$.

3 The modified Newton-AGSOR method

Based on the extension of the AGSOR method introduced in the previous section, next we will use the AGSOR method as an inner iteration method for the modified Newton method to solve a class of large sparse nonlinear systems with block two-by-two complex symmetric Jacobian matrices.

Now, we focus on the nonlinear system described as

$$\begin{aligned} F(x)=0, \end{aligned}$$

(10)

where $F:\mathbb {D} \subset \mathbb {C}^{2n} \rightarrow \mathbb {C}^{2n}$ is continuously differentiable and its Jacobian matrix is large sparse and complex symmetric with the following form

$$\begin{aligned} F'(x)= \left( \begin{array}{cc} W(x) &{} iT(x) \\ iT(x) &{} W(x) \\ \end{array} \right) . \end{aligned}$$

In the above expression, $W(x) \in \mathbb {R}^{n \times n}$ and $T(x) \in \mathbb {R}^{n \times n}$ are symmetric matrices and W(x) satisfies the positive definite condition. It should be noted that the condition for T(x) is weaker than the modified Newton DPMHSS (MN-DPMHSS)[19] and the modified Newton-MDPMHSS (MN-MDPMHSS)[6] methods.

For simplicity of later discussion, we disassemble F(x) as follows:

$$\begin{aligned} {F}(x)= \left( \begin{array}{cc} P(x) \\ Q(x) \\ \end{array} \right) ,\\ \end{aligned}$$

where P(x) , Q(x) $\in \mathbb {C}^{n}$.

When we use AGSOR method as the inner iteration for the modified Newton method, it is equivalent to using AGSOR method to solve the two Newton equations with the following form:

$$\begin{aligned} {F'}(x_{k})d_{k}= & {} -F(x_{k})\ ,\quad x_{k+\frac{1}{2}}= d_{k}+x_{k};\nonumber \\ {F'}(x_{k})h_{k}= & {} -F(x_{k+\frac{1}{2}})\ ,\quad x_{k+1}= h_{k} +x_{k+\frac{1}{2}}. \end{aligned}$$

(11)

Now, we have a preliminary understanding of the basic structure and specific form of the modified Newton-AGSOR (MN-AGSOR) method. Afterwards, we can apply the MN-AGSOR method for solving nonlinear system (10).

From the above iteration table, the MN-AGSOR method can be easily rewritten as an equivalent form as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{k+\frac{1}{2}}=x_{k}-\sum \limits _{n=0}^{l_k-1}\mathcal {G}_{\alpha , \beta }^{n}(x_k)\mathcal {R}_\alpha (x_k) {F}(x_k),\\ x_{k+1}=x_{k+\frac{1}{2}}-\sum \limits _{n=0}^{m_k-1}\mathcal {G}_{\alpha , \beta }^{n}(x_k) \mathcal {R}_\alpha (x_k) {F}\left( x_{k+\frac{1}{2}}\right) , \end{array}\right. } \end{aligned}$$

(12)

where

$$\begin{aligned} \mathcal {G}_{\alpha , \beta }(x)&=\left( \begin{array}{cc} W(x) &{} 0 \\ \beta iT(x) &{} W(x) \\ \end{array} \right) ^{-1} \left( \begin{array}{cc} (1-\alpha )W(x) &{} -\alpha iT(x) \\ 0 &{} (1-\beta )W(x) \\ \end{array} \right) ,\\&=\left( \begin{array}{cc} I &{} 0 \\ \beta iS(x) &{} I \\ \end{array} \right) ^{-1} \left( \begin{array}{cc} (1-\alpha )I &{} -\alpha iS(x) \\ 0 &{} (1-\beta )I \\ \end{array} \right) ,\\ \end{aligned}$$

and

$$\begin{aligned} \mathcal {R}_{\alpha , \beta }{(x)}=\left( \begin{array}{cc} W(x) &{} 0 \\ \beta T(x) &{} W(x) \\ \end{array} \right) ^{-1}\left( \begin{array}{cc} \alpha I &{} 0 \\ 0 &{} \beta I \\ \end{array} \right) , \end{aligned}$$

with $S(x)= W(x)^{-1}T(x)$ and 0 $\ne \alpha \beta \in \mathbb {R}$.

Notice that the matrix W(x) is positive definite and, in general, we can use the Cholesky decomposition method or the conjugate gradient method to solve the two linear subsystems in (6).

In addition, we define matrices $\mathcal {M}_{\alpha ,\beta }(x)$ and $\mathcal {N}_{\alpha ,\beta }(x)$ by

$$\begin{aligned} \mathcal {M}_{\alpha ,\beta }(x)= \left( \begin{array}{cc} \frac{1}{\alpha } I &{} 0 \\ 0 &{} \frac{1}{\beta } I \\ \end{array} \right) \left( \begin{array}{cc} W(x) &{} 0 \\ \beta T(x) &{} W(x) \\ \end{array} \right) ,\\ \mathcal {N}_{\alpha ,\beta }(x)= \left( \begin{array}{cc} \frac{1}{\alpha } I &{} 0 \\ 0 &{} \frac{1}{\beta } I \\ \end{array} \right) \left( \begin{array}{cc} (1-\alpha )W(x) &{} -\alpha T(x) \\ 0 &{} (1-\beta )W(x) \\ \end{array} \right) . \end{aligned}$$

Then the Jacobian matrix ${F'}(x)$ can be split as

$$\begin{aligned} {F'}(x)=\mathcal {M}_{\alpha ,\beta }(x)-\mathcal {N}_{\alpha ,\beta }(x), \end{aligned}$$

and the following formulas hold true

$$\begin{aligned} \mathcal {G}_{\alpha ,\beta }(x)= & {} \mathcal {M}_{\alpha ,\beta }^{-1}(x)\mathcal {N}_{\alpha ,\beta }(x), \qquad \mathcal {M}_{\alpha ,\beta }(x)= \mathcal {R}_{\alpha ,\beta }(x)^{-1},\nonumber \\&{F'}(x)^{-1}=(I-\mathcal {G}_{\alpha ,\beta }(x))^{-1}\mathcal {R}_{\alpha , \beta }(x). \end{aligned}$$

(13)

Using the above equations, we can convert the expression (12) equivalently to

$$\begin{aligned} {\left\{ \begin{array}{ll} x_{k+\frac{1}{2}}=x_{k}-(I-\mathcal {G}_{\alpha ,\beta }(x_k)^{l_k}){F'}(x_k)^{-1}{F}(x_k),\\ x_{k+1}=x_{k+\frac{1}{2}}-(I-\mathcal {G}_{\alpha ,\beta }(x_k)^{m_k}){F'}(x_k)^{-1}{F}\left( x_{k+\frac{1}{2}}\right) . \end{array}\right. } \end{aligned}$$

(14)

4 Convergence analysis

The main content of this section is to analyze and prove the local convergence properties of the MN-AGSOR iteration method. We will complete our work under the Hölder continuous condition, similar to [5], which is weaker than Lipschitz continuous assumption [21].

Assume that the mapping $F:\mathbb {D}\subset \mathbb {C}^{2n}\rightarrow \mathbb {C}^{2n}$ is G-differentiable in an open domain $\mathbb {D}_0 \subset \mathbb {D}$, $F^{'}({x})$ is symmetric and continuous, and there exists a point ${x}_{*}\in \mathbb {D}_0$ satisfying $F({x}_*)=0$. For analyzing the convergence properties of the MN-AGSOR method and facilitating the symbolic operation in the proof process, we need some assumptions and appointments.

Appointment I In the article, $\Vert z\Vert$ represents the 2-norm of a matrix or a vector z. We use the symbols $\varDelta =\min \left\{ \alpha ,\beta \right\}$ and $\varLambda =\max \left\{ \left| 1-\alpha \right| ,\left| 1-\beta \right| \right\}$.

Assumption 1

Suppose ${x}_{*}\in \mathbb {D}_0$ is a solution to $F({x})=0$, and there exists a positive constant r, for any $u\in \mathbb {N}(x_*,r)\subset \mathbb {D}_0$, he following conditions hold.

• (A1) (The Bounded Condition) There exist positive constants $\eta$ and $\gamma$ satisfying

  $$\begin{aligned} \max \left\{ \; ||T(x_*)||\;,\;||W(x_*)|| \; \right\} \le \eta \quad \text {and} \quad ||{F'}(x_*)^{-1}||\le \gamma . \end{aligned}$$

• (A2) (The Hölder Condition) For some $p\in (0,1]$, there exist nonnegative constants $H_t$ and $H_\omega$ satisfying

  $$\begin{aligned} ||T(x_*)-T(x)||\le & {} H_t||x_*-x||^p,\\ ||W(x_*)-W(x)||\le & {} H_\omega ||x_*-x||^p. \end{aligned}$$

The following perturbation lemma is useful for later discussion and analysis of convergence; see Lemma 2.3.2 in [15].

Lemma 2

Assume that$M,N\in \mathbb {C}^{n \times n}$, withMbeing nonsingular and$||M^{-1}||\le \xi$. If$||M-N||\le \zeta$and$\zeta \xi < 1$, then$N^{-1}$exists and its norm satisfies

$$\begin{aligned} ||N^{-1}||\le \frac{\xi }{1-\zeta \xi }. \end{aligned}$$

Lemma 3

If$r\in (0,1/(\gamma H)^\frac{1}{p})$with$H=H_\omega +H_t$and Assumption1holds, then for any$x,v\in \mathbb {N}(x_*,r)\subset \mathbb {D}_0$, the matrix${F'}(x)$is nonsingular and the following four inequalities are true when$p\in (0,1]$, for any$x,v\in \mathbb {N}(x_*,r)$:

• (1) $||{F'}(x_*)-{F'}(x)||\le H||x_*-x||^{p}$,

• (2) $||{F'}(x)^{-1}||\le \frac{\gamma }{1-\gamma H||x_*-x||^{p}}$,

• (3) $||{F}(v)||\le \frac{H}{p+1}||v-x_*||^{p+1}+2\eta ||v-x_*||$,

• (4) $S(v)\le \frac{H\gamma }{1-\gamma H||x-x_*||^{p}}(\frac{1}{p+1}||v-x_*||^{p}+||x-x_*||^{p})||v-x_*||$,

  where $S(v)=||v-x_*-{F'}(x)^{-1}{F}(v)||$.

Proof

Using Assumption (A2), we obtain

$$\begin{aligned} ||{F'}(x)-{F'}(x_*)||&=\left| \left| \left( \begin{array}{cc} W(x)-W(x_*) &{} iT(x)-iT(x_*)\\ iT(x)-iT(x_*) &{} W(x)-W(x_*) \\ \end{array} \right) \right| \right| \\&\le \left| \left| \left( \begin{array}{cc} W(x)-W(x_*) &{} 0\\ 0 &{} W(x)-W(x_*) \\ \end{array} \right) \right| \right| \\&\quad +\,\left| \left| \left( \begin{array}{cc} 0 &{} iT(x)-iT(x_*)\\ iT(x)-iT(x_*) &{} 0 \\ \end{array} \right) \right| \right| \\&= ||W(x)-W(x_*)||+ ||T(x)-T(x_*)||\\&\le H_\omega ||x-x_*||^{p}+H_t||x-x_*||^{p}\\&=H||x-x_*||^{p}. \end{aligned}$$

Then the first formula of Lemma 3 is proved.

Moreover, the condition $r\in (0,1/(\gamma H)^\frac{1}{p})$ implies $\gamma H||x-x_*||^{p}<1$. Hence by using $||{F'}(x_*)^{-1}||\le \gamma$ and Lemma 2, we know that ${F'}(x)^{-1}$ exists and satisfies

$$\begin{aligned} ||{F'}(x)^{-1}||\le \frac{||{F'}(x_*)^{-1}||}{1-||{F'}(x_*)^{-1}|| ||{F'}(x)-{F'}(x_*)||} \le \frac{\gamma }{1-\gamma H||x-x_*||^{p}}. \end{aligned}$$

Thus the second formula of Lemma 3 is true.

Since

$$\begin{aligned} {F}(v)&={F}(v)-{F}(x_*)-{F'}(x_*)(v-x_*)+{F'}(x_*)(v-x_*)\\&=\int _0^1[{F'}(x_*+t(v-x_*))-{F'}(x_*)](v-x_*)dt+{F'}(x_*)(v-x_*)\\ \end{aligned}$$

and

$$\begin{aligned} ||{F'}(x_*)||&\le \left| \left| \left( \begin{array}{cc} W(x_*) &{} 0\\ 0 &{} W(x_*) \\ \end{array} \right) \right| \right| +\left| \left| \left( \begin{array}{cc} 0 &{} iT(x_*)\\ iT(x_*) &{} 0 \\ \end{array} \right) \right| \right| \\&=||W(x_*)||+||T(x_*)||\le 2\eta , \end{aligned}$$

then it holds that

$$\begin{aligned} ||{F}(v)||&\le \int _0^1||{F'}(x_*+t(v-x_*))-{F'}(x_*)||||v-x_*||dt+||{F'}(x_*)||||v-x_*||\\&\le \frac{H}{p+1}||v-x_*||^{p+1}+2\eta ||v-x_*||. \end{aligned}$$

So the third formula of Lemma 3 is correct.

Next, because

$$\begin{aligned}&v-x_*-{F'}(x)^{-1}{F}(v)\\&\quad =-{F'}(x)^{-1}[{F}(v)-{F}(x_*)-{F'}(x_*)(v-x_*) +({F'}(x_*)-{F'}(x))(v-x_*)]\\&\quad =-{F'}(x)^{-1}\Big [\int _0^1({F'}(x_*+t(v-x_*))-{F'}(x_*))dt\\&\qquad +\, ({F'}(x_*)-{F'}(x))\Big ](v-x_*), \end{aligned}$$

we have

$$\begin{aligned}&||v-x_*-{F'}(x)^{-1}{F}(v)||\\&\quad \le ||{F'}(x)^{-1}|| \Big [\int _0^1||{F'}(x_*+t(v-x_*))-{F'}(x_*)||dt\\&\qquad +\, ||{F'}(x_*)-{F'}(x)||\Big ]||v-x_*||\\&\quad \le \frac{\gamma }{1-\gamma H||x-x_*||^{p}}\left( \frac{H}{p+1}||v-x_*||^{p}+H||x-x_*||^{p}\right) ||v-x_*||.\\ \end{aligned}$$

Now proof of Lemma 3 is complete. $\square$

Theorem 1

Let$\varDelta =\min \left\{ \alpha ,\beta \right\}$and$\varLambda =\max \left\{ \left| 1-\alpha \right| ,\left| 1-\beta \right| \right\}$. Under the conditions of Lemma3, assume$r\in (0,r_0)$, with$r_0=min\left\{ r_1,r_2,r_3\right\}$,

$$\begin{aligned} r_1= & {} \left( \frac{1}{2\gamma \left( \frac{1}{\varDelta }H_\omega +\frac{\beta }{\varDelta } H_t\right) }\right) ^\frac{1}{p},\\ r_2= & {} \left( \frac{\sigma \theta }{2\gamma \left[ \frac{1}{\varDelta }(1+\varLambda +\sigma \theta )H_\omega +\frac{1}{\varDelta }(\sigma \theta \beta +\alpha +\beta )H_t\right] }\right) ^\frac{1}{p},\\ r_3= & {} \left( \frac{1-2\beta \gamma [(\sigma +1)\theta ]^{\mu _*}}{4\gamma H}\right) ^\frac{1}{p}, \end{aligned}$$

where$\mu _*=min\left\{ {m_*,l_*}\right\}$, $m_*=\liminf \nolimits _{k\rightarrow \infty }\;m_k$, $l_*={\liminf \nolimits _{k\rightarrow +\infty }}\;l_k$, and the constant$\mu _*$satisfies

$$\begin{aligned} \mu _*>\left\lfloor -\frac{\ln (2\eta \gamma )}{\ln ((1+\sigma )\theta )}\right\rfloor . \end{aligned}$$

(15)

Here the symbol$\lfloor x \rfloor$is an upper bound function, representing the smallest integer no less than the corresponding real numberx, the number$\sigma \in (0,\sigma _0)$is a prescribed positive constant with$\sigma _0=\frac{1-\theta }{\theta }$, and

$$\begin{aligned} \theta \equiv \theta (\alpha ,\beta ;x_*)=||\mathcal {G}_{\alpha , \beta }(x_*)||<1 \end{aligned}$$

(16)

with$\alpha , \beta$satisfying$0<\alpha \beta<\alpha +\beta <\alpha \beta \frac{1-\rho (W(x_*)^{-1}T(x_*)) }{2}+2$. Then for all$x_0\in \mathbb {N}(x_*,r)$, any positive integer sequences$\left\{ {l_k}\right\} ^\infty _{k=0}$and$\left\{ {m_k}\right\} ^\infty _{k=0}$, the iteration solution sequence$\left\{ {x_k}\right\} ^\infty _{k=0}$generated by the MN-AGSOR method is well-defined and converges to the solution$x_*$. Moreover, it holds that

$$\begin{aligned} \lim _{k\rightarrow \infty }\sup ||x_k-x_*||^\frac{1}{k}\le g(r_0,x_*)^2, \end{aligned}$$

(17)

where

$$\begin{aligned} g(s,\lambda )=\frac{\gamma }{1-\gamma Hs^p}[3Hs^p+2\eta ((1+\sigma )\theta )^\lambda ],\ \text {for}\quad s\in (0,r)\quad \text {and} \quad \lambda >\mu _*. \end{aligned}$$

Proof

The idea to prove this theorem is to find some r, such that for any vector $x\in \mathbb {N}(x_*,r)$, it holds that

$$\begin{aligned} ||\mathcal {G}_{\alpha ,\beta }(x)||\le (\sigma +1)\theta <1, \end{aligned}$$

which is satisfied if we can show $||\mathcal {G}_{\alpha ,\beta }(x_*)-\mathcal {G}_{\alpha ,\beta }(x)||<\sigma \theta$ since

$$\begin{aligned} ||\mathcal {G}_{\alpha ,\beta }(x)||\le ||\mathcal {G}_{\alpha ,\beta }(x)-\mathcal {G}_{\alpha ,\beta }(x_*)||+||\mathcal {G}_{\alpha ,\beta }(x_*)||. \end{aligned}$$

By using (16) and Assumption (A1), we obtain

$$\begin{aligned} ||\mathcal {M}_{\alpha ,\beta }(x_*)^{-1}||&=||(I-\mathcal {G}_{\alpha ,\beta }(x_*)){F'}(x_*)^{-1}||\nonumber \\&\le (1+||\mathcal {G}_{\alpha ,\beta }(x_*)||)||{F'}(x_*)^{-1}||<2\gamma . \end{aligned}$$

(18)

In addition, $r\in (0,1/(\gamma H)^\frac{1}{p})$ implies $\gamma H||x-x_*||^{p}<1$, then by Assumption (A2), we have

$$\begin{aligned}&||\mathcal {M}_{\alpha ,\beta }(x_*)-\mathcal {M}_{\alpha ,\beta }(x)||\\&\quad =\begin{Vmatrix} \left( \begin{array}{cc} \frac{1}{\alpha } I &{} 0 \\ 0 &{} \frac{1}{\beta } I \\ \end{array} \right) \left( \begin{array}{cc} W(x_*) &{} 0 \\ \beta iT(x_*) &{} W(x_*) \\ \end{array} \right) - \left( \begin{array}{cc} \frac{1}{\alpha } I &{} 0 \\ 0 &{} \frac{1}{\beta } I \\ \end{array} \right) \left( \begin{array}{cc} W(x) &{} 0 \\ \beta iT(x) &{} W(x) \\ \end{array} \right) \end{Vmatrix}\\&\quad =\begin{Vmatrix} \left( \begin{array}{cc} \frac{1}{\alpha } I &{} 0 \\ 0 &{} \frac{1}{\beta } I \\ \end{array} \right) \left( \begin{array}{cc} W(x_*)-W(x) &{} 0 \\ \beta iT(x_*)-\beta iT(x) &{} W(x_*)-W(x) \\ \end{array} \right) \end{Vmatrix}\\&\quad \le \begin{Vmatrix} \left( \begin{array}{cc} \frac{1}{\alpha } I &{} 0 \\ 0 &{} \frac{1}{\beta } I \\ \end{array} \right) \end{Vmatrix} \bigg [ \begin{Vmatrix} \left( \begin{array}{cc} W(x_*)-W(x) &{} 0\\ 0 &{} W(x_*)-W(x) \\ \end{array} \right) \end{Vmatrix} \\&\qquad +\, \begin{Vmatrix}\left( \begin{array}{cc} 0 &{} 0\\ \beta iT(x_*)-\beta iT(x) &{} 0 \\ \end{array} \right) \end{Vmatrix} \bigg ] \\&\quad \le \max \left\{ \frac{1}{\alpha },\frac{1}{\beta } \right\} \Big ( ||W(x_*)-W(x)||+\beta ||T(x_*)-T(x)||\Big ) \\&\quad \le \frac{1}{\varDelta }H_\omega ||x-x_*||^{p}+ \frac{\beta }{\varDelta }H_t||x-x_*||^p\\&\quad = \left( \frac{1}{\varDelta }H_\omega +\frac{\beta }{\varDelta } H_t\right) ||x-x_*||^p, \end{aligned}$$

and

$$\begin{aligned}&||\mathcal {N}_{\alpha ,\beta }(x_*)-\mathcal {N}_{\alpha ,\beta }(x)||\\&\quad =\begin{Vmatrix} \left( \begin{array}{cc} \frac{1}{\alpha } I &{} 0 \\ 0 &{} \frac{1}{\beta } I \\ \end{array} \right) \left( \begin{array}{cc} (1-\alpha )(W(x_*)-W(x)) &{} -\alpha (T(x_*)-T(x)) \\ 0 &{} (1-\beta )(W(x_*)-W(x)) \\ \end{array} \right) \end{Vmatrix}\\&\quad \le \begin{Vmatrix} \left( \begin{array}{cc} \frac{1}{\alpha } I &{} 0 \\ 0 &{} \frac{1}{\beta } I \\ \end{array} \right) \end{Vmatrix} \begin{Vmatrix} \left( \begin{array}{cc} (1-\alpha )(W(x_*)-W(x)) &{} 0\\ 0 &{} (1-\beta )(W(x_*)-W(x)) \\ \end{array} \right) \end{Vmatrix} \\&\qquad +\, \begin{Vmatrix} \left( \begin{array}{cc} \frac{1}{\alpha } I &{} 0 \\ 0 &{} \frac{1}{\beta } I \\ \end{array} \right) \end{Vmatrix} \begin{Vmatrix}\left( \begin{array}{cc} 0 &{} -\alpha (T(x_*)-T(x))\\ 0 &{} 0 \\ \end{array} \right) \end{Vmatrix} \\&\quad \le \max \left\{ \frac{1}{\alpha },\frac{1}{\beta }\right\} \Big [ \max \left\{ \left| 1-\alpha \right| ,\left| 1-\beta \right| \right\} ||W(x_*)-W(x)||+\alpha ||T(x_*)-T(x)||\Big ] \\&\quad \le \frac{1}{\varDelta }\left[ \varLambda H_\omega ||x_*-x||^{p}+\alpha H_t||x_*-x||^p\right] \\&\quad = \Big [ \frac{ \varLambda }{\varDelta }H_\omega +\frac{\alpha }{\varDelta } H_t\Big ]||x-x_*||^p. \end{aligned}$$

Thus, from (18) and Lemma 2, for any $x \in \mathbb {N}(x_*,r)$, we obtain

$$\begin{aligned} ||\mathcal {M}_{\alpha ,\beta }(x)^{-1}||&\le \frac{||\mathcal {M}_{\alpha , \beta }(x_*)^{-1}||}{1-||\mathcal {M}_{\alpha ,\beta }(x_*)^{-1}||||\mathcal {M}_{\alpha ,\beta }(x_*) -\mathcal {M}_{\alpha ,\beta }(x)||}\nonumber \\&\le \frac{2\gamma }{1-2\gamma \left( \frac{1}{\varDelta }H_\omega +\frac{\beta }{\varDelta } H_t\right) ||x-x_*||^p}, \end{aligned}$$

(19)

given that

$$\begin{aligned} ||x-x_*||^p<\frac{1}{2\gamma \left( \frac{1}{\varDelta }H_\omega +\frac{\beta }{\varDelta } H_t\right) )}, \end{aligned}$$

which is satisfied since $r<r_1$.

On the one hand, by direct calculations, we have

$$\begin{aligned}&||\mathcal {G}_{\alpha ,\beta }(x)-\mathcal {G}_{\alpha ,\beta }(x_*)||\nonumber \\&\quad =||\mathcal {M}_{\alpha , \beta }(x)^{-1}\mathcal {N}_{\alpha ,\beta }(x)-\mathcal {M}_{\alpha ,\beta }(x_*)^{-1}\mathcal {N}_{\alpha ,\beta }(x_*)||\nonumber \\&\quad \le ||\mathcal {M}_{\alpha ,\beta }(x)^{-1}||[||\mathcal {N}_{\alpha ,\beta }(x)-\mathcal {N}_{\alpha ,\beta }(x_*)||\nonumber \\&\qquad +\, ||\mathcal {M}_{\alpha ,\beta }(x)-\mathcal {M}_{\alpha ,\beta }(x_*)||||\mathcal {G}_{\alpha ,\beta }(x_*)||]\nonumber \\&\quad \le \frac{2\gamma \left[ \left( \frac{1}{\varDelta }H_\omega +\frac{\beta }{\varDelta } H_t\right) ||x-x_*||^p+ \left[ \frac{ \varLambda }{\varDelta }H_\omega +\frac{\alpha }{\varDelta } H_t\right] ||x-x_*||^p\right] }{1-2\gamma \left( \frac{1}{\varDelta }H_\omega +\frac{\beta }{\varDelta } H_t\right) ||x-x_*||^p}. \end{aligned}$$

(20)

On the other hand, $r<r_1$ implies

$$\begin{aligned} 1-2\gamma \left( \frac{1}{\varDelta }H_\omega +\frac{\beta }{\varDelta } H_t\right) ||x-x_*||^p>0. \end{aligned}$$

Furthermore, in order to make $||\mathcal {G}_{\alpha ,\beta }(x)-\mathcal {G}_{\alpha , \beta }(x_*)||<\sigma \theta$, we only need to show

$$\begin{aligned} \frac{2\gamma \left[ \left( \frac{1}{\varDelta }H_\omega +\frac{\beta }{\varDelta } H_t\right) ||x-x_*||^p+ \left[ \frac{ \varLambda }{\varDelta }H_\omega +\frac{\alpha }{\varDelta } H_t\right] ||x-x_*||^p\right] }{1-2\gamma \left( \frac{1}{\varDelta }H_\omega +\frac{\beta }{\varDelta } H_t\right) ||x-x_*||^p}<\sigma \theta , \end{aligned}$$

which is equivalent to

$$\begin{aligned} ||x-x_*||^p<\frac{\sigma \theta }{2\gamma \left[ \left( \frac{1}{\varDelta }+\frac{ \varLambda }{\varDelta }+\frac{1}{\varDelta }\sigma \theta \right) H_\omega +\left( \sigma \theta \frac{\beta }{\varDelta }+\frac{\alpha +\beta }{\varDelta }\right) H_t\right] }, \end{aligned}$$

and it is true since $r<r_2$. Therefore, when $r<r_1$ and $r<r_2$, we have

$$\begin{aligned} ||\mathcal {G}_{\alpha ,\beta }(x)-\mathcal {G}_{\alpha ,\beta }(x_*)||<\sigma \theta . \end{aligned}$$

Hence, for any $u\in \mathbb {N}(x_*,r)$, with $r<\min \{r_1,r_2\}$, we obtain

$$\begin{aligned} \rho (\mathcal {G}_{\alpha ,\beta }(x))&\le ||\mathcal {G}_{\alpha ,\beta }(x)||\nonumber \\&\le ||\mathcal {G}_{\alpha ,\beta }(x_*)-\mathcal {G}_{\alpha ,\beta }(x)||+||\mathcal {G}_{\alpha ,\beta }(x_*)||\nonumber \\&<(1+\sigma )\theta <1, \end{aligned}$$

(21)

since $\sigma <\sigma _0=\frac{1-\theta }{\theta }$.

Now, we can estimate the error of the iteration sequence $\left\{ {x_k}\right\} ^\infty _{k=0}$ generated by MN-AGSOR method. Using (14) and Lemma 3, we get

$$\begin{aligned}&||x_{k+\frac{1}{2}}-x_*|| =||x_k-x_*-(I-\mathcal {G}_{\alpha ,\beta }(x_k)^{l_k}){F'}(x_k)^{-1}{F}(x_k)||\\&\quad \le ||x_k-x_*-{F'}(x_k)^{-1}{F}(x_k)||+||\mathcal {G}_{\alpha ,\beta }(x_k)||^{l_k}\cdot ||{F'}(x_k)^{-1}{F}(x_k)||\\&\quad \le \frac{(p+2+((\sigma +1)\theta )^{l_k})\gamma H}{(p+1)(1-\gamma H||x_k-x_*||^{p})}||x_k-x_*||^{p+1}\\&\qquad +\, \frac{2\gamma \eta ((\sigma +1)\theta )^{l_k}}{1-\gamma H||x_k-x_*||^{p}}||x_k-x_*||\\&\quad \le \frac{\gamma }{1-\gamma H||x_k-x_*||^{p}}\left[ \frac{3+p}{1+p}H||x_k-x_*||^{p} \ +2\eta ((\sigma +1)\theta )^{l_k}\right] ||x_k-x_*||\\&\quad \le \frac{\gamma }{1-\gamma H||x_k-x_*||^{p}}\left[ 3 H||x_k-x_*||^{p} \ +2\eta ((\sigma +1)\theta )^{l_k}\right] ||x_k-x_*||\\&\quad =g(||x_k-x_*||,l_k)||x_k-x_*||, \end{aligned}$$

where

$$\begin{aligned} g(||x_k-x_*||,l_k)=\frac{\gamma }{1-\gamma H||x_k-x_*||^{p}}\left[ 3 H||x_k-x_*||^{p} \ +2\eta ((\sigma +1)\theta )^{l_k}\right] \end{aligned}$$

and $(1+\sigma )\theta <1$.

Set $\mu _*=min\left\{ {m_*, l_*}\right\}$, $m_*=\liminf \limits _{k\rightarrow \infty }\;m_k$, and $l_*={\liminf \limits _{k\rightarrow +\infty }}\;l_k$. It is clear that the function $g(s,\lambda )$ is strictly monotone decreasing with respect to $\lambda$. Additionally, by direct calculations, we have

$$\begin{aligned} \frac{\partial g(s,\lambda )}{\partial s}=\frac{\gamma Hps^{p-1}[3+2\gamma \eta ((\sigma +1)\theta )^\lambda ]}{(1-\gamma Hs^p)^2}>0, \end{aligned}$$

which implies that $g(s,\lambda )$ is strictly monotone increasing with respect to s. Then, for $x_k\in \mathbb {N}(x_*,r)$, we get

$$\begin{aligned} g(||x_k-x_*||,l_k)<\frac{\gamma }{1-\gamma Hr^p}(3Hr^p+2\eta ((1+\sigma )\theta )^{\mu _*})=g(r,\mu _*)<1, \end{aligned}$$

under the conditions that

$$\begin{aligned} 2\eta \gamma ((1+\sigma )\theta )^{\mu _*}<1, \quad \text {and}\quad r< \left( \frac{1-2\eta \gamma [(1+\sigma )\theta ]^{\mu _*}}{4\gamma H}\right) ^\frac{1}{p}. \end{aligned}$$

Actually, the above two inequalities are correct with $\mu _*$ satisfying (15) and $r<r_3$, thus, we obtain

$$\begin{aligned} ||x_{k+\frac{1}{2}}-x_*||<||x_k-x_*||. \end{aligned}$$

Similarly, it holds that

$$\begin{aligned}&||x_{k+1}-x_*||=||x_{k+\frac{1}{2}}-x_*-(I-\mathcal {G}_{\alpha ,\beta }(x_k)^{m_k}){F'}(x_k)^{-1}{F}\left( x_{k+\frac{1}{2}}\right) ||\\&\quad \le ||x_{k+\frac{1}{2}}-x_*-{F'}(x_k)^{-1}{F}(x_k)||+||\mathcal {G}_{\alpha ,\beta }(x_k)||^{m_k}\cdot ||{F'}(x_k)^{-1}{F}\left( x_{k+\frac{1}{2}}\right) ||\\&\quad \le \frac{\gamma }{1-\gamma H||x_k-x_*||^{p}}\left( \frac{1+((\sigma +1)\theta )^{m_k}}{p+1}H||x_{k+\frac{1}{2}}-x_*||^{p}\right) ||x_{k+\frac{1}{2}}-x_*||\\&\qquad +\, \frac{\gamma }{1-\gamma H||x_k-x_*||^{p}}\left( H||x_k-x_*||^{p} +2\eta ((\sigma +1)\theta )^{m_k}\right) ||x_{k+\frac{1}{2}}-x_*|| \\&\quad \le \frac{\gamma g(||x_k-x_*||,l_k)}{1-\gamma H||x_k-x_*||^{p}} \times ||x_{k}-x_*||\\&\qquad \times \, \left( \frac{2g(||x_k-x_*||,l_k)^p +1+p}{p+1}H||x_k-x_*||^{p} +2\eta ((\sigma +1)\theta )^{m_k} \right) \\&\quad \le \frac{\gamma g(||x_k-x_*||,l_k)}{1-\gamma H||x_k-x_*||^{p}}\Big ( 3H||x_k-x_*||^{p}+2\eta ((\sigma +1)\theta )^{m_k}\Big )||x_k-x_*|| \\&\quad =g(||x_k-x_*||,l_k)g(||x_k-x_*||,m_k)||x_*-x_k||\\&\quad<g(r,\mu _*)^2||x_*-x_k||\\&\quad <||x_*-x_k||. \end{aligned}$$

Therefore, for any $u_0\in \mathbb {D}(x_*,r)\subset \mathbb {D}_0$, since

$$\begin{aligned} 0\le \cdots<\Vert x_{k+1}- x_*\Vert<\Vert x_k- x_*\Vert<\cdots<\Vert x_0- x_*\Vert <r, \end{aligned}$$

then we know that the iteration solution sequence $\{x_k\}_{k=0}^\infty$ generated by the modified Newton-GSOR method is convergent to the solution $x_*$ and well-defined. Moreover, $\Vert x_{k+1}- x_*\Vert <g(r,x_*)^2\Vert u_k- x_*\Vert$ directly leads to $\Vert x_k- x_*\Vert <g(r_0,x_*)^{2k}\Vert x_0- x_*\Vert$, or equivalently,

$$\begin{aligned} \Vert x_k- x_*\Vert ^{\frac{1}{k}}<g(r_0,x_*)^{2}\Vert x_0- x_*\Vert ^{\frac{1}{k}}, \end{aligned}$$

then by letting $k\rightarrow \infty$, we establish (17), at this point, proof of this theorem is completed. $\square$

5 Numerical examples

Next, we will make comparisons between the Modified Newton-AGSOR (MN-AGSOR) method, the Modified Newton-DPMHSS (MN-DPMHSS) method [19] and the Modified Newton-MDPMHSS (MN-MDPMHSS) method [6] by several numerical experiments to show the validity and superiority of the MN-AGSOR method. As mentioned earlier, the AGSOR method contains the GSOR method (as long as the two parameters are the same), so MN-GSOR is a special form of MN-AGSOR, but in the numerical experiments, we use MN-GSOR as an independent method.

Consider the following nonlinear equations [6, 19]

$$\begin{aligned} \left\{ \begin{array}{ll} \left[ \begin{array}{cc} \tilde{u}_t\\ \tilde{u}_t \end{array}\right] - \left[ \begin{array}{cc} \alpha _1 I_n & i \beta _1 I_n\\ i\beta _1 I_n & \alpha _1 I_n \end{array}\right] \left[ \begin{array}{cc} \tilde{u}_{xx}\\ \tilde{u}_{yy} \end{array}\right] + \zeta \left[ \begin{array}{cc} \tilde{u}\\ \tilde{u} \end{array}\right] = - \left[ \begin{array}{cc} \alpha _2 I_n & i \beta _2 I_n\\ i\beta _2 I_n & \alpha _2 I_n \end{array}\right] \left[ \begin{array}{cc} {\tilde{u}}^{\frac{4}{3} }\\ {\tilde{u}}^{\frac{4}{3} } \end{array}\right] , &\quad \text {in}\quad \mathbb {D},\\ \tilde{u}(0,x,y)=\tilde{u}_0(x,y), &\quad \text {in}\quad \varOmega ,\\ \tilde{u}(t,x,y)=0, &\quad \text {in}\quad \left( 0,1\right] \times \partial \varOmega , \end{array}\right. \end{aligned}$$

(22)

where $\mathbb {D}=\left( 0,1\right] \times \varOmega$ with $(x,y)\in \varOmega =(0,1)\times (0,1)$, and $\partial \varOmega$ being the boundary of $\varOmega$. The constant $\zeta >0$ represents the magnitude of the reaction term. By discretizing the above problem on equidistant grids $\Delta t=h=1/(N+1)$, then at each temporal step of the implicit scheme, we should solve a system of nonlinear equations

$$\begin{aligned} F(u)=M(\hat{u}^{T},\hat{u}^{T})^{T}+\left( \begin{array}{cc} \alpha _2 I_n &{} i \beta _2 I_n\\ i\beta _2 I_n &{} \alpha _2 I_n\\ \end{array}\right) h\Delta t \psi (\hat{u})=0, \end{aligned}$$

(23)

where

$$\begin{aligned} M=h(1+\zeta \Delta t)I_{2n}+\frac{\Delta t}{h}\left( \begin{array}{cc} \alpha _1 I_n &{} i \beta _1 I_n\\ i\beta _1 I_n &{} \alpha _1 I_n\\ \end{array}\right) \otimes (A_N\otimes I_N+I_N\otimes A_N), \end{aligned}$$

and

$$\begin{aligned} \psi (\hat{u})=(\hat{u}_{1} ^{\frac{4}{3}}, \hat{u}_{2} ^{\frac{4}{3}}, \ldots , \hat{u}_{n} ^{\frac{4}{3}},\hat{u}_{1} ^{\frac{4}{3}}, \hat{u}_{2} ^{\frac{4}{3}}, \ldots , \hat{u}_{n} ^{\frac{4}{3}})^T \quad \text {for vector}\quad \hat{u}=(\hat{u}_{1}, \hat{u}_{2}, \ldots , \hat{u}_{n})^T, \end{aligned}$$

with $n=N \times N$ and $A_N = tridiag(-1,2,-1)$. Here $\otimes$ means the Kronecker product.

Mention that all the numerical tests are finished in Matlab (R2016a) on an Intel quad-core processor (2.79GHz, 8GB RAM). We choose the initial guess ${x}_0=1$ for all the considered iteration methods, and the program’s termination condition for the outer modified Newton iteration is

$$\begin{aligned} \frac{||F(u_k)||_2}{||F(u_0)||_2} \le 10^{-6}. \end{aligned}$$

We set the tolerance of inner iteration methods $\delta _k=\tilde{\delta }_k=\delta$ for the considered four methods.

It is easy to see that the solution of (23) is $\hat{u}_\star =0$ , and

$$\begin{aligned} F'(u)=M+\frac{4}{3} h\Delta t\left( \begin{array}{cc} \alpha _2 I_n &{} i \beta _2 I_n\\ i\beta _2 I_n &{} \alpha _2 I_n\\ \end{array}\right) \times diag \left( \hat{u}_{1} ^{\frac{1}{3}}, \hat{u}_{2} ^{\frac{1}{3}}, \ldots , \hat{u}_{n} ^{\frac{1}{3}}\right) , \end{aligned}$$

thus $F'(u_\star )=M$. In addition, we can get that

$$\begin{aligned} ||F'(u_*)-F'(u)|| \le \frac{4}{3}h\Delta t \sqrt{\alpha _2^2+\beta _2^2}||u_*-u||^\frac{1}{3}, \end{aligned}$$

for any vector $u \in N(u_\star ,r)$.

Hence, the solution sequence $\{u_k\}$ generated by the MN-AGSOR method converges to the solution $u_\star = 0$ according to the previous theoretical analysis. We obtain the optimal experimental parameters of the MN-DPMHSS method and the MN-MDPMHSS method in different situations from the article [6, 19].

First we choose $\alpha _1=\beta _1=1$ and $\alpha _2=\beta _2=1$. The optimal experimental parameters of the MN-AGOSR method and the MN-GSOR method are obtained by some experimental tests. The detailed data of the experimental optimal parameters are shown in Tables 1, 2, 3 and 4.

Table 1 The experimental optimal parameters $\alpha , \beta$ of MN-DPMHSS

Table 2 The experimental optimal parameters $\alpha , \beta$ of MN-MDPMHSS

Table 3 The experimental optimal parameters $\alpha , \beta$ of MN-AGSOR

Table 4 The experimental optimal parameters $\alpha$ of MN-GSOR

In Tables 5, 6, 7 and 8, we compare our MN-AGSOR method and MN-GSOR method with MN-DPMHSS method and MN-MDPMHSS method in the following four aspects: the step of inner iteration steps denoted as “In Step”, the step of outer iteration steps denoted as “Out Step”, the elapsed CPU time in seconds denoted as “CPU(s)”, and the error estimates denoted as “RES”.

Table 5 $\delta =0.1$, $\hbox {N}=40$

Table 6 $\delta =0.2$, $\hbox {N}=40$

Table 7 $\delta =0.4$, $\hbox {N}=30$

Table 8 $\delta =0.4$, $\hbox {N}=50$

Next we choose $\alpha _1=\alpha _2=1$, $\beta _1 = 1/2$ and $\beta _2 = -2$ for further comparison. At this time, the experimental optimal parameters of the four considered methods are listed in Table 9 for $\hbox {N}=50$, and numerical results of the four methods are presented in Tables 10 and 11, respectively.

Table 9 The experimental optimal parameters of the methods for $\hbox {N}=50$

Table 10 $\delta =0.1$, $\hbox {N}=50$

Table 11 $\delta =0.2$, $\hbox {N}=50$

According to the results of the numerical tests in Tables 5, 6, 7 and 8 and Tables 10 and 11, we can see that the inner and outer iteration steps of the MN-AGSOR method are significantly smaller than the MN-DPMHSS and MN-MDPMHSS methods, and the CPU time of the MN-AGSOR method is significantly less which implies that the modified Newton-AGSOR method is more efficient and superior than the MN-DPMHSS and the MN-MDPMHSS methods. On the other hand, we can see that the performances of the MN-GSOR method and the MN-AGSOR method are similar, but the MN-GSOR method requires only one parameter, so when we handle the scientific and engineering problems, it is better to choose the MN-GSOR method instead of the MN-AGSOR method.

6 Conclusions

For solving the nonlinear systems with block two-by-two complex symmetric Jacobian matrices,we have introduced a modified Newton-AGSOR method (MN-AGSOR) method based on the AGSOR algorithm. In the theoretical analysis, the local convergence properties of the MN-AGSOR have been discussed under the Hölder continuous condition instead of the stronger Lipschitz assumption. The numerical results confirm that the MN-AGSOR method has the advantage over the modified Newton-DPMHSS and the modified Newton-MDPMHSS methods in both CPU time and iteration steps. Because the performance of the MN-GSOR method is very close to that of the MN-AGOSR method, we prefer the MN-GSOR method in applications. Furthermore, the MN-AGSOR method needs less conditions for the Jacobian splitting matrix than the MN-DPMHSS and MN-MDPMHSS methods.