Explicit iterative algorithms for solving equilibrium problems

Abstract

The paper introduces two new extragradient algorithms for solving a pseudomonotone equilibrium problem with a Lipschitz-type condition recently presented by Mastroeni in auxiliary problem principle. The algorithm uses variable stepsizes which are updated at each iteration and based on some previous iterates. The advantage of the algorithms is that they are done without the prior knowledge of Lipschitz-type constants and also without any linesearch procedure. The convergence of the algorithms is established under mild assumptions. In the case where the equilibrium bifunction is strongly pseudomonotone, the R-linear rate of convergence of the new algorithms is formulated. Several of fundamental experiments are provided to illustrate the numerical behavior of the algorithms and also to compare with others.

1 Introduction

The paper considers some methods for approximating solutions of an equilibrium problem in a real Hilbert space H. Let C be a nonempty closed convex subset of H. Recall that an equilibrium problem (shortly, EP) for a bifunction $f:C\times C\rightarrow \mathfrak {R}$ is stated as follows:

$$\begin{aligned} \text{ Find }~x^*\in C~\text{ such } \text{ that }~f(x^*,y)\ge 0,~\forall y\in C. \end{aligned}$$

(EP)

Let us denote by EP(f, C) the solution set of problem (EP). Mathematically, problem (EP) can be considered as a general model in the sense that it unifies in a simple form numerous known models as optimization problems, fixed point problems, variational inequalites as well as Nash equilibrium problems [6,7,8, 10, 20, 26]. This can explain why problem (EP) becomes an attractive field in recent years. Together with theoretical results of solution existence, approximation methods to solutions of problem (EP) are also interesting. The first notable method for solving problem (EP) can be the proximal point method [19, 25]. The main idea of this method is to replace the original problem by a family of regularization equilibrium subproblems which can be solved more easily. The regularized solutions can converge finitely or asymptotically to some solution of the original problem.

In this paper, we are interested in the proximal-like method [9] which is also called the extragradient method [27] due to the early contributions on the saddle point problems in [21]. The convergence of the extragradient method is established in [27] under the assumptions that the bifunction is pseudomonotone and satisties a Lipschitz-type condition presented in [24]. Another method, named the modified extragradient method in [22], can be considered as an improvement of the extragradient method in [9, 27] where the complexity of the algorithm is reduced. Unlike [9, 27], the modified method in [22] only requires to proceed one value of bifunction by iteration. Some other methods for solving problem (EP) can be found, for example, in the works [1,2,3,4, 6, 13,14,15,16,17,18, 23, 28,29,30].

At this stage, it is worth mentioning that the methods in [22, 27] are used under the requirement that the Lipschitz-type constants must be known. This means that those constants must be input parameters of the algorithms. Unfortunately, Lipschitz-type constants in general are unknown or even with complex non-linear problems they are still difficult to approximate. In those cases, methods with a linesearch procedure have been considered. However, a linesearch often requires many computations at each iteration which is inherently time-consuming. Recently, the author in [11, 12] has introduced some extragradient-like algorithms with previously taking suitable stepsizes to avoid the finding of the Lipschitz-type constants of bifunction. The convergence of the methods in [11, 12] is proved under the assumption of strong pseudomonotonicity of bifunction. Without this assumption, those methods cannot converge, see in [11, Remark 2] or [12, Remark 4.6].

In this paper, motivated and inspired by the aforementioned results, we introduce two iterative algorithms with new stepsize rules for solving a pseudomonotone and Lipschitz-type equilibrium problem in a real Hilbert space. The variable stepsizes are generated by the algorithms at each iteration, based on some previous iterates, and without any linesearch procedure. Unlike the results in [22, 27], the proposed algorithms are performed without the prior knowledge of the Lipschitz-type constants. The convergence of the new algorithms is established under some standard conditions. In the case where the bifunction is strongly pseudomonotone, the R-linear rate of convergence of the algorithms has been proved contrary to the algorithms in [11, 12]. Some experiments are performed to show the numerical behavior of the proposed algorithms, and also to compare with others.

This paper is organized as follows: Sect. 2 recalls some definitions and results used in the paper. Sect. 3 presents the new algorithms and proves their convergence while Sect. 4 deals with their rate of convergence. Several fundamental experiments are provided in Sect. 5.

2 Preliminaries

Let H be a real Hilbert space and C be a nonempty closed convex subset of H. We begin with some concepts of monotonicity of a bifunction $f:C\times C\rightarrow \mathfrak {R}$, see [7, 26] for more details. The bifunction f is called:

(a) $\gamma$-strongly monotone on C if there exists $\gamma >0$ such that

$$\begin{aligned} f(x,y)+f(y,x)\le -\gamma ||x-y||^2,~\forall x,y\in C; \end{aligned}$$

(b) monotone if

$$\begin{aligned} f(x,y)+f(y,x)\le 0 ,~\forall x,y\in C; \end{aligned}$$

(c) $\gamma$-strongly pseudomonotone on C if there exists $\gamma >0$ such that

$$\begin{aligned} f(x,y)\ge 0\Longrightarrow f(y,x)\le -\gamma ||x-y||^2,~\forall x,y\in C; \end{aligned}$$

(d) pseudomonotone on C if

$$\begin{aligned} f(x,y)\ge 0\Longrightarrow f(y,x)\le 0,~\forall x,y\in C; \end{aligned}$$

It follows from the definitions that the following implications hold,

$$\begin{aligned} \mathrm{(a)}\Longrightarrow \mathrm{(b)}\Longrightarrow \mathrm{(d)}\quad \text{ and } \quad \mathrm{(a)} \Longrightarrow \mathrm{(c)}\Longrightarrow \mathrm{(d)}. \end{aligned}$$

A bifunction $f:C\times C\rightarrow \mathfrak {R}$ satisfies a Lipschitz-type condition [23] if there exist two constants $c_1,~c_2>0$ such that

$$\begin{aligned} f(x,y)+f(y,z)\ge f(x,z)-c_1||x-y||^2-c_2||y-z||^2,~\forall x,y\in C. \end{aligned}$$

Recall that the proximal mapping of a proper, convex and lower semicontinuous function $g:C\rightarrow \mathfrak {R}$ with a parameter $\lambda >0$ is defined by

$$\begin{aligned} \mathrm{prox}_{\lambda g}(x)=\arg \min \left\{ \lambda g(y)+\frac{1}{2}||x-y||^2:y\in C\right\} ,~x\in H. \end{aligned}$$

The following is a property of the proximal mapping ${prox}_{\lambda g}$ (see, [5] for more details).

Lemma 1

For all $x\in H,~y\in C$ and $\lambda >0$, the following inequality holds,

$$\begin{aligned} \lambda \left\{ g(y)-g(\mathrm{prox}_{\lambda g}(x))\right\} \ge \left\langle x-\mathrm{prox}_{\lambda g}(x),y-\mathrm{prox}_{\lambda g}(x)\right\rangle . \end{aligned}$$

Remark 1

From Lemma 1, it is easy to show that if $x=\mathrm{prox}_{\lambda g}(x)$ then

$$\begin{aligned} x\in \mathrm{Arg}\min \left\{ g(y):y\in C\right\} :=\left\{ x\in C: g(x)=\min _{y\in C}g(y)\right\} . \end{aligned}$$

We also need the following lemma (see, [5, Theorem 5.5]).

Lemma 2

Let $\left\{ x_n\right\}$ be a sequence in H and C be a nonempty subset of H. Suppose that $\left\{ x_n\right\}$ is Fejér monotone with respect to C, i.e., $||x_{n+1}-x||\le ||x_n-x||$ for all $n\ge 0$ and for all $x\in C$, and that every weak sequential cluster point of $\left\{ x_n\right\}$ belongs to C. Then, the sequence $\left\{ x_n\right\}$ converges weakly to a point in C.

3 Explicit extragradient algorithms

In this section, we introduce two extragradient algorithms for solving pseudomontone (EP) with a Lipschitz-type condition. The algorithms are explicit in the sense that they are done without previously knowing the Lipschitz-type constants of bifunction. This is particularly interesting in the case where these constants are unknown or even difficult to approximate. For the sake of simplicity in the presentation, we will use the notation $[t]_+=\max \left\{ 0,t\right\}$ and adopt the conventions $\frac{0}{0}=+\infty$ and $\frac{a}{0}=+\infty$ ($a\ne 0$). The following is the first algorithm.

Algorithm 1

Initialization Choose $x_0\in C$ and $\lambda _0>0$, $\mu \in (0,1)$.

Iterative steps Assume that $x_n \in C$ and $\lambda _n ~(n\ge 0)$ are known. Compute $x_{n+1}$, $\lambda _{n+1}$ as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n = \mathrm{prox}_{\lambda _n f(x_n,.)}(x_n),\\ x_{n+1} =\mathrm{prox}_{\lambda _n f(y_n,.)}(x_n), \end{array}\right. } \end{aligned}$$

and set

$$\begin{aligned} \lambda _{n+1}=\min \left\{ \lambda _n,\frac{\mu (||x_n-y_n||^2+||x_{n+1}-y_n||^2)}{2\left[ f(x_n,x_{n+1}) - f(x_n,y_n) -f(y_n,x_{n+1})\right] _+}\right\} . \end{aligned}$$

Stopping criterion If $y_n=x_n$ then stop and $x_n$ is a solution of EP.

It is seen that the stepsize $\lambda _{n}$ generated by the algorithm, and updated during the iteration is based on the previous iterate $x_n$ and the two current ones $y_n$ and $x_{n+1}$. This is different from the strategy to choose of diminishing and non-summable stepsizes in [11]. Comparing with linesearch algorithms, for example [27, Algorithm 2a], the stepsize in Algorithm 1 is computed more simply. Indeed, a linesearch procedure needs many computations by iteration with some finite stopping criterion, and is of course more time-consuming. As seen below, the sequence $\left\{ \lambda _{n}\right\}$ generated by Algorithm 1 is separated from 0. This is more useful than algorithms with diminishing stepsizes.

In order to obtain the convergence of Algorithm 1, we consider the following blanket assumptions imposed on the bifunction f.

(A1) f is pseudomontone on C and $f(x,x)=0$ for all $x\in C$.

(A2) f satisfies the Lipschitz-type condition.

(A3) $\limsup \limits _{n\rightarrow \infty } f(x_n,y)\le f(x,y)$ for each $y\in C$ and each $\left\{ x_n\right\} \subset C$ with $x_n\rightharpoonup x$;

(A4) f(x, .) is convex and subdifferentiable on C for every fixed $x\in C$.

Remark that under the hypothesis (A2), there exist some contants $c_1>0$, $c_2>0$ such that

$$\begin{aligned} f(x_n,x_{n+1}) - f(x_n,y_n) -f(y_n,x_{n+1})\le & {} c_1||x_n-y_n||^2+c_2||x_{n+1}-y_n||^2\\\le & {} \max \left\{ c_1,c_2\right\} (||x_n-y_n||^2+||x_{n+1}-y_n||^2). \end{aligned}$$

Thus, from the definition of $\left\{ \lambda _n\right\}$, we see that this sequence is bounded from below by $\left\{ \lambda _0,\frac{\mu }{2\max \left\{ c_1,c_2\right\} }\right\}$. Moreover, the sequence $\left\{ \lambda _n\right\}$ is non-increasing monotone. Thus, there exists a real number $\lambda >0$ such that $\lim \limits _{n\rightarrow \infty }\lambda _n=\lambda$. In fact, from the definition of $\lambda _{n+1}$, if $f(x_n,x_{n+1}) - f(x_n,y_n) -f(y_n,x_{n+1}) \le 0$ then $\lambda _{n+1}:=\lambda _n$.

We have the following first result.

Theorem 1

Under the hypotheses (A1)–(A4), the sequence $\left\{ x_n\right\}$ generated by Algorithm 1 converges weakly to some solution of problem (EP).

Proof

It follows from Lemma 1 and the definition of $x_{n+1}$ that

$$\begin{aligned} \left\langle x_n-x_{n+1}, x_{n+1}-y\right\rangle \ge \lambda _n f(y_n,x_{n+1})-\lambda _n f(y_n,y),~\forall y\in C. \end{aligned}$$

(1)

From the definition of $\lambda _{n+1}$, we get

$$\begin{aligned} f(x_n,x_{n+1}) - f(x_n,y_n) -f(y_n,x_{n+1})\le \frac{\mu (||x_n-y_n||^2+||x_{n+1}-y_n||^2)}{2\lambda _{n+1}}, \end{aligned}$$

which, after multiplying both sides by $\lambda _n>0$, implies that

$$\begin{aligned} \lambda _n f(y_n,x_{n+1})\ge & {} \lambda _n\left( f(x_n,x_{n+1}) -f(x_n,y_n)\right) \nonumber \\&-\frac{\mu \lambda _n(||x_n-y_n||^2+||x_{n+1}-y_n||^2)}{2\lambda _{n+1}}. \end{aligned}$$

(2)

Combining the relations (1) and (2), we obtain

$$\begin{aligned} \left\langle x_n-x_{n+1}, x_{n+1}-y\right\rangle\ge & {} \lambda _n\left\{ f(x_n,x_{n+1}) - f(x_n,y_n)\right\} -\frac{\mu \lambda _n}{2\lambda _{n+1}}||x_n-y_n||^2\nonumber \\&-\frac{\mu \lambda _n}{2\lambda _{n+1}}||x_{n+1}-y_n||^2-\lambda _n f(y_n,y). \end{aligned}$$

(3)

Similarly, from Lemma 1 and the definition of $y_n$, we also obtain

$$\begin{aligned} \lambda _n(f(x_n,x_{n+1})-f(x_n,y_n))\ge \left\langle y_n-x_n,y_n-x_{n+1}\right\rangle . \end{aligned}$$

(4)

From the relations (3) and (4), we obtain

$$\begin{aligned} \left\langle x_n-x_{n+1}, x_{n+1}-y\right\rangle\ge & {} \left\langle y_n-x_n,y_n-x_{n+1}\right\rangle -\frac{\mu \lambda _n}{2\lambda _{n+1}}||x_n-y_n||^2\nonumber \\&-\frac{\mu \lambda _n}{2\lambda _{n+1}}||x_{n+1}-y_n||^2-\lambda _n f(y_n,y). \end{aligned}$$

Thus, multiplying both sides of the last inequality by 2, we come to the following estimate

$$\begin{aligned} 2\left\langle x_n-x_{n+1}, x_{n+1}-y\right\rangle\ge & {} 2\left\langle y_n-x_n,y_n-x_{n+1}\right\rangle -\frac{\mu \lambda _n}{\lambda _{n+1}}||x_n-y_n||^2\nonumber \\&-\frac{\mu \lambda _n}{\lambda _{n+1}}||x_{n+1}-y_n||^2-2\lambda _n f(y_n,y). \end{aligned}$$

(5)

We have the following facts:

$$\begin{aligned}&2\left\langle x_n-x_{n+1}, x_{n+1}-y\right\rangle =||x_n-y||^2-||x_{n+1}-x_n||^2-||x_{n+1}-y||^2. \end{aligned}$$

(6)

$$\begin{aligned}&2\left\langle y_n-x_n,y_n-x_{n+1}\right\rangle =||x_n-y_n||^2+||x_{n+1}-y_n||^2-||x_n-x_{n+1}||^2. \end{aligned}$$

(7)

Combining the relations (5)–(7), we get

$$\begin{aligned} ||x_{n+1}-y||^2\le & {} ||x_{n}-y||^2-\left( 1-\frac{\mu \lambda _n}{\lambda _{n+1}}\right) ||x_n-y_n||^2\nonumber \\&-\left( 1-\frac{\mu \lambda _n}{\lambda _{n+1}}\right) ||x_{n+1}-y_n||^2+2\lambda _n f(y_n,y),~\forall y\in C,~\forall n\ge 0.\nonumber \\ \end{aligned}$$

(8)

For each $x^*\in EP(f,C)$, we have that $f(x^*,y_n)\ge 0$ and by (A1) that $f(y_n,x^*)\le 0$. Then, using $y=x^* \in C$ in relation (8), we obtain

$$\begin{aligned} ||x_{n+1}-x^*||^2\le & {} ||x_{n}-x^*||^2-\left( 1-\frac{\mu \lambda _n}{\lambda _{n+1}}\right) ||x_n-y_n||^2\nonumber \\&-\left( 1-\frac{\mu \lambda _n}{\lambda _{n+1}}\right) ||x_{n+1}-y_n||^2. \end{aligned}$$

(9)

Let $\epsilon \in (0,1-\mu )$ be some fixed number. Since $\lambda _n \rightarrow \lambda >0$,

$$\begin{aligned} \lim _{n\rightarrow \infty }\left( 1-\frac{\mu \lambda _n}{\lambda _{n+1}}\right) =1-\mu>\epsilon >0. \end{aligned}$$

Thus, there exists $n_0\ge 1$ such that

$$\begin{aligned} 1-\frac{\mu \lambda _n}{\lambda _{n+1}}>\epsilon >0,~\forall n\ge n_0. \end{aligned}$$

(10)

From the relations (9) and (10), we obtain

$$\begin{aligned} ||x_{n+1}-x^*||^2\le ||x_{n}-x^*||^2-\epsilon \left( ||x_n-y_n||^2+||x_{n+1}-y_n||^2\right) , \end{aligned}$$

or

$$\begin{aligned} a_{n+1}\le a_n-b_n, \end{aligned}$$

(11)

where $a_n=||x_{n}-x^*||^2$ and $b_n=\epsilon \left( ||x_n-y_n||^2+||x_{n+1}-y_n||^2\right)$. Thus, the limit of $\left\{ a_n\right\}$ exists and $\lim \limits _{n\rightarrow \infty }b_n=0$ which imply that $\left\{ x_n\right\}$ is bounded and

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }||x_n-y_n||^2=\lim \limits _{n\rightarrow \infty }||x_{n+1}-y_n||^2=0. \end{aligned}$$

(12)

Hence, since $||x_{n+1}-x_n||\le ||x_{n+1}-y_n||+||x_n-y_n||$, we also get

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }||x_{n+1}-x_n||^2=0. \end{aligned}$$

(13)

Now, we prove that each weak cluster point of $\left\{ x_n\right\}$ is in EP(f, C). Indeed, suppose that $\bar{x}$ is a weak cluster point of $\left\{ x_n\right\}$, i.e., there exists a subsequence, denoted by $\left\{ x_m\right\}$, of $\left\{ x_n\right\}$ converging weakly to $\bar{x}$. Since $||x_n-y_n||\rightarrow \infty$, we also have that $y_m\rightharpoonup \bar{x}$. Passing to the limit in (8) as $n=m\rightarrow \infty$ and using hypothesis (A3), the relation (12), and the fact $\lambda _m\rightarrow \lambda >0$, we obtain

$$\begin{aligned} f(\bar{x},y)\ge \limsup _{m\rightarrow \infty }f(y_m,y)\ge \frac{1}{2\lambda }\limsup _{m\rightarrow \infty }\left( ||x_{n+1}-y||^2-||x_n-y||^2\right) ,~\forall y\in C.\nonumber \\ \end{aligned}$$

(14)

On the other hand, from the triangle inequality, we have

$$\begin{aligned} \left| ||x_{n+1}-y||^2-||x_n-y||^2\right|\le & {} ||x_{n+1}-x_n||\left( ||x_{n+1}-y||+||x_n-y||\right) . \end{aligned}$$

Thus, from the boundedness of $\left\{ x_n\right\}$ and the relation (13), we get for each $y\in C$

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\left| ||x_{n+1}-y||^2-||x_n-y||^2\right| =0. \end{aligned}$$

(15)

Combining the relations (14) and (15), we get $f(\bar{x},y)\ge 0$ for all $y\in C$ or $\bar{x}\in EP(f,C)$. From the relations (9) and (10), we see that the sequence $\left\{ x_n\right\} _{n\ge n_0}$ is Fejér-monotone. Thus, Lemma 2 ensures that the whole sequence $\left\{ x_n\right\}$ converges weakly to $\bar{x}$ as $n\rightarrow \infty$. This completes the proof. $\square$

Algorithm 1 requires to compute at each iteration the values of the bifunction f at $x_n$ and $y_n$. Next, we present an algorithm, namely the explicit modified extragradient algorithm, which only needs to compute one value of f at the current approximation.

Algorithm 2

Initialization Choose $y_{-1},~y_0,~x_0\in C$ and $\lambda _0>0$, $\mu \in (0,\frac{1}{3})$.

Iterative steps Assume that $y_{n-1},~y_n,~x_n\in C$ and $\lambda _n \ge 0$ ($n\ge 1$) are known, calculate $x_{n+1}$, $y_{n+1}$ and $\lambda _{n+1}$ as follows:

Step 1 Compute $x_{n+1}= \mathrm{prox}_{\lambda _n f(y_n,.)}(x_n)$ and set

$$\begin{aligned} \lambda _{n+1}=\min \left\{ \lambda _n,\frac{\mu (||y_{n-1}-y_{n}||^2+||y_n-x_{n+1}||^2)}{2\left[ f(y_{n-1},x_{n+1}) - f(y_{n-1},y_{n})-f(y_n,x_{n+1})\right] _+}\right\} . \end{aligned}$$

Step 2 Compute $y_{n+1}= \mathrm{prox}_{\lambda _{n+1}f(y_n,.)}(x_{n+1}).$

Stopping criterion If $x_{n+1}=y_n=x_n$ then stop and $x_n$ is a solution of EP.

As for Algorithm 1, the sequence $\left\{ \lambda _n\right\}$ generated by Algorithm 2 is non-increasing monotone and $\lim \limits \lambda _n=\lambda >0$. Another point of comparison with Algorithm 1 is that Algorithm 2 uses two different stepsizes $\lambda _n$ and $\lambda _{n+1}$ per iteration. Algorithm 2 is also weakly convergent as shown in the next theorem.

Theorem 2

Under the hypotheses (A1)–(A4), the sequence $\left\{ x_n\right\}$ generated by Algorithm 2 converges weakly to some solution of problem (EP).

Proof

For all $y\in C$, we have the following equality,

$$\begin{aligned} ||x_{n+1}-y||^2= & {} ||x_n-y||^2-||x_n-y_n||^2-||y_n-x_{n+1}||^2\nonumber \\&+2 \left\langle x_n-y_n,x_{n+1}-y_n\right\rangle +2\left\langle x_n-x_{n+1},y-x_{n+1}\right\rangle . \end{aligned}$$

(16)

Lemma 1 and the definition of $x_{n+1}$ ensure that

$$\begin{aligned} \left\langle x_n-x_{n+1},y-x_{n+1}\right\rangle \le \lambda _n \left\{ f(y_n,y)- f(y_n,x_{n+1})\right\} ,~\forall y\in C. \end{aligned}$$

(17)

Similarly, from the definition of $y_{n}$ and Lemma 1, we get

$$\begin{aligned} \left\langle x_{n}-y_{n},x_{n+1}-y_{n}\right\rangle \le \lambda _n \left\{ f(y_{n-1},x_{n+1})- f(y_{n-1},y_{n})\right\} . \end{aligned}$$

(18)

Combining the relations (16)–(18), we come to the following estimate,

$$\begin{aligned} ||x_{n+1}-y||^2\le & {} ||x_n-y||^2-||x_n-y_n||^2-||y_n-x_{n+1}||^2+2\lambda _n f(y_n,y)\nonumber \\&+2\lambda _n \left\{ f(y_{n-1},x_{n+1}) - f(y_{n-1},y_{n})- f(y_n,x_{n+1})\right\} . \end{aligned}$$

(19)

From the definition of $\lambda _{n+1}$, we see that

$$\begin{aligned} f(y_{n-1},x_{n+1})-f(y_{n-1},y_{n})-f(y_n,x_{n+1}) \le \frac{\mu (||y_{n-1}-y_{n}||^2+||y_n-x_{n+1}||^2)}{2\lambda _{n+1}}, \end{aligned}$$

which together with relation (19), can be written

$$\begin{aligned} ||x_{n+1}-y||^2\le & {} ||x_n-y||^2-||x_n-y_n||^2-||y_n-x_{n+1}||^2+2\lambda _n f(y_n,y)\nonumber \\&+\frac{\lambda _n \mu }{\lambda _{n+1}}\left( ||y_{n-1}-y_{n}||^2+||y_n-x_{n+1}||^2\right) . \end{aligned}$$

(20)

Using the triangle inequality and the fact $(a+b)^2\le 2a^2+2b^2$, we obtain

$$\begin{aligned} ||y_{n-1}-y_{n}||^2\le \left( ||y_{n-1}-x_{n}||+||x_{n}-y_{n}||\right) ^2\le 2||y_{n-1}-x_n||^2+2||x_n-y_n||^2.\nonumber \\ \end{aligned}$$

(21)

From relations (20) and (21), we have

$$\begin{aligned} ||x_{n+1}-y||^2\le & {} ||x_n-y||^2-||x_n-y_n||^2-||y_n-x_{n+1}||^2+2\lambda _n f(y_n,y)\nonumber \\&+\frac{2\lambda _n \mu }{\lambda _{n+1}}||y_{n-1}-x_n||^2+\frac{2\lambda _n \mu }{\lambda _{n+1}} ||y_{n}-x_n||^2+\frac{\lambda _n \mu }{\lambda _{n+1}}||y_n-x_{n+1}||^2\nonumber \\= & {} ||x_n-y||^2-\left( 1-\frac{2\lambda _n \mu }{\lambda _{n+1}}\right) ||x_n-y_n||^2\nonumber \\&-\left( 1-\frac{\lambda _n \mu }{\lambda _{n+1}}\right) ||y_n-x_{n+1}||^2+2\lambda _n f(y_n,y)+\frac{2\lambda _n \mu }{\lambda _{n+1}}||y_{n-1}-x_n||^2.\nonumber \\ \end{aligned}$$

(22)

Adding the term $\frac{2\lambda _{n+1} \mu }{\lambda _{n+2}} ||y_n-x_{n+1}||^2$ to both sides of the inequality (22), we get

$$\begin{aligned}&||x_{n+1}-y||^2+\frac{2\lambda _{n+1} \mu }{\lambda _{n+2}} ||y_n-x_{n+1}||^2\le ||x_n-y||^2+\frac{2\lambda _n \mu }{\lambda _{n+1}}||y_{n-1}-x_n||^2\nonumber \\&\quad -\left( 1-\frac{2\lambda _n \mu }{\lambda _{n+1}}\right) ||x_n-y_n||^2-\left( 1-\frac{\lambda _n \mu }{\lambda _{n+1}}-\frac{2\lambda _{n+1} \mu }{\lambda _{n+2}}\right) ||y_n-x_{n+1}||^2\nonumber \\&\quad +2\lambda _n f(y_n,y),~\forall y\in C,~n\ge 0. \end{aligned}$$

(23)

For each $x^*\in EP(f,C)$, we have $f(x^*,y_n)\ge 0$. Thus, $f(y_n,x^*)\le 0$ because of the pseudomonotonicity of f. Now, using the relation (23) for $y=x^*$, we come to the following inequality,

$$\begin{aligned}&||x_{n+1}-x^*||^2+\frac{2\lambda _{n+1} \mu }{\lambda _{n+2}} ||y_n-x_{n+1}||^2\le ||x_n-x^*||^2+\frac{2\lambda _n \mu }{\lambda _{n+1}}||y_{n-1}-x_n||^2\nonumber \\&\quad -\left( 1-\frac{2\lambda _n \mu }{\lambda _{n+1}}\right) ||x_n-y_n||^2-\left( 1-\frac{\lambda _n \mu }{\lambda _{n+1}}-\frac{2\lambda _{n+1} \mu }{\lambda _{n+2}}\right) ||y_n-x_{n+1}||^2.\nonumber \\ \end{aligned}$$

(24)

Let $\epsilon \in (0,1-3\mu )$ be some fixed number. Since $\lambda _n\rightarrow \lambda >0$, we obtain

$$\begin{aligned}&\lim _{n\rightarrow \infty }\left( 1-\frac{2\lambda _n \mu }{\lambda _{n+1}}\right) =1-2\mu>1-3\mu>\epsilon>0,\\&\lim _{n\rightarrow \infty }\left( 1-\frac{\lambda _n \mu }{\lambda _{n+1}}-\frac{2\lambda _{n+1} \mu }{\lambda _{n+2}}\right) =1-3\mu>\epsilon >0. \end{aligned}$$

Thus, there exists $n_0\ge 1$ such that

$$\begin{aligned}&1-\frac{2\lambda _n \mu }{\lambda _{n+1}}>\epsilon >0,~\forall n\ge n_0, \end{aligned}$$

(25)

$$\begin{aligned}&1-\frac{\lambda _n \mu }{\lambda _{n+1}}-\frac{2\lambda _{n+1} \mu }{\lambda _{n+2}}>\epsilon >0,~\forall n\ge n_0. \end{aligned}$$

(26)

Thus, from the relations (24)–(26), we obtain

$$\begin{aligned}&||x_{n+1}-x^*||^2+\frac{2\lambda _{n+1} \mu }{\lambda _{n+2}} ||y_n-x_{n+1}||^2\le ||x_n-x^*||^2+\frac{2\lambda _n \mu }{\lambda _{n+1}}||y_{n-1}-x_n||^2\nonumber \\&\quad -\epsilon \left( ||x_n-y_n||^2+||y_n-x_{n+1}||^2\right) , \forall n\ge n_0, \end{aligned}$$

(27)

or

$$\begin{aligned} a_{n+1}\le a_n-b_n,~\forall n\ge n_0, \end{aligned}$$

(28)

where

$$\begin{aligned}&a_n=||x_n-x^*||^2+\frac{2\lambda _n \mu }{\lambda _{n+1}}||y_{n-1}-x_n||^2,\\&b_n=\epsilon \left( ||x_n-y_n||^2+||y_n-x_{n+1}||^2\right) . \end{aligned}$$

From the relation (28), we obtain that the limit of $\left\{ a_n\right\}$ exists, and $\lim \nolimits _{n\rightarrow \infty }b_n=0$. Thus, from the definition of $a_n$ and $b_n$, we obtain that $\left\{ x_n\right\}$ is bounded and

$$\begin{aligned} \lim _{n\rightarrow \infty }||x_n-y_n||^2=\lim _{n\rightarrow \infty }||y_n-x_{n+1}||^2=0. \end{aligned}$$

(29)

This together with the triangle inequality implies that

$$\begin{aligned} \lim _{n\rightarrow \infty }||x_n-x_{n+1}||^2=0. \end{aligned}$$

(30)

Since $\lim _{n\rightarrow \infty }a_n \in \mathfrak {R}$, from the definition of $a_n$ and (29), we also obtain

$$\begin{aligned} \lim _{n\rightarrow \infty }||x_n-x^*||^2 \in \mathfrak {R},~\forall x^*\in EP(f,C). \end{aligned}$$

(31)

Next, we prove that every weak cluster point of $\left\{ x_n\right\}$ is in EP(f, C). Indeed, suppose that $\bar{x}$ is a weak cluster point of $\left\{ x_n\right\}$, i.e., there exists a subsequence, denoted by $\left\{ x_m\right\}$, of $\left\{ x_n\right\}$ converging weakly to $\bar{x}$. From the relation (29), we also get that $y_m\rightharpoonup \bar{x}$. Now, passing to the limit in the relation (23) as $n=m\rightarrow \infty$, and using the hypothesis (A3), the relation (29), and the fact $\lambda _n\rightarrow \lambda >0$ we obtain

$$\begin{aligned} f(\bar{x},y)\ge \limsup _{m\rightarrow \infty }f(y_m,y)\ge \frac{1}{2\lambda }\limsup _{m\rightarrow \infty }\left( ||x_{n+1}-y||^2-||x_n-y||^2\right) ,~\forall y\in C.\nonumber \\ \end{aligned}$$

(32)

Arguing as in the proof of Theorem 1, we also obtain for each $y\in C$

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\left| ||x_{n+1}-y||^2-||x_n-y||^2\right| =0. \end{aligned}$$

(33)

Combining the relations (32) and (33), we get $f(\bar{x},y)\ge 0$ for all $y\in C$ or $\bar{x}\in EP(f,C)$. To finish the proof, we show that the whole sequence $\left\{ x_n\right\}$ converges weakly to $\bar{x}$ as $n\rightarrow \infty$. Indeed, assume that $\left\{ x_l\right\}$ is another subsequence of $\left\{ x_n\right\}$ converging weakly to $\widetilde{x}\ne \bar{x}$. As aforementioned, we see that $\widetilde{x}\in EP(f,C)$. The relation (31) ensures that $\lim \limits _{n\rightarrow \infty }||x_n-\bar{x}||^2\in \mathfrak {R}$ and $\lim \limits _{n\rightarrow \infty }||x_n-\widetilde{x}||^2\in \mathfrak {R}$ . Using the following identity,

$$\begin{aligned} 2 \left\langle x_n,\bar{x}-\widetilde{x}\right\rangle = ||x_n-\widetilde{x}||^2-||x_n-\bar{x}||^2+||\bar{x}||^2-||\widetilde{x}||^2, \end{aligned}$$

we have immediately that

$$\begin{aligned} \lim \limits _{n\rightarrow \infty }\left\langle x_n,\bar{x}-\widetilde{x}\right\rangle =K\in \mathfrak {R}. \end{aligned}$$

(34)

Passing to the limit in (34) as $n=m,~l\rightarrow \infty$, we obtain

$$\begin{aligned} \left\langle \bar{x},\bar{x}-\widetilde{x}\right\rangle =\lim \limits _{m\rightarrow \infty }\left\langle x_m,\bar{x}-\widetilde{x}\right\rangle =K=\lim \limits _{l\rightarrow \infty }\left\langle x_l,\bar{x}-\widetilde{x}\right\rangle =\left\langle \widetilde{x},\bar{x}-\widetilde{x}\right\rangle . \end{aligned}$$

Thus, $||\bar{x}-\widetilde{x}||^2=0$ and $\bar{x}=\widetilde{x}$. This completes the proof. $\square$

4 R-linear rate of convergence

Algorithms in [11, 12] have some special advantages that they are done without the prior knowledge of the Lipschitz-type constants of bifunction. However, in the case where the bifunction f is strongly pseudomonotone (SP) and satisfies the Lipschitz-type condition (LC), the linear rate of convergence cannot be obtained for these algorithms. In this section, we will establish the R-linear rate of convergence of Algorithms 1 and 2 under the hypotheses (SP) and (LC). In addition, as in [11, 12], we assume additionally that the function $f(x,\cdot )$ is convex, lower semicontinuous and the function $f(\cdot ,y)$ is hemicontinuous on C. Under these assumptions, problem (EP) has the unique solution, denoted by $x^\dagger$. The rate of convergence of the two proposed algorithms is ensured by the following theorem.

Theorem 3

Under the hypotheses (SP) and (LC), the sequence $\left\{ x_n\right\}$ generated by Algorithm 1 (or Algorithm 2) converges R-linearly to the unique solution $x^\dagger$ of problem (EP).

Proof

The proof is divided into two cases following that Algorithms 1 or 2 is considered.

Case 1 The sequence $\left\{ x_n\right\}$ is generated by Algorithm 1. In this case, using the relation (8) with $y=x^\dagger$, we obtain

$$\begin{aligned} ||x_{n+1}-x^\dagger ||^2\le & {} ||x_{n}-x^\dagger ||^2-\left( 1-\frac{\mu \lambda _n}{\lambda _{n+1}}\right) ||x_n-y_n||^2\nonumber \\&-\left( 1-\frac{\mu \lambda _n}{\lambda _{n+1}}\right) ||x_{n+1}-y_n||^2+2\lambda _n f(y_n,x^\dagger ),~\forall n\ge 0.\nonumber \\ \end{aligned}$$

(35)

Since $f(x^\dagger ,y_n)\ge 0$, we get that $f(y_n,x^\dagger )\le -\gamma ||y_n-x^\dagger ||^2$ by assumption (SP), where $\gamma$ is some positive real number. Thus, from relation (35), we obtain

$$\begin{aligned} ||x_{n+1}-x^\dagger ||^2\le & {} ||x_{n}-x^\dagger ||^2-\left( 1-\frac{\mu \lambda _n}{\lambda _{n+1}}\right) ||x_n-y_n||^2\nonumber \\&-\left( 1-\frac{\mu \lambda _n}{\lambda _{n+1}}\right) ||x_{n+1}-y_n||^2-2 \gamma \lambda _n ||y_n-x^\dagger ||^2. \end{aligned}$$

(36)

Since $\left\{ \lambda _n\right\}$ is non-increasing monotone and $\lambda _n\rightarrow \lambda$, we have that $\lambda _n\ge \lambda _{\infty }=\lambda$ for all $n\ge 0$. Thus, from (36), we get

$$\begin{aligned} ||x_{n+1}-x^\dagger ||^2\le & {} ||x_{n}-x^\dagger ||^2-\left( 1-\frac{\mu \lambda _n}{\lambda _{n+1}}\right) ||x_n-y_n||^2-\left( 1-\frac{\mu \lambda _n}{\lambda _{n+1}}\right) ||x_{n+1}\nonumber \\&-y_n||^2-2 \gamma \lambda ||y_n-x^\dagger ||^2. \end{aligned}$$

(37)

Let $\epsilon$ be some fixed number in the interval $\left( 0,\frac{1-\mu }{2}\right)$. We find that

$$\begin{aligned} \lim _{n\rightarrow \infty }\left( 1-\frac{\mu \lambda _n}{\lambda _{n+1}}\right) =1-\mu>2\epsilon >0. \end{aligned}$$

Thus, there exists $n_0\ge 1$ such that

$$\begin{aligned} 1-\frac{\mu \lambda _n}{\lambda _{n+1}}>2\epsilon >0,~\forall n\ge n_0. \end{aligned}$$

(38)

It follows from the relations (37) and (38) that, for all $n\ge n_0$

$$\begin{aligned} ||x_{n+1}-x^\dagger ||^2\le & {} ||x_{n}-x^\dagger ||^2-\left( 1-\frac{\mu \lambda _n}{\lambda _{n+1}}\right) ||x_n-y_n||^2-2 \gamma \lambda ||y_n-x^\dagger ||^2\nonumber \\\le & {} ||x_{n}-x^\dagger ||^2-2\epsilon ||x_n-y_n||^2-2 \gamma \lambda ||y_n-x^\dagger ||^2\nonumber \\\le & {} ||x_{n}-x^\dagger ||^2-\min \left\{ \epsilon , \gamma \lambda \right\} \left\{ 2||x_n-y_n||^2+2 ||y_n-x^\dagger ||^2\right\} \nonumber \\\le & {} ||x_{n}-x^\dagger ||^2-\min \left\{ \epsilon , \gamma \lambda \right\} ||x_n-x^\dagger ||^2\nonumber \\= & {} r ||x_{n}-x^\dagger ||^2, \end{aligned}$$

(39)

where $r=1-\min \left\{ \epsilon , \gamma \lambda \right\} \in (0,1)$. From the relation (39), we obtain by induction that

$$\begin{aligned} ||x_{n+1}-x^\dagger ||^2\le r^{n-n_0+1}||x_{n_0}-x^\dagger ||^2,~\forall n\ge n_0, \end{aligned}$$

or $||x_{n+1}-x^\dagger ||^2\le Mr^n$ for all $n\ge n_0$, where $M=r^{1-n_0}||x_{n_0}-x^\dagger ||^2$. This implies the desired conclusion.

Case 2 The sequence $\left\{ x_n\right\}$ is generated by Algorithm 2. Now, using the relation (22) with $y=x^\dagger$ and noting that $f(y_n,x^\dagger )\le -\gamma ||y_n-x^\dagger ||^2$, we obtain

$$\begin{aligned} ||x_{n+1}-x^\dagger ||^2\le & {} ||x_n-x^\dagger ||^2-\left( 1-\frac{2\lambda _n \mu }{\lambda _{n+1}}\right) ||x_n-y_n||^2\nonumber \\&-\left( 1-\frac{\lambda _n \mu }{\lambda _{n+1}}\right) ||y_n-x_{n+1}||^2\nonumber \\&-2\lambda _n \gamma ||y_n-x^\dagger ||^2+\frac{2\lambda _n \mu }{\lambda _{n+1}}||y_{n-1}-x_n||^2. \end{aligned}$$

(40)

Let $\theta$ and $\rho$ be two real numbers such that

$$\begin{aligned} \theta \in \left( 0,\frac{1-2\mu }{2}\right) \qquad \text{ and }\qquad 1<\rho <\frac{1}{2}\left( \frac{1}{\mu }-1\right) . \end{aligned}$$

(41)

Adding the term $\frac{2\lambda _{n+1} \mu \rho }{\lambda _{n+2}} ||y_n-x_{n+1}||^2$ to both sides of (40), we get

$$\begin{aligned}&||x_{n+1}-x^\dagger ||^2+\frac{2\lambda _{n+1} \mu \rho }{\lambda _{n+2}} ||y_n-x_{n+1}||^2\le ||x_n-x^\dagger ||^2+\frac{2\lambda _n \mu }{\lambda _{n+1}}||y_{n-1}-x_n||^2\nonumber \\&\quad -\left( 1-\frac{2\lambda _n \mu }{\lambda _{n+1}}\right) ||x_n-y_n||^2-\left( 1-\frac{\lambda _n \mu }{\lambda _{n+1}}-\frac{2\lambda _{n+1} \mu \rho }{\lambda _{n+2}}\right) ||y_n-x_{n+1}||^2\nonumber \\&\quad -2\lambda _n \gamma ||y_n-x^\dagger ||^2,~\forall y\in C,~n\ge 0. \end{aligned}$$

(42)

Since $\lambda _n\rightarrow \lambda >0$, we obtain

$$\begin{aligned}&\lim _{n\rightarrow \infty }\left( 1-\frac{2\lambda _n \mu }{\lambda _{n+1}}\right) =1-2\mu>2\theta>0,\\&\lim _{n\rightarrow \infty }\left( 1-\frac{\lambda _n \mu }{\lambda _{n+1}}-\frac{2\lambda _{n+1} \mu \rho }{\lambda _{n+2}}\right) =1-(1+2\rho )\mu >0. \end{aligned}$$

Thus, there exists $n_0\ge 1$ such that

$$\begin{aligned}&1-\frac{2\lambda _n \mu }{\lambda _{n+1}}>2\theta >0,~\forall n\ge n_0, \end{aligned}$$

(43)

$$\begin{aligned}&1-\frac{\lambda _n \mu }{\lambda _{n+1}}-\frac{2\lambda _{n+1} \mu \rho }{\lambda _{n+2}}>0,~\forall n\ge n_0. \end{aligned}$$

(44)

From the relations (42)–(43) and the fact $2\lambda _n \gamma \ge 2\lambda \gamma$, we have

$$\begin{aligned}&||x_{n+1}-x^\dagger ||^2+\frac{2\lambda _{n+1} \mu \rho }{\lambda _{n+2}} ||y_n-x_{n+1}||^2\le ||x_n-x^\dagger ||^2+\frac{2\lambda _n \mu }{\lambda _{n+1}}||y_{n-1}-x_n||^2\nonumber \\&\quad -\left( 2\theta ||x_n-y_n||^2+2\lambda \gamma ||y_n-x^\dagger ||^2\right) ,~n\ge n_0. \end{aligned}$$

(45)

We also have

$$\begin{aligned} 2\theta ||x_n-y_n||^2+2\lambda \gamma ||y_n-x^\dagger ||^2\ge & {} \min \left\{ \theta ,\lambda \gamma \right\} \left( 2||x_n-y_n||^2+2 ||y_n-x^\dagger ||^2\right) \nonumber \\\ge & {} \min \left\{ \theta ,\lambda \gamma \right\} ||x_n-x^\dagger ||^2. \end{aligned}$$

(46)

Combining the relations (45) and (46), we obtain

$$\begin{aligned} ||x_{n+1}-x^\dagger ||^2+\frac{2\lambda _{n+1} \mu \rho }{\lambda _{n+2}} ||y_n-x_{n+1}||^2\le & {} \left( 1-\min \left\{ \theta ,\lambda \gamma \right\} \right) ||x_n-x^\dagger ||^2\nonumber \\&+\frac{2\lambda _n \mu }{\lambda _{n+1}}||y_{n-1}-x_n||^2,~n\ge n_0.\nonumber \\ \end{aligned}$$

(47)

Set $a_n=||x_n-x^\dagger ||^2$ and $b_n=\frac{2\lambda _n \mu \rho }{\lambda _{n+1}}||y_{n-1}-x_n||^2$. From the relation (47), we get

$$\begin{aligned} a_{n+1}+b_{n+1}\le & {} \left( 1-\min \left\{ \theta ,\lambda \gamma \right\} \right) a_n+\frac{b_n}{\rho }\le r(a_n+b_n),~n\ge n_0, \end{aligned}$$

(48)

where $r=\max \left\{ 1-\min \left\{ \theta ,\lambda \gamma \right\} ,\frac{1}{\rho }\right\} \in (0,1)$. Thus, by induction, we obtain that $a_{n+1}+b_{n+1}\le r^{n-n_0+1}(a_{n_0}+b_{n_0})$ for all $n\ge n_0$, which can be reduced to $a_{n+1}=||x_{n+1}-x^\dagger ||^2\le Mr^n$ with $M=r^{1-n_0}(a_{n_0}+b_{n_0})$. This finishes the proof. $\square$

5 Computational experiments

This section presents some fundamental experiments on a model which generalizes the Nash-Cournot oligopolistic equilibrium model [10]. For a readable purpose, we present briefly this model as follows: Suppose that there are m firms producing a common homogeneous commodity. Let $p_j$ be the price of goods produced by firm j depending on the commodities of all firms j, $j=1,2,\ldots ,m$, i.e., $p_j=p_j(x_1,x_2,\ldots ,x_m)$. Denote $c_j(x_j)$ the cost of firm j which only depends on its produced level $x_j$. Then the profit made by company j is given by $f_j(x_1,x_2,\ldots ,x_m)= x_j p_j(x_1,x_2,\ldots ,x_m)-c_j( x_j)$. Let $C_j$ be the strategy set of firm j. Then $C=C_1\times C_2\times \ldots \times C_m$ is the strategy of the model. Actually, each firm j seeks to maximize its own profit by choosing the corresponding production level $x_j$ under the presumption that the production of the other firms is a input parameter. A commonly used approach to the model is based on the famous Nash equilibrium concept.

Let $x=(x_1,x_2,\ldots ,x_m)\in C$ and recall that a point $x^* =(x_1^*,x_2^*,\ldots ,x_m^*) \in C$ is called an equilibrium point of the model if

$$\begin{aligned} f_j(x_1^*,x_2^*,\ldots ,x_m^*) \ge f_j(x_1^*,\ldots , x_{j-1}^*,y_j,x_{j+1}^*\ldots ,x_m^*) \ \forall y_j \in C_j, \ \forall j=1,2,\ldots ,m, \end{aligned}$$

By setting $\psi (x,y):= -\sum _{j = 1}^m f_j(x_1^*,\ldots , x_{j-1}^*,y_j,x_{j+1}^*\ldots ,x_m^*)$ and $f(x, y):= \psi (x,y)-\psi (x,x)$, the problem of finding a Nash equilibrium point of the model can be shortly formulated as:

$$\begin{aligned} \text{ Find }~x^* \in C: f(x^*,x) \ge 0 \ \forall x \in C. \end{aligned}$$

(EP)

For the purpose of experiment, we assume that the price $p_j(s)$ is a decreasing affine function of s with $s= \sum _{j=1}^m x_j$, i.e., $p_j(s)= a_j - b_j s$, where $a_j > 0$, $b_j > 0$, and that the function $c_j(x_j)$ is increasing and affine for every j. This assumption means that the cost for producing a unit is increasing as the quantity of the production gets larger. In that case, the bifunction f can be formulated in the form $f(x,y)=\left\langle Px+Qy+q,y-x\right\rangle$, where $q\in \mathfrak {R}^m$ and P,  Q are two matrices of order m such that Q is symmetric positive semidefinite and $Q-P$ is symmetric negative semidefinite. The bifunction f satisfies the Lipschitz-type condition and is pseudomonotone. The feasible set C has the form $C=\left\{ x\in \mathfrak {R}^m:Ax\le b\right\}$ where A is a random matrix of size $l\times m$ ($l=10$ and $m=200$ or $m=300$) and $b\in \mathfrak {R}^l$ such that $x_0=y_{-1}=y_0=(1,1,\ldots ,1)\in C$. The two matrices P,  Q are generated randomly¹. All the optimization problems can be solved effectively by the function quadprog in Matlab Optimization Toolbox. All the programs are written in Matlab 7.0 and computed on a PC Desktop Intel(R) Core(TM) i5-3210M CPU @ 2.50 GHz, RAM 2.00 GB.

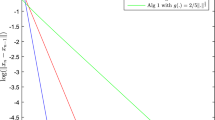
Experiment 1 In this experiment, we study the numerical behavior of Algorithm 1 (shortly, EEGA) and Algorithm 2 (EMEGA). We take $\mu =0.33$ and $\lambda _0\in \left\{ 0.2,~0.4,~0.6,~0.8,~1.0\right\}$ and perform the experiments in $\mathfrak {R}^{200}$ or $\mathfrak {R}^{300}$. Observe the characteristic of the solutions of problem (EP) that $x\in EP(f,C)$ if and only if $x=\mathrm{prox}_{\lambda f(x,.)}(x)$ for some $\lambda >0$, we use the function $D(x)=||x-\mathrm{prox}_{\lambda f(x,.)}(x)||^2$ to show the numerical behavior of algorithms EEGA and EMEGA. It is of course that $D(x)=0$ iff $x\in EP(f,C)$. The convergence of $\left\{ D(x_n)\right\}$ generated by each algorithm to 0 can be considered as the sequence $\left\{ x_n\right\}$ converges to the solution of the problem. The numerical results are shown in Figs. 1, 2, 3 and 4.

In view of these figures, we see that the proposed algorithms work better when $\lambda _0$ is larger. Moreover, Algorithm 2 (EMEGA) is better than Algorithm 1 (EEGA) in both the execution time and the obtained error after the same number of iterations.

Fig. 1

Algorithm 1 (EEGA) in $\mathfrak {R}^{200}$. The execution time is 5.97, 5.57, 5.71, 5.82, 5.25, respectively

Fig. 2

Algorithm 1 (EEGA) in $\mathfrak {R}^{300}$. The execution time is 23.84, 23.17, 23.66, 23.63, 23.34, respectively

Fig. 3

Algorithm 2 (EMEGA) in $\mathfrak {R}^{200}$. The execution time is 5.19, 5.16, 5.22, 5.12, 5.04, respectively

Fig. 4

Algorithm 2 (EMEGA) in $\mathfrak {R}^{300}$. The execution time is 22.05, 21.87, 22.69, 22.92, 21.93, respectively

Experiment 2 The purpose of this experiment is to present a comparison between the proposed algorithms (EEGA and EMEGA) and two other algorithms, namely the linesearch extragradient algorithm (LEGA) presented in [27, Algorithm 2a] and the ergodic algorithm (ErgA) proposed in [3]. We choose these algorithms to compare because they have a common feature that the Lipschitz-type constants are not the input parameters of the algorithms. The control parameters are $\mu =0.33$ and $\lambda _0=1$ (for EEGA and EMEGA); $\alpha =0.5,~\theta =0.5,~\rho =\gamma =1$ (for LEGA); and $\lambda _n=\frac{1}{n}$ (for the ErgA). The results are shown in Figs. 5, 6, 7 and 8. In each figure, the x-axis represents either the number of iterations or the execution time elapsed in second while the y-axis gives the value of $D(x_n)$ generated by each algorithm.

Fig. 5

$D_n$ and # iterations (in $\mathfrak {R}^{200}$)

Fig. 6

$D_n$ and time (in $\mathfrak {R}^{200}$)

Fig. 7

$D_n$ and # iterations (in $\mathfrak {R}^{300}$)

Fig. 8

$D_n$ and time (in $\mathfrak {R}^{300}$)

The numerical results here have illustrated that the proposed algorithms work better than other ones in both the number of iterations and the execution time. Besides, Algorithm 2 (EMEGA) is also better than Algorithm 1 (EEGA). The advantage of Algorithm 2 over Algorithm 1 is only to compute a value of bifunction at each iteration.

6 Conclusions

The paper has proposed the two explicit extragradient-like algorithms for solving an equilibrium problem involving a pseudomonotone and Lipschitz-type bifunction in a real Hilbert space. A new stepsize rule has been introduced which is not based on the information of the Lipschitz-type constants. The convergence as well as the R-linear rate of convergence of the algorithms have been established. Several experiments are reported to illustrate the numerical behavior of our two algorithms, and to compare them with other ones well known in the literature.