An augmented fully-mixed finite element method for the stationary Boussinesq problem

Abstract

In this paper we propose and analyze a new fully-mixed finite element method for the stationary Boussinesq problem. More precisely, we reformulate a previous primal-mixed scheme for the respective model by holding the same modified pseudostress tensor depending on the pressure, and the diffusive and convective terms of the Navier–Stokes equations for the fluid; and in contrast, we now introduce a new auxiliary vector unknown involving the temperature, its gradient and the velocity for the heat equation. As a consequence, a mixed approach is carried out in heat as well as fluid equation, and differently from the previous scheme, no boundary unknowns are needed, which leads to an improvement of the method from both the theoretical and computational point of view. In fact, the pressure is eliminated and as a result the unknowns are given by the aforementioned auxiliary variables, the velocity and the temperature of the fluid. In addition, for reasons of suitable regularity conditions, the scheme is augmented by using the constitutive and equilibrium equations, and the Dirichlet boundary conditions. Then, the resulting formulation is rewritten as a fixed point problem and its well-posedness is guaranteed by the classical Banach theorem combined with the Lax–Milgram theorem. As for the associated Galerkin scheme, the Brouwer and the Banach fixed point theorems are utilized to establish existence and uniqueness of discrete solution, respectively. In particular, Raviart–Thomas spaces of order k for the auxiliary unknowns and continuous piecewise polynomials of degree $\le k +1$ for the velocity and the temperature become feasible choices. Finally, we derive optimal a priori error estimates and provide several numerical results illustrating the good performance of the scheme and confirming the theoretical rates of convergence.

1 Introduction

In engineering and industry, natural convection is a largely studied phenomenon due to its presence in different applications. For instance, electrical and electronic industries use it for the thermal regulation of components and devices of industrial equipments, and the agricultural sector utilizes this model for drying applications and storage. This phenomenon can also be found in aeronautics, nuclear energy, solar collectors and environmental engineering, to name a few. In simple words, it refers to a fluid motion generated by density differences due to temperature gradients. Mathematically, it is modelled by the Navier–Stokes equations coupled to the convection–diffusion equation through the Boussinesq approximation (variations in density are neglected everywhere except in the buoyancy term), reason why it is often called the Boussinesq model.

Due its relevance, in the last decades the numerical analysis community has been vividly focused on developing accurate and efficient numerical methods for simulating this phenomenon (see, e.g. [2, 4, 6, 7, 10, 11, 13, 14, 18, 20, 21, 24], and the references therein). The above list includes temperature-dependent parameters problems and time-dependent problems. In particular, a conforming finite element method for the Boussinesq model is introduced and analized in [4]. The approach there, which corresponds to one of the first works in this direction, employs the primal method in both Navier–Stokes and heat equations, yielding the fluid velocity, the fluid pressure and the fluid temperature as the main unknowns of the system. Later, a dual-mixed formulation for the two-dimensional Boussinesq model has been proposed in [13]. Here, the gradient of the velocity and the gradient of the temperature are introduced as further unknowns (besides the velocity, pressure and temperature). The corresponding mixed finite element scheme employs Raviart–Thomas elements of lowest order for the gradients and piecewise constants for the velocity, temperature and pressure. Existence of solution and convergence of the numerical scheme are proved near a nonsingular solution and quasi-optimal error estimates are provided.

Recently, a new augmented primal-mixed variational formulation for the stationary Boussinesq model has been proposed and analyzed in [10]. This approach employs a technique previously applied to the Navier–Stokes equations (see [8]), which consists of the introduction of a modified nonlinear pseudostress tensor involving the gradient of the velocity, the convective term and the pressure. By using an equivalent statement suggested by the incompressibility condition, the pressure is eliminated. Furthermore, since the convective term forces the velocity to live in a smaller space than usual, the variational formulation for the fluid flow equations are augmented by incorporating suitable Galerkin type expressions arising from the constitutive and equilibrium equations, and the Dirichlet boundary condition. The resulting augmented formulation for the fluid flow is coupled with a primal-mixed scheme for the convection–diffusion equation, yielding the so called augmented primal-mixed coupled system, where the main unknowns are given by the aforementioned nonlinear pseudostress, the velocity, the temperature and the normal derivative of the latter on the boundary. The pressure can be easily recovered in terms of the nonlinear pseudostress and the velocity through a simple post-processing procedure. An equivalent fixed-point setting that resembles the approach from [3] is then employed to develop the continuous and discrete analyses in [10].

In this paper, we extend the results obtained in [10], and propose and analyze a new augmented fully-mixed finite element method for the stationary Boussinesq problem. Similarly to [10], we adopt the augmented mixed formulation from [8] for the fluid flow equations, whereas, in contrast to [10], we also propose an augmented mixed formulation for the convection–diffusion equation modelling the temperature. More precisely, we introduce a new auxiliary vector unknown involving the temperature, its gradient and the velocity, and derive a new mixed formulation for the convection–diffusion equation, which is also augmented by using the constitutive and equilibrium temperature equations, and the temperature boundary condition. In this way, the aforementioned auxiliary variable, together with the nonlinear pseudostress, the velocity and the temperature of the fluid, are the main unknown of the resulting coupled system. As a consequence, we obtain a new augmented fully-mixed formulation for the coupled problem, which allows the utilization of the same family of finite element subspaces for approximating the unknowns of both, the Navier–Stokes and convection–diffusion equations. This property constitutes a significative advantage from a practical point of view since it permits to unify and simplify the computational implementation of the resulting discrete scheme. In addition, we emphasize in advance that, differently from the scheme in [10], no boundary unknowns are needed here, which leads to an improvement of the method from both the theoretical and computational point of view. Concerning the solvability analysis, we proceed as in [3, 10], and introduce an equivalent fixed-point setting. In this way, assuming that the data is sufficiently small, we establish existence and uniqueness of solution of the continuous problem by means of the classical Banach fixed-point theorem, combined with the Lax–Milgram theorem. In turn, the Brouwer and the Banach fixed-point theorems are utilized to establish existence and uniqueness of solution, respectively, of the associated Galerkin scheme. We remark that no discrete inf-sup conditions are required for the discrete analysis, and therefore arbitrary finite element subspaces can be employed, which is another interesting feature of the present approach. In particular, Raviart–Thomas spaces of order k for the auxiliary unknowns and continuous piecewise polynomials of degree $\le k +1$ for the velocity and the temperature become feasible choices. Finally, we point out that an additional advantage of approximating the solution of the coupled system through this new approach is that, besides the possibility of recovering the pressure in terms of the nonlinear pseudostress and the velocity, one can compute other variables of physical relevance, such as the vorticity, the shear–stress tensor, the velocity gradient and the temperature gradient, as simple post-processing formulae of the solution. Whether this is utilized or not and, in case it is, the corresponding choice of variables to be postprocessed, strictly depend on the particular interests of the user.

1.1 Outline

We have organized the contents of this paper as follows. The remainder of this section introduces some standard notations and functional spaces. In Sect. 2 we introduce the model problem, which for our purposes, is rewritten as an equivalent first-order set of equations. Next, in Sect. 3, we derive the augmented mixed variational formulation and, by assuming sufficiently small data, we establish its well-posedness by means of a fixed-point strategy and the Banach fixed-point theorem. The associated Galerkin scheme is introduced and analyzed in Sect. 4. Its well-posedness is attained by adapting the fixed-point strategy developed for the continuous problem. In Sect. 5 we apply a suitable Strang-type lemma to derive the corresponding Céa estimate under a similar assumption on the size of the data. Finally, in Sect. 6 we present several numerical examples illustrating the good performance of the augmented fully-mixed finite element method and confirming the theoretical rates of convergence.

1.2 Preliminaries

Let us denote by $\Omega \subseteq {\mathrm {R}}^n$, $n\in \{2,3\}$, a given bounded domain with polyhedral boundary $\Gamma$, and denote by ${\varvec{\nu }}$ the outward unit normal vector on $\Gamma$. Standard notation will be adopted for Lebesgue spaces ${\mathrm {L}}^p(\Omega )$ and Sobolev spaces ${\mathrm {H}}^s(\Omega )$ with norm $\Vert \cdot \Vert _{s,\Omega }$ and seminorm $|\cdot |_{s,\Omega }$. In particular, ${{\mathrm {H}}}^{1/2}(\Gamma )$ is the space of traces of functions of ${\mathrm {H}}^1(\Omega )$ and ${{\mathrm {H}}}^{-1/2}(\Gamma )$ denotes its dual. By ${\mathbf {M}}$ and ${\mathbb {M}}$ we will denote the corresponding vectorial and tensorial counterparts of the generic scalar functional space ${\mathrm {M}}$, and $\Vert \cdot \Vert$, with no subscripts, will stand for the natural norm of either an element or an operator in any product functional space. Furthermore, as usual ${\mathbb {I}}$ stands for the identity tensor in ${\mathrm {R}}^{n\times n}$, and $|\cdot |$ denotes the Euclidean norm in ${\mathrm {R}}^n$. Also, for any vector fields ${\varvec{v}}=(v_i)_{i=1,n}$ and ${\varvec{w}}=(w_i)_{i=1,n}$ we set the gradient, divergence, and tensor product operators, as

$$\begin{aligned} \nabla {\varvec{v}}:= \left( \frac{\partial v_i}{\partial x_j}\right) _{i,j=1,n}, \quad {\mathrm {div}}\,{\varvec{v}}:= \sum _{j=1}^n \frac{\partial v_j}{\partial x_j}, {\quad \hbox {and}\quad }{\varvec{v}}\otimes {\varvec{w}}:= (v_i\,w_j)_{i,j = 1,n}. \end{aligned}$$

In addition, for any tensor fields ${\varvec{\tau }}=(\tau _{ij})_{i,j=1,n}$ and ${\varvec{\zeta }}= (\zeta _{ij})_{i,j=1,n}$, we let ${\mathbf {div}}\,{\varvec{\tau }}$ be the divergence operator ${\mathrm {div}}$ acting along the rows of ${\varvec{\tau }}$, and define the transpose, the trace, the tensor inner product, and the deviatoric tensor, respectively, as

$$\begin{aligned} {\varvec{\tau }}^{\mathtt{t}}:= & {} (\tau _{ji})_{i,j=1,n}, \quad {\mathrm {tr}}({\varvec{\tau }}) := \sum _{i=1}^n\tau _{ii}, \quad {\varvec{\tau }}:{\varvec{\zeta }}:= \sum _{i,j=1}^n\tau _{ij}\zeta _{ij}, {\quad \hbox {and}\quad }\\ {\varvec{\tau }}^{\mathtt{d}}:= & {} {\varvec{\tau }}- \frac{1}{n}\,{\mathrm {tr}}({\varvec{\tau }})\,{\mathbb {I}}. \end{aligned}$$

Then, we recall that the spaces

$$\begin{aligned} {\mathbf {H}}({\mathrm {div}};\Omega ) := \{{\mathbf {q}}\in {\mathbf {L}}^2(\Omega ):{\mathrm {div}}\,{\mathbf {q}}\in {\mathrm {L}}^2(\Omega )\}, \end{aligned}$$

and

$$\begin{aligned} {\mathbb {H}}({\mathbf {div}};\Omega ) := \{{\varvec{\tau }}\in {\mathbb {L}}^2(\Omega ):{\mathbf {div}}\,{\varvec{\tau }}\in {\mathbf {L}}^2(\Omega )\}, \end{aligned}$$

equipped with the usual norms

$$\begin{aligned} \Vert {\mathbf {q}}\Vert ^2_{{\mathrm {div}};\Omega } := \Vert {\mathbf {q}}\Vert ^2_{0,\Omega } + \Vert {\mathrm {div}}\, {\mathbf {q}}\Vert ^2_{0,\Omega } \quad \forall {\mathbf {q}}\in {\mathbf {H}}({\mathrm {div}};\Omega ), \end{aligned}$$

and

$$\begin{aligned} \Vert {\varvec{\tau }}\Vert ^2_{{\mathbf {div}};\Omega } := \Vert {\varvec{\tau }}\Vert ^2_{0,\Omega } + \Vert {\mathbf {div}}\, {\varvec{\tau }}\Vert ^2_{0,\Omega } \quad \forall {\varvec{\tau }}\in {\mathbb {H}}({\mathbf {div}};\Omega ), \end{aligned}$$

are both Hilbert spaces.

2 The model problem

The stationary Boussinesq problem consists of a system of equations where the incompressible Navier–Stokes equation is coupled with the heat equation through a convective term and a buoyancy term typically acting in direction opposite to gravity. More precisely, given an external force per unit mass ${\varvec{g}}\in {\mathbf {L}}^\infty (\Omega )$, and assuming that the boundary velocity and temperature are prescribed by ${\varvec{u}}_D\in {\mathbf {H}}^{1/2}(\Gamma )$ and $\varphi _D \in {\mathrm {H}}^{1/2}(\Gamma )$, respectively, the aforementioned system of equations is given by

$$\begin{aligned} \displaystyle -\,{\mu }\,\Delta {\varvec{u}}+ (\nabla {\varvec{u}})\,{\varvec{u}}+ \nabla p-{\varvec{g}}\,\varphi= & {} 0 {\quad \hbox {in }}\Omega ,\nonumber \\ \displaystyle {\mathrm {div}}\,{\varvec{u}}= & {} 0{\quad \hbox {in }}\Omega ,\nonumber \\ \displaystyle -\,{\mathrm {div}}({\mathbb {K}}\,\nabla \varphi )+{\varvec{u}}\cdot \nabla \varphi= & {} 0 {\quad \hbox {in }}\Omega ,\nonumber \\ \displaystyle {\varvec{u}}= & {} {\varvec{u}}_D {\quad \hbox {on }}\Gamma ,\nonumber \\ \displaystyle \varphi= & {} \varphi _D {\quad \hbox {on }}\Gamma , \end{aligned}$$

(2.1)

where the unknowns are the velocity ${\varvec{u}}$, the pressure p and the temperature $\varphi$ of a fluid occupying the region $\Omega$. Here, $\mu > 0$ is the fluid viscosity and ${\mathbb {K}}\in {\mathbb {L}}^\infty (\Omega )$ is a uniformly positive definite tensor describing the thermal conductivity, which are assumed to be known. In particular, we denote by $\kappa _{0}$ the positive constant satisfying

$$\begin{aligned} {\mathbb {K}}^{-1}\, {\varvec{c}}\cdot {\varvec{c}}\ge \kappa _{0}\,|{\varvec{c}}|^{2}\quad \forall {\varvec{c}}\in {\mathrm {R}}^{n}. \end{aligned}$$

(2.2)

As usual, the Dirichlet datum ${\varvec{u}}_{D}$ must satisfy the compatibility condition

$$\begin{aligned} \int _{\Gamma }{\varvec{u}}_{D}\cdot {\varvec{\nu }}=0. \end{aligned}$$

(2.3)

In addition, it is well known that uniqueness of a pressure solution of (2.1) (see e.g. [21]) is ensured in the space ${\mathrm {L}}^{2}_{0}(\Omega )= \big \{q\in L^{2}(\Omega ):\int _{\Omega } q= 0\big \}.$

Now, in order to derive our augmented fully-mixed formulation we first need to rewrite (2.1) as a first-order system of equations. To this end, we first introduce the nonlinear pseudostress

$$\begin{aligned} {\varvec{\sigma }}:=\mu \,\nabla {\varvec{u}}-({\varvec{u}}\otimes {\varvec{u}})-p\,{\mathbb {I}} {\quad \hbox {in }}\Omega , \end{aligned}$$

(2.4)

and then, proceeding as in [8] (see also [10]), in particular utilizing the incompressibility condition ${\mathrm {div}}\,{\varvec{u}}={\mathrm {tr}}(\nabla {\varvec{u}})=0$, we find that the equations modelling the fluid can be rewritten, equivalently, as

$$\begin{aligned} \displaystyle {\varvec{\sigma }}^{\mathtt{d}}+({\varvec{u}}\otimes {\varvec{u}})^{\mathtt{d}} \,= & {} \,\mu \,\nabla {\varvec{u}}{\quad \hbox {in }}\Omega ,\quad -\,{\mathbf {div}}\,{\varvec{\sigma }}-{\varvec{g}}\,\varphi = 0 {\quad \hbox {in }}\Omega ,\quad {\varvec{u}}= {\varvec{u}}_D {\quad \hbox {on }}\Gamma ,\nonumber \\ \displaystyle p \,= & {} \,-\frac{1}{n}\,{\mathrm {tr}}({\varvec{\sigma }}+ {\varvec{u}}\otimes {\varvec{u}})\, {\quad \hbox {in }}\Omega ,\quad \int _{\Omega }{\mathrm {tr}}({\varvec{\sigma }}+{\varvec{u}}\otimes {\varvec{u}})\, =\, 0.\, \end{aligned}$$

(2.5)

Note that the fourth equation in (2.5) allows us to eliminate the pressure p from the system and compute it as a simple post-process of the solution, whereas the last equation takes care of the requirement that $p\in L^2_0(\Omega )$.

Similarly, for the convection–diffusion equation modelling the temperature of the fluid, we now introduce the further unknown,

$$\begin{aligned} {\mathbf {p}}:= {\mathbb {K}}\,\nabla \varphi -\varphi \,{\varvec{u}}{\quad \hbox {in }}\Omega , \end{aligned}$$

so that, utilizing again the incompressibility condition ${\mathrm {div}}\, {\varvec{u}}=0{\quad \hbox {in }}\Omega$, and after simple computations, the remaining equations in the system (2.1) can be rewritten, equivalently, as

$$\begin{aligned} {\mathbb {K}}^{-1}\,{\mathbf {p}}+{\mathbb {K}}^{-1}\,\varphi \,\,{\varvec{u}}\, =\,\nabla \varphi {\quad \hbox {in }}\Omega , \quad {\mathrm {div}}\,{\mathbf {p}}= 0 {\quad \hbox {in }}\Omega ,\quad \varphi = \varphi _D {\quad \hbox {on }}\Gamma . \end{aligned}$$

(2.6)

In this way, we arrive at the full first-order system of equations given by (2.5) and (2.6), where, after eliminating the pressure, we find that the new auxiliary variables ${\varvec{\sigma }}$ and ${\mathbf {p}}$, the velocity ${\varvec{u}}$, and the temperature $\varphi$ become the main unknowns of the coupled problem. In addition, we emphasize that one of the main advantages of approximating the solution of the coupled system (2.5) and (2.6) is that, besides the possibility of recovering the pressure in terms of the nonlinear pseudostress and the velocity, one can compute further variables of interest, such as the vorticity $\varvec{\omega }$, the shear–stress $\widetilde{\varvec{\sigma }}$, the velocity gradient $\nabla {\varvec{u}}$, and the temperature gradient $\nabla \varphi$, as simple post-processes of the solution, that is

$$\begin{aligned} \varvec{\omega }\,= & {} \,\displaystyle \frac{1}{2\mu }({\varvec{\sigma }}-{\varvec{\sigma }}^{\mathtt{t}}),\quad \widetilde{\varvec{\sigma }}=\displaystyle {\varvec{\sigma }}^{\mathtt{d}} +({\varvec{u}}\otimes {\varvec{u}})^{\mathtt{d}} + {\varvec{\sigma }}^{\mathtt{t}}+ {\varvec{u}}\otimes {\varvec{u}},\nonumber \\ \nabla {\varvec{u}}\,= & {} \displaystyle \frac{1}{\mu }({\varvec{\sigma }}^{\mathtt{d}}\, +\, ({\varvec{u}}\otimes {\varvec{u}})^{\mathtt{d}}),\quad \nabla \varphi \, =\, {\mathbb {K}}^{-1}\,{\mathbf {p}}+{\mathbb {K}}^{-1}\,\varphi \,\,{\varvec{u}}. \end{aligned}$$

(2.7)

Furthermore, since the set of equations modelling the fluid (cf. (2.5)) are the same of the mixed-primal formulation utilized in [10], we remark in advance that in what follows we make use of some results already available in [10], and also adapt several arguments utilized in [10] to derive and analyze the augmented fully-mixed scheme to be proposed in the present paper.

3 The continuous problem

3.1 The augmented fully-mixed formulation

In this section we derive the weak formulation of the coupled system (2.5) and (2.6). We begin recalling that, in accordance with the last equation of (2.5) and the decomposition (see e.g. [5, 16])

$$\begin{aligned} {\mathbb {H}}({\mathbf {div}};\Omega )={\mathbb {H}}_{0}({\mathbf {div}};\Omega )\oplus {\mathrm {R}}\,{\mathbb {I}}, \end{aligned}$$

(3.1)

where

$$\begin{aligned} {\mathbb {H}}_{0}({\mathbf {div}};\Omega ):=\left\{ {\varvec{\zeta }}\in {\mathbb {H}}({\mathbf {div}};\Omega ):\int _{\Omega }{\mathrm {tr}}({\varvec{\zeta }})=0 \,\right\} , \end{aligned}$$

(3.2)

the eventual solution ${\varvec{\sigma }}\in {\mathbb {H}}({\mathbf {div}};\Omega )$ of this system is given by ${\varvec{\sigma }}= {\varvec{\sigma }}_0 + c\,{\mathbb {I}}$, where ${\varvec{\sigma }}_{0}\in {\mathbb {H}}_{0}({\mathbf {div}};\Omega )$ and (see e.g., [10, Section 3.1]):

$$\begin{aligned} c := - \dfrac{1}{n\,|\Omega |}\int _{\Omega }{\mathrm {tr}}({\varvec{u}}\otimes {\varvec{u}}) . \end{aligned}$$

(3.3)

As a consequence, and noting that ${\varvec{\sigma }}^{\mathtt{d}}= {\varvec{\sigma }}_{0}^{\mathtt{d}}$ and ${\mathbf {div}}\,{\varvec{\sigma }}^{\mathtt{d}}= {\mathbf {div}}\,{\varvec{\sigma }}_{0}^{\mathtt{d}}$, we can rewrite equations (2.5) in terms of ${\varvec{\sigma }}_0$ without modifying them. Nevertheless, for the sake of simplicity of notation, in what follows we name the unknown in ${\mathbb {H}}_{0}({\mathbf {div}};\Omega )$ simply as ${\varvec{\sigma }}$. Taking this into account, we test the constitutive equation for the fluid (first equation of (2.5)) by a function ${\varvec{\tau }}\in {\mathbb {H}}({\mathbf {div}};\Omega )$, integrate by parts and utilize the Dirichlet boundary condition for ${\varvec{u}}$ to find the variational equation

$$\begin{aligned} \int _{\Omega }{\varvec{\sigma }}^{\mathtt{d}}:{\varvec{\tau }}^{\mathtt{d}} + \mu \int _{\Omega }{\varvec{u}}\cdot {\mathbf {div}}\,{\varvec{\tau }}+\int _{\Omega }({\varvec{u}}\otimes {\varvec{u}})^{\mathtt{d}} :{\varvec{\tau }}^{\mathtt{d}}=\mu \, \langle \,{\varvec{\tau }}{\varvec{\nu }},\,{\varvec{u}}_{D}\,\rangle _{\Gamma }\quad \forall {\varvec{\tau }}\in {\mathbb {H}}_{0}({\mathbf {div}};\Omega ), \end{aligned}$$

(3.4)

where hereafter $\langle \,\cdot ,\cdot \,\rangle _{\Gamma }$ stands for the duality between ${\mathbf {H}}^{-1/2}(\Gamma )$ [resp. ${\mathrm {H}}^{-1/2}(\Gamma )$] and ${\mathbf {H}}^{1/2}(\Gamma )$ [resp. ${\mathrm {H}}^{1/2}(\Gamma )$], and the test space has been reduced to ${\mathbb {H}}_{0}({\mathbf {div}};\Omega )$ due to the decomposition (3.2) and the compatibility condition (2.3). In turn, the equilibrium equation for the fluid (second equation of (2.5)) is imposed weakly as

$$\begin{aligned} {-}\mu \,\int _{\Omega }{\varvec{v}}\cdot {\mathbf {div}}\,{\varvec{\sigma }}-\mu \,\int _{\Omega }\varphi \,{\varvec{g}}\cdot {\varvec{v}}=0 \quad \forall {\varvec{v}}\in {\mathbf {L}}^{2}(\Omega ). \end{aligned}$$

(3.5)

Next, for Eq. (2.6) we proceed similarly. We first multiply the constitutive equation for the temperature (first equation of (2.6)) by a function ${\mathbf {q}}\in {\mathbf {H}}({\mathrm {div}};\Omega )$, integrate by parts, and use the Dirichlet boundary condition for $\varphi$ to obtain

$$\begin{aligned} \int _{\Omega } {\mathbb {K}}^{-1}\,{\mathbf {p}}\cdot {\mathbf {q}}+\int _{\Omega }\varphi \,{\mathrm {div}}\,{\mathbf {q}}+\int _{\Omega }{\mathbb {K}}^{-1}\,\varphi \,{\varvec{u}}\cdot {\mathbf {q}}= \langle \,{\mathbf {q}}\cdot {\varvec{\nu }},\,\varphi _{D}\,\rangle _{\Gamma }\quad \forall {\mathbf {q}}\in {\mathbf {H}}({\mathrm {div}};\Omega ).\qquad \end{aligned}$$

(3.6)

In addition, the equilibrium equation for the temperature (second equation of (2.6)), is imposed weakly as

$$\begin{aligned} -\,\int _{\Omega } \psi \,{\mathrm {div}}\,{\mathbf {p}}= 0\quad \forall \psi \in {\mathrm {L}}^{2}(\Omega ). \end{aligned}$$

(3.7)

At this point, we realize from the third terms at the left-hand side of (3.4) and (3.6) that a suitable regularity is required for both unknowns ${\varvec{u}}$ and $\varphi$. Indeed, it follows from Cauchy–Schwarz and Hölder inequalities, and then from the continuous embedding of ${\mathrm {H}}^{1}(\Omega )$ into ${\mathrm {L}}^{4}(\Omega )$ (see [1, Theorem 4.12], [22, Theorem 1.3.4]), that there exist positive constants $c_{1}(\Omega )$ and $c_{2}(\Omega ),$ such that

$$\begin{aligned}&\left| \,\int _{\Omega } ({\varvec{u}}\otimes {\varvec{w}})^{\mathtt{d}} \, : \, {\varvec{\tau }}^{\mathtt{d}} \,\right| \nonumber \\&\quad \le c_{1}(\Omega )\,\Vert {\varvec{u}}\Vert _{1,\Omega }\,\Vert {\varvec{w}}\Vert _{1,\Omega }\,\Vert {\varvec{\tau }}\Vert _{0,\Omega }\quad \forall {\varvec{u}},\,{\varvec{w}}\in {\mathbf {H}}^{1}(\Omega )\quad \forall {\varvec{\tau }}\in {\mathbb {L}}^{2}(\Omega ), \end{aligned}$$

(3.8)

and

$$\begin{aligned}&\left| \,\int _{\Omega } \varphi \,{\varvec{u}}\cdot {\mathbf {q}}\,\right| \nonumber \\&\quad \le c_{2}(\Omega )\,\Vert \varphi \Vert _{1,\Omega }\,\Vert {\varvec{u}}\Vert _{1,\Omega }\,\Vert {\mathbf {q}}\Vert _{0,\Omega }\quad \forall \varphi \in {\mathrm {H}}^{1}(\Omega )\quad \forall {\varvec{u}}\in {\mathbf {H}}^{1}(\Omega )\quad \forall {\mathbf {q}}\in {\mathbf {L}}^{2}(\Omega ).\nonumber \\ \end{aligned}$$

(3.9)

Pursuant to the above, and for the sake of analyzing the present variational formulation of the coupled problem (2.5) and (2.6), we propose to seek ${\varvec{u}}\in {\mathbf {H}}^{1}(\Omega )$ and $\varphi \in {\mathrm {H}}^{1}(\Omega )$. In this way, similarly as in [10, Section 3.1] (see also [15, Section 3]), we augment (3.4)–(3.7) through the following redundant terms arising from the constitutive and equilibrium equations, and from both Dirichlet boundary conditions

$$\begin{aligned}&\displaystyle \kappa _1 \int _{\Omega }(\mu \,\nabla {\varvec{u}}-{\varvec{\sigma }}^{\mathtt{d}}-({\varvec{u}}\otimes {\varvec{u}})^{\mathtt{d}}):\nabla {\varvec{v}}= 0 \quad \forall {\varvec{v}}\in {\mathbf {H}}^{1}(\Omega ),\nonumber \\&\displaystyle \kappa _{2}\int _{\Omega }\,{\mathbf {div}}\,{\varvec{\sigma }}\cdot {\mathbf {div}}\,{\varvec{\tau }}+\kappa _{2}\int _{\Omega }\varphi \,{\varvec{g}}\cdot {\mathbf {div}}\,{\varvec{\tau }}= 0 \quad \forall {\varvec{\tau }}\in {\mathbb {H}}_{0}({\mathbf {div}};\Omega ),\nonumber \\&\displaystyle \kappa _{3}\int _{\Gamma }{\varvec{u}}\cdot {\varvec{v}}= \displaystyle \kappa _{3}\int _{\Gamma }{\varvec{u}}_{D}\cdot {\varvec{v}}\quad \forall {\varvec{v}}\,\in {\mathbf {H}}^{1}(\Omega ),\qquad \end{aligned}$$

(3.10)

and

$$\begin{aligned}&\displaystyle \kappa _{4} \int _{\Omega }(\nabla \varphi -{\mathbb {K}}^{-1}\,{\mathbf {p}}-{\mathbb {K}}^{-1}\varphi \,{\varvec{u}})\cdot \,\nabla \psi = 0 \quad \forall \psi \in {\mathrm {H}}^{1}(\Omega ),\nonumber \\&\displaystyle \kappa _{5}\int _{\Omega }\,{\mathrm {div}}\,{\mathbf {p}}\,{\mathrm {div}}\,{\mathbf {q}}= 0 \quad \forall {\mathbf {q}}\in {\mathbf {H}}({\mathrm {div}};\Omega ),\nonumber \\&\displaystyle \kappa _{6}\int _{\Gamma }\varphi \,\psi = \displaystyle \kappa _{6}\int _{\Gamma }\varphi _{D}\,\psi \quad \forall \psi \,\in {\mathrm {H}}^{1}(\Omega ), \end{aligned}$$

(3.11)

where $(\kappa _{1},\,\dots ,\,\kappa _{6})$ is a vector of positive parameters to be specified later.

Consequently, we arrive at the following augmented fully-mixed formulation for the stationary Boussinesq problem: Find $({\varvec{\sigma }},\,{\varvec{u}},\,{\mathbf {p}},\,\varphi )\in {\mathbb {H}}_{0}({\mathbf {div}};\Omega )\times {\mathbf {H}}^{1}(\Omega )\times {\mathbf {H}}({\mathrm {div}};\Omega )\times {\mathrm {H}}^{1}(\Omega )$ such that

$$\begin{aligned} {\mathbf {A}}(({\varvec{\sigma }},{\varvec{u}}),({\varvec{\tau }},{\varvec{v}}) ) + {\mathbf {B}}_{{\varvec{u}}}(({\varvec{\sigma }},{\varvec{u}}),({\varvec{\tau }},{\varvec{v}}))= & {} (F_{\varphi } + F_{D})({\varvec{\tau }},{\varvec{v}}) \nonumber \\&\forall ({\varvec{\tau }},{\varvec{v}}) \in {\mathbb {H}}_{0}({\mathbf {div}};\Omega )\times {\mathbf {H}}^{1}(\Omega ),\nonumber \\ \widetilde{ {\mathbf {A}}}(({\mathbf {p}},\varphi ),({\mathbf {q}},\psi )) + \widetilde{{\mathbf {B}}}_{{\varvec{u}}} (({\mathbf {p}},\varphi ),({\mathbf {q}},\psi ))= & {} \,\widetilde{F}_{D}({\mathbf {q}},\psi ) \quad \nonumber \\&\forall ({\mathbf {q}},\psi ) \in {\mathbf {H}}({\mathrm {div}};\Omega )\times {\mathrm {H}}^{1}(\Omega ),\nonumber \\ \end{aligned}$$

(3.12)

where the forms ${\mathbf {A}},$ ${\mathbf {B}}_{{\varvec{w}}},$ $\widetilde{{\mathbf {A}}},$ and $\widetilde{{\mathbf {B}}}_{{\varvec{w}}}$ are defined, respectively, as

$$\begin{aligned} \displaystyle {\mathbf {A}}(({\varvec{\sigma }},{\varvec{u}}),\,({\varvec{\tau }},{\varvec{v}})):= & {} \int _{\Omega }{\varvec{\sigma }}^{\mathtt{d}}:\,( {\varvec{\tau }}^{\mathtt{d}} - \kappa _{1}\,\nabla {\varvec{v}})\, + \int _{\Omega }(\mu \,{\varvec{u}}+\kappa _{2}\,{\mathbf {div}}\,{\varvec{\sigma }})\cdot {\mathbf {div}}\,{\varvec{\tau }}\,\nonumber \\&\displaystyle -\,\mu \,\int _{\Omega }{\varvec{v}}\cdot {\mathbf {div}}\,{\varvec{\sigma }}+\mu \,\kappa _{1}\int _{\Omega }\nabla {\varvec{u}}: \nabla {\varvec{v}}+ \kappa _{3}\int _{\Gamma }{\varvec{u}}\cdot {\varvec{v}}, \qquad \qquad \end{aligned}$$

(3.13)

$$\begin{aligned} \displaystyle {\mathbf {B}}_{{\varvec{w}}}(({\varvec{\sigma }},{\varvec{u}}),\,({\varvec{\tau }},{\varvec{v}})):= & {} \int _{\Omega }({\varvec{u}}\otimes {\varvec{w}})^{\mathtt{d}} : (\,{\varvec{\tau }}^{\mathtt{d}}-\kappa _{1}\,\nabla {\varvec{v}}), \end{aligned}$$

(3.14)

$$\begin{aligned} \displaystyle \widetilde{{\mathbf {A}}}(({\mathbf {p}},\varphi ),\,({\mathbf {q}},\psi )):= & {} \displaystyle \,\int _{\Omega }{\mathbb {K}}^{-1}\, {\mathbf {p}}\cdot ( {\mathbf {q}}-\kappa _{4}\,\nabla \psi ) + \int _{\Omega } (\varphi +\kappa _{5}\,{\mathrm {div}}\,{\mathbf {p}})\,{\mathrm {div}}\,{\mathbf {q}}\nonumber \\&\displaystyle -\,\int _{\Omega }\,\psi \,{\mathrm {div}}\,{\mathbf {p}}+\kappa _{4}\int _{\Omega }\nabla \varphi \cdot \nabla \psi +\kappa _{6}\int _{\Gamma }\varphi \,\psi , \end{aligned}$$

(3.15)

and

$$\begin{aligned} \displaystyle \widetilde{{\mathbf {B}}}_{{\varvec{w}}}(({\mathbf {p}},\varphi ),\,({\mathbf {q}},\psi )):=\,\int _{\Omega }{\mathbb {K}}^{-1}\,\varphi \,{\varvec{w}}\cdot ( {\mathbf {q}}-\kappa _{4}\nabla \psi ) . \end{aligned}$$

(3.16)

for all $({\varvec{\sigma }},{\varvec{u}}),\,({\varvec{\tau }},{\varvec{v}})\in {\mathbb {H}}_{0}({\mathbf {div}};\Omega )\times {\mathbf {H}}^{1}(\Omega ),$ for all $({\mathbf {p}},\varphi ),\,({\mathbf {q}},\psi )\,\in \,{\mathbf {H}}({\mathrm {div}};\Omega )\times {\mathrm {H}}^{1}(\Omega ),$ and for all ${\varvec{w}}\in {\mathbf {H}}^{1}(\Omega ).$ Note that ${\mathbf {A}}$ and $\widetilde{{\mathbf {A}}}$ are bilinear as well as ${\mathbf {B}}_{{\varvec{w}}}$ and $\widetilde{{\mathbf {B}}}_{{\varvec{w}}}$ [for a fixed ${\varvec{w}}\in {\mathbf {H}}^{1}(\Omega )$]. In turn, given $\varphi \in {\mathrm {H}}^{1}(\Omega )$, $F_{\varphi }$, $F_{D},$ and $\widetilde{F}_{D}$ are the bounded linear functionals given by

$$\begin{aligned} F_{\varphi }({\varvec{\tau }},{\varvec{v}}):= & {} \,\int _{\Omega }\varphi \,{\mathbf {g}}\cdot (\mu \,{\varvec{v}}-\kappa _{2}\,{\mathbf {div}}\,{\varvec{\tau }})\quad \forall ({\varvec{\tau }},{\varvec{v}})\in {\mathbb {H}}_{0}({\mathbf {div}};\Omega )\times {\mathbf {H}}^{1}(\Omega ),\qquad \end{aligned}$$

(3.17)

$$\begin{aligned} F_{D}({\varvec{\tau }},{\varvec{v}}):= & {} \kappa _{3}\,\int _{\Gamma }{\varvec{u}}_{D}\cdot {\varvec{v}}+\mu \,\langle \,{\varvec{\tau }}{\varvec{\nu }},{\varvec{u}}_{D}\,\rangle _{\Gamma }\quad \forall ({\varvec{\tau }},{\varvec{v}})\in {\mathbb {H}}_{0}({\mathbf {div}};\Omega )\times {\mathbf {H}}^{1}(\Omega ),\nonumber \\ \end{aligned}$$

(3.18)

and

$$\begin{aligned} \widetilde{F}_{D}({\mathbf {q}},\psi ):=\kappa _{6}\,\int _{\Gamma }\varphi _{D}\,\psi +\,\langle \,{\mathbf {q}}\cdot {\varvec{\nu }},\varphi _{D}\,\rangle _{\Gamma }\quad \forall ({\mathbf {q}},\psi )\in {\mathbf {H}}({\mathrm {div}};\Omega )\times {\mathrm {H}}^{1}(\Omega ).\qquad \end{aligned}$$

(3.19)

In the Sects. 3.2–3.4 below we proceed similarly as in [10] and utilize a fixed point strategy to prove that problem (3.12) is well posed. More precisely, in Sect. 3.2 we rewrite (3.12) as an equivalent fixed point equation in terms of an operator ${\mathbf {T}}$. Next in Sect. 3.3 we show that ${\mathbf {T}}$ is well defined, and finally in Sect. 3.4 we apply the classical Banach’s theorem to conclude that ${\mathbf {T}}$ has a unique fixed point.

3.2 The fixed point approach

We first set ${\mathbf {H}} :={\mathbf {H}}^{1}(\Omega ) \times {\mathrm {H}} ^{1}(\Omega )$, and define the operator ${\mathbf {S}}:{\mathbf {H}}\,\longrightarrow \, {\mathbb {H}}_{0}({\mathbf {div}};\Omega )\times {\mathbf {H}}^{1}(\Omega )$ as

$$\begin{aligned} {\mathbf {S}}({\varvec{w}},\phi ):=({\mathbf {S}}_{1}({\varvec{w}},\phi ),{\mathbf {S}}_{2}({\varvec{w}},\phi ))=({\varvec{\sigma }},{\varvec{u}})\quad \forall ({\varvec{w}},\phi )\in {\mathbf {H}}, \end{aligned}$$

(3.20)

where $({\varvec{\sigma }},{\varvec{u}})$ is the unique pair in $({\varvec{\sigma }},{\varvec{u}})\in {\mathbb {H}}_{0}({\mathbf {div}};\Omega )\times {\mathbf {H}}^{1}(\Omega )$ such that

$$\begin{aligned}&{\mathbf {A}}(({\varvec{\sigma }},{\varvec{u}}),({\varvec{\tau }},{\varvec{v}}))+ {\mathbf {B}}_{{\varvec{w}}}(({\varvec{\sigma }},{\varvec{u}}),({\varvec{\tau }},{\varvec{v}})) \,\nonumber \\&\quad =\big (F_{\phi }+F_{D}\big )({\varvec{\tau }},{\varvec{v}})\quad \forall ({\varvec{\tau }},{\varvec{v}})\in {\mathbb {H}}_{0}({\mathbf {div}};\Omega )\times {\mathbf {H}}^{1}(\Omega ). \end{aligned}$$

(3.21)

Note here that the linear functional $F_{\phi }$ is given exactly as in (3.17) but with $\phi$ instead of $\varphi$. In turn, we let $\widetilde{{\mathbf {S}}}:{\mathbf {H}}^{1}(\Omega )\,\longrightarrow \,{\mathbf {H}}({\mathrm {div}};\Omega )\times {\mathrm {H}}^{1}(\Omega )$ be the operator given by

$$\begin{aligned} \widetilde{{\mathbf {S}}}({\varvec{w}}):=(\widetilde{{\mathbf {S}}}_{1}({\varvec{w}}),\widetilde{{\mathbf {S}}}_{2}({\varvec{w}}))=({\mathbf {p}},\varphi )\quad \forall {\varvec{w}}\in {\mathbf {H}}^{1}(\Omega ), \end{aligned}$$

(3.22)

where $({\mathbf {p}},\varphi )$ is the pair in $({\mathbf {p}},\varphi )\in {\mathbf {H}}({\mathrm {div}};\Omega )\times {\mathrm {H}}^{1}(\Omega )$ such that

$$\begin{aligned} \widetilde{ {\mathbf {A}}}(({\mathbf {p}},\varphi ),({\mathbf {q}},\psi ))+ \widetilde{{\mathbf {B}}}_{{\varvec{w}}}(({\mathbf {p}},\varphi ),({\mathbf {q}},\psi )) = \,\widetilde{F}_{D}({\mathbf {q}},\psi ) \quad \forall ({\mathbf {q}},\psi )\in {\mathbf {H}}({\mathrm {div}};\Omega )\times {\mathrm {H}}^{1}(\Omega ). \end{aligned}$$

(3.23)

Having introduced the auxiliary mappings ${\mathbf {S}}$ and $\widetilde{{\mathbf {S}}}$, we now define ${\mathbf {T}}:{\mathbf {H}}\,\longrightarrow \,{\mathbf {H}}$ as

$$\begin{aligned} {\mathbf {T}}({\varvec{w}},\phi ):=({\mathbf {S}}_{2}({\varvec{w}},\phi ),\widetilde{{\mathbf {S}}}_{2}({\mathbf {S}}_{2}({\varvec{w}},\phi )))\quad \forall ({\varvec{w}},\phi )\in {\mathbf {H}}, \end{aligned}$$

(3.24)

and realize that solving (3.12) is equivalent to seeking a fixed point of ${\mathbf {T}}$, that is: Find $({\varvec{u}},\varphi )\, \in \,{\mathbf {H}}$ such that

$$\begin{aligned} {\mathbf {T}}({\varvec{u}},\varphi )= ({\varvec{u}},\varphi ). \end{aligned}$$

In this way, in what follows we focus on analyzing that ${\mathbf {T}}$ has a unique fixed point. Before doing this, we certainly need to verify that ${\mathbf {T}}$ is well defined. The next section is devoted to this matter.

3.3 Well-definiteness of the fixed point operator

In this section we show that ${\mathbf {T}}$ is well defined. For this purpose, we first notice that it suffices to prove that the uncoupled problems (3.21) and (3.23) defining ${\mathbf {S}}$ and $\widetilde{{\mathbf {S}}}$, respectively, are well posed. In this way, in the sequel we focus on the solvability analysis of (3.21) and (3.23). In this regard, we first point out that a distinctive feature of the results obtained below is that, differently from the analysis in [10] where the introduction of a boundary unknown leads to a mixed-primal formulation, in our present case both uncoupled problems (3.21) and (3.23) yield strongly elliptic bilinear forms. In addition, clearly the operator ${\mathbf {S}}$ is exactly defined as in [10, Section 3.2], and therefore throughout this work we omit most of the corresponding proofs and recall only the key properties, and results, concerning this operator, but without compromising the clarity of our reasoning. Hence, the core of our analysis will be mainly devoted to the uncoupled problem (3.23) and its influence on ${\mathbf {T}}.$

Now, concerning the well-posedness of (3.21), we first recall the stability properties of the forms ${\mathbf {A}}$ and ${\mathbf {B}}_{{\varvec{w}}}$ and the functional $F_{\phi }+F_{D}$ (cf. (3.13), (3.14), (3.17) and (3.18), respectively). In what follows, and according to a notational comment in Sect. 1 (cf. Preliminaries), $\Vert ({\varvec{\tau }},{\varvec{v}})\Vert$ denotes the product norm of a given $({\varvec{\tau }},{\varvec{v}}) \in {\mathbb {H}}_{0}({\mathbf {div}};\Omega )\times {\mathbf {H}}^{1}(\Omega )$, that is

$$\begin{aligned} \Vert ({\varvec{\tau }},{\varvec{v}})\Vert := \{ \Vert {\varvec{\tau }}\Vert ^2_{{\mathbf {div}};\Omega } + \Vert {\varvec{v}}\Vert ^2_{1,\Omega }\}^{1/2}. \end{aligned}$$

(3.25)

Then, we begin by establishing the boundedness of the forms ${\mathbf {A}}$ and ${\mathbf {B}}_{{\varvec{w}}}$, where ${\varvec{w}}\in {\mathbf {H}}^{1}(\Omega )$ is given (see [10, Lemma 3.3] for details):

$$\begin{aligned} \begin{array}{r} |{\mathbf {B}}_{{\varvec{w}}}(({\varvec{\sigma }},{\varvec{u}}),({\varvec{\tau }},{\varvec{v}}))|\, \le \,c_1(\Omega )\,(\kappa _{1}^{2}+1)^{1/2}\,\Vert {\varvec{w}}\Vert _{1,\Omega }\,\Vert {\varvec{u}}\Vert _{1,\Omega }\,\Vert ({\varvec{\tau }},{\varvec{v}})\Vert \end{array} \end{aligned}$$

(3.26)

and

$$\begin{aligned} |{\mathbf {A}}(({\varvec{\sigma }},{\varvec{u}}),\,({\varvec{\tau }},{\varvec{v}}))|\le \Vert {\mathbf {A}}\Vert \, \Vert ({\varvec{\sigma }},{\varvec{u}})\Vert \,\Vert ({\varvec{\tau }},{\varvec{v}})\Vert , \end{aligned}$$

(3.27)

for all $({\varvec{\sigma }},{\varvec{u}}),\,({\varvec{\tau }},{\varvec{v}})\in {\mathbb {H}}_{0}({\mathbf {div}};\Omega )\times {\mathbf {H}}^{1}(\Omega )$. In (3.26) the constant $c_1(\Omega )$ depends only on $\Omega$, whereas in (3.27) the constant $\Vert {\mathbf {A}}\Vert$ depends on $\Omega$, the viscosity $\mu$, and the parameters $\kappa _1$, $\kappa _2$ and $\kappa _3$.

As a consequence of the estimates (3.26) and (3.27) we obtain that the bilinear form ${\mathbf {A}} +{\mathbf {B}}_{\varvec{w}}$ is bounded, that is there exists a positive constant $\Vert {\mathbf {A}}+{\mathbf {B}}_{{\varvec{w}}}\Vert$, depending on $\mu ,$ $\Omega ,$ the stabilization parameters, and $\Vert {\varvec{w}}\Vert _{1,\Omega }$, such that for all $\,({\varvec{\sigma }},{\varvec{u}}),\,({\varvec{\tau }},{\varvec{v}})\in {\mathbb {H}}_{0}({\mathbf {div}};\Omega )\times {\mathbf {H}}^{1}(\Omega )$, there holds

$$\begin{aligned} |{\mathbf {A}}(({\varvec{\sigma }},{\varvec{u}}),\,({\varvec{\tau }},{\varvec{v}}))+{\mathbf {B}}_{{\varvec{w}}}(({\varvec{\sigma }},{\varvec{u}}),\,({\varvec{\tau }},{\varvec{v}}))|\le \Vert {\mathbf {A}} +{\mathbf {B}}_{{\varvec{w}}}\Vert \, \Vert ({\varvec{\sigma }},{\varvec{u}})\Vert \,\Vert ({\varvec{\tau }},{\varvec{v}})\Vert . \end{aligned}$$

(3.28)

Furthermore, it is not difficult to see that ${\mathbf {A}}$ is strongly elliptic. In fact, using similar arguments as in [15] we deduce that for each $\kappa _{1}\in (0,\,2\,\delta )$, with $\delta \in (0,\,2\,\mu ),$ and $\kappa _{2},\kappa _{3}> 0,$ there exists a positive constant $\alpha (\Omega )$, depending only on $\mu ,$ $\kappa _{1},$ $\kappa _{2},$ $\kappa _{3},$ and $\Omega ,$ such that (see [10, Lemma 3.3] for details)

$$\begin{aligned} {\mathbf {A}}(({\varvec{\tau }},{\varvec{v}}),\,({\varvec{\tau }},{\varvec{v}}))\ge \alpha (\Omega )\,\Vert ({\varvec{\tau }},{\varvec{v}})\Vert ^{2}\quad \forall ({\varvec{\tau }},{\varvec{v}})\in {\mathbb {H}}_{0}({\mathbf {div}};\Omega )\times {\mathbf {H}}^{1}(\Omega ). \end{aligned}$$

(3.29)

Then, combining (3.26) and (3.29), and proceeding as in [10, Lemma 3.3], we now define

$$\begin{aligned} r_{0}\,:=\dfrac{\alpha (\Omega )}{2\, (\kappa _{1}^{2}+1)^{1/2}\,c_{1}(\Omega )}, \end{aligned}$$

(3.30)

and find that for each $r\in (0,r_{0})$, and for each ${\varvec{w}}\in {\mathbf {H}}^{1}(\Omega )$ such that $\Vert {\varvec{w}}\Vert _{1,\Omega }\le r,$ the bilinear form ${\mathbf {A}} + {\mathbf {B}}_{\varvec{w}}$ is strongly elliptic with constant $\frac{\alpha (\Omega )}{2}$, that is

$$\begin{aligned} ({\mathbf {A}}+ {\mathbf {B}}_{{\varvec{w}}}\,)(({\varvec{\tau }},{\varvec{v}}),\,({\varvec{\tau }},{\varvec{v}})) \ge \dfrac{\alpha (\Omega )}{2}\,\Vert ({\varvec{\tau }},{\varvec{v}})\Vert ^{2}\, \quad \forall ({\varvec{\tau }},{\varvec{v}})\in {\mathbb {H}}_{0}({\mathbf {div}};\Omega )\times {\mathbf {H}}^{1}(\Omega ). \end{aligned}$$

(3.31)

Finally, from the Cauchy–Schwarz inequality and the trace theorems in ${\mathbb {H}}({\mathbf {div}};\Omega )$ and ${\mathbf {H}}^{1}(\Omega )$ with constants 1 and $c_0(\Omega ),$ respectively, we conclude with $M_{{\mathbf {S}}}:=\max \{ (\mu ^{2}+\kappa _{2}^{2})^{1/2},\,\kappa _{3}\,c_{0}(\Omega )\},$ that

$$\begin{aligned} \Vert F_{\phi }+F_{D}\Vert \le M_{{\mathbf {S}}}\,\{ \Vert {\varvec{g}}\Vert _{\infty ,\Omega }\, \Vert \phi \Vert _{0,\Omega }+\Vert {\varvec{u}}_{D}\Vert _{0,\Gamma }+\Vert {\varvec{u}}_{D}\Vert _{1/2,\Gamma }\}. \end{aligned}$$

(3.32)

The foregoing analysis confirms that the uncoupled problem (3.21) is well-posed (equivalently, the operator ${\mathbf {S}}$ is well-defined), which is summarized in the following Lemma.

Lemma 3.1

Let $r_0>0$ given by (3.30) and let $r\in (0,r_0)$. Assume that $\kappa _{1}\in ( 0,\,2\,\delta )$, with $\delta \,\in \,(0 ,\,2\,\mu ),$ and $\kappa _{2},\,\kappa _{3}> 0$. Then, for each $({\varvec{w}},\phi )\in {\mathbf {H}}$ such that $\Vert {\varvec{w}}\Vert _{1,\Omega }\le r$, the problem (3.21) has a unique solution $({\varvec{\sigma }},{\varvec{u}})={\mathbf {S}}({\varvec{w}},\phi ) \in {\mathbb {H}}_{0}({\mathbf {div}};\Omega )\times {\mathbf {H}}^{1}(\Omega )$. Moreover, there exists a constant $c_{{\mathbf {S}}}>0$, independent of $({\varvec{w}},\phi )$, such that

$$\begin{aligned} \Vert {\mathbf {S}}({\varvec{w}},\phi )\Vert = \Vert ({\varvec{\sigma }},{\varvec{u}})\Vert \le c_{{\mathbf {S}}}\, \{ \Vert {\varvec{g}}\Vert _{\infty ,\Omega }\, \Vert \phi \Vert _{0,\Omega }+\Vert {\varvec{u}}_{D}\Vert _{0,\Gamma }+\Vert {\varvec{u}}_{D}\Vert _{1/2,\Gamma }\} . \end{aligned}$$

(3.33)

Proof

The result follows from estimates (3.28) and (3.31), and a straightforward application of the Lax–Milgram Theorem (see for instance [16, Theorem 1.1]). We refer to [10, Lemma 3.3] for further details. $\square$

Next, we concentrate in proving that problem (3.23) is well posed. Before addressing this, we recall the following preliminary result.

Lemma 3.2

There exists $c_{3}(\Omega )>0$ such that

$$\begin{aligned} |{\varvec{v}}|^{2}_{1,\Omega }+\Vert {\varvec{v}}\Vert ^{2}_{0,\Gamma }\ge c_{3}(\Omega )\,\Vert {\varvec{v}}\Vert ^{2}_{1,\Omega }\quad \forall {\varvec{v}}\in {\mathbf {H}}^{1}(\Omega ). \end{aligned}$$

Proof

See [15, Lemma 3.3]. $\square$

In addition, analogously to the definition of the product norm (3.25), we now set

$$\begin{aligned} \Vert ({\mathbf {q}},\psi )\Vert := \{ \Vert {\mathbf {q}}\Vert ^2_{{\mathrm {div}};\Omega } + \Vert \psi \Vert ^2_{1,\Omega } \}^{1/2} \quad \forall ({\mathbf {q}},\psi ) \in {\mathbf {H}}({\mathrm {div}};\Omega )\times {\mathrm {H}}^{1}(\Omega ) . \end{aligned}$$

The following lemma establishes the well-posedness of problem (3.23), or equivalently, that the operator $\widetilde{{\mathbf {S}}}$ (cf. (3.22)) is well-defined.

Lemma 3.3

Assume that $\kappa _4\in \Big ( 0,\,\dfrac{2\,\kappa _{0}\,\widetilde{\delta }}{\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }}\,\Big )$, with $\widetilde{\delta }\,\in \,\Big (0 ,\,\dfrac{2}{\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }}\,\Big ),$ and $\kappa _{5},\,\kappa _{6}> 0$. Then, there exists $\widetilde{r}_0 > 0$ such that for each $\widetilde{r}\in (0,\widetilde{r}_0)$, problem (3.23) has a unique solution $({\mathbf {p}},\varphi ):=\widetilde{{\mathbf {S}}}({\varvec{w}}) \in {\mathbf {H}}({\mathrm {div}};\Omega )\times {\mathrm {H}}^{1}(\Omega )$ for each ${\varvec{w}}\in {\mathbf {H}}^{1}(\Omega )$ such that $\Vert {\varvec{w}}\Vert _{1,\Omega }\le \widetilde{r}.$ Moreover, there exists a constant $c_{\widetilde{{\mathbf {S}}}}>0$, independent of ${\varvec{w}}$, such that there holds

$$\begin{aligned} \Vert \widetilde{{\mathbf {S}}}({\varvec{w}})\Vert =\Vert ({\mathbf {p}},\varphi )\Vert \le c_{\widetilde{{\mathbf {S}}}}\, \{\Vert \varphi _{D}\Vert _{0,\Gamma }\, +\,\Vert \varphi _{D}\Vert _{1/2,\Gamma }\}. \end{aligned}$$

(3.34)

Proof

For a given ${\varvec{w}}\in {\mathbf {H}}^{1}(\Omega ),$ we observe from (3.15) and (3.16) that $\widetilde{{\mathbf {A}}} +\widetilde{{\mathbf {B}}}_{{\varvec{w}}}$ is clearly a bilinear form. Now, applying the Cauchy–Schwarz inequality, the trace theorem in ${\mathbf {H}}^1(\Omega )$ with constant $c_{0}(\Omega ),$ and the estimate (3.9), we deduce that

$$\begin{aligned}&|\widetilde{{\mathbf {A}}}(({\mathbf {p}},\varphi ),\,({\mathbf {q}},\psi ))|\,\\&\quad \le \, \Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }\,\Vert {\mathbf {p}}\Vert _{0,\Omega }\,\Vert {\mathbf {q}}\Vert _{0,\Omega }+ \,\kappa _{4}\,\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }\,\Vert {\mathbf {p}}\Vert _{0,\Omega }\,|\psi |_{1,\Omega }+\Vert \varphi \Vert _{0,\Omega }\,\Vert {\mathrm {div}}\,{\mathbf {q}}\Vert _{0,\Omega }\\&\quad \quad +\,\kappa _{5}\,\Vert {\mathrm {div}}\,{\mathbf {p}}\Vert _{0,\Omega }\,\Vert {\mathrm {div}}\,{\mathbf {q}}\Vert _{0,\Omega }+\kappa _{4}\,|\varphi |_{1,\Omega }\,|\psi |_{1,\Omega }\, +\,\Vert \psi \Vert _{0,\Omega }\,\Vert {\mathrm {div}}\,{\mathbf {p}}\Vert _{0,\Omega }\\&\quad \quad +\,\kappa _{6}\,c_{0}(\Omega )\,\Vert \varphi \Vert _{0,\Gamma }\,\Vert \psi \Vert _{0,\Gamma } \end{aligned}$$

and

$$\begin{aligned} |\widetilde{{\mathbf {B}}}_{{\varvec{w}}}(({\mathbf {p}},\varphi ),\,({\mathbf {q}},\psi ))|\le (\kappa _{4}^{2}+1)^{1/2}\,\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }\,c_{2}(\Omega )\, \Vert {\varvec{w}}\Vert _{1,\Omega } \,\Vert \varphi \Vert _{1,\Omega }\,\Vert ({\mathbf {q}},\psi )\Vert , \end{aligned}$$

(3.35)

for all $({\mathbf {p}},\varphi ),\,({\mathbf {q}},\psi )\in {\mathbf {H}}({\mathrm {div}};\Omega )\times {\mathrm {H}}^{1}(\Omega )$. Then, by gathering the foregoing inequalities, we find that there exists a positive constant, which we denote by $\Vert \widetilde{{\mathbf {A}}}+\widetilde{{\mathbf {B}}}_{{\varvec{w}}} \Vert ,$ depending on $\kappa _{4},$ $\kappa _{5},$ $\kappa _{6},$ $c_{0}(\Omega ),$ $c_{2}(\Omega ),$ $\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }$ and $\Vert {\varvec{w}}\Vert _{1,\Omega },$ such that

$$\begin{aligned}&|\big (\widetilde{{\mathbf {A}}}+\widetilde{{\mathbf {B}}}_{{\varvec{w}}}\big )(({\mathbf {p}},\varphi ),({\mathbf {q}},\psi ))|\\&\quad \le \Vert \widetilde{{\mathbf {A}}} + \widetilde{{\mathbf {B}}}_{{\varvec{w}}}\Vert \, \Vert ({\mathbf {p}},\varphi ) \Vert \, \Vert ({\mathbf {q}},\psi ) \Vert \quad \forall ({\mathbf {p}},\varphi ), \,({\mathbf {q}},\psi )\in {\mathbf {H}}({\mathrm {div}};\Omega ) \times {\mathrm {H}}^{1}(\Omega ). \end{aligned}$$

In turn, from (3.15) we have that

$$\begin{aligned} \widetilde{{\mathbf {A}}}(({\mathbf {q}},\psi ),\,({\mathbf {q}},\psi ))= & {} \int _{\Omega }{\mathbb {K}}^{-1}\,{\mathbf {q}}\cdot {\mathbf {q}}-\kappa _{4}\int _{\Omega }{\mathbb {K}}^{-1}\,{\mathbf {q}}\cdot \nabla \psi + \kappa _{5}\,\Vert {\mathrm {div}}\,{\mathbf {q}}\Vert ^{2}_{0,\Omega }\\&+\,\kappa _{4}\,|\psi |^{2}_{1,\Omega }+\kappa _{6}\,\Vert \psi \Vert ^{2}_{0,\Gamma }, \end{aligned}$$

and then, using the uniform positiveness of the tensor ${\mathbb {K}}^{-1}$ given by (2.2), and the Cauchy–Schwarz and Young inequalities, we obtain that for all $({\mathbf {q}},\psi )\in {\mathbf {H}}({\mathrm {div}};\Omega )\times {\mathrm {H}}^{1}(\Omega )$ and for any $\widetilde{\delta }> 0,$ there holds

$$\begin{aligned} \widetilde{{\mathbf {A}}}(({\mathbf {q}},\psi ),\,({\mathbf {q}},\psi ))\ge & {} \kappa _{0}\,\Vert {\mathbf {q}}\Vert ^{2}_{0,\Omega }-\,\kappa _{4}\,\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega } \Vert {\mathbf {q}}\Vert ^{2}_{0,\Omega }\,|\psi |_{1,\Omega }+\,\kappa _{5}\,\Vert {\mathrm {div}}\,{\mathbf {q}}\Vert ^{2}_{0,\Omega }\\&+\,\kappa _{4}\,|\psi |^{2}_{1,\Omega }+\,\kappa _{6}\,\Vert \psi \Vert ^{2}_{0,\Gamma }\\\ge & {} \Big ( \kappa _{0} -\dfrac{\kappa _{4}\,\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }}{2\,\widetilde{\delta }}\Big ) \Vert {\mathbf {q}}\Vert ^{2}_{0,\Omega }+\kappa _{5}\,\Vert {\mathrm {div}}\,{\mathbf {q}}\Vert ^{2}_{0,\Omega }\\&+\,\kappa _{4}\,\Big ( 1-\dfrac{\widetilde{\delta }\,\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega } }{2} \Big )\,|\psi |^{2}_{1,\Omega }+\,\kappa _{6}\,\Vert \psi \Vert ^{2}_{0,\Gamma }. \end{aligned}$$

Then, defining the constants

$$\begin{aligned} \displaystyle c_{4}:= & {} \min \left\{ \kappa _{0} -\dfrac{\kappa _{4}\,\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }}{2\,\widetilde{\delta }}\, ,\,\kappa _{5} \right\} ,\quad \text{ and }\quad \\ c_{5}:= & {} \min \left\{ \kappa _{4}\,\left( 1-\dfrac{\widetilde{\delta }\,\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }}{2}\right) ,\kappa _{6} \right\} , \end{aligned}$$

which are positive thanks to the hypotheses on $\widetilde{\delta }$ and $\kappa _{4}$, and applying Lemma 3.2, it follows that

$$\begin{aligned} \widetilde{{\mathbf {A}}}(({\mathbf {q}},\psi ),\,({\mathbf {q}},\psi ))\ge c_{4}\,\Vert {\mathbf {q}}\Vert _{{\mathrm {div}};\Omega }^2 +c_{5}\,\{|\psi |^2_{1,\Omega }+\Vert \psi \Vert ^{2}_{0,\Gamma } \} \ge \widetilde{\alpha }(\Omega )\,\Vert ({\mathbf {q}},\psi )\Vert ^{2},\nonumber \\ \end{aligned}$$

(3.36)

with $\widetilde{\alpha }(\Omega ):=\, \min \{c_{4},\,\,c_{5}\,c_{3}(\Omega ) \}$, which shows that $\widetilde{{\mathbf {A}}}$ is elliptic. In this way, combining now (3.35) and (3.36), we deduce that for all $({\mathbf {q}},\psi )\in {\mathbf {H}}({\mathrm {div}};\Omega )\times {\mathrm {H}}^{1}(\Omega )$, there holds

$$\begin{aligned}&\displaystyle (\widetilde{{\mathbf {A}}}+\widetilde{{\mathbf {B}}}_{{\varvec{w}}})(({\mathbf {q}},\psi ),({\mathbf {q}},\psi ))\nonumber \\&\quad \displaystyle \ge (\widetilde{\alpha }(\Omega ) - (\kappa _{4}^{2}+\,1)^{1/2}\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega } \,c_{2}(\Omega ) \Vert {\varvec{w}}\Vert _{1,\Omega } )\Vert ({\mathbf {q}},\psi )\Vert ^{2}\,\nonumber \\&\quad \ge \dfrac{\widetilde{\alpha }(\Omega )}{2}\, \Vert ({\mathbf {q}},\psi )\Vert ^{2}, \end{aligned}$$

(3.37)

provided $(\kappa _{4}^{2}+\,1)^{1/2}\,\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega } \,c_{2}(\Omega )\,\Vert {\varvec{w}}\Vert _{1,\Omega }\le \dfrac{\widetilde{\alpha }(\Omega )}{2}.$ Therefore, the ellipticity of $\widetilde{{\mathbf {A}}}+\widetilde{{\mathbf {B}}}_{{\varvec{w}}},$ with constant $\dfrac{\widetilde{\alpha }(\Omega )}{2},$ independent of ${\varvec{w}},$ is ensured by requiring $\Vert {\varvec{w}}\Vert _{1,\Omega }\le \widetilde{r}_{0},$ with

$$\begin{aligned} \widetilde{r}_{0}:=\dfrac{\widetilde{\alpha }(\Omega )}{2\,(\kappa _{4}^{2}+1)^{1/2}\,\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }\,c_{2}(\Omega )} . \end{aligned}$$

(3.38)

Next, it is easy to see from (3.19) that the functional $\widetilde{F}_{D}$ is bounded with

$$\begin{aligned} \Vert \widetilde{F}_{D}\,\Vert \le M_{\widetilde{{\mathbf {S}}}}\,\{\Vert \varphi _{D}\Vert _{0,\Gamma }+ \Vert \varphi _{D}\Vert _{1/2,\Gamma }\}, \end{aligned}$$

(3.39)

where $M_{\widetilde{{\mathbf {S}}}}:=\max \big \{\kappa _{6}\,c_{0}(\Omega ),1\big \}$ and $c_0(\Omega )$ is the norm of the trace operator in ${\mathrm {H}}^{1}(\Omega )$. Summing up, and owing to the hypotheses on $\kappa _4$, $\kappa _5$ and $\kappa _6$, we have proved that for any sufficiently small ${\varvec{w}}\in {\mathbf {H}}^1(\Omega )$, the bilinear form $\widetilde{{\mathbf {A}}}+\widetilde{{\mathbf {B}}}_{{\varvec{w}}}$ and the functional $\widetilde{F}_D$ satisfy the hypotheses of the Lax–Milgram theorem (see e.g. [16, Theorem 1.1]), which guarantees the well-posedness of (3.23) and the continuous dependence estimate (3.34) with $c_{\widetilde{{\mathbf {S}}}}:=\dfrac{2\,M_{\widetilde{{\mathbf {S}}}}}{\widetilde{\alpha }(\Omega )}$. $\square$

As a consequence of Lemmas 3.1 and 3.3 we can show now that ${\mathbf {T}}$ is also well-posed.

Lemma 3.4

Let $\kappa _{1}\in ( 0,\,2\,\delta )$, with $\delta \,\in \,(0 ,\,2\,\mu )$, $\kappa _4\in \Bigg ( 0,\,\dfrac{2\,\kappa _{0}\,\widetilde{\delta }}{\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }}\,\Bigg )$, with $\widetilde{\delta }\,\in \,\Bigg (0 ,\,\dfrac{2}{\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }}\,\Bigg ),$ and $\kappa _{2},\,\kappa _{3},\,\kappa _{5},\,\kappa _{6}> 0$. Assume that, given $r\in (0,r_0)$, the data ${\varvec{g}}$ and ${\varvec{u}}_{D}$ satisfy

$$\begin{aligned} c_{{\mathbf {S}}}\,\{r\,\Vert {\varvec{g}}\Vert _{\infty ,\Omega }+\Vert {\varvec{u}}_{D}\Vert _{0,\Gamma } +\Vert {\varvec{u}}_{D}\Vert _{1/2,\Gamma }\} < \widetilde{r}_0 , \end{aligned}$$

(3.40)

with $c_{{\mathbf {S}}}$ defined in (3.33). Then, ${\mathbf {T}}({\varvec{w}},\phi )$ is well defined for each $({\varvec{w}},\phi ) \in {\mathbf {H}}$ such that $\Vert ({\varvec{w}},\phi )\Vert \le r$. Moreover, in that case there holds

$$\begin{aligned} \Vert {\mathbf {T}}({\varvec{w}},\phi )\Vert \le c_{{\mathbf {S}}}\,\{r\,\Vert {\varvec{g}}\Vert _{\infty ,\Omega }+\Vert {\varvec{u}}_{D}\Vert _{0,\Gamma } +\Vert {\varvec{u}}_{D}\Vert _{1/2,\Gamma }\} + c_{\widetilde{{\mathbf {S}}}}\,\{\Vert \varphi _{D}\Vert _{0,\Gamma }+\Vert \varphi _{D}\Vert _{1/2,\Gamma }\}. \end{aligned}$$

(3.41)

Proof

We first observe, in virtue of Lemma 3.1, that given $({\varvec{w}},\phi ) \in {\mathbf {H}}$ such that $\Vert ({\varvec{w}},\phi )\Vert \le r$, $\,{\mathbf {S}}_2({\varvec{w}},\phi )$ is well-defined and its norm is bounded by the left hand side of (3.40). It follows, according to Lemma 3.3, that $\widetilde{{\mathbf {S}}}_2({\mathbf {S}}({\varvec{w}},\phi ))$ is also well-defined and its norm is bounded by the expression $c_{\widetilde{{\mathbf {S}}}}\,\{\Vert \varphi _{D}\Vert _{0,\Gamma }+\Vert \varphi _{D}\Vert _{1/2,\Gamma }\}$. In this way, ${\mathbf {T}}({\varvec{w}},\phi )$ is well-defined and (3.41) is obtained thanks to (3.24) and the aforementioned bounds. $\square$

3.4 Solvability analysis of the fixed-point equation

In this section we address the existence and uniqueness of a fixed-point of ${\mathbf {T}}$ (cf. (3.24)) by means of the classical Banach fixed-point theorem. We begin by establishing suitable conditions under which ${\mathbf {T}}$ maps a ball into itself.

Lemma 3.5

Assume that the stabilization parameters satisfy the hypotheses of Lemma 3.4. In addition, given $r\in (0,\min \{r_{0},\widetilde{r}_0\})$, let ${\mathbf {W}}_r:=\{ ({\varvec{w}},\phi )\in {\mathbf {H}}:\Vert ({\varvec{w}},\phi )\Vert \le r \,\}$, and assume that the data satisfy

$$\begin{aligned} c_{{\mathbf {S}}}\,\{r\,\Vert {\varvec{g}}\Vert _{\infty ,\Omega }+\Vert {\varvec{u}}_{D}\Vert _{0,\Gamma } +\Vert {\varvec{u}}_{D}\Vert _{1/2,\Gamma }\} + c_{\widetilde{{\mathbf {S}}}}\, \{\Vert \varphi _{D}\Vert _{0,\Gamma }+\Vert \varphi _{D}\Vert _{1/2,\Gamma }\} \le r\qquad \end{aligned}$$

(3.42)

where $c_{{\mathbf {S}}}$ and $c_{\widetilde{{\mathbf {S}}}}$ are the positive constants in (3.33) and (3.34), respectively. Then ${\mathbf {T}}({\mathbf {W}}_r)\subseteq {\mathbf {W}}_r$.

Proof

Given $r\in (0,\min \{r_{0},\widetilde{r}_0\})$, it is clear from (3.42) that (3.40) is satisfied, and hence ${\mathbf {T}}({\varvec{w}},\phi )$ is well defined for each $({\varvec{w}},\phi ) \in {\mathbf {W}}_r$. In addition, the same hypothesis (3.42) and the upper bound (3.41) guarantee that ${\mathbf {T}}({\varvec{w}},\phi ) \in {\mathbf {W}}_r$, which ends the proof. $\square$

Let us now recall that the Banach fixed-point theorem requires the operator ${\mathbf {T}}$ to be a contractive mapping, which, as we will see later on, is indeed true under suitable assumptions on the data ${\varvec{u}}_D$, ${\varvec{g}}$, and $\varphi _D$. To this end, we first need to show that the operator ${\mathbf {T}}$ is Lipschitz continuous, for which, according to (3.24), it suffices to show that both ${\mathbf {S}}$ and $\widetilde{{\mathbf {S}}}$ satisfy this property. We begin next with the corresponding result for ${\mathbf {S}}$. We omit details on its proof and refer to [10, Lemma 3.6].

Lemma 3.6

Let $r\in (0,r_0)$, with $r_0$ given by (3.30). Then there exists a positive constant $C_{{\mathbf {S}}},$ depending on the viscosity $\mu ,$ the stabilization parameters $\kappa _{1}$ and $\kappa _{2},$ the constant $c_{1}(\Omega )$ (cf. (3.8)), and the ellipticity constant $\alpha (\Omega )$ of the bilinear form ${\mathbf {A}}$ (cf. (3.29)), such that

$$\begin{aligned} \Vert {\mathbf {S}}({\varvec{w}},\phi )-{\mathbf {S}}(\widetilde{{\varvec{w}}},\widetilde{\phi })\Vert \le C_{{\mathbf {S}}}\,\{\Vert {\varvec{g}}\Vert _{\infty ,\Omega }\,\Vert \phi -\widetilde{\phi }\Vert _{0,\Omega }+ \Vert {\mathbf {S}}_{2}({\varvec{w}},\phi )\Vert _{1,\Omega }\,\Vert {\varvec{w}}-\widetilde{{\varvec{w}}}\Vert _{1,\Omega }\,\}, \end{aligned}$$

(3.43)

for all $({\varvec{w}},\phi ),(\widetilde{{\varvec{w}}},\widetilde{\phi })\in {\mathbf {H}}$ such that $\Vert {\varvec{w}}\Vert _{1,\Omega },\,\Vert \widetilde{{\varvec{w}}}\Vert _{1,\Omega }\le r$.

In turn, the result for the operator $\widetilde{{\mathbf {S}}}$ is established as follows.

Lemma 3.7

Let $r\in (0,\widetilde{r}_0)$, with $\widetilde{r}_0$ given by (3.38). Then there exists a positive constant $C_{\widetilde{{\mathbf {S}}}}$ depending on $\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega },$ the parameter $\kappa _{4},$ the ellipticity constant $\widetilde{\alpha }(\Omega )\,$ of the bilinear form $\widetilde{{\mathbf {A}}}$ (cf. (3.36)), and the constant $c_{2}(\Omega )$ (cf. (3.9)), such that

$$\begin{aligned} \Vert \widetilde{{\mathbf {S}}}({\varvec{w}})-\widetilde{{\mathbf {S}}}(\widetilde{{\varvec{w}}})\Vert \le C_{\widetilde{{\mathbf {S}}}}\, \Vert \widetilde{{\mathbf {S}} }_{2}({\varvec{w}})\Vert _{1,\Omega }\,\Vert {\varvec{w}}-\widetilde{{\varvec{w}}}\Vert _{1,\Omega } \end{aligned}$$

(3.44)

for all ${\varvec{w}},\widetilde{{\varvec{w}}}\in {\mathbf {H}}^{1}(\Omega )$ such that $\Vert {\varvec{w}}\Vert _{1,\Omega },\,\Vert \widetilde{{\varvec{w}}}\Vert _{1,\Omega }\le r.$

Proof

Given $r\in \big (0,\widetilde{r}_0\big )$ and ${\varvec{w}},\,\widetilde{{\varvec{w}}}\in {\mathbf {H}}^{1}(\Omega )\,$, such that $\Vert {\varvec{w}}\Vert _{1,\Omega },\,\Vert \widetilde{{\varvec{w}}}\Vert _{1,\Omega }\le r$, we let $({\mathbf {p}},\varphi ), \,\,(\widetilde{{\mathbf {p}}},\widetilde{\varphi })\in {\mathbf {H}}({\mathrm {div}};\Omega )\,\times {\mathrm {H}}^{1}(\Omega )$, such that $({\mathbf {p}},\varphi ):=\widetilde{{\mathbf {S}}}({\varvec{w}})$ and $(\widetilde{{\mathbf {p}}},\widetilde{\varphi }):=\widetilde{{\mathbf {S}}}(\widetilde{{\varvec{w}}})$. From the definition of $\widetilde{{\mathbf {S}}}$ (cf. (3.22) and (3.23)) and the bilinearity of $\widetilde{{\mathbf {A}}}$, it readily follows that

$$\begin{aligned} \widetilde{ {\mathbf {A}}}(({\mathbf {p}},\varphi )-(\widetilde{{\mathbf {p}}},\widetilde{\varphi }),\,({\mathbf {q}},\psi ) ) +\widetilde{{\mathbf {B}}}_{{\varvec{w}}}(({\mathbf {p}},\varphi ),\,({\mathbf {q}},\psi )) -\widetilde{{\mathbf {B}}}_{\widetilde{{\varvec{w}}}}((\widetilde{{\mathbf {p}}},\widetilde{\varphi }),\,({\mathbf {q}},\psi ))=0, \end{aligned}$$

for all $({\mathbf {q}},\psi )\in {\mathbf {H}}({\mathrm {div}};\Omega )\times {\mathrm {H}}^{1}(\Omega )$. Then, taking $({\mathbf {q}},\psi )=({\mathbf {p}},\varphi )-(\widetilde{{\mathbf {p}}},\widetilde{\varphi })$ in the previous identity, utilizing the bilinearity of $\widetilde{{\mathbf {B}}}_{{\varvec{w}}}$, and adding and subtracting suitable terms, we arrive at

$$\begin{aligned} (\widetilde{{\mathbf {A}}}+\widetilde{{\mathbf {B}}}_{\widetilde{{\varvec{w}}}}\,)\,(({\mathbf {p}},\varphi )-(\widetilde{{\mathbf {p}}},\widetilde{\varphi }),({\mathbf {p}},\varphi )-(\widetilde{{\mathbf {p}}},\widetilde{\varphi })) =-\,\widetilde{{\mathbf {B}}}_{{\varvec{w}}-\widetilde{{\varvec{w}}}}(({\mathbf {p}},\varphi ),({\mathbf {p}},\varphi )-(\widetilde{{\mathbf {p}}},\widetilde{\varphi })). \end{aligned}$$

In this way, we proceed as in the proof of [10, Lemma 3.6], and use the ellipticity property of the bilinear form $\widetilde{{\mathbf {A}}}+\widetilde{{\mathbf {B}}}_{\widetilde{{\varvec{w}}}}$ (cf. (3.37)), and the continuity of $\widetilde{{\mathbf {B}}}_{\varvec{w}}$ (cf. (3.35)), to obtain

$$\begin{aligned}&\displaystyle \dfrac{\widetilde{\alpha }(\Omega )}{2} \, \Vert ({\mathbf {p}},\varphi )-(\widetilde{{\mathbf {p}}},\widetilde{\varphi })\Vert ^{2}\le - \widetilde{{\mathbf {B}}}_{{\varvec{w}}-\widetilde{{\varvec{w}}}}(({\mathbf {p}},\varphi ),\,({\mathbf {p}},\varphi )-(\widetilde{{\mathbf {p}}},\widetilde{\varphi }))\,\\&\displaystyle \quad \le (\kappa _{4}^{2}+1)^{1/2}\,\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }\,c_{2}(\Omega )\,\Vert \varphi \Vert _{1,\Omega }\,\Vert {\varvec{w}}-\widetilde{{\varvec{w}}}\Vert _{1,\Omega }\,\Vert ({\mathbf {p}},\varphi )-(\widetilde{{\mathbf {p}}},\widetilde{\varphi })\Vert , \end{aligned}$$

which, denoting $C_{\widetilde{{\mathbf {S}}}}:= \dfrac{2}{\widetilde{\alpha }(\Omega )}\,(\kappa _{4}^{2}+1)^{1/2}\,\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }\,c_{2}(\Omega ),$ and recalling that $\varphi = \widetilde{{\mathbf {S}}}_{2}({\varvec{w}}),$ yields (3.44) and completes the proof. $\square$

As a consequence of Lemmas 3.6 and 3.7 we establish next the Lipschitz-continuity of ${\mathbf {T}}$.

Lemma 3.8

Given $r \in (0,\min \{r_{0},\widetilde{r}_{0}\})$, with $r_{0}$ and $\widetilde{r}_{0}$ given by (3.30) and (3.38), respectively, let ${\mathbf {W}}_r:=\{ ({\varvec{w}},\phi )\in {\mathbf {H}}\,:\quad \Vert ({\varvec{w}},\phi )\Vert \le r \,\}$, and assume that the data ${\varvec{g}},$ ${\varvec{u}}_{D},$ and $\varphi _{D}$ satisfy (3.42).

Then, there holds

$$\begin{aligned}&\displaystyle \Vert {\mathbf {T}}({\varvec{w}},\phi )-{\mathbf {T}}(\widetilde{{\varvec{w}}},\widetilde{\phi })\Vert \nonumber \\&\displaystyle \quad \le \, C_{{\mathbf {T}}}\, (\Vert {\varvec{g}}\Vert _{\infty ,\Omega } + c_{{\mathbf {S}}}\,\{r\,\Vert {\varvec{g}}\Vert _{\infty ,\Omega }+\Vert {\varvec{u}}_{D}\Vert _{0,\Gamma } +\Vert {\varvec{u}}_{D}\Vert _{1/2,\Gamma }\} )\,\Vert ({\varvec{w}},\phi )-(\widetilde{{\varvec{w}}},\widetilde{\phi })\Vert ,\nonumber \\ \end{aligned}$$

(3.45)

for all $({\varvec{w}},\phi ),(\widetilde{{\varvec{w}}},\widetilde{\phi })\in {\mathbf {W}}_r$, where $C_{{\mathbf {T}}} := C_{{\mathbf {S}}}\,\{1+r\,C_{\widetilde{{\mathbf {S}}}}\}$, and the constants $C_{{\mathbf {S}}}$ and $C_{\widetilde{{\mathbf {S}}}}$ are given by (3.43) and (3.44), respectively.

Proof

Firstly, we realize from Lemmas 3.4 and 3.5 that the stipulated assumptions on r and the data ${\varvec{g}},$ ${\varvec{u}}_{D},$ and $\varphi _{D},$ guarantee that ${\mathbf {T}}$ is well defined in ${\mathbf {W}}_r$ and that ${\mathbf {T}}({\mathbf {W}}_r)\subseteq {\mathbf {W}}_r$. Now, let $({\varvec{u}},\varphi ),\, (\widetilde{{\varvec{u}}},\widetilde{\varphi }),\, ({\varvec{w}},\phi ), \,(\widetilde{{\varvec{w}}}, \,\widetilde{\phi })\in {\mathbf {W}}_r$, such that $({\varvec{u}},\varphi )={\mathbf {T}}({\varvec{w}},\phi )$ and $(\widetilde{{\varvec{u}}},\widetilde{\varphi })={\mathbf {T}}(\widetilde{{\varvec{w}}},\widetilde{\phi })$, that is

$$\begin{aligned} {\varvec{u}}={\mathbf {S}}_{2}({\varvec{w}},\phi ),\quad \widetilde{{\varvec{u}}}={\mathbf {S}}_{2}(\widetilde{{\varvec{w}}},\widetilde{\phi }),\quad \varphi =\widetilde{{\mathbf {S}}}_{2}({\varvec{u}})\,{\quad \hbox {and}\quad }\widetilde{\varphi }=\widetilde{{\mathbf {S}}}_{2}(\widetilde{{\varvec{u}}}). \end{aligned}$$

It follows, thanks to the Lipschitz continuity of $\widetilde{{\mathbf {S}}}$ (cf. (3.44)) and the a priori estimate (3.34), that

$$\begin{aligned} \Vert \varphi -\widetilde{\varphi }\Vert _{1,\Omega }\le \Vert \widetilde{{\mathbf {S}}}({\varvec{u}})-\widetilde{{\mathbf {S}}}(\widetilde{{\varvec{u}}})\Vert \,\le & {} \, C_{\widetilde{{\mathbf {S}}}}\, \Vert \widetilde{{\mathbf {S}} }_{2}({\varvec{u}})\Vert _{1,\Omega }\,\Vert {\varvec{u}}-\widetilde{{\varvec{u}}}\Vert _{1,\Omega }\\\le & {} \,C_{\widetilde{{\mathbf {S}}}}\,c_{\widetilde{{\mathbf {S}}}}\, \Big \{ \Vert \varphi _{D}\Vert _{0,\Gamma } +\Vert \varphi _{D}\Vert _{1/2,\Gamma }\Big \}\,\Vert {\varvec{u}}-\widetilde{{\varvec{u}}}\Vert _{1,\Omega }, \end{aligned}$$

which, using from (3.42) that $c_{\widetilde{{\mathbf {S}}}}\, \{ \Vert \varphi _{D}\Vert _{0,\Gamma } +\Vert \varphi _{D}\Vert _{1/2,\Gamma }\} \le r$, yields

$$\begin{aligned} \Vert {\mathbf {T}}({\varvec{w}},\phi )-{\mathbf {T}}(\widetilde{{\varvec{w}}},\widetilde{\phi })\Vert \le \Vert {\varvec{u}}-\widetilde{{\varvec{u}}}\Vert _{1,\Omega }+\Vert \varphi -\widetilde{\varphi }\Vert _{1,\Omega } \le \{1+r\,C_{\widetilde{{\mathbf {S}}}}\}\, \Vert {\varvec{u}}-\widetilde{{\varvec{u}}}\Vert _{1,\Omega }. \end{aligned}$$

Then, combining the foregoing inequality with the fact that

$$\begin{aligned} \Vert {\varvec{u}}-\widetilde{{\varvec{u}}}\Vert _{1,\Omega }=\Vert {\mathbf {S}}_{2}({\varvec{w}},\phi )-{\mathbf {S}}_{2}(\widetilde{{\varvec{w}}}, \widetilde{\phi })\Vert _{1,\Omega }\le \Vert {\mathbf {S}}({\varvec{w}},\phi )-{\mathbf {S}}(\widetilde{{\varvec{w}}},\widetilde{\phi })\Vert , \end{aligned}$$

and then employing the Lipschitz continuity of ${\mathbf {S}}$ (cf. (3.43)) and the estimate (3.33), we deduce that

$$\begin{aligned}&\Vert {\mathbf {T}}({\varvec{w}},\phi )-{\mathbf {T}}(\widetilde{{\varvec{w}}},\widetilde{\phi })\Vert \,\\&\quad \le C_{{\mathbf {S}}}\,\{1+r\,C_{\widetilde{{\mathbf {S}}}}\}\, \{\Vert {\varvec{g}}\Vert _{\infty ,\Omega } +\Vert {\mathbf {S}}_{2}({\varvec{w}},\phi )\Vert _{1,\Omega }\,\}\, \Vert ({\varvec{w}},\phi )-(\widetilde{{\varvec{w}}},\widetilde{\phi })\Vert ,\\&\quad \le C_{{\mathbf {S}}}\,\{1+r\,C_{\widetilde{{\mathbf {S}}}}\}\\&\quad \quad \times (\Vert {\varvec{g}}\Vert _{\infty ,\Omega } + c_{{\mathbf {S}}}\,\{r\,\Vert {\varvec{g}}\Vert _{\infty ,\Omega }+\Vert {\varvec{u}}_{D}\Vert _{0,\Gamma } +\Vert {\varvec{u}}_{D}\Vert _{1/2,\Gamma }\})\,\Vert ({\varvec{w}},\phi )-(\widetilde{{\varvec{w}}},\widetilde{\phi })\Vert , \end{aligned}$$

which completes the proof. $\square$

We now observe from (3.45) that ${\mathbf {T}}$ becomes a contraction mapping if we assume additionally that

$$\begin{aligned} C_{{\mathbf {T}}}\, (\Vert {\varvec{g}}\Vert _{\infty ,\Omega } + c_{{\mathbf {S}}}\,\{r\,\Vert {\varvec{g}}\Vert _{\infty ,\Omega }+\Vert {\varvec{u}}_{D}\Vert _{0,\Gamma } +\Vert {\varvec{u}}_{D}\Vert _{1/2,\Gamma }\} ) < 1. \end{aligned}$$

(3.46)

We remark here that, while the derivation of (3.45) makes use of the fact that the second term on the left hand side of (3.42) is bounded by r, we do not apply the same upper bound to the first term in (3.42) since in that case the resulting inequality (3.46) would impose a further and unnecessary restriction on r. In other words, the idea of employing (3.42) only to bound the second term there is in order to obtain a linear combination of the data being bounded as the new restriction insuring that ${\mathbf {T}}$ is a contraction. Then, as suggested by (3.46), the existence and uniqueness of a fixed-point of ${\mathbf {T}}$, which corresponds to the unique solution of problem (3.12), follows from a straightforward application of the corresponding Banach theorem. More precisely, we have proved the following result.

Theorem 3.9

Let $\kappa _{1}\in ( 0,\,2\,\delta )$, with $\delta \,\in \,(0 ,\,2\,\mu )$, $\kappa _4\in \Bigg ( 0,\,\dfrac{2\,\kappa _{0}\,\widetilde{\delta }}{\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }}\,\Bigg )$, with $\widetilde{\delta } \in \Bigg (0 ,\dfrac{2}{\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }}\,\Bigg ),$ and $\kappa _{2},\,\kappa _{3},\,\kappa _{5},\,\kappa _{6}> 0$. Given $r \in (0,\min \{r_{0},\widetilde{r}_{0}\})$, with $r_{0}$ and $\widetilde{r}_{0}$ given by (3.30) and (3.38), respectively, let ${\mathbf {W}}_r:=\{ ({\varvec{w}},\phi )\in {\mathbf {H}}:\Vert ({\varvec{w}},\phi )\Vert \le r \,\}$, and assume that the data ${\varvec{g}},$ ${\varvec{u}}_{D},$ and $\varphi _{D}$ satisfy (3.42) and (3.46). Then, there exists a unique $({\varvec{\sigma }},{\varvec{u}},{\mathbf {p}},\varphi ) \in {\mathbb {H}}_{0}({\mathbf {div}};\Omega ) \times {\mathbf {H}}^{1}(\Omega ) \times {\mathbf {H}}({\mathrm {div}};\Omega ) \times {\mathrm {H}}^{1}(\Omega )$ solution to (3.12), with $({\varvec{u}},\varphi )\in {\mathbf {W}}_r\,$. Moreover, there holds

$$\begin{aligned} \Vert ({\varvec{\sigma }},{\varvec{u}})\Vert \le c_{{\mathbf {S}}}\, \{r\, \Vert {\varvec{g}}\Vert _{\infty ,\Omega }\, +\Vert {\varvec{u}}_{D}\Vert _{0,\Gamma }+\Vert {\varvec{u}}_{D}\Vert _{1/2,\Gamma }\}, \end{aligned}$$

(3.47)

and

$$\begin{aligned} \Vert ({\mathbf {p}},\varphi )\Vert \le c_{\widetilde{{\mathbf {S}}}}\, \{\Vert \varphi _{D}\Vert _{0,\Gamma }+\Vert \varphi _{D}\Vert _{1/2,\Gamma }\}. \end{aligned}$$

(3.48)

Proof

It suffices to apply the Banach fixed-point Theorem and then employ the a priori estimates (3.33) and (3.34). We omit further details. $\square$

4 The Galerkin scheme

In this section, we introduce and analyze the Galerkin scheme of the augmented fully-mixed formulation (3.12). As we will see in the forthcoming sections, the analysis of the corresponding discrete problem follows straightforwardly by adapting the fixed-point strategy introduced and analyzed in Sects. 3.2 and 3.3.

4.1 Preliminaries

We start by considering the generic finite dimensional subspaces

$$\begin{aligned} {\mathbb {H}}_{h}^{{\varvec{\sigma }}} \, \subseteq \,{\mathbb {H}}_{0}({\mathbf {div}};\Omega ), \quad {\mathbf {H}}_{h}^{{\varvec{u}}}\, \subseteq \, {\mathbf {H}}^{1}(\Omega ), \quad {\mathbf {H}}_{h}^{{\mathbf {p}}}\, \subseteq \, {\mathbf {H}}({\mathrm {div}};\Omega ),\quad \text{ and }\quad {\mathrm {H}}_{h}^{\varphi }\, \subseteq \, {\mathrm {H}}^{1}(\Omega ), \end{aligned}$$

(4.1)

which shall be specified later in Sect. 4.3. Hereafter, h stands for the size of a regular triangulation ${\mathcal {T}}_{h}$ of $\overline{\Omega }$ made up of triangles K (when $d=2$) or tetrahedra K (when $d=3$) of diameter $h_{K} ,$ defined as $h\,:=\max \,\{h_{K}:K\in {\mathcal {T}}_{h} \}.$ In this way, the Galerkin scheme of (3.12) reads: find $({\varvec{\sigma }}_{h},\,{\varvec{u}}_{h},\,{\mathbf {p}}_{h},\,\varphi _{h})\in {\mathbb {H}}^{{\varvec{\sigma }}}_{h}\times {\mathbf {H}}^{{\varvec{u}}}_{h}\times {\mathbf {H}}^{{\mathbf {p}}}_{h}\times {\mathrm {H}}^{\varphi }_{h}$ such that

$$\begin{aligned} {\mathbf {A}}(({\varvec{\sigma }}_{h},{\varvec{u}}_{h}),\,({\varvec{\tau }}_{h},{\varvec{v}}_{h}) )+{\mathbf {B}}_{{\varvec{u}}_{h}}(({\varvec{\sigma }}_{h},{\varvec{u}}_{h}),\,({\varvec{\tau }}_{h},{\varvec{v}}_{h}))= & {} F_{\varphi _{h}}(({\varvec{\tau }}_{h},{\varvec{v}}_{h})) +F_{D}(({\varvec{\tau }}_{h},{\varvec{v}}_{h}))\,\nonumber \\ \widetilde{ {\mathbf {A}}}(({\mathbf {p}}_{h},\varphi _{h}),\,({\mathbf {q}}_{h},\psi _{h}) )+\widetilde{{\mathbf {B}}}_{{\varvec{u}}_{h}}(({\mathbf {p}}_{h},\varphi _{h}),\,({\mathbf {q}}_{h},\psi _{h}))= & {} \,\widetilde{F}_{D}(({\mathbf {q}}_{h},\psi _{h})), \end{aligned}$$

(4.2)

for all $({\varvec{\tau }}_{h},\,{\varvec{v}}_{h},\,{\mathbf {q}}_{h},\,\psi _{h})\in {\mathbb {H}}^{{\varvec{\sigma }}}_{h}\times {\mathbf {H}}^{{\varvec{u}}}_{h}\times {\mathbf {H}}^{{\mathbf {p}}}_{h}\times {\mathrm {H}}^{\varphi }_{h}$.

Similarly to the continuous context, in order to analyze problem (4.2) we rewrite it equivalently as a fixed-point problem. Indeed, we firstly let ${\mathbf {H}}_{h}:={\mathbf {H}}^{{\varvec{u}}}_{h}\times {\mathrm {H}} ^{\varphi }_{h}$ and define ${\mathbf {S}}_{h}:{\mathbf {H}}_{h}\,\longrightarrow \,{\mathbb {H}}^{{\varvec{\sigma }}}_{h}\times {\mathbf {H}}^{{\varvec{u}}}_{h}$ by

$$\begin{aligned} {\mathbf {S}}_{h}({\varvec{w}}_{h},\phi _{h}):=({\mathbf {S}}_{1,h}({\varvec{w}}_{h},\phi _{h}),{\mathbf {S}}_{2,h}({\varvec{w}}_{h},\phi _{h})) =({\varvec{\sigma }}_{h},{\varvec{u}}_{h})\quad \forall ({\varvec{w}}_{h},\phi _{h})\,\in {\mathbf {H}}_{h},\qquad \end{aligned}$$

(4.3)

where $({\varvec{\sigma }}_{h},{\varvec{u}}_{h})$ is the unique solution of the discrete version of problem (3.21): find $({\varvec{\sigma }}_{h},\,{\varvec{u}}_{h})\in {\mathbb {H}}^{{\varvec{\sigma }}}_{h}\times {\mathbf {H}}^{{\varvec{u}}}_{h}$, such that

$$\begin{aligned}&{\mathbf {A}}(({\varvec{\sigma }}_{h},{\varvec{u}}_{h}),({\varvec{\tau }}_{h},{\varvec{v}}_{h}))+ {\mathbf {B}}_{{\varvec{w}}_{h}}(({\varvec{\sigma }}_{h},{\varvec{u}}_{h}),({\varvec{\tau }}_{h},{\varvec{v}}_{h})) \,\nonumber \\&\quad =(F_{\phi _{h}}+F_{D})({\varvec{\tau }}_{h},{\varvec{v}}_{h}) \quad \forall ({\varvec{\tau }}_{h},{\varvec{v}}_{h})\in {\mathbb {H}}^{{\varvec{\sigma }}}_{h}\times {\mathbf {H}}^{{\varvec{u}}}_{h}, \end{aligned}$$

(4.4)

where the form ${\mathbf {A}}$ and the functional $F_{D}$ are defined as in (3.13) and (3.18), respectively. In turn, with ${\varvec{w}}_{h}$ and $\phi _{h}$ given, the bilinear form ${\mathbf {B}}_{{\varvec{w}}_{h}}$ and the linear functional $F_{\phi _{h}}$ are the ones defined in (3.14) and (3.17) with ${\varvec{w}}_{h}$ and $\phi _{h}$ in place of ${\varvec{w}}$ and $\varphi$, respectively. Secondly, we define the operator $\widetilde{{\mathbf {S}}}_{h}:{\mathbf {H}}_{h}^{{\varvec{u}}}\,\longrightarrow \, {\mathbf {H}}_{h}^{{\mathbf {p}}}\times {\mathrm {H}}^{\varphi }_{h}$ as

$$\begin{aligned} \widetilde{{\mathbf {S}}}_{h}({\varvec{w}}_{h}):=(\widetilde{{\mathbf {S}}}_{1,h}({\varvec{w}}_{h}),\,\widetilde{{\mathbf {S}}}_{2,h}({\varvec{w}}_{h}))=({\mathbf {p}}_{h},\varphi _{h})\quad \forall {\varvec{w}}_{h}\in {\mathbf {H}}_{h}^{{\varvec{u}}}, \end{aligned}$$

(4.5)

where $({\mathbf {p}}_{h},\varphi _{h})$ is the unique element in ${\mathbf {H}}^{{\mathbf {p}}}_{h}\times {\mathrm {H}}^{\varphi }_{h}$ satisfying the discrete version of (3.23), namely

$$\begin{aligned} \widetilde{ {\mathbf {A}}}(({\mathbf {p}}_{h},\varphi _{h}),({\mathbf {q}}_{h},\psi _{h}))+ \widetilde{{\mathbf {B}}}_{{\varvec{w}}_{h}}(({\mathbf {p}}_{h},\varphi _{h}),({\mathbf {q}}_{h},\psi _{h}))= \widetilde{F}_{D}({\mathbf {q}}_{h},\psi _{h})\,\,\, \forall ({\mathbf {q}}_{h},\psi _{h}){\in } {\mathbf {H}}^{{\mathbf {p}}}_{h}\times {\mathrm {H}}^{\varphi }_{h}, \end{aligned}$$

(4.6)

where the bilinear form $\widetilde{{\mathbf {A}}}$ and the functional $\widetilde{F}_{D}$ are defined as in (3.15) and (3.19), respectively, whereas $\widetilde{{\mathbf {B}}}_{{\varvec{w}}_{h}}$ is the bilinear form given by (3.16) with ${\varvec{w}}_{h}$ instead of ${\varvec{w}}$. Finally, introducing the operator ${\mathbf {T}}_{h} : {\mathbf {H}}_{h}\,\longrightarrow \,{\mathbf {H}}_{h}$ given by

$$\begin{aligned} {\mathbf {T}}_{h}({\varvec{w}}_{h},\phi _{h}):=({\mathbf {S}}_{2,h}({\varvec{w}},\phi ),\widetilde{{\mathbf {S}}}_{2,h}({\mathbf {S}}_{2,h}({\varvec{w}}_{h},\phi _{h}))) \quad \forall ({\varvec{w}}_{h},\phi _{h}) \in {\mathbf {H}}_{h} , \end{aligned}$$

(4.7)

we realize that solving (4.2) is equivalent to seeking a fixed-point of the operator ${\mathbf {T}}_{h}$, that is: Find $({\varvec{u}}_{h},\varphi _{h}) \in {\mathbf {H}}_h$ such that

$$\begin{aligned} {\mathbf {T}}_{h}({\varvec{u}}_{h},\varphi _{h})= ({\varvec{u}}_{h},\varphi _{h}). \end{aligned}$$

(4.8)

4.2 Solvability analysis

Now we establish the well-posedness of problem (4.2) by studying the equivalent fixed-point problem (4.8). Before proceeding with the analysis we observe that, since in this case the operator ${\mathbf {T}}_h$ is defined on a finite dimensional space, the existence of solution can be addressed by using the well-known Brouwer fixed-point Theorem (see e.g. [9, Theorem 9.9-2]) in the following form: let W be a compact and convex subset of a finite dimensional Banach space X and let $T:W\,\longrightarrow \,W$ be a continuous mapping. Then, T has at least one fixed-point in W. As a consequence, the existence of solution can be attained with less restrictions, namely without requiring assumption (3.46). This condition will be required only to achieve uniqueness of solution by means of the Banach fixed-point theorem.

Analogously to the continuous case, we firstly study the well-definiteness of operator ${\mathbf {T}}_h$ by establishing first the well-posedness of the two discrete uncoupled problems (4.4) and (4.6). This is addressed in the following three lemmas. Their proofs follow straightforwardly by applying the same arguments utilized in Lemmas 3.1, 3.3 and 3.4, respectively, reason why most of the details are omitted.

Lemma 4.1

Assume that $\kappa _{1}\in ( 0,\,2\,\delta )$ with $\delta \,\in \,(0 ,\,2\,\mu ),$ and $\kappa _{2},\,\kappa _{3}> 0$. Then, for each $r\in (0,r_0),$ with $r_{0}$ given by (3.30), and for each $({\varvec{w}}_{h},\phi _{h})\in {\mathbf {H}}_{h}$, such that $\Vert {\varvec{w}}_{h}\Vert _{1,\Omega }\le r$, the problem (4.4) has a unique solution $({\varvec{\sigma }}_{h},{\varvec{u}}_{h})\,=:\,{\mathbf {S}}_{h}({\varvec{w}}_{h},\phi _{h}) \in {\mathbb {H}}_{h}^{{\varvec{\sigma }}}\times {\mathbf {H}}_{h}^{{\varvec{u}}}$. Moreover, with the same constant $c_{{\mathbf {S}}}>0$ from Lemma 3.3, which is independent of $({\varvec{w}}_{h},\phi _{h})$, there holds

$$\begin{aligned} \Vert {\mathbf {S}}_{h}({\varvec{w}}_{h},\phi _{h})\Vert = \Vert ({\varvec{\sigma }}_{h},{\varvec{u}}_{h})\Vert \le c_{{\mathbf {S}}}\, \{\Vert {\varvec{g}}\Vert _{\infty ,\Omega }\, \Vert \phi _{h}\Vert _{0,\Omega }+\Vert {\varvec{u}}_{D}\Vert _{0,\Gamma }+\Vert {\varvec{u}}_{D}\Vert _{1/2,\Gamma }\}. \end{aligned}$$

Proof

It is a straightforward consequence of the Lax–Milgram theorem and [10, Lemma 3]. $\square$

Lemma 4.2

Assume that $\kappa _{4}\in \Bigg ( 0,\,\dfrac{2\,\kappa _{0}\,\widetilde{\delta }}{\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }}\,\Bigg )$, with $\widetilde{\delta }\,\in \,\Bigg (0 ,\,\dfrac{2}{\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }}\,\Bigg ),$ and $\kappa _{5},\,\kappa _{6}> 0$. Then, for each $r\in (0, \widetilde{r}_{0}),$ with $\widetilde{r}_{0}$ given by (3.38), and for each ${\varvec{w}}_{h}\in {\mathbf {H}}_{h}^{{\varvec{u}}}$ such that $\Vert {\varvec{w}}_{h}\Vert _{1,\Omega }\le r$, the problem (4.6) has a unique solution $({\mathbf {p}}_{h},\varphi _{h}) \,=:\,\widetilde{{\mathbf {S}}}_h({\varvec{w}}_h)\in {\mathbf {H}}^{{\mathbf {p}}}_{h}\times {\mathrm {H}}^{\varphi }_{h}$. Moreover, with the same constant $c_{\widetilde{{\mathbf {S}}}}>0$ from (3.34), which is independent of ${\varvec{w}}_{h}$, there holds

$$\begin{aligned} \Vert \widetilde{{\mathbf {S}}}_{h}({\varvec{w}}_{h})\Vert =\Vert ({\mathbf {p}}_{h},\varphi _{h})\Vert \le c_{\widetilde{{\mathbf {S}}}}\, \{\Vert \varphi _{D}\Vert _{0,\Gamma }+\Vert \varphi _{D}\Vert _{1/2,\Gamma }\} . \end{aligned}$$

Proof

By using the same arguments as in the proof of Lemma 3.3, we find that for any ${\varvec{w}}_{h}\,\in {\mathbf {H}}_{h}^{{\varvec{u}}}$ given, the form $\widetilde{{\mathbf {A}}}+\widetilde{{\mathbf {B}}}_{{\varvec{w}}_{h}}$ is bilinear and continuous with continuity constant $\Vert \widetilde{{\mathbf {A}}}+\widetilde{{\mathbf {B}}}_{{\varvec{w}}_{h}}\Vert$, depending on the parameters $\kappa _4$, $\kappa _5$, $\kappa _6$, $|\Omega |$, $\Vert {\mathbb {K}}^{-1}\Vert$ and r. Besides, we have that $\widetilde{{\mathbf {A}}}+\widetilde{{\mathbf {B}}}_{{\varvec{w}}_{h}}$ is elliptic on ${\mathbf {H}}_{h}^{{\mathbf {p}}}\times {\mathrm {H}}_{h}^{\varphi }$ with the same constant $\widetilde{\alpha }(\Omega )$ provided the conditions already established on the constants $\kappa _{4},$ $\widetilde{\delta },$ $\kappa _{5},\kappa _{6},r$ and the given function ${\varvec{w}}_{h}$ (in place of ${\varvec{w}}$) are held, as in Lemma 3.3. In addition, $\widetilde{F}_{D}$ is clearly a linear and bounded functional as in (3.39). Then, the result is a straightforward consequence of the Lax–Milgram Theorem applied to the discrete problem (4.6). $\square$

Lemma 4.3

Let $\kappa _{1}\in ( 0,\,2\,\delta )$, with $\delta \,\in \,(0 ,\,2\,\mu )$, $\kappa _4\in \Bigg ( 0,\,\dfrac{2\,\kappa _{0}\,\widetilde{\delta }}{\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }}\,\Bigg )$, with $\widetilde{\delta }\,\in \,\Bigg (0 ,\,\dfrac{2}{\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }}\,\Bigg ),$ and $\kappa _{2},\,\kappa _{3},\,\kappa _{5},\,\kappa _{6}> 0$. Assume that, given $r\in (0,r_0)$, the data ${\varvec{g}}$ and ${\varvec{u}}_{D}$ satisfy (3.40).

Then, ${\mathbf {T}}_h({\varvec{w}}_h,\phi _h)$ is well-defined for each $({\varvec{w}}_h,\phi _h)\in {\mathbf {H}}_h$ such that $\Vert ({\varvec{w}}_h,\phi _h)\Vert \le r$. Moreover, there holds

$$\begin{aligned} \Vert {\mathbf {T}}_h({\varvec{w}}_h,\phi _h)\Vert \le c_{{\mathbf {S}}}\,\{r\,\Vert {\varvec{g}}\Vert _{\infty ,\Omega }+\Vert {\varvec{u}}_{D}\Vert _{0,\Gamma } +\Vert {\varvec{u}}_{D}\Vert _{1/2,\Gamma }\} + c_{\widetilde{{\mathbf {S}}}}\,\{\Vert \varphi _{D}\Vert _{0,\Gamma }+\Vert \varphi _{D}\Vert _{1/2,\Gamma }\}. \end{aligned}$$

Proof

By combining Lemmas 4.1 and 4.2 the result follows exactly as the proof of Lemma 3.4. $\square$

The discrete analogue of Lemma 3.5 is stated next. Its proof, being a simple translation of the arguments proving that lemma, is omitted.

Lemma 4.4

Given $r\in (0,\min \{r_{0},\widetilde{r}_0\})$, let ${\mathbf {W}}_{r,h}:=\{ ({\varvec{w}}_h,\phi _h)\in {\mathbf {H}}_h:\Vert ({\varvec{w}}_h,\phi _h)\Vert \le r \}$, and assume that the data satisfy (3.42). Then ${\mathbf {T}}({\mathbf {W}}_{r,h})\subseteq {\mathbf {W}}_{r,h}$.

Next, we address the Lipschitz continuity of ${\mathbf {T}}_h$, which, analogously to the continuous case, follows from the Lipschitz continuity of ${\mathbf {S}}_h$ and $\widetilde{{\mathbf {S}}}_h$. These results are established next in Lemmas 4.5–4.7. Their proofs are omitted since they are almost verbatim as those of the corresponding continuous estimates provided by Lemmas 3.6–3.8, respectively.

Lemma 4.5

Let $r\in (0,r_0)$, with $r_0$ given by (3.30). Then, there holds

$$\begin{aligned}&\Vert {\mathbf {S}}_{h}({\varvec{w}}_{h},\phi _{h})-{\mathbf {S}}_{h}(\widetilde{{\varvec{w}}}_{h},\widetilde{\phi }_{h})\Vert \\&\quad \le C_{{\mathbf {S}}}\,\{\Vert {\varvec{g}}\Vert _{\infty ,\Omega }\,\Vert \phi _{h}-\widetilde{\phi }_{h}\Vert _{0,\Omega }+ \Vert {\mathbf {S}}_{2,h}({\varvec{w}}_{h},\phi _{h})\Vert _{1,\Omega }\,\Vert {\varvec{w}}_{h}-\widetilde{{\varvec{w}}}_{h}\Vert _{1,\Omega }\} \end{aligned}$$

for all $({\varvec{w}}_{h},\phi _{h}),(\widetilde{{\varvec{w}}}_{h},\widetilde{\phi }_{h})\in {\mathbf {H}}_{h}$ such that $\Vert {\varvec{w}}_{h}\Vert _{1,\Omega },\,\Vert \widetilde{{\varvec{w}}}_{h}\Vert _{1,\Omega }\le r$, where $C_{{\mathbf {S}}}$ is the constant from Lemma 3.6.

Lemma 4.6

Let $r\in (0,\widetilde{r}_0)$, with $\widetilde{r}_0$ given by (3.38). Then, there holds

$$\begin{aligned} \Vert \widetilde{{\mathbf {S}}}_{h}({\varvec{w}}_{h})-\widetilde{{\mathbf {S}}}_{h}(\widetilde{{\varvec{w}}}_{h})\Vert \le C_{\widetilde{{\mathbf {S}}}}\, \Vert \widetilde{{\mathbf {S}} }_{2,h}({\varvec{w}}_{h})\Vert _{1,\Omega }\,\Vert {\varvec{w}}_{h}-\widetilde{{\varvec{w}}}_{h}\Vert _{1,\Omega } \end{aligned}$$

for all ${\varvec{w}}_{h},\widetilde{{\varvec{w}}}_{h}\in {\mathbf {H}}_{h}^{{\varvec{u}}}$ such that $\Vert {\varvec{w}}_{h}\Vert _{1,\Omega },\,\Vert \widetilde{{\varvec{w}}}_{h}\Vert _{1,\Omega }\le r$, where $C_{\widetilde{{\mathbf {S}}}}$ is the constant from Lemma 3.7.

Lemma 4.7

Given $r \in (0,\min \{r_{0},\widetilde{r}_{0}\})$, with $r_{0}$ and $\widetilde{r}_{0}$ given by (3.30) and (3.38), respectively, let ${\mathbf {W}}_{r,h}:=\{ ({\varvec{w}}_h,\phi _h)\in {\mathbf {H}}_h:\Vert ({\varvec{w}}_h,\phi _h)\Vert \le r \}$, and assume that the data ${\varvec{g}},$ ${\varvec{u}}_{D},$ and $\varphi _{D}$ satisfy (3.42). Then, there holds

$$\begin{aligned}&\displaystyle \Vert {\mathbf {T}}_h({\varvec{w}}_h,\phi _h)-{\mathbf {T}}_h(\widetilde{{\varvec{w}}}_h,\widetilde{\phi }_h)\Vert \\&\displaystyle \quad \le C_{{\mathbf {T}}}\, (\Vert {\varvec{g}}\Vert _{\infty ,\Omega } + c_{{\mathbf {S}}}\,\{r\,\Vert {\varvec{g}}\Vert _{\infty ,\Omega }+\Vert {\varvec{u}}_{D}\Vert _{0,\Gamma } +\Vert {\varvec{u}}_{D}\Vert _{1/2,\Gamma }\} )\,\Vert ({\varvec{w}},\phi )-(\widetilde{{\varvec{w}}},\widetilde{\phi })\Vert , \end{aligned}$$

for all $({\varvec{w}}_{h},\phi _{h}),(\widetilde{{\varvec{w}}}_{h},\widetilde{\phi }_{h})\in {\mathbf {W}}_{r,h}$, where $C_{{\mathbf {T}}}$ is the constant provided by Lemma 3.8.

As a consequence of the previous lemmas, and owing to the equivalence between (4.2) and (4.8), we conclude that problem (4.2) has at least one solution. More precisely, we have the following theorem.

Theorem 4.8

Let $\kappa _{1}\in ( 0,\,2\,\delta )$, with $\delta \,\in \,(0 ,\,2\,\mu )$, $\kappa _4\in \Bigg ( 0,\,\dfrac{2\,\kappa _{0}\,\widetilde{\delta }}{\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }}\,\Bigg )$, with $\widetilde{\delta } \in \Bigg (0 ,\dfrac{2}{\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }}\,\Bigg ),$ and $\kappa _{2},\,\kappa _{3},\,\kappa _{5},\,\kappa _{6}> 0$. Given $r \in \big (0,\min \{r_{0},\widetilde{r}_{0}\}\big )$, with $r_{0}$ and $\widetilde{r}_{0}$ given by (3.30) and (3.38), respectively, let ${\mathbf {W}}_{r,h}:=\{ ({\varvec{w}}_h,\phi _h)\in {\mathbf {H}}_h:\Vert ({\varvec{w}}_h,\phi _h)\Vert \le r \}$, and assume that the data ${\varvec{g}},$ ${\varvec{u}}_{D},$ and $\varphi _{D}$ satisfy (3.42). Then, the Galerkin scheme (4.2) has at least one solution $({\varvec{\sigma }}_{h},{\varvec{u}}_{h},{\mathbf {p}}_{h},\varphi _{h}) \in {\mathbb {H}}^{{\varvec{\sigma }}}_{h} \times {\mathbf {H}}^{{\varvec{u}}}_{h} \times {\mathbf {H}}^{{\mathbf {p}}}_{h} \times {\mathrm {H}}^{\varphi }_{h}$, with $({\varvec{u}}_{h},\varphi _{h}) \in {\mathbf {W}}_{r,h}$, and there hold

$$\begin{aligned} \Vert ({\varvec{\sigma }}_{h},{\varvec{u}}_{h})\Vert \le c_{{\mathbf {S}}}\, \{r\, \Vert {\varvec{g}}\Vert _{\infty ,\Omega }\, +\Vert {\varvec{u}}_{D}\Vert _{0,\Gamma }+\Vert {\varvec{u}}_{D}\Vert _{1/2,\Gamma }\}, \end{aligned}$$

(4.9)

and

$$\begin{aligned} \Vert ({\mathbf {p}}_{h},\varphi _{h})\Vert \le c_{\widetilde{{\mathbf {S}}}}\, \{\Vert \varphi _{D}\Vert _{0,\Gamma }+\Vert \varphi _{D}\Vert _{1/2,\Gamma }\}. \end{aligned}$$

(4.10)

Proof

Bearing in mind Lemmas 4.4 and 4.7, and the fact that ${\mathbf {W}}_{r,h}$ is a convex and compact subset of ${\mathbf {H}}_h$, the proof follows from a straightforward application of the Brouwer fixed-point theorem. $\square$

Finally, as already announced at the beginning of this section, we now provide the following existence and uniqueness result.

Theorem 4.9

In addition to the hypothesis of Theorem 4.8, assume that the data ${\varvec{g}}$ and ${\varvec{u}}_D$ are sufficiently small so that (3.46) is satisfied. Then, the problem (4.2) has an unique solution $({\varvec{\sigma }}_{h},{\varvec{u}}_{h},{\mathbf {p}}_{h},\varphi _{h})$ $\in \,{\mathbb {H}}^{{\varvec{\sigma }}}_{h}\times {\mathbf {H}}^{{\varvec{u}}}_{h}\times {\mathbf {H}}^{{\mathbf {p}}}_{h}\times {\mathrm {H}}^{\varphi }_{h}$, with $({\varvec{u}}_{h},\varphi _{h})\in {\mathbf {W}}_{r,h}$, and the a priori estimates (4.9) and (4.10) hold.

Proof

It follows similarly to the proof of Theorem 3.9 by a direct application of the Banach fixed-point Theorem. $\square$

We end this section by emphasizing that the solvability analysis of the Galerkin scheme does not require any discrete inf-sup conditions among $\,{\mathbb {H}}_{h}^{{\varvec{\sigma }}}$, $\,{\mathbf {H}}_{h}^{{\varvec{u}}}$, $\,{\mathbf {H}}_{h}^{{\mathbf {p}}}$, and $\,{\mathrm {H}}_{h}^{\varphi }$, and hence they can be chosen freely as arbitrary finite element subspaces of $\,{\mathbb {H}}_{0}({\mathbf {div}};\Omega )$, $\,{\mathbf {H}}^{1}(\Omega )$, $\,{\mathbf {H}}({\mathrm {div}};\Omega )$, and $\,{\mathrm {H}}^{1}(\Omega )$, respectively. This flexibility is certainly another feature of practical interest of our method. A particular choice of the discrete spaces, which is actually the canonical one, is described in the following section.

4.3 Specific finite element subspaces

Given an integer $k\ge 0$ and a subset ${\mathrm {S}}\subseteq {\mathrm {R}}^{n}$, we let as usual ${\mathrm {P}}_{k}({\mathrm {S}})$ [resp. $\widetilde{{\mathrm {P}}}_{k}({\mathrm {S}})$] be the space of polynomial functions on ${\mathrm {S}}$ of degree $\le \,k$ (resp. of degree $=\,k$), and with the same notation and definitions introduced in Sect. 4.1 concerning the triangulation ${\mathcal {T}}_{h}$ of $\overline{\Omega }$, we start defining the corresponding local Raviart–Thomas space of order k, for each $K\in {\mathcal {T}}_{h},$ as

$$\begin{aligned} {\mathbf {RT}}_{k}(K):={\mathbf {P}}_{k}(K)\, \oplus \,\widetilde{{\mathrm {P}}}_{k}(K)\,{\varvec{x}}, \end{aligned}$$

where, according to the notations described in the Sect. 1, ${\mathbf {P}}_{k}(K):=[\,{\mathrm {P}}_{k}(K) \,]^{n}$, and ${\varvec{x}}$ is the generic vector in ${\mathrm {R}}^{n}.$ Similarly, ${\mathbf {C}}(\overline{\Omega })=[{\mathrm {C}}(\overline{\Omega })]^{n}.$ Then, we introduce the finite element subspaces approximating the unknowns ${\varvec{\sigma }}$ and ${\varvec{u}}$ as the global Raviart–Thomas space of order k, and the corresponding Lagrange space given by continuous piecewise polynomials of degree $\le \,k+1$, respectively, that is

$$\begin{aligned} {\mathbb {H}}_{h}^{{\varvec{\sigma }}}:=\{ {\varvec{\tau }}_{h}\in {\mathbb {H}}_{0}({\mathbf {div}};\Omega ):{\varvec{c}}^{t}\,{\varvec{\tau }}_{h}|_{K}\in {\mathbf {RT}}_{k}(K) \quad \forall {\varvec{c}}\in {\mathrm {R}}^{n}\quad \forall K\in {\mathcal {T}}_{h} \}, \end{aligned}$$

(4.11)

and

$$\begin{aligned} {\mathbf {H}}_{h}^{{\varvec{u}}}:=\{ {\varvec{v}}_{h}\in {\mathbf {C}}(\overline{\Omega }):{\varvec{v}}_{h}|_{K}\in {\mathbf {P}}_{k+1}(K)\quad \forall K\in {\mathcal {T}}_{h} \}. \end{aligned}$$

(4.12)

In turn, we define the approximating spaces for ${\mathbf {p}}$ and the temperature $\varphi$ as the global Raviart–Thomas space of order k, and the corresponding Lagrange space given by continuous piecewise polynomials of degree $\le \,k+1,$ respectively, as follows

$$\begin{aligned} {\mathbf {H}}_{h}^{{\mathbf {p}}}:=\{ {\mathbf {q}}_{h}\in {\mathbf {H}}({\mathrm {div}};\Omega ):{\mathbf {q}}_{h}|_{K}\in {\mathbf {RT}}_{k}(K) \quad \forall K\in {\mathcal {T}}_{h} \} \end{aligned}$$

(4.13)

and

$$\begin{aligned} {\mathrm {H}}_{h}^{\varphi }:=\{ \psi _{h}\in {\mathrm {C}}(\overline{\Omega }):\psi _{h}|_{K}\in {\mathrm {P}}_{k+1}(K)\quad \forall K\in {\mathcal {T}}_{h} \}. \end{aligned}$$

(4.14)

We end this section by recalling from [16], the approximation properties of the specific finite element subspaces introduced above.

$({\mathbf {AP}}_{h}^{{\varvec{\sigma }}})$ :

There exists $C>0,$ independent of h,  such that for each $s\in (0,k+1]$, and for each ${\varvec{\sigma }}\in {\mathbb {H}}^{s}(\Omega )\,\cap \,{\mathbb {H}}_{0}({\mathbf {div}};\Omega )$ with ${\mathbf {div}}\,{\varvec{\sigma }}\in {\mathbf {H}}^{s}(\Omega ),$ there holds

$$\begin{aligned} {{\mathrm {dist}}({\varvec{\sigma }},{\mathbb {H}}_{h}^{{\varvec{\sigma }}}) := \inf _{{\varvec{\tau }}_h\in {\mathbb {H}}_{h}^{{\varvec{\sigma }}}} \, \Vert {\varvec{\sigma }}- {\varvec{\tau }}_h\Vert _{{\mathbf {div}};\Omega }} \le C\,h^{s}\,\{\Vert {\varvec{\sigma }}\Vert _{s,\Omega }+\Vert {\mathbf {div}}\,{\varvec{\sigma }}\Vert _{s,\Omega } \}. \end{aligned}$$

$({\mathbf {AP}}_{h}^{{\varvec{u}}})$ :

There exists $C>0,$ independent of h,  such that for each such that for each $s\in (0,k+1]$, and for each ${\varvec{u}}\in {\mathbf {H}}^{s+1}(\Omega ),$ there holds

$$\begin{aligned} {{\mathrm {dist}}({\varvec{u}},{\mathbf {H}}_{h}^{{\varvec{u}}}) := \inf _{{\varvec{v}}_h\in {\mathbf {H}}_{h}^{{\varvec{u}}}} \, \Vert {\varvec{u}}- {\varvec{v}}_h\Vert _{1,\Omega }} \le C\,h^{s} \,\Vert {\varvec{u}}\Vert _{s+1,\Omega }. \end{aligned}$$

$({\mathbf {AP}}_{h}^{{\mathbf {p}}})$ :

There exists $C>0,$ independent of h,  such that for each $s\in (0,k+1]$, and for each ${\mathbf {p}}\in {\mathbf {H}}^{s}(\Omega )\,\cap \,{\mathbf {H}}({\mathrm {div}};\Omega )$ with ${\mathrm {div}}\,{\mathbf {p}}\in {\mathrm {H}}^{s}(\Omega ),$ there holds

$$\begin{aligned} {{\mathrm {dist}}({\mathbf {p}},{\mathbf {H}}_{h}^{{\mathbf {p}}}) := \inf _{{\mathbf {q}}_h\in {\mathbf {H}}_{h}^{{\mathbf {p}}}} \, \Vert {\mathbf {p}}- {\mathbf {q}}_h\Vert _{{\mathrm {div}};\Omega }} \le C\,h^{s}\,\{\Vert {\mathbf {p}}\Vert _{s,\Omega }+\Vert {\mathrm {div}}\,{\mathbf {p}}\Vert _{s,\Omega } \}. \end{aligned}$$

$({\mathbf {AP}}_{h}^{\varphi })$ :

There exists $C>0,$ independent of h,  such that for each $s\in (0,k+1]$, and for each $\varphi \in {\mathrm {H}}^{s+1}(\Omega ),$ there holds

$$\begin{aligned} {{\mathrm {dist}}(\varphi ,{\mathrm {H}}_{h}^{\varphi }) := \inf _{\psi _h\in {\mathrm {H}}_{h}^{\varphi }} \, \Vert \varphi - \psi _h\Vert _{1,\Omega }} \le C\,h^{s} \,\Vert \varphi \Vert _{s+1,\Omega }. \end{aligned}$$

5 A priori error analysis

In this section, we carry out the error analysis for our Galerkin scheme (4.2). We first deduce the corresponding Céa estimate by considering the generic finite dimensional subspaces (4.1), and then we apply it to derive the theoretical rates of convergence when using the specific discrete spaces provided in Sect. 4.3. As we will see later, the a priori error estimate can be easily obtained by applying the well-known Strang Lemma for elliptic variational problems (see e.g.[23, Theorem 11.1]). This auxiliary result is stated first.

Lemma 5.1

Let V be a Hilbert space, $F\in V'$, and $A:V\times V \,\rightarrow \,{\mathrm {R}}$ be a bounded and $V-$elliptic bilinear form. In addition, let $\{V_{h}\}_{h > 0}$ be a sequence of finite dimensional subspaces of V, and for each $h > 0$ consider a bounded bilinear form $A_{h}:\,V_{h}\times V_{h}\,\rightarrow \,{\mathrm {R}}$ and a functional $F_h \in V'_h$. Assume that the family $\{A_{h}\}_{h > 0}$ is uniformly elliptic, that is, there exists a constant $\widetilde{\alpha }>0$, independent of h, such that

$$\begin{aligned} A_{h}(v_{h},v_{h})\, \ge \, \widetilde{\alpha } \,\Vert v_{h}\Vert _{V}^{2}\quad \forall v_{h}\in V_{h},\quad \forall h> 0. \end{aligned}$$

In turn, let $u\in V$ and $u_{h}\in V_{h}$ such that

$$\begin{aligned} A(u,v)=F(v)\quad \forall v\in V \quad \text{ and }\quad A_{h}(u_{h},v_{h})=F_{h}(v_{h})\quad \forall v_{h}\in V_{h}. \end{aligned}$$

Then, for each $h> 0$ there holds

$$\begin{aligned} \displaystyle \Vert u-u_{h}\Vert _{V}\le & {} C_{{\mathrm {ST}}}\,\left\{ \sup _{\mathop {w_{h}\ne 0}\limits ^{\scriptstyle w_{h} \in V_{h}}} \dfrac{|F(w_{h})-F_{h}(w_{h})|}{\Vert w_{h}\Vert _{V}}\right. \\&\displaystyle \left. + \inf _{\mathop {v_{h}\ne 0}\limits ^{\scriptstyle v_{h} \in V_{h}}} \left( \Vert u-v_{h}\Vert _{V} +\sup _{\mathop {w_{h}\ne 0}\limits ^{\scriptstyle w_{h} \in V_{h}}} \dfrac{|A(v_{h},w_{h}) -A_{h}(v_{h},w_{h}) |}{\Vert w_{h}\Vert _{V}}\right) \right\} , \end{aligned}$$

where $C_{{\mathrm {ST}}} :=\widetilde{\alpha }^{-1}\,\max \{1,\Vert A\Vert \}$.

Now, let $({\varvec{\sigma }},\, {\varvec{u}},\,{\mathbf {p}},\, \varphi )\in {\mathbb {H}}_{0}({\mathbf {div}};\Omega )\times {\mathbf {H}}^{1}(\Omega )\, \times \,{\mathbf {H}}({\mathrm {div}};\Omega )\times {\mathrm {H}}^{1}(\Omega )$ and $({\varvec{\sigma }}_{h},\, {\varvec{u}}_{h},\, {\mathbf {p}}_{h},\varphi _{h}) \in {\mathbb {H}}_{h}^{{\varvec{\sigma }}}\times {\mathbf {H}}_{h}^{{\varvec{u}}}\times {\mathbf {H}}_{h}^{{\mathbf {p}}}\times {\mathrm {H}}_{h}^{\varphi }$ be the solutions of problems (3.12) and (4.2), respectively, with $({\varvec{u}},\,\varphi )\in {\mathbf {W}}_r$ and $({\varvec{u}}_{h},\,\varphi _{h})\in {\mathbf {W}}_{r,h}$. Then we are interested in finding an upper bound for

$$\begin{aligned} \Vert ({\varvec{\sigma }},\, {\varvec{u}},\,{\mathbf {p}},\, \varphi )-({\varvec{\sigma }}_{h},\, {\varvec{u}}_{h},\, {\mathbf {p}}_{h},\varphi _{h})\Vert , \end{aligned}$$

for which we plan to estimate $\Vert ({\varvec{\sigma }},{\varvec{u}})-({\varvec{\sigma }}_{h},{\varvec{u}}_{h})\Vert$  and  $\Vert ({\mathbf {p}},\, \varphi )-({\mathbf {p}}_{h},\varphi _{h})\Vert$, separately.

In the sequel, for the sake of simplicity, we denote as usual

$$\begin{aligned} {\mathrm {dist}}(({\varvec{\sigma }},{\varvec{u}}),{\mathbb {H}}_{h}^{{\varvec{\sigma }}}\times {\mathbf {H}}_{h}^{{\varvec{u}}} ) = \inf _{({\varvec{\tau }}_{h},{\varvec{v}}_{h})\in {\mathbb {H}}_{h}^{{\varvec{\sigma }}}\times {\mathbf {H}}_{h}^{{\varvec{u}}}}\, \Vert \,({\varvec{\sigma }},{\varvec{u}})-({\varvec{\tau }}_{h},{\varvec{v}}_{h})\,\Vert \end{aligned}$$

and

$$\begin{aligned} {\mathrm {dist}}( ({\mathbf {p}},\varphi ),{\mathbf {H}}_{h}^{{\mathbf {p}}}\times {\mathrm {H}}_{h}^{\varphi } ) = \inf _{({\mathbf {q}}_{h},\psi _{h})\in {\mathbf {H}}_{h}^{{\mathbf {p}}}\times {\mathrm {H}}_{h}^{\psi }}\, \Vert \,({\mathbf {p}},\varphi )-({\mathbf {q}}_{h},\psi _{h})\,\Vert . \end{aligned}$$

In order to derive the upper bound for $\Vert ({\varvec{\sigma }},{\varvec{u}})-({\varvec{\sigma }}_{h},{\varvec{u}}_{h})\Vert$, we first notice that, according to the first equations of (3.12) and (4.2), $({\varvec{\sigma }},{\varvec{u}})$ and $({\varvec{\sigma }}_h,{\varvec{u}}_h)$ satisfy, respectively,

$$\begin{aligned}&{\mathbf {A}}(({\varvec{\sigma }},{\varvec{u}}),({\varvec{\tau }},{\varvec{v}}))+ {\mathbf {B}}_{{\varvec{u}}}(({\varvec{\sigma }},{\varvec{u}}),({\varvec{\tau }},{\varvec{v}})) \\&\quad = \big ( F_{\varphi } + F_{D}\big )({\varvec{\tau }},{\varvec{v}}) \quad \forall ({\varvec{\tau }},{\varvec{v}})\in {\mathbb {H}}_{0}({\mathbf {div}};\Omega )\times {\mathbf {H}}^{1}(\Omega ), \end{aligned}$$

and

$$\begin{aligned}&{\mathbf {A}}(({\varvec{\sigma }}_{h},{\varvec{u}}_{h}),({\varvec{\tau }}_{h},{\varvec{v}}_{h}))+ {\mathbf {B}}_{{\varvec{u}}_{h}}(({\varvec{\sigma }}_{h},{\varvec{u}}_{h}),({\varvec{\tau }}_{h},{\varvec{v}}_{h})) \\&\quad = \big (F_{\varphi _{h}} + F_{D}\big )({\varvec{\tau }}_{h},{\varvec{v}}_{h}) \quad \forall ({\varvec{\tau }}_{h},{\varvec{v}}_{h})\in {\mathbb {H}}_{h}^{{\varvec{\sigma }}}\times {\mathbf {H}}_{h}^{{\varvec{u}}}. \end{aligned}$$

Then, applying Lemma 5.1, we can obtain the desired estimate for $\Vert ({\varvec{\sigma }},{\varvec{u}})-({\varvec{\sigma }}_{h}\Vert$ as follows.

Lemma 5.2

Let $\displaystyle C_{{\mathrm {ST}}}:=\frac{2}{\alpha (\Omega )}\, \max \{1,\Vert \,{\mathbf {A}}+{\mathbf {B}}_{{\varvec{u}}}\,\Vert \}$, where $\alpha (\Omega )$ is the constant yielding the ellipticity of both ${\mathbf {A}}$ and ${\mathbf {A}}+{\mathbf {B}}_{{\varvec{w}}}$ for any ${\varvec{w}}\in {\mathbf {H}}^1(\Omega )$ (cf. (3.29) and (3.31)). Then, there holds

$$\begin{aligned}&\displaystyle \Vert ({\varvec{\sigma }},{\varvec{u}})-({\varvec{\sigma }}_{h},{\varvec{u}}_{h})\Vert \nonumber \\&\quad \le C_{{\mathrm {ST}}}\,\{( 1 + c_{1}(\Omega )\, (\kappa _{1}^{2}+1)^{1/2}\,\Vert {\varvec{u}}-{\varvec{u}}_{h}\Vert _{1,\Omega })\, {\mathrm {dist}}(({\varvec{\sigma }},{\varvec{u}}),{\mathbb {H}}_{h}^{{\varvec{\sigma }}}\times {\mathbf {H}}_{h}^{{\varvec{u}}} ) \Big . \nonumber \\&\quad \quad \displaystyle + \,c_{1}(\Omega )\,(\kappa _{1}^{2}+1)^{1/2}\,\Vert {\varvec{u}}-{\varvec{u}}_{h}\Vert _{1,\Omega } \, \Vert {\varvec{u}}\Vert _{1,\Omega } + (\mu ^{2}+\kappa _{2}^{2})^{1/2}\, \Vert {\varvec{g}}\Vert _{\infty ,\Omega }\,\Vert \varphi -\varphi _{h}\Vert _{0,\Omega } \}.\nonumber \\ \end{aligned}$$

(5.1)

Proof

Observe that, according to the previous continuous and discrete analyses in Sects. 3 and 4, respectively, we readily obtain that the bilinear forms $A:={\mathbf {A}}+{\mathbf {B}}_{\varvec{u}}$, $A_h:={\mathbf {A}}+{\mathbf {B}}_{{\varvec{u}}_h}$, and the functionals $F=F_\varphi +F_D$ and $F_h=F_{\varphi _h}+F_D$ satisfy the hypotheses of Lemma 5.1. Then, after simple algebraic computations the result follows from the aforementioned lemma. We omit further details and refer to [10, Lemma 5.3] for details. $\square$

Next, for $\Vert ({\mathbf {p}},\varphi )-({\mathbf {p}}_{h},\varphi _{h})\Vert$, we proceed similarly to the previous analysis and firstly observe from the second equations of (3.12) and (4.2), that $({\mathbf {p}},\varphi )$ and $({\mathbf {p}}_h,\varphi _h)$ satisfy, respectively

$$\begin{aligned} \widetilde{ {\mathbf {A}}}(({\mathbf {p}},\varphi ),({\mathbf {q}},\psi ))+\widetilde{{\mathbf {B}}}_{{\varvec{u}}}(({\mathbf {p}},\varphi ),({\mathbf {q}},\psi ))= & {} \widetilde{F}_{D}({\mathbf {q}},\psi ) \nonumber \\&\forall ({\mathbf {q}},\psi )\in {\mathbf {H}}({\mathrm {div}};\Omega )\times {\mathrm {H}}^{1}(\Omega ) ,\nonumber \\ \end{aligned}$$

(5.2)

and

$$\begin{aligned} \widetilde{ {\mathbf {A}}}(({\mathbf {p}}_{h},\varphi _{h}),({\mathbf {q}}_{h},\psi _{h}))+ \widetilde{{\mathbf {B}}}_{{\varvec{u}}_{h}}(({\mathbf {p}}_{h},\varphi _{h}),({\mathbf {q}}_{h},\psi _{h}))= & {} \widetilde{F}_{D}({\mathbf {q}}_{h},\psi _{h}) \nonumber \\&\forall ({\mathbf {q}}_h,\psi _h)\,\in \,{\mathbf {H}}^{\mathbf {p}}_h\times {\mathrm {H}}^\varphi _h.\nonumber \\ \end{aligned}$$

(5.3)

Then, applying again Lemma 5.1 we derive the upper bound for $\Vert ({\mathbf {p}},\varphi )-({\mathbf {p}}_{h},\varphi _{h})\Vert$ as follows.

Lemma 5.3

Let $\displaystyle C_{{\mathrm {ST}}}:=\frac{2}{\widetilde{\alpha }(\Omega )}\,\max \{1,\Vert \,\widetilde{{\mathbf {A}}}\, +\,\widetilde{{\mathbf {B}}}_{{\varvec{u}}}\,\Vert \}$, where $\widetilde{\alpha }(\Omega )$ is the constant yielding the ellipticity of both $\widetilde{{\mathbf {A}}}$ and $\widetilde{{\mathbf {A}}}+\widetilde{{\mathbf {B}}}_{{\varvec{w}}}$, for any ${\varvec{w}}\in {\mathbf {H}}^1(\Omega )$ (cf. (3.36) and (3.37) in the proof of Lemma 3.3). Then, there holds

$$\begin{aligned}&\Vert ({\mathbf {p}},\varphi )-({\mathbf {p}}_{h},\varphi _{h})\Vert \,\nonumber \\&\quad \le \displaystyle \widetilde{C}_{{\mathrm {ST}}}\, \{ (\kappa _{4}^{2}+1)^{1/2}\, \Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }\,c_{2}(\Omega )\, \Vert \, {\varvec{u}}\, -\,{\varvec{u}}_{h} \,\Vert _{1,\Omega }\, \Vert \,({\mathbf {p}},\varphi )\,\Vert \Big . \nonumber \\&\quad \quad \displaystyle +\Big .( 1+ (\kappa _{4}^{2}+1)^{1/2}\, \Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }\,c_{2}(\Omega )\, \Vert \, {\varvec{u}}\,- \,{\varvec{u}}_{h} \,\Vert _{1,\Omega }\,)\,\nonumber \\&\quad \quad \times {\mathrm {dist}}( \,({\mathbf {p}},\varphi ),{\mathbf {H}}_{h}^{{\mathbf {p}}}\times {\mathrm {H}}_{h}^{\varphi } ) \}. \end{aligned}$$

(5.4)

Proof

We proceed similarly as in proof of Lemma 5.3 in [10]. In fact, from Lemmas 3.3 and 4.1, we have that the bilinear forms $\widetilde{{\mathbf {A}}}\,+ \,\widetilde{{\mathbf {B}}}_{{\varvec{u}}}$ and $\widetilde{{\mathbf {A}}}+\widetilde{{\mathbf {B}}}_{{\varvec{u}}_{h}}$ are both bounded and elliptic with the same constant $\widetilde{\alpha }(\Omega )/2,$ which is clearly independent of h on their respective spaces. In addition, $\widetilde{F}_{D}$ is a linear and bounded functional in ${\mathbf {H}}({\mathrm {div}};\Omega )\, \times \,{\mathrm {H}}^{1}(\Omega )$ and, in particular, in ${\mathbf {H}}_{h}^{{\mathbf {p}}}\times {\mathrm {H}}_{h}^{\varphi }$. Then, a straightforward application of Lemma 5.1 to the context given by (5.2)–(5.3) provides the existence of a positive constant $\widetilde{C}_{{\mathrm {ST}}}:=\dfrac{2}{\widetilde{\alpha }(\Omega )}\,\max \{1,\Vert \,\widetilde{{\mathbf {A}}}+\widetilde{{\mathbf {B}}}_{{\varvec{u}}}\,\Vert \}$, such that

$$\begin{aligned} \displaystyle \Vert ({\mathbf {p}},\varphi )-({\mathbf {p}}_{h},\varphi _{h})\Vert \,\le & {} \, \widetilde{C}_{{\mathrm {ST}}}\,\left\{ \inf _{\mathop {({\mathbf {q}}_{h},\psi _{h})\ne {\mathbf {0}}}\limits ^{\scriptstyle ({\mathbf {q}}_{h},\psi _{h}) \in {\mathbf {H}}_{h}^{{\mathbf {p}}}\times {\mathrm {H}}_{h}^{\varphi }}}\, \Bigg ( \Vert ({\mathbf {p}},\varphi )-({\mathbf {q}}_{h},\psi _{h})\Vert \right. \nonumber \\&\displaystyle \left. +\, \sup _{\mathop {\scriptstyle ({\mathbf {r}}_{h}, \phi _{h}) \ne {\mathbf {0}}}\limits ^{\scriptstyle ({\mathbf {r}}_{h},\phi _{h}) \in {\mathbf {H}}_{h}^{{\mathbf {p}}}\times {\mathrm {H}}_{h}^{\varphi }}} \dfrac{|\widetilde{{\mathbf {B}}}_{{\varvec{u}}-{\varvec{u}}_{h}}(({\mathbf {q}}_{h},\psi _{h}),({\mathbf {r}}_{h} ,\phi _{h}))|}{\Vert \,({\mathbf {r}}_{h},\phi _{h}) \,\Vert }\,\Bigg ) \right\} .\qquad \qquad \end{aligned}$$

(5.5)

Now, we observe that the expression $\widetilde{{\mathbf {B}}}_{{\varvec{u}}-{\varvec{u}}_{h}}(({\mathbf {q}}_{h},\psi _{h}),({\mathbf {r}}_{h}, \phi _{h}))$ in the second term of (5.5) can be bounded by using the estimate (3.35) with ${\varvec{u}}-{\varvec{u}}_{h}$, $({\mathbf {q}}_{h},\psi _{h} )$ and $({\mathbf {r}}_{h},\phi _{h})$ instead of ${\varvec{w}},$ $({\mathbf {p}},\varphi )$ and $({\mathbf {q}},\psi ),$ respectively. Then, adding and subtracting $\varphi ,$ and then bounding $\Vert \varphi -\psi _{h}\Vert$ by $\Vert ({\mathbf {p}},\varphi )\, -\,({\mathbf {q}}_{h},\psi _{h})\Vert$, we obtain

$$\begin{aligned}&|\widetilde{{\mathbf {B}}}_{{\varvec{u}}-{\varvec{u}}_{h}}(({\mathbf {q}}_{h},\psi _{h}),({\mathbf {r}}_{h},\phi _{h}))|\le c_{2}(\Omega ) \,(\kappa _{4}^{2}+1)^{1/2}\, \Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }\, \Vert \, {\varvec{u}}\,\\&\quad \quad -{\varvec{u}}_{h} \,\Vert _{1, \Omega }\, \Vert \psi _{h}\Vert _{1,\Omega } \,\Vert \, ({\mathbf {r}}_{h},\phi _{h}) \,\Vert \\&\quad \le c_{2}(\Omega )\, (\kappa _{4}^{2}+1)^{1/2}\, \Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }\, \Vert \, {\varvec{u}}-{\varvec{u}}_{h} \,\Vert _{1,\Omega }\, \Vert \varphi \Vert _{1,\Omega } \,\Vert \, ({\mathbf {r}}_{h},\phi _{h}) \,\Vert \\&\quad \quad + c_{2}(\Omega )\,(\kappa _{4}^{2}+1)^{1/2} \Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega } \Vert \, {\varvec{u}}\,- \,{\varvec{u}}_{h} \,\Vert _{1,\Omega }\, \Vert \,({\mathbf {p}},\varphi )- ({\mathbf {q}}_{h},\psi _{h}) \,\Vert \,\Vert \, ({\mathbf {r}}_{h},\phi _{h}) \,\Vert , \end{aligned}$$

which yields

$$\begin{aligned}&\displaystyle \sup _{\mathop {\scriptstyle ({\mathbf {r}}_{h},\phi _{h}) \ne {\mathbf {0}}}\limits ^{\scriptstyle ({\mathbf {r}}_{h},\phi _{h}) \in {\mathbf {H}}_{h}^{{\mathbf {p}}}\times {\mathrm {H}}_{h}^{\varphi }}} \dfrac{|\widetilde{{\mathbf {B}}} _{{\varvec{u}}-{\varvec{u}}_{h}}(({\mathbf {q}}_{h},\psi _{h}),({\mathbf {r}}_{h},\phi _{h}))|}{\Vert \,({\mathbf {r}}_{h},\phi _{h}) \,\Vert } \nonumber \\&\displaystyle \quad \le \,c_{2}(\Omega ) \,(\kappa _{4}^{2}+1)^{1/2}\, \Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }\, \Vert {\varvec{u}}-{\varvec{u}}_{h} \Vert _{1,\Omega }\, \Vert \varphi \Vert _{1,\Omega } \nonumber \\&\displaystyle \quad \quad + c_{2}(\Omega )\,(\kappa _{4}^{2}+1)^{1/2}\, \Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }\, \Vert \, {\varvec{u}}-{\varvec{u}}_{h} \,\Vert _{1,\Omega }\, \Vert ({\mathbf {p}},\varphi )- ({\mathbf {q}}_{h},\psi _{h}) \Vert .\qquad \qquad \end{aligned}$$

(5.6)

Therefore, Eq. (5.4) follows by replacing (5.6) in (5.5), and then using the definition of ${\mathrm {dist}}(({\mathbf {p}},\varphi ),{\mathbf {H}}_{h}^{{\mathbf {p}}}\times {\mathrm {H}}_{h}^{\varphi })$. $\square$

We now combine the inequalities provided by Lemmas 4.4 and 4.5 to derive the a priori estimate for the total error $\Vert ({\varvec{\sigma }},{\varvec{u}},{\mathbf {p}},\varphi )-({\varvec{\sigma }}_{h},{\varvec{u}}_{h},{\mathbf {p}}_{h},\varphi _{h})\Vert .$ Indeed, by gathering together the estimates (5.1) and (5.4), it follows that

$$\begin{aligned}&\Vert ({\varvec{\sigma }},{\varvec{u}})-({\varvec{\sigma }}_{h},{\varvec{u}}_{h})\Vert +\Vert ({\mathbf {p}},\varphi )-({\mathbf {p}}_{h},\varphi _{h})\Vert \,\nonumber \\&\quad \le C_{{\mathrm {ST}}}\,(\mu ^{2}\, +\,\kappa _{2}^{2})^{1/2}\,\Vert {\varvec{g}}\Vert _{\infty ,\Omega }\,\Vert \varphi -\varphi _{h}\Vert \\&\quad \quad + \{C_{{\mathrm {ST}}}\,c_{1}(\Omega )\,( \kappa _{1}^{2}+1 )^{1/2}\,\Vert {\varvec{u}}\Vert _{1,\Omega }\, +\,\widetilde{C}_{{\mathrm {ST}}}\,c_{2}(\Omega )\,( \kappa _{4}^{2}+1 )^{1/2}\,\Vert \varphi \Vert _{1,\Omega } \, \}\, \Vert {\varvec{u}}-{\varvec{u}}_{h}\Vert \\&\quad \quad + C_{{\mathrm {ST}}} \,( 1+c_{1}(\Omega )\,(\kappa _{1}^{2}+1)^{1/2}\,\Vert {\varvec{u}}-{\varvec{u}}_{h}\Vert _{1,\Omega }\,)\,{\mathrm {dist}}( \,({\varvec{\sigma }},{\varvec{u}}),{\mathbb {H}}_{h}^{{\varvec{\sigma }}}\times {\mathbf {H}}_{h}^{{\varvec{u}}} )\\&\quad \quad +\widetilde{C}_{{\mathrm {ST}}}( 1+c_{2}(\Omega )\,(\kappa _{4}^{2}+1)^{1/2}\, \Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }\, \Vert \, {\varvec{u}}-{\varvec{u}}_{h} \,\Vert _{1,\Omega })\,{\mathrm {dist}}( ({\mathbf {p}}, \varphi ),{\mathbf {H}}_{h}^{{\mathbf {p}}}\times {\mathrm {H}}_{h}^{\varphi }). \end{aligned}$$

Then, using the estimates (3.47) and (3.48) to bound $\Vert {\varvec{u}}\Vert _{1,\Omega }$ and $\Vert \varphi \Vert _{1,\Omega }$, respectively, and then performing some algebraic manipulations, from the latter inequality we find that

$$\begin{aligned}&\Vert ({\varvec{\sigma }},{\varvec{u}})-({\varvec{\sigma }}_{h},{\varvec{u}}_{h})\Vert +\Vert ({\mathbf {p}},\varphi )-({\mathbf {p}}_{h},\varphi _{h})\Vert \nonumber \\&\quad \le {\mathbf {C}}({\varvec{g}},{\varvec{u}}_{D},\varphi _{D})\,\{ \Vert ({\varvec{\sigma }},{\varvec{u}})-({\varvec{\sigma }}_{h},{\varvec{u}}_{h})\Vert +\Vert ({\mathbf {p}},\varphi )-({\mathbf {p}}_{h},\varphi _{h})\Vert \}\nonumber \\&\quad \quad + C_{{\mathrm {ST}}} \,( 1+c_{1}(\Omega )\,(\kappa _{1}^{2}+1)^{1/2}\,\Vert {\varvec{u}}-{\varvec{u}}_{h} \Vert _{1,\Omega })\,{\mathrm {dist}}( \,({\varvec{\sigma }},{\varvec{u}}),{\mathbb {H}}_{h}^{{\varvec{\sigma }}}\times {\mathbf {H}}_{h}^{{\varvec{u}}} )\nonumber \\&\quad \quad +\widetilde{C}_{{\mathrm {ST}}}( 1+c_{2}(\Omega )\,(\kappa _{4}^{2}+1)^{1/2}\, \Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }\, \Vert \, {\varvec{u}}-{\varvec{u}}_{h} \,\Vert _{1,\Omega })\,{\mathrm {dist}}( \,({\mathbf {p}},\varphi ),{\mathbf {H}}_{h}^{{\mathbf {p}}}{\mathrm {H}}_{h}^{\varphi })\nonumber \\ \end{aligned}$$

(5.7)

where

$$\begin{aligned} {\mathbf {C}}({\varvec{g}},{\varvec{u}}_{D},\varphi _{D}):= \max \{{\mathbf {C}}_{1}({\varvec{g}},{\varvec{u}}_{D},\varphi _{D}),\,{\mathbf {C}}_{2}({\varvec{g}},{\varvec{u}}_{D},\varphi _{D})\}, \end{aligned}$$

with

$$\begin{aligned} \displaystyle {\mathbf {C}}_{1}({\varvec{g}},{\varvec{u}}_{D},\varphi _{D}):= & {} C_{{\mathrm {ST}}}\,(\mu ^{2}+\kappa _{2}^{2})\,\Vert {\varvec{g}}\Vert _{\infty ,\Omega },\\ {\mathbf {C}}_{2}({\varvec{g}},{\varvec{u}}_{D},\varphi _{D}):= & {} C_{1}(r\Vert {\varvec{g}}\Vert _{\infty ,\Omega }+\Vert {\varvec{u}}_{D}\Vert _{0,\Gamma }+\Vert {\varvec{u}}_{D}\Vert _{1/2,\Gamma } \,) +C_{2}\,(\Vert \varphi _{D}\Vert _{0,\Gamma }\,\\&+\Vert \varphi _{D}\Vert _{1/2,\Gamma } ) \end{aligned}$$

and

$$\begin{aligned} C_{1}:=c_{{\mathbf {S}}}\,C_{{\mathrm {ST}}}\,c_{1}(\Omega )\,(\kappa _{1}^{2}+1)^{1/2} \quad \text{ and }\quad C_{2}:=c_{\widetilde{{\mathbf {S}}}}\,\widetilde{C}_{{\mathrm {ST}}}\,c_{2}(\Omega )\,(\kappa _{4}^{2}+1)^{1/2}\,\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }. \end{aligned}$$

Notice that the constants multiplying the distances ${\mathrm {dist}}(({\mathbf {p}},\varphi ), {\mathbf {H}}_{h}^{{\mathbf {p}}}\times {\mathrm {H}}_{h}^{\varphi } )$ and ${\mathrm {dist}}(({\varvec{\sigma }},{\varvec{u}}), {\mathbb {H}}_{h}^{{\varvec{\sigma }}}\times {\mathbf {H}}_{h}^{{\varvec{u}}} )$ are both controlled by constants, parameters, and data only since $\Vert {\varvec{u}}-{\varvec{u}}_h\Vert$ can be controlled by (3.47) and (4.9). Also, clearly the constants ${\mathbf {C}}_{i}({\varvec{g}}, {\varvec{u}}_{D},\varphi _{D}),$ $i\in \{1,2\},$ depend linearly on ${\varvec{g}},$ ${\varvec{u}}_{D},$ and $\varphi _{D}$.

As a consequence of the above, we are now in position of establishing the main result of this section providing the requested Cea estimate.

Theorem 5.4

Assume that the data ${\varvec{g}}$, ${\varvec{u}}_{D}$ and $\varphi _{D}$ satisfy:

$$\begin{aligned} {\mathbf {C}}_i({\varvec{g}},{\varvec{u}}_D,\varphi _D) \le \frac{1}{2} \quad \forall i \in \{1,2\}. \end{aligned}$$

(5.8)

Then, there exists a positive constant $C_{3}$, depending only on parameters, data and other constants, all of them independent of h, such that

$$\begin{aligned}&\displaystyle \Vert ({\varvec{\sigma }},{\varvec{u}})-({\varvec{\sigma }}_{h},{\varvec{u}}_{h})\Vert + \Vert ({\mathbf {p}},\varphi )-({\mathbf {p}}_{h},\varphi _{h})\Vert \nonumber \\&\displaystyle \quad \le C_{3}\,\{ {\mathrm {dist}} (({\varvec{\sigma }},{\varvec{u}}),{\mathbb {H}}_{h}^{{\varvec{\sigma }}}\times {\mathbf {H}}_{h}^{{\varvec{u}}} ) + {\mathrm {dist}}(({\mathbf {p}},\varphi ),{\mathbf {H}}_{h}^{{\mathbf {p}}}\times {\mathrm {H}}_{h}^{\varphi } ) \}. \end{aligned}$$

(5.9)

Proof

From (5.8) and (5.7), it follows that

$$\begin{aligned}&\Vert ({\varvec{\sigma }},{\varvec{u}})-({\varvec{\sigma }}_{h},{\varvec{u}}_{h})\Vert +\Vert ({\mathbf {p}},\varphi )-({\mathbf {p}}_{h},\varphi _{h})\Vert \\&\quad \le 2\,C_{{\mathrm {ST}}} \,( 1+c_{1}(\Omega )\,(\kappa _{1}^{2}+1)^{1/2}\,\Vert {\varvec{u}}-{\varvec{u}}_{h} \Vert _{1,\Omega }\,)\,{\mathrm {dist}}( \,({\varvec{\sigma }},{\varvec{u}}),{\mathbb {H}}_{h}^{{\varvec{\sigma }}}\times {\mathbf {H}}_{h}^{{\varvec{u}}} )\\&\quad \quad +2\,\widetilde{C}_{{\mathrm {ST}}}( 1+c_{2}(\Omega )\,(\kappa _{4}^{2}+1)^{1/2}\, \Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }\, \Vert \, {\varvec{u}}-{\varvec{u}}_{h} \,\Vert _{1,\Omega }){\mathrm {dist}}( \,({\mathbf {p}},\varphi ),{\mathbf {H}}_{h}^{{\mathbf {p}}}{\times } {\mathrm {H}}_{h}^{\varphi } ), \end{aligned}$$

and then, the rest of the proof reduces to employ the upper bounds for $\Vert {\varvec{u}}\Vert _{1,\Omega }$ and $\Vert {\varvec{u}}_h\Vert _{1,\Omega }$ given in (3.47) and (4.9), respectively, and the triangle inequality. $\square$

Finally, we complete our a priori error analysis with the following result which provides the corresponding rate of convergence of our Galerkin scheme with the specific finite element subspaces ${\mathbb {H}}_{h}^{{\varvec{\sigma }}},$ ${\mathbf {H}}_{h}^{{\varvec{u}}},$ ${\mathbf {H}}_{h}^{{\mathbf {p}}},$ and ${\mathrm {H}}_{h}^{\varphi }$ introduced in Sect. 4.3.

Theorem 5.5

In addition to the hypotheses of Theorems 3.9, 4.8 and 5.4, assume that there exists $s>0$ such that ${\varvec{\sigma }}\in {\mathbb {H}}^{s}(\Omega ),$ ${\mathbf {div}}\,{\varvec{\sigma }}\in {\mathbf {H}}^{s}(\Omega ),$ ${\varvec{u}}\in {\mathbf {H}} ^{s+1}(\Omega ),$ ${\mathbf {p}}\in {\mathbf {H}}^{s}(\Omega ),$ ${\mathrm {div}}\,{\mathbf {p}}\in {\mathrm {H}}^{s}(\Omega ),$ and $\varphi \in {\mathrm {H}}^{s+1}(\Omega ),$ and that the finite element subspaces are defined by (4.11)–(4.14). Then, there exist $C> 0,$ independent of h,  such that there holds

$$\begin{aligned}&\displaystyle \Vert ({\varvec{\sigma }},{\varvec{u}})-({\varvec{\sigma }}_{h},{\varvec{u}}_{h})\Vert +\Vert ({\mathbf {p}},\varphi )-({\mathbf {p}}_{h},\varphi _{h})\Vert \nonumber \\&\displaystyle \quad \le C\,h^{\min \{s,k+1\}}\{\Vert {\varvec{\sigma }}\Vert _{s,\Omega }+\Vert {\mathbf {div}}\,{\varvec{\sigma }}\Vert _{s,\Omega }+\Vert {\varvec{u}}\Vert _{s+1,\Omega } +\Vert {\mathbf {p}}\Vert _{s,\Omega } +\Vert {\mathrm {div}}\,{\mathbf {p}}\Vert _{s,\Omega }\nonumber \\&\quad \quad + \Vert \varphi \Vert _{s+1,\Omega }\}. \end{aligned}$$

(5.10)

Proof

It follows from the Cea estimate (5.9) and the approximation properties $({\mathbf {AP}}_{h}^{{\varvec{\sigma }}})$, $({\mathbf {AP}}_{h}^{{\varvec{u}}})$, $({\mathbf {AP}}_{h}^{{\mathbf {p}}})$ and $({\mathbf {AP}}_{h}^{\varphi })$ specified in Sect. 4.3. $\square$

6 Numerical results

In this section we present two examples illustrating the performance of our augmented fully-mixed finite element scheme (4.2) on a set of quasi-uniform triangulations of the corresponding domains and considering the finite element spaces introduced in Sect. 4.3. Our implementation is based on a FreeFem $++$ code (see [17]), in conjunction with the direct linear solver UMFPACK (see [12]). A Picard algorithm with a fixed tolerance $tol=1e-8$ has been used for the corresponding fixed-point problem (4.8) and the iterations are terminated once the relative error of the entire coefficient vectors between two consecutive iterates is sufficiently small, i.e.,

$$\begin{aligned} \frac{\Vert {\mathbf {coeff}}^{m+1} - {\mathbf {coeff}}^m\Vert }{\Vert {\mathbf {coeff}}^{m+1}\Vert } \le \, tol, \end{aligned}$$

where $\Vert \cdot \Vert$ stands for the usual euclidean norm in ${\mathbb {R}}^N$, with N denoting the total number of degrees of freedom defining the finite element subspaces ${\mathbb {H}}_h^{{\varvec{\sigma }}}$, ${\mathbf {H}}_h^{{\varvec{u}}}$, ${\mathbf {H}}_{h}^{{\mathbf {p}}}$ and ${\mathrm {H}}^{\varphi }_h$. For each example shown below we simply take $({\varvec{u}}_h^0,\varphi _h^0)=({\mathbf {0}}, 0)$ as initial guess, and the stabilization parameters are chosen according to Lemmas 3.1 and 3.3 to be specified below on each example.

We now introduce some additional notation. The individual and total errors are denoted by:

$$\begin{aligned} \mathtt{e}({\varvec{\sigma }}):= & {} \Vert {\varvec{\sigma }}- {\varvec{\sigma }}_h\Vert _{{\mathbf {div}};\Omega },\quad \mathtt{e}({\varvec{u}}) :=\Vert {\varvec{u}}- {\varvec{u}}_h\Vert _{1,\Omega }, \quad \mathtt{e}(p):=\Vert p - p_h\Vert _{0,\Omega },\\ \mathtt{e}({\mathbf {p}}):= & {} \Vert {\mathbf {p}}- {\mathbf {p}}_h\Vert _{{\mathrm {div}};\Omega },\quad \mathtt{e}(\varphi ) :=\Vert \varphi - \varphi _h\Vert _{1,\Omega }, \end{aligned}$$

and

$$\begin{aligned} \mathtt{e}({\varvec{\sigma }},{\varvec{u}},{\mathbf {p}},\varphi ) := \{\mathtt{e}({\varvec{\sigma }})^2 + \mathtt{e}({\varvec{u}})^2 + \mathtt{e}({\mathbf {p}})^2 + \mathtt{e}(\varphi )^2\}^{1/2}, \end{aligned}$$

where p is the exact pressure of the fluid and $p_h$ is the postprocessed discrete pressure suggested by the formulae given in (2.5) and (3.3), namely,

$$\begin{aligned} p_h = -\displaystyle \frac{1}{n}\,{\mathrm {tr}}\{ {\varvec{\sigma }}_h+c_h {\mathbb {I}} + ({\varvec{u}}_h\otimes {\varvec{u}}_h)\} , \quad \mathrm{with}\quad c_h := -\frac{1}{n|\Omega |} \, \int _\Omega {\mathrm {tr}}({\varvec{u}}_h\otimes {\varvec{u}}_h). \end{aligned}$$

Similarly as in [8], we also compute further variables of interest such as the velocity gradient $\nabla {\varvec{u}}_{h}$, the shear stress tensor $\widetilde{{\varvec{\sigma }}}_{h}$, the vorticity $\varvec{\omega }_{h}$ and the temperature gradient $\nabla \varphi _{h}$ according to (2.7) in Sect. 2. Besides, it is not difficult to show that there exist $C,\widetilde{C} > 0$, independents of h, such that the following a priori estimates are satisfied:

$$\begin{aligned}&\displaystyle \Vert p - p_h\Vert _{0,\Omega }+\Vert \widetilde{{\varvec{\sigma }}} - \widetilde{{\varvec{\sigma }}}_{h}\Vert _{0,\Omega }+\Vert \nabla {\varvec{u}}- \nabla {\varvec{u}}_{h}\Vert _{0,\Omega } +\Vert \varvec{\omega } - \varvec{\omega }_h\Vert _{0,\Omega }\,\\&\quad \le C\, \{\Vert {\varvec{\sigma }}- {\varvec{\sigma }}_h\Vert _{{\mathbf {div}};\Omega } + \Vert {\varvec{u}}- {\varvec{u}}_h\Vert _{1,\Omega } \} ,\\&\quad \quad \displaystyle \Vert \nabla \varphi -\nabla \varphi _{h}\Vert _{0,\Omega }\le \widetilde{C}\,\{ \Vert {\mathbf {p}}-{\mathbf {p}}_{h} \Vert _{{\mathrm {div}};\Omega } + \Vert \varphi - \varphi _h\Vert _{1,\Omega } + \Vert {\varvec{u}}- {\varvec{u}}_h\Vert _{1,\Omega } \}, \end{aligned}$$

which says that the rates of convergence of the postprocessed variables coincide with those provided by (5.10) (cf. Theorem 5.5).

Next, as usual we let $r(\cdot )$ be the experimental rate of convergence given by

$$\begin{aligned} r(\cdot ):=\frac{\log (\mathtt{e}(\cdot )/\mathtt{e}'(\cdot ))}{\log (h/h')} \end{aligned}$$

where h and $h'$ denote two consecutive meshsizes with errors $\mathtt{e}$ and $\mathtt{e}'$.

Example 1

In our first example we illustrate the accuracy of our method in 2D by considering a manufactured exact solution defined on $\Omega :=(-1/2,3/2)\times (0,2)$. We initially take the viscosity $\mu =1$, the thermal conductivity ${\mathbb {K}}= e^{x_1+x_2}{\mathbb {I}}$ $\forall (x_1,x_2) \in \Omega$, which yields $\kappa _{0}=e^{-1/2}$ and $\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }=e^{1/2}$, and the external force ${\mathbf {g}}=(0,-1)^{\mathtt{t}}$. Later on, further numerical results with $\mu \in \{0.1, 0.05\}$ are also reported when the behavior of the iterative method with respect to small values of the viscosity is illustrated. In turn, as for the stabilization parameters, they are chosen either as the mean values of the corresponding feasible ranges, or such that the intermediate constants defining the ellipticity constants $\alpha (\Omega )/2$ and $\widetilde{\alpha }(\Omega )/2$ of the uncoupled problems (cf. Lemmas 3.1, 3.3) are maximized. In particular, for this example we take

$$\begin{aligned} \kappa _{1}= & {} \mu \quad \kappa _{2}=1,\quad \kappa _{3}=\mu ^{2}/2, \nonumber \\ \kappa _{4}= & {} \dfrac{\kappa _{0}}{\Vert {\mathbb {K}}^{-1}\Vert ^{2}_{\infty ,\Omega }}\approx 0.224,\quad \kappa _{5}=\dfrac{\kappa _{0}}{2}\,\approx \,0.303,\quad \kappa _{6}=\dfrac{\kappa _{0}}{2\Vert {\mathbb {K}}^{-1}\Vert _{\infty ,\Omega }}\,\approx \,0.1848.\nonumber \\ \end{aligned}$$

(6.1)

Table 1 Example 1: degrees of freedom, meshsizes, errors, rates of convergence, and number of iterations for the fully-mixed ${\mathbb {RT}}_0- {\mathbf {P}}_1- {\mathbf {RT}}_0- {\mathrm {P}}_1$ and ${\mathbb {RT}}_1- {\mathbf {P}}_2- {\mathbf {RT}}_1- {\mathrm {P}}_2$ approximations of the Boussinesq equations

In turn, the terms on the right-hand sides are adjusted so that the exact solution is given by the functions

$$\begin{aligned} \varphi (x_1 ,x_2 )= & {} x_1^2(x_2^2 + 1),\quad {\varvec{u}}(x_1 ,x_2 )=\left( \begin{array}{c} 1 -e^{\vartheta x_1}\cos (2\pi x_2)\\ \frac{\vartheta }{2\pi }e^{\vartheta x_1}\sin (2\pi x_2) \end{array}\right) , \quad \text{ and }\;\;\\ p(x_1 ,x_2 )= & {} -\frac{1}{2}e^{2\vartheta x_1} + \bar{p}, \end{aligned}$$

where

$$\begin{aligned} \vartheta := \frac{-8\pi ^2}{\mu ^{-1}+\sqrt{\mu ^{-2} +16\pi ^2}}. \end{aligned}$$

and the constant $\bar{p}$ is such that $\int _\Omega p=0$. Notice that $({\varvec{u}},p)$ is the well known analytical solution for the Navier–Stokes problem obtained by Kovasznay [19], which presents a boundary layer at $\{-1/2\}\times (0,2)$.

Fig. 1

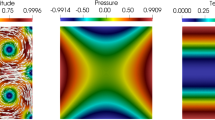
Example 1: velocity vector field, horizontal and vertical velocity with streamlines (top left, middle and right, resp), approximate temperature, magnitude of its gradient and pressure (left, middle and right of center row, resp), components $\widetilde{{\varvec{\sigma }}}_{11,h},$ $\widetilde{{\varvec{\sigma }}}_{12,h}$ of the stress (left and middle of bottom row, resp) and vorticity component $\omega _{12,h}$ obtained with $N=173571$ for the family ${\mathbb {RT}}_1- {\mathbf {P}}_2- {\mathbf {RT}}_1-\mathrm{P}_2$

Table 2 Example 1: $\kappa _1$ vs. $\mathtt{e}({\varvec{\sigma }},{\varvec{u}},\varphi ,\lambda )$ for the mixed ${\mathbb {RT}}_0-{\mathbf {P}}_{1}-{\mathbf {RT}}_{0}-{\mathrm {P}}_{1}$ (top) and ${\mathbb {RT}}_1-{\mathbf {P}}_{2}-{\mathbf {RT}}_{1}-{\mathrm {P}}_{2}$ (bottom) approximations of the Boussinesq equations with $h=0.0968$ and $\mu =1$

Table 3 Example 1: $(\kappa _4,\kappa _{5},\kappa _{6})$ vs. $\mathtt{e}({\varvec{\sigma }},{\varvec{u}},\varphi ,\lambda )$ for the mixed $\mathbb {RT}_0-{\mathbf {P}}_{1}-{\mathbf {RT}}_{0}-{\mathrm {P}}_{1}$ (top) and ${\mathbb {RT}}_1-{\mathbf {P}}_{2}-{\mathbf {RT}}_{1}-{\mathrm {P}}_{2}$ (bottom) approximations of the Boussinesq equations with $h=0.0968$ and $\mu =1$

Table 4 Example 1: convergence behaviour of the iterative method for the mixed ${\mathbb {RT}}_0-{\mathbf {P}}_{1}-{\mathbf {RT}}_{0}-{\mathrm {P}}_{1}$ (top) and ${\mathbb {RT}}_1-{\mathbf {P}}_{2}-{\mathbf {RT}}_{1}-{\mathrm {P}}_{2}$ (bottom) approximations with respect to the viscosity $\mu$ and the meshsize h

Table 5 Example 1 (with $\mu = 0.1$): degrees of freedom, meshsizes, errors, rates of convergence, and number of iterations for the fully-mixed ${\mathbb {RT}}_0- {\mathbf {P}}_1- {\mathbf {RT}}_0- {\mathrm {P}}_1$ and ${\mathbb {RT}}_1- {\mathbf {P}}_2- {\mathbf {RT}}_1- {\mathrm {P}}_2$ approximations of the Boussinesq equations

Table 6 Example 1 (with $\mu = 0.05$): degrees of freedom, meshsizes, errors, rates of convergence, and number of iterations for the fully-mixed ${\mathbb {RT}}_0- {\mathbf {P}}_1- {\mathbf {RT}}_0- {\mathrm {P}}_1$ and ${\mathbb {RT}}_1- {\mathbf {P}}_2- {\mathbf {RT}}_1- {\mathrm {P}}_2$ approximations of the Boussinesq equations

In Table 1 we summarize the convergence history for a sequence of quasi-uniform triangulations, considering the finite element spaces introduced in Sect. 4.3 with $k=0$ and $k=1$. We observe there that the rate of convergence $O(h^{k+1})$ predicted by Theorem 5.5 (when $s = k+1$) is attained in all the cases for unknowns and postprocessed variables. In turn, we also notice that $r(\varphi )$ is larger than expected, which we believe is due to the smoothness of $\varphi$ (a polynomial function of degree 2 in each one of its variables $x_1$ and $x_2$). Next, in Fig. 1 we display the approximate velocity magnitude, horizontal and vertical components of the velocity with streamlines, the approximate temperature and magnitud of its gradient, the approximate pressure, and some components of the stress and vorticity tensors of the fluid. All the figures were built using the ${\mathbb {RT}}_1- {\mathbf {P}}_2- {\mathbf {RT}}_1- {\mathrm {P}}_2$ approximation with $N=173{,}571$ degrees of freedom. In all the cases we observe that the finite element subspaces employed provide very accurate approximations to all the unknowns, thus confirming a good behaviour on the boundary layer as well.

Next, we aim to study the robustness and the stability of our method with respect to the stabilization parameters and considering a fixed mesh with $h=0.0968.$ We start by analyzing the convergence of the scheme by varying the parameters corresponding to the fluid equation. In this case, we take $\mu =1$ and observe the total error behavior considering $\kappa _{1}=\delta =\mu /(1\times 10^{n}),$ for $n=0,\dots ,4$. The parameters $\kappa _{2}$ and $\kappa _{3}$ are computed in function of $\kappa _{1}$ and $\delta ,$ and meanwhile the parameters $\kappa _{4},$ $\kappa _{5}$ and $\kappa _{6}$ are taken as in (6.1). Next, we study the error behaviour by varying now the parameters associated to the heat equation by considering each $\kappa _{i}$ as $\kappa _{i}/(1\times 10^{n})$ for $i=4,5,6,$ respectively, and $n=0,\dots ,4$, where $\kappa _{i}$ $(i=1,\dots ,6)$ as in (6.1). In Tables 2 and 3 we display the corresponding results for each case and observe, similarly as in our previous mixed-primal scheme [10], that there is a sufficiently large range for the parameters yielding a stable Galerkin scheme in the sense that the corresponding total error remains bounded. This fact certainly confirms the robustness of the fully-mixed method with respect to the stabilization parameters.

Table 7 Example 2: degrees of freedom, meshsizes, errors, rates of convergence, and number of iterations for the fully-mixed ${\mathbb {RT}}_0- {\mathbf {P}}_1- {\mathbf {RT}}_0- {\mathrm {P}}_1$ approximation of the Boussinesq equations

In turn, in Table 4 we show the behaviour of the iterative method as a function of the viscosity number and the meshsize h. We consider both ${\mathbb {RT}}_0- {\mathbf {P}}_1- {\mathbf {RT}}_0- {\mathrm {P}}_1$ and ${\mathbb {RT}}_1- {\mathbf {P}}_2- {\mathbf {RT}}_1- {\mathrm {P}}_2$ approximations, and the stabilization parameters are chosen as before. We observe here that the smaller the parameter $\mu$ the higher the number of resulting iterations. In particular, we notice that when $\mu =0.01$ the iterative method does not converge, reason why this information is not reported in those cases. However, it is also important to remark that for viscosities not smaller than 0.05 the number of iterations remains reasonably bounded. In addition, as shown in Tables 5 and 6, the rates of convergence for $\mu \in \{0.1, 0.05\}$ are still as predicted by the theory.

Therefore, for simulating problems with small viscosity, the foregoing discussion and results suggest to decrease gradually this physical parameter, using meshes with small enough size and high order approximation k, along with alternative techniques such as continuation method on the viscosity. We plan to report on these issues in a separate work.

Fig. 2

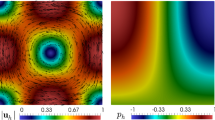
Example 2: magnitude and streamlines of the approximate velocity, temperature magnitude and vector field (top left, middle and right, resp), approximate components of the fluid stress $\widetilde{{\varvec{\sigma }}}_{13,h}$, $\widetilde{{\varvec{\sigma }}}_{23,h}$ and $\widetilde{{\varvec{\sigma }}}_{33,h}$ (left, middle and right of center row, resp), approximate components of the fluid vorticity $\omega _{12,h}$, $\omega _{13,h}$ and $\omega _{23,h}$ (left, middle and right of bottom row, resp) obtained with $N=1{,}741{,}188$ for the family ${\mathbb {RT}}_0- {\mathbf {P}}_1- {\mathbf {RT}}_0-\mathrm{P}_1$

Example 2

This example illustrates the performance of our method in 3D by considering a manufactured exact solution defined in the cube $\Omega :=(0,1)^{3}$, which is given by

$$\begin{aligned}{\varvec{u}}(x_{1},x_{2},x_{3})=\left( \begin{array}{c} 4x_{1}x_{2}x_{3}(x_{3}-1)(x_{2}-1)(x_{2}-x_{3})(x_{1}-1)^{2}\\ -4x_{1}x_{2}^{2}x_{3}(x_{2}-1)^{2}(x_{3}-1)(x_{1}-1)(x_{1}-x_{3})\\ 4x_{1}x_{2}x_{3}^{2}(x_{3}-1)^{2}(x_{2}-1)(x_{1}-1)(x_{1}-x_{2})^{2}\\ \end{array} \right) , \end{aligned}$$

and

$$\begin{aligned} p(x_{1},x_{2},x_{3})=x_{1}-\dfrac{1}{2}\quad \text{ and }\quad \varphi (x_{1},x_{2},x_{3})=e^{x_{1}+x_{2}+x_{3}} \end{aligned}$$

We take the viscosity $\mu =1$, the thermal conductivity ${\mathbb {K}}={\mathbb {I}}$, and the external force ${\mathbf {g}}=(0,0,-1)^\mathtt{{t}}$. Again, the stabilization parameters are optimally chosen, i.e.,

$$\begin{aligned} \kappa _{1}= & {} \mu ,\quad \kappa _{2}=\mu ,\quad \kappa _{3}=\mu ^{2}/2,\\ \kappa _{4}= & {} 1,\quad \kappa _{5}=1/2,\quad \text{ and }\quad \kappa _{6}=1/2. \end{aligned}$$

For this example we consider the finite element spaces introduced in Sect. 4.3 with $k=0$ on a sequence of quasi-uniform triangulations. In Table 7 the convergence history is summarized and it is observed there that the rate of convergence O(h) predicted by Theorem 5.5 is attained by all the unknowns and postprocessed variables. Next, in Fig. 2 we display the approximate velocity magnitude, streamlines, the approximate temperature gradient field and its magnitude as well as some components of the stress and vorticity tensors of the fluid. All the figures were built using the ${\mathbb {RT}}_0 - {\mathbf {P}}_1- {\mathbf {RT}}_0- {\mathrm {P}}_1$ approximation with $N=1{,}741{,}188$ degrees of freedom.