On a functional inequality arising in the analysis of finite-volume methods

Abstract

We establish a Poincaré–Wirtinger type inequality on some particular domains with a precise estimate of the constant depending only on the geometry of the domain. This type of inequality arises, for instance, in the analysis of finite volume (FV) numerical methods. As an application of our result, we prove uniform a priori bounds for the FV approximate solutions of the heat equation with Ventcell boundary conditions in the natural energy space defined as the set of those functions in $H^1(\varOmega )$ whose traces belong to $H^1(\partial \varOmega )$. The main difficulty here comes from the fact that the approximation is performed on non-polygonal control volumes since the domain itself is non-polygonal.

1 Introduction

The main goal of this paper is to study functional inequalities of the following form

$$\begin{aligned} \left| \frac{1}{m_{{\scriptscriptstyle \sigma }}} \int _{\scriptscriptstyle \sigma }u - \frac{1}{m_{{\scriptscriptstyle \mathcal {K}}}}\int _{\scriptscriptstyle \mathcal {K}}u\right| \le C \mathrm {diam}({\mathcal {K}}) \frac{1}{m_{{\scriptscriptstyle \mathcal {K}}}} \int _{\scriptscriptstyle \mathcal {K}}|Du|, \ \ \forall u\in W^{1,1}(\mathbb R^n), \end{aligned}$$

(1)

where ${\mathcal {K}}$ is a bounded connected Lipschitz domain in $\mathbb R^n$ and $\sigma$ a non empty open subset of $\partial {\mathcal {K}}$. We have denoted by $m_{{\scriptscriptstyle \mathcal {K}}}$ the volume of ${\mathcal {K}}$ and $m_{{\scriptscriptstyle \sigma }}$ the surface measure of $\sigma$, namely its $(n-1)$-dimensional Hausdorff measure. Those notations will be used all along this paper.

The fact that such an inequality holds is straightforward, for instance by applying the Bramble-Hilbert lemma (see for instance [2]). Our main purpose is to estimate the dependence of the constant C with respect to the geometry of the domain ${\mathcal {K}}$. In the particular case of a convex domain ${\mathcal {K}}$ the mean-value inequality immediately implies that

$$\begin{aligned} \left| \frac{1}{m_{{\scriptscriptstyle \sigma }}} \int _{\scriptscriptstyle \sigma }u - \frac{1}{m_{{\scriptscriptstyle \mathcal {K}}}}\int _{\scriptscriptstyle \mathcal {K}}u\right| \le \mathrm {diam}({\mathcal {K}}) \left( \sup _{{\mathcal {K}}} |Du|\right) , \ \ \forall u\in W^{1,\infty }(\mathbb R^n), \end{aligned}$$

(2)

with no geometric constant in the right-hand side. The inequality (1) has to be seen as a generalisation of (2) to less regular functions u. This loss of regularity induces that the constant in the inequality may depend on the shape of ${\mathcal {K}}$. Observe that, if ${\mathcal {K}}$ is not convex, one has to replace $\sup _{{\mathcal {K}}} |Du|$ by $\sup _{\mathrm{Conv}({\mathcal {K}})} |Du|$ in (2), where $\mathrm{Conv}({\mathcal {K}})$ is the convex hull of ${\mathcal {K}}$.

Inequalities of the form (1) play an important role in the analysis of finite volume numerical methods for elliptic or parabolic equations on general meshes, which is our main motivation. They are meant to be applied to each cell (control volume) ${\mathcal {K}}$ in a mesh of a given computational domain. They allow to prove stability estimates in (discrete) Sobolev spaces for the natural $L^2$ projections of the functions defined on $\varOmega$ and the projections of their traces. To our knowledge, such inequalities have only been established up to now in the framework of polygonal sets ${\mathcal {K}}$. However, for more complex situations, like for the discretisation of the heat equation with dynamic Ventcell boundary conditions, we are interested in proving such inequalities for non polygonal domains. We detail such an application in Sect. 6.

Let us mention some references where such inequalities are proved and/or used in the finite volume framework.

• In [7, Lemma 3.4] (see also [4, Lemma 7.2] and [5, Lemmas 6.2 and 6.3]), (1) is proved (in 2D for simplicity) when ${\mathcal {K}}$ is polygonal and convex, with a constant C depending only on the number of edges/faces of ${\mathcal {K}}$, and on the shape-regularity ratio $(\mathrm {diam}({\mathcal {K}}))^2/m_{{\scriptscriptstyle \mathcal {K}}}$.

• In [6, Lemma 6.6], the inequality is slightly generalized to a polygonal ${\mathcal {K}}$ which is simply supposed to be star-shaped with respect to a suitable ball.

• In [1], such inequalities are used for the convergence and error analysis of some approximation of non-linear Leray–Lions type operators (a model of which is the p-Laplace problem).

Finally, we refer to [9] for an example of analysis of a more complex model of a non-linear evolution equation associated with a non-linear dynamical boundary condition. This reference was in fact our main motivation for the present work. Indeed, compared to the other references above, the numerical method in [9] is derived on non-polygonal control volumes, so that an inequality like (1) is needed on non-polygonal open sets ${\mathcal {K}}$, see also Sect. 6.

The outline of the paper is the following. In Sect. 2, we state our main result (Theorem 1 in 2D) and the geometric assumptions that we shall work with in the sequel. Section 3 is devoted to the proof of the main result whereas in Sect. 4, we state and prove a sort of Poincaré–Wirtinger inequality related to the functional inequality proved in Theorem 1. Section 5 is dedicated to the extension of our main inequality in the higher dimensional case (i.e. in $\mathbb R^n$, for $n\ge 3$). Finally, in order to illustrate this work, we provide an application, as simple as possible, of Theorem 1 to the proof of uniform discrete energy estimates for a finite volume approximation of a toy system on a non-polygonal domain $\varOmega$.

2 Main result

Given a $C^1$ curve $\sigma \subset \mathbb R^2$ and a point $z_*\in \mathbb R^2\setminus \sigma$, we consider the following domain $T$:

$$\begin{aligned} T=\left\{ z_*+t(\gamma (\theta )-z_*) : t\in ]0,1[, \theta \in ]0,1[\right\} , \end{aligned}$$

where $\gamma :[0,1]\rightarrow \mathbb R^2$ is a $C^1$ parametrization of $\sigma$: $\gamma ([0,1])=\sigma$, $\gamma$ is one-to-one and $|\gamma '|$ does not vanish. Without loss of generality, we choose the parametrization $\gamma$ in such a way that $|\gamma '(\theta )|=m_{{\scriptscriptstyle \sigma }}$ for every $\theta \in [0,1]$.

We say that $T$ is a pseudo-triangle if for every $x \in \sigma$,

$$\begin{aligned} \left\{ z_*+t(x-z_*) : t\ge 0\right\} \cap \sigma = \{x\}. \end{aligned}$$

(3)

Without loss of generality, we shall assume that the vertex $z_*$ of T opposite to $\sigma$ is the origin $(0,0)$ of $\mathbb R^2$.

Theorem 1

Let $T$ be a pseudo-triangle as above. We assume that there exist $\mu , \nu >0$ such that for any sub-arc $\tilde{\sigma }\subset \sigma$, the corresponding sub-triangle $T_{\tilde{\sigma }}$ (see Fig. 1) satisfies

$$\begin{aligned} \mu \le \frac{m_{\scriptscriptstyle {T_{\tilde{\sigma }}}}}{m_{\tilde{\scriptscriptstyle {\sigma }}}} \le \nu . \end{aligned}$$

(4)

Then for every $p\in [1,+\infty [$ and every $u \in W^{1,p}(T)$,

$$\begin{aligned} \left| \frac{1}{m_{{\scriptscriptstyle \sigma }}} \int _{\sigma } u - \frac{1}{m_{\scriptscriptstyle T}}\int _T u \right| ^p \le C^p (m_{{\scriptscriptstyle \sigma }}+\mathrm {diam}(T))^p \frac{1}{m_{\scriptscriptstyle T}} \int _{T} |Du|^p, \end{aligned}$$

(5)

where $C$ only depends on the ratio $\frac{\nu }{\mu }$.

Fig. 1

The pseudo-triangle T with its curved edge $\sigma$ and one of its sub-triangle

As already noticed in the introduction, the main issue is to understand how the constant in the inequality depends on the geometry of this pseudo-triangle T.

Remark 1

For a real flat triangle T, the quantity $\frac{m_{\scriptscriptstyle {T_{\tilde{\sigma }}}}}{m_{\tilde{\scriptscriptstyle {\sigma }}}}$ does not depend on $\tilde{\sigma }$ and is equal to $\frac{m_{\scriptscriptstyle T}}{m_{{\scriptscriptstyle \sigma }}}$. In this particular case, we have $\mu =\nu$ and $m_{{\scriptscriptstyle \sigma }}\le \mathrm {diam}(T)$. Hence, we recover exactly the inequality proved in [7].

Proposition 1

Under assumption (3), the map $\theta \mapsto \text {det}\,(\gamma (\theta ), \gamma '(\theta ))$ is either nonnegative everywhere or nonpositive everywhere.

In the sequel, we assume that the orientation is chosen such that $\det (\gamma ,\gamma ') \ge 0$. Then, assumption (4) is equivalent to the following inequality

$$\begin{aligned} 2\mu m_{{\scriptscriptstyle \sigma }}\le \det \left( \gamma (\theta ), \gamma '(\theta )\right) \le 2 \nu m_{{\scriptscriptstyle \sigma }}, \ \ \forall \theta \in [0,1]. \end{aligned}$$

(6)

Proof

One can assume without loss of generality that $\gamma ([0,1])$ is contained in the half plane $\{(x,y)\in \mathbb {R}^2 : x > 0\}$. There exists a $C^1$ map $\varphi :[0,1]\rightarrow ]-\pi /2, \pi /2[$ such that for every $\theta \in [0,1]$,

$$\begin{aligned} \frac{\gamma (\theta )}{|\gamma (\theta )|} = (\cos \varphi (\theta ), \sin \varphi (\theta )). \end{aligned}$$

By (3), the map $\varphi$ is one-to-one. Hence, it is either strictly increasing or strictly decreasing. Assume for instance that $\varphi$ is strictly increasing.

This implies that for every $\theta \in [0,1)$, for every $h>0$ such that $\theta +h\in [0,1]$,

$$\begin{aligned} \begin{aligned} \text {det}\,\left( \gamma (\theta ), \frac{\gamma (\theta + h)-\gamma (\theta )}{h}\right)&= \frac{1}{h}\text {det}\,(\gamma (\theta ), \gamma (\theta + h))\\&= \frac{1}{h}|\gamma (\theta )||\gamma (\theta +h)| \sin (\varphi (\theta +h)-\varphi (\theta )) \ge 0. \end{aligned} \end{aligned}$$

Passing to the limit $h\rightarrow 0$ yields the desired result.

Assume now that (4) holds true, then let $0\le a < b \le 1$, and consider $\tilde{\sigma }=\gamma ([a,b])$. Then

$$\begin{aligned} m_{\tilde{\scriptscriptstyle {\sigma }}}= (b-a) m_{{\scriptscriptstyle \sigma }}\ \text {and} \ m_{\scriptscriptstyle {T_{\tilde{\sigma }}}}= \frac{1}{2}\int _a^b\det (\gamma (\theta ),\gamma '(\theta )) \, d\theta , \end{aligned}$$

thus thanks to (4),

$$\begin{aligned} \mu \le \frac{\int \nolimits _a^b \det (\gamma (\theta ),\gamma '(\theta )) \, d\theta }{2(b-a)m_{\sigma }} \le \nu , \end{aligned}$$

and we obtain (6) when b tends to a. Conversely, assume that (6) holds. Then (4) follows by integration of (6) on the segment $[a,b]$. $\square$

Remark 2

For some particular cases, we can estimate the constant in the inequality (5) even if the pseudo-triangle T does not satisfy assumption (4). In order to illustrate such a situation, we consider the pseudo-triangle T defined as follows (see Fig. 2)

$$\begin{aligned} T= & {} \{t \gamma (\theta ) : 0< t < 1, -\theta _0 < \theta < \pi +\theta _0\}, \text { with } \\ \gamma (\theta )= & {} \left( R\cos \theta , R \sin \theta +\frac{R}{\sin (\theta _0)}\right) , \end{aligned}$$

where $0<\theta _0<\frac{\pi }{2}$, $R>0$. Observe that $\gamma$ and $\gamma '$ are colinear for $\theta =-\theta _0$ or $\theta =\pi +\theta _0$ so that assumption (4) is not satisfied here. We decompose the pseudo-triangle T into the piece of disk P of radius R and center $A=(0,R/\sin (\theta _0))$ and the quadrilateral Q defined by: $Q=T\setminus P$.

First, we remark that assumption (4) is satisfied for the pseudo-triangle P with the ratio $\frac{\nu }{\mu }$ equal to 1 (see Remark 1). Then we can apply Theorem 1 to the pseudo-triangle P, so that there exists a constant $C_0>0$ which does not depend on R and $\theta _0$ such that

$$\begin{aligned} \left| \frac{1}{m_{{\scriptscriptstyle \sigma }}} \int _{\sigma } u - \frac{1}{m_{\scriptscriptstyle P}}\int _P u \right| \le C_0 R \frac{1}{m_{\scriptscriptstyle P}} \int _{P} |Du|. \end{aligned}$$

Moreover, since $P\subset T$ and T is convex, we can apply [4, Lemma 7.1],

$$\begin{aligned} \left| \frac{1}{m_{\scriptscriptstyle T}} \int _{T} u - \frac{1}{m_{\scriptscriptstyle P}}\int _P u \right| \le \widetilde{C_0} \frac{\left( \mathrm {diam}(T)\right) ^3}{m_{\scriptscriptstyle P}m_{\scriptscriptstyle T}} \int _{T} |Du|. \end{aligned}$$

Now, we want to control the volume of the pseudo-triangle T by the volume of P. We note that

$$\begin{aligned} m_{\scriptscriptstyle Q}=\frac{R^2}{\tan \theta _0}, \quad \quad m_{\scriptscriptstyle P}=\frac{R^2}{2}(\pi +2\theta _0), \quad \quad \mathrm {diam}(T)= R\left( 1+\frac{1}{\sin \theta _0}\right) . \end{aligned}$$

Hence

$$\begin{aligned} m_{\scriptscriptstyle Q}\le \frac{\mathrm {diam}(T)}{R} \frac{2}{\pi }m_{\scriptscriptstyle P}\end{aligned}$$

and then using that $R \le \mathrm {diam}(T)$,

$$\begin{aligned} m_{\scriptscriptstyle P}\ge \frac{\pi R}{\pi R +2\mathrm {diam}(T)} m_{\scriptscriptstyle T}\ge C_1 \frac{R}{\mathrm {diam}(T)} m_{\scriptscriptstyle T}. \end{aligned}$$

This implies

$$\begin{aligned} \left| \frac{1}{m_{{\scriptscriptstyle \sigma }}} \int _{\sigma } u - \frac{1}{m_{\scriptscriptstyle P}}\int _P u \right| \le \frac{C_0}{C_1} \mathrm {diam}(T) \frac{1}{m_{\scriptscriptstyle T}} \int _{T} |Du|, \end{aligned}$$

and

$$\begin{aligned} \left| \frac{1}{m_{\scriptscriptstyle T}} \int _{T} u - \frac{1}{m_{\scriptscriptstyle P}}\int _P u \right| \le \frac{\widetilde{C_0}}{C_1} \frac{\left( \mathrm {diam}(T)\right) ^4}{Rm_{\scriptscriptstyle T}^2} \int _{T} |Du|. \end{aligned}$$

Since $R\le \mathrm {diam}(T)$, $m_{\scriptscriptstyle T}\le (\mathrm {diam}(T))^2$, the above two inequalities yield

$$\begin{aligned} \left| \frac{1}{m_{\scriptscriptstyle T}} \int _{T} u -\frac{1}{m_{{\scriptscriptstyle \sigma }}} \int _{\sigma } u \right|\le & {} C \frac{(\mathrm {diam}(T))^4}{Rm_{\scriptscriptstyle T}^2} \int _{T} |Du|\nonumber \\\le & {} \frac{C'}{\sin (\theta _0)^2} \mathrm {diam}(T) \frac{1}{m_{\scriptscriptstyle T}}\int _{T} |Du|, \end{aligned}$$

where $C'$ is a universal constant. As expected we observe that the above inequality does not depend on R and blows up when $\theta _0$ goes to 0.

Fig. 2

A particular case which does not satisfy assumption (4)

3 Proof of Theorem 1

By Jensen’s inequality, we only need to establish the case $p=1$. We begin by proving a change of variables formula (Proposition 2) that let us express the differences between the mean values of a function on T and on $\sigma$ as a weighted integral of its gradient on T. Then, we prove in Proposition 3 that this change of variables can be realized with a diffeomorphism satisfying suitable estimates. This proposition relies on two technical Lemmas 1 and 2. Theorem 1 readily follows from those two propositions.

We notice that the existence of such a diffeomorphism is ensured by a general result of [3] but we have to be able to estimate the derivatives of this diffeomorphism in function of the geometry of T. That is why we resume explicitly the steps of [3] that allow us to control all the constants involved in the estimates.

In the sequel, we denote by $Q^2=]0,1[^2$ the unit cube in $\mathbb {R}^2$. By a standard approximation argument, one can assume that $\gamma \in C^{2}(0,1)$.

Proposition 2

Assume that there exists a Lipschitz continuous map $\varPhi : \overline{Q^2}\rightarrow \overline{T}$ such that

• 1. $\varPhi$ is a $C^1$ diffeomorphism from $Q^2$ onto $T$,

• 2. $\varPhi (0,\theta )=(0,0)$,

• 3. $\varPhi (1,\theta )=\gamma (\theta )$,

• 4. $\text {Jac}\,\varPhi (s,\theta )=2m_{\scriptscriptstyle T}s$.

Then for every $u\in W^{1,1}(T)$, we have

$$\begin{aligned} \frac{1}{m_{{\scriptscriptstyle \sigma }}} \int _{\sigma } u - \frac{1}{m_{\scriptscriptstyle T}}\int _T u = \frac{1}{2m_{\scriptscriptstyle T}}\int _T Du(x,y)\left[ s \partial _s \varPhi (s,\theta ) \right] _{(s,\theta ) =\varPhi ^{-1}(x,y)}\,dx\,dy. \end{aligned}$$

Proof

It follows from (6) that the pseudo-triangle $T$ is biLipschitz homeomorphic to a (true) triangle, see the proof of Lemma 3 in Sect. 4. In particular, $T$ is a Lipschitz domain. By a standard density argument, we can thus assume that $u\in C^{1}(\overline{T})$. Let

$$\begin{aligned} v(s,\theta )=u\circ \varPhi (s,\theta ) \text {Jac}\,\varPhi (s,\theta ). \end{aligned}$$

Then for every $(t,\theta )\in Q^2$,

$$\begin{aligned} v(1,\theta ) -v(t, \theta ) = \int _{t}^1 \partial _s v(s,\theta ) \,ds. \end{aligned}$$

Hence, thanks to the assumptions on $\varPhi$, we obtain

$$\begin{aligned} 2m_{\scriptscriptstyle T}u(\gamma (\theta )) - u\circ \varPhi (t,\theta ) \text {Jac}\,\varPhi (t,\theta ) = \int _{t}^{1} \left( \partial _s (u\circ \varPhi ) \text {Jac}\,\varPhi + 2m_{\scriptscriptstyle T}(u\circ \varPhi )\right) \,ds. \end{aligned}$$

By integrating this equality on $Q^2$ and using an obvious change of variables, we get

$$\begin{aligned} 2\frac{m_{\scriptscriptstyle T}}{m_{{\scriptscriptstyle \sigma }}} \int _{\sigma } u - \int _T u = \int _{0}^{1}\,d\theta \int _{0}^{1}\,dt \int _{t}^{1}\left( \partial _s (u\circ \varPhi ) \text {Jac}\,\varPhi + 2m_{\scriptscriptstyle T}(u\circ \varPhi )\right) \,ds. \end{aligned}$$

(7)

By Fubini theorem,

$$\begin{aligned}&\int _{0}^{1}\,d\theta \int _{0}^{1}\,dt \int _{t}^{1}\left( \partial _s (u\circ \varPhi ) \text {Jac}\,\varPhi + 2m_{\scriptscriptstyle T}(u\circ \varPhi )\right) \,ds\\&\quad = \int _{Q^2}s\left( \partial _s (u\circ \varPhi ) \text {Jac}\,\varPhi + 2m_{\scriptscriptstyle T}(u\circ \varPhi )\right) \,ds\,d\theta . \end{aligned}$$

Since $\text {Jac}\,\varPhi (s,\theta )=2m_{\scriptscriptstyle T}s$, the same change of variables gives

$$\begin{aligned}&\int _{Q^2}s\left( \partial _s (u\circ \varPhi ) \text {Jac}\,\varPhi + 2m_{\scriptscriptstyle T}(u\circ \varPhi )\right) \,ds\,d\theta \\&\quad = \int _T Du(x,y)\left[ s \partial _s \varPhi (s,\theta ) \right] _{(s,\theta ) =\varPhi ^{-1}(x,y)}\,dx\,dy + \int _{T}u. \end{aligned}$$

The claim now follows from this identity together with (7). $\square$

The proof of Theorem 1, that is the one of the inequality (5), is now a straightforward consequence of the following proposition that claims that we can build a suitable $\varPhi$ and apply Proposition 2.

Proposition 3

Under assumption (4), there exists a universal constant $C>0$ and a map $\varPhi :\overline{Q^2}\rightarrow \overline{T}$ satisfying the properties required in Proposition 2 and the additional estimate

$$\begin{aligned} \left| \partial _s \varPhi (s,\theta ) \right| \le C\frac{\nu ^3}{\mu ^3}(\mathrm {diam}(T)+m_{{\scriptscriptstyle \sigma }}), \ \ \forall (s,\theta )\in Q^2. \end{aligned}$$

(8)

The sequel of this section is thus devoted to the proof of Proposition 3. We first observe that, in the case when T is a real triangle, namely when $\sigma$ is a segment, the map $\varPhi =\phi _2$ with

$$\begin{aligned} \phi _2:(s,\theta )\in \overline{Q^2} \mapsto s \gamma (\theta ) \in \overline{T}, \end{aligned}$$

satisfies the assumptions of Proposition 2 as well as estimate (8).

In the general case where $\sigma$ is curved, we have

$$\begin{aligned} \text {Jac}\,\phi _2(s,\theta )=s\det (\gamma (\theta ), \gamma '(\theta )), \end{aligned}$$

and this quantity depends on $\theta$: we cannot choose $\varPhi =\phi _2$ anymore. Thus, we are going to right compose $\phi _2$ with a diffeomorphism of the unit cube to construct a $\varPhi : \overline{Q^2}\rightarrow \overline{T}$ satisfying Proposition 3, see Fig. 3.

Fig. 3

Construction of the diffeomorphism $\varPhi$

To simplify the notation, we define g by

$$\begin{aligned} g: (s,\theta )\in \overline{Q^2} \mapsto \text {Jac}\,\phi _2(s,\theta ) = s \det (\gamma , \gamma ')(\theta ). \end{aligned}$$

Then, we construct a first diffeomorphism $\phi _1$ of $Q^2$ such that $\phi _2\circ \phi _1$ satisfies the first three assumptions of Proposition 2 as a well as a weaker version (integrated with respect to s) of the third assumption. Obtaining the strong version of this property (that is a point-by-point equality) will be the purpose of Lemma 2.

Lemma 1

There exists a $C^1$ diffeomorphism $\phi _1 : \overline{Q^2}\rightarrow \overline{Q^2}$ such that

• 1. for every $x\in \partial Q^2$, $\phi _1(x)=x$,

• 2. for every $\theta \in [0,1]$,

  $$\begin{aligned} \int _0^1 \text {Jac}\,(\phi _2\circ \phi _1) (s,\theta )\, ds = \int _{0}^{1} g\circ \phi _1 (s,\theta ) \text {Jac}\,\phi _1(s,\theta )\,ds = m_{\scriptscriptstyle T}. \end{aligned}$$

  (9)

• 3. for every $(s,\theta )\in \overline{Q^2}$,

  $$\begin{aligned} \frac{\mu }{4\nu }\le \text {Jac}\,\phi _1(s,\theta ) \le \frac{5\nu }{\mu }. \end{aligned}$$

  (10)

Proof

Let

$$\begin{aligned} \varepsilon = \frac{\mu }{10 \nu } \end{aligned}$$

(11)

and $\zeta \in C^{\infty }_{c}(0,1)$ be a cut-off function such that $0\le \zeta \le 1+\varepsilon$, $|\zeta '|_{L^{\infty }}\le \frac{10}{\varepsilon }$ and

$$\begin{aligned} \int _{0}^1 \zeta (s)\, ds =1 \ \text { and } \ \int _{0}^1|\zeta (s)-1|\, ds <\varepsilon . \end{aligned}$$

(12)

We introduce the map

$$\begin{aligned} G : (a,b) \mapsto \int _{0}^1 s\,ds \int _{0}^{a+\zeta (s)b} \det (\gamma ,\gamma ')(\theta ) \,d\theta . \end{aligned}$$

Then $G$ is well-defined and $C^2$ on the set $\{(a,b) : 0\le a \le 1, \frac{-a}{1+\varepsilon }\le b \le \frac{1-a}{1+\varepsilon }\}$ (here, we use the fact that $\gamma \in C^{2}([0,1])$ so that $\det (\gamma , \gamma ')$ is $C^{1}([0,1])$). Moreover, we have

$$\begin{aligned} \partial _a G(a,b)= & {} \int _{0}^1 \det (\gamma ,\gamma ')(a+\zeta (s)b) s\,ds\\ \partial _b G(a,b)= & {} \int _{0}^1 \det (\gamma ,\gamma ')(a+\zeta (s)b) \zeta (s)s\,ds. \end{aligned}$$

By (6), we have

$$\begin{aligned} 2m_{{\scriptscriptstyle \sigma }}\mu \int _{0}^1 \zeta (s)s\,ds \le \partial _b G(a,b) \le 2m_{{\scriptscriptstyle \sigma }}\nu \int _{0}^1 \zeta (s)s\,ds. \end{aligned}$$

We can bound the right hand side by $2m_{{\scriptscriptstyle \sigma }}\nu$ while

$$\begin{aligned} 2m_{{\scriptscriptstyle \sigma }}\mu \int _{0}^1 \zeta (s)s\,ds\ge & {} 2m_{{\scriptscriptstyle \sigma }}\mu \left( \int _{0}^1 s\,ds -\int _{0}^1|\zeta (s)-1|\,ds\right) \\\ge & {} 2m_{{\scriptscriptstyle \sigma }}\mu \left( \int _{0}^1 s\,ds -\varepsilon \right) \ge \frac{4m_{{\scriptscriptstyle \sigma }}\mu }{5}. \end{aligned}$$

Hence we conclude that

$$\begin{aligned} 0 < \frac{4m_{{\scriptscriptstyle \sigma }}\mu }{5} \le \partial _b G(a,b) \le 2m_{{\scriptscriptstyle \sigma }}\nu . \end{aligned}$$

(13)

We claim that

$$\begin{aligned} G\left( a, \frac{-a}{1+\varepsilon }\right) \le m_{\scriptscriptstyle T}a. \end{aligned}$$

(14)

Indeed, by (6),

$$\begin{aligned} G\left( a,\frac{-a}{1+\varepsilon }\right) \le 2m_{{\scriptscriptstyle \sigma }}\nu \int _{0}^{1}s (a-\frac{a}{1+\varepsilon }\zeta (s))\,ds\le \frac{2m_{{\scriptscriptstyle \sigma }}\nu a}{1+\varepsilon } \int _{0}^1 ( 1+\varepsilon -\zeta (s))\,ds. \end{aligned}$$

By (12), this implies

$$\begin{aligned} G\left( a,\frac{-a}{1+\varepsilon }\right) \le \frac{2m_{{\scriptscriptstyle \sigma }}\nu a \varepsilon }{1+\varepsilon }\le 2m_{{\scriptscriptstyle \sigma }}\nu a \varepsilon . \end{aligned}$$

Since

$$\begin{aligned} m_{\scriptscriptstyle T}= \frac{1}{2} \int _{0}^{1} \det (\gamma , \gamma ')(\theta )\,d\theta \ge m_{{\scriptscriptstyle \sigma }}\mu , \end{aligned}$$

it follows from (11) that

$$\begin{aligned} G\left( a,\frac{-a}{1+\varepsilon }\right) \le m_{\scriptscriptstyle T}a , \end{aligned}$$

which proves our claim.

Similarly, one can prove that

$$\begin{aligned} \int _0^1 s\,ds \int _{a+\zeta (s)\frac{1-a}{1+\varepsilon }}^1 \det (\gamma , \gamma ')(\theta )\,d\theta \le m_{\scriptscriptstyle T}(1-a). \end{aligned}$$

This can be written as

$$\begin{aligned} G(1,0) - G\left( a, \frac{1-a}{1+\varepsilon }\right) \le m_{\scriptscriptstyle T}(1-a). \end{aligned}$$

Since

$$\begin{aligned} G(1,0) = \int _0^1 s\,ds \int _{0}^1 \det (\gamma , \gamma ')(\theta ) \, d\theta =m_{\scriptscriptstyle T}, \end{aligned}$$

this implies

$$\begin{aligned} G\left( a,\frac{1-a}{1+\varepsilon }\right) \ge m_{\scriptscriptstyle T}a. \end{aligned}$$

(15)

We deduce from (13), (14) and (15) that for every $a\in [0,1]$, there exists a unique $w(a)\in [-a/(1+\varepsilon ), (1-a)/(1+\varepsilon )]$ such that

$$\begin{aligned} G(a, w(a))= m_{\scriptscriptstyle T}a. \end{aligned}$$

By the implicit function theorem, the function $w$ is $C^2$ on $[0,1]$ and satisfies

$$\begin{aligned} \partial _a G(a,w(a)) + \partial _b G(a,w(a))w'(a)= m_{\scriptscriptstyle T}. \end{aligned}$$

(16)

Since $G(0,0)=0$ and $G(1,0)=m_{\scriptscriptstyle T}$, we have $w(0)=0=w(1)$.

We claim that for every $s\in [0,1]$, for every $a\in [0,1]$,

$$\begin{aligned} 1+\zeta (s)w'(a)>0. \end{aligned}$$

To this end, it would be sufficient to prove that $\partial _b G(a,w(a)) (1+\zeta (s)w'(a))>0$ but for a further use we shall derive more precise bounds on this quantity.

• By (16), we can write

  $$\begin{aligned} \partial _b G(a,w(a)) (1+\zeta (s)w'(a)) = \partial _b G(a,w(a)) + \zeta (s) (m_{\scriptscriptstyle T}-\partial _a G(a,w(a))),\nonumber \\ \end{aligned}$$

  (17)

  and thus

  $$\begin{aligned} \begin{aligned} \partial _b G(a,w(a)) (1+\zeta (s)w'(a)) =&\, \partial _b G(a, w(a)) -\partial _a G(a, w(a)) \\&+\zeta (s) m_{\scriptscriptstyle T}+(1-\zeta (s)) \partial _a G(a, w(a)). \end{aligned} \end{aligned}$$

  But

  $$\begin{aligned} \partial _b G(a, w(a)) -\partial _a G(a, w(a))= & {} \int _{0}^1 \det (\gamma ,\gamma ')(a+ \zeta (s)w(a)) (\zeta (s)-1) s\,ds \\\ge & {} - 2\nu m_{\sigma }\int _{0}^1|\zeta -1| \ge -2\nu m_{{\scriptscriptstyle \sigma }}\varepsilon =-\frac{\mu m_{\sigma }}{5}. \end{aligned}$$

  In the last inequality, we have used (12). Moreover, since $0\le \zeta \le 1+\varepsilon$,

  $$\begin{aligned} \zeta (s) m_{\scriptscriptstyle T}+(1-\zeta (s)) \partial _a G(a, w(a)) \ge \min \left( \partial _a G(a,w(a)) , (1+\varepsilon ) m_{\scriptscriptstyle T}- \varepsilon \partial _a G(a, w(a)) \right) . \end{aligned}$$

  Since $m_{{\scriptscriptstyle \sigma }}\mu \le \partial _a G(a, w(a)) \le m_{{\scriptscriptstyle \sigma }}\nu$ and $m_{\scriptscriptstyle T}\ge m_{{\scriptscriptstyle \sigma }}\mu$, we get by (11)

  $$\begin{aligned} \zeta (s) m_{\scriptscriptstyle T}+(1-\zeta (s)) \partial _a G(a, w(a)) \ge \frac{9m_{{\scriptscriptstyle \sigma }}\mu }{10}. \end{aligned}$$

  This implies

  $$\begin{aligned} \partial _b G(a,w(a)) (1+\zeta (s)w'(a))\ge \frac{m_{{\scriptscriptstyle \sigma }}\mu }{2}. \end{aligned}$$

  (18)

• Using that $m_{\scriptscriptstyle T}\le m_{{\scriptscriptstyle \sigma }}\nu$ and that $\partial _aG>0$, we obtain by (13) and (17)

  $$\begin{aligned} \begin{aligned} \partial _b G(a,w(a)) (1+\zeta (s)w'(a))&\le \partial _b G(a,w(a)) + \zeta (s) m_{\scriptscriptstyle T}\\&\le 2 \nu m_{{\scriptscriptstyle \sigma }}+ (1+\varepsilon ) m_{{\scriptscriptstyle \sigma }}\nu \le 4 m_{{\scriptscriptstyle \sigma }}\nu . \end{aligned} \end{aligned}$$

  (19)

Gathering (13), (18) and (19), we deduce that

$$\begin{aligned} \frac{\mu }{4\nu }\le 1+\zeta (s)w'(a) \le 5\frac{\nu }{\mu }. \end{aligned}$$

(20)

We now define

$$\begin{aligned} \phi _1(s, \theta ) = (s, \theta + \zeta (s) w(\theta )) , \quad \quad (s,\theta )\in \overline{Q^2}. \end{aligned}$$

It appears that $\phi _1$ is $C^1$ on $Q^2$ and satisfies $\text {Jac}\,\phi _1 (s, \theta )= 1+ \zeta (s) w'(\theta )>0$. Since for every $s\in [0,1]$, the function $\theta \mapsto \theta + \zeta (s) w(\theta )$ is continuous and increasing, it maps $[0,1]$ onto $[0,1]$. Hence $\phi _1$ is a $C^1$ diffeomorphism from $\overline{Q^2}$ onto $\overline{Q^2}$. Moreover, $\phi _1$ agrees with the identity map on $\partial Q^2$. We now turn to the proof of (9).

Let $a\in [0,1]$. By definition of $w$ and $g$,

$$\begin{aligned} \int _{0}^1 ds \int _{0}^{a + \zeta (s) w(a)} g(s,\theta )\,d \theta = m_{\scriptscriptstyle T}a. \end{aligned}$$

By definition of $\phi _1$, this can be written

$$\begin{aligned} \int _{\phi _1((0,1)\times (0,a))} g = m_{\scriptscriptstyle T}a. \end{aligned}$$

By the change of variables formula, this gives

$$\begin{aligned} \int _{0}^a d\theta \int _0^1 g\circ \phi _1(s,\theta )\text {Jac}\,\phi _1 (s,\theta )\,ds = m_{\scriptscriptstyle T}a. \end{aligned}$$

Since this holds true for any $a\in [0,1]$, by derivation we deduce

$$\begin{aligned} \int _0^1 g\circ \phi _1(s,\theta )\text {Jac}\,\phi _1 (s,\theta )\,ds = m_{\scriptscriptstyle T}, \quad \forall \theta \in (0,1); \end{aligned}$$

which completes the proof of (9).

Since $\text {Jac}\,\phi _1(s,\theta )=1+\zeta (s)w'(\theta )$, we can use (20), to obtain the estimate (10). The lemma is proven. $\square$

We proceed with the construction of the diffeomorphism $\varPhi$ that we search in the form $\phi _2\circ \phi _1\circ \phi _0$. To simplify the notation, we consider the map $g_1 : Q^2\rightarrow \mathbb R$ defined as follows:

$$\begin{aligned} g_1(s,\theta )= & {} \text {Jac}\,(\phi _2\circ \phi _1) (s,\theta ) \\= & {} g\circ \phi _1(s,\theta ) \text {Jac}\,\phi _1(s,\theta )\\= & {} s \det (\gamma , \gamma ')(\theta +\zeta (s)w(\theta ))(1+\zeta (s)w'(\theta )). \end{aligned}$$

Observe that for every $s\in (0,1]$, $\theta \in [0,1]$, $g_1(s,\theta )>0.$

Lemma 2

There exists a Lipschitz homeomorphism $\phi _0 : \overline{Q^2}\rightarrow \overline{Q^2}$ which is $C^1$ on $Q^2$ and such that

• 1. for every $\theta \in [0,1]$, $\phi _0(0,\theta )=(0,\theta )$ and $\phi _0(1,\theta )=(1,\theta )$,

• 2. for every $(s,\theta )\in Q^2$,

  $$\begin{aligned} \text {Jac}\,(\phi _2\circ \phi _1\circ \phi _0) (s,\theta ) = g_1 \circ \phi _0 (s,\theta ) \text {Jac}\,\phi _0(s,\theta ) = 2m_{\scriptscriptstyle T}s. \end{aligned}$$

• 3. for every $(s,\theta )\in Q^2$,

  $$\begin{aligned} |\partial _s \phi _0(s, \theta )|\le C, \end{aligned}$$

  where $C$ only depends on $\nu /\mu$.

Proof

For every $(s, \theta )\in \overline{Q^2}$, we denote by $v(s,\theta )$ the unique element of $[0,1]$ such that

$$\begin{aligned} \int _{0}^{v(s,\theta )} g_1(s', \theta )\,ds'=m_{\scriptscriptstyle T}s^2. \end{aligned}$$

(21)

The map $v$ is well-defined since $g_1(s, \theta )>0$ for every $s\in (0,1]$, $\theta \in [0,1]$ and also because

$$\begin{aligned} \int _{0}^{1} g_1(s', \theta )\,ds'=m_{\scriptscriptstyle T}. \end{aligned}$$

This is exactly the reason why we constructed $\phi _1$ in Lemma 1. Moreover, $v(0,\theta )=0$ and $v(1,\theta )=1$. By the implicit function theorem, $v$ is $C^{1}$ on $(0,1]\times [0,1]$ and satisfies $g_1(v(s,\theta ),\theta ) \partial _s v(s,\theta )=2m_{\scriptscriptstyle T}s$; that is,

$$\begin{aligned} v(s, \theta )\det (\gamma , \gamma ')(\theta + \zeta \circ v(s,\theta )w(\theta ))(1+\zeta \circ v(s,\theta )w'(\theta ))\partial _s v(s,\theta )=2m_{\scriptscriptstyle T}s.\nonumber \\ \end{aligned}$$

(22)

In particular, for every $(s,\theta )\in Q^2$, $\partial _s v(s,\theta )>0$.

We deduce from Lemma 1 that for every $(s,\theta )\in Q^2$,

$$\begin{aligned} m_{{\scriptscriptstyle \sigma }}\frac{\mu ^2}{2\nu }s\le g_1(s, \theta ) \le \frac{10m_{{\scriptscriptstyle \sigma }}\nu ^2}{\mu }s. \end{aligned}$$

Integrating with respect to s those inequalities between 0 and $v(s,\theta )$, using (21), and the fact that $m_{{\scriptscriptstyle \sigma }}\mu \le m_{\scriptscriptstyle T}\le m_{{\scriptscriptstyle \sigma }}\nu$, we get

$$\begin{aligned} \frac{\mu }{\sqrt{5}\nu }s \le v(s,\theta ) \le 2\frac{ \nu }{\mu }s. \end{aligned}$$

(23)

From (22) and (20),

$$\begin{aligned} 0<v(s,\theta )\partial _s v(s,\theta ) \le 4\frac{\nu ^2}{\mu ^2}s. \end{aligned}$$

(24)

In view of (23), this also implies that

$$\begin{aligned} 0<\partial _s v(s, \theta )\le 4\sqrt{5}\frac{\nu ^3}{\mu ^3}. \end{aligned}$$

(25)

A similar argument proves that $\partial _\theta v \in L^{\infty }(Q^2)$. We now define

$$\begin{aligned} \phi _0(s,\theta )=(v(s,\theta ), \theta ). \end{aligned}$$

Then $\phi _0$ is a homeomorphism from $\overline{Q^2}$ onto $\overline{Q^2}$ which is $C^1$ on $Q^2$. Moreover, $\phi _0(0,\theta )=(0, \theta )$, $\phi _0(1,\theta )=(1, \theta )$ and $\text {Jac}\,\phi _0(s,\theta ) = \partial _s v(s,\theta )$. By differentiation of (21), we get

$$\begin{aligned} 2m_{\scriptscriptstyle T}s= g_1(v(s,\theta ), \theta )\partial _s v(s,\theta )=g_1\circ \phi _0(s,\theta )\text {Jac}\,\phi _0(s,\theta ). \end{aligned}$$

This completes the proof of the lemma. $\square$

Gathering the previous results we can finally conclude the proof.

Proof (of Proposition 3)

Lemmas 1, 2 clearly show that, as announced, the map

$$\begin{aligned} \varPhi = \phi _2\circ \phi _1\circ \phi _0, \end{aligned}$$

satisfies all the assumptions of Proposition 2. The structure is summarized in Fig. 3:

• The side $\{s=0\}$ of $Q^2$ (in red solid on the figure) is pointwise preserved by $\phi _0$ and $\phi _1$ and mapped to the vertex of T (also in red) by $\phi _2$.

• The side $\{s=1\}$ of $Q^2$ (in blue dashdotted on the figure) is pointwise preserved by $\phi _0$ and $\phi _1$ and mapped to $\sigma$ by $\phi _2$.

• The horizontal segments $\{\theta =\mathrm{cte}\}$ of $Q^2$ (in magenta dashed) are preserved as a whole by $\phi _0$ then deformed by $\phi _1$ and $\phi _2$.

• The vertical segments $\{s=\mathrm{cte}\}$ (in green dotted) are preserved as a whole by $\phi _1$ and deformed by $\phi _0^{-1}$ and $\phi _2$.

Moreover, by definition, we have (using the same notation as in the proofs of the above two lemmas)

$$\begin{aligned} \varPhi (s,\theta ) = v(s,\theta )\gamma (\theta + \zeta \circ v(s,\theta )w(\theta )). \end{aligned}$$

Hence,

$$\begin{aligned} \partial _s \varPhi (s,\theta ) =&\left( \partial _s v(s,\theta )\right) \gamma (\theta + \zeta \circ v(s,\theta )w(\theta )) \\&+ v(s,\theta ) \partial _s v(s,\theta )\zeta '(v(s,\theta )) w(\theta ) \gamma '(\theta + \zeta \circ v(s,\theta )w(\theta )). \end{aligned}$$

By construction, $|\zeta '|_{L^{\infty }}\le 10/\varepsilon =100\nu /\mu$ and $|w|_{L^{\infty }}\le 1$. It then follows from (24) and (25) that

$$\begin{aligned} \left| \partial _s \varPhi (s,\theta ) \right| \le C\frac{\nu ^3}{\mu ^3}(\mathrm {diam}(T)+m_{{\scriptscriptstyle \sigma }}). \end{aligned}$$

The proof is complete. $\square$

4 A Poincaré inequality

In this section, we derive a Poincaré inequality related to Theorem 1.

Theorem 2

We consider the same assumption (4) as in Theorem 1. Then for every $p\in [1,+\infty [$ and every $u \in W^{1,p}(T)$,

$$\begin{aligned} \frac{1}{m_{\scriptscriptstyle T}} \int _T \left| u-\frac{1}{m_{{\scriptscriptstyle \sigma }}}\int _{\sigma } u\right| ^p \le C\left( \mathrm {diam}(T) + m_{{\scriptscriptstyle \sigma }}\right) ^p \frac{1}{m_{\scriptscriptstyle T}} \int _{T} |Du|^p, \end{aligned}$$

where $C$ only depends on p and on the ratio $\frac{\nu }{\mu }$.

This result is a consequence of the inequality proved in the previous section and of the following lemma whose proof is postponed at the end of the section.

Lemma 3

Under the assumption (4), for every $u\in W^{1,p}(T)$, we have

$$\begin{aligned} \frac{1}{m_{\scriptscriptstyle T}^2}\int _T\int _T |u(x)-u(x')|^p\,dx\, dx' \le C (\mathrm {diam}(T) + m_{{\scriptscriptstyle \sigma }})^p \frac{1}{m_{\scriptscriptstyle T}}\int _T|Du|^p, \end{aligned}$$

where $C$ only depends on p and on the ratio $\frac{\nu }{\mu }$.

Proof (of Theorem 2)

By the triangle inequality,

$$\begin{aligned} \frac{1}{m_{\scriptscriptstyle T}}\int _T \left| u-\frac{1}{m_{{\scriptscriptstyle \sigma }}}\int _{\sigma } u\right| ^p \le C_p \frac{1}{m_{\scriptscriptstyle T}}\int _T \left| u-\frac{1}{m_{\scriptscriptstyle T}}\int _{T} u\right| ^p +C_p \left| \frac{1}{m_{\scriptscriptstyle T}}\int _T u-\frac{1}{m_{{\scriptscriptstyle \sigma }}}\int _{\sigma } u\right| ^p. \end{aligned}$$

One can estimate the second term with Theorem 1:

$$\begin{aligned} \left| \frac{1}{m_{\scriptscriptstyle T}} \int _{T} u - \frac{1}{m_{{\scriptscriptstyle \sigma }}}\int _{\sigma } u \right| ^p \le C^p (m_{{\scriptscriptstyle \sigma }}+\mathrm {diam}(T))^p \frac{1}{m_{\scriptscriptstyle T}} \int _{T} |Du|^p, \end{aligned}$$

where $C$ only depends on the ratio $\frac{\nu }{\mu }$. By Jensen’s inequality, the first term is not larger than the quantity

$$\begin{aligned} \frac{1}{m_{\scriptscriptstyle T}^2}\int _T\int _T |u(x)-u(x')|^p\,dx\,dx', \end{aligned}$$

which is, in turn, estimated by using Lemma 3. $\square$

It remains to prove the lemma.

Proof (of Lemma 3)

Let us introduce the reference unit triangle $T_0$ defined by

$$\begin{aligned} T_0=\{(a,b)\in ]0,1[^2, \ \ b<a\}. \end{aligned}$$

On this domain, the following inequality classicaly holds

$$\begin{aligned} \int _{T_0}\int _{T_0} |v(y)-v(y')|^p\, dy\, dy'\le C_p \int _{T_0} |D v(y)|^p\, dy, \ \ \forall v\in W^{1,p}(T_0), \end{aligned}$$

(26)

with a value of $C_p>0$ depending only on p.

We introduce (see Fig. 4) the following diffeomorphism from $T_0$ onto T

$$\begin{aligned} \varPsi :(a,b)\in T_0 \mapsto a\gamma (b/a) \in T. \end{aligned}$$

We proceed now with the estimate of the derivatives of $\varPsi$. An immediate computation shows that

$$\begin{aligned} D\varPsi (a,b) = \left( \gamma (b/a)-(b/a) \gamma '(b/a), \gamma '(b/a) \right) , \end{aligned}$$

so that we get

$$\begin{aligned} \text {Jac}\,\varPsi (a,b) = \det (\gamma (b/a),\gamma '(b/a)), \end{aligned}$$

and thus, by (6) (which is a consequence of (4)), we deduce that

$$\begin{aligned} 0<2 \mu m_{{\scriptscriptstyle \sigma }}\le \text {Jac}\,\varPsi (a,b)\le 2 \nu m_{{\scriptscriptstyle \sigma }}, \ \ \forall (a,b)\in T_0, \end{aligned}$$

(27)

and

$$\begin{aligned} \Vert D \varPsi \Vert _\infty \le (\Vert \gamma \Vert _\infty + \Vert \gamma '\Vert _\infty ) \le (\mathrm {diam}(T) + m_{{\scriptscriptstyle \sigma }}). \end{aligned}$$

(28)

For any $u\in C^1(\bar{T})$ we set $v=u\circ \varPsi \in W^{1,p}(T_0)$ and we use $\varPsi$ as a change of variables

$$\begin{aligned} \int _T \int _T |u(x)-u(x')|^p\, dx\, dx'= & {} \int _{T_0}\int _{T_0} |v(y)-v(y')|^p \text {Jac}\,\varPsi (y) \text {Jac}\,\varPsi (y')\, dy\, dy'\\\le & {} \Vert \text {Jac}\,\varPsi \Vert _\infty ^2 \int _{T_0}\int _{T_0} |v(y)-v(y')|^p\, dy\,dy'. \end{aligned}$$

Then by (26) and the change of variables $x=\varPsi (y)$ again, we get

$$\begin{aligned}&\int _T \int _T |u(x)-u(x')|^p\, dx\, dx' \le C_p \Vert \text {Jac}\,\varPsi \Vert _\infty ^2 \int _{T_0} |D v(y)|^p\, dy\\&\quad \le C_p \frac{\Vert \text {Jac}\,\varPsi \Vert _\infty ^2}{\inf _{T_0} \text {Jac}\,\varPsi } \int _{T_0} |D v(y)|^p\, \text {Jac}\,\varPsi (y) dy\\&\quad = C_p \frac{\Vert \text {Jac}\,\varPsi \Vert _\infty ^2}{\inf _{T_0} \text {Jac}\,\varPsi } \int _{T}|(D v)(\varPsi ^{-1}(x))|^p\, dx\\&\quad = C_p \frac{\Vert \text {Jac}\,\varPsi \Vert _\infty ^2}{\inf _{T_0} \text {Jac}\,\varPsi } \int _{T} |D u(x)|^p \Vert D\varPsi (\varPsi ^{-1}(x))\Vert ^p\, dx\\&\quad \le C_p \frac{\Vert \text {Jac}\,\varPsi \Vert _\infty ^2 \Vert D\varPsi \Vert _\infty ^p}{\inf _{T_0} \text {Jac}\,\varPsi } \int _{T} |D u(x)|^p\,dx. \end{aligned}$$

By using the previous estimates (27) and (28) we conclude that

$$\begin{aligned} \int _T \int _T |u(x)-u(x')|^p\, dx\, dx'\le & {} C_p \frac{2m_{{\scriptscriptstyle \sigma }}\nu ^2 }{\mu }(\mathrm {diam}(T) +m_{{\scriptscriptstyle \sigma }})^p \int _{T} |D u(x)|^p\,dx\\\le & {} C_p \frac{2m_{{\scriptscriptstyle \sigma }}\nu ^2 }{\mu ^2} \mu (\mathrm {diam}(T) +m_{{\scriptscriptstyle \sigma }})^p \int _{T} |D u(x)|^p\,dx. \end{aligned}$$

Since $\mu m_{{\scriptscriptstyle \sigma }}\le m_{\scriptscriptstyle T}$, we finally obtain

$$\begin{aligned} \int _T \int _T |u(x)-u(x')|^p\, dx\, dx' \le C m_{\scriptscriptstyle T}(\mathrm {diam}(T) +m_{{\scriptscriptstyle \sigma }})^p \int _{T} |D u(x)|^p\,dx \end{aligned}$$

for a C depending only on p and $\nu /\mu$. Dividing this inequality by $m_{\scriptscriptstyle T}^2$ gives the claim. $\square$

Fig. 4

The diffeomorphism $\varPsi$

5 The higher dimensional case

Let $n\ge 2$. Let $\gamma : \overline{Q^{n-1}} \rightarrow \mathbb R^n$ be a $C^1$ map on the closure of the unit cube $Q^{n-1}=(0,1)^{n-1}$ such that $\gamma$ is one-to-one and $|\partial _1 \gamma \wedge \dots \wedge \partial _{n-1}\gamma |>0$ on $\overline{Q^{n-1}}$. We denote by $\sigma =\gamma (\overline{Q^{n-1}})$ the corresponding hypersurface and by $T$ the set:

$$\begin{aligned} T=\{s\gamma (\theta ) : s\in (0 , 1), \theta \in Q^{n-1}\}. \end{aligned}$$

We assume that for every $\theta \in \overline{Q^{n-1}}$,

$$\begin{aligned} \left\{ s\gamma (\theta ), s\ge 0\right\} \cap \sigma = \left\{ \gamma (\theta ) \right\} . \end{aligned}$$

Theorem 3

We assume that there exist $\mu , \nu >0$ such that for every $\theta \in Q^{n-1}$,

$$\begin{aligned} \mu \le \frac{\det (\gamma ,\partial _1 \gamma , \dots , \partial _{n-1}\gamma )(\theta )}{n|\partial _1\gamma \wedge \dots \wedge \partial _{n-1}\gamma |(\theta )} \le \nu . \end{aligned}$$

(29)

Then for every $p\in [1,+\infty [$ and every $u \in W^{1,p}(T)$,

$$\begin{aligned} \left| \frac{1}{m_{{\scriptscriptstyle \sigma }}} \int _{\sigma } u - \frac{1}{m_{\scriptscriptstyle T}}\int _T u \right| ^p \le C^p (\Vert D\gamma \Vert _{L^{\infty }}+\mathrm {diam}(T))^p \frac{1}{m_{\scriptscriptstyle T}} \int _{T} |Du|^p, \end{aligned}$$

where $C$ only depends on the ratio $\frac{\nu }{\mu }$.

Remark 3

Observe that the quantity in (29) is invariant with respect to the parametrization of $\sigma$. More precisely, let $\psi : Q^{n-1} \rightarrow Q^{n-1}$ be a $C^{1}$ map such that $|\text {Jac}\,\psi |>0$ everywhere and $\widetilde{\gamma }=\gamma \circ \psi$. Then

$$\begin{aligned} \partial _1\widetilde{\gamma }\wedge \dots \wedge \partial _{n-1}\widetilde{\gamma } = \left( (\partial _1 \gamma \wedge \dots \wedge \partial _{n-1}\gamma )\circ \psi \right) \text {Jac}\,\psi . \end{aligned}$$

This implies

$$\begin{aligned} \begin{aligned} \det (\widetilde{\gamma },\partial _1 \widetilde{\gamma } , \dots , \partial _{n-1}\widetilde{\gamma })&= \langle \widetilde{\gamma }, \partial _1\widetilde{\gamma }\wedge \dots \wedge \partial _{n-1}\widetilde{\gamma } \rangle \\&= \langle \widetilde{\gamma }, \left( (\partial _1\gamma \wedge \dots \wedge \partial _{n-1}\gamma )\circ \psi \right) \text {Jac}\,\psi \rangle \\&= \left( \det (\gamma ,\partial _1 \gamma , \dots , \partial _{n-1}\gamma )\circ \psi \right) \text {Jac}\,\psi . \end{aligned} \end{aligned}$$

Hence,

$$\begin{aligned} \frac{\det (\widetilde{\gamma },\partial _1 \widetilde{\gamma } , \dots , \partial _{n-1}\widetilde{\gamma })}{|\partial _1 \widetilde{\gamma } \wedge \dots \wedge \partial _{n-1}\widetilde{\gamma }|} = \frac{\det (\gamma ,\partial _1 \gamma , \dots , \partial _{n-1}\gamma )\circ \psi }{|\partial _1\gamma \wedge \dots \wedge \partial _{n-1}\gamma |\circ \psi }. \end{aligned}$$

In particular, when $\psi$ is a $C^1$ diffeomorphism, $\gamma$ satisfies (29) if and only if $\widetilde{\gamma }$ satisfies (29).

In view of Lemma 6 given in the Appendix, one can assume without loss of generality that

$$\begin{aligned} |\partial _1 \gamma \wedge \dots \wedge \partial _{n-1} \gamma |(\theta ) = m_{{\scriptscriptstyle \sigma }}, \ \ \forall \theta \in Q^{n-1}. \end{aligned}$$

(30)

Exactly as in the $2$ dimensional case, the proof of Theorem 3 is a consequence of the following two propositions.

Proposition 4

Assume that there exists a Lipschitz continuous map $\varPhi : [0,1]\times \overline{Q^{n-1}}\rightarrow \overline{T}$ such that

• 1. $\varPhi$ is a $C^1$ diffeomorphism from $(0,1)\times Q^{n-1}$ onto $T$,

• 2. $\varPhi (0,\theta )=(0,0)$,

• 3. $\varPhi (1,\theta )=\gamma (\theta )$,

• 4. $\text {Jac}\,\varPhi (s,\theta )=nm_{\scriptscriptstyle T}s^{n-1}$.

Then for every $u\in W^{1,1}(T)$, we have

$$\begin{aligned} \frac{1}{m_{{\scriptscriptstyle \sigma }}} \int _{\sigma } u - \frac{1}{m_{\scriptscriptstyle T}}\int _T u = \frac{1}{nm_{\scriptscriptstyle T}}\int _T Du(x,y)\left[ s \partial _s \varPhi (s,\theta ) \right] _{(s,\theta ) =\varPhi ^{-1}(x,y)}\,dx\,dy. \end{aligned}$$

The proof is very similar to the proof of Proposition 2 and we omit it. In particular, we observe that by (30), we have

$$\begin{aligned} \int _{\sigma } u = \int _{Q^{n-1}}u(\gamma (\theta ))|\partial _1 \gamma \wedge \dots \wedge \partial _{n-1} \gamma |(\theta )\,d\theta&= m_{{\scriptscriptstyle \sigma }}\int _{Q^{n-1}}u(\gamma (\theta ))\,d\theta \\&= m_{{\scriptscriptstyle \sigma }}\int _{Q^{n-1}}u(\varPhi (1,\theta ))\,d\theta . \end{aligned}$$

The construction of a suitable $\varPhi$ then follows the lines of the two dimensional case. More precisely, the following proposition is the analogue of Proposition 3:

Proposition 5

There exists a $\varPhi : [0,1]\times \overline{Q^{n-1}}\rightarrow \overline{T}$ satisfying the assumptions of Proposition 4 and such that

$$\begin{aligned} \left| \partial _s \varPhi (s,\theta ) \right| \le C(\mathrm {diam}(T)+\Vert D\gamma \Vert _{L^{\infty }}) \end{aligned}$$

where $C$ only depends on $\nu /\mu$.

Proof (of Theorem 3)

By Jensen’s inequality, we only need to prove the case $p=1$ and by a standard approximation argument, one can further assume that $\gamma \in C^{2}(\overline{Q^{n-1}})$. The required inequality is then a consequence of the equality given by Proposition 4, and of the construction and estimate of the map $\varPhi$ given by Proposition 5. $\square$

It remains to prove Proposition 5. As in the 2D case, we will look for $\varPhi$ in the following form

$$\begin{aligned} \varPhi = \phi _2\circ \phi _1\circ \phi _0, \end{aligned}$$

where we still denote by $\phi _2$ the map

$$\begin{aligned} \phi _2:(s,\theta )\in [0,1]\times \overline{Q^{n-1}} \mapsto s \gamma (\theta ) \in \bar{T}. \end{aligned}$$

The maps $\phi _1$ and $\phi _0$ are built in a similar way as in Sect. 3 so that we only proceed to indicate the major changes in the following two lemmas.

Lemma 4

There exists a $C^1$ diffeomorphism $\phi _1 : [0,1]\times \overline{Q^{n-1}}\rightarrow [0,1]\times \overline{Q^{n-1}}$ such that

• 1. for every $\theta \in Q^{n-1}$, $\phi _1(0,\theta )=(0,\theta )$ and $\phi _1(1,\theta )=(1,\theta )$,

• 2. for every $\theta \in Q^{n-1}$,

  $$\begin{aligned} \int _{0}^{1} \text {Jac}\,(\phi _2\circ \phi _1) (s,\theta ) \,ds = m_{\scriptscriptstyle T}. \end{aligned}$$

• 3. for every $s\in [0,1]$ and every $\theta \in \overline{Q^{n-1}}$,

  $$\begin{aligned} |\partial _s \phi _1(s,\theta )|\le C, \quad \quad C'\le \text {Jac}\,\phi _1(s,\theta ) \le C'' \end{aligned}$$

  (31)

  where $C, C'$ and $C''>0$ only depend on the ratio $\nu /\mu$.

Proof

It is divided into three steps. In the first one we detail an auxiliary construction that will be used in Step 2 in order to build, by induction, the diffeomorphism $\phi _1$. In the third and final step, we establish the required estimates (31).

Step 1: Construction of an auxiliary function

Fix $1\le k\le n-1$. Given $\theta \in \overline{Q^{n-1}}$, we use the notation $\theta ^{k-1}=(\theta _1, \dots , \theta _{k-1})$ and $\theta '=(\theta _{k+1}, \dots , \theta _{n-1})$. Assume that there exists a $C^1$ function $h:[0,1]\times \overline{Q^{n-1}}\rightarrow \mathbb R$ such that

• 1. For every $\theta '=(\theta _{k+1}, \dots , \theta _{n-1})\in \overline{Q^{n-k-1}}$,

  $$\begin{aligned} \int _{(0,1)\times Q^k} h(s, \theta ^k, \theta ')\,ds d\theta ^k=m_T, \end{aligned}$$

• 2. There exist $C<1<C'$ only depending on $\nu /\mu$ such that

  $$\begin{aligned} C nm_{{\scriptscriptstyle \sigma }}\mu s^{n-1}\le h(s,\theta ) \le C' nm_{{\scriptscriptstyle \sigma }}\nu s^{n-1}, \ \ \forall (s,\theta )\in [0,1]\times \overline{Q^{n-1}}. \end{aligned}$$

We introduce

$$\begin{aligned} \varepsilon = \frac{C\mu }{2nC'\nu } \end{aligned}$$

and a cut-off function: $\zeta \in C^{\infty }_c((0,1)\times Q^{k-1})$ such that $0\le \zeta \le 1+\varepsilon$ and

$$\begin{aligned} \int _{(0,1)\times Q^{k-1}} \zeta (s,\theta ^{k-1})\,ds d\theta ^{k-1}=1, \quad \int _{(0,1)\times Q^{k-1}} |\zeta (s,\theta ^{k-1})-1|\,ds d\theta ^{k-1}<\varepsilon . \end{aligned}$$

We can further require that

$$\begin{aligned} \Vert D\zeta \Vert _{L^{\infty }}\le \frac{C_n}{\varepsilon } \end{aligned}$$

for some constant $C_n$ which only depends on $n$. Consider the map

$$\begin{aligned} G_{\theta '} : (a,b) \mapsto \int _{(0,1)\times Q^{k-1}}\,ds d\theta ^{k-1} \int _{0}^{a+\zeta (s, \theta ^{k-1})b} h(s, \theta ^k, \theta ')\,d\theta _k. \end{aligned}$$

Then $G_{\theta '}$ is well-defined and $C^2$ on the set $\{(a,b) : 0\le a \le 1, \frac{-a}{1+\varepsilon }\le b \le \frac{1-a}{1+\varepsilon }\}$. As in the proof of Lemma 1, there exists a $C^2$ map $w:[0,1]\times \overline{Q^{n-k-1}} \mapsto [-1,1]$ such that for every $a\in [0,1]$ and every $\theta '\in \overline{Q^{n-k-1}}$, $G_{\theta '}(a, w(a, \theta ')) = m_T a$; that is,

$$\begin{aligned} \int _{(0,1)\times Q^{k-1}}\,ds d\theta ^{k-1} \int _{0}^{a+\zeta (s, \theta ^{k-1})w(a,\theta ')} h(s, \theta ^k, \theta ')\,d\theta _k=m_T a. \end{aligned}$$

Moreover, $w(0,\theta ')=0=w(1, \theta ')$ and by differentiation of the above identity with respect to $a$, one gets

$$\begin{aligned}&\int _{(0,1)\times Q^{k-1}} h\left( s, \theta ^{k-1}, a+\zeta (s, \theta ^{k-1})w(a,\theta '), \theta '\right) \nonumber \\&\quad \left( 1+\zeta (s,\theta ^{k-1})\partial _a w(a,\theta ') \right) ds\,d\theta ^{k-1} =m_{\scriptscriptstyle T}. \end{aligned}$$

(32)

As in the proof of Lemma 1, this leads to the following estimate:

$$\begin{aligned} D\le 1+\zeta (s, \theta ^{k-1})\partial _a w(a, \theta ')\le D' \end{aligned}$$

(33)

for some constants $D$, $D'>0$ which only depend on $\nu /\mu$. We omit the details.

Step 2: construction of $\phi _1$

Let $\psi _{n+1}= id_{[0,1]\times \overline{Q^{n-1}}}$ and $h_{n+1}=h_n=\text {Jac}\,\phi _2$. We construct by induction on $k=n, \dots , 0$ two sequences of maps

$$\begin{aligned} \psi _{k+1} : [0,1] \times \overline{Q^{n-1}} \rightarrow [0,1] \times \overline{Q^{n-1}}, \quad \quad h_k : [0,1]\times \overline{Q^{n-1}}\rightarrow \mathbb R\end{aligned}$$

such that for $k=0, \dots , n,$

• 1. The map $\psi _{k+1}$ is a $C^2$ diffeomorphism from $[0,1]\times \overline{Q^{n-1}}$ onto $[0,1]\times \overline{Q^{n-1}}$,

• 2. For every $\theta \in Q^{n-1}$, $\psi _{k+1}(0,\theta )=(0, \theta )$ and $\psi _{k+1}(1, \theta )=(1, \theta )$,

• 3. We have

  $$\begin{aligned} h_{k}=(h_{k+1}\circ \psi _{k+1}) \text {Jac}\,\psi _{k+1}, \end{aligned}$$

• 4. There exist two constants $0<C_k< 1< C_{k}'$ depending only on $\nu /\mu$ such that for every $s\in [0,1]$ and every $\theta \in \overline{Q^{n-1}}$,

  $$\begin{aligned} \begin{aligned} C_k \le&\, \text {Jac}\,\psi _{k+1}(s, \theta ) \le C_{k}', \\ C_k nm_{{\scriptscriptstyle \sigma }}\mu s^{n-1}&\le h_k(s, \theta ) \le C_{k}'nm_{{\scriptscriptstyle \sigma }}\nu s^{n-1} . \end{aligned} \end{aligned}$$

  (34)

• 5. We have

  $$\begin{aligned} \int _{(0,1)\times Q^k}h_k(s, \theta ^k, \theta ')\,ds d\theta ^k=m_{\scriptscriptstyle T}, \end{aligned}$$

  where $\theta ^k=(\theta _1, \dots , \theta _k)$ and $\theta '=(\theta _{k+1}, \dots , \theta _{n-1})$.

Observe that these conditions are satisfied for $k=n$. We assume that for some $k\ge 1$, $\psi _{n+1},\psi _n \dots , \psi _{k+1}$, and thus $h_n,\dots , h_k$ are already constructed and satisfy the above properties. Let $\varepsilon _k=\frac{C_k\mu }{2nC_k'\nu }$ and $\zeta _k$ a function which satisfies the properties of the function $\zeta$ introduced in Step 1, with $\varepsilon =\varepsilon _k$. We apply Step 1 to the function $h_k$ with $\zeta _k$ and $C=C_k$, $C'=C_k'$. This gives a function $w_k : [0,1]\times \overline{Q^{n-k-1}}\rightarrow [-1,1]$ satisfying the properties enumerated in Step 1.

We then construct $\psi _k$ as follows

$$\begin{aligned} \psi _k(s, \theta _1, \dots , \theta _{n-1})&= (s,\theta ^{k-1}, v_k(s, \theta ), \theta ') \\&=(s,\theta _1, \dots , \theta _{k-1}, v_k(s, \theta ),\theta _{k+1}, \dots , \theta _{n-1}) \end{aligned}$$

with

$$\begin{aligned} v_k(s, \theta ) = \theta _k + \zeta _k(s,\theta ^{k-1})w_k(\theta _{k}, \theta '). \end{aligned}$$

Since $\text {Jac}\,\psi _k = 1+\zeta _k \partial _{\theta _k} w_k$, (33) implies

$$\begin{aligned} C_{k-1}\le \text {Jac}\,\psi _k\le C_{k-1}', \end{aligned}$$

where $0<C_{k-1}<1<C_{k-1}'$ only depend on $\nu /\mu$.

Let $h_{k-1}=(h_k\circ \psi _k) \text {Jac}\,\psi _k$. By (32),

$$\begin{aligned}&\int _{(0,1)\times Q^{k-1}} h_{k-1} \\&\quad = \int _{(0,1)\times Q^{k-1}}h_k(s, \theta ^{k-1}, \theta _k+\zeta _k(s,\theta ^{k-1}) w_k(\theta _k, \theta '),\theta ') \text {Jac}\,\psi _k(s,\theta )\,ds d\theta ^{k-1} \\&\quad =m_T. \end{aligned}$$

As in the proof of Lemma 1, one can check that $h_{k-1}$ and $\psi _k$ satisfy all the remaining properties, even if it means changing the actual value of the constants $C_{k-1}$ and $C_{k-1}'$. This completes the construction by induction of $h_0, \dots , h_n$ and $\psi _1, \dots , \psi _{n+1}$. We now define

$$\begin{aligned} \phi _1=\psi _n\circ \psi _{n-1}\circ \dots \circ \psi _1. \end{aligned}$$

Then $\phi _1$ is a $C^1$ diffeomorphism from $[0,1]\times \overline{Q^{n-1}}$ onto itself and $\phi _1$ coincides with the identity on $\{0\}\times \overline{Q^{n-1}}$ and $\{1\}\times \overline{Q^{n-1}}$. By construction,

$$\begin{aligned} h_0= (h_1\circ \psi _1) \text {Jac}\,\psi _1= & {} \left( \left( (h_2\circ \psi _2) \text {Jac}\,\psi _2\right) \circ \psi _1\right) \text {Jac}\,\psi _1 \nonumber \\= & {} (h_2\circ \psi _2 \circ \psi _1) \text {Jac}\,(\psi _2\circ \psi _1) = \dots \nonumber \\= & {} (h_n\circ \psi _n\circ \dots \circ \psi _1) \text {Jac}\,(\psi _n\circ \dots \circ \psi _1) \nonumber \\= & {} (h_n\circ \phi _1) \text {Jac}\,\phi _1 \nonumber \\= & {} (\text {Jac}\,\phi _2 \circ \phi _1) \text {Jac}\,\phi _1 = \text {Jac}\,(\phi _2\circ \phi _1). \end{aligned}$$

(35)

In particular, we deduce that

$$\begin{aligned} m_{\scriptscriptstyle T}= \int _{(0,1)} h_0(s,\theta ')\,ds = \int _{(0,1)}\text {Jac}\,(\phi _2\circ \phi _1)(s,\theta ')\,ds. \end{aligned}$$

Step 3: Proof of (31)

For every $k=1, \dots , n-1,$ and every $(s,\theta )\in [0,1]\times \overline{Q^{n-1}}$, let us introduce the notation:

$$\begin{aligned}{}[(s,\theta )]^{k} = \theta ^{k}=(\theta _1, \dots , \theta _k). \end{aligned}$$

Then

$$\begin{aligned} \psi _1(s,\theta )=(s, [\psi _1(s,\theta )]^1, \theta ')=(s, \theta _1+\zeta _1(s)w_1(\theta _1, \theta '), \theta ') \end{aligned}$$

with $\theta '=(\theta _2, \dots , \theta _{n-1})$, and for every $k=1, \dots , n$,

$$\begin{aligned}&\psi _k \circ \psi _{k-1}\circ \dots \circ \psi _1 (s, \theta ) \\&\quad = \left( s, [\psi _{k-1}\circ \dots \circ \psi _1(s,\theta )]^{k-1}, \theta _k +\zeta _k(s,[\psi _{k-1}\circ \dots \circ \psi _1(s,\theta )]^{k-1})w_k(\theta _k, \theta '), \theta ' \right) \end{aligned}$$

where $\theta '= (\theta _{k+1}, \dots , \theta _n)$.

Since $\Vert w_k\Vert _{L^{\infty }}\le 1$, it follows by induction on $k=1, \dots , n$ that there exists $A_k>0$ which depends only on $\nu /\mu$ such that

$$\begin{aligned} \Vert \partial _s (\psi _{k}\circ \dots \circ \psi _1)\Vert _{L^{\infty }}\le A_k. \end{aligned}$$

In particular, $\Vert \partial _s \phi _1\Vert _{L^{\infty }}\le A_n$. The fact that $C\le \text {Jac}\,\phi _1 \le C'$, for some $C, C'>0$ depending only on $\nu /\mu$, follows from (34) and the identity

$$\begin{aligned} \text {Jac}\,\phi _1 = \prod _{k=1}^n \text {Jac}\,\psi _{k}. \end{aligned}$$

The lemma is proved. $\square$

Lemma 5

There exists an homeomorphism $\phi _0 : [0,1]\times \overline{Q^{n-1}}\rightarrow [0,1] \times \overline{Q^{n-1}}$ which is $C^1$ on $(0,1)\times Q^{n-1}$ and such that

• 1. for every $\theta \in (0,1)$, $\phi _0(0,\theta )=(0,\theta )$ and $\phi _0(1,\theta )=(1,\theta )$,

• 2. for every $(s,\theta )\in (0,1) \times Q^{n-1}$,

  $$\begin{aligned} \text {Jac}\,(\phi _2\circ \phi _1\circ \phi _0) (s,\theta ) = nm_{\scriptscriptstyle T}s^{n-1}, \end{aligned}$$

• 3. there exists a $C^1$ map $v: (0,1)\times Q^{n-1}\rightarrow [0,1]$ such that for every $(s,\theta )\in (0,1) \times Q^{n-1}$, $\phi _0(s,\theta )=(v(s,\theta ), \theta )$ and

  $$\begin{aligned} |v(s,\theta )|\le Cs , \quad |\partial _s v(s,\theta )| \le C \end{aligned}$$

  where $C$ only depends on $\nu /\mu$.

The proof is essentially the same as the proof of Lemma 2. The only difference is that now by (34) for $k=0$ and (35)

$$\begin{aligned} Cnm_{{\scriptscriptstyle \sigma }}\mu s^{n-1} \le \text {Jac}\,(\phi _2\circ \phi _1) \le C'nm_{{\scriptscriptstyle \sigma }}\nu s^{n-1}. \end{aligned}$$

The rest of the proof is the same and we omit it.

Proof (of Proposition 5)

By construction,

$$\begin{aligned} \varPhi (s,\theta ) =\phi _2\circ \phi _1 \circ \phi _0 (s,\theta )=\phi _2 (\phi _1(v(s,\theta ), \theta )). \end{aligned}$$

Hence,

$$\begin{aligned} \partial _s \varPhi (s,\theta ) = D\phi _2 (\phi _1(v(s,\theta ),\theta )) . \partial _s \phi _1(v(s,\theta ),\theta ) . \partial _s v(s,\theta ). \end{aligned}$$

By Lemma 5, $|\partial _s v|, |v| \le C$ and by Lemma 4, we have $|\partial _s \phi _1|\le C$. Hence

$$\begin{aligned} \left| \partial _s \varPhi (s,\theta ) \right| \le C(\mathrm {diam}(T)+\Vert D\gamma \Vert _{L^{\infty }}) \end{aligned}$$

where $C$ only depends on $\nu /\mu$. $\square$

6 Applications to the analysis of some finite volume methods

6.1 Regular families of meshes of a smooth domain

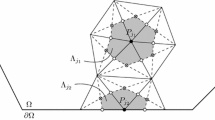
Let $\varOmega$ be a bounded domain of $\mathbb R^2$ with a $C^2$ boundary; we set $\varGamma =\partial \varOmega$. A finite volume mesh $\mathfrak {M}$ of $\varOmega$ is a finite family of compact subsets of $\overline{\varOmega }$ with non-empty interiors usually refered to as control volumes and denoted by the letter ${\mathcal {K}}$. This family is supposed to satisfy

$$\begin{aligned} \mathring{{\mathcal {K}}}\cap \mathring{{\mathcal {L}}}= & {} \emptyset , \ \ \forall {\mathcal {K}},{\mathcal {L}}\in \mathfrak {M}, {\mathcal {K}}\ne {\mathcal {L}},\\ \overline{\varOmega }= & {} \bigcup _{{\mathcal {K}}\in \mathfrak {M}} {\mathcal {K}}. \end{aligned}$$

Fig. 5

The non-polygonal mesh $\mathfrak {M}$ of $\varOmega$ and the two submeshes $\mathfrak {M}_{int}$ and $\mathfrak {M}_{ext}$

We assume that $\mathfrak {M}$ can be split into two disjoint subsets (see Fig. 5) as follows:

• The set of polygonal control volumes $\mathfrak {M}_{int}$ that satisfy: for any ${\mathcal {K}}\in \mathfrak {M}_{int}$, ${\mathcal {K}}$ is polygonal and ${\mathcal {K}}\cap \partial \varOmega$ contains at most a finite number of points.

• The set of curved control volumes $\mathfrak {M}_{ext}$ that satisfy: for any ${\mathcal {K}}\in \mathfrak {M}_{ext}$, ${\mathcal {K}}$ is a pseudo-triangle whose curved edge is contained in the boundary of the domain $\varOmega$. With any such curved control volume ${\mathcal {K}}$, we associate the (real) triangle ${\widetilde{\mathcal {K}}}$ which possesses the same vertices as ${\mathcal {K}}$ (see the dashed lines in Fig. 5). Observe that ${\widetilde{\mathcal {K}}}$ may not be included in $\overline{\varOmega }$.

We may now define the approximate mesh to be the following set of control volumes

$$\begin{aligned} \widetilde{\mathfrak {M}}= \bigcup _{{\mathcal {K}}\in \mathfrak {M}_{int}}\{ {\mathcal {K}}\} \cup \bigcup _{{\mathcal {K}}\in \mathfrak {M}_{ext}} \{{\widetilde{\mathcal {K}}}\}. \end{aligned}$$

This is a finite volume mesh made of polygonal control volumes.

The size and the regularity of such a mesh are measured by the quantities

$$\begin{aligned} \mathrm{size}(\mathfrak {M})= \max _{{\scriptscriptstyle \sigma }\in \mathcal {E}} m_{{\scriptscriptstyle \sigma }}, \ \text {and} \ \mathrm{reg}_1(\mathfrak {M})= \max _{{\mathcal {L}}\in \widetilde{\mathfrak {M}}} \frac{\mathrm {diam}({\mathcal {L}})^2}{m_{{\scriptscriptstyle \mathcal {L}}}}, \end{aligned}$$

where $\mathcal {E}$ is the set of the edges $\sigma$ of all the control volumes in the mesh $\mathfrak {M}$. Usual convergence results in the finite volume framework assume that $\mathrm{size}(\mathfrak {M})$ goes to 0 and that $\mathrm{reg}_1(\mathfrak {M})$ remains bounded. This means that control volumes are not allowed to become flat while the mesh is refined.

The main objective of this section is to prove that, if one builds a mesh $\mathfrak {M}$ of $\varOmega$ as described previously such that $\mathrm{size}(\mathfrak {M})$ is small enough, then each boundary curved control volumes ${\mathcal {K}}\in \mathfrak {M}_{ext}$ satisfies the assumptions of Theorem 1 with a ratio $\nu _{\mathcal {K}}/\mu _{\mathcal {K}}$ which is independent of ${\mathcal {K}}$. In other words, on such curved elements, the inequality (5) holds with a constant C uniformly bounded as the mesh is refined.

Proposition 6

Let $\varOmega$ be a bounded domain of class $C^2$ in $\mathbb R^2$ and $\xi _0>0$. There exists $h_0>0$ depending only on $\varOmega$ and $\xi _0$, such that for any finite volume mesh $\mathfrak {M}$ as described above, if

$$\begin{aligned} \mathrm{reg}_1(\mathfrak {M})\le \xi _0 \ \text {and} \ \mathrm{size}(\mathfrak {M})\le h_0, \end{aligned}$$

(36)

then any exterior control volume ${\mathcal {K}}\in \mathfrak {M}_{ext}$ (which is a pseudo-triangle) satisfies the assumption (6) with two values of $\mu$ and $\nu$ that satisfy $\nu /\mu =3$.

Proof

The exterior control volume ${\mathcal {K}}$ can be written in the following form (see Fig. 6)

$$\begin{aligned} \mathcal {K}=\{(1-s)\gamma (t) : s\in [0,1] , t\in [0,h]\}, \end{aligned}$$

where the opposite vertex which is supposed to be the origin (0, 0) lies inside $\varOmega$, and $\gamma :[0,h]\rightarrow \mathbb R^2$ is a normal parametrization of the curved edge $\sigma \subset \varGamma$: $\Vert \gamma '(t)\Vert =1$ for every $t\in [0,h]$.

We also introduce the associated real triangle $\widetilde{\mathcal {K}}$ with vertices $(0,0), \gamma (0)$ and $\gamma (h)$.

First, we claim that if we assume that

$$\begin{aligned} h_0<\frac{1}{2\Vert \gamma ''\Vert _{\infty }}, \end{aligned}$$

(37)

then we have

$$\begin{aligned} m_{{\scriptscriptstyle \sigma }}= h \le 2 \mathrm {diam}({\widetilde{\mathcal {K}}}). \end{aligned}$$

(38)

Indeed, let $t\in [0,h]$. By the mean value inequality, there exists $\xi _t\in [0,h]$ such that

$$\begin{aligned} \begin{aligned} \langle \gamma '(t), \gamma (h)-\gamma (0)\rangle&= h\langle \gamma '(t), \gamma '(\xi _t)\rangle \\&\ge h- h^2\Vert \gamma '\Vert _{\infty }\Vert \gamma ''\Vert _{\infty } = h-h^2\Vert \gamma ''\Vert _{\infty }\\&\ge \frac{h}{2}. \end{aligned} \end{aligned}$$

The last inequality follows from (36) and (37). The conclusion follows from the Cauchy-Schwarz inequality and the fact that the parametrization $\gamma$ is normal and satisfies $\Vert \gamma (h)-\gamma (0)\Vert \le \mathrm {diam}({\widetilde{\mathcal {K}}})$.

Then, we are going to prove relation (6). For any $t\in [0,h]$, we write the term $\det (\gamma (t),\gamma '(t))$ as follows:

$$\begin{aligned} \begin{aligned} \det \left( \gamma (t),\gamma '(t)\right) =&\det \left( \gamma (0),\frac{\gamma (h)-\gamma (0)}{h} \right) \\&+ \det \left( \gamma (0),\gamma '(t) - \frac{\gamma (h)-\gamma (0)}{h} \right) \\&+ \det \left( \gamma (t)-\gamma (0),\gamma '(t)\right) \\ :=&I_1 + I_2 + I_3. \end{aligned} \end{aligned}$$

(39)

Now, we have to control the terms $I_j$, $j=1,2,3$.

We begin with the term $I_1$. Clearly, we have

$$\begin{aligned} I_1 = \frac{2}{h}m_{\scriptscriptstyle {\mathcal {\widetilde{K}}}}. \end{aligned}$$

(40)

As regards the second term in (39), there exists $\zeta _t\in [0,h]$ such that,

$$\begin{aligned} |I_2| = \left| \det \left( \gamma (0), \gamma '(t) - \gamma '(\zeta _t)\right) \right| \le \Vert \gamma (0)\Vert \Vert \gamma ''\Vert _{\infty } h \le 2 \Vert \gamma ''\Vert _{\infty } \mathrm {diam}({\widetilde{\mathcal {K}}})^2.\qquad \quad \end{aligned}$$

(41)

Now, we are concerned by the last term in (39). There exists $\widetilde{\zeta }_t\in [0,h]$ such that,

$$\begin{aligned} |I_3| = \left| \det \left( -t\gamma '(t) + \frac{t^2}{2} \gamma ''(\widetilde{\zeta }_t) ,\gamma '(t) \right) \right| \le \frac{h^2}{2} \Vert \gamma '\Vert _\infty \Vert \gamma ''\Vert _\infty , \end{aligned}$$

and since the parametrization is normal, we deduce by (38) that

$$\begin{aligned} |I_3| \le \frac{h^2}{2} \Vert \gamma '\Vert _{\infty } \Vert \gamma ''\Vert _{\infty } \le 2 \Vert \gamma ''\Vert _{\infty } \left( \mathrm {diam}({\widetilde{\mathcal {K}}})\right) ^2. \end{aligned}$$

(42)

Gathering relations (39)–(42) we get,

$$\begin{aligned} \left| \frac{2}{h}m_{\scriptscriptstyle {\mathcal {\widetilde{K}}}}- \det \left( \gamma (t),\gamma '(t)\right) \right| \le 4 \Vert \gamma ''\Vert _{\infty } \left( \mathrm {diam}({\widetilde{\mathcal {K}}})\right) ^2. \end{aligned}$$

Thanks to the definition of $\mathrm{reg}_1(\mathfrak {M})$ and assumption (36) on $\mathrm{reg}_1(\mathfrak {M})$ we have,

$$\begin{aligned} \left| \det \left( \gamma (t),\gamma '(t)\right) - \frac{2}{h}m_{\scriptscriptstyle {\mathcal {\widetilde{K}}}}\right| \le 4 \Vert \gamma ''\Vert _{\infty } \xi _0 m_{\scriptscriptstyle {\mathcal {\widetilde{K}}}}. \end{aligned}$$

Then, we obtain

$$\begin{aligned} m_{\scriptscriptstyle {\mathcal {\widetilde{K}}}}\left( \frac{2}{h} - 4 \Vert \gamma ''\Vert _{\infty } \xi _0 \right) \le \det \left( \gamma (t),\gamma '(t)\right) \le m_{\scriptscriptstyle {\mathcal {\widetilde{K}}}}\left( \frac{2}{h} + 4 \Vert \gamma ''\Vert _{\infty } \xi _0 \right) . \end{aligned}$$

Assuming that $h_0$ satisfies, additionally to (37), the condition

$$\begin{aligned} h_0 < \frac{1}{4 \Vert \gamma ''\Vert _{\infty } \xi _0 } \end{aligned}$$

(43)

we finally proved

$$\begin{aligned} \frac{1}{h} m_{\scriptscriptstyle {\mathcal {\widetilde{K}}}}\le \det \left( \gamma (t),\gamma '(t)\right) \le \frac{3}{h} m_{\scriptscriptstyle {\mathcal {\widetilde{K}}}}, \end{aligned}$$

which exactly gives (6) with a ratio $\nu /\mu$ equal to 3 (observe that in (6), the parametrization is not normal but satisfies $|\gamma '|=m_{{\scriptscriptstyle \sigma }}$ which does not change anything to the ratio $\nu /\mu$). The claim is proved provided one chooses a $h_0$ that satisfies (37) and (43). $\square$

Fig. 6

A control volume ${\mathcal {K}}\in \mathfrak {M}_{ext}$ with a curved edge $\sigma \subset \varGamma$

6.2 Example of application: the heat equation with dynamic Ventcell boundary conditions

As an illustration of the previous discussion we shall briefly describe a finite volume approximation of the following model problem

Here, $\alpha \ge 0$ is a parameter, $u_{|\varGamma }$ denotes the trace of u on the boundary $\varGamma =\partial \varOmega$ and $\varDelta _\varGamma$ denotes the Laplace-Beltrami operator on $\varGamma$.

Remark 4

The second equation of this system has to be understood as a boundary condition associated with the heat equation. It is usually refered to as a (dynamic, if $\alpha >0$) Ventcell boundary condition, see for instance [10] for a recent work on this kind of problem.

We also refer to [9] where the result of the present paper was used as an important tool to give a complete convergence result (and as by-product a well-posedness result) for a much more complex model. This model is known as the Cahn-Hilliard equation with dynamic boundary condition. It is a fourth-order non-linear parabolic equation assorted with a non-linear dynamic boundary condition.

The natural energy space for the problem (44) is the space

$$\begin{aligned} H^{1}_{\varGamma } = \{u\in H^{1}(\varOmega ), \quad u_{|\varGamma }\in H^1(\varGamma )\}, \end{aligned}$$

endowed with the norm

$$\begin{aligned} \Vert u\Vert _{H^1_\varGamma }=(\Vert \nabla u\Vert _{L^2(\varOmega )}^2 + \Vert u_{|\varGamma }\Vert _{L^2(\varGamma )}^2 + \Vert \nabla _\varGamma u_{|\varGamma }\Vert _{L^2}^2)^\frac{1}{2}, \end{aligned}$$

where $\nabla _\varGamma$ denotes the tangential gradient on $\varGamma$.

A well-posedness result can be proved in this space, the main ingredient being the following formal energy estimate, obtained by multiplying the first equation by $\partial _t u$ and the boundary condition by $\partial _t u_{|\varGamma }$

$$\begin{aligned} \frac{d}{dt} \Vert u(t)\Vert _{H^1_\varGamma }^2&= \frac{d}{dt} \left( \int _\varOmega |\nabla u(t,.)|^2 + \int _{\varGamma } |u_{|\varGamma }(t,.)|^2 + \int _{\varGamma } |\nabla _\varGamma u_{|\varGamma }(t,.)|^2 \right) \\&= - 2 \int _\varOmega |\partial _t u|^2 - 2 \alpha \int _\varGamma |\partial _t u_{|\varGamma }|^2. \end{aligned}$$

Let $\mathfrak {M}$ be a finite volume mesh of $\varOmega$ as defined in Sect. 6.1. We recall here the main notations of the mesh $\mathfrak {M}$ (see Fig. 7) used to obtain the finite volume scheme and we refer the reader to [7], for example, for more details.

Fig. 7

Finite volume mesh $\mathfrak {M}$ of $\varOmega$

We decompose $\mathcal {E}$ (the set of all the edges in the mesh) into the subset of exterior edges $\mathcal {E}_{ext}=\{\sigma \in \mathcal {E}: \sigma \subset \varGamma \}$ and the subset of interior edges $\mathcal {E}_{int}=\{\sigma \in \mathcal {E}: \sigma \not \subset \varGamma \}$. Similarly we use the notations ${\mathcal {E}^{int}_{\scriptscriptstyle \mathcal {K}}}$ and ${\mathcal {E}^{ext}_{\scriptscriptstyle \mathcal {K}}}$ for the edges of a given control volume ${\mathcal {K}}\in \mathfrak {M}$. If $\sigma$ is an interior edge which separates the control volumes ${\mathcal {K}}$ and ${\mathcal {L}}$, we note $\sigma ={\scriptstyle {\mathcal {K}}}|{\scriptstyle {\mathcal {L}}}$. For any neighboring exterior edges $\sigma ,{\tilde{\sigma }}\in \mathcal {E}_{ext}$, we note ${ \mathbf {v}}=\sigma |{\tilde{\sigma }}$ their common vertex (that belongs to $\varGamma$).

Let us remark that we have to solve an equation on the boundary $\varGamma$, thus we have to define boundary unknowns. In this context, we define a boundary mesh $\partial \mathfrak {M}$ which is in fact equal to the set of exterior edges of the initial mesh $\mathfrak {M}$. Thus, when we want to refer to the set of exterior edges we will note $\mathcal {E}_{ext}$ and when we want to refer to the set of boundary control volumes we will note $\partial \mathfrak {M}$. At each control volume ${\mathcal {K}}\in \mathfrak {M}$ we associate a point $x_{{\scriptscriptstyle \mathcal {K}}}\in {\mathcal {K}}$ called the center of the control volume ${\mathcal {K}}$ and at each edge $\sigma \in \mathcal {E}$ we associate a center ${x_{{\scriptscriptstyle \sigma }}}\in \sigma$. We assume that they satisfy the following orthogonality condition:

$$\begin{aligned}&[x_{{\scriptscriptstyle \mathcal {K}}},x_{{\scriptscriptstyle \mathcal {L}}}] \bot \sigma , \ \ \text {and} \quad {x_{{\scriptscriptstyle \sigma }}}= [x_{{\scriptscriptstyle \mathcal {K}}},x_{{\scriptscriptstyle \mathcal {L}}}]\cap \sigma , \ \ \forall \sigma ={\scriptstyle {\mathcal {K}}}|{\scriptstyle {\mathcal {L}}}\in \mathcal {E}_{int},\\&\quad [x_{{\scriptscriptstyle \mathcal {K}}},{x_{{\scriptscriptstyle \sigma }}}] \bot e_{\scriptscriptstyle \sigma }, \ \forall \sigma \in {\mathcal {E}^{ext}_{\scriptscriptstyle \mathcal {K}}}, {\mathcal {K}}\in \mathfrak {M}_{ext}, \end{aligned}$$

where $e_{\scriptscriptstyle \sigma }$ is the chord associated with $\sigma$ in the second case.

For ${\mathcal {K}}\in \mathfrak {M}$ and any edge $\sigma \in \mathcal {E}_{\scriptscriptstyle \mathcal {K}}$, we note $d_{{\scriptscriptstyle \mathcal {K}},{\scriptscriptstyle \sigma }}$ the distance between the center $x_{{\scriptscriptstyle \mathcal {K}}}$ and the center ${x_{{\scriptscriptstyle \sigma }}}$, and for interior edges $\sigma ={\scriptstyle {\mathcal {K}}}|{\scriptstyle {\mathcal {L}}}\in \mathcal {E}_{int}$, we set $d_{{\scriptscriptstyle \mathcal {K}},{\scriptscriptstyle \mathcal {L}}}=d_{{\scriptscriptstyle \mathcal {K}},{\scriptscriptstyle \sigma }}+d_{{\scriptscriptstyle \mathcal {L}},{\scriptscriptstyle \sigma }}$.

For any vertex ${ \mathbf {v}}=\sigma |{\tilde{\sigma }}$, we define $d_{{\scriptscriptstyle \sigma },{\tilde{\scriptscriptstyle \sigma }}}$ as the length of the arc included in $\varGamma$ whose ends are ${x_{{\scriptscriptstyle \sigma }}},{x_{{\tilde{\scriptscriptstyle \sigma }}}}$ and passing through ${ \mathbf {v}}=\sigma |{\tilde{\sigma }}$ (drawn with larger dashes on Fig. 7).

With these new notations, we can now measure the regularity of the mesh with respect to the position of the centers in each control volume and each edge by the following quantity

$$\begin{aligned} \mathrm{reg}_2(\mathfrak {M})= \max \left( \max _{\begin{array}{c} {\scriptscriptstyle \mathcal {K}}\in \mathfrak {M}\\ \sigma \in \mathcal {E}_{\scriptscriptstyle \mathcal {K}} \end{array}} \frac{m_{{\scriptscriptstyle \sigma }}}{d_{{\scriptscriptstyle \mathcal {K}},{\scriptscriptstyle \sigma }}} , \max _{{ \mathbf {v}}=\sigma |{\tilde{\sigma }}} \frac{m_{{\scriptscriptstyle \sigma }}+m_{\tilde{\scriptscriptstyle {\sigma }}}}{d_{{\scriptscriptstyle \sigma },{\tilde{\scriptscriptstyle \sigma }}}} \right) . \end{aligned}$$

Finally, for simplicity, we shall assume that the interior control volumes are triangles but the approach can easily be generalized to more general convex polygonal interior control volumes.

In order to obtain the semi-discrete finite volume scheme associated with problem (44) we integrate Eq.  (44a) on all control volumes ${\mathcal {K}}\in \mathfrak {M}$ and we integrate Eq. (44b) on all boundary control volumes $\sigma \in \partial \mathfrak {M}$. Then we use a consistent two-point flux approximation for the Laplace operator in $\varOmega$ and for the Laplace-Beltrami operator on $\varGamma$. A solution of this scheme is thus a set of time-dependent unknowns

$$\begin{aligned} \mathbf {u}(t) = \bigg ((u_{{\scriptscriptstyle \mathcal {K}}}(t))_{{\scriptscriptstyle \mathcal {K}}\in \mathfrak {M}}, (u_{{\scriptscriptstyle \sigma }}(t))_{{\scriptscriptstyle \sigma }\in \partial \mathfrak {M}}\bigg )\in \mathbb R^\mathfrak {M}\times \mathbb R^{\partial \mathfrak {M}}. \end{aligned}$$

The scheme reads as follows: Find $t\mapsto \mathbf {u}(t)\in \mathbb R^\mathfrak {M}\times \mathbb R^{\partial \mathfrak {M}}$ such that,

$$\begin{aligned} \left\{ \begin{aligned}&m_{{\scriptscriptstyle \mathcal {K}}}\partial _t u_{{\scriptscriptstyle \mathcal {K}}}+ \sum _{\sigma ={\mathcal {K}}|{\mathcal {L}}\in {\mathcal {E}^{int}_{\scriptscriptstyle \mathcal {K}}}} m_{{\scriptscriptstyle \sigma }}\frac{u_{{\scriptscriptstyle \mathcal {K}}}-u_{{\scriptscriptstyle \mathcal {L}}}}{d_{{\scriptscriptstyle \mathcal {K}},{\scriptscriptstyle \mathcal {L}}}} + \sum _{\sigma \in {\mathcal {E}^{ext}_{\scriptscriptstyle \mathcal {K}}}} m_{{\scriptscriptstyle \sigma }}\frac{u_{{\scriptscriptstyle \mathcal {K}}}-u_{{\scriptscriptstyle \sigma }}}{d_{{\scriptscriptstyle \mathcal {K}},{\scriptscriptstyle \sigma }}} = 0, \quad \forall {\mathcal {K}}\in \mathfrak {M},\\&\alpha m_{{\scriptscriptstyle \sigma }}\partial _t u_{{\scriptscriptstyle \sigma }}+ \sum _{{ \mathbf {v}}={\scriptscriptstyle \sigma }|{\tilde{\scriptscriptstyle \sigma }}} \frac{u_{{\scriptscriptstyle \sigma }}-u_{{\tilde{\scriptscriptstyle \sigma }}}}{d_{{\scriptscriptstyle \sigma },{\tilde{\scriptscriptstyle \sigma }}}} + m_{{\scriptscriptstyle \sigma }}u_{{\scriptscriptstyle \sigma }}- m_{{\scriptscriptstyle \sigma }}\frac{u_{{\scriptscriptstyle \mathcal {K}}}-u_{{\scriptscriptstyle \sigma }}}{d_{{\scriptscriptstyle \mathcal {K}},{\scriptscriptstyle \sigma }}} = 0, \quad \forall \sigma \in \partial \mathfrak {M}, \end{aligned} \right. \nonumber \\ \end{aligned}$$

(45)

where, in the second formula, we conventionally denote by ${\mathcal {K}}$ the unique boundary control volume such that $\sigma \in {\mathcal {E}^{ext}_{\scriptscriptstyle \mathcal {K}}}$.

We postpone the important discussion on the choice of the discrete initial condition $\mathbf {u}(0)=\mathbf {u}^0$ to Theorem 4.

The discrete version of the $H^1_\varGamma$ norm is defined as follows

$$\begin{aligned} \Vert \mathbf {u}\Vert _{1,\mathfrak {M},\partial \mathfrak {M}} = \left( \Vert \mathbf {u}\Vert _{1,\mathfrak {M}}^2 + \Vert \mathbf {u}\Vert _{0,\partial \mathfrak {M}}^2 + \Vert \mathbf {u}\Vert _{1,\partial \mathfrak {M}}^2 \right) ^\frac{1}{2}, \end{aligned}$$

where each term is given by

$$\begin{aligned} \Vert \mathbf {u}\Vert _{1,\mathfrak {M}}^2= & {} \sum _{\sigma ={\scriptstyle {\mathcal {K}}}|{\scriptstyle {\mathcal {L}}}\in \mathcal {E}_{int}} m_{{\scriptscriptstyle \sigma }}d_{{\scriptscriptstyle \mathcal {K}},{\scriptscriptstyle \mathcal {L}}}\left( \frac{u_{{\scriptscriptstyle \mathcal {K}}}-u_{{\scriptscriptstyle \mathcal {L}}}}{d_{{\scriptscriptstyle \mathcal {K}},{\scriptscriptstyle \mathcal {L}}}}\right) ^2 + \sum _{\sigma \in \mathcal {E}_{ext}} m_{{\scriptscriptstyle \sigma }}d_{{\scriptscriptstyle \mathcal {K}},{\scriptscriptstyle \sigma }}\left( \frac{u_{{\scriptscriptstyle \mathcal {K}}}-u_{{\scriptscriptstyle \sigma }}}{d_{{\scriptscriptstyle \mathcal {K}},{\scriptscriptstyle \sigma }}}\right) ^2,\\ \Vert \mathbf {u}\Vert _{0,\partial \mathfrak {M}}^2= & {} \sum _{{\scriptscriptstyle \sigma }\in \partial \mathfrak {M}} m_{{\scriptscriptstyle \sigma }}(u_{{\scriptscriptstyle \sigma }})^2, \quad \text {and} \quad \Vert \mathbf {u}\Vert _{1,\partial \mathfrak {M}}^2 = \sum _{{ \mathbf {v}}={\scriptscriptstyle \sigma }|{\tilde{\scriptscriptstyle \sigma }}} d_{{\scriptscriptstyle \sigma },{\tilde{\scriptscriptstyle \sigma }}}\left( \frac{u_{{\scriptscriptstyle \sigma }}-u_{{\tilde{\scriptscriptstyle \sigma }}}}{d_{{\scriptscriptstyle \sigma },{\tilde{\scriptscriptstyle \sigma }}}}\right) ^2. \end{aligned}$$

Note that, in the boundary term of the definition of $\Vert \cdot \Vert _{1,\mathfrak {M}}$, we use the same convention as in (45) for the notation ${\mathcal {K}}$.

A discrete energy estimate is obtained by multiplying the first equation in (45) by $\partial _t u_{{\scriptscriptstyle \mathcal {K}}}$, the second equation by $\partial _t u_{{\scriptscriptstyle \sigma }}$ and by summing the resulting equalities on $\mathfrak {M}$ and $\partial \mathfrak {M}$. We obtain

$$\begin{aligned} \frac{d}{dt} \Vert \mathbf {u}(t)\Vert _{1,\mathfrak {M},\partial \mathfrak {M}}^2 \le 0, \end{aligned}$$

where we did not specify the form of the dissipation terms, since it is not important for our purpose.

This estimate shows that the discrete $H^1_\varGamma$ norm of the approximate solution decreases along the time and thus satisfies

$$\begin{aligned} \sup _{t\in [0,T]} \Vert \mathbf {u}(t)\Vert _{1,\mathfrak {M},\partial \mathfrak {M}} \le \Vert \mathbf {u}^0\Vert _{1,\mathfrak {M},\partial \mathfrak {M}}. \end{aligned}$$

This a priori estimate is the main tool to prove the convergence of the numerical method. However, in order to be useful, we see that the discrete initial data $\mathbf {u}^0$ needs to be a stable approximation of $u^0$ in the sense that $\Vert \mathbf {u}^0\Vert _{1,\mathfrak {M},\partial \mathfrak {M}}$ has to be bounded uniformly with respect to the mesh size, for any $u^0\in H^1_\varGamma$.

In this framework, the inequality we proved in this paper leads to the following stability result, which was our main motivation.

Theorem 4

Let $\xi _0>0$ and $h_0>0$ given by Proposition 6. There exists a $C>0$ such that for any finite volume mesh $\mathfrak {M}$ of $\varOmega$ satisfying

$$\begin{aligned} \mathrm{reg}_1(\mathfrak {M})\le \xi _0, \ \ \mathrm{reg}_2(\mathfrak {M})\le \xi _0, \quad \text {and} \quad \mathrm{size}(\mathfrak {M})\le h_0, \end{aligned}$$

and for any $u^0\in H^1_\varGamma$, we have

$$\begin{aligned} \Vert \mathbf {u}^0\Vert _{1,\mathfrak {M},\partial \mathfrak {M}} \le C \Vert u^0\Vert _{H^1_\varGamma }, \end{aligned}$$

where $\mathbf {u}^0=\bigg ( (u^0_{\scriptscriptstyle \mathcal {K}})_{{\scriptscriptstyle \mathcal {K}}\in {\scriptscriptstyle \mathfrak {M}}} , (u^0_{\scriptscriptstyle \sigma })_{{\scriptscriptstyle \sigma }\in {\scriptscriptstyle \partial \mathfrak {M}}}\bigg )$ is defined by

$$\begin{aligned} \left\{ \begin{array}{lll} u^0_{{\scriptscriptstyle \mathcal {K}}} &{} = \frac{1}{m_{{\scriptscriptstyle \mathcal {K}}}}\int _{\scriptscriptstyle \mathcal {K}}u^0(x)\, dx, \ \quad &{}\forall {\mathcal {K}}\in \mathfrak {M},\\ u^0_{{\scriptscriptstyle \sigma }}&{} = \frac{1}{m_{{\scriptscriptstyle \sigma }}} \int _{{\scriptscriptstyle \sigma }} u^0_{|\varGamma }\, dx, \ \ &{}\forall \sigma \in \partial \mathfrak {M}. \end{array} \right. \end{aligned}$$

(46)

Notice first that, in order to take advantage of the assumed regularity of the trace of $u^0$ on $\varGamma$ in the estimate of the tangential gradient term $\Vert \mathbf {u}^0\Vert _{1,\partial \mathfrak {M}}$, we absolutely need to define the boundary terms $\mathbf {u}_{\scriptscriptstyle \sigma }^0$ by using only the values of the trace of $u^0$ on $\varGamma$ and not, for instance, the values of $u^0$ on the chords associated with each boundary control volume $\sigma$.

Proof

• The estimate of the $L^2$ term $\Vert \mathbf {u}^0\Vert _{0,\partial \mathfrak {M}}$ is a straightforward consequence of Jensen’s inequality.

• For any two neighboring boundary control volumes $\sigma$ and ${\tilde{\sigma }}$, one can easily prove by using a Taylor formula on the manifold $\varGamma$, that

  $$\begin{aligned} \left| \frac{1}{m_{{\scriptscriptstyle \sigma }}}\int _{\scriptscriptstyle \sigma }u^0 - \frac{1}{m_{\tilde{\scriptscriptstyle {\sigma }}}}\int _{{\tilde{\scriptscriptstyle \sigma }}} u^0 \right| ^2 \le (m_{{\scriptscriptstyle \sigma }}+m_{\tilde{\scriptscriptstyle {\sigma }}}) \int _{{\scriptscriptstyle \sigma }\cup {\tilde{\scriptscriptstyle \sigma }}} |\nabla _{\varGamma } u^0 |^2. \end{aligned}$$

  It follows that

  $$\begin{aligned} \Vert \mathbf {u}^0\Vert _{1,\partial \mathfrak {M}}^2&= \sum _{{ \mathbf {v}}={\scriptscriptstyle \sigma }|{\tilde{\scriptscriptstyle \sigma }}} \frac{1}{d_{{\scriptscriptstyle \sigma },{\tilde{\scriptscriptstyle \sigma }}}} \left( \frac{1}{m_{{\scriptscriptstyle \sigma }}}\int _{\scriptscriptstyle \sigma }u^0 - \frac{1}{m_{\tilde{\scriptscriptstyle {\sigma }}}}\int _{{\tilde{\scriptscriptstyle \sigma }}} u^0 \right) ^2\\&\le \sum _{{ \mathbf {v}}={\scriptscriptstyle \sigma }|{\tilde{\scriptscriptstyle \sigma }}} \frac{m_{{\scriptscriptstyle \sigma }}+m_{\tilde{\scriptscriptstyle {\sigma }}}}{d_{{\scriptscriptstyle \sigma },{\tilde{\scriptscriptstyle \sigma }}}} \int _{{\scriptscriptstyle \sigma }\cup {\tilde{\scriptscriptstyle \sigma }}} |\nabla _{\varGamma } u^0 |^2,\\&\le 2 \mathrm{reg}_2(\mathfrak {M})\int _\varGamma |\nabla _{\varGamma } u^0|^2. \end{aligned}$$

• It remains to estimate the term $\Vert \mathbf {u}^0\Vert _{1,\mathfrak {M}}^2$. To this end, we first estimate the term corresponding to the interior edges as follows

  $$\begin{aligned} \sum _{\sigma ={\scriptstyle {\mathcal {K}}}|{\scriptstyle {\mathcal {L}}}\in \mathcal {E}_{int}} m_{{\scriptscriptstyle \sigma }}d_{{\scriptscriptstyle \mathcal {K}},{\scriptscriptstyle \mathcal {L}}}\left( \frac{u_{{\scriptscriptstyle \mathcal {K}}}^0-u_{{\scriptscriptstyle \mathcal {L}}}^0}{d_{{\scriptscriptstyle \mathcal {K}},{\scriptscriptstyle \mathcal {L}}}}\right) ^2&= \sum _{\sigma ={\scriptstyle {\mathcal {K}}}|{\scriptstyle {\mathcal {L}}}\in \mathcal {E}_{int}} \frac{m_{{\scriptscriptstyle \sigma }}}{d_{{\scriptscriptstyle \mathcal {K}},{\scriptscriptstyle \mathcal {L}}}} \left( u_{{\scriptscriptstyle \mathcal {K}}}^0-u_{{\scriptscriptstyle \mathcal {L}}}^0\right) ^2 \\&\le 2 \sum _{\sigma ={\scriptstyle {\mathcal {K}}}|{\scriptstyle {\mathcal {L}}}\in \mathcal {E}_{int}} \frac{m_{{\scriptscriptstyle \sigma }}}{d_{{\scriptscriptstyle \mathcal {K}},{\scriptscriptstyle \mathcal {L}}}} \left[ (u_{{\scriptscriptstyle \mathcal {K}}}^0-u_{{\scriptscriptstyle \sigma }}^0)^2 + (u_{{\scriptscriptstyle \sigma }}^0-u_{{\scriptscriptstyle \mathcal {L}}}^0)^2\right] , \end{aligned}$$

  where we have introduced the mean-values on the edges $u_{{\scriptscriptstyle \sigma }}^0$ as in (46) but for interior edges now.

  Gathering this computation with the other term in $\Vert \mathbf {u}^0\Vert _{1,\mathfrak {M}}^2$, we obtain

  $$\begin{aligned} \Vert \mathbf {u}^0\Vert _{1,\mathfrak {M}}^2&\le 2 \sum _{{\scriptscriptstyle \mathcal {K}}\in \mathfrak {M}} \sum _{\sigma \in \mathcal {E}_{\scriptscriptstyle \mathcal {K}}} \frac{m_{{\scriptscriptstyle \sigma }}}{d_{{\scriptscriptstyle \mathcal {K}},{\scriptscriptstyle \sigma }}}(u_{{\scriptscriptstyle \mathcal {K}}}^0-u_{{\scriptscriptstyle \sigma }}^0)^2. \end{aligned}$$

  We can now use Theorem 1 and Proposition 6, to obtain

  $$\begin{aligned} \Vert \mathbf {u}^0\Vert _{1,\mathfrak {M}}^2&\le C_{\xi _0} \sum _{{\scriptscriptstyle \mathcal {K}}\in \mathfrak {M}} \sum _{\sigma \in \mathcal {E}_{\scriptscriptstyle \mathcal {K}}} \frac{m_{{\scriptscriptstyle \sigma }}}{d_{{\scriptscriptstyle \mathcal {K}},{\scriptscriptstyle \sigma }}} (m_{{\scriptscriptstyle \sigma }}+\mathrm {diam}({\scriptstyle {\mathcal {K}}}))^2 \frac{1}{m_{{\scriptscriptstyle \mathcal {K}}}}\int _{\scriptscriptstyle \mathcal {K}}|\nabla u^0|^2\\&\le C_{\xi _0} \mathrm{reg}_2(\mathfrak {M})(1+\mathrm{reg}_2(\mathfrak {M}))^2 \sum _{{\scriptscriptstyle \mathcal {K}}\in \mathfrak {M}} \sum _{\sigma \in \mathcal {E}_{\scriptscriptstyle \mathcal {K}}} \mathrm {diam}({\scriptstyle {\mathcal {K}}})^2 \frac{1}{m_{{\scriptscriptstyle \mathcal {K}}}}\int _{\scriptscriptstyle \mathcal {K}}|\nabla u^0|^2 \\&\le 3 C_{\xi _0}\mathrm{reg}_2(\mathfrak {M})(1+\mathrm{reg}_2(\mathfrak {M})^2) \mathrm{reg}_1(\mathfrak {M})\int _\varOmega |\nabla u^0|^2, \end{aligned}$$

  and the claim is proved. Notice that the assumptions of Theorem 1 are satisfied with a uniform ratio $\nu /\mu$ thanks to Proposition 6, and to the fact that for interior control volumes ${\scriptstyle {\mathcal {K}}}$, which are real triangles, the ratio $\nu /\mu$ is equal to 1 (see Remark 1).

$\square$

Appendix: An intermediate result

Lemma 6

There exists a $C^{1}$ diffeomorphism $\psi :\overline{Q^{n-1}} \rightarrow \overline{Q^{n-1}}$ such that, setting $\widetilde{\gamma }=\gamma \circ \psi$, for every $\theta \in \overline{Q^{n-1}}$,

$$\begin{aligned} |\partial _1\widetilde{\gamma } \wedge \dots \wedge \partial _{n-1}\widetilde{\gamma }|(\theta )=m_{{\scriptscriptstyle \sigma }}. \end{aligned}$$

Proof

This follows from the proof of [8, Lemma 2], see also [3, Theorem 7, Proposition A.2]. However, in the former reference, all the data are assumed to be smooth. In the latter (which gives a result on more general domains than a cube), the map $\psi$ is merely $C^1$ on $Q^{n-1}$ instead of $\overline{Q^{n-1}}$. For the convenience of the reader, we detail the proof.

Let $f=\frac{1}{m_{{\scriptscriptstyle \sigma }}}|\partial _1\gamma \wedge \dots \wedge \partial _{n-1}\gamma |$. Then $\int _{Q^{n-1}}f=1$.

For every $k=1, \dots , n-1$, there exists a $C^1$ map $f_{k}:\overline{Q^{k}}\rightarrow \mathbb R$ such that $f=f_1\dots f_{n-1}$ and

$$\begin{aligned} \int _{0}^1 f_k(x_1, \dots , x_{k-1},t)\,dt =1, \quad \quad (x_1, \dots , x_{k-1})\in \overline{Q^{k-1}}. \end{aligned}$$

(47)

Indeed, let

$$\begin{aligned} f_1(x_1) = \int _{Q^{n-2}}f(x_1, t_2, \dots , t_{n-1})\,dt_2\dots dt_{n-1}, \quad \quad x_1\in [0,1] \end{aligned}$$

and then define by induction on $1\le k \le n-1$, the map $f_k$ by

$$\begin{aligned} f_1(x_1)\dots f_k(x_1, \dots , x_k)=\int _{Q^{n-1-k}}f(x_1, \dots , x_k, t_{k+1}, \dots , t_{n-1})\,dt_{k+1}\dots dt_{n-1}. \end{aligned}$$

(When $k=n-1$, the right-hand side is simply $f(x_1, \dots , x_{n-1})$.) One easily checks that (47) is satisfied. We now define the map $\rho =(\rho _1, \dots , \rho _{n-1})$ by

$$\begin{aligned} \rho _i(x_1, \dots , x_i)=\int _{0}^{x_i}f_i(x_1, \dots , x_{i-1},t)\,dt, \quad \quad 1\le i \le n-1. \end{aligned}$$

Then $x_i\mapsto \rho _i(x_1, \dots , x_i)$ maps diffeomorphically $[0,1]$ onto $[0,1]$. Moreover,

$$\begin{aligned} \text {Jac}\,\rho = \prod _{i=1}^{n-1}\frac{\partial \rho _i}{\partial x_i}=\prod _{i=1}^{n-1}f_i=f. \end{aligned}$$

We then define $\psi =\rho ^{-1}$. Then

$$\begin{aligned} 1=\text {Jac}\,(\rho \circ \psi )=((\text {Jac}\,\rho ) \circ \psi ) \text {Jac}\,\psi =(f\circ \psi ) \text {Jac}\,\psi . \end{aligned}$$

Since

$$\begin{aligned} \partial _1\widetilde{\gamma } \wedge \dots \wedge \partial _{n-1}\widetilde{\gamma }=\left( (\partial _1\gamma \wedge \dots \wedge \partial _{n-1}\gamma )\circ \psi \right) \text {Jac}\,\psi , \end{aligned}$$

this completes the proof of the lemma. $\square$