Introduction

Large-scale discontinuities, such as faults (Chigira 1992), bedding (Ma et al. 2018), and weak interlayers (Han et al. 2023), often form the boundaries of potentially sliding rock masses. Additionally, small-scale discontinuities, like joints and secondary fractures, significantly influence the integrity and mechanical properties of the rock mass (Han et al. 2017). Hence, obtaining accurate and rapid information about these discontinuities features is essential for engineering rock mass classification and slope stability analysis. Currently, traditional manual measurement remains the predominant method in fieldwork, involving geologists recording discontinuities at accessible areas using a compass and tape. Nonetheless, this method has limitations, as it is subjective and unsuitable for steep, hazardous, or inaccessible areas (Gischig et al. 2011; Gigli and Casagli 2011). At present, the interpretation of rock mass discontinuity information from point clouds obtained through non-contact measurement has become a supplementary approach in fieldwork. This approach allows for validation with manual measurements in accessible areas and enables discontinuity information acquisition in otherwise inaccessible regions.

Many scholars have made efforts to extract discontinuity information from point clouds, primarily utilizing two methodologies: point cloud segmentation and point cloud classification. Both these methodologies rely on inherent point cloud features, including spatial coordinates, normal vector, curvature, and color. Spatial coordinates and color are the fundamental attributes captured through laser scanning or photographic imagery (Park and Cho 2022). Normal vector and curvature, on the other hand, are derived through 2.5D methods involving triangulation (Slob et al. 2002; Lato and Vöge 2012; Chen et al. 2016; Zhang et al. 2018; Li et al. 2019) and searching cube (Gigli and Casagli 2011; Guo et al. 2017). An alternative option is the application of a point-based 3D method (Ferrero et al. 2009; Riquelme et al. 2014; Menegoni et al. 2019; Zhang et al. 2019) to calculate attributes for points sets composed of point and adjacent points.

The methods for calculating normal vector and curvature include the least squares method (Ferrero et al. 2009; Wang et al. 2017; Riquelme et al. 2018; Zhang et al. 2018) and principal component analysis (PCA) (Jaboyedoff et al. 2007; Otoo et al. 2011; Mah et al. 2013; Hu et al. 2020), which, however, display sensitivity to outliers. Due to its robustness in noisy data, some researchers (Vasuki et al. 2014; Chen et al. 2016; Li et al. 2019) employed the Random Sample Consensus (RANSAC) (Fischler and Bolles 1981) to achieve more reliable normal estimations, despite its limited applicability to curvature computations.

Point cloud segmentation methods partition point clouds with similar features into clusters, enabling the extraction of individual discontinuities. Classic point cloud segmentation algorithms include Hough transform (HT), RANSAC, region growth, and supervoxel. Discontinuities within rock masses tend to be geometrically planar. Therefore, HT and RANSAC have been employed by many researchers (Ferrero et al. 2009; Leng et al. 2016; Chen et al. 2017; Han et al. 2017; Yang et al. 2021) to detect planes within point clouds, with each plane representing an individual discontinuity. However, these methods have become less popular in point cloud plane extraction tasks, due to their substantial computational memory and time requirements (Daghigh et al. 2022). On the other hand, based on the normal vector and curvature relationship between the seed point and adjacent points, the region growth algorithm (Wang et al. 2017; Ge et al. 2018; Yi et al. 2023) facilitates the expansion of points belonging to the same individual discontinuity, and finally formed coherent regions to realize the extraction of individual discontinuities. However, as point cloud size and density escalate, the processing time also exhibits a pronounced increase. To mitigate the challenges of directly dealing with vast point clouds, Sun et al. (2021) proposed to voxelize the point cloud, and consider the connectivity of neighboring voxels, merging similar voxels to form supervoxels, achieving pre-segmentation of the point cloud. After that, individual discontinuities were extracted based on spatial connectivity, region planarity, and parallelism among adjacent supervoxels. Once the individual discontinuities are acquired using segmentation algorithms, the discontinuity sets can be identified by employing the K-means algorithm (Ge et al. 2017; Yi et al. 2023; Sun et al. 2021).

Point cloud classification entails grouping each point based on its distinctive features, facilitating the identification of discontinuity sets. Within the same discontinuity set, the orientations of the discontinuity do not differ significantly, resulting in multiple principal orientations, with their quantity corresponding to the number of discontinuity sets. Various methods have been developed to determine principal normal vectors equivalent to the principal orientations including 2D kernel density analysis (Riquelme et al. 2014) and 3D fast search and find density peak (Kong et al. 2020; Wu et al. 2021) based on the density of the normal vectors. Each point is then assigned the nearest principal normal vector based on its angular deviation from the principal normal vectors. Methods like K-means (Chen et al. 2016; Wu et al. 2021) and FCM (Van Knapen and Slob 2006; Vöge et al. 2013) also explore principal normal vectors as cluster centroids for point cloud classification. Nevertheless, traditional K-means and FCM may often result in incorrect cluster centroid identification when updating cluster centroid through average value. In response, scholars incorporated optimization algorithms, like particle swarm optimization (PSO) (Li et al. 2015; Song et al. 2017), differential evolution (DE) (Cui and Yan 2020), and firefly algorithm (FA) (Guo et al. 2017), to find accurate cluster centroids. There are also alternative methods for point clouds direct classification without the prerequisite for initial principal normal vector identification. For instance, Ge et al. (2022) manually selected training samples to train an artificial neural network, enabling point cloud classification and discontinuity sets identification. However, this approach needs iterative manual reselection of samples to overcome the limitation of representative training samples to ensure satisfactory outcomes, and thereby compromising efficiency. After discontinuity sets are obtained, the subsequent steps involve applying density-based spatial clustering of applications with noise (DBSCAN) (Riquelme et al. 2014; Ge et al. 2022) to further segmentation, resulting in the extraction of individual discontinuities.

This paper introduces a new approach to identify discontinuity using convolutional neural networks (CNN) and an improved FCM algorithm based on PSO. The structure of this paper is organized as follows: the data and methods employed in this paper are introduced in “Methodology.” The application of the method to results in two case studies, as well as the analysis of relevant parameters, is introduced in “Results for case.” The discussion and conclusion are respectively presented in “Discussion”4 and “Conclusion.”

Methodology

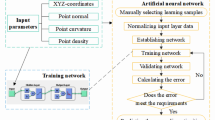
The proposed methodology in this study consists of five steps as illustrated in Fig. 1.

  • Step 1: Establishment of the convolutional neural network — AlexNet.

  • Step 2: Calculation of point cloud feature. PCA is used to calculate the normal vector and curvature.

  • Step 3: Automatic selection of learning samples. The improved FCM is used to categorize randomly selected points of a certain proportion, and these categorized points are used as learning samples.

  • Step 4: Identification of discontinuity sets using AlexNet trained by automatically categorized learning samples.

  • Step 5: Recognition of individual discontinuities using hierarchical density–based spatial clustering of applications with noise (HDBSCAN) and calculation of orientation.

Fig. 1
figure 1

Flow chart of the proposed method

Full size image

Dataset description

Case A

Case A is located along the TP-7101 highway in the Baix Camp region of Spain (Catalonia Province). It is approximately 4 km away from the nearest town, False, in the northwest direction. The scanned rock formation is composed of dark grey to black, silt–clay size, small tabular, slightly weathered meta-siltstone, and slate, measuring about 50 m in length and 6 m in height. Figure 2a is a photograph of the rock exposure at the site. The point cloud data was obtained using the Optech llris 3D laser scanner on June 10, 2004. The average distance between the laser scanner and the rock formation was 11.3 m, resulting in an approximate point cloud spacing of 5 mm. A specific region within the point cloud data, as indicated by the red rectangle in Fig. 2a, was selected as the study area. Figure 2b shows the selected region’s point cloud, consisting of a total of 86,749 points. The raw point cloud data is available at https://www.researchgate.net/publication/289523298_raw_point_cloud_data_ascii_x_y_z_intensity_metadata (Slob 2010).

Fig. 2
figure 2

Case A: a Photograph of rock exposure (Slob 2010). Red rectangle: research area of this paper. b Point cloud of the research area

Full size image

Case B

The outcrop of case B is located along Highway 15, approximately 30 km north of Kingston, Ontario, Canada. The raw point cloud data was obtained by LeicaHD S6000 scanner at a position about 10 m away from the scanning area and 2,167,515 points were obtained in total. Three distinct scan sites for placing the scanner were strategically established based on the discontinuity distribution in the outcrop. Figure 3 shows the precise locations and orientations of the three scan sites. The scanning range measures 13.28 m × 4.21 m × 3.71 m, with an average point spacing of approximately 5 mm. This outcrop exhibits the development of three nearly orthogonal discontinuity sets. Figure 3 highlights a representative discontinuity from each of the three sets. The raw point cloud data is publicly accessible and can be obtained from the RockBench repository (Lato et al. 2013).

Fig. 3
figure 3

Photograph of outcrop in case B. Three locations of the scanner and three typical individual discontinuities (Lato et al. 2009)

Full size image

AlexNet

Compared to large-scale networks burdened by high computational demands and slow processing speeds, the lightweight convolutional neural network, AlexNet (Krizhevsky et al. 2012) significantly enhances training speed through parallel training on dual GPUs. Therefore, this study used AlexNet to classify the point cloud, focusing on normal vectors serving as the network input. The AlexNet architecture suitable for discontinuity sets recognition is illustrated in Fig. 4. It consists of five convolutional layers and three fully connected layers, utilizing 1 × 3 normal vectors as input and generating an output value “i” that represents the identified discontinuity set associated with the “i” category. Given the 1 × 3 input data size, “same” convolution with a stride of 1 was utilized with no pooling layers interposed between the convolutional layers to maintain its size. The five convolutional layers have 96, 256, 384, 384, and 256 filters, respectively, each sized at 1 × 3. The learning samples used in the training process were automatically categorized using the improved FCM algorithm. The details are described in “Automatic selection of learning samples.”

Fig. 4
figure 4

The architecture of AlexNet employed in this study

Full size image

Point cloud feature

In this study, the point cloud features used for AlexNet input are normal vectors. Meanwhile, curvature is used to identify edges in point clouds. To enhance computational efficiency, instead of using different algorithms to calculate normal vectors and curvature separately, the PCA algorithm was employed in this paper to calculate both simultaneously.

Normal vector

Pi is a point member of the point cloud; K-nearest neighbor algorithm is employed to find the nearest K points of Pi in Euclidean space. As a result, Qi, comprising K points, is formed:

$$\left[\begin{array}{ccc}{x}_{1}& {y}_{1}& {z}_{1}\\ {x}_{2}& {y}_{2}& {z}_{2}\\ \vdots & \vdots & \vdots \\ {x}_{k}& {y}_{k}& {z}_{k}\end{array}\right]$$

The normal vector of the plane defined by Qi is calculated by PCA, which identifies the eigenvalues (λ1, λ2, λ3) and eigenvectors for the covariance matrix of Qi. Assuming λ1 ≦ λ2 ≦ λ3, the eigenvector corresponding to λ1 is the normal vector of Pi.

As shown in Fig. 5, the surface of the rock mass discontinuity is rough and uneven, resulting in normal vector pointing in the opposite direction at different points on the same discontinuity, which is necessary to adjust the normal vector to a unified direction. The angle θ between the normal vector \(\overrightarrow{a}\) and the reference point \(\overrightarrow{b}\) = [1 1 1] is determined by the following equation:

Fig. 5
figure 5

Normal vector direction at different points in the same discontinuity

Full size image
$$\theta =arccos\frac{\overrightarrow{a} \overrightarrow{b}}{|\overrightarrow{a}|\times |\overrightarrow{b}|}$$
(1)

When θ > 90°, \(\overrightarrow{a}\) is not pointing towards \(\overrightarrow{b}\), and the vector is flipped. Figure 6 shows the point clouds before and after normal vector adjustment in which the parameter K is set to 45, 40 for two cases, respectively. Several manual tests showed that the normal vector is more suitable when K is set as 45 for case A. Therefore, K was initialized with a value of 45 for case A. However, after a more thorough validation process in “Number of nearest neighbor K,” the optimal value of K was determined to be 40. Hence, for case B, K was set to 40. For example, in Fig. 3, the observed color of the discontinuity set where J3 is positioned shifts from black and green to green. This indicates that the normal vectors have been standardized to a consistent direction.

Fig. 6
figure 6

The 3D point cloud: The color of each point corresponds to its normal vector with K = 45, 40 for case A and case B, respectively. Left: normal vector before adjustment. Right: normal vector after adjustment. a Case A: 86,749 points. b Case B: 2,761,515 points

Full size image

Curvature

“Normal vector” has calculated the eigenvalues (λ1, λ2, λ3) for the covariance matrix of Qi. σK(Pi) determined by Eq. (2) is defined as the surface change at Pi within the surface formed by Qi.

$${\sigma }_{K}({P}_{i})\text{=}\frac{{\lambda }_{1}}{{\lambda }_{1}+{\lambda }_{2}+{\lambda }_{3}}$$
(2)

Pauly et al. (2002) observed a strong agreement between σK(Pi) and the average curvature of each point across different point cloud models. Therefore, in this method, σK(Pi) is used to replace the average curvature equivalent to reduce the computation time.

Automatic selection of learning samples

For field slope outcrop dataset, learning samples are not readily available, but should be acquired from the corresponding point cloud. In contrast to manual selection, this paper introduces an automatic method for obtaining learning samples. First, the edges, intersection of the discontinuity, are excluded to ensure that randomly chosen samples are not situated on edges with chaotic normal vectors. Then, a subset of sample points is randomly selected from the remaining point cloud, which is automatically classified using an improved FCM based on PSO, assigning a category to each sample point.

Discarded edge

Unlike the nearly parallel normal vectors exhibited by the same set of discontinuities, the normal vector of the edge appears chaotic and exhibits an angle deviation from the discontinuity, as illustrated in Fig. 7. As depicted in Fig. 8a, the curvature of edges is markedly higher than that of discontinuities. Therefore, edges are eliminated by applying a curvature threshold, denoted as r.

Fig. 7
figure 7

Normal vector direction at discontinuity and edge, respectively

Full size image
Fig. 8
figure 8

The 3D point cloud of case A: The color of each point corresponds to its curvature with K = 45. a Edges are not discarded. b Remaining 69,399 points. 17,350 points belonging to edges were discarded with p = 0.8

Full size image

The sorted elements in σK(P) are taken as the cumulative probability (0.5/n), (1.5/n), …, ([n − 0.5]/n) quantiles, where n is the number of sorted elements. The linear interpolation method is employed to compute quantiles for a given cumulative probability p between (0.5/n) and ([n − 0.5]/n). x1 and x2 are determined by Eq. (3), corresponding to quantiles y1 and y2, respectively, for the given cumulative probability p between x1 and x2. Utilizing linear interpolation, the p quantile yp is derived using Eq. (4). Figure 8b shows that the edges were discarded when r equals σK(P) when the cumulative probability p was set as 0.8.

$$\left\{\begin{array}{c}{x}_{1}=\frac{{\text{round}}\;\left(p\times n\right)-0.5}{n}\\ {x}_{2}=\frac{{\text{round}}\;\left(p\times n\right)+0.5}{n}\end{array}\right.$$
(3)

where \({\text{round}}\;\left(x\right)=\left\{\begin{array}{cc}\lceil x\rceil,& \mathrm{if }x-\lfloor x\rfloor\ge 0.5\\ \lfloor {\text{x}}\rfloor,& \mathrm{if }x-\lceil x\rceil\ge 0.5\end{array}\right.\)

$${y}_{p}={y}_{1}+\frac{p-{x}_{1}}{{x}_{2}-{x}_{1}}({y}_{2}-{y}_{1})$$
(4)

Fuzzy C-means algorithm

To obtain categorized learning samples, FCM is employed to classify a small randomly selected subset of points with known features from the point cloud with its edges removed.

The normal vectors are represented by (P1, P2, …, PN), with N representing the count of selected points. The cluster centroids are initialized as (V1, V2, …, Vc), where C is the number of discontinuity sets. The acute angle θ between Pj and Vi is determined by the following equation.

$$\theta ={\text{arccos}}|{P}_{j}\cdot {{V}_{i}}^{T}|$$
(5)

In this paper, for the grouping selected points, the distance between two points was measured using the square of the sine value of the acute angle between the normal vectors of two points, instead of the Euclidean distance. The distance between Pj and Vi is then given by the following equation:

$$D({P}_{j},{V}_{i})={{\text{sin}}}^{2}\;\theta =1-{({P}_{j}\cdot {{V}_{i}}^{T})}^{2}$$
(6)

The FCM calculates the distance between every normal vector and each cluster centroid, and assigns each point to the closest cluster centroid based on the distance. Thus, the objective function E for grouping discontinuities is expressed in the following equation.

$$E=\sum_{j=1}^{N}\sum_{i=1}^{C}{{u}_{ij}}^{2}{D}^{2}({P}_{j},{V}_{i})$$
(7)

where uij represents the membership degree of the jth normal vector belonging to the ith cluster centroid as shown in Eq. (8).

$${{u}_{i}}_{j}=\frac{1}{{D}^{2}({P}_{j},{V}_{i})}{\left[\sum_{k=1}^{C}\frac{1}{{D}^{2}({P}_{j},{V}_{k})}\right]}^{-1}$$
(8)

Once all points have been assigned to the nearest cluster centroid, the mean value for each cluster is calculated and adopted as the new cluster centroids. This iterative approach continually updates the cluster centroids until the objective function E is minimized. In this paper, the number of clusters (C) is determined by identifying color variations in the point cloud, where the colors are represented by normal vectors. Considering that the FCM heavily relies on initial centroids selection, an incorrect choice of initial centroids may lead to suboptimal clustering results and increased clustering iterations. Therefore, the PSO algorithm is applied to replace the conventional mean value for updating cluster centroids.

Particle Swarm Optimization algorithm

PSO algorithm (Kennedy and Eberhart 1995) conceptualizes birds in a foraging flock as weightless particles. Each particle has a distinct position xi = (xi1, xi2, …, xin) and velocity vi = (vi1, vi2, …, vin) in an n-dimensional space. By iteratively adjusting their movement direction and position, referencing their personal historical best position xpbest and the best position of the entire group xgbest, the particles progressively converge towards an optimal solution. The xpbest and xgbest are updated in every iteration based on the fitness function value of the particle.

The velocity and position of particles are adjusted using Eqs. (9) and (10) respectively:

$${v}_{i}^{t+1}=\omega \cdot {v}_{i}^{t}+{c}_{1}\cdot {r}_{1}\cdot ({x}_{pbest}-{x}_{i}^{t})+{c}_{2}\cdot {r}_{2}\cdot ({x}_{gbest}-{x}_{i}^{t})$$
(9)
$${x}_{i}^{t+1}={x}_{i}^{t}+{v}_{i}^{t+1}$$
(10)

where ω, known as the inertia weight, is set as 0.9 for global search. The cognitive and social learning factors, denoted as c1 and c2, respectively, are both set as 1.5. r1 and r2 are random numbers between 0 and 1.

For categorizing the selected points, the particle positions are corresponded to the normal vectors. The fitness function is the objective function E, which is minimized during the iterative process. Therefore, during the iteration process, xpbest refers to the position where a particle has its lowest fitness, while xgbest represents the position where the particle exhibits the lowest fitness in the entire group. After the iteration ends, xgbest is the cluster centroid for the selected points.

As particles move towards the optimal solution, they may encounter local extreme values that cause their velocities to quickly reduce to zero, leading to premature convergence of all particles on a local extreme. To avoid inaccurate classification due to premature convergence, this paper introduces a time threshold T. If the convergence time is less than T, the algorithm will be re-executed.

Figure 9 shows 87 points, randomly selected from the remaining points cloud, were automatically categorized by the improved FCM based on PSO with C = 4 (four colors in Fig. 6a), T = 50, and a particle count of 1000 for case A. Figure 10 shows the population’s progression in achieving a minimum fitness of 0.36075 after the 178th iteration during the twelfth cycle, taking 110.28 s.

Fig. 9
figure 9

Automatically randomly selected learning samples used for training the AlexNet for case A

Full size image
Fig. 10
figure 10

Fitness variation curve with iterations at different cycle

Full size image

Identification of discontinuity set

The categorized learning samples are used to train the network model. Once trained, the model takes the complete point cloud with calculated features as input to determine the category of each point. Points belonging to the same category are aggregated to form a discontinuity set. While achieving 100% accuracy with a CNN model is challenging, it is expected to result in some errors. However, these error points are typically sparsely distributed within the point cloud.

In Fig. 11, the network trained on the learning samples in Fig. 9 successfully identifies four discontinuity sets for case A. However, some error points are indicated within the circled area in Discontinuity sets 1, 3, and 4.

Fig. 11
figure 11

Identification of discontinuity sets for case A with one color per discontinuity set. Red circles denote the location of error points. a Discontinuity sets 1–4, b Set 1, c set 2, d set 3, and e set 4

Full size image

Analysis of individual discontinuity

Once the points belonging to a discontinuity set are identified, each discontinuity set is further segmented to obtain individual discontinuities. Then, the orientation of each discontinuity is calculated.

Recognition of individual discontinuity

DBSCAN (Ester et al. 1996) has been widely employed for the extraction of individual discontinuities from discontinuity sets in previous studies (Riquelme et al. 2014; Buyer and Schubert 2017; Singh et al. 2021). However, selecting two appropriate input parameters (the search radius (ε) and the minimum number of points (min-pts)) for DBSCAN is challenging, particularly when dealing with varying density. To address this, HDBSCAN (Campello et al. 2013) introduces the concept of mutual reachability distance and transforms DBSCAN into a hierarchical clustering algorithm, thus offering a solution for clustering issues with varying densities. The mutual reachability distance between two points is defined by Eqs. (11).

$${d}_{m{\text{reach}}}\left({p}_{i},{p}_{j}\right)={\text{max}}\left\{\left.{{\text{core}}}_{{\text{min}}-{\text{pts}}}({p}_{i}),{{\text{core}}}_{{\text{min}}-{\text{pts}}}({p}_{j}),d\left({p}_{i},{p}_{j}\right)\right\}\right.$$
(11)

where \(d({p}_{i},{p}_{j})\) represents the Euclidean distance between pi and pj. \({{\text{core}}}_{{\text{min}}-{\text{pts}}}({p}_{i})\) and \({{\text{core}}}_{{\text{min}}-{\text{pts}}}({p}_{j})\) represents the distances of pi and pj to their nearest min-pts neighbors, respectively.

Convert the minimum spanning tree generated from mutual reachable distances into a hierarchical cluster structure. Then, traverse the hierarchy and identify new clusters created by the split with sizes smaller than the minimum cluster threshold (minCluster) as “fall out of a cluster,” facilitating the condensation of the cluster tree and, ultimately, the extraction of clusters. For more comprehensive information, refer to prior studies (Campello et al. 2013).

In practice, the primary parameter, minCluster, is intuitive, fairly robust, and easy to select (McInnes and Healy 2017). Additionally, a quantity threshold, DisTh, related to the exposed area and resolution of the point cloud is set to prevent generating too small clusters that represent excessively small individual discontinuities. Both smaller regions with higher resolution and larger areas require a larger DisTh.

Calculation of orientation

In the context of a right-hand coordinate system with the Z-axis pointing vertically upwards, the orientation of the discontinuities is determined by the following equations.

$$dip=co{s}^{-1}(|C|)$$
(12)
$$\left\{\begin{array}{c}dipdirection=90^\circ -{{\text{tan}}}^{-1}\left(\frac{B}{A}\right) \, \, \, \, \, \, \, \, A>0\\ dipdirection=270^\circ -{{\text{tan}}}^{-1}\left(\frac{B}{A}\right) \, \, \, \, \, \, A<0\end{array}\right.$$
(13)

where A, B, and C are the three components computed using the PCA algorithm mentioned in “Normal vector” of the unit normal vector of the discontinuity.

Results for case

Case A: results and relevant parameters analysis

Result for case A

In Fig. 11, some points on the edges of sets 1 and 3 are misidentified as belonging to set 2. This misclassification can be attributed to the chaotic appearance and angle deviation of normal vectors at the edges, as illustrated in Fig. 7. Furthermore, the practical constraints of convolutional neural networks, which cannot achieve 100% accuracy in real-world applications, also contribute to a certain degree of classification error for points along the edges.

Figure 12 presents the clustering results of case A with minCluster = 5, and DisTh = 50. It can be observed that successful segmentation of each discontinuity set has been achieved, resulting in the extraction of individual discontinuities. Additionally, the outlier points in Fig. 11 have been eliminated.

Fig. 12
figure 12

Results of clustering for case A with one color per individual discontinuity. a Sets 1–4, b set 1, c set 2, d set 3, and e set 4

Full size image

Several labeled discontinuities in Fig. 13 were measured on-site by Slob (2010). The orientations of these discontinuities, calculated using the method proposed in this paper, are compared with the field measurements in Table 1. From the comparison, the deviations are within 5°, except for discontinuity 21, which has a dip direction deviation of 7.80°. Considering the rough and uneven nature of the rock mass discontinuity, these deviations can be considered acceptable, affirming the reliability of the proposed method.

Fig. 13
figure 13

Several labeled discontinuities are used for comparison

Full size image
Table 1 Comparison of the orientation of labeled discontinuities calculated by the proposed method and field measurements for case A
Full size table

Number of nearest neighbor K

The value of K significantly influences normal vector calculations in step 2. For each labeled discontinuity in Fig. 13, Fig. 14 shows the standard deviation of angles between the normal vectors of all points situated on the discontinuity and the corresponding discontinuity normal vector across various K values (5, 15, 40, 60, 100, 200, 500, 1000, 2000). Except for discontinuity 42, the others display a trend of initially decreasing and then increasing as K values rise. This is because a larger K may group points from different discontinuities, while a smaller K may result in differences in the same discontinuity due to its rough and uneven nature. Furthermore, discontinuity 12, 13, 21, and 31; discontinuity 11 and 41; and discontinuity 14 exhibit the minimum standard deviations at K = 40, 20, and 60, respectively. Considering that most discontinuities reach their minimum standard deviations at K = 40 and show no significant difference from those at 20 and 60, K = 40 is considered the optimal value.

Fig. 14
figure 14

Calibration of parameter K for different discontinuities labeled in Fig. 13

Full size image

Cumulative probability p

The curvature threshold r, determined by the cumulative probability p, relates to whether learning samples include positions of non-discontinuity, which in turn affects the subsequent identification results of discontinuity sets. If there are many points located on the edges in the learning samples, the FCM tends to cluster the edges as a separate set during point classification, leading to one output of the network being recognized as edges, which hampers the identification accuracy of discontinuity sets.

Figure 15a–d illustrate the removal of edges for different cumulative probabilities p. When p is set as 0.9, some points on the edges are not eliminated, but at p = 0.8, most edge points are removed. However, selecting a smaller p would remove points from discontinuities due to their rough and even nature. Therefore, it is advisable to select a p between 0.8 and 0.9 to achieve the desired results.

Fig. 15
figure 15

Point cloud with different cumulative probability p. a p = 0.9; b p = 0.8; c p = 0.7; d p = 0.6

Full size image

Time threshold and number of learning samples

By conducting a comprehensive analysis, an appropriate number of learning samples and time threshold T are determined. Figure 16 illustrates the elapsed time during multiple executions of the PSO algorithm for case A, considering various numbers of learning samples. It can be observed that there is a distinct time gap that serves as a criterion to identify premature convergence in the PSO algorithm. Figure 16 also presents the longest time for premature convergence, as well as the shortest and longest times for non-premature convergence under different numbers of learning samples. It is evident that as the number of learning samples increases, both the shortest and longest time increases. When the sample is more than 300, the shortest time of 159.15 s at a sample quantity of 300 is an acceptable range. However, the longest time increases significantly to 3233.51 s when the sample quantity is 1000, resulting in a substantial time increase. Therefore, the sample quantity should be below 300, as both the minimum and maximum times fall within an acceptable range. Furthermore, at a sample quantity of 300, the longest time required for premature convergence is 49.71 s. Taking all factors into consideration, this study sets the time threshold as 50 s.

Fig. 16
figure 16

Calibration of the learning samples quantity and threshold time T

Full size image

Optimal parameters

The optimal values for the parameters in different steps of the proposed method are as follows: In step 2, the value of K used to compute the normal vector and curvature is set as 40. For automated learning sample selection at step 3, the curvature threshold p, as analyzed in “Cumulative probability p,” is set between 0.8 and 0.9. The number of colors assigned to the point cloud determines the number of clusters C during colorization based on normal vectors. The sample quantity and time threshold, analyzed in “Time threshold and number of learning samples,” are set as less than 300 and 50 s, respectively.

Result for case B

Figure 6b displays three distinct colors with K = 40, indicating the presence of three discontinuity sets in case B, which is consistent with the results of the field investigation. Utilizing the optimal parameters described in “Optimal parameters,” a total of 184 points were randomly selected from the edge-removed point cloud of case B (p = 0.85) and subjected to classification using improved FCM. Figure 17 illustrates the distribution of the 184 points, which are categorized into three sets: 43 points in discontinuity set 1, 43 points in set 2, and 98 points in set 3.

Fig. 17
figure 17

184 learning samples for case B

Full size image

Figure 18a illustrates the results of discontinuity set identification obtained through training a network on 184 points. It can be observed that the entire point cloud is divided into three sets, and the grouping results align with Fig. 6b, demonstrating accurate grouping. Figure 18 b illustrates the clustering results of the three discontinuity sets, with minCluster = 10 and DisTh = 200.

Fig. 18
figure 18

Identification results and clustering results of discontinuity set for case B. a Discontinuity sets 1–3. One color per discontinuity set. b 518 individual discontinuities. One color per individual discontinuity

Full size image

Figure 19 shows the stereographic projection of all the discontinuity orientations in case B using an equal-angle lower hemisphere projection. The mean orientation of the three discontinuity sets obtained through our method is compared with that from the PlaneDetect software (Lato and Vöge 2012) and DSE software (Riquelme et al. 2016) in Table 2. Compared to the PlaneDetect software, set 1 and set 2 show a good agreement with a maximum deviation of 3°. Although set 3 exhibits a larger orientation deviation, it closely aligns with the results from the DSE software. This may be attributed to the rough and uneven nature of the discontinuity and differences in software recognition accuracy. Overall, the deviations are within an acceptable range.

Fig. 19
figure 19

Stereographic projection of all the discontinuity orientations in case B

Full size image
Table 2 Comparison of orientation results of case B
Full size table

Discussion

Compared to 2D or 2.5D methods that simplify surface information, potentially leading to the loss of valuable information, our approach for calculating normal vectors is a true 3D method that considers each point. Although the generated normal vector data is much larger than that of 2.5D methods, the capability of CNN to handle massive amounts of data effectively solves this problem. By combining the improved FCM with the AlexNet, the entire point cloud can be classified using a small subset of data, thereby avoiding the need to directly process the point cloud using the clustering algorithm such as the improved FCM mentioned in this paper, or the fast search and find of density peaks (CFSFDP) algorithm used by Kong et al.(2020). As a result, the data processing time is greatly reduced.

Kong et al. (2020) proposed employing CFSFDP for extracting discontinuity within two point clouds (approximately 500,000 points and 1,500,000 points). The tasks took 1.5 h and 5.5 h, respectively, using a laptop equipped with a 2.30 GHz(R) Intel Core i5-6300Q processor and 4 GB of RAM. The CFSFDP algorithm is based on the assumption that cluster centers are surrounded by neighbors with lower local density and that they are at a relatively large distance from any points with a higher local density (Rodriguez & Laio 2014). For each data point i, the local density ρi and distance δi depend only on the distances dij. Therefore, the CFSFDP algorithm requires computing the distance matrix dij between any two points, resulting in a time complexity of O(n^2) (where n is the number of points), causing a significant increase in the processing time for large datasets. Table 3 compares the processing time cost by the improved FCM, and DSE software developed by Riquelme et al. (2014), and the method proposed in this paper to case B. It is evident that even with a simplified point cloud (10% of the original point cloud, a total of 216,752 points), the processing time (3.75 h) cost by the improved FCM increases significantly. Meanwhile, compared with the DSE software, the calculation time of the method proposed in this paper is reduced from 1766.2 to 409.5 s, demonstrating the proposed method has an improved computation efficiency.

Table 3 The computation time cost by the DSE software, proposed method and improved FCM for case B
Full size table

When using the improved FCM to determine learning samples, the number of clusters is determined through color classification, which is accurate and avoids the need for iterative determination of the appropriate number of FCM clusters. Furthermore, a time threshold is incorporated to prevent premature convergence of the PSO algorithm, and the processing time is generally less than 300 s.

Manually selecting learning samples is both time-consuming and burdensome on the operator’s eyes. Furthermore, the accuracy heavily relies on the subjective selection of learning samples, which can result in incorrect identification. The iterative process of selecting and reselecting learning samples repeats until satisfactory results are achieved, leading to a significant increase in time and effort expended. The results show that the automatic sample selection method proposed in this paper is reliable and greatly improves the automation level.

In classification tasks, ANN learns complex relationships between input features and output labels through multiple layers of nodes and a fully connected structure, where each node is connected to all nodes in the preceding layer without considering the spatial structure of the data. However, CNN, with its local connections through convolutional kernels, captures spatial local features more effectively, enhancing the processing efficiency for spatially structured data. Figure 20 compares the point cloud classification obtained through two different approaches: the one proposed in this paper, which utilizes AlexNet, and the method used by Ge et al. (2022) employing artificial neural networks (ANN). The recognition results for Discontinuity set 2 and 3 are almost identical for both methods. Nevertheless, when dealing with discontinuity set 1, the ANN-based method misclassified some edge points as discontinuity set 1, leading to lower recognition precision compared to the proposed method in this paper, which yields better recognition results.

Fig. 20
figure 20

Comparison of results between our proposed method using CNN, and Ge et al. (2022) proposed method using ANN: a CNN, discontinuity sets 1–3; b ANN, discontinuity sets 1–3

Full size image

Conclusion

The article presents a new semi-automated method for identifying and extracting rock mass discontinuity using an improved FCM and CNN. The main conclusions are as follows:

A modified convolutional neural network, AlexNet, trained with learning samples automatically categorized by the Fuzzy C-Means based on particle swarm optimization, is designed for identifying discontinuity set within point clouds, which overcomes the problem of manual sample selection, simultaneously enhancing automation and accuracy, and enables the network to complete training within an exceptionally short timeframe. Individual discontinuities are extracted by segmenting the discontinuity set using HDBSCAN and the PCA is applied to calculate the normal vectors of each discontinuity, providing their orientations. HDBSCAN provides a solution for clustering issues with varying densities, and the required parameters are intuitive and easy to select.

The method was applied to two real field outcrops and compared with the results of field surveys and previous studies. By comparing the results with the field survey results of case A, the reliability of the proposed method in this study was verified. Sensitivity analysis was conducted to determine the optimal parameters, which were then applied to case B, also yielding reliable outcomes.

This study combines the improved FCM and CNN to process point clouds, addressing the issue of the time-consuming of using the improved FCM alone. It also avoids the manual selection of learning samples when using neural networks, which may potentially necessitate reselection and result in increased time and effort consumption. In addition, compared with DSE software, the proposed method also improves computational efficiency. While our method takes slightly longer during the point cloud classification using AlexNet compared to the approach proposed by Ge et al. (2022) using ANN, it achieves better results in the recognition of the discontinuity set. The lightweight network AlexNet, proposed in this paper for identifying discontinuity set from point clouds, can complete training in a short time. In summary, the proposed method considers an overall balance between computational accuracy and efficiency.

Furthermore, the method can be easily extended to calculate other parameters of the discontinuity, including trace length, spacing, and roughness. However, extracting the aperture of discontinuity from point clouds remains a challenging problem that requires further investigation in future research.