Kinematic limit analysis of the slope encapsulating a laterally loaded pile

Abstract

This study aims to present a theoretical method for the safety factor of a slope encapsulating a laterally loaded pile. The factor can be derived by the object function concerning the external work rate and internal energy dissipation based on kinematic limit analysis, after assuming the log-spiral failure mechanism of the slope. To address the core issues (the critical point depth and lateral force provided by the pile) in the analysis, the modified strain wedge technique and the soil wedge assumption were adopted to evaluate the soil resistance and extra earth pressure around the pile, respectively. Besides, the proposed method was verified by published data and numerical methods, and the slope failure mechanism was revealed by observing two wedge-shaped failure regions around the pile. Furthermore, the variations of normalized safety factors with normalized lateral loads can be empirically fitted by cubic functions, and the normalized safety factor mainly depends on the lateral load and pile location but is not sensitive to the shear strength. The safety factor of the slope encapsulating a laterally loaded pile (FoS₁) can be thus alternatively predicted by scaling the safety factor of the slope without the lateral load (FoS₀) with the corresponding normalized safety factor η.

Introduction

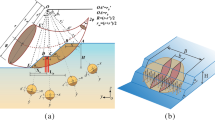
Piles have been frequently employed to sustain superstructures of bridges (Zhao et al. 2017, 2019, 2020), transmission towers, and buildings in mountainous areas (Peng et al. 2019, 2020a, b) such as western and southern hilly terrain (Ng et al. 2001; Ng and Zhang 2001; Zhang et al. 2008) in China (Fig. 1a). The pile would inevitably carry lateral loads caused by high-speed vehicles, typhoons (Liang et al. 2012), and earthquakes (Wang et al. 2021), and the lateral load would be transferred from the pile head to the slope, leading to a degeneration of slope stability and even a slope failure (Fig. 1b). Hence, the mechanical context and behavior of the slope encapsulating a laterally loaded pile are more complicated than those of the slope reinforced with anti-slide piles, and the corresponding stability analysis has become one of the significant technical issues in highway bridge engineering in mountainous areas.

Fig. 1

Slope encapsulating laterally loaded piles: a pile foundations in mountainous areas; b global instability and local instability

In the field of slope stability analysis (Liu et al. 2021), much more effort has been devoted to the slope without a laterally loaded pile and the commonly used methods include the limit equilibrium method (Ito et al. 1979; Poulos 1995), numerical simulation (Lee et al. 1991; Ni et al. 2018), and limit analysis method (Ausilio et al. 2001; Huang et al. 2013; Gao et al. 2014; Qin et al. 2017). The main thought of these methods is to sum the lateral reaction forces provided by anti-slide piles on the potential sliding block and then evaluate the slope safety factor by reducing the shear strength of soil or comparing the resisting moment with the overturning moment on the block. For the limit equilibrium method, the solutions satisfy the static equilibrium condition and Mohr–Coulomb criterion; however, certain simplified assumptions are required and the stress–strain relationship of soil is neglected (Yu et al. 1998). For the numerical simulation, the response of the pile-slope system could be preferably investigated; however, the method is challenged by intensive computations and excessive sensitiveness to input soil parameters and constitutive relation. As to the limit analysis method, the solutions can consider the stress–strain relationship of soil based on rigid-perfectly plastic assumptions, and the method has been broadly employed due to its simplicity and convenience. Hence, it is also an effective theoretical means to predict the stability of the slope encapsulating a laterally loaded pile based on the limit analysis method but has not been systematically reported yet. To the authors’ acknowledge, the lateral load transferred from the pile head to the slope would result in different mechanical responses such as the soil resistance and extra earth pressure around the pile. Two cases of slope failure ascribed to by laterally loaded piles were reported by Uto et al. (1987), but there was no further development on the failure mechanism. To tackle it, an assumption of the wedge-shaped local failure in front of the laterally loaded pile was presented (Nakasima et al. 1985), and the local failure was subsequently observed in some model experiments (Muthukkumaran 2014). In addition, three-dimensional numerical analysis was carried out to quantitatively investigate the effect of the laterally loaded pile on the slope stability, and the mechanisms of lateral load transfer from the pile to the slope were revealed (Ng et al. 2001). However, these studies failed to theoretically predict the mechanical response (Ng et al. 2001; Uto et al. 1987; Nakasima et al. 1985; Muthukkumaran 2014) and satisfy the requirement of the recent design code (JTG 2020). In conclusion, it is necessary to estimate the soil resistance and extra earth pressure in the theoretical analysis of slope stability with a laterally loaded pile.

On account of this, the assessments of degraded soil resistance in front of the pile and extra earth pressure behind the pile should be considered (Fig. 2). For the former, it is commonly estimated by reducing the standard p-y curves in the level ground (Reese and Welch 1975) with reduction coefficients (Mezazigh and Levacher 1998; Liyanapathirana and Poulos 2010; Nimityongskul et al. 2018), idealizing the soil as a series of nonlinear springs along piles (Reese et al. 2006; Jiang et al. 2020). However, the estimation would rely on measured p-y curves in the field, with a limited range of pile properties (e.g., the pile type, pile stiffness, and pile top restrains) and material properties (e.g., sand and clay). To make up these limitations, the strain wedge technique (Norris 1986; Ashour et al. 1998, 2004; Xu et al. 2013; Yang et al. 2017) has been modified to evaluate the degraded soil resistance in the mountainside (Peng et al. 2019, 2020b). It envisioned a relationship of the three-dimensional responses of laterally loaded piles to parameters of one-dimensional beam on elastic foundation. As to the latter, theoretical methods are more economically efficient and time-saving in preliminary designs; however, it has been mainly investigated by experiments (Peng et al. 2020a; Muthukkumaran 2014; Zhao et al. 2018) and numerical simulations (Ng et al. 2001; Ng and Zhang 2001; Zhang et al. 2008). Hence, the soil wedge assumption (Paik and Salgado 2003; He et al. 2015) has been employed to evaluate the extra earth pressure behind the laterally loaded pile (Peng et al. 2020b), the magnitude and distribution of which have been mentioned in previously published studies (Ng et al. 2001; Ng and Zhang 2001). In the assumption, the nonlinear distribution of the extra earth pressure is proposed based on experiments (Tsagareli 1965; Fang and Ishibashi 1986) and theoretical methods (Wang 2000), differing from the traditional Coulomb and Rankine theory.

Fig. 2

Laterally loaded pile-soil interaction in the mountainside

This paper is committed to proposing a theoretical method of the safety factor of the slope encapsulating a laterally loaded pile. The safety factor is derived by the object function concerning the external work rate and internal energy dissipation based on kinematic limit analysis, with a log-spiral failure mechanism pre-assumed. The action of the laterally loaded pile on the slope is converted into equivalent resultant lateral force on the potential sliding block. To address the assessment of the critical point depth and lateral force provided by the pile, the modified strain wedge technique and the soil wedge assumption are adopted to evaluate the soil resistance and extra earth pressure around the pile, respectively. The proposed method is first substantiated by the cases of the slopes reinforced with anti-slide piles rather than laterally loaded piles (Poulos 1995; Cao and Zaman 1999; Cai and Ugai 2000; Wei and Cheng 2009); it is then further validated by comparing with the results of the case with a laterally loaded pile (Ng et al. 2001) by finite element limit analysis and finite element method. In addition to verification, the effects of the lateral load atop the pile, pile location, and soil shear strength on slope stability are further investigated by authors. On this basis, an alternative approach for the safety factor of the slope encapsulating a laterally loaded pile can be presented by scaling the safety factor of the slope without the lateral load with the corresponding normalized safety factor.

Kinematic limit analysis

In any kinematically admissible velocity field, the load determined by the object function consisting of the rate of external work and internal energy dissipation is no less than the actual load at failure (Chen 1975), as described in Eq. (1).

$${\int }_{\Omega }{\sigma }_{ij}{\dot{\varepsilon }}_{ij}\mathrm{d\Omega }\ge {\int }_{S}{T}_{i}{v}_{i}\mathrm{d}S+{\int }_{\Omega }{X}_{i}{v}_{i}\mathrm{d\Omega }$$

(1)

where σ_ij and ${\dot{\varepsilon }}_{ij}$ denote the stress tensor and strain rate in the potential sliding block Ω, respectively; T_i corresponds to the surcharge on boundary S; v_i refers to the velocity along the velocity discontinuous surface; and X_i represents the body force.

Failure mechanism

In the analysis of the pile-slope system, a core step is to find a reasonable failure mechanism (kinematically admissible velocity field). For simplicity, the plane stability of the pile-slope system is evaluated without considering the pile geometry and soil arching effect in this study, although the pile-slope interaction is three-dimensional. As illustrated in Fig. 3, the log-spiral failure mechanism is frequently used by published studies (Ausilio et al. 2001; Yang et al. 2004; Nian et al. 2008). The failure curve is rotating about the point O with varied radius r (clockwise is denoted as positive), described by Eq. (2), and intersects the pile at point P (critical point). Point A and point B are the starting point and ending point of the curve, respectively; point C and point D are the slope toe and crest respectively. Besides, θ is the slope angle; θ_A is the rotating angle from the horizontal to OA; θ_B is the rotating angle from the horizontal to point OB; θ′ is the angle between DB and BC; θ₁ (θ₂) is the rotating angle from the horizontal to the vertical projection pint of point D (point C) on the curve; θ_P is the rotating angle from the horizontal to the critical point; r_A (r_B and r_P) symbolizes the corresponding radius at point A (B and P); x_P refers to the horizontal distance between the pile and slope toe; H_p is the horizontal project of the slope; H denotes the slope height; h characterizes the total height of the pile above the potential sliding surface.

Fig. 3

Pre-assumed log-spiral failure mechanism

$$r={r}_{\mathrm{A}}\ \mathrm{exp}\left[\left(\theta -{\theta }_{\mathrm{A}}\right)\frac{\mathrm{tan}\ \varphi }{FoS}\right]$$

(2)

The factor of safety (FoS) is generally defined concerning the shear strength of soil (internal friction angle φ and cohesion c), as shown in Eq. (3).

$$FoS=\frac{c}{{c}^{\prime}}=\frac{\mathrm{tan}\ \varphi}{\mathrm{tan}\ {\varphi}^{\prime}}$$

(3)

where φ′ and c′ are the mobilized friction angle and cohesion at failure.

Objective function

The objective function of the rate of external work and internal energy dissipation is constructed by kinematic limit analysis. The specific derivations of components of the objective function are expressed below.

External work rate

The external work rate produced by the soil self-weight consists of four components, as given in Eq. (4).

$${\dot{W}}_{\gamma }={\gamma wr}_{\mathrm{A}}^{3}\left({f}_{1}-{f}_{2}-{f}_{3}-{f}_{4}\right)$$

(4)

where γ denotes the unit weight of soil; w symbolizes the angular velocity of the potential sliding block; and f₁, f₂, f₃, and f₄ are geometry-dependent non-dimensional functions of the block concerning sections OAB, OAD, OBD, and BCD, respectively. The specific expressions of the four components could be given below (Qin et al. 2017).

$$\begin{aligned}{f}_{1}\ =\ & \frac{\mathrm{tan}\ {\varphi}^{\prime}}{1+9\ {\mathrm{tan}}^{2}\ {\varphi}^{^{\prime}}}\left\{\left(\mathrm{cos}\ {\theta}_{\mathrm{B}}+\frac{\mathrm{sin}\ {\theta}_{\mathrm{B}}}{3\ \mathrm{tan}\ {\varphi}^{\prime}}\right)\ \mathrm{exp}\ \left[3\left({\theta }_{\mathrm{B}}-{\theta }_{\mathrm{A}}\right) \right. \right. \\ & \left. \left. \mathrm{tan}\ {\varphi}^{\prime}\right]-\left(\mathrm{cos}\ {\theta}_{\mathrm{A}}+\frac{\mathrm{sin}\ {\theta}_{\mathrm{A}}}{3\ \mathrm{tan}\ {\varphi}^{\prime}}\right)\right\}\end{aligned}$$

(5)

$${f}_{2}=\frac{1}{6}\frac{L\ \mathrm{sin}\ {\theta}_{\mathrm{A}}}{{r}_{\mathrm{A}}}\left(2\ \mathrm{cos}\ {\theta}_{\mathrm{A}}-\frac{L}{{r}_{\mathrm{A}}}\right)$$

(6)

$$\begin{array}{c}{f}_{3}=\frac{\mathrm{exp}\ \left[\left({\theta}_{\mathrm{B}}-{\theta}_{\mathrm{A}}\right)\ \mathrm{tan}\ {\varphi}^{\prime}\right]}{6}\left[\mathrm{sin}\ \left({\theta}_{\mathrm{B}}-{\theta}_{\mathrm{A}}\right)-\frac{L}{{r}_{\mathrm{A}}}\mathrm{sin}\ {\theta}_{\mathrm{B}}\right]\\\qquad\quad \left[\mathrm{cos}\ {\theta}_{\mathrm{A}}-\frac{L}{{r}_{\mathrm{A}}}+\mathrm{cos}\ {\theta}_{\mathrm{B}}\ \mathrm{exp}\ \left[\left({\theta}_{\mathrm{B}}-{\theta}_{\mathrm{A}}\right)\mathrm{tan}\ {\varphi}^{\prime}\right]\right]\end{array}$$

(7)

$$\begin{array}{l}{f}_{4}={\left(\frac{H}{{r}_{\mathrm{A}}}\right)}^{2}\frac{\mathrm{sin}\ \left(\theta -{\theta }^{\prime}\right)}{2\ \mathrm{sin}\ \theta\ \mathrm{sin}\ {\theta }^{\prime}}\\\qquad \left[\mathrm{cos}\ {\theta }_{\mathrm{A}}-\frac{L}{{r}_{\mathrm{A}}}-\frac{1}{3}\frac{H}{{r}_{\mathrm{A}}}\left(\mathrm{cot}\ \theta +\mathrm{cot}\ {\theta }^{\prime}\right)\right]\end{array}$$

(8)

where L refers to the distance between point A and point D.

Internal energy dissipation rate

The internal energy dissipation rate is derived as follows.

$${\dot{W}}_{D1}={\int }_{{\theta }_{\mathrm{A}}}^{{\theta }_{\mathrm{B}}}c\left(V\ \mathrm{cos}\ \varphi \right)\frac{r\mathrm{d}\theta}{\mathrm{cos}\ \varphi}={cwr}_{\mathrm{A}}^{2}{f}_{5}$$

(9)

$${f}_{5}=\frac{\mathrm{exp}\ \left[2\left({\theta }_{\mathrm{B}}-{\theta }_{\mathrm{A}}\right)\ \mathrm{tan}\ {\varphi }^{\prime}\right]-1}{2\ \mathrm{tan}\ {\varphi }^{^{\prime}}}$$

(10)

Moreover, the slope safety factor would be affected by the laterally loaded pile (Ng et al. 2001), and the pile action should be incorporated as a resultant lateral force F and moment exerted on a possible sliding block at the depth of the critical point. The dissipation rate of the resultant lateral force and moment can be then given as:

$${\dot{W}}_{D2}={Fr}_{\mathrm{A}}\ \mathrm{sin}\ {\theta}_{\mathrm{P}}\ w\ \mathrm{exp}\ \left[\left({\theta}_{\mathrm{P}}-{\theta }_{\mathrm{A}}\right)\mathrm{tan}\ {\varphi }^{\prime}\right]-F\chi hw$$

(11)

where χ is a ratio of the distance between the critical point and action point of resultant force to the overall h.

Some geometric parameters in the formulas mentioned above could be obtained from the failure mechanism and the relative position of the pile and slope.

$$h={r}_{\mathrm{P}}\ \mathrm{sin}\ {\theta}_{\mathrm{P}}-{r}_{\mathrm{B}}\ \mathrm{sin}\ {\theta}_{\mathrm{B}}+{x}_{\mathrm{P}}\ \mathrm{tan}\ \theta$$

(12)

$${x}_{\mathrm{P}}={r}_{\mathrm{P}}\ \mathrm{cos}\ {\theta}_{\mathrm{P}}-{r}_{\mathrm{B}}\ \mathrm{cos}\ {\theta }_{\mathrm{B}}-d$$

(13)

$$d=\frac{\mathrm{sin}\ \left(\theta-{\theta }^{\prime}\right)}{\mathrm{sin}\ \theta\ \mathrm{sin}\ {\theta}^{\prime}}H$$

(14)

where d is the length of line BC.

As a consequence, the total energy dissipation rate is given as:

$${\dot{W}}_{D}={\dot{W}}_{D1}+{\dot{W}}_{D2}$$

(15)

Based on the kinematic limit analysis, the total external work rate equals the overall energy dissipation rate.

$${\dot{W}}_{\gamma }={\dot{W}}_{D}$$

(16)

Above all, the safety factor of the slope encapsulating a laterally loaded pile could be evaluated by Eq. (3), and the significative parameters (φ′ and c′) in the equation would be determined by substituting Eqs. (4–11) and Eq. (15) into Eq. (16).

Solutions for critical point depth and resultant force

The core issue in the stability analysis of the slope encapsulating a laterally loaded pile is the assessment of the critical point depth and resultant lateral force provided by the pile. In this study, the critical point is assumed as the point where the lateral deflection of piles is zero. The detailed derivation is elaborated below by employing the modified strain wedge technique and the soil wedge assumption (Fig. 4).

Fig. 4

Strain wedge in front of the pile and soil wedge behind the pile

Governing equation

The governing equation for the laterally loaded pile in the mountainside is given as:

$$EI\left(\frac{{\mathrm{d}}^{4}y}{\mathrm{d}{z}^{4}}\right)+p\left(z\right)-q\left(z\right)=0$$

(17)

where EI symbolizes the flexural rigidity of the pile; y is the pile deflection; p(z) is the soil resistance below the critical point (evaluated by the beam on elastic foundation method) or the degraded soil resistance above the critical point (quantified by the modified strain wedge technique); and q(z) is the extra earth pressure (estimated by the soil wedge assumption).

Modified strain wedge technique

The original strain wedge technique (Norris 1986; Ashour et al. 1998, 2004) was presented to evaluate the soil resistance in front of the laterally loaded pile in the level ground (Fig. 5a). In the technique, the strain wedge was characterized as three main parameters (base angle β_m, fan angle φ_m, and strain wedge depth h). Thereinto, the base angle and fan angle satisfy the assumption, β_m = π/4 + φ_m/2; the fan angle depends on the mobilization of soil strength within the strain wedge, and the strain wedge depth is equal to the critical point depth. All of them are variable with the lateral load at the pile head and estimated by iterative procedures. Whereafter, the technique has been modified to estimate the degraded soil resistance in front of the laterally loaded pile in the mountainside (Peng et al. 2019, 2020b), as illustrated in Fig. 5b where D denotes the width (diameter) of a square (circular) pile; Z₀ represents the intersection depth of the far surface (plane B₀B₁C₁C₀) and slope surface (plane B₀B₂C₂C₀); and the depth of the intersection of the (j-1)th and jth sublayer strain wedge is marked as Z_j, j = 1, 2, …, n.

Fig. 5

Three-dimensional strain wedge: a in the level ground; b in the mountainside

Besides, the linearized deflection assumption (Ashour et al. 1998) was employed in the analysis of the performance of the long flexible pile as well as that of the short rigid pile. The pile deflection was considered linear above the critical point (Fig. 6), and other details about the strain wedge technique were detailed in Ref. (Ashour et al. 1998, 2004) where δ denotes the linearized deflection angle and y₀ is the deflection at the pile head.

Fig. 6

Linearized deflection assumption and correlative strain wedge

Furthermore, the soil above each sublayer strain wedge is abstracted as the uniformly distributed load q, and the stress status within the strain wedge satisfies the static equilibrium equation in the lateral direction, Eq. (18), as depicted in the elevation view and plan view (Fig. 7).

$$p\left(z\right)={\Delta \sigma }_{i}L\left(z\right){S}_{1}+2\tau D{S}_{2}$$

(18)

where Y₀ denotes the horizontal distance from the intersection of the slope surface and far surface to the pile; σ_vi(z) and Δσ_i symbolize the effective vertical stress and lateral stress increment, respectively; τ symbolizes the side friction (Ashour et al. 1998); L(z) denotes the width of far surface; and S₁ and S₂ are pile shape coefficients (Briaud et al. 1984).

Fig. 7

Projection of modified strain wedge: a elevation view; b plan view

Geometry parameters

The base angles β_m,j and fan angle φ_m,j of different sublayer strain wedges satisfy the assumption, β_m = π/4 + φ_m/2.

$${\beta }_{\mathrm{m},j}=\frac{\pi }{4}+\frac{{\varphi }_{\mathrm{m},j}}{2}$$

(19)

The depth Z₀ and Z_j could then be defined by the wedge geometry.

$${Z}_{0}+\frac{{Z}_{0}}{\mathrm{tan}\ \theta}=h$$

(20)

$${Z}_{j}+\frac{{Z}_{j}}{\mathrm{tan}\ \theta}={Z}_{j-1}$$

(21)

Finally, the far surface width L(z) is given as:

$$\begin{array}{cc}L\left(z\right)=D+2\left(h-z\right)\ \mathrm{tan}\ {\beta}_{\mathrm{m}}\ \mathrm{tan}\ {\varphi }_{\mathrm{m}}& \left(z<{Z}_{0}\right)\end{array}$$

(22)

$$\begin{array}{cc}L\left(z\right)=D+\frac{2z\ \mathrm{tan}\ {\varphi}_{\mathrm{m}}}{\mathrm{tan}\ \theta }& \left(z<{Z}_{0}\right)\end{array}$$

(23)

Stress state

The effective vertical stress σ_vi(z) above different sublayer strain wedges is derived by Eqs. (24) and (25).

$$\begin{array}{cc}{\sigma }_{\mathrm{v}i}\left(z\right)=\gamma \left(z-\frac{{Z}_{0}}{2}\right)& \left(z\ge {Z}_{0}\right)\end{array}$$

(24)

$$\begin{array}{cc}{\sigma }_{\mathrm{v}i}\left(z\right)=\gamma \left(z-\frac{{Z}_{j}}{2}\right)& \left({Z}_{j-1}\ge z\ge {Z}_{j},j\ge 1\right)\end{array}$$

(25)

The lateral stress increment and side friction are written as Eqs. (26) and (27).

$${\Delta \sigma }_{i}={\sigma }_{\mathrm{v}i}\left[{\mathrm{tan}}^{2}\ \left(\frac{\pi }{4}+\frac{{\varphi }_{\mathrm{m}}}{2}\right)-1\right]$$

(26)

$$\tau ={\sigma }_{\mathrm{v}i}\ \mathrm{tan}\ {\varphi}_{\mathrm{m}}$$

(27)

In the strain wedge technique, the stress level (SL), expressed as Eq. (28), had been employed to characterize the relationship between the stress state of soil before yielding and the yield state. It can also define the fan angle characterizing the geometry of strain wedge, and the fan angle equals the mobilized effective friction angle of soil (Fig. 8), varied with the lateral stress. The other details of SL were sketched in Appendix 1.

$$SL=\frac{{\Delta \sigma }_{i}}{{\Delta \sigma }_{\mathrm{hf}}}=\frac{{\mathrm{tan}}^{2}\ \left(\pi /4+{\varphi }_{\mathrm{m}}/2\right)-1}{{\mathrm{tan}}^{2}\ \left(\pi /4+\varphi /2\right)-1}$$

(28)

$${\Delta \sigma }_{\mathrm{hf}}={\sigma }_{\mathrm{v}0}\left[{\mathrm{tan}}^{2}\ \left(\frac{\pi }{4}+\frac{\varphi }{2}\right)-1\right]$$

(29)

where Δσ_hf and σ_v0 represent the lateral stress increment and vertical stress in the yield status.

Fig. 8

Mobilized effective friction angle varied with lateral stress: a sand; b c-φ soil

Soil wedge assumption

To estimate the extra earth pressure, the soil wedge assumption (Peng et al. 2020b; Paik and Salgado 2003; He et al. 2015) is utilized in this study. In the assumption, two points should be noted: (i) the soil wedge depth is regarded as the critical point depth; (ii) and the soil wedge width can be considered equal to the width of the laterally loaded pile.

Soil wedge concept

The slip plane of the soil wedge behind the pile is of an angle θ₀ to the horizontal (Fig. 9). The expressions of the angle θ₀ and β₀ (the angle between the slip plane and slope surface equals to θ₀-θ) could be estimated by the stress state of the differential element of the pile and corresponding Mohr’s circle, detailed in Ref. (He et al. 2015).

Fig. 9

Elevation view of the soil wedge

$${\beta }_{0}=\frac{1}{2}\left(\varphi -\theta+\mathrm{arccos}\ \frac{\mathrm{sin}\ \theta}{\mathrm{sin}\ \varphi}\right)$$

(30)

$${\theta }_{0}=\frac{1}{2}\left(\varphi +\theta+\mathrm{arccos}\ \frac{\mathrm{sin}\ \theta}{\mathrm{sin}\ \varphi}\right)$$

(31)

Lateral earth pressure

To investigate the lateral earth pressure within the soil wedge, it is sliced into many differential elements (Fig. 10). The path line (dotted line) of minor principal stress σ₃ is assumed as an arc with radius R. As to the major principal stress σ₁, it is perpendicular to the arc (Fig. 10a) where S symbolizes the differential element length, S = (H-z)cosθ₀/sinβ; dV′ represents a component of the differential stress dV, and V′ symbolizes the resultant of dV′, perpendicular to line E₀P; ψ represents the angle between the normal line OD and the horizontal; ω is the angle between the normal line OP and the vertical, ω = 0; θ_w is the angle between the normal line OJ and the horizontal, θ_w = π/4 + φ/2; and ξ refers to the angle between the normal line OQ and the vertical, derived as Eq. (32).

Fig. 10

Principal stress on a differential element: a minor and major principal stresses; b vertical force

$$\xi =\frac{\pi }{4}+\frac{\varphi }{2}-{\theta }_{0}=\frac{1}{2}\left(\frac{\pi }{2}-\theta -{\mathrm{cos}}^{-1}\ \frac{\mathrm{sin}\ \theta}{\mathrm{sin}\ \varphi}\right)$$

(32)

The lateral earth pressure coefficient K_an and mean vertical stress ${\overline{\sigma }}_{\mathrm{v}}$ are given by Eqs. (33) and (34), respectively, the derivations of which are written in Appendices 2 and 3.

$${K}_{\mathrm{an}}=\frac{{\sigma}_{\mathrm{h}}}{{\tilde{\sigma}}_{\mathrm{v}}}=\frac{\mathrm{cos}\ \left({\theta}_{w}+\xi \right)\ \mathrm{cos}\ \theta}{\mathrm{cos}\ \left(\theta +\xi \right)\ \mathrm{cos}\ {\theta }_{\omega}}\cdot \frac{3\left(N\ {\mathrm{cos}}^{2}\ {\theta}_{w}+{\mathrm{sin}}^{2}\ {\theta }_{w}\right)}{3N-\left(N-1\right){\mathrm{cos}}^{2}\ {\theta}_{w}}$$

(33)

$$\begin{array}{l}{\overline{\sigma }}_{\mathrm{v}}=\frac{\gamma h\ \mathrm{cos}\ \theta }{1-\left({K}_{\mathrm{an}}\ \mathrm{tan}\ \varphi -{K}_{\mathrm{an}}\mathrm{tan}\ \theta +{m}_{0}\right)\frac{\mathrm{sin}\ {\beta}_{0}}{\mathrm{cos}\ {\theta }_{0}}}\\\qquad\ \times \left[{\left(1-\frac{z}{h}\right)}^{\left({K}_{\mathrm{an}}\ \mathrm{tan}\ \varphi -{K}_{\mathrm{an}}\ \mathrm{tan}\ \theta +{m}_{0}\right)\frac{\mathrm{sin}\ {\beta }_{0}}{\mathrm{cos}\ {\theta }_{0}}}-\left(1-\frac{z}{h}\right)\right]\end{array}$$

(34)

$${m}_{0}=\frac{{K}_{\mathrm{an}}\ \mathrm{sin}\ \xi\ \mathrm{cos}\ \theta}{\left(N\ {\mathrm{cos}}^{2}\ {\theta }_{w}+{\mathrm{sin}}^{2}\ {\theta}_{w}\right)\mathrm{cos}\ \left(\xi +\theta \right)}$$

(35)

The lateral earth pressure σ_h is derived by multiplying ${\overline{\sigma }}_{\mathrm{v}}$ by K_an.

$$\begin{array}{l}{\sigma}_{\mathrm{h}}=\frac{{K}_{\mathrm{an}}\gamma h\ \mathrm{cos}\ \theta }{1-\left({K}_{\mathrm{an}}\ \mathrm{tan}\ \varphi-{K}_{\mathrm{an}}\ \mathrm{tan}\ \theta+{m}_{0}\right)\frac{\mathrm{sin}\ {\beta}_{0}}{\mathrm{cos}\ {\theta}_{0}}}\\\qquad\ \times \left[{\left(1-\frac{z}{h}\right)}^{\left({K}_{\mathrm{an}}\ \mathrm{tan}\ \varphi -{K}_{\mathrm{an}}\ \mathrm{tan}\ \theta +{m}_{0}\right)\frac{\mathrm{sin}\ {\beta}_{0}}{\mathrm{cos}\ {\theta}_{0}}}-\left(1-\frac{z}{h}\right)\right]\end{array}$$

(36)

Iterative solution

The critical point depth and resultant lateral force provided by the laterally loaded pile could be derived by the governing equation, Eq. (17), adopting the modified strain wedge technique (Peng et al. 2019, 2020b) and soil wedge assumption (Ashour et al. 1998). The iterative procedures are illustrated in Fig. 11. Thereinto, the governing equation, Eq. (17), would be handled by substituting Eqs. (18) and (36). The deflection at the pile top obtained from Eq. (17) is labeled as y₀, whereas an alternative pile head deflection, evaluated by the deflection pattern δ and soil strain ε, is labeled as (y₀)_SW. Likewise, y_j refers to the lateral displacement of piles at depth Z_j obtained from by Eq. (17), whereas (y_j)_SW is estimated by the strain wedge length Y_j and soil strain ε. The nonlinear deflection pattern of the laterally loaded pile in the mountainside is depicted in Figs. 12 and 13.

Fig. 11

Iterative procedure

Fig. 12

Nonlinearized deflection pattern of the pile

Fig. 13

Comparisons between predicted deflections: a (y_j)_SW > y_j; b (y_j)_SW < y_j

Case studies

To verify the proposed method, some cases of slopes without a laterally loaded pile (Poulos 1995; Cao and Zaman 1999; Cai and Ugai 2000; Wei and Cheng 2009) and the case of the slope encapsulating a laterally loaded pile (Ng et al. 2001) have been quoted.

Slopes without a laterally loaded pile

The example slopes are composed of homogeneous materials, and the slope height, slope angle, and material parameters are listed in Table 1. A row of stabilizing piles would be required in the slopes (the pile location, x_p, is detailed in the references) since the initial safety factors of the slope are inadequate. Employing the proposed method, the safety factors of these slopes are evaluated and listed in Table 2. It indicates that the proposed method is capable of predicting the safety factor of the slope considering the pile effect.

Table 1 Parameters of these example slopes

Table 2 Comparisons between results evaluated by the proposed approach and references

Slope encapsulating a laterally loaded pile

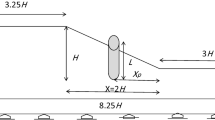
The slope is 15 m high with a slope angle of 32°, and the mechanical properties of the pile-soil system are illustrated in Fig. 14. The diameter and length of the laterally loaded pile are 2 m and 30 m, respectively, ignoring the effect of groundwater. The ultimate shear capacity of the pile is specified as V_u = 0.8f_c^0.5A (f_c denotes the concrete compressive strength, f_c = 45 MPa; A refers to the pile cross-section area) (British Standards Institution 1985). To investigate the slope stability and failure mechanism, the lateral loads V = 0.03, 0.06, 0.12, and 0.36V_u are applied to the pile head in the analysis (the design load is 0.12V_u). The predicted safety factors are compared with those from published literature, shown in Table 3.

Fig. 14

Slope encapsulating a laterally loaded pile

Table 3 Comparisons of safety factors

Table 3 indicates that the safety factors of the slope under different lateral loads evaluated by the proposed method are reasonably consistent with those obtained from the published study (Ng et al. 2001) and the finite element limit analysis program, OptumG2 (Optum Computational Engineering 2017) whose procedure is detailed in Appendix 4. It proves that the proposed method can well predict the stability of the slope encapsulating a laterally loaded pile as well as the finite element limit analysis. As expected, the safety factor of the slope reinforced with anti-slide piles (lateral load is zero) is greater than that of the unreinforced condition (the factor of safety increases from 1.90 to 2.0). It can be ascribed to an extra resisting moment provided by the pile when the lateral load equals zero, and the slope stability would be improved by the pile. It should be noted that the slope is unsafe when the lateral load reaches 0.36V_u, and the exact safety factor of the slope had not been evaluated, but simply considered a value less than 1.0 (Ng et al. 2001). Furthermore, the evolution of the safety factor of the slope encapsulating a laterally loaded pile revealed in Table 3 indicates that the slope would develop into instability with lateral loads atop the pile; the safety factor of the slope encapsulating the pile would significantly decrease with lateral loads, and it is approximately reduced by 40%, while the lateral load at the pile head increases from 0 to 0.12V_u.

Discussion

The effect of the lateral load at the pile head on the slope failure mechanism and safety factor is investigated below. The classical failure mechanism of the slope encapsulating a laterally loaded pile is visualized by finite element limit analysis (Figs. 15 and 16). The different magnitudes of the plastic multiplier are characterized by different colors, and the variation of the color from blue to red indicates the increase of the plastic multiplier. The global potential sliding surface starts from the slope toe and extends to the slope crest, and two local failures of wedge-shaped regions occur around the laterally loaded pile; thereinto, the wedge-shaped region in front of the pile would increase with lateral loads and the distance from the slope toe, and the failure mechanism under small lateral load conditions is similar to that of the slope reinforced with anti-slide piles. These observations prove the rationality of the log-spiral failure mechanism (Fig. 3), the strain wedge technique, and soil wedge assumption (Fig. 4).

Fig. 15

Slope failure mechanism under different lateral loads: a V/V_u = 0.015V_u; and b V/V_u = 0.03

Fig. 16

Slope failure mechanism for different pile locations: a x_p/H_p = 1/4; b x_p/H_p = 3/4

To better interpret the effect of the lateral load atop the pile and the pile location on the factor of safety, the normalized safety factor η and normalized lateral load α have been proposed. The former represents the ratio of the safety factor with the lateral load (FoS₁) to the one without the lateral load (FoS₀), η = FoS₁/FoS₀; the latter denotes the ratio of the lateral load (V) applied on the pile head to the ultimate shear capacity (V_u), α = V/V_u. Then, the normalized safety factor η decreases from 0.59 to 0.37 while the normalized lateral load α increases from 0.12 to 0.36 in the case (Ng et al. 2001). Furthermore, plenty of cases (α = 0, 0.03, 0.06, 0.09, and 0.12; x_p/H_p = 1/6, 1/4, 1/3, 1/2, ¾, and 1; φ = 15°, 20°, 25°, 30°, and 35°; c/γD = 0.25, 0.5, 0.75, and 1) are supplemented for a parametric study based on the original case (Ng et al. 2001), and the predictions of normalized safety factors η are illustrated in Fig. 17. The normalized safety factor, together with the safety factor of the slope, is observed to nonlinearly decrease with normalized lateral loads. It is therefore necessary to consider the effect of lateral loads on slope stability in the design of engineering practice. Furthermore, the variations of normalized safety factors with normalized lateral loads can be fitted by cubic functions (Fig. 17). The differences between the predictions of normalized safety factors and those on fitting curves are mostly less than 0.1, except for the cases of extremely small shear strength (c/γD = 0.25), and the reason for the exceptions is that the slope is already unstable even without the lateral load. In addition, the normalized safety factor is positively correlated with x_p/H_p, revealing that the effect of lateral loads on the slope stability would be weakened while the pile location moves from the slope toe to the slope crest. It can be also observed that the normalized safety factor mainly depends on the lateral load and pile location but is not sensitive to the shear strength; hence, the results and corresponding fitting curves can be generalized to cases of other shear strengths.

Fig. 17

Relationship between the normalized safety factor and normalized lateral load under different shear strengths: a x_p/H_p = 1/6; b x_p/H_p = 1/4; c x_p/H_p = 1/3; d x_p/H_p = 1/2; e x_p/H_p = 3/4; and f x_p/H_p = 1

Based on these aforementioned analyses, an alternative approach to assess the safety factor of the slope encapsulating a laterally loaded pile has been provided. It can be predicted by scaling the relatively easily obtained safety factor of the slope without the lateral load (i.e., the slope reinforced with anti-slide piles) with the corresponding normalized safety factor. By this means, the evaluation of the safety factor of the slope encapsulating a laterally loaded pile can be simplified by avoiding the derivation of the critical point depth and the resultant force provided by the pile. It is noteworthy that the prediction method of normalized safety factor has been not reported yet and could be estimated by the proposed method in this work. Cases of normalized safety factors under different conditions (e.g., pile diameter, pile location, and slope inclination) providing more useful information for the preliminary engineering design would be further investigated in subsequent research.

Conclusions

A theoretical method of the safety factor of the slope encapsulating a laterally loaded pile has been proposed by introducing the modified strain wedge technique and soil wedge assumptions to evaluate the soil resistance and extra earth pressure around the pile, respectively. After verifying the proposed method, the effect of the lateral load atop the pile, pile location, and soil shear strength on the safety factor of the slope encapsulating a laterally loaded pile is extensively investigated under different conditions. Several conclusions are listed as follows:

• (i) The safety factors of some cases evaluated by the proposed theoretical method are in good agreement with those obtained from published studies and numerical simulations. It proves that the proposed method can well evaluate the safety factor of the slope encapsulating a laterally loaded pile.

• (ii) The failure mechanism under the minute lateral load is similar to that of the slope reinforced with anti-slide piles, but for cases of greater lateral load, the lateral load transferred from the pile to the slope would further result in the local failure. Local failures of two wedge-shaped regions observed around the laterally loaded pile in the numerical simulations suggest the applicability of the strain wedge technique and soil wedge assumption; thereinto, the wedge-shaped region in front of the pile would increase with lateral loads.

• (iii) The normalized safety factor, together with the safety factor of the slope, is observed to nonlinearly decrease with normalized lateral loads; the variations of normalized safety factors with normalized lateral loads can be fitted by cubic functions. In addition, the normalized safety factor, not sensitive to the shear strength, mainly depends on the lateral load and pile location, and it is positively correlated with x_p/H_p, revealing that the effect of lateral loads on the slope stability would be weakened while the pile location moves from the slope toe to the slope crest.

• (iv) The safety factor of the slope encapsulating a laterally loaded pile can be alternatively obtained by scaling the safety factor of the slope without the lateral load with the corresponding normalized safety factor. By this means, the evaluation of the safety factor of the slope encapsulating a laterally loaded pile can be simplified by avoiding the derivation of the critical point depth and the resultant force provided by the pile, which is useful for the preliminary engineering design.

Appendices

Appendix 1 Stress level

The relationship between the stress level SL and soil strain ε was observed from isotropically consolidated drained and undrained triaxial tests (Ashour et al. 1998). It can be sketched in Fig. 18 and given as Eqs. (37) to (39).

$$\begin{array}{cc}{SL}_{i}=\frac{3.19\varepsilon }{{\left({\varepsilon }_{50}\right)}_{i}}\ \mathrm{exp}\ \left(-3.707{SL}_{i}\right)& \left(\mathrm{Stage\ I}\quad \varepsilon \le {\varepsilon }_{50}\right)\end{array}$$

(37)

$$\begin{array}{cc}{SL}_{i}=\frac{{\lambda }_{i}\varepsilon}{{\left({\varepsilon}_{50}\right)}_{i}}\ \mathrm{exp}\ \left(-3.707{SL}_{i}\right)& \left(\mathrm{Stage\ II}\quad {\varepsilon }_{50}<\varepsilon \le {\varepsilon }_{80}\right)\end{array}$$

(38)

$$\begin{array}{cc}{SL}_{i}=\mathrm{exp}\left[\mathrm{ln}\ 0.2+\frac{100\varepsilon}{m\varepsilon +{q}_{i}}\right]& \left(\mathrm{Stage\ III}\quad \varepsilon >{\varepsilon }_{80}\right)\end{array}$$

(39)

where ε₅₀ denotes the soil strain at 50% stress level; λ_i varies linearly from 3.19 (SL = 0.5) to 2.14 (SL = 0.8); and m = 59.0 and q_i = 95.4ε₅₀.

Fig. 18

Relationship between stress level and soil strain

Appendix 2 Lateral earth pressure coefficient

On the one hand, the lateral stress at point E₀ (Fig. 10), σ_h, was obtained based on the stress equilibrium equation.

$${\sigma }_{\mathrm{h}}={\sigma}_{1}\ {\mathrm{cos}}^{2}\ {\beta}_{0}+{\sigma}_{3}\ {\mathrm{sin}}^{2}\ {\beta}_{0}$$

(40)

Likewise, the lateral stress at point D (Fig. 10), σ_ah, was also obtained as follows:

$${\sigma }_{\mathrm{ah}}={\sigma}_{1}\ {\mathrm{cos}}^{2}\ \psi +{\sigma}_{3}\ {\mathrm{sin}}^{2}\ \psi$$

(41)

Substituting σ₃/σ₁ = 1/N into Eq. (41), the lateral stress σ_ah could be rearranged as:

$${\sigma }_{\mathrm{ah}}=\left({\mathrm{cos}}^{2}\ \psi +\frac{1}{N}\ {\mathrm{sin}}^{2}\ \psi \right){\sigma }_{1}$$

(42)

where N = tan²(π/4 + φ/2).

On the other hand, the vertical stress applied to the differential element E₀JPQ was evaluated, including two components (Fig. 19): (i) vertical stress applied to the quadrangle differential element E₀JG₀Q; (ii) the minor and major principal stresses on the triangular differential element G₀PQ where σ_v is the vertical stress applied on the differential element, consisting of σ_f and σ′_v; the former is parallel to line E₀G₀, and the latter is perpendicular to line E₀G₀, derived as:

$$\frac{{{\sigma }^{\prime}}_{\mathrm{v}}}{{\sigma }_{\mathrm{v}}}=\mathrm{cos}\ \theta$$

(43)

Fig. 19

Stress status on the quadrangle differential element E₀JG₀Q

Substituting that σ_v + σ_ah = σ₁ + σ₃, Eq. (43) could be given as Eq. (44):

$$\frac{{{\sigma }^{\prime}}_{\mathrm{v}}}{{\sigma}_{1}}=\mathrm{cos}\ \theta \left({\mathrm{sin}}^{2}\ \psi +\frac{1}{N}\ {\mathrm{cos}}^{2}\ \psi \right)$$

(44)

For simplification, σ′_v can be replaced by mean stress $\overline{{\sigma }^{^{\prime}}}$ (Fig. 20) where h₀ = cosθ·dz; σ₃ and σ_3v are the minor principal stress on the line G₀Q and its vertical component.

$${\overline{{\sigma }^{\prime}}}_{\mathrm{v}}=\frac{{V}^{\prime}}{S}$$

(45)

where

$${V}^{^{\prime}}={\int }_{{\theta }_{\omega }}^{\pi /2-\omega }\mathrm{d}{V}^{\prime}={\int }_{{\theta }_{\omega }}^{\pi /2-\omega }{\sigma }_{1}R\ \mathrm{sin}\ \psi \left({\mathrm{sin}}^{2}\psi +\frac{1}{N}\ {\mathrm{cos}}^{2}\ \psi \right)\mathrm{d}\psi$$

(46)

$$S=\frac{\mathrm{cos}\ \left({\theta }_{w}+\xi \right)}{\mathrm{cos}\ \left(\theta +\xi \right)}R$$

(47)

Fig. 20

Stress status on the main part of the differential element

Then, Eq. (45) could be rewritten as follows:

$${\overline{{\sigma }^{\prime}}}_{\mathrm{v}}=\frac{\mathrm{cos}\ \left(\theta +\xi \right)}{\mathrm{cos}\ \left({\theta }_{w}+\xi \right)}\ \mathrm{cos}\ {\theta }_{\omega }\left(1-\frac{N-1}{3N}\ {\mathrm{cos}}^{2}\ {\theta }_{\omega }\right){\sigma }_{1}$$

(48)

The average vertical stress ${\overline{\sigma }}_{\mathrm{v}}$ on the differential element could be given as Eq. (49).

$${\tilde{\sigma}}_{\mathrm{v}}=\frac{{\overline{{\sigma}^{\prime}}}_{\mathrm{v}}}{\mathrm{cos}\ \theta }$$

(49)

Substituting Eq. (48) into Eq. (49), it could be finally obtained as:

$${\overline{\sigma }}_{\mathrm{v}}=\frac{\mathrm{cos}\ \left(\theta +\xi \right)}{\mathrm{cos}\ \left({\theta }_{w}+\xi \right)\ \mathrm{cos}\ \theta}\ \mathrm{cos}\ {\theta }_{\omega }\left(1-\frac{N-1}{3N}\ {\mathrm{cos}}^{2}\ {\theta }_{\omega }\right){\sigma }_{1}$$

(50)

Above all, the lateral earth pressure coefficient K_an is given by Eqs. (42) and (50).

$${K}_{\mathrm{an}}=\frac{{\sigma }_{\mathrm{h}}}{{\tilde{\sigma}}_{\mathrm{v}}}=\frac{\mathrm{cos}\ \left({\theta }_{w}+\xi \right)\mathrm{cos}\ \theta }{\mathrm{cos}\ \left(\theta +\xi \right)\ \mathrm{cos}\ {\theta }_{w}}\cdot \frac{3\left(N\ {\mathrm{cos}}^{2}\ {\theta}_{w}+{\mathrm{sin}}^{2}\ {\theta}_{w}\right)}{3N-\left(N-1\right)\ {\mathrm{cos}}^{2}\ {\theta }_{w}}$$

(51)

Appendix 3 Vertical stress

To further investigate the vertical stress within the soil wedge, the triangular element G₀PQ assumed to be in the equilibrium status can be neglected in the analysis of the differential element E₀JPQ. The minor principal stress on the line G₀Q σ₃ and its vertical component σ_3v are derived as:

$${\sigma }_{3}=\frac{{K}_{\mathrm{an}}}{N\ {\mathrm{cos}}^{2}\ {\theta}_{w}+{\mathrm{sin}}^{2}\ {\theta}_{w}}{\overline{\sigma }}_{\mathrm{v}}$$

(52)

$${\sigma }_{3\mathrm{v}}={\sigma}_{3}\ \mathrm{sin}\ \xi \frac{\mathrm{cos}\ \theta }{\mathrm{cos}\ \left(\xi +\theta \right)}$$

(53)

The shear stress on the differential element E₀JG₀Q (Fig. 10) can be regarded as:

$$\tau ={\sigma }_{\mathrm{h}}\ \mathrm{tan}\ \varphi={\overline{\sigma}}_{\mathrm{v}}\ {K}_{\mathrm{an}}\ \mathrm{tan}\ \varphi$$

(54)

The equilibrium equation of the differential element E₀JMQ in the vertical can be derived as Eq. (55), ignoring the vertical stress on the line MG₀.

$$\begin{aligned}DS\mathrm{d}{\overline{\sigma }}_{\mathrm{v}} & +D{K}_{\mathrm{an}}{\overline{\sigma }}_{\mathrm{v}}\ \mathrm{tan}\ \varphi \mathrm{d}z-D{K}_{\mathrm{an}}{\overline{\sigma}}_{\mathrm{v}}\ \mathrm{tan}\ \theta \mathrm{d}z \\ & +D{\sigma}_{3}\frac{\mathrm{sin}\ \xi\ \mathrm{cos}\ \theta}{\mathrm{cos}\ \left(\xi +\theta \right)}\mathrm{d}z=DS{h}_{0}\gamma\end{aligned}$$

(55)

Substituting Eq. (52) into Eq. (55), ${\overline{\sigma }}_{\mathrm{v}}$ is obtained as:

$$\begin{array}{l}{\overline{\sigma }}_{\mathrm{v}}=\frac{\gamma h\ \mathrm{cos}\ \theta }{1-\left({K}_{\mathrm{an}}\mathrm{tan}\ \varphi -{K}_{\mathrm{an}}\mathrm{tan}\ \theta +{m}_{0}\right)\frac{\mathrm{sin}\ {\beta }_{0}}{\mathrm{cos}\ {\theta }_{0}}}\\\qquad\ \times \left[{\left(1-\frac{z}{h}\right)}^{\left({K}_{\mathrm{an}}\mathrm{tan}\ \varphi -{K}_{\mathrm{an}}\mathrm{tan}\ \theta +{m}_{0}\right)\frac{\mathrm{sin}\ {\beta }_{0}}{\mathrm{cos}\ {\theta }_{0}}}-\left(1-\frac{z}{h}\right)\right]\end{array}$$

(56)

Appendix 4 Procedure of the finite element limit analysis

The common procedures of finite element limit analysis are elaborated below (Fig. 21):

• i) Establish the numerical model according to the geometric configuration of the pile-slope system, considering the boundary effect, while the slope and the pile (free-head and fixed-end) are modeled as the Mohr–Coulomb material (associated flow rule) and the linear elastic material, respectively.

• ii) The boundary condition is selected as the standard boundary condition, that is, the lateral displacement is constrained at the left and right boundaries of the model, and the bottom of the model is fixed; the lateral load atop the pile could be applied as the distributed load (Fig. 21a).

• iii) The total element number and initial element number are 10,000 and 1000, respectively; and the adaptive remeshing technique is adopted in the analysis (Fig. 21b).

Fig. 21

Finite element limit analysis: (a) boundary condition and load condition; (b) adaptive remeshing technique