An analytical solution of scattering of semi-circular hill on cylindrical SH waves

Abstract

Irregular topography can induce scattering and diffraction of incident seismic waves and cause topographic amplification effects. In this paper, a theoretical model for the scattering and diffraction of cylindrical SH waves caused by a semi-circular hill is established for the first time to reveal the influence of source characteristics on the topographic amplification effects. The analytical solution of the theoretical model is derived via the wave function expansion method and image theory, and its accuracy is verified by checking the given boundary conditions. Base on the presented solution, the influences of source location, incident wave frequency, and hill radius on amplitude amplification are systematically investigated. Comparison of amplitude amplification around the hill caused by cylindrical waves and plane waves indicates that the effect of source distance on topographic amplification effects is not negligible unless the source distance exceeds 15 times the hill radius. It suggests that much attention should be paid to the effects of source location on topographic amplification effects, especially when the source is near the topography.

Introduction

Irregular topography can induce the scattering and diffraction of incident seismic waves, which markedly alters the travel law of seismic waves. Field observations and model experiments have shown that in some cases, the vibration amplitudes of irregular topography are much greater than those of flat topography, exhibiting significant topographic amplification effects (Trifunac and Hudson 1971; Hough et al. 2010; Massa et al. 2014; Li et al. 2019b). Strong vibration can cause damage to buildings and even endanger human life, therefore studying wave scattering and diffraction induced by irregular topography has been one of the most important subjects in earthquake engineering (Geli et al. 1988; Ferraro et al. 2009).

Considering that field observations and model experiments can only give some qualitative analysis, extensive numerical and analytical methods have been employed to deepen the understanding of wave scattering induced by irregular topography. The numerical methods mainly include finite element method (Komatitsch and Vilotte 1998; Cavallaro et al. 2008; Li et al. 2019a), finite difference method (Boore 1972; Opršal and Zahradník 1999), and boundary element method (Wong and Jennings 1975; Panji et al. 2014). The numerical methods are convenient to address the wave scattering problems with complex surface geometries and geological conditions, but its accuracy depends on the quality of meshes which will inevitably introduce numerical errors. In contrast, the analytical methods are only capable of tackling a few simple wave scattering problems, while they can provide us a profound understanding of the mechanism of wave scattering and test the accuracy of numerical methods, hence obtaining an analytical solution is very encouraging. The analytical methods mainly include wave function expansion method, integral equation method, and perturbation method (Mow and Pao 1971). The wave function expansion method is the most widely employed due to its high precision and relatively simple mathematical derivation.

At present, most theoretical studies on this subject presuppose the incident seismic waves as plane waves, and there are several analytical solutions to the scattering of plane SH waves caused by various-shaped concave topographies (Trifunac 1972; Wong and Trifunac 1974; Cao and Lee 1989; Yuan and Liao 1994; Tsaur and Chang 2008, 2010; Zhang et al. 2012a, 2012b; Gao et al. 2012; Le et al. 2017) and convex topographies (Yuan and Men 1992; Yuan and Liao 1996; Lee et al. 2006; Hayir et al. 2001; Qiu and Liu 2005; Lin et al. 2010; Amornwongpaibun and Lee 2013; Lee and Amornwongpaibun 2013). Besides, a few analytical solutions to the scattering of plane P, SV and Rayleigh waves caused by irregular topography have been presented (Lee and Cao 1989; Cao and Lee 1990; Todorovska and Lee 1991; Liang et al. 2005a, 2005b, 2006).

It is acceptable to treat the incident seismic waves as plane waves when the earthquake source is far away from the irregular topography. However, when the earthquake source is located in the vicinity of irregular topography, the wavefront curvature of incident seismic waves is considerable, resulting in the propagation path of incident seismic waves and plane waves significantly different. In such case, the effects of source location on wave scattering induced by irregular topography should be taken into account. To theoretically study the effects of source location on wave scattering, the incident seismic waves can be assumed as spherical waves or cylindrical waves, and several analytical solutions have been proposed for the scattering of cylindrical SH waves caused by concave topographies (Gao and Zhang 2013; Zhang et al. 2015). However, as far as we know, analytical solutions for cylindrical SH wave scattering caused by convex topographies are rare. Herein, we present an analytical solution on the scattering of cylindrical SH waves caused by a semi-circular hill, aiming to reveal the effects of earthquake source on wave scattering by convex topographies. The specific process of this paper is given as follows. Firstly, the model of a semi-circular hill on an elastic half-space subject to a buried anti-plane line source is established, and the corresponding series solution is derived through the wave function expansion method and image theory. Secondly, the relationship between the accuracy of the series solution and its truncation orders is discussed by checking the residuals of boundary conditions. Lastly, based on the series solution, the effects of source location, incident wave frequency, and hill radius on vibration amplitudes of the surface and interior of the hill are systematically discussed.

Theoretical formula

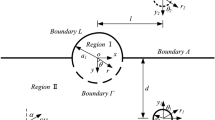
The 2D theoretical model in this study is depicted in Fig. 1. This figure illustrates a semi-circular hill with radius a sitting on an elastic, isotropic, and homogeneous half-space, with buried anti-plane line source below the hill. The material properties of the model are given by the shear modulus μ and shear wave velocity c.

Fig. 1

Schematic diagram of the theoretical model of a semi-circular hill subjected to a buried anti-plane line source

To simplify the issue, we divide the theoretical model into an exterior region S and an interior region Ω by a semi-circular auxiliary boundary as shown in Fig. 1 (Yuan and Men 1992). In these two regions, two Cartesian and two polar coordinate systems are defined. Both origins of the Cartesian coordinate system (x, y) and polar coordinate system (r, θ) are set at the center of hill bottom. The origins of the Cartesian coordinate system (x₁, y₁) and polar coordinate system (r₁, θ₁) are placed at the line source. The horizontal y-axis (or y₁-axis) is set as positive to the right direction, and the angles θ (or θ₁) are measured from the vertical direction x-axis (or x₁-axis) clockwise towards to the y-axis (or y₁-axis). The location of the line source is denoted by (r₀, θ₀) in the polar coordinate system (r, θ) and (-x₀, -y₀) in the Cartesian coordinate system (x, y). For the issue studied herein, we set a virtual line source for the reflected wave generated by the half-space. The origins of the Cartesian coordinate system (x₂, y₂) and polar coordinate system (r₂, θ₂) are placed at the virtual line source, and the angle θ₂ is measured from the vertical direction x₂-axis anticlockwise towards to the horizontal direction y₂-axis.

The displacement field W within the entire model must satisfy the elastic-wave equation:

$$ \frac{\partial^2W}{\partial {r}^2}+\frac{1}{r}\frac{\partial W}{\partial r}+\frac{1}{r^2}\frac{\partial^2W}{\partial {\theta}^2}+{k}^2W=\frac{\delta \left(r-{r}_0\right)\delta \left(\theta -{\theta}_0\right)}{r} $$

(1)

where δ(·) is the Dirac delta function, k = ω/c is the wavenumber, and ω is the circular frequency. The time factor exp(-iωt) has been omitted for the steady waves.

Besides, the displacement fields should satisfy the traction-free boundary condition on the horizontal ground surface and hill surface:

$$ {\tau}_{\theta z}=\frac{\mu \partial W}{r\partial \theta }=0,\kern2.5em \theta =\pm \pi /2,\kern4em r>a\kern1.5em $$

(2)

$$ {\tau}_{rz}=\frac{\mu \partial W}{\partial r}=0,\kern1.25em -\pi /2<\theta <\pi /2,\kern2em r=a $$

(3)

Considering that the exterior region S and interior region Ω are welded together, the continuities of displacement and stress at the auxiliary boundary are also required:

$$ \left\{\begin{array}{c}{W}^{\left(\varOmega \right)}\left(a,\theta \right)={W}^{(S)}\left(a,\theta \right)\\ {}{\tau}_{rz}^{\left(\varOmega \right)}\left(a,\theta \right)={\tau}_{rz}^{(S)}\left(a,\theta \right)\kern1em \end{array}\right.,-\pi \le \theta \le -\frac{\pi }{2}\cup \frac{\pi }{2}\le \theta \le \pi \kern0.75em $$

(4)

The incident wave W⁽ⁱ⁾ is emitted by the line source, and its mathematical form in polar coordinate system (r₁, θ₁) is as follows:

$$ {W}^{(i)}=\frac{i}{4\mu }{H}_0^{(1)}\left(k{r}_1\right)\kern0.5em $$

(5)

where ${H}_0^{(1)}\left(\bullet \right)$represents the Hankel function of the first kind with order 0.

Based on the image theory, the reflected wave W^(r) induced by the half-space can be written in polar coordinate system (r₂, θ₂) as follows:

$$ {W}^{(r)}=\frac{i}{4\mu }{H}_0^{(1)}\left(k{r}_2\right)\kern1.25em $$

(6)

According to coordinate relations:

$$ {x}_2=2{x}_0-{x}_1,{y}_2={y}_1 $$

(7)

$$ {x}_1=x+{x}_0,{y}_1=y+{y}_0 $$

(8)

The incident wave W⁽ⁱ⁾ and the reflected wave W^(r) can be rewritten in the Cartesian coordinate system (x, y) as follows:

$$ {W}^{(i)}=\frac{i}{4\mu }{H}_0^{(1)}\left(k\sqrt{x^2+{y}^2+2{x}_0x+2{y}_0y+{x}_0^2+{y}_0^2}\right)\kern1em $$

(9)

$$ {W}^{(r)}=\frac{i}{4\mu }{H}_0^{(1)}\left(k\sqrt{x^2+{y}^2-2{x}_0x+2{y}_0y+{x}_0^2+{y}_0^2}\right) $$

(10)

We can define W^(ff) = W⁽ⁱ⁾ + W^(r) as a free-field displacement which represents the displacement of half-space at the absence of the hill, and its mathematical form in polar coordinate system (r, θ) is as follows:

$$ {W}^{(ff)}=\frac{i}{4\mu}\left[{H}_0^{(1)}\left(k\sqrt{r^2+2{x}_0r\cos \theta +2{y}_0r\sin \theta +{x}_0^2+{y}_0^2}\right)+{H}_0^{(1)}\left(k\sqrt{r^2-2{x}_0r\cos \theta +2{y}_0r\sin \theta +{x}_0^2+{y}_0^2}\right)\right] $$

(11)

And, relevant stress components are derived as follows:

$$ {\displaystyle \begin{array}{c}{\tau}_{\theta z}^{(ff)}=\frac{\mu \partial {W}^{(ff)}}{r\partial \theta }=\frac{ik}{4r}\left\{H{\prime}_0^{(1)}\left(k\sqrt{r^2+2{x}_0r\cos \theta +2{y}_0r\sin \theta +{x}_0^2+{y}_0^2}\right)\frac{-{x}_0r\sin \theta +{y}_0r\cos \theta }{\sqrt{r^2+2{x}_0r\cos \theta +2{y}_0r\sin \theta +{x}_0^2+{y}_0^2}}\right.\\ {}\left.+{H^{\prime}}_0^{(1)}\left(k\sqrt{r^2-2{x}_0r\cos \theta +2{y}_0r\sin \theta +{x}_0^2+{y}_0^2}\right)\frac{x_0r\sin \theta +{y}_0r\cos \theta }{\sqrt{r^2-2{x}_0r\cos \theta +2{y}_0r\sin \theta +{x}_0^2+{y}_0^2}}\right\}\end{array}} $$

(12)

$$ {\displaystyle \begin{array}{c}{\tau}_{rz}^{(ff)}=\frac{\mu \partial {W}^{(ff)}}{\partial r}=\frac{ik}{4}\left\{H{\prime}_0^{(1)}\left(k\sqrt{r^2+2{x}_0r\cos \theta +2{y}_0r\sin \theta +{x}_0^2+{y}_0^2}\right)\frac{r+{x}_0\cos \theta +{y}_0\sin \theta }{\sqrt{r^2+2{x}_0r\cos \theta +2{y}_0r\sin \theta +{x}_0^2+{y}_0^2}}\right.\\ {}\left.+H{\prime}_0^{(1)}\left(k\sqrt{r^2-2{x}_0r\cos \theta +2{y}_0r\sin \theta +{x}_0^2+{y}_0^2}\right)\frac{r-{x}_0\cos \theta +{y}_0\sin \theta }{\sqrt{r^2-2{x}_0r\cos \theta +2{y}_0r\sin \theta +{x}_0^2+{y}_0^2}}\right\}\end{array}} $$

(13)

where $H{\hbox{'}}_0^{(1)}\ \left(\bullet \right)$is the first derivative of ${H}_0^{(1)}\ \left(\bullet \right)$.

Substituting θ = ± π/2 into Eq. (12) deduces ${\tau}_{\theta z}^{(ff)}=0$ which means the free-field displacement W^(ff) satisfy the traction-free boundary condition Eq. (2).

Since the expressions of W^(ff) and ${\tau}_{rz}^{(ff)}$ are quite complex, further derivation via the separation variable method in this study is cumbersome. We expand W^(ff) and ${\tau}_{rz}^{(ff)}$ into Fourier series over the interval [-π,π] as follows:

$$ {W}^{(ff)}=\sum \limits_{m=0}^{+\infty }{M}_m\cos m\theta +{N}_m\sin m\theta \kern0.5em $$

(14)

$$ {\tau}_{rz}^{(ff)}=\mu k\sum \limits_{m=0}^{+\infty }{M}_m^{\prime}\cos m\theta +{N}_m^{\prime}\sin m\theta $$

(15)

where

$$ \left\{\begin{array}{c}{M}_m=\frac{1}{\Delta_m\pi }{\int}_{-\pi}^{\pi }{W}^{(ff)}\cos m\theta d\theta, \kern1.25em \\ {}{N}_m=\frac{1}{\pi }{\int}_{-\pi}^{\pi }{W}^{(ff)}\sin m\theta d\theta, \kern2.75em \\ {}\begin{array}{c}{M}_m^{\prime }=\frac{1}{\Delta_m\pi }{\int}_{-\pi}^{\pi}\frac{1}{\mu k}{\tau}_{rz}^{(ff)}\cos m\theta d\theta, \\ {}{N}_m^{\prime }=\frac{1}{\pi }{\int}_{-\pi}^{\pi}\frac{1}{\mu k}{\tau}_{rz}^{(ff)}\sin m\theta d\theta .\kern1.5em \end{array}\end{array}\right. $$

(16)

$$ {\Delta}_m=\left\{\begin{array}{c}2,m=0\\ {}1,m\ne 0\end{array}\right. $$

(17)

Because of the presence of the hill and auxiliary boundary, two extra waves are generated. The first wave is the outgoing waves W^(d) in the exterior region S, while the second one is the standing waves W^(Ω) inside the interior region Ω. Both the outgoing waves and standing waves can be expressed as a series form of Bessel functions.

The mathematical form of W^(d) is given as follows:

$$ {W}^{(d)}=\sum \limits_{m=0}^{+\infty }{H}_m^{(1)}(kr)\left({A}_m{\delta}_m^{(1)}\cos m\theta +{B}_m{\delta}_m^{(2)}\sin m\theta \right) $$

(18)

where ${\delta}_m^{(1)}=1+{\left(-1\right)}^m$ and ${\delta}_m^{(2)}=1-{\left(-1\right)}^m$ and A_m and B_m are the unknown coefficients.

Relevant stress components are derived as follows:

$$ {\tau}_{\theta z}^{(d)}=\frac{\mu \partial {W}^{(d)}}{r\partial \theta }=\frac{\mu }{r}\sum \limits_{m=0}^{+\infty }{H}_m^{(1)}(kr)\left(-{A}_m{\delta}_m^{(1)}m\sin m\theta +{B}_m{\delta}_m^{(2)}m\cos m\theta \right) $$

(19)

$$ {\tau}_{rz}^{(d)}=\frac{\mu \partial {W}^{(d)}}{\partial r}=\mu k\sum \limits_{m=0}^{+\infty }H{\prime}_m^{(1)}(kr)\left({A}_m{\delta}_m^{(1)}\cos m\theta +{B}_m{\delta}_m^{(2)}\sin m\theta \right)\kern0.5em $$

(20)

Substituting θ = ± π/2 into Eq. (19) deduces ${\tau}_{\theta z}^{(d)}=0$ which indicates the outgoing wave field W^(d) satisfies the traction-free boundary condition (Eq. (2)).

The total wave fields W^(S) and ${\tau}_{rz}^{(S)}$of the exterior region are the superposition of free wave fields and outgoing wave fields, as follows:

$$ {W}^{(S)}={W}^{(d)}+{W}^{(ff)} $$

(21)

$$ {\tau}_{rz}^{(S)}={\tau}_{rz}^{(d)}+{\tau}_{rz}^{(ff)}\kern2.25em $$

(22)

The mathematical form of W^(Ω) is given as follows:

$$ {W}^{\left(\varOmega \right)}=\sum \limits_{m=0}^{+\infty }{J}_m(kr)\left({C}_m\cos m\theta +{D}_m\sin m\theta \right) $$

(23)

where J_m(·) represents the Bessel function with order m, C_m, and D_m are the unknown coefficients.

Relevant stress components are expressed as follows:

$$ {\tau}_{\theta z}^{\left(\varOmega \right)}=\frac{\mu \partial {W}^{\left(\varOmega \right)}}{r\partial \theta }=\frac{\mu }{r}\sum \limits_{m=0}^{+\infty }{J}_m(kr)\left(-{C}_mm\sin m\theta +{D}_mm\cos m\theta \right) $$

(24)

$$ {\tau}_{rz}^{\left(\varOmega \right)}=\frac{\mu \partial {W}^{\left(\varOmega \right)}}{\partial r}=\mu k\sum \limits_{m=0}^{+\infty }{J}_m^{\prime }(kr)\left({C}_m\cos m\theta +{D}_m\sin m\theta \right)\kern1em $$

(25)

Now, defining two functions Φ(θ) and Ψ(θ) as follows:

$$ \Phi \left(\theta \right)=\left\{\begin{array}{c}0,-\pi /2+2 l\pi \le \theta \le \pi /2+2 l\pi \\ {}{W}^{\left(\varOmega \right)}\left(a,\theta \right)-{W}^{(S)}\left(a,\theta \right),\mathrm{other}\kern0.75em \end{array},l=0,\pm 1,\pm 2,\dots \kern10em \right. $$

(26)

$$ \Psi \left(\theta \right)=\left\{\begin{array}{c}{\tau}_{rz}^{\left(\varOmega \right)}\left(a,\theta \right),-\pi /2+2 l\pi \le \theta \le \pi /2+2 l\pi \\ {}{\tau}_{rz}^{\left(\varOmega \right)}\left(a,\theta \right)-{\tau}_{rz}^{(S)}\left(a,\theta \right),\mathrm{other}\kern5.75em \end{array},l=0,\pm 1,\pm 2,\dots \right.\kern7em $$

(27)

According to Eqs. (3) and (4), the values of Φ(θ) and Ψ(θ) are equal to zero. Expanding Φ(θ) and Ψ(θ) into Fourier series over interval [-π,π] and making the coefficients of the series equal to zero can lead to the following equations:

$$ \sum \limits_{m=0}^{+\infty}\left[{H}_m^{(1)}(ka){A}_m{\delta}_m^{(1)}-{C}_m{J}_m(ka)+{M}_m\right]{\lambda}_{mn}=0\kern1.25em $$

(28)

$$ \sum \limits_{m=0}^{+\infty}\left[{H}_m^{(1)}(ka){B}_m{\delta}_m^{(2)}-{D}_m{J}_m(ka)+{N}_m\right]{\mu}_{mn}=0\kern1.75em $$

(29)

$$ {C}_n{J}_n^{\prime }(ka)-\sum \limits_{m=0}^{+\infty}\left[{H^{\prime}}_m^{(1)}(ka){A}_m{\delta}_m^{(1)}+{M}_m^{\prime}\right]{\lambda}_{mn}=0\kern1.25em $$

(30)

$$ {D}_n{J}_n^{\prime }(ka)-\sum \limits_{m=0}^{+\infty}\left[{H^{\prime}}_m^{(1)}(ka){B}_m{\delta}_m^{(2)}+{N}_m^{\prime}\right]{\mu}_{mn}=0\kern1.5em $$

(31)

where

$$ {\lambda}_{m n}=\left\{\begin{array}{c}\frac{1}{2},\kern19.5em m=n\\ {}\frac{\varepsilon_n}{2\pi}\frac{-2m\cos \frac{n\pi}{2}\sin \frac{m\pi}{2}+2n\cos \frac{m\pi}{2}\sin \frac{n\pi}{2}}{m^2-{n}^2},m\ne n\end{array}\right.\kern1.5em $$

(32)

$$ {\mu}_{m n}=\left\{\begin{array}{c}0,\kern17.5em m=n=0\\ {}\frac{1}{2},\kern17.25em m=n\ne 0\\ {}\frac{\varepsilon_n}{2\pi}\frac{-2n\cos \frac{n\pi}{2}\sin \frac{m\pi}{2}+2m\cos \frac{m\pi}{2}\sin \frac{n\pi}{2}}{m^2-{n}^2},m\ne n\end{array}\right.\kern1em $$

(33)

$$ {\varepsilon}_n=\left\{\begin{array}{c}1,\kern1.75em n=0\\ {}2,\kern1.75em n\ne 0\end{array}\right.\kern0.5em $$

(34)

Then, substituting Eqs. (30) and (31) into Eqs. (28) and (29) derives the following equations:

$$ \sum \limits_{m=0}^{+\infty }{\delta}_m^{(1)}\left[{H}_m^{(1)}(ka){\lambda}_{mn}-H{\prime}_m^{(1)}(ka){P}_{mn}\right]{A}_m=\sum \limits_{m=0}^{+\infty }-{M}_m{\lambda}_{mn}+{M}_m^{\prime }{P}_{mn} $$

(35)

$$ \sum \limits_{m=0}^{+\infty }{\delta}_m^{(2)}\left[{H}_m^{(1)}(ka){\mu}_{mn}-{H^{\prime}}_m^{(1)}(ka){Q}_{mn}\right]{B}_m=\sum \limits_{m=0}^{+\infty }-{N}_m{\mu}_{mn}+{N}_m^{\prime }{Q}_{mn}\kern0.5em $$

(36)

where

$$ {P}_{mn}=\sum \limits_{l=0}^{+\infty}\frac{J_l(ka)}{J_l^{\prime }(ka)}{\lambda}_{ml}{\lambda}_{ln}\kern0.75em $$

(37)

$$ {Q}_{mn}=\sum \limits_{l=0}^{+\infty}\frac{J_l(ka)}{J_l^{\prime }(ka)}{\mu}_{ml}{\mu}_{ln} $$

(38)

and m, n = 0,1,2,…

The unknown coefficients A_m and B_m can be solved numerically by truncating Eqs. (35) and (36) into finite terms. Specifically, the indexes m and n are truncated to M and N terms, where M is the number of truncation of series solutions and N is the number of equations. Besides, N should be greater than M; thus the truncated equations become over-determined and should be solved by the least-squares method.

After solving Eqs. (35)–(36) and obtaining the value of coefficients A_m and B_m, the unknown coefficients C_n and D_n can be deduced from Eqs. (30) and (31) as follows:

$$ {C}_n=\frac{1}{J{\prime}_n(ka)}\sum \limits_{m=0}^{+\infty}\left[H{\prime}_m^{(1)}(ka){A}_m{\delta}_m^{(1)}+{M}_m^{\prime}\right]{\lambda}_{mn}=0 $$

(39)

$$ {D}_n=\frac{1}{J_n^{\prime }(ka)}\sum \limits_{m=0}^{+\infty}\left[{H^{\prime}}_m^{(1)}(ka){B}_m{\delta}_m^{(2)}+{N}_m^{\prime}\right]{\mu}_{mn}=0\kern12.25em $$

(40)

Finally, we can calculate the wave field at any point within the theoretical model by Eqs. (21) and (23).

Validation of theoretical solution

The accuracy of the series solution can be verified by checking the correctness of the displacement and stress continuous conditions at the auxiliary boundary. Because the value of the incident waves W⁽ⁱ⁾ is frequency-dependent, and obviously not equal to 1, we take the normalized displacement residuals ΔW and stress residuals Δτ_rz at the auxiliary boundary as follows:

$$ \Delta W=\left|{W}^{\left(\varOmega \right)}-{W}^{(S)}\right|/{W}_0\kern3.5em $$

(41)

$$ \Delta {\tau}_{rz}=\left|{\tau}_{rz}^{\left(\varOmega \right)}-{\tau}_{rz}^{(S)}\right|/{\tau}_0\kern2.25em $$

(42)

where ${W}_0=2\left|{W}^{(i)}\left(0,0\right)\right|=\left|i/2\mu {H}_0^{(1)}\left(k{r}_0\right)\right|$ is the value of the free field displacement W^(ff) at the origin of the Cartesian coordinate system (x, y) and τ₀ = μkW₀.

To reduce the number of variables, the dimensionless frequency is defined as follows:

$$ \eta =\frac{2a}{\lambda }=\frac{ka}{\pi}\kern0.5em $$

(43)

where λ = 2π/k is the wavelength of the incident waves.

Figures 2, 3, 4 illustrate the variations of the displacement residuals ΔW and stress residuals Δτ_rz at the auxiliary boundary with increasing truncation order M when line source is located at r₀ = 2a, θ₀= −180^o and the values of dimensionless frequencies are η = 1.0, 2.0 and 3.0, respectively. The abscissa in the figures is the angle variable θ ranging from 90^o to 270^o.

Fig. 2

The normalized displacement residuals and stress residuals at the auxiliary boundary when η = 1.0

Fig. 3

The normalized displacement residuals and stress residuals at the auxiliary boundary when η = 2.0

Fig. 4

The normalized displacement residuals and stress residuals at the auxiliary boundary when η = 3.0

As seen in Figs. 2, 3, 4, as the truncation order M increases, the displacement residuals ΔW and the stress residuals Δτ_rz gradually decrease to a small number, which means the error of series solution is negligible provided M is large enough. Note that the values of ΔW and Δτ_rz at the rims of the hill (θ = 90^o or 270^o) are significantly higher than the rest of the auxiliary boundary. This is because the included angles of the rims are greater than π and it can cause stress singularity. Fortunately, the influence of stress singularity on the accuracy of the displacement solutions is comparatively small because the displacements at the rims are finite. Therefore, the displacement solution can relatively quickly converge to the true solution (Yuan and Liao 1996).

Results and discussion

In this section, the displacement distribution on surface and interior of the hill are systematically discussed for different dimensionless frequencies and source locations. Consistent with the above section, the displacement amplitude |W| is normalized by W₀.

The comparison of surface displacement induced by cylindrical waves and plane waves

Figure 5 demonstrates the normalized amplitudes of surface displacement of half-space (−3 ≤ y/a ≤ −3) induced by the plane waves (Yuan and Men 1992) and cylindrical waves. The solid lines represent the case of the plane waves and short dashed and dashed lines correspond to the case of the cylindrical waves with source distance r₀ = 2a, 15a.

Fig. 5

Comparison of normalized amplitudes of surface displacement for a semi-circular hill subject to plane SH waves and cylindrical SH waves. The incident angles α of the plane waves and the source locations (r₀, θ₀) of the cylindrical waves are given. The results in (a)–(c) are for dimensionless frequency η = 0.5, and those in (d)–(f), (g)–(i), (j)–(l) correspond to η = 1.0, 2.0, and 3.0, respectively

As seen in Fig. 5, the surface displacement distribution for near-source (r₀ = 2a) cylindrical waves is quite different from that of plane waves. The displacement amplitudes on hill surface excited by the near-source cylindrical waves are generally smaller than those excited by the plane waves when the incident direction is vertical to half-space. However, when the incident direction is oblique or horizontal to half-space, the displacement amplitudes on hill surface caused by the near-source cylindrical waves are larger than those caused by the plane waves. For example, the displacement amplitudes at the hilltop (y/a = 0) are 1.96 for plane waves (solid line) and 1.74 for near-source cylindrical waves (short dashed line) in Fig. 5(d). But those values in Figs. 5(e) and (f) are 0.66 versus 0.86 and 0.40 versus 0.58, respectively. Moreover, when the dimensionless frequency is high, the topographic effect at certain locations for the plane waves and near-source cylindrical wave is contrary. For instance, as shown in Fig. 5(g), when the dimensionless frequency η = 2.0, the displacement amplitudes at the hilltop are 1.32 for plane waves and 0.53 for near-source cylindrical waves. In addition, those values are 0.13 versus 1.38 in Fig. 5(j). The above results indicate that we cannot simply view the cylindrical waves as plane waves, and the influence of source distance on amplitudes should be handled.

Then, we compare the results for far-source (r₀ = 15a) cylindrical waves (dashed line) and plane waves (solid lines). The surface displacements between them are in good accord, except a little difference on the horizontal ground due to the geometric attenuation effect of the cylindrical waves. The average differences in the surface displacements (−3 ≤ y/a ≤ −3) between far-source cylindrical waves and plane waves are only 1.94, 3.48, and 4.01% in Figs. 5(a)–(c), and those values in (d)–(f) are 2.32, 7.10, and 4.39%, in Figs. 5(g)-(i) are 5.87, 4.87, and 6.33% and in Figs. 5(j)–(l) are 5.67, 4.70, and 4.38%. Since these values are small, e.g., most of them are less than 5% and the maximum is only 7.10%, one can conclude that the cylindrical waves can be regarded as the plane waves when the source distance is greater than 15 times the hill radius.

The relationship between the surface displacement and dimensionless frequency

The main influencing factors on the responses of the semi-circular hill are incident wave frequency, radius of the hill and source location. In previous subsection, the effects of source location on displacement amplitudes have been investigated. This subsection focuses on the effects of incident wave frequency and radius of the hill, and they are expressed by the dimensionless frequency.

Fig. 6 shows the normalized amplitudes of surface displacement of half-space (-3 ≤ y/a ≤ -3) for different dimensionless frequencies when source distance r₀ = 5a and source angles θ₀ = -180^o, -135^o, -90^o, respectively.

Fig. 6

The normalized amplitudes of surface displacement for a semi-circular hill with different dimensionless frequencies. The results in (a)–(b) are for source location (r₀ = 5a, θ₀ = −180^o) and those in (c)–(d) and (e)–(f) correspond to (r₀ =5a, θ₀ = −135^o) and (r₀ = 5a, θ₀ = −90^o), respectively

As depicted in Fig. 6, when the dimensionless frequency is not greater than 1.0, the displacement amplitudes variation along surface is relatively slow and only one single peak value is observed on hill surface. For example, when the dimensionless frequency η = 0.2, the surface displacement peaks for θ₀= −180^o, −135^o, and −90^o are 1.49, 1.45, and 1.40, and all of them appear near at the hilltop (y/a = 0), and the average differences in displacement amplitudes between hilltop and other points of hill surface are only 6.17, 6.45, and 6.73%, respectively. Besides, the source angles have significant impact on the location and corresponding frequency of the maximum displacements. For instance, the maximum displacement in Figs. 6(a) and (b) is 1.891 located at y/a = 0 and η = 1.0, in Figs. 6(c) and (d) is 1.796 located at y/a = 0.77 and η = 0.7, and in Figs. 6(e) and (f) is 1.803 located at y/a =0.88 and η = 0.7. The above results indicate that the topographic amplification effects widely exist for different source angles when the dimensionless frequency is not greater than 1.0.

Then, we can see that when the dimensionless frequency is greater than 1.0, there are multiple displacement peaks on hill surface, and the number of the peaks increase as the dimensionless frequency increases. Furthermore, the displacement peaks for θ₀= −180^o are large, and significant topographic amplification effects are observed, while the displacement peaks for θ₀= −90^o are small and mostly show the topographic reduction effects. It makes sense because the wave energy is primarily concentrated in the incident direction, and the energy of the diffraction wave will decrease as the incident wave frequency increases. Therefore, the displacement amplitudes for θ₀= −180^o is generally greater than that for θ₀= −90^o, especially when the dimensionless frequency is large.

The relationship between the internal displacement and dimensionless frequency

Due to the difference of wave propagation path, the displacement distributions of the interior and surface of the hill are different. Figure 7 illustrates the normalized amplitudes of internal displacement along vertical direction (θ = 0^o) of the semi-circular hill for different dimensionless frequencies when r₀ = 5a and θ₀ = −180^o, −135^o, and −90^o, respectively.

Fig. 7

The normalized amplitudes of internal displacement along vertical direction (θ = 0^o) of the semi-circular hill with different dimensionless frequencies. The results in (a)-(b) are for source location (r₀ = 5a, θ₀ = −180^o), and those in (c)-(d) and (e)-(f) correspond to (r₀ =5a, θ₀ = −135^o) and (r₀ = 5a, θ₀ = −90^o), respectively

As shown in Fig. 7, when the dimensionless frequency η ≤ 0.5, the displacement will increase monotonously with increasing elevation, and the maximum displacement appears at the hill surface (x/a = 1.0). But this monotonicity will be altered with the increased dimensionless frequency, and the internal displacement is possibly greater than the surface displacement. For example, when η ≥ 0.5, as the elevation increases, the displacement for θ₀ = −90^o first decreases then increases, and the maximum displacement appears at the hill bottom (x/a = 0.0) rather than the hill surface. Moreover, the characteristics of displacement distribution vary with source angles. For instance, when η ≥ 2.0, the displacements for θ₀ = −180^o are large in the middle and small at both ends, and the maximum displacements appear near x/a = 0.5, showing significant amplitude amplification effects, while the surface displacements exhibit amplitude reduction effects. On the contrary, the displacements for θ₀ = −135^o and −90^o are small in the middle and large at both ends, and the maximum displacements appear at the hill surface or hill bottom. Above results indicate that the surface displacements are possibly smaller than the internal displacements when the dimensionless frequency is large. Especially when the source is located directly below the hill, the surface displacements are reduced but the internal displacements could be amplified.

The displacements induced by transient waves

In above subsections, we have analyzed the effects of steady waves on the distribution of surface and internal displacements of semi-circular hill. However, the actual seismic waves are transient waves, and the results of single frequency are unable to fully embody the features of transient motions. In this subsection, the transient responses for semi-circular hill are given through the inverse fast Fourier Transform.

The incident wave is assumed as Ricker wavelet:

$$ R(t)=\left(2{\pi}^2{f}_c^2{t}^2-1\right)\exp \left(-{\pi}^2{f}_c^2{t}^2\right) $$

(44)

where f_c = 1.0Hz represents the predominant frequency.

Because the amplitude spectrum of the wavelet is approximate to zero at 4Hz, we take the calculation frequencies ranging from 0 4Hz and the interval is 1/24Hz. For comparison, both the dimensionless frequencies for transient waves η_c = 2af_c/c and steady waves η = 2af/c are set to 1.0. Figure 8 shows normalized amplitudes of displacement around the hill caused by transient waves and steady waves when r₀ = 5a and θ₀ = −180^o, −135^o, and −90^o, respectively.

Fig. 8

Comparison of transient waves and steady waves on displacement distributions of the semi-circular hill when the dimensionless frequency η = 1.0. The results in (a)-(c) are surface displacements, and those in (d)-(f) correspond to internal displacements along vertical direction (θ = 0^o)

As illustrated in Fig. 8, the overall distribution of displacement amplitudes of transient responses and steady responses is consistent, but there are some differences. Firstly, the amplitude fluctuations of the transient waves are lower than those of steady waves. For example, in Fig. 8(a), the maximum differences in displacement amplitudes on hill surface are equal to 1.77 and 0.82 for steady waves and transient waves, respectively. Secondly, the maximum responses of transient waves are less than that of steady waves for θ₀= −180^o, but it is contrary for θ₀= −135^o and −90^o. For example, the maximum displacements for transient waves and steady waves in Fig. 8(a) are 1.44 and 1.89, in Fig. 8(b) are 1.34 and 1.24, and in Fig. 8(c) are 1.23 and 1.11. That is because for steady waves with η = 1.0, the maximum displacement for θ₀ = −180^o is at a peak along η-axis (as seen in Fig. 6(a)). Therefore, transient waves which contain other frequencies have a lower amplitude than steady waves. While the maximum displacement for θ₀= −135^o and −90^o are located in the middle of two peaks along η-axis (as seen in Figs. 6(c) and (e)), thus transient waves have a larger amplitude than steady waves. Thirdly, the displacement amplitudes at the hill bottom (x/a = 0.0) for transient waves are less than those for steady waves. It could be due to the transient waves are finite wave trains, while the steady waves are infinite wave trains, therefore the intensity of wave superposition at the hill bottom of the transient waves is lower than that of steady waves.

Conclusions

In this paper, a novel series solution for the dynamic response of semi-circular hill subject to the cylindrical SH wave is derived by wave expansion method. The influence of source location and dimensionless frequency on displacement distributions around the hill is systematically analyzed. The main conclusions are drawn as follows:

• (1) When the source distance is small, the displacements of the hill surface caused by cylindrical waves are generally smaller than those caused by plane waves for the case of vertical incidence, but it is contrary to the cases of oblique incidence and horizontal incidence. As source distance increases, the difference between them decreases. When the source distance is larger than 15 times of the radius of the hill, this difference is negligible.

• (2) When the dimensionless frequency is not greater than 1.0, the topographic amplification effects widely exist in different source angles. But when the dimensionless frequency is greater than 1.0, the topographic amplification effects mainly occur in the case of vertical incidence, and the case of horizontal incidence mainly exhibits topographic reduction effects.

• (3) The displacements of hill surface are larger than the displacements inside the hill when the dimensionless frequency is not larger than 1.0, and when the dimensionless frequency is larger than 1.0, the displacements of hill surface are possibly smaller than that inside the hill.

• (4) When the predominant frequency of transient waves is the same with the frequency of steady waves, the displacement amplitude distributions of the hill caused by transient and steady waves are consistent on the whole, but there are some differences, such as the amplitude fluctuations of the former is lower than that of the latter.