Wave and current-induced dynamic response in a multilayered poroelastic seabed

Abstract

Waves and currents often coexist in ocean, which significantly changes the pore pressure and stress state in the seabed. Besides, stratification is a basic feature of a seabed due to natural deposition or artificial construction. An analytical solution to the dynamic response of a multilayered seabed to combined wave and current loading is proposed in this study. The seabed is modeled using Biot’s fully dynamic theory, where the effects of inertia and the compressibility of solids and fluids are included. Unlike previous investigations, stratification of seabed and non-linear interactions between waves and the current are considered in this study. The present solution is firstly validated against an existing analytical solution and a model test. Comprehensive parametric study is then conducted to study the influences of soil layering, current and waves on the dynamic response of a multilayered seabed. A seabed with layered soil properties (e.g. shear modulus, permeability) has substantially different pore pressure and stress state from a homogeneous seabed under combined wave and current loading. The current significantly influences the seabed response. An opposing current is beneficial to prevent both soil liquefaction and shear failure, and a following current is more likely to cause seabed instability. The present solution is a practical tool to evaluate seabed stability in an ocean environment with multiple layers, especially where waves and currents are prevailing.

Introduction

Research on seabed response to oceanic loadings has been carried out and has attracted extensive attention in recent years due to growing reported failures of seabed and marine structures (e.g. Zen et al. 1985; Lundgren et al. 1989; Ulker et al. 2012; Ye et al. 2018). The oceanic loadings (e.g. wave loading or current loading or both) excite excess pore pressure, decrease the effective stress, and may cause shear failure and significant movement of sediment, thus posing threat to marine structures and the seabed. When waves and current coexist and interact with each other, the original characteristics of the wave (e.g. wave length) is changed by the current, causing significantly different seabed response from only wave loading, which may even worsen the safety conditions of marine structures and the seabed (Ye 2012). Thus, it is essential to study the response of seabeds to oceanic loadings, especially combined wave and current loading.

In the past few decades, considerable efforts have been devoted to the wave-induced seabed response. A detailed review about wave-induced seabed response can be found in Jeng (2003) and Ulker and Rahman (2009). Recently, more and more research has paid attention to the wave and current-induced seabed response. Different assumptions, such as the compressibility of soil particles and pore fluids, the accelerations due to soil and fluid motion, degree of saturation, the assumption of semi-infinite seabed, and so on, have been considered or ignored in the analyses. Ye and Jeng (2012) were the first to numerically investigate the response of a porous seabed to wave and current loading by adopting the u-p approximation (partially dynamic theory). Zhang et al. (2013) proposed an analytical solution for wave and current-induced dynamic response in a semi-infinite porous seabed. Liao et al. (2015) presented a new analytical approximation for wave and current-induced dynamic response of soil and investigated the effects of wave and current parameters on pore pressure. Yang and Ye (2017) investigated wave and current-induced residual liquefaction in a loose seabed floor and found that the progressive liquefaction process is significantly affected by wave height, permeability and saturation of seabed soil.

However, due to complex natural geological processes or artificial construction, the seabed is generally highly inhomogeneous (e.g. Davis 1969; Zhou et al. 2011; Zhang et al. 2016; Yang and Ye 2018), and great efforts have been made to investigate the dynamic response of an inhomogeneous seabed to wave loading. Yamamoto (1981) and Rahman et al. (1994) studied the response to storm loading of an inhomogeneous seabed with several layers. Hsu et al. (1995) studied soil response and liquefaction in a layered seabed to wave loading using a semi-analytical method. Zhou et al. (2011) comprehensively investigated the wave-induced response in a multilayered porous seabed. Ulker (2014) studied the dynamic response of saturated, layered porous media to harmonic waves using a semi-analytical method. Recently, Peng et al. (2017) investigated the wave-induced oscillatory response in a spatially random heterogeneous porous seabed and found that soil properties affect seabed response significantly. Moreover, the results of Wang et al. (2018) indicate that Biot’s fully dynamic theory should be considered in seabed response analysis, and their results show that seabed response is significantly affected by several wave and seabed parameters, including wave period, pore fluid compressibility, soil permeability, shear modulus, and so on. Based on the above review, both solution to response of an uniform seabed to combined wave and current loading and that to response of a layered seabed to wave loading have been reported in the literature. However, the dynamic response of a multilayered seabed to combined wave and current loading is still unclear.

In this paper, an analytical solution to the dynamic response of a multilayered seabed to combined wave and current loading is proposed. The seabed is modeled using Biot’s fully dynamic theory, where the inertia effects and compressibility of solids and fluids are included. The correctness and accuracy of the proposed method are validated against an existing analytical solution and a model test. Comprehensive parametric study is then conducted to study the influences of soil layering, current and waves on the dynamic response of a multilayered seabed.

Governing equations and boundary conditions

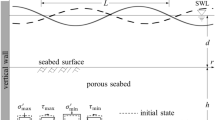
A schematic diagram of the model in this study is presented in Fig. 1. Ocean waves propagating with current over a multilayered porous seabed is considered. The porous sediment is assumed to be homogeneous and isotropic in each layer and governed by Biot’s fully dynamic theory. The origin of the coordinate system is set at the water/seabed interface, and the z-axis points downward. The thickness of the n-th layer is h_n.

Fig. 1

Combined wave and current loading on a multilayered porous seabed

Governing equations of Biot’s fully dynamic theory

Biot’s fully dynamic theory is used to describe the multilayered porous seabed. The governing equations of poroelastic media are given by the following physical laws (Biot 1956; Zienkiewicz et al. 1980; Ding et al. 2013; Feng et al. 2019a):

$$ {\sigma}_{ij}=\lambda {\delta}_{ij}e+2\mu {e}_{ij}-{\delta}_{ij}p $$

(1)

$$ \left({\dot{u}}_{i,i}+{\dot{w}}_{i,i}\right)=-\frac{\phi }{K_f^{\prime }}\dot{p} $$

(2)

$$ {\sigma}_{ij,j}=\rho {\ddot{u}}_i+{\rho}_f{\ddot{w}}_i $$

(3)

$$ -\frac{\rho g}{k}{\dot{w}}_i={p}_{,i}+{\rho}_f{\ddot{u}}_i+\frac{\rho_f}{\phi }{\ddot{w}}_i $$

(4)

In the above equations, a dot above a symbol indicates the derivative with respect to time; the subscript index following a comma indicates a spatial derivative; δ_ij is the Kronecker delta; σ_ij is the total stress tensor; p is the pore fluid pressure; ρ is the bulk density of the seabed; ρ_f is the density of the seawater; e_ij = (u_{i, j} + u_{j, i})/2 is the strain tensor of the solid phase; e = e_ii is the dilatational strain of the solid phase; w_i = ϕ(U_i − u_i) is the relative displacement vector, where ϕ is the porosity, and u_i and U_i are the solid and fluid displacements, respectively; λ and μ are drained Lame coefficients; k is the coefficient of permeability; and ${K}_f^{\prime }$ is the bulk modulus of the pore fluid. If the seabed contains even a very small amount of air, ${K}_f^{\prime }$ greatly decreases (Yamamoto et al. 1978) and can be expressed as (Yamamoto et al. 1978; Jeng and Cha 2003; Wang et al. 2018):

$$ \frac{1}{K_f^{\prime }}=\frac{1}{K_f}+\frac{1-{S}_r}{p_{w0}} $$

(5)

where K_f is the bulk modulus of pore water (2 × 10⁹ N/m²); S_r is the degree of saturation of the seabed; and p_w0 is the absolute static pressure. For a fully saturated seabed, ${K}_f^{\prime }={K}_f$. Eq. (5) is only applicable for nearly saturated soil, and it works well for seabed soil in an offshore area since the saturation of such generally is larger than 90% (Yang and Ye 2017).

Boundary and continuity conditions

Before solving the response of a multilayered porous seabed in Fig. 1, the boundary and continuity conditions must be specified.

• 1) Boundary conditions at the seabed surface (z = 0)

In this study, the third-order analytical solution of combined wave and current loading proposed by Ye and Jeng (2012) is adopted to apply the pressure loading on the multilayered seabed, which has proved to be accurate enough to describe the wave-current interaction.

The dynamic pressure acting on the seabed can be expressed as

$$ {\displaystyle \begin{array}{l}{P}_b\left(x,t\right)=\frac{\rho_f gH}{2\cosh \left({k}_0d\right)}\left[1-\frac{\omega_2{k}_0^2{H}^2}{2\left({U}_0{k}_0-{\omega}_1\right)}\right]\cos \left({k}_0x-{\omega}_0t\right)\\ {}\kern4em +\frac{3{\rho}_f{H}^2}{8}\left[\frac{\omega_1\left({\omega}_1-{U}_0{k}_0\right)}{2\sinh^4\left({k}_0d\right)}-\frac{g{k}_0}{3\sinh \left(2{k}_0d\right)}\right]\cos 2\left({k}_0x-{\omega}_0t\right)\\ {}\kern4em +\frac{3{\rho}_f{k}_0{H}^3{\omega}_1\left({\omega}_1-{U}_0{k}_0\right)}{512}\frac{\left(9-4{\sinh}^2\left({k}_0d\right)\right)}{\sinh^7\left({k}_0d\right)}\cos 3\left({k}_0x-{\omega}_0t\right)\\ {}\kern3em ={P}_1\cos \left({k}_0x-{\omega}_0t\right)+{P}_2\cos 2\left({k}_0x-{\omega}_0t\right)+{P}_3\cos 3\left({k}_0x-{\omega}_0t\right)\end{array}} $$

(6)

where ρ_f is the density of seawater; k₀ = 2π/L is the wave number; and g is the gravitational acceleration. As shown in Fig. 1, U₀ is the current velocity; d is the static water depth; h is the considered seabed thickness; L and H are the wave length and wave height, respectively; and η is the wave amplitude.

The dispersion relationship is as follows:

$$ {\omega}_0={\omega}_1+{\left({k}_0H\right)}^2{\omega}_2 $$

(7)

where

$$ {\omega}_1={U}_0{k}_0+\sqrt{g{k}_0\tanh \left({k}_0d\right)} $$

(8)

$$ {\omega}_2=\frac{\left[9+8\mathit{\sin}{h}^2\left({k}_0d\right)+8\mathit{\sin}{h}^4\left({k}_0d\right)\right]}{64\mathit{\sin}{h}^4\left({k}_0d\right)}\left({\omega}_1-{U}_0{k}_0\right) $$

(9)

The vertical effective normal stress vanishes at the seabed surface, and the shear stress here is small and can be reasonably neglected. The pore pressure at the seabed surface is equal to the water pressure induced by the wave and current:

$$ {\sigma}_{zx}^1\left({k}_x,0,\omega \right)=0,{\sigma^{\prime}}_{zz}^1\left({k}_x,0,\omega \right)=0,{p}^1\left({k}_x,0,\omega \right)={\hat{\overline{P}}}_b $$

(10)

where ${\sigma}_{zz}^{\prime }$ is the vertical effective stress and ${\hat{\overline{P}}}_b$ denotes the wavenumber-frequency (k_x, ω) form of P_b(x, t) and can be expressed as

$$ {\hat{\overline{P}}}_b=2{\pi}^2\sum \limits_{m=1}^3{P}_m\left[\delta \left(\omega +m{\omega}_0\right)\delta \left({k}_x-m{k}_0\right)+\delta \left(\omega -m{\omega}_0\right)\delta \left({k}_x+m{k}_0\right)\right] $$

(11)

• 2) Continuity conditions between the interfaces (z = z_n)

According to Deresiewicz and Skalak (1963), the displacement, the stress and the pore pressure should be continuous at the interfaces:

$$ {u}_z^n\left({k}_x,{z}_n,\omega \right)={u}_z^{n+1}\left({k}_x,{z}_n,\omega \right),{u}_x^n\left({k}_x,{z}_n,\omega \right)={u}_x^{n+1}\left({k}_x,{z}_n,\omega \right) $$

(12a)

$$ {\sigma}_{zx}^n\left({k}_x,{z}_n,\omega \right)={\sigma}_{zx}^{n+1}\left({k}_x,{z}_n,\omega \right),{\sigma}_{zz}^n\left({k}_x,{z}_n,\omega \right)={\sigma}_{zz}^{n+1}\left({k}_x,{z}_n,\omega \right) $$

(12b)

$$ {p}^n\left({k}_x,{z}_n,\omega \right)={p}^{n+1}\left({k}_x,{z}_n,\omega \right),{w}_z^n\left({k}_x,{z}_n,\omega \right)={w}_z^{n+1}\left({k}_x,{z}_n,\omega \right) $$

(12c)

• 3) Boundary conditions at the seabed bottom (z = z_N)

The bottom of the multilayered seabed is considered as rigid and impermeable. Thus, there is no displacement and vertical flow here:

$$ {u}_z^N\left({k}_x,{z}_N,\omega \right)=0,{u}_x^N\left({k}_x,{z}_N,\omega \right)=0,{w}_z^N\left({k}_x,{z}_N,\omega \right)=0 $$

(13)

Analytical solution to a multilayered porous seabed

General solution to the governing equations

The governing equations (Eqs. 1–4) can also be expressed in the form of the first-order ordinary differential ones in the wavenumber-frequency (k_x, ω) domain (Feng et al. 2016):

$$ \frac{\mathrm{d}}{\mathrm{d}z}\mathbf{f}(z)=\left(\begin{array}{cc}\mathbf{0}& {\mathbf{A}}_1\\ {}{\mathbf{A}}_2& \mathbf{0}\end{array}\right)\mathbf{f}(z) $$

(14)

where f(z) is the displacement-stress vector and is given by

$$ \mathbf{f}(z)={\left[{\tilde{u}}_z,\ {\tilde{\zeta}}_z,{\tilde{\overline{\sigma}}}_{zx},{\tilde{\overline{\sigma}}}_{zz},\tilde{p},{\tilde{u}}_x\right]}^T $$

(15)

In the above equation, the normal combination displacement of porous media is defined as

$$ {\tilde{\zeta}}_z=\left(1-\phi \right){\tilde{u}}_z+\phi {\tilde{U}}_z={\tilde{u}}_z+{\tilde{w}}_z $$

(16)

where ${\tilde{\overline{\sigma}}}_{zx}=-{\tilde{\sigma}}_{zx}$, ${\tilde{\overline{\sigma}}}_{zz}=-{\tilde{\sigma}}_{zz}^{\prime }$, and ${\tilde{\sigma}}_{zz}^{\prime }={\tilde{\sigma}}_{zz}+\tilde{p}$. The matrices A₁ and A₂ are consistent with those in Feng et al. (2016) after α, M, m^′and κ are replaced by 1, ${K}_f^{\prime }/\phi$, ρ_f/ϕ and k/ρg, respectively.

Considering the boundary conditions in Eq. (10) and Eq. (13), a new displacement-stress vector, i.e. ${\left[{\tilde{u}}_x^n,{\tilde{u}}_z^n,{\tilde{w}}_z^n,{\tilde{\sigma}}_{zx}^n,{\tilde{\sigma}}_{zz}^{\prime n},{\tilde{p}}^n\right]}^T$, should be used in this paper. The general solution has the following form:

$$ {\displaystyle \begin{array}{l}{\left[{\tilde{u}}_x^n,{\tilde{u}}_z^n,{\tilde{w}}_z^n,{\tilde{\sigma}}_{zx}^n,{\tilde{\sigma}}_{zz}^{\prime n},{\tilde{p}}^n\right]}^T={\mathbf{L}}^n\left({k}_x,\omega \right){\mathbf{W}}^n\left({k}_x,z,\omega \right)\\ {}=\left[\begin{array}{cc}{\mathbf{L}}_{11}^n& {\mathbf{L}}_{12}^n\\ {}{\mathbf{L}}_{21}^n& {\mathbf{L}}_{22}^n\end{array}\right]{\left[{\mathbf{W}}_d^n{\left({k}_x,z,\omega \right)}^T\kern0.5em {\mathbf{W}}_u^n{\left({k}_x,z,\omega \right)}^T\right]}^T\end{array}} $$

(17)

where ${\mathbf{L}}_{11}^n$, ${\mathbf{L}}_{12}^n$, ${\mathbf{L}}_{21}^n$ and ${\mathbf{L}}_{22}^n$ are defined to have columns that contain the response of three types of plane wave in the n-th layer, and the expressions of them are enclosed in the Appendix. It is noteworthy that ${\left[{\tilde{u}}_z^n,\ {\tilde{\zeta}}_z^n,{\tilde{\overline{\sigma}}}_{zx}^n,{\tilde{\overline{\sigma}}}_{zz}^n,{\tilde{p}}^n,{\tilde{u}}_x^n\right]}^T$ in Feng et al. (2016) is replaced by ${\left[{\tilde{u}}_x^n,{\tilde{u}}_z^n,{\tilde{w}}_z^n,{\tilde{\sigma}}_{zx}^n,{\tilde{\sigma}}_{zz}^{\prime n},{\tilde{p}}^n\right]}^T$ here, thus ${\mathbf{L}}_{11}^n$, ${\mathbf{L}}_{12}^n$, ${\mathbf{L}}_{21}^n$ and ${\mathbf{L}}_{22}^n$ are different from ${\mathbf{L}}_1^n$ and ${\mathbf{L}}_2^n$ in Feng et al. (2016).

A stable transmission and reflection matrix method for a multilayered porous seabed

The transmission and reflection matrix (TRM) method was first proposed by Kennett (1983). Lu and Hanyga (2005) and Xu et al. (2008) extended the method to layered poroelastic media. In this section, a stable and efficient TRM method is developed to solve the dynamic response of a multilayered seabed under wave and current loading. The method not only has concise mathematical expression, but also explicitly exhibits the physical mechanism of wave propagation (see Fig. 2). The down-going and the up-going wave vectors in Eq. (17) can be rewritten as (Feng et al. 2016)

$$ {\mathbf{W}}_d^n\left({k}_x,z,\omega \right)={\mathbf{E}}^n\left(z-{z}_{n-1}\right){\mathbf{W}}_d^n\left({k}_x,{z}_{n-1},\omega \right) $$

(18)

$$ {\mathbf{W}}_u^n\left({k}_x,z,\omega \right)={\mathbf{E}}^n\left({z}_n-z\right){\mathbf{W}}_u^n\left({k}_x,{z}_n,\omega \right) $$

(19)

where

$$ {\mathbf{E}}^n(z)=\operatorname{diag}\left[{\mathrm{e}}^{-{a}_1^nz}\kern0.5em {\mathrm{e}}^{-{a}_2^nz}\kern0.5em {\mathrm{e}}^{-{b}^nz}\right] $$

(20)

Fig. 2

(a) Actual reflection and transmission at an interface; (b) equivalent reflection and transmission at an interface

Based on Eq. (17), the continuity conditions (Eq. 12) for the n-th interface between the porous layers are recast as follows:

$$ \left[\begin{array}{cc}-{\mathbf{L}}_{11}^{n+1}& {\mathbf{L}}_{12}^n\\ {}-{\mathbf{L}}_{21}^{n+1}& {\mathbf{L}}_{22}^n\end{array}\right]\left[\begin{array}{c}{\mathbf{W}}_d^{n+1}\left({k}_x,{z}_n,\omega \right)\\ {}{\mathbf{W}}_u^n\left({k}_x,{z}_n,\omega \right)\end{array}\right]=\left[\begin{array}{cc}-{\mathbf{L}}_{11}^n& {\mathbf{L}}_{12}^{n+1}\\ {}-{\mathbf{L}}_{21}^n& {\mathbf{L}}_{22}^{n+1}\end{array}\right]\left[\begin{array}{c}{\mathbf{W}}_d^n\left({k}_x,{z}_n,\omega \right)\\ {}{\mathbf{W}}_u^{n+1}\left({k}_x,{z}_n,\omega \right)\end{array}\right],1\le n\le N-1 $$

(21)

Inversion of the matrix on the left-hand side of Eq. (21) gives the expression as follows:

$$ \left[\begin{array}{c}{\mathbf{W}}_d^{n+1}\left({k}_x,{z}_n,\omega \right)\\ {}{\mathbf{W}}_u^n\left({k}_x,{z}_n,\omega \right)\end{array}\right]=\left[\begin{array}{cc}{\mathbf{T}}_{dd}^n& {\mathbf{R}}_{du}^n\\ {}{\mathbf{R}}_{ud}^n& {\mathbf{T}}_{uu}^n\end{array}\right]\left[\begin{array}{c}{\mathbf{W}}_d^n\left({k}_x,{z}_n,\omega \right)\\ {}{\mathbf{W}}_u^{n+1}\left({k}_x,{z}_n,\omega \right)\end{array}\right] $$

(22)

${\mathbf{T}}_{dd}^n$, ${\mathbf{T}}_{uu}^n$ and ${\mathbf{R}}_{du}^n$, and ${\mathbf{R}}_{ud}^n$ describe the actual transmission and reflection at each interface (see Fig. 2a). For example, ${\mathbf{T}}_{dd}^n$ and ${\mathbf{R}}_{ud}^n$ denote the downward transmission and upward reflection of a down-going wave, respectively.

The dynamic pressure acting on the seabed generates dynamic waves. In fact, wave propagation in the multilayered system is very complicated, such that repeated reflection and transmission will happen at each interface (see Fig. 2b). However, Eq. (22) only includes the wave propagation information at the n-th interface, but is not a recursive form to connect the information of the other layers. To simplify the analysis, Eq. (22) is improved as follows:

$$ {\mathbf{W}}_d^{n+1}\left({k}_x,{z}_n,\omega \right)={\overset{\frown }{\mathbf{T}}}_{dd}^n{\mathbf{W}}_d^n\left({k}_x,{z}_n,\omega \right) $$

(23)

$$ {\mathbf{W}}_u^n\left({k}_x,{z}_n,\omega \right)={\overset{\frown }{\mathbf{R}}}_{ud}^n{\mathbf{W}}_d^n\left({k}_x,{z}_n,\omega \right) $$

(24)

The complicated repeated reflection and transmission processes are equivalent to global transmission (i.e. ${\overset{\frown }{\mathbf{T}}}_{dd}^n$) and global reflection (i.e. ${\overset{\frown }{\mathbf{R}}}_{ud}^n$) as shown in Fig. 2b, namely, the down-going wave vector in the (n + 1)-th layer (${\mathbf{W}}_d^{n+1}\left({k}_x,{z}_n,\omega \right)$) and the up-going wave vector in the n-th layer (${\mathbf{W}}_u^n\left({k}_x,{z}_n,\omega \right)$) can be expressed as the product of the down-going wave vector in the n-th layer (${\mathbf{W}}_d^n\left({k}_x,{z}_n,\omega \right)$). Substituting Eq. (23) and Eq. (24) into Eq. (22), the following recursive formulas can be obtained:

$$ {\overset{\frown }{\mathbf{T}}}_{dd}^n={\left(\mathbf{I}-{\mathbf{R}}_{du}^n{\overset{\frown }{\overline{\mathbf{R}}}}_{ud}^{n+1}\right)}^{-1}{\mathbf{T}}_{dd}^n $$

(25)

$$ {\overset{\frown }{\mathbf{R}}}_{ud}^n={\mathbf{R}}_{ud}^n+{\mathbf{T}}_{uu}^n{\overset{\frown }{\overline{\mathbf{R}}}}_{ud}^{n+1}{\overset{\frown }{\mathbf{T}}}_{dd}^n $$

(26)

where ${\overset{\frown }{\overline{\mathbf{R}}}}_{ud}^{n+1}={\mathbf{E}}^{n+1}\left({h}_{n+1}\right){\overset{\frown }{\mathbf{R}}}_{ud}^{n+1}{\mathbf{E}}^{n+1}\left({h}_{n+1}\right)$.

According to the boundary conditions at the seabed bottom, the following equation is obtained:

$$ {\mathbf{L}}_{11}^N{\mathbf{W}}_d^N\left({k}_x,{z}_N,\omega \right)+{\mathbf{L}}_{12}^N{\mathbf{W}}_u^N\left({k}_x,{z}_N,\omega \right)=\mathbf{0} $$

(27)

Following Eq. (24), ${\overset{\frown }{\mathbf{R}}}_{ud}^N$ can be derived from Eq. (13):

$$ {\overset{\frown }{\mathbf{R}}}_{ud}^N=-{\left[{\mathbf{L}}_{12}^N\right]}^{-1}{\mathbf{L}}_{11}^N $$

(28)

Then, ${\overset{\frown }{\mathbf{R}}}_{ud}^n\left({k}_x,\omega \right)$ and ${\overset{\frown }{\mathbf{T}}}_{dd}^n\left({k}_x,\omega \right)$ can be determined based on Eq. (25) and Eq. (26).

Furthermore, using the boundary conditions at the seabed surface, the following equation is obtained:

$$ {\mathbf{L}}_{21}^1{\mathbf{W}}_d^1\left({k}_x,0,\omega \right)+{\mathbf{L}}_{22}^1{\mathbf{W}}_u^1\left({k}_x,0,\omega \right)=\hat{\overline{\mathbf{F}}}\left({k}_x,\omega \right) $$

(29)

where $\hat{\overline{\mathbf{F}}}\left({k}_x,\omega \right)={\left[0,\kern0.5em 0,\kern0.5em {\hat{\overline{P}}}_b\right]}^T$.

Combining Eq. (24) and Eq. (29) yields

$$ {\mathbf{W}}_d^1\left({k}_x,0,\omega \right)={\left[{\mathbf{L}}_{21}^1+{\mathbf{L}}_{22}^1{\mathbf{E}}^1\left({h}_1\right){\overset{\frown }{\mathbf{R}}}_{ud}^1{\mathbf{E}}^1\left({h}_1\right)\right]}^{-1}\hat{\overline{\mathbf{F}}}\left({k}_x,\omega \right) $$

(30)

After the down-going wave vector ${\mathbf{W}}_d^1\left({k}_x,0,\omega \right)$ in the top layer is determined, it is straightforward to obtain all the down-going and up-going wave vectors in an arbitrary layer using Eq. (23) and Eq. (24). Moreover, after determining the wave vectors of an arbitrary layer, the displacement and stress can be given by Eq. (17). It should be noted that the horizontal normal stress, ${\tilde{\sigma}}_{xx}^{\prime n}$, is needed to analyze the seabed dynamic response. Based on the obtained displacement and the constitutive equation (Eq. 1), ${\tilde{\sigma}}_{xx}^{\prime n}$ can be derived as follows:

$$ {\tilde{\sigma}}_{xx}^{\prime n}=\left[{\mathbf{L}}_{xx1}^n\kern0.5em {\mathbf{L}}_{xx2}^n\right]{\left[\begin{array}{cc}{\mathbf{W}}_d^n{\left({k}_x,z,\omega \right)}^T& {\mathbf{W}}_u^n{\left({k}_x,z,\omega \right)}^T\end{array}\right]}^T $$

(31)

where the expressions of ${\mathbf{L}}_{xx1}^n$and ${\mathbf{L}}_{xx2}^n$ are given as follows:

$$ {\mathbf{L}}_{xx1}^n=\left[{H}_n{\left({k}_1^n\right)}^2+2{\mu}_n{\left({a}_1^n\right)}^2\kern0.5em {H}_n{\left({k}_2^n\right)}^2+2{\mu}_n{\left({a}_2^n\right)}^2\kern0.5em 2{\mu}_n{k}_x{b}^n\right] $$

(32)

and

$$ {\mathbf{L}}_{xx2}^n=\left[{H}_n{\left({k}_1^n\right)}^2+2{\mu}_n{\left({a}_1^n\right)}^2\kern0.5em {H}_n{\left({k}_2^n\right)}^2+2{\mu}_n{\left({a}_2^n\right)}^2\kern0.5em -2{\mu}_n{k}_x{b}^n\right] $$

(33)

The expressions of the variables in Eq. (32) and Eq. (33) are included in the Appendix.

The time domain solution can be further derived. Let $\hat{\overline{\varOmega}}\left({k}_x,z,\omega \right)$ represent all the wavenumber-frequency domain variables; thus, $\hat{\overline{\varOmega}}\left({k}_x,z,\omega \right)$ due to combined wave and current loading can be expressed as:

$$ \hat{\overline{\varOmega}}\left({k}_x,z,\omega \right)={\hat{\overline{\varOmega}}}^{\ast}\left({k}_x,z,\omega \right){\hat{\overline{P}}}_b $$

(34)

where ${\hat{\overline{\varOmega}}}^{\ast}\left({k}_x,z,\omega \right)$ denotes Green’s function of the seabed dynamic response to a vertical force with unit magnitude acting on the seabed surface.

Applying the double-inverse Fourier transform to Eq. (34) and using the Dirac δ function yields

$$ {\displaystyle \begin{array}{l}\varOmega \left(x,z,t\right)={\left(\frac{1}{2\pi}\right)}^2{\int}_{-\infty}^{\infty }{\int}_{-\infty}^{\infty }{\hat{\overline{\varOmega}}}^{\ast}\left({k}_x,z,\omega \right){\hat{\overline{P}}}_b{e}^{i\left(\omega t-{k}_xx\right)} d\omega d{k}_x\\ {}\kern3.5em =\frac{1}{2}\sum \limits_{m=1}^3{\int}_{-\infty}^{\infty }{\int}_{-\infty}^{\infty }{\hat{\overline{\varOmega}}}^{\ast}\left({k}_x,z,\omega \right){P}_m\Big[\delta \left(\omega +m{\omega}_0\right)\delta \left({k}_x-m{k}_0\right)\\ {}\kern8em +\delta \left(\omega -m{\omega}_0\right)\delta \left({k}_x+m{k}_0\right)\Big]{e}^{i\left(\omega t-{k}_xx\right)} d\omega d{k}_x\\ {}\kern3.5em =\frac{1}{2}\sum \limits_{m=1}^3{P}_m\left[{\hat{\overline{\varOmega}}}^{\ast}\left(m{k}_0,z,-m{\omega}_0\right){e}^{- im\left(\omega t-{k}_0x\right)}+{\hat{\overline{\varOmega}}}^{\ast}\left(-m{k}_0,z,m{\omega}_0\right){e}^{im\left(\omega t-{k}_0x\right)}\right]\end{array}} $$

(35)

where Ω(x, z, t) represents all the spatial-temporal domain variables.

Model validation

To validate the model, an analytical solution proposed by Hsu et al. (1995) and a laboratory model test conducted by Lu (2005) are adopted.

Hsu et al. (1995) presented an analytical solution to wave-induced response of a two-layer seabed. The input data are listed in Table 1. Figure 3 shows the profiles of the absolute value of wave-induced pore pressure, where p₀ is the maximum pressure acting on the seabed surface. In Fig. 3, the markers denote the results reported by Hsu et al. (1995), and the solid lines represent the results in this study, which agree very well for various conditions.

Table 1 Input data for model validation (Hsu et al. 1995)

Fig. 3

Comparison between the solution proposed by Hsu et al. (1995) (markers) and the solution in this study (solid lines)

Lu (2005) conducted a series of laboratory tests to investigate the dynamic response of a homogeneous sand bed to waves in a flume which was 60 m long, 1.5 m wide and 1.8 m high. The sand bed consisted of coarse sand. The pore pressure at four points with depth was monitored in the tests. The characteristics of the regular wave were H = 12 cm, d = 0.4 m and T = 1.2 s. The sand properties reported by Lu (2005) were as follows: shear modulus μ = 10⁷ N/m², Possion’s ratio ν = 0.3, permeability k = 10⁻³ m/s, porosity ϕ = 0.39, mean size of sand particles d₅₀ = 0.44 mm and degree of saturation S_r = 98%. The comparison of the wave-induced dynamic pore pressure at the four points between the present analytical solution and the experimental data of Lu (2005) is shown in Fig. 4, which shows good agreement.

Fig. 4

Comparison between the experimental data reported by Lu (2005) (markers) and the solution in this study (solid lines)

Response and stability of the multilayered seabed under combined wave and current loading

The dynamic pore pressure, vertical effective stress, horizontal effective stress and shear stress induced by combined wave and current loading can be obtained by Eq. (35). In order to investigate the response of the multilayered seabed and seabed stability under combined wave and current loading, it is meaningful to conduct a comprehensive parametric study. Two groups of parameters involved in the analytical solution need be specified as follows.

• (1) Wave and current parameters: current velocity U₀, wave height H, wave period T and water depth d. These parameters determine the wavelength through the wave dispersion relationship as shown in Eqs. (7–9).

• (2) Soil properties: soil permeability k_n, shear modulus μ_n, Poisson’s ratio ν_n, porosity ϕ_n, solid skeleton density ρ_sn, pore fluid density ρ_fn, degree of saturation S_rn and thickness of sub-layer h_n, where the subscript n denotes the n-th layer of the multilayered seabed. Among these parameters, the soil permeability, shear modulus and degree of saturation play dominant roles (Jeng and Cha 2003; Ye and Jeng 2012; Wang et al. 2018).

In the following part, without special mention, a three-layer seabed is adopted. The total thickness of the three layers is 30 m, and the thickness of each sub-layer is 10 m. The values of the needed parameters are enclosed in Table 2. If the influence of a specific parameter is investigated, the value of the parameter is changeable and will be specified.

Table 2 Input data for parametric study

Effect of soil layering

In this section, four different cases are first studied as shown in Fig. 5. Case 1 considers a single-layer seabed and wave loading. Case 2 considers a three-layer seabed and wave loading. Case 3 considers a single-layer seabed and combined wave and current loading. Case 4 considers a three-layer seabed and combined wave and current loading. For the single-layer seabed cases, the permeability is 10⁻² m/s. For the three-layer seabed cases, the permeability of three sub-layers (k₁, k₂ and k₃) are 10⁻⁴, 10⁻³ and 10⁻² m/s, respectively. Figure 5a illustrates the vertical distributions of the maximum pore pressure in the seabed for the four different cases. The pore pressure of the single-layer case in the upper part (i.e. approximately z/h = 0.4) is larger than that of the respective three-layer case. The variation is contrary in the deeper part. The difference of other stress responses in the upper part of the seabed between single-layer cases and three-layer cases is also significant, as shown in Fig. 5b, 4c, d. It can be concluded that soil layering significantly affects the dynamic response of the seabed for both sole wave loading condition and wave-current loading condition. More detailed influence of properties of layered soil is illustrated as follows.

Fig. 5

Effect of soil layering and current on the dynamic response of the seabed: (a) pore pressure; (b) vertical effective stress; (c) shear stress; (d) horizontal effective stress

Seabed soil is characterized by wide range of shear modulus and has been studied by some researchers (e.g. Zhou et al. 2011). In order to investigate the effect of shear modulus on the seabed response, the shear modulus of the three-layer seabed is assumed as follows: (1) case A1: μ₁:μ₂:μ₃ = 0.5:1:2; (2) case A2: μ₁:μ₂:μ₃ = 1:1:1 and (3) case A3: μ₁:μ₂:μ₃ = 2:1:0.5, where μ₂ = 10⁷ N/m². Figure 6 shows the dynamic response with depth of the seabed to combined wave and current loading. It is noteworthy that the results for cases A1 and A3 have a sharp change at z/h = 1/3 and 2/3 (the two interfaces), which further confirms the effect of soil layering. Figure 6b shows that the vertical effective stress of case A3 is significantly smaller than that of case A1 when z/h is smaller than 2/3, and the variation is contrary when z/h is larger than 2/3. Figure 6c shows that the shear stress of case A3 is overall greatly larger than that of case A1. Therefore, the shear modulus has substantial influence on the seabed response, and different distribution of the shear modulus leads to significantly different pore pressure and stress state in the seabed.

Fig. 6

Seabed response for various shear modulus combinations (μ₂ = 10⁷ N/m²): (a) pore pressure; (b) vertical effective stress; (c) shear stress; (d) horizontal effective stress

Soil permeability is a vital factor for seabed response. Herein, three permeability combinations are studied: (1) case B1: k₁:k₂:k₃ = 0.1:1:10, (2) case B2: k₁:k₂:k₃ = 1:1:1 and (3) case B3: k₁:k₂:k₃ = 10:1:0.1, where k₂ = 10⁻³ m/s. Figure 7 shows the seabed response for various seabed permeability combinations to combined wave and current loading. The effect of permeability is significant in the upper part of the seabed (z/h is approximately larger than 0.6, 0.5, 0.7 and 0.4 for pore pressure, vertical effective stress, shear stress and horizontal effective stress, respectively), and the effect can be ignored in the respective lower part. Figure 7a–d shows that pore pressure, shear stress and horizontal effective stress of case B3 are larger than those of case B1 in the upper part, while variation of the vertical effective stress is contrary. Therefore, the permeability highly affects the flow of pore fluid and the conduction of pore pressure, and different distribution of permeability leads to significantly different pore pressure and stress states in the seabed.

Fig. 7

Seabed response for various seabed permeability combinations (k₂ = 10⁻³ m/s): (a) pore pressure; (b) vertical effective stress; (c) shear stress; (d) horizontal effective stress

The presence of gas in marine sediment can affect the compressibility of the seabed. Therefore, the degree of saturation is another important factor in the seabed response. Figure 8 illustrates the vertical distributions of the relative difference of pore pressure for various degrees of saturation under combined wave and current loading. The pore pressure substantially increases with increasing degree of saturation for all the permeability combinations. The reason is that the compressibility of gas is extremely larger than that of the seawater. Comparison among Fig. 8a–c further confirms the effect of permeability on the seabed response.

Fig. 8

Vertical distributions of the relative difference of pore pressure for various degrees of saturation (k₂ = 10⁻³ m/s)

Effect of current and waves

Comparison between wave loading cases and wave-current loading cases shows that the effect of current on pore pressure and vertical effective stress is significant (see Fig. 5a, b). In Fig. 5c, it is interesting that soil layering mainly affects the shear stress in the upper part of the seabed, while current mainly affects that in the lower part. Since shear stress is very important for evaluating seabed stability, it is essential to consider the effect of soil layering and current together on the seabed response and stability.

Current velocity is an important parameter for evaluating the seabed response (Ye and Jeng 2012). In this study, the effect of current velocity in a three-layer seabed is investigated. Vertical distributions of relative difference of the wave-current induced response are shown in Figs. 9 and 10 for two kinds of permeability combinations. The first kind of combination is k₁ = 10⁻² m/s, k₂ = 10⁻³ m/s and k₃ = 10⁻⁴ m/s, while the second one is k₁ = 10⁻⁴ m/s, k₂ = 10⁻³ m/s and k₃ = 10⁻² m/s. Figures 9 and 10 indicate that a following current notably increases the pore pressure and the vertical effective stress, and an opposing current significantly decreases them. For shear stress, the variation is similar in medium and deep parts of the seabed, but is contrary in the very shallow part (Figs. 9c, 10c). The larger the magnitude of the current velocity is, the more significant the phenomena will be. This implies that a following current is more likely to make the seabed unstable. Figures 9 and 10 also show that even for the same magnitude of current velocity, the relative differences of the seabed response to opposing current are overall greater than those to the following current. The results are consistent with previous studies for a single-layer seabed (Ye and Jeng 2012).

Fig. 9

Seabed response for various current velocities (k₁, k₂, k₃ = 10⁻², 10⁻³, 10⁻⁴ m/s): (a) pore pressure; (b) vertical effective stress; (c) shear stress; (d) horizontal effective stress

Fig. 10

Seabed response for various current velocities (k₁, k₂, k₃ = 10⁻⁴, 10⁻³, 10⁻² m/s): (a) pore pressure; (b) vertical effective stress; (c) shear stress; (d) horizontal effective stress

The effect of wave characteristics on the seabed response is shown in Figs. 11 and 12. Figure 11 illustrates the vertical distributions of the relative difference of pore pressure for various wave periods. For all three permeability combinations, a medium wave period (i.e. T = 8 s) overall generates the largest pore pressure. With the wave period further increasing (i.e. T = 12, 15 s), the variation of pore pressure becomes stable, but is notably larger than that of the small wave period case (i.e. T = 5 s) in the deeper part (z/h > 0.2). As for water depth, Fig. 12 reveals that its influence is not significant.

Fig. 11

Vertical distributions of the relative difference of pore pressure for various wave periods (k₂ = 10⁻³ m/s)

Fig. 12

Vertical distributions of the relative difference of pore pressure for various water depths (k₂ = 10⁻³ m/s)

Seabed stability under combined wave and current loading

It is well known that soil may liquefy instantaneously under dynamic loading because of the buildup of excess pore pressure (Liao et al. 2018; Chen et al. 2019; Feng et al. 2019b). To investigate the potential of instantaneous liquefaction in the seabed under combined wave and current loading, the liquefaction criterion proposed by Zen and Yamazaki (1990) is adopted, which is expressed as

$$ \left({\gamma}_s-{\gamma}_w\right)z-\left[{P}_b\left(x,t\right)-p\left(x,z,t\right)\right]\le 0 $$

(36)

where γ_s and γ_w are the unit weights of soil and water, respectively. In this section, the wave height is 6 m, and the other needed parameters are enclosed in Table 2, except for permeability.

Figure 13 shows the liquefied zone in the seabed under various conditions. The magnitudes of opposing and following current velocities are both 2 m/s. In Fig. 13, only the upper part of the seabed can liquefy. For all the three permeability combinations, the liquefied zone enlarges as the current changes from opposing current to following current, which implies that the opposing current is beneficial to prevent soil liquefaction, and the following current is harmful. It should be noted that the liquefied zone is smaller if the upper layer is more permeable. The reason is that larger permeability is beneficial for dissipation of pore pressure.

Fig. 13

Soil liquefaction zone in the seabed under combined wave and current loading: (a) k₁, k₂, k₃ = 10⁻², 10⁻³, 10⁻⁴ m/s; (b) k₁, k₂, k₃ = 10⁻³, 10⁻³, 10⁻³ m/s; (c) k₁, k₂, k₃ = 10⁻⁴, 10⁻³, 10⁻² m/s

To investigate the potential of shear failure in the seabed under combined wave and current loading, the Mohr–Coulomb failure criterion is adopted. Shear failure occurs when stress angle ϕ_s is larger than the internal friction angle ϕ_u. For sandy soils, the stress angle is related to effective stresses and shear stress of the soil, and can be expressed as

$$ \sin {\phi}_s=\frac{\sqrt{{\left({\sigma}_{oz}^{\prime }-{\sigma}_{ox}^{\prime}\right)}^2+4{\sigma}_{zx}^2}}{\left({\sigma}_{oz}^{\prime }+{\sigma}_{ox}^{\prime}\right)} $$

(37)

where ${\sigma}_{oz}^{\prime }$ and ${\sigma}_{ox}^{\prime }$ are vertical and horizontal effective normal stresses induced by wave-current loading and the self-weight of the soil, respectively, and σ_zx is the shear stress induced by wave-current loading.

Figure 14 shows the stress angle in the seabed under the combined wave and current loading. The shear failure zone expands as the current changes from opposing current to following current. Thus, the opposing current is beneficial to prevent both soil liquefaction and shear failure, and the following current is more likely to cause seabed instability. Figure 14 also reveals that larger permeability in the upper layer leads to smaller shear failure zone, which further confirms the effect of soil layering.

Fig. 14

Stress angle in the seabed under combined wave and current loading: (a) k₁, k₂, k₃ = 10⁻², 10⁻³, 10⁻⁴ m/s; (b) k₁, k₂, k₃ = 10⁻³, 10⁻³, 10⁻³ m/s; (c) k₁, k₂, k₃ = 10⁻⁴, 10⁻³, 10⁻² m/s

Summary and conclusions

In this paper, an analytical solution to the response of a multilayered seabed to combined wave and current loading is proposed. The seabed is modeled using Biot’s fully dynamic theory, where the inertia effects and compressibility of solids and fluids are included. The correctness and accuracy of the proposed method are validated against an existing analytical solution and a model test. The effects of several important factors are then comprehensively investigated in terms of pore pressure, effective stresses and shear stress. Some major conclusions can be drawn as follows.

Soil layering significantly affects the dynamic response of the seabed for both sole wave loading condition and wave-current loading condition. A seabed with layered soil properties (e.g. shear modulus, permeability) has a substantially different pore pressure and stress state from a homogeneous seabed under combined wave and current loading. The liquefied zone and shear failure zone in the seabed are smaller if the upper layer is more permeable. It is noteworthy that the pore pressure obviously increases with the increase of degree of saturation.

Current substantially influences the seabed response. A current with medium wave period (e.g. T = 8 s in this study) generates the largest pore pressure. A following current notably increases the pore pressure, vertical effective stress and shear stress, and an opposing current significantly decreases them. The overall effect of current on seabed stability is also evaluated. The results indicate that the opposing current is beneficial to prevent both soil liquefaction and shear failure, and the following current is more likely to cause seabed instability.

Appendix

The solution matrices ${\mathbf{L}}_{11}^n$, ${\mathbf{L}}_{12}^n$, ${\mathbf{L}}_{21}^n$ and ${\mathbf{L}}_{22}^n$ in Eq. (17) can be given as follows:

$$ {\mathbf{L}}_{11}^n=\left(\begin{array}{ccc}-\mathrm{i}{k}_x& -\mathrm{i}{k}_x& -\mathrm{i}{b}^n\\ {}-{a}_1^n& -{a}_2^n& -{k}_x\\ {}-{\xi}_1^n{a}_1^n& -{\xi}_2^n{a}_2^n& -{\xi}_s^n{k}_x\end{array}\right) $$

(A1)

$$ {\mathbf{L}}_{12}^n=\left(\begin{array}{ccc}-\mathrm{i}{k}_x& -\mathrm{i}{k}_x& \mathrm{i}{b}^n\\ {}{a}_1^n& {a}_2^n& -{k}_x\\ {}{\xi}_1^n{a}_1^n& {\xi}_2^n{a}_2^n& -{\xi}_s^n{k}_x\end{array}\right) $$

(A2)

$$ {\mathbf{L}}_{21}^n=\left(\begin{array}{ccc}2{\mu}_n{k}_x\mathrm{i}{a}_1^n& 2{\mu}_n{k}_x\mathrm{i}{a}_2^n& 2{\mu}_n{\varOmega}_n\mathrm{i}\\ {}2{\mu}_n{k}_x^2-{H}_n{\left({k}_1^n\right)}^2& 2{\mu}_n{k}_x^2-{H}_n{\left({k}_2^n\right)}^2& 2{\mu}_n{k}_x{b}^n\\ {}{M}_n\left(1+{\xi}_1^n\right){\left({k}_1^n\right)}^2& {M}_n\left(1+{\xi}_2^n\right){\left({k}_2^n\right)}^2& 0\end{array}\right) $$

(A3)

$$ {\mathbf{L}}_{22}^n=\left(\begin{array}{ccc}-2{\mu}_n{k}_x\mathrm{i}{a}_1^n& -2{\mu}_n{k}_x\mathrm{i}{a}_2^n& 2{\mu}_n{\varOmega}_n\mathrm{i}\\ {}2{\mu}_n{k}_x^2-{H}_n{\left({k}_1^n\right)}^2& 2{\mu}_n{k}_x^2-{H}_n{\left({k}_2^n\right)}^2& -2{\mu}_n{k}_x{b}^n\\ {}{M}_n\left(1+{\xi}_1^n\right){\left({k}_1^n\right)}^2& {M}_n\left(1+{\xi}_2^n\right){\left({k}_2^n\right)}^2& 0\end{array}\right) $$

(A4)

where

$$ {a}_1^n=\sqrt{k_x^2-{\left({k}_1^n\right)}^2},{a}_2^n=\sqrt{k_x^2-{\left({k}_2^n\right)}^2},{b}^n=\sqrt{k_x^2-{\left({k}_s^n\right)}^2} $$

(A5)

$$ {H}_n={\lambda}_n+2{\mu}_n,{\varOmega}_n={k}_x^2-{\left({k}_s^n\right)}^2/2 $$

(A6)

$$ {\xi}_{1,2}^n=\frac{\left({\lambda}_n+{M}_n+2{\mu}_n\right){\left({k}_{1,2}^n\right)}^2-{\rho}^n{\omega}^2}{\rho_f^n{\omega}^2-{M}_n{\left({k}_{1,2}^n\right)}^2},{\xi}_s^n=-\frac{\rho_f^n}{\gamma_n} $$

(A7)

$$ {M}_n={K}_f^{\prime }/{\phi}_n,{\gamma}_n=\frac{\rho_f^n}{\phi_n}-\frac{\mathrm{i}{\rho}^ng}{\omega {k}_n} $$

(A8)

$$ {\left({k}_{1,2}^n\right)}^2=\frac{B_n\mp \sqrt{B_n^2-4{A}_n{C}_n}}{2{A}_n},{\left({k}_s^n\right)}^2=\frac{C_n}{\mu^n{\gamma}_n{\omega}^2} $$

(A9)

$$ {A}_n={M}_n\left({\lambda}_n+2{\mu}_n\right) $$

(A10)

$$ {B}_n=\left[{\gamma}_n\left({\lambda}_n+{M}_n^2+2{\mu}_n\right)+{M}_n\left({\rho}_n-2{\rho}_f^n\right)\right]{\omega}^2 $$

(A11)

$$ {C}_n=\left[{\rho}_n{\gamma}_n-{\left({\rho}_f^n\right)}^2\right]{\omega}^4 $$

(A12)