Introduction

Over the past 20 years,numerous marine structures, such as breakwater, have been constructed offshore. The stability of offshore marine structures under ocean wave loading is the main concern of ocean engineers involved in design. Understanding of the dynamic response characteristics of seabed foundation for ocean waves is a key factor when evaluating the stability of offshore structures during their service period.

In the offshore environment, newly deposited Quaternary seabed soil is widely distributed, for example, the loose silty soil in the zone of the estuary of the Yellow River in China. A great number of offshore structures have been built on Quaternary sediment worldwide. The particle arrangement of Quaternary seabed soil generally is relatively loose. Under cyclic ocean wave loading (wave height must be great enough, resulting in wave-induced cyclic shear stress ratio \(\tau /\sigma ^\prime _0\) at a position in the seabed that is greater than a critical magnitude, which can make contractive plastic deformation occur in seabed soil. This critical magnitude of cyclic shear stress ratio \(\tau /\sigma ^\prime _0\) is dependent on the relative density \(D_r,\) property, etc. of seabed soil, soil particles would re-arrange their relative positions to a more dense status, accompanying a pore water drainage process (some pore water in a seabed is drained out through the seabed surface driven by an upward pore pressure gradient, making room for soil particles to re-arrange their relative position). In this process, pore water pressure builds up, making soil liquefy, or soften. Therefore, it would bring great risk to build a marine structure on a newly deposited Quaternary seabed floor. In this study, the wave-induced dynamic response characteristics of newly deposited seabed soil, rather than very dense seabed soil (elastic deformation is dominant) is exactly the focus.

On the problem of wave–seabed interaction, there have been a series of investigations in the previous literature. An analytical solution was first proposed to study the wave-induced dynamics of seabed soil based on Biot’s theory. Due to the limitation of analytical methods, seabed soil must be very dense soil in which elastic deformation was dominant under wave loading. Dense seabed soil could be infinite (Yamamoto et al. 1978; Madsen 1978) or finite (Hsu and Jeng 1994; Jeng and Hsu 1996) in depth; also the seabed could be isotropic or anisotropic, and one layer or multi-layers (Zhou et al. 2013). The ocean wave (progressive wave, standing wave or short-crested wave Hsu and Jeng 1994) adopted in these analytical solutions were all derived based on Stokes wave theory. The governing equation for seabed soil dynamics used was the consolidation equation, ‘\(u-p\)’ approximation, or the ‘\(u-w\)’ equation (Liao et al. 2015). Generally, the uncoupled method was adopted in the abovementioned analytical solutions. There was no feedback from seabed soil to ocean wave when seabed soil responded to wave loading. Fortunately, there were also a few coupled analytical solutions that were proposed for wave–seabed interaction (Lee et al. 2002), in which the continuity of pore pressure and fluid exchange on the seabed surface could be considered. However, the existence of offshore structures on the seabed floor could not be taken into consideration.

In addition to the analytical solution, a numerical solution was also a useful tool to investigate the wave-induced dynamics of seabed soil. In the early stages, an elastic soil model was used to describe the dynamics of seabed soil in most of the previous literature (Jeng 2003), assuming seabed soil was in a very dense state. Naturally, very dense seabed soil rarely exists in offshore areas. Newly deposited seabed soil should be a concern of ocean engineers involved in structure design. Due to the flexibility of the numerical model, it was possible to describe the nonlinear behavior of loose seabed soil adopting some advanced soil models. In the previous literature, there were basically two types of methods widely used to study the pore pressure response in loose seabed soil for wave loading. The first method was based on the following governing equation:

$$\begin{aligned} \frac{\partial p}{\partial t}=c_v \bigtriangledown ^2 p+f \end{aligned},$$
(1)

where p was the pore pressure in loose seabed, and \(c_v\) was the consolidation coefficient. f was a source term to describe the mechanism of pore pressure buildup in loose seabed soil under wave loading. It was expressed by Seed et al. (1976) and Seed and Rahman (1978) as

$$\begin{aligned} f=\frac{\sigma ^\prime _{z0}}{N_L}\frac{1}{T}, \end{aligned}$$
(2)

where \(\sigma ^\prime _{z0}\) was the initial vertical effective stress. T was the period of wave loading. \(N_L\) was the cyclic number of loading making loose soil reach the liquefaction state. Generally, It was directly related to the shear stress ratio \(\tau /\sigma ^\prime _{z0}.\) \(N_L\) could be determined by fitting and regressing laboratory dynamic test data for the soil, following:

$$\begin{aligned} N_L=\left( \frac{1}{a}\frac{\tau }{\sigma ^\prime _{z0}}\right) ^{\frac{1}{b}}. \end{aligned}$$
(3)

in which \(\tau\) was the amplitude of shear stress; a and b were the fitting coefficients. Generally, they were dependent on the relative density of soil \(D_r.\)

Some researchers have successfully obtained the closed form solution of Eq. (1) using an analytical method for the problem of pore pressure buildup in loose seabed soil under ocean wave loading (Rahman and Jaber 1986; Cheng et al. 2001). However, their solutions basically were only limited to one-dimensional cases. For 2-D or 3-D cases, numerical methods were widely used to solve this type of problem (Li and Jeng 2008). In most previous investigations, regardless of analytical or numerical solution, the amplitude of wave-induced shear stress in a seabed (used in Eq. (1)), was determined by poro-elastic theory, assuming that the seabed soil was very dense. This assumption was contradictory with the mechanism of pore pressure build up in loose seabed soil. There were two reasons for this contradiction. Firstly, elastic deformation was not the dominant component in a loose seabed under ocean wave loading; secondly, wave-induced shear stress in a loose seabed should gradually reduce in the process of pore pressure build-up. When seabed liquefied at a position, shear stress at this position should become zero finally (Ye and Wang 2015, 2016). This dynamic response mechanism of loose seabed soil could not be effectively described by poro-elastic theory. The amplitude of wave-induced shear stress in a seabed determined by poro-elastic theory was a constant, rather than a decreasing value. As a result, the action of an ocean wave in loose seabed was highly overestimated if shear stress was determined by poro-elastic theory; and the pore pressure ratio \(r_u=p_\mathrm{{excess}}/\sigma ^\prime _{z0}\) in sandy seabed soil could be much greater than 1.0, maybe at 3.0–5.0 (Jeng and Zhao 2015), (of course, \(r_u\) could be reasonably a little greater than 1.0 in cohesive soil). Obviously, this poro-elastic theory based method was insufficient to study the dynamic characteristics of loose seabed soil in regard to ocean wave. Until recently, there were still several similar works published adopting poro-elastic theory to determine wave-induced shear stress in loose seabed, and further estimating the pore pressure buildup process.

The second method was that elasto-plastic constitutive soil models were used to describe the nonlinear behaviour of loose seabed soil under wave loading. Sassa et al. (2001) proposed an effective model to study the pore pressure buildup in loose seabed soil under wave loading based on the concept of a two-layer fluid system and a moving boundary. A simplified constitutive equation

$$\begin{aligned} \frac{\mathrm{{d}}v^{{p}}}{\mathrm{{d}}t}=\beta \left[ v^{{p}}_{\infty }\left( \frac{\tau }{\sigma ^\prime _z}\right) -v^p\right] \end{aligned}$$
(4)

was used to describe the plastic volume strain rate of loose seabed soil under cyclic loading, in which \(v^{{p}}\) was plastic volume strain, “\(\infty\)” represented the ultimate state. Even though the above constitutive equation is simple, the predicted results of pore pressure buildup agreed with test data very well. However, effective stress in loose seabed could not be determined by this model proposed by Sassa et al. (2001); After that, several similar works have also been conducted by Liu et al. (2009) and Xu and Dong (2011) to extend Sassa’s model to two dimensions and the random ocean wave case. Oka et al. (1994) developed a FEM model incorporating a nonlinear elasto-plastic constitutive soil model to study the dynamics of loose seabeds regarding linear ocean wave adopting a one-dimensional case. Similar work was also performed by Lu and Cui (2004). After that, Dunn et al. (2006) investigated the wave-induced liquefaction in loose seabed around buried pipelines under linear progressive water waves, adopting a widely verified advanced soil model Pastor–Zienkiewicz Model Mark-III (PZIII) proposed by Zienkiewicz and Mroz (1984) and Pastor et al. (1990). Ou (2009) and Jeng and Ou (2010) further extended the PZIII model from 2-D to 3-D. Their work promoted the investigation of wave-induced liquefaction in loose seabeds to a new level. The purpose of this study is to further explore and reveal the dynamic response characteristics of loose seabeds for ocean waves in the same framework, letting us more deeply understand the mechanism of wave-induced liquefaction in loose seabeds.

As a type of offshore structure, breakwaters are widely constructed to protect harbors, regulate sediments transportation, etc. In front of a breakwater, a standing wave generally is formed if an incident wave is perpendicular to the breakwater. Actually, a standing wave is more dangerous than a short-crested wave (oblique reflection) for the stability of breakwater if wave parameters are the same. Therefore, it is meaningful to study the standing wave-induced dynamics of loose seabed foundation. Some laboratory wave flume tests have been conducted for this problem (Wang et al. 2014; Kirca et al. 2013). However, only the result of pore pressure and some qualitative phenomena have been observed. Presently, it is short of numerical results on this problem to comprehensively and deeply understand the response characteristics of loose seabed foundation for standing waves.

In this study, taking a semi-coupled numerical model FSSI–CAS 2D (Ye et al. 2013) as the tool, the standing wave-induced liquefaction mechanism of newly deposited loose seabed soil is investigated. The advanced soil constitutive model—Pastor–Zienkiewicz Mark III (PZIII) proposed by Pastor et al. (1990) is used to describe the complicated nonlinear dynamic behaviour of loose seabed soil. The change of void ratio e,  and corresponding permeability k of soil is considered in this computation. Additionally, the stiffness matrix [K] highly depending on an effective stress state is also updated using current effective stress in the computation, to fully consider the nonlinearity of the dynamics of loose seabeds regarding ocean waves. Results indicate that FSSI–CAS 2D incorporating the PZIII model has effectively and precisely captured a series of nonlinear dynamic response characteristics of loose seabeds for standing ocean waves.

Numerical model and constitutive model

Dynamic Biot’s equations known as the “\(u-p\)” approximation proposed by Zienkiewicz et al. (1980) are used to govern the dynamic response of the porous seabed soil under seismic wave loading:

$$\begin{aligned} \frac{\partial \sigma _x^\prime }{\partial x} + \frac{\partial \tau _{xz}}{\partial z} = - \frac{\partial p_s}{\partial x} +\rho \frac{\partial ^2 u_s}{\partial t^2} , \end{aligned}$$
(5)
$$\begin{aligned} \frac{\partial \tau _{xz}}{\partial x} + \frac{\partial \sigma _z^\prime }{\partial z} +\rho g= - \frac{\partial p_s}{\partial z} +\rho \frac{\partial ^2 w_s}{\partial t^2} , \end{aligned}$$
(6)
$$\begin{aligned} k \nabla ^2p_s -\gamma _w n \beta \frac{\partial p_s}{\partial t}+ k\rho _f \frac{\partial ^2 \epsilon _v}{\partial t^2} =\gamma _w \frac{\partial \epsilon _v}{\partial t}, \end{aligned}$$
(7)

where \((u_s, w_s)=\) the soil displacements in the horizontal and vertical directions, respectively; \(n=\) soil porosity; \(\sigma _x^\prime\) and \(\sigma _z^\prime =\) are effective normal stresses in the horizontal and vertical directions, respectively; \(\tau _{xz}=\) shear stress; \(p_s=\) the pore water pressure; \(\rho =\rho _fn+\rho _s(1-n)\) is the average density of porous seabed; \(\rho _f =\) the fluid density ; \(\rho _s =\) solid density; \(k=\) the Darcy’s permeability; \(g=\) the gravitational acceleration, \(\gamma _w\) is unit weight of water and \(\epsilon _v\) is the volumetric strain. In Eq. (7), the compressibility of pore fluid (\(\beta\)) and the volumetric strain (\(\epsilon _v\)) are defined as

$$\begin{aligned} \beta =\left( \frac{1}{K_f}+\frac{1-S_r}{p_{w0}}\right) , \quad {\text{ and }} \quad \epsilon _v =\frac{\partial u_s}{\partial x} +\frac{\partial w_s}{\partial z}, \end{aligned}$$
(8)

where \(S_r =\) the degree of saturation of the seabed, \(p_{w0} =\) the absolute static pressure and \(K_f =\) the bulk modulus of pore water, generally, \(K_f=2.24\times 10^9\) N/m\(^2.\) Here, the compressibility of pore fluid \(\beta\) is taken to consider the unsaturation of seabed soil, which is only applicable for nearly saturated soil. In fact, the saturation of seabed soil in offshore areas generally is greater than 90%, which is in the application range of \(\beta .\)

A Finite Element Model (FE) methodology is used to solve the above governing Eqs. (5)–(7), and the Generalized Newmark scheme (implicit scheme) is adopted to calculate time integration when solving the above governing equations (Chan 1988). For the problem of fluid–structure–seabed interaction (FSSI), an integrated numerical model FSSI–CAS 2D was developed by Ye (2012a). In FSSI–CAS 2D, the Volume Average Reynold Average Navier Stokes (VARANS) equation (Hsu et al. 2002) governs wave motion and porous flow in porous seabeds. The above dynamic Biot’s equation governs the dynamic behaviour of offshore structure and its seabed foundation. A coupled algorithm is developed to couple VARANS equation and Biot’s dynamics equation together. More detailed information about the coupled model can be found in Ye et al. (2013), Ye (2012a) and Zienkiewicz et al. (1999).

Void ratio e and the related Darcy’s permeability k of soil change are based on the deformation characteristics of granular materials. In the previous investigation, this variation process generally was not considered based on a small deformation assumption, namely, void ratio e and permeability k were kept constant. In this study, the standing wave-induced variation of the void ratio of seabed soil is considered to follow the formulation

$$\begin{aligned} e_{n+1}=(1+e_n)\exp {\left( \frac{\Delta p}{Q}+\Delta \epsilon _\mathrm{{vs}}\right) }-1\end{aligned},$$
(9)

which is established on the prospect of a large deformation, where n stands for \(n\mathrm{{th}}\) time step, \(\Delta p\) is the incremental pore pressure, \(\Delta \epsilon _\mathrm{{vs}}\) is the incremental volumetric strain of soil, and \(Q=1/\beta\) is the compressibility of pore water. Correspondingly, the permeability of seabed soil k changes following

$$\begin{aligned} k=C_f\frac{e^3}{1+e} \end{aligned},$$
(10)

where \(C_f\) is an empirical coefficient, determined by (Miyamoto et al. 2004)

$$\begin{aligned} C_f=k_0\frac{1+e_0}{e_0^3} \end{aligned},$$
(11)

where \(e_0\) is the initial void ratio. Additionally, the hydrostatic water pressure, as well as the hydrodynamic pressure acting on the seabed floor, as the boundary values in the FE computation, are variable, based on the wave-induced deformation of the seabed floor. Under wave loading, the void ratio of loose seabed soil would decrease, leading to the subsidence of the seabed surface. As a result, the hydrostatic pressure acting on the seabed surface would change, especially in the cases involving a large deformation.

A soil model Pastor–Zienkiewicz-Mark III (PZIII) proposed by Pastor et al. (1990) is adopted to describe the dynamic behavior of loose seabed soil under seismic wave loading. The reliability of PZIII has been validated by a series of laboratory tests involving monotonic and cyclic loading, especially by the centrifuge tests in the VELACS project (Zienkiewicz et al. 1999). This model is one part of the heritage of Olek Zienkiewicz (Pastor et al. 2011).

Verification

The validity and reliability of the developed semi-coupled numerical model FSSI–CAS 2D have been widely verified by Ye (2012a). Adopting the analytical solution proposed by Hsu and Jeng (1994), and a series of laboratory wave flume tests conducted by Lu (2005) for regular wave and cnoidal waves, by Tsai and Lee (1995) for standing wave, by Mizutani et al. (1998) for submerged breakwater, and by Mostafa et al. (1999) for composite breakwater, the developed semi-coupled numerical model FSSI–CAS 2D was used to reproduce the dynamic response of elastic seabed foundations and/or breakwaters. The good agreement between the predicted numerical results and the corresponding experimental data indicated that FSSI–CAS 2D was highly reliable for the problem of wave–seabed–structure interaction. Furthermore, the validity and reliability of FSSI–CAS 2D for the problem of wave-loose seabed soil interaction was also verified by a wave flume test (Teh et al. 2003) and a geotechnical centrifuge test (Sassa and Sekiguchi 1999). More detailed information about the verification work can be found in Ye (2012a); and related works have been published in Ye et al. (2013).

Computational domain, parameters, boundary conditions and hydrodynamic loading

Fig. 1
figure 1

Schematic of the computational domain, boundary conditions and hydrodynamic loading

Full size image

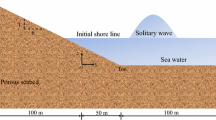
As illustrated in Fig. 1, a flat seabed 400m long and 20m thick is chosen as the computational domain (Noted: \(z=0\) is set at the bottom of the domain; and \(x=0\) is set at the left lateral side). The horizontal mesh size is 1 m; and it is 0.5 m vertically. In total, 12,000 4-nodes FE elements are generated. It has been illustrated by Ye et al. (2013) that numerical results of soil dynamics obtained by FSSI–CAS 2D are convergent, if the mesh size is less than L / 40,  where L is wave length. In this study, the wave length is about 70 m. Therefore, the mesh size used is in the range of convergence. In computation, the following boundary conditions are applied. First, the bottom of the seabed foundation is impermeable and fixed. Second, the two lateral sides are fixed only horizontally. Third, hydrostatic pressure is applied on the surface of the seabed. In each time step, the hydrostatic pressure acting on the seabed floor, which is as the boundary values on the seabed surface, is updated as \(p_s=\rho g d_0+\rho g s_v,\) where \(d_0\) is the initial water depth. \(s_v\) is the residual vertical subsidence plus the oscillatory vertical displacement of points on the seabed floor resulting from wave loading. Fourth, standing wave-induced dynamic pressure acting on the seabed is also applied accompanying hydrostatic pressure, expressed as a second-order formulation (Tsai et al. 2000 proved that the predicted results were much closer to experiment data if the nonlinearity of the standing wave was considered):

$$\begin{aligned} P_b(x,t)= & {} \frac{\rho _f gH}{\cosh \lambda d} \cos (\lambda x) \cos (\omega t) \nonumber \\&+\left\{ \frac{1}{8}\frac{\lambda H \cosh ^2(\lambda d)}{\sinh (\lambda d)} +\frac{3(\omega ^{-4}-\omega ^4)}{\cosh (2\lambda d)} \right\} \nonumber \\&\times \cos (2 \lambda x) \cos (2 \omega t) -\frac{1}{2}\lambda H \sinh (\lambda d) \cos (2 \omega t) \nonumber \\&+\frac{1}{8}\frac{\lambda H \cosh ^2(\lambda d)}{\sinh (\lambda d)} (1-\omega ^4) \cos (2 \lambda x) \end{aligned},$$
(12)

where \(\rho _f\) is the density of sea water, g is gravity, H is wave height, \(\lambda =2\pi /L\) is wave number, where L is wave length, and \(\omega =T/2\pi\) is angle frequency. Here, \(d=d_0+s_v\) is the immediate water depth. Figure 2 shows the nonlinear standing wave-induced hydrodynamic water pressure on the seabed floor in one period. It is observed that the distribution of hydrodynamic pressure on the seabed induced by the wave crest and the wave trough is clearly different. Furthermore, the hydrodynamic pressure under nodes does not always remain zero. It is indicated that there is an effect of nonlinearity of the standing wave on the hydrodynamic pressure. When applying the hydrostatic and hydrodynamic water pressure on the seabed floor, the effective stresses on the seabed surface must be guaranteed as 0.

Fig. 2
figure 2

Nonlinear standing wave-induced hydrodynamic water pressure on the seabed floor (\(H=1.5\) m, \(d_0=10\) m, \(T=8.0\) s)

Full size image

The parameters of loosely deposited seabed soil for the PZIII constitutive model are listed in Table 1, which were determined by Zienkiewicz et al. (1999) for Nevada sand (\(D_r=60\)%) when attending the VELACS project hosted by the American National Science Foundation (NSF). Actually, these model parameters for PZIII can be determined by conducting a series of laboratory tests for real soils sampled from the offshore seabed floor. The initial void ratio e,  saturation of seabed soil used in computation is 0.333, and 98%, respectively. Correspondingly, the initial permeability of seabed soil is \(1.0\times 10^{-5}\) m/s. The initial water depth \(d_0\) of sea water over the seabed floor is 10 m. Wave height and wave period are set as 1.5 m and 8.0 s, respectively. The symmetrical line \(x=200\) m is forced to exactly locate below an anti-node when applying the nonlinear standing wave in computation. Then the computational results on two lines \(x=200\) m under the anti-node and \(x=217.7\) m under the node are recorded, taking as the representatives to understand the dynamics of loose seabed soil under a standing wave.

Table 1 Model parameters of loose seabed soil for PZIII in analysis
Full size table

Results

In an offshore environment, the seabed soil generally experiences a long-term consolidation process under hydrostatic pressure. There is not any excess pore pressure in seabed soil before ocean wave loading is applied. This initial consolidation state is first determined (Ye 2012b). Then, it is taken as the initial condition for the following dynamic analysis. It is noted that the compression is taken as a negative value, and tension is taken as a positive value in this study.

Effective stresses and pore pressure

Analysis of wave-induced effective stresses and pore pressure in a seabed is the key to understanding the dynamics of loosely deposited offshore seabed soil for an ocean wave. Here, we focus our attention on the standing wave-induced response characteristics of effective stresses and pore pressure. Figures 3 and 4 show the time history of effective stresses and pore pressure at three typical buried depths on line \(x=200\) m (under the anti-node) and \(x=217.7\) m (under the node), respectively. In Fig. 3, it is clearly observed that pore pressure in loose seabed builds up under wave loading at the three buried depths. Correspondingly, mean effective stress \(I_1\) is reduced from their initial values, and then gradually approaches the liquefaction status. The build-up of pore pressure is not unlimited, it is highly related to overburdened soil weight. The residual pore pressure at \(z=18.5\) m (buried depth \(=\) 1.5 m) stops to build up at \(t=200\) s. After that, there is only oscillatory pore pressure under wave loading. Meanwhile, it is also found that the loose seabed soil at \(z=18.5\) m becomes partially liquefied (because the mean effective stress \(I_1\) is not zero) also at \(t=200\) s. It is proven that the stop of build-up of residual pore pressure is highly related to soil liquefaction. Additionally, it is also observed in Fig. 3 that the amplitude of wave-induced oscillatory pore pressure is inversely related to buried depth. The amplitude of oscillatory pore pressure at \(z=18.5\) m (buried depth \(=\) 1.5 m) is significantly greater than that at \(z=10\) m (buried depth \(=\) 10 m) and \(z=2\) m (buried depth \(=\) 18 m). Meanwhile, the magnitude of residual pore pressure build-up is positively related to buried depth.

Fig. 3
figure 3

Time history of pore pressure, mean effective stress and shear stress at three typical buried depths (18.5, 10.0, and 2.0 m) on \(x=200\) m under the anti-node

Full size image

For the seabed soil at \(z=18.5\) m, it becomes practically liquefied at \(t=200\) s under the standing wave loading. Until to about \(t=425\) s, the mean effective stress \(I_1\) completely becomes zero. This means the seabed soil at \(z=18.5\) m becomes fully liquefied. As we know, a fully liquefied soil behaves like a kind of heavy fluid. It cannot transmit shear waves. Correspondingly, the shear stress \(\tau _{xz}\) becomes zero from \(t=425\) s. It is indicated that the developed numerical model FSSI–CAS 2D incorporating the PZIII model could effectively simulate the post-liquefaction behavior of loose seabed soil to some extent. For the seabed soil at \(z=10\) m, residual pore pressure builds up 120 kPa, this means effective stress \(I_1\) decreases to about 2 kPa from its initial 80 kPa at \(t=500\) s. It is indicated that the seabed soil here also becomes partially liquefied when \(t=500\) s. For the seabed soil at \(z=2\) m, its residual pore pressure only builds up 125 kPa, its mean effective stress \(I_1\) is about 82 kPa at \(t=500\) s, which is far away from zero stress status. The seabed soil at \(z=2\) m does not liquefy until \(t=500\) s. The sequence of liquefaction from the upper seabed to the lower seabed shows that the wave-induced liquefaction in loose seabed soil is a progressive process from top to bottom (it will be analyzed in the following part). For shear stress \(\tau _{xz}\) on line \(x=200\) m under the anti-node, there is a common characteristics that it increases at an early stage, then gradually decreases to a small value accompanying mean effective stress \(I_1\) decrease; and it becomes zero if seabed soil become fully liquefied; otherwise, there is still an oscillation even if seabed soil is partially liquefied because it still can transmit a shear wave under such a state.

Fig. 4
figure 4

Time history of pore pressure, mean effective stress and shear stress at three typical buried depths (18.5, 10.0, and 2.0 m) on \(x=217.7\) m under node

Full size image

On the one hand, the response of pore pressure and effective stress in loose seabed soil under nodes has a series of common characteristics with that under anti-nodes, for example, residual pore pressure building up, and effective stresses reducing correspondingly. It is observed that pore pressure at \(z=2\) m under the node has been built up to about 45 kPa at \(t=500\) s; however, the mean effective stress \(I_1\) at this position only increases at an early stage, and then continuously reduces. The final value of \(I_1\) at this position when \(t=500\) s is basically the same with its initial value. It is shown that the dynamic response of pore pressure and effective stress in loose seabed soil under nodes, on the other hand, is significantly different with that under anti-nodes. Firstly, the magnitude of residual pore pressure build-up under nodes is significantly less than that under anti-nodes, for example, the magnitude of residual pore pressure at position \(z=10\) m and \(z=2\) m under anti-nodes is about 120 and 125 kPa, respectively, at \(t=500\) s; however, it is only 110 and 45 kPa at their counterpart position under the nodes at the same time. This difference is positively related to buried depth. Secondly, the mean effective stress \(I_1\) in the upper seabed under nodes cannot approach a zero stress state, for example, \(I_1\) at position (\(x=217.7\) m, \(z=18\) m) under the node is about 4 kPa, far away from a zero stress state at \(t=500\) s; however, the seabed soil at position (\(x=200\) m, \(z=18.5\) m) under the anti-node can approach this zero stress state, namely full liquefaction. It is found that all seabed soil at the three typical positions under nodes does not liquefy at \(t=500\) s. However, it does not mean that there is completely no liquefaction in the upper seabed soil under the nodes. The subsequent liquefaction analysis shows that there is indeed a liquefaction zone between the depth \(z=10\) m to \(z=18\) m in the upper seabed under the nodes. Due to the fact that seabed soil at the three typical positions under the node does not liquefy, there is always an oscillating part for shear stress \(\tau _{xz}\) on the three positions; and their oscillatory amplitude are much greater than their counterpart under the anti-nodes.

The difference of dynamic response of pore pressure and effective stress in loose seabed soil under anti-nodes and nodes is dependent on the loading characteristics of the standing wave. As illustrated in Fig. 2, the standing wave-induced hydrodynamic water pressure on the seabed under the anti-nodes is much greater than that under the nodes. Therefore, the dynamic response of loose seabed soil under the anti-nodes is much stronger. As a result, the speed of residual pore pressure build-up in the seabed under anti-nodes is much faster than that under nodes; and the magnitude of build-up is also greater than that under nodes. However, it is interesting to find in Figs. 3 and 4 that the amplitude of oscillatory shear stress under the anti-nodes is much less than that under the nodes of a standing wave. The reason is that seabed soil under the anti-nodes is always on the symmetrical lines of wave loading; while, seabed soil under the nodes is always on the anti-symmetrical lines of wave loading.

Except for pore pressure build-up, there is another diffusion mechanism when a loose seabed is loaded by a standing wave. Pore water moves from the zone under anti-nodes with high residual excess pore pressure toward to the zone under nodes with low residual excess pore pressure, resulting in the further increase of residual pore pressure in the seabed zone under the nodes, and the decrease of residual pore pressure in the seabed zone under the anti-nodes. As analyzed above, the hydrodynamic water pressure acting on the seabed zone under the nodes is apparently weak, compared with that under anti-nodes. However, it is shown by Fig. 4 that residual pore pressure can reach up to 20, 110 and 45 kPa at buried depths of 2, 10 and 18 m, respectively, on line \(x=217.7\) m under the node. This remarkable residual pore pressure in the seabed zone under nodes is mostly caused by this diffusion mechanism of pore pressure in seabed soil. Actually, diffusion of pore pressure always exists in a seabed until excess residual pore pressure dissipates completely.

Distribution of standing wave-induced dynamic pore pressure and effective stress in the loose seabed at time \(t=35\) T are illustrated in Fig. 5 (only \(x=100\) m to 300 m is shown). It is clearly observed that there are a series of zones with high dynamic pore pressure, exactly under anti-nodes of a standing wave. These high pressure zones distribute alternately in the seabed. In the zones under nodes of a standing wave, wave-induced dynamic pore pressure is less, forming alternate low pore pressure zones. Corresponding to the distribution of dynamic pore pressure, the distribution of effective stress also owns obvious periodicity. In the zones with high residual pore pressure, wave-induced dynamic effective stress is also great (positive value means total effective stress decreases). Additionally, there are some zones under the nodes of a standing wave and in the lower seabed, in which effective stresses of seabed soil become larger based on their initial value. It means that the seabed soil in these zones will never become liquefied under standing wave loading. This characteristics is significantly different with that induced by a progressive wave. Another interesting phenomenon observed is that the size of zones with high dynamic residual pore pressure is different. This is due to the fact that the size of a zone with high dynamic residual pressure enlarges when it is under the wave crest, and shrinks when it is under the wave trough.

Fig. 5
figure 5

Distribution of standing wave-induced dynamic pore pressure and mean effective stress \(I_1\) in the loose seabed at \(t=35\) T

Full size image
Fig. 6
figure 6

Time history of lateral pressure coefficient \(K_0=\frac{\sigma ^\prime _x}{\sigma ^\prime _z}\) at typical positions

Full size image

In the static state, the lateral pressure coefficient \(K_0=\sigma ^\prime _x / \sigma ^\prime _z\) generally is 0.5 in a homogeneous seabed soil. Under a dynamic state, this coefficient is variable. Figure 6 demonstrates the variation characteristics of the lateral pressure coefficient under standing wave loading. For very dense seabed soil, recoverable elastic deformation is the dominant deformation. As a result, \(K_0\) regularly vibrates around 0.5, like a harmonic function, sine or cosine. However, the variation characteristics of \(K_0\) is significantly different in loosely deposited seabed soil. Due to the existence of plastic deformation in loose seabed soil, the median of \(K_0\) will take place with a permanent shift toward a greater value, regardless if under anti-nodes or nodes. Additionally, the residual median, as well as the amplitude of the oscillation part of \(K_0\) under anti-nodes are both significantly greater than that under nodes. As a whole, the lateral pressure coefficient \(K_0\) in loose seabed soil increases gradually at an early stage until the liquefaction state. After that, residual median and oscillation amplitude basically remain stable. These response characteristics of \(K_0\) indicate that the decrease of effective stress \(\sigma ^\prime _x\) and \(\sigma ^\prime _z\) are not synchronous when pore pressure is building up under wave loading. The speed of the \(\sigma ^\prime _x\) decrease is less than that of \(\sigma ^\prime _z.\)

Fig. 7
figure 7

Definition of stress angle \(\theta _\mathrm{{MC}}\) based on Mohr–Coulomb criteria in granular seabed soil

Full size image

Stress angle could be another important physical parameter to study the response characteristics of loose seabed soil in relation to a standing wave. Stress angle is defined based on the conception of the Mohr–Coulomb criteria (illustrated in Fig. 7) as:

$$\begin{aligned} \theta _\mathrm{{MC}}=\arctan { \left\{ \frac{\frac{\sigma ^\prime _1-\sigma ^\prime _3}{2}}{ \frac{c}{\tan {\phi }}+\frac{\sigma ^\prime _1+\sigma ^\prime _3}{2}} \right\} } \end{aligned},$$
(13)

where \(\theta _\mathrm{{MC}}\) is the stress angle, c and \(\phi\) are the cohesion and internal friction angle of seabed soil. \(\sigma ^\prime _1\) and \(\sigma ^\prime _3\) are the maximum and minimum principle stresses.

Fig. 8
figure 8

Time history of stress angle at typical positions on \(x=200\) m under the anti-node of a standing wave

Full size image

The variation characteristics of stress angle at two typical positions in the loose seabed are demonstrated in Fig. 8. If seabed soil is dense, there is basically only elastic deformation in it. Then, there is only the oscillating part for the stress angle, like a harmonic sine or cosine function, regardless of buried depth. However, the variation characteristics of stress angle in loose seabed are also significantly different from that in a dense seabed. In Fig. 8, it is observed that stress angle in loose seabed decreases in the early stages; and then it gradually increases until approaching liquefaction state. After that, for example \(t=200\) s for the soil at (\(x=200\) m, \(z=18.5\) m), the maximum, minimum and median value of the stress angle basically are stable. However, the amplitude of the stress angle is great, for example, it is about 35\(^\circ\) at (\(x=200\) m, \(z=18.5\) m). It is also observed that the time needed for the stress angle decreasing to then increase is positively related to buried depth. Because of this variation of characteristics of stress angle in loose seabed under wave loading, it could be taken as a feasible method to judge the occurrence of wave-induced liquefaction in the future.

Displacement

Previous literature has proved that liquefied soil behaves like a kind of heavy fluid. In the above analysis, it has been known that the loose seabed soil in the upper seabed becomes liquefied under continuous standing wave loading. Then, with the overlying sea water, a two-layer fluid system is formed. Under standing wave loading, the liquefied seabed soil is supposed to vibrate driven by the overlying wave motion. The standing wave-induced displacement of the seabed surface is illustrated in Fig. 9. It is observed that the horizontal displacement of loose seabed soil is apparently small. However, the vertical displacement is considerable. There is vertical subsidence of the loose seabed soil accompanying pore water drainage out of the seabed surface.

Fig. 9
figure 9

Time history of standing wave-induced displacement of seabed soil at the surface. It is shown that liquefied seabed soil has a significant vertical vibration driven by ocean waves

Full size image

The most important characteristic of vertical displacement is that its amplitude is gradually increasing under wave loading. Before seabed soil becomes liquefied, the amplitude of vertical displacement is less. After liquefaction, its amplitude gradually increases due to the fact that the wave-induced liquefaction zone in loose seabed becomes larger and larger. At \(t=500\) s, the amplitude of vertical displacement reaches up to about 30 cm (it is great). Actually, this is a kind of resonance phenomenon in the two-layer fluid system driven by the overlying wave motion. This resonance phenomenon also has been observed in a series of wave flume tests in the laboratory (Sassa and Sekiguchi 1999; Wang et al. 2014; Kirca et al. 2013). It is indicated that the developed model FSSI–CAS 2D and PZIII soil model is reliable to understand the dynamic response of offshore loosely deposited seabed soil.

Progressive liquefaction

It has been widely verified that loose seabed soil could liquefy under ocean wave loading by laboratory tests (Sassa and Sekiguchi 1999) and field records (Sassa et al. 2006). There are, generally, two types of liquefaction mechanisms in seabed soil. They are (1) momentary liquefaction and (2) residual liquefaction. Momentary liquefaction can only occur in very dense sand. Its effect on the transient stability of offshore structures is minor. However, momentary liquefaction could boost the scouring of seabed soil around offshore structures. Residual liquefaction is due to the pore pressure build up in loose soil under cyclic loading. The liquefaction occurring in offshore loose seabed soil in this study is exactly the residual liquefaction. Generally, residual liquefaction in seabed foundation has a fatal effect on the stability of offshore structures. Once residual liquefaction occurs in seabed soil, bearing capacity of seabed soil is basically completely lost. A standing wave generally is formed in front of the breakwater, quaywall, etc. Understanding of residual liquefaction induced by a standing wave in seabed soil in front of a breakwater and/or quaywall is important and necessary for offshore engineers involved in design of offshore structures.

In this study, a parameter named the residual liquefaction potential \(L_\mathrm{{potential}}\) is defined to investigate the liquefaction characteristics of a loose seabed under standing wave loading:

$$\begin{aligned} L_\mathrm{{potential}}=\frac{\sigma ^\prime _{zd}}{-\sigma ^\prime _{z0}+\alpha c} \end{aligned},$$
(14)

where \(\sigma ^\prime _{zd}=\sigma ^\prime _{z}-\sigma ^\prime _{z0}\) is wave-induced dynamic vertical effective stress; \(\sigma ^\prime _{z0}\) is initial vertical effective stress; \(\sigma ^\prime _{z}\) is current vertical effective stress. c is cohesion of seabed soil; \(\alpha\) is a material coefficient. In Eq. 14, the cohesion of seabed soil is considered. From the point of review that cohesive soil is much more difficult to become liquefied under cyclic loading, it is indicated that cohesion of soil could effectively boost the liquefaction resistance of soil \(L_r=-\sigma ^\prime _{z0}+\alpha c\) (Liu and Jeng 2016). Therefore, cohesion c of soil must be considered when defining liquefaction potential (in Eq. 14). Due to the fact that macroscopic cohesion c of soil is not absolutely equivalent to the microscopic liquefaction resistance of soil particles, a material coefficient must be added to cohesion c of soil in Eq. 14. Currently, investigation on the effect of cohesion of soil on its liquefaction resistance is limited. In this study, cohesion c is zero because the seabed is assumed to be sandy soil. Then, there is no effect of \(\alpha\) on \(L_\mathrm{{potential}}\) for sandy seabed soil. However, \(\alpha\) must be quantitatively determined based on laboratory tests for silty soil and cohesive soil when evaluating their liquefaction potential under cyclic loading.

In theory, when \(L_\mathrm{{potential}}\) is greater than or equal to 1.0, sandy soil becomes liquefied. But actually, \(L_\mathrm{{potential}}\) of sandy soil will not exceed 1.0 either in numerical computation or in laboratory tests (Ishihara 1993; Wu et al. 2004). The reason is that sandy soil is a non-cohesive granular material. It can not bear any tensile stress as silty and cohesive soil. There is no yield surface and plastic potential surface in the tension stress space. Therefore, sandy seabed soil is difficult to reach a fully liquefied status (\(L_\mathrm{{potential}}=1.0\)) in numerical computation. In laboratory tests, this phenomenon is also observed, for instance, Ishihara (1993) found that \(L_\mathrm{{potential}}\) in silty sands or sandy silts containing some amount of fines stopped build up when it reached about 0.9–0.95. If liquefaction was strictly defined as the occurrence of \(L_\mathrm{{potential}}=1.0,\) then seabed soils would never“liquefy” despite the fact that they may have behaved as liquefiable materials. Some laboratory soil tests (Wu et al. 2003, 2004; Kammerer et al. 2002) performed at U.C. Berkeley also shown that liquefaction still could occur when the residual excess pore pressure did not reach the downward initial vertical effective stress, namely when \(L_\mathrm{{potential}}< 1.\) Here, this liquefaction is referred as to partial liquefaction. Based on the above recognition, it is defined that seabed sandy soil will liquefy if the \(L_\mathrm{{potential}} \ge \alpha _r,\) in which \(\alpha _r\) is also a coefficient depending on the soil characteristics. Its range generally is 0.78–0.99 (Wu et al. 2004). Based on previous investigation, \(\alpha _r\) is determined as 0.86 for the loose seabed soil in this study (Ye et al. 2015).

Fig. 10
figure 10

Vertical distribution of standing wave-induced residual pore pressure and oscillatory pore pressure on symmetrical line \(x=200\) m

Full size image

The essence of residual soil liquefaction in a loose seabed is the build-up of residual pore pressure under wave loading. When excess residual pore pressure is equal to or greater than the initial contact effective stress between soil particles, sandy soil become liquefied. It is highly necessary for us to understand the vertical distribution characteristics of residual pore pressure under anti-nodes of a standing wave. In Fig. 10, this vertical distribution characteristic of residual pore pressure, as well as oscillatory pore pressure at different times on \(x=200\) m under anti-nodes of a standing wave are shown. It is clearly observed that residual pore pressure in a loose seabed continuously builds up with time. However, there is a limitation line to constrain the build-up of residual pore pressure. Residual pore pressure cannot exceed this limitation line. Actually, this limitation line is the abovementioned liquefaction resistance line (LRL). When wave-induced residual pore pressure reaches LRL at a depth, the seabed soil at this depth becomes liquefied. The time needed for residual pore pressure reaching LRL is positively related to buried depth of seabed soil. It means the standing wave-induced liquefaction in loose seabed is a progressive process, initiating at the surface, and gradually propagating downward, as illustrated in Fig. 11. At \(t=500\) s, the residual liquefaction depth is about 11.5m (\(z=9.5\) m).

Fig. 11
figure 11

Depth of the frontier of the standing wave-induced residual liquefaction zone

Full size image

The vertical distribution of oscillatory pore pressure on \(x=200\) m also owns interesting characteristics. It is found that oscillatory pore pressure in loose seabed is significantly greater than that in dense seabed. It is also observed that the vertical distribution of oscillatory pore pressure is oscillating in the upper liquefied seabed soil; while, it is regular in lower non-liquefied seabed soil, for example, the liquefaction depth is about 10 m (\(z=10\) m) at \(t=400\) s. At this time, the distribution of oscillatory pore pressure in the upper 10 m seabed is oscillatory; while, it is not in lower 10 m seabed. These typical distribution characteristics could be adopted to predict the wave-induced residual liquefaction depth in numerical computation in the future.

Fig. 12
figure 12

Stress path at a series of typical positions on \(x=200\) m and \(x=217.7\) m in a loose seabed under standing wave continuous loading

Full size image

Stress path is another important way to characterise wave-induced liquefaction in a loose seabed. Figure 12 shows a series of stress paths at several typical positions on \(x=200\) m under the anti-node, and \(x=217.7\) m under the nodes. It is found that all stress states at an initial time are located on an initial \(K_0\) line. If a seabed is in a dense state, only elastic deformation could occur under wave loading. Their stress paths are only some tiny closed loops in a p–q coordinate system. However, the situation is completely different if the seabed soil is loose. Under wave continuous loading, effective stress in a loose seabed decreases resulting from the build-up of pore pressure. As a result, the stress state gradually moves toward the zero stress state (namely the liquefaction state). At the end of computation, the stress state at a series of positions on \(x=200\) under the anti-node in the upper seabed reaches/approaches a zero stress state, becoming liquefied. However, others in the lower seabed do not approach the zero stress state. The stress paths on \(x=217.7\) m under the node is a little different from that on \(x=200\) m as shown in Fig. 12a. The stress state at \(z=10\) m under the nodes is far away from liquefaction state at the end of computation. It is indicated that the residual liquefaction depth under the nodes is clearly shallower than that under the anti-nodes of a standing wave. This point can be clearly observed in Fig. 13.

Fig. 13
figure 13

Predicted residual liquefaction zone in a loose seabed at \(t=35\) T under standing wave loading

Full size image

The liquefaction zone shown in Fig. 13 is predicted based on the definition of liquefaction potential \(L_\mathrm{{potential}}.\) When \(L_\mathrm{{potential}} \ge 0.86\) at a position, it is predicted that the seabed soil here becomes liquefied. In Fig. 13, it is found that there is a liquefaction zone only under anti-nodes when \(t=20\) T. while, the soil under nodes basically does not fully liquefy until this time. The distribution of a standing wave-induced liquefaction zone in a loose seabed also owns periodicity. After applied 50 periods by the standing wave, the liquefaction zone in a loose seabed substantially enlarges, making the upper seabed soil under the nodes of a standing wave becoming liquefied; and these previous periodic liquefaction zones are linked together. The shape of the liquefaction zone frontier is wavy as affected by the motion of a standing wave.

Stress-strain relation

The dynamic response of a loose seabed to a standing wave has shown some nonlinear characteristics in the above analysis. Stress-strain relations demonstrated in Figs. 14 and 15 further prove the nonlinearity of dynamics of loose seabed soil to a standing wave. In Fig. 14, it is observed that there is cyclic mobility at all positions under the anti-node in a loose seabed. The mobility speed is relatively slow in an early stage. At the end of computation, the shear strain at position (\(x=200\) m, \(z=18.5\) m) is about 0.25%; and it is only 0.003% at position(\(x=200\) m, \(z=2\) m). It is indicated that the magnitude of shear strain is negatively related to buried depth, even though shear stress is positively related to buried depth. From the relation of \(\tau _{xz}\)–\(\epsilon _v,\) it is found that loose seabed soil is contractive under wave loading; and the magnitude of contraction has a negative relation with buried depth. The contraction of seabed soil represents that there is pore water being drained from the surface of the seabed.

Fig. 14
figure 14

Stress-strain relation at three typical positions on \(x=200\) m under the anti-node of a standing wave

Full size image
Fig. 15
figure 15

Stress-strain relation at three typical positions on \(x=217.7\) m under the node of a standing wave

Full size image

Stress-strain relation on \(x=217.7\) m under the node of a standing wave as demonstrated in Fig. 15 shows different characteristics from that on \(x=200\) m under the anti-node. First, the magnitude of shear stress on \(x=217.7\) m under the node is much greater than the counterparts on \(x=200\) m under the anti-node, for example, \(\tau _{xz}\) at position (\(x=217.7\) m, \(z=18.5\) m) is a maximum over 3 kPa; while, it is only about 75 Pa at position (\(x=200\) m, \(z=18.5\) m). Additionally, the magnitude of shear strain on \(x=217.7\) m is also greater than the counterparts on \(x=200\) m, for example, shear strain on position (\(x=217.7\) m, \(z=18.5\) m) reaches 3% at the end of computation. At the upper seabed under the nodes of a standing wave, there is also obviously cyclic mobility of shear strain. However this cyclic mobility at the middle and lower seabed is invisible. In Fig. 15, it is observed that the stress-strain relation at \(z=10\) m and \(z=2\) m under the nodes basically is elastic. There is basically no irrecoverable plastic deformation in the lower seabed under the nodes of a standing wave. It also can be observed that loose seabed soil on \(x=217.7\) m also is all contractive under wave loading; however, the magnitude of contraction is less than the counterpart on \(x=200\) m.

Parametric study

The effect on wave characteristics (wave height, period and water depth) and soil characteristics (permeability and saturation) on the progressive liquefaction process in a loose seabed under a standing wave is illustrated in Figs. 16 and 17, respectively. In Fig. 16, it is found that the effect of wave height H is most significant; and the effect of water depth d is not important. After 50 cycles of wave loading, the liquefaction depth reaches 15.5 m for the case in which \(H=3.0\) m; while it is only 6.5 m if \(H=1.0\) m. Their difference is significant. Overall, standing wave-induced liquefaction depth in a loose seabed floor is positively related to wave height and wave period; and negatively related to water depth.

Fig. 16
figure 16

Effect of wave characteristics on the progressive liquefaction process in a loose seabed floor under a standing wave

Full size image
Fig. 17
figure 17

Effect of soil characteristics on the progressive liquefaction process in a loose seabed floor under a standing wave

Full size image

In Fig. 17, it is observed that permeability and saturation of soil both could significantly affect the progressive liquefaction process. It is shown that there is no liquefaction occurring in a loose seabed if permeability k is not less than \(1.0\times 10^{-2}\) m/s. Overall, liquefaction depth is negatively related to permeability. However, its effect basically disappears when permeability is less than \(1.0\times 10^{-5}.\) It is indicated that the effect of permeability of soil to the residual liquefaction process has a range limitation. Finally, for a loose seabed floor, wave-induced liquefaction depth is positively related to saturation of soil.

Conclusion

Quaternary newly deposited loose seabed soil is widely distributed in offshore areas in the world. Wave-induced residual liquefaction in a loose seabed floor brings great risk to the stability of offshore structures in extreme climates. The understanding of the characteristics of wave-induced residual liquefaction in a loose seabed is meaningful for engineers involved in the design of offshore structures. In this study, standing wave-induced residual liquefaction has been investigated deeply and comprehensively adopting a validated integrated numerical model. It is shown that the integrated numerical model FSSI–CAS 2D incorporating the PZIII soil model can effectively and precisely captures a series of nonlinear dynamic response characteristics of a loose seabed floor under standing wave loading. The computational results further confirm the wave-induced liquefaction in loose seabed soil is progressively downward, initiating at the seabed surface. Besides, it is found that two physical processes, including vertical distribution of oscillatory pore pressure and time history of stress angle possibly could be used to judge the occurrence of wave-induced residual liquefaction in loose seabeds in the future. It is also found that the progressive liquefaction process is significantly affected by wave height, permeability and saturation of seabed soil.