KAGO: an approximate adaptive grid-based outlier detection approach using kernel density estimate

Abstract

Outlier detection approaches show their efficacy while extracting unforeseen knowledge in domains such as intrusion detection, e-commerce, and fraudulent transactions. A prominent method like the K-Nearest Neighbor (KNN)-based outlier detection (KNNOD) technique relies on distance measures to extract the anomalies from the dataset. However, KNNOD is ill-equipped to deal with dynamic data environment efficiently due to its quadratic time complexity and sensitivity to changes in the dataset. As a result, any form of redundant computation due to frequent updates may lead to inefficiency while detecting outliers. In order to address these challenges, we propose an approximate adaptive grid-based outlier detection technique by finding point density using kernel density estimate (KAGO) instead of any distance measure. The proposed technique prunes the inlier grids and filters the candidate grids with local outliers upon a new point insertion. The grids containing potential outliers are aggregated to converge on to at most top-N global outliers incrementally. Experimental evaluation showed that KAGO outperformed KNNOD by more than an order of $\approx$3.9 across large relevant datasets at about half the memory consumption.

1 Introduction

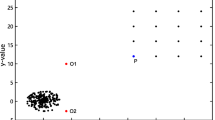
Anomaly¹ or outlier detection relates to the task of filtering patterns in data that deviate from normal behavior. These non-conforming or deviating patterns are often designated as anomalies, outliers, exceptions or aberrations [6]. Figure 1 demonstrates the outliers and normal patterns in a 2-D data. The points which appear in isolation from the expected patterns are shown as outliers, while the two groups of accumulated points in close neighborhood of each other form the clusters.

Motivation: Outlier detection finds its importance in a wide range of applications such as network intrusion detection [19, 34], credit card transactions [30], healthcare [11], detecting faults in safety critical system [20]. In all the aforementioned applications, there exists a possibility of frequent data updates in a dynamic environment [2, 3, 27, 37]. For example, consider the following scenarios: a credit card transaction in a place far from its usual location of use may indicate a fraud. Similar transactions carried out in such unexpected locations in course of time may reaffirm the involvement of fraudulent means. On the contrary, as the count of such transactions increases from a particular new location, the prior usage of credit card from this new place may appear legal instead of being suspicious. In both the cases, if a new transaction is mapped to the entry of a data point upon the base dataset², then as the number of transactions increase with the passage of time, we may either have new outliers (fraudulent transactions from a new location) or conforming patterns of data (expected transactions from a usual place).

Fig. 1

Illustration of outliers in a 2-D data

However, against every new insert upon the base dataset, involving all the points in their entirety to detect anomalies may lead to following disadvantages:

• The run time of the outlier detection algorithm may increase disproportionately (Tables 1, 2 and 3).

• Every new update may lead into an increased consumption of computing resources.

• A delayed extraction of outliers due to processing of data in totality against frequent changes.

Baseline method and the associated challenges: A prominent method viz. (namely) the K-Nearest Neighbors outlier detection [7] (KNNOD) algorithm relies on the measure of distance to extract outliers. For each point $x \in D$ (base dataset), the algorithm identifies the distance of x with its K$^{th}$ nearest neighbor ($d_{K}$ (say)). If t is considered as a threshold value, then all the data points whose $d_{K}$ value is more than t are considered as outliers, while rest of the points remain as inliers (Refer Fig. 2). However, with the size and velocity of data growing continually, the discovery of outliers in an automated manner becomes crucial. Against every new update made to the base dataset, a KNN-based approach may require re-computation of the K-Nearest Neighbors for each data item. Since KNNOD has a quadratic time complexity, such an approach may suffer from high response time, resource constraint and redundant computation in a dynamic environment. Therefore, while handling frequently changing data (insertion in this work), it is critical to develop a mechanism that provides an adaptive extension to KNNOD [7] without incorporating any redundant computation.

In our pursuit to design an efficient version of KNNOD [7], we aim to identify outliers based on point density instead of directly using any distance-based techniques (e.g., KNN). This is due to the fact that in variable density regions of a data-space, distance-based methods are rendered inappropriate [1, 7] while filtering outliers. Regions of uniform density in different subspaces have often been ignored resulting in detection of false outliers [10]. Therefore, adopting a density-based approach to extract outliers based on the statistical properties of data may resolve such issues. Our proposed technique revolves around the use of the probability density approximation method viz. kernel density estimation (KDE) [18, 24, 28, 29, 31] while finding point densities. Contrary to the KNN-based method [7] for outlier detection which is sensitive to data updates, KDE evaluates point density taking into consideration the statistical features of the dataset. Therefore, our proposed approach leads towards robustness in a dynamic data environment as compared to the static KNNOD [7] method.

Table 1 Tabular summary about the motivation behind our work

Fig. 2

Brief illustration of the scheme adopted in case of KNNOD algorithm (2D)

Fig. 3

Brief illustration of the scheme adopted for the KAGO algorithm (2D)

Table 2 Brief overview of the baseline method and our proposed approach in this paper

Foundation of the proposed approach: In this work, we propose an approximate adaptive grid-based outlier detection algorithm using kernel density estimate (KAGO) in order to address the bottlenecks faced by KNNOD [7] working on a static snapshot of data (Sect. 3 presents details of the KAGO algorithm). Initially, we divide the d-dimensional data-space into grids such that there are $p^{d}$ grid cells in total with p being the number of partitions per dimension. For an individual grid cell, we measure the density (local density)³ of all the data points within it by applying a suitable KDE function [24, 29]. The grid cell itself is treated as the local neighborhood for any point within it (Refer Fig. 3). On finding the density estimate of each point within a grid cell, we compute the grid local outlier score (glos) for individual points within the cell. The average glos taking all the points within a grid provides a measure of the mean grid local outlier score (mglos) for the concerned cell. Subsequently, we find the mglos values of all the non-empty grid cells (maximum $p^{d}$) lying across the data-space. The grid cells with higher mglos values above a certain threshold (algorithm determined) are pruned, while those with lower mglos values are considered as candidate outlier grids (COG). From the grid cells belonging to COG, we are able to filter the top-N global outliers based on their glos estimate. The value of N is set as the square root of updated dataset size ($|D^\prime |$). However, with possible fluctuations in COG post any given point insertion, the KAGO algorithm may end up detecting lesser than N outliers. This may happen due to persistent insertion of data points in a subspace resulting into formation of higher density grids.

While computing the local density of all the points within a grid cell, the KAGO algorithm only takes into consideration the reduced sub-space of the cell itself instead of whole data-space. For any grid cell $g_{c},c=1,2,3,\ldots ,p^{d}$, we consider multiple cell bound kernel centers⁴ [24, 39] to have an influence on the local density of any point. Given that the data points are d-dimensional, any grid cell $g_{c}$ will have $2^{d}$ corners and a center point. If $g_{c}$ contains more than $2^{d}+1$ points then, it is considered to be a relatively denser grid, otherwise a sparse grid. As per the KAGO algorithm, a sparsely populated grid allows most points within it to behave as kernel centers. However, we adopt an opportunistic scheme for the densely populated grids where only a set of points representing $g_{c}$ cast their influence as kernel centers. The biased sampling of kernel centers depending on grid density enables to improve the overall efficiency of the KAGO algorithm while extracting a maximum of top-N global outliers. Our proposed algorithm therefore aims to provide an efficient outlier detection mechanism incrementally at a minimum loss of accuracy.

Since the kernel centers involved in the point density computation remain localized to the grid cell itself, KAGO effectively determines the degree of local outlierness for a point in the data-space instead of relying on any global threshold [5]. The idea of finding top-N global outliers depends on the aggregation of local outliers from individual grid cells within COG. The motivation behind involving local outliers lies on the fact that real world datasets at times exhibit variable distribution properties at different regions of the data-space. As a result, it is often more desirable to converge on the anomaly status of a point based on the density variation with points in its local neighborhood (grid cell in our case) instead of relying on any global density measure.

Our contribution(s): Next, we briefly mention the contributions made in this paper.

• 1. We propose an approximate adaptive extension to KNNOD [7] in the form of KAGO algorithm.

• 2. Use grid structure for subspace creation instead of any expensive clustering technique.

• 3. Facilitate inlier pruning by focusing on a set of candidate outlier grids (COG). This prevents unnecessary checking of inlier points for not being anomalous.

• 4. Introduce an opportunistic scheme of kernel center selection based on the grid density for a cost effective design of the KAGO algorithm.

• 5. Prove the efficiency of KAGO over KNNOD [7].

Table 3 Major notations used in the paper

Organization of paper: Section 2 presents the important definitions related to the work along with problem formulation. This is followed by a detailed description of the KAGO algorithm in Sect. 3. The analysis of time complexity of KAGO is provided in Sect. 4. This is followed by the experimental observations covering results from relevant datasets proving the efficiency of KAGO over KNNOD in Sect. 5. Some of the key analytical points affecting the proposed algorithm and the related work are mentioned in Sects. 6 and 7. The paper concludes by highlighting the conclusion and future work in Sect. 8.

2 Preliminaries and problem formulation

In this section, we present the definitions of ideas and concepts that have been used while developing the KAGO algorithm. We also provide a formal representation of our problem in contention.

2.1 Local outlier

A point $x_{i}$ is termed as a local outlier if the data density at $x_{i}$ is substantially lower than the densities at $x_{i}$’s neighboring points. As shown in Fig. 4, the density at point $x_{i}$ appears relatively lesser than that of its neighboring points. Therefore, $x_{i}$ is more likely to be a local outlier where the neighborhood taken into consideration is the containing grid cell.

Fig. 4

Illustration of local outliers within a grid cell using localized density

Following steps are involved in designating a point $x_{i}$ as local outlier:

• 1. Compute the density at point $x_{i}$ along with the densities at $x_{i}$’s neighboring points.

• 2. Estimate $x_{i}$’s local outlierness score. This is based on the deviation of density at $x_{i}$ contrary to those lying in its neighborhood.

2.2 Neighborhood

For any point $x_{i} \in D$ (base dataset)$[1 \le i \le n, |D|=n]$ and a grid cell $g_{c},c=1,2,3,....p^{d}$, $x_{i}$’s neighborhood or local neighborhood is represented by the corresponding $g_{c}$ that contains $x_{i}$.

2.3 Kernel centers

Let S be any sample of data ($S \subseteq D$), then we denote a kernel center by $Lc_{j}, 1 \le j \le m$, such that $|S|=r$ and $m\le r$. Typically S represents the set of points within a grid cell $g_{c},1 \le k \le p^{d}$ and $Lc_{j}$ is a data point sampled from S. The chosen set of kernel centers must adequately represent the data distribution of S [29].

For any given kernel center $Lc_{j}$, there exists a kernel function $K_{h}$. The influence of a kernel center $Lc_{j}$ on the density of a point $x_{i} \in S, [1 \le i \le r]$ is estimated on the basis of distance from $Lc_{j}$ to the concerned point $x_{i}$ and is given as: $K_{h} (|x_{i} - Lc_{j}|)$.

2.4 Kernel density estimate (KDE)

The kernel density estimate (KDE) is a non-parametric method applied to compute the probability density function (PDF) of any data sample $S=\{x_{1},x_{2},x_{3},.....,x_{r}\}$. For any given point $x_{i} \in S$ where $1 \le i \le r$, the KDE on dataset S is used to estimate the likelihood of a point $x_{i}$ being drawn from S. The probability estimated through the kernel density estimator may be interpreted as the “point density” at any $x_{i} \in S$. In context of this work, the overall density at $x_{i}$ is given as the average of individual density contributions made by all the chosen kernel centers. The following equation gives the measure of overall local density at $x_{i}$.

$$\begin{aligned} f_{D} (x_{i}) = \frac{1}{l}\sum _{j=1}^{l}K_{h} (|x_{i} - Lc_{j}|) \end{aligned}$$

(1)

where l is the number of influencing kernel centers, $K_{h} (.)$ represents the kernel function, h is the kernel bandwidth or the smoothing factor and $Lc_{j}$ represents the $j^{th}$ kernel center. In this paper, we adopt the cosine similarity [23] measure for evaluating the distance between $x_{i}$ and $Lc_{j}$.

Fig. 5

Gaussian kernel as univariate KDE with different kernel bandwidth

For illustrative purpose, in Fig. 5, we have shown the effect of three kernel centers, each of them a carrying a Gaussian kernel function (red curve). The final density function across all kernels assumes the shape of a curve represented by blue color. From Fig. 5 (a) (left), we observe that the kernel bandwidth (h) takes a value of 0.1 resulting in sharper curves as compared to Fig. 5 (b) (left) with $h=0.3$ having flatter curves.

2.5 Kernel functions

A variety of kernel functions may be applied for estimating the density using KDE [29]. The Gaussian kernel [1] is one of the most frequently used kernel functions. In this paper, we use the Gaussian kernel as our KDE function.

$$\begin{aligned} K_{Gauss} (v) = \frac{1}{h (\sqrt{2\pi })}exp (-\frac{1}{2}\frac{v^{2}}{h^{2}}) \end{aligned}$$

(2)

where v signifies the distance from a kernel center $Lc_{j}$ to the target point $x_{i}$. Here, $1\le j \le m, 1\le i \le r \hspace{.1cm} (|S|=r,m\le r)$ with S being the data sample. The kernel bandwidth h is also known as the smoothing factor that controls smoothness of the curve obtained from KDE function. A higher value of h ensures a smoother curve of the density function $f_{D} (.)$ (Refer Fig. 5).

2.6 Grid local outlier score (glos)

Let $S=\{x_{1},x_{2},x_{3},....,x_{r}\}$ be the set of points in a grid cell such that $|S|=r$, then $\forall x_{i} \in S, i=1,2,3,\ldots ,r$, the glos value is defined as follows: Given a set of kernel centers $Lc=\{Lc_{1},Lc_{2},Lc_{3},....,Lc_{m}\}$ where $Lc \subseteq S$ and $m \le r$, the glos value of a target point $x_{i} \in S$ is measured as:

$$\begin{aligned} glos (x_{i})=z-score\bigg (f_{D} (x_{i}),\frac{1}{m}\sum _{j=1}^{m}f_{D} (Lc_{j})\bigg ) \end{aligned}$$

(3)

where $z-score (P,Q)= \frac{P-Q}{\sigma _{Q}}$ [40] signifies that if Q is the mean of a set of values, then how many standard deviations the value P is below or above Q. Therefore, from Eq. 3, we observe that variable P is equivalent to the overall local density at point $x_{i}$ i.e., $f_{D} (x_{i})$, while variable Q represents the mean local density of all the chosen kernel centers $Lc_{j} \in Lc$ where $1 \le j \le m$ and $m \le r$. The value of $glos (x_{i})$ effectively measures the degree of difference between the local density of $x_{i}$ to that of its neighboring kernel centers within the same grid cell. A smaller $glos (x_{i})$ value indicates a higher probability of point $x_{i}$ being an outlier.

2.7 Mean grid local outlier score (mglos)

Let $S=\{x_{1},x_{2},x_{3},....,x_{r}\}$ represent the set of points in any grid cell $g_{c}, c=1,2,3,\ldots ,p^d$, then we define the mglos value of any $g_{c}$ by the following equation:

$$\begin{aligned} mglos (g_{c})= \frac{1}{r}\sum _{i=1}^{r}glos (x_{i}) \end{aligned}$$

(4)

2.8 Adaptive anomaly detection

Let the initial outliers be defined by a mapping: f: D $\rightarrow$ O where O represents the set of outliers obtained from the non-adaptive algorithm. Let an insertion sequence of i points be made over a base dataset $D (|D|=n, i<<n)$. After i insertions let $D^{\prime }$ be the new dataset, then an adaptive outlier detection is defined as a mapping h : D$^{\prime }$ $\rightarrow$ O$^{\prime }$, where O$^{\prime }$ represents the outliers produced from the adaptive version. The outliers obtained through $h (D^\prime )$ is similar to the one time outliers f (D$^{\prime }$) produced by the non-adaptive algorithm.

2.9 Problem formulation

For k number of insertions where k $\in {\mathbf {N}}$, ${\mathcal {R}}^{d}$, let $T_{non-adaptive}$ be the total time taken by the non-adaptive algorithm, $T_{point-adaptive}$ be the time taken by the point-based approximate adaptive method against every insertion. Let $O_{non-adaptive}$ and $O_{point-adaptive}$ be the respective set of clusters obtained after i number of updates, then we establish the following objectives:

• $T_{point-adaptive} < T_{non-adaptive}$

• $O_{point-adaptive} \approx O_{non-adaptive}$

3 The KAGO algorithm

3.1 Framework of the KAGO algorithm

The KAGO algorithm is built around the framework as listed in phases below (Refer Fig. 6).

• 1. Phase-1 Build grid structure: Initially, the whole data-space $D:|D|=n$ is divided into grids. The usage of grids eliminates the task of any clustering [24] technique for demarcating noiseless points from outliers.

• 2. Phase-2 Compute glos, mglos, COG values: From the existing grid structure containing the base dataset D, the glos value of each data point from all the grid cells is evaluated using the KDE technique (Gaussian kernel) [1]. This is followed by the computation of mglos values for individual grids. Grids with higher mglos values beyond a certain threshold determined in course of the algorithm are inducted into the set of candidate outlier grids (COG).

• 3. Phase-3 New point insertion: The next phase deals with the insertion of a new data point. A newly inserted point occupies a single grid. As a result, the glos and mglos values of that concerned grid are updated accordingly. This may result in a change within the set COG. A cell previously belonging to COG may cease to exist within it post insertion of a new point due to reduced mglos value.

• 4. Phase-4 Filter top-N global outliers from the updated COG set: From the set of updated COG, the potential outlier data points are aggregated. Based on the glos value of the data points, the top-N global outliers are segregated for the current iteration.

• 5. Repetition of Phases 3 and 4 until all the data points are inserted.

Fig. 6

KAGO framework

3.2 Theoretical model

Let $O=\{o_{1},o_{2},o_{3},.....,o_{m}\}$ be the set of outliers from base dataset $D=\{x_{1},x_{2},x_{3},.....,x_{n}\}$ such that $O \subseteq D$ and $m \le n$. Each item in D is represented by a d-dimensional vector $\implies x_{i}=\{x_{i1},x_{i2}....,x_{id}\}$ where $x_{iq} \in {\mathcal {R}}^{}, 1 \le i \le n, 1 \le q \le d$. Let $x_{n+1}$ be the new data point added to D. Therefore, D changes to $D^\prime$ where $D^\prime = \{x_{1},x_{2}....,x_{n},x_{n+1}\}$ becomes the current set of points from which the updated outliers are to be extracted. We aim to address the issue of re-computing outliers post increase in the size of the dataset. The new set of outliers can be obtained by applying the KNNOD [7] algorithm on $D^\prime$. However, we avoid this procedure by developing a less expensive scheme in form of the KAGO algorithm.

Let $O_{KNNOD}$ and $O^\prime _{KNNOD}$ be the set of outliers obtained by executing KNNOD upon dataset D and $D^\prime$. Also, let $O^\prime _{KAGO}$ be the set of outliers obtained by executing the proposed KAGO algorithm incrementally, then we may have the following interpretations:

If $O_{KNNOD} \leftarrow KNNOD (D); O^\prime _{KNNOD} \leftarrow KNNOD (D^\prime )$ $;O^\prime _{KAGO} \leftarrow KAGO (D^\prime )$ then we establish the following objectives: $Time_{KAGO} (D^\prime ) < Time_{KNNOD} (D^\prime )$ and $O^\prime _{KAGO} \simeq O^\prime _{KNNOD}$.

3.3 Steps of the KAGO algorithm

Prior to insertion of any new data point, we execute the first two phases of our proposed KAGO algorithm. This includes creation of the grid structure (GridStruct) for base dataset D and identification of the set COG wrt. D. We define a new term called Algorithm-Components (Algo-Comp). The GridStruct and COG are included as a part of the Algo-Comp along with the base dataset D. Once the Algo-Comp values are determined, the algorithm receives a new incoming point. The pre-determined Algo-Comp values are then used by the KAGO algorithm for extracting the new set of outliers incrementally.

Next, we present the steps of our proposed KAGO algorithm supported by necessary explanation as and when required. The parameter taken by KAGO is the number of partitions per dimension denoted as p. For readers’ convenience, we also mention the pseudo-code (Refer Algorithm 1) of the KAGO algorithm.

• 1. Step 1- Set the AlgoComp

  • (a) Load the base dataset D.

  • (b) Set the no. of grid cells to $p^{d}$.

  • (c) Create GridStruct by dividing the dataspace containing D into $p^{d}$ d-dimensional grids.

  • (d) Set the variable $VolGrid = 2^{d}+1$. VolGrid gives a measure of the minimum number of points per grid required for it to be a relatively denser grid.

  • (e) $COG \leftarrow \phi$.

  • (f) For each d-dimensional non-empty grid cell $g_{c}, [1 \le c \le p^{d}]$,

    If ($|g_{c}| = 0$), process the next grid.

    If |g_c| > VolGrid), where $|g_{c}|=r (say)$, then $g_{c}$ is considered to be relatively dense. For a dense grid $g_{c}$, KAGO selects m kernel centers$[m = 3]$ within that grid such that it represents the data distribution within the grid $g_{c}$ (Fig. 7). The chosen kernel centers within $g_{c}$ are:

    $x_{i} \in g_{c}[1 \le i \le r]$, and $x_{i}$ is closest to the centroid of $g_{c}$.

    $x_{i} \in g_{c}[1 \le i \le r]$, and $x_{i}$ is closest to the minimal point⁵ of $g_{c}$.

    $x_{i} \in g_{c}[1 \le i \le r]$, and $x_{i}$ is closest to the maximal point⁶ of $g_{c}$.

    If ($|g_{c}| \le VolGrid$) with $|g_{c}|=r (say)$, then the grid $g_{c}$ is considered to be a sparse grid. Under this scenario, m kernel centers $[m \le r]$ within $g_{c}$ influence the local density of any point within $g_{c}$ (Figs. 7 and 8).

    Estimate the KDE (Defined in Sect. 2) of $\forall x_{i}[i=1,2,3,....,r] \in g_{c}$.

    $\forall x_{i} \in g_{c}[i=1,2,3,\ldots ,r]$, compute $glos (x_{i})$ (Fig. 9) (Defined in Sect. 2).

    Compute $mglos (g_{c})$ (Fig. 9) (Defined in Sect. 2).

  • (g) Sort the non-empty grids cells in GridStruct according to their increasing $mglos (g_{c})$ value where $c \in [1, p^{d}]$.

  • (h) $COG \leftarrow COG$ $\cup$ $\{g_{c}\}$ such that $g_{c} \in$ the top 50% non-empty grids from GridStruct with lowest $mglos (g_{c})$ scores. Designate top N points from COG as potential outliers based on their increasing glos value (Fig. 10).

• 2. Step 2- New point insertion A new point npt (say) is inserted upon D. The base dataset D therefore changes to $D^\prime$ where $|D^\prime |=|D|+1$.

• 3. Step 3- Identify the affected grid Post insertion of new point npt, KAGO identifies the affected grid cell $g_{c}[1 \le c \le p^{d}]$ where npt gets positioned (Fig. 11). The strength of $g_c (|g_c|=r)$ (say) increases by 1. Therefore $|g_{c}|=r+1$.

• 4. Step 4- Update the variables related to AlgoComp wrt. affected grid

  • (a) For the affected grid cell $g_{c}[1 \le c \le p^{d}]$ where $[|g_{c}|=r+1 (say)]$,

    If ($|g_{c}| > VolGrid$), then $g_{c}$ is considered to be a dense grid cell. KAGO selects m kernel centers$[m = 3]$ (Similar to Step 1 (f) (ii)) such that it represents the data distribution within $g_{c}$.

    If ($|g_{c}| \le VolGrid$), then it continues to be a sparse grid. Under this scenario m kernel centers$[m \le |g_{c}|]$ influence the local density of any point within the grid cell.

    Estimate the updated KDE of $\forall x_{i} [i=1,\ldots ,r+1] \in g_{c}$.

    $\forall x_{i} \in g_{c}[i=1,2,3,\ldots ,r+1]$, compute the updated $glos (x_{i})$.

    Compute the updated value of $mglos (g_{c})$.

  • (b) Sort the non-empty grids cells in GridStruct according to their updated $mglos (g_{c})$ value in increasing order post insertion of npt.

  • (c) Update the set COG by selecting a maximum of top 50% non-empty grids⁷ from GridStruct according to the updated $mglos (g_{c})$ values. An inlier grid prior to addition of npt will not become a part of COG post insertion in spite of a relatively lesser mglos score.

  • (d) If $COG \leftarrow \phi$, there are no outliers post insertion of npt. Go to Step 6.

• 5. Step 5- Filter a maximum of top-N global outliers Gather all data points from the updated set of COG. Sort the data points in increasing order of their glos and extract a maximum of top-N⁸ global outliers (Fig. 12). A point having an inlier status prior to addition of npt will not be an outlier after its insertion even if it has a relatively lesser glos value.

• 6. Set $D \leftarrow D^{\prime }$.

• 7. Repeat Steps 2 to 6 till k number of points are inserted.

Fig. 7

Selection of kernel centers for relatively denser grids

Fig. 8

Identification of denser and sparser grids

Fig. 9

Finding of glos and mglos values

Fig. 10

Sorting the grids in COG based on their increasing mglos values

Fig. 11

Affected grid post insertion of new point

Fig. 12

Extracting at most top-N global outliers

4 Time and space complexity of the KAGO algorithm

The time complexity of KAGO is determined through analyzing individual steps of the algorithm (Refer Sect. 3). The first five component steps (Step 1(a) to 1(e)) within Step 1 of the KAGO algorithm mainly involve loading of the base dataset and creation of grid structure. As a result, Step 1 involves a constant running time of ${\mathcal {O}} (1)$. For Step 1(f), two scenarios may arise while processing a certain grid cell $g_c \hspace{.1cm} [1\le c \le p^d]$. If $g_{c}$ is a dense grid $(|g_{c}| > VolGrid)$ as per KAGO, then the algorithm considers three kernel centers to have an influence for determining point wise glos values. Considering grid strengths not exceeding $n (|D|=n)$, a running time of ${\mathcal {O}} ( (3r+3r)*g_{c}) \simeq {\mathcal {O}} (1)$ [$\because r,g_{c}<< n, |g_{c}|=r$, ${\mathcal {O}} (3r)$ each for kernel center selection and KDE computation $\forall x_i \in g_c, i=1,2,\ldots ,r, r>VolGrid$ ] is required for Step 1(f(ii)). However, for sparse grids $(|g_{c}| \le VolGrid)$ (Step 1(f(iii))), ${\mathcal {O}} (r^2*g_{c}) \approx {\mathcal {O}} (1)$ time is required given that all the r points within a $g_{c}$ act as kernel centers. For skewed datasets with certain highly dense grids ($r \approx n$), a combined running time of ${\mathcal {O}} (1)+{\mathcal {O}} (n*g_{c})$ is involved for evaluation of $glos (x_{i}) [1 \le i \le n]$.

The mglos value for each grid takes either ${\mathcal {O}} (r)$ or ${\mathcal {O}} (n)$ time (Step 1(f(vi))) depending on grid density. Step 1 (g) involves sorting of grids on the basis of their increasing mglos values which leads towards completion in ${\mathcal {O}} (g_{c}*\log g_{c}) \simeq {\mathcal {O}}(1)\hspace{.1cm} [\because |g_{c}|<< n]$ time. Step 1 (h) also involves a constant time. The following steps 2 and 3 take ${\mathcal {O}} (1)$ time where the insertion of new point and its grid cell identification takes place. The next step (Step 4) deals with updation of glos value for each point within the affected grid and mglos value for the grid itself. Depending on the grid density, Step (4(a)) involves a total time of ${\mathcal {O}} (r^2)$ (sparse grid) or ${\mathcal {O}} (r) \hspace{.1cm} [r \le n]$ (dense grid). Sorting of grids post insertion of new point takes ${\mathcal {O}} (g_{c}*\log g_{c}) \simeq {\mathcal {O}}(1)$ time. The new list of COG is rebuilt in constant time.

While deciding the final set of outliers (Step 5), all the potential outliers lying within COG are sorted at a cost of ${\mathcal {O}} (g_{c}*r\log (g_{c}*r))$ [Taking an average grid density of r] or ${\mathcal {O}} (n\log n) \hspace{.1cm} [r \approx n$] based on their increasing glos values. We assume the initial size of top-N outliers as $\sqrt{n}$. Therefore, checking a point for its outlier status is done by comparing it with the previous list involves a running time of ${\mathcal {O}} (\sqrt{n*n})\simeq {\mathcal {O}} (n)$ time. Contrary to quadratic running time of KNNOD [7], the overall time complexity (worst case) of KAGO is therefore ${\mathcal {O}} (n+n\log n) \simeq {\mathcal {O}} (n\log n)$ for a skewed distribution otherwise ${\mathcal {O}} (1) \hspace{.1cm} [\because r, g_{c}<< n]$ for uniformly distributed grids.

Space complexity analysis The storage required for executing the KAGO algorithm is influenced by both the number of points (n) and dimensions (d). For storing the base dataset ${\mathcal {O}}(n * d)$ space is required. We additionally maintain two 2-D matrices for storing the grid structure and the point densities. This consumes a space of ${\mathcal {O}}(r*p^d)$ where r ($r \approx n$ for denser grid cells) may be considered as the size of each grid cell. In order to store COG and the set of outliers, a storage space of around ${\mathcal {O}}(n+p^d)$ is required. If $d<< n$, then $p^d$ may be taken as a constant entity given that the value of p is not substantially high. Increasing the value of p may lead to creation of more grid cells involving higher computational cost overall. The KAGO algorithm will therefore have a linear space complexity in the average case.

However, scaling the value of $d \hspace{.1cm} (d>>n)$ may eventually result in consumption of exponential amount of space. This is due to a significant increase in the number of grid cells ($p^d$) which would require additional storage. Therefore with increase in number of dimensions, the advantages derived from the efficient designing of KAGO may be nullified with a much higher memory overhead.

Table 4 Datasets and their partition size used in experiments

5 Experimental evaluation

In this section, we provide key experimental observations and their analysis thereby proving the efficiency of KAGO over KNNOD [7] and some other benchmark outlier detection methods. We also compared the memory usage between both the algorithms. Further, evaluation of correctness of results was performed based on Rand-index (RI) and F1-scores (https://nlp.stanford.edu/IR-book/html/htmledition/).

5.1 Experimental setup, datasets used and observations

We simulated our proposed KAGO algorithm in C++ on a Linux platform (Intel (R) Xeon (R) CPU E5530 @ 2.40GHz) with 32GB RAM. The experiments were performed on two network intrusion detection dataset(s): NSL-KDD (PCA (Principal Component Analysis) [36] reduced to 3 and 4 dimensions respectively) (See https://www.unb.ca/cic/datasets/nsl.html) and a bidding data for market advertisement: A1 for Yahoo! Search (See https://webscope.sandbox.yahoo.com/catalog.php?datatype=a). In this paper, we use the PCA reduced NSL-KDD datasets by the name of NSL-KDD3 and NSL-KDD4 respectively, while the Yahoo! bidding data have been named as A1-Yahoo! (Refer Table 4 for dataset details). In addition, we also used the Vowel dataset from UCI Machine Learning Repository [9] for conducting our experiments.

Fig. 13

Efficiency comparison between KAGO and KNNOD, number of COG and top-N outliers post every insertion for NSL-KDD3 (NSL-KDD PCA reduced to 3 dimensions)

Fig. 14

Efficiency comparison between KAGO and KNNOD, number of COG and top-N outliers post every insertion for NSL-KDD4 ((NSL-KDD PCA reduced to 4 dimensions))

Fig. 15

Efficiency comparison between KAGO and KNNOD, number of COG and top-N outliers post every insertion for A1 - Yahoo! Search Marketing Advertiser Bidding Data

Prior to execution of KAGO, we involve the entire dataset to decide the starting and ending point of each dimension. The minimum and the maximum end for each dimension is decided by the following relations:

$$\begin{aligned}&Min = min\{min\{D_{1}\}, min\{D_{2}\},...., min\{D_{d}\}\} \end{aligned}$$

(5)

$$\begin{aligned}&Max = max\{max\{D_{1}\}, max\{D_{2}\},...., max\{D_{d}\}\} \end{aligned}$$

(6)

Here, $min\{D_{i}\},max\{D_{i}\} \hspace{.1cm} [1 \le i \le d]$ represent the minimum and maximum of all the values along $i^{th}$ dimension. The GridStruct (Refer Sect. 3) is therefore constructed with its origin containing Min (Eq. 5) and every dimension extends to an identical length till Max (Eq. 6). The purpose of building GridStruct with entire dataset is to ensure the positioning of newly added points within the same co-ordinate system as the base dataset points while executing KAGO.

For our experimental purpose, in case of dense grid ($|g_{c}| > VolGrid,c=1,2,3,\ldots ,p^d$), we select three kernel centers (centroid, minimal, maximal) ($m=3$, Refer Sect. 3) to exert influence on each $x_{i}\in g_{c} \hspace{.1cm} [1 \le i \le r, r > VolGrid]$ while evaluating $x_{i}'$s kernel density. In case of a sparse grid ($|g_{c}| \le VolGrid$), $\forall x_{i}\in g_{c} \hspace{.1cm} [1 \le i \le r, r \le VolGrid]$, we assume each $x_{i}$ to behave as an influential kernel center within $g_{c}$. Therefore, for any sparse grid $g_{c},|g_{c}|=r$ (say), we assume $m=r$. Next, we describe our observations based on experiments conducted for each dataset while detecting a maximum of top-N outliers through the KAGO algorithm dynamically.

Observations for NSL-KDD3: For NSL-KDD3 dataset, the value of parameter p (# partitions/dimension) was taken to be 5. As a result, the total number of grid cells within GridStruct is 125[$\because \#Grids = p^d,d=3 \hspace{.1cm} (\#dimensions)$]. After analyzing the entire dataset (25000 points), the Min and Max values were computed to be $-$4.09628 and 111.051, respectively. The origin of the co-ordinate system is therefore located at (−4.09628, −4.09628, −4.09628), while the maximal point of GridStruct should be at (111.051, 111.051, 111.051). For each of the 125 grid cells, the grid height (h) in every dimension is identical to a value of 23.0295.

Key result(s): The base dataset size was taken to be 20000 with 5000 additional points were inserted one at a time. Prior to insertion of any new point npt (say), there were five grids filled with data points: 1, 26, 51, 76 and 101. Grid #1 was the only dense grid with more than 8 $(\because VolGrid =2^d+1)$ points. From Fig. 13 (top figure), we observed that our proposed KAGO algorithm (lower curve) consistently outperformed KNNOD [7] till the entry of the final point. Based on our observation, a maximum speedup of about 6660 times ($\approx$ order 3.8) was achieved by KAGO when 4000th point was inserted. However, a curve dip (Fig. 13 (top figure)) was observed after 615th and 3954th insertion in case of KAGO. Reason(s): The high speedup of KAGO can be attributed to its grid-based approach of dealing with subspaces instead of  the entire dataset scan. The efficiency curve dip (Fig. 13 (top figure)) for KAGO occurred because two new grids: Grid# 101 and Grid# 76 were affected when 615th and 3954th point were inserted. These newly affected grids remain sparse due to which the time required to compute the glos values of the points within the affected grid is less as compared to the denser grids.

Key result(s): The number of COG (Candidate Outlier Grids) was consistent throughout the insertion process of all the data points (Figure 13 (middle figure)). Reason(s): A constancy in the number of COG implies that no new grids were affected due to point insertion and that the list of initial COG with probable outliers remains untouched after repeated addition of points. It may also be the case that a single grid in a COG of any iteration had been dismantled by a newly affected grid, while rest of the grids with erstwhile COG retain their position. No deviation in the number of COG also means that the potential outliers were selected post every insertion from the three COG (for NSL-KDD3 dataset), while at most top-N (N=$\lfloor \sqrt{D} \rfloor , D=20000$) outliers were selected.

Key result(s): We observed a steady decrease in the number of top-N outliers from 141 to 131 after all the insertions were made. Reason(s): The reason for this steady decrease in the number of outliers may be attributed to the increase in glos values of the data points due to a dense neighborhood within affected grids. Redundant insertions on certain grid(s) initiate this phenomenon where a previous outlier point may gradually lose its outlier status due to a sufficiently filled containing parent grid with a higher mgols value.

Observations for NSL-KDD4: The parameter p’s value was taken to be 5 resulting in a total of 625 grid cells ($\because d=4$). The base dataset size equaled 20000 facilitating insertion of 5000 points. The Min and Max values for NSL-KDD4 dataset were −6.28682 and 111.051 respectively, with a grid height h of 23.4676 in each of the four dimensions. Prior to insertion of any new data point, a total of five grids were filled with Grid# 1 being the densest containing 19985 points.

Key result(s): On observing the results for subsequent insertions from Fig. 14 (top figure), we found that KAGO achieved a maximum speedup of around 6445 times ($\approx$ order 3.8) over KNNOD post insertion of the last point. No change was was observed in the number of COG throughout all point insertions (Fig. 14 (middle figure)). However, a curve dip (Fig. 14 (top figure)) was observed after 615th, 2991st and 3955th insertion was made. Reason(s): Similar reasons as applicable for the previous dataset. The newly affected grids in this case were: Grid# 101, Grid# 126 and Grid# 76, respectively, over all insertions.

Key result(s): For the set of outliers (Fig. 14 (bottom figure)), we observed that upon entry of the first point, a total of 141 outliers were extracted which reduced to 124 post entry of the 5000th point. Reason(s): This is because upon entry of any new point, a sparse grid may turn into a dense grid resulting in an overall increase of the mglos score of that affected grid. This results in a significant decrease in the number of top-N global outliers.

Table 5 Key experimental results (KAGO vs. KNNOD)

Observations for A1-Yahoo!: Parameter p was assigned a value of 5. The dataset being used consisted of four dimensions resulting in a total of 625 grid cells. The base dataset size was fixed at 15000 with an additional 3000 points were added one at a time. The Min and Max values were calculated to be 0 and 1133, respectively, with a grid height h equaling 226.6 per dimension. Post insertion of all the data points, we observed that (Refer Fig. 15 (top figure)) for A1-Yahoo! dataset, the KAGO algorithm outperformed KNNOD [7] by an order $\approx 3.92$ (around 8403 times faster).

Key result(s): We observed that there is a periodic dip in the efficiency graph (Refer Fig. 15 (top figure)) for KAGO over subsequent point insertions. Reason(s): Initially preceding any insertion, 6 grids were filled with data points: Grid# 46 (321 points), Grid# 17 (404 points), Grid# 22 (227 points), Grid# 47 (3928 points), Grid# 16 (5779 points) and Grid# 21 (4341 points). Once the new insertions were made, a new grid (Grid# 52) started filling up from the 37th insertion periodically. The new grid continued to be a sparse grid till the entry of first seventeen points with each point behaving as kernel centers. Further insertion into the same grid transformed Grid# 52 into a relatively denser grid. However, the total number of points within Grid# 52 was still less than the other affected grid (Grid #47) during repeated insertions. As per the KAGO algorithm (Sect. 3), a running time of ${\mathcal {O}} (3r+3r)$ (Sect. 4) is required for a dense grid while computing the glos value of individual points. Let |Grid# 47|= r1 and |Grid# 52|= r2, $\because r2 < r1$ across all insertions, we observe a periodic dip in the time required by KAGO (Fig. 15 (top figure)) when Grid# 52 is affected.

Key result(s): Contrary to the previous datasets, we observed that the number of COG (Refer Fig. 15 (middle figure)) remained as three till the insertion of the 36th point. While 37th point was inserted, the number of COG increased to 4. Reason(s): This may be possible when new grids are affected (previously empty) post insertion of data points. We observed that a new grid (Grid# 52) was targeted when the 37th point was entered. Upon observing the set of populated grids prior to any data insertion, we clearly noticed that Grid# 52 was previously empty. This triggers a re-shuffle of the new COG list resulting in an addition of one or more grids as potential outlier grids based on the updated mglos values.

Key result(s): The set of top-N (N = 122) outliers after the entry of the first point experienced a sharp decrease (Refer Fig. 15 (bottom figure)) till the entry of the 890th point (N = 28). During this phase of steep decrease in the number of top-N outliers, Grid# 47 and #52 were repeatedly affected. From the insertion of 891st point, no more reduction in outliers was observed. Reason(s): This may happen when the glos values of existing points are at least as low as the value necessary for retaining the outlier status due to previous insertion and the new points are a part of the dense grids. Redundant positioning of new points in previously affected grids ensures a higher glos value for the contained points within the grid itself therefore ensuring a decrease or constancy in the number of outliers. A brief summary of experimental results comparing KAGO with KNNOD [7] on all the datasets has been shown in Table 5.

Comparison of KAGO with other prominent outlier detection algorithms We also compared KAGO with some of the other well-established anomaly detection algorithms viz. LOF [4], iLOF [22], MiLOF [26] and DILOF [21]. We primarily focused on comparing the efficiency of these algorithms with that of KAGO.

Fig. 16

Efficiency comparison between KAGO and LOF, number of COG and top-N outliers post every insertion for the Vowel dataset

Fig. 17

Efficiency comparison between KAGO and LOF for NSL-KDD3, NSl-KDD4 and A1-Yahoo! dataset

Observations wrt. LOF [4]: While drawing comparisons with LOF [4], we used all the four datasets (Refer Table 4). For Vowel, we chose the size of base dataset as 100. A total of 400 points were inserted upon the base dataset in a point wise manner. For the other three datasets viz. NSL-KDD3, NSL-KDD4 and A1-Yahoo!, the partitions were made as shown in Table 5. The parameter p was assigned a value of 3 with each data point having three dimensions. Therefore, the data space was divided into 27 grid cells. From Fig. 16 (top figure), we observe that the KAGO algorithm consistently maintained a better efficiency than LOF [4]. A highest efficiency of the order of $\approx$ 1.34 was achieved in favour of KAGO after 400th insertion.

We further noticed that (Refer Fig. 16) there is an occasional dip in the curve corresponding to KAGO after 147th and 148th insertion, respectively. Subsequently, a dip also occurred at the end of 257th insertion. Similar phenomenon was observed for three more timestamps before the final insertion. Moreover, the COG curve (Fig. 16 (middle figure)) showed a fluctuating tendency unlike the previous cases. In addition, the set of outliers (Figure 16 (bottom figure)) appeared to diminish after the addition of 130th point.

Reason(s): With increasing updates, the quadratic running time of LOF results in it being outperformed by our proposed KAGO algorithm on a consistent basis. As the size of base dataset increases with additional inserts, KAGO continues to achieve a greater efficiency over LOF.

The temporal dip in the efficiency curve of KAGO may be attributed to the processing of a sparse grid after a given insertion has taken place. This happens when either a grid gets newly affected due to an insert or the grid cell is yet to obtain a dense status. However, a significant dip observed against the above entries was mostly due to insertion happening in a sparse grid cell with very lesser number of data points.

Table 6 Key experimental results (KAGO vs. LOF)

The varying size of COG at various phases of point insertions is mainly due to the grid cells moving in and out of contention for producing outliers. In case of a grid cell being targeted with repeated insertions, the size of COG is likely to shrink with more number of denser points. However, we also observed that as new grids are affected, the COG expands and accommodates more number of grid cells with potential outliers. Along with COG, a consistent reduction in the number of top-N outliers happens when repeated insertions take place across the data space. Effectively, the sparse regions gradually become dense resulting in diminishing outliers.

As observed, the KAGO algorithm consistently outperformed LOF [4] across all the four datasets: NSL-KDD3, NSL-KDD4, A1-Yahoo! and Vowel (Refer Fig. 17, Fig. 16). While in case of NSL-KDD3 and NSL-KDD4, KAGO achieved an overall efficiency of the order of $\approx$ 3.90 and 3.98 respectively, for A1-Yahoo!, KAGO outperformed LOF by an order of $\approx$ 4.12. Table 6 provides a brief summary of the results obtained while comparing the efficiency of KAGO over LOF.

Fig. 18

Efficiency comparison of KAGO with iLOF, MiLOF and DILOF for Vowel dataset

Comparisons with other algorithms: We further evaluated the effectiveness of KAGO in terms of efficiency and performance for Vowel [9] dataset and compared with methods: iLOF, MiLOF and DILOF (Fig. 18). Experimentally, we observed that KAGO was about 10,715 times faster than iLOF (order of $\approx$ 4) post insertion of 100$^{th}$ point or a window size of 200. Upon comparing with MiLOF and DILOF for similar insertion timestamp, KAGO achieved an overall efficiency of about 507 times and 169.82 times, respectively, thereby outperforming both the algorithms.

In terms of performance, the KAGO algorithm showed a higher RI score as compared to LOF. For the NSL-KDD3 dataset, KAGO achieved an accuracy measure of about 47.56%, while LOF was about 39.97%. In case of NSL-KDD4 dataset, the proposed algorithm achieved a better RI measure with 40.78% accuracy while LOF measured about 37.78%. The Vowel dataset recorded the highest improvement with KAGO showing an enhanced accuracy of about 38% wrt. (with respect to) LOF. For A1-Yahoo! dataset, identical values were achieved by both the algorithms (RI = 1.0).

Furthermore, while validating the outliers by computing the F1-score, we observed that KAGO was about 7% higher in comparison with iLOF [22] algorithm for the NSL-KDD3 dataset. Similar observations were made while comparing the algorithms for NSL-KDD4 with KAGO outperforming iLOF by about 3%. The iLOF algorithm achieved a validation score of about 54.83% against KAGO which equivalently resulted for about 57.94%. In case of A1-Yahoo! dataset, both the algorithms achieved similar results with an F1 measure of 1.0 in either case.

5.2 Support vector data description

In order to characterize the involved data by identifying meaningful spaces, a suitable description of data domain is considered an essential feature. In this regard, the use of support vector data description (SVDD) enables finding of a spherical boundary around the data and filter outliers [33]. In context of our experimental analysis, we treat a test instance ${\mathbf {z}}$ (say) as an accepted support vector if it lies at a distance less than or equal to the mean radius $\mathbf {R_{s}^2}$ (say) of the sphere (denser region) with ${\mathbf {a}_{\mathbf {s}}}$ being the center (Eq. 7).

$$\begin{aligned} ||{{\mathbf {z}} - \mathbf {a}_{\mathbf {s}}}||^2 \le \mathbf {R_{s}^2} \end{aligned}$$

(7)

Support vectors which fall outside this description are neglected, e.g., outliers. While expanding Eq. 7, a support vector may be expressed in terms of its inner products ${\mathbf {z}}.{\mathbf {z}}$ [33]. However, in our case, we replace by a Gaussian Kernel function (Refer Sect. 2) that has been used in finding the KDE-based local outliers.

While demonstrating our comparisons for individual dataset, we state the outlier instances implying that the accepted support vectors are determined. Since the glos value is directly dependent on KDE, the kernel density estimate comparison has been provided by representing the appropriate glos value of the outliers. The SVDD objects were identified for comparing KAGO with KNNOD [7] and LOF [4]. Due to presence of numerous values, we have included the SVDD comparisons in an online supplementary material (OSM)⁹ Since a large number of superfluous support vectors are identified, a limited observation is presented in the OSM.

5.3 Memory usage

The high efficiency of KAGO over KNNOD [7] in terms of CPU execution time is achieved along with a significant reduction in memory consumption (Refer Table 7). For each dataset, we observed that the memory usage due to KAGO is approximately half as that of the KNNOD algorithm. Contrary to KAGO, a larger share of memory consumption due to KNNOD results from its storage of K-nearest neighbors for each data point in form of KNN matrix. The KAGO algorithm on the other hand allocates space only for the filled up grids within GridStruct facilitating the storage of glos value for each point. The grid indices and outliers occupy additional memory space.

Table 7 Memory usage comparison between KAGO and KNNOD [7]

5.4 Brief outlier analysis

We conducted a brief study of outliers obtained through both KAGO and KNNOD [7] algorithm. For KNNOD, the size of K-Nearest Neighbor (KNN) and a cutoff threshold determines the outliers for a given dataset. In our experimental procedure, we initially identified the distances of each point $x_{i} \in D \hspace{.1cm} [1 \le i \le n]$ with its Kth nearest neighbor $K (x_{i})$ (say). The mean of all such distances is treated as the threshold $K_{th}$ (say). The value of K ($\lceil \sqrt{n}/10\rceil$) [12] was chosen to be 15, 15 and 12 for NSL-KDD3, NSL-KDD4 and A1-Yahoo! datasets. Any point whose $K (x_{i})$ is greater than $K_{th}$ obtained an outlier status.

Table 8 Measures required for outlier analysis metrics

Table 9 Algorithm correctness evaluation

We evaluated the RI measure and F1-score¹⁰ for comparing the quality of results related to KAGO and KNNOD [7] (Table 9). RI provides a measure of the percentage of correct decisions. The calculation of RI is based on the evaluation of TP (True Positive), FP (False Positive), True Negative (TN), False Negative (FN). The RI measure is given as:

$$\begin{aligned} RI = \frac{TP+TN}{TP+FP+FN+TN} \end{aligned}$$

(8)

The F-measure penalizes FN more than FP contrary to the RI measure. For our outlier evaluation purpose, we measure the F1-score given by:

$$\begin{aligned}&Precision (p) = \frac{TP}{TP+FP} \hspace{.3cm} Recall (r) = \frac{TP}{TP+FN} \end{aligned}$$

(9)

$$\begin{aligned}&F1-score = \frac{2pr}{p+r} \end{aligned}$$

(10)

Table 8 provides an estimate of individual measures required to obtain the desired values of outlier quality metrics. From Table 9, we observed that while evaluating the RI for both NSL-KDD3 and NSL-KDD4 dataset, our proposed algorithm KAGO achieved an accuracy of around 47.50% and 40.78% respectively. This elevated accuracy was about 9% and 1% higher as compared to KNNOD. No change in accuracy was observed in case of A1-Yahoo! dataset. The reason for obtaining a better accuracy in case of KAGO as compared to KNNOD can be attributed to repeated inlier pruning based on glos value across point insertions instead of filtering outliers based on any predetermined threshold. The exactness wrt. both the algorithms have been compromised to a certain extent; however, the usage of KAGO has ensured a more efficient and effective outlier detection scheme compared to KNNOD (Refer Tables 5 and 9) $\therefore T_{point-adaptive} < T_{non-adaptive}$ and $O_{point-adaptive} \approx O_{non-adaptive}$.

6 Key analytical points of the KAGO algorithm

In this section, we dwell on the probable reasons behind certain assumptions made for our proposed algorithm. We also present few proofs related to some key possibilities in this work.

• 1. Point (s): In the KAGO algorithm, any grid $g_{c} \hspace{.1cm} [1 \le c \le p^{d}]$ is considered as sparse or relatively dense depending on the number of contained points within $g_{c}$ which is below or above a threshold $VolGrid = 2^d+1$.

  Analysis/Reason(s): If the average number of points per grid ($|D|/\#Grids$) was taken instead of VolGrid, then there exists a possibility that a reasonably filled up subspace (grid) might be potentially inducted into COG in spite of being an inlier grid. In order to prevent this scenario, we incorporated the threshold VolGrid. Any $d-$dimensional grid cell contains $2^d$ corners and a center point. As a combination of these points can exert distinct influence as kernel centers on any point within $g_{c}$, we assumed VolGrid to be the threshold between a sparse and a relatively denser grid. By no means we impose the fact that any for $g_{c}, |g_{c}|>VolGrid$, the grid is an absolute dense grid, and hence, we use term “relativly dense” wrt. our KAGO algorithm.

• 2. Point (s): Three kernel centers are used for a dense grid, while all the data points within any sparse grid are involved as kernel centers.

  Reason(s) For any sparse grid $g_{c} \hspace{.1cm} [1 \le c \le p^{d}]$, we have $|g_{c}| \le VolGrid$. As compared to the size of base dataset D wrt. any given insertion, $g_{c}<< |D|$. Therefore, a selective choice of kernel centers from $g_{c}$ may not represent the data distribution within completely. Moreover, due to sparse nature of the concerned grid, the included points in $g_{c}$ might be spatially dispersed. As result, $\forall x_{i} \in g_{c} \hspace{.1cm} [1 \le i \le r, r\le VolGrid]$, $x_{i}$ can potentially act as a kernel center having a distinct impact on KDE (local density) of any other point within $g_{c}$. Due to these reasons in the KAGO algorithm, each data point within a sparse grid is treated as kernel centers.

  In case of a dense grid ($|g_{c}| > VolGrid$), the points within $g_{c}$ are very close to each other. Effectively, a similar influence of such close neighboring points on KDE of any $x_{i} \in g_{c} \hspace{.1cm} [1 \le i \le r, r >VolGrid]$ will lead to redundant computation. In order to efficiently compute the KDE $\forall x_{i} \in g_{c}$, we chose to represent the data distribution within a dense $g_{c}$ with three kernel centers including minimal, maximal and centroid points of the grid.

• 3. Point(s): A relatively denser grid with higher number of points may belong to the set COG.

  Analysis/reason(s): The COG is identified based on increasing mglos value of the grids. However, post sorting of all the non-empty grids, a certain grid $g_{c} \hspace{.1cm} [|g_{c}|>VolGrid]$ may not obtain a sufficiently higher mglos so as to be pruned like an inlier grid. As a result $g_{c}$ continues to be a part of COG and produces the potential outliers.

• 4. Selected COG always may not extract the top-N global outliers post first insertion.

  Reason(s): This is an exceptional scenario which may arise if repeated insertions result in single point filled grids. Under such a case, the dense grids will be pruned as inlier grids. However, due increase in the number of sparse grids, the list of COG may not include such potential outlier grids resulting in a fall in top-N global outliers initially. On the contrary, if we increase the percentage of COG, then unnecessary computations may be involved in accessing the points which are not outliers possessing a higher glos value.

Lemma 1

5. Let $q_{max} = max\{|COG|\} = \lceil \frac{\#Grids}{2}\rceil$ produced from D. Let q ($q<q_{max}$) be the size of COG prior to any insertion, then $\forall x_{i},i=1,2,3,\ldots ,k$, where $D=D+{x_{i}}$, we have $0 \le$ |COG| $\le q_{max}$.

Proof

With every insertion $x_{i}$, the $'mglos'$ value of the affected grid $g_{c},[1 \le c \le p^d]$ gets updated. The new list of grids is produced to give a new COG. It is possible that the grids in old COG may become sufficiently dense to move out of new COG, while a previously inlier grid will not become a part of new $COG \implies |COG|=0$.

If the old COG retains some of its grids post $x_{i}$’s insertion, while some grids are removed due to increase in $'mglos'$ value, then $|COG|<q$. If no loss in new COG is observed due to redundant insertion on same grid (s), $|COG|=q, \therefore 0 \le$ |COG| $\le q.$ However, if previously empty grids are affected across insertions then at most all the grids may become non-empty. In that case, $q = q_{max} \therefore 0 \le$ |COG| $\le q_{max}$.

Lemma 2

Degree of outlierness $\forall p \in D \propto 1/glos (p)$.

Proof

From definition of $'glos'$ value for any $p \in D$ (Sect. 2), we have $glos (p) =$ f(z-score(p)) [40]. $\because$ $z-score (P,Q)= \frac{P-Q}{\sigma _{Q}}$ where P is the density of x wrt. any grid $g_{c}$ and Q is the mean local density of the included kernel centers within $g_{c}$, $\therefore$ if $z-score (P,Q)>>0 \implies \frac{P-Q}{\sigma _{Q}}>>0 \implies P>>Q$ $[\sigma _{Q} \ne 0].$ Therefore, a highly dense point p has higher $'glos'$ value. A low density point ($P<<Q$) has low $'glos'$ value and hence an higher probability of being an outlier. Effectively, grids containing points with lower $'glos'$ values are more probable to become a part of COG.

7 Related work

A study regarding incremental outlier detection known as iLOF [22] provides an insight about handling high velocity data streams. A similar work: I-IncLOF [14] considers sliding window to designate a set of points as inliers or outliers. The concept of KDE is also employed in another method involving data streams [24] for detecting local outliers. Another work that uses the local KDE [32] provides a simple yet efficient technique to find the density based outliers. The work proposed by Tang et’al introduces a relative density-based outlier score (RDOS) in order to measure the degree of local outlierness. The distribution of density for an object is computed by leveraging the idea of local KDE and extended nearest neighbors of the object.

Use of K-nearest neighbor classification is also done in [16] for detecting outliers in HTTP traffic data. The approach in this work incrementally learns the new traffic anomalies with advent of more data samples. An alternative novel adaptive outlier detection approach known as GEM [13] efficiently detects anomalies at a given level of significance. Moreover, for detecting online anomalies in unmanned vehicles, another research [15] has been carried out with encouraging results. We also covered a traditional KNN-based anomaly detection approach for detecting outliers in large scale traffic data [7], a method which we chose to extend in an adaptive manner. Few prominent distance-based algorithms were also proposed [17, 25] to extract outliers from large datasets and are also scalable over large data streams [5].

Among the latest works in outlier detection, a prominent survey [35] by Wang et’al extensively covers the evolution of relevant algorithms over a period of last two decades. Apart from categorizing the various outlier detection techniques based on their scheme of extraction, the work also assesses the associated challenges and advantages with these algorithms. While emphasizing the density-based outlier extraction approach, the survey [35] suggests the possibility of finding outliers from a lower density region containing inliers. A simiar survey [38] on anomaly detection by Xu et’al also highlighted the advantages and limitations of various classes of such algorithms. Distance-based outlier detection approaches were said to have issues related to parameter sensitivity and performance.

The application of outlier detection has found its usage in traffic problems. Anomalies in spatio-temporal traffic flow in urban areas [8] have been highlighted. The flow distribution is considered within a given time duration which enables construction of the flow distribution probability (FDP). The FDP uses both the spatial and the temporal information. However, a KNN-based outlier detection scheme is adopted involving distance measures.

Challenges: Most of these existing outlier detection techniques either apply a distance-based approach which remains a costly option for dynamic environment or involve streaming data with expensive computations. Moreover, a lot of these methods also end up detecting only local outliers. Our grid-based approach coupled with the usage of KDE enables us to provide a global outlier detection algorithm without neglecting the regional sub-spaces. This makes our approach more robust to extract outliers from sub-spaces with varied densities.

8 Discussion and conclusion

In this work, we proposed an adaptive extension to the KNNOD [7] outlier detection algorithm known as KAGO. Our proposed approach relies on local density derived through KDE instead of any distance measure while determining the local outlier status of a point. The local outliers obtained from different sub-spaces designated through grids combine to produce a set of at most top-N global outliers. In a dynamic setup with incoming data points, KAGO enables an efficient outlier detection by selectively handling the data points within the affected grid instead of entire data-space. Experimental results on large network datasets and a market bidding data showed the greater efficiency of KAGO over KNNOD, $\therefore T_{point-adaptive} < T_{non-adaptive}$ (Refer Sect. 2). We also provided a brief description about the approximate correctness of the identified anomalies across datasets which shows that $O_{point-adaptive} \approx O_{non-adaptive}$ (Refer Sect. 2).

A potential limitation of the proposed approach may involve the choice of number of partitions per dimension (p). A large value of p would lead to creation of more grid cells resulting in complex computation. On the contrary, a lesser number of grid cells may result in overlooking of outliers from sub-spaces with low densities. Therefore, a trade-off exists between the grid size and the accuracy of the proposed approach. Our choice of p in the experimental procedure was aimed at generating a reasonable number of grid cells for computation. The accumulation of grid cells in COG potentially overrides the effect of the size of a cell. We have made a conscious effort not to reduce the value of p any further while extracting outliers from regions of varied granularity.

Another important factor is the formation of set COG. As per KAGO algorithm, half of the non-empty grid cells with lesser mglos scores constitute the initial formation of COG. With repeated insertions, the size of COG may reduce significantly. The extent of reduction in the size of COG may be influenced by the initial choice of the number of grid cells within it. This may have an impact on the overall extraction of outliers from the entire data space. We additionally observed that upon insertion of new data points, there exists a possibility of dense grid cells being filled up. In that case, the sparse regions of the data space may retain similar outlier configuration across insertions. The scheme followed by the KAGO algorithm requires computation of COG for finding such outliers from sparse regions. Although the number of such grid cells within the COG may be relatively less, this may involve redundant computation in extracting the desired outliers.

As a part of our future work, we intend to compare our method with other state of the art outlier detection algorithms. Also, it will be interesting to observe the influence or other kernels apart from the Gaussian kernel on the overall outliers extraction process.