1 Introduction

Fault detection and isolation (FDI) is an important issue in many applications, such as chemical plants [1, 2], power plants [3, 4], to ensure the reliability, safety and efficient operation as well as higher performance of the whole system. A fault is defined as an unallowable deviation of a variable or parameter of the system from the normal condition [5]. The FDI problem is the task of responding to abnormal events in a process and consists of three steps, indicating if there is a fault, determining the location and estimating the size and nature of the fault [6]. Toward these end, a set of residuals are generated which are sensitive to faults and insensitive to disturbances and modeling errors. These residuals should be zero mean in the normal conditions. Then, the residuals are used to make decisions on the occurrence of a fault and on the type of the fault occurred.

An extensive research on FDI methods has already been reported in the literature which can be classified into two general categories, model-free [7,8,9] and model-based methods. Model-based methods are divided into quantitative methods, such as observer-based or Kalman filter-based methods, qualitative (knowledge-based) methods, such as fuzzy methods, and data-driven methods, such as neural network-based methods. Venkatasubramanian et al. have summarized a collection of these methods in a three-part review paper [10,11,12] with applications in process chemical engineering. Hwang et al. [13] have written a survey paper that focuses mainly on the quantitative model-based approach for FDI. Parity relation method is another quantitative model-based method which has been used by some researchers [14, 15]. Kalman filter (KF) is a well-known recursive technique for state and parameter estimation. Using the extended Kalman filtering (EKF) for fault detection and diagnosis in chemical processes has been demonstrated in [16, 17]. In [18], a KF has been proposed for FDI in a continuous stirred tank reactor (CSTR) to cope with external disturbances and unpredictable faults. Saravanakumar et al. [19] has also used a bank of KFs for detecting and isolating incipient additive faults in Wind Turbine Generators DFIG and PMSM under possible changes in the reference/disturbance as well as modeling/parametric uncertainties. In [20], a method based on the EKF has been proposed for sensor FDI in interior permanent-magnet synchronous motors (IPMSMs).

On the other hand, knowledge-based and data-driven approaches have received considerable attention in the recent years [21, 22]. Soft computing techniques such as fuzzy inference systems (FISs) and neural networks (NNs) are able to approximate smooth nonlinear functions with arbitrary accuracy and are important in developing intelligent FDI techniques for nonlinear systems. Neural networks due to their fast and robust implementation, their performance in learning any nonlinear mappings and their ability for pattern recognition have been effectively used for FDI purposes. A survey paper by Angeli et al. [23] focuses on numerical and artificial intelligence FDI methods. Various applications of FIS and NN methods in FDI can be found in [24,25,26,27,28]. Simani et al. [29] proposed a fault diagnosis scheme based on the identification of fuzzy model, in order to detect and isolate the faults in a wind turbine simulator. Garci [30] has applied parameter estimation to devise nonlinear FDI techniques using multi-layer perceptron neural network (MLPN) as functional approximator. Benkouider et al. [31] presented a diagnosis algorithm in batch and semi-batch reactor using the EKF for estimating the heat transfer coefficient of the reactor and a probabilistic NN for fault classification.

FDI schemes were developed for nonlinear systems based on neuro-fuzzy networks (NFN) [32,33,34] by merging FIS and NN, which utilize the transparency property derived from FIS and the learning ability from NN. Viharos et al. [35] provided a survey on the application of neuro-fuzzy systems for technical diagnostics and measurement. Khireddine et al. [36] presented a scheme for FDI via artificial neural networks and fuzzy logic to deal with sensors and actuator fault of a three links SCARA robot. In [37], a NFN-based scheme for FDI of a steam generator is presented. First, a NFN of Takagi–Sugeno model trained using locally linear model tree (LOLIMOT) algorithm is used for residual generation and then a NFN of Mamdani model is employed for decision making. The most widely used type of NFNs is referred to as adaptive neuro-fuzzy inference system (ANFIS) by Jang [38]. Banu et al. [39] have used ANFIS-based dedicated observers for sensor fault detection in a CSTR. In [40], an ANFIS-based fault detection and diagnosis of pneumatic valve used in cooler water spray system in cement industry has been developed.

In summary, quantitative approaches use an analytical model of the system for FDI purposes. One of the major advantages of these approaches is having control over the behavior of the residuals. Also, the model parameters have physical meaning that can be used for fault isolation and the variables status may be an index for the magnitude of the occurred fault. On the other hand, qualitative and data-driven approaches such as NN-based and NFN-based techniques are powerful techniques for developing models with arbitrary accuracy, but they lead to “black-box” and “gray-box” models, respectively. Therefore, they do not give reasonable physical interpretation to the process dynamics. Meanwhile, these methods need larger computational facilities and memory for large-scale systems, resulting in more hardware and software efforts. This issue is considered as the basic challenge for using these approaches in industries. Nevertheless, these methods are capable of accommodating human knowledge in the decision-making process of FDI to increase the reliability of the fault diagnostic system.

The major motivation of this work is to combine the advantages of the aforementioned FDI approaches in order to develop a new method to overcome the drawbacks of previous methods. There are similar techniques in the literature for some applications [41, 42]. In [41], a fault detection and isolation scheme for a dual spool gas turbine engine is developed. A dynamic neural network-based multiple-model scheme is proposed in which a bank of dynamic neural networks acts as an estimator of the various faulty modes. Tong et al. [42] combined data-driven and observer-design methodology for FDI in hybrid process systems by integrating Gaussian mixture models (GMM), subspace model identification (SMI), and unknown input observer (UIO) theory. In this paper, an approach based on the combination of EKF and NFN is proposed for both actuator and sensor fault detection and identification (FDI). Firstly, an EKF is designed to estimate the system output and to generate accurate residuals by a mathematical model of the process. Then, the generated residuals are fed to a classifier network which is a NFN. This NFN maps the patterns from the mean value of the residual space into a decision space. The mean of the residuals, as a valuable feature, is a useful tool for detecting various faults of the system. By averaging the residual over a period of time, the false alarm due to spike-like disturbances can be avoided. On the other hand, since the residuals have physical interpretation, they can be directly used for generating NFN rules. We will use LOLIMOT algorithm to train the NFN. This network assigns a locally linear model to each faulty mode of the system in which the validity of each model is determined based on the fuzzy rules.

This paper is organized as follows. Next section presents the proposed FDI method, which is based on the EKF approach for residual generation and NFN approach for decision making. In Sect. 3, the overall model of the CSTR process is described to be used for case study. The simulation results of the implementation of the proposed method on the CSTR model are presented in Sect. 4. Finally, the conclusions are given in Sect. 5.

2 The proposed FDI method

A remarkable point in the model-based and data-driven methods is that each one gives an approach completely independent of the other. For instance, model-based methods try to model all conditions of the system and to consider a distinct model for each faulty mode. Indeed, many of these methods use a bank of observers, each one responsible for detecting a special fault leading to high computational complexity in the fault diagnosis problem.

On the other hand, data-driven methods do not require a detailed mathematical model of the system, leading to a large amount of features without physical interpretations. Thus, one has to select some features without knowing much about them. This will increase the computational burden of the problem and makes it improper for real-time applications.

In this paper, we introduce a technique for FDI which is based on a combination of model-based and data-driven methods and employs the benefits of each method to result in an efficient FDI method.

Given a nonlinear system model, the EKF is designed to estimate the state variables of the system. The difference between the actual system output and the output estimated by EKF is considered as the residuals. Then, the obtained residuals are used for training NFN. A unique feature of the residuals is that they have a physical interpretation and are limited to the number of the system outputs. Unlike model-based methods, in which there exist a lot of features, the number of features is limited in the proposed method.

In normal conditions, the mean of the residuals remains close to zero, but when a fault occurs, correlation between the normal condition model and the actual system is disturbed, causing some of these residuals to be nonzero. However, a challenge in employing the residuals as features is that they may change dynamically when a fault occurs. These dynamic changes can reduce the performance of the neural network. So, these dynamic features must somehow be converted into static and fixed characteristics for each fault.

In the proposed FDI method, we assume that the mathematical model of the system and the residuals of the Kalman filter in various faulty modes are available. With these assumptions, the algorithm of the proposed fault diagnosis method using an EKF and NFN is introduced as follows:

  1. a.

    The EKF is designed according to the mathematical model of the system.

  2. b.

    Residuals of the various faulty modes are collected as data, and the mean of each residual in different and distinct time window are considered as the features.

  3. c.

    If the features have severe dynamic changes, the static features should be extracted from the dynamic ones. “Severe dynamic change” may refer to a big gradient in the residuals.

  4. d.

    NFN rules are obtained by some qualitative analysis on the extracted features.

  5. e.

    Output layer parameters are obtained from the extracted features using least squared error (LSE) method.

In the next sections, these steps are described in detail. Figure 1 shows a general schematic diagram of the introduced fault diagnosis system.

Fig. 1
figure 1

Structure of fault diagnosis system using EKF and NFN

Full size image

2.1 Extended Kalman filter (EKF)

The KF is an optimal state estimator which is applied to stochastic dynamic systems. Information of the states (which is expressed by the covariance matrix) is corrected at each step using the previous estimations and the new data. The EKF is a generalization of the KF for nonlinear system in which the system is linearized around the last estimation of the filter. The EKF algorithm for continuous-time systems is summarized as follows [43]:

  1. 1.

    Consider the system equations as:

    $$\begin{aligned} \dot{\varvec{x}} = \varvec{f}\left( {\varvec{x},\varvec{u},\varvec{w},t} \right),\quad \;\varvec{w} \sim N\left( {0,\varvec{Q}} \right) \hfill \\ \varvec{y} = \varvec{h}\left( {\varvec{x},\varvec{v},t} \right),\quad \quad \quad \varvec{v} \sim N\left( {0,\varvec{R}} \right) \hfill \\ \end{aligned}$$
    (1)

    where t is the time, x is the state vector, u is the plant input vector, y is the output vector, and w and v are zero mean normally distributed process and measurement noise vectors with covariance matrices Q and R, respectively.

  2. 2.

    Obtain the matrices of the system linearized around the estimated variables of the KF (\(\hat{\varvec{x}}\)):

    $$\varvec{A} = \left. {\frac{{\partial \varvec{f}}}{{\partial \varvec{x}}}} \right|_{{\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}} ,\quad \varvec{B} = \left. {\frac{{\partial \varvec{f}}}{{\partial \varvec{u}}}} \right|_{{\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}} ,\quad \varvec{L} = \left. {\frac{{\partial \varvec{f}}}{{\partial \varvec{w}}}} \right|_{{\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}} ,\quad \varvec{C} = \left. {\frac{{\partial \varvec{h}}}{{\partial \varvec{x}}}} \right|_{{\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}} ,\quad \varvec{M} = \left. {\frac{{\partial \varvec{h}}}{{\partial \varvec{v}}}} \right|_{{\varvec{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} }}}$$
    (2)
  3. 3.

    Calculate the corresponding covariance matrices:

    $$\tilde{\varvec{Q}} = \varvec{LQL}^{T} , \tilde{\varvec{R}} = \varvec{MRM}^{T}$$
    (3)
  4. 4.

    Execute the following KF equations recursively:

    $$\begin{aligned} \hat{\varvec{x}}\left( 0 \right) & = E\left[ {\varvec{x}\left( 0 \right)} \right] \\ \varvec{P}\left( 0 \right) & = E\left[ {\left( {\varvec{x}\left( 0 \right) - \hat{\varvec{x}}\left( 0 \right)} \right)\left( {\varvec{x}\left( 0 \right) - \hat{\varvec{x}}\left( 0 \right)} \right)^{T} } \right] \\ \varvec{\dot{\hat{x}}}\left( t \right) & = \varvec{f}\left( {\hat{\varvec{x}},\varvec{u},\varvec{w}_{0} ,t} \right) + \varvec{K}\left[ {\varvec{y} - \varvec{h}\left( {\hat{\varvec{x}},\varvec{v}_{0} ,t} \right)} \right],\quad w_{0} = 0,\quad v_{0} = 0 \\ \varvec{K} & = \varvec{PC}^{T} \tilde{\varvec{R}}^{ - 1} \\ \dot{\varvec{P}} & = \varvec{AP} + \varvec{PA}^{T} + \tilde{\varvec{Q}} - \varvec{PC}^{T} \tilde{\varvec{R}}^{ - 1} \varvec{CP} \\ \end{aligned}$$
    (4)

where K is the Kalman gain, P is the error covariance matrix, and \(\hat{\varvec{x}}\left( 0 \right)\) and P(0) are the initial values of the estimated states and covariance matrix. The idea of utilizing the KF in FDI systems is based on the fact that the residuals in stochastic linear systems are white noise with zero mean, as long as the KF is fully compliant with the model of the system. For using the KF for fault diagnosis purposes, it must be set based on the normal condition of the system. In this case, when a fault is occurred, the mean of the residuals will be nonzero. The idea of multiple-model KF (MMKF) approach in the model-based FDI methods includes designing a bank of KF, each one sensitive to a certain fault [44, 45]. The FDI system based on multiple-model EKF (MMEKF), as shown in Fig. 2, consists of a bank of parallel EKF. A normal EKF model provides with the best estimation of the system under its normal operating condition, but other filters are designed for faulty modes, each filter for a specific fault. As can be seen in Fig. 2, the EKF is getting feedback from the residuals. What is important for the EKF is the accurate estimate of the original system state variables, in both the normal and faulty conditions. Therefore, an intelligent KF is a filter that can match with various operating conditions of the system and modify its parameters for accurate estimation of the system state variables in each circumstance.

Fig. 2
figure 2

FDI system based on the MMEKF

Full size image

Residuals of the various faulty modes are generated from the EKF, and the mean of the residuals is collected as the features. These features are employed to make decisions on the occurrence of a fault and on the type of the fault occurred. Toward this end, a NFN is designed.

2.2 Neuro-fuzzy structure design by the extracted features from the residuals

In this section, a NFN is designed for FDI using the features obtained from the residuals. What is notable about this method and distinguishes it from other methods is simultaneous utilization of model-based and data-driven techniques. The main advantage of using the model is to provide the residuals which have physical interpretation from system behavior. The residuals behavior is zero mean in the normal condition, but the mean of all residuals or some of them will exceed from zero in the faulty condition. So, the mean of the residuals contain useful information from the faulty condition.

Now suppose that the system has p outputs and consequently p residuals. The mean of these p residuals over a period of time will be as the inputs of the NFN. The averaging interval is selected by experience and is dependant to the system dynamics. If the averaging interval be very small, the calculated mean value is not really a mean and the fault amplitude may be obtained incorrectly, and if it be very large, the occurrence of some transient faults may not be diagnosed.

Let’s consider k different types of the faults (faulty modes). The network should be trained by various values of each fault. Usually this is performed using small, medium and large quantities of the faults. Thus, for the jth faulty mode, commensurate with its importance or possession of the data, there exist n(j) different categories, each one representing a different amplitude of this fault, in which n is a function that determines the number of data categories corresponding to each faulty mode. A linear model is obtained for each category, and in fact, different amplitudes of the fault are identified using locally linear models. The validity of each model is determined based on its associated fuzzy rule. Figure 3 shows the structure of this NFN. As can be seen, the inputs of the blocks are not required to be the same for modeling different types of faults. This allows the designer to remove unnecessary inputs according to available information and experiences from the system. This network has k outputs (the same number as the various faulty modes), each one of which estimates the amplitude of a certain fault. At the following, the relations of this network are given for a system with two outputs \(\left\{ {x_{1} ,x_{2} } \right\}\), whose residual are the inputs of the network.

Fig. 3
figure 3

NFN proposed for fault diagnosis

Full size image

The rules corresponding to normal condition:

$${\text{If}}\quad \left( {x_{1} \in A_{0} } \right)\; {\text{and}}\; \left( {x_{2} \in B_{0} } \right),\;{\text{then}}\;\varvec{F}_{0} = \varvec{X}_{0}\varvec{\theta}_{0} ,\;\varvec{\omega}_{0} = { \hbox{min} }\left( {A_{0} \left( {x_{1} } \right), B_{0} \left( {x_{2} } \right)} \right),\,\; {\text{and}}\;{\text{NCI}} =\varvec{\omega}_{0} \varvec{F}_{0}$$
(5)

Here, the features are considered as the inputs of locally linear models and are denoted by X. Also, \(\varvec{F}_{0} ,\varvec{ X}_{0} ,\varvec{ \theta }_{0}\) are outputs, inputs and parameters of the locally linear models in the normal condition, respectively. The parameter “NCI” (normal condition index) is an index indicating the normal condition of the system, which is 1 in normal condition and close to 0 in faulty condition. It is used in order to recognize an unknown fault occurrence.

The rules corresponding to the jth faulty mode:

$$\begin{aligned} & {\text{If}}\;\left( {x_{1} \in A_{ji} } \right)\;{\text{and}}\;\left( {x_{2} \in B_{ji} } \right),\;{\text{then}}\;\varvec{F}_{ji} = \varvec{X}_{ji}\varvec{\theta}_{ji} ,\quad i = 1,2, .., n\left( j \right) \\ &\varvec{\omega}_{ji} = \hbox{min} \left( {A_{ji} \left( {x_{1} } \right), B_{ji} \left( {x_{2} } \right)} \right),\;{\text{and}}\;\varvec{y}_{j} = \mathop \sum \limits_{i = 1}^{n\left( j \right)}\varvec{\omega}_{ji} \varvec{F}_{ji} ,\quad j = 1,2, .., k \\ \end{aligned}$$
(6)

where \(\varvec{X}_{ji}\) represents the features of the ith category of the jth faulty mode, and Aji and Bji are the membership functions associated to these features. Also, \(\varvec{F}_{ji}\) is the output corresponding to the ith category of the jth faulty mode. yj is the total output corresponding to the jth faulty mode. These membership functions are chosen according to their corresponding feature amplitudes in each faulty mode illustrated in the next sections.

The parameters of each model are obtained using the least squared error (LSE) method applied to the train data as follows:

$$\varvec{\theta}_{ji} = \left( {\varvec{X}_{ji}^{T} \varvec{X}_{ji} } \right)^{ - 1} \varvec{X}_{ji}^{T} \varvec{F}_{ji}$$
(7)

According to the above description, it can be seen that the number of the locally linear model (N) is calculated to be:

$$N = \mathop \sum \limits_{j = 1}^{k} n\left( j \right)$$
(8)

3 Description of the CSTR process

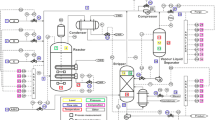
In order to demonstrate the proposed method, a model of CSTR process is developed in which an irreversible and exothermic reaction takes place and run in a liquid–gas phase. Figure 4 shows the schematic diagram of the CSTR process. A feeding flow of reactant enters into the reactor, resulting in an exothermic reaction with the catalyst therein. A stirring system mixes the fluid perfectly and a product with uniform concentration leaves the reactor. A jacket is fitted around the reactor, and a coolant flows through it. This jacket has the task of removing the heat from the reactor.

Fig. 4
figure 4

CSTR process and its control loops used by Luyben [46]

Full size image

This process has been completely investigated by Luyben, and its differential equations have been well expressed [46]. Various CSTRs have been employed in the literatures which differ in their control valves location. In this work, we have used the model studied by Luyben.

This model consists of three control valves for process control. One of these valves has been designed in order to control the pressure of the gas generated in the reactor by controlling the output flow of this gas. The second valve controls the level of the product in the reactor using the output flow of the product, and the third one controls the temperature within the reactor and consequently the temperature of the product using the coolant flow. The goal of this process is to produce a product with a desired concentration and temperature after entering a feeding reactant with a certain concentration and specific temperature into the reaction vessel.

The measurable outputs of this process are the level (L), the temperature (T) and concentration (CA) of final product, the coolant temperature (Tc), and the pressure within the vessel (P). The equations describing this process are as follows:

$$\begin{aligned} \frac{{{\text{d}}V}}{{{\text{d}}t}} & = F_{i} - F \\ \frac{{{\text{d}}C_{A} }}{{{\text{d}}t}} & = \frac{{F_{i} }}{V}\left( {C_{Ai} - C_{A} } \right) - r_{A} \\ \frac{{{\text{d}}T}}{{{\text{d}}t}} & = \frac{{F_{i} }}{V}\left( {T_{i} - T} \right) + \frac{{r_{A} \left( { - \Delta H} \right)}}{{\rho C_{p} }} - \frac{{UA\left( {T - T_{\text{c}} } \right)}}{{V\rho C_{p} }} \\ \frac{{{\text{d}}T_{c} }}{{{\text{d}}t}} & = \frac{{F_{c} }}{{V_{j} }}\left( {T_{ci} - T_{\text{c}} } \right) + \frac{{UA\left( {T - T_{\text{c}} } \right)}}{{V_{j} \rho_{j} C_{pj} }} \\ \frac{{{\text{d}}n}}{{{\text{d}}t}} & = r_{A} V - F_{vg} \\ PV_{g} & = nRT \\ r_{A} & = C_{d} C_{A} k_{0} {\text{e}}^{ - E/RT} \\ \end{aligned}$$
(9)

where the last equation is known as the reaction kinetic law. The parameters of this process are given in Table 1.

Table 1 Parameters of the CSTR
Full size table

4 Simulation results

4.1 Designing FDI system

To evaluate the proposed FDI algorithm, we simulate and apply it on the CSTR process for sensor and actuator fault diagnosis. Two types of sensor faults and two types of actuator faults are studied here. Hence, the designed diagnosis system has 4 outputs whose magnitudes demonstrate the magnitude of the fault identified by the NFN. The data corresponding to the fault of different parts are obtained by simulating the system in MATLAB/Simulink. The faults selected for this study are listed in Table 2. Different magnitudes of each fault are considered for training the network. In order to design a fault diagnosis system, the algorithm presented in the previous section will be run step by step.

Table 2 Train data set
Full size table

Step 1

Design the EKF

The state variables of the system are \(\varvec{X} = \left[ {\begin{array}{*{20}c} V & {C_{A} } & {T } \\ \end{array} \begin{array}{*{20}c} {T_{c} } & n \\ \end{array} } \right]\). The Jacobian matrices A and C required in the EKF and also, the initial values of the matrices P, Q and R are as follows:

$$\begin{aligned} {\mathbf{A}} & = \left[\begin{array}{lllll} 0 & 0 & 0 & 0 & 0 \\ {F_{i} \frac{{(C_{A} - C_{Ai} )}}{{V^{2} }}} & { - \frac{{F_{i} }}{V} - C_{d} k_{0} {\text{e}}^{ - E/RT} } & {\frac{{ - C_{d} C_{A} k_{0} E{\text{e}}^{- E/RT} }}{{RT^{2} }}} & 0 & 0 \\ {F_{i} \frac{{(T - T_{i} )}}{{V^{2} }} + UA\frac{{(T - T_{c} )}}{{\rho C_{p} V^{2} }}} & { - \frac{\Delta H}{{\rho C_{p} }}C_{d} k_{0} {\text{e}}^{ - E/RT} } & { - \frac{{F_{i} }}{V} - \frac{UA}{{V\rho C_{p} }} - \frac{{C_{d} C_{A} k_{0} E{\text{e}}^{ - E/RT} }}{{RT^{2} }} \times \frac{\Delta H}{{\rho C_{p} }}} & {\frac{UA}{{V\rho C_{p} }}} & 0 \\ 0 & 0 & {\frac{UA}{{V_{j} \rho_{j} C_{pj} }}} & { - \frac{{F_{c} }}{{V_{j} }} - \frac{UA}{{V_{j} \rho_{j} C_{pj} }}} & 0 \\ {r_{A} } & {VC_{d} k_{0} {\text{e}}^{ - E/RT} } & {\frac{{VC_{d} C_{A} k_{0} E{\text{e}}^{ - E/RT} }}{{RT^{2} }}} & 0 & 0 \\ \end{array} \right] \\ {\mathbf{C}} & = \left[\begin{array}{lllll} 1 &\quad 0 &\quad 0 &\quad 0 &\quad 0 \\ 0\quad &\quad 1 &\quad 0 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad 1 &\quad 0 &\quad 0 \\ 0 &\quad 0 &\quad {\frac{nR}{{V_{g} }}} &\quad 0 &\quad {\frac{RT}{{V_{g} }}} \\ \end{array} \right]\,\,\,\,,\,\,\,\,{\mathbf{P}} = { 10}^{{{ - }\, 4}} \, \times \left[ \begin{array}{lllll} 1& 0& 0& 0& 0 \hfill \\ 0&1&0&0&0 \hfill \\ 0& 0& 1& 0& 0 \hfill \\ 0& 0& 0& 1& 0 \hfill \\ 0& 0& 0& 0& 1 \hfill \\ \end{array} \right] \\ {\mathbf{Q}} & = \left[ \begin{array}{*{20}c} {0.01} & {0.01} & {0.01} & {0.01} & {0.01} \\ {0.01} & {0.01} & {0.01} & {0.01} & {0.01} \\ {0.01} & {0.01} & {0.01} & {0.01} & {0.01} \\ {0.01} & {0.01} & {0.01} & {0.01} & {0.01} \\ {0.01} & {0.01} & {0.01} & {0.01} & {0.01} \\ \end{array} \right]\,\,\,\,,\,\,\,\,{\mathbf{R}} = \left[{\begin{array}{llll} {23} & 0 & 0 & 0 \\ 0 & {0.0055} & 0 & 0 \\ 0 & 0 & {3600} & 0 \\ 0 & 0 & 0 & {44.8} \\ \end{array} } \right] \\ \end{aligned}$$
(10)

Step 2

Extracting fault features using the mean of the residuals

In this step, the features are extracted from the residuals generated from the difference of the actual system output and the output estimated by EKF. The primary feature is obtained by averaging the original data over a period of time. An averaging window with the length of 100 data is selected for this reason. Using the “primary” term is because that the mean of some residuals may have dynamic behavior. An example of the dynamic changes in the mean behavior of the residual of the state variable V is shown in Fig. 5.

Fig. 5
figure 5

Mean of the residuals in the various faulty modes

Full size image

Step 3

Extracting static features from dynamic ones

As it is shown in Fig. 5, the residual of the state variable V in the faulty mode 1 has linear dynamic behavior. This dynamic behavior occurs, while the fault amplitude is constant during the corresponding period. This issue affects the performance of the NFN assigning a static linear model to the fault behavior in each section. On the other hand, if one wants to consider the dynamic in the linear model, the history of the residuals should be used as input to the model. This not only increases the computational costs, but also some tests are required to determine length of the historical data, complicating the design procedure. In such a condition, the method introduced in [47] makes the procedure simple and effective. Here, the slope of the residual of the state variable V, which is approximately constant, is employed as the static feature. Figure 6 shows the results of this conversion, and Fig. 7 represents the fault amplitude corresponding to the various faulty modes.

Fig. 6
figure 6

Static features of the residuals in the trained data sets

Full size image
Fig. 7
figure 7

Fault amplitude corresponding to the various faulty modes in the trained data sets

Full size image

Step 4

Determining NFN rules from the extracted features

Now, using the extracted features from the residuals, the NFN rules are determined. The number of the rules required for designing fault diagnosis system is at least equal to the number of the various faulty modes which in this case study is equal to 15. However, the traditional NFN with 5 inputs and 4 membership function for each input will need to 45 = 1024 fuzzy rules. As mentioned before, this reduction in the number of rules is a result of employing the residuals as the features. These residuals have physical interpretation and allow one to analyze simply the system status. The rules in each operating condition of the system are as follows.

The rules corresponding to the normal condition:

$$\begin{aligned} & {\text{If}}\;\left( {V \in A_{0} } \right)\;{\text{and}}\;(C_{a} \in B_{0} )\;{\text{and}}\;\left( {T \in C_{0} } \right)\;{\text{and}}\;\left( {T_{c} \in D_{0} } \right)\;{\text{and}}\;\left( {P \in E_{0} } \right),\quad {\text{then}}\;\varvec{F}_{0} = \varvec{X}_{0}\varvec{\theta}_{0} \\ &\varvec{\omega}_{0} = { \hbox{min} }\left( {A_{0} \left( V \right),\;B_{0} \left( {C_{a} } \right), C_{0} \left( T \right), D_{0} \left( {T_{c} } \right),E_{0} \left( P \right)} \right),\;NCI =\varvec{\omega}_{0} \varvec{F}_{0} \\ \end{aligned}$$
(11)

The rules corresponding to the first faulty mode:

$$\begin{aligned} & {\text{If}}\left( {V \in A_{1i} } \right)\; {\text{and}}\; (C_{a} \in B_{1} )\; {\text{and}}\; \left( {T \in C_{1} } \right)\; {\text{and}}\; \left( {T_{c} \in D_{1} } \right)\; {\text{and}}\; \left( {P \in E_{1} } \right),\,\;{\text{then}}\;\varvec{F}_{1i} = \varvec{X}_{1i}\varvec{\theta}_{1i} \quad i = 1,2,3 \\ &\varvec{\omega}_{1i} = { \hbox{min} }\left( {A_{1i} \left( V \right), B_{1} \left( {C_{a} } \right), C_{1} \left( T \right), D_{1} \left( {T_{c} } \right),E_{1} \left( P \right)} \right),\quad \varvec{y}_{1} = \mathop \sum \limits_{i = 1}^{3}\varvec{\omega}_{1i} \varvec{F}_{1i} \\ \end{aligned}$$
(12)

The rules corresponding to the second faulty mode:

$$\begin{aligned} & {\text{If}}\left( {V \in A_{2} } \right)\; {\text{and}}\; (C_{a} \in B_{2} )\; {\text{and}}\; \left( {T \in C_{2i} } \right)\; {\text{and}}\; \left( {T_{c} \in D_{2i} } \right)\; {\text{and}}\; \left( {P \in E_{2i} } \right),\,\;{\text{then}}\;\varvec{F}_{2i} = \varvec{X}_{2i}\varvec{\theta}_{2i} \quad i = 1,2,3 \\ &\varvec{\omega}_{2i} = { \hbox{min} }\left( {A_{2} \left( V \right), B_{2} \left( {C_{a} } \right), C_{2i} \left( T \right), D_{2i} \left( {T_{c} } \right),E_{2i} \left( P \right)} \right),\quad \varvec{y}_{2} = \mathop \sum \limits_{i = 1}^{3}\varvec{\omega}_{2i} \varvec{F}_{2i} \\ \end{aligned}$$
(13)

The rules corresponding to the third faulty mode:

$$\begin{aligned} & {\text{If}}\left( {V \in A_{3i} } \right)\; {\text{and}}\; (C_{a} \in B_{3} )\; {\text{and}}\; \left( {T \in C_{3} } \right)\; {\text{and}}\; \left( {T_{c} \in D_{3} } \right)\; {\text{and}}\; \left( {P \in E_{3} } \right),\,\;{\text{then}}\;\varvec{F}_{3i} = \varvec{X}_{3i}\varvec{\theta}_{3i} \quad i = 1,2,3,4 \\ &\varvec{\omega}_{3i} = { \hbox{min} }\left( {A_{3i} \left( V \right), B_{3} \left( {C_{a} } \right), C_{3} \left( T \right), D_{3} \left( {T_{c} } \right),E_{3} \left( P \right)} \right),\quad \varvec{y}_{3} = \mathop \sum \limits_{i = 1}^{4}\varvec{\omega}_{3i} \varvec{F}_{3i} \\ \end{aligned}$$
(14)

The rules corresponding to the fourth faulty mode:

$$\begin{aligned} & {\text{If}}\left( {V \in A_{4} } \right)\; {\text{and}}\; (C_{a} \in B_{4} )\; {\text{and}}\; \left( {T \in C_{4i} } \right)\; {\text{and}}\; \left( {T_{c} \in D_{4} } \right)\; {\text{and}}\; \left( {P \in E_{4} } \right),\,\;{\text{then}}\;\varvec{F}_{4i} = \varvec{X}_{4i}\varvec{\theta}_{4i} \quad i = 1,2,3,4 \\ &\varvec{\omega}_{4i} = { \hbox{min} }\left( {A_{4} \left( V \right), B_{4} \left( {C_{a} } \right), C_{4i} \left( T \right), D_{4} \left( {T_{c} } \right),E_{4} \left( P \right)} \right),\quad \varvec{y}_{4} = \mathop \sum \limits_{i = 1}^{4}\varvec{\omega}_{4i} \varvec{F}_{4i} \\ \end{aligned}$$
(15)

The above membership functions are selected so as to be related to the features in each faulty mode (see Fig. 6). For example, the membership functions of the input variable “V” in faulty mode 3 are shown in Fig. 8. Because there are four different amplitudes for this feature, four membership functions have been chosen whose horizontal axis’ values are equivalent to the amplitudes of the features.

Fig. 8
figure 8

Membership functions of “V” in faulty mode 3

Full size image

Step 5

Obtaining output layer parameters

The NFN consists of some locally linear model, each one of which takes the task of modeling a faulty mode. The fuzzy rules in such a system are to determine the validity of each local model. This is performed by using the superposition of fuzzy membership functions. The parameters of each model are obtained using LSE method as in (7). Since 15 different conditions have been considered for this system, 15 locally linear models are required for designing NFN.

4.2 Results analysis

In this section, we first train the designed network. Toward this end, 15 different feature sets are used, each one of which representing one situation of the system, as shown in Figs. 6 and 7. These feature sets have been obtained from the mean of the residuals or its derivative along with a data window corresponding to each situation. Then, the trained NFN is evaluated using the test data. In these tests, the performance of the designed system is investigated on 8 different data sets which have different values of the trained data. In each test data set, the system is initially in the normal mode and then, a specific fault takes place in the system at arbitrary moment. This is exactly consistent with reality. Besides, the EKF is a model-based estimator and works based on the dynamic equation of the system, which can be easily implemented on a microcontroller. Also, the proposed NFN is composed of some locally linear models and a few numbers of fuzzy rules, and thus, its implementation on a microcontroller is not very difficult. These demonstrate the possibility and feasibility of online implementation of the proposed method. Table 3 shows the various modes of the test data in the order of their occurrence. For each faulty mode, two different amplitudes are chosen to verify the effectiveness of the proposed FDI method in detection and identification of different types of the faults with different amplitudes. The extracted features of the test data residuals and the fault amplitude corresponding to the various faulty modes are depicted in Figs. 9 and 10, respectively.

Table 3 Test data set information
Full size table
Fig. 9
figure 9

Extracted features of the residuals in test data sets

Full size image
Fig. 10
figure 10

Fault amplitude corresponding to the various faulty modes in the test data sets

Full size image

Table 4 shows the mean squared error (MSE) criterion for NFN train and test data. Each column of this table corresponds to a specific faulty mode. As can be seen, for each test, only the column associated with that faulty mode has a nonzero value and the others are zero or close to zero. The correlation between fault mode 1 and 3 is because of their dependence to the input variable V. As can be seen from Fig. 9, this input has a significant correlation with the first and third faulty modes. Table 5 demonstrates the maximum correlation between different faulty modes. To compensate the errors introduced by the correlations in the outputs, the fuzzy membership functions in different faulty modes have been chosen so that the NFN can isolate the faults with correlation.

Table 4 MSE of test and train
Full size table
Table 5 Correlation between different fault types
Full size table

The results of the system performance for the test data sets are displayed in Fig. 11. This figure shows that the proposed FDI method is able to detect, isolate and identify various sensor and actuator faults with different amplitudes. The major advantages of the proposed method are listed as:

Fig. 11
figure 11

Result of fault detection and identification for test data sets

Full size image
  1. a.

    Possible to be implemented online.

  2. b.

    No need to a bank of observers for fault diagnosis.

  3. c.

    No need to model the faults.

  4. d.

    Acceptable accuracy in the estimation of sensor and actuator fault.

  5. e.

    Using the physical inference of various conditions of the state variables in extracting features of the residuals for generating NFN rules which lead to a reduction in FIS rules.

For better evaluation of the performance of the proposed method, the relative error and mean error of the estimation in different faulty modes in the test are depicted in Fig. 12. As can be seen, the maximum mean error is devoted to the level actuator fault which is about 10%. Large error in the faulty mode 1 and 2 may be related to the dynamic features therein (see Fig. 9). Meanwhile, this fault diagnosis method can estimate sensor fault better than the actuator fault.

Fig. 12
figure 12

Accuracy of the estimation of different faults in the test

Full size image

Comparison with other FDI methods is an alternative approach for evaluating the performance of the proposed EKF-NFN method. Figure 13 shows the result of the EKF-NFN method in comparison with the EKF method (proposed in [17]) for different fault types. As can be seen, the proposed method has better performance than the EKF method. Also, the MSE criterion for EKF-NFN is equal to 0.196, while for EKF is 0.343. These results demonstrate the effectiveness of the proposed FDI approach.

Fig. 13
figure 13

Comparison of the proposed method with EKF method

Full size image

5 Conclusions

In this paper, a fault detection and identification (FDI) method has been proposed for nonlinear systems based on EKF and NFN. This method uses the capabilities of both model-based and data-driven approaches. It is shown that the mean of the residuals can be used for FDI as a valuable feature which possess the fault information. The major advantages of using the residuals in designing the NFN are firstly limitation of their number to the number of outputs (hence, the number of the used features are not too many) and secondly the physical interpretation that helps with determination of fuzzy rules. This leads to a significant decrease in the required fuzzy rules in the proposed method over other methods. In the NFN developed in this work, a locally linear model is assigned to each faulty mode of the system in which the validity of each model is determined based on the corresponding fuzzy rules. Finally, a fault diagnosis system is designed and tested on the CSTR plant. Its results demonstrate the acceptable performance of the presented algorithm in detecting, isolating and identifying various sensor and actuator faults with different amplitudes. The main advantages of the proposed method are: no need to a bank of observers, no need to the fault modeling and also reduction in the fuzzy rules because of using the residuals. The dependence on the mathematical model of the system can be mentioned as the major disadvantage of the proposed approach which is an unavoidable property of the model-based methods.