Improved 3D reconstruction method based on the Scheimpflug principle

Abstract

This paper proposes a 3D reconstruction scheme for monocular cameras based on an improved line structure cursor positioning method and the Scheimpflug principle to overcome the limitations of current calibration methods for line-structured light 3D reconstruction and binocular stereo vision matching. Unlike the traditional line structure cursor positioning method, the line-structured light is projected on a blank area of a high-precision chessboard target to avoid the low corner point extraction accuracy caused by the intersection of the structured light strip and the chessboard target. The 3D coordinates of the point in the camera coordinate system can be obtained by combining the linear equation between the origin and the center point of the light stripe on the target and the plane equation of the target. The light plane equation is obtained through data fitting on the basis of the 3D information of the light stripe center of two or more pictures. The experimental system allows the position relationship of the light source, lens, and complementary metal oxide semiconductor to meet the Scheimpflug conjugate’s clear imaging conditions for improving the visual range of the measurement system. Results show that the measurement system obtains good measurement accuracy and robustness.

1 Introduction

Line-structured light is widely used in 3D contour detection of object surfaces because of its noncontact feature, large measurement range, and fast response [1, 2]. The calibration accuracy of the line-structured light determines the measurement accuracy of the system [3]. At present, the line structure cursor positioning technique proposed by Huynh is commonly used to fit the light plane using the principle of cross ratio invariance [4, 5]. This method uses the collinear corner points of three known coordinates on the chessboard target and utilizes the principle of cross ratio invariance to find the intersection coordinates of the three points. A light plane equation is fitted after obtaining the point coordinates of multiple light planes. This calibration method is simple, fast, and highly accurate. However, it requires intersecting the line-structured light with the chessboard target, and has certain limitations in extracting the target corner points and the center line of the light stripe [6, 7].

This paper proposes an improved line structure cursor positioning method to address the above-mentioned limitations. The line-structured light is projected on the blank area of the chessboard target, and the central feature point of the light stripe is extracted [8, 9]. A straight line equation between the feature point and the origin of the camera coordinate system can be obtained using the internal parameters of the camera and the normalized image plane. The plane equation of the chessboard target can be obtained from its rotation and translation matrices relative to the camera coordinate system [10]. The 3D coordinates of the feature points in the camera coordinate system can be obtained using the two above equations, and then the 3D coordinates of all feature points can be determined [11, 12]. At least two chessboard targets with different attitude pictures under line-structured light projection are required to fit the light plane rather than using one picture. The chessboard target is replaced with a displacement platform and the object to be measured. The 3D topography of the object surface is restored by taking multiple pictures, coordinate transformation, and data fitting on the basis of the advantages of the large measurement range of the Scheimpflug principle [13,14,15].

2 Measurement principle

2.1 Scheimpflug principle

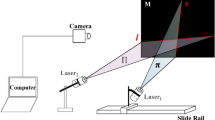
The imaging optical path used by the measurement system is shown in Fig. 1, where $O_{{\text{c}}} X_{{\text{c}}} Y_{{\text{c}}} Z_{{\text{c}}}$ is the camera coordinate system, ${\text{Ouv}}$ is the pixel coordinate system, and $O_{{\text{w}}} X_{{\text{w}}} Y_{{\text{w}}} Z_{{\text{w}}}$ is the world coordinate system. The distance from $O_{{\text{c}}}$ to $O_{{\text{s}}}$ is the focal length, $\alpha$ is the angle between the imaging and lens planes, and $\theta$ is the angle between the light and lens planes. The line-structured light is projected by a laser light source to a blank area on the plane of the chessboard target. The laser light, lens main plane, and complementary metal oxide semiconductor (CMOS) intersect at point $O_{{\text{l}}}$. The imaging formula is expressed as:

$$\frac{1}{l} + \frac{1}{{l^{^{\prime}} }} = \frac{1}{{l_{0} }} + \frac{1}{{l_{0}^{^{\prime}} }}$$

(1)

where $l$ and $l^{^{\prime}}$ are the object and image distances of $P$, respectively, and $l_{0}$ and $l_{0}^{^{\prime}}$ are the object and image distance of point $Q$, respectively. On the basis of the similarity of $\Delta P^{^{\prime}} {\text{MO}}_{{\text{m}}}$ and $\Delta P{\text{NO}}_{{\text{m}}}$, we have

$$l^{^{\prime}} \tan \left( {\frac{\pi }{2} - \alpha } \right) = l\tan \left( {\frac{\pi }{2} - \beta } \right)$$

(2)

where $\frac{\pi }{2} - \alpha$ is the angle between the imaging plane and the optical axis of the lens, and is replaced by $\varphi$, and $\frac{\pi }{2} - \beta$ is the angle between the light and lens planes, and is replaced by $\theta$. Thus, Eq. (2) can be rewritten as:

$$l^{^{\prime}} \tan \varphi = l\tan \theta$$

(3)

Fig. 1

Scheimpflug imaging principle and system optical path diagram

Equation (3) is the mathematical expression of the Scheimpflug principle. For the light path that meets the Scheimpflug condition, any object moving in the direction of the light plane can become a clear image on the imaging plane [13, 14].

As shown in Fig. 1, the point corresponding to point $P$ on the imaging plane is $P^{^{\prime}}$, and the point corresponding to point $Q$ on the imaging plane is $Q^{^{\prime}}$.The distance between $P$ and $Q$ is $h$, and the corresponding distance on the imaging plane is $x$. The geometric relationship of $h$ and $x$ can be expressed as:

$$h = \frac{lx\sin \varphi }{{l^{^{\prime}} \sin \theta + x\sin \;(\theta + \varphi )}}$$

(4)

The system resolution calculated using Eq. (4) is expressed as:

$$\frac{dh}{{dx}} = \frac{{ll^{^{\prime}} \sin \theta \sin \varphi }}{{\left[ {l^{^{\prime}} \sin \theta + x\sin (\theta + \varphi )} \right]^{2} }}$$

(5)

where $\frac{dh}{{dx}}$ is the physical distance corresponding to a single pixel. The smaller the $\frac{dh}{{dx}}$, the higher will be the system accuracy.

As shown in Fig. 2, increasing $\theta$ and decreasing $\varphi$ can improve the resolution of the system, and the resolution is maximum when $\varphi { + }\theta$ is around $60^{ \circ }$. Therefore, $\beta$ should be decreased and $\alpha$ should be increased to satisfy this condition during the measurement. Thus, $\beta$ is chosen between $50^{ \circ }$ and $65^{ \circ }$ because the proposed calibration method aims to control $\alpha$ within $6^{ \circ }$.

Fig. 2

a Effect of $\varphi$ and $\theta$ on resolution; b effect of $\varphi { + }\theta$ on resolution

2.2 Calibration principle

As shown in Fig. 1, the coordinate of point $P$ on the laser strip in the camera coordinate system is $\left( {x_{{\text{c}}} ,y_{{\text{c}}} ,z_{{\text{c}}} } \right)^{T}$, and the coordinate in the world coordinate system is $\left( {x_{{\text{w}}} ,y_{{\text{w}}} ,z_{{\text{w}}} } \right)^{T}$. The projection of $P$ in the pixel coordinate system is $P^{^{\prime}}$. Let the coordinates of $P^{^{\prime}}$ in the camera coordinate system be $\left( {x_{{\text{c}}}^{^{\prime}} ,y_{{\text{c}}}^{^{\prime}} ,z_{{\text{c}}}^{^{\prime}} } \right)^{T}$. The $X_{e} O_{e} Y_{e}$ plane is a virtual plane, which is 1 unit away from the origin of the camera coordinate system, and the projection of point $P$ on this plane is $P^{\prime \prime }$. Let $P^{\prime \prime }$ be $\left( {x_{{\text{c}}}^{\prime \prime } ,y_{{\text{c}}}^{\prime \prime } ,1} \right)^{T}$ in the camera coordinate system and $\left( {u,v,1} \right)^{T}$ in the pixel coordinate system. On the basis of the calibration rule, we have:

$$\left( {\begin{array}{*{20}c} u \\ v \\ 1 \\ \end{array} } \right) = M\left( {\begin{array}{*{20}c} {x_{{\text{c}}}^{\prime \prime } } \\ {y_{{\text{c}}}^{\prime \prime } } \\ 1 \\ \end{array} } \right)$$

(6)

$$\left( {\begin{array}{*{20}c} {x_{{\text{c}}} } \\ {y_{{\text{c}}} } \\ {z_{{\text{c}}} } \\ 1 \\ \end{array} } \right){ \, = \,}\left( {\begin{array}{*{20}c} R & T \\ {0^{T} } & 1 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {x_{{\text{w}}} } \\ {y_{{\text{w}}} } \\ {z_{{\text{w}}} } \\ 1 \\ \end{array} } \right)$$

(7)

where $M$ is the internal parameter matrix of the camera, and $R$ and $T$ are the rotation matrix and translation vector between the world and the camera coordinate systems, respectively [10]. The coordinates of point $P^{\prime \prime }$ in the camera coordinate system can be obtained using Eq. (6):

$$\left( {\begin{array}{*{20}c} {x_{{\text{c}}}^{\prime \prime } } \\ {y_{{\text{c}}}^{\prime \prime } } \\ 1 \\ \end{array} } \right) = M^{ - 1} \left( {\begin{array}{*{20}c} u \\ v \\ 1 \\ \end{array} } \right)$$

(8)

The equations of the chessboard target plane in the world and camera coordinate systems are expressed as:

$$A_{{\text{w}}} X + B_{{\text{w}}} Y + C_{{\text{w}}} Z + D_{0} = 0,$$

(9)

$$A_{{\text{c}}} X + B_{{\text{c}}} Y + C_{{\text{c}}} Z + D_{1} = 0.$$

(10)

On the basis of Eqs. (7), (8), and (9), the plane equation of the chessboard target in the camera coordinate system can be obtained as:

$$\left( {\begin{array}{*{20}c} {A_{{\text{c}}} } & {B_{{\text{c}}} } & {C_{{\text{c}}} } & {D_{1} } \\ \end{array} } \right){ = }\left( {\begin{array}{*{20}c} 0 & 0 & 1 & 0 \\ \end{array} } \right)\left( {\begin{array}{*{20}c} R & T \\ {0^{T} } & 1 \\ \end{array} } \right)$$

(11)

In the camera coordinate system, the 3D coordinates of point $P$ can be obtained from the straight line equations of points $P$ and $P^{\prime \prime }$ and the plane equations of the chessboard target, which can be expressed as:

$$\left( {\begin{array}{*{20}c} {x_{{\text{c}}} } & {y_{{\text{c}}} } & {z_{{\text{c}}} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\frac{{ - D_{1} x_{{\text{c}}}^{\prime \prime } }}{{A_{{\text{c}}} x_{{\text{c}}}^{\prime \prime } + By_{{\text{c}}}^{\prime \prime } + C}}} & {\frac{{ - D_{1} y_{{\text{c}}}^{\prime \prime } }}{{A_{{\text{c}}} x_{{\text{c}}}^{\prime \prime } + By_{{\text{c}}}^{\prime \prime } + C}}} & {\frac{{ - D_{1} }}{{A_{{\text{c}}} x_{{\text{c}}}^{\prime \prime } + By_{{\text{c}}}^{\prime \prime } + C}}} \\ \end{array} } \right)$$

(12)

The 3D coordinates of all feature points on a calibration image in the camera coordinate system can be repeated. The position of the chessboard target is changed to obtain the 3D coordinates of the center point of the light strip on at least two pictures in the camera coordinate system. Then, the equation of the light plane in the camera coordinate system can be fitted as:

$$A_{{\text{l}}} X + B_{{\text{l}}} Y + C_{{\text{l}}} Z + D_{2} = 0$$

(13)

The object to be measured is placed on a displacement platform for linear motion at a uniform speed and captured at every fixed distance. In the camera coordinate system, the 3D coordinates of the feature points on each picture can be obtained using Eqs. (12) and (13). Then, the 3D contour information of the object surface can be reconstructed [11, 12].

3 Experiment and discussion

The experimental system device is shown in Fig. 3a. The camera used is Daheng VEN-134-90U3M, with a resolution of 1280 × 1024. The chessboard target uses a 13 × 10 ceramic target. The lens, CMOS, and line laser generators are placed on sliding guides and intersect at one point. The angle between the lens main plane and the CMOS can be changed by changing the angle between the guide rails. The lines of the structured light are projected to a chessboard target. The position of the target is changed, and four photo-plane calibration pictures are captured, as shown in Fig. 3b. The light source is turned off, and eight chessboard target pictures are captured at different positions to calibrate the camera [10, 11]. Then, the feature points in the center of the light strip on the chessboard target are extracted. In the camera coordinate system, the 3D coordinates of the center point of the light strip of the four pictures are obtained using the linear and the chessboard target plane equations. The light plane is fitted using the least square method.

Fig. 3

a Experimental device; b light plane calibration picture

The main methods used to extract the center of the light strip include the Steger algorithm, gray center of gravity, and direction template methods. The Steger algorithm has the highest extraction accuracy, but is the slowest among the three methods [16]. The two other methods have fast extraction speed, but their extraction accuracy is lower than that of the Steger algorithm. Table 1 lists the time required for several algorithms to process the same image [6,7,8,9].

Table 1 Extraction time of the three algorithms

The gray center of gravity method is developed on the basis of the extremum and threshold methods. This method adopts the principle of weighted average of pixels whose gray value is greater than the threshold value and less than the extremum as the center point of light stripe. In this manner, although the gray value on the cross section of the light stripe fails to meet the strict Gaussian distribution, the gray center of gravity method can still extract the coordinates of the center point. Figure 4 shows the principle of gray center of gravity.

Fig. 4

Principle diagram of gray center of gravity

The first scan is performed along the cross section of the light stripe to obtain the pixel with the highest gray value. The maximum gray value is recorded as $G_{\max }$. Then, the threshold $T$ is set based on $G_{\max }$. The difference $\Delta G$ between the threshold and maximum value is generally 10–20 based on experience. Then, whether the gray value of the pixel point on the cross section of the light stripe is greater than the threshold $T$ is determined. If so, the coordinate $j$ and gray value $I(i,j)$ of the point on the cross section are recorded. After the scan is completed, all gray values greater than the threshold are recorded. For the number of pixels $L$, the weighted average of the center points of the light stripes is calculated in accordance with Eq. (14).

$$x_{j} = \frac{{\sum\nolimits_{i = 1}^{L} {I(i,j) \cdot j} }}{{\sum\nolimits_{i = 1}^{L} {I(i,j)} }}$$

(14)

The threshold value of the gray center of gravity method differs on each cross section of the light stripe. Based on the gray distribution of different light stripe cross sections, the corresponding adjustments are performed to maximize the use of the gray value information near the extreme point. Based on the extreme value method and threshold value method, the adjustment is optimized, and the accuracy of extraction of the center point of the light stripe is improved. At the same time, compared with the Steger center extraction algorithm, the grayscale center of gravity method involves less calculation, has a faster extraction speed, and is more suitable for real-time measurement occasions. Figure 5 compares the extraction effect of the gray center of gravity method and Steger algorithm. Figure 5b shows the extraction effect of the gray center of gravity method using a $7\; \times \;7$ template to perform median filtering on the image. The figure shows that the center line of the light stripe has good continuity, no line breakage, and relatively smooth overall curve. Figure 5c displays the center line of the light stripe extracted by Steger algorithm. Although the algorithm extracts lines smoothly and continuously in areas with high light intensity distribution density, continuous broken lines appear in the upper and lower areas with weak light intensity distribution density, and numerous pixels are missed compared with the gray center of gravity method.

Fig. 5

a Light streak diagram. b Effect picture of gray center of gravity method. c Steger algorithm renderings

In summary, although the accuracy of Steger light stripe center extraction algorithm currently shows the highest accuracy among all center extraction algorithms, the method requires substantial calculation, a long center extraction time, and only accommodates regions with weak light intensity distribution in the image. The center point may not be extracted. Grayscale centroid method can achieve desirable extraction accuracy under the premise of selecting a suitable threshold value and median filtered image. A minimal calculation amount is required, and the extraction speed is fast. At the same time, the system selects the final gray center of gravity method as the method for extracting the center of light stripes to achieve real-time measurement in the next step.

The light plane and camera calibration parameters are summarized in Table 2. The four chessboard target planes and the fitted light plane coefficients are shown in Table 3.

Table 2 Camera parameters

Table 3 Planar parameters and translation vectors

After light-plane calibration, the mouse (Fig. 6a) is placed on the guide rail, and the line-structured light is projected on the mouse to show the robustness of the algorithm for the white object with the least light absorption capacity. A 1280 × 960 image is captured every 1 mm, and the three-dimensional (3D) coordinates of the light strip center on each picture in the camera coordinate system are calculated. Reverse engineering software Geomagic Studio 2015 is used to process the point cloud data, and the results are shown in Fig. 6b. The figure shows that the details of the mouse arc can be accurately obtained by our method, and the measurement results are satisfactory. The object to be measured with a Phillips screwdriver is replaced to verify the measurement effect of the system on objects with high reflectivity and small volume (Fig. 6c). Given its small size, an image with 1280 × 1024 size is captured every 0.5 mm, and the obtained measurement results are shown in Fig. 6d. The system can extract the center point of the light stripe and complete the 3D topography measurement task regardless of the object with white reflective surface or the surface with small surface roughness and high reflectivity. Finally, the test object is replaced with a drill bit with 2 mm diameter, and an 800 × 600 image is captured at 0.5 mm intervals. The results are shown in Fig. 6f. The proposed method can reliably measure objects of any shape.

Fig. 6

a Tested mouse. b Mouse point cloud. c Tested phillips screwdriver. d Phillips screwdriver point cloud. e Tested bit. f Bit point cloud

4 Conclusion

In this paper, an improved line structure cursor determination method and Scheimpflug theorem are used to realize 3D reconstruction of monocular cameras. Results show that the proposed method can accurately extract the chessboard corners and the light strip center point compared with the traditional method. The measurement system uses an optical structure that satisfies the Scheimpflug’s theorem, thereby increasing the detection range. The influence of the angle between the planes on the system resolution is analyzed, and the range of the angle between the planes is determined to improve the detection accuracy of the system. The future work will focus on the acceleration of the light strip center extraction and point cloud coordinate calculation to achieve real-time 3D measurement.