1 Introduction

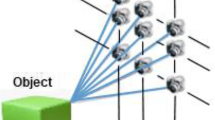
Three-dimensional (3D) sensing and imaging [1–3] have been a subject of research due to their diverse benefits and widely applications in Multi-areas. Integral imaging (II) [4, 5] is an autostereoscopic or multiscopic 3D display, meaning that it displays a 3D image without the use of special glasses on the part of the viewer. It achieves this by placing an array of micro-lens (similar to a lenticular lens) in front of the image, where each lens looks different depending on viewing angle. Thus, rather than displaying a 2D image that looks the same from every direction, it reproduces a 4D light field, creating stereo images that exhibit parallax when the viewer moves. Each of the elemental images captured through a micro-lens or pinhole forms a de-magnified 2D image with its own perspective. To reconstruct the 3D scene from the elemental images, all we need to do is to conduct the rays coming from the elemental images through the same micro-lens array used for the recording. This process will form a 3D image where the object is originally located. The lens array used to record the elemental images is referred to as pickup lens array, while the display one is called display micro-lens array.

Reconstructing a 3D scene from a set of elemental images may be carried out optically or computationally. Optical reconstruction, used for directly view 3D display, is accomplished by displaying the elemental images on a 2D display panel such as an LCD along with a display micro-lens array. Because of diffraction and limitations of optical devices, direct optical reconstruction would introduce image quality degradation. Computational II (CII) reconstruction, on the other hand, is accomplished by digitally simulating geometric ray propagation through a virtual display micro-lens array to process the elemental images obtained optically by direct pickup and thus reconstructing the volume of a 3D scene. This approach has many applications in which volume pixels (voxels) of 3D images are needed for further image processing, such as extracting surface profiles of 3D images. Another advantage of CII is the ability to generate the viewing angle of the reconstructed objects without optically displaying the elemental images. However, the existing CII reconstruction method has several limitations. For instance, the reconstructed images using CII technique in Ref. [5] produce the 3D images viewed from one particular view point through the array. In Ref. [6], the reconstruction algorithm uses triangulation and NCC (Normalized Cross Correlation) with limited numbers of the elemental images (or sampled elemental images) to achieve a 3D image from a simplex viewpoint, which results in great time consumption.

In this paper, we propose a new CII reconstruction algorithm based on ASIFT [7]. The proposed method still uses the limited information of the elemental images to reconstruct the 3D scene, but it will reconstruct the 3D targets at any distance from a virtual display micro-lens array without suffering the limiting effects of device degradations of an optical reconstruction setup and diffraction. More importantly, the proposed algorithm reduces the time cost and improves the accuracy.

2 Review of depth extraction in integral imaging

Stereo disparity matching is one kind of 3D reconstruction technologies [8, 9] in which the 3D spatial geometry of a scene is obtained by analyzing two different perspective views of the 3D scene captured by two cameras placed at different locations and mating the stereo parallax information. The commonly used stereo parallax matching method, requiring two or more cameras, is not only too bulky and not suitable for mobile devices, but also requires hardware synchronization to capture multiple views simultaneously in order to avoiding motion blurring or undesired motion parallax. On the other hand, an integral image system can integrate the camera sensor and a micro-lens array in a very compact package and capture multiple elemental images in one single shot. Besides the advantages of compactness and view synchronization, camera calibration is much more relaxed due to its integration nature than in a conventional multi-view camera system. In parallax matching algorithms, binocular vision can be influenced by defective pixels only using two pixels for stereo matching. In an II system, multiple views are simultaneously acquired and redundant matching pixels are readily available from several elemental images. Such redundancy thus reduces the influence of defective pixels [6]. Finally, an II system with a two-dimensional micro-lens array is capable of capturing both horizontal and vertical parallax, which can potentially result in more accurate stereo parallax matching and 3D scene reconstruction. Compared with the conventional stereo technique, the main drawback of an II system lies in the very limited small baseline among adjacent elemental images and their relatively low-pixel resolution.

Figure 1 shows the geometric configuration of an II setup used in this paper. An object point, \(x\), is assumed to be at a distance \(l_{\text{o}}\) from the micro-lens array and for an image point, \(X_{i}\), through the ith lenslet. Each of the lenslet has a diameter of \(\varphi_{\text{p}}\) and 100 % fill factor is assumed. The gap between the micro-lens array and the camera sensor is \(g_{\text{p}}\). By using the triangular relationship, the mapping between the object and image points is given by

Fig. 1
figure 1

Schematic layout of an integral imaging setup and the geometric relationship between object point and image point

Full size image
$$(i\phi_{\text{p}} - x)/l_{\text{o}} = (X_{i} - i\phi_{\text{p}} )/g_{\text{p}}$$
(1)

where \(\phi_{\text{p}}\) is diameter of the lenslets and \(g_{\text{p}}\) is the gap between the micro-lens array and the camera sensor. A 100 % fill factor is assumed for the micro-lens array. For two different lenslets, Eq. (1) is rewritten as

$$X_{i}=\frac{{i\phi_{\text{p}} - x}}{{l_{\text{o}} }}g_{\text{p}} + i\phi_{\text{p}}$$
(2)

and

$$X_{j}=\frac{{j\phi_{\text{p}} - x}}{{l_{\text{o}} }}g_{\text{p}} + j\phi_{\text{p}}.$$
(3)

Subtracting Eqs. (3) and (2) gives the stereo parallax information between these two views:

$$X_{j} - X_{i}=(j - i)(1 + g_{\text{p}} /l_{\text{o}} )\phi_{\text{p}}$$
(4)

Theoretically, using the Eq. (4), the depth of the 3D object point, \(l_{\text{o}}\), can be obtained by extracting the two corresponding pixel coordinates in a pair of elemental images. This is a triangulation technique. The first step is therefore to acquire an image if plane P that contains several elemental images provided by each micro-lens. To improve the quality of this image, we digitally enhance its contrast and get rid of the noise. Furthermore, we calibrate our images to achieve rectification.

Figure 2 demonstrates two elemental images captured by our experimental setup. The simplest method to obtain the depth of the object points and generate depth map is to apply a stereo parallax matching algorithm on 2D images captured from multiple viewing perspectives. By choosing the elemental image near to the center field of view as the reference, we determine the corresponding points and compute their parallax between the reference image and other elemental images to obtain depth map by using the normalized cross-correlation (NCC) parallax matching algorithm [5]. The cross-correlation of two pixels in two elemental images is given by

Fig. 2
figure 2

The stereo parallax match between two elemental images

Full size image
$$C[(i,j),(i^{'} ,j^{'} )] = \frac{{\sum\limits_{p = - t}^{t} {\sum\limits_{q = - t}^{t} {I_{1} (X_{i} + p,\;Y_{j} + q)I_{2} (X_{{i^{'} }} + p,\;Y_{{j^{'} }} + q)} } }}{{\left[ {\sum\limits_{p = - t}^{t} {\sum\limits_{q = - t}^{t} {I_{1}^{2} (X_{i} + p,\;Y_{j} + q)\sum\limits_{p = - t}^{t} {\sum\limits_{q = - t}^{t} {I_{2}^{2} (X_{{i^{'} }} + p,\;Y_{{j^{'} }} + q)} } ]} } } \right]^{\frac{1}{2}} }}$$
(5)

where \(I_{1}\) and \(I_{2}\) are two elemental images, \(p\) and \(q\) are sizes of sampling window. \((i, \, j)\) and \((i^{\prime}, \, j^{\prime})\) are central coordinates of the sampling window in two images, respectively.

The main advantage of similarity criterion is that it is not limited by changes of two cells image brightness. For a \((2 \times j + 1) \times (2 \times j + 1)\) lens array, we calculate all the depth information with respect to the center reference image. The optimized depth value is obtained by computing a similarity criterion of \(M\) by changing the value z each time:

$$M(z) = \sum\limits_{i = - m}^{m} {\sum\limits_{j = - n}^{n} {C[(i,\;j - 1),\;(i,\;j)] + } } \sum\limits_{i = - m}^{m} {\sum\limits_{j = - n}^{n} {C[(i - 1,\;j),\;(i,\;j)]} }$$
(6)

The z value corresponding to the maximum value of \(M\) on the curve is regarded as the extracted depth \(Z\) of the object point. It is worth pointing out, however, that the NCC method alone has high computation cost due to the iteration nature of the algorithm. To meet the need of real-time applications, in this paper, we adopt ASIFT operator to improve computation efficiency which is further explained in Sect. 3.

3 ASIFT algorithm

When the relative space position of two elemental images changes smaller, light intensity is good enough; SIFT(Scale-invariant feature transform) algorithm in image matching performs very well. But for 3D reconstruction, match points that we can get are too sparse according to previous experiments. In our paper, we use Fig. 3 as system structure and experimental array image. The distance between the micro-lens and the 3D object are about 200 mm (Cube) and 500 mm (Kidney). The size of lens array is 100 mm × 100 mm with each lens diameter at 1 mm and the focal length is 3 mm. In order to ensure the number of elemental image and resolution, we chose 200 × 200 pixels as resolution of each image.

Fig. 3
figure 3

System Structure and Images array

Full size image

After cutting same size elemental images, we use SIFT algorithm to extract match points [10–13]. As is shown in Fig. 4, there are only 30 pairs of points with some error match points in bad light condition.

Fig. 4
figure 4

Match points (including error match points)

Full size image

We cannot achieve 3D dense reconstruction by only 30 pairs of points including mismatch points. So, we adopt ASIFT algorithm. But it does not mean that SIFT can be used instead of the ASIFT in the case of high-intensity light source. The main reason is as described in Fig. 5; ASIFT simulates all distortions caused by the variation of the camera optical axis because the algorithm introduces two more parameters in order to achieve full affine invariant [14]. Then, we can get more match points even in lower light condition. In the end, we use the same method to match corresponding points as SIFT. In other words, ASIFT simulates three parameters scale, camera longitude angle, and latitude angle (which is equivalent to the tilt) and also normalizes the other three parameters (translation and rotation). This is affine invariant in the true sense [15].

Fig. 5
figure 5

Overview of the ASIFT algorithm [5]. The square images A and B represent the compared images u and v. ASIFT simulates all distortions caused by a variation of the camera optical axis direction

Full size image

Affine Transformation Matrix A can be decomposed into

$$A = \left[ {\begin{array}{*{20}c} a & b \\ c & d \\ \end{array} } \right] = \lambda \left[ {\begin{array}{*{20}c} {\cos \psi } & { - \sin \psi } \\ {\sin \psi } & {\cos \psi } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} t & 0 \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\cos \phi } & { - \sin \phi } \\ {\sin \phi } & {\cos \phi } \\ \end{array} } \right] = \lambda R(\psi )T_{t} R(\phi )$$
(7)

where \(\lambda > 0\), \(\phi \in [0,\pi )\). As is shown in Fig. 6, \(\phi\) and \(\theta = arc\;\cos \;1/t\) are the camera optical axis longitude and latitude, respectively. The image is a flat physical object. The small parallelogram on the top represents a camera looking at \(u\). A third angle \(\psi\) parameterizes the camera spin, and \(\lambda\) is a zoom parameter.

Fig. 6
figure 6

Camera model

Full size image

In order to have ASIFT invariant to any affine transformations, we need to sample the tilt \(t\) and angle \(\phi\) with a high enough precision. The sampling steps \(\Delta t\) and \(\Delta \phi\) must be fixed experimentally by testing several natural images. Figure 7 illustrates the irregular sampling results: \(\theta\) and \(\phi\) on the observation hemisphere, where \(\Delta t = \sqrt 2\) and \(\Delta \phi = 72^{ \circ } /t\). The samples accumulate near the equator.

Fig. 7
figure 7

Sampling of the parameters [7] θ = arccos 1/t and φ. The samples are the black dots. Top perspective illustration of the observation hemisphere (only t = 2, 2\(\sqrt 2\), 4 are shown). Bottom zenith view of the observation hemisphere. The values of θ are indicated on the figure

Full size image

Original image is \(u(x,\;y)\), it can be changed to \(u(tx,\;y)\) when it tilted \(t\) on the \(x\) axis. For digital images, tilt images are determined by directional t-subsampling. It requires antialiasing filter processing on the \(X\) axis in order to minimize the distortion of the image. The filter is performed by Gaussian convolution which standard deviation is \(c\sqrt {t^{2} - 1}\). In the Ref. [11], Lowe recommended value \(c = 0.8\). In the Ref. [5], it proved that image distortion is smaller at this value. We do some rotation transform and tilt transform to images, which can simulate and generate some images taken from different horizontal angles and vertical angles. In this way, we can make sure simulative images keep approximation in different view angle \(\theta\) and \(\phi\). All the tilted images will be matched using SIFT algorithm. Figure 8 shows 715 pairs of match points with ASIFT which is better than SIFT in same light condition.

Fig. 8
figure 8

ASIFT Match Points

Full size image

4 Optimization algorithm

Theoretically, binocular parallax can get depth Z. The existence of various error such as system noise and detector defects affects the depth accuracy. In this case, using multiple elemental images will provide enough redundancy to improve signal-to-noise ratio. However, the number of cell image also cannot be too much. The pixels of the camera are fixed, while the number of cell image is too much, it will seriously reduce the number of a single-elemental image pixels, thus reducing the resolution of the 3D reconstruction.

In this paper, we pick \(3 \times 3\) elemental images, and calculate optimize the depth using

$$Z = \arg \;\hbox{min} \sum\limits_{i = 1}^{n} {(Z - z_{i} )}^{2}$$
(8)

where \(z_{i} = \frac{fT}{{x^{l} - x^{t} }}\), \(f\) is focal length, \(T\) is pitch of lens, \(x^{l}\) and \(x^{t}\) are coordinates of matching points, n is number of lens. Optimized depth value can be used as the object point depth of the central image. Using Eq. (9) can calculate x and y coordinates.

$$\left\{ {\begin{array}{*{20}c} {x = - (Z/g)X_{0} } \\ {y = - (Z/g)Y_{0} } \\ \end{array} } \right.$$
(9)

where X 0 and Y 0 are corresponding coordinates in the center image.

Obviously, through registration algorithm we have got enough match points; however, we find that in some parts, no match shows up. So in this place, we usually adopt region growing method which is used to complete calculation for the dense points. Figure 9 shows disparity map after regional growth process. The cube and kidney model has been obvious distinguished.

Fig. 9
figure 9

Disparity map of elemental images

Full size image

5 Experimental result

In this paper, we mainly do two aspects of experiment:

5.1 The contrast experiment in depth accuracy

This experiment selects one point on Cube and one point on Kidney model, respectively. We pick up some feature points near selected points and corresponding points on redundant elemental images to optimize the final depth z. In Fig. 10, we can get intuitionistic contrast data.

Fig. 10
figure 10

Data contrast figure in depth values with match points (\(\circ\)), measured points using optical platform (+) and optimal points by redundant match points (blue lines)

Full size image

As we can see in Table 1, the more feature points we can provide, in other words, the more redundancy images in the calculation, the optimized value will be closer to real value, and the depth error will be smaller.

Table 1 Error analysis
Full size table

5.2 Synthesis time in the PLY 3D data and display

In this paper, we use IBM X230 desktop (Intel core i7-3520 M CPU 8G RAM) and 64 bits operating system as the experiment platform. Table 2 shows time consumption with NCC algorithm and ASIFT algorithm. Obviously, ASIFT algorithm has good performance.

Table 2 Time consumption in NCC and ASIFT algorithm
Full size table

In the end, we use Matlab (2013a) to create 3D data.PLY file which format is X, Y, Z, R, G, B, ALPA (default 255), Fig. 11 is the generated 3D images seen from different angles with Meshlab software.

Fig. 11
figure 11

3D reconstruction in different view angles on Meshlab

Full size image

6 Conclusion

In our work, we reviewed some previous paper, and adopt the latest used ASIFT operator instead of NCC algorithm to accomplish image registration. In this way, we greatly reduce the time consumption. Meanwhile, combining with regional similarity principle, we adopt simple optimization method to realize higher precision measurement of depth value. The algorithm in our paper enhances real-time performance in Medical 3D imaging, and has a very broad application prospects in many fields.