Introduction

Rock mass in the earth’s crust is broken on scales from millimeters to kilometers, and fluid flow and mass transfer often occur in both the porous rock matrix and interconnected fracture networks for fractured porous rock. The matrix predominantly stores mass (e.g., hydrocarbons, water) and heat, governing long timescale processes. Fractures, in contrast to the rock matrix, exhibit significantly higher permeabilities and are widely recognized as the primary conduits for fluid and solute migration (Hu et al. 2022; Sweeney et al. 2020). Understanding the interaction between these physical systems is of utmost importance for numerous natural and engineering applications such as groundwater resource extraction (Luo et al. 2020), hydrocarbon extraction from unconventional reservoirs (Kim et al. 2021), CO2 sequestration (Chen et al. 2022), geothermal energy extraction (Salimzadeh et al. 2019), and high-level radioactive nuclear waste disposal (Zhang et al. 2022).

Our ability to comprehend subsurface systems relies, in part, on the development of accurate numerical models capable of capturing the diverse mechanisms of physics occurring within fractures and the surrounding matrix, and their interactions. However, it is important to note that no single model currently exists as a universal solution. Models employed for simulating flow and transport processes in fractured porous media can be categorized into three types—equivalent porous medium (EPM) model, discrete fracture network (DFN) model, and discrete fracture-matrix (DFM) model (Applegate and Appleyard 2022; Khafagy et al. 2022a, b; Wei et al. 2020). Each model utilizes a distinct set of underlying methods, which come with their own inherent advantages and disadvantages.

The accurate simulation of flow in fractured porous media hinges on effectively characterizing complex fracture network geometries and accurately representing the coupled flow dynamics within fractures and the surrounding matrix. The EPM, DFN, and DFM models address (or do not address) these issues in different ways. Specifically, the EPM model regards the fractured geologic medium as a continuum medium and considers that the permeability of the fractured geologic medium is equivalent to that of a continuum porous medium (Mortazavi et al. 2022; Wang et al. 2022a, b; Weijermars and Khanal 2019; Xue et al. 2022). The EPM model has been successfully applied to solve large-scale water yield problems in fractured geologic media, making it widely utilized in geological engineering practice (Chen et al. 2020; Scanlon et al. 2003; Song et al. 2018; Zhang et al. 2020). The EPM model provides a simplified approach for representing flow within fractured rock mass and is renowned for its ease of implementation compared to other models.

To more thoroughly consider the impact of fracture networks, some scholars have proposed multicontinuum methods building upon the foundation of the EPM model (Bosma et al. 2017; Sweeney et al. 2020). The dual-porosity model is a quintessential multicontinuum approach, which, to a certain extent, describes the phenomenon of preferential flow and accounts for the exchange of water flow between the fracture system and the matrix system. This method proves effective and suitable for reservoirs characterized by dense and extensive fracture distributions (Hu et al. 2021; Ma et al. 2023a, b; Pham and Falta 2022). However, its principal limitation lies in relying on empirical transfer functions for fluid transport between the matrix and fractures, leading to a homogenized fracture domain that substantially obscures detailed fracture information. In practice, the effectiveness of this method also requires assessment and validation.

The DFN model focuses solely on water flow within fractures and does not account for penetration into the rock matrix. It is a suitable method for accurately characterizing fracture geometry, spatial connectivity, and flow behavior (Feng et al. 2020; Huang et al. 2021; Khafagy et al. 2022a, b; Yaghoubi 2019). By excluding the matrix, the DFN model can utilize existing numerical methods that specifically address flow within fractures (Berrone et al. 2019; Geetha Manjari and Sivakumar Babu 2022); however, the DFN model necessitates a substantial amount of fracture investigation data and extensive computational effort, which limits its practical application in engineering. Furthermore, the absence of rock matrix representation restricts its applicability to specific scenarios, such as flow in impermeable rocks.

Unlike the DFN model, the DFM model explicitly represents both the fracture network and the surrounding porous matrix. Although the DFM model is newer compared to the DFN and EPM models, there are still implementation challenges that need to be addressed (Jia and Xian 2022; Mi et al. 2017; Zhao et al. 2019). The DFM model effectively captures the complexities of fracture network geometries and accurately represents the coupled flow dynamics within the fractures and the surrounding matrix, thus offering a high-fidelity representation of the fracture-matrix system. However, challenges related to meshing and numerical methods have restricted its applicability to simpler problems (Ţene et al. 2017; Wang et al. 2022a, b; Younes et al. 2023; Zhao et al. 2018). Generally, the DFM model represents the fracture network as (n—1)-dimensional fractures coupled with an (n)-dimensional mesh that represents the matrix. Consequently, the meshes utilized in the DFM model are inherently multidimensional, which introduces additional complexities in solving the governing equations for flow and transport (Hyman and Dentz 2021; Li et al. 2019, 2023; Liu et al. 2020).

Certain regional-scale and long-term hydrogeological problems necessitate more precise descriptions of water head or velocity distributions, particularly for applications such as hydrogeochemical evolution and nuclide migration within fractures. When using the DFN or DFM model, accurately characterizing all fractures becomes impractical due to limitations in current investigation techniques, high investigation effort, and associated costs. One possible approach to overcome these challenges is to utilize the EPM method, which reduces model complexity and computational cost by not explicitly including fractures in the models (Wei et al. 2021). To apply the EPM model, researchers introduced the concept of the representative elementary volume (REV) to describe the hydraulic characteristics of the equivalent continuum model in hydrogeology (Dou et al. 2019; Liang et al. 2019; Liu et al. 2021; Loyola et al. 2021). Researchers have proposed several methods to assess the occurrence of the REV through numerical simulations (Rong et al. 2013; Young et al. 2020); however, this evaluation method does not provide a clear criterion for assessing suitability.

Previous research indicates that the presence of fractures significantly influences the head value, and neglecting fractures can result in estimation errors in the groundwater quantity and velocity (Koohbor et al. 2020; Qi-Zhen et al. 2012; Xing et al. 2021a, b). Furthermore, various studies have demonstrated that fractures have a substantial impact on simulation results (Jarrahi et al. 2019; Zareidarmiyan et al. 2021; Zeng et al. 2021). However, a convenient and efficient method for evaluating the influence of fractures on the suitability of the EPM model is still lacking. The permeability of a fractured geologic medium is determined by many factors, among which the most important parameters are fracture permeability and matrix permeability (Baghbanan and Jing 2008; Bou Jaoude et al. 2022). Further, fracture permeability is mainly controlled by the fracture aperture. Some scholars have carried out a series of research projects on the seepage of fractured rock mass based on these factors (Bisdom et al. 2016; Dou et al. 2018; Mi et al. 2014); however, the influence of fracture aperture and matrix permeability of fractured rock mass on the suitability of the EPM model remains unclear.

The objective of this study, conducted within a two-dimensional (2D) framework, was to assess the impact of fracture aperture and rock matrix permeability on the suitability of the EPM model. To accomplish this, a 2D DFM prototype model was generated using statistical parameters of fractures from the Three Gorges Dam Project area in China. Subsequently, multiple sets of DFM models were created, varying the fracture aperture and matrix permeability of the fractured rock mass. The influence of these parameters on the suitability of the EPM model was analyzed. This study provides valuable insights into the impact of fracture aperture and matrix permeability on the suitability of the EPM method for fractured rock masses. The findings offer a scientific basis for determining the applicability of this method to address water-head-related hydrogeological issues in fractured geological media at specific sites.

Methodology

Two-dimensional (2D) discrete fracture-matrix model

The DFM model combines the advantages of the DFN model and the EPM model. The equations of water flow are established with the equivalent continuous medium model and discrete medium model, respectively, and then the coupling calculation is carried out according to the basic principle for establishing the DFM model, that is, the hydraulic heads at the contact of the two media are the same and the flow at the nodes is balanced. The finite element method can be used to solve the equation of the DFM model of seepage in fractured rock mass (Hu et al. 2022; Sweeney et al. 2020; Zheng et al. 2021)—for a more detailed introduction to the DFM model, refer to (Binda et al. 2021; Dodangeh et al. 2023; Ma et al. 2023a, b). This model can obviously consider the influence of fracture and matrix permeability on seepage at the same time.

Mathematical model of water flow in 2D discrete fractures

The DFN model considers that the rock mass itself is impermeable, and the fracture is regarded as a discrete independent model. The mathematical model representing the anisotropy of the medium is established with fracture parameters, to determine the real flow state of the fluid in the fracture network (Fu et al. 2013; Lopes et al. 2022; Su et al. 2022). The nomenclature is summarized in the Appendix.

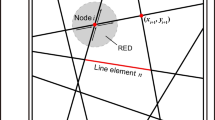
In the fracture network, line elements and their two end nodes form the basic units. If node i is an endpoint of line element j, then element j is said to be connected to node i. The degree of node i is the number of line elements connected to it. Assuming the selection of a 2D fracture study domain ABCD, which includes fracture intersection point i, a closed curve passing through the midpoints of all connected line elements is constructed centered on point i, forming a representative domain. According to the assumption of single-phase incompressible fluid flow and the principle of mass conservation for steady seepage, the seepage equation within the representative domain can be written as:

$${\left(\sum\limits_{j=1}^{N'}{q}_{j}\right)}_{i}+{Q}_{i}=0$$
(1)

where qj represents the flow rate into or out of node i through line element j; N′ is the degree of node i; Qi is the source-sink term at node i.

If there are N nodes and M line elements in the fracture study area, then N equations of the form of Eq. (1) can be formed, which can be written in matrix form as follows:

$$\mathbf{A}\mathbf{q}+\mathbf{Q}=0$$
(2)

where A is an aggregation matrix reflecting the aggregation relationship between the line elements and nodes in the fracture network. The matrix A has the number of rows equal to the number of nodes and the number of columns equal to the number of fracture line elements; \(\mathbf{q}={\left({q}_{1},{q}_{2},\cdots ,{q}_{N}\right)}^{{\text{T}}}\); \(\mathbf{Q}={\left({Q}_{1},{Q}_{2},\cdots ,{Q}_{N}\right)}^{{\text{T}}}\).

The specific discharge formula of incompressible fluid flow in a laminar regime within a fracture consisting of two parallel and smooth surfaces is given by the cubic law (He et al. 2021; Wang et al. 2020a, b; Xing et al. 2021a, b), as follows:

$$q=\frac{\gamma }{4\mu }{J}_{{\text{f}}}{\int }_{0}^{b/2}\left({b}^{2}-{4y}^{2}\right)dy=\frac{{\gamma b}^{3}}{12\mu }{J}_{{\text{f}}}$$
(3)

The average velocity of water flowing through this fracture is:

$$V=\frac{{\gamma b}^{2}}{12\mu }{J}_{{\text{f}}}={K}_{{\text{f}}}{J}_{{\text{f}}}$$
(4)

where q is the specific discharge; μ is the dynamic viscosity coefficient of the fluid; γ is the specific gravity of groundwater; Jf is the hydraulic gradient of fracture water flow; Kf is the permeability coefficient of the fracture.

From single-fracture seepage Eqs. (3) and (4), it can be known that the flow rate of the jth line element is:

$${q}_{j}=\frac{{\left({K}_{{\text{f}}}\right)}_{j}{b}_{j}\Delta {H}_{j}}{{l}_{j}}={R}_{j}{\Delta H}_{j}$$
(5)

where Kf is the permeability coefficient of the fracture; bj and lj represent the width and length of the line element, respectively; ΔHj denotes the head difference between the two ends of the j-line element.

The hydraulic conductivity of the j-line element is:

$${R}_{j}=\frac{\gamma {b}_{j}^{2}}{12\mu }\bullet \frac{{b}_{j}}{{l}_{j}}$$
(6)

written in matrix form:

$$\mathbf{q}=\mathbf{R}\bullet \Delta \mathbf{H}$$
(7)

where ∆H = ATH, ΔH is the column vector representing the head difference between the two ends of the line element, ∆H = (∆H1,∆H2),…,∆HM)T, A is the aggregation matrix reflecting the relationship between line elements and nodes in the fracture network, and H is the vector nodal heads; q = (q1,q2,…,qM)T; R = diag(R1,R2,…,RM).

By combining Eqs. (2) and (7), the final seepage solution formula for the DFN model can be obtained:

$$\left({\mathbf{A}\mathbf{R}\mathbf{A}}^{{\text{T}}}\right)\mathbf{H}=\mathbf{Q}$$
(8)

Mathematical model of water flow in a 2D continuous medium

The EPM model depicts fractured rock mass as a continuum seepage medium, and equally distributes fracture fluid in the whole rock mass; it considers fractured rock mass as a seepage medium with a symmetric permeability tensor (Chen et al. 2021a, b; Zhang et al. 2017). The 2D steady seepage in a saturated medium, based on Darcy’s law, can be expressed as:

$$\frac{\partial }{\partial x}=\left({T}_{x}\frac{\partial h}{\partial x}\right)+\frac{\partial }{\partial y}\left({T}_{y}\frac{\partial h}{\partial y}\right)+W=0$$
(9)

where Tx and Ty are the transmissivities in the x and y directions; h = h(x, y) is the head function; W represents the source-sink term per element area.

For the Neumann boundary \({\Gamma }_{2}\), the inflow or outflow per unit length on this boundary is known, and there are flow boundary conditions:

$${K}_{n}\frac{\partial h}{\partial n}{\left|\right.}_{{\Gamma }_{2}}=q\left(x,y\right)$$
(10)

where n is the external normal direction of \({\Gamma }_{2}\); q(x, y) is the known flow rate. If the boundary is impermeable, then q = 0.

The solution to the initial-boundary value problem of seepage partial differential equations can be transformed into finding the extremal function of a certain functional. Therefore, solving Eq. (9) is equivalent to finding the minimal function of the following functional:

$$I\left(h\right)=\underset{\Omega }{\overset{}{\iint }}\left\{\frac{1}{2}\left[{K}_{x}{\left(\frac{\partial h}{\partial x}\right)}^{2}+{K}_{y}{\left(\frac{\partial h}{\partial y}\right)}^{2}\right]\right\}{\text{d}x\text{d}y}+\underset{{\Gamma }_{2}}{\overset{}{\int }}qh\mathrm{d\Gamma }$$
(11)

The seepage area Ω is discretized and divided into m disjoint units e, each unit contains M nodes, and the interpolation function is Ni, thus the head expression of the unit from any point is:

$$h=\sum_{i=1}^{M}{N}_{i}{h}_{i}$$
(12)

The seepage area Ω is decomposed into the sum of individual elements, and the boundary \({\Gamma }_{1}\) is decomposed into the sum of line elements, resulting in:

$$I\left(h\right)=\sum_{e=1}^{m}{I}^{e}\left(h\right)=\sum_{e=1}^{m}\underset{e}{\overset{}{\iint }}\left\{\frac{1}{2}\left[{K}_{x}{\left(\frac{\partial h}{\partial x}\right)}^{2}+{K}_{y}{\left(\frac{\partial h}{\partial y}\right)}^{2}\right]\right\}{\text{d}x\text{d}y}+\underset{{\Gamma }_{1}}{\overset{}{\int }}qh{\text{d}}\Gamma$$
(13)

By substituting Eq. (12) into Eq. (13), I(h) becomes a function of the hydraulic heads at each node. The sought function h should be the minimal function of the functional I(h); therefore, it must satisfy:

$$\frac{\partial I}{{\partial h}_{i}}=\sum_{e=1}^{m}\frac{{\partial I}^{e}}{{\partial h}_{i}}=0$$
(14)

If the functional I is a quadratic function of h and its derivatives, then the functional Ie for any element e is also quadratic. Consequently, the solution equations are transformed into:

$$\mathbf{K}\mathbf{h}=\mathbf{F}$$
(15)

where F is a known constant term; The expression for an individual element in matrix K is as follows:

$${K}_{ij}^{e}=\underset{e}{\overset{}{\iint }}\left({K}_{x}\frac{{\partial N}_{i}}{\partial x}\frac{{\partial N}_{j}}{\partial x}+{K}_{y}\frac{{\partial N}_{i}}{\partial y}\frac{{\partial N}_{j}}{\partial y}\right){\text{d}}x{\text{d}y}$$
(16)

The corresponding relationship between elements in the whole conductivity matrix and elements in the unit conductivity matrix is as follows:

$${K}_{ij}=\sum_{k=1}^{{m}_{i}}{K}_{ij}^{{e}_{k}}$$
(17)

where mi is the number of units with common nodes i, j. Because there are few related nodes in each node, the overall conductivity matrix is a highly sparse symmetrical matrix.

In Eq. (15), the vector at the right end of the medium number is also obtained by superimposing the vector at the right end of the unit. The calculation formula of each element in the vector at the right end of the unit is:

$${F}_{i}^{e}=\underset{e}{\overset{}{\iint }}{wN}_{i}\mathrm{d\Omega }+\underset{{\Gamma }_{1}}{\overset{}{\int }}{qN}_{i}\mathrm{d\Gamma }$$
(18)

where w is the amount of infiltration or evaporation water; q is the inflow per unit area of the boundary.

Solution of the 2D discrete fracture-matrix model

In order to solve the problem of 2D steady flow in areas where continuous media and fractured media are adjacent to each other, this study uses the discrete fracture-matrix coupling flow method (Fig. 1). The key of the method is, firstly, the corresponding integral seepage matrices of fractured media and continuous media in the whole seepage area are established respectively, and then based on the principle of equal water head and flow balance of the common nodes of the two types of media, the integral seepage matrix of the whole seepage area is formed for further finite element analysis, which is actually an integral solution method (Guo et al. 2023; Hyman et al. 2022; Mi et al. 2017).

Fig. 1
figure 1

Schematic diagram of a discrete fracture-matrix model

Full size image

According to the seepage theory of fracture network in section ‘Mathematical model of water flow in 2D discrete fractures’, the steady flow equation of a 2D fracture network can be written as follows:

$${\mathbf{A}\mathbf{R}\mathbf{A}}^{{\text{T}}}\mathbf{h}=\mathbf{Q}$$
(19)

where A is the aggregation matrix; R is the coefficient matrix of hydraulic conductivity of fracture; h is the node head; Q is the source-sink term.

Based on the Ritz finite element method, the process of fracture seepage is the same as that of continuous medium seepage theory, described in section ‘Mathematical model of water flow in a 2D continuous medium’. Each fracture segment is regarded as a line element to discretize the fracture seepage area. If the two ends of line element j are node i and node i + 1, respectively, there is an elemental seepage matrix as follows:

$${\mathbf{K}}^{j}=\frac{{K}_{j}}{{l}_{j}}\left[\begin{array}{cc}1& -1\\ -1& 1\end{array}\right]$$
(20)
$${K}_{j}=\frac{{\gamma b}^{3}}{12\mu }$$
(21)

For line element j, there is an equation as follows:

$${\mathbf{K}}^{j}{\mathbf{h}}^{j}=\left[\begin{array}{cc}\frac{{\gamma b}_{j}^{3}}{12{\mu l}_{j}}& -\frac{{\gamma b}_{j}^{3}}{{12\mu l}_{j}}\\ -\frac{{\gamma b}_{j}^{3}}{{12\mu l}_{j}}& \frac{{\gamma b}_{j}^{3}}{{12\mu l}_{j}}\end{array}\right]\left\{\begin{array}{c}{h}_{i}\\ {h}_{i+1}\end{array}\right\}=\left\{\begin{array}{c}{Q}_{i}\\ {Q}_{i+1}\end{array}\right\}$$
(22)

where Qi and Qi+1 are the known flow rates of node i and node i + 1, respectively.

The overall permeability matrix (K) is obtained by superimposing all element permeability matrices, and finally, the finite element equation is:

$$\mathbf{K}\mathbf{h}=\mathbf{Q}$$
(23)

And there is:

$$\mathbf{K}={\mathbf{A}\mathbf{R}\mathbf{A}}^{{\text{T}}}$$
(24)

when coupling the fractured system and the continuous medium system, the fractured medium can be discretized by the line element, and the continuous medium can be discretized by the triangular element (Fig. 2). All nodes are numbered uniformly to obtain a permeability matrix of every triangular element. These matrices are assembled together according to node connection relationships to form the overall permeability matrix, after which the boundary conditions are added to solve the seepage flow.

Fig. 2
figure 2

Schematic diagram of the fracture and matrix spatial discretization

Full size image

Suitability evaluation of the EPM model

For a study area with known fracture geometry parameters and rock matrix permeability, the DFM model can be used to solve the hydraulic head of each node in the study area, and the DFM simulation results are taken as the reference value of the hydraulic head in the study area. Accordingly, the EPM model is used to calculate the hydraulic head of each node of the same study area. Finally, comparing the simulation results of the EPM model with those of the DFM model, the hydraulic head error of each node from the EPM model simulation can be solved, and the error is used to evaluate the suitability of the EPM model.

When utilizing the EPM model to solve for the hydraulic head of each node in the fractured rock mass, the fractured rock mass is characterized as a continuum seepage medium, equally distributing the water in the whole rock mass. The aquifer is assumed to be homogeneous, thus the hydraulic head at any position in the study area can be obtained by:

$${H}_{p}={H}_{b1}+\frac{{l}_{p{\text{AB}}}}{{l}_{{\text{AD}}}}\left({H}_{b2}-{H}_{b1}\right)$$
(25)

where Hp is the hydraulic head at any position p in the study area, lpAB is the distance from position p in the study area to boundary AB, lAD is the AD boundary length, and Hb1 and Hb2 are the hydraulic heads at the left and right boundaries, respectively, of the study area.

After obtaining the simulation results of the EPM model and the DFM model in the study area, this study mainly uses three calculation methods to quantitatively evaluate the influence of fracture aperture and rock matrix permeability on the suitability of the EPM model, including the commonly used mean absolute error (MAE) and root mean square error (RMSE) values and the suitable rate of the EPM model proposed to express the suitability of the EPM model more intuitively.

In statistics, the MAE is the average value of the absolute errors. It is a measure of the errors between pairs of observations expressing the same phenomenon, which can suitably reflect the actual situation of the prediction errors. The calculation formula is as follows:

$${\text{MAE}}=\frac{\sum\limits_{i=1}^{m}\left|{{\text{predicted}}}_{i}-{{\text{actual}}}_{i}\right|}{m}$$
(26)

The RMSE is a statistical metric commonly used to quantify the deviation between observed values and true values. It is calculated as the square root of the mean of the squared differences between observed and true values, divided by the number of observations m. The formula for calculating RMSE is as follows:

$${\text{RMSE}}=\sqrt{\frac{1}{m}\sum_{i=1}^{m}{\left({{\text{predicted}}}_{i}-{{\text{actual}}}_{i}\right)}^{2}}$$
(27)

The MAE is conceptually simpler and easier to explain than the RMSE. It is just the average absolute vertical or horizontal distance between each point in the scatter plot and the y = x line. In addition, the contribution of each error to MAE is proportional to the absolute value of the error. This is in contrast to RMSE which involves squaring the error; thus, some larger errors will make RMSE increase more than MAE.

To provide a more intuitive and straightforward evaluation of the EPM model’s suitability, the suitable rate was utilized to assess its performance. The relative error is calculated as follows:

$$\delta_i=\frac{H_i^{'}-H_i}{H_\text{max}-H_\text{min}}$$
(28)

where \({\delta }_{i}\) represents the relative error at node i, while \({H}_{i}{^\prime}\) and Hi correspond to the hydraulic head values at node i obtained from the DFM and EPM models, respectively. Additionally, Hmax denotes the maximum hydraulic head value in the study area, and Hmin represents the minimum water head value. Based on the relative error, a criterion was established to determine the suitability of the EPM model at each node. If the relative error at node i is less than or equal to 0.15, the EPM model simulation results are considered satisfactory. Conversely, if the relative error exceeds 0.15, the EPM model’s performance is deemed inadequate at that particular node. This can be expressed as:

$${e}_{i}=\left\{\begin{array}{c}1,{\delta }_{i}\le 0.15\\ 0,{\delta }_{i}>0.15\end{array}\right.$$
(29)

where ei represents the suitability of the EPM model at node i. A value of 1 indicates that the EPM model is suitable for that node, while a value of 0 suggests that the EPM model is unsuitable. To assess the overall suitability of the EPM model, the suitable rate is computed by dividing the number of suitable nodes by the total number of nodes:

$$\eta =\frac{\sum\limits_{i=1}^{{N}_{{\text{t}}}}{e}_{i}}{{N}_{{\text{t}}}}$$
(30)

where η denotes the suitability of the EPM model, ranging from 0 to 1. The η closer to 0 indicates poor suitability, while the η closer to 1 implies better suitability. Nt represents the total number of nodes in the study area.

By systematically varying the fracture aperture and matrix permeability in the study area, different fracture networks are generated, allowing for the suitability of the EPM model for each network to be calculated, thus enabling an exploration of the impact of fracture aperture and matrix permeability on the EPM model’s suitability.

Numerical model setup

This study employed a numerical simulation method to obtain simulated heads, enabling the evaluation of the EPM model’s suitability. The parameters in the numerical model were primarily determined based on the investigation results from the Three Gorges Dam Project in China (Wang et al. 2020a, b). The statistical characteristics of four fracture groups in the area are presented in Table 1. To model the fracture trace length and aperture, a lognormal distribution was assumed following the work of Tonon and Chen (2007). Additionally, the fracture orientation probability distribution was considered to follow a normal distribution based on the studies by Chen et al. (2008) and Ni et al. (2017). Fracture density was treated as constant, defined as the total number of fractures divided by a given area.

Table 1 Geometric parameters of fracture for generating the initial DFM model
Full size table

In this study, a 2D fracture network model with dimensions of 20 × 20 m was generated using the Monte Carlo method based on fracture geometric parameters. It is worth noting that boundary conditions play a crucial role in investigating the seepage behavior of fractured rock masses. This study defined the left and right boundaries as constant-head boundaries, with hydraulic heads set to 2 and 0 m, respectively. The upper and lower boundaries were considered impermeable, allowing water to enter from the left boundary and exit from the right boundary. The fluid flow was assumed to be steady.

To solve for the head values at each node of the fracture network, MATLAB software was used, taking into account the generated computational domain, boundary conditions, fracture distribution, and parameters. As the fracture network generated through the Monte Carlo simulation method exhibits certain randomness, the operations were repeated for all models 200 times (realizations). This approach was adopted to reduce random errors while considering the trade-off between computational burden and accuracy requirements.

The influence of the fracture aperture on the permeability of fractured rock mass was quantitatively studied. Nine fracture apertures were set in this study (Table 2), which was modified by the classification standard of the fracture aperture in ISRM 1978 (Mechanics 1978). Other geometric parameters of fractures were controlled, and the permeability of the rock matrix was set to 0 m/s, which means that the matrix is impermeable. These DFN models were used to quantitatively analyze the influence of fracture aperture on the permeability of fractured rock mass when the rock matrix permeability is neglected.

Table 2 Classification standard of fracture aperture (modified by ISRM,1978)
Full size table

In previous studies, the matrix permeability of fractured rock mass is often neglected, which often leads to a larger error in judgment on the suitability of the EPM model. The permeability of the rock matrix and fracture aperture control the overall permeability of fractured rock mass at the same time; thus, the influence of both of them on the suitability of the EPM model was studied (Chen et al. 2021a, b). According to Table 2, nine different fracture apertures were selected to build fracture network models (Fig. 3), while the other geometric parameters of fractures are kept constant. As shown in Fig. 4, the matrix permeability of the fractured rock mass gradually increases from 0 to 0.01 m/s, and 12 different matrix permeability values of fractured rock mass were used for the numerical simulation. Totally, 108 fracture network models with different parameters were generated, and 21,600 numerical calculations were performed. The DFM model was used to quantitatively study the influence of fracture aperture and rock matrix permeability on the suitability of the EPM model.

Fig. 3
figure 3

2D DFM models with nine different apertures; ‘Original’ refers to the original fracture aperture, set at a value of 0.27 mm

Full size image
Fig. 4
figure 4

Twelve 2D DFM models with different rock matrix permeability of fractured rock mass

Full size image

Results and discussion

Simulation results of the DFN model

The DFN model was used to explore the influence of fracture aperture on the permeability of fractured rock mass when the matrix permeability is ignored. The hydraulic conductivity K is the smallest when the fracture aperture is 0.1 mm (K = 9.086 × 10–7 m/s), and the largest K is 0.9086 m/s when the fracture aperture is 10 mm. The overall K of fractured rock mass increases exponentially with the increase of fracture aperture, and K is proportional to the third power of the fracture aperture.

If the matrix permeability of fractured rock mass was to be ignored, the DFN model was used to solve the head of each node in the study area, and the simulation results were taken as the reference value of the head in the study area. The EPM model was used to obtain the hydraulic head results of each node in the study area. Finally, by comparing the EPM model simulation results with the DFN simulation results, the hydraulic head error of each node in the study area was calculated to evaluate the suitability of the EPM model. The three calculation methods were mainly used to quantitatively evaluate the influence of fracture aperture on the suitability of the EPM model, including the commonly used MAE and RMSE values and the suitability of the ECM model. These models were all run 200 times to reduce the error caused by randomness. The results show that, when the rock matrix permeability was neglected, with the increase of fracture aperture, the MAE value was 0.1252 m, the RMSE value was 0.1673 m, and the suitability of the EPM model was 0.8783. Under the condition of ignoring the permeability of rock matrix and keeping other fracture geometric parameters unchanged, the change of fracture aperture has no effect on the water head distribution in fractured rock mass, and thus does not affect the suitability of the EPM model.

Simulation results of the DFM model

The DFM model was used to quantitatively study the influence of fracture aperture and rock matrix permeability on the suitability of the EPM model. The results were shown in Fig. 5. With the fracture aperture increasing gradually, the MAE tends to increase gradually. When the fracture aperture increases to a certain limit, the MAE value begins to increase, and finally reaches the maximum value of 0.1252. When the fracture aperture increases beyond this limit, the MAE value will not change. RMSE value keeps the same trend as the MAE value; it gradually increases with the fracture aperture. When the fracture aperture increases to a certain limit, the RMSE value begins to increase and finally reaches the maximum value of 0.1673, and then increases the fracture aperture, and the RMSE value does not change. The matrix permeability of fractured rock mass mainly affects the starting point and endpoint of increases of MAE and RMSE. The influence of fracture aperture on the suitability of the EPM model is emphatically analyzed considering the permeability of rock matrix. Generally, when the permeability coefficient of rock matrix is small, the fracture aperture has little influence on the suitability of the EPM model. When the matrix permeability coefficient is relatively larger, the suitability of the EPM model shows a decreasing trend with the increase of fracture aperture, gradually decreasing from the maximum of 0.9599 to finally 0.8793. When the fracture aperture is relatively smaller, the matrix permeability of fractured rock mass significantly affects the suitability of the EPM model. The greater the permeability, the greater the suitability of the EPM model. The matrix permeability also affects the inflection point where the suitability decreases, and the end point where the suitability tends to be stable (Fig. 5a). With the increase of matrix permeability, the inflection point of decrease will be delayed—in other words, only when the fracture aperture is larger will the fracture aperture affect the suitability of the EPM model. When the permeability of the rock matrix is smaller, the change of fracture aperture will not affect the suitability of the EPM model, which is consistent with the characteristics that the suitability of the EPM model remains unchanged with the increase of fracture aperture when the permeability of rock matrix is ignored (section ‘Simulation results of the DFN model’). The change trends of RMSE and MAE with aperture and matrix permeability are similar (Fig. 5b,c), which are generally reversed compared with the suitability change trend.

Fig. 5
figure 5

Influence of fracture aperture on the suitability of the EPM model: a suitability value, b MAE value, c RMSE value

Full size image

This research also focuses on the influence of the permeability of the rock matrix on the suitability of the EPM model, which is widely ignored by many scholars. The research results are plotted in Fig. 6. With the gradual increase of the permeability of rock matrix, the suitability of the EPM model gradually increases. No matter what the fracture aperture values are, the suitability of the EPM model gradually increases with matrix permeability, starting from the minimum of 0.8783 and finally reaching 0.9599, then tends to be stable. Different fracture apertures have different starting points and end points of the change curve. With the increase of fracture aperture, the starting point and end point will be delayed correspondingly. The trends of MAE and RMSE are consistent. With the increase of matrix permeability, the values of MAE and RMSE gradually decrease, and different fracture apertures have different starting points and end points of curve decline. Using suitability rates, MAE, and RMSE methods to study the influence of permeability of rock matrix on the suitability of the EPM model, the results are very similar, but the suitability rate of the EPM model will reach the stable point faster than the MAE and RMSE.

Fig. 6
figure 6

Influence of matrix permeability on the suitability of the EPM model: a suitability value, b MAE value, c RMSE value

Full size image

Suitability evaluation of the EPM model

Curve fitting is carried out based on the influence of the permeability of rock matrix on the suitability of the EPM model. The results are shown in Fig. 7. It can be found that the fitting results of the suitability vs. different fracture apertures have the same form, and the fitting curve perfectly conforms to the Boltzmann formula (Hashemireza et al. 2023):

Fig. 7
figure 7

Fitting curve of influence of the matrix permeability on the suitability of the EPM model

Full size image
$$y=\frac{{A}_{1}-{A}_{2}}{1+{e}^{\left(x-{x}_{0}\right)/w}}+{A}_{2}$$
(31)

The significance of each parameter in the fitted formula was further explored. Among them, A1 is the lowest value of the curve. Regardless of the variations in fracture apertures, A1 consistently remains at 0.8783, a value that is also indicative of the suitability rate of the EPM model when the permeability of the rock matrix is ignored. As mentioned in section ‘Simulation results of the DFM model’, this value is not affected by the fracture aperture. A2 is the highest value of the curve, remaining constant at 0.9599 across different fracture apertures, indicating that once the matrix permeability increases to a certain limit, the influence of the existence of fractures on the permeability of fractured rock mass is minimal and can be approximately ignored. The permeability of the fractured rock mass can be approximately considered equal everywhere, and then the EPM model can be perfectly used for fractured rock mass. In the case of different fracture apertures, w in the fitting formula fluctuates little and can be approximately regarded as a constant, which represents the changing intensity of the curve when the suitability increases the most. With different fracture apertures, the absolute value of parameter x0 changes to become larger, and it reduces with fracture aperture increase. This study focused on the influencing factors of changing x0. The results show that x0 is related to the rock permeability when the matrix permeability of the fractured rock mass is ignored. As shown in Fig. 8, the fitting parameter x0 is proportional to log10K. Here, K represents the overall permeability K of the fractured rock mass obtained when not considering matrix permeability. In this way, when evaluating the suitability of the EPM model for a site, one can consider the influence of fracture matrix permeability on the EPM model, or consider fracture matrix permeability to modify the suitability of the EPM model according to the existing site conditions. Firstly, without considering the permeability of rock matrix, the suitability of the EPM model for this site is A1, and the rock permeability K can be obtained at the same time; A2 and w are fixed values, which are roughly 1 and 0.478 respectively. Then, x0 is calculated according to the formula with the rock permeability K, and the influence curve of matrix permeability of fractured rock mass on the suitability of the EPM model is combined to quantitatively evaluate the influence of matrix permeability of fractured rock mass on the suitability of the EPM model.

Fig. 8
figure 8

Relationship between the fitting parameter x0 and permeability of the fractured rock mass when matrix permeability of fractured rock mass is ignored

Full size image

Conclusions

In this study, the influence of fracture aperture and matrix permeability of fractured rock mass on the suitability of the EPM model was explored by the numerical simulation method. By keeping the geometric parameters unchanged and by changing the related parameters of fracture aperture and matrix permeability of the fractured rock mass, the fracture network is generated by the Monte Carlo simulation method and hydraulic head is solved by the DFM model. A total of 108 sets of EPM models were built to analyze the influence of comprehensive fracture aperture and matrix permeability of fractured rock mass on the suitability of this model. To reduce the influence of randomness on the results, 200 random simulations as well as a total of 21,600 numerical simulation experiments were carried out for each model.

The results indicate that when the matrix permeability of fractured rock mass is neglected, the overall hydraulic conductivity K of the fractured rock mass increases exponentially with the increase of fracture aperture, and K is proportional to the third power of fracture aperture. With the increase of fracture aperture, MAE, RMSE and the suitability of the EPM models remain unchanged, which is to say, that the change of fracture aperture does not affect the suitability of the EPM model. Considering the combined influence of fracture aperture and matrix permeability of fractured rock mass on the suitability of the EPM model, with the increase of fracture aperture, the suitability of the EPM model tends to decrease, and the difference in matrix permeability of the fractured rock mass mainly affects the inflection point where the suitability decreases. With the increase of matrix permeability, the inflection point will be delayed. With the gradual increase of the matrix permeability of fractured rock mass, the suitability of the EPM model gradually increases, and different fracture apertures affect the starting point and end point of the curve. With the increase of fracture aperture, the starting point and end point will be delayed correspondingly. According to the influence of matrix permeability on the suitability of the EPM model, the curve-fitting result perfectly accords with the Boltzmann formula. When evaluating the suitability of the EPM model of a site, the influence of matrix permeability on the suitability of the EPM model can be quantitatively calculated.

The present study provides valuable insight into the influence of fractures and matrix on the suitability of the EPM method for addressing hydraulic-head-related hydrogeological issues in fractured geological media. While the effects of fracture aperture and matrix permeability were examined in this study, it is important to note that other fracture geometric parameters, such as uneven distribution and fracture roughness, were not comprehensively considered. Additionally, the study focused on a 2D fracture network, whereas in three-dimensional (3D) space, the complexities of water flow and transmission in fractured rock masses are amplified due to factors like fracture connectivity and spatial positioning. Therefore, it is essential to conduct further investigations to determine the suitability conditions of the EPM model in 3D space, accounting for a broader range of fracture geometric parameters.