Introduction

Generating realistic geological facies models from limited, sparse data is an important task in hydrogeology. Given a set of core data, aquifer properties such as hydraulic conductivities from well-pumping tests, and hydrogeologic conceptual models, hydrogeologists often are tasked to estimate the underlying geologic facies models that match field observations and known geologic features. The geological facies models then can be used for many applications such as well-field pumping optimization and contaminant-transport predictions. Because the quality of the conclusions using the numerical groundwater-flow and contaminant-transport models is directly dependent on the quality of the geological facies models, simulating reliable and realistic geological facies becomes an important area of research in hydrogeology.

The field of geostatistics has many methods of geostatistical simulations that can convert a small array of data points (i.e., measurements) into a complete geologic facies model that can imitate real geologic features (Deutsch and Journel 1992). This task is similar to spatial interpolation, but note that such methods must be able to generate multiple solutions that all respect field observations. A popular approach called multi-point statistics (MPS) can use an initial training image and a set of measurements to generate multiple images that have the same geologic features and that honor the conditioning data (e.g., Lochbühler et al. 2014; Honarkhah and Caers 2012; Mariethoz and Renard 2010). MPS generally works by copying the patterns provided within the training image and placing them on the basis of where the hard data points are located. By iteratively repeating this process, entire geologic facies models can be generated to exhibit geological structures similar to those in the training image, along with conditioning on the measurements; furthermore, MPS is also capable of generating images that exhibit nonstationarity (Mariethoz et al. 2015).

Another technique is object-based methods (OBM). By controlling the shapes and distribution of geometric objects, realistic geological features can be generated (Michael et al. 2010; Hauge et al. 2007; Deutsch and Wang 1996). The use of parameterized geometric shapes allows OBM to have a much lower risk of accidentally generating nonrealistic geologic features. The problem with OBM is that it is limited to geologic features that can be geometrically parameterized. The OBM method is not very general—for every type of geologic feature, a separate object model must be designed and tested. Conditioning with OBM also can be challenging because it is difficult to back-calculate which object parameters produce results that honor observed data (Holden et al. 1998).

Because of the recent, rapid success of deep machine learning, many of the deep learning methods are starting to be applied to the field of hydrogeology (Shen et al. 2018). Particularly, generative adversarial networks (GAN) introduced by Goodfellow et al. (2014) has increasingly gained popularity. GAN is composed of two neural network agents called the generator and the discriminator. The generator is tasked with transforming a randomly generated latent vector into a realistic image. The job of the discriminator is to decide whether a given image is real (an image from the training set) or fake (an image produced by the generator). During training, both agents get progressively better at their tasks. As the discriminator gets better at distinguishing between real and fake images, the generator is forced to learn how to make more realistic images to fool the discriminator. After training, the result is a generator that is exceptionally good at generating realistic images such as photographs of human faces (Karras et al. 2019). Such a generator can instead be used to generate realistic geological facies. Given a random latent vector, a generator can transform that vector into a realistic geological model. If the latent vector is adjusted, then the generated images also change, but they continue to resemble a realistic geologic model. GAN can be used essentially as a dimensionality reduction method that can be coupled with data assimilation for parameter inversion (e.g., Laloy et al. 2018; Bao et al. 2020, 2022).

Researchers have applied a variety of GAN architectures to a range of geological modeling scenarios. Specifically, experimenting with both unconditioned and conditioned models, Dupont et al. (2018) used GAN to generate river channel facies. For conditioning the model, they used a blurred version of the measurement array to facilitate the use of gradient descent. Nesvold and Mukerji (2019) used a Wasserstein GAN trained on 20,000 multispectral satellite images of 40 modern river deltas. Markov Chain Monte Carlo method of conditioning with hard and soft data was performed with the trained model. Mosser et al. (2020) employed GAN to, a priori, generate a geological model for a stochastic seismic waveform inversion. Bayesian inversion was performed using the Metropolis-adjusted Langevin algorithm to find generated earth models that honor seismic observations. The differential nature of deep neural networks was used to calculate the gradient for the discrepancies within seismic observations. Laloy et al. (2018) applied spatial GAN to produce two-dimensional (2D) and three-dimensional (3D) geological facies models. The spatial GAN is composed entirely of convolution neural networks (CNN). The use of CNN allows for more flexibility for the size of the generated images.

To generate conditioned geological models, a common technique is to iteratively adjust the latent vector until the generator produces a geologic model that matches with observed geological facies (Mosser et al. 2020; Nesvold and Mukerji 2019; Dupont et al. 2018; Laloy et al. 2018). Methods such as Markov Chain Monte Carlo and gradient descent often are used to calibrate the latent vector. The conditioning process generally involves iteratively generating many hypothetical geological models and recording their mismatch with observed data. After numerous iterations, enough simulation data are collected to allow determination of the appropriate latent vectors. Instead of directly manipulating the latent vectors, researchers also have explored alternate methods for incorporating conditioning data into their GAN architecture—for example, Chan and Elsheikh (2018) produced conditioned results by extending the original GAN with an extra network that learns to perform the conditioning operation. During training, the extra network learns to map an initial set of randomly generated unconditioned latent vectors into a new set of conditioned latent vectors that produce geologic models to honor conditioning data. Song et al. (2021a) applied progressive growing GANs for geomodelling and quickly generating realistic channelized facies models. Based on that, Song et al. (2021b) proposed a framework called GANSim, which is a geomodelling workflow that can directly take sparse well facies data and global features (e.g., channel width) as inputs of the generator for conditioning, together with the original latent vector. In GANSim, input pipelines for different conditioning data (i.e., well data and global features) are designed within the architecture of the generator, and an extra type of condition-based loss function is introduced to enforce the consistency between the input conditioning data and generated geologic models. Song et al. (2022a) proposed to include facies probability maps as another input conditioning data for GANSim. Song et al. (2022b) recently improved GANSim in various aspects and extended the method to generate 3D geologic models of karst cave reservoirs with good results.

Although GAN has been applied extensively in the field of hydrogeology and has gained a degree of success, it also has some issues to be resolved, in particular, for the conditioning of measurements and stability of training—for example, Song et al. (2021b) have shown that their networks can still produce images where the GAN ignores some of the conditioning points. To mitigate this, they proposed enlarging the conditioning points with the intent of increasing the mismatch error, a problem that is not unique to Song et al. (2021b). Chan and Elsheikh (2018) also mentioned a similar issue, and they noted that they cannot fully guarantee that conditioning is strictly honored, but only that it is honored with high probability. Aside from issues with the conditioning behavior of the GAN, another common problem with these networks is their instability. GAN is known to lose variety in its generated output, a behavior known as mode collapse. Because GAN involves two agents competing against each other, any flaws in the agents or the competition process can cause GAN to fail. To deal with this problem, researchers have introduced a variety of methods to reduce instability (Arjovsky et al. 2017; Karras et al. 2017; Heusel et al. 2017). Nesvold and Mukerji (2019) used a Wasserstein GAN because its earth mover’s distance loss function can yield a more stable GAN training session. Song et al. (2021b) used progressive growing GAN for their work because training GAN in successive layers, instead of all at once, was shown to be a more stable method (Karras et al. 2017).

To mitigate the aforementioned issues using GAN, researchers have performed experiments to better understand how the parameters used by these networks affect their performance. Song et al. (2021b) conducted an array of experiments with various weights for global features and well facies loss terms in their loss function. Lopez-Alvis et al. (2020) performed experiments on variational autoencoders and studied how changes in the regularization weight and the noise distribution affect how the generator maps from one latent space into another. Lucic (2018) used a large array of numerical experiments with a variety of GAN architectures and found that, overall, parameters optimization is necessary. They explained that because of GAN’s sensitivity to its parameters, researchers cannot simply assume that the parameters they found for their work can be applied to all scenarios. Even given the same machine learning model, a different application of the model requires researchers to develop their own set of optimal parameters.

To resolve issues with applying this conditioning behavior to these generative machine learning models, it is important to establish a better understanding of how these networks learn this conditioning behavior. When this mechanism is better understood, researchers can make improved decisions about which architecture hyperparameters must be changed to yield better results.

In this work, a novel metric for measuring various aspects of conditioned progressive growing GANs is proposed. Specifically, a newly defined metric called the conditioning ratio was calculated across the layers of a conditioned progressive growing GAN during training. The conditioning ratio determines the magnitude of the influence of the conditioning input. This metric is used by the discriminator during training as a method to reduce model collapse. However, the conditioning ratio becomes a more valuable metric when applied to the layers of a generator within PGGAN’s architecture. What makes the PGGAN architecture special is that it trains a generator in stages, with each stage learning to produce a higher resolution image using the output of the previous stage. By measuring the conditioning ratio at each of these stages, the growth and development of the conditioning behavior can be observed. Within the context of GANs, the conditioning ratio metric fills the gap for a metric that focuses on the variance of generated images and measures how they are influenced by conditioning input. This process also was repeated for various network architecture hyperparameter values to observe how these changes affect the networks’ learning of the conditioning behavior. The results of these experiments can help researchers when designing new conditioned GAN architectures. This is possible by using the proposed metric to measure which layers first learn the conditioning behavior and observe how each layer contributes to the overall performance of the generator. The proposed metric could also help guide the design of the training process by predicting the final performance of the generator without needing to wait for the entire training process to complete.

Methodology

Training images

In this work, a GAN was trained to generate realistic images of channelized aquifers. To train the GAN model, the training images were generated by cutting out sections of a source image. For this study, the source image was a 2500 × 2500-pixel image containing channelized aquifers trending along the east–west direction (Fig. 1; Zahner et al. 2016). The source image contained two facies: one facies with high hydraulic conductivity in the channels, and another with low conductivity outside the channels. The training images were generated by randomly clipping out 128 × 128-pixel images out of the source image. To produce a validation set of images, the randomly clipped images were flipped horizontally to ensure the new images had never been seen by the trained model. Horizontal flipping is sufficient to generate the validation set of images because convolutional neural networks are known to produce results that are not invariant to various spatial transformations such as flips and rotation (Azulay and Weiss 2018). Data augmentation techniques take advantage of this property by spatially transforming training images to increase the size of the training set (Hernández-García and König 2018). The goal of the GAN was to generate 128 × 128 images of the same channelized aquifers in a way that imitates the channel connectivity of the source image. After training, the models were first verified by visual inspection that the channel connectivity of the generated images were properly imitated before starting experiments with the conditioning ratio.

Fig. 1
figure 1

Shows the source image used to generate the training data. The source image has a resolution of 2500 × 2500 and contains channelized facies that are oriented along the east–west direction (Zahner et al. 2016). Training images are made by randomly clipping out 128 × 128 sections of the source image

Full size image

Progressive growing GAN

A progressive growing GAN architecture was used for this study. PGGAN is a GAN architecture first introduced by Karras et al. (2017) as a method to improve stability during training of GAN. PGGAN works by first training the generator and discriminator in creating and discriminating images that are of a very low resolution, such as a 4 × 4 image. The training images for this first training session are just the original training images downsampled until they are at the matching training resolution. After the networks have learned to generate realistic 4 × 4 pixel images, an additional layer is added to both networks. The networks then begin to learn how to produce realistic 8 × 8 images. To ease the training process, the output of the first layer is resampled to the new resolution before being sent to the newly added layer. Thus, for the generator, the 4 × 4 images generated by the first layer then are upsampled into 8 × 8 images before being sent into the new layer. To further ease the training process, the generator first outputs just the upsampled output of the first layer, without using the newly appended layer. As training progresses, the influence of the new layer is linearly increased until, by the end of the training stage, the generator’s output is the upsampled image of the first layer that has been modified by the new second layer. When the networks have mastered the second stage with 8 × 8 images, the training moves to the next stage with a greater resolution. For this work, each successive stage doubled the number of pixels along the edges of the images (4 then 8 then 16, and so on). This process continued until the networks could generate realistic images of the same resolution as the original training images. the final resolution was a 128 × 128 image for this study. As the networks are grown during training, the networks first learn to replicate broad features that can be seen in low-resolution versions of the training images. As the training resolution increases, the networks learn to replicate finer and finer details until the original resolution is achieved. Experiments by Karras et al. (2017) showed that this progressive architecture not only produces more stable results but also yields realistic images of much greater resolution than previously achieved.

Original GAN architectures were known to have problems with the lack of variety of the generated images (Lala et al. 2018). The generator would produce realistic images, but only a few types of images, instead of the full variety available in the training set. To remedy this, Karras et al. (2017) incorporated a technique called minibatch discrimination into the PGGAN architecture (Salimans et al. 2016). Minibatch discrimination begins with calculating the standard deviation for each spatial location across all the images in the batch sent to the discriminator. The average of the standard deviations is calculated, yielding a single value. This value then is broadcasted into an array of the same dimensions as one of the images. Finally, this array of the mean of standard deviations is appended to each of the images in the batch as a new feature. This mean of standard deviations is used as a metric for mode collapse. If the mean is small, then the variety of the generated images has dropped and mode collapse has occurred. If the mean is large, then the generated images have a great variety and the generator has trained properly. Appending this feature to the images allows the discriminator to quickly learn and identify when mode collapse is taking place. To trick the discriminator, the generator is forced to learn a new mapping that does not have any mode collapse.

Conditioned PGGAN

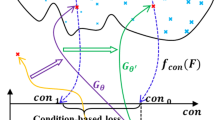
To have the PGGAN generate realistic images that are conditioned to well data, this work uses the GANSim architecture introduced by Song et al. (2021b). A minor difference in the architecture used by this study is how the conditioning data is introduced into the generator. In the original GANSim architecture introduced by Song et al. (2021b), the conditioning data was introduced into the network as a two-layer array. For this work, conditioning data is instead introduced as a single-layer array. The conditioning data are formatted as a 2D array that contains the location of the wells and the facies type known at those points. For this study, the elements of the array could take one of three possible values: ‘1’ represents the high conductivity facies, ‘–1’ represents the low conductivity facies, and ‘0’ represents areas where the facies type is unknown. The conditioning array is injected into the generator of the PGGAN by downsampling the conditioning array, convolving the result with a small convolutional layer, and appending the resulting block to the blocks within the generator’s architecture. Because the generator contains a set of blocks responsible for convolving images at each resolution stage, a downsampled and convolved conditioning array is appended to the blocks of each resolution stage. The downsampling method used for the conditioning layers is the average pooling method. With the conditioning data introduced at various resolutions, the generator is given the opportunity to learn how to incorporate the data, from broad structures down to the fine structures of the images. Figure 2 shows the structure of the generator within the PGGAN architecture and shows how information from the conditioning array is incorporated into the generated image.

Fig. 2
figure 2

Expanded view of the generator side of the conditioned PGGAN architecture. The architecture is the same as the GANSim architecture introduced by Song et al. (2021b). The generator begins with a randomly generated latent variable. The latent variable is sent through a fully connected neural network (FCN) with its result reshaped into the \(n \times n \times 128\) dimensions. This generator begins with a starting resolution of \(2 \times 2\) (this parameter is varied in the experiments). Concatenated with this 128-block is a \(n \times n \times 4\) block that contains information from the initial conditioning array. This generator uses four conditioning layers for its conditioning blocks (this parameter is varied in the experiments). This 4-block is made by first downsampling (DS) the initial array many times until it produces an image that matches the \(n \times n\) dimensions of the blocks. The downsampling method used for the conditioning arrays is the average pooling method. This downsampled image then is sent through two consecutive convolutional neural networks using a 3 × 3 kernel (“Two CNN 3 × 3”). After the 128-block and the conditioning 4-block are concatenated together to form a \(n \times n \times 132\) block, the result then is upsampled (US) using the nearest-neighbor method to double the resolution to form a \(2n \times 2n \times 132\) block, the final block produced from this resolution stage. For the next resolution stage, the final 132-block output from the previous stage is sent through another set of convolution neural networks to produce a new 128-block for the resolution stage. The process repeats for many more stages until the final 132-block has the same side dimensions of the final image (\(128 \times 128\) for this example). The final 132-block is sent through a single convolution neural network layer to produce the final generated images. For this work, a minor change was made where the conditioning input was introduced using only one layer instead of using two layers as outlined by Song et al. (2021b) on the original GANSim architecture

Full size image

To generate the conditioning arrays used for training and validation, conditioning masks are used. Conditioning masks are sparse, 2D arrays filled mostly with zeros except for locations where a conditioning point is located. To create these conditioning masks, the process starts by creating a 128 × 128 array filled with a random, uniform distribution of ones and zeros. This array is multiplied element-wise with another random array created in the same way. After several iterations of multiplying with another random array, the result is a conditioning mask array that contains a sparse distribution of ones in an array filled with zeroes. This conditioning mask then can be multiplied element-wise with a training image of a channelized aquifer to create a conditioning array that can be used by the generator. To change the overall density of the conditioning points, increasing the number of multiplication iterations increases the sparsity of the points. For this study, 10 iterations were used. This method for generating the conditioning masks allows the spatial distribution and the number of conditioning points to be randomized. This was done to ensure the generator does not learn to rely on these attributes of the conditioning array.

Loss functions and training procedure

The discriminator is tasked with converting an image channelized aquifer into a numerical score that reflects how realistic the image is, with more realistic images yielding larger values. The goal of the optimizer is to adjust the discriminator until it yields high scores for images from the training set and low scores for images made by the generator. The optimizer does this by adjusting the parameters of the discriminator in a way that minimizes the value of the loss function. The loss function used to train the discriminator in the PGGAN is similar to the loss function used for WGAN-GP architecture (Gulrajani et al. 2017).

$$\begin{aligned} { \mathbf{L}(\mathbf{D}) = \mathbb {E}_{\mathbf{z} \sim \mathbf{p}_{\mathbf{z}}}\left\{\mathbf{D}\left[G\left(\mathbf{z}\right)\right]\right\} - \mathbb {E}_{\mathbf{x} \sim \mathbf{p}_{\mathbf{x}}}[\mathbf{D}(\mathbf{x})] + \lambda \mathbb{E}_{\hat{\mathbf{x}} \sim \mathbf{p}_{\hat{\mathbf{x}}}}[({\Vert \nabla _{\hat{\mathbf{x}}}\mathbf{D}(\hat{\mathbf{x}})\Vert }_{2} - 1)^2]} \end{aligned}$$
(1)

The loss function shown in Eq. (1) uses the outputs of the discriminator \(\textbf{D}\) and the generator \(\textbf{G}\) evaluated using images \(\hat{\textbf{x}}\) and latent vectors \(\textbf{z}\). For this study, the latent vectors have a length of 128. The discriminator loss function is composed of three main terms. The first two terms are responsible for adjusting the discriminator so that it outputs a small score for images made by the generator and a large score for images taken from the training set. The last term is the gradient penalty term. It is responsible for ensuring that the discriminator does not change too much to the point of causing instability in the GAN training process. In the last term, \(\lambda\) sets the weight for the gradient penalty term; it was set to \(\lambda = 10\) for this study. \(\hat{\textbf{x}}\) is a random linear interpolation between an image made by the generator (\(\mathbf {x_G}\)) and an image sampled from the training set (\(\textbf{x}\)). \(\hat{\textbf{x}}\) is defined as \(\hat{\textbf{x}} = \varepsilon \textbf{x} + (1 - \varepsilon )\mathbf {x_G}\) where \(\varepsilon\) is a weight with its value randomly sampled from a uniform distribution between zero and 1 [\(\varepsilon \sim\)uniform(0, 1)].

The loss function used by this study is the same as what was presented by Song et al. (2021b). Because the PGGAN training process operates in stages of different resolutions, the loss function must be modified such that it can be evaluated in different resolutions.

$$\begin{aligned} \mathbf { L(G) = -\mathbb {E}_{z \sim p_{z}}\left\{D[G(z)] \right\} + \text {ln}({\Vert \{U[G(z)] - x_{ref}\}\odot I\Vert }_{2})} \end{aligned}$$
(2)

The discriminator loss function is composed of two main terms. The first term in the loss function is responsible for adjusting the generator such that it produces images that maximize the corresponding score given by the discriminator. This term essentially encourages the generator to produce images that fool the discriminator into thinking the images are real and are from the training set. The second term in the loss function is responsible for ensuring the generator learns to produce images that respect the conditioning data. The images made by the generator are first upsampled so that the resulting image is the same 128 × 128 resolution as the training images [\(\mathbf{U}(\mathbf{G}(\boldsymbol{z})\))]. The upsampling method used for this is the nearest neighbor. The generated and upsampled images are compared to the reference images (\(\mathbf {x_{\text {ref}}}\)) used to generate the conditioning arrays. The difference between the two arrays then is multiplied element-wise (\(\odot\)) with the conditioning mask \(\textbf{I}\). This makes sure the sum of errors only considers differences at sites where the conditioning data are given. After calculating the L2 norm, a natural logarithm was applied to the result to ensure the value of this term does not grow too large to the point of causing trouble with the training process. Including the natural logarithm to the original loss function presented by Song et al. (2021b) is a minor modification intended to improve stability during the training process.

The optimization method called Adam (Kingma and Ba 2014) was used to train both the generator and discriminator. The Adam optimizer was used with \(\beta _1=0\), \(\beta _2=0.99\), and \(\epsilon _1={10}^{-8}\), which are standard values used by Karras et al. (2017) and Song et al. (2021b). Unlike previous PGGAN, the generator and discriminator used two different learning rate values, instead of using the default value of \(\text {lr} = 0.001\) for each. The learning rate for the generator was \({\text {lr}}_{\text {G}} = 0.001\), but the learning rate for the discriminator was reduced to \({\text {lr}}_{\text {G}} = 0.00002\). The concept of having the generator and discriminator use two different learning rates was first investigated by Heusel et al. (2017). They found that having two separate learning rates allows the GAN system to approach a Nash equilibrium and therefore improve the stability of the GAN training process. Because this study involves performing a set of experiments that changes the architecture of the networks, the training method must be set up such that it can train a wide variety of architectures without needing to change the training hyperparameters.

The PGGAN training procedure involves multiple stages, one for each training resolution. Given training resolutions of 4 × 4 up to a resolution of 128 × 128, there are up to 6 training stages. In each stage, the GAN transitions from performing its tasks from the current resolution to the next higher output resolution. For this study, the entire GAN training process goes through 200,000 iterations, so about 33,000 iterations are distributed evenly to each of the training stages. In each iteration, the networks train through a batch of 32 images. Within each training stage, the generator only outputs an upscaled version of the image produced by the previous layer. But as training progresses, the weight for the new convolution layer linearly increases such that by the end of the training stage, the generator outputs an image produced by the new layer. A summary of the entire training procedure for PGGAN is shown in Algorithm 1.

Algorithm 1
figure a

Training procedure for a progressive growing GAN

Full size image

Measurement of the conditioning ratio

The generator of the conditioned PGGAN architecture has two main inputs: the latent vector, and the conditioning array. Previous works have studied the influence the latent vector has on the output (Mosser et al. 2020; Nesvold and Mukerji 2019; Dupont et al. 2018). This means to produce a range of images that respects observations, only the latent vector can be manipulated to achieve this. But the conditioned PGGAN architecture has two inputs, the latent vector and the conditioning input. The latent vector can be used to generate variability in the images, while the conditioning input ensures the generated images respect observation data. This study focuses more on the influence the conditioning array has on the output image. The generator is designed to use the conditioning array to produce conditioned images, but this performance must be measured. This measurement is done by using a process similar to minibatch discrimination. To evaluate the conditioning behavior of a trained generator, the generator transforms a batch of 50 latent vectors and conditioning arrays into a batch of realistic images. In this batch, all the latent vectors are randomly generated. But for the conditioning arrays, the first 25 arrays are all the same, while the last 25 arrays are all different. The last 25 conditioning arrays are randomly generated and a new set of conditioning arrays are generated every time the conditioning ratio is recalculated. This is done to reduce the artifacts that may be introduced by any single batch of conditioning inputs. For each set of 25 images, the mean of the pixel-wise variance is calculated using the same process as minibatch discrimination. If the generator has been trained correctly, then the mean variance for the images that used the same conditioning array should be lower than the mean variance for the images that used different conditioning arrays. Dividing the mean variance for images that used the same conditioning array by the mean variance for images that used different conditioning arrays yields a useful metric defined as the “conditioning ratio”. A summary of the conditioning ratio metric is presented in Algorithm 2. Figure 3 shows example batches of generated images with a high and low value for the conditioning ratio. A conditioning ratio less than one means that the generator has the expected behavior of reducing the variance of generated images due to the introduction of conditioning data. To get a stable value for the conditioning ratio, the generator evaluates 1,000 batches and then reports the average value across all the batches as the final conditioning ratio for a given generator. Since the conditioning ratio uses the mean of the pixel-wise variance of the generated images, the standard errors of the means could be computed by using the standard deviation of the pixel-wise variance. However, this standard error was found to quickly vanish because of the large number of pixels used. For example, 8 × 8 images generate 50 times already yields a sample size of 3,200. Variations from simply retraining the GAN model produce a larger variance on the metric than from the inherent variances from calculating the metric. Note that the conditioning ratio measures the influence conditioning data has on the variance of the generated images. It does not measure the proportion of correctly produced point data among all input point data.

Algorithm 2
figure b

Calculating the conditioning ratio metric

Full size image
Fig. 3
figure 3

Example batches of generated images with different conditioning ratios. For each batch (a–b), the first 25 images (above the center red dividing line) were generated with different latent vectors but the same conditioning array. However, for the second 25 images (below the center red dividing line), the images were generated with different latent vectors and different conditioning arrays. The two 25-image batches were placed on top of each other (with the middle row containing a five images from batch 1 and b five images from batch 2) to highlight any visual similarities or differences between the two batches. Note that for large conditioning ratios, such as in section ‘Trends across the number of conditioning layers’, this means the generator will produce realizations with a variance that does not significantly change, even when the conditioning data is held constant while the latent variable is varied. Visually, this means the two batches will look like each other and the boundary between the two batches is difficult to distinguish. When the conditioning ratio is close to zero, such as in section ‘Trends across the number of conditioning layers’, the generator will produce realizations with variances lower than what the conditioning data allows. Visually, this means the two batches will be easy to distinguish since one of the batches will look like copies of the same image

Full size image

One of the advantages of using the conditioning ratio is that it can be evaluated regardless of the resolution at which the generator operates. When using pixel-wise variance maps, comparisons become difficult to interpret when comparing between variance maps of different dimensions. The conditioning ratio resolves this issue by summarizing the variance of generated images with a single normalized value, thereby allowing comparison of variance maps with different resolutions. This allows the conditioning ratio to be evaluated not only for a completely trained generator, but also for the generators throughout the entire training process, giving insight into how the conditioning behavior of the generator changes throughout the training process. Because the generator of the PGGAN process is composed of layers that generate images at different resolutions, the conditioning ratio also can be evaluated for different layers within a single generator. The conditioning behavior can be monitored as information propagates through the generator’s network. Note that the conditioning ratio still has its utility, even when evaluated during later stages of training where early low resolution CNN layers are no longer required to produce realistic and conditioned images. Studying the changes of the conditioning ratio of these early layers can yield insight into how the PGGAN learns its conditioning task and how the performance of early layers influences the performance of later layers.

Network architecture experiments

When investigating the conditioning behavior of the generator from a PGGAN process, the conditioning layers within the generator become an important network component to study. Song et al. (2021b) used 16 conditioning layers for each stage with the generator. This study explores a range of values for the number of conditioning layers. A range from 4 to 128 layers was explored. The number of layers can be important because it can change the conditioning behavior of the generator. If the number of conditioning layers is too small, then the generator might not be able to learn how to use the conditioning array to generate conditioned outputs. If the number of conditioning layers is too large, then the generator might rely too much on the conditioning array and lose the variety introduced by the latent vector.

Another important architectural component of the generator network is the starting resolution for the PGGAN process. Song et al. (2021b) used 4 × 4 as their starting resolution but did not explore other starting resolutions. This study investigates the effects of changing the starting resolution and how it competes with other network architecture parameters. Intuitively, having a larger starting resolution would make the generator have a harder time learning to replicate broad-scale structures. These experiments were designed to test whether this intuition remains true in practice. This study will experiment with starting resolutions of 4 × 4 and 8 × 8. This study will also investigate how changing the starting resolution will affect the number of conditioning layers necessary to produce a properly trained conditioned GAN.

Results

Trends across the number of conditioning layers

Several PGGAN models were trained with a range of values for the number of conditioning layers. Values ranging from 4 to 128 conditioning layers were explored. A starting resolution of 4 × 4 and 8 × 8 also was explored. Figure 4 shows the result of plotting the conditioning ratio against a varying number of conditioning layers, including the conditioning ratio plot for a 4 × 4 and an 8 × 8 starting resolution. For both starting resolutions, the generators sharply transitioned from a high conditioning ratio to a low ratio as the number of conditioning layers increased. However, the transition for the 8 × 8 series occurs sooner than the transition for the 4 × 4 series transitions at. The 4 × 4 series begins to transition at 48 conditioning layers, while the 8 × 8 series begins to transition at only 12 conditioning layers. After the transition, the conditioning ratio for the 8 × 8 series begins to increase as the number of conditioning layers increases.

Fig. 4
figure 4

The conditioning ratio plotted against the number of conditioning layers. There are two data series, one for generators with a 4 × 4 starting resolution and one for generators with an 8 × 8 starting resolution. Both series show the conditioning ratio decreasing as the number of conditioning layers increases. Note that the 8 × 8 series transitions at a lower number of conditioning layers than where the 4 × 4 series transitions

Full size image

Figure 5 shows batches of images generated by various generators trained within the 4 × 4 series in Fig. 4. Focus is placed on the transition period that occurs at 48, 56, and 64 conditioning layers. As the conditioning ratio drops, the variance of the generated conditioned images is reduced. All three batches were given the same number of conditioning points, so the conditioning array is not responsible for the drop in image variance.

Fig. 5
figure 5

Example batches made by generators with different amounts of conditioning layers. As the number of conditioning layers increases, the conditioning ratio drops. This figure showcases how this drop of the conditioning ratio changes the generated images during this transition period. The batches are generated with the same method shown in Fig. 3. As the conditioning number drops, the variance of the conditioned images drops. This is true even when all three image batches are given the same amount of conditioning points

Full size image

Trends across training iterations

As the networks went through the PGGAN training process, the conditioning ratio was calculated for each resolution within the generator. For the series of generators with a 4 × 4 starting resolution, the conditioning ratio plots were made for the 8 × 8, 16 × 16, 32 × 32, 64 × 64, and 128 × 128 outputs of the generator. The conditioning ratios were calculated throughout the 200,000-iteration process. Figure 6 shows this set of conditioning ratio plots for the 4 × 4 starting resolution generators with 8, 16, 32, and 64 conditioning layers. Figure 6 shows trends that are common across all four conditioning ratio plots. During the start of the training session, the conditioning ratios for each of the resolution stages drop in sequence. Training begins with the 8 × 8 stage dropping to a low conditioning ratio before the rest of the stages follow suit. For the generators with 8 and 16 conditioning layers (Fig. 6a,b), the conditioning ratios for most of the resolution stages remain close to one, while the 4 × 4 and 8 × 8 resolution stages have their conditioning ratios widely vary throughout the training. Figure 6c shows the 32 × 32 conditioning layer generator with most of the stages sharing very similar conditioning ratios throughout the training session. Except for the 8 × 8 resolution stage, the conditioning ratios of the remaining stages began by dropping down close to zero before bouncing back up and approaching the final value. For Fig. 6d, all resolution stages approached zero, except for the 4 × 4 stage, which became unstable and produced conditioning ratios well above 1.

Fig. 6
figure 6

The conditioning ratio versus training iteration plots for PGGANs that use a starting resolution of 4 × 4. Each subfigure shows the plot for a generator trained with a given number of conditioning layers. Within each plot, each series is a set of conditioning ratios for a given output resolution within the generator

Full size image

For the 4 × 4 starting resolution series, Fig. 6 shows that the conditioning ratio transitions from high to low between 32 and 64 conditioning layers. To better understand this transition, additional tests were done at 48 and 56 conditioning layers. Figure 7 shows the additional set of conditioning ratio plots for this transition period. The plots of Fig. 7 show that as the number of conditioning layers increases, the variation between the conditioning ratios increases. In Fig. 7a, except for 8 × 8 stages, all other stages have their conditioning ratios closely following each other throughout the U-shaped trend, with differences no greater than 0.2. However, in Fig. 7c, the cluster of stages expands to the point of having a maximum difference of 0.4. The final generator produces a range of conditioning ratios, with higher conditioning ratios corresponding to higher output resolutions.

Fig. 7
figure 7

The conditioning ratio versus training iteration plots for the generators that use a starting resolution of 4 × 4. Each subfigure shows the plot for a generator trained with a given number of conditioning layers. Within each plot, each series is a set of conditioning ratios for a given output resolution within the generator. These plots focus on when the final output of the generator transitions from a high to low conditioning ratio between 32 and 64 conditioning layers (Fig. 4)

Full size image

As with Fig. 6, Fig. 8 shows the conditioning plots for the series of generators with an 8 × 8 starting resolution. Figure 8 shows the plots for generators trained with 8, 16, 32, and 64 conditioning layers. The figures show that for generators with 16 conditioning layers or greater, the majority of the stages begin with an initial conditioning ratio of one, then sharply trend down toward zero before rising back up toward the final value. This trend of having an initial drop is similar to what was found for the 4 × 4 starting resolution generators (Fig. 7, although the drops were not as sharp as what was found for the 8 × 8 starting resolution generators in Fig. 8. The 8 × 8 series begin their initial drops sooner, at 40,000 iterations, as compared to the 4 × 4 series with their initial drops that start at 60,000 iterations. During the slow upward trend in the conditioning ratio, there is a small but consistent bump at 170,000 iterations for the final resolution stage of 128 × 128. At the end of the training session, the conditioning ratio of the trained generator varies, based on the output resolution of the stage, with higher resolutions yielding higher conditioning ratios. Note that this trend is consistent with what was found in Fig. 7c.

Fig. 8
figure 8

The conditioning ratio versus training iteration plots for PGGANs that use a starting resolution of 8 × 8. Each subfigure shows the plot for a generator trained with a given number of conditioning layers. Within each plot, each series is a set of conditioning ratios for a given output resolution within the generator

Full size image

For the 8 × 8 starting resolution series, Fig. 9 shows that the conditioning ratio transitions from high to low between 8 and 16 conditioning layers. To better understand this transition period, additional models were trained with 12 and 14 conditional layers. Figure 9 shows the set of additional conditioning ratio plots for this transition period. The plots of Fig. 9 show that as the number of conditioning layers increases, the magnitude of the initial drop of the conditioning number increases. With eight conditioning layers (Fig. 9a), the 16 × 16 stage only dips as low as 0.5, while the rest of the higher resolution stages remain close to one. With 12 conditioning layers (Fig. 9b), the 16 × 16 stage dips down farther to 0.45, while the rest of the higher resolution stages continue to remain close to one. However, with 14 conditioning layers (Fig. 9c), the rest of the high-resolution stages finally perform the distinct drop of the conditioning ratio × iteration 60,000. Compared to the transition slope for the 4 × 4 starting resolution series, the transition slope for the 8 × 8 series is much steeper. Even with the additional experiments, there was no 8 × 8 series model that yielded a conditioning ratio between 0.4 and 0.6.

Fig. 9
figure 9

The conditioning ratio versus training iteration plots for generators that use a starting resolution of 8 × 8. Each subfigure shows the plot for a generator trained with a given number of conditioning layers. Within each plot, each series is a set of conditioning ratios for a given output resolution within the generator. These plots focus on when the final output of the generator transitions from a high to low conditioning ratio between 8 and 16 conditioning layers (Fig. 4)

Full size image

Discussion

Some of the trends in the results are reasonable and can be intuitively explained. One example is the trend where, during training, all conditioning ratios begin at a value of one before dropping down and then rising back up to their final value. At the start of the training sessions, the generator begins at a conditioning ratio of one because the later stages have not yet learned how to use the conditioning array or even learn how to produce realistic images yet, so the initial images are essentially randomly generated images with no influence by the conditioning array. As training continues, the conditioning ratio drops because the generator quickly learns that it can yield a lower value for the loss function, through the second term of Eq. (2), if it incorporates the conditioning array into the output of the generator. Afterward, the conditioning ratios begin to rise because the variance between the generated images increases as the resolution of the generated images also increases. This explains why the conditioning ratio of the fully trained generator increases with the resolution of the output image (see iteration 200,000 of Fig. 8d). The specific paths the conditioning ratio takes during training will vary, based on the resolution stage and other hyperparameters, but the general U-shaped trend holds true for the majority of the tested models. The U-trend indicates that, at least for the conditioned PGGAN architecture, the generator prefers to first learn to copy data from the conditioning array into output; then it learns how to adjust the output to be more realistic and imitate the variance of the training images. This initial dependence on the conditioning array could explain why Song et al. (2021b) found issues with “local pixel noise” in which the generator produces images with outstanding pixels that match the conditioning data but do not match the surrounding geologic facies. The generator learns to ignore the influence of the conditioning as it seeks to produce more realistic images. To fix this, Song et al. (2021b) proposed enlarging the conditioning points with the intent of increasing the mismatch error. Another method to explore is training the discriminator to be more sensitive to these outstanding conditioning points.

Although the experiments reveal trends that are easily explainable, the results also show trends that are not intuitive. The most substantial example is the plot shown in Fig. 4. The intuition behind the experiments was that having a lower starting resolution gives the generator a better opportunity to learn how to replicate these broad-scale features in the images and to learn how to incorporate conditioning data into these large-scale features. Having another resolution stage also provides an additional path to inject conditional data into the generator. Both of these reasons indicate that a generator with a 4 × 4 starting resolution should require fewer conditioning layers in order to have the same performance as an 8 × 8 starting resolution generator. Yet the results in Fig. 4 shows the opposite result, with the 8 × 8 starting resolution generators transitioning from a high to low conditioning ratio at a smaller number of conditioning layers than the 4 × 4 transition. A possible explanation for why this occurs is that the early stages of the generator can become a burden if the resolution is too small. Note that many of the plots for the 4 × 4 starting resolution series show the first stage (8 × 8) following trends that are different from what the rest of the higher resolution stages follow. Figure 9c shows the first two stages reaching a conditioning ratio of zero. Plots from the 8 × 8 starting resolution series (Fig. 9a–c) only show divergent behaviour from the first stage of the generator, which has an 8 × 8 resolution. Note that conditioning ratios above 1 have the same meaning as the conditioning ratio equal to 1, which means the model is producing outputs that are not properly constrained by conditioning inputs. A conditioning ratio of more than 1 rarely occurs and is most likely to occur with very low resolution images (such as 4 × 4) where a small pixel count is most likely to produce a set of values that yields a conditioning ratio value greater than 1. This case is unlikely to occur with images of larger resolutions. In Fig. 9c, the first stage even climbs upward like the rest of the stages, unlike the first stage in Fig. 7a. The burden of the early stages also shows in the delay of the initial drop of the conditioning ratio during training. The 8 × 8 series begin their initial drops sooner, at 40,000 iterations, compared to the 4 × 4 series with their initial drops starting at 60,000 iterations.

On top of revealing nonintuitive learning behaviors within the training of conditioned PGGAN generators, the conditioning ratio has proven to be a useful metric for tuning the parameters of these generators. Figure 5 showcases this tuning process using the conditioning ratio metric. Recall that a generator with a large conditioning ratio will produce a variety of realistic images that do not respect the conditioning data. A generator with a small conditioning ratio produces images that respect conditioning data, but at the cost of producing images with low variance. Therefore, the ideal generator that produces realistic conditioned images with high variance will have a conditioning ratio that is between these two extremes, whereby the lower extreme is 0 and the upper extreme is 1. In practice, these extremes can be verified by measuring the conditioning ratio of the conditioned GAN model when it exhibits one of two types of training failure. If there is almost no variance in the generated images when the conditioning input is held constant, even while the latent variable is varied, then the measured conditioning ratio will be close to zero. However, if the variance of the generated images does not reduce when the conditioning input is held constant versus when the conditioning input is varied, then the conditioning ratio will be one. For some architecture parameters, such as the number of conditioning layers, a simple binary search using the conditioning ratio metric can quickly find the optimal value for these parameters. When tuning the parameter, the target value for the conditioning ratio is 0.5. A conditioning ratio of 0.5 means that the generator is able to properly produce images that respect the conditioning input but does so in way that does not severely reduce the variance of the generated images beyond what the conditioning input can justify. To use the conditioning ratio for tuning parameters, first select the tuning parameter of interest. For the case of Fig. 5, the parameter of interest is the number of conditioning layers in the GAN architecture. Next, run the GAN model with various values for the tuned parameter and calculate the conditioning ratio of the model’s output for each of these runs. Some parameter values will yield a GAN with a conditioning ratio close to one, while other parameter values will make the GAN have a conditioning ratio close to zero. Since the conditioning ratio is continuous, then there must exist a parameter value such that it will produce a GAN with a conditioning ratio of 0.5. This parameter value can be found using the binary search algorithm. At the conditioning ratio of 0.5, the model produces images that respect the conditioning input. Also at 0.5, the model does not over rely on the conditioning input to the point where the model only produces one image when the conditioning input is varied, even when the latent variable is varied. For the example shown in Fig. 5, a binary search with the conditioning ratio will find 56 conditioning layers to be close to the optimal value.

Conclusions

This study introduces a set of experiments that focus on investigating the performance of conditioned progressive growing generative adversarial networks (PGGANs). The generators of these PGGANs are tasked with converting a latent variable and a conditioning array into images of geologically realistic channelized aquifers that match with point data from well observations. Conditioning data are injected into the generator by downsampling the conditioning array and appending additional conditioning layers to the existing layers within the generator. Focus was placed on investigating the conditioning performance of these networks and how their performance changes in response to alterations of the network architecture. To measure the conditioning performance of the network, a metric called the conditioning ratio was defined. The conditioning ratio is essentially the variance of images generated with the same conditioning data divided by the variance of images generated with different conditioning data. Low conditioning ratios indicate strong or excessive conditioning behavior and high ratios mean little to no conditioning. By measuring the conditioning ratio, the experiments can provide information about how the conditioning behavior changes across many different scenarios. The conditioning ratio was measured on each of the resolution stages within the generator while it was training. This measurement process also was done for varying numbers of conditioning layers and with different starting resolutions.

The experiments and measurements of the conditioning ratio yielded plots that provide great insight into how the conditioning behavior arises within these networks. The results revealed a common U-shaped trend where, during training, the conditioning ratio starts at a high ratio and then quickly drops before climbing back up toward the final value. The results also show that PGGANs with lower starting resolutions can require more conditioning layers than generators with a higher starting resolution. Overall, the experiments demonstrated that measuring the conditioning ratios within layers of the generators provides a valuable method for monitoring the performance of these networks. Researchers can reduce the computational demands of exploring new GAN architectures by using the conditioning ratio to trim off redundant high-resolution layers of the progressive GAN process or by stopping the training process early when the conditioning ratios detect a trend that predicts a failure at the end of training.

Future applications for these experiments include using conditioning ratios across PGGAN generator layers as diagnostic tools useful for the design of future GAN architectures that produce images of higher dimensions or can receive a wider variety of conditioning data. The techniques introduced in this work also can be extended to GAN architectures designed to find mappings between state and parameters space, thereby helping in the design of more efficient surrogates for groundwater models.