Introduction

Groundwater systems have finite yields, and groundwater resources can be overexploited due to both natural factors (e.g., ecological water consumption and climate-driven changes) and human activities (e.g., drinking, irrigation and industrial consumption; Krogulec 2018; Smith and Pollock 2012). To improve the sustainability of an aquifer and obtain environmental benefits, there is a need to increase the groundwater yield via managed aquifer recharge (MAR) techniques (Bansal 2017; Rodriguez-Escales et al. 2018). Artificial groundwater recharge is an efficient and controllable MAR technique that is widely used (Ali and Islam 2019; Qi et al. 2020). Recently, many studies have focused on applying artificial groundwater recharge approaches (e.g., infiltration ponds, irrigation, streams, wells and other temporary reservoirs) to unconfined aquifers to mitigate the flood risk of stormwater in humid areas, augment natural groundwater in arid areas, control the intrusion of seawater in coastal areas, and dispose of wastewater (e.g., soil-aquifer treatment or geo-purification; Liang et al. 2018; Zlotnik et al. 2017). However, excessive groundwater recharge activities may lead to waterlogging, salinization, the flooding of building basements and the restriction of plant growth, among other negative influences (Bouwer et al. 1999; Chang et al. 2016). To properly evaluate and manage artificial groundwater recharge, water-table fluctuations must be estimated both before and after MAR by using mathematical modeling (Masetti et al. 2016).

There are two main categories of mathematical modeling methods: numerical methods and analytical methods (Aguila et al. 2019; Jeong and Park 2019). Numerical methods (e.g., the MODFLOW and boundary element methods) can incorporate real field conditions with complex geometries of boundaries, heterogeneous aquifer properties and multiple recharge basins and pumping wells etc. (Saeedpanah and Azar 2017; Yeh and Chang 2013). Analytical methods can obtain direct solutions of the groundwater flow equation, which is constructed based on simplified assumptions. Analytical methods are preferred in the study of groundwater flow problems in aquifer systems with simple aquifer boundary and homogeneous formation properties due to the simplicity of parameter inputs and the fast computation time, and they are often used to verify the accuracy of other numerical methods (Kacimov et al. 2016; Manglik and Rai 2015; Sanayei and Javdanian 2020). In the past half a century, analytical methods have been extensively employed in the study of artificial groundwater recharge—for example, many researchers use the Boussinesq equation to study the interaction between surface water and groundwater in unconfined aquifers (Dralle et al. 2014; Moutsopoulos 2010). However, because the Boussinesq equation is nonlinear, it is difficult to obtain the solution directly (Gravanis and Akylas 2017; Mandayi and Seyyedian 2014). In order to avoid the complexity of the solution, the linearized form of the Boussinesq equation is generally applied to obtain its analytical solution (Bansal and Teloglou 2013; Mahdavi 2019).

Earlier analytical models were developed based on the assumption of a constant rate of recharge (Dagan 1967; Hantush 1967); however, while this assumption can be leveraged to effectively estimate the fluctuations in the water table in a short time, the infiltration rate will decrease due to clogging of the soil pores in the bottom of the recharge basin caused by deposition (e.g., silt and clay deposition; Pholkern et al. 2015; Rai et al. 2006). In recent years, researchers have used the linearized one-dimensional (1D) Boussinesq equations to study water-table fluctuations at the 1D scale (e.g., on cross sections or profiles of infiltration basins or streams) on the basis of time-varying recharge rates. Rai et al. (2001) derived an analytical solution to the linearized 1D Boussinesq equation using the finite Fourier sine transforms, and estimated water-table fluctuations from an overlying strip basin profile on the basis of a time-varying recharge rate. They used a number of piecewise linear elements to approximate the nature of time varying recharge rate. They then approximated some complex time-varying recharge rates for one, or more than one, cycle of wet and dry periods with the help of linear elements of different lengths and slopes. Bansal (2012) obtained analytical expressions for the hydraulic head and flow rate under the conditions of an upward-sloping bed, zero slope condition, and instantaneous rise in the stream water with the linearized 1D Boussinesq equation on the basis of a vertical time-varying recharge rate. The method was validated to demonstrate the effects of bed slope, stream rise rate and recharge rate on the aquifer baseflow using a numerical example. Liang and Zhang (2013) used the linearized 1D Boussinesq equation to derive closed-form solutions for the water table and lateral discharge per unit width in a horizontally heterogeneous unconfined aquifer on the basis of time-dependent sources and fluctuating river stages. They then compared the lateral discharge in heterogeneous unconfined aquifers with that in equivalent homogeneous aquifers using a numerical example. And the results demonstrated that these solutions are valid for this kind of heterogeneity and fluctuations of recharge/discharge and river stage, as long as the Dupuit assumption is valid. Jiang and Tang (2015) developed a general approximate method by introducing a new variable to predict the water table response in a semi-infinite aquifer system with a vertical or sloping boundary based on the linearized 1D Boussinesq equation. They then applied this method to constant, sudden, linear and periodic change situations of water level variation resting on vertical or sloping boundaries, which demonstrate that the proposed method has a good accuracy and versatility over a wide range of applications. Most recently, Hayek (2019) presented the approximate solutions of the linearized 1D Boussinesq equation by introducing an empirical function with four parameters, and applied the proposed analytical solutions to describe flow in horizontal unconfined aquifers induced by a sudden change in boundary head. Results based on this technique showed that there was good accuracy to solve the problems of recharging and dewatering of an unconfined aquifer.

However, the existing analytical solutions mainly focus on transient water-table fluctuations for single artificial recharge events; in contrast, few studies have focused on the analysis and modeling of multiyear water-table fluctuations under the condition of intermittent artificial recharge. A variable water table makes the boundary condition dynamic (Jiang and Tang 2015). Because of erratic and nonperiodic variations in the recharge rate, it is difficult to quantitatively describe the multistage processes of artificial groundwater recharge by mathematical methods under field conditions (Manglik and Rai 2015). In contrast, multiyear observations of water-table fluctuations in a recharge pond can intuitively reflect the recharge process and reflect the decline in the water table due to a decreased recharge rate. This study attempts to obtain an analytical solution of the linearized 1D Boussinesq equation by using boundary variations of the water table as the solution variables based on Laplace transforms. Then, improved analytical models are developed to simulate the water-table fluctuations under transient recharge, spreading recharge and multistage recharge conditions. Finally, a synthetic example is presented to confirm the validity of the improved analytical models in the modeling of water-table fluctuations in a basin with intermittent artificial groundwater recharge over multiple years.

Methodology

Analytical solution for transient recharge

To describe the water-table fluctuations under artificial recharge with mathematical methods, many assumptions are made as follows (Chipongo and Khiadani 2015; Schmidtke et al. 1982). The aquifer is homogeneous, isotropic, and laterally unconfined with constant aquifer coefficients and a constant percolation rate. The aquifer is underlain by a horizontal impermeable base that receives vertical downward recharge from the infiltration site. The rate of percolation is very small compared with the permeability, and thus, downward-percolating groundwater is almost completely refracted in the direction of the water table. Due to the symmetry of the model, the stream is used as the boundary on one side, while the other side is unbounded. Moreover, the rising range of the water table is less than 50% of the initial depth of saturation. Under these conditions, one can define the phase as phase 1 transient-type recharge (Fig. 1). For the unbounded side of the recharge domain (0 ≤ x < ∞), the fluctuations in the groundwater flow can be approximately expressed by the linearized 1D Boussinesq equation (Korkmaz 2013; Rai et al. 2001):

Fig. 1
figure 1

Vertical cross section of the flow system for transient recharge

Full size image
$$ \frac{\partial^2h}{\partial {x}^2}+\frac{R\left(x,t\right)}{K}=\frac{1}{a}\frac{\partial h}{\partial t} $$
(1)

where h is the height relative to initial water table, x is the riparian distance measured from the center of the stream (x = 0), t is the time of observation, K is the hydraulic conductivity, and R(x, t) is a function of the recharge rate and is defined as:

$$ R\left(x,t\right)=\left\{\begin{array}{cc}R(t)& 0\le x\le l\\ {}0& x>l\end{array}\right. $$
(2)

where l is half of the width of the stream and R(t) is a function of the time-varying recharge rate. When the riparian distance is larger than half of the width of the stream [x > l, R(x, t) = 0], Eq. (1) is written as:

$$ \frac{\partial^2h}{\partial {x}^2}=\frac{1}{a}\frac{\partial h}{\partial t} $$
(3)

Using the variation in the water table (S = h – h0) as the variable, Eq. (3) is written as:

$$ \frac{\partial^2S}{\partial {x}^2}=\frac{1}{a}\frac{\partial S}{\partial t} $$
(4)
$$ a=\frac{K\overline{h}}{\varepsilon } $$
(5)

where ε is the specific yield of the aquifer and \( \overline{h} \) is the weighted mean depth of saturation \( \overline{h} \) = (h0 + ht)/2, in which ht is the boundary water table at time t and h0 is the initial height of the boundary water table at t = 0.

The initial boundary conditions of Eq. (4) are:

$$ S\left(x,0\right)=0 $$
(6)
$$ S\left(\infty, t\right)=0 $$
(7)
$$ S\left(0,t\right)={h}_t-{h}_0={S}_t $$
(8)

where St is the variation in the boundary water table at time t.

In this study, the Laplace transform method is used to obtain the analytical solution of the linearized Boussinesq equation (Danierhan et al. 2013; Ren and Zhang 1999; Zhang 1983). By utilizing the Laplace transform methods, Eq. (4) is then written as:

$$ \frac{d\overline{S}\left(x,P\right)}{dx^2}=\frac{1}{a}P\overline{S}\left(x,P\right)-\frac{1}{a}S\left(x,0\right) $$
(9)

Upon substituting Eq. (6) into Eqs. (9), Eqs. (9) becomes:

$$ a\frac{d^2\overline{S}\left(x,P\right)}{dx^2}-P\overline{S}\left(x,P\right)=0 $$
(10)

The preceding equation is a homogeneous ordinary-differential equation with constant coefficients. Its characteristic equation is:

$$ {ar}^2-P=0\kern1em r=\pm \sqrt{\frac{P}{a}} $$
(11)

The general solution of Eq. (10) is:

$$ \overline{S}\left(x,P\right)={c}_1{e}^{\sqrt{\frac{p}{a}x}}+{c}_2{e}^{-\sqrt{\frac{p}{a}}x} $$
(12)

Utilizing the Laplace transform for Eqs. (7) and (8) yield the following:

$$ \overline{S}\left(\infty, t\right)=0 $$
(13)
$$ \overline{S}\left(0,t\right)=\frac{S_t}{P} $$
(14)

Upon substituting Eqs. (13) and (14) into Eq. (12), one can obtain c1 = 0 and c2 = St/P, and substituting c1 and c2 into Eq. (12) yields:

$$ \overline{S}\left(x,P\right)=\frac{S_t}{P}{e}^{-\sqrt{\frac{p}{a}}x} $$
(15)

An inverse Laplace transform results in:

$$ \frac{e^{-\mu \sqrt{p}}}{P}\overline{\to}\operatorname{erfc}\left(\frac{\mu }{2\sqrt{t}}\right) $$
(16)
$$ \mu =\frac{x}{\sqrt{a}} $$
(17)

Utilizing the inverse Laplace transform of Eqs. (16) and (17) for Eq. (15), the following expression for the variation in the water table can be obtained:

$$ S\left(x,t\right)={S}_t\cdot \operatorname{erfc}\left(\frac{x}{2\sqrt{at}}\right) $$
(18)

When the water table changes continuously, Eq. (18) will be written as:

$$ S{\left(x,{t}_j\right)}_T=\sum \limits_{j=1}^M\left\{\left({h}_j-{h}_{j-1}\right)\cdot \operatorname{erfc}\left[\frac{x}{2\sqrt{a\left({t}_j-{t}_{j-1}\right)}}\right]\right\} $$
(19)

where j is the frequency of the calculation (j = 1, 2, 3,..., M), hj is the height of the boundary water table at time tj (h0 = 0), erfc (λ) is the complementary error function and S(x, tj)T is the variation in the water table that is calculated by analytical solution for transient recharge (AS-T) at the riparian distance x.

Analytical solution for multistage recharge

However, the downward rate of percolation decreases with a rise in the water table, and the groundwater exhibits a spreading-type recharge trend due to the gravitational force. Some study showed that when the rising range of the water table is more than 50% of the initial depth of saturation, there was an obvious spreading-type recharge trend of groundwater flow (Manglik et al. 2013). In fact, the groundwater hydrograph became increasingly elongated and the groundwater mound grew mainly laterally with the continuation of groundwater recharge process under the condition of multi-stage recharge. One can define this phase as phase 2 spreading-type recharge (Fig. 2a). However, the calculation result of complementary error function erfc(λ) of Eq. (18) will gradually decrease with the increase of riparian distance x. Under these conditions, the variations in the water table will be underestimated by Eq. (18) due to the lateral growth of groundwater mounds. Therefore, an index is needed to estimate the calculation error of the water table at the riparian distance x caused by spreading recharge. In this study, time is chosen as the solution index:

Fig. 2
figure 2

Vertical cross sections of the flow system for a spreading recharge and b multistage recharge

Full size image
$$ u=\frac{v}{n}=\frac{Ki}{n}=\frac{K\frac{1}{m}\sum \limits_{a=1}^m\frac{h_a}{x_a}}{n}=\frac{K}{mn}\sum \limits_{a=1}^m\frac{h_a}{x_a} $$
(20)
$$ {t}_l=\frac{x}{u} $$
(21)

where u is the flow velocity of groundwater, v is the rate of percolation, n is the porosity of the aquifer medium, i is the hydraulic gradient of groundwater movement, the riparian distance x is divided into m hydrologic units, ha/xa is the hydraulic gradient between two adjacent hydrologic units, and the hydrologic units are defined by the density of groundwater monitoring network, and tl is the time index associated with the distance x. The expression for the variation in the water table during phase 2 is calculated as:

$$ S\left(x,{t}_l\right)=\left({h}_M-{h}_0\right)\cdot \operatorname{erfc}\left(\frac{x}{2\sqrt{a{t}_l}}\right) $$
(22)
$$ S{\left(x,{t}_j\right)}_s=\sum \limits_{j=1}^M\left\{\left({h}_j-{h}_{j-1}\right)\cdot \operatorname{erfc}\left[\frac{x}{2\sqrt{a\left({t}_j-{t}_{j-1}\right)}}\right]\right\}+\left({h}_m-{h}_0\right)\cdot \operatorname{erfc}\left(\frac{x}{2\sqrt{a{t}_l}}\right) $$
(23)

where S(x, tl) is the calculation error of the water table at the riparian distance x due to spreading recharge, (hM – h0) is the variation in the water table during the simulation period and S(x, tj)S is the variation in the water table that is calculated by analytical solution for spreading recharge (AS-S) at the riparian distance x.

When artificial groundwater recharge stops, the water table decreases gradually but has a certain hydraulic gradient. With a new stage of artificial groundwater recharge, there will be two recharge processes: one is the self-recharge process caused by the initial hydraulic gradient (spreading-type self-recharge), and the other is the artificial groundwater recharge process. One can define this phase as phase 3 multistage-type recharge (Fig. 2b). However, the water-table fluctuations caused by artificial recharge may have a certain delay effect with an increase in the riparian distance x due to the limited groundwater flow velocity (Delottier et al. 2018; Zhan and Zlotnik 2002). To estimate the water-table fluctuations in this phase, there is a need to add the transient variations in the water table caused by artificial groundwater recharge during the delayed period. Therefore, the variations in the water table during phase 3 will be calculated for two situations:

$$ S{\left(x,{t}_j\right)}_m=\left\{\begin{array}{c}\sum \limits_{j-1}^M\left\{\left({h}_j-{h}_{j-1}\right)\cdot \operatorname{erfc}\left[\frac{x}{a\left({t}_j-{t}_{j-1}\right)}\right]\right\}+\left({h}_M-{h}_0\right)\cdot \operatorname{erfc}\left(\frac{x}{2\sqrt{a{t}_l}}\right)+{S}_{tl}\kern1em \mathrm{Delayed}\ \mathrm{period}\\ {}\sum \limits_{j-1}^M\left\{\left({h}_j-{h}_{j-1}\right)\cdot \operatorname{erfc}\left[\frac{x}{2\sqrt{a\left({t}_j-{t}_{j-1}\right)}}\right]\right\}+\left({h}_M-{h}_0\right)\cdot \operatorname{erfc}\left(\frac{x}{2\sqrt{a{t}_l}}\right)\kern1em \mathrm{other}\ \mathrm{period}\end{array}\right. $$
(24)

where Stl is the transient variation in the water table calculated by Eq. (18) and S(x, tj)M is the variation in the water table that is calculated by analytical solution for multistage recharge (AS-M) at the riparian distance x.

Study area and data

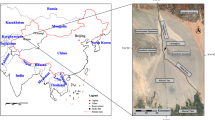
The Tarim River, which is located in Northwest China, is one of the largest inland rivers in Central Asia and even the world (Fig. 3). Because of the relatively low precipitation (20–50 mm) and high potential evapotranspiration (2,500–3,000 mm) in this region, the consumption of groundwater cannot be satisfied by the natural recharge conditions; therefore, groundwater recharge is highly dependent on the Tarim River. In the 1970s, the Tarim River was cut off downstream due to unreasonable engineering facilities (estuarine barrage), which resulted in a significant decline in the water table. To replenish the groundwater and restore the ecological environment downstream, intermittent water conveyance through the stream was implemented from Daxihaizi Reservoir during the water-rich period upstream.

Fig. 3
figure 3

Location of the study area—Base on map sources: GS (2020) 4401

Full size image

The downstream region of Tarim River has a typical desert arid climate in the continental warm temperate zone, with the Taklimakan Desert in the southwest and the Kuruk Desert in the northeast. The unconfined aquifers beneath the alluvial plain on both sides of the riparian area are composed mainly of silty fine sand with fine particles and a uniform texture. The unconfined aquifer is basically consistent with the homogeneous and isotropic of Dupuit assumption within the scope of influence of artificial recharge. To test the application of the analytical models under field conditions, monitoring data from 9 years (from 2009 to 2017) in the Kardayi section and Alagan section were used to study the multiyear variations in the water table for transient recharge, spreading recharge and multistage recharge under intermittent artificial recharge. The Kardayi section (E, see Fig. 3) is located approximately 110 km from Daxihaizi Reservoir, and the profile passes through the centers of three monitoring wells at horizontal distances of 50 m (E1), 150 m (E2) and 300 m (E3), respectively. And the Alagan section (G) is located approximately 180 km from Daxihaizi Reservoir, and the profile passes through the centers of three monitoring wells at horizontal distances of 50 m (G2), 150 m (G3) and 300 m (G4), respectively. The water table is observed once every 30 days on average, and the stream flow is continuously observed during the water conveyance period.

Results and discussion

Characteristics of artificial groundwater recharge

There were 14 stages of water conveyance in the downstream region of Tarim River from 2009 to 2017 with varying mean stream flow of 4.501–95.416 m3 s−1 and durations of 10–221 days (Fig. 4), and the total volume of water was 0.072–11.722 × 108 m3. The water table declined continuously due to the finite amount of groundwater recharge in 2008 and 2009; as a result, the water table almost reached the base of the aquifer on 30 July 2010 in the downstream of Tarim River. The initial hydraulic gradient was small during this period, which basically satisfies the initial horizontal base of the Dupuit assumption.

Fig. 4
figure 4

Intermittent water conveyance from 2009 to 2017

Full size image

The boundary hydraulic condition may be saturated under large amounts of groundwater recharge, which may result in simulation errors. To confirm the validity of the analytical solutions and test their application to simulations of water-table fluctuations for multiyear artificial groundwater recharge, the variations in the water table at x = 50 m in the Kardayi section (110 km) and Alagan section (180 km) of the downstream of Tarim River were selected as the boundary conditions of the analytical solutions (Fig. 5). Due to the difference in distance from the upstream source, the water level fluctuation in the Kardayi section was on 14 August 2010, and the water level fluctuation in the Alagan section was on 10 Sept. 2010 during the stages of water conveyance in 2010. As shown in Fig. 5, the water table of the unconfined aquifer rose continuously due to artificial recharge, satisfying the transient recharge condition of the linearized Boussinesq equation in the short term. However, the rise of the water table decreased gradually with the continuous process of artificial recharge due to a decrease in the vertical recharge rate. In addition, Fig. 5 also shows that the water table at x = 50 m rose and fell alternately for several years due to intermittent artificial recharge and cut-off of the stream in different monitoring sections. Since the solution conditions of the analytical models are the variations in the boundary water table, the solutions can also be solved according to the corresponding analytical methods during the subsidence stage of the water table.

Fig. 5
figure 5

The variations in the water table from 2009 to 2017 at a distance of 50 m: a the Kardayi section and b the Alagan section

Full size image

Numerical results for transient water-table fluctuations

The fluctuation in the water table depends mainly on the downward percolation of stream water during the transient-type recharge phase. To demonstrate the applicability of Eq. (18), the variations in the water table at a distance of 50 m at t = 10, 25, 48 and 90 days (the Kardayi section (110 km), since 14 Aug. 2010) and at t = 13, 33, 45 and 67 days (the Alagan section (180 km), since 10 Sept. 2010) were selected as the boundary solution conditions. The values of the other controlling parameters are shown in Table 1: K is the average hydraulic conductivity of the downstream of Tarim River, ε is the average specific yield of the downstream of Tarim River, the initial height of the water table is defined as h0 = 0, S is the variation in the water table, St is the variation in the water table at t, ħ is the weighted mean depth of saturation, and t, ħt is the weighted mean depth of saturation at t.

Table 1 Parameters of soil and groundwater samples
Full size table

In order to validate the AS-T model (Eq. 18), MODFLOW module in GMS (Groundwater Modeling System) software is used to simulate water-table fluctuations. Because the case study focuses on water-table fluctuations at the 1D scale, the width of the section is assumed infinitely small; however, to obtain better visualizations, the width of the section is expanded to 300 m in the result maps. The stream is defined as the recharge region boundary (x = 50 m), and the other boundary is defined as the specified head boundary. A sufficiently large extent in x-direction is chosen to ensure the same flow domain as in the analytical solution within the different simulation period. The stress periods are set to 10, 25, 48 and 90 days in the Kardayi section, and the average recharge rates are 0.05908, 0.06049, 0.04955 and 0.03463 m/day, respectively. The stress periods are set to 13, 33, 45 and 67 days in the Alagan section, and the average recharge rates are 0.08631, 0.05264, 0.05041 and 0.04083 m/day respectively. The other control parameters are the same as used for the analytical model. The numerical results of the Kardayi section (t = 10, 25, 48 and 90 days) and Alagan section (t = 13, 33, 45 and 67 days) are shown in Figs. S1 and S2 of the electronic supplementary material (ESM).

Figure 6 presents the comparison results of water-table profiles by using the AS-T model and MODFLOW in the Kardayi section (Fig. 6a) and Alagan section (Fig. 6b). Evidently, the water table rose with continuous artificial groundwater recharge, and the groundwater hydrograph became increasingly elongated due to there being no limiting boundary on one side. The fitting results of the variations in the water table (h–h0) are in good agreement between the analytical model (AS-T model) and the numerical model (MODFLOW) results without obvious deviations at different time scales in both the Kardayi and Alagan sections. Thus, the solution procedure presented in the preceding can effectively simulate the behavior of the variations in the water table during the initial phase of recharge. To analyze the effects of the hydraulic conductivity K and specific yield ε on the water-table fluctuations, the variations in the water table for different values of K and ε were calculated by using Eq. (18).

Fig. 6
figure 6

Water-table profiles at different times in the a Kardayi section and b Alagan section

Full size image

Figure 7a,c,e show the water-table profiles of Kardayi section (110 km) for different values of K (K, 2 K, 3 K) at t = 25, 48 and 90 days, respectively. The water table spread laterally with the increasing hydraulic conductivity, which resulted in the groundwater mound drifting toward the right interface. The groundwater hydrograph became increasingly elongated as K increased because of the acceleration of the flow velocity. Figure 7b,d,f show the water-table profiles of Kardayi section for different values of ε (ε, 2ε, 3ε) at t = 25, 48 and 90 days, respectively. The height of the water table subsided with the increasing specific yield, and the groundwater mound drifted toward the left interface with the increasing specific yield. The groundwater hydrograph became increasingly shorter as the value of ε increased because more water was stored in the pore space. These phenomena highlight the importance of the hydraulic conductivity and specific yield in the determination of transient variations in the water table and further confirm the ability of Eq. (18) to estimate transient water-table fluctuations.

Fig. 7
figure 7

Water-table profiles at t = 25, 48 and 90 days for different values of K and ε (the Kardayi section)

Full size image

Simulation results for multiyear water-table fluctuations

The AS-T model can be applied to estimate the transient-state water-table fluctuations well; however, spreading-type recharge and a delay in groundwater fluctuation were observed with the continuous artificial recharge and the elongation of the groundwater hydrograph. As shown in Fig. 6, the simulation result of the water table at the farther riparian distance was underestimated with the elongation of the groundwater hydrograph; the reason for this discrepancy was that the vertical rising rate was relatively small, and the movement of groundwater was mainly lateral spreading. To reduce the errors caused by this spreading and delay effect for multistage artificial recharge, the delay indexes were calculated by Eqs. (20) and (21). In this study, the mean flow velocity with ū = 2.56 m/day was chosen due to the multiyear artificial recharge. Then, the mean delay indexes at the riparian distance of x = 150 m and x = 300 m were computed from Eq. (21) by using x = 50 m in the Kardayi section and Alagan section as the initial boundary condition (Table 2).

Table 2 Statistics of the simulation results by using the AS-T, AS-S and AS-M models
Full size table

To test the accuracy and robustness of the proposed analytical solutions, the multiyear variations in the water table under different movement modes were calculated by using Eqs. (19), (23) and (24). In this study, the variations in the water table at a distance of 50 m from 14 Aug. 2010 to 15 Dec. 2017 in the Kardayi section and from 10 Sept. 2010 to 15 Dec. 2017 in the Alagan section were selected as the water-table boundary conditions (Fig. 5a,b). The values of the other controlling parameters were as follows: the hydraulic conductivity was K = 10 m/day, the specific yield was ε = 0.07, the multiyear-average-weighted mean depths of saturation ħ were 3.09 m in the Kardayi section and 4.16 m in the Alagan section, and the multiyear mean delay indexes tl were 39 and 98 days at 150 and 300 m, respectively.

The comparison results among the water-table fluctuations obtained by using the AS-T, AS-S and AS-M models in the Kardayi section and Alagan section are presented in Fig. 8. The simulation values of the water table rose and fell alternately for multiyear simulations due to intermittent artificial recharge and cut-off of the stream in different monitoring sections. The delayed period caused by multistage artificial groundwater recharge was lengthened with an increase in the riparian distance. Table 2 presents the statistical results of different analytical solutions. As shown in Table 2, the results confirm that the spreading effect and delay effect had considerable influences on the fluctuations in the water table for multiple years. The AS-T model can better reflect the variations in the water table during the initial phase of transient recharge; however, the AS-T model underestimated the maximum, minimum and mean variations in the water table for multiple years due to the neglect of the spreading effect and delay effect of the groundwater recharge. In contrast, the AS-S model, which considers the effect of spreading-type recharge on the movement of groundwater, can better reflect the maximum and minimum variations in the water table, but it underestimated the mean variation in the water table for the multiyear simulation by neglecting the delay effect. Finally, the AS-M model, which considers the spreading effect and delay effect of the groundwater recharge comprehensively, can better reflect the maximum, minimum and mean variations in the water table for multiple years.

Fig. 8
figure 8

Modeling results of water-table variations by using the AS-T, AS-S and AS-M models

Full size image

Fitting precision for multistage water-table fluctuations

To compare the fluctuations in the water table for multiple years, the cumulative variations in the water table simulated by the AS-T, AS-S and AS-M models are shown in Fig. 9. The fluctuation trends of the three analytical models were consistent at different riparian distances. However, the AS-T and AS-S models underestimated the cumulative variations in the water table under intermittent artificial groundwater recharge conditions for multiple years. The cumulative variations in the water table obtained by the AS-M model matched the observation results much better than those produced by the AS-T and AS-S models. In addition, the simulation errors of water table caused by the spreading effect and delay effect increased with an increase in the riparian distance. As shown in Fig. 9, the simulation results had more obvious deviations at the riparian distance of x = 300 m than that at x = 150 m due to the spreading effect and delay effect of the groundwater recharge.

Fig. 9
figure 9

Comparison among the cumulative variations in the water table by using the AS-T, AS-S and AS-M models

Full size image

The fitting results of the AS-T, AS-S and AS-M models are presented in Tables 3 and 4. In this study, five criteria were used to assess the performance of these simulation models. The best fitting results between the simulations and observations were as follows: Bias = 0, mean absolute error (MAE) = 0, root mean squared error (RMSE) = 0, Nash-Sutcliffe efficiency (NSE) = 1 and coefficient of determination (R2) = 1. As shown in Tables 3 and 4, the Bias, MAE and RMSE values of the simulation by the AS-M model were lower than the corresponding values simulated by the AS-T and AS-S models. In addition, the AS-M model had higher NSE and R2 values than the AS-T and AS-S models.

Table 3 Fitting results for the comparison among the AS-T, AS-S and AS-M models for Kardayi
Full size table
Table 4 Fitting results for the comparison among the AS-T, AS-S and AS-M models for Alagan
Full size table

Figure 10 illustrates the scatter plots of the water table simulated by the AS-M model in the Kardayi section (Fig. 10a,b) and Alagan section (Fig. 10c,d). Evidently, the results simulated by the AS-M model were regularly distributed around the standard values without obvious deviations, and the linear regression line is close to 1:1 (i.e., linear) at the riparian distance of x = 150 m and x = 300 m in different monitoring sections. The NSE increased to 0.806 and 0.677 and R2 increased to 0.817 and 0.702 at the riparian distance of x = 150 m and x = 300 m in the Kardayi section, respectively. And the NSE increased to 0.794 and 0.795 and R2 increased to 0.802 and 0.810 at the riparian distance of x = 150 m and x = 300 m in the Alagan section, respectively. These findings indicate good conformity and fits between the simulated and observed values, and highly accurate results were obtained by the AS-M model under multiyear intermittent artificial groundwater recharge conditions. Moreover, the improved analytical models seemed to be adequate for simulating the water-table fluctuations over multiple years and were highly adaptable to multistage artificial groundwater recharge conditions.

Fig. 10
figure 10

Scatter plots of simulation results by the AS-M model in the Kardayi section and Alagan section. The dashed line represents the 1:1 line, and the solid line represents the fitting line

Full size image

Limitations

Although the analytical solutions and improved analytical models in this study can obtain quantitative results in the simulation of transient-type and multiyear water-table fluctuations, some limitations should be considered in practical applications. First, the recharge assumption for the solution was for a homogeneous, isotropic, unconfined aquifer; however, the aquifer may be heterogeneous with horizontal stratification, which is not considered in the aforementioned study. Second, the uncertainties of parameters such as hydraulic conductivity (K) and specific yield (ε) may result in nonunique results—for example, the solutions in this study provide only an average recharge condition for multiple years. Therefore, it is necessary to conduct a comprehensive site investigation and hydraulic analysis in practical applications. Third, the simulation scope of water-table fluctuation was larger than half of the width of the stream (i.e., x > l), which limited the application of the model to cases near the riparian zone (i.e., x < l). Fourth, this study considered only a single recharge source, whereas different water-table fluctuations would be obtained when multiple recharge sources are incorporated. Finally, some other factors may influence the fluctuations in the water table such as clogging of the soil pores beneath the bottom of the basin, climate change, saturated boundary hydraulic condition, or the local pumping of groundwater. In summary, this study presents relatively simple configurations with which to quantify the fluctuations in the water table due to an intermittent artificial groundwater recharge basin for multiple years.

Conclusions

The study focuses on an investigation of water-table fluctuations caused by intermittent artificial groundwater recharge for multiple years in a homogeneous, unconfined aquifer. First, the analytical solution and improved analytical model are derived by using the linearized 1D Boussinesq equation; then, the responses of water-table fluctuations to changes in each controlling parameter are explored. In addition, the effects and validity of the models are analyzed by comparing the simulation results with the observation results of a case study.

The results indicate that the analytical solutions of the linearized Boussinesq equation in this study exhibit better stability and convergence and can estimate the variations in the water table during the transient-type recharge phase, in which the aquifer’s parameters (e.g., hydraulic conductivity and specific yield) have significant influence on water-table fluctuation. In addition, the improved analytical models, which consider the spreading effect and delay effect comprehensively, can better estimate the water-table fluctuations for multiple years. Although some discrepancies between the simulations and observations remain, the improved analytical models can obtain more accurate results for multiyear water-table fluctuations according to the case study. Therefore, the present analytical solutions and improved analytical models are feasible for estimating water-table fluctuations under intermittent artificial groundwater recharge conditions for multiple years. Additionally, the proposed methods can be applied to the study and management of artificial groundwater recharge for transient and multiyear periods in aquifers with similar aquifer conditions.