1 Introduction

Surface infiltration using basins is one of the most popular methods of artificial groundwater recharge for storage or to dispose of treated wastewater. Other methods include vadose injection and direct aquifer injection wells (Asano et al. 2006, Pliakas et al. 2005). Where soils are permeable and aquifers unconfined, surface infiltration is the most favored method due to efficient space utilization and minimal maintenance requirements (Bouwer 2002). Other advantages of surface infiltration over injection wells include purification as water percolates through the vadose zone into the underlying aquifers as well as better clogging control (Asano et al. 2006). Artificial groundwater recharge is increasingly becoming important in restoring depleted groundwater levels, managing saltwater intrusion of freshwater in coastal aquifers, storing excess storm water or treated wastewater for future use and for preventing land subsidence problems (Smith and Pollock 2010). A key aspect in the design of surface infiltration basins is the estimation of groundwater mounding beneath the basin (Sumner et al. 1999) and mitigating preventable mound growth (Eusuff and Lansey 2004). Mounding may reduce infiltration rates and threaten basements, landfills and other structures (Bouwer et al. 1999).

In the past half a century, researchers have developed both analytical and numerical methods for determining the groundwater mounding during artificial recharge and the subsequent decay after infiltration has stopped. Analytical solutions such as those developed by Glover (1960), Hantush (1967), Rao and Sarma (1981), Singh (2012) and Swamee and Ohja (1997) are a direct solution of the governing groundwater flow equation. Numerical methods include specialized groundwater software such as FEFLOW, SUTRA, FEHM and MODFLOW or computer programs such as MATLAB, MATHCad and Maple employing finite difference or finite element methods to complex problems (Warner 1987). Warner et al. (1989) compared and evaluated three analytical solutions each for circular and rectangular basins. Considering ease of implementation and accuracy, Warner et al. (1989) highly endorsed Glover (1960) and Hantush (1967) proving that besides the method of linearizing transmissivity both methods yield identical solutions (Smith and Pollock 2010). Recent developments have disproved the accuracy of these methods because the assumptions made that (1) the aquifer is homogeneous, isotropic, infinite, and resting on a horizontal impermeable base; (2) the hydraulic properties of the aquifer remain constant with both time and space; (3) the rate of percolation is constant with respect to time and space; (4) the flow due to percolation is vertically downward until it reaches the water table; (5) the water table remains below the bottom of the spreading basin; (6) the height of the water table above the base of the aquifer is approximately equal to the average head over the depth of saturation; and (7) the rise of the water table relative to the initial depth of saturation does not exceed 50 %, are unrealistic.

Numerical methods tend to have fewer assumptions as a result produce results higher than both Glover (1960) and Hantush (1967) solutions (Marino 1975; Singh 2012). What is not yet clear is how recent analytical solutions agree with each other and how well they compare with numerical methods. The objective of this paper is to review recently developed analytical models and evaluate them against numerical methods. In addition the paper seeks to extend these results to soil with varying infiltration rates. The results of this study will provide a basic guide for selecting groundwater mounding estimation methods. A key aspect in our study is predicting the growth of the mound due to recharge as time varies.

2 Theory

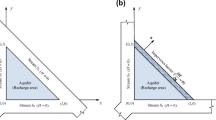
Analytical solutions for predicting the groundwater mound below recharge basins are based on the groundwater flow equation; they are a direct solution to the governing partial differential equation describing the flow of water in two dimensions. Based on the geometry in Fig. 1, the groundwater flow equation is:

$$ T\left(\frac{\partial^2h}{\partial {x}^2}+\frac{\partial^2h}{\partial {y}^2}\right)+{V}_a=f\frac{\partial h}{\partial t} $$
(1)

where the terms are defined in Fig. 1.

Fig. 1
figure 1

Rectangular recharge basin geometry

Full size image

2.1 Glover’s Solution

Glover (1960) solved Eq. (1) considering different scenarios such as instantaneous and continuous recharge, steady and transient state, circular and rectangular recharge areas as well as different length to width ratios. The assumptions made were that:

  1. i.

    the height of the mound was relatively small in comparison to the initial saturated thickness H,

  2. ii.

    transmissivity was constant and calculated as the product of the hydraulic conductivity K and the initial saturated thickness H: (T = KH),

  3. iii.

    the initial ground water mound height and far-field boundary conditions from basin was zero,

  4. iv.

    the aquifer is infinite, isotropic and homogeneous and

  5. v.

    there was no other recharge or pumping.

The simplified Glover’s solution for predicting growth is (Glover 1960; Molden et al. 1984; Smith and Pollock 2010; Warner et al. 1989):

$$ h\left(x,y,t\right)-H=\frac{V_at}{4f}{\displaystyle \underset{0}{\overset{1}{\int }}\left(erf\frac{u_2}{\sqrt{\tau }}-erf\frac{u_1}{\sqrt{\tau }}\right)}\left(erf\frac{u_4}{\sqrt{\tau }}-erf\frac{u_3}{\sqrt{\tau }}\right)d\tau $$
(2)

where

$$ {u}_1=\frac{x-\frac{W}{2}}{\left(\frac{4T}{tf}\right)}; \kern0.75em {u}_2=\frac{x+\frac{W}{2}}{\left(\frac{4T}{tf}\right)}; \kern0.75em {u}_3=\frac{y-\frac{L}{2}}{\left(\frac{4T}{tf}\right)}\ \mathrm{and}\kern0.75em {u}_4=\frac{y+\frac{L}{2}}{\left(\frac{4T}{tf}\right)} $$
(3)

and

$$ erfz=\frac{2}{\sqrt{\pi }}{\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-{z}^2}}dz $$
(4)

where all the parameters are defined in Fig. 1. After recharge stops percolation continues for several days due to the saturated vadose zone. Infiltration stops at t0; mound decay is found by superimposing an equivalent recharge mound with a negative infiltration rate (Hantush 1967).

Glover (1960) also provided solutions for determining the groundwater mound beneath a long recharge strip assuming that at L ≥ 5 W, the rectangular basin functioned essentially as an infinitely long strip after some time. The infiltration mound beneath a long strip is:

$$ h\left(x,y,t\right)=\frac{V_at}{2}\left[M\left({u}_4\right)-M\left({u}_3\right)\right] $$
(5)

where

$$ M\left(\beta \right)=\frac{2}{\sqrt{\pi }}{\displaystyle \underset{0}{\overset{\beta }{\int }}{e}^{-{u}^2}du+\frac{2{\beta}^2}{\sqrt{\pi }}}{\displaystyle \underset{\beta }{\overset{\infty }{\int }}\frac{e^{-{u}^2}}{u^2}}du $$
(6)

and

$$ {u}_3=\frac{x-\frac{W}{2}}{\sqrt{\frac{4Tt}{f}}}\kern0.5em \mathrm{and}\kern0.5em {u}_4=\frac{x+\frac{W}{2}}{\sqrt{\frac{4Tt}{f}}} $$
(7)

Tables were initially used for numerical evaluation of analytical expressions (Glover 1960; Hantush 1967). However this practice has been replaced by the use of software such as MATLAB, Maple and Mathcad for solving numeric equations. All complex integrals and special functions encountered in some analytical solutions in this study were computed using MATLAB.

2.2 Hantush’s Solution

Hantush (1967) made improvements to the solutions presented by Glover (1960). Hantush assumed the initial groundwater table was horizontal with boundary conditions defined by a slope of zero at both the center and infinite distance away from the basin. In addition Hantush (1967) used a linearization method to determine the transmissivity expressed as the product of the hydraulic conductivity and the average saturated thickness (Eq. (12)). Hantush commended Baumann’s approach for determining mound heights at distances more than 0.5 L and 0.5 W away from the basin (Hantush 1967). However, Baumann’s approach is time-independent. In addition it requires the conversion of the rectangular recharge area into an equivalent circular area (Warner et al. 1989). Hantush’s solution for predicting groundwater mound growth is:

$$ h\left(x,y,t\right)-H=\frac{v_at}{4f}\left\{F\left[\left(\frac{W}{2}+x\right)n,\left(\frac{L}{2}+y\right)n\right]+F\left[\left(\frac{W}{2}+x\right)n,\left(\frac{L}{2}-y\right)n\right]+F\left[\left(\frac{W}{2}-x\right)n,\left(\frac{L}{2}+y\right)n\right]+F\left[\left(\frac{W}{2}-x\right)n,\left(\frac{L}{2}-y\right)n\right]\right\} $$
(8)

where

$$ F\left(\alpha, \beta \right)={\displaystyle \underset{0}{\overset{1}{\int }}\left[erf\left(\frac{\alpha }{\sqrt{\tau }}\right)erf\left(\frac{\beta }{\sqrt{\tau }}\right)\right]}d\tau $$
(9)
$$ \alpha =\left(\frac{W}{2}\pm x\right)n\kern0.75em \beta =\left(\frac{L}{2}\pm y\right)n $$
(10)

and

$$ n={\left(\frac{4tT}{f}\right)}^{-\frac{1}{2}} $$
(11)

where

$$ \widehat{T}=K\overline{b} $$
(12)

and

$$ \overline{b}=\frac{1}{2}\left(H+h\left(x,y,t\right)\right) $$
(13)

The integral of the product of the error function in Eq. (9) cannot be determined analytically hence MATLAB was used. Hantush (1967) also made the same assumptions as those made by Glover (1960) regarding mound decay and mound growth beneath a long recharge strip. His subsequent solution for predicting groundwater mound decay is (Asano et al. 2006; Hantush 1967; Warner et al. 1989):

$$ h\left(x,y,t\right)=H+\left(h\left(x,y,t\right)-h\left(x,y,t-{t}_0\right)\right) $$
(14)

where

$$ h\left(x,y,t-{t}_0\right)=\frac{V_a\left(t-{t}_0\right)}{4f}\left[F\left[\left(\frac{W}{2}+x\right){n}_0,\left(\frac{L}{2}+y\right){n}_0\right]+F\left[\left(\frac{W}{2}+x\right){n}_0,\left(\frac{L}{2}-y\right){n}_0\right]+F\left[\left(\frac{W}{2}-x\right){n}_0,\left(\frac{L}{2}+y\right){n}_0\right]+F\left[\left(\frac{W}{2}-x\right){n}_0,\left(\frac{L}{2}-y\right){n}_0\right]\right] $$
(15)

and

$$ {n}_0={\left(\frac{4\left(t-{t}_0\right)T}{f}\right)}^{-\frac{1}{2}} $$
(16)

where h(x, y, t) is as defined in Eq. (8), F (α, β) can still be evaluated using MATLAB and t 0 is the time since recharge stopped. Hantush’s solution for determining the height of the mound beneath a long rectangular recharge strip for x < W/2 is:

$$ {h}^2\left(x,y,t\right)-{H}^2=\frac{T{V}_at}{Kf}\left\{4{i}^2 erfc\left(\frac{\frac{W}{2}-x}{\sqrt{\frac{4Tt}{f}}}\right)-4{i}^2 erfc\left(\frac{\frac{W}{2}+x}{\sqrt{\frac{4Tt}{f}}}\right)\right\} $$
(17)

where

$$ {i}^n erfc(z)=-z{n}^{-1}{i}^{n-2} erfc(z)+{(2n)}^{-1}{i}^{n-2} erfc(z) $$
(18)

and

$$ erfc(z)=1-erf(z) $$
(19)

For x > W/2 mound height beneath a long rectangular recharge strip is:

$$ {h}^2\left(x,y,t\right)-{H}^2=\frac{T{V}_at}{Kf}\left\{4{i}^2 erfc\left(\frac{x-\frac{W}{2}}{\sqrt{\frac{4Tt}{f}}}\right)-4{i}^2 erfc\left(\frac{\frac{W}{2}+x}{\sqrt{\frac{4Tt}{f}}}\right)\right\} $$
(20)

where i 2 erfc(z) and erfc(z) are defined in Eqs. (18) and (19) respectively.

2.3 Rao and Sarma’s Solution

Rao and Sarma (1981) used the finite Fourier Transform to solve Eq. (1). The assumptions made were that a rectangular impermeable boundary 2 W and 2 L existed around the basin parallel to the x and y directions of the basin. The slope at the center was assumed to be zero and the initial groundwater table horizontal. However, these conditions are much harder to achieve in practical situations. Their solution is (Warner et al. 1989; Rao and Sarma 1981):

$$ h\left(x,y,t\right)-H=\frac{2{V}_a TLWt}{KfAB}+\frac{8{V}_a{A}^2{B}^2}{K{\pi}^4}\left({\displaystyle \sum_{m=1}^{\infty }{\displaystyle \sum_{n=1}^{\infty}\left[\frac{1}{mn\left({m}^2{A}^2+{n}^2{B}^2\right)}\left(1- \exp \left(-\frac{T{\pi}^2}{f}\times \frac{t\left({m}^2{A}^2+{n}^2{B}^2\right)}{A^2{B}^2}\right)\right)\times \sin \left(\frac{m\pi W}{2B}\right)\times \sin \left(\frac{n\pi L}{2A}\right)\times \cos \left(\frac{m\pi x}{B}\right)\times \cos \left(\frac{n\pi y}{A}\right)\right]}}\right) $$
(21)

or

$$ h\left(x,y,t\right)-H=\frac{V_a HLWt}{2 fAB}+\frac{8{V}_a{A}^2{B}^2}{K{\pi}^4}\left({\displaystyle \sum_{m=1}^{\infty }{\displaystyle \sum_{n=1}^{\infty}\left[\frac{1}{mn\left({m}^2{A}^2+{n}^2{B}^2\right)}\left(1- \exp \left(-\frac{T{\pi}^2}{f}\times \frac{t\left({m}^2{A}^2+{n}^2{B}^2\right)}{A^2{B}^2}\right)\right)\times \sin \left(\frac{m\pi W}{2B}\right)\times \sin \left(\frac{n\pi L}{2A}\right)\times \cos \left(\frac{m\pi x}{B}\right)\times \cos \left(\frac{n\pi y}{A}\right)\right]}}\right) $$
(22)

where A and B are the length and width of the underlying aquifer expressed along the x and y axes respectively.

Due to the infinite sums, Eqs. (21) and (22) require significant computation time; as the number of terms in the summation increases, the solution becomes more accurate. Griffin and Warrington (1988) reviewed the solution presented by Rao and Sarma (1981). The authors stated that this solution yields results closest to Hantush’s when A/L = B/W =200. In addition, the authors concluded that Rao and Sarma’s solution converges when m = n ≥ 150 (Griffin and Warrington 1988).

2.4 Swamee and Ohja’s Approximation to the Hantush Solution

The product of error functions in Hantush’s mound function makes it impossible to obtain analytical results without the use of numerical evaluation. The algebraic approximation for Hantush’s mound function developed by Swamee and Ohja (1997) is:

$$ F\left(\alpha, \beta \right)={\left[1+{\left(\frac{0.5785}{\alpha}\right)}^{2.75}+{\left(\frac{0.5785}{\beta}\right)}^{2.75}+{\left(\frac{0.36}{\alpha \beta}\right)}^{2.4}\right]}^{-0.325} $$
(23)

where α and β are defined in Eq. (10). Swamee and Ohja (1997) demonstrated the accuracy and the applicability of Eq. (23) in place of the tabular solution and concluded that this was a practical alternative.

2.5 Vatankhah’s Approximation to the Hantush Solution

In a review of Swamee and Ohja (1997), Vatankhah (2013) argued that with a maximum and average percentage error up to 42.5 and 8 % respectively the solution was inappropriate. Instead Vatankhah (2013) proposed the following solution for predicting Hantush’s mound function:

$$ F\left(\alpha, \beta \right)={\left(0.485f\left(\alpha \right)f\left(\beta \right)+0.418g\left(\alpha \right)g\left(\beta \right)+0.0095\right)}^{4.15} $$
(24)

where

$$ f\left(\alpha \right)={\left\{1- \exp \left(\frac{-{\alpha}^{1.5}\left(0.007+2.45{\alpha}^{1.9}\right)}{0.52+{\alpha}^{1.9}}\right)\right\}}^{0.12} $$
(25)

and

$$ g\left(\alpha \right)={\left\{1- \exp \left(\frac{-{\alpha}^{1.5}\left(0.001+11.18{\alpha}^{1.9}\right)}{0.0025+{\alpha}^{1.9}}\right)\right\}}^{0.12} $$
(26)

where α and β are defined in Eq. (10).

Nadarajah (2009) developed another approximation to Hantush (1967) which is not included in this paper.

2.6 Singh’s Solution

Singh (2012) reported that assumptions made by both Hantush (1967) and Glover (1960) were unrealistic. The author argued that assuming the mound height was too small in comparison with the saturated thickness was inappropriate and the solutions were essentially for a confined aquifer. Singh (2012) suggested the following correction to be applied to Hantush and Glover's solutions:

$$ hc\left(x,y,t\right)=\left(h\left(x,y,t\right)-H\right)+H\left\{2-\sqrt{1-\frac{\left(h\left(x,y,t\right)-H\right)}{2H}}\right\} $$
(27)

where hc(x, y, t) is the corrected mound height (m) and h(x, y, t) is the corresponding height calculated from Hantush’s solution and the rest as defined before. Singh (2012) compared the results from Eq. (27) with those obtained using MODFLOW and concluded that the correction can be applied to obtain results comparable to those from complicated solutions.

2.7 FEFLOW

FEFLOW (finite element subsurface flow) is a finite element simulator of groundwater, solute mass, and energy transport through porous media (Diersch 2012). In FEFLOW, either Darcy or Richards’ equations can be used. The former is used strictly for fully saturated models and the latter for unsaturated or variably saturated models. However, Richards’ equation is applicable for saturated models as well. With both equations, finite element formulations are used with initial conditions and boundary conditions as they occur in the model to compute hydraulic head at different locations (Diersch and Perrochet 2012).

Developing the model in FEFLOW constituted defining a square model area, 1000 × 1000 m allowing estimation of mound height up to 950 m away from the center of the basin. Common approaches model one quadrant of the aquifer since there is no flow between quadrants and heads are symmetrical. The water table was assumed flat with an initial head of 30 m prior to recharge and all boundaries around the model area were set to a fixed head equal to 30 m. Sensitivity analysis of the mesh size and meshing mode revealed that the hydraulic head was consistent with a meshing size greater than 3000 using transport mapping. Since the aquifer is unconfined, it was defined by only one layer set at an elevation of 100 m below the top of the model. Model properties were set to “unconfined aquifer” and “transient state” to enable groundwater mound values to be read for different recharge times. Recharge rate of 0.27 m/day was applied to the top grid layer on a rectangular patch 100 m × 100 m to simulate leakage through the square basin. Other hydraulic parameters i.e., the fillable porosity of 0.25 and horizontal hydraulic conductivity of 13.6, 5.2 and 1.6 m/day were also applied to the entire layer. The model was then run and the hydraulic head h0 at the center of the basin recorded for different recharge times.

To compute mound decay, initial head in the model was set to the hydraulic head after 365 days of recharge. While maintaining all the other properties of the model, the recharge rate was changed to zero to indicate that recharge stopped after 365 days. This allowed the recharge mound that had formed to dissipate and drain away from beneath the basin. With the model still in “transient state”, h0 was computed to estimate the head after recharge had stopped.

3 Results

Performance of the solutions were compared for a test basin with; V a = 0.274 m/day, f = 0.25, H = 30 m, L = W = 100 m; t = 0–365 days and K = 13.6; 5.2 and 1.6 m/day (Asano et al. 2006).

3.1 Mound Growth During Recharge

Solutions for predicting groundwater mounding beneath recharge basin (Eqs. (2), (8), (21), (23), (24) and (27)) were used to compute the rise in mound height, h0-H beneath the hypothetical basin, and the results presented in Table 1. Investigating the effect of varying hydraulic properties K, V a and f on maximum mound height was beyond the scope of this paper mainly because similar work has already been done (Rai et al. 2001) while Mahdavi and Seyyedian (2013) reported that as K increases mound height below the basin reduces as a result of flow becoming smoother away from the recharge source. However to generate general trends on the behavior of different analytical solutions, mound heights were computed for three value of K i.e., 13.6, 5.2 and 1.6 m/day representing very rapid, rapid and moderately rapid infiltration rates respectively.

Table 1 Comparison of analytical solution with FEFLOW under various hydrogeologic conditions
Full size table

Table 1 indicates that mound growth is rapid for t ≤ 50 days and grows at a slower rate with prolonged recharge periods. Finnemore (1995) reported that due to the assumptions made in the derivation of analytical methods (Section 2.1) mound growth is infinite though at much slower rates. This implies that hydraulic capacity can be increased with minimal mound growth. Reduced infiltration rates during wet seasons and the necessity of cycles of wetting and drying to control clogging limits recharge to a few months (Bouwer 2002). This is the period within which mound growth is rapid. In addition, minimum variation in mound heights predicted by analytical solutions is observed for t ≤ 50 days hence choosing analytical solutions will be insignificant.

For all three values of K, the variation in Glover’s solution decreases with increasing K. According to Warner et al. (1989) if Glover (1960) is preferred for simplicity of computation T = KH must be replaced by \( \widehat{T}=K\overline{b} \). Glover (1960) is desirable over Hantush (1967) because it does not contain the complex integral of the product of the error function known as the mound function F (α, β) which was simplified using integration by parts. Mound heights predicted using Singh (2012)’s correction are consistent for all three values of K. More so, mound heights estimated using Vatankhah (2013), Hantush (1967) and Rao and Sarma (1981) are analogous for all values of K. The deviation between FEFLOW and analytical solutions decreases as K decreases. A similar trend is observed between Swamee and Ohja (1997) and Hantush (1967). When K = 1.6 m/day, there is a closest match between FEFLOW and analytical solutions. Likewise, Swamee and Ohja (1997) shows good agreement with Hantush (1967) for the same value of K.

Vatankhah (2013) yields values equivalent to Hantush (1967) with a maximum difference of 0.1 m. Considering that mound height is in the order of metres, this difference is negligible. In fact Vatankhah (2013) is as accurate as Hantush (1967) up to 1 decimal place. The author claimed to have developed a mound height function that is accurate, easy to compute with a maximum percentage error of 1 % and an average percentage error of 0.3 %. The maximum calculated error in this report was 0.9 % and the average percentage error 0.27 % which is within the limits stated by the author. Results indicate that when A/L = B/W ≥ 1000 and m = n ≥ 10,000, Rao and Sarma (1981) is as accurate as Hantush (1967) with a maximum error of 0.3 %, the same results up to two decimal places (Table 1).

FEFLOW predicts mound heights higher than analytical solutions (up to 25 % for the highest K value). This is consistent with Sumner et al. (1999) and Rai and Manglik (2012) that numerical solutions yield higher results. Such a deviation is however unacceptable. It is likely that one of the approaches is erroneous. Singh (2012) claimed that his correction was easy to compute but similar to MODFLOW. We find a poor match between Singh and FEFLOW (for the values of parameters we have chosen). At low K value, Singh overestimates FEFLOW.

For analytical solutions the growth of the infiltration mound is inversely proportional to hydraulic conductivity, i.e., as K increases h0-H decreases. Since the difference between solutions such as Singh (2012) and Glover (1960) is consistent for different values of K, thus it can be assumed that the deviation of FEFLOW from analytical solution decreases as K decreases. This implies that FEFLOW converges to lower values as K decreases. As a result, the variation between FEFLOW and analytical solutions diminishes with decreasing values of K.

3.2 Mound Growth in Equivalent Long Strip

According to Glover (1960) a recharge area with L/W ≥ 5, functions essentially as a long strip at a late time. Bouwer (2002) states that infiltration mounds beneath a recharge structure can be reduced by using a long rectangular strip instead of the equivalent circular or square area. The area in the test basin (100 m × 100 m) was converted into a long recharge strip with a ratio of R = L/W = 6.25, 16, 25, 64, 100 and 400 maintaining all the other parameters constant.

Figure 2 shows the mound profiles obtained using various solutions for the first recharge strip with a ratio of L/W = 6.25. All solutions, except Singh (2012) and FEFLOW indicate that a smaller mound develops beneath a long recharge strip as compared to a square basin (Fig. 2). This is because Singh (2012) imitates numerical solutions. When compared with numerical solution of the original square basin, lower recharge mounds are observed for both FEFLOW and Singh (2012). To investigate the effect of increasing length-to-width ratios, mound heights were computed using Hantush (1967) for different recharge times. It was noted that as R increases, mound height decreases. Up to 1.0 m mound height difference is observed between R = 1 and R = 400. In fact, approximately 78.5 % of mound growth for R = 1 is evaded when R = 400 is used, for K = 1.6 m/day. Where mounding is problematic, this can be essential. The study has revealed that if there are no land restrictions, converting square basins into long strips can limit mound growth.

Fig. 2
figure 2

Mound heights for a rectangular area and an equivalent long recharge strip

Full size image

3.3 Mound Decay after Recharge Stops

The mound formed during recharge dissipates when recharge stops. Eq. (13) and the respective mound height approximations were used to compute the deterioration of the groundwater recharge mound after recharge. Bianchi and Haskell (1968) showed observed growth and decay mound for two ponds in a field study. Pond 2 had the following properties: K = 7.9248 m/day, V a = 0.10668 m/day, f = 0 0.052, H = 24.384 m, L = W = 90 m (Bianchi and Haskell 1968). Recharge was applied for t = 10.92 days and stopped allowing the mound to dissipate. Mound profiles for the falling hydrograph were calculated and plotted on Fig. 3 together with field observations. These results are consistent with Bianchi and Haskell (1968). A good match among analytical solutions was noted. About 75 % of the mound formed during recharge was dissipated after half the recharge time (t = 5 days). This suggests that the mound decays faster than it forms (Bouwer et al. 1999). However, the observed mound decays much slower. This is because the saturated zone continues to drain after recharge has stopped (Bianchi and Haskell 1968). Interestingly however, FEFLOW predicts mound heights that are similar to analytical solutions for the decaying mound (Fig. 4). Observed mound heights for the falling hydrograph were high due to vadose drainage (Bianchi and Haskell 1968).

Fig. 3
figure 3

Mound heights predicted using different analytical solutions for recharge mound decay

Full size image
Fig. 4
figure 4

Comparison of numeric methods and observation for predicting recharge mound decay

Full size image

4 Discussion

The use of Hantush (1967) solution to compute mound profiles for test basins is widespread. All except Singh’s (2012) solution produce results comparable to Hantush (1967). We demonstrated all mathematical solutions developed for modelling artificial recharge beneath a rectangular recharge basin provide credible results within their limitations. To obtain results comparable to Hantush (1967), simple modifications of Rao and Sarma (1981), Swamee and Ohja (1997) and Glover (1960) can be made. Using values of m = n ≥ 104 and A/L = B/W ≥ 103, Rao and Sarma (1981) yields exactly the same values as Hantush (1967). If Glover (1960) is preferred, transmissivity T must be calculated from Hantush (1967)’s linearization method Eq. (12). Swamee and Ohja (1997)’s approximation of F (α, β) can be used for low K values. Subsequently, Singh’s (2012) correction can then be applied to analytical solutions for results that compare with more complex solutions such as FEFLOW. We endorse the approximation of F (α, β) by Vatankhah (2013). In its simplicity it is the best approximation developed so far as a substitute for F (α, β). This is essential if quick approximation of mound heights is required without the use of numerical methods.

We find FEFLOW overestimates the mound height compared to analytical solutions for the models we selected. In addition when Singh (2012) correction is applied to Hantush (1967) or any other analytical solution the results obtained are in agreement with FEFLOW at early time. Bianchi and Haskell (1968) established theoretical solutions yielded results comparable to field observations. However Sumner et al. 1999 stated that numerical solutions predict higher mound heights compared to analytical solutions. Even if Bianchi and Haskell (1968) were thorough in their investigation, their findings alone are insufficient for evaluation against theoretical approaches. More field observations are required to establish the match between numerical solutions and observed data.

5 Model Applications and Limitations

Many writers have attested to the analogy between numerical and observed recharge mounds (Carleton 2010; Flint and Ellett 2004; Sumner et al. 1999; Vauclin et al. 1979) to point a few. Hydrologists are concerned about the applications of these models in relation to different hydrodynamic properties. The results discussed above indicate that the various models have both strengths and weaknesses. Since these results were generated based on a hypothetical basin, it was vital to test the performance of all models in a practical scenario.

Uppasit et al. (2012) applied artificial recharge to a deep aquifer underlain by a shallow aquifer and separated by a confining layer for a period of 55 days. A total recharge amount of 25 797 m3 was applied from two basins of area 600 m2 and 660 m2. From a detailed hydrogeological characteristics investigation, the porosity and hydraulic conductivity of the shallow layer were established to be 0.22 and 7.78 m/day, respectively. It was observed that the maximum mound growth below the basin was 3.33 m after 35 days after which the mound started to dissipate to the original water table elevation by the end of recharge in 55 days. Nevertheless, the data in the paper was not holistic enough to reproduce a FEFLOW model as such only analytical solutions were compared. Singh’s (2012) solution came closest to this value by up to 0.01 m at 35 days but continued to rise until the end of time while the rest underestimated the maximum mound. Since Singh’s (2012) was developed to imitate numerical solutions, it can be argued that numerical solutions are analogous to observed mounds. However Singh (2012) is also a modification of Hantush’s solution and due to that it shows an ever steadily rising recharge mound.

In an isolated investigation by Bala et al. (2013) recharge was applied through a percolation tank, 8 m by 8 m and 0.6 m deep. Other parameters were as follows; K = 14.4 m/day, V a = 0.33 m/day, f = 0 0.403 and H = 12.1 m. Figure 5 shows a comparison of both numerical and analytical solutions for the basin above. On one hand, observed mounds indicate that mound rise is gradual unlike analytical mounds which show rapid mound growth at the onset. Moreover, analytical results are closest to observed groundwater mound where they converge. On the other hand, Singh (2012) and FEFLOW overestimates observed recharge mounds. While the former is closer to observed at the onset, the variation is double for the latter. Further investigations were conducted using field data from Bianchi and Haskell (1968) and the results plotted in Fig. 6. The similarity between Figs. 5 and 6 is no mere coincidence. Rather a clear indication that analytical models are more superior in predicting mound rise during artificial recharge. This endorses the enduring popularity of Hantush’s (1967) solution

Fig. 5
figure 5

Comparison of computed and observed recharge mounds for a real case study

Full size image
Fig. 6
figure 6

Comparison of models in predicting recharge mounds for a real case study

Full size image

6 Conclusion

After computing recharge mound heights with different analytical solutions, we observed minor deviations among analytical solutions. However, comparison with FEFLOW indicated that numerical solutions overestimate mound heights when compared with analytical solutions. Table 2 highlights our findings in terms of the application of each solution under various conditions which can be summarized as:

Table 2 Mound profiles computed from various solutions for predicting mound growth
Full size table
  1. 1.

    We have noted that most analytical solutions yield similar results for t < 50 days. Often recharge cycles are within this time range; the selection among analytical solutions therefore is not crucial.

  2. 2.

    As already been established analytical solutions underestimate numerical solutions. However, the correction suggested by Singh is not generic. In fact Singh’s correction overestimates mound growth compared to both numerical and analytical solutions for all K values.

  3. 3.

    Negligible differences were observed between analytical and numerical solutions for predicting mound decay. However, numerical solutions are recommended if decaying mound is to be determined for longer periods of time.

  4. 4.

    If mound growth is problematic, converting circular or square basins into rectangular with a high R = L/W ratio significantly increases mound growth. In fact more than 75 % mound growth is avoided with R = 400.

  5. 5.

    Finally, when compared to observed infiltration mounds analytical solutions are a closer match for three practical scenarios.