Introduction

Hydraulic conductivity quantifies the ease with which water can move through the intergranular pore and fracture spaces of the formation. In hydrogeological problems, it is one of the most important petrophysical properties of rocks that can be generally measured in the laboratory using rock samples, and by aquifer tests performed in the field or at the aquifer scale, for instance from aquifer modeling. The study is mostly performed at the well log scale, which attempts to calculate hydraulic conductivity purely from well-logging measurements influenced by only the near vicinity of the borehole at a given depth. In porous media, the hydraulic conductivity is related theoretically to the grain-size, porosity and fracture characteristics. In primary porosity rocks, other textural properties of rocks are also taken into account such as cementation exponent or tortuosity factor. Geophysical interpretation approaches usually use some empirical method or statistical tool for the evaluation (Idrysy and De Smedt 2007; Ross et al. 2007; Odong 2013). Borehole geophysical measurements are part of the in-situ investigations that are used primarily to detect the variation of hydraulic conductivity along a borehole and to correlate it between neighboring boreholes. In oilfield applications, the direct determination of permeability as a related quantity is possible by means of the nuclear magnetic resonance (NMR) log. The surface geophysical application of its technique known as magnetic resonance sounding (MRS) is an emerging method in hydrogeology (Roy and Lubczynski 2003). Borehole NMR has been adapted from the oilfield for hydrogeological applications, using boreholes typical of environmental and hydrogeological investigations (Walsh et al. 2013). Although borehole NMR is very expensive, it has the added advantage of not only providing effective porosity, it can also be used to determine the pore-size distribution and pore-fluid characteristics to provide a better estimate of the hydraulic properties of rocks. The effective pore-radius based permeability prediction also has promising results both in the laboratory and in hydrocarbon exploration fields (Glover and Walker 2009). The indirect (in-situ) methods for hydraulic conductivity estimation are based on the determination of formation porosity and bound-water saturation (Timur 1968). Alger (1966) connected formation factor to effective grain-size, which allowed for calculation of hydraulic conductivity from borehole logs. As a continuation, Csókás (1995) suggested a well-logging technique to estimate hydraulic conductivity and other freshwater quality parameters for unconsolidated sediments, which requires the preliminary calculation of porosity, pore-water resistivity and true resistivity of the aquifer. The theory of freshwater assessment by means of well-logging information was summarized in Alger and Harrison (1989). In this framework, the reservoir parameters (including hydraulic conductivity) are connected to physical quantities that are measurable by well-logging probes. For extracting the unknown petrophysical parameters some deterministic or inverse modeling-based procedure is usually applied. A resistivity and porosity log-based approach can be found in Khalil et al. (2011), while example inversion applications can be found in Drahos (2005), Szabó and Dobróka (2013a).

Most types of well logs used in oilfields are commonly applicable in hydrogeology practice. Spontaneous potential and natural gamma-ray intensity logs are used for lithology identification and calculation of shale volume. Gamma-gamma and neutron-neutron intensity measurements give an accurate estimate of porosity. Resistivity tools are mainly sensitive to the water saturation that is calculated by them. In a regular case, the above well log types fulfill the requirements; however, there are some other advanced techniques that could give further information. Acoustic measurements are typically used for porosity estimation but, in shallow applications, nuclear logs work better. In secondary porosity rocks, the sonic log gives lower porosity reading than true porosity of the formation, because the acoustic waves avoid vugs and fractures as a result of the Fermat’s principle. Full-wave sonic logs may provide more detailed information on porosity, elastic parameters and horizontal stress conditions in the vicinity of the borehole. The separation of Stoneley waves propagating in the borehole enables the determination of the permeability of porous formations. Permeability is generally estimated from the inversion or statistical processing of Stoneley transit-time data with an advantage that they do not require the prior knowledge of porosity (Buffin 1996). Recently a non-linear statistical model was suggested by Szabó and Kalmár (2013) for improving the description of the relation between the characteristics of Stoneley waves and permeability. Their findings suggest that the circumferential borehole acoustic or optical images used in fractured formations should be completed with full-wave sonic logs for a more accurate and reliable interpretation.

When the currently used data processing methods are evaluated, one can see that each of them have their own weaknesses. The assumed model can be ambiguous and the data sets may be noisy or not sensitive enough to give a good estimate to hydraulic properties. Moreover, the interpretation results are often in contradiction with those determined from core samples. The estimation error of permeability may reach one to one and a half orders of magnitude. To reduce the uncertainty, the borehole surveys are frequently expanded with ground geophysical measurements. In Perdomo et al. (2014), hydraulic parameters are estimated by a joint application of well-logging resistivity and direct current electric measurements. Slater (2007) combined surface induced-polarization measurements with borehole flowmeter data, ground penetrating radar tomographic data and neutron-log-derived porosity information. Guérin (2005) presents the advantages of the application of electromagnetic methods. In the hydrogeological assessment of underground mines, quantitative information can be extracted from the joint inversion of borehole seismic and in-mine geoelectric data, used for instance, in detecting tectonic disturbances and fault zones in coal seam series, water inrush and in estimating the thickness of impervious layers (Dobróka et al. 1991).

In addition to the present measurement techniques, the introduction of an independent data processing method is of utmost importance. The simultaneous application of the new method and the existing ones can improve the accuracy and reliability of the estimation result. In this paper, an alternative approach based on multivariate statistical principles is presented, which processes all borehole logs together to give an estimate to the vertical distribution of formation hydraulic conductivity. Factor analysis is normally used to reduce the dimensionality of multivariate statistical problems, and to extract latent information from the data set that is non-measurable. The basic principle of the theory of factor analysis can be found in the paper of Lawley and Maxwell (1962). Several geophysical applications showed that the extracted factor variables correlate to some petrophysical properties of geological formations. Szabó (2011) introduced a factor analysis-based method to estimate the shale volume of sedimentary rocks. The statistical technique gave proper estimates for several domestic and some overseas deep wells in hydrocarbon fields (Szabó and Dobróka 2013b). The method was also tested in some shallow freshwater wells drilled in Hungary. Szabó et al. (2014) proposed a regression relationship between one of the factors and shale volume for eastern Hungary. Similar results were recently published by Asfahani (2014), who processed nuclear logs including natural gamma-ray intensity, density and neutron-porosity data and long- and short-normal electrical logs by factor analysis to characterize the large extended basaltic areas in southern Syria. It was concluded that the factor responsible for the largest part of variance of original logs (i.e. first factor) can be interpreted as a shale factor, which is useful for separating different lithological units. The hydraulic conductivity of groundwater formations is strongly related to shale volume in primary porosity rocks. In this study, it is assumed that the well log of the first factor correlates adequately with hydraulic conductivity, which is useful to extract the relevant parameter from borehole geophysical measurements. The feasibility of the statistical method is presented by synthetic modeling experiments and field studies, and the interpretation results are validated by independent laboratory and aquifer tests.

Theory of the method

According to Darcy’s law, hydraulic conductivity is the proportionality factor between Darcy’s velocity of water flow and hydraulic gradient, which in rocks with predominantly primary porosity, depends on the density and viscosity of pore-water, grain-size and pore-size distribution, porosity and water saturation. The spatial distribution of the related parameters can be derived from well-logging measurements. In the literature regarding the forementioned parameters, some empirical or approximate formula is normally used to calculate hydraulic properties such as hydraulic conductivity, transmissivity and storativity. The hydraulic conductivity K is directly proportional to intrinsic permeability expressing the measure of the aquifer’s ability to transmit water through its pore spaces. The Kozeny-Carman equation is one of the most widely used formulas for the estimation of hydraulic conductivity given in units of cm/s (Bear 1972)

$$ K=\frac{\rho_{\mathrm{w}}g}{\upmu}\frac{d^2}{180}\frac{\varPhi^{\mathtt{3}}}{{\left(1-\varPhi \right)}^2}, $$
(1)

where d (cm) is the grain diameter, Φ (v/v) is the porosity of formation, ρ w (g/cm3) is the density of pore-fluid, μ (g/cm/s) is the dynamic viscosity and g (cm/s2) is the normal acceleration of gravity. In Eq. (1), the dominant grain diameter d (cm) can be found from grain-size analysis (Juhász 2002)

$$ d=\frac{d_{10}+{d}_{\mathtt{60}}}{2}\sqrt{\frac{d_{10}}{d_{60}}}, $$
(2)

where d 10 (cm) and d 60 (cm) are the representative sample diameters at 10 and 60 % cumulative frequencies, respectively. As rock samples can be taken from boreholes and porosity can be estimated from well logs, the vertical distribution of hydraulic conductivity can be calculated continuously along the borehole. A new statistical method is presented in this paper that makes use of suitable well logs sensitive to hydraulic properties of rocks to give an estimate to hydraulic conductivity for the entire logging interval.

The method of factor analysis is applied to borehole logs in the following manner. Let the column vector d l contain the data of the l-th measured variable along the borehole. The readings of all data types are gathered in data matrix D

$$ {D}_{il}={d}_i^l, $$
(3)

where i = 1,2,…,N is the total number of measuring points in the processed depth-interval and l = 1,2,…,L is the number of geophysical tools measuring different physical quantities in the investigated borehole. The input data must be standardized in the first step of the analysis

$$ {\widehat{D}}_{il}=\frac{\left({D}_{il}-{\overline{D}}_l\right)}{\sqrt{\frac{1}{N-1}{\displaystyle \sum_{i=1}^N{\left({D}_{il}-{\overline{D}}_l\right)}^2}}}, $$
(4)

where \( {\overline{D}}_l \) represents the arithmetic mean of the data measured by the l-th probe. Factor analysis reduces the N-by-L matrix in Eq. (4) to a lower dimension by the matrix decomposition

$$ \widehat{\mathbf{D}}=\mathbf{F}{\mathbf{W}}^{\mathrm{T}}+\mathbf{E}, $$
(5)

where F denotes the N-by-M matrix of factor scores, W is the L-by-M matrix of factor loadings, E is the N-by-L matrix of residuals, M is the number of factors extracted from a higher number of observed variables, that is, M < L (T indicates the matrix transpose operator). The factor scores given in a column of matrix F represent a well log of the extracted statistical variable. Matrix W contains the weights of individual data corresponding to the extracted factors. Practically, the factor loadings represent the degree of correlation between each factor and measured data type. Since the factors are assumed to be linearly independent (F T F/N = I), the correlation matrix of the standardized data is

$$ \mathbf{R}=\frac{1}{N}{\widehat{\mathbf{D}}}^{\mathrm{T}}\widehat{\mathbf{D}}=\mathbf{W}{\mathbf{W}}^{\mathrm{T}}+\boldsymbol{\Psi}, $$
(6)

where Ψ = E T E/N is the diagonal matrix of specific variances (I is the identity matrix). If the notation of communalities represented by the elements of the main diagonal of matrix R c = WW T is introduced, it can be realized that matrix Ψ represents the part of variance of the observations that are not explained by the common factors. Normally W and Ψ are estimated by an iterative algorithm that minimizes the following type of objective functions

$$ \varOmega \left(\mathbf{W},\boldsymbol{\Psi} \right)=\mathrm{t}\mathrm{r}{\left(\mathbf{R}\hbox{-} \mathbf{W}{\mathbf{W}}^{\mathrm{T}}-\boldsymbol{\Psi} \right)}^2= \min, $$
(7)

where tr denotes the trace of the square matrix given in the argument. Function Ω must be minimized with respect to factor loadings and specific variances simultaneously. For solving the optimization problem the use of the maximum likelihood method is generally applied, which can give a robust solution (Jöreskog 1969). Assuming that W and Ψ are known, the factor logs can be extracted by the maximization of the following log-likelihood function

$$ \lg (P)=-\frac{1}{2}\left[ \lg \left|2\pi\;\boldsymbol{\Psi} \right|+\left(\widehat{\mathbf{D}}-\mathbf{F}{\mathbf{W}}^{\mathrm{T}}\right){\boldsymbol{\Psi}}^{-1}{\left(\widehat{\mathbf{D}}-\mathbf{F}{\mathbf{W}}^{\mathrm{T}}\right)}^{\mathrm{T}}\right]= \max . $$
(8)

After solving Eq. (8), an unbiased estimate to factor scores can be given by the hypothesis of linearity (Bartlett 1953)

$$ {\mathbf{F}}^{\mathrm{T}}={\left({\mathbf{W}}^{\mathrm{T}}{\boldsymbol{\Psi}}^{-1}\mathbf{W}\right)}^{-1}{\mathbf{W}}^{\mathrm{T}}{\boldsymbol{\Psi}}^{-1}{\widehat{\mathbf{D}}}^{\mathrm{T}}. $$
(9)

The optimal number of factors can be set by statistical tests (Bartlett 1950) or a non-iterative approach (Jöreskog 2007). The resultant factors are usually rotated for an easier interpretation. Since factor loadings are defined non-uniquely, an orthogonal transformation WW T = W*W*T can be applied to factor loadings, where W* = WV holds for a suitably chosen M-by-M orthogonal matrix V. In this study, the varimax algorithm suggested by Kaiser (1958) is used to generate rotated factors, which can be directly compared to hydraulic conductivity of groundwater formations.

The resultant factors can be related with formation parameters in regression analysis. Szabó et al. (2014) showed a strong exponential connection between the first factor (i.e. first column of matrix F) and shale volume in groundwater formations, where the regression coefficients obtained were approximately the same for different areas in eastern Hungary. As hydraulic conductivity is inversely proportional to shale content in primary porosity rocks (Benson and Trast 1995; Sallam 2006; Shevnin et al. 2006), it is assumed that the first factor variable is also sensitive to hydraulic conductivity. In this study, a linear relationship between the first factor and the decimal logarithm of hydraulic conductivity is demonstrated

$$ \hbox{-} \lg (K)={aF}_1^{\ast }+b, $$
(10)

where a, b are site specific constants and F *1 is the first factor scaled into an arbitrary interval. Equation (10) is confirmed by synthetic modeling experiments (see section ‘Synthetic modeling experiments’) and well-site studies (see section ‘Well-site applications’). The Pearson’s correlation coefficient R=\( \operatorname{cov}\left(K,{F}_1^{*}\right)/{\sigma}_{\mathrm{K}}{\sigma}_{{\mathrm{F}}_1^{*}} \) characterizes the strength of the linear connection between the given factor and the logarithm of hydraulic conductivity, where cov is the sample covariance operator, \( {\sigma}_{\mathrm{K}}\;\mathrm{and}\;{\sigma}_{{\mathrm{F}}_1^{*}} \) are the standard deviations of the correlated quantities, respectively. For statistical experiments using an exactly known model the misfit between the noisy and noiseless synthetic data is measured by the relative data distance

$$ {D}_{\mathrm{d}}=\sqrt{\frac{1}{NL}{\displaystyle \sum_{i=1}^N{{\displaystyle \sum_{l=1}^L\left(\frac{d_{il}^{\left(\mathrm{m}\right)}-{d}_{il}^{\left(\mathrm{c}\right)}}{d_{il}^{\left(\mathrm{m}\right)}}\right)}}^2}}, $$
(11)

where d (m) il and d (c) il denote the l-th measured and calculated data in the i-th depth point, respectively. Multiplying D d by 100, the measure of misfit is given in percent. The closeness of hydraulic conductivities estimated from different sources can be measured also by the Pearson’s correlation coefficient.

Synthetic modeling experiments

Consider the petrophysical model with exactly known parameters such as effective porosity (POR), water saturation in the immediate vicinity of the borehole flushed by mud (SX0) and that of the undisturbed formation away from the borehole including only pore-water (SW), shale volume (VSH), sand volume (VSD), dominant grain-size (D) and hydraulic conductivity (K). The model parameters vary vertically along the borehole. The model represents a shallow unconsolidated sedimentary geological formation made up of five inhomogeneous beds (model-well-1). In the near-surface region, not only freshwater but gas (normally air) may fill the pore space. The air saturation can be calculated by SG = 1 – SW, which can be divided into movable (SGM = SX0 – SW) and irreducible (SGIR = 1 – SX0) parts. The lithology from the top to the bottom is silty sand (42 % air and 58 % water), fine-grained sand (42 % air and 58 % water), shale (100 % water), fine-grained sand (35 % air and 65 % water) and shaly sand (100 % water). Typical grain-sizes are set from the literature (Wentworth 1922), while hydraulic conductivities are calculated by Eq. (1). In Well-1 bulk density (DEN), natural gamma-ray intensity (GR), spontaneous potential (SP), deep resistivity (RD), shallow resistivity (RS), neutron-neutron intensity (NN) logs are applied. The parameters of the petrophysical model are usually related to borehole geophysical measurements empirically. These mathematical relations called probe response equations can be used to predict data in a forward modeling procedure. The values of theoretical data would be measured along the borehole, if the geological structure was characterized by the assumed (exactly known) model parameters. Most types of borehole geophysical data can be expressed as a linear combination of the physical properties of rock matrix and fluid components weighted by the relative volumes of rock constituents. The following set of response functions can be used for the solution of forward problem in groundwater formations (Alberty and Hashmy 1984)

$$ \mathrm{DEN}=\mathrm{P}\mathrm{O}\mathrm{R}\left[\left(\mathrm{S}\mathrm{X}0\cdot \mathrm{DEMF}\right)+\left(1-\mathrm{S}\mathrm{X}0\right)\mathrm{D}\mathrm{E}\mathrm{G}\right]+\mathrm{V}\mathrm{S}\mathrm{H}\cdot \mathrm{DESH}+\mathrm{V}\mathrm{S}\mathrm{D}\cdot \mathrm{DESD}, $$
(12)
$$ \mathrm{G}\mathrm{R}=\mathrm{GRSD}+\frac{1}{\mathrm{DEN}}\left(\mathrm{V}\mathrm{S}\mathrm{H}\cdot \mathrm{GR}\mathrm{S}\mathrm{H}\cdot \mathrm{DESH}+\mathrm{V}\mathrm{S}\mathrm{D}\cdot \mathrm{GR}\mathrm{S}\mathrm{D}\cdot \mathrm{DESD}\right), $$
(13)
$$ \mathrm{S}\mathrm{P}=\mathrm{SPSD}+\mathrm{V}\mathrm{S}\mathrm{H}\left(\mathrm{SPSH}\hbox{-} \mathrm{SP}\mathrm{S}\mathrm{D}\right)=\mathrm{V}\mathrm{S}\mathrm{H}\cdot \mathrm{SP}\mathrm{S}\mathrm{H}-C\cdot \lg \left(\frac{\mathrm{RMF}}{\mathrm{RW}}\right)\left(1-\mathrm{V}\mathrm{S}\mathrm{H}\right), $$
(14)
$$ \mathrm{N}\mathrm{N}=\mathrm{P}\mathrm{O}\mathrm{R}\cdot \mathrm{N}\mathrm{N}\mathrm{F}+\mathrm{V}\mathrm{S}\mathrm{H}\cdot \mathrm{N}\mathrm{N}\mathrm{S}\mathrm{H}+\mathrm{V}\mathrm{S}\mathrm{D}\cdot \mathrm{N}\mathrm{N}\mathrm{S}\mathrm{D}, $$
(15)
$$ \frac{1}{\sqrt{\mathrm{RD}}}=\left[\frac{{\mathrm{VSH}}^{\left(1-\mathrm{V}\mathrm{S}\mathrm{H}/2\right)}}{\sqrt{\mathrm{RSH}}}+\frac{{\left(\sqrt{\mathrm{POR}}\right)}^{\mathrm{BM}}}{\sqrt{\mathrm{BA}\cdot \mathrm{R}\mathrm{W}}}\right]{\left(\sqrt{\mathrm{SW}}\right)}^{\mathrm{BN}}, $$
(16)
$$ \frac{1}{\sqrt{\mathrm{RS}}}=\left[\frac{{\mathrm{VSH}}^{\left(1-\mathrm{V}\mathrm{S}\mathrm{H}/2\right)}}{\sqrt{\mathrm{RS}\mathrm{H}}}+\frac{{\left(\sqrt{\mathrm{POR}}\right)}^{\mathrm{BM}}}{\sqrt{\mathrm{BA}\cdot \mathrm{R}\mathrm{M}\mathrm{F}}}\right]{\left(\sqrt{\mathrm{SX}0}\right)}^{\mathrm{BN}}, $$
(17)
$$ \mathrm{P}\mathrm{O}\mathrm{R}+\mathrm{V}\mathrm{S}\mathrm{H}+\mathrm{V}\mathrm{S}\mathrm{D}=1. $$
(18)

In Eqs. (12)–(17), there are additional quantities called zone parameters that express the physical properties of the solid and fluid parts of the groundwater formation. The detailed list of zone parameters practically chosen as constant in the forward modeling procedure can be found in Table 1. Equation (18) is the material balance equation for the rock environment, which is used to constrain the domain of model parameters in the interpretation procedure. Response Eqs. (12)–(17) can be used to generate synthetic borehole logs. In the test, these data are contaminated with some amount of random noise to produce quasi measured logs. By the processing of the noisy data it demonstrates how accurately the statistical procedure reconstructs the parameters of the exact model. The experiment evaluates the performance of the method, namely it characterizes its accuracy, stability and noise sensitivity.

Table 1 Groundwater-zone parameters chosen for synthetic modeling experiments
Full size table

The method of factor analysis is tested on synthetic well-logging data calculated on model-well-1. The workflow of the method is detailed in Szabó et al. (2014). Borehole logging data are calculated to each depth by substituting the actual values of model parameters (POR, SX0, SW, VSH, VSD) to Eqs. (12)–(17). As a result, six types of well logs (GR, SP, DEN, NN, RS, RD) in 250 depth levels are given, where the total number of data is 1,500. The synthetic data set is contaminated by random noise by adding a random number to each data generated from Gaussian probability distribution with zero mean and a scale parameter proportional to the noise level. The values of zone parameters are listed in Table 1. The correlation matrix in Table 2 shows that data variables represented by noisy synthetic data are relatively strongly correlated. The first two factors (i.e. first and second columns of matrix F) are calculated, because they explain 90.8 % and 9.2 % of total variance of measured data, respectively. Table 3 contains the loadings of the factors calculated by Eq. (8) for the case of the synthetic data set including 5 % Gaussian distributed noise. The largest weights on the first factor are given by lithology sensitive logs (GR and SP), while those of the second one are obtained by resistivity logs (RS and RD). These results are consistent with earlier studies (Szabó 2011; Szabó and Dobróka 2013b; Szabó et al. 2014). Asfahani (2014) also concluded that the first factor expresses the presence of clay in basaltic formations, and can be termed as a clay factor, while the second factor can be used to separate different lithological units according to their resistivity response; therefore, it can be termed as a resistivity factor. Two uncorrelated factors are calculated with the factor loadings by Eq. (9), which are then rotated and scaled to the interval of 0 and 100 (in earlier studies the same interval was chosen for the sake of comparability). The linear connection between the first factor and hydraulic conductivity in Fig. 1 is based on Eq. (10). The regression model is lg(K) = −0.033F *1 – 2.72, where coefficients a, b are obtained highly reliably (a min = –0.034, a max = –0.032 b min = –2.75 b max = –2.70 with 95 % confidence bounds). The Pearson’s correlation coefficient between lg(K) and F *1 is R = –0.98, which indicates a strong correlation and inverse proportionality between the variables. In Fig. 2, the input logs, the petrophysical model and the estimated hydraulic conductivity logs are illustrated, where GR log primarily correlates with shale volume of the formations. Since the resistivity of mud-filtrate (RMF) is lower than that of the pore-water (RW), a sand aquifer is at higher potential than shale (reverse SP). Shales are not invaded by mud; therefore, RS and RD logs overlap. The porous formations are flooded by a more conductive mud filtrate than the original pore-water. Normally in water-saturated rocks, the mud causes lower RS values than RD. The RD curve ascends more in the first, second and fourth layers where the pore space is partially saturated with air. The air effect appears as a separation between the nuclear logs, which provide porosity estimates for Eq. (1). The composition and saturation of the modelled rocks are represented by the last two tracks of Fig. 2. Beside the two factors, the well logs of the hydraulic conductivity estimated from Eq. (1) and Eq. (10) are plotted in track 7. The K(KOZENY) and K(FA) logs show a close agreement with a correlation coefficient of R = 0.98.

Table 2 Correlation matrix of synthetic borehole logging data in case of exactly known inhomogeneous model
Full size table
Table 3 Factor loadings derived from synthetic wellbore data in case of inhomogeneous model for Well-1
Full size table
Fig. 1
figure 1

Hydraulic conductivity versus factor scores derived from synthetic well-logging data contaminated by 5 % Gaussian distributed noise for the model-well-1

Full size image
Fig. 2
figure 2

Synthetic borehole logs calculated for model-well-1. GR is natural gamma-ray intensity, SP is spontaneous potential, DEN is density, NN is neutron-neutron intensity, RS and RD are shallow and deep resistivity logs, respectively. Dominant grain diameter is in track 5. The well logs of the extracted factors are in track 6. Hydraulic conductivity (K) logs are estimated from Kozeny-Carman equation (red curve) and factor analysis (FA, black curve), separately (track 7). SX0 is water saturation in the invaded zone, SW is water saturation in the virgin zone (track 8), POR is porosity, VSH is shale content, VSD is sand volume (track 9)

Full size image

Factor analysis as a data processing method is necessarily affected by the propagation of errors. The factor logs are estimated with a certain accuracy depending on the noise level of input data. A set of additional synthetic tests are performed using different level of uncertainties of wellbore data calculated on model-well-1 to examine the noise sensitivity of the factor analysis algorithm. In Table 4 the test results for data sets with different data distances based on Eq. (11) are listed. Beside Gaussian noise up to 10 %, some non-Gaussian typed (asymmetric) data distribution are also generated by adding outliers to the Gaussian distributed data (five times higher amount of noise is added randomly to the 10 % of the given Gaussian distributed data). Two factors are calculated in each case. The magnitude and sign of factor loadings do not vary significantly, as they show a low-rate decay for lithology dependent logs with increasing data distances. The coefficients for the regression connection between the hydraulic conductivity and the first-scaled factor show high accuracy and little variation. Estimation errors are directly proportional to data noises and are relatively small even in highly noisy cases. The Pearson’s correlation coefficients show strong and steady relationship between the two variables. Non-Gaussian tests show that factor analysis is properly resistant against data distributions different from Gaussian type. The regression connection between the factor and hydraulic conductivity can also be recognized beside extreme noises. The synthetic tests show a reliable and stable statistical algorithm.

Table 4 Results of noise sensitivity tests in case of inhomogeneous model and noisy synthetic well-logging data sets
Full size table

Well-site applications

Validation with Kozeny-Carman model

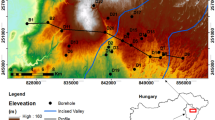
The suggested statistical method works properly when applied to real data sets. The following example shows a Hungarian case study. In the Pannonian Basin Province of Central Europe, a thick Tertiary sedimentary sequence including hydrocarbon and thermal-water reservoirs was deposited over the Mesozoic and older basement rocks. The overlying unconsolidated Quaternary formations mainly consist of freshwater-bearing gravel or sand aquifers confined by shales. The shallow part of well B-1 is investigated, which is located in Baktalórántháza, Szabolcs-Szatmár-Bereg County, North-East Hungary (Fig. 3). The aim of the survey and earlier results of factor analysis can be found in Szabó et al. (2014).

Fig. 3
figure 3

Location map of the investigated well sites, in a view of the northern hemisphere of the Earth from above the North Pole

Full size image

In this study, factor analysis is applied to borehole logs to evaluate the hydraulic conductivity of geological formations between the interval of 105 and 486 m, where 176 core samples were previously collected. The processed well logs include: natural gamma-ray intensity (GR), spontaneous potential (SP), shallow resistivity (RS), gamma-gamma intensity (GG) and neutron-neutron intensity (NN). The total number of data is 19,075 which are processed together in one interpretation procedure. The strength of correlation between the measured variables is moderate, as is seen in Table 5. The correlation coefficients are even smaller than they are assumed in the calculations of the synthetic case (Table 2). Singular value decomposition (SVD) of the data covariance matrix shows that the total variance of input data can be explained by two lithological factors. The first factor is responsible for 82 % of data variance, while the second factor explains the 18 % of observed information. In the previous study, the first factor log was identified as a shale indicator. Now a comparison is made between the first factor and hydraulic conductivity coming from grain-size analysis and porosity information. The factor loadings for well B-1 are listed in Table 6, where the GR and RS logs bear the heaviest influence on the first factor. Factor scores are scaled by the same procedure as in section ‘Synthetic modeling experiments’. Figure 4 shows the regression relationship between the first scaled factor and the decimal logarithm of hydraulic conductivity calculated by Eq. (1). Dominant grain-sizes are calculated by Eq. (2) from d 10 and d 60 values of grain-size distribution curves measured on core samples. Porosity in Eq. (1) was calculated from the neutron log using Eq. (15). The zone parameters for the neutron response can be obtained from the neutron-neutron vs. gamma-gamma crossplot (NNSD = 7.5 kcpm, NNSH = 4.0 kcpm, NNF = 1.0 kcpm). The regression function suggested in Eq. (10) approximates well the relationship between the two variables, where the Pearson’s correlation coefficient (R = –0.79) indicates an unequivocal inverse proportionality. This index number is highly dependent on the level of data noise and the uncertainty of positioning the places of core sampling. The regression function is lg(K) = −0.046F *1 − 3.38, where coefficients a = [–0.052,–0.041] and b = [–3.66,–3.11] are estimated with 95 % level of significance.

Table 5 Correlation matrix of borehole logging data observed in well B-1
Full size table
Table 6 Factor loadings derived from borehole geophysical data collected from well B-1
Full size table
Fig. 4
figure 4

Regression relation between the hydraulic conductivity calculated from core measurements and the scores of the first factor derived from borehole logs measured in well B-1

Full size image

The input borehole logs and the interpretation results are illustrated in Fig. 5. The GR log indicates the boundary between the Pleistocene and Pannonian (late Miocene) complex at around 240 m. The latter dominantly consists of clayey sands, silts and marls, while the former is formed mainly by coarse-grained sands and gravels. At the top of the lithology column Holocene flood sediments can be found. A GR-log-based method proposed by Larionov (1969) can be applied to give an independent estimate to shale volume (indicated by VSH in the last track). The formation porosity (POR) is extracted from the neutron log by Eq. (15), while the volume of sand is calculated by Eq. (18). As the entire interval is fully water-saturated, thus the water saturation in the flushed and the virgin zone is 100 % (SX0 = SW = 1). In the fifth track, the well log of the first scaled factor is plotted. Hydraulic conductivity K(CORE) values indicated by red circles are calculated by Eq. (1) in the places of core sampling. The same quantity derived from factor analysis is represented by the black curve of K(FA). The hydraulic conductivity logs show a close fit to confirm the feasibility of the statistical method.

Fig. 5
figure 5

Borehole logs measured from well B-1 (tracks 1–4). GR is natural gamma-ray intensity, SP is spontaneous potential, GG is gamma-gamma intensity, NN is neutron-neutron intensity, RS is shallow resistivity log. The well log of the first factor is in track 5. D10 and D60 are representative grain diameters at 10 and 60 % cumulative frequencies, DOMINANT is dominant grain diameter (track 6). Hydraulic conductivity (K) logs are estimated from grain-size analysis made on core samples (red circles) and factor analysis (black curve), separately (track 7). POR is porosity, VSH is shale content, VSD is sand volume (track 8)

Full size image

Validation with aquifer test

The drilling of Well FL-800 was part of a project of US Geological Survey and US Environmental Protection Agency to characterize the lithostratigraphy and regional hydrogeology of the Ordovician Sinnipee Group situated in Waupun, Fond du Lac County, Wisconsin, USA (Fig. 3). The aim of the study was to acquire useful information to manage and protect the groundwater supply. For this task, detailed laboratory measurements made on core samples, borehole geophysical and hydrogeological surveys were performed at the investigation site (Dunning and Yeskis 2007). The Ordovician Sinnipee Group is considered a bedrock aquifer, which consists of the Platteville, Decorah and Galena Dolomite formations (from the bottom to the top). They are overlain only by a thin layer of unconsolidated deposits of Quaternary age. The principal lithology of the Sinnipee Group is dolomite and shaly dolomite in the logged interval. Core measurements indicate a primary porosity of 2–4 % in the dolomite, while primary porosity is up to 10 % in shaly intervals. The dolomite is quite massive and in some levels the fractures and bedding-plane partings are responsible for secondary porosity and permeability. These features were identified by the acoustic borehole televiewer, single-hole directional reflection and cross-hole radar tomography measurements. Borehole geophysical results showed that water is transmitted primarily along bedding-plane partings. In some isolated intervals, horizontal hydraulic conductivity was estimated by hydraulic tests, which proved to be highly consistent with heat-pulse flow-meter (flow velocity and volume) data. In this study, horizontal hydraulic conductivities calculated from slug tests using the method of Hvorslev (1951) are directly compared to the results of factor analysis.

Borehole logging measurements in well FL-800 suitable for factor analysis includes: natural gamma-ray intensity (GR), short- and long-spaced neutron-neutron intensity (NN-N for near receiver and NN-F for far receiver), electric resistivity (RES-16: short normal, RES-64: long normal, LAT: lateral) and temperature (TEMP) logs. The processed interval is between elevation 910 and 750 feet (277.4 and 228.6 m) above mean sea level referenced to National Geodetic Vertical Datum of 1929 in the United States of America (NGVD 29). The total number of data is 11,298. Table 7 shows the correlation matrix of the borehole logs, which indicates moderate correlation between the measured variables on the average. Three factor logs are calculated, where SVD results show that 79.1 % of total variance is explained by the first factor, 14.9 % by the second factor and 6 % by the third factor. The factor loadings for well FL-800 are listed in Table 8, which shows some difference compared to the case of primary porosity rocks. The first factor appears to be principally a resistivity factor, while the second one is affected more by lithology and water content. In these fractured formations the first factor seems to be directly proportional to resistivity, while it is inversely related to natural gamma-ray log. After scaling the first factor as in section ‘Synthetic modeling experiments’, the logarithm of hydraulic conductivities obtained from slug tests can be plotted with respect to the factor scores. The regression relationship is illustrated in Fig. 6, which shows that the inverse connection is even stronger (R = –0.90) than in section ‘Validation with Kozeny-Carman model’. The regression function is lg(K) = −0.05F *1 + 2.84, where the coefficients estimated with 95 % significance bounds are a = [–0.08, –0.02] and b = [1.47, 4.21].

Table 7 Correlation matrix of borehole geophysical data acquired in well FL-800
Full size table
Table 8 Factor loadings derived from borehole geophysical data measured in well FL-800
Full size table
Fig. 6
figure 6

Regression relation between the hydraulic conductivity calculated from aquifer tests and the scores of the first factor estimated from well logs observed in well FL-800

Full size image

The boundary of Galena Dolomite and Decorah formations runs at 810 elevation in feet (246.9 m) and the top of the Platteville Formation is at around 790 elevation in feet (240.8 m). The GR log provides information on shale content, of which maximum is ~40 % in the Decorah Formation. The highest permeability zones are in the argillaceous dolomite above 870 elevation in feet (265.2 m), which was obtained from flow-meter tests. The acoustic televiewer images showed earlier also a high density of subvertical fractures and bedding-plane partings in the same interval. In the Decorah Formation, the larger porosity of shale causes a relative higher permeability than in the massive dolomite of Platteville Formation. The permeable zones are also indicated by the separation of resistivity logs of different penetrations. The well logs of the factors are plotted in the fifth track in Fig. 7. The logarithm of hydraulic conductivity LG_K(ST) values represented by red circles are obtained from slug test results, while the continuous curve of LG_K(FA) is estimated from factor analysis. The overall fit between the results is sufficient to confirm the validity of the method.

Fig. 7
figure 7

Borehole logs measured from well FL-800 (tracks 1–4). GR is natural gamma-ray intensity, NN(NEAR) and NN(FAR) are short- and long spaced neutron-neutron intensity, RES-16 and RES-64 short and long normal resistivity, LAT is lateral resistivity, TEMP is temperature log. The extracted three factors are in track 5. Hydraulic conductivity (K) logs estimated from slug tests (red circles) and factor analysis (black curve), separately (track 6). Conversion: 1 m = 3.2808 ft, 1 cm/s = 2834.65 ft/day

Full size image

In this section, the feasibility of factor analysis has been demonstrated for two different geological settings. An acceptable fit between the estimates of hydraulic conductivity derived separately from factor and core analysis was achieved in well B-1 (Fig. 8a). In the Pleistocene, the matching points of the crossplot show bigger discrepancies from the black straight line representing the equation lgK(FA) = lgK(CORE), while the misfit is smaller in the lower hydraulic conductivity Miocene formation. In well FL-800, a closer fit between the estimates of factor analysis and slug tests is indicated for the entire depth interval (Fig. 8b), where the equality lgK(FA) = lgK(ST) is represented by black straight line in the figure. The accomplished synthetic and field experiments infer that the statistical method gives a reliable evaluation of hydraulic conductivity of groundwater formations.

Fig. 8
figure 8

Regression relation between hydraulic conductivity estimations. a The decimal logarithm of hydraulic conductivity was estimated from factor and laboratory analysis in well B-1. b The decimal logarithm of hydraulic conductivity was estimated from factor analysis and slug tests in well FL-800. Conversion: 1 cm/s = 2,834.65 ft/day

Full size image

Conclusions

A multivariate statistical approach applied to borehole logging data is suggested for the estimation of hydraulic conductivity. The factor analysis-based method has been proven to be a powerful tool in solving hydrogeophysical problems, for instance in earlier studies factor analysis was used to evaluate the shaliness of groundwater formations (Szabó 2011; Szabó and Dobróka 2013b; Szabó et al. 2014). As a continuation, a new statistical procedure is introduced in this paper to extract the vertical distribution of formation hydraulic conductivity purely from borehole geophysical observations. As a result, it provides continuous in-situ information to interpolate hydraulic conductivity between cored or pumped intervals. Synthetic modeling experiments using noisy data sets show that the estimation results are consistent, accurate and outlier resistant. Since the estimation error of permeability or hydraulic conductivity can normally reach one order of magnitude, any additional information given from a different source may increase the reliability of the hydrogeological interpretation. The estimation error can be effectively reduced by the suggested method, because of a large number of observed variables and statistical sample. The method of factor analysis jointly processes suitable data within the logging interval allowing some shorter intervals of missing data. The process requires only a few seconds of CPU time using a quad-core processor-based workstation.

The paper also gives an overview on the practical issues on the application of the method. Numerical results confirm the validity of the regression formula defined in Eq. (10). The regression coefficients must be set for each well using core or aquifer test data. Even with the lack of this information, the formula gives a first approximation of hydraulic conductivity. On the basis of earlier results, the method is tested first in shallow clastic aquifers (section ‘Validation with Kozeny-Carman model’), where a strong inverse proportionality is shown between the first factor and hydraulic conductivity. Another field case is presented to demonstrate the feasibility of the method also in fractured sedimentary rocks (section ‘Validation with aquifer test’). Both studies confirm the validity of regression Eq. (10) where some deviations in the regression constants can be experienced because of the different measurement units of hydraulic conductivity. In sedimentary rocks with intergranular porosity, the first factor is mainly sensitive to shale content, where the factor loadings show positive correlation with the lithology logs (GR and SP). In these rocks the permeability is inversely proportional to shale content. In secondary or mixed porosity systems, where the mineral composition and textural (or structural) properties are more complex, the first factor may be influenced by other properties different from lithology (e.g. pore-fluid content and secondary permeability). In section ‘Validation with aquifer test’, a massive dolomite complex is studied, in which shale volume is directly proportional to permeability. The loading of the first factor for the GR log appears to be negative and smaller than those of the resistivity logs. The interpretation of factors related to fractured rocks should be further analyzed in forthcoming research. The presented results show that reliable information on the distribution of hydraulic conductivity can be extracted from borehole geophysical data sets, which may improve the solution of hydrogeological problems. The method can be extended to multiple (two- or three-dimensional) borehole applications as it was shown earlier in Szabó et al. (2012) to support ground geophysical and hydrogeological surveys even in regional scales.