Quasi-static collapse of two-dimensional granular columns: insight from continuum modelling

Abstract

We investigate numerically the mechanism governing the quasi-static collapse of two-dimensional granular columns using a recently proposed continuum approach, the particle finite element method (PFEM), which inherits both the solid mathematical foundation of the traditional finite element method and the flexibility of particle methods in simulating ultra-large deformation problems. The typical collapse patterns of granular columns are reproduced in the PFEM simulation and the physical mechanism behind the collapse phenomenon is provided. The collapse processes obtained from the PFEM simulation are compared to experimental observations and discrete element modeling, where a satisfactory agreement is achieved. The effects of the macro density and friction angle of the granular matter, as well as the roughness of the wall surfaces on the quasi-static collapse, are also investigated in this paper. Furthermore, our simulations reveal new quasi-static collapse patterns, as supplements to the ones already observed in the experimental tests, due to the change of the roughness of the basal surface.

1 Introduction

Granular materials may behave like a solid, a liquid, or even a gas under different conditions [1]. Due to their complex behaviour that they exhibit, granular materials remain poorly understood and continue to attract attention from researchers in both academia and industry. Numerous experiments have been conducted to provide a better understanding of granular materials and improve guidelines for engineering practice, among which the dynamic/quasi-static collapse of granular columns under the action of gravity [2–4] is a typical example.

To date, a considerable amount of research effort has been devoted to investigating the dynamic collapse of granular columns. Such laboratory tests were initially introduced by two separate research groups simultaneously, Lube et al. [2, 5] and Lajeunesse et al. [3, 6]. Experimental results from both groups revealed that: (a) the shape of the final deposit mainly depends on the initial aspect ratio of the column; (b) during the collapse process, there exists a static region within which the granules are undisturbed; (c) the relation between the deposit shape (measured by the normalised final height and width) and the initial aspect ratio can be expressed as a simple power law, the factor of which differs for columns with low and high aspect ratios; and (d) in the case of axisymmetric collapse, the normalised final height tends to be constant when the initial aspect ratio is sufficiently large. To identify the dominant factors that govern the collapse, such experiments were then widely studied under different conditions [7–12] (i.e. different roughness and inclination of the basal plane, in air or underwater, etc.) in physical modelling.

From the perspective of numerical analysis, the dynamic collapse of granular columns has also been extensively investigated using both the discrete element method (DEM) and continuum approaches. The DEM [13] treats the granular column as an assembly of independent elements called particles or grains, whose motions are predicted via Newton’s law of motion associated with appropriate constitutive relations linking the contact force and overlap that may occur between particles (or grains). So far, the dynamic collapse of granular columns has been studied by a bulk of researchers using the DEM [14–18]. This is, to a large extent, due to its feature that arbitrarily large deformation can be handled naturally. In addition, the DEM simulation can consider the effect of microscopic properties of particles (i.e. particle surface roughness, particle shapes etc.) on the macroscopic mechanical behaviour [19, 20]. However, it is worth noting that the computing cost of the DEM simulation is highly intensive rendering the number of particles used in the simulation is usually far less than that in the physical modeling. In contrast to DEM modelling, the simulation based on continuum approaches makes use of macroscopic constitutive models and may provide insight into the effect of the macroscopic material properties, which in fact are easily obtained through laboratory tests and are more frequently referred to by engineers. However, the large deformation and moving boundaries involved in the problem are challenging for the popular traditional finite element method (FEM) [21]. This is because large deformation usually leads to a severely distorted finite element mesh, and the boundary evolution cannot be captured accurately due to the fixed mesh topology in the traditional FEM. To overcome these issues, some alternative numerical tools have to be employed. For example, Chen et al. [22] developed a three-dimensional model of the smoothed particle hydrodynamics method for the analysis of granular column collapse which successfully reproduced the flow pattern as well as the final deposit. Holsapple [23] presented a finite-difference continuum model to evaluate the performance of standard continuum plasticity Mohr-Coulomb and/or Drucker-Prager models on predicting granular columns collapse problem and showed that the classical plasticity models very accurately predict such a cliff collapse problem. The effects of the internal frictional angle of granular matter on the dynamic collapse of granular columns were investigated by Mast et al. [24] using the material point method. Recently, a novel continuum approach called particle finite element method (PFEM), were adopted for the simulation of granular flow problems [25–28], in particular the dynamic collapse of granular columns [29, 30]. The PFEM [28, 31–33] makes use of particles to represent materials, as in meshfree particle methods, but solves the governing equations via a standard finite element procedure. As a result, this technique inherits not only the ability of meshfree particle methods to cope with arbitrary changes in geometry, but also the solid mathematical foundation of the traditional FEM. It is shown [25–28, 30, 34] that the PFEM is particularly suitable for simulating granular materials which show both solid-like and fluid-like behaviour.

Compared to the extensive works that are available on the dynamic collapse, the quasi-static spreading of granular columns attracts less attention despite its importance in industry. It is true that in many, if not most, industrial processes (in particular soil-related processes) the inertial effect of granular materials is commonly negligible and thus the problem can be treated as quasi-static. Typical examples include the movement of soil retaining walls in geotechnical engineering and soil cutting using blades in tillage. To the best of the authors knowledge, the earliest published data on the quasi-static collapse of granular columns were attributed to M$\acute{e}$riaux [4], with additional results documented in [35] by Owen et al., who also provided insight into the effect of the microscopic characteristics and properties of the granules on quasi-static collapse from the numerical point of view. In [35], both two-dimensional and three-dimensional modelling was conducted using the discrete element method (DEM). It was reported that the collapse is independent of the particle stiffness, particle-wall friction, and particle-particle friction whereas it is very sensitive to the particle shape.

In this study, we attempt to provide insight into the quasi-static collapse of two-dimensional granular columns from a continuum simulation perspective. This is achieved by employing the PFEM developed in [26]. This version of the PFEM makes use of the classic plastic theory with the Mohr-Coulomb model to represent granular matter which is deemed to be appropriate for describing quasi-static behaviour of granular matter [36]. In addition, the singularity of the Mohr-Coulomb yield surface is no longer a problem because the finite element formulation is reformulated as a standard second-order cone programming problem [37] in which the cones can be treated natually using an advanced optimisation algorithm [38]. The simulation results from the PFEM, including the collapse patterns, the evolution of the granular bed height at the fixed and moving walls, and the final deposition are compared with available experimental data [4, 35] and DEM simulation results [35] with the mechanism behind the flow being discussed. Various collapse types observed in experiments are explained from the perspective of numerical modeling. The effects of the macroscopic material properties and the roughness of the walls on the collapse mechanism are studied in detail. Furthermore, some new collapse types are discovered due to the change of basal roughness in our simulations.

The paper is organised as follows. Section 2 describes the problems considered as well as the associated governing equations. Section 3 briefly introduces the solution scheme for the initial boundary-value problems. Simulation results as well as discussions are then presented in Sect. 4 before conclusions are drawn in Sect. 5.

2 Problem description

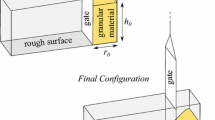
Figure 1 illustrates the experimental setup for the quasi-static collapse of two-dimensional granular columns. This quasi-static collapse experiment was originally conducted by M$\acute{e}$riaux [4] and then by Owen et al. [35]. In the experiments [4, 35], the granular materials were deposited in a cubic box (see Fig. 1). The wall on the left hand side is fixed, while the wall on the right hand side can move. The initial length and height of the column are represented by $L_i$ and $H_i$, respectively, and the initial aspect ratio of the column is defined by $A=H_i/L_i$. The collapse is induced by retreating the wall on the right hand side from the fixed wall.

Although in experiments the collapse of a granular column proceeds very slowly and can be regarded as quasi-static, the problem here is studied through a complete dynamic analysis in continuum modeling, the governing equations of which are summarised as follows:

Fig. 1

Schematic representation of the quasi-static collapse of two-dimensional granular column

• (a) Momentum conservation equations for the granular matter

  $$\begin{aligned}&\varvec{\nabla }^{\textsf {{\tiny T}}}\varvec{\sigma }+ \varvec{b} = \rho \ddot{\varvec{u}},~~\text {in}~V \end{aligned}$$

  (1)

• (b) Mass conservation equation

  $$\begin{aligned}&\rho J = \rho _0 \end{aligned}$$

  (2)

• (c) Rigid-perfectly plastic constitutive model for the granular matter

  $$\begin{aligned}&F(\varvec{\sigma }) \le 0\nonumber \\&\dot{\varvec{\varepsilon }} = \dot{\lambda }\nabla _\sigma G(\varvec{\sigma }) \nonumber \\&\dot{\lambda } F(\varvec{\sigma }) = 0,~~\dot{\lambda } \ge 0 \end{aligned}$$

  (3)

• (d) Classical Coulomb model [39] for frictional contact between the granular matter and walls

  $$\begin{aligned}&g_N\ge 0,\quad p\ge 0,\quad p\,g_N=0 \nonumber \\&|q| - \mu p \le 0 \end{aligned}$$

  (4)

• (e) Boundary conditions

  $$\begin{aligned}&\varvec{u} = \bar{\varvec{u}},~~\text {on}~\varGamma _u \end{aligned}$$

  (5)
  $$\begin{aligned}&\varvec{N}^{\textsf {{\tiny T}}}\varvec{\sigma }= \bar{\varvec{t}},~~\text {on}~\varGamma _t \end{aligned}$$

  (6)

  where

• $\varvec{\sigma }$ is the stress

• $\varvec{b}$ is the body force

• $\rho$ and $\rho _0$ are bulk densities of the granular material at time t and $t_0$

• J is the determinant of the deformation gradient tensor

• $\varvec{u}$ is the displacement

• V is the material domain under consideration

• $\varvec{\varepsilon }=\varvec{\nabla }\varvec{u}$ is the linear strain

• F is the yield function

• G is the plastic potential

• $\dot{\lambda }$ is the plastic multiplier

• $g_N$ is the gap between the granular matter and the rigid surface

• p is the contact pressure which is positive corresponding to compression

• q is the tangential stress

• $\mu$ is the friction coefficient between the material and the rigid surface

• $\bar{\varvec{u}}$ is the prescribed displacement on boundary

• $\bar{\varvec{t}}$ is the prescribed traction on boundary

• $\varvec{N}$ consists of components of outward normal to the corresponding boundaries.

In the above equations, a superposed dot denotes differentiation with respect to time, and, in two-dimensional cases, the $\varvec{\nabla }$ is the usual linear operator.

Remark 1

The governing equations proposed above are on the basis of the infinitesimal strain theory which may lead to several errors. The most serious one is the generation of strains as a result of rigid body motion. However, it has been shown in [26, 40] that this and related errors are relatively minor for the kind of time steps used in typical granular flow simulations. As such, the price to pay for the convenience of being able to operate with usual infinitesimal strain theory appears to be very small. Under the infinitesimal strain assumption, the mass conservation or continuity equation (2) degrades to $\rho = \rho _0$. It should be emphasized that, due to the fact that mesh node position will be updated at each incremental analysis, volume change may happen in the situation that Poisson’s rate is not euqal to 0.5 or the dilation angle of the granular matter is greater than zero. As a result, the density of the material have to be updated according to equation (2) explicitly at the end of each incremental analysis step even though the infinitesimal deformation is assumed. In this study, the elastic deformation is neglected and the dilation angle is set to be zero which prevent the volume change. As a result, Eq. (2) is always fulfilled.

Remark 2

As shown in (3), the granular materials are represented by a rigid plastic constitutive model with a non-associated flow rule. In our simulations, both the yield function and the plastic potential obey the Mohr-Coulomb failure criterion in the present work, that

$$\begin{aligned} F= & {} \sqrt{(\sigma _{xx}-\sigma _{yy})^2 + 4\sigma _{xy}^2} + (\sigma _{xx}+\sigma _{yy})\sin \phi -2c\cos \phi \nonumber \\ G= & {} \sqrt{(\sigma _{xx}-\sigma _{yy})^2 + 4\sigma _{xy}^2} + (\sigma _{xx}+\sigma _{yy})\sin \psi \end{aligned}$$

(7)

where $\phi$ is the friction angle, c is the cohesion, and $\psi$ is the dilation angle with $\psi =0^\circ$ implying that plastic flow takes place at constant volume. Although it is simple, such a classical rate-independent plastic model is perhaps the most widely used one for describing quasi-static behaviour of granular materials [36]. Furthermore, recent studies show that this model is also valid for predicting the dynamic collapse of granular columns [23, 29, 41]. Notably, the model utilised here ignores any elastic, reversible behaviour of the granular material. Such a treatment is appropriate when deformation in the material is dominated by plastic flow as shown in [28, 29]. For the numerical studies of the collapse of granular columns using more sophisticated models, we refer the readers to [24, 27, 30, 42]

3 Solution scheme

A variety of numerical solution schemes are available for solving the governing equations presented in the above section. In this work, they are tackled using the Finite Element Method (FEM) in mathematical programming (MP) [43–46]. In particular [26], the governing finite element equations are reformulated as a standard optimisation problem, for example as a second-order cone programming program, which is then solved directly using advanced optimisation engines. Some key advantages associated with this MP-based method [26] include the natural treatment of the singularity of the Mohr-Coulomb yield criterion [43] and the predictable and rapid convergence behaviour of solutions from the modern mathematical programming algorithms[38, 45, 47] among others. Notably, the utilised MP-based method can handle the frictional contact between rigid and deformable bodies straightforward and the corresponding frictional contact algorithm has been documented in [26]. In this paper, the utilised solution scheme is documented briefly in the “Appendix” for the sake of completeness. Also in [26], this MP-based solution scheme was embeded into the particle finite element procedure, which is adopted here for the numerical studies of quasi-static collapse of granular columns.

4 Numerical simulation and discussion

In this section, the quasi-static collapse of two-dimensional granular columns described in Sect. 2 is studied numerically using the recently-developed PFEM [26]. In our simulations, the speed of the movement of the wall on the right hand side is set to be $V=6$ mm/s (if not otherwise specified). In such a circumstance, the inertial effects are negligible (which will be shown later). The material parameters of the granular matter follow those quoted in [4, 35] for sands, if not defined otherwise, and are: density $\rho =1.49\,\hbox {g/cm}^3$, friction angle $\phi =28^\circ$, dilatancy angle $\psi =0^\circ$, and cohesion $c=0$. The frictional coefficient between the wall and the granular material is $\mu _w=\tan \phi _w$ with $\phi _w=25^\circ$ and the basal surface is assumed to be rough, namely its friction coefficient $\mu _b=\tan \phi$.

Fig. 2

Collapse of the granular column with the initial aspect ratio $A=0.5$ and length $L_i=70$ mm at the normalised time a $t/\text {T}=0.01$, b $t/\text {T}=0.3$, (c) $t/\text {T}=0.7$, and d $t/\text {T}=1.0$. Colours are proportional to the norm of the velocity, $\Vert v\Vert$ (mm/s) (colour figure online)

Fig. 3

Collapse of the granular column with the initial aspect ratio $A=3.0$ and length $L_i=36.7$ mm at the normalised time a $t/\text {T}=0.01$, b $t/\text {T}=0.2$, c $t/\text {T}=0.55$, and d $t/\text {T}=1.0$. Colours are proportional to the norm of the velocity, $\Vert v\Vert$ (mm/s) (colour figure online)

Fig. 4

Collapse of the granular column with the initial aspect ratio $A=5.5$ and length $L_i=20$ mm at the normalised time a $t/\text {T}=0.01$, b $t/\text {T}=0.2$, c $t/\text {T}=0.3$, d $t/\text {T}=0.7$, e $t/\text {T}=1.0$. Colours are proportional to the norm of the velocity, $\Vert v\Vert$ (mm/s) (colour figure online)

4.1 Collapse patterns

To capture different collapse patterns, the collapse of granular columns of initial aspect ratio A ranging from 0.1 to 11 are simulated numerically. The typical collapse patterns obtained from the PFEM simulation are illustrated in Figs. 2, 3 and 4. From these figures we can see that the collapse patterns of the granular columns chiefly depend on the magnitude of their initial aspect ratios, which is in line with the observations in the experimental tests [4].

Figure 2 shows the collapse evolution for a granular column with a small initial aspect ratio, e.g. $A=0.5$. The normalised time $\bar{(t)}$ is estimated via the current accumulated horizontal displacement of the moving wall divided by its total displacement when the final deposit is formed. As illustrated, the column collapses only partially with a failure plane propagating from the bottom right of the column (adjacent to the moving wall) up to its free surface. The initial failure plane is oriented towards the horizontal at an angle smaller than $(\phi /2+45^\circ )=59^\circ$. Note that, when an associated plastic flow rule is assumed (e.g. $\psi =\phi =28^\circ$), the angle of the initial failure plane estimated from the simulation is roughly $59^\circ$. This can be seen in Fig. 2a where the dashed line represents the predicted failure plane with associated flow. During the collapse process, the material near the fixed wall remains static while a triangular block of material moves down towards the moving wall. As the wall displaces, the column gradually spreads so that the static region keeps increasing while the moving wedge shrinks steadily. When the column comes to rest, an almost flat sloping surface is obtained, as shown in Fig. 2d, with its angle being around $26^\circ$ (which is smaller than the angle of repose of the sand, $28^\circ$, reported in [4, 20]). This is in contrast to the final configuration resulting from dynamic collapse [16, 18] where a curved sloping surface is formed and the slope angle at the toe of the deposit is very low. Such a difference is attributable to the effect of the inertial forces.

For a column of a moderate initial aspect ratio (e.g. $A=3.0$ as shown in Fig. 3), the whole free surface of the column begins to move once the wall retreats. Rather than breaking the free surface of the granular column as in Fig. 2a, the interface between the static and moving regions shown in Fig. 3a propagates from the bottom right to the left side of the column. The interface obtained here is very similar to the one observed in the dynamic collapse; nevertheless, in the sequential quasi-static collapse the part of the free surface adjacent to the fixed wall deforms much faster than the part close to the moving wall, which has also been observed in the experimental tests [4]. As a result, a downward slope from the fixed wall is formed in quasi-static collapse (see Fig. 3b), which differs from the slope which tilts downwards the moving wall in dynamic collapse [2, 3, 23, 26]. It was reported in [4] that the collapse pattern for granular columns with large aspect ratios will evolve to be the same as that observed for columns with small aspect ratios as the collapse proceeds (e.g. Fig. 2b) at the moment the aspect ratio of the column is close to one. Such a transition in collapse pattern is also reproduced by the PFEM simulation (see Fig. 3b–d), and the mechanism behind it can be seen from the simulation results. As illustrated in Fig. 3b, the reason for this transition lies in the fact that the length of the static region approximately equals its height, and the left part of the column’s top free surface is very close to the failure plane when the aspect ratio is close to one. Further displacement of the wall leads to the situation that the left part of the free surface reaches the failure plane, and then the shape of the dynamic region changes to be triangular which results in the transition of the collapse pattern. The angle of the final slope surface is around $26^\circ$, which again is close to, but smaller than, the material friction angle. The finite element mesh shown in Fig. 3 highlights the issues related to large changes of geometry, for example mesh distortion and free-surface evolution, which are handled without difficulty by the PFEM.

Figure 4 shows the collapse of a column with a high initial aspect ratio $A=5.5$. Surprisingly, the collapse pattern in this quasi-static case is quite similar to that in the dynamic case at the very beginning of the collapse process [2, 3]. The free surface of the column remains flat and the upper material drops without any deformation as the wall retreats (see Fig. 4a, b), and a triangular region, within which the granular material is undisturbed, exists at the bottom of the column. Such a static region increases gradually as the collapse proceeds, and when the free surface tends to be close to the failure plane, the free surface near the fixed wall declines faster than it does close to the moving wall (see Fig. 4c). This leads to the collapse pattern being transferred to that for columns with a moderate initial aspect ratio. Similar features of the final deposit (see Fig. 4d), as described in the above, are then exhibited.

Fig. 5

Comparison of internal structure of the deposit: a results from [35], b DEM solution from [35], c PFEM solution

The above collapse patterns obtained from our simulation coincide with those observed in experimental tests [4, 35]. However, our results show that the angle of the final profile is somewhat smaller than the friction angle of the material, implying that it may not be equal to the maximum angle of repose of the material (even though the collapse is quasi-static). Further numerical studies show that, in addition to the aspect ratio of the granular column, the basal roughness is also a key factor in quasi-static granular collapse. Other collapse patterns can be found by adjusting the basal roughness, and will be discussed later in this paper. To illustrate the internal flow, the column with aspect ratio $A=5.5$ is also painted accordinly to differentiate six alternating layers. Figure 5 shows the internal structure of the deposit obtained from the PFEM simulation where the results from the two-dimensional DEM simulation and the experimental test are also depicted. Altough the strata boundaries are recovered qualitatively in both the PFEM and DEM simulations, there are some appreciable differences. The first one is that the strata boundaries in the experimental test (Fig. 5a) are more sharply defined than these in the DEM and PFEM simulations (Fig. 5b, c). In addition, neither the PFEM nor the DEM simulation reproduced the kink of the second black layer which were observed in the experimental test (see Fig. 5a). However, it was reported that the kink can be reproduced when the three-dimensional DEM modelling was conducted [35].

4.2 Evolution of column height and length and effect of the wall speed

In the above section, the computed collapse patterns for the granular columns in quasi-static cases are qualitatively comparable to those observed in the experiment. In this section, a quantitative study on the collapse process is carried out. To this end, the collapse of a granular column with a high initial aspect ratio $A=5.5$ is revisited with a focus on the evolution of the height and the length of the granular bed.

Fig. 6

Evolution of the height of the granular columns at the fixed wall (a) and the moving wall (b) against the bed length

Figure 6 illustrates plots of the height of both sides of the granular bed against its length from the PFEM simulation. The experimental and DEM simulation data documented in [35] are provided as well for comparison. As shown, the results obtained from the PFEM simulations with different moving speeds of the wall at $V=$2 mm/s, 6 mm/s, and 10 mm/s agree well with each other which echoes the finding in [4, 35] that the velocity of the moving wall has no significant influence on the results as long as the collapse can be approximately regarded as quasi-static. Figure 6 also shows that the PFEM simulation results correspond well with the results from two-dimensional DEM simulations documented in [35]. For the bed height at the fixed wall (Fig. 6a), the simulation results from both the DEM and PFEM modelling are always lower than the experimental results. Regarding the height at the moving wall (Fig. 6b), the results from the PFEM simulation are lower than the experimental results before the bed length reaches 4 cm, after which the situation is reversed.

From Fig. 6a we can also see that the deformation process of the bed height at the fixed wall can be divided approximately into two stages. In the first stage (before the bed length reaches 4 cm), the bed height declines sharply, whereas in the second stage the rate of the decrease slows down significantly. This is because in the first stage, the bed’s top surface is far away from the failure plane and collapse is of the type shown in Fig. 4a, b. When the bed length is around 4 cm, the surface at the fixed wall is very close to the failure plane and thus no significant dropping occurs afterwards. The free surface of the granular column adjacent to the moving wall, on the other hand, is always further away from the failure plane, and thus the bed height near the moving wall decreases smoothly as shown in Fig. 6b. Notably, the 4-cm threshold for the change of the bed height near the fixed wall is just for the column with $A=5.5$. Generally speaking, for columns with intermediate or high aspect ratios, the threshold is the transition between the collapse patterns shown in Fig. 4b, c, respectively.

The overall agreement between the PFEM solution and experimental data is generally satisfactory. Regarding the deviation of the simulation results from the experimental results, this may stem partially from the fact that the problem was modelled under plane-strain conditions, whereas the actual deformation is three-dimensional (due to the effect of the front and back walls). Previous studies on the quasi-static collapse of granular columns show that numerical predictions are more accurate when three-dimensional DEM simulations are conducted [35]. Similar conclusions were also drawn in [41] where the dynamic collapse of granular columns was investigated. Moreover, the studies in [35] also show that the accuracy of the simulations can be improved when non-circular particles are utilised in the DEM modelling, which corresponds to increasing the macro friction angle. Further simulation results regarding the effect of the macro friction angle on the mode of collapse will be given in Sect. 4.4.

4.3 Deposition profile

M$\acute{e}$riaux [4] conducted a series of experiments to investigate the relations between the initial aspect ratio and the normalised height and length of the final profile. It was found [4] that the relation can be expressed as a power law which is similar to that for dynamic collapse [2, 3]. The power laws obtained by M$\acute{e}$riaux [4] can be summarised as follows:

$$\begin{aligned}&\frac{H_i}{H_f} = \left\{ \begin{array}{lcl} 1, &{}~A \le 1 \\ a_sA^\alpha , &{}A > 1 \\ \end{array}\right. \end{aligned}$$

(8)

$$\begin{aligned}&\frac{L_f-L_i}{L_i} =\left\{ \begin{array}{ll} c_sA, &{} ~A \le 2 \\ b_sA^\beta , &{} ~A >2 \end{array}\right. \end{aligned}$$

(9)

where $H_f$ and $L_f$ are the height and the length of the final deposit, and $a_s$, $b_s$, $c_s$, $\alpha$, and $\beta$ are material dependent coefficients [4].

Fig. 7

Normalised final height (a) and length (b) of final profiles as functions of the aspect ratio

The PFEM simulation results, as well as the experimental data for sands, are plotted in Fig. 7. As can be seen, for $A\le 1$, the numerical predictions for the normalised height obey Eq. (9) exactly. For $A>1$, the estimated $a_s$ and $\alpha$ for the best-fit curve to the simulation results are 1.0 and 0.57, respectively, which are within the ranges proposed by M$\acute{e}$riaux [4] (who found that $a_s$ is close to 0.9 and $\alpha =0.55\pm 0.05$ for sands). Regarding the normalised final length, the estimated $c_s$, $b_s$, and $\beta$ for the best-fit curves to PFEM simulation results are 1.15, 1.1, and 0.8 which are close to the values given by M$\acute{e}$riaux [4] for sands as well.

4.4 Effect of friction angle

The results regarding the final deposition profile are expected to improve by increasing the friction angle of the granular matter. Figure 8 shows the results of the simulation with the friction angles $\phi =25^\circ$, $30^\circ$, and $35^\circ$, respectively. It can be seen that, for a column with a small aspect ratio (i.e. $A\le 1.0$), the normalised final height and length of the deposit are insensitive to the macro friction angle. In cases where the aspect ratio $A>1.0$, however, the macro friction angle does affect the shape of the final deposit. A larger friction angle results in a smaller normalised final height (which means a larger final height) and a smaller normalised final length (which means a shorter final length). As indicated in Fig. 8, the simulation results with $\phi =35^\circ$ match the experimental data very well.

Fig. 8

Effect of the friction angle on normalised final height (a) and length (b) of depositions

Fig. 9

Effect of the friction angle $\phi$ on the evolution of bed heights at the fixed wall (a) and the moving wall (b) with $\rho =1.5$ g/cm$^3$, $\psi =0^\circ$, $\phi _w=0.5\phi$

It is remarkable that, although the increase of friction angle improves the match of the final profiles, it does not eleminate the difference in the bed height evolution process at the first collapse stage for a column with a high aspect ratio (for example $A=5.5$) whose quasi-static spreading involves a transition of the collapse pattern. This can be seen from Fig. 9, where the bed height evolution process is insensitive to the friction angle when the bed length is less than 4 cm (implying the first collapse stage). Such an insensitivity is due to the fact that, for a bed length smaller than 4 cm, the column undergoes the collapse pattern shown in Fig. 4b where the top surface of the column remains flat. When the bed length is larger than 4 cm (second collapse stage), an increase of the friction angle results in changes of bed height evolution.

Fig. 10

Evolution of the height of the granular columns at the fixed wall and the moving wall against the bed length. a Effect of surface roughness $\mu =\tan \phi _w$ with $\rho =1.5$ g/cm$^3$, $\phi =30^\circ$, $\psi =0^\circ$ and b effect of density $\rho$ with $\phi =30^\circ$, $\psi =0^\circ$, $\phi _w=0.5\phi$

4.5 Effect of the roughness of side walls and the granular density

Figure 10a illustrates the effect of the surface roughness of the walls on the collapse. It appears that the effect of the walls roughness is rather trivial, which is in line with the finding in [35]. In addition, it is unsurprising that the evolution process for the bed heights at both the fixed and moving walls is the same regardless of the macro density of the granular matter (see Fig. 10b). This indicates that quasi-static collapse is independent of the macro density of the material. Such independence has been observed also in dynamic granular flow problems [28, 29]. It is worth noting here that the investigation of the sensitivity to the macro density was performed while keeping the rest of the other macro mechanical properties constant. For an assembly of granular matter, a change in density is always associated with a change of the void ratio, and thus of the macroscopic friction angle.

4.6 Effect of basal roughness

Despite the numerous investigations of the influence of the basal surface on dynamic granular collapse [14, 29], little attention has been paid to its effect on quasi-static column collapse. The numerical results that have been presented in this paper, so far, are all based on the assumption that the basal surface is rough (e.g. $\mu =\tan \phi$). In the following, the basal roughness will be decreased to investigate its influence on quasi-static column collapse.

Fig. 11

Collapse of a granular column with aspect ratio on a basal surface with friction coefficient $\mu =\tan (\frac{1}{4}\phi )$ at the normalised time a $t/\text {T}=0.01$, b $t/\text {T}=0.3$, c $t/\text {T}=0.4$, d $t/\text {T}=0.67$, and e $t/\text {T}=1.0$. Colours are proportional to the norm of the velocity, $\Vert v\Vert$ (mm/s) (colour figure online)

Fig. 12

Collapse of a granular column with aspect ratio on a basal surface with friction coefficient $\mu =\tan (\frac{1}{8}\phi )$ at the normalised time a $t/\text {T}=0.01$, b $t/\text {T}=0.1$, c $t/\text {T}=0.3$, d $t/\text {T}=0.4$, e $t/\text {T}=0.65$, and f $t/\text {T}=1.0$. Colours are proportional to the norm of the velocity, $\Vert v\Vert$ (mm/s) (colour figure online)

Fig. 13

Collapse of a granular column with an initial aspect ratio $A=0.5$ on a perfectly smooth basal surface with retreatment displacement at a 1.2 mm, b 6 mm, c 17 mm, d 44 mm, and e 62 mm. Colours are proportional to the norm of the velocity, $\Vert v\Vert$ (mm/s) (colour figure online)

Fig. 14

Collapse of a granular column with aspect ratio $A=5.5$ on a basal surface with friction coefficient $\mu =\tan (\frac{1}{8}\phi )$ at the normalised time a $t/\text {T}=0.01$, b $t/\text {T}=0.03$, c $t/\text {T}=0.3$, d $t/\text {T}=0.4$, e $t/\text {T}=0.5$, f $t/\text {T}=0.7$, and g $t/\text {T}=1.0$. Colours are proportional to the norm of the velocity, $\Vert v\Vert$ (mm/s) (colour figure online)

We first focus on the granular column with a low aspect ratio $A=0.5$. Figure 11 shows the evolution of the collapse with the basal friction coefficient $\mu =\tan (\frac{1}{4}\phi )$. It can be seen that the collapse pattern at the beginning is similar to that shown in Fig. 2a where $\mu =\tan \phi$ was assumed. However, a new collapse pattern emerges when the collapse proceeds. In contrast to the failure plane propagating from the bottom-right of the column to the top surface as shown in Fig. 2a, b, the new pattern consists of a failure plane breaking through the bottom of the column. Due to this new collapse pattern, a wavy sloping surface, rather than a flat sloping surface, forms when the column comes to rest and the profile angle is smaller than that obtained previously. A further decrease of the friction coefficient, for example $\mu =\tan (\frac{1}{8}\phi )$, leads to the appearance of other new failure patterns (see Fig. 12). As illustrated in Fig. 12c the new failure mode is ’V-shaped’, which is similar to the one in the problem of an accretionary wedge [48, 49]. Further movement of the wall leads to the emergence of more V-shape failure planes (see Fig. 12c, d). The final profile of the column in this case possesses a wavy sloping surface as well and a further decrease in the profile angle (see Fig. 12f). When the basal surface is perfectly smooth (e.g. $\mu =0$), the evolution of the collapse is totally different in that the heights at both lateral sides of the granular bed are always approximately equal with the presence of a wavy top surface in between (see Fig. 13). As can be seen, V-shaped failure planes are again involved when the basal surface is smooth.

Similar phenomena have been observed for columns with high aspect ratios and low basal roughness in our simulations. Thus, here we only present the collapse of a column with $A=5.5$ and $\mu =\tan (\frac{1}{8}\phi )$ as an illustration (see Fig. 14).

5 Conclusions

The quasi-static collapse of two-dimensional granular columns is studied using a novel continuum approach, the Particle Finite Element Method (PFEM).

Three typical collapse patterns for granular columns with small, intermediate and large initial aspect ratios are predicted by the PFEM, with the evolution of the static region in the granular matter being discussed. The transition of the collapse patterns when the aspect ratio is close to one is explained, based on the physical mechanism behind the collapse phenomenon. The results from the PFEM simulations for the evolution of the granular bed heights at both the fixed wall and moving agree well with those from the DEM simulations, and are also comparable to those observed in experiments. In addition, satisfactory agreement is achieved between the simulated and experimental normalised heights and lengths of the final profile, even though the simulations assume plane-strain conditions.

Parametric studies show that the collapse of columns with an intermediate to large aspect ratio ($A\ge 1$) is influenced considerably by the macro friction angle, but this is less marked for columns with small aspect ratios ($A<1$). For a column with a large aspect ratio, the macro friction angle only affects the second stage of failure due to the specific collapse patterns involved. The macro density of the granular matter has no influence on the collapse mechanism and the influence of the roughness of the side walls is very limited. In contrast, the effect of the roughness of the basal surface is significant. Indeed, the numerical studies show that the change of basal roughness not only affects the collapse process quantitatively, but may lead to new failure patterns which have yet to be observed in experimental tests for the quasi-static collapse of granular columns.

It is worthnoting that the three-dimensional modelling may further improve the agreement rate, in particular in terms of the strata boundaries. Regarding the constitutive model, the simple Mohr-Coulomb model is utilised here and both the dilation angle and the friction angle of the material are assumed to be constant. This model is valid for describing the behaviour of loose granular matter; however it fails when dense granular matter undergoing large deformation is considered. This is because plastic deformation leads to the change of the porosity of granular matter that has a considerable influence on the friction angle and dilation angle of the granular matter. Further development of the PFEM for using more realistic model is currently underway.

Appendix

1.1 Time discretisation

The momentum conservation equations (1) can be discretised using $\theta$-method [50] as:

$$\begin{aligned}&{\varvec{\nabla }}^\textsf {{\tiny T}}[ \theta _1{\varvec{\sigma }}_{n+1} + (1-\theta _1){\varvec{\sigma }}_n] + {\varvec{b}} = \rho \displaystyle \frac{{\varvec{v}}_{n+1}-{\varvec{v}}_n}{\varDelta t}, \end{aligned}$$

(10)

$$\begin{aligned}&\theta _2{\varvec{v}}_{n+1} + (1-\theta _2){{\varvec{v}}_n} = \displaystyle \frac{{\varvec{u}}_{n+1}-{\varvec{u}}_n}{\varDelta t}, \end{aligned}$$

(11)

where ${\varvec{v}}$ are velocities, subscripts n and $n+1$ refer to the known and new, unknown states, and $\varDelta t=t_{n+1}-t_n$ is the time step. Rearranging the above equations leads to

$$\begin{aligned}&{\varvec{\nabla }}^\textsf {{\tiny T}}{\varvec{\sigma }}_{n+1} + \tilde{\varvec{b}} = \tilde{\rho }\frac{\varDelta {\varvec{u}}}{\varDelta t^2}, \end{aligned}$$

(12)

$$\begin{aligned}&{\varvec{v}}_{n+1} = \displaystyle \frac{1}{\theta _2}\left[ \frac{\varDelta {\varvec{u}}}{\varDelta t} - (1-\theta _2){\varvec{v}}_n\right] , \end{aligned}$$

(13)

where $\varDelta {\varvec{u}} = {\varvec{u}}_{n+1}-{\varvec{u}}_n$ and

$$\begin{aligned} \tilde{\rho }= & {} \displaystyle \frac{\rho }{\theta _1\theta _2}, \end{aligned}$$

(14)

$$\begin{aligned} \tilde{\varvec{b}}= & {} \displaystyle \frac{1}{\theta _1}{\varvec{b}} + \tilde{\rho }\displaystyle \frac{{\varvec{v}}_n}{\varDelta t} + \displaystyle \frac{1-\theta _1}{\theta _1}{\varvec{\nabla }}^\textsf {{\tiny T}}\varvec{\sigma }_n, \end{aligned}$$

(15)

The natural boundary conditions (6) are approximated in an analogous manner leading to

$$\begin{aligned} \varvec{N}^\textsf {{\tiny T}}{\varvec{\sigma }}_{n+1} = \tilde{\varvec{t}},\,\text {on}\,S, \end{aligned}$$

(16)

where

$$\begin{aligned} \tilde{\varvec{t}} = \frac{1}{\theta _1}{\varvec{t}} - \frac{1-\theta _1}{\theta _1}{\varvec{N}}^\textsf {{\tiny T}} {\varvec{\sigma }}_n. \end{aligned}$$

(17)

Following [26], the above problem can be stated in terms of a min-max problem:

$$\begin{aligned} \begin{array}{lcl} \underset{\varDelta \varvec{u}}{\text {min}}~~\underset{(\varvec{\sigma },\varvec{r})_{n+1}}{\text {max~~}} &{}~&{} \langle \varvec{\sigma }_{n+1},\varvec{\nabla }(\varDelta \varvec{u})\rangle _V - \langle \tilde{\varvec{b}},\varDelta {\varvec{u}} \rangle _V - \langle \tilde{\varvec{t}},\varDelta {\varvec{u}}\rangle _S \\ &{}~&{} -\frac{1}{2}\varDelta t^2\langle {\varvec{r}}_{n+1},{\tilde{\rho }}{}^{-1}{\varvec{r}}_{n+1}\rangle _V + \langle {\varvec{r}}_{n+1},\varDelta {\varvec{u}}\rangle _V \\ \text {subject to} &{}~&{}F({\varvec{\sigma }}_{n+1}) \le 0 \end{array} \end{aligned}$$

(18)

on the basis of the Hellinger-Reissner variational principle. In above, ${\varvec{r}}_{n+1}$ are a set of variables interpreted as dynamic forces [26], and the notation

$$\begin{aligned} \langle {\varvec{x}},{\varvec{y}}\rangle _A = \int _A{\varvec{x}}^\textsf {{\tiny T}}\varvec{y}\,\text {d} A \end{aligned}$$

(19)

is utilised. The equivalence between the optimisation problem (18) and the governing equations at hand is established by demonstrating that the Euler-Lagrange equations associated with (18) indeed reproduce the governing equations [26].

1.2 Spatial discretisation

Using the standard finite element notation, the following approximations

$$\begin{aligned}&{\varvec{\sigma }}(\varvec{x}) \approx {\varvec{N}}_\sigma \hat{\varvec{\sigma }}, \end{aligned}$$

(20)

$$\begin{aligned}&{\varvec{r}}({\varvec{x}}) \approx \varvec{N}_r\hat{\varvec{r}}, \end{aligned}$$

(21)

$$\begin{aligned}&{\varvec{u}}({\varvec{x}}) \approx \varvec{N}_u\hat{\varvec{u}}, \end{aligned}$$

(22)

$$\begin{aligned}&{\varvec{\nabla }} {\varvec{u}} \approx \varvec{ B}_u\hat{\varvec{u}}, \end{aligned}$$

(23)

are introduced for the state variables, where $\hat{\varvec{\sigma }}$, $\hat{\varvec{r}}$ and $\hat{\varvec{u}}$ are the nodal variables, $\varvec{N}$ matrices contain the shape functions, and $\varvec{B}_u = \varvec{\nabla } \varvec{N}_u$. Substituting the above approximations into the variational principle (18) results in the following discrete principle:

$$\begin{aligned} \begin{array}{lcl} \underset{\varDelta \hat{\varvec{u}}}{\text {min}}~~\underset{(\hat{\varvec{\sigma }},\hat{\varvec{r}})_{n+1}}{\text {max~~}} &{}~&{} \hat{\varvec{\sigma }}_{n+1}^\textsf {{\tiny T}}\varvec{B}\varDelta \hat{\varvec{u}} - {\varvec{f}}^\textsf {{\tiny T}}\varDelta \hat{\varvec{u}}\\ &{}~&{}-\frac{1}{2}\varDelta t^2\hat{\varvec{r}}_{n+1}^\textsf {{\tiny T}}\varvec{D}\hat{\varvec{r}}_{n+1}+ \hat{\varvec{r}}_{n+1}^\textsf {{\tiny T}}\varvec{A}\varDelta \hat{\varvec{u}} \\ \text {subject to} &{}~&{} F(\hat{\varvec{\sigma }}_{n+1}^j) \le 0,~~j=1,\ldots ,n_\sigma \end{array} \end{aligned}$$

(24)

where $n_\sigma$ is the number of Gauss integration points, and

$$\begin{aligned}&{\varvec{B}} = \int _V \varvec{N}_\sigma ^\textsf {{\tiny T}}{\varvec{B}_u}\,\text {d} V, \end{aligned}$$

(25)

$$\begin{aligned}&{\varvec{f}} = \int _V \varvec{N}_u^\textsf {{\tiny T}}\tilde{\varvec{b}}\,\text {d} V + \int _S \varvec{N}_u^\textsf {{\tiny T}}\tilde{\varvec{t}}\,\text {d} S, \end{aligned}$$

(26)

$$\begin{aligned}&{\varvec{D}} = \int _V \varvec{N}_r^\textsf {{\tiny T}}\tilde{\rho }{}^{-1}\varvec{N}_\sigma \,\text {d} V, \end{aligned}$$

(27)

$$\begin{aligned}&{\varvec{A}} = \int _V \varvec{N}_u^\textsf {{\tiny T}} {\varvec{N}_r}\,\text {d} V. \end{aligned}$$

(28)

Then, solving the minimisation part of (24) gives a maximisation problem as:

$$\begin{aligned} \begin{array}{lcl} \underset{(\hat{\varvec{\sigma }},\hat{\varvec{r}})_{n+1}}{\text {maximise}} &{}~&{} -\frac{1}{2}\varDelta t^2\hat{\varvec{r}}_{n+1}^\textsf {{\tiny T}}\varvec{D}\hat{\varvec{r}}_{n+1} \\ \text {subject to} &{}~&{}\varvec{B}^\textsf {{\tiny T}}\hat{\varvec{\sigma }}_{n+1} + \varvec{A}^\textsf {{\tiny T}}\hat{\varvec{r}}_{n+1} = \varvec{f}\\ &{}~&{} F(\hat{\varvec{\sigma }}_{n+1}^j) \le 0,~~j=1,\ldots ,n_\sigma \end{array} \end{aligned}$$

(29)

At this stage, the contact constrains (4) are imposed on all potential contact nodes (i.e. mesh nodes located on the boundaries), which leads to a final problem of the type:

$$\begin{aligned} \begin{array}{lcl} \underset{(\hat{\varvec{\sigma }},\hat{\varvec{r}},p_j)_{n+1}}{\text {maximize}} &{}~&{} -\frac{1}{2}\varDelta t^2\hat{\varvec{r}}_{n+1}^\textsf {{\tiny T}}\varvec{D}\hat{\varvec{r}}_{n+1}-\sum _{j=1}^{n_c}{ g_{0j} p_j} \\ \text {subject to} &{}~&{}\varvec{B}^\textsf {{\tiny T}}\hat{\varvec{\sigma }}_{n+1} + \varvec{A}^\textsf {{\tiny T}}\hat{\varvec{r}}_{n+1} + {\varvec{E}}^\textsf {{\tiny T}}\varvec{\rho } = \varvec{f}\\ &{}~&{} F(\hat{\varvec{\sigma }}_{n+1}^i) \le 0,~~i=1,\ldots ,n_\sigma \\ &{}~~&{} p_j = -\varvec{n}^\textsf {{\tiny T}}\varvec{\rho }_j,~~~j=1,\ldots , n_c \\ &{}~~&{} q_j = -\hat{\varvec{n}}^\textsf {{\tiny T}}\varvec{\rho }_j \\ &{}~&{} |q_j| - \mu p_j \le 0 \end{array} \end{aligned}$$

(30)

where $\varvec{\rho } = (\rho _1,\rho _2)^\textsf {{\tiny T}}$ are the nodal forces, $\varvec{n}=(n_1,n_2)^\textsf {{\tiny T}}$ and $\hat{\varvec{n}} = (-n_2,n_1)^\textsf {{\tiny T}}$ are the normal and the tangential of the rigid boundary, $\varvec{E}$ is an index matrix of zeros and ones, and $n_c$ is the number of potential contacts.

The above problem can be transformed into a standard form of the second-order cone program (SOCP) and then solved using the high performance optimization solver MOSEK [38]. The transformation of (30) into SOCP standard form is straightforward and has been documented in [40]. In the course of solving the problem, the kinematic variables (displacement increments and plastic multipliers) are recovered as the dual variables, or Lagrange multipliers, associated with the discrete equilibrium constraints.