1 Introduction

Recently, aiming to improve safety, efficiency, mobility and so on, many researchers have proposed lane following control schemes (for example [1,2,3]). In the case when the vertical force between wheels and a road surface becomes too small, handling stability becomes worse and good lane following performance cannot be expected. On the other hand, we have to also consider a method to improve ride comfort of autonomous vehicles. To improve both of handling stability and ride comfort of vehicles, based on a quarter vehicle model, various active suspension control schemes [4,5,6,7,8,9,10,11,12,13,14] have been provided. Control schemes [15,16,17] have been also developed based on a half vehicle model. Based on a full vehicle model, the authors of the reference papers [18,19,20] have provided controllers.

Fig. 1
figure 1

Quarter vehicle model

Full size image

It is assumed that vehicles run on a highway. If design parameters are set in the controlled vehicles proposed in [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] so as to further improve handling stability for a road surface such as large bumps, ride comfort may deteriorate even for a road surface such as that with not so large bumps. Very recently, to address the problem, a nonlinear active suspension control scheme [21] has been proposed. As shown in numerical simulation results of the reference paper [21], even if the relative tire load exceeds a dangerous value in a passive vehicle, both ride comfort and steering stability can be significantly improved in the controlled vehicle. However, in the nonlinear control scheme, the authors do not consider varying vehicle mass. In the practical case, vehicle mass varies greatly. Using the proposed control scheme [21], we have to redesign a controller every time vehicle mass varies. Until now, many robust active suspension controllers have been proposed (For example [22,23,24]). As far as authors know, there is no robust control scheme in which both ride comfort and steering stability can be significantly improved.

In the paper, we propose a new robust active suspension control scheme based on a control scheme [21]. In the robust control scheme, even if vehicle mass varies, redesign of a controller is not required. To achieve this, at first, we propose a design method for an ideal vehicle model. In the ideal vehicle model, even if vehicle mass varies, good ride comfort and good handling stability can be achieved by setting only one design parameter. After that, to make the real vehicle track the designed ideal vehicle model, we will develop a robust tracking controller.

2 Dynamic equation

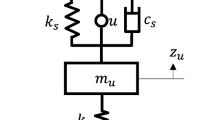
Figure 1 shows a quarter vehicle model. Table 1 shows the explanation of the parameters used in the figure and equations below. The new states are defined by \(x_b(t)=z_s(t)-z_r(t)\), \(x_t(t)=z_u(t)-z_r (t)\), \(\xi (t)=\ddot{z}_s(t)\). Then, we have [21]

$$\begin{aligned}{} & {} \left. \begin{aligned} \dot{{\varvec{x}}}(t)&=A{\varvec{x}}(t)+\frac{1}{m_s}{\varvec{b}}\mu (t)-{\varvec{d}}\ddot{z}_r(t)\\ \mu (t)&={\dot{u}}(t)+\alpha u(t),~~{\varvec{x}}(t)=[{\varvec{x}}_{b}(t)^T~{\varvec{x}}_{t}(t)^T]^T\\ {\varvec{x}}_{b}(t)&=[x_b(t)~{\dot{x}}_b(t)~\xi (t)]^T,~~{\varvec{x}}_{t}(t)=[x_t(t)~{\dot{x}}_t(t)]^T \end{aligned}\right\} , \end{aligned}$$
(1)
$$\begin{aligned}{} & {} \left. \begin{aligned} A&=\left[ \begin{array}{cc}A_b&{}A_{bt}\\ A_{tb}&{}A_t\end{array}\right] ,~A_b=\Omega _b+{\varvec{b}}_b{\varvec{a}}_{1b}^T,~A_{bt}={\varvec{b}}_b{\varvec{a}}_{1t}^T\\ \Omega _b&={\varvec{c}}_b{\varvec{d}}_b^T+{\varvec{d}}_b{\varvec{b}}_b^T,~{\varvec{c}}_b=[1~0~0]^T,~{\varvec{d}}_b=[0~1~0]^T\\ {\varvec{b}}_b&=[0~0~1]^T,~{\varvec{b}}=[{\varvec{b}}_b^T~0~0]^T,~{\varvec{d}}=[{\varvec{d}}_b^T~{\varvec{b}}_t^T]^T\\ {\varvec{a}}_{1b}&=-[\alpha k_{ss}~~k_{ss}+\alpha c_{ss}~~c_{ss}(1+m_{su})+\alpha ]^T\\ {\varvec{a}}_{1t}&=[\alpha k_{ss}-c_{ss}k_{tu}~~k_{ss}+\alpha c_{ss}]^T,~~{\varvec{b}}_t=[0~1]^T\\ c_{ss}&=\frac{c_s}{m_s},~k_{ss}=\frac{k_s}{m_s},~m_{su}=\frac{m_s}{m_u},~k_{tu}=\frac{k_t}{m_u}\\ A_{tb}&=-m_{su}{\varvec{b}}_t{\varvec{b}}_b^T,~A_t={\varvec{c}}_t{\varvec{b}}_t^T-k_{tu}{\varvec{b}}_t{\varvec{c}}_t^T,~{\varvec{c}}_t=[1~0]^T \end{aligned}\right\} , \end{aligned}$$
(2)

where \(\alpha\) is a positive design parameter. The signal \(\mu (t)\) is the control input to be designed below, and the real control input u(t) is generated by the solution of the second equation of (1).

Table 1 Meaning of symbols
Full size table

In this paper, the control objective is to develop a robust active suspension controller against varying sprung mass that satisfies the following conditions [21].

\({\varvec{\textrm{C1}}}\):

Passenger resonance frequency exists in the neighborhood of 1–2 [Hz]. To improve the ride comfort of passengers, the magnitude of the vertical acceleration of the vehicle body \(m_s\) must be reduced to as small as possible with respect to the road surface displacement frequency neighborhood of 1–2 [Hz].

\({\varvec{\textrm{C2}}}\):

To achieve good handing stability, the vehicle must be controlled so that the relative tire load \(R_t(t)=k_tx_t(t)/(m_s+m_u )g\) can satisfy \(|R_t(t)|\le r_{tu}<1,\) where \(r_{tu}\) is a design parameter.

To develop a robust active suspension controller that can achieve the above conditions, the following assumptions are made for the vehicle (1).

\({\varvec{A1}}\):

The elements of the state \({\varvec{x}}(t)\) can be measured.

\({\varvec{A2}}\):

The derivatives of the road displacement \(z_r(t)^{(i)},~~i=0\cdots 2\) are unknown but bounded.

\({\varvec{A3}}\):

Parameters \(m_u\), \(k_s\) and \(c_s\) do not vary and are known.

\({\varvec{A4}}\):

The nominal value \({\overline{k}}_t\) is known, but \(k_t\) is unknown, and there exist known constants \(m_{sU}\) and \(m_{sL}\) such that \(m_{sU}\ge m_s\ge m_{sL}>0\). Sprung mass \(m_s\) can be measured, but there exist measurement errors.

3 Development of ideal vehicle model

To meet the design objective, we introduce an ideal vehicle model. Since the design scheme of the ideal vehicle model is very complex, we will explain the design scheme briefly. At first, we design two vehicle models \({\varvec{x}}_i(t), i=U, L\) given by

$$\begin{aligned}{} & {} \left. \begin{aligned} {\varvec{x}}_i(t)&={\varvec{x}}_{0i}(t)+{\varvec{d}}{\dot{x}}_b(t),~~{\varvec{x}}_{0i}(0)={\varvec{x}}(0)-{\varvec{d}}{\dot{x}}_b(0)\\ \dot{{\varvec{x}}}_{0i}(t)&=A_i{\varvec{x}}_i(t)+{\varvec{b}}\frac{1}{m_{si}}\mu _{i}(t)-{\varvec{d}}\xi (t),~~i=U, L\\ \mu _i(t)&=\mu _{ci}(t)+\mu _{ti}(t) \end{aligned} \right\} , \end{aligned}$$
(3)
$$\begin{aligned}{} & {} A_i=\left[ \begin{array}{cc}\Omega _b+{\varvec{b}}_b{\varvec{a}}_{1bi}^T&{}{\varvec{b}}_b{\varvec{a}}_{1ti}^T\\ -m_{siu}{\varvec{b}}_t{\varvec{b}}_b^T&{}{\overline{A}}_t\end{array}\right] ,~m_{siu}=\frac{m_{si}}{m_u},~i=U,L, \end{aligned}$$
(4)

where \({\overline{A}}_t\) is a matrix in which \(k_{tu}\) in \(A_t\) is replaced by \({\overline{k}}_{tu}={\overline{k}}_t/m_u\), \({\varvec{a}}_{1bi}\) and \({\varvec{a}}_{1ti}\) are vectors in which the parameters \(k_{tu}\) and \(m_s\) of \(c_s/m_s\), \(k_s/m_s\) and \(m_s/m_u\) in \({\varvec{a}}_{1b}\) and \({\varvec{a}}_{1t}\) are replaced by \({\overline{k}}_{tu}\) and \(m_{si}\). The parameters \({\varvec{a}}_{1b}\) and \({\varvec{a}}_{1t}\) are defend in the fourth and fifth equations of (2). The parameters \(m_{si}, i=U, L\) are defined in the assumption \({\varvec{\textrm{A4}}}\). Using \(\ddot{x}_b(t)=\xi (t)-\ddot{z}_r(t)\) in (3), we have

$$\begin{aligned} \dot{{\varvec{x}}}_i(t)=A_i{\varvec{x}}_i(t)+{\varvec{b}}\frac{1}{m_{si}} \mu _i(t)-{\varvec{d}}\ddot{z}_r(t),~{\varvec{x}}_i(0)={\varvec{x}}(0). \end{aligned}$$
(5)

In the vehicle model \({\varvec{x}}_U(t)\), the situation is considered where the sprung mass \(m_s\) becomes maximum \(m_U\) and in the vehicle model \({\varvec{x}}_L(t)\), the situation is considered where the sprung mass \(m_s\) becomes minimum \(m_L\). The model inputs \(\mu _i(t),~~i=U, L\) are designed by using the same scheme proposed in [21]. After the two vehicle models are designed, to design an ideal vehicle model for varying sprung mass values, the two vehicle models are linearly combined.

The signal \(\mu _{ci}(t),~i=U, L\) are input signals mainly to keep good ride comfort in each vehicle model, and are given by

$$\begin{aligned} \left. \begin{aligned}&\mu _{ci}(t)=-\frac{m_{si}}{r_{ci}}{\varvec{b}}^TP_{ci}{\varvec{x}}_i(t)\\&A_i^TP_{ci}+P_{ci}A_i-\frac{1}{r_{ci}}P_{ci}{\varvec{b}}{\varvec{b}}^TP_{ci}=-Q_{ci} \end{aligned} \right\} , \end{aligned}$$
(6)

where \(r_{ci}>0\) and \(Q_{ci}>0,~i=U, L\) are design parameters and set by using a trial and error method so that the sprung mass acceleration \(|\xi _i(t)|=|[0~ 0~ 1~ 0~ 0]{\varvec{x}}_i(t)|\) can becomes small in each vehicle model and the condition \({\varvec{\textrm{C1}}}\) can be achieved.

Only in case of \(|R_{ti}(t)|\ge r_u\) where \(R_{ti}(t)={\overline{k}}_t{\varvec{c}}_t^T{\varvec{x}}_{ti}(t)\) \(/(m_{si}+m_u)/g\) and \(r_u\) is a design parameter such that \(1>r_{tu}> r_u>0\) (\(r_{tu}\) is design parameter defined in condition \({\varvec{\textrm{C2}}}\).), the input signals \(\mu _{ti}(t),~i=U, L\) work so as to keep the relative tire loads in the range \(|R_{ti}(t)|\le r_{tu}\), and are given by

$$\begin{aligned}{} & {} \left. \begin{aligned}&\mu _{ti}(t)\\&\quad =-m_{si}\beta _i f_\varepsilon (R_{ti}){\varvec{b}}^TP_{ti}{\varvec{\varepsilon }}_i(t)\\&\qquad +m_{si}f_\omega (R_{ti})\big ({\widehat{\omega }}_{\varepsilon 0 i}(t)+\omega _{\varepsilon i}(t)\big )\\&A_{ci}^TP_{ti}+P_{ti}A_{ci}=-Q_{ti},~Q_{ti}>0\\&A_{ci}=A_i-\frac{1}{r_{ci}}{\varvec{b}}{\varvec{b}}^TP_{ci} \end{aligned} \right\} , \end{aligned}$$
(7)
$$\begin{aligned}{} & {} \left. \begin{aligned} {\varvec{\varepsilon }}_i(t)&={\varvec{x}}_i(t)-{\varvec{x}}_{ri}(t),~\omega _{\varepsilon i}(t)=-{\varvec{b}}^TA_{ci}{\varvec{x}}_{ri}(t)\\ {\varvec{x}}_{ri}(t)&=-\big [\frac{m_{si}+m_u}{m_{si}}\eta (t)~\frac{m_{si}+m_u}{m_{si}}{\dot{\eta }}(t)~\frac{m_u}{m_{si}}{\widehat{w}}(t)~0~0\big ]^T\\ {\widehat{\omega }}_{\varepsilon 0 i}(t)&={\mathcal {L}}^{-1}\big [\frac{s}{T_t s+1}{\mathcal {L}}[{\varvec{b}}^T{\varvec{x}}_{ri}(t)]\big ] \end{aligned} \right\} , \end{aligned}$$
(8)
$$\begin{aligned}{} & {} \left. \begin{aligned} {\widehat{w}}(t)&=\ddot{\eta }(t),\\ \eta (t)&={\mathcal {L}}^{-1}\bigg [\frac{1}{s^2+2\zeta _r\omega _r s+\omega _r^2}\frac{1}{T_rs+1}\\&\quad \times \big ({\mathcal {L}}[\xi (t)]-s{\mathcal {L}}[{\dot{x}}_b(t)]\big )\bigg ] \end{aligned} \right\} , \end{aligned}$$
(9)
$$\begin{aligned}{} & {} \left. \begin{aligned} f_\varepsilon (R_{ti})&=\left\{ \begin{array}{ll} 0&{}\quad \text {if }|R_{ti}(t)|<r_{u}\\ |R_{ti}(t)-\textrm{sgn}(R_{ti})r_u|&{}\quad \text {if }|R_{ti}(t)|\ge r_{u} \end{array} \right. \\ f_\omega (R_{ti})&=\left\{ \begin{array}{ll} 0&{}\quad \text {if }|R_{ti}(t)|<r_{u}\\ 1&{}\quad \text {if }|R_{ti}(t)|\ge r_{u} \end{array} \right. \end{aligned}\right\} , \end{aligned}$$
(10)

where \(T_r\), \(\zeta _r\), \(\omega _r\), \(T_t>0\), \(\beta _i>0\) and \(Q_{ti}>0,~i=U, L\) are design parameters. In (9), \({\widehat{w}}(t)\) denotes the estimate of \(w(t)=\ddot{z}_r(t)\) [21]. The design parameters are determined by using a trial and error method so that the state norms \(\Vert {\varvec{\varepsilon }}_i(t)\Vert , i=U, L\) defined in (8) can be reduced. If the state norms \(\Vert {\varvec{\varepsilon }}_i(t)\Vert\) including the estimate \({\widehat{w}}(t)\) of the load disturbance \(w(t)=\ddot{z}_r(t)\) can be reduced, the tire deflections \(|x_{ti}(t)|=|[0~ 0~ 0~ 1~ 0]{\varvec{x}}_i(t)|, i=U, L\) can be reduced and the relative tire loads \(|R_{ti}(t)|\) can be also reduced as shown in the reference paper [21].

To develop an ideal vehicle model \({\varvec{x}}_d(t)\) adaptable for any \(m_s\), we will integrate the two vehicle models as

$$\begin{aligned} \left. \begin{aligned} {\varvec{x}}_d(t)&=[{\varvec{x}}_{bd}(t)^T~{\varvec{x}}_{td}(t)^T]^T=T_U{\varvec{x}}_U(t)+T_L{\varvec{x}}_L(t)\\ T_U&=\beta _m\textrm{diag}\left[ \frac{m_{sU}}{{\widehat{m}}_s}~\frac{m_{sU}}{{\widehat{m}}_s}~\frac{m_{sU}}{{\widehat{m}}_s}~1~1\right] \\ T_L&=(1-\beta _m)\textrm{diag}\left[ \frac{m_{sL}}{{\widehat{m}}_s}~\frac{m_{sL}}{{\widehat{m}}_s}~\frac{m_{sL}}{{\widehat{m}}_s}~1~1\right] \end{aligned} \right\} , \end{aligned}$$
(11)

where \({\widehat{m}}_s\) is the measured value of \(m_s\) and \(\beta _m\) is a parameter determined by

$$\begin{aligned} \beta _mm_{sU}+(1-\beta _m)m_{sL}={\widehat{m}}_s,~1\ge \beta _m\ge 0. \end{aligned}$$
(12)

Lemma 1

The ideal vehicle model is given by

$$\begin{aligned}{} & {} \left. \begin{aligned} \dot{{\varvec{x}}}_d(t)&={\overline{A}}{\varvec{x}}_d(t)+\frac{1}{{\widehat{m}}_s} {\varvec{b}}\mu _d(t)-{\varvec{d}}\ddot{z}_r(t),~{\varvec{x}}_d(0)={\varvec{x}}(0)\\ \mu _d(t)&=\beta _m{\varvec{a}}_{\mu U}^T{\varvec{x}}_U(t)+(1-\beta _m) {\varvec{a}}_{\mu L}^T{\varvec{x}}_L(t)\\&\quad +\beta _m\mu _U(t)+(1-\beta _m)\mu _L(t)\\ {\varvec{a}}_{\mu i}&=\big [m_{si}({\varvec{a}}_{1bi}-\overline{{\varvec{a}}}_{1b} )^T~(m_{si}{\varvec{a}}_{1ti}-{\widehat{m}}_s\overline{{\varvec{a}}}_{1t})^T\big ]^T \end{aligned}\right\} , \end{aligned}$$
(13)
$$\begin{aligned}{} & {} \left. {\overline{A}}=\left[ \begin{array}{cc}{\overline{A}}_b&{}{\varvec{b}}_b\overline{{\varvec{a}}}_{1t}^T\\ -{\overline{m}}_{su}{\varvec{b}}_t{\varvec{b}}_b^T&{}{\overline{A}}_t\end{array}\right] ,~ \begin{array}{l}{\overline{A}}_b=\Omega _b+{\varvec{b}}_b\overline{{\varvec{a}}}_{1b}^T\\ {\overline{m}}_{su}=\frac{{\widehat{m}}_s}{m_u} \end{array} \right\} , \end{aligned}$$
(14)

where \(\overline{{\varvec{a}}}_{1b}\) and \(\overline{{\varvec{a}}}_{1t}\) are vectors in which the parameters \(k_{tu}\) and \(m_s\) of \(c_s/m_s\), \(k_s/m_s\) and \(m_s/m_u\) in \({\varvec{a}}_{1b}\) and \({\varvec{a}}_{1t}\) are replaced by \({\overline{k}}_{tu}\) and \({\widehat{m}}_s\). The parameters \({\varvec{a}}_{1b}\) and \({\varvec{a}}_{1t}\) are defend in the fourth and fifth equations of (2).

Proof

From (5), (11) and (12), we can derive (13) and (14) very easily. \(\square\)

It is expected that good ride comfort can be maintained in the ideal vehicle model for any sprung mass \({\widehat{m}}_s\). This fact will be ascertained by using numerical simulation results. As for \(R_{td}(t)={\overline{k}}_t/({\widehat{m}}_s+m_u)/g\) \(\times {\varvec{c}}_t^T{\varvec{x}}_{td}(t)\), the relation \(|R_{td}(t)|\le r_{ru}\) holds for any sprung mass \({\widehat{m}}_s\). Since model controllers (7)-(10) are designed so that the relations \(|R_{ti}(t)|\le r_{tu},~i=U, L\) can hold, for the relative tire load \(R_{td}(t)\), we have

$$\begin{aligned} |R_{td}(t)|= & {} \bigg |\frac{\beta _m (m_{sU}+m_u)}{{\widehat{m}}_s+m_u}R_{tU}(t)\nonumber \\{} & {} +\frac{(1-\beta _m) (m_{sL}+m_u)}{{\widehat{m}}_s+m_u}R_{tL}(t)\bigg |\le r_{tu}. \end{aligned}$$
(15)

4 Development of controller

To force the real vehicle to track the ideal vehicle model, consider the tracking errors \(\widetilde{{\varvec{x}}}_b(t)={\varvec{x}}_b(t)-{\varvec{x}}_{bd}(t)\) and \(\widetilde{{\varvec{x}}}_t(t)={\varvec{x}}_t(t)-{\varvec{x}}_{td}(t)\). Then, we have

$$\begin{aligned}{} & {} \dot{\widetilde{{\varvec{x}}}}_b(t)\nonumber \\{} & {} \quad ={\overline{A}}_b\widetilde{{\varvec{x}}}_b(t) +\frac{1}{m_s}{\varvec{b}}_b\big (\mu (t)-\mu _d(t)+ {\widehat{m}}_s\overline{{\varvec{a}}}_{1t}^T\widetilde{{\varvec{x}}}_t(t)\big )\nonumber \\{} & {} \qquad +{\varvec{b}}_b\big (\widetilde{{\varvec{e}}}_b^T\widetilde{{\varvec{x}}}(t )+{\widetilde{e}}_{bd}(t)\big ),~~\widetilde{{\varvec{x}}}_b(0)=[0~0~0]^T, \end{aligned}$$
(16)
$$\begin{aligned}{} & {} \dot{\widetilde{{\varvec{x}}}}_t=A_t\widetilde{{\varvec{x}}}_t(t)-m_{su} {\varvec{b}}_t{\varvec{b}}_b^T\widetilde{{\varvec{x}}}_b(t)-{\varvec{b}}_t{\widetilde{e}}_{td} (t),~\widetilde{{\varvec{x}}}_t(0)=[0~0]^T ,\end{aligned}$$
(17)
$$\begin{aligned}{} & {} \left. \begin{aligned} \widetilde{{\varvec{e}}}_b&=\widetilde{{\varvec{a}}}_1+\bigg [0~0~0~\frac{{\widetilde{m}}_s}{m_s}\overline{{\varvec{a}}}_{1t}^T\bigg ]^T,~ {\varvec{a}}_1=[{\varvec{a}}_{1b}^T~{\varvec{a}}_{1t}^T]^T\\ {\widetilde{e}}_{bd}(t)&=-\frac{{\widetilde{m}}_s}{m_s{\widehat{m}}_s}\mu _d(t)+\widetilde{{\varvec{a}}}_1^T{\varvec{x}}_d(t),~ \widetilde{{\varvec{a}}}_1={\varvec{a}}_1-\overline{{\varvec{a}}}_1\\ \overline{{\varvec{a}}}_1&=[\overline{{\varvec{a}}}_{1b}^T~\overline{{\varvec{a}}}_{1t}^T]^T,~{\widetilde{m}}_s=m_s-{\widehat{m}}_s,~~{\widetilde{k}}_{tu}=k_{tu}-{\overline{k}}_{tu}\\ {\widetilde{e}}_{td}&={\widetilde{k}}_{tu}{\varvec{c}}_t^T{\varvec{x}}_{td}(t)+\frac{{\widetilde{m}}_s}{m_u}{\varvec{b}}_b^T{\varvec{x}}_{bd}(t) \end{aligned} \right\} , \end{aligned}$$
(18)

where \(\widetilde{{\varvec{e}}}_b\) is bounded unknown vector, \({\widetilde{e}}_{bd}(t)\) and \({\widetilde{e}}_{td}(t)\) are bonded signals. The vector \(\widetilde{{\varvec{e}}}_b\) and the signals \({\widetilde{e}}_{bd}(t)\), \({\widetilde{e}}_{td}(t)\) becomes zero if \({\widetilde{k}}_{tu}=0\) and \({\widetilde{m}}_s=0\).

To develop a robust active suspension controller, consider the state given by

$$\begin{aligned} \left. \begin{aligned} {\varvec{\varepsilon }}_b(t)&=\widetilde{{\varvec{x}}}_b(t)-{\varvec{{\varvec{x}}}}_c(t), ~~{\varvec{\varepsilon }}_b(0)=[0~0~0]^T\\ {\varvec{x}}_{c}(t)&=\frac{\beta _{tc}}{{\overline{m}}_{su}}\big [\int _0^t {\varvec{c}}_{t}^T\widetilde{{\varvec{x}}}_{t}(\tau )d\tau \\&\quad {\varvec{c}}_{t}^T\widetilde{{\varvec{x}}}_{t}(t)~~{\varvec{b}}_ t^T\widetilde{{\varvec{x}}}_{t}(t)\big ]^T, \end{aligned} \right\} \end{aligned}$$
(19)

where \(\beta _{tc}\ge 1\) is a design parameter. Then, we have

$$\begin{aligned}{} & {} \dot{{\varvec{\varepsilon }}}_b(t)\nonumber \\{} & {} \quad ={\overline{A}}_b{\varvec{\varepsilon }}_b(t) +\frac{1}{m_s}{\varvec{b}}_b\big (\mu (t)-\mu _d(t)\nonumber \\{} & {} \qquad +{\widehat{m}}_s\overline{{\varvec{a}}}_{1b}^T{\varvec{x}}_c(t) +\overline{{\varvec{a}}}_\varepsilon ^T\widetilde{{\varvec{x}}}(t)\big )\nonumber \\{} & {} \qquad +{\varvec{b}}_b\bigg ({\widetilde{e}}_{\varepsilon d}(t) +\widetilde{{\varvec{e}}}_\varepsilon ^T\widetilde{{\varvec{x}}}(t) +\frac{{\widetilde{m}}_s}{m_s}\overline{{\varvec{a}}}_{1b}^T{\varvec{x}}_c(t)\bigg ), \end{aligned}$$
(20)
$$\begin{aligned}{} & {} \dot{\widetilde{{\varvec{x}}}}_t(t)=A_{tc}\widetilde{{\varvec{{\varvec{x}}}}}_t(t) -m_{su}{\varvec{b}}_t{\varvec{b}}_b^T{\varvec{\varepsilon }}_b(t)-{\varvec{b}}_t{\widetilde{e}}_{td}(t), \end{aligned}$$
(21)
$$\begin{aligned}{} & {} \left. \begin{aligned} \overline{{\varvec{a}}}_\varepsilon&={\widehat{m}}_s[0~0~0~\overline{{\varvec{a}}}_{1t}^T]^T +\beta _{tc}[{\widehat{m}}_s{\varvec{b}}_b^T~~m_u{\overline{k}}_{tu}{\varvec{c}}_t^T]^T\\ {\widetilde{e}}_{\varepsilon d}(t)&={\widetilde{e}}_{bd}(t) +\frac{\beta _{tc}}{{\overline{m}}_{su}}{\widetilde{e}}_{td}(t), ~A_{tc}=A_t-\frac{\beta _{tc}m_s}{{\widehat{m}}_s}{\varvec{b}}_t{\varvec{b}}_t^T\\ \widetilde{{\varvec{e}}}_\varepsilon&=\widetilde{{\varvec{e}}}_b\\&\quad +\beta _{tc}\bigg [\frac{{\widetilde{m}}_s(m_s+{\widehat{m}}_s)}{m_s{\widehat{m}}_s}{\varvec{b}}_b^T~\frac{1}{{\overline{m}}_{su}} \bigg ({\widetilde{k}}_{tu}+\frac{{\widetilde{m}}_s{\overline{k}}_{tu}}{m_s} \bigg ){\varvec{c}}_t^T\bigg ]^T \end{aligned} \right\} . \end{aligned}$$
(22)

Although the system matrix \(A_t\) is not a stable matrix, the system matrix \(A_{tc}\) becomes an asymptotically stable matrix due to introduction of the signal \({\varvec{\varepsilon }}_b(t)\) including the signal \({\varvec{x}}_{c}(t)\). If the signal \({\varvec{\varepsilon }}_b(t)\) becomes stable and small, then the state \(\widetilde{{\varvec{x}}}_t(t)\) becomes also stable because the signal \({\widetilde{e}}_{td}(t)\) is bounded.

Based on the tracking error systems (20) and (21), a robust controller is developed as

$$\begin{aligned} \left. \begin{aligned} {\dot{u}}(t)&=-\alpha u(t)+\mu (t)\\ \mu (t)&=\mu _d(t)-{\widehat{m}}_s\overline{{\varvec{a}}}_{1b}^T{\varvec{x}}_c(t) -\overline{{\varvec{a}}}_\varepsilon ^T\widetilde{{\varvec{x}}}(t)\\&\quad -{\widehat{m}}_s\beta _c\big (\beta _c+\Vert \widetilde{{\varvec{x}}}(t) \Vert ^2+\Vert {\varvec{x}}_c(t)\Vert ^2\big ){\varvec{b}}_b^TP{\varvec{\varepsilon }}_b(t)\\ {\overline{A}}_b^TP+P{\overline{A}}_b&=-Q,~~\beta _c\ge 1,~~Q>0 \end{aligned} \right\} , \end{aligned}$$
(23)

where \(\beta _c\) and Q are design parameters. For \(\alpha >0\), since the matrix \({\overline{A}}_b\) becomes a Hurwitz matrix, Lyapunov equation has a positive definite matrix \(P>0\).

For the controlled vehicle system (20), (21) and (23), we have the following theorem.

Theorem 1

In case of \({\widetilde{m}}_s=0\) and \({\widetilde{k}}_t=k_t-{\overline{k}}_t=0\), we obtain \(\Vert \widetilde{{\varvec{x}}}(t)\Vert =0,\) where \({\widetilde{m}}_s\) is defined in the third equation of (18). In case of \({\widetilde{m}}_s\ne 0\) or \({\widetilde{k}}_t\ne 0\), the tracking error \(\widetilde{{\varvec{x}}}(t)\) becomes stable. In addition to the fact, there exists a constant value \(\rho _\varepsilon \ge 0\) independent of the design parameter \(\beta _c\) such that \(\Vert {\varvec{\varepsilon }}_b(t)\Vert ^2\le \rho _\varepsilon /\beta _c\).

Proof

At first, we will show \(\Vert \widetilde{{\varvec{x}}}(t)\Vert =0\) in case of \({\widetilde{m}}_s=0\) and \({\widetilde{k}}_t=0\). Since \(\Vert \widetilde{{\varvec{e}}}_\varepsilon \Vert =0\) and \({\widetilde{e}}_{\varepsilon d}(t)=0\), the derivative of the positive definite function \(V(t)={\varvec{\varepsilon }}_b(t)^TP{\varvec{\varepsilon }}_b(t)\) is given by

$$\begin{aligned} {\dot{V}}(t)= & {} -{\varvec{\varepsilon }}_b(t)^TQ{\varvec{\varepsilon }}_b(t) -2\frac{{\widehat{m}}_s}{m_s}\beta _c\big (\beta _c+\Vert \widetilde{{\varvec{x}}}(t)\Vert ^2\nonumber \\{} & {} +\Vert \widetilde{{\varvec{x}}}_c(t)\Vert ^2\big ){\varvec{\varepsilon }}_b(t)^TP {\varvec{b}}_b{\varvec{b}}_b^TP{\varvec{\varepsilon }}_b(t). \end{aligned}$$
(24)

From (24) and \(\Vert {\varvec{\varepsilon }}_b(0)\Vert =0\), we can obtain \(\Vert {\varvec{\varepsilon }}_b(t)\Vert =0\). In (21), the matrix \(A_{tc}\) includes uncertainties but asymptotically stable. In addition to the fact, since \({\widetilde{e}}_{td}(t)=0\) and \(\Vert \widetilde{{\varvec{x}}}_t(0)\Vert =0\), we can conclude that \(\Vert \widetilde{{\varvec{x}}}(t)\Vert =0\).

Next, in case of \({\widetilde{m}}_s\ne 0\) or \({\widetilde{k}}_t\ne 0\), we will show that \(\widetilde{{\varvec{x}}}(t)\) becomes stable. The derivative of V(t) is given by

$$\begin{aligned} {\dot{V}}(t)= & {} -{\varvec{\varepsilon }}_b(t)^TQ{\varvec{\varepsilon }}_b(t) -2\frac{{\widehat{m}}_s}{m_s}\beta _c\big (\beta _c+ \Vert \widetilde{{\varvec{x}}}(t)\Vert ^2+\Vert \widetilde{{\varvec{x}}}_c(t)\Vert ^2\big )\nonumber \\{} & {} \times {\varvec{\varepsilon }}_b(t)^TP{\varvec{b}}_b{\varvec{b}}_b^TP{\varvec{\varepsilon }}_b(t) +2{\varvec{\varepsilon }}_b(t)^TP{\varvec{b}}_b\nonumber \\{} & {} \times \bigg ({\widetilde{e}}_{\varepsilon d}(t) +\widetilde{{\varvec{e}}}_\varepsilon ^T\widetilde{{\varvec{x}}}(t) +\frac{{\widetilde{m}}_s}{m_s}\overline{{\varvec{a}}}_{1b}^T{\varvec{x}}_c(t)\bigg ). \end{aligned}$$
(25)

Since \({\widetilde{e}}_{\varepsilon d}(t)\), \(\Vert \widetilde{{\varvec{e}}}_\varepsilon \Vert\), \({\widetilde{m}}_s/m_s\Vert \overline{{\varvec{a}}}_{1b}\Vert\) are bounded and \(\beta _c\ge 1\), there exists a constant \(\rho _{\varepsilon 1}\) independent of design parameter \(\beta _c\) such that the second and third terms of the right side of (25) are less than and equal to \(\rho _{\varepsilon 1}/\beta _c\). Using the fact in (25), we can obtain

$$\begin{aligned} {\dot{V}}(t)\le -\delta _\varepsilon V(t)+\frac{\rho _{\varepsilon 1}}{\beta _c},~~\delta _\varepsilon =\frac{\lambda _{\textrm{min}}[Q]}{\lambda _{\textrm{max}}[P]}. \end{aligned}$$
(26)

From (26), \({\varvec{\varepsilon }}_b(t)\) is stable and we can have \(\Vert {\varvec{\varepsilon }}_b(t)\Vert ^2\le \rho _{\varepsilon }/\beta _c\), \(\rho _{\varepsilon }=\rho _{\varepsilon 1}/(\delta _\varepsilon \lambda _{\textrm{min}}[P])\). From (21), we can obtain that the tracking error \(\widetilde{{\varvec{x}}}_t(t)\) is also stable, and then, we have from (19) that \({\varvec{b}}_b^T\widetilde{{\varvec{x}}}_b(t)\) and \({\varvec{d}}_b^T\widetilde{{\varvec{x}}}_b(t)\) are stable.

Multiplying \([0~0~0~{\varvec{b}}_t^T]\) in the first equation of (13) from left and integrating, we have

$$\begin{aligned} {\varvec{b}}_t^T\widetilde{{\varvec{x}}}_{td}(t)=-{\overline{k}}_{tu} \int _{0}^{t}{\varvec{c}}_t^T\widetilde{{\varvec{x}}}_{td}(\tau )d\tau -{\overline{m}}_{su}{\varvec{d}}_b^T{\varvec{x}}_{bd}(t)-{\dot{z}}_r(t). \end{aligned}$$
(27)

From assumption \({\varvec{A2}}\) and (27), \(\int _0^t{\varvec{c}}_t^T{\varvec{x}}_{td}(\tau )d\tau\) is bounded, and then, we can have that \(\int _0^t{\widetilde{e}}_{td}(\tau )d\tau\) is also bounded. Using the facts in the relation obtained by multiplying \({\varvec{b}}_t^T\) in (17) from left and integrating, we have that \(\int _0^t{\varvec{c}}_t^T\widetilde{{\varvec{x}}}_{t}(\tau )d\tau\) is bounded, and then, we can conclude that \(\widetilde{{\varvec{x}}}(t)\) is stable. \(\square\)

From theorem 1, in case of \({\widetilde{m}}_s=0\) and \({\widetilde{k}}_t=0\), good performance can be assured without redesign of the controller even if vehicle mass varies greatly. In case of \({\widetilde{m}}_s\ne 0\) or \({\widetilde{k}}_t\ne 0\), if \(|{\widetilde{e}}_{td}(t)|\) is small, it can be expected that as the design parameter \(\beta _c\) becomes large, \(\Vert \widetilde{{\varvec{x}}}_t(t)\Vert\) and \(|{\varvec{b}}_b^T\widetilde{{\varvec{x}}}_b(t)|\) become small. The control performance in case of \({\widetilde{m}}_s\ne 0\) or \({\widetilde{k}}_t\ne 0\) are shown in the next section. When measurements errors exist in practical applications, there is a possibility where large vibrations occur for a high feedback gain \(\beta _c\).

5 Numerical simulation results

The numerical simulations are carried out to confirm usefulness of the proposed robust active suspension controller. The nominal vehicle parameter values are shown in Table 2 [21].

Fig. 2
figure 2

Passive vehicle and ideal vehicle model

Full size image
Fig. 3
figure 3

Responses of controlled vehicle

Full size image
Fig. 4
figure 4

Robust performance of controlled vehicle

Full size image
Table 2 Nominal values of vehicle parameters
Full size table

The design parameters of (9) and a controller (23) are set as \(T_r=0.01\), \(\omega _r=2\), \(\zeta _r=1\) and \(\alpha =1\), \(Q=I\). The road surface displacement \(z_r(t)\) is given by

$$\begin{aligned} {\dot{z}}_r(t)= & {} -\frac{1}{T_{zr}}z_r(t)+\frac{1}{T_{zr}}w_r(t), ~T_{zr}=0.005 \end{aligned}$$
(28)
$$\begin{aligned} w_r(t)= & {} \left\{ \begin{array}{ll} \frac{h_z}{2}\left( \sin \left( \omega _z-\frac{\pi }{2}\right) +1\right) &{}\quad \text {if } 0\le t\le \frac{2\pi }{\omega _{zr}}\\ 0&{}\quad \text {if }\frac{2\pi }{\omega _{zr}}<t \end{array} \right. , \end{aligned}$$
(29)

where \(h_z\) is the amplitude and \(\omega _z\) is the frequency of the uneven road surface.

The design parameters for an ideal vehicle model are set so that the conditions C1 and C2 can be achieved in the range of \(h_z\in [9~13]\) [cm] and \(\omega _z\in [0.5~3.5]\) [Hz].

$$\begin{aligned}{} & {} \left. \begin{aligned} Q_U&=Q_bQ_b^T+10^3{\varvec{q}}_a{\varvec{q}}_a^T+Q_s{\textrm{diag}}[10^5~10]Q_s^T\\&\quad +10^5Q_u{\textrm{diag}}[1~0.3]Q_u\\ Q_{tU}&=Q_bQ_b^T+{\varvec{q}}_a{\varvec{q}}_a^T+Q_sQ_s^T+Q_uQ_u^T\\ {\varvec{q}}_a&=[0~~0~~1~~0~~0]^T,~~Q_s=Q_b-Q_t\\ Q_b&=\left[ \begin{array}{cc}1~0~0~0~0\\ 0~1~0~0~0\end{array}\right] ^T,~~ Q_u=\left[ \begin{array}{cc}0~0~0~1~0\\ 0~0~0~0~1\end{array}\right] ^T\\ \beta _U&=m_s10^7,~~m_{sU}={\overline{m}}_s+65 \end{aligned} \right\} , \end{aligned}$$
(30)
$$\begin{aligned}{} & {} \left. \begin{aligned} Q_L&=Q_bQ_b^T+10^3{\varvec{q}}_a{\varvec{q}}_a^T+Q_s{\textrm{diag}}[10^5~10]Q_s^T\\&\quad +6\times 10^6Q_u{\textrm{diag}}[1~0.3]Q_u\\ Q_{tL}&=Q_{tU},~~\beta _L=m_s10^7,~~m_{sL}={\overline{m}}_s-65 \end{aligned} \right\} . \end{aligned}$$
(31)

In the designed models, the parameters \(r_{tu}\) and \(r_u\) are set as \(r_{tu}=0.6\) and \(r_u=0.45\).

In the matrixes \(Q_i, i=U, L\), to meet \({\varvec{\textrm{C1}}}\) in each vehicle model (5), coefficients of \({\varvec{q}}_a{\varvec{q}}_a^T\) are set to be a large value. However, when the coefficients of \({\varvec{q}}_a{\varvec{q}}_a^T\) are only set to be large, vibrations appear in suspension stroke and tire deflection. To avoid the vibrations, coefficients corresponding to \(Q_s\) and \(Q_u\) are also set to be large values. To meet \({\varvec{\textrm{C2}}}\), we mainly use high feedback gains \(\beta _i, i=U, L\) in each vehicle model (5). The coefficients in \(Q_{ti}, i=U, L\) are set to be one.

We can set any values of \(m_{sU}\) and \(m_{sL}\). When a nominal situation has two passengers in standard-size vehicles, it is considered that increase/decrease of the sprung mass may about 15 [%]. Under the notion, we set the values of \(m_{sU}\) and \(m_{sL}\).

Figure 2 a–f shows variations of maximum values of \(|R_t(t)|\) and \(|\xi (t)|\) of the passive vehicle (\(u(t)=0\)). Figure 2g–l shows variations of maximum values of \(|R_{td}(t)|\) and \(|\xi _d(t)|=|{\varvec{b}}^T{\varvec{x}}_d(t)|\) of the ideal vehicle model. In the passive vehicle, the values of vehicle parameters are nominal values except the sprung mass \(m_s\). In Fig. 2, x-axis denotes amplitude \(h_z\) [cm] and y-axis denotes frequency \(\omega _z\) [Hz] of road surface displacement \(z_r(t)\). In Fig. 2a,c,e, for clarity, the maximum relative tire loads are set as \(\max |R_t(t)| = 0.8\) in the case when \(\max |R_t(t)| > r_{tu} =0.6\).

As shown in Fig. 2 a,c,e in the passive vehicle, handling performance becomes very poor (\(|R_t(t)|>r_{tu}=0.6\)) in some regions of \(h_z\) and \(\omega _z\). Compared with the passive vehicle, the performance of the designed ideal vehicle model becomes much better. In addition to the fact, by setting the measured vehicle mass \({\widehat{m}}_s\), we can easily obtain the ideal vehicle model with high performance compared with passive vehicle without redesigning.

In the case of \(m_s={\widehat{m}}_s\) and \(k_t={\overline{k}}_t\), as shown in Theorem 1, the behavior of the controlled vehicle and an ideal vehicle model becomes the same. Therefore, consider the case where there exist uncertainties such as \(m_s={\widehat{m}}_s(1+\Delta _m/100)\) and \(k_t={\overline{k}}_t(1+\Delta _k/100\)), where \(\Delta _m\) and \(\Delta _k\) denote measured error and parameter uncertainty. In case of \({\widehat{m}}_s=320\) [kg], \(\omega _z=2\) [Hz], \(h_z=13\) [cm] \(\Delta _m =5\) [%] and \(\Delta _k=-10\) [%], Fig. 3 shows responses of the controlled vehicle for various \(\beta _c\). In Fig. 3 a,b, thick solid lines show responses of the ideal vehicle model. When \(\Delta _k\) becomes larger than 10 [%], the maximum value of \(|R_t(t)|\) becomes larger and the maximum value of \(|\xi (t)|\) becomes smaller. If \(\Delta _k\) becomes too large, the maximum value of \(|R_t(t)|\) exceeds \(r_{tu}\). When \(\Delta _m\) becomes smaller than -10 [%], the maximum value of \(|R_t(t)|\) becomes larger and the maximum value of \(|\xi (t)|\) becomes larger. If \(\Delta _m\) becomes too small, the maximum value of \(|\xi (t)|\) becomes very large.

As shown in Fig. 3 c, the maximum error of \(\Vert {\varvec{\varepsilon }}_b(t)\Vert\) becomes small as the design parameter \(\beta _c\) becomes larger. When \(\beta _c\) is 300, the maximum error of \(\Vert {\varvec{\varepsilon }}_b(t)\Vert\) becomes almost zero. As shown in Fig. 3 a,b, as the \(\beta _c\) becomes larger, the error between the controlled vehicle and the ideal vehicle model becomes smaller.

To investigate the effects of uncertainties \(\Delta _m\) and \(\Delta _k\) on the controlled vehicle, in Fig. 4, we show variations of maximum values of \(|R_t(t)|\) and \(|\xi (t)|\) for various \(\Delta _m\) and \(\Delta _k\). In the controlled vehicle, the design parameter is set as \(\beta _c=300\). In Fig. 4, x-axis denotes \(\Delta _m\) and y-axis denotes \(\Delta _k\).

As shown in Fig. 4, even if there exist measured errors in \({\widehat{m}}_s\), steering performance and ride comfort little vary, while, as shown in Fig. 4 a, as \(\Delta _k\) becomes large, the maximum values of \(|R_t(t)|\) becomes large and close to \(r_{tu}=0.6\). However, as \(\Delta _k\) becomes small, the maximum values of \(|R_t(t)|\) become small. The variations of \(|\xi (t)|\) against the variations of \(\Delta _k\) become small as shown in Fig. 4 b,d,f.

From the facts stated above, we can conclude that in the case when \(|\Delta _m|\le 5\) [\(\%\)] and \(|\Delta _k|\le 10\) [\(\%\)], in the controlled vehicle, good handling performance and good ride comfort can be maintained even if vehicle masses vary greatly.

6 Conclusion

We proposed a design method of an ideal vehicle model in which good steering performance and good ride comfort can be maintained even if vehicle mass varies greatly. To achieve a good control performance, a robust tracking controller is developed to force the actual vehicle follow the ideal vehicle model. Using numerical simulation results, it is shown that in the case for small uncertainties, good handling performance and good ride comfort can be maintained in the controlled vehicle even if vehicle mass varies greatly.