1 The problem of dynamic obstacles avoidance

Controlling a vehicle (manual or automatic) in various traffic settings involves negotiation with numerous static (e.g., parked vehicles, traffic islands, road signs) and dynamic (other vehicles, pedestrians) objects. Interactions with the dynamic obstacles are, evidently, more complicated for managing, and uncertainties in estimating their positions and velocities raise severe challenges to the safe navigation of human drivers and pedestrians. A formal view of the interaction between the traffic participants is especially important for autonomous vehicles control systems operating in mixed traffic and interacting with humans driving vehicles.

There are several approaches to the planning/dynamic obstacle avoidance algorithms. However, some of them have significant limitations for performing correctly in real-world situations [1]. Some exploit simplified models of moving obstacles’ dynamics [1, 2] where the objects follow traffic regulations [1, 3, 4], while others are based on the kinematic patterns of drivers and pedestrians in specific motion maneuvers [5,6,7].

In reactive collision avoidance, the driving trajectory is constructed in reaction to the instantaneously observed moving objects [2, 8, 9]. These algorithms are affected by the “time horizon”—the duration of the time window chosen for forecasting the objects’ expected displacements. Typically, for human drivers, the time horizon is 1–2 s [10]. Improper selection of time horizon may cause erroneous estimates of an object’s future location [5, 8] and time to collision (TTC), and may result in a collision [1, 11, 12]. Given the time horizon, the precision of drivers’ estimates of distances and velocities decreases when the distance to or speed of the moving objects increases or lighting and other environmental conditions worsen [13, 14].

According to the National Safety Council (NSC) in the US (https://www.nsc.org/safety-training/defensive-driving), human and automated driving should be defensive: “..the driving behavior that saves lives, time, and money, despite the conditions around, and the actions of others, that best provides preventative methods for traffic incidents”. In addition to being alert, focused, and obeying traffic rules, defensive driving also demands continuous scanning of the environment and the ability to forecast unpredictable behavior of other drivers. For this purpose, we propose the Maneuverability Maps (MM) that represent the possible future avoidance maneuvers of a vehicle regarding the mobile obstacles over a variety of time horizons and the possible safe maneuvers that can prevent a crash. MM can serve as a part of Advanced Driver-Assistance Systems or Autonomous Vehicle (AV) control system.

Our previous papers presented the algorithm for avoiding vehicle–pedestrian interaction [15, 16] and investigated its properties with the agent-based simulation environment (SAFEPED). In this paper, we extend the proposed algorithm for vehicle-vehicle interaction.

The structure of the paper is as follows:

Section 2 briefly reviews the algorithmic for computing maneuvers for a vehicle capable of accelerating, decelerating, and steering, which avoids collision with an obstacle moving along a straight trajectory. It begins with explaining the rationale behind selecting one of two alternatives, accelerating or braking, and proceeds to a combination of the decision for changing speed with the decision to change direction in avoiding a crash.

Section 3 is devoted to the avoidance of obstacles moving along a curved trajectory. It explains the dependency of maneuver outcomes to the time horizon selected for forecasting the obstacles motion. Finally, it presents a method for selecting the proper forecast time horizon of motion planning, and introduces the maneuverability map as a useful instrument for computing optimal avoidance maneuvers.

Section 4 presents a case study which exhibits the advantage of using a maneuverability map over arbitrary selected constant forecast time horizon in realistic urban road interaction. Finally, Sect. 5 provides a discussion and concluding remarks.

2 Collision avoidance in vehicle—vehicle interaction

A collision can be avoided by a combination of braking, accelerating, and steering maneuvers. To present the concept, we start with the case of two potentially colliding vehicles that cannot steer, and then continue with the description of the case where all three maneuvers are possible.

2.1 The case of braking/accelerating only

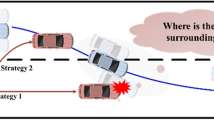
The scenario in Fig. 1 considers two vehicles, \({\varvec{A}}\) (blue) and \({\varvec{B}}\) (red), approaching a road intersection, both constrained to a narrow road and, thus, able to brake or accelerate only. \({\varvec{A}}\) and \({\varvec{B}}\) will crash if they maintain their current speeds \({V}_{A}\) and \({V}_{B}\).

Fig. 1
figure 1

Vehicle \({\varvec{A}}\) resolves a possible collision with vehicle \({\varvec{B}}\) by braking or accelerating: a \({\varvec{A}}\) accelerates to avoid a crash; b \({\varvec{A}}\) decelerates before \({\varvec{B}}\)’s front edge reaches the potential crash point c \({\varvec{A}}\) decelerates to avoid a crash with the back edge of \({\varvec{B}}\); d displacement CC of A for the given time horizon

Full size image

The dashed lines \({l}_{A}\) and \({r}_{A}\) represent the trajectories of left and right edges of \({\varvec{A}}\) respectively that moves from left to right, and \({l}_{B}\) and \({r}_{B}\) the trajectories of the left and right edges of \({\varvec{B}}\) respectively that moves downwards. \({D}_{B1}\) is the distance from the front of \({\varvec{B}}\) to \({l}_{A}\), and \({D}_{B2}\) is the distance from the rare end of \({\varvec{B}}\) to \({r}_{A}\). \({D}_{A1}\) and \({D}_{A2}\) are the distances of the back and front edges of \({\varvec{A}}\) to the left and right edges of \({\varvec{B}}\) respectively (Fig. 1a–c). The time to the collision between the front edge of \({\varvec{B}}\) and the left edge of \({\varvec{A}}\) is \(\Delta {t}_{1}^{TTC}=\frac{{D}_{B1}}{{V}_{B}}\), and between the front edge of vehicle \({\varvec{A}}\) and the right back side of \({\varvec{B}}\) is \(\Delta {t}_{2}^{TTC}=\frac{{D}_{B2}}{{V}_{B}}\).

Let us assume that \({\varvec{B}}\) ignores \({\varvec{A}}\) by maintaining its initial speed, and it is up to \({\varvec{A}}\) to avoid the collision. If \({\varvec{A}}\) decelerates, it must not pass \({D}_{A2}\) before the period \(\left[\Delta {t}_{1}^{TTC}\Delta {t}_{2}^{TTC}\right]\), when \({\varvec{B}}\) will leave the zone of a potential crash. If \({\varvec{A}}\) accelerates, it must pass \({D}_{A1}\) at \(\Delta {t}_{1}^{TTC}\). An object moving at an initial speed of \({v}_{0}\) and accelerating with a constant acceleration a, covers, during \(\Delta t\), a distance \(D\):

$$\begin{array}{*{20}c} {D = v_{0} \cdot \Delta t + \frac{{a \cdot \Delta t^{2} }}{2},} \\ \end{array}$$
(1)

thus, the acceleration/deceleration necessary to avoid the collision is:

$$\begin{array}{*{20}c} {a = \frac{{2 \cdot \left( {D - v_{0} \cdot \Delta t} \right)}}{{\Delta t^{2} }}.} \\ \end{array}$$
(2)

Let \(d^{\max }\) be the maximal deceleration and \(a^{\max }\) the maximal acceleration of \({\varvec{A}}\).

If \(V_{A} \cdot \Delta t_{2}^{{{\text{TTC}}}} + \frac{{d^{\max } \cdot \left( {\Delta t_{2}^{{{\text{TTC}}}} } \right)^{2} }}{2} > D_{A2}\), then \({\varvec{A}}\) is incapable of avoiding the crash by braking. Otherwise, vehicle \(B\) safely passes the intersection first if the acceleration of \(A\) is lower than \(a_{1}\):

$$\begin{array}{*{20}c} {a_{1} = \frac{{2 \cdot \left( {D_{A2} - V_{A} \cdot \Delta t_{2}^{{{\text{TTC}}}} } \right)}}{{\left( {\Delta t_{2}^{{{\text{TTC}}}} } \right)^{2} }}} \\ \end{array}$$
(3)

If \(V_{A} \cdot \Delta t_{1}^{{{\text{TTC}}}} + \frac{{a^{\max } \cdot \left( {\Delta t_{1}^{{{\text{TTC}}}} } \right)^{2} }}{2} < D_{A1} ,\) then \({\varvec{A}}\) is incapable of avoiding the crash by accelerating. Otherwise, vehicle \({\varvec{A}}\) safely passes the intersection first if the acceleration of \(A\) is higher than \(a_{2}\):

$$\begin{array}{*{20}c} {a_{2} = \frac{{2 \cdot \left( {D_{A1} - V_{A} \cdot \Delta t_{1}^{{{\text{TTC}}}} } \right)}}{{\left( {\Delta t_{1}^{{{\text{TTC}}}} } \right)^{2} }}} \\ \end{array}$$
(4)

In what follows, we assume that \({\varvec{A}}\) tries to avoid the collision by choosing the maneuver that demands a minimal deviation from its current speed. The optimal acceleration is, thus,

$$\begin{array}{*{20}c} {a_{{{\text{optimal}}}} = \min \left( {\left| {a_{1} } \right|,\left| {a_{2} } \right|} \right).} \\ \end{array}$$
(5)

Let at every time moment t, the driver, human or computer, plans the maneuvers for a time horizon \(\Delta t^{h}\). Then, in the above scenario, the vehicle’s velocity at the end of \(\Delta t^{h}\) is given by:

$$\begin{array}{*{20}c} {V_{{t + \Delta t^{h} }} = v_{t} + a \cdot \Delta t^{h} } \\ \end{array}$$
(6)

Velocities within the range \(VC_{{t + \Delta t^{h} }} \in \left[ {v_{t} + a_{1} \cdot \Delta t^{h} , v_{t} + a_{2} \cdot \Delta t^{h} } \right]\) are unsafe and lead to a crash; velocities outside this range are considered safe.

In this example, the direction of the displacement always coincides with the velocity vector. The displacement of \({\varvec{A}}\) for the time horizon \(\Delta t^{h}\) (Fig. 1c) is:

$$\begin{array}{*{20}c} {S_{{t + \Delta t^{h} }} = v_{t} \cdot \Delta t^{h} + \frac{{a \cdot \left( {\Delta t^{h} } \right)^{2} }}{2},} \\ \end{array}$$
(7)

and the range for unsafe displacement is

$$\begin{array}{*{20}c} {CC \in \left[ {\begin{array}{*{20}c} {v_{t} \cdot \Delta t^{h} + \frac{{a_{1} \cdot \left( {\Delta t^{h} } \right)^{2} }}{2}, } \\ { v_{t} \cdot \Delta t^{h} + \frac{{a_{2} \cdot \left( {\Delta t^{h} } \right)^{2} }}{2}} \\ \end{array} } \right].} \\ \end{array}$$
(8)

2.2 General case—braking, accelerating, and steering

In the case of steering, the set of unsafe displacements becomes two-dimensional, and its shape depends on the relative motion of \({\varvec{A}}\) toward \({\varvec{B}}\). To construct this set, we follow Fiorini and Shiller [17]. They proposed the Relative Collision Cone (RCC): the relative velocities of \({\varvec{A}}\) that remain within the RCC lead to a crash, while the relative velocities of \({\varvec{A}}\) outside RCC are safe (Fig. 2a). By mapping RCC to the absolute velocities space, we obtain the Absolute Collision Cone (ACC), see Fig. 2b.

Fig. 2
figure 2

Identifying the set of velocities that guarantee no collision in case of a straight motion of A: a the relative velocities are out of RCC; b in case of straight motion \(v<{V}_{A}^{+}\& v>{V}_{A}^{-}\) c \(v\in {VV}^{+} \& v\in {VV}^{-}\)

Full size image

The domain \({VV}^{-}\) in Fig. 2c represents the set of reduced velocities of \({\varvec{A}}\) that give way to B, while the domain \({VV}^{+}\) represents the set of increased velocities of \({\varvec{A}}\) that allow \({\varvec{B}}\) to pass the potential crash zone after A leaves that potential crash zone.

In the case of straight motion (Fig. 2b), we consider the avoidance maneuver as optimal if it can be performed with the minimal change of the vehicle speed equal to\(\mathrm{min}\left({V}_{A}^{-},{V}_{A}^{+}\right)\). For the case of unconstrained motion of\({\varvec{A}}\), the optimal avoidance is within the two infinite sets—\({VV}^{-},{VV}^{+}\) (Fig. 2c) and we call \({VV}^{-}\) “accelerate-and-steer” and \({VV}^{+}\) “brake-and-steer” sets of velocities.

2.3 Motion along circular arcs

The motion of ground vehicles is constrained by kinematic and dynamic features such as maximal accelerating/deceleration capabilities and minimal turning radius. To account for the displacement along a non-straight trajectory, Waizman et al. [16] consider displacements along a circular arc (Fig. 3a). In this figure, \({\varvec{A}}\) can avoid a collision with \({\varvec{B}}\) by constructing a “synthetic” obstacle \({O}_{B}\) based on the obstacle’s dimension and its current speed, using the ACC procedure.

Fig. 3
figure 3

The set of velocities that guarantee no collision in case of a circular motion of \({\varvec{A}}\) a unconstraint vehicle must steer out of \({O}_{B}\) b Set of available displacements AS, set of safe displacements \({ASS}^{-}\), the optimal displacement \({S}^{-}\in {ASS}^{-}\) for brake-and-steer avoidance for the time horizon \({\Delta t}^{h}\) c the optimal displacement \({S}^{+}\in {ASS}^{+}\) for accelerate-and-steer avoidance for the time horizon \({\Delta t}^{h}\)

Full size image

In Fig. 3a, \({\varvec{A}}\) can avoid the collision by sharp left turn (denoted \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{1}\)) or by a moderate right turn (denoted \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{2}\)). The locus of available displacements is denoted by AS in Fig. 3b and is formed by the maximal acceleration/deceleration and the minimal turning radius for a given time horizon \({\Delta t}^{h}\). The minimal and maximal longitudinal displacements (\(S\mathrm{min}, S\mathrm{max}\)), which depend on the current speed of A and on its maximal deceleration/acceleration, determine the rear and front boundaries of AS (Fig. 3b). The minimal turning radius (\(R\mathrm{min}\)), determines the radii of the lateral boundaries of AS.

The set of all collision displacements for brake-and-steer maneuvers—\({CSS}^{-}\) (Fig. 3b) resides between \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{1}\) and \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{2}\), which forms the closest safe bypass trajectories of \({\varvec{A}}\) from the left and right sides of obstacle \({O}_{B}\) accordingly. The shape of \({O}_{B}\) is derived from ACC (for more details, see [16]). The set of available brake-and-steer safe displacements \({ASS}^{-}\) is a result of subtracting \({CSS}^{-}\) from the AS.

The collision displacements for accelerate-and-steer maneuvers—\({CSS}^{+}\) (Fig. 3c) include the area of ACC and the areas between ACC and \({\varvec{A}}\). The set of available accelerate-and-steer safe displacements \({ASS}^{+}\), similarly to \({VV}^{+}\), includes displacements over \({CSS}^{+}\) with a higher velocity of the current velocity vector of \({\varvec{A}}\) and therefore is associated with acceleration (Fig. 3c).

The displacement for the optimal unconstrained motion is selected from the safe displacements requiring minimal effort (acceleration/deceleration/steering) to maneuver the vehicle. If the endpoint of the current velocity vector of \({\varvec{A}}\) falls inside the set of collision displacements (\({\mathrm{CSS}}^{-}\) or \({\mathrm{CSS}}^{+}\)), the control system (automatic or manual) identifies the optimal displacement inside the set of the safe displacements (\({\mathrm{ASS}}^{-}\) or \({\mathrm{ASS}}^{+}\)). The optimal displacement requires minimal energy to be applied and, therefore, corresponds to the minimal combination of longitudinal and lateral acceleration for \({\varvec{A}}\). The optimal displacement from \({\mathrm{ASS}}^{-}\), is denoted by \({S}^{-}\)(Fig. 3b), and the one from \({ASS}^{+}\) is denoted by \({S}^{+}\) (Fig. 3c).

2.4 Switching between the brake and accelerate maneuvers

During the motion, the size of the safe “brake-and-steer” and “accelerate-and-steer” displacements may change (Fig. 4) and can result in a qualitative change in the optimal maneuver. At time \(t\) (Fig. 4a), “brake-and-steer” is selected because \({\mathrm{ASS}}^{-}\)> \({ASS}^{+}\). “Accelerate-and-steer” is selected at time \(t+\Delta t\) in the situation described in (Fig. 4b) as vehicles \({\varvec{A}}\) and \({\varvec{B}}\) approach each other and \({\mathrm{ASS}}^{+}\)> \({\mathrm{ASS}}^{-}\). Selecting the most extensive set of safe displacements between \({ASS}^{-}\) and \({ASS}^{+}\) preserves more options for further maneuvering of \({\varvec{A}}\), i.e., leaves more options for avoiding a collision.

Fig. 4
figure 4

Safe displacements loci in \({\varvec{A}}\) reaction to \({\varvec{B}}\): a at the time t the area of a safe “brake-and-steer” \({\mathrm{ASS}}_{t}^{-}\) is 70% of its total area, while safe “accelerate-and-steer” \({\mathrm{ASS}}_{t}^{+}\) is just empty; b at the next moment \(t+\Delta t\) \({\mathrm{ASS}}_{t+\Delta t}^{-}\) decreases to 15% of the total area while \({ASS}_{t+\Delta t}^{+}\) increases to 20%

Full size image

3 Predicting maneuvering of mobile obstacles

3.1 The effect of forecast time horizon on maneuverability

As already mentioned, drivers predict the location of moving obstacles 1–2 s. ahead of time and control their vehicles respectively [10]. Let us consider this prediction in the case of non-linear motion. Figure 5 presents the loci of safe displacements \({ASS}^{-}\) and \({ASS}^{+}\) for vehicle \({\varvec{A}}\) in reaction to vehicle \({\varvec{B}}\) for three different forecast time horizons \({\tau }_{1}<{\tau }_{2} <{\tau }_{3}\) and three predicted locations \({P}_{\tau 1}^{A}\), \({P}_{\tau 2}^{A}\) and \({P}_{\tau 3}^{A}\) of \({\varvec{A}}\) along its anticipated trajectory. The velocity vectors of \({\varvec{B}}\) for these three horizons are different, and as shown, \({ASS}_{\tau 1}^{+}<{ASS}_{\tau 2}^{+}<{ASS}_{\tau 3}^{+}\) while\({ASS}_{\tau 1}^{-}>{ASS}_{\tau 2}^{-}>{ASS}_{\tau 3}^{-}\).

Fig. 5
figure 5

Increasing forecast time \({\varvec{\tau}}\) affects the relative size of the \({ASS}_{\tau }^{-}\) and \({ASS}_{\tau }^{+}\) domains, thus resulting in different accelerating/braking decision

Full size image

Since the vehicle’s maneuverability option is defined by the largest of the two safe zones, an algorithm for establishing the optimal time horizon is suggested as follows:

Construct safe “brake-and-steer” and “accelerate-and-steer” domains \({ASS}_{\tau }^{-}\) and \({ASS}_{\tau }^{+}\) for the series of time horizons between 0 and 2 s. for \({\tau }_{i}=\left\{\Delta \tau \cdot i:i=\mathrm{0,1}..16,\Delta \tau =0.125 sec\right\}\).

Select the maximal of 32 areas of the obtained safe displacements:

$$\overline{i} = \arg \max f\left( i \right) \in \left\{ {i:i = 0,1..16} \right\},$$
$$f\left( i \right) = \max \left( {\left\{ {ASS^{ - } \left( {\tau_{i} } \right),ASS_{\tau }^{ + } \left( {\tau_{i} } \right)} \right\}} \right)$$

where \(\overline{\tau } = \tau_{{\overline{i}}}\) is considered as the optimal time horizon that can be braking-and-steering or accelerating-and-steering, depending on which of \({ASS}^{-}\left(\overline{\tau }\right)\) or \({ASS}^{+}\left(\overline{\tau }\right)\) is selected.

3.2 Constant vs. optimal forecast time horizon

Figure 6 presents a scenario, in which vehicle \({\varvec{A}}\), with a maximal speed of 45 km/h, approaches the roundabout at a speed of 40 km/h, while vehicle \({\varvec{B}}\) exiting the roundabout at a speed of 40 km/h by turning left without using its turning signals. Vehicle \({\varvec{A}}\) can choose to brake, assuming that \({\varvec{B}}\) does not leave the roundabout, maintain its current speed or even accelerate, assuming that \({\varvec{B}}\) will exit the roundabout. The intermediate option for \({\varvec{A}}\) is to decrease the speed at the beginning (between Fig. 6a, b) and then accelerate (Fig. 6c, d) after realizing that \({\varvec{B}}\) is exiting the roundabout. Let us investigate the outputs of this scenario in case of the constant and optimal horizon time \(\tau\)

Fig. 6
figure 6

Vehicle \({\varvec{A}}\) brakes in the period between a and b assuming vehicle \({\varvec{B}}\) continues in the roundabout decision and then accelerates on the segment between c and d when realizing that \({\varvec{B}}\) leave the roundabout

Full size image

Figure 7a–c presents A’s speed for constant \({\tau }_{A}=0.5, 1.0\, \mathrm{sec\ and}\ 2.0\,\mathrm{ sec}\). If there are no obstacles to avoid or sharp turns of the road, vehicle A increases its speed to a maximum of 45 km/h. It starts reacting to vehicle B between time t ≈ 1.0 s. (\(\tau\) = 2.0 s, Fig. 7c) and ≈1.1 s (\(\tau\) = 0.5 s, Fig. 7a) from the beginning of the interaction. In the case of variable \(\tau \in \left[0.0-2.0\right]\) sec. (Fig. 7d) vehicle A reacts as earlier as in the case of \(\tau\) = 0.5 s. As can be seen, in all cases, \({\varvec{A}}\) first brakes and then accelerates, and acceleration depends on \(\tau\) – the speed of \({\varvec{A}}\) decreases to 26 km/h for \({\tau }_{A} = 0.5\) and to 32–33 km/h for \({\uptau }_{\mathrm{A}}\) = 1.0 and \({\uptau }_{\mathrm{A}}\) = 2.0. In case of the optimal time horizon that varies during the movement, the decrease in speed is minimal, to ≈ 36 km/h (Fig. 9d).

Fig. 7
figure 7

Change of A’s speed in time for the constant and variable forecast time a \(\tau\) = 0.5 s, b \(\tau\) = 1.0 s, c \(\tau\) = 2.0 s, d optimal \(\tau\) that varies within [0.0 2.0] during motion

Full size image

3.3 Maneuverability map

Let us analyze the scenario in Fig. 6 for introducing the Maneuverability Indices and the Maneuverability Map. Let us define for vehicle A at some moment t of the interaction with vehicle B, the Maneuverability Index for braking (\({MI}_{t}^{-}(\tau )\)) as the ratio between the area of the safe displacements for braking maneuvers—\({ASS}_{t}^{-}\left(\tau \right)\) and the area of all (safe and unsafe) available displacements—\(AS_{t}^{ - } \left( \tau \right)\) for a given time horizon \(\tau\):

$$\begin{array}{*{20}c} {MI_{t}^{ - } \left( \tau \right) = \frac{{ASS_{t}^{ - } \left( \tau \right)}}{{AS_{t}^{ - } \left( \tau \right)}}.} \\ \end{array}$$
(9)

Similarly, the Maneuverability Index for accelerating is given by

$$\begin{array}{*{20}c} {MI_{t}^{ + } \left( \tau \right) = \frac{{ASS_{t}^{ + } \left( \tau \right)}}{{AS_{t}^{ + } \left( \tau \right)}}.} \\ \end{array}$$
(10)

As mentioned, we consider forecast times \(|\tau \in \left[0.0 2.0\right]\ \mathrm{at \,resolution\, of }\,0.125\,\mathrm{ sec}\). However, the forecast time \(\tau\) above Time to Collision (TTC) is meaningless because it leads to a certain crash. The area in the MM map where \(\tau >\mathrm{TTC}\) is marked with gray. If \({MI}_{t}^{-}(\tau )=1\) or \({MI}_{t}^{+}\left(\tau \right)=1\) then, for the given τ, there is no risk of collision. Similarly, if \({MI}_{t}^{-}(\tau )=0\) and \({MI}_{t}^{+}\left(\tau \right)=0\), then there are no safe displacements neither for braking nor for accelerating and resolution of a collision depends on the other vehicles’ maneuvers. We call this state “near-crash”.

The Maneuverability Map presents \({MI}_{t}^{-}\left(\tau \right)\) and \({MI}_{t}^{+}\left(\tau \right)\) as a function of \(\tau\) and t and consists of the acceleration and deceleration sections. Figure 8 presents the Maneuverability Maps for the scenario shown in Fig. 6. Forecast time \({\overline{\tau }}^{-}\) is defined as the highest of \({MI}_{t}^{-}(\tau )\). Forecast time \({\overline{\tau }}^{+}\) is defined as the highest of and \({MI}_{t}^{+}\left(\tau \right)\). If \({MI}_{t}^{-}({\overline{\tau }}^{-})< {MI}_{t}^{+}({\overline{\tau }}^{+})\), the optimal forecast time is\(\overline{\tau }={\overline{\tau }}^{+}\), otherwise\(\overline{\tau }={\overline{\tau }}^{-}\). The optimal forecast \(\overline{\tau }\) appears on the map as a solid black line, on the braking section if \(\overline{\tau }={\overline{\tau }}^{-}\) or on accelerating section if\(\overline{\tau }={\overline{\tau }}^{+}\).

Fig. 8
figure 8

Maneuverability map for a adjustable and b constant \(\tau = 1.0\, \mathrm{sec}\). Color denotes the values of the Maneuverability Index; the forecast time \(\tau\) above TTC is excluded (a gray area) as leading to a crash

Full size image

In both cases, vehicle \({\varvec{A}}\) changes, while moving, from the “Brake and Steer” to “Accelerate-and-steer” maneuvers, but the dynamics of these changes are different. For the adjustable time horizon (Fig. 8a), \({\varvec{A}}\) accelerates from 40 to 45 km/h during the time interval \([0, 1.1 \,\mathrm{sec}]\), but at \(t \approx 1.1\) (point a′ in Fig. 8a), some displacements of \({\varvec{A}}\) become unsafe due to the approaching vehicle \({\varvec{B}}\). As a result, the brake maneuverability index for \({\varvec{A}}\) decreases on the \(\left[1.1, 1.5 \,\mathrm{sec}\right]\) time interval (segment a′–b′ in Fig. 8a) and \({\varvec{A}}\) slows down to 38 km/h. At \(t = 1.5\), \({\varvec{B}}\) turns toward the exit of the roundabout and \({\varvec{A}}\) switches to accelerate-and-steer maneuvers. From t = 1.8 s. (point c′ in Fig. 8a), the optimal time horizon of A decreases as being limited by the TTC—until t ≈2.6 s. Shortly after that (point d′ in Fig. 8a, \(t \approx 2.9 \,\mathrm{sec}\)), the two vehicles drive away from each other.

For the constant time horizon of \(\tau = 1.0 \,\mathrm{sec}.\) (Fig. 8b), \({\varvec{A}}\) starts with a “Brake-and-Steer” maneuver, and, when switching to “Accelerate and steer” one, its speed is lower than the speed at the switching moment in case of the adjustable time horizon. At the end of the interaction, A's speed is 45 km/h in both cases.

3.4 The computational cost

Maneuvers’ computations using the MM consist of (a) establishing optimal forecast time \(\overline{\tau }\) and (b) identifying the optimal displacement \(\overline{S }\). As mentioned above, the first part includes constructing the areas of the safe displacements for 32 time horizons between 0 to 2 s. for \(\tau_{i} = \left\{ {\Delta \tau \cdot i:i = 0,1..16,\;\Delta \tau = 0.125\; {\text{sec}}} \right\}\).

The second part exploits the area of safe displacement associated with the optimal \(\overline{\tau }\) as an input.

As mentioned, in this paper we use SAFEPED for all the simulations. SAFEPED software is developed in standard C++. The simulations below are done on a standard desktop computer with i3-4170 CPU, two physical cores.

The red section of the graph in Fig. 9 represents the time required for determining the optimal \(\overline{\tau }\) as described above during the interaction between the two-vehicle. As shown, the average CPU time is ≈ 10 ms. The blue section corresponds to the period when the vehicles do not interact, and the optimal displacement computations are performed at an average of ≈1 ms.

Fig. 9
figure 9

CPU time for motion planning in case of one mobile obstacle and case of no obstacles

Full size image

3.5 Avoidance of multiple obstacles

So far, we have discussed two-vehicle interactions. However, the proposed algorithm can be extended to multiple vehicles scenarios. Generally, the set of safe “Brake-and-Steer” displacements \({ASS}^{-}\) for vehicle \({\varvec{A}}\) (Fig. 10a)—is the result of subtracting form the set of available displacements \(AS\), multiple sets of colliding displacements (\({\mathrm{CSS}}_{B}^{-},{\mathrm{CSS}}_{C}^{-}\)) and \({\mathrm{ASS}}^{+}\) for “Accelerate-and-Steer” (Fig. 10b) is the result of subtracting (\({\mathrm{CSS}}_{B}^{+},{\mathrm{CSS}}_{C}^{+}\)) form the set of available displacements. Identifying the optimal forecast time \(\overline{\tau }\) with regard to \(N\) obstacles requires the computation of both \({\mathrm{ASS}}^{-}\) and \({\mathrm{ASS}}^{+}\) for all permutations (with repetitions) of forecast times— \(\tau_{i} = \left\{ {\Delta \tau \cdot i:i = 0,1..16,\;\Delta \tau = 0.125\;{\text{ sec}}} \right\}\) for all obstacles:

$${\text{ASS}}_{{\left[ {1,2 \ldots N} \right]}}^{{ - \left[ {i_{1} i_{2} \ldots i_{N} } \right]}} = {\text{AS}}\backslash \left( {{\text{CSS}}_{1}^{{ - \tau_{i1} }} \cup {\text{CSS}}_{2}^{{ - \tau_{i2} }} \cup \cdots \cup {\text{CSS}}_{N}^{{ - \tau_{iN} }} } \right):i_{1} = 0,1..16,i_{2} = 0,1 \ldots 16 \ldots ,i_{N} = 0,1 \ldots 16$$
(11)
$${\text{ASS}}_{{\left[ {1,2..N} \right]}}^{{ + \left[ {i_{1} i_{2} \cdots i_{N} } \right]}} = {\text{AS}}\backslash \left( {{\text{CSS}}_{1}^{{ + \tau_{i1} }} \cup {\text{CSS}}_{2}^{{ + \tau_{i2} }} \cup \cdots \cup {\text{CSS}}_{N}^{{ + \tau_{iN} }} } \right):i_{1} = 0,1 \ldots 16,i_{2} = 0,1 \ldots 16 \ldots i_{N} = 0,1 \ldots 16$$
(12)
Fig. 10
figure 10

Constructing set of available displacements for multiple obstacles for a braking-and-steering b accelerating-and-steering maneuvers

Full size image

The number of permutations in total is:

$$\begin{array}{*{20}c} {\overline{A}_{16}^{N} = 16^{N} } \\ \end{array}$$
(13)

Sequential computation of the algorithm, in this case, may become time-consuming. Parallelizing:

Estimating \({{CSS}_{j}^{{-\tau }_{i}}, CSS}_{j}^{{+\tau }_{i}}:i=0..16,j=\mathrm{0,1}..N\)

Subsequent computing:

$${ASS}_{\left[\mathrm{1,2}..N\right]}^{-\left[{i}_{1}{i}_{2}\cdots {i}_{N}\right]}, {ASS}_{\left[\mathrm{1,2}..N\right]}^{+\left[{i}_{1}{i}_{2}\cdots {i}_{N}\right]}$$

significantly reduce execution time.

Finding: \(\mathrm{max}\left({\mathrm{ASS}}_{\left[\mathrm{1,2}..N\right]}^{-\left[{i}_{1}{i}_{2}\cdots {i}_{N}\right]}\right),\mathrm{max}\left({\mathrm{ASS}}_{\left[\mathrm{1,2}..N\right]}^{+\left[{i}_{1}{i}_{2}\cdots {i}_{N}\right]}\right)\) using numerical tools for non-linear optimization e.g., the steepest descent can significantly reduce number of \({\mathrm{ASS}}^{-}\) and \({\mathrm{ASS}}^{+}\) computations and consequently reduce the computation cost.

4 A case study

This section demonstrates that using adjustable forecast time has an advantage in forming avoidance maneuvers in an urgent situation even if the behavior of the active agent is not optimal. Normally, if the endpoint of the current velocity vector of an agent is out of the set of safe displacements, the control system selects an optimal displacement which requires minimal energy to be applied (0). In this experiment, we qualify urgent steering conditions if there is no safe displacement, neither for braking nor for accelerating, in the current direction of the agent’s motion. In this case, we set the control system to select displacement, which requires maximal energy to be applied. Consequently, A reacts to B and steers in the most forceful way, making its maneuvering less smooth.

Let A (Fig. 11) be the maneuvering vehicle and \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D}\)– is the shortest trajectory of A toward B. The experiment runs are repeated ten times for two maximal speeds of B—30 and 35 km/h, and five maximal speeds of A—25, 30, 35, 40, and 45 km/h. The speed of A affects the kinematic limits of its maneuvering (i.e., braking distance and minimal turning radius). The rate of the angular rotation of B depends on its speed and affects the ability of \({\varvec{A}}\) to make an accurate forecast of \({\varvec{B}}\)’s motion. The start time of \({\varvec{B}}\) is set to 0.0 s, while the start time of \({\varvec{A}}\) is set with a time delay of

$$\begin{array}{*{20}c} {\Delta t = \frac{{D_{1} }}{{V_{1} }} - \frac{{D_{2} }}{{V_{2} }}} \\ \end{array}$$
(14)

such that if both \({\varvec{A}}\) and \({\varvec{B}}\) do not react to each other, they crash. For all combinations of speeds, \({\varvec{A}}\) starts moving later than \({\varvec{B}}\). The point of collision between \({\varvec{A}}\) and \({\varvec{B}}\) is at distance \(D_{1} = 47m\) from the start point of \({\varvec{A}}\) along its trajectory and at distance \(D_{{2}} { = 27}\;{\text{m}}\) from the start point of \({\varvec{B}}.\) As mentioned, If vehicles \({\varvec{A}}\) and \({\varvec{B}}\) are “blind” and do not react to each other, they meet each other at the same point for all combinations of their initial speed due to different time delays.

Fig. 11
figure 11

Vehicle B, which does not react on A, turns left. A avoids collision with B. \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D}\)– is the shortest trajectory leading \({\varvec{A}}\) to a collision with \({\varvec{B}}\). The range is the length of \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{D}\)

Full size image

The results in Table 1 show that:

  • In the runs with adjustable time horizon, \({\varvec{A}}\) always lets \({\varvec{B}}\) to pass and takes a left bypass; in the runs with constant time horizon, \({\varvec{A}}\) always avoids \({\varvec{B}}\) taking a right bypass.

  • The minimal distance between the vehicles and the TTC are higher for the adjustable forecast. In the cases of \({\varvec{A}}\)-30 km/h velocities, the crash is avoided only in the case of adjustable forecast.

  • For the scenarios without a crash, the minimal distance between the vehicles is slightly higher when the of the speed of \({\varvec{A}}\) is higher for both constant and adjustable forecast.

  • In the case of no-crash, the TTC and the minimal distance loosely depend on the vehicles’ speeds and vary within the intervals 0.2–0.7 m and 0.02–0.05 s. In the case of the adjustable forecast, the distance and the TTC are double than for the constant forecast.

Table 1 The speed of A, the shortest range between A and B, and the TTC at the moment of their closest proximity in case of no-crash for the constant and adjustable time horizon
Full size table

The maneuverability maps for the adjustable and the constant time horizon \(\tau = 2.0\,\text{s}\) are presented in Fig. 12 in the scenario where \({\varvec{A}}\) and \({\varvec{B}}\) speeds are 35 km/h. At the time \({t}_{1}=1.0\,\text{s}\) in both cases \({\varvec{A}}\) switches to “Accelerate-and-Steer” because of insignificant advantage over “Brake-and-Steer.” In the case of adjustable forecast, the optimal forecast time is \(\tau =0.0 \, \text{s}\) and remains up to \({t}_{2}=1.7\, \text{s}\), when \({\varvec{A}}\) returns to “Brake-and-Steer” maneuver (Fig. 12a). It begins turning intensively because of the urgent steering conditions. The arc length of the sharp turning displacement is larger than that of the straight velocity vector. As a result, the speed of \({\varvec{A}}\) shows slight growth for some 0.1 s. At \({t}_{3}=2.1\, \text{s}\), \({\varvec{A}}\) switches again to “Accelerate-and-Steer” (Fig. 12a) to bypass \({\varvec{B}}\) from the left, however keeping the same speed till \({t}_{4}=2.7sec.\). Then it slightly accelerates until \({t}_{5}=3.2sec.\) when it leaves \({\varvec{B}}\) behind and returns to the initial path.

Fig. 12
figure 12

Maneuverability map for the case of \({\varvec{A}}\) − 35 \({\varvec{B}}\) − 35 km/h a adjustable forecast t1 = 1.0 s, t2 = 1.7 s, t3 = 2.1 s, t4 = 2.7 s, t5 = 3.2 s b 2.0 s constant forecast t1 = 1.0 s, t2 = 1.5 s, t3 = 2.8 s, t4 = 3.5 s

Full size image

For the fixed \(\tau =2.0\,\text{s}\), at the beginning of \({\varvec{B}}\boldsymbol{^{\prime}}{\varvec{s}}\) left turn, the momentary linear paths of \({\varvec{A}}\) and \({\varvec{B}}\) intersect few meters ahead of \({\varvec{A}}\). Algorithm associates the area of intersection with the area of potential crash. Therefore, \({\varvec{A}}\) begins the “Accelerate-and-Steer” maneuver at \({t}_{1}=1.0 \,\mathrm{sec}.\) As \({\varvec{B}}\) further turns left, momentary linear paths of \({\varvec{B}}\) turns left as well. As a result, the area of potential crash moves forward ahead of \({\varvec{A}}\) at an increasing rate. Consequently, vehicle \({\varvec{A}}\) starts speeding up at \({t}_{2}=1.5 \,\mathrm{sec}\) till \({t}_{3}=2.8 \mathrm{s}\) (Fig. 12b). At \({t}_{3}\) \({\varvec{A}}\) returns from urgent steering condition. At \({t}_{4}=3.5s\) it leaves \({\varvec{B}}\) behind and returns to the initial path (Fig. 12b).

5 Discussion

Providing vehicles with collision alert systems and autonomic driving capabilities becomes a common practice with the advance of the Driver-Assistance Systems. This paper proposes an algorithm for motion planning and collision avoidance that resolves uncertainty in predicting maneuvering of a dynamic obstacle that moves along a non-linear trajectory.

Given a moving object (a vehicle or a pedestrian), the algorithm accounts for the kinematic state of the surrounding moving objects and the short history of their behavior, calculates the optimal forecast time for estimating the set of available safe displacements for this object, and chooses the optimal displacement. The algorithm performs at a rate of 100 times per second in our simulations. Using a realistic road situation, we demonstrate that the proposed method generates the maneuver which requires the lowest possible energy to avoid a crash.

The essence of the algorithm is the maneuverability maps that represent the set of available displacements at a high time resolution for all reasonable forecast times. The maneuverability maps approach can be part of training human drivers in “defensive-driving” courses.

The proposed approach can be integrated into the control system of a driverless vehicle operating in a heterogeneous environment and sharing roads with human-driven vehicles, pedestrians, and other road users. This control system must include a sensing component for estimating the surrounding vehicles and pedestrians' dimensions and their relative motion. Data sharing between vehicles (V2V) and between the road infrastructure and road users (I2V) is the key feature of smart transportation systems. It is based on arrays of on-board, off-board sensors, as well as fast communication channels between all road users. Sensing based on video processing is one of the major methods used in modern smart transportation systems, it is well studied, widely used, and has zero environmental impact. Experience in using video processing to evaluate traffic scenes began in the early ‘90 s [18], and today it has grown to real-world autonomous driving applications [19]. In their control system [19], the image processing performs in bounds of typical configuration—with 10 Hz for images with a resolution of 782 × 582 [pix] on a Linux PC with a real-time kernel patch. The optimization procedure runs on a real-time rapid pace prototyping system with a cycle time of 25 Hz. SAFEPED’s 100 Hz performing motion planning algorithm may easily be integrated into a control system with a processing rate such as the one discussed in [19]. The implementation of active sensors, such as LIDAR [20] and Doppler radar [21] are yet in development because it requires additional resources and time-consuming signal processing.