From Concentration to Quantitative Regularity: A Short Survey of Recent Developments for the Navier–Stokes Equations

Abstract

In this short survey paper, we focus on some new developments in the study of the regularity or potential singularity formation for solutions of the 3D Navier–Stokes equations. Some of the motivating questions are the following. Are certain norms accumulating/concentrating on small scales near potential blow-up times? At what speed do certain scale-invariant norms blow-up? Can one prove explicit quantitative regularity estimates? Can one break the criticality barrier, even slightly? We emphasize that these questions are closely linked together. Many recent advances for the Navier–Stokes equations are directly inspired by results and methods from the field of nonlinear dispersive equations.

1 Introduction

This short survey paper is concerned with recent developments in the study of the regularity or potential singularity formation for solutions of the 3D Navier–Stokes equations

$$\begin{aligned} \partial _tU-\Delta U+U\cdot \nabla U+\nabla P=0,\qquad \nabla \cdot U=0. \end{aligned}$$

We mostly focus on the whole-space case $\mathbb {R}^3$ or localize away from physical boundaries. We will mainly concentrate on two topics, concentration of solutions on small scales on the one hand and quantitative regularity on the other hand, and show how these subjects are related. The study of these questions is recent for the Navier–Stokes equations. Indeed all the main results in this paper were published in the last five years.

In 2003 Escauriaza, Seregin and Šverák [29] were able to prove the blow-up of the critical borderline norm $L^3$ for singular solutions of 3D Navier–Stokes, provided such solutions exist. This paper was followed by a tremendous amount of works proving analogous results for many kind of evolution equations with a scaling symmetry¹ [15, 28, 41, 42, 44, 58, 61, 62]... These results are all qualitative, with the exception of the work by Merle and Raphaël [58] for nonlinear Schrödinger, which gives a quantitative blow-up rate for a critical norm of radially symmetric solutions.

A breakthrough for the Navier–Stokes equations was achieved by Tao in 2019 [84]. He was able to explicitly quantify the rate of blow-up of the critical $L^3$ norm near a potential first-time singularity

$$\begin{aligned} \limsup _{t\rightarrow T^*}\frac{\Vert U(\cdot ,t)\Vert _{L^3(\mathbb {R}^3)}}{\big (\log \log \log (T^*-t)\big )^{c}}=\infty , \end{aligned}$$

(1.1)

for a universal constant $c\in (0,\infty )$. Previously, only abstract quantitative results were known, which were based on abstract quantification of the seminal (qualitative) result of Escauriaza, Seregin and Šverák [29] and the use of persistence of singularities, see for instance [72].

Some techniques described in this paper are directly inspired by methods introduced for nonlinear dispersive equations. In this vein, let us mention the ‘stacking of scales scheme’ used to prove quantitative regularity estimates in Section 6 and Section 7 inspired by [58], and the ‘mild criticality breaking’ result in Section 9 inspired by [13].

Explicit quantitative estimates: for what purpose? Blow-up rates and quantitative regularity estimates are two sides of the same coin. Let us outline five motivations for the study of quantitative regularity and blow-up rates:

• (1) In the field of PDEs, there seems to be very few quantitative rates for critical norms near the maximal time of existence.

• (2) Quantitative regularity estimates with explicit bounds under a priori boundedness of critical norms enable to break (to some limited extent) the criticality barrier. For instance in Section 9, we use the result of Tao [84] to derive a new regularity criteria in terms of a slightly supercritical Orlicz norm.

• (3) Blow-up rates for critical norms such as (1.1) may enable to rule out certain blow-up scenarios for which the numerically computed growth of the $L^3$ norm is too slow. However, the extremely slow triple logarithmic rate in (1.1) means testing it may be beyond computing capacities, as is emphasized in Hou’s recent paper [34].

• (4) As is well understood for dispersive equations, finding blow-up rates and concentration estimates is a first step toward understanding potential blow-up profiles.

• (5) In turbulence theory, cascade processes are the dominant feature of the inertial range, where nonlinear inertial effects dominate (or are in balance with) viscous dissipative effects. Beyond certain scales though, so-called ‘Kolmogorov scales’, for very high wavenumbers or small spatial scales, dissipative effects dominate. Estimating those dissipative scales quantitatively is one of the main objectives of the quantitative regularity theory, see Section 5.3 and Objective C.

Outline of the paper This survey paper is partly based on several talks given in the past three years. Further comments and topics are found in the habilitation thesis [71]. The first three sections are devoted to ‘weak concentration’ (Section 2), ‘strong concentration’ (Section 4) and a fundamental tool for the quantitative regularity, namely local-in-space smoothing (Section 3). The rest of the paper is concerned with quantitative regularity and blow-up rates for critical norms. Section 5 describes three facets of quantitative regularity: blow-up rates, quantitative regularity estimates and quantitative estimates for dissipative scales. Moreover, two cases are studied, the case of $L^{5}_{t,x}$ which is a toy model, and the case of $L^\infty _tL^3_x$ studied by Tao. Section 6 focuses on the strategy to estimate the dissipative scales in a quantitative manner. Section 7 concentrates on the Type I case. Section 8 reviews some recent developments in the wake of [84]. Section 9 shows that the scaling barrier can be slightly broken thanks to good quantitative estimates in the critical case. This section is based on the paper [8]. There a (partial) answer to a question asked in [84] about the blow-up of certain Orlicz norms is given. Finally in Section 10, we summarize some results in two tables.

Notice that C and c are universal positive constants that may change from line to line.

2 Weak Concentration

In this paper we distinguish between:

• ‘weak concentration’ of norms near a potential blow-up time $T^*$; these results assert the existence of points x(t) (or a sequence of points $x_n$) and scales $\lambda (t)$ (or a sequence of scales $\lambda _n$) such that certain norms accumulate on $B_{x(t)}(\lambda (t))$ as $t\rightarrow T^*$;

• ‘strong concentration’ of norms near a potential space-time blow-up point $(x^*,T^*)$;² these results assert the existence of scales $\lambda (t)$ (or a sequence of scales $\lambda _n$) such that certain norms accumulate on shrinking balls $B_{x^*}(\lambda (t))$ as $t\rightarrow T^*$.

A short review of concentration for certain nonlinear PDEs The first results on concentration near potential singularities date back to more than 30 years ago. They mainly fall into the class of ‘weak concentration’. The study of ‘mass concentration’ i.e. concentration of the $L^{2}$ norm for the nonlinear Schrödinger equations has triggered a lot of developments in this direction, in the wake of the seminal results by Weinstein [86], Merle and Tsutsumi [59], Nawa [64, Theorem B and Theorem C] and [65, Theorem B], Merle [56, 57]. These results were followed by many others: Bourgain [11], Nawa and Tsutsumi [66], Hmidi and Keraani [32, Corollary 1.8] for nonlinear Schrödinger, Kenig, Ponce and Vega [43, Corollary 1.4] for the KdV equation, Merle and Zaag [60, Theorem 1, (ii)] for the semilinear wave equation... We also refer to the books by Cazenave [17, Section 6.5], Tao [82] and Sulem and Sulem [80, Section 5.2.4 and Section 14.3.2].

There are also a number of results that fall into the category of ‘strong concentration’ results, especially for the nonlinear Schrödinger equation, for radially symmetric solutions: Merle and Tsutsumi [59], Tsutsumi [85, Theorem 1.1], Holmer and Roudenko [33, Theorem 1.2]...

The topic of concentration is also strongly tied to proving the blow-up of certain critical norms. The recent paper of Mizoguchi and Souplet on the semilinear heat equation states a strong concentration property for a Type I singularity [62, Lemma 3.1] that is key to proving the blow-up of a critical norm in that case; see also Miura and Takahashi [61] without the Type I assumption.

As for fluids, we mention two results dealing with the possible energy concentration in solutions of Euler and Navier–Stokes equations. These results are a bit orthogonal to the concentration results on which we focus in this paper, but are also interesting directions. Chae and Wolf [19] proved that for 3D Euler under a Type I condition there is no concentration of the energy into isolated points at possible blow-up times. For 3D Navier–Stokes, Arnold and Craig [3, Theorem 4.5] gave a lower bound on the energy concentrating set.

Weak concentration for the Navier –Stokes equations Li, Ozawa and Wang [51, Theorem 1.2] prove what we believe is the first concentration result for potential blow-up solutions of the 3D Navier–Stokes equations. It is proved that for any Leray–Hopf solution U that first blows-up at time $T^*\in (0,\infty )$, one has for any $q\in [1,\infty ]$, the following concentration of the $L^q$ norm:

$$\begin{aligned} \Vert U(\cdot ,t)\Vert _{L^q(|\cdot -x_n|\lesssim \omega (t_n)^{-1})}\gtrsim \omega (t_n)^{1-\frac{3}{q}}, \end{aligned}$$

(2.1)

where $t_n\rightarrow T^*$, $x_n\in \mathbb {R}^3$ and $\omega (t_n):=\Vert U(\cdot ,t_n)\Vert _{L^\infty (\mathbb {R}^3)}\overset{t\rightarrow T^*}{\longrightarrow }\infty$. The proof is based on: (i) selecting a sequence of times $t_n$ on which one has large growth of the $L^\infty$ norm of the solution, (ii) showing that the low frequencies $\lesssim \omega (t_n)$ contribute to a large part of the growth of the $L^\infty$ norm of U.

Let us make two comments on this result. First, it is a concentration result that holds for any Leray–Hopf solution that blows-up. The price to pay for this generality is the fact that the concentration is weak, i.e. not localized in space. Second, the concentration (2.1) holds for any norm in the Lebesgue scale, no matter whether the norm is subcritical ($q\in (3,\infty ]$), critical ($q=3$) or supercritical ($q\in [1,3)$). Notice that in this last case, the lower bound in (2.1) goes to zero as $t\rightarrow T^*$. In the case of $q\in (3,\infty ]$, one can bound the right hand side of (2.1) from below by $(T^*-t_n)^{-\frac{1}{2}(1-\frac{3}{q})}$ thanks to Leray’s [50] lower bound, see (5.1) below, and get the concentration on a ball of size $\sqrt{T^*-t_n}$.

Existence results of mild solutions with $L^q_{\text {uloc}}$ initial data also enable to prove weak concentration for potential blow-up solutions to the Navier–Stokes equations. This was remarked in [54, Corollary 1.1], where the existence of mild solutions in $L^q_{\text {uloc}}$ is combined with a simple scaling argument to yield that for every $t\in (0, T^*)$, there exists $x(t)\in \mathbb {R}^3$, such that for any $q\in [3,\infty ]$,³

$$\begin{aligned} \Vert U(\cdot , t)\Vert _{L^{q}(|\cdot -x(t)|\le \sqrt{T^*-t})}\gtrsim (T^*-t)^{-\frac{1}{2}(1-\frac{3}{q})}. \end{aligned}$$

(2.2)

This strategy is robust enough to apply to the half-space $\mathbb {R}^3_+$ as in [54].

In [39, Theorem 1.6 (i)], Kang, Miura and Tsai prove a statement that can be read as weak concentration result for the supercritical $L^2$ norm near potential singularities of the Navier–Stokes equations: there exists $\gamma _{\text {univ}}\in (0,\infty )$, $S\in (0,\infty )$ and a function $x=x(t)\in \mathbb {R}^3$ such that for all $t\in (0,T^*)$,

$$\begin{aligned} \frac{1}{\sqrt{T^*-t}}\int _{B_{x(t)}\left( \sqrt{\frac{T^*-t}{S}}\right) }|U(x,t)|^2\, dx>\gamma _{\text {univ}}. \end{aligned}$$

This result is in the vein of the one of Bradshaw and Tsai [12, Theorem 8.2], see also Grujić and Xu [31, Theorem 4.1].

The bottom line is that ‘weak concentration’ results are in general a consequence of global regularity results or local well-posedness results and hence use a limited amount of specific structure of the equations. In order to have ‘strong concentration’ results, one needs more localized regularity results at the price of additional a priori assumptions such as a Type I bound on U. This is the topic of the next section.

3 Local-in-Space Smoothing

The idea behind local-in-space smoothing is very natural. Assume that one is given a rough initial data, for instance finite-energy or $L^2_{\text {uloc}}$ i.e. of uniformly locally finite energy, that happens to be more integrable, i.e. critical or subcritical, on some fixed ball, say $B_0(1)$ to fix the ideas. For Navier–Stokes the general question becomes:

Is the local smoothing due to the heat part of the equation strong enough to compensate for the nonlocal effects of the pressure that tend to propagate irregularities of the solutions from large-scale spatial scales to $B_0(1)$?

The answer is yes in many situations, when the local ‘regular’ data is taken in critical or subcritical Lebesgue, Lorentz or Besov spaces. More surprisingly, such results remain even true for the Navier–Stokes equations in the half-space with no-slip boundary condition, where nonlocal effects are known to be strong, see for instance [36, 37, 76]. When the answer is yes, we call such results ‘local-in-space short-time smoothing’. The solution U then satisfies bounds of the type

$$\begin{aligned} \sup _{t \in (0,S(M))} t^{\frac{1}{2}} \Vert U(\cdot ,t)\Vert _{L^\infty (B_0(\frac{1}{2})))} \lesssim 1 \end{aligned}$$

(3.1)

under the condition that $\Vert U_0\Vert _{L^3(B_0(1))}\lesssim 1$ and for a short time $S=S(M)\ll 1$, where M quantifies the large-scale or global ‘background’ assumption on the solution. Typically M is taken to be the $L^2_{\text {uloc}}$ norm of the initial data, which controls the local energy of the associated solution on a certain time interval. This line of research was pioneered by Jia and Šverák in the seminal paper [35]. We find three main classes of methods of proofs that we sketch below. For more details and in particular statements of theorems, we refer to [35, Theorem 3.1, Sections 2 and 3], [6, Theorem 1, Sections 2 and 4], [71, Chapter 5], [39, Theorem 1.1 and Section 3] and [46, Theorem 1.6 and Section 5].

Let us stress that local-in-space smoothing is a versatile tool that proved to be efficient in many situations, such as the existence proof of self-similar solutions [35], strong concentration (see below Section 4) and quantitative regularity (see below Section 5 and Section 7). For the last point in particular, it is important to have quantitative versions of local-in-space smoothing, see for instance [9, Theorem 5.1].

Local-in-space smoothing also helps us gain understanding of a very natural question: for which initial data does the associated solution exhibit improved regularity properties?

3.1 Lin Type Compactness Methods

We work with U a global-in-time local energy solution to the Navier–Stokes equations on $\mathbb {R}^3\times (0,\infty )$ with initial data $U_0\in L^2_{\text {uloc}}(\mathbb {R}^3)$ with some mild decay at space infinity in order to rule out parasitic solutions and get a formula for the pressure.⁴ Assume that $U_0|_{B_0(1)}\in L^q(\mathbb {R}^3)$, with $q\in [3,\infty ]$.⁵

The compactness method proceeds in two steps. One first decomposes the solution U to the Navier–Stokes equations into a mild solution a originating from the critical or subcritical data $U_0|_{B_0(1)}$⁶ and a perturbation V solving a perturbed Navier–Stokes system, with critical or subcritical drift terms and initial data locally zero in $B_0(1)$. The perturbation has small energy locally in $B_0(\frac{1}{2})$ near the initial time and can be extended by zero backward in time. Hence, the regularity of V falls into the realm of epsilon-regularity results, which is the second step of this method.

The method for establishing the epsilon-regularity for the perturbed equation is inspired from the compactness method [52] that Lin used to prove epsilon-regularity for the Navier–Stokes equations. Since the equation for the perturbation V is a Navier–Stokes equation with drift terms, one needs to discriminate between subcritical and critical drifts:

• For subcritical drifts ($q\in (3,\infty ]$), one has improved Hölder regularity for the limit equation in the compactness argument, hence one can directly prove local space-time Hölder regularity near the initial time of the perturbation V. This was done in [35].

• For critical drifts ($q=3$), there is no improved Hölder regularity at the limit in general. One therefore aims at first proving a subcritical Morrey bound for the perturbation that just misses boundedness; see [38]. Then one can combine this subcritical information for V with subcritical information for the mild solution a away from initial time to apply standard epsilon-regularity results for the Navier–Stokes equations to give boundedness of V up to the initial time; see for instance [38, Section 5.3]. It is also possible using information from the initial data to bootstrap the regularity of the perturbation to be Hölder continuous near the initial time; see for instance [6, Section 3].

In the half-space with no-slip boundary condition, we were able to use the compactness method to prove local-in-space smoothing for subcritical and critical data in the Lebesgue scale; see [2]. This work relies on the new estimates for the harmonic pressure obtained in [53]. The compactness scheme is convenient, because in the critical case, the smallness of the drift can be incorporated in the scheme, which avoids proving regularity for the limiting Stokes equation with drift terms, as is done for the whole-space in [35, Lemma 2.2] in the subcritical case or [38, Section 4] in the critical case.

The bottom line is that the compactness method is flexible to handle both the global and the local settings and the regularity away or near boundaries.

3.2 Caffarelli–Kohn–Nirenberg Type Methods

The general scheme of the method is exactly as the one previous of the previous method: decomposition $U=a+V$ and smallness of the local energy of the perturbation V (first step) and epsilon regularity for the perturbed Navier–Stokes equation with drift terms (second step). The difference is in the way the epsilon regularity is proved. In the paper [6, Section 2], we prove an epsilon regularity result for the perturbed Navier–Stokes equations with critical drift terms by using an iteration scheme à la Caffarelli, Kohn and Nirenberg [14]. The criticality of the drift a associated to $L^3$ data causes difficulties, as was the case for the compactness method, and therefore only enables to propagate a subcritical Morrey bound for the perturbation V.

The main advantage of this method lies in the fact that given the current state of the art, it is the only method that manages to handle data locally small in the borderline endpoint Besov space $B^{-1+\frac{3}{q}}_{q,\infty }$ for $q\in (3,\infty )$; see [6, Appendix C]. The results can also be localized, see [6, Theorem 3].

3.3 Scaled Local Energy Methods

This approach was started by Kang, Miura and Tsai [39]. Roughly speaking, it relies on working with the scale-invariant energy and pressure

$$\begin{aligned} E_r(t):=\frac{1}{r}\int _{B_0(r)}|U(\cdot ,t)|^2 +\frac{1}{r}\int _0^t\int _{B_0(r)}|\nabla U|^2+\frac{1}{r^2}\int _0^t\int _{B_0(r)}|p|^\frac{3}{2}, \end{aligned}$$

and propagating the smallness at the initial time, i.e. of $\sup _{r\in (R,1)}E_r(0)$ where R is a given non-negative scale, forward-in-time via local energy estimates and a nonlinear Gronwall-type inequality for

$$ \mathscr {E}_{R,\hat{R}}(t)=\sup _{r\in [R,\hat{R}]}\sup _{s\in (0,t)}E_r(s), $$

for a well-chosen parameter $\hat{R}$.

There are two main advantages of this method. The first advantage is a technical one. The first step of the previous two methods, which consists in splitting the solution into $U=a+V$ where a is the mild solution and V the perturbation is not needed here any longer. One directly works with the solution. The second advantage is that it enables to directly prove local-in-space smoothing for small scaled local kinetic energy [39, Theorem 1.1].

All the local-in-space smoothing results in the local setting mentioned so far are for suitable solutions. Hence the pressure is a priori assumed to be in the Lebesgue space $L^\frac{3}{2}$. Building upon the method of Kang, Miura and Tsai [39], Kwon [46, Theorem 1.6] was able to extend the local-in-space smoothing result for data locally in $L^3$ to the class of dissipative solutions, for which the pressure is merely a distribution. Moreover in [46, Theorem 1.6] the time interval for which the local-in-space smoothing occurs is independent of the pressure.

4 Strong Concentration

As mentioned above, see the preamble of Section 2, strong concentration is the accumulation of norms near potential blow-up points, on balls centered at a singularity, whereas ‘weak concentration’ shows accumulation near blow-up times and is not well localized in space.

Given the current state of the art, strong concentration can be proved in two cases:

• either under some symmetry assumption on the solution, such as radial symmetry for solutions of the nonlinear Schrödinger equation, see for instance [33, 59, 85],

• or under a Type I assumption, see for instance [62, Lemma 3.1] for the semilinear heat equation.

In principle, strong concentration results for the Navier–Stokes equations are simply deduced from local-in-space smoothing results by a contradiction argument, under the condition that one has a good workable notion of Type I.⁷ We assume that the solution satisfies the following generalized Type I bound: for fixed $M,~T^*\in (0,\infty )$ and a fixed radius $r_0\in (0,\infty ]$,

$$\begin{aligned} \sup _{\bar{x}\in \mathbb {R}^3}\sup _{r\in (0,r_0)}\sup _{T^*-r^2<t<T^*}r^{-\frac{1}{2}}\left( \int _{B_{\bar{x}}(r)}|U(x,t)|^2dx\right) ^\frac{1}{2}\le M. \end{aligned}$$

(4.1)

In order to make sense of the condition (4.1) in the case when $r_0>\sqrt{T^*}$, we may extend U by zero in negative times.⁸ That condition ensures that blow-up profiles belong to the class of local energy solutions in which local-in-space smoothing results are proved, see Section 3.

In [6], strong concentration of the critical $L^3$, $L^{3,\infty }$ and Besov norms $B^{-1+\frac{3}{q}}_{q,\infty }$ ($q\in (3,\infty )$) are proven. Figure 1 explains the idea to deduce strong concentration of the $L^3$ norm from local-in-space smoothing for critical $L^3$ data. For a solution U satisfying the Type I bound (4.1), first blowing-up at $T^*$ and such that the space-time point $(0,T^*)$ is a singularity, we have

$$\begin{aligned} \Vert U(\cdot ,t)\Vert _{L^3\left( B_0\left( \sqrt{\frac{T^*-t}{S(M)/2}}\right) \right) }>\gamma _{\text {univ}}, \end{aligned}$$

(4.2)

for all $t\in (t_*(T^*,M,r_0),T^*)$ and S(M) a time appearing in the local-in-space smoothing estimate (3.1).

Fig. 1

Concentration near potential Type I singularities via quantitative local-in-space short-time smoothing

In [39, Theorem 1.6 (ii)] Kang, Miura and Tsai prove the strong concentration of the scaled energy on concentrating balls. Their result holds under the generalized Type I condition (4.1). There exists $\gamma _{\text {univ}}\in (0,\infty )$ and $S(M)\in (0,\infty )$ such that for all $t\in (t_*(T^*,M,r_0),T^*)$,

$$\begin{aligned} \frac{1}{\sqrt{T^*-t}}\int _{B_{0}\left( \sqrt{\frac{T^*-t}{S(M)}}\right) }|U(x,t)|^2\, dx\gtrsim 1. \end{aligned}$$

Notice that under the stronger ODE blow-up Type I condition (4.2), this result simply follows from (4.3) and interpolation.

Figure 6 on page 24 summarizes some results about weak and strong concentration for the Navier–Stokes equations, as well as local-in-space smoothing.

The bottom line is that strong concentration of certain scale-invariant quantities is at the heart of quantitative regularity, in particular for proving quantitative estimates of dissipative scales; see Sections 5.3, 6 and 7.2 below. From now on the paper is concerned with such questions relating to quantitative regularity.

5 Three Facets of Quantitative Regularity

In our view, there are three main objectives for the quantitative regularity theory: (i) quantitative blow-up rates, see Objective A below, (ii) quantitative regularity estimates, see Objective B below, (iii) quantitative estimates of dissipative scales, see Objective C below. The last objective is in some sense more fundamental, since the two others will in general follow from it. We formulate the general objectives in a somewhat loose way. In the rest of the paper, we will explain how the examples fit into that abstract framework. In particular in this section we illustrate the objectives in two cases: the case of a priori control in $L^5(\mathbb {R}^3\times (-1,0))$ which is a critical non-borderline space,⁹ and the case of a priori control in $L^\infty (-1,0;L^3(\mathbb {R}^3))$¹⁰ which is a critical borderline space.

5.1 Quantitative Blow-up Rates

It is known since the seminal work of Leray [50] that subcritical norms blow-up with an algebraic rate near a potential blow-up time $T^*$, i.e.

$$\begin{aligned} \Vert U(\cdot ,t)\Vert _{L^q(\mathbb {R}^3)}\gtrsim (T^*-t)^{-\frac{3}{2}(\frac{1}{3}-\frac{1}{q})}\quad \text {for } q\in (3,\infty )~\text { and }~t\in [0,T^*). \end{aligned}$$

(5.1)

Objective A

Show that for certain critical spaces $L^p_t\mathcal A_x$ and $\mathcal B$,¹¹ there exists an explicit positive function $\mathscr {F}$ or $\mathscr {F}_{p,\mathcal A}$ on $[0,\infty )$ such that $\mathscr {F}(s),\ \mathscr {F}_{p},\mathcal {A}(s)\overset{s\rightarrow 0}{\longrightarrow }\infty$ and for a smooth solution with enough decay¹²U to the Navier–Stokes equations on $\mathbb {R}^3\times (0,T^*)$ blowing-up at time $T^*$,

$$\begin{aligned} \frac{\Vert U\Vert _{L^p(0,t;\mathcal A)}}{\mathscr {F}(T^*-t)}\gtrsim 1\quad \textit{when}~t~\textit{is sufficiently close to } T^*\end{aligned}$$

(5.2)

or

$$\begin{aligned} \frac{\Vert U(\cdot ,t)\Vert _{\mathcal B}}{\mathscr {F}_{p,\mathcal A}(T^*-t)}\gtrsim 1\quad \textit{when}~t~\textit{is sufficiently close to } T^*. \end{aligned}$$

(5.3)

${The \,toy \,model\,L^5_{t,x}}$ Using the same reasoning as (5.5), the quantitative estimate (5.6) combined with Leray’s blow-up rate (5.1) imply that

$$\begin{aligned} \Vert U\Vert _{L^5(0,t;L^5(\mathbb {R}^3))}\gtrsim \left( \log \left( \frac{T^*}{T^*-t}\right) \right) ^\frac{1}{5}\quad \text {for all }~t\in \left( \tfrac{T^*}{2},T^*\right) . \end{aligned}$$

Not surprisingly, this estimate is compatible with (and actually a consequence of) the Leray blow-up rate (5.1) in the case $q=5$.

${The\,case\,of}\,L^\infty _tL^3_{x}$ The critical borderline case $q=3$ was open until 2019 and a remarkable paper of Tao [84]. There Tao proves the rate (1.1). Notice that this rate follows from the lower bound (5.2) proved in [84] with $p:=\infty$, $\mathcal A:=L^3(\mathbb {R}^3)$ and $\mathscr {F}(s):=(\log \log \log s)^{c}$, for a universal constant $c\in (0,\infty )$.

5.2 Quantitative Regularity Estimates

Objective B

Show that for certain critical spaces $L^p(-1,0;\mathcal A)$ and $\mathcal B$, there exists an explicit positive function $\mathscr {G}$ on $[0,\infty )$,¹³ such that for a critically bounded smooth solution U (with enough decay) of the Navier–Stokes equations on $\mathbb {R}^3\times (-1,0)$,

$$\begin{aligned} \Vert U\Vert _{L^{\infty }\left( \mathbb {R}^3\times \left( -\frac{1}{2},0\right) \right) }\le \mathscr {G}(\Vert U\Vert _{L^p(-1,0;\mathcal A)},\Vert U(\cdot ,0)\Vert _{\mathcal B}). \end{aligned}$$

(5.4)

We previously remarked that certain qualitative regularity results in terms of critical norms can be quantified abstractly, see [9, Introduction]. This is the case of the Escauriaza, Seregin and Šverák [29] result that can be abstractly quantified via the use of the persistence of singularities [72]. The focus of this survey paper is to derive an explicit formula for $\mathscr {G}$.

Let us also note that a general quantitative result such as (5.4) with an increasing function $\mathscr {G}$ can be combined with the Leray blow-up rate (5.1) to yield quantitative blow-up rates of the form (5.2)–(5.3). Indeed, by scaling¹⁴

$$\begin{aligned} \frac{1}{\sqrt{t}}\mathscr {G}\left( \Vert U\Vert _{L^\infty (0,t;L^3(\mathbb {R}^3))}\right)= & {} \frac{1}{\sqrt{t}}\mathscr {G}\left( \Vert U_{\sqrt{t}}\Vert _{L^\infty (0,1;L^3(\mathbb {R}^3))}\right) \nonumber \\\ge & {} \frac{1}{\sqrt{t}}\Vert U_{\sqrt{t}}\Vert _{L^\infty \left( \mathbb {R}^3\times \left( \frac{1}{2},1\right) \right) }\nonumber \\= & {} \Vert U\Vert _{L^\infty \left( \mathbb {R}^3\times \left( \frac{t}{2},t\right) \right) }\nonumber \\\ge & {} C(T^*-t)^{-\frac{1}{2}}. \end{aligned}$$

(5.5)

It remains to invert $\mathscr {G}$ to get a blow-up rate for $\Vert U\Vert _{L^\infty (0,t;L^3(\mathbb {R}^3))}$.

${The\,toy\,model}\,L^5_{t,x}$ Using the strategy described in Section 6 below,¹⁵ one can prove the following quantitative estimate:

$$\begin{aligned} \Vert U\Vert _{L^{\infty }\left( \mathbb {R}^3\times \left( -\frac{1}{2},0\right) \right) }\lesssim \exp \left( \Vert U\Vert _{L^5(\mathbb {R}^3\times (-1,0))}^5\right) , \end{aligned}$$

(5.6)

where $C\in (0,\infty )$ is a universal constant. Here

$$\begin{aligned} p=5,\quad \mathcal A=L^5(\mathbb {R}^3),\quad \text {and}\quad \mathscr {G}(A,B)\simeq \exp (A^5) \end{aligned}$$

in the notation of the general form estimate (5.4).

${The\,case\,of}\,L^\infty _tL^3_{x}$ Tao shows that for classical solutions to the Navier–Stokes equations on belonging to the critical space $L^{\infty }(-1,0; L^{3}(\mathbb {R}^3))$,

$$\begin{aligned} \Vert U\Vert _{L^{\infty }\left( \mathbb {R}^3\times \left( -\frac{1}{2},0\right) \right) }\lesssim \exp \exp \exp \left( \Vert U\Vert _{L^{\infty }(-1,0;L^3(\mathbb {R}^3))}^{c}\right) , \end{aligned}$$

(5.7)

where $c\in (0,\infty )$ is a universal constant. Here

$$\begin{aligned} p:=\infty ,\quad \mathcal A:=L^3(\mathbb {R}^3),\quad \text {and}\quad \mathscr {G}(A,B)\simeq \exp (\exp (\exp (A^c))) \end{aligned}$$

in the notation of the general form estimate (5.4).

5.3 Quantitative Estimates of Dissipative/Kolmogorov Scales

Objective C

Show that for certain critical spaces $L^p(-1,0;\mathcal A)$ and $\mathcal B$,¹⁶ there exists an explicit positive function $\mathscr {H}$ on $[0,\infty )$ such that for a critically bounded smooth solution with enough decay U to the Navier–Stokes equations on $\mathbb {R}^3\times (-1,0)$, dissipative effects take over the nonlinearity¹⁷ for physical scales

$$\begin{aligned} \lambda \le \mathscr {H}\left( \Vert U\Vert _{L^\infty (-1,0;\mathcal A)},\Vert U(\cdot ,0)\Vert _{\mathcal B}\right) \end{aligned}$$

(5.8)

or Fourier scales

$$\begin{aligned} N\ge \mathscr {H} \left( \Vert U\Vert _{L^\infty (-1,0;\mathcal A)},\Vert U(\cdot ,0)\Vert _{\mathcal B}\right) . \end{aligned}$$

The threshold between the scales where diffusive effects dominate vs. where nonlinear effects dominate is measured by the smallness vs. concentration of certain scale-critical quantities $\mathscr {S}$. Once this threshold is estimated in a quantitative way, regularity criteria (epsilon-regularity, local smoothing...) imply the quantitative bounds stated in Objective B. The estimate of dissipative scales is hence the heart of the matter.

Figure 2 summarizes the general strategy in the three main cases described in this survey paper.

${The\,toy\,model}\,L^5_{t,x}$ For solutions of the Navier–Stokes equations critically bounded in $L^5(\mathbb {R}^3\times (-1,0))$, we work with the following scale-invariant Weissler–Kato type norms

$$\begin{aligned} (-t)^\frac{1}{5}\Vert U(\cdot ,t)\Vert _{L^5(\mathbb {R}^3)}\quad \text {for }~t\in (-1,0). \end{aligned}$$

(5.9)

If the quantity defined by (5.9) is small for all sufficiently small times $0>t>t_*(A)$, then Caffarelli, Kohn and Nirenberg type epsilon-regularity results imply the quantitative bound (5.6).¹⁸

Objective Cin the $L^5_{t,x}$ case: If the following statement

$$\begin{aligned} \mathscr {S}(t):=(-t)^\frac{1}{5}\Vert U(\cdot ,t)\Vert _{L^5(\mathbb {R}^3)}<\varepsilon \end{aligned}$$

(5.10)

fails for a certain $t\in (-1,0)$, find a quantitative upper bound $t_*\in (-1,0)$ for t.

Estimate (5.10) together with $\varepsilon$-regularity criteria then implies the quantitative bound (5.6). It can be shown, applying the general strategy outlined in Section 6, that

$$\begin{aligned} -t>\frac{1}{2}\exp \left( -\tfrac{32\Vert U\Vert _{L^5(\mathbb {R}^3\times (-1,0))}^5}{\varepsilon ^5}\right) =:-t_*(A). \end{aligned}$$

(5.11)

Hence, $\mathscr {H}(A,B):=-t_*(A)=\exp (-\frac{32A^5}{\varepsilon ^5})$ with the notation of Objective C.

${The\,case\,of}\,L^\infty _tL^3_{x}$ Tao works with globally defined quantities due to a Fourier based approach. His analysis is based on the following scale-invariant quantities

$$\begin{aligned} \mathscr {S}(N;x,t):=N^{-1}|P_{N}U(x,t)|\quad \text {for }~ (x,t)\in \mathbb {R}^3\times (-1,0), \end{aligned}$$

(5.12)

where $P_N$ is the Littlewood–Paley projection on the frequency $N\in (0,\infty )$. Indeed, if the quantity $\mathscr {S}(N;x,t)$ defined by (5.12) is small in terms of $A:=\Vert U\Vert _{L^{\infty }_{t}L^{3}_{x}(\mathbb {R}^3\times (-1,0))}$, uniformly in $(x,t)\in \mathbb {R}^3\times (-\frac{1}{2},0)$ and for high frequencies $N\ge N_*(A)$, then $\Vert U\Vert _{L^{\infty }_{x,t}(\mathbb {R}^3\times (-\frac{1}{8},0))}$ can be estimated explicitly in terms of A and $N_*$. Related observations were made previously by Cheskidov and Shvydkoy [25, 26] and Cheskidov and Dai [24], but without the bounds explicitly stated. There the frequency $N_*$ is called the Kolmogorov scale and denoted $\Lambda$. If $N^{-1}\Vert P_{N}U\Vert _{L^{\infty }_{x,t}}\ll 1$ is small, then $N\Vert P_NU\Vert ^2_{L^\infty _{t,x}}\ll N^2\Vert P_NU\Vert _{L^\infty _{t,x}}$ so that the diffusion dominates the nonlinearity, heuristically at least, since some of the frequencies in the paraproduct are neglected, see [83].

From this perspective, Tao’s aim is the following.

Tao’s Objective C: Assume

$$\begin{aligned} A:=\Vert U\Vert _{L^{\infty }_{t}L^{3}_{x}(\mathbb {R}^3\times (-1,0))}<\infty . \end{aligned}$$

If the following statement

$$\begin{aligned} N^{-1}\Vert P_{N}U\Vert _{L^{\infty }_{x,t}(\mathbb {R}^3\times (-\frac{1}{2},0))}<\varepsilon (A) \end{aligned}$$

(5.13)

fails for $\varepsilon (A)= A^{-c}$ and a certain frequency N, find a quantitative upper bound $N_*(A)$ for N.

In Tao’s paper [84, Theorem 5.1], it is shown that

$$\begin{aligned} \mathscr {H}(A,B):=N_*(A)\simeq \exp \exp \exp (A^{c}) \end{aligned}$$

(5.14)

with the notations of Objective C.

Fig. 2

Quantitative regularity via concentration: a summary of the method

6 A General Strategy for Quantitative Estimates of Dissipative Scales

In this part we describe a general strategy to fulfill Objective C, i.e. to estimate quantitatively the dissipative scales. The scheme is based on the study of the concentration of certain scale-invariant quantities $\mathscr {S}$, such as the Weissler–Kato norm (5.10) in the case of $L^5_{t,x}$ or the frequency bubbles (5.12) in the case of $L^\infty _tL^3_x$. One can summarize the idea as follows:

• (Step-1) Propagation of concentration If a certain scale-invariant quantity $\mathscr {S}$ concentrates at a given scale, then it will concentrate at many disjoint scales. One relies on various tools such as bilinear estimates or local-in-space smoothing when applying quantitative Carleman inequalities. For this, one needs to work in space-time regions where one has good quantitative regularity properties: epochs and annuli of quantitative regularity.

• (Step-2) Summation of scales and coercivity of the standing assumption The standing critical assumption

  $$\begin{aligned} \Vert U\Vert _{L^\infty (-1,0;\mathcal A)}<\infty \quad \text {or}\quad \Vert U(\cdot ,0)\Vert _{\mathcal B}<\infty \end{aligned}$$

  implies an upper bound on the number of disjoint scales where the scale-invariant quantity $\mathscr {S}$ concentrates, which directly yields a quantitative estimate of the estimate of dissipative scales $\mathcal H$ in Objective C.

6.1 The Toy Model $L^5_{t,x}$

Let us now sketch the proof in the toy model case see Fig. 3. Assume that

$$\begin{aligned} A:=\Vert U\Vert _{L^5(\mathbb {R}^3\times (-1,0))}<\infty \end{aligned}$$

and that (5.10) fails for a certain t. In order to estimate the dissipative scales quantitatively, see Objective C above, we argue in the following two-step way:

• (Step-1) Backward propagation of Weissler–Kato norm concentration Using the proof of the well-posedness theory for subcritical $L^5$ data [16] we get

  $$\begin{aligned} \Vert U(\cdot ,t)\Vert _{L^5(\mathbb {R}^3)}>\frac{\varepsilon }{(-t)^{\frac{1}{5}}}~ \Rightarrow ~ \Vert U(\cdot ,t')\Vert _{L^5(\mathbb {R}^3)}>\frac{\varepsilon /2}{(-t')^{\frac{1}{5}}}\quad \text {for all }~t'\in (-1,2t). \end{aligned}$$

• (Step-2) Summation of scales and coercivity of the standing assumption Integrating the concentration for $t'\in (-1,2t)$,

  $$\begin{aligned} \Vert U\Vert _{L^5(\mathbb {R}^3\times (-1,0))}^5\ge \int _{-1}^{2t}\Vert U(\cdot ,t')\Vert _{L^5(\mathbb {R}^3)}^5\, dt' \ge -\frac{\varepsilon ^5}{32}\log (-2t). \end{aligned}$$

  Hence, we get the estimate (5.11), which is the upper bound for the times where the Weissler–Kato norm concentrates.

Fig. 3

Quantitative regularity via concentration of scale-critical quantities: the toy model $L^5_{t,x}$

6.2 The Case of $L^\infty _tL^3_x$

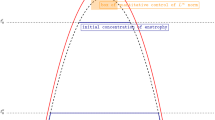
We now sketch the strategy of Tao to prove his main Objective C described on page 13. A slightly different summary of the strategy is given in [9, Section 1.1] and in [84, Section 1]. Assume that

$$\begin{aligned} A:=\Vert U\Vert _{L^{\infty }(-1,0;L^{3}_{x}(\mathbb {R}^3))}<\infty \end{aligned}$$

(6.1)

and that (5.13) fails for $\varepsilon (A)= A^{-c}$ and a certain frequency N. Hence, there exists $(x_0,t_0)\in \mathbb {R}^3\times (-\frac{1}{2},0)$ such that

$$\begin{aligned} N^{-1}|P_{N}u(x_0,t_0)|> A^{-c}. \end{aligned}$$

(6.2)

We call this the ‘initial concentration’.

(Step-1):

Propagation of concentration The idea is to transfer the initial concentration (6.2) in space and time in order to get a lower bound on the $L^3(\mathbb {R}^3)$ norm at time zero. That propagation of concentration, or ‘frequency bubbling’, relies on:

(i):

Backward frequency bubbling For all $n\in \mathbb {N}$, there exists a frequency $N_{n}\in (0,\infty )$, $(x_{n}, t_{n})\in \mathbb {R}^3\times (-1,t_{n-1})$ such that

$$\begin{aligned} N_{n}^{-1}|P_{N_{n}}u(x_{n},t_{n})|> A^{-c} \end{aligned}$$

(6.3)

with

$$\begin{aligned} x_{n}=x_{0}+A^{O(1)}(-t_{n})^{\frac{1}{2}},\quad N_{n}\simeq A^{O(1)}|-t_{n}|^{-\frac{1}{2}}. \end{aligned}$$

(6.4)

(ii):

Transfer of concentration in Fourier space to physical space In order to use quantitative Carleman inequalities, see the next point, one needs to transfer the information on the concentration in Fourier space to physical space quantities, namely a scale-invariant enstrophy. To do this it seems important to have a priori control of a global scale-invariant norm, such as (6.1).

(iii):

Large-scale and forward-in-time propagation of concentration Using quantitative versions of the Carleman inequalities in [29], see [84, Propositions 4.2 and 4.3], Tao shows that the lower bounds on the scale-invariant enstrophy can be transferred to a lower bound on the $L^{3}$ norm of U at the final moment of time 0. The applicability of the quantitative Carleman inequalities to the vorticity equation requires the ‘epochs of regularity’ in the previous step and the existence of ‘good spatial annuli’ where the solution enjoys good quantitative estimates. Specifically, Tao shows that for certain admissible time scales S,¹⁹ one has the concentration of the $L^3$ norm on the annulus $\{S^\frac{1}{2}\le |\cdot -x_{0}|\le \exp (A^c)S^\frac{1}{2}\}$, i.e.

$$\begin{aligned} \int _{S^\frac{1}{2}\le |x-x_{0}|\le \exp (A^c)S^\frac{1}{2}} |U(x,0)|^3 dx\ge \exp (-\exp (A^{c})). \end{aligned}$$

(6.5)

(Step-2):

Summation of scales and coercivity of the standing assumption Summing (6.5) over admissible time scales S such that the annuli $\{S^\frac{1}{2}\le |\cdot -x_{0}|\le \exp (A^c)S^\frac{1}{2}\}$ are disjoint, one eventually obtains

$$\begin{aligned} A^3\ge \int _{\mathbb {R}^3}|U(x,0)|^3dx\gtrsim \log (N)\exp (-\exp (A^{c})). \end{aligned}$$

This concludes the proof of the triple exponential upper bound (5.14) for N.²⁰

Let us note that ideas in a similar spirit were used by Merle and Raphaël in [58] to prove a quantitative rate of blow-up of a critical norm for radial solutions of a supercritical nonlinear Schrödinger equation; see [58, Theorem 2]. In particular a lower bound on annuli analogous to (6.5) is obtained and the final $\log$ blow-up rate is obtained by a similar stacking of scales argument; see [58, Section 4.2].

7 Quantitative Regularity in the Type I Case

We focus here on the quantitative regularity results in the Type I case proved in [9]. Let us emphasize that the regularity in the Type I case is proved only for axisymmetric flows²¹ [21, 22, 45]. We now show how the results in [9] fulfill the three objectives stated in Section 5.

7.1 Three Facets of the Quantitative Regularity in the Type I Case

Answer to Objective A

Result A

([9, Theorem A], localized quantitative rate of blow-up) Assume that U is a smooth solution with sufficient decay to the Navier–Stokes equations and that $T^*$ is a first blow-up time.

Assume in addition that $(0,T^*)$ is a Type I singular point i.e.

$$\begin{aligned} A:=\Vert U\Vert _{L^{\infty }(0,T^*;L^{3,\infty }(\mathbb {R}^3))}<\infty . \end{aligned}$$

Then the above assumptions imply that there exists $S(A)\simeq A^{-30}$ such that for any $t\in (\frac{T^*}{2},T^*)$ and

$$\begin{aligned} R\in \left( \sqrt{\tfrac{T^*-t}{S(A)}},e^{A^{1022}}\sqrt{T^*}\right) \end{aligned}$$

we have

$$\begin{aligned} \int _{|x|<R} |U(x,t)|^3 dx\ge \frac{\log \left( \frac{R^2}{A^{802}(T^*-t)}\right) }{\exp (\exp (A^{1025}))}. \end{aligned}$$

(7.1)

Estimate (7.1) is written in a scale-invariant form. Notice that this estimate implies an estimate of the form (5.3). Indeed taking $R=(T^*-t)^{\frac{1}{2}-\delta }$ for $\delta >0$ and small, we have (5.3) with $\mathcal B:=L^3(B_0((T^*-t)^{\frac{1}{2}-\delta })))$, $p:=\infty$, $\mathcal A:=L^{3,\infty }(\mathbb {R}^3)$, $\mathscr {F}_{p,\mathcal A}\simeq -\log \big (A^{802}(T^*-t)^{2\delta }\big )$ and $|T^*-t|\lesssim _{A}1$.

Notice that contrary to (1.1), it is stated in (7.1) that the norm blows-up not only along a subsequence but pointwise for $t\rightarrow T^*$. This is due to the fact that the quantitative regularity under the a priori Type I control, see Result B, just involves the $L^3$ norm at the final time and not the whole $L^\infty _tL^3_x$ norm of the solution as the estimate (5.7) of [84].

Answer to Objective B

Result B

([9, Proposition 2.1, estimate (52)], localized quantitative regularity) Assume that U is a smooth solution with sufficient decay to the Navier–Stokes equations.

Assume in addition that U satisfies the Type I bound

$$\begin{aligned} A:=\Vert U\Vert _{L^{\infty }(-1,0;L^{3,\infty }(\mathbb {R}^3))}<\infty . \end{aligned}$$

Then, letting

$$\begin{aligned} t_*= & {} t_*(A,U(\cdot ,0))\\:= & {} -A^{-c}\exp \left( -\exp \exp (A^{1024})\int _{B_{0}(\exp (A^{1023}))}|U(\cdot ,0)|^3\right) , \end{aligned}$$

the following quantitative boundedness holds

$$\begin{aligned} \Vert U\Vert _{L^\infty (B_{0}(A^{c}\sqrt{-t_*})\times (t_*/2,0))}\lesssim \frac{A^{-c}}{\sqrt{-t_*}}, \end{aligned}$$

(7.2)

with $c\in (0,\infty )$ a universal constant.

Notice that (7.2) involves the a priori Type I control in $L^\infty _tL^{3,\infty }_x$ and the control of the $L^3$ norm at the final time. Given the current state of the art, such assumptions are needed to prove the regularity; a mere Type I assumption is at this point not enough to beat the scaling except in the axisymmetric case and the self-similar case.²² For more insights on the qualitative regularity in borderline endpoint critical spaces such as the Lorentz space $L^{3,\infty }$ or the Besov space $B^{-1+\frac{3}{p}}_{p,\infty }$, see [1].²³

Estimate (7.2) also implies a localized quantitative bound in the spirit of (5.4) with $\mathcal B:=L^3(B_0(\exp (A^{1023})))$, $p:=\infty$, $\mathcal A:=L^{3,\infty }(\mathbb R^3)$,

$$\begin{aligned} \mathscr {G}(A,B)\simeq \exp \big (\exp (\exp (A^c))B),\quad{} & {} \text {where }~ A:=\Vert U\Vert _{L^{\infty }(-1,0;L^{3,\infty }(\mathbb {R}^3))}\\{} & {} \text {and }~B:=\int _{B_0(\exp (A^{1023}))}|U(\cdot ,0)|^3. \end{aligned}$$

Answer to Objective C

Result C

([9, Proposition 2.1, estimate (50)], quantitative estimates of dissipative/Kolmogorov scales) Assume that U is a smooth solution with sufficient decay to the Navier–Stokes equations.

Assume in addition that U satisfies the Type I bound

$$\begin{aligned} A:=\Vert U\Vert _{L^{\infty }(-1,0;L^{3,\infty }(\mathbb {R}^3))}<\infty . \end{aligned}$$

Then the threshold determining where the dissipative effects dominate the nonlinear effects is estimated as follows:

$$\begin{aligned} t_*= & {} t_*(A,U(\cdot ,0))\nonumber \\:= & {} -A^{-c}\exp \left( -\exp \exp (A^{1024})\int _{B_{0}(\exp (A^{1023}))}|U(\cdot ,0)|^3\right) . \end{aligned}$$

(7.3)

It is not surprising that the definition of $t_*$ already appears in Result B, since Result B is (almost) an immediate consequence of Result C and a regularity criteria (namely a local-in-space short-time regularity result). More precisely, $-t_*$ defined by (7.3) is the time after which the following scale-invariant enstrophy

$$\begin{aligned} \mathscr {S}(A;t):=(-t)^{\frac{1}{2}}\int _{B_{0}\left( A^c(-t)^{\frac{1}{2}}\right) }|\omega (x,t)|^2 dx \end{aligned}$$

(7.4)

is smaller than a given small number $\varepsilon (A)=A^{-c}$, where $\omega =\nabla \times U$ is the vorticity as is usual.

Estimate (7.3) also implies a quantitative bound like (5.8) with $\mathcal B:=L^3(B_0(\exp (A^{1023})))$, $p:=\infty$, $\mathcal A:=L^{3,\infty }(\mathbb {R}^3)$,

$$\begin{aligned} \mathscr {H}(A,B)\simeq A^{-c}\exp \big (-\exp \exp (A^{1024})B\big ),\quad{} & {} \text {where }~ A:=\Vert U\Vert _{L^{\infty }(-1,0;L^{3,\infty }(\mathbb {R}^3))}\\{} & {} \text {and }~ B:=\int _{B_0(\exp (A^{1023}))}|U(\cdot ,0)|^3. \end{aligned}$$

7.2 Quantitative Estimates of Dissipative Scales in the Type I Case

The general scheme to get the estimate (7.3) is a physical space parallel to Tao’s Fourier based strategy described in Section 6.2. Assume that $\mathscr {S}(A;t)$ defined by (7.4) concentrates, i.e. is not small, for a certain time t. Then, the goal is to find an upper bound $t_*$ for t. More precisely, assume that

$$\begin{aligned} \mathscr {S}(A;t):=(-t)^{\frac{1}{2}}\int _{B_{0}\left( A^c(-t)^{\frac{1}{2}}\right) }|\omega (x,t)|^2 dx>A^{-c}, \end{aligned}$$

(7.5)

for a $t\in (-1,0)$ not too close to $-1$. We call this the ‘initial concentration’.

Fig. 4

Quantitative regularity in the Type I case via concentration of a scale-invariant enstrophy Step-1: backward (label 2 above), large-scale (label 3 above) and forward propagation of enstrophy concentration (label 4 above)

Fig. 5

Quantitative regularity in the Type I case via concentration of a scale-invariant enstrophy Step-2: summation of scales

• (Step-1) Propagation of concentration For this step we refer to Fig. 4. The idea is to transfer the initial concentration (7.5) in space and time in order to get a lower bound on the localized $L^3$ norm at time zero. That propagation of concentration relies on:

  • (i) Backward propagation of concentration For all $t'\in (-1,t)$ such that $-t'$ is not too close to $-t$, we have

    $$\begin{aligned} (-t')^{\frac{1}{2}}\int _{B_{0}\left( A^c(-t')^{\frac{1}{2}}\right) }|\omega (x,t')|^2 dx>A^{-c}. \end{aligned}$$

  • (ii) Large-scale and forward-in-time propagation of concentration It is shown that for certain admissible time scales S,²⁴ one has the concentration of the $L^3$ norm on the annulus $\{S^\frac{1}{2}\le |\cdot |\le \exp (A^c)S^\frac{1}{2}\}$, i.e.

    $$\begin{aligned} \int _{S^\frac{1}{2}\le |\cdot |\le \exp (A^c)S^\frac{1}{2}} |U(x,0)|^3 dx\ge \exp (-\exp (A^{c})). \end{aligned}$$

    (7.6)

    The role of the Type I bound is to show that the solution U obeys good quantitative estimates in certain space-time regions, epochs of quantitative regularity and annuli of quantitative regularity, which is needed to apply the Carleman inequalities to the vorticity equation, see [29], see [84, Proposition 4.2 and Proposition 4.3].

• (Step-2) Summation of scales and coercivity of the standing assumption We refer to Fig. 5 for this step. Summing (7.6) over all permissible disjoint annuli finally gives us the desired lower bound for $-t'$. We note that the localized $L^{3}$ norm of U at time 0 plays a distinct role to that of the Type I condition described in the previous step. Its sole purpose is to bound the number of permissible disjoint annuli that can be summed. This concludes the proof of the single exponential upper bound in $\int _{B_{0}(\exp (A^{1023}))}|U(\cdot ,0)|^3$ for t, see (7.3).

Notice that quantitative local-in-space smoothing, see Section 3 above, is a fundamental tool to achieve the backward propagation of enstrophy concentration in (Step-1) above as well as to go from Result C to Result B.

7.3 A Comparison with Tao’s Strategy

We outline here the two main differences between: on the one hand Tao’s strategy [84] for the quantitative regularity in the case of a priori control of the solution in the borderline critical space $L^\infty _tL^3_x$ and on the other hand the strategy of [9] for the quantitative regularity in the case of a priori control of the solution in the borderline endpoint critical space $L^\infty _tL^{3,\infty }_x$ with additional control of the $L^3$ norm of $U(\cdot ,0)$. There are two main aspects, see below. The first aspect is the decisive difference that also explains the second point. Let us state these two differences for the sake of clarity.

Fourier space vs. physical space We already underlined this aspect above. Tao works with the frequency bubbles of concentration (5.12), which are scale-invariant quantities defined in Fourier space. Therefore these quantities involve the solution $U(\cdot ,t)$ on the whole-space $\mathbb {R}^3$. On the contrary, the analysis of [9] relies on the localized scale-invariant enstrophies (7.4). Those quantities are defined in physical space and involve the solution U only on the ball $B_{0}(A^c(-t)^{\frac{1}{2}})$. Therefore, one can obtain localized results, such as the blow-up rate (7.1) of Result A.

Global scale-critical vs. criticality along a sequence of times/at a given time This aspect is a consequence of the point made above about Fourier vs. physical space approach. In Tao’s work, there is a step, see ‘Transfer of concentration in Fourier space to physical space’ in Section 6.2, that consists in transferring the concentration of frequency bubbles to concentration of a scale-invariant enstrophy, see [84, equation (5.6)]. That localized $L^2$ norm of the vorticity is needed to work with quantitative Carleman inequalities in order to propagate the concentration at large scales and forward in time. The process of transfer is based on the fact that the solution is bounded in $L^\infty (-1,0;L^3(\mathbb {R}^3))$. In the case of the strategy described in Section 7.2 above in the Type I case, this step is not needed.

This remark has several implications:

• (1) The scheme developed in the Type I case, see Section 7.2, enables to handle the case when a global scale-critical standing assumption is lacking, which is the case in [9, Theorem B] that quantifies Seregin’s 2012 criteria [73].

• (2) In a related vein, we get regularity at time $t=0$ for large $L^3$ data at $t=-1$ if the profile at time $t=0$ is quantitatively small; see [1, Theorem 4.1 (i)] for a qualitative statement and [9, Proposition 4.4] for a quantitative statement.

8 Some Further Developments

There are many interesting research developments in the wake of the two papers [9, 84]. Let us review some of them.

Very recently, the paper [5] was able to give a localized version of Tao’s blow-up rate (1.1). For a smooth suitable weak solution U to the Navier–Stokes equations on $B(0,4)\times (0,T^*)$, that possesses a singular point $(x_0,T^*)\in B(0,4)\times \{T^*\}$, then for all $\delta >0$ sufficiently small

$$ \limsup _{t\uparrow T^*} \frac{\Vert U(\cdot ,t)\Vert _{L^{3}(B(x_0,\delta ))}}{\left( \log \log \log \left( \frac{1}{(T_*-t)^{\frac{1}{4}}}\right) \right) ^{\frac{1}{1129}}}=\infty . $$

In that sense, this bound is a true quantification of the qualitative Escauriaza, Seregin and Šverák [29] criteria, which is also localized but qualitative. The main difficulty with the localization is related to showing that the local solution possesses quantitative annuli and epochs of regularity, which is required in (Step-1)(iii).

The quantitative regularity for solutions $U\in L^\infty _tL^d_x$ to the Navier–Stokes equations in higher dimensions $d\ge 4$ was handled by Palasek in [69]. This work gives an effective quantification of the qualitative result by Dong and Du [27]. For the blow-up rate, one pays the price of an additional logarithm compared to the result in dimension three (1.1).

Palasek [68] was also able to improve upon the triple logarithmic rate (1.1) obtained by Tao in [84]: in the case of axisymmetric solutions for instance, the triple logarithm is replaced by a double logarithm. Without any symmetry assumption on the solution, a similar improvement can be obtained by replacing the $L^3$ norm by the scale-invariant norm $\Vert r^{1-\frac{3}{q}}U\Vert _{L^\infty _tL^q_x}$ for $q\in (3,\infty )$ and $r:=|x_h|$.

Finally, let us mention a related research line that aims at quantifying the regularity of axisymmetric solutions satisfying a critical or slightly supercritical Type I a priori bound. In the wake of the result of Pan [70], De Giorgi methods were intensively used to improve upon the regularity beyond the Type I case (see [21, 22, 45, 48]) by slightly breaking the a priori scale-invariant assumption. This research was carried by Seregin [74, 75] and Chen, Tsai and Zhang [23]. In this last paper, a double-logarithmic quantitative blow-up rate for the $\dot{B}^{-1}_{\infty ,\infty }(\mathbb {R}^3)$ norm of U is obtained; see [23, Theorem 1.4]. Using Harnack inequalities instead of the Carleman inequalities used by Tao [84], Ożański and Palasek [67] recover the blow-up rate of the $L^{3,\infty }(\mathbb {R}^3)$ norm of U; see [67, Corollary 1.2]. In addition, they obtain a quantitative bound of the form (5.4) in terms of the $L^\infty _tL^{3,\infty }_x$ norm of the solution only; see [67, Theorem 1.1]. For other developments, see [47].

9 Mild Criticality Breaking and a Conjecture of Tao

Recently, in [84, Remark 1.6], Tao conjectured that if a solution first loses smoothness at time $T^*>0$, then the Orlicz norm $\Vert U(\cdot ,t)\Vert _{L^{3}(\log \log \log L)^{-c}(\mathbb {R}^3)}$ must blow-up as t tends to $T^*$. Result D provides a positive answer to Tao’s conjecture, at the cost of one additional logarithm.

Result D

(Blow-up of slightly supercritical Orlicz norms; [8, Theorem 2]) There exists a universal constant $\theta \in (0,1)$ such that the following holds.

Let U be a Leray–Hopf solution to the Navier–Stokes equations on $\mathbb {R}^3\times (0,\infty )$ with initial data $U_0\in L^2(\mathbb {R}^3)\cap L^4(\mathbb {R}^3)$. Assume that U first blows-up at $T^*\in (0,\infty )$. Then

$$\begin{aligned} \lim \sup _{t\uparrow T^*}\int _{\mathbb {R}^3}\frac{|U(x,t)|^3}{\left( \log \log \log \left( (\log (e^{e^{3e^{e}}}+|U(x,t)|))^\frac{1}{3}\right) \right) ^\theta }dx=\infty . \end{aligned}$$

As far as we know, Result D is the first result of this type for the Navier–Stokes equations concerned with slight criticality breaking in borderline spaces. Previously, it was shown for non-borderline spaces by Chan and Vasseur [20] that if U is a Leray–Hopf solution satisfying

$$ \int _{0}^{\infty }\int _{\mathbb {R}^3}\frac{|U|^5}{\log (1+|U|)}dxdt<\infty $$

then U is smooth on $\mathbb {R}^3\times (0,\infty )$. Subsequent improvements were obtained in [49] and [10]; see also [63]. Let us mention that the techniques used in these papers cannot be used to treat the borderline case considered in Result D.

A new method for transferring subcriticality of the data forward in time The method for proving Result D relies on the following lemma and on a careful tuning of the parameters (estimating the $L^{3-\mu }$ norm for a well-chosen parameter $\mu$). Lemma E is directly inspired by the recent result of Bulut [13] for a nonlinear supercritical defocusing Schrödinger equation.

Result E

(‘mild criticality breaking’; [8, Theorem 1]) For all $M,\, A\in [1,\infty )$ sufficiently large, there exists $\delta (M,A)\in (0,\frac{1}{2}]$ such that the following holds. Let U be a suitable weak Leray–Hopf solution to the Navier–Stokes equations on $\mathbb {R}^3\times (0,\infty )$ with initial data $U_0\in L^2(\mathbb {R}^3)\cap L^4(\mathbb {R}^3)$.

Assume that

$$\begin{aligned} \Vert U_0\Vert _{L^2},~\Vert U_0\Vert _{L^4}\le M, \end{aligned}$$

and that

$$\begin{aligned} \Vert U\Vert _{L^\infty (0,\infty ;L^{3-\delta (M,A)}(\mathbb {R}^3))}\le A. \end{aligned}$$

Then, the above assumptions imply that U is smooth on $\mathbb {R}^3\times (0,\infty )$. Moreover, there is an explicit formula for $\delta (M,A)$, see [8, equation (26)], and $\delta (M,A)\rightarrow 0$ when $M\rightarrow \infty$ or $A\rightarrow \infty$.

We call Result E a ‘mild breaking of the criticality’, or a ‘mild supercritical regularity criteria’ as opposed to strong criticality breaking results obtained for instance in the axisymmetric case [23, 70, 74, 75], see Section 8. Indeed, the supercritical space $L^{\infty }_tL^{3-\delta (M,A)}$ in which we break the scaling depends on the size A of the solution in this supercritical space via $\delta (M,A)$. In other words this can be considered as a non-effective regularity criteria, hence the term ‘mild’. Moreover, given a solution U, assume that you knew all the $L^\infty _tL^{3-\delta }_x$ norms for $\delta \rightarrow 0$. Then the question whether Lemma E applies to U or not becomes a question about how fast

$$\begin{aligned} \Vert U\Vert _{L^\infty (0,\infty ;L^{3-\delta }(\mathbb {R}^3))} \end{aligned}$$

grows when $\delta \rightarrow 0$. Of course one would have regularity if the solution was a priori bounded in the critical space $L^\infty _tL^3_x$. The result shows that with $L^4$ initial data one can relax the exponent 3 to a slightly supercritical $3-\delta (M,A)$. Let us also remark that the initial condition $U_0\in L^4(\mathbb {R}^3)$ can be replaced by any subcritical initial condition $U_0\in L^{3+}(\mathbb {R}^3)$.

The main idea of the proof of Lemma E is to transfer subcritical information from the initial time forward in time. In a nutshell, subcritical energy estimates are combined with quantitative regularity estimates as obtained by Tao [84]. Hence, the growth of the subcritical norm along the evolution can be estimated.²⁵ In that perspective the main objective is the following.

Objective D

Prove that there exists $\delta (M,A)\in (0,\frac{1}{2}]$ and $K(M,A)\in [1,\infty )$ such that for all $U_0\in L^2(\mathbb {R}^3)\cap L^4(\mathbb {R}^3)$ and any suitable weak Leray–Hopf solution associated to the initial data $U_0$, if

$$\begin{aligned} \Vert U_0\Vert _{L^2},~\Vert U_0\Vert _{L^4}\le M, \end{aligned}$$

and

$$\begin{aligned} \Vert U\Vert _{L^\infty (0,\infty ;L^{3-\delta (M,A)}(\mathbb {R}^3))}\le A, \end{aligned}$$

then

$$\begin{aligned} \Vert U\Vert _{L^\infty (0,T;L^4(\mathbb {R}^3))}\le K(M,A). \end{aligned}$$

for any $T>0$.

This then obviously implies the result stated in Result E. The crucial point is that K(M, A) is uniform in time.

Let us emphasize that the only a priori globally controlled quantity is a supercritical $L^\infty _tL^{3-}$ norm. We are not aware of any regularity mechanism enabling to break the critically barrier based on the sole knowledge of such a supercritical bound. Therefore, the idea, following Bulut [13], is to transfer the subcritical information coming from the initial data $U_0\in L^4(\mathbb {R}^3)$ to arbitrarily large times by using three ingredients:

• (1) the control of the critical $L^\infty _tL^3_x$ norm via interpolation between the supercritical norm $L^\infty _tL^{3-\delta (M,A)}_x$ and the subcritical $L^\infty _tL^4_x$ norm

  $$\begin{aligned} \Vert U\Vert _{L^\infty (0,T;L^3(\mathbb {R}^3))}\le & {} \Vert U\Vert _{L^\infty (0,T;L^{3-\delta }(\mathbb {R}^3))}^\frac{3-\delta }{3+3\delta }\Vert U\Vert _{L^\infty (0,T;L^4(\mathbb {R}^3))}^\frac{4\delta }{3+3\delta }\\\le & {} A^\frac{3-\delta }{3+3\delta }K^\frac{4\delta }{3+3\delta }; \end{aligned}$$

• (2) the quantitative control of the critical non borderline $L^5_{t,x}$ norm (see [8, Proposition 3]) in terms of the critical norm $\Vert U\Vert _{L^\infty (0,\infty ;L^{3}(\mathbb {R}^3))}$, and the supercritical $L^2$ and subcritical $L^4$ norms of the initial data $U_0$

  $$\begin{aligned} \Vert U\Vert _{L^5(0,T;L^5(\mathbb {R}^3))}\le C(M)\exp \exp \exp \left( C_{\text {univ}}\left( A^\frac{3-\delta }{3+3\delta }K^\frac{4\delta }{3+3\delta }\right) ^c\right) ; \end{aligned}$$

  this hinges on the quantitative bounds on solutions belonging to the critical space $L^{\infty }_{t}L^{3}_{x}$, which were established by Tao in [84], see (5.7); this step enables the slicing of the interval (0, T) into a T-independent number m of disjoint epochs $I_j=(t_j,t_{j+1})$, such that $\Vert U\Vert _{L^5(I_j; L^5(\mathbb {R}^3))}\le \varepsilon$. Moreover,

  $$\begin{aligned} \varepsilon ^5m=\sum _{j=1}^m\Vert U\Vert _{L^5(I_{j};L^5(\mathbb {R}^3))}^5\le & {} \Vert U\Vert _{L^5(0,T;L^5(\mathbb {R}^3))}^5\\\le & {} C(M)\exp \exp \exp \left( \left( A^\frac{3-\delta }{3+3\delta }K^\frac{4\delta }{3+3\delta }\right) ^c\right) ; \end{aligned}$$

• (3) an $L^4$ energy estimate [8, Proposition 4] under the $L^5_{t,x}$ control of U, which enables the transfer the subcritical information from time $t_j$ to $t_{j+1}$

  $$\begin{aligned} \mathscr {E}_{4,t_{j+1}}\le & {} \Vert U(\cdot ,t_j)\Vert _{L^4(\mathbb {R}^3)}^4+C\Vert U\Vert _{L^5(\mathbb {R}^3\times I_j)}\mathcal E_{4,t_{j+1}}\\\le & {} \Vert U(\cdot ,t_{j+1})\Vert _{L^4(\mathbb {R}^3)}^4+C\varepsilon \mathscr {E}_{4,t_{j+1}}, \end{aligned}$$

  where $\mathscr {E}_{4,t_{j+1}}$ is the $L^4$ energy, see [8, equation (13)], and eventually to T

  $$\begin{aligned} \Vert U\Vert _{L^\infty (0,T;L^4(\mathbb {R}^3))}^4=\max _{1\le j\le m+1}\left\{ \Vert U\Vert _{L^\infty (I_j;L^4(\mathbb {R}^3))}^4\right\} \le 64M^4 2^m. \end{aligned}$$

  (9.1)

  One then designs the number K(M, A) and $\delta (M,A)$ to bound the right hand side (9.1) above by $(K(M,A))^4$.

Fig. 6

Weak and strong concentration: a selection of results

Fig. 7

Qualitative vs. explicit quantitative regularity: a selection of results

10 Summary of Selected Results

Figure 6 on page 24 summarizes some results about weak and strong concentration for the Navier–Stokes equations, as well as local-in-space smoothing. Figure 7 on page 24 summarizes qualitative and quantitative regularity results for the Navier–Stokes equations.