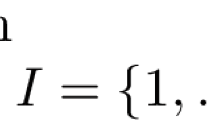E′-Convex Sets and Functions: Properties and Characterizations

Abstract

The main properties of evenly convex sets and functions have been deeply studied by different authors, and a duality theory for evenly convex optimization problems has been well developed as well. In this theory, the notion of $\text {e}^{\prime }$-convexity appears as a necessary requirement for obtaining important results in strong and stable strong duality. This fact has motivated the authors to study possible properties of this kind of convexity in sets and functions, which is closely connected to even convexity.

1 Introduction

In [10] Wernel Fenchel introduced the concept of evenly convex set in $\mathbb {R}^{n}$ trying to generalize the polarity theory to nonclosed convex sets. A set is e-convex if it can be expressed as an intersection of an arbitrary family (possibly empty) of open halfspaces. In the literature dealing with these sets, they are abbreviated as e-convex sets, so we warn the reader to avoid any possible confusion with e-convex sets in [22]. Characterizations of e-convex sets can be found in [2] and [12] and their basic properties were studied in [14]. They appear to be very useful in the study of geometrical properties of the feasible set of a linear inequality system containing strict inequalities; see [13]. In a natural way, e-convex sets allow the definition of e-convex functions, introduced in [21] as those extended real-valued functions whose epigraghs are e-convex. Moreover, in [15] a suitable conjugation pattern for e-convex functions defined on locally convex spaces, the c-conjugation, was defined. Its suitability refers that a proper function is e-convex if and only if it is equal to its double c-conjugate.

Since any closed convex set is e-convex, the class of convex lower semicontiuous functions can be considered as a subclass of the e-convex functions. This fact motivated that Fajardo et al. in [7] extended some well-known properties of convex lower semicontinuous functions to e-convex functions. The notion of e$^{\prime }$-convexity appeared in that paper, firstly, trying to obtain the counterpart of a well-known result (see [1, Sect. 2]): Let X be a locally convex space and $f,g: X \to \overline {\mathbb {R}}$ be two proper lower semicontinuous convex functions such that domf ∩domg≠∅. Then

$$ \text{cl}(\text{epi} f^{\ast}+\text{epi} g^{\ast})= \text{epi} (f+g)^{\ast}, $$

(1)

where f^∗ and g^∗ are the Fenchel conjugate functions of f and g, respectively. If we assume that f and g are e-convex, it is not necessarily true, and if we take c-conjugate functions instead of Fenchel ones the closure is not an appropriate hull. In [7, Remark 1] it is also stated that the e-convex hull is not enough to reach the equality, fact that motivated them to introduce the notion of e$^{\prime }$-convexity; see [7, Definition 2]. Moreover, in this paper, and using the c-conjugation scheme, a Fenchel-type dual problem for a primal one where both objective function and feasible set are e-convex were built. Optimization problems where the objective function and the feasible set are e-convex have potential applications in mathematical applications, in an analogous way than evenly quasiconvex optimization is used in [19].

In [3] an alternative dual problem (GD_c) for a general primal (GP) was built by means of the c-conjugation scheme, via the perturbational approach. Weak duality was assured and sufficient conditions for Fenchel strong duality, called regularity conditions, were obtained. In addition, relationships between e-convexity and other closedness-type notions in infinite dimensional locally convex spaces were deduced.These connections were used for achieving regularity conditions for (GP) and (GD_c), which were particularized for Fenchel duality case and compared with the one obtained in [7]. Fajardo et al. [5] states the analysis of regularity conditions for Lagrange duality. In [9] Fenchel–Lagrange duality is considered, where dual problems are expressed via the c-conjugates of the functions involved in the primal problem. Fajardo and Vidal [8] studies sufficient conditions and characterizations for stable strong duality in this generalized framework for Fenchel and Lagrange dualities. In addition, a comparison of the optimal values and solutions of the three alternative dual problems (Fenchel, Lagrange and Fenchel–Lagrange) is achieved in [6]. Finally, in the recent paper [4], converse and total duality as well as new results on subdifferential theory for e-convex functions have been also studied, developed initially in [15] .

E-convex properties have been deeply studied, as the reader can observe, whereas e$^{\prime }$-convexity has been a necessary tool for the achievement of generalized duality results. Something was asking to be done: the study of interesting properties or characterizations of e$^{\prime }$-convex sets and functions, if there were any. As it will be shown in the following section, an e$^{\prime }$-convex set is defined over the space $W\times \mathbb {R}$, where $W=X^{\ast } \times X^{\ast }\times \mathbb {R}$. Since this space can be a bit difficult to deal with due to its high dimension, we will try to obtain a characterization of such kind of sets, but without using ideas based on separation hyperplanes. To this aim, and inspired in [10, 11], we shall define two new operators which will allow us to characterize the e$^{\prime }$-convexity of a given subset and, in spirit of [21], we will analyze the main properties that e$^{\prime }$-convex sets and functions inherit from the e-convex case.

The organization is as follows. In Section 2, we present the main properties for e-convex sets and functions, together with all the necessary results, in order to make the paper self-contained. The idea of this section is to give a general perspective of e-convexity, since its properties have been taken as a reference for the purpose of studying the e$^{\prime }$-convexity. Section 3 is dedicated to the study of the e$^{\prime }$-convex sets and Section 4 presents the main properties of the e$^{\prime }$-convex functions. Finally, Section 5 concludes.

2 Preliminaries

Let X be a separated locally convex space, lcs in brief, equipped with the σ(X,X^∗) topology induced by X^∗, its continuous dual space endowed with the σ(X^∗, X) topology. The notation 〈x,x^∗〉 stands for the value at x ∈ X of the continuous linear functional x^∗∈ X^∗. For a set $D\subseteq X$ we denote its convex hull and its closure by convD and clD, respectively. Moreover, if D≠∅, the indicator function $\delta _{D}:X \to \overline {\mathbb {R}}= \mathbb {R} \cup \{\pm \infty \}$ is defined by

$$ \delta_{D}(x)=\left\{ \begin{array}{ll} 0 &\quad \text{if }x\in D,\\ +\infty &\quad \text{otherwise.} \end{array} \right. $$

According to [2], a set $C\subseteq X$ is e-convex, if for every point x₀∉C, there exists x^∗∈ X^∗ such that 〈x − x₀, x^∗〉 < 0, for all x ∈ C. Since X is assumed to be a nontrivial lcs, X^∗≠ 0. From the definition of e-convex set, the entire space X is e-convex. As a consequence of Hahn–Banach theorem, every closed or open convex set is e-convex as well.

The class of e-convex sets captures some important properties from the subclass of closed convex sets. For instance, it is immediate that the intersection of an arbitrary family of e-convex sets is e-convex. Moreover, if C is an e-convex set, αC is also e-convex, for all α > 0. Nevertheless, the image of an e-convex set from a linear transformation is not, in general, an e-convex set. In particular, the sum of two e-convex sets is not necessarily an e-convex set (see [12, Example 3.1]).

The next two propositions show basic properties of e-convex sets whose proofs in their respective references have been done in $\mathbb {R}^{n}$, but they can be extended to general locally convex spaces with no further difficulties.

Proposition 1

[21, Proposition 1.2] Let $C_{1} \subseteq X$ and $C_{2} \subseteq Y$ be two non-empty subsets, with X and Y locally convex spaces. Then C₁ × C₂ is e-convex in X × Y if and only if C₁ and C₂ are e-convex sets in X and Y, respectively.

For a set $C\subseteq X$, the e-convex hull of C, econvC, is the smallest e-convex set in X containing C. This operator is well defined because X is e-convex and the class of e-convex sets is closed under intersection. Moreover, for all $C\subseteq X$, it always holds $C\subseteq \text {conv} C \subseteq \text {econv} C\subseteq \text {cl} C$.

Proposition 2

[13, Proposition 2.3] Let $C_{1} \subseteq X$ and $C_{2} \subseteq Y$ be non-empty subsets with X and Y locally convex spaces. Then, it holds

$$ \text{econv} (C_{1} \times C_{2}) = \text{econv} (C_{1}) \times \text{econv}(C_{2}). $$

Considering now a function $f:X \to \overline {\mathbb {R}}$, we denote by

$$ \text{dom} f= \{x\in X : f(x)<+\infty\} $$

the effective domain of f and by

$$ \text{epi} f = \{(x,r) \in X \times \mathbb{R} : f(x)\leq r\} $$

its epigraph. We say that f is proper if epif does not contain vertical lines, i.e., $f(x)>-\infty$ for all x ∈ X, and domf≠∅. By clf we denote the lower semicontinuous hull of f, which is the function whose epigraph equals cl(epif). A function f is lower semicontinuous, lsc in brief, if for all x ∈ X, f(x) = clf(x), and e-convex if epif is e-convex in $X\times \mathbb {R}$. Clearly, any lsc convex function is e-convex, but the converse does not hold in general as we can see below.

Example 1

(cf. [6, Example 2.1]) Let $f:\mathbb {R} \to \overline {\mathbb {R}}$ be the function defined as

$$ f(x)=\left\{ \begin{array}{ll} x&\quad\text{if }x>0,\\ +\infty&\quad\text{otherwise.} \end{array} \right. $$

Clearly, $\text {epi} f=\{(x,y)\in \mathbb {R}^{2}~|~x>0, y\geq x\}$ is e-convex in $\mathbb {R}^{2}$ since for every x₀∉epif, there exists a non-trivial hyperplane whose intersection with epif is empty. However, epif is not closed and, consequently, f is not lsc.

The e-convex hull of a function $f:X \rightarrow \overline {\mathbb {R}}$, econvf, is defined as the largest e-convex minorant of f. The next propositions show important properties of e-convex functions which have been presented in [21] for $X=\mathbb {R}^{n}$, whose proofs can be generalized to locally convex spaces with no extra effort.

Proposition 3

[21, Proposition 3.1] Let $f:X\rightarrow \overline {\mathbb {R}}$ be an e-convex function and α > 0. Then αf is e-convex.

Proposition 4

[21, Proposition 3.2] Let $\{f_{i} :X \rightarrow \overline {\mathbb {R}}, i\in I\}$ be a family of e-convex functions, then $f=\sup _{i\in I}f_{i}$ is e-convex.

Proposition 5

[21, Proposition 3.3] Let $f,g:X\rightarrow \overline {\mathbb {R}}$ be two proper e-convex functions. Then f + g is e-convex.

Based on the generalized convex conjugation theory introduced by Moreau in [17], a suitable conjugation scheme for e-convex functions is provided in [15]. Let us consider the space $W:=X^{\ast }\times X^{\ast }\times \mathbb {R}$ with the coupling functions $c:X\times W\rightarrow \overline {\mathbb {R}}$ and $c^{\prime }:W\times X\rightarrow \overline {\mathbb {R}}$ given by

$$ c(x,(x^{\ast},u^{\ast },\alpha ))=c^{\prime}\big((x^{\ast },u^{\ast},\alpha ),x\big) :=\left\{ \begin{array}{ll} \langle x,x^{\ast }\rangle &\quad \text{if }\langle x,u^{\ast}\rangle <\alpha, \\ +\infty &\quad \text{otherwise.} \end{array} \right. $$

Given two functions $f:X\rightarrow \overline {\mathbb {R}}$ and $g:W\rightarrow \overline {\mathbb {R}}$, the c-conjugate of f and the c$^{\prime }$-conjugate of g are defined as the functions $f^{c}:W\rightarrow \overline {\mathbb {R}}$ and $g^{c^{\prime }}:X\rightarrow \overline {\mathbb {R}}$, such that

$$ \begin{array}{@{}rcl@{}} f^{c}(x^{\ast },u^{\ast },\alpha )&:=&\sup_{x\in X}\{c(x,(x^{\ast},u^{\ast },\alpha ))-f(x)\},\\ g^{c^{\prime }}(x)&:=&\sup_{(x^{\ast },u^{\ast },\alpha )\in W}\left\{c^{\prime }\left( (x^{\ast },u^{\ast },\alpha ),x\right) -g(x^{\ast},u^{\ast },\alpha )\right\} , \end{array} $$

respectively, with the conventions $(+\infty ) +(-\infty )=(-\infty ) + (+\infty ) =(+\infty ) - (+\infty )=(-\infty ) -(-\infty )=-\infty$.

Functions of the form $x \in X \to c(x,(x^{\ast },u^{\ast },\alpha ))-\upbeta \in \overline {\mathbb {R}}$, with (x^∗, u^∗, α) ∈ W and $\upbeta \in \mathbb {R}$ are called c-elementary, and, in a similar way, functions of the form $(x^{\ast },u^{\ast },\alpha )\in W \to c^{\prime }((x^{\ast },u^{\ast },\alpha ),x)-\upbeta \in \overline {\mathbb {R}}$ with x ∈ X and $\upbeta \in \mathbb {R}$ are called $c^{\prime }$-elementary. In [15] it is shown the following characterization for a proper e-convex function, which can be understood as the e-convex version of [20, Theorem 12.1] for proper convex and lsc functions.

Theorem 1

Let $f:X\rightarrow \overline {\mathbb {R}}$, not identically $+\infty$ or $-\infty$. Let $\mathcal {E}_{f}$ be the set of c-elementary functions minorizing f, i.e.,

$$ \mathcal{E}_{f}:=\{a:X \rightarrow \overline {\mathbb{R}}: a \text{ is c-elementary and } a \leq f \}. $$

Then f is a proper e-convex function if and only if $f=\sup \{a:a \in \mathcal {E}_{f}\}$.

Definition 1

[7, p. 379] A function $g:W \to \overline {\mathbb {R}}$ is e$^{\prime }$-convex if it is the pointwise supremum of sets of $c^{\prime }$-elementary functions, and the e$^{\prime }$-convex hull of an extended real valued function g defined on W, denoted by e$^{\prime }\text {conv} g$, is the largest e$^{\prime }$-convex minorant of it.

It is immediate that the epigraph of a $c^{\prime }$-elementary function is the intersection of an open and a closed half-spaces in $W \times \mathbb {R}$, therefore it is an e-convex set. We conclude that any $c^{\prime }$-elementary function is e-convex, so it follows directly that any $e^{\prime }$-convex function is e-convex. The following theorem has been proved in [16, Proposition 6.1, Proposition 6.2, and Corollary 6.1], containing what can be understood as the counterpart of Fenchel–Moreau theorem for e-convex and e$^{\prime }$-convex functions.

Theorem 2

Let $f:X\to \mathbb {R}\cup \{+\infty \}$ and $g:W \to \overline {\mathbb {R}}$. Then

• i) f^c is e$^{\prime }$-convex and $g^{c^{\prime }}$ is e-convex.

• ii) $\text {econv} f=f^{c{c^{\prime }}}$ and $\mathrm {e}^{\prime }\text {conv} g=g^{{c^{\prime }}c}$.

• iii) f is e-convex if and only if $f^{c c^{\prime }}=f$ and g is e$^{\prime }$-convex if and only if $g^{c^{\prime } c}=g$.

• iv) $f^{cc^{\prime }} \leq f$ and $g^{c^{\prime } c} \leq g$.

Remark 1

[7, p. 379] According to iii) in Theorem 2, given $f:X\rightarrow \mathbb {R}\cup \{+\infty \}$, we say that it is e-convex in x ∈ X if $f(x)=f^{cc^{\prime }}(x)$. Given $g:W\rightarrow \overline {\mathbb {R}}$, it is said to be e$^{\prime }$-convex in (x^∗, y^∗, α) ∈ W when $g(x^{\ast },y^{\ast },\alpha )=g^{c^{\prime } c}(x^{\ast },y^{\ast },\alpha )$.

The next result follows from Theorem 2 and Remark 12 in [15].

Theorem 3

Let $f:X\rightarrow \overline {\mathbb {R}}$ be a proper convex function. Then f is e-convex if and only if f is lsc in econv(domf).

3 E$^{\prime }$-convex Sets

In this section we will study some algebraic properties of the class of e$^{\prime }$-convex sets as well as a characterization of them by using general operators instead of supporting hyperplanes. To this aim, we begin recalling the definition of e$^{\prime }$-convex set from [7].

Definition 2

[7, Definition 2] A set $D\subseteq W\times \mathbb {R}$ is e$^{\prime }$-convex if there exists an e$^{\prime }$-convex function $k:W\rightarrow \overline {\mathbb {R}}$ such that D = epik. The e$^{\prime }$-convex hull of an arbitrary set $D\subseteq W\times \mathbb {R}$ is defined as the smallest e$^{\prime }$-convex set containing D, and it will be denoted by e$^{\prime }\text {conv} D$.

This type of envelope allowed to obtain the counterpart of (1) with the c-conjugation scheme in [7]:

$$ \mathrm{e}^{\prime}\text{conv}(\text{epi} f^{c} + \text{epi} g^{c})=\text{epi}(f+g)^{c} $$

under a certain additivity hypothesis between the sets $\mathcal {E}_{f}$ and $\mathcal {E}_{g}$. See [7, Corollary 5] for more details.

As described in the Introduction, e$^{\prime }$-convex sets are important in the establishment of regularity conditions for strong and stable strong duality on e-convex optimization problems. For this reason, the rest of the section aims to investigate further properties as well as a characterization of this class of sets. As any e$^{\prime }$-convex function is e-convex as well, it follows that any e$^{\prime }$-convex set is e-convex.

3.1 Characterization of e$^{\prime }$-convex Sets

Given $C\subseteq \mathbb {R}^{n}$ and $F\subseteq \mathbb {R}^{n}\times \mathbb {R}$, Fenchel in [10] and Goberna et al. in [11] defined, on the one hand, the negative polar of C and, on the other hand, the weak dual cone of C and the symmetrical expression of K, as the sets

$$ \begin{array}{@{}rcl@{}} C^{e} &:=&\{y\in \mathbb{R}^{n}~|~\langle x,y\rangle <1~\text{ for all } x\in C\},\\ C^{\leq} &:=&\left\{{a \choose b} \in \mathbb{R}^{n} \times \mathbb{R} ~|~ \langle a,x \rangle \leq b~\text{ for all } x \in C \right\},\\ F_{\leq} &:=&\left\{x \in \mathbb{R}^{n} ~|~ \langle a,x \rangle \leq b~\text{ for all } {a \choose b} \in F \right\}, \end{array} $$

respectively. Using these operators, in [10] and [11] it was shown that a set $C\subseteq \mathbb {R}^{n}$ is e-convex if and only if

$$ C=C^{ee}\quad \text{ or } \quad C=(C^{\leq})_{\leq}, $$

(2)

so a natural question arises: is it possible to adapt these operators into the e$^{\prime }$-convexity scheme keeping somehow these characterizations? Without further ado, we will define two new operators which can be viewed as their e$^{\prime }$-convex counterparts.

Definition 3

Let $K\subseteq W \times \mathbb {R}$. We define the General Dual Cone (GDC) of K as the set

$$ K^{GDC} := \{(x,\gamma)\in X\times \mathbb{R} ~|~ c^{\prime}((x^{\ast},y^{\ast},\alpha),x)-\gamma \leq \upbeta~\text{ for all } (x^{\ast},y^{\ast},\alpha,\upbeta)\in K\} $$

and, by convention, we establish that $(\emptyset _{W\times \mathbb {R}})^{GDC} = X \times \mathbb {R}$, being $\emptyset _{W\times \mathbb {R}}$ the empty set of the space $W\times \mathbb {R}$.

Let us observe that $(W\times \mathbb {R})^{GDC}=\emptyset _{X\times \mathbb {R}}$, and that in general, K^GDC is not necessarily a cone. For instance, if

$$ K=\{(x,y,\alpha, \upbeta) \in \mathbb{R}^{4} ~|~ x- \upbeta \le 0 \text{ and } y - \alpha < 0\}, $$

we have $K^{GDC}= \{1\} \times \mathbb {R}_{+}$, which clearly is not a cone. We can ensure that K^GDC is a cone if its projection onto $\mathbb {R}^{2}$ reduces to the origin, which can be proved easily. Nevertheless, although K^GDC is not necessarily a cone, we have kept this word in the name because K^GDC represents the generalization of C^≤ in our context. In the following proposition we give conditions guaranteeing the nonemptiness of K^GDC if K is nonempty and proper.

Proposition 6

Let us assume that X is a reflexive space, and that $K \subset W \times \mathbb {R}$ is a nonempty convex set such that its projections onto $X^{\ast } \times \mathbb {R}$

$$ \begin{array}{@{}rcl@{}} K_{1}&:=& \{(x^{\ast}, \upbeta) ~|~ (x^{\ast}, y^{\ast}, \alpha,\upbeta) \in K \text{ for some } (y^{\ast}, \alpha) \in X^{\ast} \times \mathbb{R}\},\\ K_{2} &:= & \{(y^{\ast}, \alpha) ~|~ (x^{\ast}, y^{\ast}, \alpha,\upbeta) \in K \text{ for some } (x^{\ast}, \upbeta) \in X^{\ast} \times \mathbb{R}\} , \end{array} $$

verify that K₁ is closed, with 0 ∈ K₁, K₂ is compact, K₁ ∩ (−K₂) = ∅, the projection of K₁ onto $\mathbb {R}$ is bounded from below but not from above, the projection of K₁ onto X^∗ is bounded and the projection of K₂ onto $\mathbb {R}$ is bounded from below by 0, then K^GDC is nonempty.

Proof

In first place, lets us observe that K^GDC is nonempty if and only if there exits $(x,\gamma ) \in X \times \mathbb {R}$ such that $K_{1} \subset H^{\le }_{(x,-1), \gamma }$ and $K_{2} \subset H^{< }_{(x,-1),0}$, where

$$ \begin{array}{@{}rcl@{}} H^{\le}_{(x,-1), \gamma}&=& \{(x^{\ast}, \upbeta) \in X^{\ast} \times \mathbb{R} ~|~ \langle x,x^{\ast} \rangle -\gamma \le \upbeta\},\\ H^{< }_{(x,-1),0} &=& \{(y^{\ast}, \alpha) \in X^{\ast} \times \mathbb{R} ~|~ \langle x,y^{\ast} \rangle -\alpha <0\}. \end{array} $$

Under the hypothesis, with X reflexive, according to Theorem 1.1.5 in [23], there exist $(x,\delta ) \in (X \times \mathbb {R})\setminus \{0\}$ and $\alpha _{1}, \alpha _{2} \in \mathbb {R}$ verifying, for all (x^∗,β) ∈ K₁ and (y^∗, α) ∈ K₂,

$$ \langle x,x^{\ast} \rangle +\delta\upbeta \le \alpha_{1} <\alpha_{2} \le \langle x,-y^{\ast} \rangle -\delta\alpha. $$

(3)

Let us observe that, since 0 ∈ K₁, α₁ ≥ 0. Since the projection of K₁ onto $\mathbb {R}$ is not bounded from above, but its projection onto X^∗ is bounded, δ ≤ 0. We distinguish two cases. In the case δ = 0, naming $\inf _{(x^{\ast }, \upbeta ) \in K_{1}}\{ \upbeta \} =C_{1}$ and $\inf _{(y^{\ast }, \alpha ) \in K_{2}}\{ \alpha \} =C_{2} \ge 0$ by hypothesis, we have

$$ \langle x,x^{\ast} \rangle -\upbeta \le \alpha_{1} - C_{1}=\gamma \text{ and } \langle x,y^{\ast} \rangle - \alpha< -\alpha_{1}-C_{2} \le 0 $$

for all (x^∗,β) ∈ K₁ and (y^∗, α) ∈ K₂, and (x,γ) ∈ K^GDC.

On the other hand, if δ < 0, multiplying by $\frac {1}{ |\delta |}$ in (3) and naming $z= \frac {1}{ |\delta |} x$ and $\gamma =\frac {1}{ |\delta |} \alpha _{1}$, we have

$$ \langle z,x^{\ast} \rangle -\upbeta \le \gamma \quad\text{ and }\quad \langle z,y^{\ast} \rangle -\alpha< 0, $$

for all (x^∗,β) ∈ K₁ and (y^∗, α) ∈ K₂, and (z,γ) ∈ K^GDC. □

Remark 2

The hypothesis about K₁ and K₂ in the above proposition can be replaced by the hypothesis 0∉cl(K₁ + K₂), keeping the hypothesis about their projections onto X^∗ and $\mathbb {R}$ and that 0 ∈ K₁, and applying Theorem 1.1.7 in [23].

Definition 4

Let $H\subseteq X \times \mathbb {R}$. We define the General Symmetrical Expression (GSE) of H as the set

$$ H_{GSE} := \{(x^{\ast},y^{\ast},\alpha,\upbeta)\in W \times \mathbb{R} ~|~ c^{\prime}((x^{\ast},y^{\ast},\alpha),x)-\gamma \leq \upbeta ~\text{ for all } (x,\gamma)\in H\} $$

and, by convention, we establish that $(\emptyset _{X \times \mathbb {R}})_{GSE} = W \times \mathbb {R}$, being $\emptyset _{X\times \mathbb {R}}$ the empty set of the space $X\times \mathbb {R}$.

Observing that $(X\times \mathbb {R})_{GSE}=\emptyset _{W\times \mathbb {R}}$, we present the following proposition concerning nonemptiness of the General Symmetrical Expression of a nonempty and proper set.

Proposition 7

Given a nonempty convex set $H\subset X\times \mathbb {R}$ such that H as well as its projection onto X have nonempty interior, the projection of H onto $\mathbb {R}$ is bounded from below but not from above, the projection of H onto X^∗ is bounded, then H_GSE is nonempty.

Proof

In this case, H_GSE is nonempty if and only if there exists $(x^{\ast },y^{\ast },\alpha ,\upbeta )\in W \times \mathbb {R}$ such that $H \subset H^{\le }_{(x^{\ast },-1), \upbeta } \cap H^{<}_{(y^{\ast },0), \alpha }$, where

$$ \begin{array}{@{}rcl@{}} H^{\le}_{(x^{\ast},-1), \upbeta}&=& \{(x, \gamma) \in X \times \mathbb{R} ~|~ \langle x,x^{\ast} \rangle -\gamma \le \upbeta\} ,\\ H^{<}_{(y^{\ast},0), \alpha}&=&\{(x, \gamma) \in X \times \mathbb{R} ~|~ \langle x,y^{\ast} \rangle <\alpha\}. \end{array} $$

According to the hypothesis, applying Corollary 1.1.4 in [23] to H and to its projection onto X, there exist supporting hyperplanes to both convex sets, i.e.,

$$ \langle x,x^{\ast} \rangle +\delta\gamma \le \upbeta\quad \text{ and }\quad \langle x,y^{\ast} \rangle \le \alpha $$

for all (x,γ) ∈ H. Taking into account the hypothesis, δ ≤ 0. In the case δ = 0, it holds (x^∗, y^∗,β−C,α + 1) ∈ H_GSE, where $C=\inf _{(x, \gamma ) \in H}\{ \gamma \}$. If δ < 0, we can argue as in the proof of Proposition 6 leading to H_GSE≠∅. □

Now, we study which properties are verified by these operators. First and foremost, applying their definitions it is not difficult to prove that given an arbitrary set $K\subseteq W\times \mathbb {R}$, the following inclusion

$$ K\subseteq (K^{GDC})_{GSE} $$

(4)

is always fulfilled. To obtain the opposite containment, we need some extra results.

Proposition 8

Let $K\subseteq W\times \mathbb {R}$ and $H\subseteq X\times \mathbb {R}$. Then, the set K^GDC is e-convex and the set H_GSE is e$^{\prime }$-convex.

Proof

To begin with, suppose that the sets K and H are nonempty. To see that K^GDC is e-convex, we define the function $f:X\to \overline {\mathbb {R}}$ such that

$$ f(x)=\sup_{(x^{\ast},y^{\ast},\alpha,\upbeta)\in K} \{c(x,(x^{\ast},y^{\ast},\alpha))-\upbeta\}, $$

with $K\subseteq W\times \mathbb {R}$. This function is e-convex by definition and it is easy to see that (x,γ) ∈epif if and only if c(x,(x^∗, y^∗, α))−β≤ γ for all (x^∗, y^∗, α,β) ∈ K. This fact is equivalent to $c^{\prime }((x^{\ast },y^{\ast },\alpha ),x)-\gamma \leq \upbeta$ for all (x^∗, y^∗, α,β) ∈ K, which means that (x,γ) ∈ K^GDC due to Definition 3. In this way, K^GDC = epif and K^GDC is an e-convex set of $X\times \mathbb {R}$.

Now we move onto the second part. Let us define $g:W\to \overline {\mathbb {R}}$ such that

$$ g(x)=\sup_{(x,\upbeta)\in H} \{c^{\prime}((x^{\ast},y^{\ast},\alpha),x)-\upbeta\}, $$

with $H\subseteq X\times \mathbb {R}$. Similarly, but applying Definition 4, we conclude that H_GSE = epig and, consequently, H_GSE is an e$^{\prime }$-convex set in $W\times \mathbb {R}$.

Finally, for the nonproper case, it is a direct consequence of Definitions 3 and 4. □

Now our purpose is to analyze the behaviour of the operators GDC and GSE regarding inclusion and intersection. The proofs of the following lemmas are consequences of Definitions 3 and 4 and, for this reason, we have omitted them.

Lemma 1

Let $K\subseteq W\times \mathbb {R}$ and $H\subseteq X\times \mathbb {R}$. If $L\subseteq K$ and $J\subseteq H$, then $K^{GDC}\subseteq L^{GDC}$ and $H_{GSE}\subseteq J_{GSE}$.

Lemma 2

Let $K_{1}, K_{2}\subseteq W\times \mathbb {R}$ and $H_{1}, H_{2}\subseteq X\times \mathbb {R}$. Then

• (i) $K_{1}^{GDC} \cap K_{2}^{GDC} \subseteq (K_{1} \cap K_{2})^{GDC}$.

• (ii) $(H_{1})_{GSE} \cap (H_{2})_{GSE} \subseteq (H_{1} \cap H_{2})_{GSE}$.

Motivated by (2), we establish the main result of this section.

Proposition 9

Let $K\subseteq W\times \mathbb {R}$, then K is e$^{\prime }$-convex if and only if

$$ K=\left( K^{GDC}\right)_{GSE}. $$

(5)

Proof

First, let us suppose that K is e$^{\prime }$-convex. If $K=\emptyset _{W\times \mathbb {R}}$, as we have seen in Definitions 3 and 4, $K^{GDC}=X\times \mathbb {R}$ and $(K^{GDC})_{GSE}=(X\times \mathbb {R})_{GSE}=\emptyset _{W\times \mathbb {R}}$, so (5) is fulfilled. If $K=W\times \mathbb {R}$, applying (4) we easily get $\left (K^{GDC} \right )_{GSE}=W\times \mathbb {R}$. Hence, we can assume that K is a proper subset of $W\times \mathbb {R}$. By hypothesis K is e$^{\prime }$-convex, so there exists a function $h:W\to \overline {\mathbb {R}}$ such that

$$ h(\cdot)=\sup_{(x,\gamma)\in {\Delta}} \{c^{\prime}(\cdot,x)-\gamma\}, $$

(6)

where ${\Delta } \subseteq X\times \mathbb {R}$ and epih = K. As K is a proper set, ${\Delta }\neq \emptyset _{X\times \mathbb {R}}$ and by using Definition 3, ${\Delta } \subseteq K^{GDC}$ since $K=\text {epi} h=\bigcap _{(x,\gamma )\in {\Delta }} \text {epi}\{c^{\prime }(\cdot ,x)-\gamma \}$. In this way, by virtue of Lemma 1 we have

$$ \left( K^{GDC}\right)_{GSE} \subseteq {\Delta}_{GSE}. $$

(7)

From Definition 4 and (6), we obtain that Δ_GSE = epih = K, and by (7), $(K^{GDC})_{GSE} \subseteq {\Delta }_{GSE}=K$. Finally, applying (4), we get (5).

The converse is a direct application of Proposition 8 to the set H = K^GDC. □

Remark 3

By virtue of (4), K is e$^{\prime }$-convex if and only if

$$ \left( K^{GDC}\right)_{GSE} \subseteq K. $$

Remark 4

Applying (4) and Proposition 8 we have that, for every $K\subseteq W\times \mathbb {R}$, it holds $K\subseteq \mathrm {e}^{\prime }\text {conv} K \subseteq (K^{GDC})_{GSE}$. Using Lemma 1 and Proposition 9, a simple calculation shows that $(K^{GDC})_{GSE}=\mathrm {e}^{\prime }\text {conv} K$.

3.2 Properties of e$^{\prime }$-convex Sets

This section focuses on the analysis of those properties which do not hold when e-convexity is replaced by e$^{\prime }$-convexity. From the definition of e$^{\prime }$-convex set and the fact that every e$^{\prime }$-convex function is e-convex, it is natural to wonder what kind of differences separates the class of e-convex sets which are epigraphs and are contained in $W\times \mathbb {R}$, from the class of e$^{\prime }$-convex sets.

E-convex sets which are closed are important in convex optimization, but they are not included in the family of e$^{\prime }$-convex sets.

Proposition 10

No proper closed convex set which is the epigraph of a certain function $g: W \to \overline {\mathbb {R}}$ is e$^{\prime }$-convex.

Proof

Let $K\subseteq W\times \mathbb {R}$ be a proper e$^{\prime }$-convex set. By Definition 2, we have that there exists a function $h:W\to \mathbb {R}$ defined as

$$ h(y^{\ast},z^{\ast},\alpha)=\underset{(x,\upbeta)\in S}{\sup} \{c^{\prime}((y^{\ast},z^{\ast},\alpha),x)-\upbeta\}, $$

where $S \subset X\times \mathbb {R}$, which satisfies

$$ K=\text{epi} h=\bigcap_{(x,\upbeta)\in S} \text{epi}(c(x,\cdot)-\upbeta). $$

(8)

Now, the idea is to prove that K cannot be closed, and to do that, we shall check that given any $(\overline {x}^{\ast },\overline {y}^{\ast },\overline {\alpha },\overline {\gamma })\in K$, the point $(\overline {x}^{\ast },0,0,\overline {\gamma })\in \text {cl} K \setminus K$. It is clear that $(\overline {x}^{\ast },0,0,\overline {\gamma })\notin K$ because this point does not belong to any epigraph of the c$^{\prime }$-elementary functions that build epih. By (8), K is the solution set of the system

$$ \{\langle (x,-1),(x^{\ast},\gamma) \rangle \leq \upbeta,~ \langle (x,-1),(y^{\ast},\alpha) \rangle < 0~\text{ for all }(x,\upbeta) \in S\}. $$

Bearing in mind that [12, Proposition 1.1] can be extended to general locally convex spaces, we have

$$ \text{cl} K = \bigcap_{(x,\upbeta)\in S} \left\{(x^{\ast},y^{\ast},\alpha,\gamma)\in W ~|~ \langle (x,-1),(x^{\ast},\gamma) \rangle \leq \upbeta,~ \langle (x,-1),(y^{\ast},\alpha) \rangle \leq 0\right\}. $$

To conclude the proof, a matter of computation shows that $(\overline {x}^{\ast },0,0,\overline {\gamma })\in \text {cl} K$ since it comes from a point $(\overline {x}^{\ast },\overline {y}^{\ast },\overline {\alpha },\overline {\gamma })$ which belongs to K. □

Remark 5

In view of the above proposition, a necessary condition for an e-convex set in $W\times \mathbb {R}$ to be e$^{\prime }$-convex is not to be closed.

Now, once we know that the class of e$^{\prime }$-convex sets and the class of closed convex sets have no element in common, let us continue our work analyzing what kind of properties the family of e$^{\prime }$-convex sets does verify. It is clear that the class of e$^{\prime }$-convex sets is closed under intersections, moreover, as a consequence of the monotonicity of the $\mathrm {e}^{\prime }\text {conv}$ hull operator,

$$ \mathrm{e}^{\prime}\text{conv} \left( \bigcap_{i \in I} K_{i} \right) \subseteq \bigcap_{i\in I} \mathrm{e}^{\prime}\text{conv} (K_{i}), $$

where {K_i}_i∈I is an arbitrary family of sets in $W\times \mathbb {R}$.

Proposition 11

Let γ > 0 and $K\subseteq W\times \mathbb {R}$ be e$^{\prime }$-convex, then γK is e$^{\prime }$-convex.

Proof

We shall prove that γK is the epigraph of an e$^{\prime }$-convex function. By hypothesis K is e$^{\prime }$-convex, so there exists an e$^{\prime }$-convex function $h:W\to \overline {\mathbb {R}}$ such that

$$ h(y^{\ast},z^{\ast},\alpha):=\sup_{(x,b)\in S} \{c^{\prime}((x^{\ast},y^{\ast},\alpha),x)-b \}, $$

with $S \subset X\times \mathbb {R}$ in such a way that epih = K. Now, let us define the function

$$ H(x^{\ast},y^{\ast},\alpha):=\gamma h \left( \frac{1}{\gamma}{x^{\ast}},\frac{1}{\gamma}{y^{\ast}},\frac{1}{\gamma}{\alpha} \right) $$

(9)

for all (x^∗, y^∗, α) ∈ W, with γ > 0 by hypothesis, and take an arbitrary point (x^∗, y^∗, α,β) ∈epiH. By virtue of (9),

$$ \gamma h \left( \frac{x^{\ast}}{\gamma},\frac{1}{\gamma}{y^{\ast}},\frac{1}{\gamma}{\alpha} \right) \leq \upbeta, $$

or, equivalently,

$$ \left( \frac{1}{\gamma}{x^{\ast}},\frac{1}{\gamma}{y^{\ast}},\frac{1}{\gamma}{\alpha},\frac{1}{\gamma}{\upbeta}, \right) \in \text{epi} h=K, $$

so we can conclude that (x^∗, y^∗, α,β) ∈ γK. The converse inclusion is analogous. Consequently, epiH = γK and we only have to prove that H is e$^{\prime }$-convex. Since

$$ c^{\prime}\left( \left( \frac{x^{\ast}}{\gamma},\frac{1}{\gamma}{y^{\ast}},\frac{1}{\gamma}{\alpha} \right),x \right) = \frac{1}{\gamma} c^{\prime}((x^{\ast},y^{\ast},\alpha),x), $$

we can write

$$ H(x^{\ast},y^{\ast},\alpha)=\gamma \sup_{(x,b)\in S} \left\{\frac{1}{\gamma} c^{\prime}((x^{\ast},y^{\ast},\alpha),x)-b \right\}. $$

Defining the set $T := \{(x, \gamma b) \in X \times \mathbb {R} ~|~ (x, b) \in S\}$, since γ is assumed to be strictly positive, we obtain

$$ \begin{array}{@{}rcl@{}} H(x^{\ast},y^{\ast},\alpha) &= & \sup_{(x,b)\in S} \{c^{\prime}((x^{\ast},y^{\ast},\alpha),x)-\gamma b\}\\ &= & \sup_{(x,\upbeta)\in T} \{c^{\prime}((x^{\ast},y^{\ast},\alpha),x)-\upbeta\}, \end{array} $$

and we conclude that H is an e$^{\prime }$-convex function. □

The next result was of interest in [8].

Lemma 3

[8, Lemma 3.2] Let $C\subseteq W\times \mathbb {R}$ be a non-empty set. Then, C is e$^{\prime }$-convex if and only if for all x^∗∈ X^∗ and $\delta \in \mathbb {R}$, C + {(x^∗,0,0,δ)} is e$^{\prime }$-convex.

Remark 6

In general, we cannot assure that the sum of an e$^{\prime }$-convex set and a point will be e$^{\prime }$-convex. To show this fact, we need the following result.

Proposition 12

[8, Proposition 2.7] A necessary condition for a non-empty set $K \subseteq \mathbb {R}^{4}$ to be e$^{\prime }$-convex is that the boundary of its projection onto $\mathbb {R}^{2}$, corresponding to the second and third coordinates, contains the origin.

Next example illustrates what is pointed out in Remark 6.

Example 2

Let $X=\mathbb {R}$ and $C\subseteq \mathbb {R}^{4}$ be the e$^{\prime }$-convex set

$$ C=\text{epi} c(1,\cdot)=\{(x,y,\alpha,\upbeta) \in \mathbb{R}^{4} ~|~ x -\upbeta\leq 0,y-\alpha<0\}. $$

Let us define

$$ C^{\prime}:=C+\{(1,1,0,0)\}=\{(x,y,\alpha,\upbeta) \in \mathbb{R}^{4} ~|~ x-\upbeta \leq 1,y-\alpha <1\}. $$

Then, since

$$ \text{Pr}_{\mathbb{R}^{2}}(C^{\prime})=\{(y,\alpha)\in \mathbb{R}^{2} ~|~ y-\alpha<1\}, $$

it is clear that 0₂ does not belong to $\text {bd}(\text {Pr}_{\mathbb {R}^{2}}(C^{\prime }))$ and, due to Proposition 12, we see that $C^{\prime }$ is not e$^{\prime }$-convex.

4 E$^{\prime }$-convex Functions

This section is divided in two parts. The first part will focus on the analysis of the main properties that the e$^{\prime }$-convex functions satisfy. Finally, we will conclude the section obtaining sufficient conditions to ensure when an e$^{\prime }$-convex function has an e-convex domain.

4.1 Properties of e$^{\prime }$-convex Functions

In this section we shall study if the class of e$^{\prime }$-convex functions is closed under certain operations that preserve e-convexity. Recall from the definition of an e-convex function that the indicator function of an e-convex set is evidently an e-convex function.

Applying the definition of e$^{\prime }$-convex function and due to Proposition 12, it is not difficult to show that the family of e$^{\prime }$-convex functions is closed under the supremum operator. Moreover, following similar steps as in the last part of the proof of Proposition 11, we have the following result.

Proposition 13

Let γ > 0 and $h:W\rightarrow \overline {\mathbb {R}}$ be an e$^{\prime }$-convex function, then γh is e$^{\prime }$-convex.

As the following result shows, certain indicator functions can be e$^{\prime }$-convex as well.

Proposition 14

Let $\hat {x}^{\ast } \in X^{\ast }$ and $A=\{\hat {x}^{\ast }\} \times \{0\} \times \mathbb {R}_{++}\subseteq W$. Then, $\delta _{A}:W\to \overline {\mathbb {R}}$ is an e$^{\prime }$-convex function.

Proof

According to Remark 1, it is enough to prove that $\delta _{A}^{c^{\prime } c}(x^{\ast },y^{\ast },\alpha )=\delta _{A}(x^{\ast },y^{\ast },\alpha )$ for every (x^∗, y^∗, α) ∈ W and, then, the function δ_A will be e$^{\prime }$-convex. Since, for all x ∈ X,

$$ \begin{array}{@{}rcl@{}} \delta_{A}^{c^{\prime}} (x) &=& \underset{(x^{\ast},y^{\ast},\alpha)\in A}{\sup} \{c(x,(x^{\ast},y^{\ast},\alpha))-\delta_{A}(x^{\ast},y^{\ast},\alpha)\}\\ &=& \underset{(\hat{x}^{\ast},0,\alpha)\in A}{\sup} \{c(x,(\hat{x}^{\ast},0,\alpha))\}=\langle x,\hat{x}^{\ast}\rangle, \end{array} $$

we have that $\text {dom} \delta _{A}^{c^{\prime }}=X$ and, consequently,

$$ \delta_{A}^{c^{\prime} c}(x^{\ast},y^{\ast},\alpha)=\underset{x\in X}{\sup} \{c(x,(x^{\ast},y^{\ast},\alpha))-\langle x,\hat{x}^{\ast} \rangle\}. $$

Now, we have to study two different cases. The first one is when (x^∗, y^∗, α) ∈ A, i.e., $(x^{\ast },y^{\ast },\alpha )=(\hat {x}^{\ast },0,\alpha )$, with α > 0, then

$$ \delta_{A}^{c^{\prime} c}(\hat{x}^{\ast},0,\alpha)=\underset{x\in X}{\sup} \{c(x,(\hat{x}^{\ast},0,\alpha))-\langle x,\hat{x}^{\ast} \rangle\}=0=\delta_{A}(\hat{x}^{\ast},0,\alpha). $$

Let us analyze what happens with $(x^{\ast },y^{\ast },\alpha )\notin A$. If $y^{\ast }\neq 0_{X^{\ast }}$, we can always find x ∈ X such that 〈x,y^∗〉≥ α, independently of the value of α. If $y^{\ast } = 0_{X^{\ast }}$ and α ≤ 0, we have that $\delta _{A}^{c^{\prime } c} (x^{\ast },0,\alpha )=+\infty$. Finally, if $y^{\ast }=0_{X^{\ast }}$, α > 0 and $x^{\ast }\neq \hat {x}^{\ast }$, then a matter of computation shows that

$$ \delta_{A}^{c^{\prime} c} (x^{\ast},0,\alpha)=\underset{x\in X}{\sup}\{\langle x,x^{\ast}\rangle - \langle x,\hat{x}^{\ast} \rangle\}=\underset{x \in X}{\sup} \{\langle x, x^{\ast} - \hat{x}^{\ast} \rangle\}=+\infty. $$

Hence, for every (x^∗, y^∗, α)∉A, we get

$$ \delta_{A}^{c^{\prime} c} (x^{\ast},y^{\ast},\alpha)=+\infty=\delta_{A}(x^{\ast},y^{\ast},\alpha), $$

concluding that the function δ_A is e$^{\prime }$-convex. □

Remark 7

It has been impossible to characterize the sets in W whose indicator function is e$^{\prime }$-convex. We would just want to point out that a little change in the description of the set in the above proposition leads to a non-e$^{\prime }$-convex function, as the following example shows.

Example 3

Let $W=\mathbb {R}^{3}$ and $A=\{(1,1)\} \times \mathbb {R}_{++}$. In this case epiδ_A = {(1,1,α,β) : α > 0,β≥ 0}, and its projection on the second and third coordinate is the set $\{1 \} \times \mathbb {R}_{++}$, whose boundary does not contain the origin. According to Proposition 12, epiδ_A is not an e$^{\prime }$-convex set.

Next proposition establishes one of the main differences between the classes of e-convex and e$^{\prime }$-convex functions. It shows that the class of e$^{\prime }$-convex functions has empty intersection with the class of lsc and convex functions, being its proof a direct consequence of Proposition 10.

Proposition 15

No proper closed convex function $g:W \to \overline {\mathbb {R}}$ can be e$^{\prime }$-convex.

Recalling Proposition 5, the sum of two proper e-convex functions is e-convex as well. However, this fact is no longer true for e$^{\prime }$-convex functions as the following example shows.

Example 4

Let $h_{1},h_{2}:\mathbb {R}^{3}\to \overline {\mathbb {R}}$ be two e$^{\prime }$-convex functions defined as

$$ \begin{array}{@{}rcl@{}} h_{1}(y^{\ast},z^{\ast},\alpha) & = &c^{\prime} ((y^{\ast},z^{\ast},\alpha),1) \quad \text{ and}\\ h_{2}(y^{\ast},z^{\ast},\alpha) & =& c^{\prime}((y^{\ast},z^{\ast},\alpha),-1). \end{array} $$

If we define the function h := h₁ + h₂, a matter of computation yields

$$ \begin{array}{@{}rcl@{}} \text{dom} h &= & \text{dom} h_{1} \cap \text{dom} h_{2}\\ & = & (\mathbb{R}\times \{(z^{\ast},\alpha)\in \mathbb{R}^{2}~|~z^{\ast}<\alpha \}) \cap (\mathbb{R} \times \{(z^{\ast},\alpha) \in \mathbb{R}^{2} ~|~ -z^{\ast}<\alpha\})\\ & = & \mathbb{R}\times \{(z^{\ast},\alpha)\in \mathbb{R}^{2}~|~-\alpha<z^{\ast}<\alpha\}=:{\Omega}, \end{array} $$

and

$$ h(y^{\ast},z^{\ast},\alpha)=\left\{ \begin{array}{ll} 0&\quad\text{if } -\alpha<z^{\ast}<\alpha,\\ +\infty&\quad\text{otherwise.} \end{array} \right. $$

Now, taking into account that the function

$$ \begin{array}{@{}rcl@{}} h^{c^{\prime}}(x) & =& \underset{(y^{\ast},z^{\ast},\alpha)\in{\Omega}}{\sup} \{c^{\prime} ((y^{\ast},z^{\ast},\alpha),x)-h(y^{\ast},z^{\ast},\alpha)\}\\ & =& \underset{(y^{\ast},z^{\ast},\alpha)\in{\Omega}}{\sup} \{c^{\prime}((y^{\ast},z^{\ast},\alpha),x)\} \end{array} $$

has $\text {dom} h^{c^{\prime }}=\{0\}$, we get, for instance,

$$ h^{c^{\prime} c}(1,2,1)=\underset{x\in \{0\}}{\sup} \left\{\langle x,1\rangle - h^{c^{\prime}}(x) \right\}=0, $$

but $h(1,2,1)=+\infty$ since (1,2,1)∉domh. Hence, a straightforward application of Theorem 2 shows that h is not e$^{\prime }$-convex.

Remark 8

Example 4 also allows us to show that the necessary condition for a set in $\mathbb {R}^{4}$ to be e$^{\prime }$-convex stated in Proposition 12 is not sufficient: the set ${\Omega } \times \mathbb {R} \subset \mathbb {R}^{4}$ verifies that necessary condition, but it is not an e$^{\prime }$-convex set, since h is not e$^{\prime }$-convex, being h the only function such that ${\Omega } \times \mathbb {R}=\text {epi} h$. In fact, $h=\delta _{\Omega \times \mathbb {R}}$.

To conclude this subsection, we would like to point out that the characterization offered by Theorem 3 for e-convex functions has no meaning when we try to translate it into the subclass of proper e$^{\prime }$-convex functions. The reason for this is that if a function h is defined on W, it does not make any sense to talk about the properties of h on $\mathrm {e}^{\prime }\text {conv}(\text {dom} h)$, which is a subset of $W \times \mathbb {R}$. In the following section we will present some results about the domain of an e$^{\prime }$-convex function.

4.2 Domain of e$^{\prime }$-convex Functions

In this section we shall study conditions to know when an e$^{\prime }$-convex function has an e-convex domain. Results for e-convex functions defined on $\mathbb {R}^{n}$ can be found in [21].

The next results will be of interest in the sequel.

Definition 5

[23, Chapter 1] Let $M\subseteq Y$ be a linear subspace of a general vector space Y and let $A\subseteq Y$ be a non-empty subset. The algebraic interior of A with respect to M is

$$ \text{aint}_{M} A=\left\{ a\in Y ~|~ \forall x \in M, \exists \delta>0 ~|~ \forall \lambda \in [0,\delta], a+\lambda x \in A \right\}. $$

If M = aff(A − A), being affA the affine hull of A, aint_MA is denoted by ⁱA and it is called the relative algebraic interior of A. Moreover, if $A\subseteq Y$ is convex, the segment $[a,x[=\{(1-\lambda )a+\lambda x ~|~ \lambda \in [0,1[\} \subseteq {}^{\mathrm {i}} A$ for all a ∈ⁱA and x ∈ A.

Lemma 4

[23, Proposition 2.1.4] Let $f : X \to \overline {\mathbb {R}}$ be a convex function. If there exists x₀ ∈ X such that $f(x_{0})=-\infty$, then $f(x)=-\infty$ for every x ∈ⁱ(domf).

The next proposition extends Lemma 2.5 in [21] to locally convex spaces.

Proposition 16

If $f : X \to \overline {\mathbb {R}}$ is e-convex such that $f(x_{0})=-\infty$ for some x₀ ∈domf, then $f(x)=-\infty$ for all x ∈domf.

Proof

Since f is e-convex, it is also convex, so applying Lemma 4, $f(x)=-\infty$ for all x ∈ⁱ(domf). Take $\overline {x} \in \text {dom} f\backslash {}^{\mathrm {i}}(\text {dom} f)$ with $f(\overline {x})\in \mathbb {R}$. Then, $(\overline {x},f(\overline {x})-1)\notin \text {epi} f$, so by virtue of the e-convexity of f, there exists $(x^{\ast },\gamma ) \in X^{\ast } \times \mathbb {R}$ such that

$$ \langle (x-\overline{x},\lambda-f(\overline{x})+1),(x^{\ast},\gamma)\rangle<0 $$

(10)

for all (x,λ) ∈epif. Since $\overline {x} \in \text {dom} f\backslash {}^{\mathrm {i}}(\text {dom} f)$, the segment $[a,\overline {x}[\subseteq {}^{\mathrm {i}}(\text {dom} f)$ for all a ∈ⁱ(domf). Defining $x_{\lambda }=\lambda \overline {x}+ (1-\lambda ) a$ for all λ ∈ [0,1[, $f(x_{\lambda })=-\infty$ for all λ ∈ [0,1[, and

$$ (x_{\lambda},f(\overline{x})),(x_{\lambda},f(\overline{x})-2) $$

belong to epif, for all λ ∈ [0,1[. Replacing them in (10) we get

$$ \langle (x_{\lambda}-\overline{x},1),(x^{\ast},\gamma)\rangle < 0, \langle (x_{\lambda}-\overline{x},-1),(x^{\ast},\gamma)\rangle < 0, $$

respectively. Making $\lambda \rightarrow 1$, we get γ = 0. Taking γ = 0 in (10), we have $\langle x-\overline {x},x^{\ast }\rangle < 0$ for all (x,λ) ∈epif, which is a contradiction since $\overline {x} \in \text {dom} f$. Hence, $f(\overline {x})=-\infty$. □

Proposition 17

Let $f:X\to \overline {\mathbb {R}}$ be an improper function such that $f(x_{0})=-\infty$ for some x₀ ∈domf. Then, f is e-convex if and only if domf is e-convex and $f \equiv -\infty$ on its domain.

Proof

It is a direct consequence of Propositions 1 and 16, and that $\text {epi} f=\text {dom} f\times \mathbb {R}$ if $f\equiv -\infty$ on its domain. □

Having in mind that any e$^{\prime }$-convex function is e-convex, the following results come from Propositions 16 and 17 directly.

Corollary 1

Let $h:W\rightarrow \overline {\mathbb {R}}$ be a function such that $h(y^{\ast }_{0},z^{\ast }_{0},\alpha _{0})=-\infty$ for some $(y^{\ast }_{0},z^{\ast }_{0},\alpha _{0})\in \text {dom} h$. Then, if h is e$^{\prime }$-convex, h equals $-\infty$ over domh.

Corollary 2

Let $h:W\rightarrow \overline {\mathbb {R}}$ be an improper convex function. If h is e$^{\prime }$-convex, then domh is e-convex.

Corollary 3

Let h₁, h₂ be two e$^{\prime }$-convex functions with at least one of them improper. Then h₁ + h₂ is e$^{\prime }$-convex and it has e-convex domain.

The purpose for the rest of the section is to analyze the proper case. First of all, we establish the following result, which comes directly form the fact that any e$^{\prime }$-convex function is e-convex as well and the generalization of [21, Proposition 2.7] for general spaces. As it happened for e-convex functions (see [21, Example 2.8]), the converse in the following result does not hold in general.

Proposition 18

Let $h:W \to \overline {\mathbb {R}}$ be a proper e$^{\prime }$-convex function which is upper bounded on its domain. Then domh is e-convex.

Now, let $h:W\rightarrow \overline {\mathbb {R}}$ be a proper e$^{\prime }$-convex function such that

$$ h(\cdot)=\underset{(x,\upbeta)\in S}{\sup} \left\{ c^{\prime} (\cdot,x)-\upbeta \right\} $$

(11)

being S an arbitrary proper subset of $X\times \mathbb {R}$. Pursuing the objective of finding conditions for the domain of a general e$^{\prime }$-convex function to be e-convex could be too ambitious. The reason is that the arbitrariness of S complicates the development of the aforementioned conditions over the domain.

Let us see an equivalent formula to express the domain of a general function h defined as in (11). On the one hand,

$$ \text{dom} h = \left\{(x^{\ast},y^{\ast},\alpha)\in \text{dom}(c^{\prime}(\cdot,x)-\upbeta)~\text{ for all }(x,\upbeta)\in S, \sup_{S}\left\{\langle x,x^{\ast}\rangle - \upbeta\right\}<+\infty \right\}. $$

On the other hand, defining the sets

$$ \begin{array}{@{}rcl@{}} D &:= & \left\{x^{\ast} \in X^{\ast} ~|~ \sup_{(x,\upbeta) \in S} \langle x,x^{\ast}\rangle -\upbeta < \infty \right\},\\ C_{(x,\upbeta)} &:= & \left\{(y^{\ast},\alpha)\in X^{\ast} \times \mathbb{R} ~|~ \langle x,y^{\ast}\rangle < \alpha \right\} \quad\text{ for all }(x,\upbeta) \in S, \end{array} $$

(12)

the following equality offers no difficulty to be checked

$$ \text{dom} h = D\times \bigcap_{(x,\upbeta) \in S} C_{(x,\upbeta)}. $$

(13)

Let us observe that actually the sets C_(x,β) are open half-spaces:

$$ C_{(x, \upbeta)} = H_{(x,-1),0}^{<}=\{(y^{\ast},\alpha)\in X^{\ast} \times \mathbb{R} ~|~ \langle (x,-1),(y^{\ast},\alpha)\rangle < 0\}, $$

therefore, they are e-convex sets. Since the class of e-convex sets is closed under intersection and finite product, if the set D were an e-convex subset of X^∗, domh would be e-convex in W. Let us assume that D≠∅.

Lemma 5

If $\sup _{(x,\upbeta ) \in S, x^{\ast } \in D} \{\langle x,x^{\ast }\rangle - \upbeta \}$ is finite, then the set D defined in (12) is e-convex in X^∗.

Proof

Take any constant $\overline {M}\in \mathbb {R}$ such that $\langle x,x^{\ast }\rangle \leq \overline {M}$ for all (x,β) ∈ S and x^∗∈ D. For any point $\overline {x}^{\ast } \notin D$, there exists $(\overline {x}, \bar \upbeta )\in S$ such that $\langle \overline {x},\overline {x}^{\ast }\rangle >\overline {M}$. Since $(\overline {x}, \bar \upbeta )\in S$, $\langle \overline {x},x^{\ast }\rangle \leq \overline {M}$ for all x^∗∈ D. Then $\langle \overline {x},x^{\ast }\rangle \leq \overline {M} < \langle \overline {x},\overline {x}^{\ast }\rangle$, for all x^∗∈ D or, equivalently, $\langle \overline {x}, x^{\ast } - \overline {x}^{\ast } \rangle < 0$ for all x^∗∈ D, concluding that D is e-convex in X^∗. □

The next result establishes a sufficient condition for an e$^{\prime }$-convex function to have e-convex domain.

Proposition 19

Let $h: W \to \overline {\mathbb {R}}$ be the function defined in (11). If S and the set D in (12) are bounded, then domh is e-convex.

Proof

According to [18, Theorem 6.4.1], the image of a bounded set through a continuous linear functional is also bounded, so the supremum in Lemma 5 is finite. Hence, D is e-convex and domh is e-convex in W. □

Finally, we conclude showing that the converse in Proposition 19 does not hold in general as we can see in the following example.

Example 5

Let $h:W\rightarrow \overline {\mathbb {R}}$ be a function such that

$$ h(\cdot)=\underset{(x,\upbeta) \in \mathbb{R} \times \mathbb{R}_{+}}{\sup} \left\{ c^{\prime}(\cdot,x)-\upbeta \right\}. $$

Hence, $\text {dom} h=\{0\} \times \{0\} \times \mathbb {R}_{++}$, which is e-convex, h is e$^{\prime }$-convex by its definition, but the set S is not bounded.

5 Conclusions

In this paper we investigate not only basic algebraic properties of the e$^{\prime }$-convex sets and functions, but also a characterization of e$^{\prime }$-convex sets. This characterization is motivated by the general dual cone and general symmetric expression operators. In addition, we prove that the class of e$^{\prime }$-convex sets does not intersect with the family of closed and convex sets of appropriate dimension. We also study which properties from e-convex sets remain still true for the family of e$^{\prime }$-convex sets. Regarding e$^{\prime }$-convex functions, we have studied some properties that they inherit from e-convex functions. Finally, we have analyzed sufficient conditions to guarantee when an e$^{\prime }$-convex function has an e-convex domain.

There are still some areas for future research. For example, it would be worthwhile investigating further conditions over the arbitrary set S in (11) implying the e-convexity of the domain of the function. Another possible continuation might be to give more precise characterizations of e$^{\prime }$-convex sets in terms of supporting hyperplanes as was done in the case of e-convex sets.