An Algorithm to Solve Equilibrium Problems and Fixed Points Problems Involving a Finite Family of Multivalued Strictly Pseudo-Contractive Mappings

Abstract

The aim of this paper is to introduce and study a new iterative algorithm for finding a common element of the set of fixed points of a finite family of multivalued strictly pseudo-contractive mappings and the set of solutions of equilibrium problems in Hilbert spaces. Strong convergence of the proposed method is established under suitable control conditions. Application to optimization problems with constraints is provided to support our main results. Furthermore, numerical example is given to demonstrate the implementability of our algorithm.The algorithm and its convergence results improve and develop previous results in the field.

1 Introduction

Let H be a real Hilbert space and let C be a nonempty, closed and convex subset of H. Let F be a bifunction of C × C into $\mathbb {R}$, where $\mathbb {R}$ is the real numbers. The equilibrium problem for F is to find x ∈ C such that

$$ F (x,y)\geq 0 \quad \forall y \in C. $$

(1)

The set of solutions is denoted by EP(F). Equilibrium problems which were introduced by Fan [9] and Blum and Oettli [10] have had a great impact and influence on the development of several branches of pure and applied sciences. Equilibrium problems include variational inequality problems as well as fixed point problems, complementarity problems, optimization, saddle point problems and Nash equilibrium problems as special cases. Equilibrium problems provide us with a systematic framework to study a wide class of problems arising in finance economics, optimization and operation research etc., which motivate the extensive concern. In recent years, equilibrium problems have been deeply and thoroughly researched, see [3, 4, 10, 12, 18, 22, 30] and the references therein. However, there are few iterative algorithms developed for the approximation of solutions of equilibrium problems.

Let (X, d) be a metric space, K be a nonempty subset of X and T : K → 2^K be a multivalued mapping. An element x ∈ K is called a fixed point of T if x ∈ Tx. For single valued mapping, this reduces to Tx = x. The fixed point set of T is denoted by Fix(T) := {x ∈ D(T) : x ∈ Tx}.

A point x ∈ X is called an endpoint (or stationary point) of T if x is a fixed point of T and T(x) = {x}. We shall denote by End(T) the set of all endpoints of T. We see that for each mapping T, End(T) ⊂Fix(T). Thus, the concept of endpoints seems to be more difficult (but more important) than the concept of fixed points. However, both concepts are equivalent when T is a single-valued mapping since, in this case, End(T) = Fix(T). Next is an example of a multivalued mapping T with Fix(T)≠∅, Tp = {p} for all p ∈ Tp.

Example 1

Let $X =\mathbb {R}$ (the reals with usual metric). Define T : [− 1,1] → 2^[− 1,1] by

$$ Tx= \left \{ \begin{array}{ll} \left[-1, \frac{2}{3}x \sin{\frac{1}{x}}\right],\quad& x\in(0, 1],\\ \{0\},&x=0,\\ \left[\frac{2}{3}x \sin{\frac{1}{x}}, 1\right],& x\in [-1, 0). \end{array} \right. $$

Then, clearly Fix(T) = {0}.

Many problems arising in different areas of mathematics, such as game theory, control theory, dynamic systems theory, signal and image processing, market economy and in other areas of mathematics, such as in non-smooth differential equations and differential inclusions, optimization theory equations, can be modeled by the equation

$$ x\in Tx, $$

where T is a multivalued nonexpansive mapping. The solution set of this equation coincides with the fixed point set of T.

For several years, the study of fixed point theory for multi-valued nonlinear mappings has attracted, and continues to attract, the interest of several well known mathematicians (see, for example, Brouwer [7], Kakutani [14], Nash [19, 20]).

Nonsmooth differential equations

A large number of problems from mechanics and electrical engineering leads to differential inclusions and differential equations with discontinuous right-hand sides, for example, a dry friction force of some electronic devices. Below are two models.

$$ \frac{du}{dt} = f(t,u)\quad\text{ a.e. }~t\in I:=[-a,a],~u(0)=u_{0}, $$

(2)

a, u₀ fixed in $\mathbb {R}$. These types of differential equations do not have solutions in the classical sense. A generalized notion of solution is what is called a solution in the sense of Fillipov.

Consider the following multi-valued initial value problem.

$$ \left\{\begin{array}{rcl} -\frac{d^{2}u}{dt^{2}}&\in& u-\frac{1}{4}-\frac{1}{4}\text{sign}(u-1)\text{ on } {\Omega} = (0,\pi);\\ u(0)&=&0;\\ u(\pi)&=&0. \end{array}\right. $$

(3)

Under some conditions, the solutions set of equations (2) and (3) coincides with the fixed point set of some multi-valued mappings.

Let K be a nonempty subset of a normed space E. The set K is called proximinal (see, e.g., [21]) if for each x ∈ E, there exists u ∈ K such that

$$ d(x,u) =\inf\{\|x-y\|:y\in K\}=d(x,K), $$

where d(x, y) = ∥x − y∥ for all x, y ∈ E. Every nonempty, closed and convex subset of a real Hilbert space is proximinal. Let CB(K), K(K) and P(K) denote the family of nonempty closed bounded subsets, nonempty compact subsets, and nonempty proximinal bounded subsets of K respectively. The Hausdorff metric on CB(K) is defined by:

$$ H(A,B)=\max\left\{\sup_{a\in A}d(a,B),~\sup_{b\in B}d(b,A)\right\} $$

for all A, B ∈ CB(K). A multi-valued mapping $T:D(T)\subseteq E\rightarrow CB(E)$ is called L-Lipschitzian if there exists L > 0 such that

$$ H(Tx,Ty)\leq L\|x-y\|\quad \forall x,y\in D(T). $$

When L ∈ (0,1), we say that T is a contraction, and T is called nonexpansive if L = 1.

Different iterative processes have been developed to approximate fixed points of multi-valued nonexpansive mappings (see, e.g., [1, 15] and the references therein) and their generalizations (see, e.g., [13]).

Recently, viscosity iterative algorithms for finding a common element of the set of fixed points for single-valued nonexpansive mappings and the set of solutions of variational inequality problems have been investigated by many authors; (see, e.g., [21, 31] and the references therein). For example, Moudafi [16] introduced the explicit viscosity approximation method for nonexpansive mappings.

Let C be a nonempty, closed and convex subset of a real Hilbert space H. Let f : C → C be a contraction mapping and T be a single-valued nonexpansive mapping on C. Let {x_n} be a sequence defined by

$$ \left\{ \begin{array}{lll} x_{0}\in C,\\ x_{n+1}= \alpha_{n} f(x_{n}) +(1-\alpha_{n})Tx_{n}, \end{array} \right. $$

(4)

where {α_n} is a sequence in (0,1). Then, the sequence {x_n} generated by (4) converges strongly to x^∗∈Fix(T), which is a unique solution of the following variational inequality:

$$ \langle x^{\ast} - f(x^{\ast}), x^{\ast}-p \rangle\leq 0\quad \forall p\in \text{Fix}(T). $$

In 2007, Takahashi and Takahashi [27] investigate Moudafi’s viscosity method (4) for finding a common element of the solutions set of (1) and the fixed points set of a nonexpansive mapping in a Hilbert space, and proved the following strong convergence theorem.

Theorem 1

[27] Let Cbe a nonempty, closed and convex subset a real Hilbert space H. Let Fbe a bifunction from$C\times C\to \mathbb {R}$satisfying the following assumptions:

• (A1) F(x, x) = 0 for all x ∈ C;

• (A2) Fis monotone, i.e., F(x, y) + F(y, x) ≤ 0 for all x, y ∈ C;

• (A3) for each x, y, z ∈ C,

  $$ \lim_{t \to 0} F(tz +(1-t)x,y) \leq F(x, y); $$

• (A4) for each x ∈ C, y → F(x, y) is convex and lower semicontinuous.

Let f : C → Cbe a contraction and T : C → Cbe a nonexpansive mapping such that Fix(T) ∩ EP(F)≠∅.

Let {x_n} and {u_n} be sequences defined iteratively from arbitrary x₀ ∈ Cby:

$$ \left\{ \begin{array}{l} F(u_{n}, y)+ \frac{1}{r_{n}}\langle y-u_{n}, u_{n}-x_{n}\rangle \geq 0\quad\forall y \in C, \\ x_{n+1}= \alpha_{n} f(x_{n})+ (1-\alpha_{n}) Tu_{n}, \end{array} \right. $$

(5)

where {α_n}⊂ (0,1) and$\{r_{n}\}\subset ]0,\infty [$satisfy:

• (i) $\lim _{n\to \infty }\alpha _{n}=0$;

• (ii) ${\sum }_{n=0}^{\infty } |\alpha _{n}- \alpha _{n-1}| < \infty$;

• (iii) $\lim _{n \to \infty }\inf r_{n}> 0$ and ${\sum }_{n=0}^{\infty } |r_{n+1}- r_{n}| < \infty$.

Then, the sequences {x_n} and {u_n} generated by (5)converge strongly to x^∗∈Fix(T) ∩ EP(F).

The important class of single-valued k-strictly pseudo-contractive maps on Hilbert spaces was introduced by Browder and Petryshyn [2] as a generalization of the class of nonexpansive mappings.

Definition 1

Let K be a nonempty subset of a real Hilbert space H. A map T : K → H is called k-strictly pseudo-contractive if there exists k ∈ (0,1) such that

$$ \|Tx-Ty\|^{2}\leq \|x-y\|^{2}+k\|x-y-(Tx-Ty)\|^{2} \quad \forall x,y\in K. $$

Motivated by approximating fixed points of multivalued mappings, Chidume et al. [8] introduced the following important class of multivalued strictly pseudo-contractive mappings in real Hilbert spaces which is more general than the class of multivalued nonexpansive mappings.

Definition 2

A multi-valued mapping $T:D(T)\subseteq H \to CB(H)$ is said to be k-strictly pseudo-contractive, if there exists k ∈ (0,1) such for all x, y ∈ D(T), we have

$$ \big(H(Tx,Ty)\big)^{2} \leq \|x-y\|^{2}+k\|(x-u)-(y-v)\|^{2}\quad\forall u\in Tx, v\in Ty. $$

(6)

If k = 1 in (6), the map T is said to be pseudo-contractive.

Remark 1

It is easily seen that any multivalued nonexpansive mapping is k-strictly pseudocontractive for any k ∈ (0,1). Moreover, the converse is not true (see, for example, Djitte and Sene [20]).

With this definition at hand, many mathematicians proved some strong convergence theorems for approximating fixed points of multivalued k-strictly pseudo-contractive mappings under some compactness conditions (see, for example, Sene et al. [24], Chidume et al. [8]).

Motivated by Takahashi and Takahashi [27] and the fact that the class of multivalued strictly pseudo-contractive mappings properly includes that of multivalued nonexpansive maps, we construct a new iterative algorithm which is a combination of Krasnoselskii–Mann algorithm and viscosity method for approximating a common element of the set of fixed points of a finite family of multivalued strictly pseudo-contractive mappings and the set of solutions of equilibrium problems which is also the solution of some variational inequality problems. Furthermore, we applied our main results to constrained convex minimization problems. The algorithm and results presented in this paper improve and extend some recents results. Finally, our method of proof is of independent interest.

2 Preliminaries

Let us recall the following definitions and results which will be used in the sequel.

Let H be a real Hilbert space. Let {x_n} be a sequence in H and let x ∈ H. Weak convergence of x_n to x is denoted by $x_{n} \rightharpoonup x$ and strong convergence by x_n → x. Let K be a nonempty, closed convex subset of H. The nearest point projection from H to K, denoted by P_K assigns to each x ∈ H the unique P_Kx with the property

$$ \|x-P_{K}x\| \leq \|y-x\| $$

for all y ∈ K. It is well known that P_Kx satisfies

$$ \langle x-P_{K}x, y-P_{K}x\rangle \leq 0 $$

for all y ∈ K.

Definition 3

Let H be a real Hilbert space and T : D(T) ⊂ H → 2^H be a multivalued mapping. I − T is said to be demiclosed at 0 if for any sequence {x_n}⊂ D(T) such that {x_n} converges weakly to p and d(x_n, Tx_n) converges to zero, then p ∈ Tp.

Lemma 1

(Demiclosedness principle, [6]) Let Hbe a real Hilbert space, Kbe a nonempty closed and convex subset of H. Let T : K → CB(K) be a multivalued nonexpansive mapping with convex-values. Then I − T is demi-closed at zero.

Lemma 2

[7] Let Hbe a real Hilbert space. Then for any x, y ∈ H, the following inequality hold:

$$ \|x+ y\|^{2} \leq \|x\|^{2}+ 2\langle y, x+y \rangle. $$

Lemma 3

(Xu, [29]) Assume that {a_n} is a sequence of nonnegative real numbers such that a_n+ 1 ≤ (1 − α_n)a_n + α_nσ_nfor all n ≥ 0, where {α_n} is a sequence in (0,1) and {σ_n} is a sequence in$\mathbb {R}$such that

• (a) ${\sum }_{n=0}^{\infty } \alpha _{n} = \infty$,

• (b) $\limsup _{n\to \infty } \sigma _{n}\leq 0$ or ${\sum }_{n=0}^{\infty } |\sigma _{n} \alpha _{n}| < \infty$.

Then$\lim _{n\rightarrow \infty }a_{n}=0$.

Lemma 4

[17] Let Kbe a nonempty closed convex subset of a real Hilbert space H and T : K → Kbe a mapping.

• (i) If T is a k-strictly pseudo-contractive mapping, then Tsatisfies the Lipschitzian condition

  $$ \|Tx-Ty\| \leq \frac{1+k}{1-k}\|x-y\|. $$

• (ii) If Tis a k-strictly pseudo-contractive mapping, then the mapping I − T is demiclosed at 0.

Lemma 5

(Sene et al. [24]) Let Kbe a nonempty, closed and convex subset of a real Hilbert space Hand$\lambda _{i}\in ]0,1[, i=1,\dots ,n$such that${\sum }_{i=1}^{n}\lambda _{i}=1$. Then,

$$ \left\|{\sum}_{i=1}^{n}\lambda_{i} u_{i} \right\|^{2}={\sum}_{i=1}^{n}\lambda_{i}\|u_{i}\|^{2} -{\sum}_{i<j}\lambda_{i}\lambda_{j}\|u_{i}-u_{j}\|^{2}\qquad\forall u_{1},u_{2},\dots,u_{n}\in K. $$

The following lemma appears implicitly in [10].

Lemma 6

[10] Let Cbe a nonempty closed convex subset of Hand letFbe a bifunction of C × Cinto$\mathbb {R}$satisfies (A1)–(A4). Let r > 0 and x ∈ H. Then, there exists z ∈ Csuch that

$$ F(z, y)+ \frac{1}{r}\langle y-z, z-x\rangle \geq 0\quad \forall y \in C. $$

The following lemma was also given in [28].

Lemma 7

[28] Assume that$F :C\times C \to \mathbb {R}$satisfies (A1)–(A4). For r > 0 and x ∈ H, define a mapping T_r : H → Cas follows

$$ T_{r}(x)= \left\{z\in C,~F (z, y)+ \frac{1}{r} \langle y-z, z-x\rangle \geq 0,~ \forall y\in C\right\} $$

for all x ∈ H. Then, the following hold:

• 1. T_ris single-valued;

• 2. T_ris firmly nonexpansive, i.e., ∥T_r(x) − T_r(y)∥² ≤〈T_rx − T_ry, x − y〉 for any x, y ∈ H;

• 3. Fix(T_r) = EP(F);

• 4. EP(F) is closed and convex.

3 Main Results

We now prove the following result.

Theorem 2

Let Cbe a nonempty, closed and convex subset of a real Hilbert space H. Let Fbe a bifunction from$C\times C\to \mathbb {R}$satisfying (A1)–(A4) and f : C → Cbe a contraction with coefficient b. Let m ≥ 1 be a fixed number and for 1 ≤ i ≤ m, let$T_{i}:C\rightarrow CB(C)$be a multivalued k_i-strictly pseudo-contractive mapping such that$G:= \bigcap _{i=1}^{m} \text {Fix}(T_{i}) \cap EP(F)\neq \emptyset$and T_ip = {p} ∀p ∈ G.

Let {x_n} and {v_n} be sequences defined iteratively from arbitrary x₀ ∈ Cby

$$ \left\{ \begin{array}{l} F(v_{n}, y) + \frac{1}{r_{n}}\langle y-v_{n}, v_{n}-x_{n}\rangle \geq 0~~\forall y \in C, \\ y_{n} = \lambda_{0} v_{n} + {\sum}_{i=1}^{m} \lambda_{i}{u_{n}^{i}},~~{u_{n}^{i}}\in T_{i}v_{n}, \\ x_{n+1} = \alpha_{n} f(x_{n})+ (1-\alpha_{n})y_{n}, \end{array} \right. $$

(7)

where λ₀ ∈]μ,1[, $\mu := \max \limits \{k_{i},i=1,\dots ,m\}$and λ_i ∈]0,1[ such that {α_n}⊂ (0,1) and$\{r_{n}\}\subset ]0,\infty [$satisfy:

• (i) $\lim _{n\to \infty }\alpha _{n}=0$,

• (ii) ${\sum }_{n=0}^{\infty } \alpha _{n}= \infty$,

• (iii) λ₀ + λ₁ + ⋯ + λ_m = 1,

• (iv) $\lim _{n\to \infty }\inf r_{n}> 0$.

Assume that the mappings I − T_iare demiclosed at the origin. Then, the sequences {x_n} and {y_n} generated by (7) converge strongly to x^∗∈ G, which is the unique solution of the variational inequality:

$$ \langle x^{\ast} - f(x^{\ast}), x^{\ast} - p \rangle \leq 0\quad \forall p\in G. $$

(8)

Proof

From $(I-f)$ is strongly monotone and G is closed convex, then the variational inequality (8) has a unique solution in G. Below, we use x^∗ to denote the unique solution of (8).

Let $p\in G$. Then from $v_{n}= T_{r_{n}}x_{n}$, we have

$$ \|v_{n}-p\|=\|T_{r_{n}}x_{n}-T_{r_{n}}p\| \leq \|x_{n}-p\|\quad \forall n\geq 0. $$

We prove that the sequences $\{x_{n}\}$ and $\{y_{n}\}$ are bounded. Using (7) and Lemma 5, we have

$$ \begin{array}{@{}rcl@{}} \|y_{n}-x^{\ast}\|^{2}&=&\left\|\lambda_{0}(v_{n}-x^{\ast}) + {\sum}_{i=1}^{m}\lambda_{i}({u_{n}^{i}}-x^{\ast})\right\|^{2}\\ &=&\lambda_{0}\|v_{n}-x^{\ast}\|^{2} + {\sum}_{i=1}^{m} \lambda_{i}\|{u_{n}^{i}}-x^{\ast}\|^{2} - {\sum}_{i=1}^{m}\lambda_{0}\lambda_{i}\|{u_{n}^{i}}-v_{n}\|^{2}\\ && - {\sum}_{1\leq i<j}^{m} \lambda_{i}\lambda_{j}\|{u_{n}^{i}}-{u_{n}^{j}}\|^{2}. \end{array} $$

Using that, for $i=1,\dots , m$, T_ix^∗ = {x^∗}, we get

$$ \begin{array}{@{}rcl@{}} \|y_{n}-x^{\ast}\|^{2} &\leq&\lambda_{0}\|v_{n}-x^{\ast}\|^{2} + {\sum}_{i=1}^{m} \lambda_{i} \left( H(T_{i}v_{n},T_{i}x^{\ast})\right)^{2} - {\sum}_{i=1}^{m} \lambda_{0}\lambda_{i}\|{u_{n}^{i}}-v_{n}\|^{2}\\ && - {\sum}_{1\leq i<j}^{m} \lambda_{i}\lambda_{j}\|{u_{n}^{i}}-{u_{n}^{j}}\|^{2}. \end{array} $$

Since, for $i=1,\dots ,m$, T_i is k_i-strictly pseudo-contractive, we have

$$ \begin{array}{@{}rcl@{}} \|y_{n}-x^{\ast}\|^{2} &\leq&\lambda_{0}\|v_{n}-x^{\ast}\|^{2} + {\sum}_{i=1}^{m} \lambda_{i}\left( \|v_{n}-x^{\ast}\|^{2} + k_{i}\|{u_{n}^{i}}-v_{n}\|^{2}\right)\\ && - {\sum}_{i=1}^{m} \lambda_{0}\lambda_{i}\|{u_{n}^{i}}-v_{n}\|^{2} - {\sum}_{1\leq i<j}^{m} \lambda_{i}\lambda_{j}\|{u_{n}^{i}}-{u_{n}^{j}}\|^{2}. \end{array} $$

Hence,

$$ \|y_{n}-x^{\ast}\|^{2} \leq \|v_{n}-x^{\ast}\|^{2} - {\sum}_{i=1}^{m} \lambda_{i}(\lambda_{0}-k_{i})\|{u_{n}^{i}}-v_{n}\|^{2}. $$

(9)

Since λ₀ ∈]μ,1[, we obtain

$$ \|y_{n}-x^{\ast}\| \leq \|v_{n}-x^{\ast}\| \leq \|x_{n}-x^{\ast}\|. $$

(10)

From (7) and (10), we have

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-x^{\ast}\| &= & \|\alpha_{n} f(x_{n}) + (1-\alpha_{n}) y_{n} -x^{\ast}\|\\ &\leq& \alpha_{n} \|f(x_{n}) - f(x^{\ast})\| + (1-\alpha_{n}) \|y_{n} -x^{\ast}\| + \alpha_{n}\|f(x^{\ast})- x^{\ast}\|\\ &\leq&(1-\alpha_{n}(1- b))\|x_{n}-x^{\ast}\| + \alpha_{n}\|f(x^{\ast})- x^{\ast}\|\\ &\leq& \max\left\{\|x_{n} - x^{\ast}\|, \frac{\|f(x^{\ast})- x^{\ast}\|}{1- b}\right\}. \end{array} $$

By induction, it is easy to see that

$$ \|x_{n}-x^{\ast}\| \leq \max\left\{\|x_{0} - x^{\ast}\|,\frac{\|f(x^{\ast}) - x^{\ast}\|}{1- b}\right\},\quad n \geq 1. $$

Hence, {x_n} is bounded and also are {f(x_n)}, and {y_n}.

Consequently, by inequality (9) and property of μ we obtain

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-x^{\ast}\|^{2} &= & \|\alpha_{n} f(x_{n})+ (1-\alpha_{n}) y_{n} -x^{\ast}\|^{2}\\ &\leq& \|\alpha_{n}(f(x_{n})-x^{\ast}) + (1-\alpha_{n})(y_{n} -x^{\ast})\|^{2}\\ &\leq& {\alpha_{n}^{2}} \|f(x_{n}) - x^{\ast}\|^{2} + (1-\alpha_{n})^{2} \|y_{n} - x^{\ast}\|^{2}\\ &&+2 \alpha_{n}(1-\alpha_{n})\|f(x_{n}) - x^{\ast}\| \|y_{n} - x^{\ast}\|\\ &\leq& {\alpha_{n}^{2}} \|f(x_{n}) - x^{\ast}\|^{2} + (1-\alpha_{n})^{2}\|v_{n}-x^{\ast}\|^{2}\\ &&-(1-\alpha_{n})^{2} {\sum}_{i=1}^{m} \lambda_{i}(\lambda_{0}-k_{i})\|{u_{n}^{i}}-v_{n}\|^{2}\\ &&+2 \alpha_{n}(1-\alpha_{n})\|f(x_{n}) - x^{\ast}\| \|x_{n} - x^{\ast}\|. \end{array} $$

Thus, for every i, 1 ≤ i ≤ m, we get

$$ \begin{array}{@{}rcl@{}} (1-\alpha_{n})^{2} {\sum}_{i=1}^{m} \lambda_{i}(\lambda_{0}-k_{i})\|{u_{n}^{i}}-v_{n}\|^{2} &\leq& \|x_{n}-x^{\ast}\|^{2} - \|x_{n+1}-x^{\ast}\|^{2} + {\alpha_{n}^{2}} \|f(x_{n}) -x^{\ast}\|^{2}\\ &&+ 2 \alpha_{n}(1-\alpha_{n})\|f(x_{n}) - x^{\ast}\| \|x_{n} - x^{\ast}\|. \end{array} $$

Since {x_n} and {f(x_n)} are bounded, there exists a constant B > 0 such that for every i, 1 ≤ i ≤ m,

$$ (1-\alpha_{n})^{2} {\sum}_{i=1}^{m} \lambda_{i}(\lambda_{0}-k_{i})\|{u_{n}^{i}}-v_{n}\|^{2} \leq \|x_{n}-x^{\ast}\|^{2} - \|x_{n+1}-x^{\ast}\|^{2} + \alpha_{n} B. $$

(11)

Now we prove that {x_n} converges strongly to x^∗. We divide the rest of the proof into two cases.

Case 1

Assume that there is n₀ ∈ N such that {∥x_n − p∥} is decreasing for all n ≥ n₀. Since {∥x_n − x^∗∥} is monotonic and bounded, {∥x_n − x^∗∥} is convergent. Clearly, we have

$$ \|x_{n}-x^{\ast}\|^{2} - \|x_{n+1}-x^{\ast}\|^{2}\to 0. $$

This implies from (11) that

$$ \lim_{n\to \infty} {\sum}_{i=1}^{m} \lambda_{i}(\lambda_{0}-k_{i})\|{u_{n}^{i}}-v_{n}\|^{2} =0\quad\forall i=1,\dots,m. $$

Since λ₀ ∈]μ,1[, we have

$$ \lim_{n \to \infty} \|v_{n}-{u_{n}^{i}}\|^{2} =0. $$

Since ${u_{n}^{i}}\in T_{i}v_{n}$ for each n, it follows that

$$ \lim_{n\to \infty} d(v_{n}, T_{i}v_{n})=0\quad \forall i=1,\dots,m. $$

(12)

Let p ∈ G, then for each n, we have

$$ \begin{array}{@{}rcl@{}} \|v_{n}-p\|^{2}&=& \|T_{r_{n}}x_{n}-T_{r_{n}}p\|^{2}\\ &\leq&\langle T_{r_{n}}x_{n}-T_{r_{n}}p, x_{n}-p\rangle\\ &\leq& \langle v_{n}-p,x_{n}-p\rangle\\ &=&\frac{1}{2}(\|v_{n}-p\|^{2} + \|x_{n}-p\|^{2}- \|x_{n}-v_{n}\|^{2}) \end{array} $$

and hence,

$$ \|v_{n}-p\|^{2}\leq \|x_{n}-p\|^{2}- \|x_{n}-v_{n}\|^{2}. $$

(13)

Therefore, from (7) and inequality (13), we get

$$ \begin{array}{@{}rcl@{}} \|x_{n+1}-x^{\ast}\|^{2}&=&\|\alpha_{n} f(x_{n}) + (1-\alpha_{n}) y_{n} -x^{\ast}\|^{2}\\ &\leq& (1-\alpha_{n})^{2}\|y_{n}- x^{\ast}\|^{2} + 2\alpha_{n}\langle f(x_{n}) -x^{\ast}, x_{n+1}-x^{\ast} \rangle\\ &\leq& (1-\alpha_{n})^{2}\|v_{n}-x^{\ast}\|^{2} + 2\alpha_{n}\langle f(x_{n}) -x^{\ast}, x_{n+1}-x^{\ast} \rangle\\ &\leq & (1- \alpha_{n})^{2}\|v_{n}-x^{\ast}\|^{2} + 2\alpha_{n} \langle f(x_{n})- f(x^{\ast}), x_{n+1}- x^{\ast} \rangle\\ &&+2\alpha_{n}\langle f(x^{\ast})-x^{\ast}, x_{n+1}-x^{\ast} \rangle\\ &\leq& (1 - \alpha_{n})^{2}(\|x_{n} - x^{\ast}\|^{2} - \|x_{n} - v_{n}\|^{2}) + 2\alpha_{n} b\|x_{n} - x^{\ast}\|\| x_{n+1} - x^{\ast}\|\\ &&+ 2\alpha_{n}\|f(x^{\ast})-x^{\ast}\| \|x_{n+1}-x^{\ast}\|\\ &= & (1- 2\alpha_{n}+ {\alpha_{n}^{2}})\|x_{n}-x^{\ast}\|^{2}- (1- \alpha_{n})^{2}\|x_{n}-v_{n}\|^{2}\\ &&+ 2\alpha_{n} b \|x_{n}-x^{\ast}\| \|x_{n+1}-x^{\ast}\| + 2\alpha_{n}\|f(x^{\ast}) - x^{\ast}\| \|x_{n+1} - x^{\ast}\|\\ &\leq&\|x_{n}-x^{\ast}\|^{2}+ \alpha_{n}\|x_{n}-x^{\ast}\|^{2}-(1-\alpha_{n})^{2}\|x_{n}-v_{n}\|^{2}\\ &&+ 2\alpha_{n} b\|x_{n}-x^{\ast}\| \|x_{n+1} - x^{\ast}\| + 2\alpha_{n}\|f(x^{\ast}) - x^{\ast}\|\|x_{n+1} - x^{\ast}\|, \end{array} $$

and hence

$$ \begin{array}{@{}rcl@{}} (1 - \alpha_{n})^{2}\|x_{n} - v_{n}\|^{2} &\leq& \|x_{n} - x^{\ast}\|^{2} - \|x_{n+1} - x^{\ast}\|^{2} + \alpha_{n}\|x_{n} - x^{\ast}\|^{2}\\ && + 2\alpha_{n} b\|x_{n} - x^{\ast}\|\|x_{n+1} - x^{\ast}\| + 2\alpha_{n}\|f(x^{\ast}) - x^{\ast}\|\|x_{n+1} - x^{\ast}\|. \end{array} $$

So, we have

$$ \lim_{n\rightarrow \infty} \|x_{n}-v_{n}\|= 0. $$

Next, we prove that $\limsup _{n\to +\infty }\langle x^{\ast }-f(x^{\ast }), x^{\ast }-x_{n}\rangle \leq 0$. Since H is reflexive and {x_n} is bounded, there exists a subsequence $\{x_{n_{j}}\}$ of {x_n} such that $x_{n_{j}}$ converges weakly to a in C and

$$ \limsup_{n\to +\infty}\langle x^{\ast}-f(x^{\ast}), x^{\ast} - x_{n}\rangle=\lim_{j\to +\infty}\langle x^{\ast}-f(x^{\ast}), x^{\ast}-x_{n_{j}}\rangle. $$

From (12) and the fact that the operators I − T_i are demiclosed, we obtain $a\in \bigcap _{i=1}^{m} \text {Fix}(T_{i})$. Without loss of generality, we can assume that $v_{n_{k}}\rightharpoonup a$. Let us show a ∈ EP(F). It follows by Lemma 7 and (A2) that

$$ \frac{1}{r_{n}}\langle y-v_{n}, v_{n}-x_{n}\rangle \geq F(y,v_{n}) $$

and hence

$$ \left\langle y-v_{n_{k}}, \frac{ v_{n_{k}}- x_{n_{k}}}{r_{n_{k}}}\right\rangle \geq F(y, v_{n_{k}}). $$

Since $\frac { v_{n_{k}}-x_{n_{k}}}{r_{n_{k}}}\to 0$ and $v_{n_{k}}\rightharpoonup a$, it follows from (A4) that F(y, a) ≤ 0 for all y ∈ C. For t with 0 < t < 1 and y ∈ C, let y_t = ty + (1 − t)a. Since y ∈ C and a ∈ C, we have y_t ∈ C and hence F(y_t, a) ≤ 0. So, from (A1) and (A4) we have

$$ 0 =F(y_{t},y_{t}) \leq t F(y_{t},y)+(1-t)F(y_{t},a)\leq t F(y_{t},y) $$

and hence 0 ≤ F(y_t, y). From (A3), we have F(a, y) ≥ 0 for all y ∈ C and hence a ∈ EP(F). Therofore, a ∈ G.

Hence,

$$ \begin{array}{@{}rcl@{}} \limsup_{n\to +\infty}\langle x^{\ast} - f(x^{\ast}), x^{\ast}-x_{n}\rangle &=& \lim_{k\to +\infty}\langle x^{\ast}- f(x^{\ast}), x^{\ast}-x_{n_{k}}\rangle\\ &=&\langle x^{\ast}-f(x^{\ast}), x^{\ast}-a)\rangle\leq 0. \end{array} $$

Finally, we show that x_n → x^∗. From (7) and Lemma 2, we get that

$$ \begin{array}{@{}rcl@{}} \|x_{n+1} - x^{\ast}\|^{2} & = & \|\alpha_{n} f(x_{n})+ (1- \alpha_{n}) y_{n} -x^{\ast}\|^{2}\\ & \leq & \|\alpha_{n} (f(x_{n})-f(x^{\ast})) + (1-\alpha_{n})(y_{n}-x^{\ast})\|^{2}\\ && +2 \alpha_{n} \langle x^{\ast} - f(x^{\ast}), x^{\ast}-x_{n+1}\rangle\\ & \leq & \left( \alpha_{n} \|f(x_{n})-f(x^{\ast})\| + \|(1-\alpha_{n})(y_{n}-x^{\ast})\|\right)^{2}\\ && + 2\alpha_{n} \langle x^{\ast}-f(x^{\ast}), x^{\ast}-x_{n+1}\rangle\\ & \leq & \left( \alpha_{n} b\|x_{n} - x^{\ast}\| + (1 - \alpha_{n}) \|y_{n} - x^{\ast}\|\right)^{2} + 2\alpha_{n} \langle x^{\ast} - f(x^{\ast}), x^{\ast} - x_{n+1} \rangle\\ &\leq& \left( (1-\alpha_{n}(1- b)) \|x_{n}-x^{\ast}\|\right)^{2} + 2\alpha_{n} \langle x^{\ast} - f(x^{\ast}), x^{\ast}-x_{n+1} \rangle\\ &\leq& (1-\alpha_{n}(1- b))\|x_{n}-x^{\ast}\|^{2} + 2\alpha_{n} \langle x^{\ast}-f(x^{\ast}), x^{\ast}-x_{n+1}\rangle. \end{array} $$

From Lemma 3, its follows that x_n → x^∗.

Case 2

Assume that the sequence {∥x_n − x^∗∥} is not monotonically decreasing. Set B_n = ∥x_n − x^∗∥² and $\tau : \mathbb {N}\to \mathbb {N}$ be a mapping defined for all n ≥ n₀ (for some n₀ large enough) by $\tau (n)= \max \limits \{k\in \mathbb {N} : k\leq n,~ B_{k}\leq B_{k+1}\}$.

We have τ is a non-decreasing sequence such that $\tau (n)\to \infty$ as $n\to \infty$ and B_τ(n) ≤ B_τ(n)+ 1 for n ≥ n₀. Let $i\in \mathbb {N}^{\ast }$, from (11), we have

$$ \left( 1-\alpha_{\tau(n)}\right)^{2} {\sum}_{i=1}\lambda_{i}(\lambda_{0}-k_{i}) \left\|v_{\tau(n)}-u_{\tau(n)}^{i}\right\|^{2} \leq \alpha_{\tau(n)} B. $$

Furthermore, we have

$$ \lim_{n\to +\infty} {\sum}_{i=1}^{m}\lambda_{i}(\lambda_{0}-k_{i}) \left\|v_{\tau(n)}-u_{\tau(n)}^{i}\right\|^{2} =0. $$

Since λ₀ ∈]μ,1[, we can deduce

$$ \lim_{n\rightarrow \infty}\left\|v_{\tau(n)}-u_{\tau(n)}^{i}\right\|^{2} =0. $$

Since $u_{\tau (n)}^{i}\in T_{i} v_{\tau (n)}$, it follows that

$$ \lim_{n\rightarrow \infty} d\left( v_{\tau(n)}, T_{i} v_{\tau(n)}\right)=0\quad\forall i=1,\dots,m. $$

By a similar argument as in Case 1, we can show that x_τ(n) and y_τ(n) are bounded in C and $\limsup _{\tau (n)\to +\infty }\langle x^{\ast }- f(x^{\ast }), x^{\ast }-x_{\tau (n)})\rangle \leq 0$. We have for all n ≥ n₀,

$$ \begin{array}{@{}rcl@{}} 0 &\leq& \|x_{\tau(n)+1}-x^{\ast} \|^{2} - \|x_{\tau(n)}-x^{\ast}\|^{2}\\ &\leq& \alpha_{\tau(n)} \left[- (1- b)\|x_{\tau(n)}-x^{\ast}\|^{2} + 2\langle x^{\ast}-f(x^{\ast}), x^{\ast}-x_{\tau(n)+1} \rangle\right], \end{array} $$

which implies that

$$ \|x_{\tau(n)}-x^{\ast}\|^{2} \leq \frac{ 2}{1- b} \langle x^{\ast}-f(x^{\ast}), x^{\ast}- x_{\tau(n)+1}\rangle. $$

Then, we have

$$ \lim_{n\rightarrow \infty} \|x_{\tau(n)}-x^{\ast}\|^{2} =0. $$

Therefore,

$$ \lim_{n\rightarrow \infty} B_{\tau(n)}=\lim_{n\rightarrow \infty} B_{\tau(n)+1}=0. $$

Furthermore, for all n ≥ n₀, we have B_τ(n) ≤ B_τ(n)+ 1 if n≠τ(n) (that is, n > τ(n)); because B_j > B_j+ 1 for τ(n) + 1 ≤ j ≤ n. As consequence, we have for all n ≥ n₀,

$$ 0\leq B_{n}\leq \max\{B_{\tau(n)},~B_{\tau(n)+1}\} = B_{\tau(n)+1}. $$

Hence, $\lim _{n\rightarrow \infty }B_{n}=0$, that is {x_n} converges strongly to x^∗. This completes the proof. □

We now apply Theorem 2 when multivalued mappings are nonexpansive mappings with convex-values. In this case demiclosedness assumption is not necessary.

Theorem 3

Let Cbe a nonempty, closed and convex subset of a real Hilbert space H. Let Fbe a bifunction from$C\times C\to \mathbb {R}$satisfying (A1)–(A4) and f : C → Cbe a contraction with coefficient b. Let m ≥ 1 be a fixed number and 1 ≤ i ≤ m, let$T_{i}:C\rightarrow CB(C)$be a multivalued nonexpansive mapping and convex-values such that$G:=\bigcap _{i=1}^{m} \text {Fix}(T_{i}) \cap EP(F)\neq \emptyset$and T_ip = {p} ∀p ∈ G.

Let {x_n} and {v_n} be sequences defined iteratively from arbitrary x₀ ∈ Cby:

$$ \left \{ \begin{array}{l} F(v_{n}, y)+ \frac{1}{r_{n}}\langle y-v_{n}, v_{n}-x_{n}\rangle \geq 0~~\forall y \in C, \\ y_{n}= \lambda_{0} v_{n} + {\sum}_{i=1}^{m} \lambda_{i}{u_{n}^{i}},~~{u_{n}^{i}}\in T_{i}v_{n}, \\ x_{n+1}= \alpha_{n} f(x_{n})+ (1-\alpha_{n})y_{n}, \end{array} \right. $$

(14)

where λ_i ∈]0,1[, $i=0,\dots ,m$ such that {α_n}⊂ (0,1) and$\{r_{n}\}\subset ]0,\infty [$satisfy:

• (i) $\lim _{n\rightarrow \infty }\alpha _{n}=0$,

• (ii) ${\sum }_{n=0}^{\infty } \alpha _{n}= \infty$,

• (iii) λ₀ + λ₁ + ⋯ + λ_m = 1.

• (iv) $\lim _{n\rightarrow \infty }\inf r_{n}> 0$.

Then, the sequences {x_n} and {v_n} generated by (14) converge strongly to x^∗∈ G, which is a unique solution of the following variational inequality (8).

Proof

Since every multivalued nonexpansive mapping is multivalued strictly pseudo-contractive mapping, then, the proof follows from Lemma 1 and Theorem 2. □

Since every single-valued mapping can be viewed as a multivalued mapping, we obtain from Lemma 4 the following corollary.

Corollary 1

Let Cbe a nonempty, closed and convex subset of a real Hilbert space H. Let f : C → Cbe a contraction with coefficient b. Let m ≥ 1 be a fixed number and 1 ≤ i ≤ m, let$T_{i}:C\rightarrow C$be a k_i-strictly pseudo-contractive mapping such that$\bigcap _{i=1}^{m}\text {Fix}(T_{i})\neq \emptyset$. Let {x_n} and {v_n} be sequences defined iteratively from arbitrary x₀ ∈ Cby:

$$ \left\{ \begin{array}{l} y_{n}= \lambda_{0} v_{n} + {\sum}_{i=1}^{m} \lambda_{i}T_{i} x_{n},\\ x_{n+1}= \alpha_{n} f(x_{n})+ (1-\alpha_{n})y_{n}, \end{array} \right. $$

(15)

where λ₀ ∈]μ,1[, $\mu := \max \limits \{k_{i}, i=1,\dots ,m\}$, λ_i ∈]0,1[, $i=1,\dots ,m$and {α_n} is a real sequence in (0,1) satisfying:

• (i) $\lim _{n\rightarrow \infty }\alpha _{n}=0$,

• (ii) ${\sum }_{n=0}^{\infty } \alpha _{n}= \infty$,

• (iii) λ₀ + λ₁ + ⋯ + λ_m = 1.

Then, the sequences {x_n} and {v_n} generated by (15) converge strongly to$x^{\ast } \in \bigcap _{i=1}^{m} \text {Fix}(T_{i})$, which is the unique solution of the variational inequality

$$ \langle x^{\ast}-f(x^{\ast}), x^{\ast}-p\rangle\leq 0\quad \forall p\in \bigcap_{i=1}^{m} \text{Fix}(T_{i}). $$

Proof

Put F(x, y) = 0 for all x, y ∈ C and r_n = 1, we get u_n = x_n in Theorem 2. The proof follows from Theorem 2 and Lemma 4. □

Let K be a nonempty, closed and convex subset of a real Hilbert space, let T : K → P(K) be a multivalued map and P_T : K → CB(K) be defined by

$$ P_{T}(x):=\{y\in Tx:~ \|y-x\| = d(x, Tx)\}. $$

We will need the following result.

Lemma 8

(Song and Cho [25]) Let Kbe a nonempty subset of a real Banach space and T : K → P(K) be a multi-valued map. Then the following are equivalent:

• (i) x^∗∈Fix(T);

• (ii) P_T(x^∗) = {x^∗};

• (iii) x^∗∈Fix(P_T). Moreover, Fix(T) = Fix(P_T).

Now, using the similar arguments as in the proof of Theorem 2 and Lemma 8, we obtain the following result by replacing T by P_T and removing the rigid restriction on Fix(T) (Tp = {p} ∀p ∈ F(T)).

Theorem 4

Let Cbe a nonempty, closed and convex subset of a real Hilbert space H. Let Fbe a bifunction from$C\times C\to \mathbb {R}$satisfying (A1)–(A4) and f : C → Cbe a contraction with coefficient b. Let T : C → CB(C) be a multivalued mapping such that G := Fix(T) ∩ EP(F)≠∅. Assume that P_Tis k-strictly pseudo-contractive.

Let {x_n} and {v_n} be sequences defined iteratively from arbitrary x₀ ∈ Cby:

$$ \left\{ \begin{array}{l} F(v_{n}, y)+ \frac{1}{r_{n}}\langle y-v_{n}, v_{n}-x_{n}\rangle \geq 0~~\forall y \in C, \\ y_{n} = \lambda_{0} v_{n} + (1-\lambda_{0})u_{n},~~u_{n}\in P_{T}v_{n},\\ x_{n+1} = \alpha_{n} f(x_{n})+ (1-\alpha_{n})y_{n}, \end{array} \right. $$

(16)

where λ₀ ∈]k,1[ and {α_n}⊂ (0,1) and$\{r_{n}\}\subset ]0,\infty [$satisfy:

• (i) $\lim _{n\rightarrow \infty }\alpha _{n}=0$,

• (ii) ${\sum }_{n=0}^{\infty } \alpha _{n}= \infty$,

• (iii) $\lim _{n\rightarrow \infty }\inf r_{n}> 0$.

Assume that the mappings I − P_Tis demiclosed at the origin. Then, the sequences {x_n} and {y_n} generated by (16) converge strongly to x^∗∈ G, which is the unique solution of the variational inequality:

$$ \langle x^{\ast}-f(x^{\ast}), x^{\ast}-p \rangle\leq 0\quad \forall p\in G. $$

4 Application to Constrained Optimization Problems

Convex optimization theory is a powerful tool for solving many practical problems in operational research. In particular, it has been widely used to solve practical minimization problems over complicated constraints [5, 11], e.g., convex optimization problems with a fixed point constraint and with a variational inequality constraint. Consider the following constrained optimization problem: Let C be a nonempty, closed and convex subset a real Hilbert space H. Given a convex objective function $g : C \to \mathbb {R}$, the problem can be expressed as

$$ \begin{array}{@{}rcl@{}} \text{Minimize }~g(x)\quad\text{subject to }~x\in C. \end{array} $$

The set of solutions of (17) is denoted by Sol(g).

Proposition 1

[26] Let Hbe a real Hilbert space. Let A : H → Hbe a monotone mapping such that K := D(A) is closed and convex. Assume that Ais bounded on bounded subsets and hemi-continuous on K. Then, the bifunction F(x, y) := 〈Ax, y − x〉 satisfies conditions (A1)–(A4).

The following basic results are well known.

Lemma 9

Let Hbe a real Hilbert space and Kbe a nonempty closed and convex subset of H. Let$g: H \to \mathbb {R}$be a real valued differentiable convex function. Let ∇g : K → Hdenotes the differential map associated to g. Then the following hold. If gis bounded, then gis locally Lipschitzian, i.e., for every x₀ ∈ Kand r > 0, there exists γ > 0 such that g is γ-Lipschitzian on B(x₀, r), i.e.,

$$ |g(x)-g(y)|\leq \gamma\|x-y\|\quad\forall x,y\in B(x_{0},r). $$

Lemma 10

Let Kbe a nonempty, closed convex subset of Hand let$g:K\to \mathbb {R}$a real valued differentiable convex function. Then x^∗is a minimizer of gover Kif and only if x^∗solves the following variational inequality 〈∇g(x^∗), x − x^∗〉≥ 0 for all x ∈ K.

Remark 2

Let K be a nonempty, closed convex subset of H. Let $g: K \to \mathbb {R}$ a real valued differentiable convex function. It is well known that the differential map associated to g is monotone.

Lemma 11

Let Kbe a nonempty, closed and convex subset of a real Hilbert space Hand$g: K \to \mathbb {R}$be a real valued differentiable convex function. Assume that gis bounded. Then the differentiable map, ∇g : K → His bounded.

Proof

For x₀ ∈ K and r > 0, let B := B(x₀, r). We show that ∇g(B) is bounded. From Lemma 9, there exists γ > 0 such that

$$ |g(x)-g(y)|\leq \gamma\|x-y\|\quad\forall x,y\in B. $$

(17)

Let z^∗∈∇g(B) and x^∗∈ B such that z^∗ = ∇g(x^∗). For u ∈ H, since B is open, there exists t > 0 such that x^∗ + tu ∈ B. Using the fact that z^∗ = ∇g(x^∗), the convexity of g and the inequality (17), it follows

$$ \langle z^{\ast}, tu\rangle\leq g(x^{\ast}+tu)-g(x^{\ast})\leq t\gamma\|u\|. $$

So that, 〈z^∗, u〉≤ γ∥u∥ ∀u ∈ H. Therefore, ∥z^∗∥≤ γ. Hence, ∇g(B) is bounded. □

Theorem 5

Let Cbe a nonempty, closed and convex subset of a real Hilbert space H. Let$g: C \to \mathbb {R}$a real valued continuously differentiable convex and bounded function and f : C → Cbe a contraction with coefficient b. Let m ≥ 1 be a fixed number and 1 ≤ i ≤ m, let T_i : C → CB(C) be a multivalued k_i-strictly pseudo-contractive mapping such that$G:=\bigcap _{i=1}^{m} \text {Fix}(T_{i}) \cap \text {Sol}(g) \neq \emptyset$and T_ip = {p} ∀p ∈ G. Assume that I − T_iare demiclosed at the origin.

Let {x_n} and {v_n} be sequences generated iteratively from arbitrary x₀ ∈ C by:

$$ \left\{ \begin{array}{l} \langle \nabla g(v_{n}),y-v_{n}\rangle + \frac{1}{r_{n}}\langle y-v_{n}, v_{n}-x_{n}\rangle \geq 0~~\forall y \in C, \\ y_{n} = \lambda_{0} v_{n} + {\sum}_{i=1}^{m} \lambda_{i}{u_{n}^{i}},~~{u_{n}^{i}}\in T_{i}v_{n},\\ x_{n+1} = \alpha_{n} f(x_{n})+ (1-\alpha_{n})y_{n}, \end{array} \right. $$

where λ₀ ∈]μ,1[, $\mu := \max \limits \{k_{i},~ i=1,\dots ,m\}$ and λ_i ∈]0,1[ such that {α_n}⊂ (0,1) and $\{r_{n}\}\subset ]0,\infty [$ satisfy:

• (i) $\lim _{n\rightarrow \infty }\alpha _{n}=0$,

• (ii) ${\sum }_{n=0}^{\infty } \alpha _{n}= \infty$,

• (iii) λ₀ + λ₁ + ⋯ + λ_m = 1,

• (iv) $\lim _{n\rightarrow \infty }\inf r_{n}> 0$.

Then, the sequence {x_n} converges strongly to x^∗ solution of (17).

Proof

Let F(x, y) := 〈∇g(x), y − x〉 for all x, y ∈ C. From the properties of g, Proposition 1, Remark 2 and Lemma 11, it follows that ∇g is monotone, continuous and bounded on bounded subset on C. So, F satisfies (A1)–(A4). Using the assumption that (17) has a solution and Lemma 10, we have x^∗ is solution of (17) if and only if x^∗∈ EP(F). Then, the proof follows from Theorem 2. □

5 Numerical Example

In this section, we present a numerical example to illustrate the convergence behavior of our iteration scheme (16).

Let $\langle \cdot , \cdot \rangle : \mathbb {R}^{3}\times \mathbb {R}^{3} \to \mathbb {R}$ be the inner product defined by

$$ \langle x,y\rangle= x_{1}\cdot y_{1}+x_{2}\cdot y_{2}+x_{3}\cdot y_{3} $$

and let $\|\cdot \|: \mathbb {R}^{3} \to \mathbb {R}$ be the usual norm defined by $\|x\|= \sqrt {{x_{1}}^{2}+{x_{2}}^{2}+{x_{2}}^{2}}$ for any $x=(x_{1}, x_{2}, x_{3})\in \mathbb {R}^{3}$. For all $x\in \mathbb {R}^{3}$, let $T: \mathbb {R}^{3} \to CB(\mathbb {R}^{3})$ defined by

$$ Tx= \left \{ \begin{array}{ll} \left[0, \frac{x}{2}\right],\quad & x\in {(0, \infty) }^{3},\\ \left[\frac{x}{2}, 0\right],\quad& x\in {(-\infty, 0]}^{3}. \end{array} \right. $$

Then P_T is strictly pseudo-contractive. In fact, $P_{T}(x) = \{\frac {x}{2}\}$ for all $x \in \mathbb {R}^{3}$. It is easy to see that Fix(T) = {0}. Let F(x, y) := y² + yx − 2x², $f(x)=\frac {1}{3}x$ and $T_{r}(x)= \{z\in \mathbb {R}^{3}, f(z, y) + \frac {1}{r} \langle y-z, z-x\rangle \geq 0~\forall y\in \mathbb {R}^{3}\}$. We can observe that $T_{r}(x)=\frac {1}{1+3r}x$ and 0 ∈Fix(T) ∩ EP(F). Choose $r=1,~\alpha _{n}=\frac {1}{n+1}$ and $\lambda _{0}=\frac {1}{2}$. Then, the scheme (16) can be simplified as

$$ \left\{ \begin{array}{l} v_{n}=\frac{1}{4}x_{n},\\ y_{n}=\frac{3}{16}x_{n},\\ x_{n+1}= \frac{1}{3n+3}x_{n}+\frac{3n}{ 16n+16}x_{n},~~ n\geq 1. \end{array} \right. $$

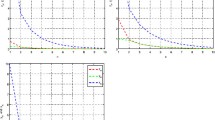
Taking the initial point x₁ = (1,2,3), the result of the numerical example obtained by using MATLAB is given in Fig. 1 where it is shown that the sequence of iterates {x_n} strongly converges to 0.

Fig. 1

Two dimensions