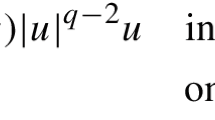1 Introduction

Let N be an integer ≥ 3, Ω be a bounded domain in \(\mathbb {R}^{N}\) with smooth boundary ∂Ω, p be in [1,N) and \(p^{\ast }=\frac {Np}{N-p}\). Let \(W^{1,p}_{0}({\Omega })\) be the usual Sobolev space with the following norm

$$\|u\|_{1,p} = \left\{{\int}_{\Omega}|\nabla u|^{p}dx\right\}^{\frac{1}{p}}\qquad\forall u\in W^{1,p}_{0}({\Omega}). $$

We consider the following Dirichlet problem:

$$ \left\{\begin{array}{ll} - \text{div}(|\nabla u|^{p-2}\nabla u)=f(x,u) & \text{ in } {\Omega},\\ u=0 & \text{ on } \partial{\Omega}. \end{array}\right. $$
(1)

In [3,4,5, 8], one has proved (1) has non-trivial solutions if f is continuous on \(\overline {\Omega }\times \mathbb {R}\) and satisfies the following conditions

  • (C 1 ) There exist r ∈ (p,p ∗− 1) and a positive real number α such that

    $$|f(x,t)|\leq \alpha(1+|t|^{r-1})\qquad\forall (x,t) \in {\Omega}\times \mathbb{R}. $$

  • (C 2 ) f(x,0) = 0 for every x in Ω and \(\lim _{t\to 0}\frac {f(x,t)}{|t|^{p-2}t} =0\) uniformly in Ω.

  • (C 3 ) \(\lim _{|t|\to \infty }\frac {f(x,t)}{|t|^{p-2}t} =\infty \) uniformly in Ω.

  • (C 4 ) There exist \(C\in [0,\infty )\), 𝜃 > p such that

    $$0 \leq f(x,t)t -\theta F(x,t) \qquad\text{ a.e. in } {\Omega}\times\{t\in\mathbb{R}: |t|>C\}, $$

    where \(F(x,t) = {{\int }_{0}^{t}}f(x,\xi )d\xi \) for every (x,t) in \({\Omega }\times \mathbb {R}\).

In the present paper, we prove the following result.

Theorem 1

Assume f is a Carath é odory function on \({\Omega }\times \mathbb {R}\) and satisfies the following conditions

  • (f 1 ) there exist r ∈ (p,p ∗), \(\omega \in \mathcal {K}_{p,r}\) (see Definition 1) and \(b\in L^{\frac {r}{r-1}}({\Omega })\) such that

    $$|f(x,t)|\leq |\omega(x)t|^{r-1} + b(x)\qquad \forall (x,t) \in {\Omega}\times \mathbb{R}, $$

  • (f 2 ) there exists d ∈ L 1(Ω)such that |f(x,t)|≤ d(x)forevery x in Ωand |t|≤ C,

  • (f 3 ) there is a non-positive function d 1in\(L^{\frac {2N}{p}}({\Omega })\)suchthat \(d_{1}(x)\le \frac {f(x,t)}{|t|^{p-2}t}\)forevery \((x,t)\in {\Omega }\times \mathbb {R}\),

  • (f 4 ) f(x,0) = 0forevery x in Ωand \(\lim _{t\to 0}\frac {f(x,t)}{|t|^{p-2}t} =0\)a.e. in Ω,

  • (f 5 ) \(\lim _{|t|\to \infty }\frac {f(x,t)}{|t|^{p-2}t} =\infty \)a.e.in Ω,and

  • (f 6 ) there exist 𝜃 > p and d 2 ∈ L 1(Ω)suchthat

    $$d_{2}(x) \leq f(x,t)t -\theta F(x,t) \qquad \textit{a.e. in} ~ {\Omega}\times\{t\in\mathbb{R}: |t|>C\}. $$

Then there is a non-trivial weak solution in\(W^{1,p}_{0}({\Omega })\)of theproblem (1).

Remark 1

In many applications, \(\frac {f(x,t)}{|t|^{p-2}t}\) is non-negative for t≠0 and |f(x,t)| is well-controlled when |t| is sufficiently small. This observation is the motivation of (f 2) and (f 3). Here, we consider the case, in which the positivity of \(\frac {f(x,t)}{|t|^{p-2}t}\) can be disturbed by a non-positive function d 1 in \(L^{\frac {2N}{p}}({\Omega })\).

Remark 2

If f is continuous on \(\overline {\Omega }\times \mathbb {R}\) and satisfies the conditions (C 1), (C 2), (C 3), and (C 4), then f satisfies (f 1)– (f 6). Furthermore, |w|r−1 may be not integrable on Ω and the convergences in (f 4) and (f 5) may be not uniform on Ω (see Example 4). Therefore our theorem improves the corresponding results in [3,4,5, 8].

We study some method to construct weight functions in weighted Sobolev embeddings and the Nemytskii operator from Sobolev spaces into Lebesgue spaces (see Theorems 4 and 5) in Section 2. We apply these results to prove the existence of non-trivial solutions of a class of super-linear p-Laplace problems in the last section.

2 Nemytskii Operators

Definition 1

Let σ be a measurable function on Ω. We put

$$T_{\sigma}u = \sigma u\qquad\forall u\in W^{1,p}_{0}({\Omega}). $$

We say

  1. (i)

    σ is of class \(\mathcal {C}_{p,s}\) if T σ is a continuous mapping from \(W^{1,p}_{0}({\Omega })\) into L s(Ω);

  2. (ii)

    σ is of class \(\mathcal {K}_{p,s}\) if T σ is a compact mapping from \(W^{1,p}_{0}({\Omega })\) into L s(Ω).

We have the following results.

Theorem 2

Let α 1 and α 2 be in \([1,\infty )\) such that α 1 < α 2 . Let \(\omega _{1}\in \mathcal {C}_{p,\alpha _{1}}\) , \(\omega _{2}\in \mathcal {C}_{p,\alpha _{2}}\) be such that ω 1 and ω 2 are non-negative. Let β ∈ (α 1,α 2)and \(\omega = \omega _{1}^{\frac {\alpha _{1}(\alpha _{2}-\beta )}{\beta (\alpha _{2} -\alpha _{1})}}\omega _{2}^{\frac {\alpha _{2}(\beta -\alpha _{1})}{\beta (\alpha _{2} -\alpha _{1})}}\) . Then \(w \in \mathcal {C}_{p,\beta }\) .

Proof

There is a positive real number C 1 such that

$$ \left\{{\int}_{\Omega}\omega_{i}^{\alpha_{i}}|u|^{\alpha_{i}} dx\right\}^{1/\alpha_{i}}\le C_{1}\|u\|_{1,p}\qquad \forall u \in W^{1,p}_{0}({\Omega}), i= 1,2. $$
(2)

Since \(\beta = \frac {\alpha _{2}-\beta }{\alpha _{2} -\alpha _{1}}\alpha _{1} + \frac {\beta -\alpha _{1}}{\alpha _{2} -\alpha _{1}}\alpha _{2}\), by Hölder’s inequality and (2), we get

$$\begin{array}{@{}rcl@{}} \left\{{\int}_{\Omega}\omega^{\beta}|u|^{\beta} dx\right\}^{1/\beta}&=&\left\{{\int}_{\Omega}\omega_{1}^{\frac{\alpha_{2}-\beta}{\alpha_{2} -\alpha_{1}}\alpha_{1}}|u|^{\frac{\alpha_{2}-\beta}{\alpha_{2} -\alpha_{1}}\alpha_{1}}\omega_{2}^{\frac{\beta-\alpha_{1}}{\alpha_{2} -\alpha_{1}}\alpha_{2}}|u|^{\frac{\beta-\alpha_{1}}{\alpha_{2} -\alpha_{1}}\alpha_{2}} dx\right\}^{1/\beta}\\ &\le& \left\{\left\{{\int}_{\Omega}\omega_{1}^{\alpha_{1}}|u|^{\alpha_{1}} dx\right\}^{\frac{\alpha_{2}-\beta}{\alpha_{2} -\alpha_{1}}}\left\{{\int}_{\Omega}\omega_{2}^{\alpha_{2}}|u|^{\alpha_{2}} dx\right\}^{\frac{\beta-\alpha_{1}}{\alpha_{2} -\alpha_{1}}}\right\}^{1/\beta}\\ &\le& \left\{\left\{{\int}_{\Omega}\omega_{1}^{\alpha_{1}}|u|^{\alpha_{1}} dx\right\}^{\frac{1}{\alpha_{1}}\frac{\alpha_{2}-\beta}{\alpha_{2} -\alpha_{1}}\alpha_{1}}\left\{{\int}_{\Omega}\omega_{2}^{\alpha_{2}}|u|^{\alpha_{2}} dx\right\}^{\frac{1}{\alpha_{2}}\frac{\beta-\alpha_{1}}{\alpha_{2} -\alpha_{1}}\alpha_{2}}\right\}^{1/\beta}\\ &\le& C_{1}\|u\|_{1,p}\quad\forall u \in W^{1,p}_{0}({\Omega}). \end{array} $$

□

Theorem 3

Let s be in \([1,\frac {Np}{N-p})\) , α be in (0,1), \(\omega \in \mathcal {C}_{p,s}\) and 𝜃 be measurable functions on Ωsuch that ω ≥ 0and |𝜃|≤ ω α . Then 𝜃 is of class \(\mathcal {K}_{p,s}\) .

Proof

Since T ω is in \(\mathcal {C}_{p,s}\), T ω is continuous from \(W^{1,p}_{0}({\Omega })\) into L s(Ω) and there is a positive real number C 2 such that

$$ \left\{{\int}_{\Omega}|u|^{s}\omega^{s} dx\right\}^{1/s}\le C_{2}\|u\|_{1,p}\qquad\forall u \in W^{1,p}_{0}({\Omega}). $$
(3)

Since ω α(x) ≤ 1 + ω(x) for every x in Ω and 1 and ω are in \(\mathcal {C}_{p,s}\), ω α belongs to \(\mathcal {C}_{p,s}\). Thus, T 𝜃 is in \(\mathcal {C}_{p,s}\). Let M be a positive real number and {u n } be a sequence in \(W^{1,p}_{0}({\Omega })\), such that ∥u n ∥1,p ≤ M for any n. By Rellich–Kondrachov’s theorem (Theorem 9.16 in [2]), {u n } has a subsequence \(\{u_{n_{k}}\}\) converging to u in L s(Ω) and \(\{u_{n_{k}}\}\) converging weakly to u in \(W_{0}^{1,p}({\Omega })\), therefore \(\|u\|_{1,p} \leq \liminf _{k \to \infty } \|u_{n_{k}}\|_{1,p} \leq M\). We shall prove \(\{T_{\theta }(u_{n_{k}})\}\) converges to T 𝜃 (u) in L s(Ω).

Let ε be a positive real number. Choose a positive real number δ such that

$$ (2C_{2}M)^{s}\delta^{(\alpha-1)s} < \frac{\varepsilon^{s}}{2}. $$
(4)

Put \({\Omega }^{\prime } =\{x\in {\Omega } : \omega (x)> \delta \}\). By (3) and (4), we have

$$\begin{array}{@{}rcl@{}} {\int}_{\Omega}|\theta(u_{n_{k}}-u)|^{s}dx &=& {\int}_{\Omega}|u_{n_{k}}-u|^{s}|\theta|^{s}dx\\ & \leq& {\int}_{{\Omega}^{\prime}}|u_{n_{k}}-u|^{s}\omega^{\alpha s}dx +{\int}_{\Omega\setminus {\Omega}^{\prime}}|u_{n_{k}}-u|^{s}\omega^{\alpha s}dx \\ &\leq& \delta^{(\alpha-1)s}{\int}_{{\Omega}^{\prime}}|u_{n_{k}}-u|^{s}\omega^{s} dx + \delta^{\alpha s}{\int}_{\Omega\setminus {\Omega}^{\prime}}|u_{n_{k}}-u|^{s}dx \\ &\leq& \delta^{(\alpha-1)s}{\int}_{\Omega}|u_{n_{k}}-u|^{s}\omega^{s} dx + \delta^{\alpha s}{\int}_{\Omega}|u_{n_{k}}-u|^{s}dx \\ &\leq& \delta^{(\alpha-1)s}\left(C_{2}\|u_{n_{k}}-u\|_{1,p}\right)^{s} +\delta^{\alpha s}{\int}_{\Omega}|u_{n_{k}}-u|^{s}dx\\ &\leq& \delta^{(\alpha-1)s}(2C_{2}M)^{s} + \delta^{\alpha s}{\int}_{\Omega}|u_{n_{k}}-u|^{s}dx\\ &\leq& \frac{\varepsilon^{s}}{2} +\delta^{\alpha s}{\int}_{\Omega}|u_{n_{k}}-u|^{s}dx. \end{array} $$
(5)

Since \(\{u_{n_{k}}\}\) converges in L s(Ω), there is an integer k 0 such that

$$ {\int}_{\Omega}|u_{n_{k}}-u|^{s}dx \le \delta^{-\alpha s}\frac{\varepsilon^{s}}{2}\qquad\forall k\ge k_{0}. $$
(6)

Combining (5) and (6), we get the theorem. □

Corollary 1

Let p ∈ [1,N), \(s \in \left (1,\frac {Np}{N-p}\right )\) , \(\eta \in \left (\frac {sNp}{Np-s(N-p)},\infty \right )\) and 𝜃 ∈ L η(Ω). Then 𝜃 is in \(\mathcal {K}_{p,s}\) .

Proof

Let β ∈ (0,1) be such that \(\beta \eta = \frac {sNp}{Np-s(N-p)}\) and ω = |𝜃|1/β. Then ω is in \(L^{\frac {sNp}{Np-s(N-p)}}({\Omega })\). Since \(\frac {Np-s(N-p)}{Np}+\frac {s(N-p)}{Np}=1\), by Hölder’s inequality, we have

$${\int}_{\Omega}|\omega u|^{s}dx\le {\int}_{\Omega}\left(|\omega|^{\frac{sNp}{Np-s(N-p)}}\right)^{\frac{Np-s(N-p)}{Np}}\left({\int}_{\Omega}|u|^{\frac{Np}{N-p}}\right)^{\frac{s(N-p)}{Np}}\qquad\forall u\in W^{1,p}_{0}({\Omega}), $$

which implies that T ω is continuous at 0 in \(W^{1,p}_{0}({\Omega })\). Thus, T ω is a linear continuous map from \(W^{1,p}_{0}({\Omega })\) into L s(Ω). By Theorem 3, 𝜃 is of class \(\mathcal {K}_{p,r}\). □

Example 1

Let N = 5, p = 3, s = 4 and \({\Omega } =\{x\in \mathbb {R}^{5}: |x| < 1\}\). Then \(\frac {sNp}{Np - s(N-p)} =\frac {4\cdot 5\cdot 3}{5\cdot 3-4(5-3)}=\frac {60}{7}<10\). Put \(\omega _{0}= |x|^{-\frac {1}{30}}\cos (16|x|)\). Then ω 0 is in L 10(Ω). Thus by Corollary 1, ω 0 is of class \(\mathcal {K}_{p,s}\).

Corollary 2

Let p ∈ [1,N), \(s \in \left (1,\frac {Np}{N-p}\right )\) , α be in (0,1) and \(\eta \in \mathcal {C}_{p,p}\) . Then \(\theta =\eta ^{\alpha \frac {p(p^{\ast }-s)}{s(p^{\ast } -p)}}\) is of class \(\mathcal {K}_{p,s}\) .

Proof

Put ω 1 = η, ω 2 = 1, α 1 = p, α 2 = p ∗, β = s. By the Embedding theorem of Sobolev, \(\omega _{2} \in \mathcal {C}_{p,p^{\ast }}\). By Theorem 2, we see that \(\eta ^{\frac {p(p^{\ast }-s)}{s(p^{\ast } -p)}}\in \mathcal {C}_{p,s}\). Thus by Theorem 4, \(\eta ^{\alpha \frac {p(p^{\ast }-s)}{s(p^{\ast } -p)}}\) is of class \(\mathcal {K}_{p,s}\). □

Example 2

Let \({\Omega } =\{x\in \mathbb {R}^{5}: \|x\| < 1\}\), p = 3, s = 4, \(\alpha = \frac {3}{4}\) and η(x) = (1 −∥x∥2)−1 for every x in Ω. By Theorem 8.4 in [7], \(\eta \in \mathcal {C}_{p,p}\). Note that \(p^{\ast }=\frac {Np}{N-p} = \frac {15}{2}\) and

$$\alpha\frac{p(p^{\ast}-s)}{s(p^{\ast} -p)}= \frac{3}{4}\frac{3}{4}\frac{7}{9}=\frac{7}{16}. $$

Put \(\theta (x) = (1-\|x\|^{2})^{-\frac {7}{16}}\) for every x in Ω. Then \(\theta \in \mathcal {K}_{3,4}\).

Theorem 4

Let s be in (1,p ∗), ω be in \(\mathcal {K}_{p,s}\) , b be in \(L^{\frac {s}{s-1}}({\Omega })\) and g be a Carath é odory function from \({\Omega } \times \mathbb {R}\) into \(\mathbb {R}\) . Assume

$$ |g(x,z)| \leq |\omega(x)|^{s-1}|z|^{s-1} + b(x)\qquad \forall (x,z) \in {\Omega} \times \mathbb{R}. $$
(7)

Put

$$N_{g}(v)(x)= g(x,v(x)) \qquad \forall v \in W^{1,p}_{0}({\Omega}), x \in {\Omega}. $$

Wehave

  1. (i)

    N g is a continuous mapping from \(W_{0}^{1,p}({\Omega })\)into \(L^{\frac {s}{s-1}}({\Omega })\).

  2. (ii)

    If A is a bounded subset in \(W_{0}^{1,p}({\Omega })\),then \(\overline {N_{g}(A)}\)is compact in \(L^{\frac {s}{s-1}}({\Omega })\).

Proof

(i) Put μ = s, \(q= \frac {s}{s-1}\) and

$$g_{1}(x,\zeta)=g(x,\omega(x)^{-1}\zeta)\qquad \forall (x,\zeta) \in {\Omega} \times \mathbb{R}, $$

By (7), we have

$$|g_{1}(x,\zeta)| \leq |\zeta|^{s-1} + b(x)\qquad \forall (x,\zeta) \in {\Omega} \times \mathbb{R}. $$

On the other hand

$$N_{g}(v) = N_{g_{1}}\circ T_{|\omega|}(v)\qquad\forall v \in W^{1,p}_{0}({\Omega}). $$

Since \(w \in \mathcal {K}_{p,s}\), applying Theorem 2.3 in [5], we get the theorem. □

Theorem 5

Let s ∈ (1,p ∗), ω be in \(\mathcal {K}_{p,s}\) , a function \(b \in L^{\frac {s}{s-1}}({\Omega })\) and g be a Carath é odory function from \({\Omega } \times \mathbb {R}\) into \(\mathbb {R}\) . Assume

$$|g(x,z)| \leq |\omega(x)|^{s-1}|z|^{s-1} + b(x)\qquad \forall (x,z) \in {\Omega} \times \mathbb{R}. $$

Put

$$\begin{array}{@{}rcl@{}} G(x,t)&=&{{\int}_{0}^{t}}g(x,\xi)d\xi \qquad \forall (x,t) \in {\Omega},\\ {\Psi}_{g}(u)&=&{\int}_{\Omega}G(x,t) dx \qquad \forall u \in W^{1,p}_{0}({\Omega}). \end{array} $$

We have

  1. (i)

    {N G (w n )}converges to N G (w)in L 1(Ω)when {w n }weakly converges to w in \(W^{1,p}_{0}({\Omega })\).

  2. (ii)

    Ψ g is a continuously Fréchet differentiable mapping from\(W^{1,p}_{0}({\Omega })\)into\(\mathbb {R}\)and

    $$D{\Psi}_{g}(u)(\phi)={\int}_{\Omega}g(x,\xi)\phi dx \qquad \forall u, \phi \in W^{1,p}_{0}({\Omega}). $$
  3. (iii)

    If A is a bounded subset in \(W^{1,p}_{0}({\Omega })\),then there is a positive real number M suchthat

    $$|{\Psi}_{g}(v)| + \|D{\Psi}_{g}(v)\|\le M \qquad\forall v \in {A}. $$

Proof

Let μ = s, \(q= \frac {s}{s-1}\) and g 1 be as in the proof of Theorem 4. Put

$$\begin{array}{@{}rcl@{}} G_{1}(x,t) &=& {{\int}_{0}^{t}}g(x,\xi)d\xi \qquad \forall (x,t) \in {\Omega},\\ {\Psi}_{g_{1}}(u)&=&{\int}_{\Omega}{\int}_{0}^{u(x)}g_{1}(x,\xi)d\xi dx \qquad \forall u \in L^{p}({\Omega}). \end{array} $$

By [5, Theorem 2.8], \(N_{G_{1}}\) is continuous from \(L^{\frac {s}{s-1}}({\Omega })\) into L 1(Ω) and \({\Psi }_{g_{1}}\) is a continuously Fréchet differentiable mapping from \(L^{\frac {s}{s-1}}({\Omega })\) into \(\mathbb {R}\). We see that N G = N G 1 ∘ T ω and Ψ g =Ψ g 1 ∘ T ω . By Theorem 3, we get the theorem. □

Remark 3

If ω = 1, Theorems 4 and 5 have been proved in [1, 5, 6].

Example 3

Let \({\Omega } =\{x\in \mathbb {R}^{5}: \|x\| < 1\}\), p = 3, s = 4, \(\alpha = \frac {3}{4}\) and ρ(x) = \((\frac {1}{2}-\|x\|^{2})^{2}(1-\|x\|^{2})^{-\frac {7}{16}}\) for every x in Ω. By Example 2, \(\rho \in \mathcal {K}_{3,4}\). Put \(a(x) = \rho (x)^{s -1} = (\frac {1}{2}-\|x\|^{2})^{6}(1-\|x\|^{2})^{-\frac {21}{16}}\) for every x in Ω. Thus, a is not integrable on Ω and Theorem 5 improves corresponding results in [1, 5, 6].

3 Proof of Theorem 1

Put

$$ J(u)=\frac{1}{p}\|u\|_{1,p}^{p}-{\int}_{\Omega}F(x,u)dx\qquad \forall u\in W_{0}^{1,p}({\Omega}). $$
(8)

By [3, Theorem 9], Theorem 5 and (f 1), J is continuously Fréchet differentiable on \(W_{0}^{1,p}({\Omega })\) and

$$ DJ(u)(v)={\int}_{\Omega}|\nabla u|^{p-2}\nabla u\cdot\nabla vdx-{\int}_{\Omega}f(x,u)\cdot vdx\qquad \forall u,v\in W_{0}^{1,p}({\Omega}). $$
(9)

In order to prove the theorem, we need the following lemmas.

Lemma 1

Under condition (f 3)and (f 4), there exist positive numbers ρ and η such that J(u) ≥ η for all u in \(W_{0}^{1,p}({\Omega })\) with ∥u∥ = ρ .

Proof

Suppose on the contrary that

$$\inf\left\{J(u): u \in W^{1,p}_{0}({\Omega}), \|u\|_{1,p} = \frac{1}{n}\right\} \leq 0\qquad\forall n\in\mathbb{N}. $$

Then, there is a sequence {u n } in \(W^{1,p}_{0}({\Omega })\) such that \(\|u_{n}\|_{1,p} =\frac {1}{n}\) and \(J(u_{n}) < \frac {1}{n^{p+1}}\). Note that \(p<\frac {2Np}{2N-p}< \frac {Np}{N-p}\). By replacing {u n } by its subsequence, by [2, Theorem 4.9], we can suppose that \(\lim _{n\to \infty }u_{n}(x) =0\) for every x in Ω, \(\left \{\frac {u_{n}}{\|u_{n}\|_{1,p}}\right \}\) strongly (resp. pointwise) converges to w in \(L^{\frac {2Np}{2N-p}}({\Omega })\) (resp. on Ω) and \(\frac {|u_{n}|}{\|u_{n}\|_{1,p}}\le v\) with a function v in \(L^{\frac {2Np}{2N-p}}({\Omega })\). We have

$$\begin{array}{@{}rcl@{}} \frac{1}{n} &>& \frac{J(u_{n})}{\|u_{n}\|_{1,p}^{p}}= \frac{1}{p}- {\int}_{\Omega}\frac{F(x,u_{n}(x))}{\|u\|_{1,p}^{p}}dx = \frac{1}{p}- {\int}_{\Omega}{{\int}_{0}^{1}}f(x,su_{n}(x))\frac{u_{n}(x)}{\|u\|_{1,p}^{p}}dsdx\\ &=&\frac{1}{p}- {\int}_{\Omega}{{\int}_{0}^{1}}\frac{f(x,su_{n}(x))}{(su_{n}(x))^{p-2}su_{n}(x)}s^{p}\frac{|u_{n}(x)|^{p}}{\|u\|_{1,p}^{p}}dsdx. \end{array} $$

Since \(d_{1}\in L^{\frac {2N}{p}}({\Omega })\), d 1 v p is integrable on Ω and, by (f 3)

$$\frac{f(x,su_{n}(x))}{(su_{n}(x))^{p-2}su_{n}(x)}s^{p}\frac{|u_{n}(x)|^{p}}{\|u\|_{1,p}^{p}}\ge s^{p}d_{1}(x)\frac{|u_{n}(x)|^{p}}{\|u\|_{1,p}^{p}} \ge s^{p}d_{1}(x)v^{p}(x)$$

for all \(x\in {\Omega }, s\in (0,1), n\in \mathbb {N}\).

Hence, by the generalized Fatou lemma ([9, p.85]), and (f 4)

$$\begin{array}{@{}rcl@{}} 0&=& \liminf_{n\to\infty} \frac{1}{n}= \frac{1}{p} - \limsup_{n\to\infty}{\int}_{\Omega}{{\int}_{0}^{1}}\frac{f(x,su_{n}(x))}{(su_{n}(x))^{p-2}su_{n}(x)}s^{p}\frac{|u_{n}(x)|^{p}}{\|u\|_{1,p}^{p}}dsdx\\ &\ge& \frac{1}{p} - {\int}_{\Omega}{{\int}_{0}^{1}}\limsup_{n\to\infty}\left[\frac{f(x,su_{n}(x))}{(su_{n}(x))^{p-2}su_{n}(x)}s^{p}\frac{|u_{n}(x)|^{p}}{\|u\|_{1,p}^{p}}\right]dsdx =\frac{1}{p}. \end{array} $$

This contradiction implies the lemma. □

Lemma 2

Let ρ be as in Lemma 1. Under conditions (f 3)and (f 5), there is e in \(W^{1,p}_{0}({\Omega })\setminus B(0,\rho )\) such that J(e) < 0.

Proof

Let \(u\in W^{1,p}_{0}({\Omega })\) be such that ∥u∥1,p = 1 and u > 0 on Ω. By (8), we have

$$\begin{array}{@{}rcl@{}} J(nu) &=& \frac{n^{p}}{p}-{\int}_{\Omega}{\int}_{0}^{nu(x)}f(x,s)dsdx= \frac{n^{p}}{p}-{\int}_{\Omega}{{\int}_{0}^{1}}f(x,\xi nu(x))nu(x)d\xi dx\\ &=&\frac{n^{p}}{p}\left[1-p{\int}_{\Omega}{{\int}_{0}^{1}}\frac{f(x,\xi nu(x))}{(\xi nu(x))^{p-1}}\xi^{p-1} u(x)^{p}d\xi dx\right]. \end{array} $$

By Sobolev’s embedding theorem, u belongs to \(L^{\frac {2Np}{2N-p}}({\Omega })\). By (f 3), d 1|u|p is integrable and \(\frac {f(x,\xi n u(x))}{|\xi n u(x)|^{p-2}\xi n u(x)}\xi ^{p-1}|u(x)|^{p}\ge \xi ^{p-1}d_{1}(x)|u(x)|^{p}\) for every integer n, x ∈ Ω and ξ ∈ (0,1). Hence, by the generalized Fatou lemma and (f 5), one has

$$\begin{array}{@{}rcl@{}} &&\limsup_{n\to\infty}\left[1-p{\int}_{\Omega}{{\int}_{0}^{1}}\frac{f(x,\xi nu(x))}{|\xi n u(x)|^{p-2}\xi n u(x)}\xi^{p-1} |u(x)|^{p}d\xi dx\right]\\ &=&1-\liminf_{n\to\infty}\left[p{\int}_{\Omega}{{\int}_{0}^{1}}\frac{f(x,\xi nu(x))}{|\xi n u(x)|^{p-2}\xi n u(x)}\xi^{p-1} |u(x)|^{p}d\xi dx\right]\\ &\le& 1- p{\int}_{\Omega}{{\int}_{0}^{1}}\liminf_{n\to\infty}\left[\frac{f(x,\xi nu(x))}{|\xi n u(x)|^{p-2}\xi n u(x)}\xi^{p-1} |u(x)|^{p}\right]d\xi dx = -\infty, \end{array} $$

which implies \(\lim _{n\to \infty }J(nu)= -\infty \). Hence, we get the lemma. □

Lemma 3

Assume (f 1), (f 2), (f 3), (f 5)and (f 6)hold. Let {u n }be a sequence in \(W_{0}^{1,p}({\Omega })\) such that {J(u n )}is bounded and \(\lim _{n\to \infty }(1+||u_{n}||_{1,p})\|DJ(u_{n})\| = 0\) . Then {u n }has a subsequence converging in \(W_{0}^{1,p}({\Omega })\) .

Proof

Put Ω n = {x ∈ Ω : |u n (x)|≤ C} for every \(n\in \mathbb {N}\). By (f 2) and (f 6), we get

$$\begin{array}{@{}rcl@{}} {\int}_{\Omega}[f(x,u_{n})u_{n}\,-\,\theta F(x,u_{n})]dx \!&=&\! \left({\int}_{\Omega\setminus{\Omega}_{n}}\,+\, {\int}_{{\Omega}_{n}}\right)[f(x,u_{n})u_{n}\,-\,\theta F(x,u_{n})]dx\\ \!&\ge&\! {\int}_{\Omega\setminus {\Omega}_{n}}d_{2}dx \,+\, {\int}_{{\Omega}_{n}}\left[f(x,u_{n})u_{n}\,-\,\theta {\int}_{0}^{u_{n}(x)}\!f(x,t)dt\right]dx\\ &\ge& \,-\,{\int}_{\Omega}|d_{2}|dx \,-\,C(1\,+\,\theta){\int}_{{\Omega}_{n}}|d(x)|dx\\ & \ge& \!-\|d_{2}\|_{L^{1}({\Omega})}\,-\, C(1+\theta)\|d\|_{L^{1}({\Omega})}, \end{array} $$

which implies

$$\begin{array}{@{}rcl@{}} &&{\int}_{\Omega}\left[\left(\frac{\theta}{p} -1\right)|\nabla u_{n}|^{p}-\theta F(x,u_{n})+f(x,u_{n})u_{n})\right]dx\\ &\ge& {\int}_{\Omega}\left(\frac{\theta}{p} -1\right)|\nabla u_{n}|^{p}dx -\|d_{2}\|_{L^{1}({\Omega})} - C(1+\theta)\|d\|_{L^{1}({\Omega})}\qquad\forall n\in\mathbb{N}. \end{array} $$
(10)

By (8) and (9), there are a positive real number M and a sequence {u n } in \(W^{1,p}_{0}({\Omega })\) such that

$$\begin{array}{@{}rcl@{}} -M&\le& {\int}_{\Omega}\left(\frac{1}{p}|\nabla u_{n}|^{p}-F(x,u_{n})\right)dx \le M\qquad\forall n\in\mathbb{N},\\ -M&\le&{\int}_{\Omega}(|\nabla u_{n}|^{p}-f(x,u_{n})u_{n})dx\le M\qquad\forall n\in\mathbb{N}. \end{array} $$

It follows that

$$ {\int}_{\Omega}\left[\left(\frac{\theta}{p} -1\right)|\nabla u_{n}|^{p}-\theta F(x,u_{n})+f(x,u_{n})u_{n})\right]dx \le (1+\theta)M\quad \forall n\in\mathbb{N}. $$
(11)

Combining (10) and (11), we get

$${\int}_{\Omega}\left(\frac{\theta}{p} -1\right)|\nabla u_{n}|^{p}dx\le (1+\theta)M + \|d_{2}\|_{L^{1}({\Omega})}+ C(1+\theta)\|d\|_{L^{1}({\Omega})}\qquad\forall n\in\mathbb{N}, $$

which implies {u m } is bounded in \(W^{1,p}_{0}({\Omega })\). By Theorem 4, there is a subsequence \(\{u_{n_{k}}\}\) of {u n } such that \(\{u_{n_{k}}\}\) weakly (resp. strongly) converges to u in \(W^{1,p}_{0}({\Omega })\) (resp. in \(L^{\frac {p}{p-1}}({\Omega })\)) and \(\{N_{f}(u_{n_{k}})\}\) is bounded in L p(Ω). Since \(\lim _{n\to \infty }\|DJ(u_{n_{k}})\|=0\) and \(\{u_{n_{k}}-u\}_{k}\) is bounded in W 1,p(Ω), we have

$$\lim_{k\to\infty}{\int}_{\Omega}f(x,u_{n_{k}})(u_{n_{k}}-u)dx =\lim_{k\to\infty}{\int}_{\Omega}N_{f}(u_{n_{k}})(u_{n_{k}}-u)dx=0 $$

and

$$\begin{array}{@{}rcl@{}} &&\lim_{k\to\infty}\left|{\int}_{\Omega}|\nabla u_{n}|^{p-2}\nabla u_{n_{k}}\nabla(u_{n_{k}}-u)dx -{\int}_{\Omega}f(x,u_{n_{k}})(u_{n_{k}}-u)dx\right|\\ &\le& \lim_{k\to\infty}\|Du_{n_{k}}\| \|u_{n_{k}}-u\|_{1,p}=0. \end{array} $$

Hence

$$\lim_{k\to\infty}{\int}_{\Omega}|\nabla u_{n}|^{p-2}\nabla u_{n_{k}}\nabla(u_{n_{k}}-u)dx =0. $$

Thus, by [3, Theorem 10], \(\{u_{n_{k}}\}\) strongly converges to u in W 1,p(Ω). □

Proof Proof of Theorem 1

Using the Mountain-pass theorem with the Palais–Smale condition, by Lemmas 1, 2, and 3, we obtain a non-trivial weak solution for the problem (1). □

Example 4

Let N = 5, p = 3, r = 4, α > 0, \({\Omega } =\{x\in \mathbb {R}^{5}: \|x\| < 1\}\),

$$\begin{array}{@{}rcl@{}} \omega_{0}(x)&=&|x|^{-\frac{1}{30}}\cos(16|x|) \qquad \forall x\in{\Omega},\\ \omega_{1}(x)&=&\left(\frac{1}{2}-\|x\|^{2}\right)^{2}(1-\|x\|^{2})^{-\frac{7}{6}}\qquad\forall x\in{\Omega},\\ \varphi_{0}(t) &=& \left\{ \begin{array}{ll} |t|^{r-2}t(1-|t|)&\text{ if } |t| \le 1,\\ 0&\text{ if } |t| \in\mathbb{R}\setminus [-1,1], \end{array} \right.\\ \varphi_{1} (t) &=& \left\{\begin{array}{ll} 0&\text{ if } |t| \le 1,\\ |t| - 1&\text{ if } |t| \in [1,2],\\ 1&\text{ if } |t| \ge 2. \end{array} \right.\\ f(x,t)&=&\omega_{0}(x)^{r-1}\varphi_{0}(t)+\omega_{1}(x)^{r-1}|t|^{p-2}t\varphi_{1}(t)\qquad\forall (x,t)\in {\Omega}\times \mathbb{R}. \end{array} $$

Let ω = |ω 0| + ω 1, C = 1, \(d(x)=|x|^{-\frac {1}{30}}\), d 1(x) = −d(x) and \(d_{2}(x)=|x|^{-\frac {1}{30}}\) for every x in Ω. We see that \(d_{1} \in L^{\frac {2N}{p}}({\Omega })\), d 2 ∈ L 1(Ω) and d ∈ L 1(Ω). By Examples 1 and 2, ω is in \(\mathcal {K}_{p,r}\). Thus, f satisfies conditions (f 1)– (f 5). Since \(\lim _{|x|\to 0}\omega _{0}(x) =\infty \) and \(\lim _{|x|\to \frac {1}{2}}\omega _{1}(x) =0\), the convergences in (f 4) and (f 5) are not uniform on Ω.

Let 𝜃 = 4. For every x in Ω, we have

$$\begin{array}{@{}rcl@{}} \theta F(x,t) &\le& \theta\left({{\int}_{0}^{1}}+{{\int}_{1}^{t}}\right)f_{1}(x,\xi)d\xi \le 4|\omega_{0}(x)|^{r-1} +4\omega_{1}^{r-1} (x){{\int}_{0}^{t}}(|\xi|^{3}\xi - \xi^{3} ) d\xi\\ &=& 4|\omega_{0}(x)|^{3} + 4\omega_{1}(x)^{3}{\int}_{1}^{|t|}(\xi^{4} - \xi^{3} )d\xi\\ &=&4|\omega_{0}(x)|^{3} +\omega_{1}(x)^{3}\left[\frac{4}{5}|t|^{5} - \frac{4}{5} -t^{4} +1\right]\\ &=&4|\omega_{0}(x)|^{3} + \omega_{1}(x)^{3}\left[\frac{4}{5}|t^{5}|+\frac{1}{5} -t^{4}\right]\\ & \le& 4|\omega_{0}(x)|^{3}+\omega_{1}(x)^{3}[|t|^{5} -t^{4}]\\ &=&4|\omega_{0}(x)|^{3}+\omega_{1}(x)^{3}t^{4}[|t| -1]\\ &\le& 4|\omega_{0}(x)|^{r-1} +\omega_{1}(x)^{3}t^{4}\\ &=&4|\omega_{0}(x)|^{3} +f_{1}(x,t)t \qquad\forall |t|\in [1 , 2],\\ \theta F(x,t) &\le& 4|\omega_{0}(x)|^{r-1}+ {\theta{\int}_{0}^{t}}\varphi_{1}(t)\omega_{1}(x)^{r-1}|\xi|^{2}\xi d\xi\\ &\le& 4|\omega_{0}(x)|^{3}+{\theta{\int}_{0}^{t}}\omega_{1}(x)^{3}|\xi|^{2}\xi d\xi\\ & = &4|\omega_{0}(x)|^{3}+\omega_{1}(x)^{3}t^{4}\\ &=& 4|\omega_{0}(x)|^{3}+f_{1}(x,t)t \qquad\forall |t|\ge 2. \end{array} $$

Thus, we get (f 6).

Therefore, we can apply Theorem 1 to f with C = 1. Since ω r−1(x) ≥\((1-\|x\|^{2})^{-\frac {21}{16}}\) for every x in Ω, ω r−1 is not integrable on Ω. Therefore, the results in [3,4,5, 8] can not be applied to solve (1) in this case.