1 Introduction

Gears are critical transmission components in rotating machinery with extensive application field especially in modern industrial areas. The whole machinery’s performance and production efficiency are directly affected by the working state of gears [1]. The stable operation is directly affected by the state of gear motion whether the gear run normally or not [2, 3]. Therefore, it is very crucial to identify the early faults before the gears develop into serious state. However, in practical applications, it is difficult to predict the formation and development of gear fault in advance because while the vibration around the gearbox is perceived, the gear fault has been a severe condition. Up to now, the research of the gear failure mechanism in early and middle condition is not mature. For the practical applications, it is important to develop the research of gear failure on vibration characteristics of gear box.

Recently, many theoretical types of research are developed on the vibration of gearbox by gear failure, few type are based on practical application. And there is a certain gap between theory and practical application. Generally, fault detection of gear teeth is the collection of fault signal samples site, and the identification of the gear fault type according to the information by the signal collection [4]. Since the measured signal is interfered with strong noise background, de-noising for the extraction of useful characteristics from the original signal is the first important stage. At present, the common methods of signal de-noising are various, such as Empirical mode decomposition method (EMD) [5, 6], Local mean decomposition method (LMD) [7, 8], Singular value decomposition method (SVD) [9,10,11] wavelet analysis method [12,13,14]. In practical, the methods are limited by some problems. EMD is affected by mode aliasing which is occurred frequently in the decomposition process, and the quality of signal decomposition is reduced in the condition [15, 16]. LMD also generates mode aliasing which makes the decomposition and extraction of fault features incomplete, and lead to decomposition failure on the whole time scale [17,18,19]. The effect of Wavelet de-noising method is depended on the calculation and selection of reasonable parameters [20, 21].

Beside the de-noising methods above, the singular value decomposition (SVD) is a better method to deal with problems of mode aliasing and endpoint effect. The singular value of effective feature is distinguished from original signal by SVD which is based on the singular value matrix of the characteristic signal. In the method, characteristic information of the noise signal is eliminated, the useful characteristic signal is reconstructed. As it is invariant, stable and effective for the de-noising, SVD is applied to the filtering of nonlinear signals, such as practical application of de-noising in fault identification of gear fault [22].

However, the accuracy of de-noising in fault identification by SVD is depended on the calculations of τ and m, which is highly subjective and unreliable in theory at present. Although suitable parameters of τ and m are calculated by a new method which is called k-SVD, the determination of k is restricted by other conditions, and affects the de-noising effect of SVD [23, 24].

It is urgency to reasonably determinate the values of τ and m in SVD respectively. For the value of τ, although is appropriate to any value in theory, the determination in practical applications is directly affected by the vibration signal. In the case that τ is too small, the correlation is concentrated to between different elements of the delay vector, and the reconstructed phase space is meaningless. Contrary, while τ is too large, it leads to loss of noise delay coordinates of mutual information elements, and the reconstructed phase space is unable to reflect the initial dynamic behavior. The parameter m controls the phase space, determines the accuracy of de-noising and identification. While m is large, the phase space is too large, and makes the calculation tedious and complex. Contrary, while m is small, the reconstructed information is unrealizable for the extraction from mutation signals [25, 26].

In order to improve the SVD for de-noising, an improved singular value decomposition (ISVD) is developed based on autocorrelation function with Cao’s algorithm for the parameter of τ and m. For the determination of τ, the autocorrelation function is closely related to the shape of the attractor in the reconstructed phase space and approximated the principal element direction of the signal system. Empirically, while the decay of autocorrelation function is approximated to 1/e, the optimal delay time is obtained [35]. For the determination of m, Cao’s algorithm which is based on the False Nearest Neighbor (FNN) method, makes the calculation of m only related to τ, and overcomes the influence of various thresholds on m [27, 28].

In this paper, ISVD is proposed for the vibration signal de-noising of gear pitting fault identification. Firstly, the parameter of τ and m of the Hankel matrix for SVD are optimized by autocorrelation function and Cao’s algorithm respectively. Secondly, simulation of ISVD by autocorrelation function and Cao’s algorithm is conducted to verify the proposed method. Thirdly, the experiment of tooth surface pitting failure is conducted by ISVD method to verify the effectiveness of the proposed method.

2 Theory of the SVD method

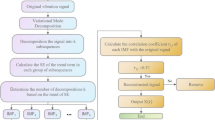
Fig. 1 shows the flowchart of ISVD for de-noising. In the flow, the optimal τ is calculated by the autocorrelation function method of fault signal sequence; m is calculated by the Cao’s algorithm of fault signal phase space, based on them, the phase space of the effective characteristic signals and noise signals are obtained respectively; then the optimal de-nosing order is calculated by the singular value difference spectrum (DSSV) method of the characteristic signal; finally, the inverse operation of Hankel matrix is used to reconstruct the characteristic signal after de-noising. It retains the effective signal value and rid the noise signal value, then reconstructs the effective signal in a suitable order. Essentially, SVD is a method of matrix orthogonalization in the mathematical view, which decomposes the given matrix into two matrixes Um×m and Vn×n, as shown: [29,30,31,32].

$$\boldsymbol{H}\boldsymbol{=}\boldsymbol{US}V^{T}$$
(1)

where S is the singular value matrix of the real matrix H, in S, σi is the singular value of the real matrix H, and \(\sigma _{1}\geq \sigma _{2}\geq \cdot \cdot \cdot \geq \sigma _{i}\geq \sigma _{r}\geq 0\), where r is the rank of the matrix H.

Fig. 1
figure 1

Flowchart of the ISVD method for de-noising

Full size image

For the signals \(x=(x_{1},x_{2},\cdot \cdot \cdot ,x_{m})\), the de-noising is described as follows:

(i):

Establishment of a Hankel matrix H based on X, H is expressed by Eq. 2.

$$\boldsymbol{H}= \begin{bmatrix} x_{1} & x_{2} & \cdots & x_{n}\\ x_{1\times \tau +1} & x_{1\times \tau +2} & \cdots & x_{1\times \tau +n}\\ \vdots & \vdots & \ddots & \vdots \\ x_{\left(m-1\right)\times \tau +1} & x_{\left(m-1\right)\times \tau +2} & \cdots & x_{\left(m-1\right)\times \tau +n} \end{bmatrix}$$
(2)

where m is the embedded dimension, τ is delay time, N is the length of the signal, and n = N − (m − 1) × τ.

(ii):

Calculation of the orthogonal matrix S = diag(σ1, σ2, …, σr) on H by SVD.

(iii):

Ordination of the elements such as σ1, σ2, …, σr, in S, to satisfy the condition of σ1 ≥ σ2 ≥ … σk ≫ σk+1 ≥ σk+2 ≥ … ≥ σr > 0.

(iv):

Finding out the mutation point k in Step. (iii), retaining the elements from σ1 to σk, and defining the other elements equal to 0 as (σk+1, σk+2, …, σr) = (0, 0, …, 0).

(v):

Reconstruction of the singular value matrix according to the order k in Step.(iv), to achieve the characteristic signal of de-noising.

k is investigated by Singular values difference spectrum (DSSV) D and the elements in D is d = σi − σi+1, where i = r − 1. The DSSV sequence Di is constructed shown in Eq. 3.

$$D_{i}=\{d_{i}|i=1,2,\cdots ,r-1\}$$
(3)

While the difference spectrum of singular value is positioned on the mutation point, the spectrum value di is the maximum in the whole sequence Di. It is expressed by:

$$d_{\max }=\max D_{i}=\max \{d_{i}|i=1,2,\cdots ,r-1\}$$
(4)

Based on of Eq. 4, the sequence number corresponding to the maximum SVDS dmax = Max (Di) is calculated of the signal. According to the above principle, the new singular value matrix SNew is obtained from the effective characteristic signal, as shown in Eq. 5:

$$S_{\mathrm{New}}=diag(\sigma _{1}^{H},\sigma _{2}^{H},\sigma _{3}^{H},\cdots ,\sigma _{i}^{H},0,\cdots ,0)$$
(5)

where, σH is the singular value left over.

(vi):

Reconstruction of characteristic signals \(X_{i}^{H}\), show as follow:

$$X_{i}^{H}=u_{1}^{H}\sigma _{1}^{H}v_{_{1}}^{H}+u_{2}^{H}\sigma _{2}^{H}v_{_{2}}^{H}+\cdots +u_{h}^{H}\sigma _{i}^{H}v_{h}^{H}$$
(6)

where, \(u_{i}^{H}\) is element of the matrix U, \(v_{i}^{H}\) is element of the matrix V.

3 Characteristic parameters of ISVD method

In this section, the two parameters of τ and m are optimized by the combination of autocorrelation and the advantages of Cao’s algorithm.

3.1 The parameter of delay time τ

A measured time series is x(t), and the autocorrelation function of the sequence after normalization processing is shown in Eq. 7 [33, 34]:

$$C(\tau )=\frac{\sum _{i=1}^{N}[x(i+\tau )-\overline{x}][x(i)-\overline{x}]}{\sum _{i=1}^{N}[x(i)-\overline{x}]^{2}}$$
(7)

where, N is sample size, τ is delay time, \(\overline{x}\) is average value of the samples,

$$\overline{x}=\frac{1}{N}\sum _{i=1}^{N}x\left(i\right)$$

The research shows, the corresponding time is selected while the value of the autocorrelation function exactly decayed to 1/e by the autocorrelation function method, as the optimal value of the τ of the effective phase space feature vector [35].

3.2 The parameter of embedded dimension m

The principle of Cao’s algorithm is expressed as the list [36]:

(i):

On the definition, an m-dimension “embedding space”, the time series vector \(\overset{\rightarrow }{X}_{m}(i)\) at the ith phase point is defined as

$$\overset{\rightarrow }{X}_{m}(i)=[x(i),x(i+\tau ),x(i+2\tau ),\cdots ,x(i+(m-1)\tau )]^{T}$$
(8)

where, x(i) is the signal corresponding to the time series; i is the time-series sequence number, i = 1, 2, …, N − (m − 1)τ.

Then the Euclidean distance Rm(i) from \(\overset{\rightarrow }{X}_{m}(i)\) to the nearest neighbor \(\overset{\rightarrow }{X}_{m}^{NN}(i)\) is calculated as:

$$R_{m}(i)=\left\| \overset{\rightarrow }{X}_{m}(i)-\overset{\rightarrow }{X}_{m}^{NN}(i)\right\|$$
(9)

where, \(\left\| \cdot \right\|\) is the ∞‑norm, and all the normalizations followed are ∞‑norm.

(ii):

While the m-dimensional phase space is extended to m + 1, similarly, the ith phase point is \(\overset{\rightarrow }{X}_{m+1}(i)\), and the Euclidean distance \(R_{m+1}(i)\) of \(\overset{\rightarrow }{X}_{m+1}(i)\) to the nearest neighbor point \(\overset{\rightarrow }{X}_{m+1}^{NN}(i)\) is calculated:

$$R_{m+1}(i)=\left\| \overset{\rightarrow }{X}_{m+1}(i)-\overset{\rightarrow }{X}_{m+1}^{NN}(i)\right\|$$
(10)
(iii):

The relationship between E(m) and m is shown:

$$E(m)=\frac{1}{N-m\tau }\sum _{i=1}^{N-m\tau }\frac{\left\| \overset{\rightarrow }{X}_{m+1}(i)-\overset{\rightarrow }{X}_{m+1}^{NN}(i)\right\| }{\left\| \overset{\rightarrow }{X}_{m}(i)-\overset{\rightarrow }{X}_{m}^{NN}(i)\right\| }$$
(11)
$$E_{1}(m)=\frac{E\left(m+1\right)}{E\left(m\right)}$$
(12)
(iv):

Continue increasing the dimension of the phase space m1, and make it larger than m, then repeat the calculation of the first three steps. Based on the results of each calculation, the relationship between E1(mi) and mi is charted. While E1(mi) in the graph reaches a plateau within a certain threshold, the corresponding mi is the optimal m of the \(\overset{\rightarrow }{X}_{m}(i)\).

(v):

In practical applications, a criterion is defined to judge the smoothness of the finite sequence change of E1(mi) and mi, it is shown as:

$$E^{*}(m)=\frac{1}{N-m\tau }\sum _{i=1}^{N-m\tau }\left\| \overset{\rightarrow }{X}_{m+1}(i)-\overset{\rightarrow }{X}_{m+1}^{NN}(i)\right\|$$
(13)
$$E_{2}(m)=\frac{E^{*}\left(m+1\right)}{E^{*}\left(m\right)}$$
(14)

From the equations, in a range of mi, if E2(m) = 1 the signal is random; if E2(m) within a certain threshold are not all equal to 1, the signal is the deterministic signal.

3.3 Evaluation of de-noising effect

The definition of SNR is expressed, shown as in follow:

$$SNR=10\lg \left[\frac{\sum _{i=1}^{N}x^{2}\left(i\right)}{\sum _{i=1}^{N}[x(i)-z(i)]^{2}}\right]$$
(15)

where, z(i) is the de-noising signal.

The definition of RMSE for root-mean-square error evaluation is expressed, shown as in follow:

$$RMSE=\sqrt{\frac{\sum _{i=1}^{N}[x(i)-z(i)]^{2}}{N}}$$
(16)

where, N is the length of x(i).

4 Numerical simulation

Fig. 2 is flowchart of the simulation for the signal de-noising. Firstly, the model of signal is based on the noise-free signal fth(t), the coupling signal f0(t) is formed by the combination of a random noise signal ξG‑noise(t) and impulse signal ξG‑pulse(t). Fig. 3 is the obtained time-domain diagram of the coupling signal after fitting simulations. And the expression of the simulation signal is shown as

$$f_{0}(t)=f_{\mathrm{th}}(t)+\xi _{G-\text{noise}}(t)+\zeta _{G-\text{pulse}}(t)$$
(17)
Fig. 2
figure 2

Flowchart of the signal de-noising

Full size image
Fig. 3
figure 3

Time domain diagram of coupled signals

Full size image

The other parameters are shown in Table 1.

Table 1 Input parameters of the simulation signal
Full size table

Base on the signal, the operation of de-nosing by the simulation is listed as:

(i):

Determine τ

Fig. 4 is the result of autocorrelation value by τ. It is calculated based on f0(t) by the autocorrelation function. While C(τ) = 1/e, the corresponding time value is the optimal τ of f0(t). From Fig. 4, the optimal τ = 8.

Fig. 4
figure 4

The autocorrelation function

Full size image
(ii):

Determine m

Fig. 5 is the results of m − E1(m) and m − E2(m), which calculated by Eqs. 13 and 14. The blue line shows that while m varies from 1 to 4, the value of E1(m) is rapidly approaching to 1. While m = 5, the value of E1(m) = 1 for the first time, and While m > 5, E1(m) = 1. The red line shows that E2(m) = 1 in the range 1 < m < 19 except the point of m = 1, 2, 3, 5, 15, 17, and 19. The analysis above shows that the certain motion characteristics and the optimal value of the embedding dimension is m = 5.

Fig. 5
figure 5

The relationship between E1(m), E2(m) and m of simulation signals

Full size image
(iii):

SVD of simulation signals

Fig. 6 is the difference spectrum and singular value by m, the first four singular values σ1 = 51.64, σ2 = 41.26, σ3 = 27.52 and σ4 = 27.64. The value of σ3 is the singular values mutates which separates the phase space of the effective signal and the noise signal. Meanwhile, in the singular value difference spectrum sequence, the first three large difference spectra are d1 = 10.39, d2 = 13.74, and d3 = 0.12 respectively, the maximum difference spectrum is d2.

Fig. 6
figure 6

Singular value and differential spectrum of signal

Full size image
(iv):

Determine de-noising order

Fig. 7 is the simulation results of the relationship between σ and DSSV. In the case that σ1 and σ2 are selected for the reconstructed signal, many information is lost; in the case of selecting σ1, σ2 and σ3, it contains a little noise information; in the case of selecting σ1, σ2, σ3, and σ4, the reconstructed signal is distorted; In the case of selecting from σ1 to σ5, a large amount of noise information is mixed in the reconstructed signals. As a result, the selection of σ1σ2 and σ3 is suitable because the effective information of the obtained characteristic signal remains relatively completely and has a good effect of de-noising.

Fig. 7
figure 7

Relationship between valid singular values and characteristic signals

Full size image

The signals are decomposed of f0(t) by the principle of the SVD method, and the σ1 to σ4 are obtained. Combined with Cao’s algorithm, the optimum parameters are m = 5 and τ = 8. Finally, as shown in Fig. 8, the inverse solution of singular value is used to reconstruct the effective characteristic signal after de-noising. From the figure the reconstructed effective signal is proximity to the pure signal, which indicates that ISVD has the potential for de-noising.

Fig. 8
figure 8

Time domain diagram of the coupled signal after de-noising

Full size image

As shown in Table 2, after the de-noising by ISVD. And the SNR = 31.31 dB, RMSE = 0.34 are acquired by Eqs. 15 and 16. It reminds ISVD has a good de-noising potential.

Table 2 Evaluation of de-noising effect of simulation signal
Full size table

5 Experimental verification

Fig. 9a is shown the experiment layout. Fig. 9b is the photograph of experiment. On the outer side of the gearbox, four measurement points are set as Points I, II, III and IV with four uniaxial acceleration sensors for the collection of vibration signal.

Fig. 9
figure 9

Structural layout of the test bed. a Experimental schematic diagram. b Field diagram. 1. Input the motor and shaft; 2. Measured gear box; 3. Torque transducer; 4. Magnetic powder loader

Full size image

The speed of input is 1500 r/min; the input current of the magnetic powder is P = 38 W; the modulus of gear is mo = 2 mm. The gear material is 18CrNiMo7 steel.

5.1 Experimental data

Fig. 10 is shown the waveforms of vibration signal which were collected at four measurement points. The signals are affected by a large numbers of interference signals.

Fig. 10
figure 10

Time domain diagram of vibration acceleration at points before de-noise

Full size image

5.2 Determination of τ

Table 3 is the calculation results. The minimum value of τ is τ = 8, which is calculated by the autocorrelation function method as while τ = 8 at each measurement point, the autocorrelation function C(τ) ≈ 1/e.

Table 3 The delay time at each measurement point
Full size table

5.3 Determination of m

Fig. 11 is the results of the computation of m by the Cao’s method in each measurement point. From Fig. 11a–d, in the range of 1 ≤ m ≤ 3, while m is increased, E1(m) is decreased as the domination of noise in the phase space. in the case of m = 3, the minimum value of E1(m) is occurred as E1(m) = 0.5 in Points I, II and IV, and in Point III, the minimum is E1(m) = 0.45. The results indicate that noise content at measurement point III is the highest. While 3 ≤ m ≤ 6, E1(m) is increases sharply with the increase of m. in the case of m = 6, E1(m) ≥ 0.8, which indicates that the content of pseudo-nearest neighbor points of fault characteristics is decreased. While m > 6, the value of E1(m) is slowly approached to 1 as m is increased.

Fig. 11
figure 11

Relationship between E(m) and m of experimental signals. a Measurement point I; b Measurement point II; c Measurement point III; d Measurement point IV

Full size image

The value of E2(m) is used to determine the type of fault characteristic signals. In Fig. 11, while 1 ≤ m < 6, E2(m) is approached to 1 fluctuant, while 6 ≤ m ≤ 19, the value of E2(m) is approximated to 1, In addition, while m = 6, the E2(m) value approaches constant value 1 for the first time. Indicating that there are certain vibration characteristics at the four measuring points. It indicates that the fault characteristics are affected by random signals. At this point, m is weak to the fault characteristics, which also makes the calculation of dimension meaningless. Finally, the optimal value of m is m = 6.

5.4 The ISVD of experimental data

Based on the calculation above, the parameters are set as: τ = 8 and m = 6. Fig. 12 is the singular value of the experimental data which is decomposed at the measurement Points I, II, III, and IV by ISVD method. Fig. 12a is the singular value distribution graph. While m < 2, the singular values of the four measurement points are σ > 800, while m > 2, the singular value in each point is smooth stability to a certain value as σI = 900, σII = 900, σIII = 700, σIV = 900 the mutated point is m = 2 or m = 3. Fig. 12b is the Singular value difference spectrum to supplement the determination of reconstruction order. In the figure, while m = 3, 5 and 6, the difference spectrum values are approximately close to 50. With the combination of results by Fig. 12a,b, the optimum reconstruction order is DSSV = 3.

Fig. 12
figure 12

The ISVD diagram of experimental data at each measurement point. a Singular value distribution graph; b Singular value difference spectrum

Full size image

5.5 Determine the de-noising order

Fig. 13 is the reconstructed signal with fault characteristics of four measuring points in time-domain by Eq. 6. In the figures, the green wave is original signal, the brown wave is the de-noising signal. From the figures, the impact vibration generated by backlash and transmission error is dominant and effectively reduced after reconstruction. From the figures, the acceleration value of de-noising signal is much smaller than original one in each time. In addition, the trend of de-noising signal and original signal are same.

Fig. 13
figure 13

Time domain diagram of vibration acceleration at measurement points after de-noising. a Measurement point I; b Measurement point II; c Measurement point III; d Measurement point IV

Full size image

The effect of signal de-noising is evaluated by SNR method and RMSE, the results are showed in Table 4. From the results, SNR ≥45 dB, and RMSE <0.4 in all measurement points. It reveals a better effect of de-noising by ISVD. In addition, it reveals that the de-noising effect of signals at Points I and II is better than Points III and IV.

Table 4 Evaluation of de-noising effect of experimental data
Full size table

5.6 Experimental results and analysis

Fig. 14 is the frequency response diagram of de-noising signals and original signals in each measurement point from Fig. 13 by Fourier transform. In Fig. 14, Fig. 14a,c and d are similar, because Point 1 Point III and Point IV are meshed. In the figures, the effective signals are retained in the frequency range of 300 Hz < f < 800 Hz and 1.2 kHz < f < 1.7 kHz as the different rotation speeds of each axis, signals of other frequencies are noise which is de-noised by ISVD. Fig. 14b are the signals in Point II which near the input source and affected by more vibrations. In the figure, the signal of noise is de-noised in ineffective range of frequency, and the effective signal is retained.

Fig. 14
figure 14

Frequency response characteristics at each measurement point. a Measurement point I; b Measurement point II; c Measurement point III; d Measurement point IV

Full size image

6 Conclusions

In this research, a new method of ISVD is proposed for the vibration signal de-noising of gear pitting fault identification. Simulation and experiments have been conducted to prove the efficiency of ISVD. The conclusions are listed as follows:

(i):

The theory of ISVD is expressed, the method for the determination of parameters τ and m for SVD are optimized by autocorrelation function and Cao’s algorithm respectively. The signal after de-noising is reconstructed by the inverse of the Hankel matrix.

(ii):

In the simulation, the ISVD method is employed to de-noise the artificial vibration signal in a mathematical model of gear pitting fault, the results are SNR = 31.3 dB and RMSE = 0.34. The simulation results reveal that ISVD has a good effect on de-noising of the fault vibration signal.

(iii):

In the experiment, the ISVD method is adopted to de-noising the vibration signal of gear pitting fault identification, the results demonstrate SNR >45 dB, and RMSE <0.4. The experiment results reveal that ISVD has a good effect on de-noising of the fault vibration signal.