Abstract
Graphs are ubiquitous in computer science. Moreover, in various application fields, graphs are equipped with attributes to express additional information such as names of entities or weights of relationships. Due to the pervasiveness of attributed graphs, it is highly important to have the means to express properties on attributed graphs to strengthen modeling capabilities and to enable analysis. Firstly, we introduce a new logic of attributed graph properties, where the graph part and attribution part are neatly separated. The graph part is equivalent to first-order logic on graphs as introduced by Courcelle. It employs graph morphisms to allow the specification of complex graph patterns. The attribution part is added to this graph part by reverting to the symbolic approach to graph attribution, where attributes are represented symbolically by variables whose possible values are specified by a set of constraints making use of algebraic specifications. Secondly, we extend our refutationally complete tableau-based reasoning method as well as our symbolic model generation approach for graph properties to attributed graph properties. Due to the new logic mentioned above, neatly separating the graph and attribution parts, and the categorical constructions employed only on a more abstract level, we can leave the graph part of the algorithms seemingly unchanged. For the integration of the attribution part into the algorithms, we use an oracle, allowing for flexible adoption of different available SMT solvers in the actual implementation. Finally, our automated reasoning approach for attributed graph properties is implemented in the tool AutoGraph integrating in particular the SMT solver Z3 for the attribute part of the properties. We motivate and illustrate our work with a particular application scenario on graph database query validation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Graphs are ubiquitous in computer science. Moreover, in various application fields, graphs are equipped with attributes to express additional information such as names of entities or weights of relationships. Due to the pervasiveness of attributed graphs, it is highly important to have the means to express properties on attributed graphs to strengthen modeling capabilities and to enable analysis. Properties on attributed graphs specify complex patterns on the graph structure and specify conditions on the attribute values of the graph. Examples of application areas include model-based engineering where properties of graphical models are expressed, the formal analysis and verification of systems where the states are modeled as graphs, the formal modeling and analysis of sets of semi-structured documents (especially if they are related by links), or of graph queries in the graph database domain.
As a first basic contribution, we introduce a novel intuitive, dedicated logic for formulating attributed graph properties, where the graph and attribution parts are neatly separated. The graph part uses graphs and graph morphisms as first-class citizens. In particular, we revert for this graph part to the logic of nested graph conditions as initially defined by Habel and Pennemann [21]. A similar approach was introduced by Rensink [43] first. The origins can be found in the notion of graph constraints [23], introduced in the area of graph transformation [44], in connection with the notion of (negative) application conditions [14, 20], as a form to limit the applicability of graph transformation rules. These graph constraints originally had a very limited expressive power, while nested conditions have been shown [21, 39] to have the same expressive power as first-order logic (FOL) on graphs as introduced by Courcelle [9]. For integration of the attribution part with the graph part of the new logic for attributed graph properties, we revert to the so-called symbolic approach to graph attribution [35], where the attributes are represented symbolically by variables whose possible values are specified by a set of constraints making use of algebraic specifications.
Apart from being able to express in an elegant and formal way attributed graph properties, we want to be able to automatically reason about these properties. A first question to be answered is whether a given attributed graph property is satisfiable at all. We have addressed this question already in earlier work for graph properties without attributes [27]. In case an attributed graph property is satisfiable, a second question to be answered is which attributed graphs satisfy the property in particular. We have addressed this further question by a symbolic model generation approach for graph properties without attributes already in [46]. In particular, we identified that in most application scenarios, it is desirable to be able to explore graphs satisfying the graph property or even to get a complete and compact overview of the graphs satisfying the graph property. More formally speaking, we designed an algorithm \(\mathcal {A}\), which returns for a given graph property p a finite set \(\mathcal {S}\) of so-called symbolic models such that
-
\(\mathcal {S}\) jointly covers all graphs G satisfying the graph property p (completeness of \(\mathcal {S}\)),
-
\(\mathcal {S}\) does not cover any graph G violating the graph property p (soundness of \(\mathcal {S}\)),
-
\(\mathcal {S}\) contains no superfluous symbolic models not necessary for completeness (compactness of \(\mathcal {S}\)),
-
\(\mathcal {S}\) allows for each of its symbolic models the immediate extraction of a finite graph G, satisfying the graph property p and being minimal (minimal representable \(\mathcal {S}\)),
-
\(\mathcal {S}\) allows for an enumeration of further finite graphs G satisfying the graph property p (explorable \(\mathcal {S}\)).
Such an algorithm is also desirable for attributed graphs.
The second main contribution of this paper is therefore twofold. We extend our refutationally complete tableau-based reasoning method for graph properties [27] to the case with attributes. Moreover, we extend our symbolic model generation approach for graph properties [46] to the case with attributes. In addition, we show that it inherits all properties mentioned above of the algorithm for the non-attributed case also strengthening compactness. Moreover, we show that it comes up with an extra property for \(\mathcal {S}\). In particular, we show that it does not generate symbolic models with overlapping covered attributed graphs (nonambiguity of \(\mathcal {S}\)). For showing that all other properties are inherited from the case without attributes, we exploit the fact that our new logic for attributed graph properties neatly separates the graph part from the attribution part and that our algorithm relies only on a abstract level on categorical constructions specific to attributed graphs. Consequently, we can leave the graph part of previous algorithm seemingly unchanged. For the attribute part, we assume and make use of an oracle, allowing for flexible adoption of different available SMT solvers in the actual algorithm implementation. In fact, our refutation procedure and symbolic model generation algorithm for attributed graph properties are highly integrated: Since the latter is designed to compute a complete overview of all possible models, it is at the same time able to refute a property if the overview turns out to be empty. Note that, in general, our symbolic model generation algorithm might not terminate because we support FOL on graphs for the graph part already. It is designed, however, (also if nonterminating) to gradually deliver better underapproximations of the complete set of symbolic models by returning a stream of symbolic models.
Finally, we present the implementation of our algorithm in the tool AutoGraph delegating the attribute part of the reasoning to the SMT solver Z3 [28]. We start the paper with presenting a concrete scenario, where our approach can be applied. In particular, we select the graph database domain [2, 3, 53] and show that we can formally model and reason about the validity of graph database queries from a prominent case study in this domain on social network queries [51, version 0.3.0].
Compared to earlier work in [46], we extended the entire approach by allowing attribute constraints in graph properties, which strengthens its overall applicability. We have moreover added the property of nonambiguity and improved the notion of compactness. In particular, we have extended the application scenario started in [46], where we investigate the validity of graph database queries, by allowing for attribute constraints in the queries as illustrated by the examples in Figs. 2, 3, 4, and 5. This extension, which is based on earlier work on symbolic graphs making use of algebraic specifications from [35], requires the usage of SMT solvers such as Z3 at various steps in our model generation algorithm such as in Definition 19 (to attempt) to decide satisfiability of attribute constraints. Furthermore, exchanging the considered category from typed graphs to typed attributed graphs resulted in the need to inspect fundamental properties (see Appendix B) of the underlying category (i.e., the category of typed attributed graphs in our case) required for higher level constructions such as \( shift \) in Definition 17 according to their soundness proofs such as Lemma 1.
This paper is structured as follows: In Sect. 2, we give an overview over related work. In Sect. 3, we discuss graph databases as an application domain where graph queries are to be analyzed. In Sect. 4, we recall the formalism of algebraic specifications required for attribute handling in a self-contained way and introduce the category GraphsSTA of typed attributed graphs. In Sect. 5, we introduce attributed graph properties over typed attributed graphs together with basic operations on them such as \( shift \) and conversion of graph properties into conjunctive normal form. In Sect. 6, we adapt our tableau-based reasoning procedure to typed attributed graphs, which has been initially developed in [27]. In Sect. 7, we present the extension of our symbolic model generation algorithm [46] to attributed graph properties, and, in particular, show that it still fulfills the requirements listed before. In Sect. 8, we describe the implementation of the algorithm in our tool AutoGraph, focussing also on modifications required by extending our work to the handling of attributes and attribute constraints. In Sect. 9, we take a closer look at our application scenario and apply our tool AutoGraph to analyze the graph queries introduced before. We conclude the paper in Sect. 10 together with an overview of future work.
2 Related work
Instead of using a dedicated logic for graph properties such as the one introduced in Sect. 5, graph properties may be defined in terms of some existing logic allowing the application of its associated reasoning methods. We structure the Related Work section in three parts. We start with describing approaches that follow the idea of using some existing logic and continue with approaches following the idea of working with a dedicated logic for graph properties. We conclude with a description of the integration of attribute constraints in all these approaches to automated reasoning on graph properties.
In particular, Courcelle presented in [9] a graph logic defined in terms of first-order (or monadic second-order) logic. In that approach, graphs are defined axiomatically using predicates \( node (n)\), asserting that n is a node and \( edge (n_1, n_2)\) asserting that there is an edge from \(n_1\) to \(n_2\). In [18], such a translation-based approach for finding models of graph-like properties is followed. OCL properties are translated into relational logic, and reasoning is then performed by Kodkod, which is a SAT-based constraint solver for relational logic. In a similar vein, in [4] reasoning for feature models is provided based on a translation into input for different general-purpose reasoners. Analogously, in [50], the Alloy analyzer [50] is used to synthesize in this case large, well-formed, and realistic models for domain-specific languages. Based on Alloy, the Aluminum tool [31] computes minimal models, which are smaller than a provided maximum (i.e., assuming the small-world hypothesis from Alloy), by minimizing initially non-minimal models computed by Alloy. Moreover, Aluminum supports the interactive exploration of the model space (but is not compact as isomorphism is only approximated). However, Aluminum inherits some general problems from Alloy: The use of a small-world hypothesis, the required complex manual encoding, as well as the usage of general-purpose SMT solvers instead of domain-specific solvers such as AutoGraph limits the usability of Aluminum. Reasoning for domain-specific modeling is addressed also in [24, 25] using the FORMULA approach taking care of dispatching the reasoning to the state-of-the-art SMT solver Z3 [28]. In [45], another translation-based approach is presented to reason with so-called partial models, which express uncertainty about the information in the model during model-based software development.
In principle, all the previously exemplarily presented approaches from the model-based engineering domain represent potential use cases for our automated reasoning approach for graph-like properties. We are in particular able to automatically refute unsatisfiable graph properties and, for satisfiable graph properties, to generate symbolic models that are complete (in case of termination), sound, compact, minimally representable, nonambiguous, and explorable in combination. We therefore believe that our approach has the potential to considerably enhance the type of analysis results, in comparison with the results obtained by using off-the-shelf SAT-solving technologies. Following this idea, in contrast to the translation-based approach, it is possible, for example, to formalize a graph-like property language such as OCL [42] by a dedicated logic for graph properties [21] and apply corresponding dedicated automated reasoning methods as developed in [27, 34, 37, 38]. The advantage of such a graph-dedicated approach as followed in this paper is that graph axioms are natively encoded in the reasoning mechanisms of the underlying algorithms and tooling. Therefore, they can be built to be more efficient than generic-purpose methods, as demonstrated, for example, in [37,38,39], where such an approach outperforms some standard provers working over encoded graph conditions. Moreover, the translation effort for each graph property language variant (e.g., OCL) into a formal logic already dedicated to the graph domain is much smaller than a translation into some more generic logic, which in particular makes translation errors less probable. Another approach following this idea is presented in [49] where uncertainty about a graph-based model, which possibly occurs in partial models, may be resolved by graph transformation steps. The authors of [37, 39] present a satisfiability solving algorithm for graph properties [21]. This solver attempts to find one finite model (if possible), but does not generate a compact and gradually complete finite set of symbolic models allowing to inspect all possible finite models including a finite set of minimal ones. In contrast to [37, 39], our symbolic model generation algorithm is interleaved directly with a refutationally complete tableau-based reasoning method [27], inspired by rules of a proof system presented previously in [38], but in that work the proof rules were not shown to be refutationally complete.
When it comes to integrating attribute constraints in all the previous approaches mentioned above, we can observe that most translation-based approaches usually come with attribute support for the properties and the corresponding reasoning. This is presumably because they can rely on the underlying solvers for coping with attribute constraints. All dedicated automated reasoning approaches up until now do not support attributes. However, there exists one recent work [11] integrating attribute support into static analysis techniques for graph transformation. As in our approach, it is based on formalizing graph attribution using symbolic graphs as introduced in [35, 36]. In particular, the tool SyGrAV and a framework for the analysis of symbolic graph transformation systems also make use of the Z3 solver to handle attribute constraints. SyGrAV allows the usage of nested negative application conditions, which are used to restrict rule applications in symbolic graph transformation systems. This approach, however, is not concerned with automated reasoning for attributed graph properties.
3 Application scenario
In this section, we focus on an application scenario from the graph database domain in which our automated reasoning approach for attributed graph properties can be applied. We revert to a prominent case study in this domain concerned with social network queries [51, version 0.3.0, p. 25]. It was developed by the Linked Data Benchmark Council (LDBC) as a benchmark for following up the progress in graph data management technologies.
Analogous to the relational database domain [48], queries can be formalized and validated by subjecting them to static analysis. As argued also in the relational domain, querying a database should not depend on how and where the data are stored. For relational databases, the relational model [8] has therefore been designed as an underlying theory for modeling databases and their queries with the mathematical notion of a relation. A relational database consists of one (or more) relations of arity prescribed by the given database schema. A relational query is basically a mapping of a given database to a relation of fixed arity. Following this idea (cf. [6] and [26]), graphs and graph properties have been used to model graph databases and their queries. In this graph model, a graph G (possibly typed over a given type graph TG) models a graph database instance. A graph query q for a graph database G maps G to one (or more) patterns (or subgraphs) of a specific form in G.
The first step in our application scenario (cf. (1) in Fig. 1) is the formalization of graph queries as attributed graph properties: We described the first four “complex read queries” from the LDBC Social Network Benchmark case study [51, version 0.3.0, p. 25] into the typed attributed graph properties presented in Figs. 2, 3, 4, and 5. Note, arguments of the graph queries are translated into variables \( arg_i \) in their graph property counterparts. Technically, graph properties allow for the combination (by propositional operators such as conjunction and negation) of statements of existence of (sub)graphs in a given host graph also allowing more complex statements using nesting. In addition to graph conditions such as in [21, 46], we also allow for the usage of attributes and attribute constraints.
Graph property \(p^{3}\) modeling query 1 of the LDBC Social Network Benchmark [51, version 0.3.0, p. 25] searching for persons \( P_{res} \) (with a given \( firstName \)-value of \( arg_2 \)) that are reachable by a path of \( knows \)-edges of length 1–3 from a person \( P \) given by the id \({arg_1}\)
Graph property \(p^{4}\) modeling query 2 of the LDBC Social Network Benchmark [51, version 0.3.0, p. 25] searching for persons \( P_{res} \) (known by a person given by the id \({arg_1}\)) and for messages \( M_{res} \) created by \( P_{res} \) before a given time \( arg_2 \)
Graph property \(p^{4}\) modeling query 3 of the LDBC Social Network Benchmark [51, version 0.3.0, p. 25] searching for persons \( P_{res} \) (known by a person given by the id \({arg_3}\)) that created at least one message \( M \) in the time interval \([ arg_1 , arg_1 + arg_2 )\) from country X or Y (with names given by \( arg_3 \) and \( arg_4 \), respectively) without being located in X or Y
Graph property \(p^{6}\) modeling query 4 of the LDBC Social Network Benchmark [51, version 0.3.0, p. 25] searching for tags \( T_{res} \) that are attached to posts created (in the time interval \([ arg_2 , arg_2 + arg_3 )\)) by a person known by a person given by the id \({arg_1}\) such that, in addition, there are no posts created by such persons before that time interval
Adapted UML-Class Diagram of the LDBC Social Network Benchmark [51, version 0.3.0, p. 15]
The second step in our application scenario (cf. (2) in Fig. 1) is the application of our automated reasoning approach for graph query analysis. As described also for the relational domain [48], many query optimization tasks rely on the following three types of questions to be answered (cf. (2a)–(2c) in Fig. 1): Can a query q ever deliver a non-empty result (nonemptiness problem)? Does query \(q_1\) always deliver the same result as query \(q_2\) (equivalence problem)? Is the result of query \(q_1\) always contained in the result of query \(q_2\) (containment problem)? In particular, the first question that can be answered automatically by our approach for a given graph database query is whether there exists a graph database for which the query result is non-empty as illustrated in Fig. 1. In particular, our refutationally complete reasoning method for attributed graph properties implemented in our tool AutoGraph returns an empty set of symbolic models iff there exists no model for the given attributed graph property. Then, we know that the graph database query is invalid. On the other hand, our symbolic model generation algorithm returns a non-empty set of symbolic models iff there exist finite models for the attributed graph property. In this case, we know that the original query is valid. In addition, however, we can explore minimal example models for the property that can be extracted immediately from each symbolic model. For our application scenario, this means that we get example graph databases for our query that deliver non-empty results. In fact, the symbolic models generated describe all different minimal graph databases that can serve as witnesses for the validity of a query because our symbolic model generation algorithm delivers a finite, complete, minimal representable, nonambiguous, and compact overview of all graph databases delivering a non-empty result. Finally, a flexible exploration starting from any such minimal graph database to bigger ones that are still witnesses for the validity will be feasible by checking suitable candidates (constructed as supergraphs of the minimal models using atomic graph modifications) for being still witnesses for the validity of the given query.
In the graph database domain, compared to the relational domain, it is not common to have a database schema but often a conceptual model [10] is present. Such a conceptual model is given by the UML-Class Diagram depicted (adapted with minor corrections and completions from the LDBC Social Network Benchmark) in Fig. 6 for our case study. We can integrate such conceptual models describing the structure of all graph databases to be queried into our graph model and analysis approach by flattening the inheritance structure of the UML-Class Diagram to obtain a type graph, by modeling the multiplicity constraints as special attributed graph properties (cf. to Fig. 10c, d, e.g) and by forbidding parallel edges of the same type by graph properties as in Fig. 10b.
Finally, with our application scenario, we can also answer, analogous to the nonemptiness problem, further questions when given multiple graph queries at once. Firstly, the nonemptiness problem can be answered for a set of queries by using a conjunction of attributed graph properties instead of a single one. Such a set of queries is then jointly valid if they are able to deliver non-empty answer sets on a common graph. Secondly, we could answer the abovementioned equivalence or containment problem for two given queries as a basis for query optimization (analogous to query optimization in the relational database domain [1, 48]). For two graph queries \(q_1\) and \(q_2\), we can state their equivalence \(q_1 \equiv q_2\) or containment \(q_1 \subseteq q_2\) using a logical equivalence or implication in a single nested graph condition.
The analysis questions introduced in our application scenario here are answered for the example graph queries of our case study mentioned above in our evaluation in Sect. 9 by using our automated reasoning approach for attributed graph properties implemented in the tool AutoGraph.
4 Preliminaries
In this section, we provide, in a self-contained way, fundamentals, which are used in the remainder of this paper. Firstly, in Sect. 4.1, we introduce algebraic specifications along the lines of [16]. Secondly, in Sect. 4.2, we introduce symbolic typed attributed graphs based on algebraic specifications from [35, 36].
4.1 Algebraic specifications
We introduce in our notation the well-known algebraic specifications, which are used in this paper for the handling of attribute values in Sect. 4.2. Algebraic specifications can be used to describe data and functional programs. Furthermore, since SMT solvers such as Z3 support the formalism of algebraic specifications, we are able to employ them for our purposes in subsequent sections.
A signature consists of sorts S and symbols for operations O. The elements of O are equipped with an empty list of input-sorts are OR with an empty list of inputs are and a unique output sort. Elements of O with an empty list of input of sorts are called constants.
Definition 1
(Signature) \(\Sigma ^p=(S,O, type _{O}:O\rightarrow S^+)\) is a signature if S and O are finite.
To allow for the symbolic handling of attribute values (using terms and equations later on), we equip signatures with sorted variables distinguishable from the operations of the signature.
Definition 2
(Signature with Variables) Given a signature \(\Sigma ^p\) (as in Definition 1), \(\Sigma =(\Sigma ^p,X, type _{X}:X\rightarrow S)\) is a signature with variables if \(X\cap O=\emptyset \).
Example 1
(Signature with Variables) We employ the well-established notation for signatures with variables as for the following signature, which captures boolean expressions (in Definition 30, we provide a signature only including the built-in operations supported by AutoGraph via Z3).
Among other usages (explained later on), we specify attribute values in Sect. 4.2 based on (the recursively defined) terms over a given signature. The terms are well typed in the sense that they respect the sorts declared for variables, constants, and operations. Note, we define the terms for subsets of the variables X given in the signature with variables.
Definition 3
(Terms) Given a signature with variables \(\Sigma \) (as in Definition 2), \(s\in S\), and \(X'\subseteq X\). We define  to be the smallest set s.t.
to be the smallest set s.t.
-
 if \( type _{X}(x)=s\) and \(x\in X'\),
if \( type _{X}(x)=s\) and \(x\in X'\), -
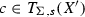 if \(c\in O\) and \( type _{O}(c)=s\), and
if \(c\in O\) and \( type _{O}(c)=s\), and -
 if \(f{\,\in \,}O\), \( type _{O}(f)=s_1{\cdots }s_{n+1}{\cdot }s\), and
if \(f{\,\in \,}O\), \( type _{O}(f)=s_1{\cdots }s_{n+1}{\cdot }s\), and  (for each \(1\le i\le n+1\)).
(for each \(1\le i\le n+1\)).
Also, we define
-
\( sort _{\Sigma }(t) =s\) whenever
 ,
, -
 , and
, and -
 .
.
The last two items from the previous definition are to be understood as follows. On the one hand, terms of arbitrary type without variables (such as \(\mathsf {and} (\mathsf {true},\mathsf {false})\) of sort \(\mathsf {bool}\) when using the signature in Example 1) are collected in the set  and represent values. On the other hand, terms containing variables are used to describe sets of values in a symbolic way; for example, the statements \(x>4\) and \(\mathsf {endsWith} (s, \text {{``suffix''}})\) where x and s are variables can be expressed by using signatures with variables comprising the used integer and string operations and variables, respectively.
and represent values. On the other hand, terms containing variables are used to describe sets of values in a symbolic way; for example, the statements \(x>4\) and \(\mathsf {endsWith} (s, \text {{``suffix''}})\) where x and s are variables can be expressed by using signatures with variables comprising the used integer and string operations and variables, respectively.
Variable substitutions are required for manipulation of terms such as in instantiations, simplifications, and equivalence proofs. A variable substitution determines for each variable x (possibly occurring in a term t) a replacement term (of equal type) to be inserted in t for each occurrence of the variable x.
Definition 4
(Variable Substitution) Given the two signatures with variables \(\Sigma _1=(\Sigma ^p,X_1, type _{X_1})\) and \(\Sigma _2=(\Sigma ^p,X_2, type _{X_2})\) with common underlying signature \(\Sigma ^p\) (as in Definition 2), each function \(\sigma :A\rightarrow B\) where \(A\subseteq X_1\), \(X_1-X_2\subseteq A\) (that is, \(\sigma \) replaces at least the variables not known by \(\Sigma _2\)), and  is a variable substitution, written \(\sigma \in \mathcal {V}_{\Sigma _1,\Sigma _2} \), if \( sort _{\Sigma _2}(\sigma (x)) = sort _{\Sigma _1}(x) \) for each \(x\in A\). Furthermore, the variable substitution \(\sigma \) is implicitly extended to a function of type
is a variable substitution, written \(\sigma \in \mathcal {V}_{\Sigma _1,\Sigma _2} \), if \( sort _{\Sigma _2}(\sigma (x)) = sort _{\Sigma _1}(x) \) for each \(x\in A\). Furthermore, the variable substitution \(\sigma \) is implicitly extended to a function of type  , which recursively replaces all occurrences of a variable \(x\in A\) in a given term by the replacement \(\sigma (x)\in B\).
, which recursively replaces all occurrences of a variable \(x\in A\) in a given term by the replacement \(\sigma (x)\in B\).
An algebraic specification extends a signature with variables by a finite set of term rewrite rules, which are called equations. The equations are of the form \((\ell ,r)\), where \(\ell \) and r are terms of equal sort, possibly making use of variables, and are usually written \(\ell =r\). The equations are used to resolve on the one hand semantic confusion between terms to be considered equal (e.g., \(\mathsf {zero} =\mathsf {minus} (\mathsf {zero})\)). On the other hand, equations determine the semantics of an operation contained in the signature as in functional programming languages (consider the equations from Example 2). For many relevant theories, these equations are applied as in functional programming from left to right to simplify terms, in particular terms without variables.
Definition 5
(Algebraic Specification) Given a signature with variables \(\Sigma \) (as in Definition 2), \( SP =(\Sigma , EQ )\) is an (algebraic) specification if
-
 ,
, -
\( EQ \) is finite, and
-
\( sort _{}(\ell ) = sort _{}(r) \) for each \((\ell ,r)\in EQ \).
The equations of the following algebraic specification can be used to rewrite terms containing the operations \(\mathsf {and} \) and \(\mathsf {not} \) into equivalent terms (defined below) without these operations (i.e., into the terms \(\mathsf {true} \) or \(\mathsf {false} \)).
Example 2
(Algebraic Specification) Equations of type \(\mathsf {bool} \) that could be added to the signature from Example 1 leading to a reasonable algebraic specification are:
The equations of a specification already determine certain terms to be equivalent but this basic equivalence is insufficient and is therefore extended to a congruence \(\cong \) w.r.t. the operators from the signature by allowing application of equations to subterms. As a base case, a term \(t_1\) can be rewritten into an equivalent term \(t_2\) by use of an equation \((\ell ,r)\) of the specification at hand by replacing (using a variable substitution \(\sigma \) fixing the variables occurring in the equation) \(t_1=\sigma (\ell )\) by \(t_2=\sigma (r)\).
Definition 6
(Equivalence of Terms) Given a specification \( SP \) (as in Definition 5), we define  to be the least equivalence s.t. \(t_1\cong _{{1}}t_2\) whenever there are \((\ell ,r)\in EQ \) and \(\sigma \in \mathcal {V}_{\Sigma ,\Sigma } \) s.t. \(t_1=\sigma (\ell )\) and \(t_2=\sigma (r)\).
to be the least equivalence s.t. \(t_1\cong _{{1}}t_2\) whenever there are \((\ell ,r)\in EQ \) and \(\sigma \in \mathcal {V}_{\Sigma ,\Sigma } \) s.t. \(t_1=\sigma (\ell )\) and \(t_2=\sigma (r)\).
The congruence \(\cong \) mentioned above is obtained by allowing term rewritings based on \(\cong _{{1}}\) on any level.
Definition 7
(Congruence of Terms) Given a specification \( SP \) (as in Definition 5), we define  to be the least equivalence s.t. \(t_1\cong t_2\) if
to be the least equivalence s.t. \(t_1\cong t_2\) if
-
\(t_1 \cong _{{1}}t_2\) or
-
there is some \(f\in O\) with \( type _{O}(f)=s_1{\cdots }s_{n+1}{\cdot }s\),
 (for each \(1\le i\le n+1\) and \(1\le j \le 2\)) with \(t^1_i \cong t^2_i\) (for each \(1\le i\le n+1\)) and \(t_j=f(t^j_1,\dots ,t^j_{n+1})\) (for each \(1\le j \le 2\)).
(for each \(1\le i\le n+1\) and \(1\le j \le 2\)) with \(t^1_i \cong t^2_i\) (for each \(1\le i\le n+1\)) and \(t_j=f(t^j_1,\dots ,t^j_{n+1})\) (for each \(1\le j \le 2\)).
Example 3
(Congruence of Terms) Using Equation 1 from Example 2, we can simplify the term \(\mathsf {and} (\mathsf {true},\mathsf {false})\) to \(\mathsf {false} \) by term rewriting (using either \(\cong _{{1}}\) or \(\cong \)).
Subsequently, we implicitly assume that algebraic specifications include a propositional fragment based on the sort \(\mathsf {bool} \) as well as the propositional constants \(\mathsf {true} \) (required for satisfiability in Definition 8) and \(\mathsf {false} \) (required for type graphs as discussed in the paragraph preceding Definition 12).
We call terms of type \(\mathsf {bool} \) (attribute) constraints and use them in attributed graphs to specify/restrict variable values. For these constraints, we define the satisfaction as follows.
Definition 8
(Satisfaction of Constraints) For a specification \( SP \) (as in Definition 5), a single constraint  (as in Definition 3), a set
(as in Definition 3), a set  of constraints, and a variable substitution \(\sigma \in \mathcal {V}_{\Sigma ,\Sigma } \) (as in Definition 4), we define that
of constraints, and a variable substitution \(\sigma \in \mathcal {V}_{\Sigma ,\Sigma } \) (as in Definition 4), we define that
-
\(\sigma \) satisfies \(\phi \), written \(\sigma \models \phi \), if \(\sigma (\phi )\cong \mathsf {true} \),
-
\(\phi \) is satisfiable by \( SP \) if \(\exists \sigma \in \mathcal {V}_{\Sigma ,\Sigma }.\,\sigma \models \phi \),
-
\(\sigma \) satisfies \(\varPhi \), written \(\sigma \models \varPhi \), if \(\forall \phi \in \varPhi .\,\sigma \models \phi \),
-
\( SP \) satisfies \(\phi \), written \( SP \models \phi \), if \(\forall \sigma \in \mathcal {V}_{\Sigma ,\Sigma }.\,\sigma \models \phi \),
-
\(\varPhi \) is satisfiable by \( SP \) if \(\exists \sigma \in \mathcal {V}_{\Sigma ,\Sigma }.\,\forall \phi \in \varPhi .\,\sigma \models \phi \), and
-
\( SP \) satisfies \(\varPhi \), written \( SP \models \varPhi \), if \(\forall \phi \in \varPhi .\, SP \models \phi \).
SMT solvers such as Z3 are typically shipped with built-in data types, operations, and equations on, for example, booleans, integers, and strings. Thus, in practice, users of such solvers and, hence, also users of higher level tools such as AutoGraph do not need to construct custom algebraic specifications and custom equations when using such built-in datatypes only.
Note, users of our tool AutoGraph may extend the basic algebraic specification to introduce further sorts and operations (including equations) for use in constraints in attributed graphs. However, while SMT solvers are often sufficient for the few built-in fragments mentioned before, satisfaction and satisfiability of constraints cannot be decided for arbitrary specifications with more complex equations. Constraints where the employed SMT solver is not capable of deciding satisfiability pose problems to our model generation procedure: The handling of this problem is explicitly addressed in Sect. 8.
4.2 Symbolic typed attributed graphs
Symbolic typed attributed graphs, as introduced in [35, Definition 1] together with a framework of graph transformation on these graphs, may include vertex attributes and edge attributes similarly to EGraphs [13]. That is, any number of vertex attributes (edge attributes) is mapped on the one hand to a vertex (an edge), called source, and, on the other hand, to an assigned element, called target. However, in EGraphs, the target of an attribute is an element of the employed data algebra, whereas in symbolic typed attributed graphs, the target is a variable of the algebraic specification. Moreover, in symbolic typed attributed graphs, a set of constraints is used to describe the values that such a variable can take. Note, the set of constraints may be satisfiable by more than one variable substitution. A set of constraints is more expressive than a single constraint because only a finite set of constraints can be translated in general into a single constraint using finite conjunction in the obvious way.
We introduce the category of symbolic typed attributed graphs stepwise starting with plain graphs.
Definition 9
(Plain Graph) Plain graphs \(G^p\) are tuples of the form \((V,E, src :E\rightarrow V, trg :E\rightarrow V)\).
Note, to simplify notation, we facilitate the usual notation for selectors for tuples such as for plain graphs. For example, we denote the vertices of a plain graph \(G^p_i\) by \(V_{G^p_i}\) or simply by \(V_i\).
In the next step, plain graphs are extended by an algebraic specification, an attribution consisting of attribute variables, attribute vertices, and attribute edges together with the source and target mappings similarly available in EGraphs, and constraints restricting the possible values of the attribute variables.
Definition 10
(Symbolic Attributed Graph) Given a plain graph \(G^p\) (as in Definition 9), a specification \( SP \) (as in Definition 5) with finite set X, and an attribution \(A=( AX , type _{ AX }: AX \rightarrow S, AV , src_{AV} : AV \rightarrow V, trg_{AV} : AV \rightarrow AX , AE , src_{AE} : AE \rightarrow E, trg_{AE} : AE \rightarrow AX )\). Then, \(G^{ sa }{\,=\,}(G^p, SP ,A,\varPhi )\) is a symbolic attributed graph if there is a signature \(\Sigma _A\) s.t.
-
\(X\cap AX =\emptyset \),
-
\(\Sigma _A=(\Sigma ^p,X\cup AX , type _{ X }\cup type _{ AX })\), and
-

See Fig. 7 for an example of a symbolic attributed graph and the simplified notation. Note, the empty graph, written \(\emptyset \), is assumed to have either the constraint set \(\varPhi =\emptyset \) or \(\varPhi =\{\mathsf {true} \}\) when this fact is to be expressed more explicitly as in Fig. 12.
A symbolic attributed graph \(G^{7}\) in two notations (left/right). The used specification from Example 2 is not depicted. The single constraint \(\varPhi \) is depicted separately from the graph structure at the bottom. Note, the constraint can be satisfied by three different variable substitutions
A symbolic attributed graph morphism f (see Def 11) has to be compatible with the operations of the source and target graphs
Five symbolic (typed) attributed graph morphisms. The type graph is given in Fig. 12a. Also, \(D_3\) satisfies the graph property  (an extension of this graph property is given in Fig. 12b) according to Definition 16 because the required morphisms \(q_2\) and \(q_4\) can be found such that the two triangles commute (see Fig. 11 for an example with more explanations on the satisfaction of graph properties)
(an extension of this graph property is given in Fig. 12b) according to Definition 16 because the required morphisms \(q_2\) and \(q_4\) can be found such that the two triangles commute (see Fig. 11 for an example with more explanations on the satisfaction of graph properties)
The subsequently introduced notion of a morphism between symbolic attributed graphs is extended with compatibility w.r.t. typing in Definition 14. As for now, the morphism maps vertices, edges, and attributes in a way compatible with the various source and target operations (see Fig. 8). Also note, attribute variable mappings must not restrict satisfying variable substitutions; i.e., a variable substitution \(\sigma \) satisfying the constraint of the target symbolic attributed graph \(G_2^{ sa }\) must already have satisfied the constraint of the source symbolic attributed graph \(G_1^{ sa }\) after application of the symbolic attributed graph morphism.
For example, consider the symbolic (typed) attributed graph morphism \(m_4\) from Fig. 9, where each variable substitution satisfying the constraint of \(G_4\) also satisfies the constraint of \(G_2\) (in this example, no variable renaming is performed by \(m_4\) as it maps the attribution variable x from \(G_2\) to the attribution variable x from \(G_4\)).
Definition 11
(Symbolic Attributed Graph Morphism) If \(G_1^{ sa }\) and \(G_2^{ sa }\) are symbolic attributed graphs (as in Definition 10) with specification \( SP =(\Sigma , EQ )\), then \(f=(f_V:V_1{\,\rightarrow \,}V_2,f_E:E_1\rightarrow E_2,f_{ AX }: AX _1\rightarrow AX _2,f_{ AV }: AV_1 {\,\rightarrow \,} AV_2 ,f_{ AE }: AE_1 \rightarrow AE_2 )\) is a symbolic attributed graph morphism of type \(G_1^{ sa }\rightarrow G_2^{ sa }\), written \(f:G_1^{ sa }\rightarrow G_2^{ sa }\), if (see Fig. 8)
-
\( src_2 \circ f_E = f_V \circ src_1 \),
-
\( trg_2 \circ f_E = f_V \circ trg_1 \),
-
\( src_{AV_2} \circ f_{ AV } = f_V \circ src_{AV_1} \),
-
\( trg_{AV_2} \circ f_{ AV } = f_{ AX } \circ trg_{AV_1} \),
-
\( src_{AE_2} \circ f_{ AE } = f_E \circ src_{AE_1} \),
-
\( trg_{AE_2} \circ f_{ AE } = f_{ AX } \circ trg_{AE_1} \),
-
\( type _{ AX _2}\circ f_{ AX }= type _{ AX _1}\), and
-
for all \(\sigma \in \mathcal {V}_{\Sigma _{A_2},\Sigma _{A_2}} \):Footnote 1 \(\sigma \models \varPhi _2\) implies \(\sigma \models f_{ AX }(\varPhi _1)\).
Moreover, the composition \(f_2\circ f_1:G_1^{ sa }\rightarrow G_3^{ sa }\) of symbolic attributed graph morphisms \(f_1:G_1^{ sa }\rightarrow G_2^{ sa }\) and \(f_2:G_2^{ sa }\rightarrow G_3^{ sa }\) is defined componentwise.
A symbolic attributed graph \(G^{ sa }\) is extended to a symbolic typed attributed graph G (or graph for short) when a type graph \( TG \) is available such that a typed attributed graph morphism from \(G^{ sa }\) to \( TG \) can be determined, which, by definition, has to satisfy the compatibilities discussed before. In practice, we often use the single constraint \(\mathsf {false} \) for type graphs to allow arbitrary values in symbolic attributed graphs to be typed.
Definition 12
((Symbolic Typed Attributed) Graph) For a given symbolic attributed graph morphism \(\tau :G^{ sa }{\,\rightarrow \,} TG \) (as in Def 11), we define \(G=(G^{ sa }, TG ,\tau :G^{ sa }{\,\rightarrow \,} TG )\) to be a (symbolic typed attributed) graph.
We introduce grounded graphs as those symbolic typed attributed graphs where the set of attribute constraints \(\varPhi \) can be satisfied by a unique variable substitution, whereas for typed attributed graphs, also infinite and empty sets of such variable substitutions are allowed.
Definition 13
(Grounded Graph) A graph is a grounded graph, if its set of attribute constraints \(\varPhi \) is satisfiable by a unique variable substitution. For a graph \(G_s\), we denote all grounded graphs \(G_g\) obtainable from \(G_s\) by only adding further attribute constraints to \(G_s\) by \( grounded (G_s) \).
Subsequently, we assume a fixed symbolic attributed graph \( TG \) used as a type graph and lift symbolic attributed graph morphisms to symbolic typed attributed graphs by requiring that the two symbolic attributed graph morphisms used for typing are compatible in the sense of the commutation of the triangle in the following definition.
Definition 14
((Symbolic Typed Attributed) Graph Morphism) Given two (symbolic typed attributed) graphs \(G_1=(G_1^{ sa }, TG ,\tau _1)\) and \(G_2=(G_2^{ sa }, TG ,\tau _2)\) (as in Def 12) over a common type graph \( TG \) and a symbolic attributed graph morphism \(f:G_1^{ sa }\rightarrow G_2^{ sa }\) (as in Def 11). We define f to be a (symbolic typed attributed graph) morphism and also to be of type \(G_1\rightarrow G_2\) if \(\tau _2\circ f=\tau _1\).

We are binding the definitions of graphs and morphisms from before into the single notion of a category.
Theorem 1
(Category GraphsSTA of Symbolic Typed Attributed Graphs) For a fixed type graph \( TG \), we obtain the category GraphsSTA by using the symbolic typed attributed graphs as defined in Definition 12 as objects, the symbolic typed attributed graph morphisms as defined in Definition 11 between them as morphisms, the composition of symbolic typed attributed graph morphisms also defined in Definition 11, and symbolic typed attributed graph identity morphisms based on the componentwise identities.
Proof
(idea) By the well definedness of the involved notions of symbolic typed attributed graphs and symbolic typed attributed morphisms.
In the following, we denote that \(f:G\rightarrow G'\) is a mono as  , an epi as \(f:G\twoheadrightarrow G'\), and an iso as
, an epi as \(f:G\twoheadrightarrow G'\), and an iso as  (see Lemma 11).
(see Lemma 11).
Note, for specifications where attribute constraint satisfiability is undecidable, we can also not decide whether an element is a graph morphism because, by definition, an implication on attribute constraint satisfaction must be decided. In Sect. 8, we handle this problem explicitly for our symbolic model generation procedure.
5 Properties over GraphsSTA
In this section, we introduce graph properties over symbolic typed attributed graphs with basic operations.
On the one hand, graph properties (for labeled graphs) with attribute constraints without nesting have been introduced in [32] and extended with operators from propositional logic in [33]. On the other hand, graph properties (for labeled graphs) without attribute constraints but with nesting have been introduced in [21]. In the following, we integrate both ideas and introduce (nested) graph properties on symbolic typed attributed graphs from Sect. 4.2.
Graph conditions of the simple form  state that G is to be contained as a subgraph in every model. The expressive power of first-order logic on graphs is then obtained by allowing conjunction, negation, and nesting of graph conditions of this form.
state that G is to be contained as a subgraph in every model. The expressive power of first-order logic on graphs is then obtained by allowing conjunction, negation, and nesting of graph conditions of this form.
Definition 15
(Graph Conditions and Graph Properties) The set \(\mathcal {C}_{G} \) of (graph) conditions over a graph G is inductivelyFootnote 2 defined by:
-
\(\wedge S\in \mathcal {C}_{G} \) if S is a finite subset of \(\mathcal {C}_{G} \),
-
\(\lnot c\in \mathcal {C}_{G} \) if \(c\in \mathcal {C}_{G} \), and
-
 if \(c\in \mathcal {C}_{G'} \).
if \(c\in \mathcal {C}_{G'} \).
A (graph) property is a condition over the empty graph \(\emptyset \).
Notation 1
We use further operators to ease the usage of graph properties, introduced as abbreviations, such as

We also allow infix and mixfix notation for \(\wedge \) and \(\vee \) (e.g., as in \(\wedge \{c_1,c_2,c_3\}=c_1\wedge c_2\wedge c_3\)).
When presenting graph conditions in figures, we abbreviate (for notational simplicity) existential quantifications of the form  by \(\exists (G',c)\) when the morphism m is clear from the context and where \(G'\) is the least subgraph of \(G_2\) containing all graph elements that are fresh in \(G_2\) w.r.t. \(G_1\). This notation is used in, for example, Fig. 2.
by \(\exists (G',c)\) when the morphism m is clear from the context and where \(G'\) is the least subgraph of \(G_2\) containing all graph elements that are fresh in \(G_2\) w.r.t. \(G_1\). This notation is used in, for example, Fig. 2.
Graph properties may be employed to specify a diverse set of properties to be satisfied by concrete models. Firstly, the graph property in Fig. 10a states a simple negative pattern by means of the symbolic typed attributed graph \(G^{7}\) from Fig. 7. Secondly, the graph properties from Figure 10b, d, and Fig. 10c specify lower/upper bounds (i.e., multiplicity statements) on graph elements that are mapped to common graph elements in the type graph. Finally, the graph property given in Fig. 10e describes an infinite sequence of nodes by essentially formalizing the Peano axioms. The last example also demonstrates that any stepwise construction of minimal models adding a finite number of elements cannot terminate in general.
Various examples of graph properties showing the diversity of properties expressible by graph properties. a Graph property \(p^{10a}=\lnot \exists (m, true )\) states that the symbolic attributed graph \(G^{7}\) from Fig. 7 (equipped with suitable vertex and edge types not depicted for simplicity) is not a subgraph of any desired model. That is, the pattern described by \(G^{7}\) can be understood to be prohibited. b Graph property \(p^{10b}=\lnot \exists (m, true )\) states that there are no parallel edges of type \(T_E\) between vertices of types \(T_{V1}\) and \(T_{V2}\), respectively. c Graph property \(p^{10c}=p^{10c}_1\wedge p^{10c}_2\) states that (\(p^{10c}_1\)) there are at least two vertices of type \(T_V\) and that (\(p^{10c}_2\)) there are not three or more vertices of type \(T_V\). d Graph property \(p^{10d}=p^{10d}_1\wedge p^{10d}_2\wedge p^{10b}\) states that (\(p^{10d}_1\)) at least two edges of type \(T_E\) exit every vertex of type \(T_{V1}\), and that (\(p^{10d}_2\)) not three or more edges of type \(T_E\) exit any vertex of type \(T_{V1}\), and (\(p^{10b}\) from Fig. 10b) is used to simplify the property (no mergings of target vertices need to be considered in the property) in contexts where preventing parallel edges is reasonable. e Graph property \(p^{10e}=p^{10e}_1\wedge p^{10e}_2\wedge p^{10e}_3\), with unique vertex and edge types (not depicted for simplicity), states that (\(p^{10e}_1\)) there is at least one vertex without predecessor vertex, (\(p^{10e}_2\)) every vertex has a successor vertex, and (\(p^{10e}_3\)) there is no vertex with two predecessor vertices. The infinite graph

Definition 16
(Satisfaction of Graph Conditions) A graph condition \( c_{inp} \) from \(\mathcal {C}_{C} \) is satisfied recursively by a monomorphism  , written \(q\models c_{inp} \), as follows:
, written \(q\models c_{inp} \), as follows:
-
\(q\models \wedge S\) if \(q \models c\) for each \(c\in S\)
-
\(q\models \lnot c\) if not \(q\models c\)
-
 if some
if some  satisfies \(q'\circ m=q\) and \(q'\models c\).
satisfies \(q'\circ m=q\) and \(q'\models c\). 
Also, a graph G
satisfies a graph property p (see Definition 15), written \(G\models p\), if the unique mono  satisfies p. Finally, \(\llbracket p\rrbracket \) is the set of all graphs satisfying p and two properties \(p_1\) and \(p_2\) are equivalent, written \(p_1\equiv p_2\), iff \(\llbracket p_1\rrbracket =\llbracket p_2\rrbracket \).
satisfies p. Finally, \(\llbracket p\rrbracket \) is the set of all graphs satisfying p and two properties \(p_1\) and \(p_2\) are equivalent, written \(p_1\equiv p_2\), iff \(\llbracket p_1\rrbracket =\llbracket p_2\rrbracket \).
Consider Fig. 11 for an example for the satisfaction of a graph property making use of nesting, conjunction, and existential quantification where types, attributes, attribute constraints, and negation are left out for simplicity.
For the given graph property \(p_1\) with its subconditions \(p_2\), \(p_3\), and \(p_4\), we derive that the graph \( G_{host} \) satisfies \(p_1\) as follows. Step 1: \( G_{host} \) satisfies \(p_1\) because the unique mono  satisfies \(p_1\). Step 2: i satisfies \(p_1\) because we can determine some \(q_1\) (mapping \(v_0\) to \(v_a\) and \(v_1\) to \(v_b\)) such that \(q_1\circ m_1=i\) (trivial) and \(q_1\) satisfies \(p_2\). Step 3: \(q_1\) satisfies \(p_2\) because \(q_1\) satisfies \(p_3\) and \(q_1\) satisfies \(p_4\). Step 4a: \(q_1\) satisfies \(p_3\) because we can determine some \(q_3\) (mapping \(v_0\) to \(v_a\) and \(v_1\) to \(v_b\)) such that \(q_2\circ m_2=q_1\) and \(q_2\) satisfies \( true \) (trivial). Step 4b: \(q_1\) satisfies \(p_4\) because we can determine some \(q_4\) (mapping \(v_0\) to \(v_a\) and \(v_1\) to \(v_b\)) such that \(q_4\circ m_3=q_1\) and \(q_4\) satisfies \( true \) (trivial). Note, instead of choosing \(q_1\) as above in Step 1, we could have selected \(q_2\) (mapping \(v_0\) to \(v_b\) and \(v_1\) to \(v_a\)). However, then we would have to derive that \(q_2\) satisfies \(p_2\). This is not possible because \(q_2\) does not satisfy \(p_3\) because there is no morphism \(q_3'\) with same type as \(q_3\) such that \(q_3'\circ m_2 = q_2\) because vertex \(v_a\) has no loop
satisfies \(p_1\). Step 2: i satisfies \(p_1\) because we can determine some \(q_1\) (mapping \(v_0\) to \(v_a\) and \(v_1\) to \(v_b\)) such that \(q_1\circ m_1=i\) (trivial) and \(q_1\) satisfies \(p_2\). Step 3: \(q_1\) satisfies \(p_2\) because \(q_1\) satisfies \(p_3\) and \(q_1\) satisfies \(p_4\). Step 4a: \(q_1\) satisfies \(p_3\) because we can determine some \(q_3\) (mapping \(v_0\) to \(v_a\) and \(v_1\) to \(v_b\)) such that \(q_2\circ m_2=q_1\) and \(q_2\) satisfies \( true \) (trivial). Step 4b: \(q_1\) satisfies \(p_4\) because we can determine some \(q_4\) (mapping \(v_0\) to \(v_a\) and \(v_1\) to \(v_b\)) such that \(q_4\circ m_3=q_1\) and \(q_4\) satisfies \( true \) (trivial). Note, instead of choosing \(q_1\) as above in Step 1, we could have selected \(q_2\) (mapping \(v_0\) to \(v_b\) and \(v_1\) to \(v_a\)). However, then we would have to derive that \(q_2\) satisfies \(p_2\). This is not possible because \(q_2\) does not satisfy \(p_3\) because there is no morphism \(q_3'\) with same type as \(q_3\) such that \(q_3'\circ m_2 = q_2\) because vertex \(v_a\) has no loop
For the tableau procedure in Sect. 6, we introduce the construction \( shift \) as a modification of the corresponding construction from [14, Construction 3.12, p. 15] where \( shift \) is employed in the context of the analysis of \(\mathcal {M}\)-adhesive transformation systems. The operation from [14] is adapted here by requiring that all involved morphisms are monomorphisms as required for conditions and for satisfaction (Definition 15 and Definition 16).
While \( shift \) is defined homomorphically on conjunction and negation, for existential quantification all possible overlappings of two positive graph patterns are constructed to compute all situations in which both positive patterns are satisfied. In the following definition, this means that the condition \( shift (m_1,\exists (m_2,c)) \) describes the occurrence of the positive pattern \(\exists (m_2,c)\) in the context of the other positive pattern \(\exists (m_1, true )\).
Consider Fig. 12 for an example of a graph property with attribute constraints that is shifted along a monomorphism where overlappings are constructed (K in following definition is an overlapping of \(C_1\) and \(C_2\) where \(m_1'\) and \(m_2'\) are injective and jointly epimorphic) and attribute constraints are handled suitably.
Definition 17
(Operation
\( shift \)) Given a graph condition from \(\mathcal {C}_{C} \) and a monomorphism  , then \( shift \) is defined recursively as follows:
, then \( shift \) is defined recursively as follows:
-
\( shift (m_1,\wedge S) =\wedge \{ shift (m_1,c) \mid c\in S\}\),
-
\( shift (m_1,\lnot c) =\lnot shift (m_1,c) \), and
-
 where \(\mathcal {F}\) is a set of representatives for the isomorphism quotient of \(\{(m_2',m_1')\in \mathcal {E'}\mid m_2'\circ m_1=m_1'\circ m_2\}\) where \(\mathcal {E'}\) is the set of pairs of jointly epimorphic morphisms from Definition 32. Here, \((m_2',m_1')\) and \((m_2'',m_1'')\) are isomorphic, if some isomorphism
where \(\mathcal {F}\) is a set of representatives for the isomorphism quotient of \(\{(m_2',m_1')\in \mathcal {E'}\mid m_2'\circ m_1=m_1'\circ m_2\}\) where \(\mathcal {E'}\) is the set of pairs of jointly epimorphic morphisms from Definition 32. Here, \((m_2',m_1')\) and \((m_2'',m_1'')\) are isomorphic, if some isomorphism  satisfies \(m_2''=i\circ m_2'\) and \(m_1''=i\circ m_1'\).
satisfies \(m_2''=i\circ m_2'\) and \(m_1''=i\circ m_1'\). 
An example of an application of the \( shift \)-operation. a The type graph \( TG \) (used in this figure) over the specification from Definition 30. We omit the vertex and edge types Vertex and Edge in the other subfigures below as they are unique. b A graph property  , which is a condition over the empty graph \(G_0=\emptyset \) by definition, where all graphs are typed over the type graph \( TG \) from above. c One of the diagrams required for computing
, which is a condition over the empty graph \(G_0=\emptyset \) by definition, where all graphs are typed over the type graph \( TG \) from above. c One of the diagrams required for computing  showing that the result (which is a disjunction) contains at least
showing that the result (which is a disjunction) contains at least  . Firstly, (in the upper rectangle) \(C_1\) is constructed from \(G_1\) and \(G_2\) by some (possibly partial) overlapping, and secondly, (in the lower rectangle) \(D_3\) is constructed from \(C_1\) and \(G_4\) by some (possibly partial) overlapping such that elements that are already in \(G_2\) are overlapped. During the overlapping process, the constraints of the result are the constraints of the two source graphs where variables are renamed according to the variable mappings from the source graphs into the constructed overlapping. Note, the graph \(D_3\) satisfies the graph property p. d An alternative overlapping to \(D_3\). e An alternative overlapping to \(D_3\). f An alternative overlapping to \(D_3\) with unsatisfiable constraint. g An alternative overlapping to \(C_1\)
. Firstly, (in the upper rectangle) \(C_1\) is constructed from \(G_1\) and \(G_2\) by some (possibly partial) overlapping, and secondly, (in the lower rectangle) \(D_3\) is constructed from \(C_1\) and \(G_4\) by some (possibly partial) overlapping such that elements that are already in \(G_2\) are overlapped. During the overlapping process, the constraints of the result are the constraints of the two source graphs where variables are renamed according to the variable mappings from the source graphs into the constructed overlapping. Note, the graph \(D_3\) satisfies the graph property p. d An alternative overlapping to \(D_3\). e An alternative overlapping to \(D_3\). f An alternative overlapping to \(D_3\) with unsatisfiable constraint. g An alternative overlapping to \(C_1\)
The definition of \( shift \) is of course important for the implementation. However, in proofs we only build upon the following lemma stating the required compatibility.
Lemma 1
(Compatibility of \( shift \) and \(\models \)) Given a graph condition \(c\in \mathcal {C}_{C} \), a monomorphism  , and a monomorphism
, and a monomorphism  . Then, \(m'\circ m\models c\) iff \(m'\models shift (m,c) \).
. Then, \(m'\circ m\models c\) iff \(m'\models shift (m,c) \).

Proof
(idea) Analogous to the proof of the corresponding earlier result [14, Lemma 3.11, p. 15] using Lemma 14.
To simplify our reasoning, our symbolic model generation algorithm operates on the subset of conditions in conjunctive normal form (CNF).
Definition 18
(Graph Conditions in Conjunctive Normal Form (CNF)) A graph condition is in CNF if it is a conjunction of clauses. A clause is a disjunction of literals. A literal is a positive literal

or a negative literal

where (in both cases)  is no isomorphism, the attribute constraint of \(C'\) is satisfiable, and c is in CNF.
is no isomorphism, the attribute constraint of \(C'\) is satisfiable, and c is in CNF.
For example, the condition \(\wedge \{\vee \{\}\}\) is in CNF and is equivalent to \( false \).
For translating conditions into equivalent conditions in CNF, we introduce the second operation \([\cdot ]\) on conditions, which is similar to an operation in [27, 38, 39].
Definition 19
(Conversion to CNF) The conversion operation \([\cdot ]:\mathcal {C}_{G} \rightarrow \mathcal {C}_{G} \) executes the following steps:
-
Step 1: remove operators besides \(\wedge \), \(\vee \), \(\lnot \), and \(\exists \) according to the abbreviations from Notation 1,
-
Step 2: remove any existential quantifications of isomorphisms (e.g.,
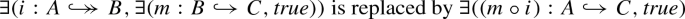
by moving the isomorphism i into the literal of the next nesting level),
-
Step 3: remove all unsatisfiable existential quantifications (i.e., replace
 by \(\vee \emptyset \) when the attribute constraints of the graph B are not satisfiable),
by \(\vee \emptyset \) when the attribute constraints of the graph B are not satisfiable), -
Step 4: move all negations inwards across \(\wedge \) and \(\vee \), dropping duplicate negations as expected, until reaching an existential quantification, and
-
Step 5: apply distributive and associative laws for \(\wedge \) and \(\vee \) to finally enforce the required CNF structure.
In Step 3, we require the existence of an oracle that decides these satisfiability questions in all cases. In Sect. 8, we explain in more detail how we handle cases where SMT solvers such as Z3 designed to implement that oracle are unable to decide satisfiability questions on attribute constraints.
As for FOL, the conversion to CNF entails the conversion of subconditions of the shape \((a_1\wedge b_1)\vee \dots \vee (a_n\wedge b_n)\), which results in a CNF with \(2^n\) clauses of size n. However, in our approach, the conversion of graph conditions into CNF graph conditions usually has no great impact on the runtime of our overall algorithm because subconditions from different existential quantifiers are not combined in the conversion; that is, we perform the conversion on each nesting level of the \(\exists \)-quantifier and, hence, we obtain quite small CNF conditions. For FOL, this is different: After skolemization, which removes existential quantifiers, all subconditions are related to each other resulting in huge formulas. Note, skolemization is not needed for graph conditions according to [39, p. 100]. Also note, the size of the graphs and the morphisms contained in the condition are not relevant for the conversion in our case, which is an important difference to the FOL scenario. However, attribute constraints have to be checked by AutoGraph for satisfiability by the employed SMT solver during the conversion to CNF to check for unsatisfiable attribute constraints (see Step 3 in Definition 19). These general explanations are supported by our runtime examinations that are presented in [47] where Alloy is applied to generate models for two graph queries without attributes that we encoded in the Alloy input language. However, apparently due to lacking support for strings and integer arithmetic, Alloy is not able to determine models for Alloy-encoded versions of the graph properties with attributes and attribute conditions from Figs. 3, 4, and 5.
6 Tableau procedure
In this section, we adapt the tableau procedure for graph conditions without attributes and attribute constraints from [27] to graph conditions over the symbolic typed attributed graphs as introduced in Sect. 4.2. To handle the additional attributes and attribute constraints, we adapted the underlying operations \( shift \) and \([\cdot ]\) as explained before.
Intuitively, using the tableau procedure, we perform in our algorithm, for a given graph property, a recursive case distinction to finally return all most explicit cases that cannot be split further. Subsequently, in Sect. 6.1, we start with an intuitive explanation on the steps for splitting, recursive application, and termination backed up by fundamental lemmas. Afterward, in Sect. 6.2, we present formal definitions for the construction of (nested) tableaux implementing the three discussed steps.
6.1 Recursive case distinction principle
Step 1 (Splitting): we are translating the given graph condition c in CNF into a disjunctive normal form, i.e., into a disjunction of conjunctions of literals. This conversion is executed in Sect. 6.2 by construction of a tableau T where each branch B of the tableau T corresponds to one clause of the disjunctive normal form to be constructed.
The obtained condition \(\vee S\) is then considered compositionally (assuming here and subsequently an enclosing existential quantification in the form of \(\exists (i_C,\vee S)\) using the unique mono  ). That is, we can consider each clause of the disjunctive normal form (given by an element of S) separately without altering the set of models of the graph property. Hence, we may consider one branch B of the tableau T constructed in isolation.
). That is, we can consider each clause of the disjunctive normal form (given by an element of S) separately without altering the set of models of the graph property. Hence, we may consider one branch B of the tableau T constructed in isolation.
Lemma 2
(Sound and Complete Branching) If S is a subset of \(\mathcal {C}_{C} \), then

Each clause \(\wedge L\) considered separately from the other clauses contains either at least one positive literal (Step 2) or only negative literals (Step 3).
Step 2 (Recursive Application): To prepare the clause \(\wedge L\) for recursive application, we are merging the elements of L into a single positive literal by application of the \( shift \) construction. Firstly, one positive literal \(\ell \) is selected from L and all other graph conditions from \(S=L-\{\ell \}\) are lifted into \(\ell \) using the \( shift \) construction.
Lemma 3
(Sound and Complete Lifting) If S is a given subset from \(\mathcal {C}_{C} \), then  .
.
Also note, the operation \([\cdot ] \), which is additionally applied in the formal tableau construction in Sect. 6.2, is sound and complete as follows.
Lemma 4
(Sound and Complete \([\cdot ] \)) If c is a condition from \(\mathcal {C}_{C} \), then \(\llbracket \exists (i_C,c)\rrbracket =\llbracket \exists (i_C,[c])\rrbracket \).
Finally, we recursively apply the presented algorithm to the condition c of the positive literal  obtained. Note, since m is no isomorphism due to the operation \([\cdot ]\), the graph \(C'\) is strictly greater than the graph C. This recursive application is justified by the following lemma.
obtained. Note, since m is no isomorphism due to the operation \([\cdot ]\), the graph \(C'\) is strictly greater than the graph C. This recursive application is justified by the following lemma.
Lemma 5
(Sound and Complete Nesting) If c is a condition in \(\mathcal {C}_{C'} \), then  .
.
Step 3 (Termination): As a complementary case to Step 2 we consider clauses containing no positive literal, that is, clauses containing any number of negative literals of the form  . Due to the construction of the operation \([\cdot ]\), the monomorphisms m of these negative literals are no isomorphisms and, hence, the unique monomorphism
. Due to the construction of the operation \([\cdot ]\), the monomorphisms m of these negative literals are no isomorphisms and, hence, the unique monomorphism  already satisfies these negative literals proving that C is a model of all negative literals contained in the clause. Also, the graph C minimally represents all models of the considered case in the sense that it is the least graph contained in all these models.
already satisfies these negative literals proving that C is a model of all negative literals contained in the clause. Also, the graph C minimally represents all models of the considered case in the sense that it is the least graph contained in all these models.
Lemma 6
(Sound and Complete Termination) Let L be a set of negative literals \(\lnot \exists (m_i,c_i)\) from \(\mathcal {C}_{C} \) where each \(m_i\) is no isomorphism. Then, C is the unique least element of \(\llbracket \exists (i_C,\wedge L)\rrbracket \) in the sense of
-
existence: C is an element of \(\llbracket \exists (i_C,\wedge L)\rrbracket \)
-
unique least: for each graph \(C'\in \llbracket \exists (i_C,\wedge L)\rrbracket \), there exists some monomorphism

The algorithm terminates at this point with conditions of the form \(\llbracket \exists (i_C,\wedge L)\rrbracket \), which cannot be broken down into multiple such conditions using a case distinction as mentioned before and which are called therefore most explicit.
Note, the proofs of these lemmas presented here are contained in Appendix.
Subsequently, we formalize the presented description of the algorithm by introducing definitions for the construction of tableaux and, for the recursive application of our steps, of nested tableaux.
6.2 Recursive construction of tableaux
Nested tableau (consisting of connected tableaux \(T_0\), ..., \(T_5\)) for the graph property \(p^{13}\). The condition used for each of the tableaux is given above it (that is, \(p^{13}\) for \(T_0\) and the corresponding openers for the other tableaux). In the middle branch of \(T_0\), we obtain \( false \) because  is reduced by \([\cdot ] \) to \( true \) by removal of the isomorphism. We extract from the nested branches ending in \(T_4\), \(T_5\), and \(T_3\) the symbolic models
is reduced by \([\cdot ] \) to \( true \) by removal of the isomorphism. We extract from the nested branches ending in \(T_4\), \(T_5\), and \(T_3\) the symbolic models  ,
,  , and
, and  , according to Definition 29. Here, \(s_2\) is a refinement of \(s_1\), according to Definition 25, and, hence, would be removed by compaction as explained in Sect. 7.4. Since \(s_1\) and \(s_3\) cover disjoint sets of graphs already, disambiguation (as explained in Sect. 7.5) does not split them up further
, according to Definition 29. Here, \(s_2\) is a refinement of \(s_1\), according to Definition 25, and, hence, would be removed by compaction as explained in Sect. 7.4. Since \(s_1\) and \(s_3\) cover disjoint sets of graphs already, disambiguation (as explained in Sect. 7.5) does not split them up further
The algorithm intuitively presented before is now formalized by means of the tableau-based reasoning method that was introduced in [27]. Regular tableaux are used to perform the splitting executed in Step 1 from above and were directly inspired by the construction of tableaux for plain FOL reasoning [22]. Then, nested tableaux are used to handle the recursive application of Step 2 from above.
Provided a condition in CNF and an empty tableau that is obtained using the initialization rule, we are using repeatedly the extension rule to construct branches of graph conditions by selecting one literal from each clause (note, a condition is unsatisfiable if it contains an empty clause) of the given condition. Then, we apply the lift rule to merge all literals that are contained in a branch into a single positive literal provided that the branch contains at least one such positive literal as a starting point.
Definition 20
(Tableaux for Graph Conditions, Open, and Closed Branches) Given a condition c in CNF over C, a tableau T for c is a finite tree whose nodes are conditions constructed using the rules below. A branch in a tableau T for c is a maximal path in T. Moreover, a branch B is closed if \( false \) is in B; otherwise, it is open. Finally, a tableau is closed if all of its branches are closed; otherwise, it is open.
-
initialization rule: A tree with a single root node \( true \) is a tableau for c.
-
extension rule: If B is a branch of a tableau for c and \(\vee S\) is a clause in c, then if \(S\ne \emptyset \) and \(S\cap B=\emptyset \), then append each element of S as a child node to the leaf of B or if \(S=\emptyset \) and \( false \notin B\), then append \( false \) as a child node to the leaf of B.
-
lift rule: if B is a branch of a tableau for c, \(\ell \) and

are in B,
 is not in B, then append \(\ell '\) as a child node to the leaf of B.
is not in B, then append \(\ell '\) as a child node to the leaf of B.
Semi-saturated tableaux are the desired results of the iterative tableaux construction where no further rules are applicable.
Definition 21
(Semi-saturated (Branch of a) Tableau) Let T be a tableau for condition c over C. A branch B of T is semi-saturated if it is either closed or
-
B is not extendable with a new node using the extension rule and
-
if \(E=\{\ell _1, \dots , \ell _n\}\) is the non-empty set of literals contained in nodes added to B using the extension rule (i.e., not by the lift rule), then there is a positive literal
 in E such that the literal in the leaf node of B is equivalent to
in E such that the literal in the leaf node of B is equivalent to 
Also, we call \(\ell \) the hook of B.
Finally, T is semi-saturated if all branches of T are semi-saturated.
Note, the set E in the definition above contains all literals that are to be integrated using the lift rule in the leaf node of B.
Following the description of the algorithm from before, we recursively construct further tableaux for the inner conditions \(c'\) of the leaf nodes  contained in the semi-saturated tableau at hand. That is, the next analysis step is to construct a tableau for condition \(c'\). The iterative (possibly nonterminating) execution of this procedure results in (possibly infinitely many) tableaux where each tableau may result in the construction of a finite number of further tableaux. This relationship between a tableau and the tableaux derived from the leaf literals of open branches results in a so-called nested tableau (see Fig. 13 for an example of a nested tableau).
contained in the semi-saturated tableau at hand. That is, the next analysis step is to construct a tableau for condition \(c'\). The iterative (possibly nonterminating) execution of this procedure results in (possibly infinitely many) tableaux where each tableau may result in the construction of a finite number of further tableaux. This relationship between a tableau and the tableaux derived from the leaf literals of open branches results in a so-called nested tableau (see Fig. 13 for an example of a nested tableau).
Definition 22
(Nested Tableaux, Opener of Tableau, Context of Tableau, Nested Branch of Nested Tableau, Semi-saturated Nested Tableau) Given a condition c over C and a partially ordered set \((I, \le , i_0)\) with minimal element \(i_0\), a nested tableau \( NT \) for c is constructed using the rules below and is, for some \(I'\subseteq I\), a familyFootnote 3 of triples \(\{\langle T_i,j,c_j\rangle \}_{i \in I'}\) that contain a tableau \(T_i\), an index \(j\in I'\), and a condition \(c_j\).Footnote 4
-
initialization rule: If \(T_{i_1}\) is a tableau for c, then the family containing only \(\langle T_{i_1}, i_0, true \rangle \) for some index \(i_1>i_0\) is a nested tableau for c and C is called context of \(T_{i_1}\).
-
nesting rule: If \( NT \) is a nested tableau for c with index set \(I'\), \(\langle T_n,k,c_k\rangle \) is in \( NT \) for index n, the literal
 is a leaf of \(T_n\), \(\ell \) is not the condition in any other triple of \( NT \), \(T_j\) is a tableau for \(c_n\), and \(j>n\) is some index not in \(I'\), then assign the triple \(\langle T_j,n,\ell \rangle \) to \( NT \) to index j, \(\ell \) is called opener of \(T_j\), and \(A_j\) is called context of \(T_j\).
is a leaf of \(T_n\), \(\ell \) is not the condition in any other triple of \( NT \), \(T_j\) is a tableau for \(c_n\), and \(j>n\) is some index not in \(I'\), then assign the triple \(\langle T_j,n,\ell \rangle \) to \( NT \) to index j, \(\ell \) is called opener of \(T_j\), and \(A_j\) is called context of \(T_j\).
A nested branch \( NB \) of the nested tableau \( NT \) is a maximal sequence of branches \(B_{i_1},\dots ,B_{i_k},B_{i_{k+1}},\dots \) of the tableaux \(T_{i_1},\dots ,T_{i_k},T_{i_{k+1}},\dots \) in \( NT \) starting with a branch \(B_{i_1}\) in the initial tableau \(T_{i_1}\) of \( NT \), such that if \(B_{i_{k}}\) and \(B_{i_{k+1}}\) are consecutive branches in the sequence, then the leaf of \(B_{i_k}\) is the opener of \(T_{i_{k+1}}\). \( NB \) is closed if it contains a closed branch; otherwise, it is open. \( NT \) is closed if all its nested branches are closed. Finally, \( NT \) is semi-saturated if each tableau in \( NT \) is semi-saturated.
The definitions for the construction of the (nested) tableaux above correspond closely to the ones in [46] as expected because they operate on the categorical level. This also implies that only the operations \( shift \) and \([\cdot ]\) occurring in the definitions above needed to be adapted (see Lemmas 1, 4).
In addition to semi-saturation, we require the notion of a saturated nested tableaux, which requires (informally) that all tableaux of the given nested tableau are semi-saturated and that hooks are selected in a fair way not postponing indefinitely the influence of a positive literal for detecting inconsistencies leading to closed nested branches.
It has been shown in [27] that the tableau-based reasoning method using nested tableaux for conditions c is sound and refutationally complete. In particular, soundness means that if we are able to construct a nested tableau where all its branches are closed, then the original condition c is unsatisfiable. Refutational completeness means that if a saturated nested tableau includes an open branch, then the original condition is satisfiable (vice versa, unsatisfiability is always determined in finite time when the saturated nested tableau includes no open branch). In fact, each open finite or infinite branch in such a nested tableau defines a finite or infinite model of the property, respectively. Incompleteness can be caused in tableaux for FOL by unfair selection of formulas (confer [22, page 117, Fig. 4] for an example where the unsatisfiable condition \(Q \wedge \lnot Q\) is treated unfairly by never being selected). In our case, the set of conditions from which a hook is to be selected in a fair way changes from one tableau to the next because conditions that are not selected are lifted into the hook resulting (possibly) in multiple different conditions. These conditions are called the successors (cf. [27]) of the conditions that are selected and lifted. To ensure refutational completeness, we ensure that the impact of a condition affects the nested branch eventually by not postponing the selection of one of these successors as a hook indefinitely. Confer to [27, p. 29] for the discussion in the original paper.
However, recall again that the usage of attributes and attribute constraints in the graphs contained in the conditions leads to situations where the employed SMT solvers cannot decide satisfiability. This has an impact on the construction of tableaux because the operation \([\cdot ]\), as explained before, employs SMT solvers to check satisfiability and it is applied in the lift rule in Definition 20.
7 Symbolic model generation
In this section, we present our symbolic model generation algorithm \(\mathcal {A} \). We first formalize the requirements from the Introduction for the generated set of symbolic models, then present our algorithm, and subsequently verify that it indeed adheres to these formalized requirements. In particular, we want our algorithm to extract symbolic models from all open finite branches in a saturated nested tableau constructed for a graph property p.
Since there are infinite saturated nested tableaux, such as the one that would be constructed for the graph property \(p^{10e}\) given in Fig. 10e, we have an incomplete procedure in the sense that the gradual construction of a nested tableau for a graph property p may not terminate. However, due to the undecidability of FOL on graphs, no alternative sound and complete algorithm could also accomplish termination. In order to be able to find a complete set of symbolic models without knowing beforehand whether the construction of a saturated nested tableau terminates, we introduce the key notions of k-semi-saturation and k-termination to reason about nested tableaux up to depth k, which are in some sense a prefix of a saturated nested tableau. Note, the verification of our algorithm, in particular for completeness, is accordingly based on induction on k. Informally, this means that by enlarging the depth k during the construction of a saturated nested tableau, we eventually find all finite open branches and thus finite models. This procedure will at the same time guarantee that we will be able to extract symbolic models from finite open branches even for the case of an infinite saturated nested tableau. For example, we will be able to extract the graph  with a single vertex from a finite open branch of the infinite saturated nested tableau for property \(p^{10e}_1\vee p^{10e}\) from Fig. 10e.
with a single vertex from a finite open branch of the infinite saturated nested tableau for property \(p^{10e}_1\vee p^{10e}\) from Fig. 10e.
7.1 Sets of symbolic models
The symbolic model generation algorithm \(\mathcal {A}\) should generate for each graph property p a set of symbolic models \(\mathcal {S}\) satisfying all requirements described in Introduction (i.e., soundness, completeness, minimal representability, compactness, and nonambiguity). A symbolic model in its most general form is a graph condition over a graph C, where C is available as an explicit component. A symbolic model then represents a (possibly empty) set of graphs (as defined in Definition 24).
Definition 23
(Symbolic Model, Remainder) If c is a condition over C according to Definition 15, then \(\langle C,c\rangle \) is a symbolic model. The condition c is called remainder of the symbolic model.
We define the graphs that are covered by a given symbolic model as follows.
Definition 24
(Graphs Covered by a Symbolic Model) \(If \langle C,c\rangle \) is a symbolic model, then  is equal to \(\llbracket \exists (i_C,c)\rrbracket \), i.e., the models of \(\exists (i_C,c)\). For a set \(\mathcal {S}\) of symbolic models, \( covered (\mathcal {S}) =\bigcup \{ covered (s) \mid s\in S\}\).
is equal to \(\llbracket \exists (i_C,c)\rrbracket \), i.e., the models of \(\exists (i_C,c)\). For a set \(\mathcal {S}\) of symbolic models, \( covered (\mathcal {S}) =\bigcup \{ covered (s) \mid s\in S\}\).
Also note, each graph G that is covered by a given symbolic model \(\langle C,c\rangle \) subsumes the graph C by means of some monomorphism as stated in the following lemma.
Lemma 7
(Existence of the Covering Monomorphism) If \(\langle C,c\rangle \) is a symbolic model and \(G\in covered (\langle C,c\rangle ) \), then there is some monomorphism  .
.
For later use, we also define when one symbolic model is entirely subsumed by another w.r.t. the covered graphs.
Definition 25
(Refinement of Symbolic Model) Given two symbolic models \(\langle C_1,c_1\rangle \) and \(\langle C_2,c_2\rangle \) s.t. \(\llbracket \exists (i_{C_2},c_2)\rrbracket \subseteq \llbracket \exists (i_{C_1},c_1)\rrbracket \), then \(\langle C_2,c_2\rangle \) is a refinement of \(\langle C_1,c_1\rangle \), written

The set of all such symbolic models \(\langle C_2,c_2\rangle \) is denoted by  .
.
Based on these definitions, we formalize the first five requirements (that is, except for explorability) from Sect. 1 to be satisfied by the sets of symbolic models returned by algorithm \(\mathcal {A}\).
Definition 26
(Soundness, Completeness, Minimal Representability, Compactness, and Nonambiguity) Let \(\mathcal {S}\) be a set of symbolic models, and let p be a graph property.
-
\(\mathcal {S}\) is sound w.r.t. p if
\( covered (\mathcal {S}) \subseteq \llbracket p\rrbracket \),
-
\(\mathcal {S}\) is complete w.r.t. p if
\( covered (\mathcal {S}) \supseteq \llbracket p\rrbracket \),
-
\(\mathcal {S}\) is minimally representable w.r.t. p if
for each \(\langle C,c\rangle \in \mathcal {S} \): \(C \models p\) and for each \(G\in covered (\langle C,c\rangle ) \) there is a mono
 ,
, -
\(\mathcal {S}\) is compact if for each \(\langle C,c\rangle \in \mathcal {S} \): \( covered (\mathcal {S}) \ne covered (\mathcal {S}-\{\langle C,c\rangle \}) \), and
-
\(\mathcal {S}\) is nonambiguous if for all distinct \(\langle C_1,c_1\rangle ,\langle C_2,c_2\rangle \in \mathcal {S} \): \( covered (\langle C_1,c_1\rangle ) \cap covered (\langle C_2,c_2\rangle ) =\emptyset \).
See Table 1 for distinguishing examples for compactness and nonambiguity when considering, for simplicity, graph part and attribute constraints in isolation. In Sect. 7.4 and Sect. 7.5, we show how both properties can be enforced, respectively. Subsequently, we discuss the generation of sets of symbolic models by algorithm \(\mathcal {A}\).
7.2 Symbolic model generation algorithm \(\mathcal {A}\)
We briefly describe the three main steps of algorithm \(\mathcal {A}\), which generates for a given graph property p a sound, complete, and minimally restrictive set of symbolic models \(\mathcal {A} (p)\) (see Fig. 14 for a visualization). The algorithm consists of three steps: the generation of symbolic models and the (optional) compaction and disambiguation of symbolic models, which are discussed in detail in Sects. 7.3, 7.4, and 7.5. Afterward, in Sect. 7.6, we discuss the explorability of the obtained set of symbolic models.
Step 1 (Generation of symbolic models in Sect. 7.3). We apply the tableau and nested tableau rules from Sect. 4 to iteratively construct a nested tableau for the given graph property p. Then, symbolic models are extracted from certain nested branches of this nested tableau that cannot be extended. Since the construction of the nested tableau may not terminate due to infinite nested branches, we construct the nested tableau in breadth-first manner and extract the symbolic models whenever possible. Moreover, to eliminate a source of nontermination, we select the hook in each branch in a fair way not postponing the successors of a positive literal that was not chosen as a hook yet indefinitely [27, p. 29] ensuring at the same time refutational completeness of our algorithm. This step ensures that the resulting set of symbolic models is sound, complete (provided termination), and minimally representable. The symbolic models extracted from the intermediately constructed nested tableau \( NT \) for growing k are denoted \(\mathcal {S}_{ NT ,k}\).
Step 2 (Compaction of sets of symbolic models in Sect. 7.4). We remove all symbolic models from \(\mathcal {S}_{ NT ,k}\) resulting in \(\mathcal {S}_{comp}\) that do not contribute to the set of graphs jointly covered thereby enforcing compactness. This second step of our algorithm \(\mathcal {A}\) preserves soundness, completeness, and minimal representability and additionally ensures compactness.
Step 3 (Disambiguation of sets of symbolic models in Sect. 7.5). We split the set \(\mathcal {S}_{comp}\) of symbolic models obtained before resulting in \(\mathcal {S}_{res}\) such that the graphs that are covered by the symbolic models from \(\mathcal {S}_{comp}\) do not overlap pairwise, thereby enforcing nonambiguity. This third step of our algorithm \(\mathcal {A}\) preserves soundness, completeness, minimal representability, and compactness and additionally ensures nonambiguity.
7.3 Generation of \(\mathcal {S}_{ NT ,k}\)
By applying a breadth-first construction, we construct nested tableaux that are for increasing k, both k-semi-saturated (i.e., all branches occurring up to index k in all nested branches are semi-saturated) and k-terminated (i.e., no nested tableau rule can be applied to a leaf of a branch occurring up to index k in some nested branch).
Definition 27
(k-Semi-saturated Nested Branches, k-Terminated Nested Branches) Given a nested tableau \( NT \) for condition c over C, if \( NB \) is a nested branch of length k of \( NT \) and each branch B contained at index \(i\le k\) in \( NB \) is semi-saturated, then \( NB \) is k -semi-saturated. If every nested branch of \( NT \) of length n is \(\mathop {min}(n,k)\)-semi-saturated, then \( NT \) is k -semi-saturated. If \( NB \) is a nested branch of \( NT \) of length n and the nesting rule cannot be applied to the leaf of any branch B at index \(i\le \mathop {min}(n,k)\) in \( NB \), then \( NB \) is k -terminated. If every nested branch of \( NT \) of length n is \(\mathop {min}(n,k)\)-terminated, then \( NT \) is k -terminated. If \( NB \) is a nested branch of \( NT \) that is k -terminated for each k, then \( NB \) is terminated. If \( NT \) is k -terminated for each k, then \( NT \) is terminated.
We define the \(k'\)-remainder of a branch, which is a refinement of the condition of that tableau that is used by the subsequent definition of the set of extracted symbolic models.
Symbolic model generation algorithm \(\mathcal {A}\) with optional components for compaction and disambiguation. In each component, the tool AutoGraph is applied to 1, n, and \(2^n-1\) graph properties, respectively. Symbolic model generation obtains the set \(\mathcal {S}_{ NT ,k}\) of symbolic models from a nested tableau \( NT \). Then, compaction (using Lemma 8) constructs n graph properties for the n symbolic models in \(\mathcal {S}_{ NT ,k} \) and removes symbolic models not contributing to the covered graphs resulting in \(\mathcal {S}_{comp}\). Finally, disambiguation (using Lemma 10) constructs \(2^n-1\) graph properties for the n symbolic models in \(\mathcal {S}_{comp} \) in each of its iterations, which disambiguates \(\mathcal {S}_{comp} \) until no further disambiguation is necessary resulting in \(\mathcal {S}_{res}\) assuming that all applications of the algorithm terminate
Definition 28
(\(k'\)-Remainder of a Branch) Given a tableau T for a condition c over C, a monomorphism  , a branch B of T, and a prefix P of B of length \(k'>0\). If R contains (a) each condition contained in P unless it has been used in P by the lift rule (being
, a branch B of T, and a prefix P of B of length \(k'>0\). If R contains (a) each condition contained in P unless it has been used in P by the lift rule (being  or \(\ell \) in the lift rule in Definition 20) and (b) the clauses of c not used by the extension rule in P (being
or \(\ell \) in the lift rule in Definition 20) and (b) the clauses of c not used by the extension rule in P (being  in the extension rule in Definition 20), then
in the extension rule in Definition 20), then

is the \(k'\) -remainder of B.
The set of symbolic models extracted from a nested branch \( NB \) is a set of certain \(k'\)-remainders of branches of \( NB \). In the example given in Fig. 13, we extracted three symbolic models from the four nested branches of the nested tableau.
Definition 29
(Symbolic Model Extracted from a Nested Branch) If \( NT \) is a nested tableau for a condition c over C, \( NB \) is a k-terminated and k-semi-saturated nested branch of \( NT \) of length \(n\le k\), B is the branch at index n of length \(k'\) in \( NB \), B is open, B contains no positive literals, then the \(k'\) -remainder of B is the symbolic model extracted from \( NB \). The set of all such extracted symbolic models from k-terminated and k-semi-saturated nested branches of \( NT \) is denoted \(\mathcal {S}_{ NT ,k} \)
Based on the previously introduced definitions of soundness, completeness, and minimal representability of sets of symbolic models w.r.t. graph properties, we are now ready to verify the corresponding results on the algorithm \(\mathcal {A}\).
Theorem 2
(Soundness) If \( NT \) is a nested tableau for a graph property p, then \(\mathcal {S}_{ NT ,k} \) is sound w.r.t. p.
Theorem 3
(Completeness) If \( NT \) is a finite terminated nested tableau for a graph property p, k is the maximal length of a nested branch in \( NT \), then \(\mathcal {S}_{ NT ,k} \) is complete w.r.t. p.
The presented algorithm \(\mathcal {A}\) does not terminate for all graph properties as can be seen from the example in Fig. 10e where the nested tableau under construction is never semi-saturated. However, the set of the symbolic models that are extracted at any point during the breadth-first construction of the (possibly infinite) nested tableau \( NT \) is a gradually extended underapproximation of the set of symbolic models \(\langle C,c\rangle \) with finite graphs C that can be extracted from \( NT \). Moreover, during such a breadth-first construction, the set of openers  of the branches that end nonterminated nested branches constitutes an overapproximation. This overapproximation encodes a lower bound on missing symbolic models in the sense that each symbolic model that may be discovered by further tableau construction (and each graph satisfying the graph property that is not covered by some symbolic model extracted already) contains some \(G_2\) as a subgraph.
of the branches that end nonterminated nested branches constitutes an overapproximation. This overapproximation encodes a lower bound on missing symbolic models in the sense that each symbolic model that may be discovered by further tableau construction (and each graph satisfying the graph property that is not covered by some symbolic model extracted already) contains some \(G_2\) as a subgraph.
Furthermore, the extracted symbolic models \(\langle C,c\rangle \) are most explicit in the sense of minimal representability because the conditions c contained in them are conjunctions of negative literals that are satisfied by C already. Of course, the graph C may still have a set of attribute constraints that is satisfiable by various variable substitutions and, therefore, SMT solvers such as Z3 may be employed to derive examples of these variable substitutions resulting in grounded graphs (see Definition 13) to obtain most explicit graphs that have a unique meaning w.r.t. the attributes as well.
Theorem 4
(Minimal Representability) If \( NT \) is a nested tableau for a graph property p, then \(\mathcal {S}_{ NT ,k} \) is minimally representable w.r.t. p.
In the next subsection, we explain how to modify sets of symbolic models extracted so far to additionally enforce compactness and nonambiguity.
7.4 Compaction of sets of symbolic models
The finite set of symbolic models \(\mathcal {S}_{ NT ,k} \) as obtained in the previous section is modified in this second step as follows to enforce compactness. This second step is intended to simplify \(\mathcal {S}_{ NT ,k}\), and hence, it may be aborted at any point, which may be necessary occasionally because compaction (and disambiguation as well) is resource intensive and possibly nonterminating.
The following lemma supports the compaction of a set of symbolic models \(\mathcal {S} \) into some subset \(\mathcal {S} '\) of it by testing an emptiness condition. This emptiness condition can be expressed by refutability of a graph property.
Lemma 8
(Compaction) A subset \(\mathcal {S} '\) of the set \(\mathcal {S} \) covers the same graphs as \(\mathcal {S} \) iff \( covered (\mathcal {S}-\mathcal {S} ')- covered (\mathcal {S} ') \,{=}\,\emptyset \) iff \(\vee \{\exists (i_C,c)\mid \langle C,c\rangle \in \mathcal {S}-\mathcal {S} '\} \wedge \lnot \vee \{\exists (i_C,c)\mid \langle C,c\rangle \in \mathcal {S} '\}\) is refutable.
We apply this lemma by testing for each symbolic model s in \(\mathcal {S}_{ NT ,k}\) whether it can be removed from \(\mathcal {S}_{ NT ,k}\) without altering the set of covered graphs. This iteration over the symbolic models may not terminate because the tableau procedure is only refutationally complete; i.e., AutoGraph is only guaranteed to terminate on unsatisfiable graph properties. The resulting set \(\mathcal {S}_{comp}\) of symbolic models is compact as desired.
Theorem 5
(Compactness) If \( NT \) is a nested tableau for a graph property p, then \(\mathcal {S}_{comp} \subseteq \mathcal {S}_{ NT ,k} \) is compact.
Note, in [46], a weaker form of compactness has been enforced, which may be called binary compactness because it considers only two symbolic models at once.
As a special case, we consider sets of symbolic models where the conditions contained in the symbolic models are equivalent to \( true \). While such sets of symbolic models (with at least two elements) are ambiguous (e.g., the union of both minimal models proves the ambiguity), we can enforce compactness as follows.
Lemma 9
(Compactness for Symbolic Models with Trivial Remainder) The set of symbolic models \(\mathcal {S} =\{\langle C_i,\wedge \emptyset \rangle \mid i\in I\}\) is compact iff for all two distinct symbolic models \(\langle C_1,\wedge \emptyset \rangle \) and \(\langle C_2,\wedge \emptyset \rangle \) contained in \(\mathcal {S} \), there is no monomorphism  .
.
We apply this lemma by removing \(\langle C_2,\wedge \emptyset \rangle \) from the set \(\mathcal {S} \) if such a monomorphism  is found. As expected, compactification using Lemma 9 is usually much faster than compaction using Lemma 8 and also terminates in each case. However, even in this simple case, we are required to find monomorphisms, which amounts to the NP-complete subgraph isomorphism problem. Nonetheless, since the handled graphs are typed and small (by construction, we generate minimal models by operating only on the graphs from the conditions rather than operating on instance graphs), the required time for finding the monomorphisms is usually not problematic.
is found. As expected, compactification using Lemma 9 is usually much faster than compaction using Lemma 8 and also terminates in each case. However, even in this simple case, we are required to find monomorphisms, which amounts to the NP-complete subgraph isomorphism problem. Nonetheless, since the handled graphs are typed and small (by construction, we generate minimal models by operating only on the graphs from the conditions rather than operating on instance graphs), the required time for finding the monomorphisms is usually not problematic.
Usually, the symbolic model generation procedure does not generate symbolic models with trivial remainder as required by Lemma 9. However, this lemma can be applied anyway in application scenarios where only the minimal models and not the remainders are of interest. Hence, replacing the remainders of the symbolic models obtained from AutoGraph by \(\wedge \emptyset \) implements, from this perspective, the selection of these minimal models and the above lemma then allows their compaction more efficiently than with Lemma 8 (before the replacement). The resulting compact set of symbolic models is then to be understood only as an enumeration of minimal models of the graph property from which the set \(\mathcal {S}_{ NT ,k}\) has been generated.
7.5 Disambiguation of sets of symbolic models
Subsequently, we enforce nonambiguity of the ultimately obtained set \(\mathcal {S}_{res} \) of symbolic models.
As a first step, we claim that a set of symbolic models is compact whenever it is nonambiguous showing that enforcing compactness can be skipped when nonambiguity is to be enforced (see Table 1 again for examples on the relationship between nonambiguity and compactness).
Corollary 1
(Nonambiguity implies Compactness) If \( NT \) is a nested tableau for a graph property p and \(\mathcal {S} \subseteq \mathcal {S}_{ NT ,k} \), then \(\mathcal {S} \) is compact if it is nonambiguous.
The following lemma demonstrates how a set of symbolic models \(\mathcal {S} \) is disambiguated by considering all combinations of symbolic models in \(\mathcal {S} \). For each such combination, which is given by a partitioning \((\mathcal {S}-\mathcal {S} ',\mathcal {S} ')\) for \(\mathcal {S} '\subsetneq \mathcal {S} \), we compute the symbolic models describing the graphs covered by \(\mathcal {S}-\mathcal {S} '\) and not covered by \(\mathcal {S} '\). The difference in this lemma can be expressed similarly as in Lemma 8.
Lemma 10
(Disambiguation) Let \(\mathcal {S} \) be some given set of symbolic models. Then, the set \( covered (\mathcal {S}) \) is equal to the set \(\bigcup \{ \bigcap \{ covered (s) \mid s\in \mathcal {S}-\mathcal {S} '\}- covered (\mathcal {S} ') \mid \mathcal {S} '\subsetneq \mathcal {S} \}\).
However, for computational complexity, we can observe that the number of cases, given by the subsets \(\mathcal {S} '\), is exponential in the size of \(\mathcal {S} \). Furthermore, for each partitioning, we obtain a condition that is a conjunction of positive and negative literals and, hence, we apply AutoGraph to each of these conditions to obtain for each set \(\mathcal {S} '\) a set of equivalent symbolic models. While the set of symbolic models generated by one of these graph properties may be ambiguous, the sets generated for the different sets of symbolic models \(\mathcal {S} '\) are nonambiguous.
For disambiguation, we recursively apply Lemma 10 to split generated symbolic models enforcing nonambiguity of the set \(\mathcal {S}_{res}\) obtained upon termination.
As for the generation of symbolic models explained in the previous subsection and the compaction procedure explained above, we may also abort the disambiguation procedure prematurely (e.g., once the designated resources are used up) still obtaining a meaningful result that is still sound, complete, minimally representable, and explorable but, due to the abortion, possibly ambiguous.
Currently, we are unable to prevent noncompactness or ambiguity of the set of symbolic models generated by algorithm \(\mathcal {A}\) on the fly (e.g., by preventing some kinds of symmetries) during the computation without a similar impact on runtime.
7.6 Exploration of sets of symbolic models
We believe that the exploration of further graphs satisfying a given property p based on the symbolic models is often desirable. In fact, \( covered (\mathcal {S}_{res})\) can be explored according to Definition 24 by selecting \(\langle C,c\rangle \in \mathcal {S}_{res} \), by generating a mono  to a new finite candidate graph G, and by deciding \(m\models c\). Then, an entire automatic exploration can proceed by selecting the symbolic models \(\langle C,c\rangle \in \mathcal {S}_{res} \) in a round-robin manner using an enumeration of the monos leaving C in each case. However, the exploration may also be guided interactively restricting the considered symbolic models and monos.
to a new finite candidate graph G, and by deciding \(m\models c\). Then, an entire automatic exploration can proceed by selecting the symbolic models \(\langle C,c\rangle \in \mathcal {S}_{res} \) in a round-robin manner using an enumeration of the monos leaving C in each case. However, the exploration may also be guided interactively restricting the considered symbolic models and monos.
For example, consider Fig. 13 where a set of two symbolic models is obtained by application of algorithm \(\mathcal {A}\) to the graph property \(p^{13}\). In an interactive exploration, we may want to decide whether the graph

also satisfies \(p^{13}\). In fact, since there is a monomorphism  from the minimal model of \(s_1\) to the graph to be tested that satisfies the remainder of \(s_1\), we derive
from the minimal model of \(s_1\) to the graph to be tested that satisfies the remainder of \(s_1\), we derive  . However, the choice of the symbolic model is also in this case relevant because any morphism
. However, the choice of the symbolic model is also in this case relevant because any morphism  from the minimal model of \(s_3\) to the graph to be tested does not satisfy the remainder of \(s_3\) thereby not allowing the derivation of
from the minimal model of \(s_3\) to the graph to be tested does not satisfy the remainder of \(s_3\) thereby not allowing the derivation of  .
.
An entire enumeration is often not feasible, since many properties (e.g., \( true \)) have infinitely many models. However, we believe that it may prove useful in many application scenarios to obtain a finitely representable guidance to construct every possible finite model if needed. The set of symbolic models represents such a guidance indeed.
As mentioned above, we will take advantage of explorability more explicitly in the future. In particular, it could be adapted to generate large sets of graphs or large, realistic graphs, for example, in the context of performance testing.
Moreover, in the context of coverage-based testing, the minimal models that we derive directly from our symbolic models are not necessarily already realistic enough to the user. This is true in particular when using attribute constraints as in the class diagram in Fig. 6 because SMT solvers such as Z3 are not designed to return satisfying models for attribute constraints that take the intended meaning of the variables such as first name or spoken languages into account. The user might want to enlarge the models (possibly interactively) and determine whether this enlargement is consistent with the specification. However, we believe that the minimal models of a condition, which we are able to generate, are most likely already reasonable test input sets.
Construction step that is implemented as a part of AutoGraph and that is used iteratively by AutoGraph to generate symbolic models where \(\ell \) is a literal, \(\ell _s\) is a list of literals, and L is a set of literals. Rule 1 stops further generation if the current result \( res \) is unsatisfiable by having a subcondition that is equivalent to \( false \). Rule 2 ensures that hooks are selected from the queue \( q\text {-}pre \) (if it is not empty) where fairness of hook selection is enforced by prioritizing and ordering the positive literals that are successors of positive literals not chosen as hooks before. Rule 3 if the queue \( q\text {-}pre \) cannot be used to select a hook and no clause remains, the nested branch is terminated and a symbolic model can be extracted by taking \(\langle G,\wedge neg \rangle \) where G is the codomain of \( cm \). Rule 4 implements the lifting rule (see Definition 20) for negative literals taken from \( neg \). Rule 5 implements the lifting rule (see Definition 20) for positive literals taken from \( q\text {-}pre \); if the morphism of the resulting positive literal is an isomorphism, as forbidden for literals in CNF, we move an equivalent condition in CNF into the current hook (also implementing the lift rule) instead of moving the literal to the queue \( q\text {-}post \) because the conversion of the positive literal into CNF may not result in a conjunction of positive literals that could be added to the queue \( q\text {-}post \). Rule 6 implements the nesting rule (see Definition 22). Rule 7 implements the extension rule (see Definition 20) constructing for each literal of a certain clause a new configuration to represent the different nested branches
8 Implementation
In this section, we introduce AutoGraph by focussing in Sect. 8.1 on the external characteristics and limitations of AutoGraph (deferring a discussion on the features until Sect. 9 where we apply AutoGraph to examples and measure the performance) and in Sect. 8.2 on the implementation details of the tableau construction procedure from algorithm \(\mathcal {A} \) presented in Sect. 6.
8.1 Functional properties of AutoGraph
We implemented the algorithm \(\mathcal {A}\) platform-independently using Java as our new tool AutoGraph. The inputs and outputs of AutoGraph (i.e., attributed graph properties, the contained attributed graph morphisms with their attributed graphs, the used attributed constraints with their algebraic specifications, the used type graphs, and the generated sets of symbolic models) are XML files satisfying a custom XSD schema [52]. We support the different use cases from Fig. 1 as follows: For an invalid query, we return an empty set of symbolic models; for a valid query, we either return only the first symbolic model generated or generate (if possible) the entire set of symbolic models (optionally executing compaction or disambiguation).
For the attributes and attribute constraints, AutoGraph uses Z3 via its Java bindings and has built-in support for the specification in Definition 30 to allow for attributes and attribute constraints over booleans, integers, and strings. Using custom algebraic specifications implementing complex functional programs is problematic for the automated reasoning of AutoGraph in general because Z3 will fail to decide satisfiability when attribute constraints are too complex. Many SMT solvers such as Z3 have, besides deciding satisfiability, also support for generating some (or a sequence) of models for satisfied properties. While AutoGraph does not compute certain grounded graphs, using this feature this may be of interest in various application domains. Finally, AutoGraph uses Z3 to simplify attribute constraints and, hence, to keep them small. This is helpful because attribute constraints are growing in the algorithm due to the operation \( shift \) where, intuitively, the union of two sets of attribute constraints is computed (actually, the variables occurring in the sets of attribute constraints of the graphs \(C_1\) and \(C_2\) in Definition 17 are renamed according to \(m_1'\) and \(m_2'\) before computing the union of the two resulting sets).
When converting a graph condition into CNF in Step 3 (see Definition 19), we need to check whether the set of attribute constraints of the contained graphs are satisfiable. However, the SMT solver may time out without returning a definite answer to such a satisfiability problem (as opposed to the oracle assumed in Sect. 6 and Sect. 7) depending on the attribute constraints. In this case, we assume satisfiability by default, which may result in the generation of symbolic models without grounded graphs (a scenario that does not occur in Sect. 7 due to the assumption of an oracle) and, in addition, it may be the reason for a nonterminating computation of AutoGraph in cases where the known unsatisfiability would have prevented further execution by removal of the considered literal (see Step 3 in Definition 19). Alternatively, we could have assumed that sets of attribute constraints are unsatisfiable when the SMT solvers do not deliver a definite result. The premature abortion of the tableau-based symbolic model generation procedure would imply that refutational completeness is no longer satisfied as not all symbolic models are generated.
For the computational complexity of the symbolic model generation algorithm, we may notice that some elementary constructions used (such as conversion to CNF using \([\cdot ] \), existence and enumeration of monomorphisms of a given type, and pair factorization as used in \( shift \)) have exponential worst case execution time. However, as explained at the end of Sect. 5, the operation \([\cdot ] \) has typically no noticeable impact and the problems of deciding existence and of enumeration of monomorphisms of a given type as well as pair factorization are applied during the execution of our algorithm, by design, only on minimal models instead of arbitrary instance graphs. Hence, we believe, also based on our tool-based evaluation in Sect. 9, that in many practical applications the runtime will be acceptable.
For decreased overall execution times, AutoGraph supports the usage of multithreading for various of its building blocks: in particular for the three high-level operations of tableau-based symbolic model generation (which is considered in more detail below), compaction, and disambiguation. For the symbolic model generation, we consider all open nested branches in parallel, and for compaction and disambiguation, we check the satisfiability of the constructed graph properties in parallel using AutoGraph.
8.2 Implementation details of AutoGraph
For limiting the memory consumption during the symbolic model generation, we discard the parts of the nested tableau that are not required for subsequent computations as follows. The implemented algorithm uses a queue (used to enforce the breadth-first construction) of configurations where every configuration represents the last branch of a nested branch of the nested tableau currently constructed (the parts of the nested tableau not given by these branches are thereby not represented in memory). The algorithm starts with a single initial configuration, applies one construction rule (see Fig. 15) inserting all results of that rule application to the queue, and terminates once the queue of configurations is empty.
The configurations contain the information that is necessary to continue the further construction of the nested tableau (also ensuring fair selection of hooks) and to extract the symbolic models whenever one is obtained.
The configurations are tuples of the form \(( inp , res , neg , q\text {-}pre , q\text {-}post , cm )\) where \( inp \) is a condition c over C in CNF (the construction of the tableau starts with an initially provided condition in CNF from which clauses are removed one after another resulting in the remaining input condition \( inp \)), \( res \) is \( \bot \) when no hook has been selected or a positive literal

into which the other literals from the branch are lifted, \( neg \) is a list of negative literals over C from clauses already handled (this list is emptied as soon as a positive literal has been chosen for \( res \)), \( q\text {-}pre \) is a queue of positive literals over C from which the first element is chosen for the \( res \) component, \( q\text {-}post \) is a queue of positive literals: Once \( res \) is a chosen positive literal

, we shift the elements from \( q\text {-}pre \) over m to obtain elements of \( q\text {-}post \), and \( cm \) is the composition of the morphisms from the openers of the nested branch constructed so far and is used to eventually obtain symbolic models (if they exist).
The implemented algorithm is started with the queue containing, for a graph property p, the unique initial configuration \(([p], \bot ,\lambda ,\lambda ,\lambda , id _{\emptyset })\) where \(\lambda \) denotes the empty list.
The construction rules return for each single configurations a finite set of such configurations and are checked in the order given where only the first applicable rule is used. The construction rules are explained for better readability directly in Fig. 15.
For soundness of the implemented algorithm based on the construction rules, reconsider Definition 28 where the set R used in the condition  recovers the desired information similarly to how it is captured in the configurations. The separation into different elements in the configurations then allows for queue handling and determinization.
recovers the desired information similarly to how it is captured in the configurations. The separation into different elements in the configurations then allows for queue handling and determinization.
9 Evaluation
In this section, we analyze the four graph database queries, which were formalized as graph properties in Figs. 2, 3, 4, and 5, by checking their validity and by generating symbolic models for them by application of AutoGraph. See Fig. 1 again for a visualization of the general workflow. Note, the algorithm \(\mathcal {A}\) implemented in AutoGraph performs the refutability check, the satisfiability check, and the model generation at once. Hence, the set of symbolic models generated by AutoGraph is sufficient (if AutoGraph terminates) to answer the three given questions of whether a graph query is valid, invalid, and how graph databases look like when the graph query can be matched.
As a first step of our evaluation, we have applied AutoGraph to the four graph properties and all binary combinations of them measuring the number of symbolic models generated as well as the duration of the generation where compaction and disambiguation have not been performed.
From the results presented in Table 2, we can draw the conclusion that all four queries are valid queries; i.e., for each of the four queries, at least one graph database exists that matches the query. Also, for the binary combinations, we derive that the queries do not exclude each other; that is, there are for each case graph databases that simultaneously match both queries. The four graph properties do not use a deep nested structure, which results in a narrow nested tableau in the beginning of the computation. This leads to the situations that some threads have no available leafs to work on in the beginning. Still, we can already observe a reasonable speedup when using multiple threads for the given graph properties.
As a second step, we can inspect the symbolic models generated. They are depicted in Fig. 16 where their remainders have been omitted for readability.
Minimal models generated by AutoGraph for the graph properties from Figs. 2, 3, 4, and 5. a The three minimal models generated for graph property \(p^{3}\) from Figure 2. b The unique minimal models generated for graph property \(p^{4}\) from Fig. 3. c The two minimal models generated for graph property \(p^{4}\) from Fig. 4. d The unique minimal model generated for graph property \(p^{6}\) from Fig. 5. e A minimal model generated by AutoGraph when requiring at least one vertex of type \(\text {Forum}\) and the satisfaction of all multiplicity constraints stated in the class diagram given in Fig. 6. These multiplicity constraints have been formalized by graph properties along the lines of Fig. 10c, d
10 Conclusion and outlook
We presented an automated reasoning approach for attributed graph properties. It includes both a refutationally complete tableau-based reasoning method and a symbolic model generation procedure. The attributed graph properties are equivalent to FOL on graphs for the graph part. Our algorithms assume the existence of an oracle for solving attribute constraints in the properties. It allows for flexible adoption of different available SMT solvers in the actual implementation. Attribute reasoning is neatly separated from graph reasoning by a dedicated logic for attributed graph properties separating both parts.
Our refutation procedure and symbolic model generation algorithm are highly integrated. Since the latter is designed to compute a complete overview of all possible models, it is at the same time able to refute a property if the overview turns out to be empty. Our symbolic model generation algorithm is innovative in the sense that it is designed to generate a finite set of symbolic models that is sound, complete (upon termination), compact, nonambiguous, minimally representable, and flexibly explorable. Moreover, the algorithm is parallelizable because every employed thread can work on one leaf of the nested tableau to be constructed. The approach is implemented in our tool, called AutoGraph.
As future work, we will attempt to determine descriptions of subsets of graph properties for which termination of AutoGraph is guaranteed. Moreover, we aim at applying, evaluating, and optimizing our approach further w.r.t. other application scenarios such as test generation for the graph database domain [7], but also to other domains such as model-driven engineering, where our approach can be used, for example, to generate test models for model transformations [5, 19, 30]. We also aim at generalizing our approach to more expressive graph properties able to encode, for example, path-related properties [29, 40, 41]. We moreover aim at supporting graph properties to state temporal properties on graphs where nodes and edges are equipped with attributes specifying their life span. Finally, the work on exploration of extracted symbolic models as well as reducing their number during tableau construction is an ongoing task. In particular, we are working on algorithms for the generation of a subset of the complete set of symbolic models that is suitably diverse. These extensions are valuable when the complete set of symbolic models is too large or its generation requires too many resources.
We would like to thank the reviewers for their thoughtful comments and efforts toward improving our manuscript.
Notes
Firstly, the algebraic specification used is given by \((\Sigma _{A_2}, EQ )\) where \(\Sigma _{A_2}\) is the signature with variables obtained for the attribution \(A_2\) of \(G_2^{ sa }\) and the signature \(\Sigma \) from \( SP \) as in Definition 10. Secondly, \(f_{AX}: AX _1\rightarrow AX _2\) is a member of \(\mathcal {V}_{\Sigma _{A_1},\Sigma _{A_2}} \) according to Definition 4.
The empty conjunction \(\wedge \emptyset \) is the base case of the inductive definition.
Formally, the family is a map that assigns one triple to each \(i\in I'\).
Intuitively, a triple \(\langle T_i,j,c_i\rangle \) is either generated by the initialization rule or is generated by the nesting rule and \(T_i\) is a tableau for a condition \(c_i\) that is the inner condition of some literal \(\ell =\exists (m,c_i)\) that is in a leaf node of the parent tableau \(T_j\) that is assigned to index j in \( NT \).
References
Abiteboul, S., Hull, R., Vianu, V. (eds.): Foundations of Databases: The Logical Level, 1st edn. Addison-Wesley Longman Publishing Co., Inc., Boston, MA (1995)
Angles, R., Arenas, M., Barceló, P., Hogan, A., Reutter, J.L., Vrgoc, D.: Foundations of modern graph query languages. CoRR, abs/1610.06264 (2016)
Angles, R., Gutierrez, C.: Survey of graph database models. ACM Comput. Surv. 40(1), 1:1–1:39 (2008)
Bak, K., Diskin, Z., Antkiewicz, M., Czarnecki, K., Wasowski, A.: Clafer: unifying class and feature modeling. Softw. Syst. Model. 15(3), 811–845 (2016)
Baudry, B.: Testing model transformations: a case for test generation from input domain models. In: Model-Driven Engineering for Distributed Real-Time Systems, Chap. 3, pp. 43–72. Wiley (2013). https://doi.org/10.1002/9781118558096.ch3
Beyhl, T., Blouin, D., Giese, H., Lambers, L.: On the operationalization of graph queries with generalized discrimination networks. In: Echahed and Minas [12], pp. 170–186
Blanco, R., Tuya, J.: A test model for graph database applications: an MDA-based approach. In: Vos Tanja E.J. Eldh, S., Prasetya, W. (eds.) Proceedings of the 6th International Workshop on Automating Test Case Design, Selection and Evaluation, A-TEST 2015, Bergamo, Italy, August 30–31, 2015, pp. 8–15. ACM (2015)
Codd, E.F.: A relational model of data for large shared data banks. Commun. ACM 13(6), 377–387 (1970)
Courcelle, B.: The expression of graph properties and graph transformations in monadic second-order logic. In: Rozenberg [44], pp. 313–400
Daniel, G., Sunyé, G., Cabot, J.: Umltographdb: mapping conceptual schemas to graph databases. In: Comyn-Wattiau, I., Tanaka, K., Song, I.-Y., Yamamoto, S., Saeki, M. (eds.) Conceptual Modeling—35th International Conference, volume 9974 of Lecture Notes in Computer Science, pp. 430–444 (2016)
Deckwerth, F.: Static verification techniques for attributed graph transformations. Ph.D. thesis, Darmstadt University of Technology, Germany (2017)
Echahed, R., Minas, M. (eds.): Graph Transformation—9th International Conference, ICGT 2016, in Memory of Hartmut Ehrig, Held as Part of STAF 2016, Vienna, Austria, July 5–6, 2016, Proceedings, volume 9761 of Lecture Notes in Computer Science. Springer (2016)
Ehrig, H., Ehrig, K., Prange, U., Taentzer, G.: Fundamentals of Algebraic Graph Transformation. Springer, Berlin (2006)
Ehrig, H., Golas, U., Habel, A., Lambers, L., Orejas, F.: \(\cal{M}\)-adhesive transformation systems with nested application conditions. Part 2: embedding, critical pairs and local confluence. Fundam. Inform. 118(1–2), 35–63 (2012). https://doi.org/10.3233/FI-2012-705
Ehrig, H., Heckel, R., Rozenberg, G., Taentzer, G., (eds.): Graph Transformations, 4th International Conference, ICGT 2008, Leicester, United Kingdom, September 7–13, 2008. Proceedings, volume 5214 of Lecture Notes in Computer Science. Springer (2008)
Ehrig, H., Mahr, B.: Fundamentals of algebraic specification 1: equations und initial semantics. In: EATCS Monographs on Theoretical Computer Science, vol. 6. Springer, Heidelberg (1985). https://doi.org/10.1007/978-3-642-69962-7
Giese, H., König, B. (eds.): Graph Transformation—7th International Conference, ICGT 2014, Held as Part of STAF 2014, York, UK, July 22–24, 2014. Proceedings, volume 8571 of Lecture Notes in Computer Science. Springer (2014)
Gogolla, M., Hilken, F.: Model validation and verification options in a contemporary UML and OCL analysis tool. In: Oberweis, A., Reussner, R.H., (eds.) Modellierung 2016, 2.-4. März 2016, Karlsruhe, volume 254 of LNI, pp. 205–220. GI (2016)
González, C.A., Cabot, J.: Test data generation for model transformations combining partition and constraint analysis. In: Ruscio, D.D., Varró, D. (eds.) Theory and Practice of Model Transformations—7th International Conference, ICMT 2014, Held as Part of STAF 2014, York, UK, July 21–22, 2014. Proceedings, volume 8568 of Lecture Notes in Computer Science, pp. 25–41. Springer (2014)
Habel, A., Heckel, R., Taentzer, G.: Graph grammars with negative application conditions. Fundam. Inform. 26(3/4), 287–313 (1996)
Habel, A., Pennemann, K.-H.: Correctness of high-level transformation systems relative to nested conditions. Math. Struct. Comput. Sci. 19(2), 245–296 (2009)
Hähnle, R.: Tableaux and related methods. In Robinson, J.A., Voronkov, A. (eds.) Handbook of Automated Reasoning (in 2 volumes), pp. 100–178. Elsevier and MIT Press (2001)
Heckel, R., Wagner, A.: Ensuring consistency of conditional graph rewriting—a constructive approach. Electr. Notes Theor. Comput. Sci. 2, 118–126 (1995)
Jackson, E.K., Levendovszky, T., Balasubramanian, D.: Reasoning about metamodeling with formal specifications and automatic proofs. In: Whittle, J., Clark, T., Kühne, T. (eds.) Model Driven Engineering Languages and Systems, 14th International Conference, MODELS 2011, Wellington, New Zealand, October 16–21, 2011. Proceedings, volume 6981 of Lecture Notes in Computer Science, pp. 653–667. Springer (2011)
Jackson, E.K., Sztipanovits, J.: Constructive techniques for meta- and model-level reasoning. In: Engels, G., Opdyke, B., Schmidt, D.C., Weil, F. (eds.) Model Driven Engineering Languages and Systems, 10th International Conference, MoDELS 2007, Nashville, USA, September 30–October 5, 2007, Proceedings, volume 4735 of Lecture Notes in Computer Science, pp. 405–419. Springer (2007)
Krause, C., Johannsen, D., Deeb, R., Sattler, K.-U., Knacker, D., Niadzelka, A.: An SQL-based query language and engine for graph pattern matching. In: Echahed and Minas [12], pp. 153–169
Lambers, L., Orejas, F.: Tableau-based reasoning for graph properties. In: Giese and König [17], pp. 17–32
Microsoft Corporation. Z3. https://github.com/Z3Prover/z3. Accessed 19 Sept 2017
Milicevic, A., Near, J.P., Eunsuk, K., Jackson, D.: Alloy*: a general-purpose higher-order relational constraint solver. In: Bertolino, A., Canfora, G., Elbaum, S.G. (eds.) 37th IEEE/ACM International Conference on Software Engineering, ICSE 2015, Florence, Italy, May 16–24, 2015, Volume 1, pp. 609–619. IEEE Computer Society (2015)
Mougenot, A., Darrasse, A., Blanc, X., Soria, M.: Uniform random generation of huge metamodel instances. In: Paige, R.F., Hartman, A., Rensink, A. (eds.) Model Driven Architecture—Foundations and Applications, 5th European Conference, ECMDA-FA 2009, Enschede, The Netherlands, June 23–26, 2009. Proceedings, volume 5562 of Lecture Notes in Computer Science, pp. 130–145. Springer (2009)
Nelson, T., Saghafi, S., Dougherty, D.J., Fisler, K., Krishnamurthi, S.: Aluminum: principled scenario exploration through minimality. In: Notkin, D., Cheng, B.H.C., Pohl, K. (eds.) 35th International Conference on Software Engineering, ICSE ’13, San Francisco, CA, USA, May 18–26, 2013, pp. 232–241. IEEE Computer Society (2013)
Orejas, F.: Attributed graph constraints. In: Ehrig et al. [15], pp. 274–288
Orejas, F., Ehrig, H., Prange, U.: A logic of graph constraints. In: Fiadeiro, J.L., Inverardi, P. (eds.) Fundamental Approaches to Software Engineering, 11th International Conference, FASE 2008, Held as Part of the Joint European Conferences on Theory and Practice of Software, ETAPS 2008, Budapest, Hungary, March 29-April 6, 2008. Proceedings, volume 4961 of Lecture Notes in Computer Science, pp. 179–198. Springer (2008)
Orejas, F., Ehrig, H., Prange, U.: Reasoning with graph constraints. Formal Asp. Comput. 22(3–4), 385–422 (2010)
Orejas, F., Lambers, L.: Symbolic attributed graphs for attributed graph transformation. ECEASST 30, (2010). https://doi.org/10.1016/j.jsc.2010.09.009
Orejas, F., Lambers, L.: Lazy graph transformation. Fundam. Inform. 118(1–2), 65–96 (2012)
Pennemann, K.-H.: An algorithm for approximating the satisfiability problem of high-level conditions. Electr. Notes Theor. Comput. Sci. 213(1), 75–94 (2008)
Pennemann, K.-H.: Resolution-like theorem proving for high-level conditions. In: Ehrig et al. [15], pp. 289–304
Pennemann, K.-H.: Development of correct graph transformation systems, Ph.D. Thesis. Dept. Informatik, Univ. Oldenburg (2009)
Poskitt, C.M., Plump, D.: Verifying monadic second-order properties of graph programs. In: Giese and König [17], pp. 33–48
Radke, H.: HR* graph conditions between counting monadic second-order and second-order graph formulas. ECEASST 61, (2013). https://doi.org/10.14279/tuj.eceasst.61.831.831
Radke, H., Arendt, T., Becker, J.S., Habel, A., Taentzer, G.: Translating essential OCL invariants to nested graph constraints focusing on set operations. In: Parisi-Presicce, F., Westfechtel, B. (eds.) Graph Transformation—8th International Conference, ICGT 2015, Held as Part of STAF 2015, L’Aquila, Italy, July 21–23, 2015. Proceedings, volume 9151 of Lecture Notes in Computer Science, pp. 155–170. Springer (2015)
Rensink, A.: Representing first-order logic using graphs. In: Ehrig, H., Engels, G., Parisi-Presicce, F., Rozenberg, G. (eds.) Graph Transformations, Second International Conference, ICGT 2004, Rome, Italy, September 28–October 2, 2004, Proceedings, volume 3256 of Lecture Notes in Computer Science, pp. 319–335. Springer (2004)
Rozenberg, G. (ed.).: Handbook of graph grammars and computing by graph transformations, vol. 1: foundations. World Scientific (1997). https://doi.org/10.1142/3303
Salay, R., Chechik, M.: A generalized formal framework for partial modeling. In: Egyed, A., Schaefer, I. (eds.) Fundamental Approaches to Software Engineering—18th International Conference, FASE 2015, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2015, London, UK, April 11–18, 2015. Proceedings, volume 9033 of Lecture Notes in Computer Science, pp. 133–148. Springer (2015)
Schneider, S., Lambers, L., Orejas, F.: Symbolic model generation for graph properties. In: Huisman, M., Rubin, J. (eds). Fundamental Approaches to Software Engineering—20th International Conference, FASE 2017, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2017, Uppsala, Sweden, April 22–29, 2017, Proceedings, volume 10202 of Lecture Notes in Computer Science, pp. 226–243. Springer (2017)
Schneider, S., Lambers, L., Orejas, F.: Symbolic model generation for graph properties (extended version). Number 115 in Technische Berichte des Hasso-Plattner-Instituts fr Softwaresystemtechnik an der Universität Potsdam. Universitätsverlag Potsdam, Hasso Plattner Institute (Germany, Potsdam), 1 edition, 2 (2017)
Schweikardt, N., Schwentick, T., Segoufin, L.: Algorithms and Theory of Computation Handbook. Chapter Database Theory: Query Languages, vol. 19, pp. 1–34. Chapman & Hall/CRC, Boca Raton (2010)
Semeráth, O., Varró, D.: Graph constraint evaluation over partial models by constraint rewriting. In: Guerra, E., van den Brand, M. (eds.) Theory and Practice of Model Transformation—10th International Conference, ICMT 2017, Held as Part of STAF 2017, Marburg, Germany, July 17–18, 2017, Proceedings, volume 10374 of Lecture Notes in Computer Science, pp. 138–154. Springer (2017)
Semeráth, O., Vörös, A., Varró, D.: Iterative and incremental model generation by logic solvers. In: Stevens, P., Wasowski, A. (eds.) Fundamental Approaches to Software Engineering—19th International Conference, FASE 2016, Held as Part of the European Joint Conferences on Theory and Practice of Software, ETAPS 2016, Eindhoven, The Netherlands, April 2–8, 2016, Proceedings, volume 9633 of Lecture Notes in Computer Science, pp. 87–103. Springer (2016)
The Linked Data Benchmark Council (LDBC). Social network benchmark. https://github.com/ldbc/ldbc_snb_docs. Accessed: 21 Aug 2017
The World Wide Web Consortium (W3C). W3c xml schema definition language (xsd) 1.1 part 1: Structures (2012)
Wood, P.T.: Query languages for graph databases. SIGMOD Rec. 41(1), 50–60 (2012)
Author information
Authors and Affiliations
Corresponding author
Appendices
Some details on AutoGraph
Definition 30
(Z3 Signature)
Furthermore, we assume sufficient operations for constructing values of \(\mathsf {string}\) as terms such as \(\mathsf {a},\dots ,\mathsf {z},\mathsf {0},\dots ,\mathsf {9},\mathsf {-},\mathsf {SPACE}:{}\rightarrow \mathsf {string} \).
Categorical preliminaries and properties of GraphsSTA
Lemma 11
(GraphsSTA: Characterization of the Monomorphisms, Epimorphisms, and Isomorphisms) A graph morphism \(f:G\rightarrow G'\) from the category GraphsSTA is a mono(morphism) (epi(morphism)) (iso(morphism)), if each of its components is injective (surjective) (bijective), respectively. And, for isomorphisms, we additionally require that the reversed implication from Definition 11 holds as well, i.e., for all \(\sigma \in \mathcal {V}_{\Sigma _{A_2},\Sigma _{A_2}} \): \(\sigma \models f_{ AX }(\varPhi _1)\) implies \(\sigma \models \varPhi _2\).
Proof
(idea) Due to the componentwise characterization.
Definition 31
(\(\mathcal {E}\)-\(\mathcal {M}\)-Factorization) Given a category, a set \(\mathcal {E}\) of epimorphisms, and a set \(\mathcal {M}\) of monomorphisms. The category has \(\mathcal {E}\)-\(\mathcal {M}\) -Factorizations, if
-
(existence) for each \(f:A\rightarrow C\) there are \((e:A\twoheadrightarrow K)\in \mathcal {E}\) and
 s.t. \(m\circ e=f\) and
s.t. \(m\circ e=f\) and -
(uniqueness) for \((e':A\twoheadrightarrow K')\in \mathcal {E}\) and
 with \(m'\circ e'=f\) there is
with \(m'\circ e'=f\) there is  with \(i\circ e=e'\) and \(m'\circ i=m\).
with \(i\circ e=e'\) and \(m'\circ i=m\).
Definition 32
(Jointly Epimorphic Morphisms [13, Definition A.16, p. 334]) Two morphisms \(e_1:A_1\rightarrow B\) and \(e_2:A_2\rightarrow B\) of a category are Jointly Epimorphic, if any two morphisms \(g,h:B\rightarrow C\) are equal whenever \(g\circ e_i=h\circ e_i\) (for each \(1\le i \le 2\)).
Pair Factorization (cf. [13, Definition 5.25, p. 122]) has the intuition that any two morphisms \(f_1\) and \(f_2\) with common codomain C coincide (in the sense of mapping to the same elements) on a well-defined subgraph K of C. That K does not include further elements (on which the two morphisms do not coincide) is expressed by stating that the morphisms \(e_1\) and \(e_2\) are jointly epimorphic and the coincidence is expressed by stating that m is a monomorphism together with the commutation.
Definition 33
(\(\mathcal {E'}\)-\(\mathcal {M}\)-Pair Factorization) For a given category, a set \(\mathcal {E'}\) of pairs \((f_1,f_2)\) of jointly epi morphisms, and a set \(\mathcal {M}\) of monomorphisms. The category has \(\mathcal {E'}\)-\(\mathcal {M}\)
-Pair Factorizations, if for each two morphisms \(f_1:A_1\rightarrow C\) and \(f_2:A_2\rightarrow C\) there are \((e_1:A_1\rightarrow K,e_2:A_2\rightarrow K)\in \mathcal {E'}\) and  s.t. \(m\circ e_i=f_i\) (for each \(1\le i\le 2\)).
s.t. \(m\circ e_i=f_i\) (for each \(1\le i\le 2\)).
Definition 34
(Binary Coproduct) A category has binary coproducts, if for every \(A_i\) (with \(1\le i\le 2\)) there are \(f_i:A_i\rightarrow C\) (for each \(1\le i\le 2\)) s.t. (the following universal property holds) for all \(g_i:A_i\rightarrow X\) there is a unique \(h:C\rightarrow X\) with \(h\circ f_i=g_i\) (for each \(1\le i\le 2\)).
Lemma 12
(GraphsSTA has Binary Coproducts)
Proof
(idea) The binary coproduct C with morphisms \(f_1\) and \(f_2\) from Definition 34 is constructed componentwise using the disjoint union, as usual.
For the category GraphsSTA, we use as \(\mathcal {E}\) the set of all epimorphisms, as \(\mathcal {M}\) the set of all monomorphisms, and as \(\mathcal {E'}\) the set of all pairs of jointly epimorphic morphisms.
Lemma 13
(GraphsSTA has \(\mathcal {E}\)-\(\mathcal {M}\)-Factorization)
Proof
(idea) The morphisms e and m, required according to Definition 31, are constructed componentwise for a morphism f.
Lemma 14
(GraphsSTA has \(\mathcal {E'}\)-\(\mathcal {M}\)-Pair Factorization)
Proof
(idea) Analogously to [13, Remark 5.26, p. 122], we construct the \(\mathcal {E'}\)-\(\mathcal {M}\)-Pair Factorizations using \(\mathcal {E}\)-\(\mathcal {M}\)-Factorizations (based on Lemma 13) and binary coproducts (based on Lemma 12).
Proofs
Proof of Lemma 2
Part1 (\(\subseteq \)).
for some q:C G
G
for some \(c\in S\)
Part2 (\(\supseteq \)).
for some \(c\in S\)
for some 
Proof of Lemma 5
Part1 (\(\subseteq \)).

for some 

for some 
Part2 (\(\supseteq \)).
for some 

Proof of Lemma 6
Part1 (C is an element).
for 
for each \(1\le i\le n\) simultaneously
there is no  such that \(q_i\models c_i\) and \(q_i\circ m_i=q\)
such that \(q_i\models c_i\) and \(q_i\circ m_i=q\)
Part2 (unique least element).
for some 
Proof of Lemma 3
Part1 (\(\subseteq \)).

for some 

for some 
also
Part2 (\(\supseteq \)).
for some 
for some 
also

Proof of Lemma 8
Part1.1 (if).
because \( covered (\mathcal {S}-\mathcal {S} ') \subseteq covered (\mathcal {S}) \)
Part1.2 (only if).
because \( covered (\mathcal {S})- covered (\mathcal {S} ') \subseteq covered (\mathcal {S}-\mathcal {S} ') \)
because \(\mathcal {S} '\subseteq \mathcal {S} \) implies \( covered (\mathcal {S} ') \subseteq covered (\mathcal {S}) \)
Part2.
Proof of Lemma 9
-
Part1 (if). Fix some \(\langle C,\wedge \emptyset \rangle \in \mathcal {S} \).
Assume for the contradiction \( covered (\mathcal {S}) = covered (\mathcal {S}-\{\langle C,\wedge \emptyset \rangle \}) \). Hence, for each \(G\in covered (\langle C,\wedge \emptyset \rangle ) \) there is some other \(\langle C',\wedge \emptyset \rangle \in \mathcal {S} \) s.t. \(G\in covered (\langle C,\wedge \emptyset \rangle ) \).
Note that \(C\in covered (\langle C',\wedge \emptyset \rangle ) \). Hence, we are able to pick some \(\langle C',\wedge \emptyset \rangle \) s.t. \(C\in covered (\langle C',\wedge \emptyset \rangle ) \).
Hence, there is a monomorphism
 .
.This is a contradiction.
-
Part2 (only if). Fix distinct \(\langle C,\wedge \emptyset \rangle \in \mathcal {S} \) and \(\langle C',\wedge \emptyset \rangle \in \mathcal {S} \).
Assume for the contradiction that
 is a monomorphism.
is a monomorphism.Hence \( covered (\langle C,\wedge \emptyset \rangle ) \subseteq covered (\langle C',\wedge \emptyset \rangle ) \).
Hence \( covered (\mathcal {S}) = covered (\mathcal {S}-\{\langle C,\wedge \emptyset \rangle \}) \).
Hence \(\mathcal {S} \) is not compact.
This is a contradiction.
Proof of Corollary 1
-
Let \(\mathcal {S} \) be nonambiguous, (sound,) complete, minimally representable.
-
We show that \(\mathcal {S} \) is compact.
-
Fix some \(\langle C,c\rangle \in \mathcal {S} \).
-
We show that \( covered (\mathcal {S}) \ne covered (\mathcal {S}-\{\langle C,c\rangle \}) \).
-
We show that \(C\in covered (\mathcal {S}) \).
From minimally representability we have that \(C\models p\).
From completeness we that \(C\in covered (\mathcal {S}) \).
-
We show that \(C\notin covered (\mathcal {S}-\{\langle C,c\rangle ) \).
Assume for the contradiction that \(\langle C',c'\rangle \in \mathcal {S}-\{\langle C,c\rangle \) such that \(C\in covered (\langle C',c'\rangle ) \).
Then, \( covered (\langle C',c'\rangle ) \cap covered (\langle C,c\rangle ) \ne \emptyset \) contradicts nonambiguity because \(\langle C',c'\rangle \ne \langle C,c\rangle \).
-
Lemma 15
(Satisfaction is a Congruence) Let \(c_1\) and \(c_2\) be conditions from \(\mathcal {C}_{C} \) such that \(\{q\mid q\models c_1\}=\{q\mid q\models c_2\}\). Then all following items are satisfied.
-
\(\{q\mid q\models \wedge (S\cup \{c_1\})\} =\{q\mid q\models \wedge (S\cup \{c_2\})\}\) for all finite \(S\subseteq \mathcal {C}_{C} \).
-
\(\{q\mid q\models \lnot c_1\} =\{q\mid q\models \lnot c_2\}\).
-
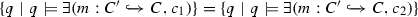 for every
for every  .
.
Proof of Lemma 15
Fix \(c_1,c_2\in \mathcal {C}_{C} \).
Assume (A) that \(\{q\mid q\models c_1\}=\{q\mid q\models c_2\}\). In each case, we show only one direction wlog.
-
Fix some \(S\subseteq \mathcal {C}_{C} \) that is finite.
Fix some
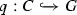 such that \(q\models \wedge (S\cup \{c_1\})\).
such that \(q\models \wedge (S\cup \{c_1\})\).Hence, \(q\models \wedge S\) and \(q\models c_1\).
From (A) we have that \(q\models c_2\).
Hence, \(q\models \wedge (S\cup \{c_2\})\).
-
Fix some
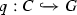 such that \(q\models \lnot c_1\).
such that \(q\models \lnot c_1\).Hence, not \(q\models c_1\).
From (A) we have that not \(q\models c_2\).
Hence, \(q\models \lnot c_2\).
-
Fix some
 .
.Fix some
 such that
such that  .
.Hence, there is some
 such that \(q\models c_1\) and \(q\circ m=q'\).
such that \(q\models c_1\) and \(q\circ m=q'\).From (A) we have that \(q\models c_2\).
Hence,
 .
.
Proof of Lemma 4
The construction steps of \([\cdot ]\) replace subterms.
By structural induction relying on Lemma 15, it is sufficient to consider how one condition \(c_1\) is replaced by another condition \(c_2\) over same graph in the sense of \(\{q\mid q\models c_1\}=\{q\mid q\models c_2\}\).
We verify for all five steps of the operation \([\cdot ]\) that the property is rephrased equivalently.
-
Step 1: The unfolding of abbreviations is sound by default.
-
Step 2: We assume that
 has been replaced by \(c_2\).
has been replaced by \(c_2\).We perform an induction on \(c_1\).
-
Case: \(c_1=\lnot c_1'\) and, hence,
 for some \(c_2'\)
for some \(c_2'\)
As induction hypothesis, we assume that \(\{q\mid q\models c_1'\}=\{q\mid q\models c_2'\}\). We have to show
 , which is the direct consequence from Lemma 15.
, which is the direct consequence from Lemma 15. -
Case: \(c_1{=}\wedge \{c_{0,1},\dots ,c_{n,1}\}\) and, hence, \(c_2{=}\wedge \{c_{0,2},\dots ,c_{n,2}\}\) for some \(c_{0,2}\), ..., \(c_{n,2}\) As induction hypothesis we assume that \(\{q\mid q\models c_{i,1}\}=\{q\mid q\models c_{i,2}\}\) (for \(0\le i\le n\)) We have to show
 , which is the direct consequence from Lemma 15.
, which is the direct consequence from Lemma 15. -
Case:
 and, hence, \(c_2=\exists (m\circ i,c_1')\)
and, hence, \(c_2=\exists (m\circ i,c_1')\)
We have to show
 , which holds directly application of Definition 16.
, which holds directly application of Definition 16.
-
-
Step 3: We show that
 if
if 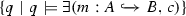 is empty. This is trivially the case because \(\{q\mid q\models \vee \emptyset \}\) is also empty.
is empty. This is trivially the case because \(\{q\mid q\models \vee \emptyset \}\) is also empty. -
Step 4: The mentioned replacement rules
\(\lnot (\wedge S){\mathop {=}\limits ^{\cdot }}\vee \{\lnot c\mid c\in S\}\),
\(\lnot (\vee S){\mathop {=}\limits ^{\cdot }}\wedge \{\lnot c\mid c\in S\}\), and
\(\lnot \lnot c{\mathop {=}\limits ^{\cdot }}c\)
are obviously sound in the sense of:
\(\{q\mid q\models lhs \}=\{q\mid q\models rhs \}\).
-
Step 5: The mentioned replacement rules
\(\wedge (S\cup \{\wedge S'\}){\mathop {=}\limits ^{\cdot }}\wedge (S\cup S')\),
\(\vee (S\cup \{\vee S'\}){\mathop {=}\limits ^{\cdot }}\vee (S\cup S')\),
\(\wedge (S\cup \{\vee S'\}){\mathop {=}\limits ^{\cdot }}\vee \{\wedge (S\cup \{c\})\mid c\in S'\}\), and
\(\vee (S\cup \{\wedge S'\}){\mathop {=}\limits ^{\cdot }}\wedge \{\vee (S\cup \{c\})\mid c\in S'\}\)
are obviously sound in the sense of:
\(\{q\mid q\models lhs \}=\{q\mid q\models rhs \}\).
Rights and permissions
About this article
Cite this article
Schneider, S., Lambers, L. & Orejas, F. Automated reasoning for attributed graph properties. Int J Softw Tools Technol Transfer 20, 705–737 (2018). https://doi.org/10.1007/s10009-018-0496-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10009-018-0496-3










 if
if 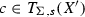 if
if  if
if  (for each
(for each  ,
, , and
, and .
. ,
, (for each
(for each 



 if
if 
 if some
if some  satisfies
satisfies 

 where
where  satisfies
satisfies 

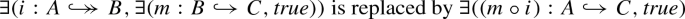
 by
by 


 is not in B, then append
is not in B, then append  in E such that the literal in the leaf node of B is equivalent to
in E such that the literal in the leaf node of B is equivalent to 
 is a leaf of
is a leaf of  ,
,


 s.t.
s.t.  with
with  with
with  .
. is a monomorphism.
is a monomorphism.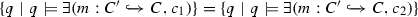 for every
for every  .
.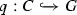 such that
such that 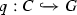 such that
such that  .
. such that
such that  .
. such that
such that  .
. has been replaced by
has been replaced by  for some
for some  , which is the direct consequence from Lemma
, which is the direct consequence from Lemma  , which is the direct consequence from Lemma
, which is the direct consequence from Lemma  and, hence,
and, hence,  , which holds directly application of Definition
, which holds directly application of Definition  if
if 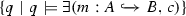 is empty. This is trivially the case because
is empty. This is trivially the case because