Parallel reachability analysis of hybrid systems in XSpeed

Abstract

Reachability analysis techniques are at the core of the current state-of-the-art technology for verifying safety properties of cyber-physical systems (CPS). The current limitation of such techniques is their inability to scale their analysis by exploiting the powerful parallel multi-core architectures now available in modern CPUs. Here, we address this limitation by presenting for the first time a suite of parallel state-space exploration algorithms that, leveraging multi-core CPUs, enable to scale the reachability analysis for linear continuous and hybrid automaton models of CPS. To demonstrate the achieved performance speedup on multi-core processors, we provide an empirical evaluation of the proposed parallel algorithms on several benchmarks comparing their key performance indicators. This enables also to identify which is the ideal algorithm and the parameters to choose that would maximize the performances for a given benchmark.

1 Introduction

Hybrid automaton (HA) is a popular formal framework for modeling and verifying safety properties in biological [7, 8] and cyber-physical systems [42]. HA combines the logical, discrete-mode-based representation of finite automata with a dynamical, continuous-state-based representation (for each mode) of differential equations. An HA is called safe, if a given set of bad states is not reachable from a set of initial states. Hence, safety can be proved in a HA through reachability analysis. Even though safety verification for HA [35] is in general an undecidable problem, there has been a great effort to introduce semi-decision procedures based on over-approximation techniques [29, 30] where the set of reachable states is generally stored as a collection of continuous sets, each of which being represented in a symbolic fashion. However, the main two challenges to be addressed within such set-based methods remain precision and scalability. In the last decade, there has been an increasing interest in developing efficient techniques for reachability analysis in HA, using different symbolical representations to compute and to approximate the reachable sets. The tool Checkmate [48] uses convex polyhedral approximations for computing reachable regions, and it has been applied in the verification of a fairly complex analog circuit design such as the delta-sigma (AI) modulator [32].

The same circuit was analyzed using the tool $d/\mathrm{d}t$ [3], which employs linear differential inclusions and non-convex polyhedra for approximating reachable sets. $\textsc {PHAVer}$ [28], which implements the HyTech algorithms [36], adopts instead polytopes to compute and to approximate the reachable sets. $\textsc {SpaceEx}$ [12, 13, 15, 27] extends the capabilities of $\textsc {PHAVer}$ [28], by implementing also the Le Guernic–Girard (LGG) method [30, 31], a very scalable reachability technique that uses support functions to compute the over-approximations by guaranteeing a certain level of precision of the reachable sets in linear HA. $\textsc {HModest}$ [34] and Hydentify [15] use, respectively, PHAVer and SpaceEx in their toolchain as back-end applications for their analysis.

Other tools, such as Flow* [17], NLTOOLBOX [19], HySAT/iSAT [25, 26], dReach [38], C2E2 [21, 23] and CORA [1], can perform the reachability analysis also on nonlinear hybrid models. Flow* [17] and NLTOOLBOX [19] use polynomial approximations for the flowpipe computation such as Taylor models [11] and Bernstein polynomials [20], respectively. HySAT/iSAT [25, 26] and dReach [38] are satisfiability checkers computing reachable sets for nonlinear hybrid systems using interval constraint-propagation techniques [45]. CORA [1] is a MATLAB toolbox integrating various matrix set representations and operations on them as well as reachability algorithms of various dynamic system classes.

All the aforementioned tools use only a single core of the CPU, and they are currently not able to scale the reachability analysis by taking advantage of the powerful parallel multi-core architectures available for free in our modern CPUs.

Related Work Although we are not aware of similar attempts in the field of hybrid systems, there has been instead a great effort in the past to develop distributed and multi-core parallel algorithms for reachability analysis in the field of explicit-state [5, 6, 22, 37, 39] and timed automata [9, 10, 16, 18] model checking.

A first generation of algorithms [5, 9, 10] was conceived to run on distributed systems consisting of several interconnected nodes, each one with its own processor and memory. The main performance bottleneck of these algorithms is generally the communication overhead required to exchange the states (yet to be explored) among the nodes. In particular, in [10] Behrmann showed that when the communication overhead is high, a random load balancing strategy may lead to an unstable workload distribution where the load of one or more nodes drops quickly to zero staying idle some of their time and causing a waste of the available computational resources. To mitigate such problem, the author proposed the use of a proportional controller with the current average load as a set point to decide, with low overhead, whether some successors states generated by a node should be redirected or not to another node. However, it is not clear whether such load balancing strategy and its relative overhead would be also beneficial for parallel algorithms running on multi-core architectures.

The increased availability of economic multi-cores CPU and many-cores GPU has lead more recently to the development of a second generation of parallel reachability analysis algorithms [6, 22, 37, 39] that can benefit of the lower communication overhead of the shared-memory systems. In these architectures, the performance depends also on the efficiency of the shared data structures used to keep track of the visited states [39] or of the states to explore [18, 37], and on the use of lockless algorithms to access these data structures avoiding mutual exclusion [18, 37]. For example, lockless shared hash tables to store visited states for multi-core reachability of timed automata were provided in [18] as an adaptation of Laarman et al. [39]. Part of our work took instead inspiration from the parallel lock-free breadth-first-search algorithm introduced by Holzmann [37] for the SPIN multi-core model checking implementation.

Our contribution We propose a suite of parallel state-space exploration algorithms that enable to scale the reachability analysis for linear continuous and hybrid automaton (HA) models of CPS by leveraging multi-core CPUs. For linear continuous models, we propose two algorithms, ParSup and Time-Slice. ParSup is an implementation of a support function-based algorithm by sampling functions in parallel. Time-Slice is an algorithm by slicing the time horizon and computing the reachable states in the time slices in parallel. Time-Slice, however, is limited on dynamics with fixed deterministic input. For HA models, we propose three algorithms, A-GJH, TP-BFS and AsyncBFS. A-GJH is an adaptation of G. J. Holzmann’s lock-free, parallel breadth-first-search algorithm [37] that was recently implemented in the SPIN model checker. We show that the adapted algorithm for HA and symbolic states has a drawback in load balancing and many CPU cores remain underutilized for certain models. For this reason, we provide TP-BFS that improves considerably the load balancing, by estimating the cost of the post-operations (both discrete and continuous), and using this estimate to balance the load by a task-level parallelization. Lastly, AsyncBFS is an asynchronous HA exploration algorithm which removes the thread synchronization overhead necessary for a breadth-first exploration. We provide an empirical evaluation of the parallel algorithms on various benchmarks on continuous and hybrid systems and demonstrate the achieved performance speedup on multi-core processors. We provide a comparison of the algorithms on the benchmarks and identify parameters to choose the ideal algorithm to draw maximum performance on any benchmark.

This work is an extension of our earlier published work [33, 46]. The additional contributions presented here are:

• We improve the Time-Slice algorithm to work for systems having singular dynamics.

• We evaluate ParSup and Time-Slice on diverse benchmarks for linear continuous systems and demonstrate its performance in comparison with the $\textsc {SpaceEx-\!LGG}$ scenario.

• We propose an asynchronous breadth-first exploration algorithm AsyncBFS for HA, in order to avoid synchronization overhead.

• We evaluate the proposed parallel HA exploration algorithms on a diverse set of hybrid systems benchmarks. We provide a comparison of the proposed algorithms on the benchmarks and identify parameters to choose the ideal algorithm to draw maximum performance on any HA.

• The reachability algorithm in the tool XSpeed is extended with fixed point computation.

XSpeed can analyze SpaceEx models using the Hyst [4] model transformation and translation tool for HA. Experiments show a significant speed up on various benchmarks using our parallel exploration algorithms, when compared to $\textsc {SpaceEx-\!LGG}$ (Le Guernic–Girard) algorithm [27, 40]. The tool and the benchmarks reported in the paper can be downloaded from http://xspeed.nitmeghalaya.in.

Paper organization The rest of the paper is organized as follows. Section 2 presents the preliminaries for the paper. In Sect. 3, we present our state-space exploration algorithms for linear continuous models. In Sect. 4, we discuss the challenges of parallel HA exploration, particularly load balancing and synchronization, and present our proposed solutions. An empirical evaluation of our algorithms is presented in Sect. 5. We conclude in Sect. 6.

2 Preliminaries

A hybrid automaton is a mathematical model of a system exhibiting both continuous and discrete dynamics. A state of a hybrid automaton is an n-tuple $(x_1,x_2,\ldots ,x_n)$ representing the values of the n continuous variables in an n-dimensional system at an instance of time.

Definition 1

A hybrid automaton is a tuple $(\mathcal {L}, \mathcal {X}, Inv, Flow, Init, \mu , \mathcal {G}, \mathcal {M})$ where:

• $\mathcal {L}$ is the set of locations of the hybrid automaton.

• $\mathcal {X}$ is the set of continuous variables of the hybrid automaton.

• $Inv: \mathcal {L} \rightarrow 2^{\mathbb {R}^n}$ maps every location of the automaton to a subset of $\mathbb {R}^n$, called the invariant of the location. An invariant of a location defines the constraint on the states within the location of the automaton.

• Flow is a mapping of the locations of the automaton to ODE equations of the form $\dot{x} = f(x), x \in \mathcal {X}$, called the flow equation of the location. A flow equation defines the evolution of the system variables within a location.

• Init is a tuple $(\ell _{init}, \mathcal {C} _{init})$ such that $\ell _{init} \in \mathcal {L}$ and $\mathcal {C} _{init} \subseteq Inv(\ell _{init})$. It defines the set of initial states of the automaton.

• $\mathcal {G} \subseteq 2^{\mathbb {R}^n}$ is the set of guard sets of the automaton.

• $\mathcal {M} \subseteq \mathbb {R}^n \rightarrow \mathbb {R}^n$ is the set of assignment maps of the automaton.

• $\mu \subseteq \mathcal {L} \times \mathcal {G} \times \mathcal {M} \times \mathcal {L}$ is the set of transitions of the automaton. A transition from a source location to a destination location in $\mathcal {L}$ may trigger when a states of the hybrid automaton lies in the guard set of the transition from $\mathcal {G}$. The map $\mathcal {M}$ of the transition transforms the state s in the source location to the new state $s'$ in the destination location. $\Box$

A reachable state is a state attainable at any time instant $0 \le t \le T$ under its flow and transition dynamics starting from an initial state in Init. The flow dynamics in a location $\ell$ evolves a state x to another state y after T time units such that $flow(x,T)=y$ and $flow(x,t) \in \textit{ Inv(} \ell$) for all $t \in [0,T]$, where flow is the solution to the flow equation of $Flow(\ell )$. Reachability analysis tools produce a conservative approximation of the reachable states of the automaton over a time horizon. Reachable states can be expressed as a union of symbolic states. A symbolic state is a tuple (loc, $\mathcal {C}$) such that $loc \in \mathcal {L}$ and $\mathcal {C} \subseteq \mathbb {R}^n$ is a continuous set. Reachability analysis algorithms require an efficient representation of the continuous set $\mathcal {C}$. In this paper, our focus will be on representing the continuous set as a compact convex set using its support function.

Definition 2

[47] Given a non-empty compact convex set $\mathcal {X} \subset \mathbb {R}^n$, the support function of $\mathcal {X}$ is a function $sup_{\mathcal {X}}:\mathbb {R}^n \rightarrow \mathbb {R}$ defined as:

$$\begin{aligned} sup_{\mathcal {X}}(\ell ) = max \{\ell \cdot x : x \in \mathcal {X} \} \end{aligned}$$

(1)

$\Box$

where $\ell \cdot x$ denotes the inner product of the vectors $\ell$, x$\in \mathbb {R}^n$. Intuitively, the support function of a convex set $\mathcal {X}$ in a direction $\ell$ defines the hyperplane given by: $\ell \cdot x = sup_{\mathcal {X}}(\ell )$ that is tangent to $\mathcal {X}$. Figure 1 shows this intuition [40]. A compact convex set $\mathcal {X}$ is uniquely determined by its support function with the following equality:

$$\begin{aligned} \mathcal {X} = \bigcap _{\ell \in \mathbb {R}^n} \{ x \in \mathbb {R}^n : \ell \cdot x \le sup_{\mathcal {X}}(\ell ) \} \end{aligned}$$

(2)

Equation 2 says that a convex set can be defined as the intersection of infinitely many halfspaces with normal $\ell \in \mathbb {R}^n$ and distance $sup_{\mathcal {X}}(\ell )$.

Definition 3

Let $\mathcal {X}$ be a non-empty compact convex set and $\mathcal {D}$ be a finite set of arbitrary directions $\ell \in \mathbb {R}^n$, called the template directions. A template polyhedral approximation of the convex set $\mathcal {X}$ is then defined as:

$$\begin{aligned} Poly_\mathcal {D} (\mathcal {X}) = \bigcap _{\ell \in \mathcal {D}}{\ell \cdot x \le sup_{\mathcal {X}}(\ell )} \end{aligned}$$

(3)

$\Box$

It is easy to see that a template polyhedral approximation of a convex set $\mathcal {X}$ is an over-approximation of $\mathcal {X}$, i.e., $\mathcal {X} \subseteq Poly_\mathcal {D} (\mathcal {X})$.

Fig. 1

Illustration of the notion of support function of a convex set $\mathcal {X}$

In Algorithm 1 [27], we show a generic reachability algorithm for hybrid automata. The algorithm maintains two data structures, Wlist and R. Wlist is the list of symbolic states waiting to be explored for reachable states, and R is the list of already visited reachable symbolic states. Wlist and R are commonly known as the waiting list and the passed list, respectively. Init is a symbolic state depicting the initial states given as an input. Wlist and R are initialized to Init and $\emptyset$, respectively, in line 2. A symbolic state S is removed from the Wlist at each iteration and explored for reachable states in line 4. The operators PostC and PostD are applied consecutively. PostC takes a symbolic state as argument and computes a conservative over-approximation of the reachable states under the continuous dynamics of the location, commonly referred as the flowpipe. The flowpipe is a symbolic state, say $R'$ which is included in R in line 5. The operator PostD is applied on $R'$ which returns a set of symbolic states under the discrete dynamics, shown as $R''$ in line 6. If $R''$ is not contained in R, it is added to Wlist for further exploration in line 8.

Fixed Point Computation A reachability algorithm is said to have reached the fixed-point solution when it can find no new reachable states. In order to reach a fixed point, we perform a containment operation. The containment operation checks whether a successor symbolic state is contained in the list of already explored states, i.e., the passed listR. When it is contained in R, it is not added to the waiting list. When a symbolic state, say s, is partially contained in R, the difference symbolic state of $s-R$ can be added to the waiting list. However, computing the exact difference of symbolic states is expensive, and therefore, tools like SpaceEx implement an approximate but cheap difference computation on symbolic states. In order to avoid an expensive difference, we choose to include a partially contained symbolic state entirely in the waiting list in our implementation. However, when a successor symbolic state is subsumed by a symbolic state in the passed list R, it is not added to the waiting list Wlist, in order to avoid duplication of work and to detect a fixed point. Currently, we do not replace symbolic states in the waiting list by a subsuming successor state. This, along with the cheap difference operation, may result in some redundant computations in our proposed algorithms. The containment operation in parallel algorithms needs to be handled carefully when the Wlist and R data structures are shared by the threads. We explain the details when we describe each of the proposed algorithms later in the text.

3 Parallel reachability analysis of continuous systems

In this section, we consider continuous linear systems with inputs and initial states. The dynamics of the systems is of the form:

$$\begin{aligned} \dot{x} = Ax(t) + u(t), u(t) \in \mathcal {U}, x(0) \in \mathcal {X} _0 \end{aligned}$$

(4)

where $x(t) \in \mathbb {R}^n$, A is a $n \times n$ matrix, $\mathcal {X} _0$, $\mathcal {U} \subseteq \mathbb {R}^n$ is the set of initial states and the set of inputs, respectively, given as compact convex sets. We assume that both the initial and the input set are given by their support function representation. The input set $\mathcal {U}$ essentially models the uncertainty in the dynamics or the control inputs to the system. We first discuss the algorithm proposed in [31] for computing reachable states using support functions. The algorithm partitions the time horizon T into discrete time steps $\delta = T/N$ with $N \in \mathbb {N}$. It computes an over-approximation of the reachable set in the time horizon by a set of convex sets represented by their support functions, as shown in Eq. 5.

$$\begin{aligned} Reach_{[0, T]}(\mathcal {X} _0) \subseteq \bigcup _{i=0}^{N-1}({\varOmega }_i) \end{aligned}$$

(5)

$Reach_{[0,T]}(\mathcal {X} _0)$ denotes the set of reachable states from the initial set $\mathcal {X} _0$, in the closed time interval [0, T]. Each convex set ${\varOmega }_i$ is an over-approximation of the set of reachable states in the time interval [$i\delta , (i+1)\delta$]. The ${\varOmega }_i$’s are given by the following relation:

$$\begin{aligned} \begin{aligned}&{\varOmega }_{i+1} = {\varPhi }_{\delta } {\varOmega }_i \oplus \mathcal {W} \\&{\varOmega }_{0} = CH(\mathcal {X} _0,{\varPhi }_{\delta } \mathcal {X} _0 \oplus \mathcal {V}) \end{aligned} \end{aligned}$$

(6)

where $\oplus$ and CH stand for Minkowski sum and convex hull operation over sets, respectively, ${\varPhi }_{\delta } = e^{\delta A}$ and $\mathcal {W}$, $\mathcal {V}$ are convex sets given as follows:

$$\begin{aligned} \begin{aligned}&\mathcal {V} = \delta \mathcal {U} \oplus \alpha \mathcal {B} \\&\mathcal {W} = \delta \mathcal {U} \oplus \beta \mathcal {B} \end{aligned} \end{aligned}$$

(7)

$\alpha , \beta$ are constants depending on $\mathcal {X} _0$, $\mathcal {U}$, $\delta$ and the matrix A of the dynamics. $\mathcal {B}$ is a unit ball in the considered norm. ${\varOmega }_0$ subsumes the reachable states in the interval [0, $\delta$], i.e., $Reach_{[0, \delta ]}(\mathcal {X} _0)$. In Eq. 6, it is computed by considering the reachable states at time $\delta$ when there is no input, given by ${\varPhi }_{\delta } \mathcal {X} _0$ and bloating it with the set $\mathcal {V}$ using the Minkowski sum operation in order to include the effect of inputs. The set $\mathcal {V}$ also additionally ensures that the convex hull of $\mathcal {X} _0$ and the bloated set ${\varPhi }_{\delta } \mathcal {X} _0 \oplus \mathcal {V}$ subsumes $Reach_{[0,\delta ]}(\mathcal {X} _0)$. The computation of the subsequent ${\varOmega }_i$s in Eq. 6 is based on the following relation:

$$\begin{aligned} Reach_{[(i+1)\delta , (i+2)\delta ]}(\mathcal {X} _0) \subseteq Reach_{[\delta ,\delta ]}({\varOmega }_i) \end{aligned}$$

(8)

where i goes from 0 to $N-2$. $Reach_{[\delta ,\delta ]}({\varOmega }_i)$ is computed by taking the reachable states at time $\delta$ when there is no input, given by ${\varPhi }_{\delta } {\varOmega }_i$ and bloating it with the set $\mathcal {W}$ using the Minkowski sum operation in order to include the effect of inputs. Template polyhedral approximation of the set ${\varOmega }_i$ can be obtained by sampling its support function in the set of template directions in $\mathcal {D}$. A template polyhedral approximation of a convex set from its support function representation makes some of the inefficient operations on support functions like the symbolic set intersection efficient. However, this efficiency comes at the expense of loss of precision of the set representation depending on the number of template directions and the choice of directions.

The algorithm considers a set of bounding directions, say $\mathcal {D}$, to sample the support functions of ${\varOmega }_i$ and obtains a set of template polyhedra $Poly_\mathcal {D} ({\varOmega }_i)$ whose union over-approximates the reachable set. The support function of ${\varOmega }_i$ is computed with the following relation obtained using the properties of support functions:

$$\begin{aligned} \begin{aligned}&sup_{{\varOmega }_{i+1}}(\ell ) = sup_{{\varOmega }_{i}}({\varPhi }_{\delta }^{T} \ell ) + sup_{\mathcal {W}}(\ell ) \\&sup_{{\varOmega }_0}(\ell ) = max \big (sup_{\mathcal {X} _0}(\ell ), sup_{X_0}({\varPhi }_{\delta }^{T}\ell ) + sup_{\mathcal {V}}(\ell )\big ) \\ \end{aligned} \end{aligned}$$

(9)

Simplification of Eq. 6 yields the following relation:

$$\begin{aligned} sup_{{\varOmega }_i}(\ell ) = sup_{{\varOmega }_0}\big (({\varPhi }_{\delta }^{t})^i \ell \big ) + \sum _{j=0}^{i-1}sup_{\mathcal {W}}\big ( ({\varPhi }_{\delta }^{t})^j \ell \big ) \end{aligned}$$

(10)

We now present two approaches to parallelize reachability algorithm for continuous systems using support functions presented in Sects. 3.1 and 3.2.

3.1 Parallel samplings over template directions

The LGG scenario implemented in SpaceEx [27] computes reachable states using support function algorithm with the provision of templates in box, octagonal and p uniform direction. Bounding box directions has 2n directions ($x_i=\pm \, 1, x_k=0, k\ne i$), whereas Octagonal has $2n^2$ directions ($x_i=\pm \, 1, x_j=\pm \, 1, x_k=0, k\ne i, k \ne j$), which gives more precise polyhedral approximations. The support function algorithm scales well for high-dimensional systems when the number of template directions are linear in the dimension n of the system. To compute finer approximations with directions quadratic in n, we trade-off scalability.

Conceptually, the support function algorithm is easy to parallelize by sampling over the template directions in parallel [31]. In our approach, we have adopted a multithreading architecture consisting of a master thread spawning a worker thread for each direction in the template $\mathcal {D}$. We refer to this parallel implementation of the support function algorithm as ParSup. The pseudocode of a master thread is shown in Algorithm 2. A shared support function matrix M having R rows and N columns is allocated to store the computed support function samples by different worker threads, where R is the number of template directions in $\mathcal {D}$ and $N = T/\delta$ is the number of iterations. An entry M(i, j) in the matrix stores the support function of ${\varOmega }_j$ in the ith direction $d_i \in \mathcal {D}$. Each worker thread is given an exclusive access to a unique row of M to store the computed support function samples, resulting in no write contention among the threads (see lines 2–4 in Algorithm 3). The master thread waits for all the worker threads to complete, populating the matrix M. After all the worker threads have finished, the master thread computes the template polytope $Poly_{\mathcal {D}}({\varOmega }_{j})$ for each convex set ${\varOmega }_{j}$, obtained from the support functions (see lines 7–9 in Algorithm 2). However, computing each template polytope $Poly_{\mathcal {D}}({\varOmega }_{j})$ is independent from one another; therefore, they can be evaluated in parallel. Finally, each computed template polytope can be stored in a unique location in $R_{approx}[j]$ represented by an array data structure comprising the reachable set.

3.1.1 Running multiple instances of GLPK

It is worth noting that when the initial set $\mathcal {X} _0$ in a location dynamics in Eq. 4 is given as a polytope, the convex sets ${\varOmega }_i$ in Eq. 6 are also polytopes. Sampling the support function of a polytope corresponds in solving a linear programming problem (LPP). For example, the support function algorithm implemented in $\textsc {SpaceEx-\!LGG}$ scenario expects an initial set $\mathcal {X} _0$ and an input set $\mathcal {U}$ to be polytopes and samples their support function using the GLPK (GNU Linear Programming Kit) library [44], an open-source and optimized linear program solver. ParSup also assumes the initial and input sets to be polytopes and uses the same library to sample the support functions. Since the multithreading architecture in ParSup proposes to sample the support functions along different directions in parallel, it corresponds to solving LPPs in parallel by the threads. We implement this by running multiple instances of the solver, one instance per thread. However, the original GLPK implementation is not thread-safe since it defines a global shared data. The shared data can be modified by the different running instances in threads to result in a race condition. To overcome this, we modify the library code by defining the shared data as thread local by allocating it from the stack. This ensures thread safety of the implementation and allows the multiple instances to solve the LPPs in parallel.

3.2 Time-sliced reachability analysis

We also explore another possible parallelization approach where we compute the reachable states at distinct time in the time horizon and treat them as initial states, from which computing independently in parallel new reachable states. Essentially, the idea is to partition the time horizon into intervals and to compute the reachable states in these intervals in parallel. The union of the reachable states in each interval will be the reachable states over the entire time horizon. We refer to this parallelization technique as Time-Slice. For load balancing, the time horizon T can be partitioned equally of size $T_p=T/N$, N being the degree of parallelization. The limitation of Time-Slice is that it requires the input set $\mathcal {U}$ to be a singleton set.

Proposition 1

Given a linear dynamics of the form $\dot{x} = Ax(t) + u(t), u(t) \in \mathcal {U}$, if the input set $\mathcal {U} =v$ is a singleton set, the set of states reachable at time $t_i=iT_p$ is defined as:

$$\begin{aligned} \mathcal {S} (t_i) = e^{AiT_p}.\mathcal {X} _0 \oplus A^{-1}\left( e^{AiT_p}-I\right) (v) \end{aligned}$$

(11)

where I is the identity matrix.

Proof

Solving the differential equation $\dot{x} = Ax(t) + u(t), u(t) \in \mathcal {U}$ gives:

$$\begin{aligned} \begin{aligned} x(t)&= e^{tA}x_0 + \int _{0}^{t} e^{(t - y)A}u(y) dy \\&= e^{tA}x_0 + \int _{0}^{t} e^{(t - y)A}v dy \\&= e^{tA}x_0 + A^{-1} (e^{At}-I)(v) \\ \end{aligned} \end{aligned}$$

When $x(0) \in \mathcal {X} _0$, we apply Minkowski sum to get:

$$\begin{aligned} \mathcal {X} (t) = e^{tA}\mathcal {X} _0 \oplus A^{-1} (e^{At}-I)(v) \end{aligned}$$

Substituting $t = i T_p$:

$$\begin{aligned} \begin{aligned} \mathcal {X} (i(T_p)) = \mathcal {S} (t_i) = e^{A(i T_p)}.\mathcal {X} _0 \oplus A^{-1}\left( e^{A (i T_p)} - I\right) (v) \end{aligned} \end{aligned}$$

$\square$

Let ${\varPhi }_1 = e^{A(i T_p)}$ and ${\varPhi }_2 = A^{-1}(e^{A (i T_p)} - I)$, the support function of the $\mathcal {S} (t_i)$ is given by:

$$\begin{aligned} sup_{\mathcal {S} (t_i)}(\ell ) = sup_{\mathcal {X} _0}\left( {\varPhi }_{1}^{T}\ell \right) + sup_{v}\left( {\varPhi }_{2}^{T}\ell \right) \end{aligned}$$

(12)

Note that if the matrix A is not invertible, we can still compute ${\varPhi }_2$ using Eq. (13) [27].

$$\begin{aligned} \left( \begin{array}{lll} {\varPhi }_1 &{}\quad {\varPhi }_2 &{}\quad {\varPhi }_3 \\ 0 &{}\quad I &{}\quad I\delta \\ 0 &{}\quad 0 &{}\quad I \\ \end{array}\right) = exp \left( \begin{array}{lll} A\delta &{}\quad I\delta &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad I\delta \\ 0 &{}\quad 0 &{}\quad 0 \end{array}\right) \end{aligned}$$

(13)

where $\delta =i T_p$, exp is matrix exponentiation function and ${\varPhi }_3 = A^{-2}(e^{A \delta } - I - I\delta )$.

The reachable states in each time interval $I_i = [iT_p,(i+1)T_p]$ starting from states $x \in S(t_i)$ are defined as $R(S_i)$ and can be computed sequentially using Eq. 6. Computation of $R(S_i)$ can also be in parallel over the template directions as proposed in Sect. 3.1.

Proposition 2

An approximation of the reachable states in time horizon T can be computed by the following relation:

$$\begin{aligned} Reach_{[0,T]}(\mathcal {X} _0) \subseteq \bigcup _{i=0}^{N-1} R(\mathcal {S} _i) \end{aligned}$$

(14)

Proof

$R(\mathcal {S} _i)$ is computed using Eq. 6 with a discretization time step $\delta$ with $\mathcal {S} _i$ as the initial set. Since $S_i$ gives the exact set of states reachable at time instant $t=iT_p$, the correctness argument shown in [31] guarantees that $Reach_{[I_i]}(\mathcal {X} _0) \subseteq R(\mathcal {S} _i)$. Therefore, we have:

$$\begin{aligned} \begin{aligned} Reach_{[0,T]}(\mathcal {X} _0)&= \bigcup _{i=0}^{N-1}Reach_{[I_i]}(\mathcal {X} _0) \subseteq \bigcup _{i=0}^{N-1}R(S_i) \\ \end{aligned} \end{aligned}$$

$\square$

In Sect. 5, we show empirically that computing the reachable states using Time-Slice sometimes produces more precise results with respect to the sequential counterpart. The approximation error in the computation of ${\varOmega }_0$ in Eq. 6 propagates in the sequential algorithm. In our algorithm, since we compute the exact reachable states at partition time points in the time horizon and re-compute ${\varOmega }_0^{t_i}$ using them, the propagation of the error in ${\varOmega }_0$ may diminish.

4 Parallel HA exploration

In this section, our focus will be on the problem of reachability analysis of hybrid systems modeled as HA. Reachability analysis of hybrid systems introduces greater challenges due to its multimodal nature, where modes signify potentially different dynamics of the system. There is switching between the system modes which is generally guarded by constraints and there can be instantaneous changes in the system states upon switching. Reachability analysis of HA presents further scopes of parallelization. We discuss some of them here.

4.1 Parallel breadth-first search

Our parallel breadth-first search (BFS) is based on the observation that in Algorithm 1, and the post-operations on the symbolic states in Wlist are independent and therefore can be potentially parallelized. In a multithreading BFS implementation, threads can compute the PostC and PostD operations in parallel on the symbolic states in Wlist. One may choose to have the data structures Wlist and R as either local to the thread or shared among the threads. Both choices have its pros and cons. In an implementation with shared Wlist and R, read and write access to the data structures must be disciplined with semaphores or locks in order to have consistency. Locking, however, incurs an additional overhead in terms of performance. On the other hand, an implementation with local copies of Wlist and R may have redundant computations since threads do not have a global view of the waiting and the passed lists, and therefore, symbolic states may be re-explored redundantly by threads. As a result, although such an implementation may not incur any locking overhead, it still may incur a performance overhead due to redundant computations. In our implementation, we propose to have a shared Wlist and R, however, with no locking overhead.

In Algorithm 4, we show how to avoid the overhead of the mutual exclusion discipline by adapting the parallel lock-free breadth-first search algorithm proposed in [37] to HA exploration. Our adapted algorithm is referred as A-GJH (Adapted Gerard J. Holzmann’s) algorithm in the paper. The algorithm uses a three-dimensional array Wlist as the data structure for storing the symbolic states to be explored (see line 3). An element of the array Wlist is a list of symbolic states. Essentially, it provides two copies of Wlist, each being a two-dimensional array of list of symbolic states. At each iteration, symbolic states are read from the Wlist[t] copy and new symbolic states are written to the $Wlist[1-t]$ copy. At the first iteration, the value of t is set to 0, and at each subsequent iteration of the main while loop (see line 36), it is re-assigned to $1-t$. In this way, the write Wlist copy becomes the read Wlist copy and vice versa, after the end of each iteration of the main loop. There are N threads, one thread per core, which computes the post-operations in parallel. All the symbolic states present in the row Wlist[t][w] are sequentially processed by the thread indexed by w (see lines 9–14). The reachable states explored by the threads using the PostC operator are accumulated in the temporary array of passed list $R'$ (see line 12). Each thread gets an access to a unique row of $R'$, and therefore, locking the data structure is not required. The synchronization at line 16 ensures that the PostC computation by the threads is complete. This is when the contents of the temporary passed list $R'$ are copied to the global passed list R (see line 18) sequentially.

A multi-threaded computation of PostD is shown in lines 20–31. The symbolic states in $R'[w]$ are sequentially processed by the thread indexed by w (see the loop at line 21). An application of the PostD operator on a symbolic state results in a list of successor symbolic states to be processed in the next iteration (see line 23). Each successor state is checked for containment in the global passed list R (see line 25). Note that here too, no locking on the passed list R is required, since all threads have only read accesses on R. When a successor state is not contained in R, it is added to the list $Wlist[1-t][w'][w]$, where $w'$ is randomly selected between 0 and $N-1$ (see line 27). This random distribution of new states across rows of $Wlist[1-t]$ is with the intention of balancing the load. Since each thread indexed at w writes to the list at $Wlist[1-t][w'][w]$, there is no write contention in $Wlist[1-t]$. When all the N threads terminate and synchronize (see line 32), the exploration of symbolic states of Wlist[t] is complete. The synchronization of threads ensures a breadth-first exploration. The algorithm terminates when there are no successor states in $Wlist[1-t]$ for further exploration or when the exploration reaches a certain depth. A proof of correctness of the algorithm is shown in Appendix.

4.2 Load balancing

The clever use of the data structures in A-GJH algorithm provides freedom from locks and a reasonable load balancing when there are sufficiently large number of symbolic states in the waiting list at each BFS iteration. At the iterations where the waiting list has a few symbolic states, A-GJH does not result in an ideal load balancing since a random distribution of the symbolic states in the waiting list may not occupy all the available of cores of the processor. For this reason, there are benchmarks for hybrid systems reachability analysis where an improper load balancing results in a low utilization of the available cores. Table 1 shows the performance and CPU utilization of A-GJH algorithm when compared to the sequential counterpart (denoted as Seq-BFS) and $\textsc {SpaceEx-\!LGG}$ scenario (denoted as SpaceEx). The results are taken on a four-core CPU, with hyperthreading disabled. It can be seen that while A-GJH running on a four-core processor provides some improvements in performance when compared to $\textsc {SpaceEx-\!LGG}$ LGG and the sequential BFS, the CPU core utilization remains very modest. The best utilization is 76% in the NAV 5 $\times$ 5 benchmark for an exploration bounded to a depth of seven, and the worst is 25% in the Bouncing ball, Platoon and TTEthernet benchmarks. In these models, there are very few symbolic states for exploration at each BFS iteration, keeping most of the CPU cores idle. A 25% CPU core utilization means that only one of the four cores is utilized by the algorithm. This says that there is, on an average, only one symbolic state in the waiting list at each iteration during the BFS of the HA. The algorithm maps the exploration of the only symbolic state to a core, keeping the other three cores idle.

Table 1 Moderate CPU utilization and performance speedup with A-GJH on a four-core machine

Fig. 2

Illustrating load balancing problem with flowpipes of varying cost. a Reachable states after two levels in depth of BFS, having four new symbolic states to explore. b Reachable states after three levels in depth of BFS

Moreover, Holzmann’s state-space exploration algorithm in SPIN is intended for explicit states in concurrent and distributed systems where states are equivalent in terms of its exploration cost. Hence, a random distribution of states to available cores balances the exploration load. This is not the case for symbolic states in HA since they can be substantially different from each other in terms of the cost of its exploration. This is illustrated on a $3 \times 3$ navigation benchmark [24] in Fig. 2. The benchmark models the motion of an object in a 2D plane partitioned as a $3 \times 3$ grid. Each cell in the grid has a width and height of one unit and has a desired velocity $v_d$. In Fig. 2, the cells are numbered from 1 to 9 and the respective desired velocities are shown with a directed vector. Note that there is no desired velocity shown in cell 3 and 7 to distinguish them from the others. Cell 3 is the target, whereas cell 7 is the unsafe region. The actual velocity of the object in a cell is given by the differential equation $\dot{v} = A(v - v_d)$, where A is a $2\times 2$ matrix. There is an instantaneous change of dynamics on crossing over to an adjacent cell. The green box is an initial set where the object can start with an initial velocity. The red region shows the reachable states under the hybrid dynamics after a finite number of cell transitions. Figure 2 shows the reachable states after two and three levels in depth of BFS exploration in Algorithm 4. There are four symbolic states, $S_1$, $S_2$, $S_3$ and $S_4$, waiting to be explored after a BFS till two levels of depth, shown in blue. The symbolic states $S_1$, $S_2$ are {1, $B_1$}, {1, $B_2$} and $S_3$, $S_4$ are {5, $B_3$} and {5, $B_4$}, respectively, where 1 and 5 are the location ids and $B_1$, $B_2$, $B_3$ and $B_4$ are the blue regions in the boundary of location with ids 1 and 4, 1 and 2, 4 and 5, 2 and 5, respectively. Algorithm 4 spawns four threads, one each to compute the flowpipe from the symbolic states. In a four core processor, this seems an ideal load division. However, observe in Fig. 2b that out of the four flowpipes, the two from $S_1$ and $S_2$ do not lead to new states since they start from the boundary of location id 1 and the dynamics pushes the reachable states outside the location invariant. This implies that the flowpipe computation cost for $S_1$ and $S_2$ is low and the two cores assigned to these flowpipe computation finish early and wait at the synchronization point until the remaining two busy cores complete. Such a situation keeps the available cores underutilized due to the idle waiting of 50% of the cores. Similarly, the cost of PostD operation also varies causing idle waiting of threads assigned to low-cost computations. Therefore, we see that an adaptation of the Holzmann’s parallel BFS to HA exploration does not always result in an ideal load balancing.

4.3 Task parallel algorithm

In the following, we propose an alternative approach to address the problem of improper load balancing in A-GJH. Our idea is to quantify the cost of the PostC operation on a symbolic state, based on the number of atomic tasks it involves. We measure the atomic tasks across all PostC operation on symbolic states during a BFS iteration as the total workload, at the present iteration. For an effective load balancing, this workload is distributed evenly between the cores of the processor by assigning nearly equal number of atomic tasks to each core. Similar tasks distribution is applied also to the computation of discrete transitions (PostD). Algorithm 5 shows this approach. Note that the notion of an atomic task is algorithm dependent and is also based on intuition. For example, in the PostC implementation using the support function algorithm, we choose a function sampling as the atomic task since we believe it is the logically non-divisible and independent task in the operation. In principle, one may further disintegrate a support function sampling into lower level tasks, though that might not be intuitive in the context of a PostC operation in HA.

In particular, the algorithm uses a shared two-dimensional array Wlist of list of symbolic states (see line 3) and a shared passed list R of symbolic states. The first dimension of size two provides two copies of Wlist, one for reading and one for writing, similar to Algorithm 4. The size of the second dimension is N and equals the number of symbolic states in Wlist waiting for exploration. Initially, N is set to one and it is modified after each iteration (see line 40). An estimate of the cost of computing a flowpipe (PostC) from a symbolic state is obtained using the function $flow\_cost$ (see line 9). After the flowpipe costs for all symbolic states in Wlist are computed, the flowpipe computations are broken into atomic tasks and inserted into a tasks list (see line 10). The atomic tasks are evenly assigned to the processor cores (see lines 12–14). The results of the atomic tasks computed in parallel are then joined together to obtain a flowpipe (see line 19). The flowpipes computed by the threads are added to the passed list R (see lines 22–24). Similar load division is carried out for PostD operation. The results of the atomic tasks for PostD are similarly joined together to obtain the successor symbolic states (see lines 26–28) computed in parallel. The successor states obtained from each flowpipe are tested for containment in R (see line 32). A successor state is added to the write list $Wlist[1-t][w]$, by a thread indexed at w (see line 33) only when it is not contained in R (see lines 31–35). This is to avoid work duplication and for fixed point detection. The exclusive access of the threads to the columns of $Wlist[1-t]$ eliminates any write contention. Note that for the containment checking at line 32, the threads do not need to acquire a lock on R since the access is only for reading. The algorithm terminates when there is no symbolic state in Wlist, or when the number of completed BFS iterations equals the preset bound. A proof of correctness of the algorithm is shown in Appendix.

In this proposed algorithm, it is important to devise an efficient method to find the cost of PostC and PostD operations, for an effective load balancing. Efficient methods and data structures for splitting the PostC and PostD operations into atomic tasks and merging the task results are important in order to ensure that the extra overhead incurred in the algorithm is not more than the gain due to parallelism. In the next section, we propose procedures to efficiently compute the cost of post-operations in a support function-based algorithm.

4.3.1 Task parallelism in support function algorithm

In this section, we show a realization of the task parallel algorithm, particularly in the support function-based algorithm discussed in Sect. 3. In the task parallel version, we consider a support function sample as the logical atomic task. The cost of a PostC computation is defined as the number of function samples required in the computation.

Definition 4

Given a time horizon T, a time discretization factor N, a set of template directions $\mathcal {D}$ and an initial symbolic state $S=(loc,\mathcal {C})$, the cost of computing the flowpipe with PostC(S) is given by $flow\_cost(S) = j.|\mathcal {D} |$ where $j = max \big \{ i \mid 0 \le i \le N \textit{ and }\forall \textit{ } 0 \le k \le i, {\varOmega }_k \vdash Inv(loc) \big \}$.

We say that a convex set ${\varOmega }\vdash Inv(loc)$ if and only if ${\varOmega }\cap Inv(loc) \ne \emptyset$. Since computing a polyhedral approximation of convex sets ${\varOmega }$ requires sampling support function in each direction of the set of template directions $\mathcal {D}$, the $flow\_cost$ essentially gives us the number of support function samplings, i.e., the atomic tasks to be completed in order to compute the flowpipe. To compute $flow\_cost$, it is necessary to find the longest sequence ${\varOmega }_0$ to ${\varOmega }_j$ satisfying the location invariant Inv(loc). Assuming polyhedral invariants, checking the invariant satisfaction can be performed using the following proposition.

Proposition 3

[41] Given a polyhedron $\mathcal {I} = \bigwedge _{i=1}^{m} \ell _{i}\cdot x \le b_i$ and a convex set ${\varOmega }$ represented by its support function $sup_{{\varOmega }}$, ${\varOmega }\vdash \mathcal {I}$ if and only if $-sup_{{\varOmega }}(-\ell _i) \le b_i$, for all $1 \le i \le m$.

A procedure to identify the largest sequence is to apply Proposition 3 to each convex set starting from ${\varOmega }_0$ iteratively until we find a ${\varOmega }_j$ such that ${\varOmega }_j \nvdash Inv(loc)$. The time complexity of the procedure is $O(m\cdot N \cdot f)$, where f is the time for sampling the support function, m is the number of invariant constraints and N is the time discretization factor. We propose a cheaper algorithm with fewer support functions samplings for a class of linear dynamics $\dot{x} = Ax(t) + u$, with u being a fixed input. Fixed input leads to deterministic dynamics allowing to compute the reachable states symbolically at any time point.

Proposition 4

Given an initial set $\mathcal {X} _0$ and dynamics $\dot{x} = Ax(t) + u$, the set of states reachable at time t is given by:

$$\begin{aligned} X(t)=e^{At}x_0 \oplus A^{-1}(e^{At}-I)(v) \end{aligned}$$

(15)

where $\oplus$ denotes Minkowski sum operator. If A is not invertible, then the expression $A^{-1}(e^{At}-I)$ can be computed using relation (13). The idea of the procedure shown in Algorithm 6 is to use a coarse time step to compute reachable states using Proposition 4 and detect an approximate time of crossing the invariant. Once the invariant crossing time is detected, similar search is followed by narrowing the time step for a finer search near the boundary of the invariant for a desired precision. The procedure is illustrated on a toy model of a counter clockwise circular rotation dynamics as shown in Fig. 3a. The model has two locations with the same dynamics but different invariants. The transition assignment maps do not modify the variables. Figure 3b illustrates the procedure. The initial set on the location is shown in blue. The red sets are the reachable images of the initial set computed at coarse time steps to detect invariant crossing, followed by computing the images at finer time steps shown in green near the invariant boundary for detecting an upper bound on the time of crossing the invariant with a desired precision. After computing this time, say $t'$, the $flow\_cost$ is obtained using Definition 4 with $j=t'/\tau$. However, the problem with the procedure is when it is possible for a reachable image to exit and re-enter the invariant within the chosen time step. In such cases, the approximation error in the time returned by the procedure can be substantial. Constant dynamics and convex invariant $\mathcal {I}$ will not have such a scenario and the approximation error on the detected time of invariant crossing can be bounded.

Theorem 1

For a class of dynamics $\dot{x} = k$ , where k is a constant, let t be the exact time when reachable states from a given initial set $\mathcal {X} _0$ violate the convex location invariant $\mathcal {I}$. Let $\delta _C$ and $\delta _F$ be the coarse and fine time steps chosen to detect approximate time $t'$ of invariant violation, then the approximation error $|t-t'| \le \delta _F$.

Proof

Constant dynamics have a fixed direction of evolution, and therefore, convexity property of the invariant set $\mathcal {I}$ ensures that the reachable states cannot exit and re-enter the invariant set. The set of reachable states at time t, $X(t) = X_0 \oplus kt$, is a convex set when $X_0$ is a convex set and can be exactly represented using its support function. Algorithm 6 samples the support function of X(t) at $\delta _F$ time steps to identify the time instant $t'$ of crossing $\mathcal {I}$, which implies $|t-t'| \le \delta _F$. $\square$

Note that the precision of the cost function only decides the quality of load balancing. It does not affect the approximation error in the resulting reachable set in Algorithm 5. Approximation guarantees of the algorithm follow from the proves in the paper [31].

Fig. 3

a A hybrid automaton of a system with rotation dynamics. b Searching time of invariant crossing with widening and narrowing time steps. The red and the green sets are computed at coarse and fine time steps, respectively

4.4 Discrete-jump cost computation

The PostD computation performs the flowpipe intersection with the guard set followed by image computation. Considering a flowpipe having sets ${\varOmega }_0$ to ${\varOmega }_j$, each of these sets is applied with intersection operation and a map for non-empty intersection. Assuming intersection and image computation as the atomic task, the cost of PostD on a flowpipe $\cup _{i=0}^{j} {\varOmega }_i$ will be j, which can be obtained from the $flow\_cost$ computation in Definition 4. The addition of the cost of post- operations for all symbolic states in the waiting list is used to uniformly distribute atomic tasks of post-operations across the cores using multithreading. Further details on the data structures and task distribution are omitted for simplicity. The task parallel version of the support function algorithm is referred as TP-BFS in the text.

4.5 Asynchronous HA exploration

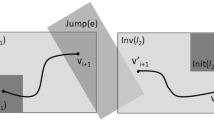
The symbolic states of a HA may also be explored by threads asynchronously, unlike in Algorithm 1. A reachability algorithm for HA can be seen as an iterative application of the PostC and PostD operators, resulting in a sequence of symbolic states. A BFS of an HA may be desirable when the goal is to obtain a shortest sequence of successive symbolic states, obtained upon PostC and PostD operations, that leads to an unsafe state. An asynchronous BFS (AsyncBFS) may be advantageous in safety checking routines, to efficiently find the reachability to an unsafe state, not necessarily via the shortest such sequence. This is because the search of an unsafe state can be performed by threads in parallel, by exploring the different sequences of symbolic states. The difference of this algorithm to the earlier proposed parallel BFS is the absence of threads synchronization at the end of each BFS iteration, incurring no waiting time delay. PostC and PostD computations for symbolic states are computed independently by threads in parallel. The AsyncBFS algorithm needs no Wlist, saving in memory, and it has a thread-shared passed list R. When new symbolic states are generated due to the application of post-operations, the algorithm creates threads for the newly generated symbolic states to compute their successors. The absence of a shared waiting list provides no global view of the symbolic states to be explored at an instance of time. This may result in threads redundantly computing reachable regions. The passed list is implemented as a lockless hash table, a data structure borrowed from [39]. The hash table structure is shown in Fig. 4. Recall from Definition 1 that a symbolic state is a tuple $(loc,\mathcal {C})$, $loc \in \mathcal {L}$ and $C \subseteq \mathbb {R}^n$. Symbolic states $(loc,\mathcal {C})$ are stored as records in the hash table, with their loc as the hash key. When a thread needs to write a symbolic state in the passed list, it can do so by only locking the hash table bucket corresponding to the key loc of the symbolic state. In this way, threads can modify the passed list without needing to lock it entirely. Figure 5 shows a pictorial view of a multi-threaded asynchronous exploration of HA. The figure shows that the symbolic state init is explored by thread T1. The k new symbolic states are explored by the threads that are spawned by T1, namely T1.1–T1.k and similarly for the symbolic states in the depths further.

Fig. 4

The structure of the hash table storing the passed list

Fig. 5

A schematic of a multi-threaded asynchronous exploration of HA

Algorithm 7 shows the details of the asynchronous BFS. R is the hash table implementation of the passed list, initially empty. It is invoked in a thread by passing the initial symbolic state s and an initial depth of zero. Application of PostC on s results in the flowpipe $R'$, a symbolic state with the same location component as in s. Therefore, a lock is acquired on R[s.loc] by the thread before inserting the flowpipe $R'$ into R[s.loc] (see lines 3–5). The PostD operation is applied on $R'$ to get a list of successor states in succ. A thread is created to explore each symbolic state in succ, that is not already contained in R, recursively (see lines 10–18). The main thread waits for the completion of its spawned threads (see line 20). The union of all the passed list R stored in the data structure L for each L[loc] gives the reachable states of the HA.

Table 2 Speedup, memory overhead and CPU utilization gain using ParSup

5 Evaluation

We have implemented the proposed parallel state space exploration algorithms in the tool XSpeed. We present an evaluation of the algorithms on various benchmarks on continuous and hybrid systems. The tool and the benchmarks reported in the paper can be downloaded from http://xspeed.nitmeghalaya.in. We make a performance comparison with the $\textsc {SpaceEx-\!LGG}$ (Le Guernic– Girard) scenario [27] and with a sequential implementation of the support function-based algorithm in [31], which is referred as SeqSup in the text.

5.1 Evaluation on continuous systems

In the following, we provide a brief description of the benchmarks we have used to test and evaluate the ParSup and Time-Slice algorithm.

Five-Dimensional System We consider a five- dimensional linear continuous system as a benchmark from [29]. The dynamics of the system is of the form $\dot{x} = A x(t) + u(t)$, where $u(t) \in \mathcal {U}$. Since we require the inputs set $\mathcal {U}$ to be a singleton set for our parallel state space exploration algorithm, we consider $\mathcal {U}$ = (0.01, 0.01, 0.01, 0.01, 0.01). We consider the initial set $\mathcal {X} _0$ as a hyperbox of side 0.02 centered at (1, 0, 0, 0, 0). For the matrix A, the reader may refer to [29].

Vehicle Platoon This benchmark is proposed in [43] to evaluate reachability analysis methods and tools for continuous and hybrid systems. It models a platoon of three moving vehicles and a leader. The vehicles communicate with each other, its relative distance, velocity and acceleration w.r.t. the vehicle ahead. The state variables of the model are [$e_1$, $v_1$, $a_1$, $e_2$, $v_2$, $a_2$, $e_3$, $v_3$, $a_3$], where $e_i$, $v_i$ and $a_i$ denote the relative distance, the relative velocity and the relative acceleration of vehicle i to its successor. The dynamics of the system is defined as $\dot{x}= A x(t) + B a_L$, where A is a constant dynamics matrix, B is a constant input matrix and $a_L$ is the acceleration of the leader vehicle as an uncertain input. The bound on the uncertainty in acceleration is $a_L \in [-9,1]$. The goal is to verify that the relative distance $e_i$ between the vehicles keeps within the safety limits. The effect of loss of communication between the vehicles can be modeled as an hybrid automaton. The model of the system with no loss of communication is purely continuous. We provide results here on the continuous model, assuming no loss of communication.

Helicopter Controller To evaluate the performance on high-dimensional systems, we consider the benchmark of Helicopter Controller from [27, 49]. This models the controller of a Westland Lynx military Helicopter with 8 continuous variables. The controller is a 20 variables LTI system and the control system having 28 variables in total. We consider an initial set $\mathcal {X} _0$ to be a hyperbox and the input set $\mathcal {U}$ to be the origin {0}.

Fig. 6

An illustration of parallel state-space exploration in sliced time horizon. a Reachable states computed by individual threads in 0.5 time unit. b Reachable states computed by individual threads in 0.75 time unit. c Reachable states computed by individual threads in 1 time unit

Fig. 7

Reachable state space of the state vector [$x_8$, time] of the Helicopter model is shown (green by Time-Slice and red by SeqSup). Time-Slice shows more precise results than the sequential counterpart. a 16 slices. b 64 slices. c 1000 slices

Building The benchmarks models the 8 floors of the Los Angeles University building, where each floor has three degrees of freedom [2]. We consider three reduced order models with 7, 17 and 25 state variables. The reduced order models have lower dimension than the original model of 48 state variables, but they retain the characteristics of the original model. The system follows affine dynamics $\dot{x} = A x(t) + B u(t)$, $u(t) \in \mathcal {U}$. The uncertain input $\mathcal {U}$ is the set of values in [0.8, 1].

Fig. 8

Performance speedup using Time-Slice w.r.t. the sequential algorithm and SpaceEx-LGG. aTime-Slice versus SeqSup. bTime-Slice versus $\textsc {SpaceEx-\!LGG}$

Table 2 shows the performance speedup, memory overhead and the gain in CPU utilization with ParSup in Sect. 3.1. The speedup w.r.t SpaceEx and the sequential implementation (SeqSup) is separately shown in the table. The memory overhead column shows the memory in excess used in ParSup w.r.t. SeqSup. The gain in CPU utilization is computed as (CPU utilization of ParSup minus CPU utilization of SeqSup). For instance, the CPU utilization of the first benchmark (Buildr-6) using ParSup and SeqSup are 81.49 and 12.41%, respectively, resulting in a total gain of 69.08%. The experiments were performed on i7-4770, 3.40 GHz, 4 cores, hyperthreading enabled processor with 8 GB RAM. The results are an average of 10 runs over a time horizon of 20 units and a time step of 0.001 s in box template directions. A maximum speedup of $13.03\times$, $3.21\times$, $7.80\times$ and $5.87\times$ is observed for the Building, Five-Dimensional System, Platoon and Helicopter Controller benchmarks, respectively, when compared to the $\textsc {SpaceEx-\!LGG}$ algorithm. The gain in CPU utilization shows how our parallel algorithm exploits the cores of the processor effectively with a reasonable memory overhead due to thread management.

Figure 6 illustrates our idea of parallel exploration by slicing the time horizon. The figure shows that a time horizon of 5 units is sliced into five intervals each of size 1 unit. Five threads compute the reachable sets in parallel starting from initial sets $\mathcal {S} (t=0)$, $\mathcal {S} (t=1)$, $\mathcal {S} (t=2)$, $\mathcal {S} (t=3)$ and $\mathcal {S} (t=4)$. Figure 7 shows the gain in precision in the Helicopter Controller model in a time horizon of 10 units, with box template directions and a time step of $1e-3$, for partition sizes of 16, 64 and 1000, respectively. The algorithm shows a performance gain of $1.5\times$ compared to SeqSup by partitioning the time horizon into 16 intervals. However with 64 and 1000 partitions, the performance degrades without any considerable gain in precision.

Figure 8 shows the performance speedup by Time-Slice with varying partition size in comparison with SeqSup and $\textsc {SpaceEx-\!LGG}$ in a time horizon of 20 units, time step of $1e{-}3$, box template directions. We show that selecting the right partition size is important to obtain the best performance. Partitioning beyond a limit may result in better precision but degrades the performance due to the overhead of parallelization. We observe that the best partition size is related to the number of cores in the processor. In our experiments, the best partition size shows to be around 8, which is the same as the number of parallel threads (4 $\times$ 2) in a hyperthreading enabled quad core processor.

Fig. 9

HA model of a switch (CM1) and an end system (SM3) of a fault-tolerant Time-Triggered Ethernet

5.2 Evaluation on hybrid systems

We present an evaluation of the A-GJH, TP-BFS and the AsyncBFS algorithms on hybrid systems benchmarks. We implement A-GJH and TP-BFS with multithreading using the OpenMP compiler directives and the AsyncBFS algorithm using the standard thread class in C++. We evaluate on a 12 core Intel Xeon(R) CPU E5-2670 v3, 2.30 GHz, hyperthreading disabled processor with 62 GB RAM. We first provide a brief description of the hybrid systems benchmarks that we have used for the evaluation.

Navigation The navigation benchmark is described in Sect. 4.2. We consider here a variant of the navigation benchmark [12]. The variant adds a non-deterministic disturbance to the position dynamics, $\dot{x}=v+u$, $\dot{v}=A(v - v_d)$, $u_{min} \le u \le u_{max}$. Moreover, some of the transitions are blocked to model obstacles between certain grids. The size of the problem instances varies from 400 to 900 locations. The Nav01 and Nav02 instances have 400 locations, whereas Nav03–Nav09 and Nav10–Nav15 instances have 625 and 900 locations, respectively. These benchmarks are suitable for evaluating the performance of our parallel exploration algorithms since they contain many HA locations.

Vehicle Platoon This benchmark extends the one described in Sect. 5.1 with the assumption that the communication between the vehicles may get lost and get restored non-deterministically. The dynamics of the system varies in the communicating and non-communicating modes, making it a hybrid system[43].

TTEthernetTime-Triggered Ethernet (TTEthernet) is a HA model of a clock synchronization algorithm in a fault-tolerant network configuration consisting of switches and end systems [14]. The end systems and switches communicate with each other in order to have the local clocks of the end systems synchronized. The maximal clock drift between any two end systems is observed, defined as the precision of the synchronization algorithm. Safety property of the fault-tolerant clock synchronization algorithm is defined by providing bounds on the maximal clock drift. The benchmark is scalable by including as many switches and end systems. We consider a network with two switches and five end systems. Figure 9 shows the HA model of a switch and an end system only. The switches are denoted as CMs and the end systems as SMs in the HA. The automaton CM1 consists of the real variables x, the local clock with rate 1, and cm1 which stores the data particular to the clock synchronization algorithm. The automaton SM3 consists of the real variables sm3, the local clock with rate 1 and drift3 which ranges from $-\,1e{-}3$ to $1e{-}3$, describing the absolute value of the maximum clock drift in the SM. The communication between the CMs and SMs is modeled by transitions in the HA with synchronization labels as snd and sync. The value of the parameter delay is considered as 20.

Filtered Oscillator This is a switched oscillator system with a series of first-order filters. The oscillator has two variables, x and y with an affine dynamics such that x, y oscillate between two equilibria. The dynamics of a filter reduces the oscillation amplitude of the output variable x. The HA model consists of four locations, each having the dynamics to reach one of the two equilibria. In addition, all the locations have the same filtering dynamics. The guards of the HA are shown by the blue lines in Fig. 10, which are at the boundary of the location invariants. Addition of filters in series further diminishes the oscillation amplitude x. The number of filters in series is a parameter, giving a $k+2$-dimensional oscillator system with k filters. To test the performance scalability with increasing dimensions, we run our algorithms on systems having no filter (Oscillator), 4 filters (F-Osci4), 8 filters (F-Osci8), 16 filters (F-Osci16) and 32 filters (F-Osci32), respectively.

Fig. 10

Reachable state space of a Filtered Oscillator in depth 4. The blue lines show the switching planes

Fig. 11

A speedup comparison of sequential BFS, A-GJH, TP-BFS and AsyncBFS w.r.t. $\textsc {SpaceEx-\!LGG}$ on 4, 6 cores. a Speedup comparison on 4 cores. b Speedup comparison on 6 cores

Fig. 12

A speedup comparison of sequential BFS, A-GJH, TP-BFS and AsyncBFS w.r.t. $\textsc {SpaceEx-\!LGG}$ on 8, 12 cores. a Speedup comparison on 8 cores. b Speedup comparison on 12 cores

Fig. 13

A speedup comparison of parallel algorithms w.r.t. the sequential version on 4, 6, 8 and 12 cores. a Nav01. b Nav10. c Nav15. d Platoon. e TTEthernet. f 16th order Filtered Oscillator

In Figures 11 and 12, we report the performance speedup of the proposed algorithms w.r.t. SpaceEx (LGG) scenario on 4, 6, 8 and 12 cores CPU, respectively. A comparison of speedup of our proposed parallel algorithms w.r.t. the sequential implementation is shown in Fig. 13. The results for the navigation instances are for a local time horizon of 40 units in each HA location. The time horizon for the Filtered Oscillator, Platoon and TTEthernet models are set to 10, 20 and 500 units, respectively, in each HA location. The time step for the experiments on the Filtered Oscillator models is $1e{-}4$, and it is $1e{-}3$ for the TTEthernet and Platoon models, $1e{-}2$ for navigation instances 1–12 and 0.005 unit for navigation instances 13–15, respectively. All flowpipe computations are using the box template directions. For performance comparison, the parameters in $\textsc {SpaceEx-\!LGG}$ and XSpeed are set to similar values. The performance on reaching a fixed point is compared. The clustering and set-aggregation parameter is set as 100 and thull in $\textsc {SpaceEx-\!LGG}$. XSpeed performs similar clustering and set aggregation. In the TTEthernet model, a fixed point is not found in both the tools. For a comparison on the TTEthernet model, we compute the reachable states bounded by a depth of 11 levels of BFS in XSpeed. We count the number of post-operations for this depth in XSpeed and apply the same number of post-operations in $\textsc {SpaceEx-\!LGG}$ using the iter-max parameter. The results show that our proposed parallel algorithms perform better than the sequential counterpart and $\textsc {SpaceEx-\!LGG}$ on all the benchmarks. The performance also automatically increases with the increase in the number of cores in the processor.

Table 3 Average symbolic states in the waiting list-AvgW

Fig. 14

Comparison of memory, CPU utilization and speedup of the proposed algorithms A-GJH, TP-BFS and AsyncBFS w.r.t. the sequential BFS algorithm on a $3\times 3$ navigation benchmark. a Memory. b CPU utilization. c Performance speedup

5.3 Discussion

We observe that the performance of A-GJH, TP-BFS and AsyncBFS is related to the average number of symbolic states in the waiting list during the HA exploration. We define average waiting symbolic states = $(\sum _{i=1}^{k} S_i)/k$, where $S_i$ denotes the number of symbolic states in the waiting list after i levels of exploration during a BFS. We refer this indicator as AvgW. Since the key idea in A-GJH and AsyncBFS is to explore the symbolic states in the waiting list in parallel, the AvgW provides a measure of the degree of parallelism in the model. Note that although AsyncBFS is asynchronous and does not follow a breadth-first search, AvgW still gives a measure of the degree of parallelism that AsyncBFS can exploit.

Remark 1

The AvgW depends on the HA model, the reachability algorithm and its parameters.

The AvgW for the benchmarks using the BFS algorithm in XSpeed with the standard parameter options is shown in Table 3. Our first observation from Figs. 11 and 12 is that the performance speedup in models having high AvgW is generally greater than the models with low AvgW. This is intuitive and says that the parallel exploration algorithms results in greater speedup on models having a larger degree of parallelism. Our second observation is that the TP-BFS algorithm gives better performance speedup than the other two parallel algorithms, on models with low AvgW. It can be verified on the Filtered Oscillator, TTEthernet and Platoon models, all of which have AvgW of 1. In these models, A-GJH, AsyncBFS does not enhance the performance of the sequential counterpart since there is no scope of parallel exploration of symbolic states in the waiting list. On the other hand, TP-BFS disintegrates the PostC and PostD operations over a symbolic state into atomic tasks and executes them in parallel on the CPU cores. Therefore, it shows a performance speedup even on models with AvgW of 1.

Figures 11 and 12 also show that for models with AvgW greater than 1, AsyncBFS displays the maximum speedup in some models, whereas TP-BFS shows maximum speedup in the other models. We observe that the AvgW of these benchmarks on the BFS algorithm in XSpeed with the chosen parameters is not very high. In order to understand the relation between the algorithms performance to AvgW, we conducted further experiments on models by varying the $\textit{AvgW}$. In order to have high $\textit{AvgW}$ on models, we disable the set-aggregation parameter in the PostD operation in XSpeed. In a PostD operation, the convex sets of the flowpipe that intersects with the guard are identified, followed by the application of transition assignment operation. When the set-aggregation parameter is enabled, the resulting convex sets are aggregated into a few convex sets by the aggregation method. Such an aggregation results in fewer flowpipe computations in the following BFS iterations. However, this operation introduces approximation error in the computed reachable set. When set aggregation is disabled in PostD, every guard intersected and transformed convex set, which is not already contained in the passed list, is added to the waiting list. This increases the AvgW of the model and incurs an additional performance penalty. Therefore, the set-aggregation parameter of a reachability algorithm allows to tune the accuracy versus performance trade-off. We considered an instance of the navigation benchmark with 625 locations and disabled the set aggregation in the PostD operation in order to increase the number of symbolic states in the waiting list. We observe that with no set aggregation in XSpeed, the number of threads in the AsyncBFS algorithm increased rapidly, with an increase in the exploration levels. The algorithm consumed the memory of the experimenting system just in exploring states till three levels of BFS and did not terminate the execution even after one hour. The sequential BFS terminated exploring the same depth with 85,510 symbolic states in 287.67 s and the A-GJH algorithm explored the same in 56.80 s. However with set aggregation enabled, an average of 215 symbolic states were explored till depth six and the execution completed in 1.23, 0.43, 0.40 and 0.38 s by the sequential BFS, A-GJH, TP-BFS and AsyncBFS algorithms, respectively. We further perform an experiment on a smaller instance of the navigation benchmark (9 locations) by increasing the exploration depth and with the set aggregation disabled. Figure 14 shows the performance speedup, memory and CPU utilization of all the algorithms with varying AvgW on the horizontal axis. Along the horizontal axis, the AvgW is shown for increasing levels of BFS exploration, from left to right. In Fig. 14a, it is evident that the memory overhead of AsyncBFS grows rapidly with increasing AvgW. We observe that the A-GJH algorithm performs better than the other algorithms when the AvgW is sufficiently larger than the number of available cores, as illustrated in Fig. 14c. AsyncBFS performs better than the others till a certain exploration depth d. Approximately $\textit{AvgW}^d$ threads are spawned by the algorithm in a d depth exploration. Therefore, for models with high degree of parallelism, the number of threads in AsyncBFS grows rapidly with an increase in the exploration depth. This in turn increases the memory consumption and other thread resources in the system. However, the absence of thread synchronization overhead keeps it a viable option to draw performance on models with not very high AvgW, for small depths of exploration. Figure 14b shows that all the proposed parallel algorithms display more than 90% CPU utilization when AvgW is high, far better than 20% CPU utilization in the sequential counterpart.

6 Conclusion

We introduce a suite of two parallel state-space exploration algorithms, ParSup and Time-Slice for linear continuous systems and three parallel state-space exploration algorithms, A-GJH, TP-BFS and AsyncBFS for HA models. ParSup and Time-Slice show considerable performance speedup on continuous system benchmarks with linear dynamics. Time-Slice algorithm also shows a gain in accuracy w.r.t. the sequential algorithm; however, it is limited to systems with fixed input. A-GJH is an adaption of the parallel breadth-first search algorithm in the SPIN model checker. We show that A-GJH algorithm does not show an ideal load balancing on certain HA models, and therefore, we present a task parallel variant for an improved load balancing. Both A-GJH and TP-BFS algorithm incur a necessary thread synchronization overhead in order to have a breadth-first exploration. We also present an asynchronous HA exploration algorithm to avoid the synchronization overhead. Performance evaluation on benchmarks displays considerable speedup in all the proposed algorithms w.r.t. the sequential counterparts and $\textsc {SpaceEx-\!LGG}$. We show that the performance of the parallel algorithms is dependent on the parameter AvgW, the average number of symbolic states in the waiting list during a BFS. We illustrate that A-GJH algorithm shows the best performance when AvgW is much larger than the available cores. TP-BFS shows the best performance when AvgW is very low. AsyncBFS shows the best performance when AvgW is large and the BFS is bounded to a small depth.

Appendix

Claim 1

A-GJH algorithm performs a BFS of a HA with the number of BFS levels $=$ bound.

Proof

We show the correctness of the algorithm by the following loop invariant of the repeat–until loop of thealgorithm:

At the beginning of the $j^{th}$ iteration of the repeat–until loop, the data structure R contains all the states of the HA reachable from Init with $j-1$ levels of BFS.

We use a level of a BFS to signify the frontiers of states reachable from Init. For example, PostC(Init) denotes all states reachable up to a BFS level/frontier of 1 from Init, and PostC(PostD(PostC(Init))) denotes all states reachable up to a BFS level/frontier of 2 from Init and so on.

At initialization, R is assigned to Init. Therefore, the loop invariant is true at initialization, which says that at the beginning of the first iteration of the repeat–until loop, R contains all the states of the HA reachable from Init with no BFS.

We now show that the loop invariant is maintained. In lines 8 to 15, PostC operator is applied to every symbolic state in Wlist[t] and the result is included in R. The states reachable by PostD transitions are added to $Wlist[1-t]$ for exploration in the next iteration. Therefore, at each iteration, the BFS frontier is increased by 1, maintaining the loop invariant. Parallel exploration causes no race condition and write contention on the shared data structure Wlist and R. The justifications are the same as in the G.J. Holzmann’s algorithm in the SPIN model checker [37].

The termination of the algorithm is evident from the termination condition of the repeat–until. The loop terminates either when there are no new symbolic states for further exploration in Wlist[t] or when the predetermined bound on the BFS levels is reached. It is clear that one of the condition must be eventually true, and hence, the algorithm must terminate.

At termination, the loop condition must be false, which means either $level=bound$ or $Wlist[t] = \emptyset$. In the former condition, the loop invariant at termination says that R contains all the states of the HA reachable from Init with bound levels of BFS, which is our claim. Termination due to the later condition implies that the fixed point has been found before BFS levels could reach the bound. In both cases, our claim holds. $\square$

Claim 2

TP-BFS algorithm performs a BFS of a HA with the number of BFS levels $=$ bound.

Proof

The correctness of the algorithm can be proved using the same loop invariant used in the proof of claim 1. The arguments for the validity of the loop invariant are same except for the invariant maintenance. In lines 7 to 28, the PostC and PostD operations increase the BFS frontier/level by 1, maintaining the loop invariant. The PostC and PostD operations are split into atomic tasks and inserted into a tasks list data structure. Since the algorithm provides a partitioned access of the tasks in the tasks list data structure to the threads executing in parallel in the cores, the threads access exclusive portions in memory, with no read–write contention. Such an exclusive access to the tasks list data structure by the threads makes locking needless. The read–write switching of the data structure Wlist is the same as in the A-GJH algorithm, which makes the accesses to the symbolic states in the waiting list lock-free, during the BFS [37].

The termination proof of the algorithm is the same as the termination proof of A-GJH algorithm in claim 1. $\square$