Introduction

Since the beginning of twentieth century, it is reported in the literature studies on thermal decomposition of solids [1,2,3,4,5,6]. Methods to acquire kinetic model parameters, such as activation energy and frequency factor, can be found in the literature. For example, those proposed by Kissinger [7], Flynn and Wall [8], Ozawa [9] and a more accurate method known as the Kissinger-Akahira-Sunose (KAS) [10]. Also, thermal analysis data can be treated by means of the model fitting or the isoconversional methods [11]. Artificial neural network has also been applied to understand kinetic process [12, 13]. An optimization method, in which it is not required the numerical solution of differential or integral equations, has been recently proposed in the literature [14]. However, these methods are based on the assumption of an integer order derivative model.

The first mention to the fractional calculus was made in a letter from l’Hôpital to Leibniz in 1695. After this, several definitions were proposed and a theoretical and historical review can be found in [15,16,17]. One important application on a kinetic process is the use of fractional derivative to model anomalous luminescence decay, which results in a single solution both to exponential and non-exponential behavior [18]. From these results, one can suppose other kinetic models also described by a fractional order derivative.

Knowledge of the thermal behavior of drugs is critical in the pre-formulation stage as some unit operations require or generate heat [19]. In this context, good manufacturing practices of drug product include the development of stability studies to ensure the quality of the final product and to promote public health [20]. Therefore, the pharmaceutical industry continually searches for analytical techniques and data processing protocols that help in understanding the stability of pharmaceutical systems. Therefore, thermoanalytical techniques are very useful to drug product developments and the fractional derivative methodology can add important information to understand this process.

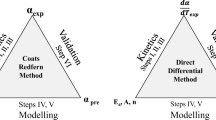
In this work, it will be given the mathematical background necessary to perform the fractional derivative analysis along with two examples to validate the fractional differential equation solution method. Since the KAS method is derived starting from the assumption of an integer order derivative kinetic model, this method will not work properly for fractional kinetic data. However, it is not possible to determine if the process follows an integer or fractional kinetics from experimental data and one may be lead to apply this method as a first analysis. The non-isothermal decomposition data of lumefantrine, first drug elected for treatment of uncomplicated and severe Plasmodium falciparum malaria [21], will be treated by the model fitting method, considering a single-step process. The KAS analysis will be carried out using simulated fractional kinetic data. This method also will be applied to experimental data to infer about the number of steps necessary to define the whole process. Hereafter, a multistep fitting procedure, considering the general kinetic equation proposed by Cai and Liu [22] with fractional order derivative, will be carried out.

Fractional calculus background

To present the kinetic analysis from a fractional calculus viewpoint, it is necessary to give some definitions and results for fractional integral and its derivatives. The n-order Riemann-Liouville integral, Jn, can be used to calculate a multiple integral of order \(n \in \mathbb {N}^{*}\) [15]

$$ J^{\sf n} f(t) = {{\int}_{0}^{t}}{\int}_{0}^{x_{1}}\dots{\int}_{0}^{x_{\sf n}} f\left( x_{{\sf n}+1}\right)dx_{{\sf n}+1}dx_{\sf n}{\dots} dx_{1} = \frac{1}{\Gamma({\sf n})}{{\int}_{0}^{t}} \frac{f(x)}{\left( t-x\right)^{1-{\sf n}}}dx $$
(1)

in which Γ(n) is the Gamma function. For the application given in this work, all definitions are left-sided on the half-axis \(\mathbb {R}^{+}\). The integer order Riemann-Liouville integral can be extended for non-integer indexes [23], γ, and one is left with

$$ J^{\gamma} f(t) = \frac{1}{\Gamma(\gamma)}{{\int}_{0}^{t}} \frac{f(x)}{\left( t-x\right)^{1-\gamma}}dx $$
(2)

Equation 2 is called Riemann-Liouville fractional integral and the associated fractional derivative is given by

$$ D^{\gamma} f(t) = \frac{d^{\sf n}}{dt^{\sf n}} \left( J^{{\sf n}-\gamma}f(t)\right) $$
(3)

Since the fractional derivative of a constant, L, is a function dependent on t, then \(\left (D^{\gamma } L \right )(t) \neq 0\). Therefore, the Riemann-Liouville fractional derivative is not appropriate to describe a dynamical process. An alternative definition is called Caputo fractional derivative and it is given by [15, 16]

$$ {D}_{*}^{\gamma} f(t) = J^{{\sf n}-\gamma} \frac{d^{\sf n} f}{dt^{\sf n}} $$
(4)

In this definition, if the function f(t) is constant, then \({D}^{\gamma }_{*} f(t) = 0\). From this point of view, the Caputo derivative is more appropriate to describe kinetic processes and it will be considered in this work.

The Caputo representation has properties under the Laplace transform which allows, in some cases, the acquisition of analytical solution for simple differential equations [15, 18]. However, in several applications, this analytical solution is not possible. Therefore, it is convenient to introduce the Grünwald-Letnikov fractional derivative, given by [15]

$$ D_{GL}^{\gamma}f(t) = \underset{h\rightarrow0}{\lim} \sum\limits_{i=0}^{\frac{t-t_{0}}{h}} \frac{(-1)^{i}}{h^{\gamma}} \binom{\gamma}{i} \left[f\left( t - ih \right) \right] $$
(5)

in which the maximum integer lower than \(\frac {t-t_{0}}{h}\) has to be considered as the upper limit. This representation for fractional derivative can be related to both, Riemann-Liouville or Caputo representations, depending on how it is defined. If the function f(t) obeys certain conditions of continuity and integrability, the Grünwald-Letnikov derivative coincides with Riemann-Liouville definition. [15]

The relation between Caputo and Grünwald-Letnikov fractional derivatives is obtained by considering that, for n = 1, Riemann-Liouville and Caputo derivatives are related as [24]

$$ {D}_{*}^{\gamma} f(t) = D^{\gamma} \left[f(t) - f(0)\right] $$
(6)

Therefore, the Caputo fractional derivative representation, with 0 < γ < 1, as a Grünwald-Letnikov series is given by

$$ {D}_{*}^{\gamma}f(t) = \underset{h\rightarrow0}{\lim} \sum\limits_{i=0}^{\frac{t-t_{0}}{h}} \frac{(-1)^{i}}{h^{\gamma}} \binom{\gamma}{i} \left[f\left( t - ih \right) - f(0) \right] $$
(7)

Expliciting the first term,

$$ {D}_{*}^{\gamma}f(t) = \underset{h\rightarrow0}{\lim} \frac{1}{h^{\gamma}}\left[f\left( t\right) - f(0) \right] + \sum\limits_{i=1}^{\frac{t-t_{0}}{h}} \frac{(-1)^{i}}{h^{\gamma}} \binom{\gamma}{i} \left[f\left( t - ih \right) - f(0) \right] $$
(8)

Equation 8 will play an important role in the solution of differential equations of fractional order. For numerical implementation, it is convenient to approximate \({D}_{*}^{\gamma }f(t) \approx \frac {1}{h^{\gamma }}\left [f\left (t\right ) - f(0) \right ] + {\sum }_{i=1}^{\frac {t-t_{0}}{h}} \frac {(-1)^{i}}{h^{\gamma }} \binom {\gamma }{i} \left [f\left (t - ih \right ) - f(0) \right ]\) for low values of h.

Kinetic models as ordinary differential equations

To study the kinetics of solid thermal reactions, such as decomposition or polymorphic conversion, kinetic models are employed to fit experimental data of thermogravimetry (TG) or differential scanning calorimetry (DSC) curves [25]. A differential equation with adjustable parameters which can represent ideal and also non-ideal kinetic models was proposed by Cai and Liu [22]:

$$ \frac{d\alpha(t)}{dt} = k(T) \alpha(t)^{m}\left( 1 - q\alpha(t)\right)^{n} $$
(9)

Equation 9 will be used in this work for non-isothermal analysis. Usually the left hand side of this equation is rewritten as \(\frac {d\alpha }{dT}\frac {dT}{dt}\), but since the Caputo fractional derivative has no simple form for composite functions as in usual calculus [15], this step will not be considered in this work.

Numerical solution for fractional derivative models

If the integer order derivative is replaced by the fractional derivative, only a few values of m, n, and q enables analytical solutions. However, using (8) in (9) and, in analogy with the Euler method, choosing α(t) = αr on the left hand side and α(t) = αr− 1 in the right hand side of Eq. 9, one obtains

$$ \frac{1}{h^{\gamma}}\left[\alpha_{r} - \alpha_{0} \right] + \sum\limits_{i=1}^{\frac{t-t_{0}}{h}} \frac{(-1)^{i}}{h^{\gamma}} \binom{\gamma}{i} \left[\alpha_{r-i} - \alpha_{0} \right] = k(T) \alpha_{r-1}^{m}\left( 1 - q\alpha_{r-1}\right)^{n} $$
(10)

after a rearrangement:

$$ \alpha_{r} = \alpha_{0} - \sum\limits_{i=1}^{\frac{t-t_{0}}{h}} (-1)^{i} \binom{\gamma}{i} \left[\alpha_{r-i} - \alpha_{0} \right] + h^{\gamma}k(T) \alpha_{r-1}^{m}\left( 1 - q\alpha_{r-1}\right)^{n} $$
(11)

The geometrical interpretation of fractional derivative is not common; however, this analogy is justified by the obtained results for some known solutions of differential equations, as discussed in the next section.

Numerical method validation

To validate the numerical method presented in this work, two examples with known analytical solution will be considered: (a) an equation for fractional decay and (b) the Avrami-Erofeev equation. The first case can be represented by the equation

$$ {D}_{*}^{\frac{1}{2}} \alpha(t) = - \alpha(t) $$
(12)

which has an analytical solution given by \(\alpha (t) = \alpha (0)\left [ e^{t} - e^{t}\text {erf}\left (\sqrt {t}\right ) \right ]\), with erf(x) being the error function. The recursive formula for Eq. 12, as obtained in the previous section, is given by

$$ \alpha_{n} = \alpha_{0} - \sum\limits_{i=1}^{n} {c}_{i}^{\frac{1}{2}} \left[\alpha_{n-i} - \alpha_{0}\right] - \alpha_{n-1}h^{\frac{1}{2}} $$
(13)

with \(c_{i}^{\gamma } = (-1)^{i} \binom {\gamma }{i}\). The numerical solution for h = 0.001 is given in Fig. 1 along with the analytical solution .

Fig. 1
figure 1

Exact (dashed) and numerical (dotted) solutions for the half order decay of Eq. 12

Full size image

To complete the validation, it is considered an integer order derivative case for Avrami-Erofeev model

$$ \frac{d\alpha(t)}{dt} = 2\left( 1-\alpha(t)\right)\left( -\ln(1-\alpha(t)) \right)^{\frac{1}{2}} $$
(14)

in which it was used the same procedure adopted for the fractional order differential equation setting γ = 1. Eq. 14 has analytical solution given by \(\alpha (t) = 1 - e^{-t^{2}}\) and can be rewritten as the recursive formula,

$$ \alpha_{n} = \alpha_{0} - \sum\limits_{i=1}^{n} {c_{i}^{1}} \left[\alpha_{n-i} - \alpha_{0}\right] + 2\left( 1-\alpha_{n-1}\right)\left( -\ln(1-\alpha_{n-1}) \right)^{\frac{1}{2}} $$
(15)

The solution for h = 0.001 is given in Fig. 2.

Fig. 2
figure 2

Exact (dashed) and numerical (dotted) solutions for γ = 1

Full size image

The accuracy of the numerical solution will depend on the values of h and therefore a convergence analysis is required for each problem to be solved.

Experimental procedure

The thermal behavior of lumefantrine was evaluated by DSC and TG/differential thermal analysis (DTA). DSC curves were obtained for lumefantrine in the DSC60 Shimadzu, calibrated with indium (melting Tonset = 156.63 oC, ΔHfus = 28.45 J g− 1) under a dynamic nitrogen atmosphere at 50 mL min− 1. The sample was heated from room temperature up to 400 ∘C with heating rate set as 10 ∘C min− 1 in a closed aluminum crucible. The lumefantrine sample was about 1.5 mg, accurately weighted.

TG simultaneous DTA curves were obtained using a Shimadzu DTG60, with heating rate set as 10 ∘C min− 1 starting from room temperature up to 600 ∘C under a dynamic nitrogen atmosphere at 50 mL min− 1 in an alumina crucible with sample mass about 2.5 mg. For the kinetic studies, the TG data were obtained at the heating rates of 5, 10, 15, and 20 ∘C min− 1, also from room temperature up to 600 ∘C, in the same experimental conditions.

Results and discussion

The necessary steps used in the present work has considered three heating rates to solve (11), together with a multiobjective error function defined as

$$ EN=\sum\limits_{i=1}^{3}||\alpha_{\text{calc},\beta_{i}}-\alpha_{\exp,\beta_{i}}||^{2} $$
(16)

with \(\alpha _{\text {calc},\beta _{i}}\) and \(\alpha _{\exp }\) representing, respectively, the calculated and experimental conversion rates at each heating rate, βi. The fourth data was used to validate the results using the root-mean-squared-deviation (rmsd)

$$ \text{rmsd}=\sqrt{\frac{||\alpha_{\text{calc}}-\alpha_{\exp}||^{2}}{N}} $$
(17)

in which N is the number of data points. The program was implemented on MATLAB®; environment using the function fminsearchbnd [26] that uses the simplex method of Lagarias et. al. [27] with the possibility to impose boundaries in the parameters to be fitted.

Experimental data

DSC curve for lumefantrine (Fig. 3, black) indicates an endothermic event, not followed by a mass loss in the TG curve (Fig. 3, red) and confirmed by DTA curve (Fig. 3, blue). This behavior indicates a physical phenomenon related to the melting (Tonset = 128.1 ∘C, Hfus = 77.39 J g− 1) as expected [28]. After melting, the degradation process started at about 250 ∘C, confirmed by the two steps of mass loss in the TG curve, 69% (corresponding to the loss of the OH, 3 Chlorine atoms, located at the side chain and part of the cyclic carbon chain) and 19% (another part of the cyclic carbon chain) of weight loss, as described by Freitas-Marques et al. [25].

Fig. 3
figure 3

Thermal behaviour of lumefantrine. DSC (left axis, black), TG (right axis, red) and DTA (right axis, blue) curves

Full size image

The non-isothermal TG curves of lumefantrine, obtained at the heating rates of 5, 10 , 15, and 20 ∘C min− 1 were used to determine the conversion rate, α, as a function of the temperature. Figure 4 presents these experimental data to be treated in this work for integer and fractional derivative kinetic models. The data presented only one single event during the whole process, which can be verified by the one step of the decomposition curves. As expected, it is observed a curve displacement as the heating rate is increased [29].

Fig. 4
figure 4

Experimental data for β = 5 (dashed), β = 10 (dotted), β = 15 (dashed and dotted) and β = 20 (full line) oC min− 1

Full size image

Model-fitting method

The model-fitting method was applied to experimental results. The data for β = 5,10,20 ∘C min− 1 were used in the adjustment, while the data for β = 15 ∘C min− 1 was used to validate the parameters found. The values of m, q, and n relative to ideal models were obtained in reference [22]. The results are presented in Table 1.

Table 1 Model-fitting results
Full size table

The ideal models considered were R2 and R3, which stands for phase boundary controlled reactions, A1.5 and A2, describing nucleation and growth reactions, F1 for first-order reaction and F2 for second-order reaction.

Except for F2 model, in which integer order kinetics was retrieved in the most general case, in all adjustments, it was found the fractional kinetics as the best model to describe the one-step reaction, particularly for A1.5, A2, and F1 models. The results for adjustment considering the general model is presented in Table 2.

Table 2 General fitting result
Full size table

In this case, the parameters m, q, and γ are more appropriated to describe the A2 fractional model, given by m = 0.511148, n = 0.793815, q = 1.003138, and γ = 0.60844. Therefore, one may infer that for a single-step process, there is a larger contribution from A2 fractional model to the simultaneous reactions. The results for ideal models are presented in Fig. 5 and for general model in Fig. 6.

Fig. 5
figure 5

Experimental data (full line) and results for a R2, b R3, c A1.5, d A2, e F1, and f F2 ideal models with integer (dots) and fractional (dashed) order derivative

Full size image
Fig. 6
figure 6

Experimental data (full line) and result for general model with fractional order derivative (dashed)

Full size image

Application of the KAS method in simulated fractional kinetic data

Another kinetic analysis can be performed by the model free methods. [30] However, these methods are all based on the assumption of an integer order derivative kinetic model. In this section, a single-step process with fractional order derivative will be simulated in four different heating rates and the KAS method will be applied to these data. This model-free method is derived starting from the equation [7, 10]

$$ \frac{d\alpha(T)}{dT} = Ae^{-\frac{E_{a}}{RT}}f(\alpha(T)) $$
(18)

with α-dependent term on the right hand side of Eq. 9 expressed as f(α). By separating the variables

$$ \frac{d\alpha}{f(\alpha)} = Ae^{-\frac{E_{a}}{RT}}dT $$
(19)

and integrating this equation, one obtains

$$ \ln\left( \frac{\beta}{T^{2}} \right) = \ln\left( \frac{AR}{E_{a}G(\alpha)} \right) - \frac{E_{a}}{RT} $$
(20)

in which \(G(\alpha )={\int \limits }_{0}^{\alpha }\frac {d\alpha }{f(\alpha )}\). Therefore, the method consists in plot \(\ln \left (\frac {\beta }{T^{2}} \right )\) versus \(\frac {1}{T}\) for different values of α.

Equations 9 and 11 were used to simulate the conversion rate data for β = 5, 10, 15, and 20 ∘C min− 1 with parameters set as γ = 0.7, A = 3.74 × 1010 s− 1, Ea = 110.72 kJ mol− 1, m = 0.337951, n = 0.856039, and q = 1.002758, which is the fractional Avrami-Erofeev A1.5 model. The curves are presented in Fig. 7.

Fig. 7
figure 7

Simulated data for fractional kinetics and β = 5,10,15,20 oC min− 1

Full size image

Considering these data and applying the KAS method, the results are obtained and presented in Table 3.

Table 3 Activation energy according to conversion degree, α, by the KAS method
Full size table

It is possible to see an approximate constant values for the activation energy for a single-step reaction, but with a large error considering the value of Ea = 110.72 kJ mol− 1 used in the simulation. Therefore, if the process occours obeying a fractional kinetics, using this model-free method to determine the activation energy may lead to wrong results, although, since the activation energy remains approximately constant, it is possible to infer if the process is multistep or not.

KAS method applied to lumefantrine data

As observed from simulated data, the KAS method may give wrong results for activation energy if the kinetics follows a fractional order derivative. However, it still can give insights if the reaction is multistep or not. Thus, the TG experimental data of lumefantrine at 5,10,15, and 20 ∘C min− 1 were used and Fig. 8 presents the KAS linear correlation.

Fig. 8
figure 8

KAS plot for different values of α

Full size image

In Table 4, the results for the activation energy according to the conversion rate, α. The increasing value for activation energy with α indicates a multistep process. Therefore, these data will be divided in five subintervals and the adjustment will be performed again considering the general kinetic equation.

Table 4 Activation energy according to conversion degree, α, by the KAS method
Full size table

General multistep method

The general equation (9) with variable derivative order will be used to perform the multistep analysis. Since experimental data shows amplified noises for α < 0.025 when β= 5 ∘C min− 1 and oscillations for α > 0.95, it was considered results in the range 0.025 < α < 0.95 for all heating rates (Table 5).

It is observed an increasing of the activation energy in each subinterval considered, as indicated by KAS method. Since the fractional derivative order is between 0.9 and 1, the similar results for activation energy obtained in the adjustment and retrieved by KAS method is expected. It is interesting to point out that results in intervals [0.7,0.85] and [0.85,0.95] are below the results presented in Table 4 for α = 0.8 and α = 0.9, respectively, which coincides with the superestimated activation energy predicted by KAS method when applied to fractional kinetic data, as discussed in Section 2.

This result indicates a integer order kinetics in the beginning of the process and a fractional kinetics process for α > 0.3. Besides, since the parameters do not correspond to any ideal model, it suggests a complex process in which more than one reaction occurs simultaneously, according to Cai and Liu work [22]. The results are presented in Fig. 9

Fig. 9
figure 9

Experimental data (full line) and results obtained by the general multistep with variable derivative order (dashed)

Full size image

Conclusions

It was given the necessary mathematical background of fractional calculus to the development of this work. The method to solve fractional differential equations was validated by considering two different examples, one with integer and the other with fractional derivative orders, which has analytical solutions, demonstrating the accuracy of the numerical method.

Table 5 Adjustment of 5 subintervals with fractional derivative considering the general model
Full size table

Although the KAS method starts from the assumption of an integer order kinetic model, it was possible to observe that , despite the error in determining the activation energy for simulated fractional kinetic data, it still gives insights if the process is multistep or not. Four heating rates experimental data for lumefantrine were used to test the fractional kinetic model. The first assumption was considering the process as a single step and it was applied the model-fitting method considering some ideal models. For this case, a better performance for fractional model, with A1.5, A2, and F1 fractional models presenting smaller rmsd, was observed.

The KAS method was applied to lumefantrine experimental data and results obtained through a multistep process were observed. To perform the new adjustment, it was considered the general model proposed by Cai and Liu [22] with variable derivative order to fit five data subintervals. It was observed that the process initiates as an integer order kinetics until α = 0.3 and then follows a fractional kinetic model. The activation energy for each subinterval has an increasing behavior, as observed in KAS results, and for fractional steps, smaller activation energies were observed than predicted by the KAS method, which is consistent with the preliminar analysis done in this work. Also, the rmsd obtained in this method was 100 times smaller than the single-step analysis. Therefore, these results indicate that the process is multistep with simultaneous reactions, since the parameters do not correspond to any ideal model, and with variable derivative order during the advance of the reaction.

From Eqs. 4 and 11, one can see that the fractional derivative and the solution of a fractional differential equation at time t1 depends on all values for t < t1 and in this sense, the fractional derivative has a kind of “memory.” From this point of view, the fractional kinetic model can be understood as a process in which all previous reaction coordinates have influence on the current reaction coordinate. Therefore, the fractional kinetic model presents a useful generalization in thermal analysis both in the adjustment numerical process, since it increases the degrees of freedom, and in the physical interpretation of the reaction. Further works are necessary to provide more insights and new methodologies to treat experimental data.