On the role of skewness and kurtosis in tempered stable (CGMY) Lévy models in finance

Abstract

We study the structure and properties of an infinite-activity CGMY Lévy process $X$ with given skewness $S$ and kurtosis $K$ of $X_{1}$, without a Brownian component, but allowing a drift component. The jump part of such a process is specified by the Lévy density which is $C\mathrm {e}^{-Mx}/x^{1+Y}$ for $x>0$ and $C\mathrm {e}^{-G|x|}/|x|^{1+Y}$ for $x<0$. A main finding is that the quantity $R=S^{2}/K$ plays a major role, and that the class of CGMY processes can be parametrised by the mean $\mathbb{E}[X_{1}]$, the variance $\mathrm {Var}[X_{1}]$, $S$, $K$ and $Y$, where $Y$ varies in $[0,Y_{\mathrm {max}}(R))$ with $Y_{\mathrm {max}}(R)=(2-3R)/(1-R)$. Limit theorems for $X$ are given in various settings, with particular attention to $X$ approaching a Brownian motion with drift, corresponding to the Black–Scholes model; for this, sufficient conditions in a general Lévy process setup are that $K\to 0$ or, in the spectrally positive case, that $S\to 0$. Implications for moment fitting of log-return data are discussed. The paper also exploits the structure of spectrally positive CGMY processes as exponential tiltings (Esscher transforms) of stable processes, with the purpose of providing simple formulas for the log-return density $f(x)$, short derivations of its asymptotic form, and quick algorithms for simulation and maximum likelihood estimation.

1 Introduction

Lévy models in finance have evolved for the purpose of mitigating some of the shortcomings of the Black–Scholes model. Here the assumption is that the price of a financial asset evolves as a geometric Brownian motion $\mathrm {e}^{X}$, where $X_{t}=m t+\sigma W_{t}$, with $W$ being a standard Brownian motion. Thus the log-returns over a period of length $h$ are i.i.d. and follow a normal distribution with mean $m h$ and variance $\sigma ^{2} h$ for some $m$ and $\sigma ^{2}$. Some of the problems with this model are that it does not accommodate jumps in the asset price, as occurring for example at a market crash, and that observed log-returns often have a shape different from the normal. Specific differences from the Black–Scholes model are heavier tails and a sharper mode, often argued to be tantamount to a kurtosis larger than that of the normal distribution, and some degree of asymmetry, for which the skewness is the most naive quantitative measure. All of these drawbacks can potentially be avoided when using a Lévy model.

Some classical expositions of the theory and applications of Lévy models in finance are Cont and Tankov [15] and Schoutens [50]. For the general theory of Lévy processes, see Sato [48], Bertoin [8] and Kyprianou [33]. A Lévy process $X$ has a decomposition as

$$ X_{t} = mt+\omega W_{t}+J_{t}, $$

(1.1)

where $mt$ is a linear drift, $W$ a standard Brownian motion and $J$ a pure jump process. We are particularly interested in the jump component and therefore consider only processes with $\omega =0$ in the following. The main characteristic of such a jump process is its Lévy measure $\nu$, which with a few exceptions we throughout assume absolutely continuous with density $n(x)\ge 0$. Properties of $\nu$ are $\int _{\{|x|>\epsilon \}} \nu (\mathrm {d}x)<\infty$ and $\int _{\{|x|\le \epsilon \}} x^{2}\nu (\mathrm {d}x)<\infty$ for some (and then all) $\varepsilon >0$. The process is said to have finite activity if $\lambda =\int _{\mathbb{R}} \nu (\mathrm {d}x)<\infty$ and is then a compound Poisson process with Poisson rate $\lambda$ and density $n(x)/\lambda$ of the jumps. The sample paths of $J$ are of finite variation if and only if $\int _{\{|x|\le \epsilon \}} x\nu (\mathrm {d}x)<\infty$. The picture is roughly that jumps in $[x,x+\mathrm {d}x)$ occur at the rate $n(x)\,\mathrm {d}x$. In the infinite-activity case, $J$ is not completely specified by $n(x)$, but involves an additional condition, which in the present paper we take as the form of the so-called Lévy exponent or cumulant function $\log \mathbb{E}[\mathrm {e}^{sJ_{1}}]$ (see also Sect. 4). The process is called spectrally positive or negative if $n(x)\equiv 0$ for $x<0$ resp. $x>0$; otherwise, we refer to it as two-sided. For the financial interpretation, we assume the time scale is chosen such that $X_{1}=m+J_{1}$ is the log-return (daily or whatever).

For a process of the form (1.1), the $k$th cumulant $\kappa _{k}$ is defined as the $k$th derivative of $\kappa (s)=\log \mathbb{E}[\mathrm {e}^{sX_{1}}]$ at $s=0$. Here $\kappa _{1}=\mathbb{E}[X_{1}]$ and $\kappa _{2}=\mathrm {Var}[X_{1}]$. The first $n$ cumulants are in one-to-one correspondence with the first $n$ moments of $X_{1}$; see e.g. Asmussen and Bladt [4] for a survey and a new representation in terms of matrix exponentials. The normalised cumulants are $\kappa _{k}^{*}=\kappa _{k}/\kappa _{2}^{k/2}$, $k=2,3,4,\ldots$ In particular, if $Z=(X_{1}-\mathbb{E}[X_{1}])/(\mathrm {Var}[X_{1}])^{1/2}$, then $S=\kappa _{3}^{*}=\mathbb{E}[Z^{3}]$ is the skewness and $K=\kappa _{4}^{*}=\mathbb{E}[Z^{4}]-3$ the kurtosis, sometimes also called excess kurtosis, measuring the deviations from the Black–Scholes model. Indeed, for a Lévy process, $K\ge 0$ with equality if and only if $X$ is a Brownian motion with drift.

The most popular jump parts of $X$ in finance are the normal inverse Gaussian (NIG) process, the generalised hyperbolic (GH) process, the Meixner process, the CGMY process and the variance gamma (VG) process. The present paper concentrates on the CGMY model where

$$\begin{aligned} n(x) &= \textstyle\begin{cases} C\frac{1}{x^{1+Y}}\mathrm {e}^{-Mx} &\quad \text{for } x>0, \\ C\frac{1}{|x|^{1+Y}}\mathrm {e}^{-G|x|}& \quad \text{for } x< 0 \end{cases}\displaystyle \end{aligned}$$

(1.2)

and

$$\begin{aligned} \kappa (s) = \textstyle\begin{cases} C\Gamma (-Y) ((M-s)^{Y}-M^{Y}+(G+s)^{Y}-G^{Y} )+sm,&\quad Y\ne 0,1, \\ C ((M-s)\log (M-s )-M\log M \\ \qquad +(G+s)\log (G+s )-G\log G )+sm, &\quad Y=1, \\ -C\log (1-s/M)-C\log (1+s/G)+sm,&\quad Y=0, \end{cases}\displaystyle \qquad \quad \end{aligned}$$

(1.3)

where $-\infty < Y<2$ (see Sect. 4 for remarks on the special role played by $Y=0$ or $Y=1$). This process has finite activity for $Y<0$, finite variation for $0\le Y<1$ and infinite variation for $1\le Y<2$. The central purpose is to shed light on the relation of the skewness $S$ and the kurtosis $K$ to other features of the process. For such purposes, the mean $\kappa _{1}$ and the variance $\kappa _{2}$ are essentially dummy quantities since they just represent location and scale. The main two features of $X$ we study are (A) how to express the parameters in terms of cumulants, and (B) giving conditions in terms of cumulants in order that $X$ is close to a BM with drift. The motivation for studying both (A) and (B) comes from numerous statements in the financial literature in the spirit that $S$ accounts for asymmetry and $K$ for a sharper mode and heavier tails than for the Black–Scholes model.

Our main result related to question (A) is the following. Define

$$ R=\frac{S^{2}}{K} = \frac{\kappa _{3}^{2}}{\kappa _{2}\kappa _{4}}, \qquad Y_{\mathrm {max}}(R)=\frac{2-3R}{1-R}. $$

(1.4)

Theorem 1.1

Given constants $\mathring {{\kappa }}_{2}>0,\mathring {{\kappa }}_{3}>0,\mathring {{\kappa }}_{4}>0$, an infinite-activity two-sided CGMY process $X$ with given rate parameter $Y$ and cumulants $\kappa _{k}=\mathring {{\kappa }}_{k}$, $k=2,3,4$, exists if and only if $\mathring {{R}}=\mathring {{\kappa }}_{3}^{2}/(\mathring {{\kappa }}_{2}\mathring {{\kappa }}_{4})\le 2/3$ and $0\le Y< Y_{\mathrm {max}}(\mathring {{R}})$. In that case, the parameters $C,G,M$ are unique and given by the expressions stated in Theorem 8.2in Sect. 8.

The most obvious interpretation of Theorems 1.1 and 8.2 is that $\mathring {{\kappa }}_{2} ,\mathring {{\kappa }}_{3} ,\mathring {{\kappa }}_{4}$ are the empirical cumulants of a data set, say a series of log-returns. The result then tells us how to fit a CGMY process matching cumulants and in particular skewness and kurtosis; this leaves open the choice of $Y$, and we return to this below in topic (E). The reason that we omit fitting the empirical mean is that this can simply be done by a subsequent appropriate choice of $m$ in (1.1), as is standard at least in the NIG and Meixner cases. However, $\mathring {{\kappa }}_{2}=\kappa _{2} ,\mathring {{\kappa }}_{3}=\kappa _{3},\mathring {{\kappa }}_{4}=\kappa _{4}$ could also be cumulants 2–4 of a given CGMY process. The result then describes how to reconstruct the parameters $C,G,M$ in terms of these cumulants and $Y$.

The basic equations $\kappa _{k}=\mathring {{\kappa }}_{k}$, $k=2,3,4$, mean that

$$ \mathring {{\kappa }}_{k} = C\Gamma (Y-k)\bigl(M^{Y-k}+(-1)^{k}G^{Y-k}\bigr), \qquad k=2,3,4. $$

(1.5)

Numerically, one could of course treat this as a 4-dimensional fixed point problem (Küchler and Tappe [32, Sect. 6] study a similar 6-dimensional problem for a generalised tempered stable process). In contrast, an analytic solution of (1.5) appears at first sight a complicated task. One difficulty is that there are four unknowns, but only three equations, so that there may well be more than one solution. Another is that $\mathring {{R}}$ does not reduce in any promising way. Our approach is to note that the problem is easy for the spectrally positive case where the relevant equations are (1.5) with the $G$-terms deleted. These equations are treated in Sect. 6, and the analysis determines in a rather straightforward way what goes on in the non-skewed case $S=0$, studied in Sect. 7. In contrast, the case $S\ne 0$ is more tricky and treated in Sect. 8. The approach is a careful study of the structure of $X$ as difference between positive and negative jumps introducing $\pi _{2}$, the fraction of $\kappa _{2}$ coming from positive jumps, as auxiliary unknown. We show that $\pi _{2}$ is the solution of a transcendental equation of the form $\varphi _{Y}(\pi _{2})=A$ for a fairly well-behaved $\varphi _{Y}$ and a constant $A$ depending on $Y$ and $R$. Given $\pi _{2}$, there are then simple expressions for $C,G,M$ in terms of $\kappa _{2},R,K,Y$.

Concerning question (B), one has the following general result. Write

$$ \mu =\mathbb{E}[X_{1} ],\qquad \sigma ^{2}=\kappa _{2}=\mathrm {Var}[X_{1} ], \qquad (X^{*}_{t})_{t\ge 0}= \big((X_{t}-\mu t) /\sigma \big)_{t \ge 0}. $$

Theorem 1.2

Consider the whole class of Lévy processes $X$, and let $S$ denote the skewness, $K$ the kurtosis of $X$. In order that $X^{*}\Rightarrow W$ in the Skorokhod space $D[0,\infty )$, it is then sufficient that either (a) $K\to 0$ or (b) each $X$ is spectrally positive and $S\to 0$.

An equivalent formulation of (a) is that for a sequence $(X_{n})$ of Lévy processes with kurtosis $K_{n}$ of $X_{n}$, it is sufficient for $X^{*}_{n}\Rightarrow W$ that $K_{n}\to 0$. Similar remarks apply to (b) and at other places in the paper.

The situation of the theorem, $X^{*}$ being close to $W$, is of particular interest in finance, since then the given Lévy process model is close to the Black–Scholes model $X_{t}=\mu t+\sigma W_{t}$. This indicates that at least for some problems like in-the-money options, there is no need for the more sophisticated Lévy model and one could just price by the much simpler BM machinery. Note also that convergence of skewness or kurtosis or higher moments is not a necessary condition for $X^{*}\Rightarrow W$ – convergence may still hold even if some uniform integrability fails. We shall see examples of this in parts (b), (c) of Proposition 6.7.

Despite its simplicity, Theorem 1.2 does not seem to be all that well known. The earliest reference for part (a) we are aware of is Arizmendi [2] where, however, the setup and proof is extremely abstract. Part (a) also follows from Fomichov et al. [20, Lemma 2.1] which, however, relies on rather intricate CLT bounds from Rio [42]. We therefore give a much more elementary proof in the Appendix, which also applies to prove the apparently new part (b). For some further relevant literature and relation to the Wasserstein distance, see item 2) in Sect. 11.

We proceed to describe some further topics (C), (D), (E) of the paper.

(C) The $R$ in (1.4) plays a fundamental role in view of Theorem 1.1. Concerning its interpretation, one may note that whereas $S$ and $K$ are scale-invariant characteristics of the distribution of $X_{1}$, then $R$ is also a time-invariant quantity: if $S(t)$ and $K(t)$ are the skewness and kurtosis of $X_{t}$, then $S(t)=S/t^{1/2}$ and $K(t)=K/t$, so that $S(t)^{2}/K(t)$ is independent of $t$. With this motivation, we review and extend in Sect. 5 various inequalities related to $R$. In particular, we obtain $R<2/3$ for the CGMY process. These inequalities should be compared with $R\le 1$ for a general Lévy process and $R\le 3/4$ for one with a completely monotone Lévy measure; for a discussion of the relevance of complete monotonicity and its applications in a Lévy process context, see e.g. Carr et al. [11], Jeannin and Pistorius [27], Hackmann and Kutznetsov [24]. For an NIG process, $R<3/5$, and in the Meixner case, $R<2/3$; see the Appendix. Note that an upper bound on $R$ may be seen either as an upper bound on $|S|$ given $K$, or as a lower bound on $K$ given $S\ne 0$.

(D) is an observation relevant for computations: for the NIG and Meixner processes, the density $f(x)$ of $X_{1}$ is explicit, at least to some degree, but for the CGMY process, it is usually not considered to be available in closed form. Accordingly, the numerical calculation of $f(x)$ has been done by rather complicated methods; the most widely used appears to be Fourier inversion, starting from Carr and Madan [13], Carr et al. [11]. In Sect. 6, we point out some simple expressions for $f(x)$ in terms of stable densities $f_{0}(x)$. Such $f_{0}(x)$ are not explicit either, but given the availability of software for stable distributions, the expressions allow a straightforward numerical computation of $f(x)$, an issue of relevance for example for pricing European options or for maximum likelihood estimation. The basic fact is that a spectrally positive CGMY process is an Esscher transform of a stable process. For exploitations of this in a somewhat different vein, see e.g. Madan and Yor [34], Poirot and Tankov [40].

(E), outlined in Sect. 10, concerns the choice of $Y$ in the fitting setting of Theorems 1.1 and 8.2, an issue left open there. Essentially, we see this as an extra degree of freedom compared to the NIG and Meixner processes, where $\kappa _{1},\kappa _{2},S,K$ are in one-to-one correspondence with the parameter sets. In contrast, a CGMY process allowing $m\ne 0$ with given $\kappa _{1},\kappa _{2},S,K$ is over-parametrised since it has five parameters $C,G,M,Y,m$ rather than four. This freedom can be utilised to choose $Y$ according to specific features of financial interest, of which we discuss tail properties (relevant, say, for pricing out-of-the-money options), higher order cumulants and finer path properties (relevant, say, in a high-frequency context).

The rest of the paper is organised as follows. Section 2 contains values of cumulants from various financial studies, guidelining what is the interesting range. Some first remarks on limit theorems are in Sect. 3, and Sect. 4 gives some further relevant preliminaries. Some concluding remarks are in Sect. 11. Finally, the Appendix contains the proofs of the limit theorems and some supplements on the NIG and Meixner models (for some of which we have no immediate reference).

2 Some data

Table 1 below contains some key quantities related to a small selection of financial Lévy models in the literature (here $R_{4}=\kappa _{4}^{2}/(\kappa _{2}\kappa _{6})$, see also Sect. 5). Most of the models have been fitted from historical data (series of log-returns), the few marked by an ^∗ by calibration, where one looks for parameters matching observed option prices as well as possible. Calibration is not based on statistical principles, but has the advantage of circumventing the problem that the issue of risk-neutrality is non-trivial for Lévy processes. In fact, there exists an infinity of equivalent risk-neutral versions and the choice among them is largely subjective. Some popular choices are, however, around, in particular the Esscher transform (exponential tilting, cf. Cont and Tankov [15, Chap. 9]) and the so-called mean-reversion, cf. Schoutens [50, Sect. 6.2.2]. When calibrating, one instead considers the resulting fit to be the market’s view of a risk-neutral model.

Table 1 Cumulants, etc., for a selection of models from the literature

The models in Table 1 are:

E1–E6: empirical cumulants reported in Schoutens [50, Table 4.1] for some popular indices. E1 is S&P500 for the period 1970–2001, with the 19 October 1987 outlier removed. E2–E6 all have period 1997–1999 and are S&P500, Nasdaq-Composite, DAX, SMI and CAC-40;

N1–N3: NIG distributions fitted from historical data, Deutsche Bank in Rydberg [46], Brent oil and SAP in Benth and Saltyte-Benth [7];

$\text{N}1^{*}$: an NIG distribution calibrated from S&P500 in Schoutens [50, Sect. 6.3];

M1–M3: Meixner distributions fitted from historical data, $\text{M1} = \text{Nikkei 225}$ and $\text{M2} = \text{SMI}$ from Schoutens [49] and $\text{M3} = \text{Banco do Brasil}$ from Fajardo Barbachan and Pereira Coutinho [19];

$\text{M}1^{*}$: a Meixner distribution calibrated from S&P500 in Schoutens [50, Sect. 6.3];

C1–C2: CGMY distributions fitted from historical data, $\text{C1} = \text{IBM}$ and $\text{C2} = \text{SPX}$ from Carr et al. [11].

$\text{C}1^{*}$–$\text{C}2^{*}$: calibrated CGMY distributions, $\text{C}1^{*}= \text{spx0210}$ in Carr et al. [11] and $\text{C}2^{*}= \text{S\&P500}$ in Schoutens [50, Sect. 6.3].

The rough picture is that the skewness $S$ is most often negative, i.e., substantial losses are more likely than substantial gains. This effect is, however, much more marked for calibrated models than for models based on historical data. In fact, large values of $R$ only occur for calibrated models.

3 Remarks on limit theorems

Most aspects of weak convergence in the standard $J_{1}$-topology on the Skorokhod space $D[0,\infty )$ simplify greatly for Lévy processes. In particular, since $t=1$ is a continuity point of $X$, convergence in distribution of $X_{1}$ is in general a necessary condition, but for Lévy processes it is also sufficient; cf. Kallenberg [28, Theorem 15.17]. In statements like “$X$ converges to a gamma process” or $X^{*}\Rightarrow W$ (where $W$ is standard Brownian motion), we understand convergence in one of these equivalent senses.

The cumulants of $X^{*}$ are $\kappa _{1}^{*}=0$, $\kappa _{2}^{*}=1$ and $\kappa ^{*}_{k}=\kappa _{k}/\kappa _{2}^{k/2}$ for $k>2$. In particular, $\kappa _{3}^{*}=S$, $\kappa _{4}^{*}=K$. The most obvious parameter set of a CGMY model is $(m,C,G,M,Y)$, but according to Theorem 1.1, one-to-one alternatives are

$$\begin{aligned} &(\kappa _{1},\kappa _{2},\kappa _{3},\kappa _{4},Y)=(\mu ,\sigma ^{2}, \kappa _{3},\kappa _{4},Y),\qquad (\kappa _{1},\kappa _{2},\kappa _{3}^{*}, \kappa _{4}^{*},Y)=(\mu ,\sigma ^{2},S,K,Y), \\ &\big(\mu ,\sigma ^{2},R\,{\mathrm{sign}}(S),K,Y\big). \end{aligned}$$

The asymptotic results of the paper involve limits where some or more parameters in one of these parametrisations are fixed and the rest varying. Some main cases of such results in the $(m,C,G,M,Y)$ parametrisation are given in the following two results (partly overlapping results when $Y<1$ are in Küchler and Tappe [32]).

Proposition 3.1

Consider the class of CGMY models with parameters $m,C,G,M,Y$. Then $X^{*}\Rightarrow W$ provided either (a) $C\to \infty$ with $G,M,Y$ fixed, (b) $Y\uparrow 2$ with $C,G,M$ fixed, or (c) $M,G\to \infty$ with $C,Y$ fixed.

In view of the explicit expression

$$ K = \frac{\kappa _{4}}{\kappa _{2}^{2}} = \frac{\Gamma (4-Y)(M^{Y-4}+G^{Y-4})}{C\Gamma (2-Y)^{2} (M^{Y-2}+G^{Y-2})^{2}}$$

for $K$ (cf. (4.4) below), this is a direct corollary of Theorem 1.2 (note that we have $\Gamma (2-Y)\to \infty$ when $Y\uparrow 2$). However, Proposition 3.1 is also easily proved without reference to that result. In fact, the case $C\to \infty$ is just the standard CLT for $X^{*}_{t}$ as $t\to \infty$ (note that Lévy processes are the continuous-time analogue of random walks). The $G,M\to \infty$ case is also straightforward since it essentially is a rescaling of the $C\to \infty$ case; cf. the final paragraph in Sect. 4. The central limit behaviour for $Y$ close to 2 has certainly been observed at least at the heuristic level, and it can be proved using the standard approach of convergence of characteristic functions; the details are much as the proof, in the Appendix, of Proposition 6.7.

Proposition 3.2

Assume $m=0$. Then:

(a) As $Y\downarrow 0$ with $C,G,M$ fixed, $X$ converges to an sVG process.

(b) As $G,M\downarrow 0$ with $C,Y$ fixed, $X$ converges to a symmetric stable process with $\alpha =Y$.

(c) As $C\downarrow 0$ with $G,M,Y$ fixed, $X/C^{1/Y}$ converges to a symmetric stable process with $\alpha =Y$.

(For stable processes, see Samorodnitsky and Taqqu [47], Nolan [37]. In (a), sVG stands for a special variance gamma process; see Sect. 4.) Here the case $C\downarrow 0$ is equivalent to the small-time behaviour, which is a notoriously difficult topic in Lévy processes; cf. e.g. Doney and Maller [17]. However, it is treated in a somewhat more general context than CGMY in Rosiński [45], and part (c) is a special case of results there. Proposition 3.2 is most easily proved by using that for a pure jump process, convergence in distribution of $X_{1}$ is implied by vague convergence of the Lévy measure $\nu (\mathrm {d}x)$; see Kallenberg [28, Theorem 15.14]. The vague convergence is in turn implied by pointwise convergence of $n(x)$ together with some bound allowing a dominated convergence argument. This easily gives Proposition 3.2. For example, in part (c), the Lévy density of $X/C^{1/Y}$ for $x>0$ is

$$ \frac{C}{(C^{1/Y})^{Y}}\frac{1}{x^{1+Y}}\mathrm {e}^{-MC^{1/Y}x} = \frac{1}{x^{1+Y}}\mathrm {e}^{-MC^{1/Y}x}$$

with the stable Lévy density $x^{-1-Y}$ as majorant as well as limit when $C\to 0$, and similarly for $x<0$.

4 Further preliminaries

A Lévy process of the form (1.1) is traditionally represented in terms of its characteristic triplet $(a,\omega , \nu )$ by the specification

$$ \log \mathbb{E}[\mathrm {e}^{sX_{1}}] = as+\omega s^{2}/2+\int _{-\infty}^{ \infty }(\mathrm {e}^{sx}-1-x\mathbb{I}_{\{|x|\le b\}} )\,\nu (\mathrm {d}x). $$

The range of $s$ always includes the imaginary axis, but in our examples where exponential moments exist, also an open real interval around $s=0$. The $x\mathbb{I}_{\{|x|\le b\}}$ term may be omitted in the finite-variation case, but is indispensable otherwise where so-called compensation of small jumps is necessary. The traditional choice is $b=1$, but it can in principle be any $b>0$. Changing $b=1$ to some other $b$ then also changes $a$. See Cont and Tankov [15, Sect. 4.5] for the choice of $a$ leading to the form (1.3) of $\kappa (s)$ in the CGMY process.

For a process $X_{t}=mt+J_{t}$ without a Brownian component,

$$ \kappa _{k} = \int _{-\infty}^{\infty }x^{k}n(x)\,\mathrm {d}x, \qquad k=2,3,\ldots $$

(4.1)

We can write $X$ as the independent difference of two spectrally positive Lévy processes, $X=X^{+}-X^{-}$, where $X^{+},X^{-}$ have Lévy measures $n^{+}(x)=n(x)$ resp. $n^{-}(x)=n(-x)$ for $x>0$ and $n^{+}(x)=n^{-}(x)=0$ for $x<0$. If $\kappa _{k}^{+},\kappa _{k}^{-}$ are the corresponding cumulants, we therefore have

$$ \kappa _{k} = \kappa _{k}^{+}+\kappa _{k}^{-}\text{ for }k=2,4,\ldots , \qquad \kappa _{k} = \kappa _{k}^{+}-\kappa _{k}^{-} \text{ for }k=3,5, \ldots $$

(4.2)

For negative non-integer $x$, $\Gamma (x)$ is defined by starting with the standard values in the interval $(0,1)$ and then using the recurrence relation $\Gamma (x+1)=x\Gamma (x)$. For the CGMY process, this gives in particular that

$$\begin{aligned} \Gamma (2-Y) &= (1-Y)\Gamma (1-Y) = Y(Y-1)\Gamma (-Y), \\ \Gamma (-Y) &= -\frac{1}{Y}\Gamma (1-Y) = \frac{1}{Y(Y-1)}\Gamma (2-Y) \end{aligned}$$

(4.3)

for $Y\ne 0,1$. The reason that $Y=0$ or $Y=1$ requires special treatment is that $\Gamma (0)= \infty$ since

$$\Gamma (\varepsilon ) = \Gamma (1+\varepsilon )/\varepsilon \ \sim \ 1/\varepsilon \qquad \text{as }\varepsilon \downarrow 0. $$

For more details on the case $Y=1$, see Rosiński [45] and Küchler and Tappe [32]. By insertion of the form of $n(x)$ in (4.1), (4.2), the cumulants of a two-sided CGMY process come out as

$$ \kappa _{k} = C\Gamma (k-Y)\bigl(M^{Y-k}+(-1)^{k} G^{Y-k}\bigr), \qquad k\ge 2, $$

(4.4)

an expression valid also when $Y=0$ or $Y=1$. The CGMY process has also been considered with different $C$ and $Y$ on the positive and negative axis. It also goes under other names, in particular the tempered stable process (cf. Koponen [31], Rosiński [45], Bianchi et al. [9, 10], Grabchak [22], Küchler and Tappe [32]), but note that the terminology is somewhat ambiguous. We do not give a detailed review of history and references, but refer to Cont and Tankov [15, Remark 4.4] and Schoutens [50, Sect. 5.3.9]. Note the connection of the acronym CGMY to the authors Carr, Geman, Madan, Yor of [11].

For the NIG process,

$$\begin{aligned} n(x) &= \frac{\alpha \delta}{ \pi |x|}K_{1} (\alpha |x| ) \mathrm {e}^{ \beta x},\qquad x\in \mathbb{R}, \\ \kappa (s) &= \delta \Big(\sqrt{\alpha ^{2}-\beta ^{2}}-\sqrt{\alpha ^{2}-( \beta +s)^{2}}\Big), \end{aligned}$$

where $\alpha ,\delta >0$, $|\beta |<\alpha$ and $\mu \in \mathbb{R}$. As usual, $K_{1}(z)$ denotes the modified Bessel function of the third kind with index 1. For the Meixner process,

$$\begin{aligned} n(x) &= d \frac{\exp (bx/a)}{x\sinh (\pi |x|/a)} = 2d \frac{\exp (bx/a-\pi |x|/a )}{|x| (1-\exp (-2\pi |x|/a) )}, \\ \kappa (s) &= 2d\log \bigl(\cos (b/2)\bigr)-2d\log \Big(\big(\cos (as+b)/2 \big)\Big), \end{aligned}$$

where $a,d>0$, $|b|<\pi$ and $m\in \mathbb{R}$. Both the NIG and Meixner processes have infinite variation.

For the gamma process with density $\gamma ^{\alpha }x^{\alpha -1}\mathrm {e}^{-\gamma x}/\Gamma (\alpha )$ of $X_{1}$, we refer to $\alpha$ as the shape parameter and to $\gamma$ as the rate parameter. The Lévy density is $\alpha \mathrm {e}^{-\gamma x}/x$, $x>0$. It is thus a spectrally positive CGMY process with $C=\alpha$, $M=\gamma$ and $Y=0$. The VG process is the difference $X^{+}-X^{-}$ between two independent gamma processes $X^{+},X^{-}$ with parameters, say, $\alpha ^{+},\gamma ^{+}$ for $X^{+}$ and $\alpha ^{-},\gamma ^{-}$ for $X^{-}$. Thus the CGMY process with $Y=0$ is VG with $\gamma ^{+}=M$ and $\gamma ^{-}=G$, $\alpha ^{+}=\alpha ^{-}=C$. That is, the shape parameters of $X^{+},X^{-}$ are identical, and we use the acronym sVG for this case ($s$ for same). The class of GH processes includes the NIG, but is more complicated (e.g. $n(x)$ is only available in integral form), and in most financial examples we have seen, the NIG performs as well. For these reasons we omit discussion of the GH process and VG processes with $\alpha ^{+}\ne \alpha ^{-}$ in this paper. We also do not go into the compound Poisson case $\int n(x)\,\mathrm {d}x<\infty$ (meaning $Y<0$ in the CGMY case), since here the log-returns have an atom at zero, a somewhat controversial feature from the financial point of view.

Scaling a jump process by $v>0$, i.e., replacing $X_{t}$ by $X_{t}/v$, changes $n(x)$ to $vn(vx)$. In particular, for the CGMY process, the parameters $C,G,M$ change to $C/v^{Y},vG,vM$, while $Y$ is left unchanged. In relation to Proposition 3.1, this shows in particular that in the spectrally positive case, the CLT in the limit $M\to \infty$ follows from that in the limit $C\to \infty$ (take $v=1/M$). Additivity properties of Lévy processes then apply to the two-sided case.

5 Inequalities

Recall that $R=S^{2}/K=\kappa _{3}^{2}/(\kappa _{2}\kappa _{4})$. Recall also that a function $g(x)$ on $(0,\infty )$ is called completely monotone if it is a (possibly continuous) mixture of exponentials, i.e., if $g(x)=\int _{0}^{\infty }\mathrm {e}^{-ax}\,V(\mathrm {d}a)$ for some nonnegative measure $V(\mathrm {d}a)$ on $(0,\infty )$. We call $n(x)$ completely monotone if both $n^{+}(x)$ and $n^{-}(x)$ are such. For example, it is shown in Carr et al. [11] that for the spectrally positive CGMY process, $V$ exists and has density $(a-M)^{Y}/\Gamma (1+Y)$, $a>M$.

If the $\kappa _{k}$ are the cumulants of a general random variable $Z$ (not necessarily of the form $Z=X_{1}$ for a Lévy process), one has $S^{2}\le K+2$ and this inequality is sharp. See Rohatgi and Székely [43], where also the inequality $R\le 1$ in part (a) of the following result can be found (but with a different proof than the one we give in the Appendix).

Proposition 5.1

For a Lévy process $X$, we have $R\le 1$, with equality if and only if $X=z_{0}N^{(\lambda )}$ for some $z_{0}\ne 0$ and some $\lambda > 0$, where $N^{(\lambda )}$ is a Poisson process with rate $\lambda$. If, furthermore, $n(x)$ is completely monotone, then $R\le 3/4$, with equality if and only if $X$ is spectrally positive or negative with $\textit{exponential}(a_{0})$ jumps in the positive resp. negative direction for some $a_{0}>0$.

Proposition 5.2

For a Lévy process $X$, we have $R_{4}=\kappa _{4}^{2}/(\kappa _{2}\kappa _{6})=K^{2}/ \kappa ^{*}_{6} \le 1$, with equality if and only if $X=z_{0}(N^{(\lambda ^{+})}-N^{(\lambda ^{-})})$ for some $z_{0}>0$ and independent $N^{(\lambda _{+})},N^{(\lambda _{-})}$. If, furthermore, $n(x)$ is completely monotone, then $R_{4}\le 2/5$, with equality if and only if $X^{+}$, $X^{-}$ are both compound Poisson with $\textit{exponential}(a_{0})$ jumps, but possibly different $\lambda ^{+},\lambda ^{-}$.

In the course of the paper, we also show the following result.

Proposition 5.3

For the CGMY process with $0\le Y<2$, one has $R\le 2/3=0.667$ and the range of $R_{4}$ is $[0,3/10]=[0,0.300]$. For NIG, we have $R\le 3/5=0.600$ and the range of $R_{4}$ is $[0.171,0.238]$. For Meixner, one has $R<2/3=0.667$ and the range of $R_{4}$ is $[0.240,0.340)$.

6 Spectrally positive CGMY processes

Proposition 6.1

Given constants $\mathring {{\kappa }}_{2}>0,\mathring {{\kappa }}_{3}>0,\mathring {{\kappa }}_{4}>0$, an infinite-activity spectrally positive CGMY process $X$ with cumulants $\kappa _{k}=\mathring {{\kappa }}_{k}$, $k=2,3,4$, exists if and only if $\mathring {{R}}=\mathring {{\kappa }}_{3}^{2}/(\mathring {{\kappa }}_{2}\mathring {{\kappa }}_{4})\le 2/3$. In that case, the parameters $C,M,Y$ are unique and given by

$$ Y=\frac{2-3 \mathring {{R}}}{1- \mathring {{R}}},\quad M=\sqrt{ \frac{(2-Y)(3-Y)\mathring {{\kappa }}_{2}}{\mathring {{\kappa }}_{4}}}= \frac{\sigma \sqrt{ \mathring {{R}}/ \mathring {{K}}}}{1- \mathring {{R}}}, \quad C= \frac{\mathring {{\kappa }}_{2}M^{2-Y}}{\Gamma (2-Y)}. $$

(6.1)

In particular, $X$ is gamma if and only if $\mathring {{R}}=2/3$. Furthermore, we have

$$ R_{4} = \frac{\mathring {{\kappa }}_{4}^{2}}{\mathring {{\kappa }}_{2}\mathring {{\kappa }}_{6}} = \frac{(2-Y)(3-Y)}{(5-Y)(4-Y)}\in (0,3/10]. $$

(6.2)

A related result appears in Küchler and Tappe [32, Proposition 5.4], but is in terms of $\kappa _{1},\kappa _{2},\kappa _{3}$ rather than $\kappa _{2},\kappa _{3},\kappa _{4}$. In particular, $M$ is written there as $(2-Y)\kappa _{2}/\kappa _{3}$.

Proof of Proposition 6.1

We first verify (6.1), (6.2) when $\mathring {{\kappa }}_{2}=\kappa _{2} ,\mathring {{\kappa }}_{3}=\kappa _{3},\mathring {{\kappa }}_{4}=\kappa _{4}$ are the cumulants of a spectrally positive CGMY process. Here, always for $Y\ne 0,1$,

$$\begin{aligned} \kappa _{1} &= -C\Gamma (-Y)YM^{Y-1}+m = C\Gamma (1-Y)M^{Y-1}+m, \end{aligned}$$

(6.3a)

$$\begin{aligned} \kappa _{2} &= C\Gamma (2-Y)M^{Y-2} = C\Gamma (-Y)Y(Y-1)M^{Y-2}, \end{aligned}$$

(6.3b)

$$\begin{aligned} \kappa _{3} &= C\Gamma (3-Y)M^{Y-3} = -C\Gamma (-Y)Y(Y-1)(Y-2)M^{Y-3}, \end{aligned}$$

(6.3c)

$$\begin{aligned} \kappa _{4} &= C\Gamma (4-Y)M^{Y-4} = C\Gamma (-Y)Y(Y-1)(Y-2)(Y-3)M^{Y-4}, \end{aligned}$$

(6.3d)

$$\begin{aligned} \kappa (s) &= C\Gamma (-Y) \bigl((M-s)^{Y}-M^{Y}\bigr) +sm \end{aligned}$$

(6.3e)

$$\begin{aligned} & = \frac{\kappa _{2}}{Y(Y-1)}M^{2-Y} \bigl((M-s)^{Y}-M^{Y}\bigr)+sm, \qquad s< M. \end{aligned}$$

(6.3f)

These are just the standard formulas (4.4) for CGMY with the $(-1)^{k} G^{Y-k}$ term deleted, with the exception of (6.3f) which follows from (6.3e), (4.3) and (6.3b). This immediately gives

$$ R = \frac{S^{2}}{K} = \frac{\kappa _{3}^{2}}{\kappa _{2}\kappa _{4}} = \frac{\Gamma (3-Y)^{2}}{\Gamma (2-Y)\Gamma (4-Y)} = \frac{2-Y}{3-Y}.$$

(6.4)

In particular, the infinite-activity condition $0\le Y<2$ translates into $R\le 2/3$, with the gamma case $Y=0$ corresponding to $R=2/3$. We then also obtain $\kappa _{4}/\kappa _{2}=(2-Y)(3-Y)/M^{2}$. Solving for $M$, we get the asserted expression. The one for $C$ follows from (6.3b) and then gives (6.3e). Finally, (6.2) follows from

$$ \kappa _{6} = \frac{(5-Y)(4-Y)}{M^{2}}\kappa _{4}= \frac{(5-Y)(4-Y)}{(2-Y)(3-Y)}\frac{\kappa _{4}^{2}}{\kappa _{2}}. $$

It is now clear that the connection between $C,M,Y$ and $\kappa _{2},\kappa _{3},\kappa _{4}$ is one-to-one and also in the case of general $\mathring {{\kappa }}_{2},\mathring {{\kappa }}_{3},\mathring {{\kappa }}_{4}$ that $\mathring {{R}}\le 2/3$ is a necessary condition for existence of $X$. That it is also sufficient follows by first noting that $C,M,Y$ as defined in (6.1) are legitimate parameters and then invoking the one-to-one correspondence. □

We next turn to topic (D) of the introduction, expressing the density $f(x)$ of $X_{1}$ in terms of $\alpha$-stable densities. For these, numerical methods are well developed in packages like Matlab or Nolan’s stable program (see the preface in Nolan [37]). They provide a quick and easy access to $f(x)$ by means of the following Proposition 6.2; for the two-sided case, we recommend discretising the convolution formula

$$ f(x) = \int _{0}^{\infty }f^{+}(x+y)f^{-}(y)\,\mathrm {d}y. $$

(6.5)

For stable distributions and processes, see again Samorodnitsky and Taqqu [47] and Nolan [37]. A nuisance is the different parametrisations in use. Here the conventions for a stable distribution $S_{\alpha}(\sigma ,\beta ,m)$ are the most widely adapted ones, see [47], but in the parametrisation $S(\alpha ,\beta ,\gamma ,\delta ,0)$ used in [37] and in Matlab, one has $\gamma = \sigma$, $\delta =\beta \sigma ^{ \alpha}\tan (\pi \alpha /2)$ for an $S_{\alpha}(\sigma ,\beta ,m)$-distribution. Note that $\beta =1$ resp. $m=0$ corresponds to the underlying stable process being spectrally positive, resp. strictly stable.

Proposition 6.2

Let $f(x)$ be the density of $X_{1}$ in a spectrally positive CGMY process with parameters $C,M,Y\in (0,2)$, $m=0$ and let $f_{0}(x)$ be the density of a strictly $\alpha$-stable distribution $S_{\alpha}(\sigma ,1,0)$, where $\alpha =Y$. If $Y\ne 1$ and one lets $\sigma = (-C\Gamma (-Y)\cos (\pi Y/2) )^{1/Y}$, then

$$ f(x)= \exp \big(-Mx-C\Gamma (-Y)M^{Y} \big)f_{0}(x). $$

(6.6)

If $Y=1$ and one lets $\sigma =C\pi /2$, then

$$f(x)= \exp \big(-Mx+CM\log M \big)f_{0}(x). $$

Proof

Assume first $Y\ne 1$. We first note that $\sigma$ is well defined since $\Gamma (-Y)<0$ and $\cos (\pi Y/2)>0$ for $0< Y<1$, whereas $\Gamma (-Y)>0$ and $\cos (\pi Y/2)<0$ for $1< Y< 2$.

It is well known, see [47, Prop. 1.2.12], that the log-Laplace transform defined as $\psi (z)=\log \int \mathrm {e}^{-zx}f_{0}(x)\, \mathrm {d}x$ is finite for all $z>0$ and given by $\psi (z)=-\gamma z^{\alpha}$ when $\alpha =Y\ne 1$, where

$$ \gamma = \sigma ^{\alpha}/\cos (\pi \alpha /2) = -C\Gamma (-Y). $$

Hence the $f(x)$ in (6.6) equals $\exp (-Mx-\psi (M) )f_{0}(x)$ and is therefore a proper density, with cumulant function

$$\begin{aligned} \log \int \mathrm {e}^{sx}f(x)\,\mathrm {d}x &= \psi (M-s)-\psi (M) \\ & = -\gamma \bigl((M-s)^{\alpha}-M^{\alpha}\bigr) \\ &= C\Gamma (-Y)\big((M-s)^{Y}-M^{Y}\bigr),\qquad s< M, \end{aligned}$$

(6.7)

as should be.

If $Y=1$, one has $\psi (z)=(2\sigma /\pi ) z\log z=Cz\log z$. The rest of the proof is just the same as in (6.7). □

Remark 6.3

One example of application of Proposition 6.2 is simulation of $X_{1}$, where in the spectrally positive case with $Y<1$, one may use acceptance–rejection with $f_{0}$ as proposal density and $\mathrm {e}^{-Mx}$ as acceptance probability. The case $Y\ge 1$ is more complicated since there $\mathrm {e}^{-Mx}$ is unbounded on the support ℝ of $X_{1}$; it has been treated by the author in [3]. Note that simulation from $f_{0}$ is standard; see in particular Chambers et al. [14]. Simulating $X^{+}_{1}$ and $X^{-}_{1}$ separately, we immediately get an algorithm for the two-sided case. This appears often to be much quicker and simpler than the methods appearing in the literature which also in many cases are only approximate. See in particular Asmussen and Rosiński [5], Ballotta and Kyriakou [6], Karlsson [29], Kim [30], Rosiński [44], Zhang and Zhang [51]. However, the acceptance probability and hence the efficiency is highly parameter-dependent. For the case $Y<1$, more sophisticated versions of the algorithm are in Devroye [16] (that paper does not connect to CGMY processes and the financial relevance).

As another application, we give a quick proof of the following corollary, appearing in Küchler and Tappe [32, Theorem 7.7] (for the case $Y<1$ only) and proved there by a more intricate argument. Here $f(x)\sim g(x)$ means $f(x)/g(x)\to 1$ in the limit under consideration.

Corollary 6.4

Assume $Y\ne 1$. Then $f(x) \sim C\exp (-Mx-C\Gamma (-Y)M^{Y})\frac{1}{x^{1+Y}}$ as $x\to \infty$.

Proof

According to Nolan [37, Theorem 1.2], we have $f_{0}(x)\sim \widetilde{C}/x^{1+Y}$, where

$$\begin{aligned} \widetilde{C} &= 2\alpha \gamma ^{\alpha}\sin (\pi \alpha /2)\Gamma ( \alpha )/\pi \\ &= -2YC\Gamma (-Y)\cos (\pi Y/2)\sin (\pi Y/2)\Gamma (Y)/\pi \\ & = 2C \Gamma (1-Y)\Gamma (Y) \cos (\pi Y/2)\sin (\pi Y/2)/\pi . \end{aligned}$$

But it is standard that $\Gamma (1-Y)\Gamma (Y)=\pi /\sin (\pi Y)$ and $2\sin \theta \cos \theta =\sin (2\theta )$. This gives $\widetilde{C}=C$. □

Remark 6.5

The corresponding result for the two-sided case and $Y\ne 0,1$ is

$$ f(x) \sim \exp \Big(-Mx+C\Gamma (-Y)\bigl((G+M)^{Y}-M^{Y}-G^{Y}\bigr) \Big)\frac{1}{x^{1+Y}}, \qquad x\to \infty . $$

(6.8)

This follows from (6.5) and Corollary 6.4 by writing $f(x)/f_{0}(x)$ as

$$\begin{aligned} &\exp \big(-Mx-C\Gamma (-Y)(M^{Y}+G^{Y})\big)\int _{0}^{ \infty }\frac{f_{0}(x+y)}{f_{0}(x)}\mathrm {e}^{-(G+M)y}f_{0}(y)\, \mathrm {d}y. \end{aligned}$$

Here the integral goes to $\exp (-\psi (G+M))$ by dominated convergence, using that $f_{0}(x+y)/f_{0}(x)\le 1$ for large $x$ and $f_{0}(x+y)/f_{0}(x)\to 1$.

Example 6.6

Using Proposition 6.2 and the Matlab routines for stable densities, we produced the plots in Fig. 1 for selected values of $K$ and $R$. We considered three values $1/2$, 1 and 4 of the kurtosis $K$, took the variance $\sigma ^{2}=\kappa _{2}$ equal to one, centered to mean zero and for each $K$ used three values $1/4$, $3/4$, $6/4=3/2$ of $Y$, corresponding to $R=7/11=0.64$, $R=5/9=0.56$ resp. $R=1/3=0.33$. We also supplemented the plot with the normal density $\varphi (x)$ with the same mean 0 and variance 1, corresponding to the Black–Scholes model.

Fig. 1

Examples of the form of $f(x)$ in the spectrally positive case

It is seen in Fig. 1 that decreasing $K$ with $Y$ fixed makes the fit closer to the normal. The same is true when increasing $Y$ or, equivalently, decreasing $R$. Theoretically, this is explained by parts (a) and (b) of the following result.

Proposition 6.7

Consider the class of spectrally positive CGMY processes. Then $X^{*}\Rightarrow W$ in a limit where either (a) $K\to 0$ or (b) $S\to 0$ or (c) $K\to \infty$ and $R\to 0$ sufficiently fast that $R\log K=S^{2}(\log K)/K\to 0$.

Proposition 6.8

As $R\uparrow 2/3$ with $\sigma ^{2},K$ fixed, $X$ converges in distribution to a gamma process with rate parameter $\gamma =\sqrt{6/K}/\sigma$ and shape parameter $\sigma ^{2}\gamma ^{2}=6/K$.

Remark 6.9

Note that (a) $K\to 0$ in Proposition 6.7 implies (b) $S\to 0$ since $R\le 2/3$. However, (c) allows $S\to \infty$, only at a slower rate than $\sqrt{K/\log K}$. Also one does not necessarily have that (a) $K\to 0$ when (b) $S\to 0$. These findings may be surprising since in most cases of a CLT, both the skewness and kurtosis go to 0. More precisely, this is equivalent to a suitable uniform integrability condition.

Note also that $\kappa _{2},\kappa _{3},\kappa _{4}$ are in one-to-one correspondence with $\sigma ^{2},K,R$. In Proposition 6.8, $R\uparrow 2/3$ is equivalent to either of $S\uparrow \sqrt{2\kappa _{2}\kappa _{4}/3}$ or $Y\downarrow 0$. Similar remarks apply at several other places in the paper.

7 Non-skewed CGMY processes

In general, a distribution which has vanishing skewness is not always symmetric. In other words, if it is the distribution of a random variable $Z$, then $Z$ and $-Z$ need not have the same distribution. However, if $S=0$ in a CGMY process, then the expression for $\kappa _{3}$ shows that $G=M$ so that symmetry holds for all $X_{t}$. Since, as noted in Sect. 2, the skewness is quite small in many financial data sets, studying the case $S=0$ is therefore a convenient start in the financial context.

When $S=0$, one has necessarily $G=M$ as said, so that the absolute value of the contribution of negative jumps has the same distribution as that from the positive jumps. However, compared to the spectrally positive case, there is an important difference: the cumulants do not specify what is the common skewness in the positive and negative parts. This leaves us with one degree of freedom, which translates into freedom in choosing $Y$.

Proposition 7.1

(a) A CGMY process with given $\kappa _{2}>0,\kappa _{4}>0$ and $\kappa _{3}=S=0$ exists for any $-\infty < Y<2$. The parameters $C,G,M,Y$ are in one-to-one correspondence with $\kappa _{2} ,\kappa _{4},Y$ by means of the formulas

$$ G=M=\sqrt{\frac{(2-Y)(3-Y)\kappa _{2}}{\kappa _{4}},}\qquad C= \frac{\kappa _{2}}{2\Gamma (2-Y)}M^{2-Y}. $$

(7.1)

(b) We have

$$ Y=\frac{5-9R_{4}-\sqrt{R_{4}^{2}+14R_{4}+1}}{2-2R_{4}}. $$

Proof

Noting that $\kappa _{k}^{+}=\kappa _{k}^{-}=\kappa _{k}/2$ for $k$ even, part (a) is immediate from Proposition 6.1. We also get $R_{4}^{+}=R_{4}^{-}=R_{4}$. Therefore (6.2) holds, which can be rewritten as $0= Y^{2}(1-R_{4})-Y(5-9R_{4})+6-20R_{4}$. That $Y$ is the solution with negative sign in front of the square root can be verified by first noting that $R_{4}\in (0,1)$ when $-\infty < Y<2$ and then checking that the solution with positive sign is $>2$ in this range of $R_{4}$. □

An illustration of the influence of the choice of $Y$ on the shape of the density of $X_{1}$ is in Fig. 2. We took the variance $\sigma ^{2}=\kappa _{2}$ equal to one, considered three values $1/2$, 1 and 4 of the kurtosis $K$ and three values $1/4$, $3/4$, $6/4=3/2$ of $Y$, and computed $f(x)$ by a discretised version of (6.5). We also supplemented the plot with the normal density $\varphi (x)$ with the same mean 0 and variance 1, corresponding to the Black–Scholes model.

Fig. 2

Examples of the form of $f(x)$ in the non-skewed case

The picture is rather much the same as in the spectrally positive case: increasing $Y$ or decreasing $K$ makes $f(x)$ closer to the normal. An analogue of Propositions 6.7, 6.8 follows. Note that a symmetric CGMY model has three free parameters $Y, M, C$ or equivalently $Y,\sigma ,K$ (note that this set is in one-to-one correspondence with $Y, M, C$ according to (7.1)).

Proposition 7.2

Consider a symmetric CGMY model given by $Y,\sigma ,K$. Then:

(a) $X^{*}\Rightarrow W$ as either (a) $K\to 0$ or (b) $Y\uparrow 2$ with $K$ fixed or (c) $K\to \infty$ and $Y\uparrow 2$ so fast that $(2-Y)\log K\to 0$.

(b) As $Y\downarrow 0$ with $\sigma ,K$ fixed, $X$ converges to an sVG process with rate parameter $\gamma =\sqrt{6/K}/\sigma$ and shape parameters $\alpha ^{+}=\alpha ^{-}=\kappa _{2}\gamma ^{2}/2=3/K$.

8 Asymmetric CGMY processes

Let $Y\in (0,2)$ be given and define $Q=(4-Y)/(2-Y)$, $Q_{1}=(1+Q)/2$,

$$ g_{Y}(\pi )=(1-\pi )^{Q}+\pi ^{Q},\qquad h_{Y}(\pi )=\pi ^{Q_{1}}-(1- \pi )^{Q_{1}}, \qquad \varphi _{Y}(\pi )= \frac{h_{Y}(\pi )^{2}}{g_{Y}(\pi )}. $$

Lemma 8.1

(a) For fixed $Y$, the function $\varphi _{Y}(\pi )$ is continuous and increases strictly from 0 to 1 in the interval $\pi \in [1/2,1]$. Furthermore, $\varphi _{Y}(\pi )\sim 1-\pi$ as $\pi \uparrow 1$.

(b) For fixed $\pi \in (1/2,1)$, the function $\varphi _{Y}(\pi )$ is strictly increasing in $Y$ with $\lim _{Y\uparrow 2}\varphi _{Y}( \pi )=\pi$.

For an illustration of the function $\varphi _{Y}$, see Fig. 3 below. The function $\varphi _{Y}$ plays a fundamental role in our main result to follow on the structure of two-sided CGMY processes with given skewness and kurtosis. More precisely, a fixed point problem in terms of $\varphi _{Y}$ determines the fractions

$$ \pi _{2} = \frac{M^{Y-2}}{M^{Y-2}+G^{Y-2}},\qquad \pi _{4} = \frac{M^{Y-4}}{M^{Y-4}+G^{Y-4}}$$

(8.1)

of $\kappa _{2}$ resp. $\kappa _{4}$ provided by positive jumps. Let further $\ell$ be the function given by $\ell (\pi )=\pi /(1-\pi )$, with inverse $\ell ^{-1}(a)=a/(1+a)$.

Fig. 3

The function $\varphi _{Y}(\pi )$

For definiteness, we have taken $\mathring {{S}}>0$ or, equivalently, $\mathring {{\kappa }}_{3}>0$ in the following main result. If $\mathring {{\kappa }}_{3}<0$, as is typical in financial data, one should just proceed as in (8.2a)–(8.2b) and then interchange $M$ and $G$.

Theorem 8.2

Given constants $\mathring {{\kappa }}_{2}>0,\mathring {{\kappa }}_{3}>0,\mathring {{\kappa }}_{4}>0$, an infinite-activity two-sided CGMY process $X$ with given rate parameter $Y$ and cumulants $\kappa _{k}=\mathring {{\kappa }}_{k}$, $k=2,3,4$, exists if and only if $\mathring {{R}}=\mathring {{\kappa }}_{3}^{2}/(\mathring {{\kappa }}_{2}\mathring {{\kappa }}_{4})\le 2/3$ and $0\le Y< Y_{\mathrm {max}}(\mathring {{R}})$, where $Y_{\mathrm {max}}(R)$ is defined as $Y_{\mathrm {max}}(R)=(2-3R)/(1-R)$. In that case, the parameters $C,G,M$ are unique and given by

$$\begin{aligned} M^{2} &= \frac{\pi _{2}\mathring {{\kappa }}_{2}}{\pi _{4}\mathring {{\kappa }}_{4}} \frac{\Gamma (4-Y)}{\Gamma (2-Y)}, \qquad G^{2} = \frac{(1-\pi _{2})\mathring {{\kappa }}_{2}}{(1-\pi _{4})\mathring {{\kappa }}_{4}} \frac{\Gamma (4-Y)}{\Gamma (2-Y)}, \end{aligned}$$

(8.2a)

$$\begin{aligned} C &= \frac{\pi _{2}^{2}\mathring {{\kappa }}^{2}_{2}}{\pi _{4}\mathring {{\kappa }}_{4}} \frac{\Gamma (4-Y)}{\Gamma (2-Y)^{2}}M^{-Y} = \frac{(1-\pi _{2})^{2}\mathring {{\kappa }}^{2}_{2}}{(1-\pi _{4})\mathring {{\kappa }}_{4}} \frac{\Gamma (4-Y)}{\Gamma (2-Y)^{2}}G^{-Y}. \end{aligned}$$

(8.2b)

Here $\pi _{2},\pi _{4}\in (1/2,1)$, $\ell (\pi _{4})=\ell (\pi _{2})^{Q}$, and $\pi _{2}$ is the unique solution in $(1/2,1)$ of the equation $\varphi _{Y}(\pi _{2})=A$, where $A=\mathring {{R}}(3-Y)/(2-Y)$.

Proof

We first consider the case where $\mathring {{\kappa }}_{2}=\kappa _{2} ,\mathring {{\kappa }}_{3}=\kappa _{3},\mathring {{\kappa }}_{4}=\kappa _{4}$ are the cumulants of a two-sided CGMY process. We have $1-\pi _{2}=G^{Y-2}/(M^{Y-2}+G^{Y-2})$ which together with (8.1) gives $\ell (\pi _{2})=(M/G)^{Y-2}$. Since $\kappa _{3}>0$ and $Y-2<0$, we have $M< G$ and so $\pi _{2}\in (1/2,1)$. Similarly, $\ell (\pi _{4})=(M/G)^{Y-4}$, giving $\ell (\pi _{4})=\ell (\pi _{2})^{Q}$, and $\pi _{4}\in (1/2,1)$ follows. In particular, $\pi _{4}$ is determined from $\pi _{2}$ as

$$ \pi _{4} = \frac{\ell (\pi _{2})^{Q}}{1+\ell (\pi _{2})^{Q}} = \frac{\pi _{2}^{Q}}{g_{Y}(\pi _{2})} = \frac{\pi _{2}^{Q}}{\pi _{2}^{Q}+(1-\pi _{2})^{Q}}. $$

(8.3)

Now $\kappa _{3}$ is the difference between the contributions from positive resp. negative jumps, i.e., $\kappa _{3}=\kappa _{3}^{+}-\kappa _{3}^{-}$, where

$$ \kappa _{3}^{+}=C\Gamma (3-Y)M^{Y-3}, \qquad \kappa _{3}^{-}=C \Gamma (3-Y)G^{Y-3}. $$

Here $\kappa _{3}^{+}>\kappa _{3}$ when $\kappa _{3}>0$, so that we can write $\kappa ^{+}_{3}=(1+\theta )\kappa _{3}$, $\kappa ^{-}_{3}=\theta \kappa _{3}$ for some $\theta >0$. Using (6.4) on the positive resp. negative parts, we get

$$ \frac{2-Y}{3-Y} = \frac{(1+\theta )^{2}\kappa _{3}^{2}}{\pi _{2}\kappa _{2} \pi _{4}\kappa _{4}}= \frac{\theta ^{2}\kappa _{3}^{2}}{(1-\pi _{2})\kappa _{2} (1-\pi _{4})\kappa _{4}}, $$

(8.4)

implying $(1+1/\theta )^{2}=\ell (\pi _{2})\ell (\pi _{4})$. Therefore

$$\begin{aligned} \theta &= \frac{1}{\sqrt{\ell (\pi _{2})\ell (\pi _{4})}-1} = \frac{1}{ \ell (\pi _{2})^{Q_{1}}-1} = \frac{(1-\pi _{2})^{Q_{1}}}{h_{Y}(\pi _{2})}, \end{aligned}$$

implying $1+\theta = \pi _{2}^{Q_{1}}/h_{Y}(\pi _{2})$. Also, using (8.4) in the first two steps and (8.3) in the third gives

$$ A=\frac{(1-\pi _{2})(1-\pi _{4})}{ \theta ^{2}}= \frac{\pi _{2}\pi _{4}}{(1+\theta )^{2}}= \frac{ \pi _{2}^{1+Q}}{g_{Y}(\pi _{2})} \frac{h_{Y}(\pi _{2})^{2}}{\pi _{2}^{1+Q}} = \varphi _{Y}(\pi _{2}). $$

The expressions (8.2a), (8.2b) now follow from Proposition 6.1.

Consider next the case of general $\mathring {{\kappa }}_{k}$. By the preceding case, we must have $A<1$ which is equivalent to $Y<(2-3\mathring {{R}})/(1-\mathring {{R}})$. Define $\pi _{2},\pi _{4},C,G,M$ as in (8.2a)–(8.2b). To check that the two expressions for $C$ in (8.2b), say $C_{+}$, $C_{-}$, coincide, we note that the definition of $\pi _{4}$ is equivalent to $\ell (\pi _{4})=\ell (\pi _{2})^{Q}$ and that $1-Q=-2/(2-Y)$ so that

$$ \biggl(\frac{M}{G}\biggr)^{Y-2} = \bigg( \frac{\ell (\pi _{2})}{\ell (\pi _{4})}\bigg)^{(Y-2)/2} = \ell (\pi _{2})^{(1-Q)(Y-2)/2} = \ell (\pi _{2}). $$

The desired conclusion $C_{+}=C_{-}$ then follows from $2-Q=-Y/(2-Y)$ because

$$ \frac{C_{+}}{C_{-}} = \frac{\ell (\pi _{2})^{2}}{\ell (\pi _{4})} \bigg(\frac{M}{G}\bigg)^{-Y} = \ell (\pi _{2})^{2-Q}\pi _{2}^{-Y/(Y-2)} = 1. $$

Let $X$ be the process given by the defined $C,G,M$ and predescribed $Y$. With $\kappa _{k}$ being its cumulants, it remains to check that $\kappa _{2}=\mathring {{\kappa }}_{2},\kappa _{3}=\mathring {{\kappa }}_{3},\kappa _{4}=\mathring {{\kappa }}_{4}$. First, we have

$$\begin{aligned} \kappa _{2} &= C\Gamma (2-Y) (M^{Y-2}+G^{Y-2} ) = C_{+}\Gamma (2-Y)M^{Y-2}+C_{-} \Gamma (2-Y)G^{Y-2}. \end{aligned}$$

Here $C_{+}\Gamma (2-Y)M^{Y-2}$ equals

$$ \frac{\pi _{2}^{2}\mathring {{\kappa }}_{2}^{2}\Gamma (4-Y)}{\pi _{4}\mathring {{\kappa }}_{4}\Gamma (2-Y)}M^{-2} = \frac{\pi _{2}^{2}\mathring {{\kappa }}_{2}^{2}\Gamma (4-Y)}{\pi _{4}\mathring {{\kappa }}_{4}\Gamma (2-Y)} \frac{\pi _{4}\mathring {{\kappa }}_{4}\Gamma (2-Y)}{\pi _{2}\mathring {{\kappa }}_{2}\Gamma (4-Y)} = \pi _{2}\mathring {{\kappa }}_{2}. $$

Analogously, $C_{-}\Gamma (2-Y)G^{Y-2}=(1-\pi _{2})\mathring {{\kappa }}_{2}$ and adding gives $\kappa _{2}=\mathring {{\kappa }}_{2}$. Similarly, $C_{+}\Gamma (4-Y)M^{Y-4}=\pi _{2}\mathring {{\kappa }}_{4}$, $C_{-}\Gamma (4-Y)G^{Y-4}=(1-\pi _{2})\mathring {{\kappa }}_{4}$ and $\kappa _{4}=\mathring {{\kappa }}_{4}$.

Finally, let $\pi _{2}^{\#}$ be the ratio between the parts of $\kappa _{2}$ provided by positive resp. negative jumps of $X$ and $A^{\#}=\kappa _{3}^{2}/(\kappa _{2}\kappa _{4})(3-Y)/(2-Y)$. Then $\varphi _{Y}(\pi _{2}^{\#})=A^{\#}$ by the first case. Also, $\ell (\pi _{2}^{\#})=(M/G)^{Y-2}$ which was shown above to equal $\ell (\pi _{2})$. Hence $\pi _{2}^{\#}=\pi _{2}$, giving $A^{\#}=A$. That $\kappa _{3}=\mathring {{\kappa }}_{3}$ then follows since by the definition of $\pi _{2}$,

$$ \mathring {{\kappa }}^{2}_{3}= \mathring {{\kappa }}_{2}\mathring {{\kappa }}_{4}\frac{2-Y}{3-Y}A=\kappa _{2} \kappa _{4}\frac{2-Y}{3-Y}A^{\#}=\kappa _{3}^{2}. $$

 □

Recall that in the infinite-activity case, $Y$ can take any value in $[0,Y_{\mathrm {max}}(R))$ for fixed $\kappa _{2},\kappa _{3},\kappa _{4}$, where $Y_{\mathrm {max}}(R)=(2-3R)/(1-R)$.

Theorem 8.3

Consider the class of two-sided CGMY models with $\kappa _{2},S>0,K$ fixed and $Y$ varying in $(0,Y_{\mathrm {max}}(R))$. Then:

(a) As $Y\uparrow Y_{\mathrm {max}}(R)$, it holds that $X$ converges in $D[0,\infty )$-distribution to the spectrally positive CGMY process with the same $\kappa _{2},\kappa _{3},\kappa _{4}$.

(b) As $Y\downarrow 0$, it holds that $X$ converges in $D[0,\infty )$-distribution to the sVG process with parameters $\alpha ^{+}=\alpha ^{-}=C_{0}$, $G_{0}$, $M_{0}$, where $C_{0},G_{0},M_{0}$ are given by (8.2a), (8.2b) with $Y=0$, $\pi _{2}$ defined as the solution of $f_{0}(\pi _{2})=3R/2$, and $\pi _{4}$ given by (8.3). Here $\pi _{2},\pi _{4}$ both are in the open interval $(1/2,1)$.

Theorem 8.4

Consider the class of two-sided CGMY models. Then $X^{*}\Rightarrow W$ if either (a) $K\to 0$ or (b) $\limsup K<\infty$ and $Y\uparrow 2$, or (c) $K\to \infty$ and $Y\uparrow 2$ sufficiently fast that $(2-Y)\log K\to 0$.

Remark 8.5

Note that $Y\uparrow 2$ is only possible if $R\to 0$ so that $S\to 0$ in both of (a) and (b). As in the spectrally positive case, $S\to \infty$ is possible in (c).

9 Fitting: further numerical examples

In a fitting perspective, our examples relate to volatility/skewness/kurtosis fitting of historical data. They also illuminate the range of the shape of the log-return density in the CGMY model. Using moment fitting rather than ML is (at least at first sight) appealing since it does not involve calculation of $f(x)$ for many different parameter sets. In contrast, CGMY cumulants are easily calculated, and hence so are the moments.

If “data” refers to series of log-returns over a period, the empirical moments $\stackrel{\circ}{m}_{k}$ are what are readily calculated, but the empirical cumulants $\mathring {{\kappa }}_{k}$ can then be obtained from standard formulas like

$$\begin{aligned} \kappa _{1}&=m_{1},\qquad \kappa _{2}=m_{2}-m_{1}^{2}, \qquad \kappa _{3}=m_{3}-3m_{1}m_{2}+2m_{1}^{3}, \\ \kappa _{4}&=m_{4}-4m_{1}m_{3}-3m_{2}^{2}+12m_{1}^{2}m_{2}-6m_{1}^{4}. \end{aligned}$$

However, “data” may also be a Lévy process, say an NIG process with given parameters to which we want to find a fit by a CGMY process, and in such situations, the cumulants $\mathring {{\kappa }}_{k}$ are usually given by explicit formulas.

The fitting equations $\kappa _{k}=\mathring {{\kappa }}_{k}$, $k=2,3,4$, were solved in Theorem 8.2 for the CGMY model. For the NIG and Meixner processes, the task is not difficult; see Appendices B and C. Again, $R=S^{2}/K=\kappa _{3}^{2}/(\kappa _{2}\kappa _{4})$ plays a fundamental role. The outcome is that always $R<3/5$ for an NIG process (as is well known) and that actually the fitting equations have a unique solution for $\alpha ,\beta ,\delta$ when $\mathring {{R}}=\mathring {{S}}^{2}/\mathring {{K}}<3/5$. In the Meixner case, $R<2/3$ and there is a unique solution for $a,b,d$ when $\mathring {{R}}<2/3$. The quantity $\mathring {{R}}$ also plays an important technical role since looking at the equation $\mathring {{R}}=R$ is a convenient first step in the solution.

Example 9.1

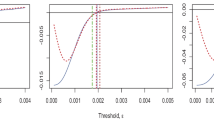
As data skewness $\mathring {{S}}$ and kurtosis $\mathring {{K}}$, we took as one of the more extreme examples in Table 1 those in $\text{N}1^{*}$, the NIG distribution calibrated from S&P500 in Schoutens [50, Sect. 6.3] with the modification that we changed the sign of the skewness from negative to positive. This gives $\mathring {{S}}=2.21$, $\mathring {{K}}=10.6$, $\mathring {{R}}=0.46$, $Y(\mathring {{R}})=1.146$. The NIG parameters are $\alpha =6.19$, $\beta =3.90$, $\delta =0.152$, $m=0$. Moment/cumulant fitting a CGMY process with $\kappa _{2}=1$ for selected values of $Y\in [0,Y(\mathring {{R}}))$ produced the results in Table 2 and Fig. 4 (where for comparison we also included the Meixner cumulant fit).

Fig. 4

Meixner and CGMY cumulant fits of NIG distribution $\text{N1}^{*}$

Table 2 Fitted parameters

Example 9.2

We now turn the situation around and imagine that the data have the shape of the CGMY distribution with $Y=1/3$ in Example 9.1. We then performed ML fitting of an NIG and a Meixner distribution, using that the continuous version of minus log-likelihood is cross-entropy; the estimate is given by

$$ (\alpha ,\beta ,\delta ,m) = \operatorname*{arg\,min}_{\alpha ,\beta ,\delta ,m} - \int \log f_{\alpha ,\beta ,\delta ,m}(x)f_{C,G,M,Y,m}(x)\,\mathrm {d}x$$

in the NIG case, and similarly for Meixner. The results are plotted in Fig. 5. For the maximisation, we used Matlab’s fminsearch routine. The ML fitted NIG parameters came out as $\delta =1.38$, $\alpha =0.790$, $\beta =0.531$, $m= -0.429$, whereas for Meixner they are $a= 2.37$, $b=1.45$, $d=0.177$, $m= -0.408$.

Fig. 5

NIG and Meixner fits of $Y=1/3$ CGMY distribution

Example 9.3

As data, we simulated $N=500$ observations from the $Y=1/3$ CGMY distribution in Example 9.1, corresponding roughly to the number of trading days in two years. From these, we performed ML estimation of $(C,G,M,Y,m)$, using Matlabs fminsearch routine with three different starting points $(C_{0},G_{0},M_{0},Y_{0},m_{0})$ taken as the cumulant fits with different $Y=Y_{0}$. The first was determined by taking a step size 0.01 of $Y$ and using the $Y_{0}=Y$ giving the highest likelihood. For the second, we took $Y_{0}=0.25$, corresponding to a value fairly close to the true 0.33, and the third had $Y_{0}=0.75$, a value quite far from 0.33.

The experiment was repeated a number of times using different seeds for the simulation, and the results of two of these are reported in Table 3 and Fig. 6, resp. Table 4 and Fig. 7. Here C-fit means fitting $C,G,M$ to match the empirical cumulants $\mathring {{\kappa }}_{2},\mathring {{\kappa }}_{3},\mathring {{\kappa }}_{4}$ as in Theorem 8.2, and $m$ then chosen to match $\mathring {{\kappa }}_{1}$. The number $L$ is minus the log-likelihood divided by $N$; for the model, it is reported as the entropy $-\int f(x) \log f(x)\,\mathrm {d}x$, such that by the law of large numbers and consistency of ML estimates, the $L$-values for ML fits should be close to the entropy. The results show that the ML fit may be quite different for different initial conditions of the likelihood maximisation, in particular for the $Y$-component. However, visually the fits are quite similar except possibly very near the mode, and they are also quite close to the C-fits except for the $Y_{0}=0.75$ case.

Fig. 6

Data and fits for first simulated data set

Fig. 7

Data and fits for second simulated data set

Table 3 Fits for first simulated data set

Table 4 Fits for second simulated data set

The picture in the further experiments not reported here was quite similar. Here $Y$ in the C-fits with highest likelihood invariably came out as $Y=Y_{0}=0.11$, and the resulting ML fits had $Y$ in the range 0.07–0.11. For $Y_{0}=0.25$, $Y$ was most often in the range 0.25–0.31, but also values 0.07–0.11 occurred. For $Y_{0}=0.75$, $Y$ was most often in the range 0.07–0.11, but sometimes also in 0.25–0.31. Between the three different initial values of $Y_{0}$, the first (determined from the C-fit with highest likelihood) always gave the highest likelihood (meaning smallest $L$) of the corresponding ML fit.

10 Choosing $Y$

How to choose $Y$ depends on the context and we have no universal recommendation. Some possibilities follow.

1) An obvious follow-up of the procedure of fitting the first four moments is to choose $Y$ to fit the 5th or 6th moment or, equivalently, cumulants 5 or 6. A difficulty is that empirical higher-order cumulants have a very substantial statistical uncertainty. Financial data are often nearly symmetric, and one would therefore expect this uncertainty to be particularly marked for the 5th cumulant. For example, in our $\sigma =1$, $K=10.6$ case in Examples 9.1, 9.2, with $S$ changed from 2.21 to 0, the correct values of cumulants 4–6 are 10.6, 0, 433, whereas simulation estimates of the standard deviation on the empirical values with the given sample size $N=500$ were 10.1, 114, 433. For an attempt to remedy such problems, see Hosking [25]. An explicit formula for fitting the 6th cumulant or, equivalently, $R_{4}$ was given in Proposition 7.1(b) for the purely symmetric case. For skewed data, we have no other suggestion than to search through a range of $Y$-values. Computationally, this is very fast.

2) If the aim is to fit the center of the distribution, maximum likelihood is the approach which is precisely designed to perform this task. For the CGMY process, the maximisation has to be done by a numerical algorithm, typically requiring starting values of the parameters $m,C,G,M,Y$. Our study in Example 9.3 indicates that different choices of this starting value may lead to quite different ML estimates, in particular of $Y$ (we have not seen this observation in the literature). Figures 4, 5 clearly show that doing moment fitting alone has its pitfalls. We therefore think that using some form of the more demanding ML procedure cannot be dispensed with. For CGMY, Example 9.3 indicates that the likelihood surface may have a quite intricate form with local maxima, so that an ML search should be performed from different starting points for the same data. However, it is also suggested that the moment fit with the $Y$ giving the highest likelihood is quite close to the global ML fit. These observations are of course preliminary, and more research is required. For computing the log-likelihood, our use of the connection of $f(x)$ to stable densities appears to be more straightforward than the traditional use of Fourier inversion.

3) In the ML setup in 2), the parameters are most often not of intrinsic interest – different sets are of equal quality if they match the data equally well. A context where the particular value of $Y$ is crucial is, however, finer path properties. In a wider Lévy process perspective, $Y$ plays the role of the so-called Blumenthal–Getoor index which is known to govern many such properties. One may estimate $Y$ from this point of view via the sample path $p$-variation; see for example Norvaiša and Salopek [38], Aït-Sahalia and Jacod [1] and references there.

4) In problems like pricing far-from-the-money options, the tail of the underlying return distribution plays a crucial role. All of the tails in CGMY, NIG, Meixner, VG, etc., models are semi-heavy, meaning $\mathbb{P}[X_{1}>x ]\sim \delta \mathrm {e}^{-\beta x}x^{\eta}$ as $x\to \infty$, for some $\delta ,\beta ,\eta$. For CGMY, integration in Corollary 6.4 and (6.8) gives $\beta =M,\eta =-1-Y$, and one could find the $\widehat{M}$ with the best match of the empirical tail by using the Hill estimator (see e.g. Resnick [41, Sect. 4.4]) to the exponentiated data which under the CGMY model have asymptotic tail $x^{-M}h(x)$, where $h(x)=\delta /(\log x)^{1+Y}$. However, it is generally considered impossible among statisticians to estimate features such as $Y$ of the slowly varying function $h$. One would therefore rather as in 1) search through a range of $Y$-values to find the $Y$ making the moment-matched $M$ equal to $\widehat{M}$.

Viewing $R_{4}=R_{4}(K,R,Y)$, $M=M(K,R,Y)$, $G=G(K,R,Y)$ as functions of $K,R,Y$ for a fixed $\kappa _{2}$, we computed $R_{4},M,G$ for $\kappa _{2}=1$ in a range of the parameter set $K,R,Y$ and the range $0.01< Y/Y_{\mathrm {max}}(R)<0.95$. The numerical results indicate that $R_{4}$ does not depend on $K$, whereas $M$ scales as $1/K$ and $G$ as $K$. That is,

$$\begin{aligned} R_{4}(K,R,Y) &\equiv R_{4}(1,R,Y), \\ M(K,R,Y)&=\frac{1}{K}M(1,R,Y), \\ G(K,R,Y)&=KG(1,R,Y). \end{aligned}$$

For these reasons, we have only taken $K=1$ in Fig. 8, illustrating the shape of the functions $R_{4},M,G$.

Fig. 8

Selected characteristics as function of $Y/Y_{\mathrm {max}}(R)$ for $K=1$: (left) $R_{4}$, (middle) $M$, (right) $G$

11 Concluding remarks

Our starting point was a wish to look into some frequently occurring heuristics in the financial literature: that a non-zero kurtosis explains a sharper mode of the empirical log-returns than would be compatible with the Black–Scholes model, and that quantitatively, a model fitting the empirical kurtosis $\mathring {{K}}$ would give a good fit around the mode. We investigated these features for CGMY, but we also touched upon two other popular Lévy models, NIG and Meixner.

The outcome was not that supportive of this heuristics: models with the same kurtosis $K$ may lead to quite different shapes of the log-return density $f(x)$ around the mode; cf. the right panels in Figs. 1, 2 and 4, 5. However, for the CGMY model, these differences could largely be removed by taking into account the value of the parameter $Y$, which was found to be subject to choice even for given values of the first four moments/cumulants. One of our main findings is that in the range $Y< Y_{\mathrm {max}}(R)$, there is a one-to-one correspondence and that in this range, the shape of the log-return distribution is quite variable. In particular, it is not universally true that the kurtosis $K$ alone governs the sharpness of the mode and heaviness of the tails; one needs to take also the value of $Y$ into account. These and related features were substantiated by a number of limit results, proved in various different settings according to which parameters/cumulants are fixed and which are varying.

Some further remarks:

1) Lévy models capture some stylised facts of the log-returns like the presence of jumps, distributions with a different shape than the normal (more marked modes and heavier tails), but certainly not all. One exception is the autocorrelation of the squared returns. Extensions covering this are time-transformed Lévy models (Carr et al. [12]) or regime-switching ones (Asmussen and Bladt [4] and references there).

2) Theorem 1.2 can alternatively also be derived from bounds in terms of the $W_{p}$-Wasserstein distance, which in the simplest case of distributions on the line with cumulative distribution functions $F_{1},F_{2}$ has the form

$$ W_{p}(F_{1},F_{2}) = \int _{0}^{1} |F_{1}^{-1}(q)-F_{2}^{-1}(q) |^{p} \,\mathrm {d}q. $$

In particular, Fomichov et al. [20, Lemma 2.1] states that the $W_{2}$-distance between the distribution of $X^{*}_{1}$ and the standard normal distribution is bounded by $C_{4}\sqrt{K}$ for some $C_{4}$. Since $W_{p}$-convergence implies weak convergence, this gives part (a) of Theorem 1.2 as well as the upper bound ${\mathrm {O}}(\sqrt{K})$ on the rate of $W_{2}$-Wasserstein convergence. The $C_{4}$ originates from Berry–Esseen-type CLT bounds in [42, Theorem 4.1] (see also Mariucci and Reiss [35, Theorem 5]), but numerical values do not appear to be easily available. Thus the $C_{4}\sqrt{K}$ bound is hardly quantitative.

Similarly, replacing Rio [42, Theorem 4.1] by Petrov [39, Theorem 16] gives a bound $C_{3}S$ on the $W_{1}$-Wasserstein distance in the spectrally positive case, giving part (b) of Theorem 1.2. Similar results for the Kolmogorov distance can be obtained using the ordinary Berry–Esseen bound or the Wasserstein distance via Petrov [39, 1.8.32] and Huber and Ronchetti [26, Corollary 4.3].

It also follows from Fomichov et al. [20, Corollary 3.3] that the $W_{2}$-distance between the trajectories of $X^{*}$ and BM $W$ on a compact interval can be bounded by a multiple of $(K\log K)^{1/4}$. Financially, this is of relevance when dealing with path-dependent options, e.g. of Asian or barrier type.

3) For a given set of data, cumulant inequalities like those of Sect. 5 may provide guidelines on which model to choose or not to choose. For example, if the empirical value of $R=\kappa _{3}^{2}/ (\kappa _{2}\kappa _{4})=S^{2}/K$ fails to satisfy $\mathring {{R}}\le 1$, this is an indication that a Lévy model may not be appropriate. Similarly, $\mathring {{R}}$ being less than 1 but quite close could be taken as a warning not to use any of CGMY, NIG, Meixner, VG or any other completely monotone class of Lévy models. Similar remarks apply to $R_{4}= \kappa _{4}^{2}/(\kappa _{2}\kappa _{6})$. Here the range is $(0,0.30]$ for CGMY, with the more narrow intervals $[0.171,0.238]$ for NIG and $[0.240,0.340]$ for Meixner (see also the numerical values reported in Table 1). This illustrates also that as a 5-parameter family, CGMY is potentially a more flexible class than the 4-parameter NIG and Meixner ones. Our limited number examples did, however, not include cases where CGMY fits the shape of financial returns better than NIG or Meixner.

Appendices

Appendix A: Proofs

In this Appendix, we slightly change notations. The time index $t$ of a stochastic process is not written with a subscript as in $X_{t}$, but with an argument in brackets as in $X(t)$.

Various techniques for proving functional limit theorems have been outlined in Sect. 3. We add here that even if subtraction is not continuous in $D[0,\infty )$, it is so in ℝ, and it therefore suffices to establish a limit of $X(1)$ or $X^{*}(1)$ separately for the positive and negative parts and then subtract. We also repeatedly use the fact from analysis that for the convergence $x\to x_{\infty}$ in a metric space, say $D[0,\infty )$, it suffices that every subsequence $(x_{n})$ of $x$ has a further subsequence $(x_{n_{k}})$ such that $x_{n_{k}}\to x_{\infty}$ as $k\to \infty$.

Proof of Theorem 1.2

(a) Consider a sequence $(X_{n})$ of Lévy processes. We can write $X^{*}_{n}=(1-\sigma _{n}^{2})^{1/2}W+J^{*}_{n}$, where $J^{*}_{n}$ is the jump part with Lévy measure, say, $\nu _{n}$ and centered to mean 0 and $\mathrm {Var}[X_{n}^{*}(1)]=1$. Thus the cumulants are $\kappa _{1,n}=0$, $\kappa _{2,n}=1$ and

$$ \kappa _{k,n} = \int _{-\infty}^{\infty }x^{k}\nu _{n}(\,\mathrm {d}x), \qquad k=3,4,\ldots $$

Further, we have $\int x^{2}\nu _{n}(\,\mathrm {d}x)=\sigma _{n}^{2}$. The assumption is that $\kappa _{4,n}\to 0$, and we must prove that $X_{n}(1)\Rightarrow V$, where $V$ is standard normal.

Consider first the pure jump case $\sigma _{n}^{2}=\kappa _{2,n}=1$. If each $\nu _{n}$ is concentrated on $\{x:|x|\le 1\}$, we have for $k>4$ that $\kappa _{k,n}\le \kappa _{4,n}$ and hence $\kappa _{k,n}\to 0$. Also $\kappa _{3,n}\to 0$ since $\kappa _{3,n}^{2}\le \kappa _{2,n}\kappa _{4,n}\to 0$ by a general Lévy process inequality. Thus all cumulants and hence all moments converge, which is sufficient (e.g. Kallenberg [28, Chap. 5, Exercise 11]). In the case of a general support of the $\nu _{n}$, write $X_{n}(1)= X_{n}'(1)+ X_{n}''(1)$, where $X_{n}'(1)$ is the part of $X_{n}(1)$ coming from jumps of sizes $x$ with $|x|>1$ and $X_{n}''(1)$ the rest. Then

$$ \mathrm {Var}[X_{n}''(1) ] = \int _{\{|x|>1\}}x^{2}\nu _{n}(\,\mathrm {d}x) \le \int _{-\infty}^{\infty }x^{4}\nu _{n}(\,\mathrm {d}x) = \kappa _{4,n} \longrightarrow 0.$$

Thus $X_{n}''(1)\to 0$ and $\mathrm {Var}X_{n}'(1)\to 1$ so that we can neglect $X_{n}''(1)$ and use what was proved for the finite support case to get $X_{n}'(1)\Rightarrow V$ and hence $X_{n}(1)\Rightarrow V$.

In the presence of a Brownian component, it suffices to show that each subsequence has a further subsequence $(n_{k})$ with $X_{n_{k}}(1)\Rightarrow V$. This is clear if $\sigma _{n}^{2}\to 0$ along the subsequence. Otherwise, we can choose $n_{k}$ with $\sigma _{n_{k}}^{2}\to \sigma ^{2}$ for some $0<\sigma ^{2}\le 1$. Define $\widetilde{J}_{n}=J_{n}/\sigma _{n}$. Then the pure jump process $\widetilde{J}_{n}$ has mean 0, variance 1 and cumulants $\widetilde{\kappa}_{k,n}=\kappa _{k,n}/\sigma _{n}^{k}$, $k>2$. Thus $\widetilde{\kappa}_{4,n}\to 0$ because $\sigma ^{2}>0$, and we can use what was already proved to conclude that $\widetilde{J}_{n_{k}}(1)\Rightarrow \widetilde{V}$. Hence

$$\begin{aligned} X_{n_{k}}(1) = (1-\sigma _{n_{k}}^{2})^{1/2}W(1)+ \sigma _{n_{k}}\widetilde{J}_{n_{k}}(1) \Longrightarrow (1-\sigma ^{2})^{1/2}W(1)+ \sigma \widetilde{V}\ \stackrel{d}{=} \ V. \end{aligned}$$

The proof of (b) is almost the same, noting that by positivity we can replace the bounds in terms of $\kappa _{4,n}$ by bounds in terms of $\kappa _{3,n}$. □

Proof of Proposition 5.1

Adding a Brownian component increases $\kappa _{2}$, but leaves $\kappa _{3},\kappa _{4},\ldots$ unchanged, so that we may assume that $X$ has no Brownian component. Let $Z$ be a random variable with $\mathbb{P}[Z\in \mathrm {d}x]= x^{2}\nu (\mathrm {d}x)/\kappa _{2}$. Then $\mathbb{E}[Z^{k}]=\kappa _{k+2}/\kappa _{2}$, and thus the inequality $\mathbb{E}[Z^{2}] \ge (\mathbb{E}[Z])^{2}$ means that $\kappa _{3}^{2}/(\kappa _{2}\kappa _{4})\le 1$ as claimed in the first part. Equality holds if and only if $Z$ and then $\nu$ is degenerate at some $z_{0}$ (then $\lambda =\nu (\{z_{0}\})$.

For the second part, assume that we have $n(x)=\int _{0}^{\infty }\mathrm {e}^{-ax}\,V^{+}(\mathrm {d}a)$ for $x>0$ and $n(x)=\int _{0}^{\infty }\mathrm {e}^{-a|x|}\,V^{-}(\mathrm {d}a)$ for $x<0$, so that

$$ \kappa ^{\pm}_{k} = \int _{0}^{\infty }x^{k} \int _{0}^{\infty } \mathrm {e}^{-ax}\,V^{\pm}(\mathrm {d}a). $$

Define $V=V^{+}+V^{-}$. Using that an $\text{exponential}(a)$ random variable $U_{a}$ has the $k$th moment $k!/a^{k}$, we get that for $k$ even,

$$\begin{aligned} \kappa _{k} = \kappa _{k}^{+} + \kappa _{k}^{-} &= \int _{0}^{\infty }x^{k} \int _{0}^{\infty }\mathrm {e}^{-ax}\,V(\mathrm {d}a)\,\mathrm {d}x \\ & = \int _{0}^{\infty }\int _{0}^{\infty }x^{k}\mathbb{P}[U_{a}\in \mathrm {d}x]\,a^{-1}V(\mathrm {d}a)\,\mathrm {d}x \\ & = k! \int _{0}^{\infty }a^{-k-1}V(\mathrm {d}a) = k! \, \kappa _{4} \mathbb{E}[Z^{4-k}/4!], \end{aligned}$$

where now $Z$ has distribution

$$ \mathbb{P}[Z\in \mathrm {d}a] = \frac{a^{-5}V(\mathrm {d}a)}{\int _{0}^{\infty }b^{-5}V(\mathrm {d}b)} = \frac{a^{-5}V(\mathrm {d}a)}{\kappa _{4}/4!}.$$

(A.1)

Similarly,

$$ |\kappa _{k}| \le \kappa _{k}^{+} +\kappa _{k}^{-} = k!\,\kappa _{4} \mathbb{E}[Z^{4-k}]/4! \qquad \text{for }k\text{ odd}.$$

(A.2)

Since $\mathbb{E}[Z^{0}]=1$, this gives

$$ \frac{S^{2}}{K} = \frac{\kappa _{3}^{2}}{\kappa _{2}\kappa _{4}} \le \frac{(3!\,\kappa _{4}\mathbb{E}[Z]/4!)^{2}}{(2!\,\kappa _{4}\mathbb{E}[Z^{2}]/4! )( 4!\,\kappa _{4}\mathbb{E}[Z^{0}]/4!)} \le \frac{6^{2}}{2\cdot 24} = \frac{3}{4}. $$

Equality holds if and only if $Z$ and then $V$ is degenerate at some $a_{0}$. However, the inequality in (A.2) is strict if $X$ is spectrally two-sided. Thus the necessary and sufficient condition for equality is that $X$ is either spectrally positive with $V=V^{+}$ degenerate at some $a_{0}$ or spectrally negative with $V=V^{-}$ degenerate at some $-a_{0}$. □

Remark A.1

The methods in the proof of Proposition 5.1 give similar bounds on other normalised cumulants. For example, for a spectrally positive finite-variation process, we get $\kappa _{3}\kappa _{4}\le \kappa _{2}\kappa _{5}$ and (use Hölder’s inequality with $\mathbb{P}[Z\in \mathrm {d}x]= x\nu (\mathrm {d}x)/\kappa _{1}$) also $\kappa _{2}^{2}\le \kappa _{1}\kappa _{3}$.

Proof of Proposition 5.2

For the first part, let $Z$ be as in the first part of the proof of Proposition 5.1. Then just use $(\mathbb{E}[Z^{2}])^{2}\le \mathbb{E}[Z^{4}]$, with equality if and only if $Z^{2}$ is degenerate at some $z_{0}^{2}$ (then $\lambda ^{+}=\nu (\{z_{0}\})$, $\lambda ^{-}=\nu (\{-z_{0}\})$). For the second part, use that $\mathbb{E}[Y^{-1}]\ge (\mathbb{E}[Y])^{-1}$ for $Y>0$ by Jensen’s inequality and the convexity of $y\mapsto 1/y$, $y>0$. Taking $Y=Z^{2}$ with now $Z$ as in (A.1), this gives

$$ \frac{\kappa _{4}^{2}}{\kappa _{2}\kappa _{6}} = \frac{\kappa _{4}^{2}}{(2!\,\kappa _{4}\mathbb{E}[Z^{2}]/4! )( 6!\,\kappa _{4}\mathbb{E}[Z^{-2}]/4!)} \le \frac{1}{(1/12)\cdot 30} = \frac{2}{5}. $$

Equality holds if and only if $Z^{2}$ is degenerate at some $a_{0}^{2}$, which is the same as the stated condition. □

Proof of Proposition 5.3, range of $R_{4}$ for CGMY

Assume without loss of generality that $G<\infty$ and let $\rho =M/G$. Then

$$\begin{aligned} R_{4}\ &= \frac{\Gamma (4-Y)^{2}}{\Gamma (2-Y)\Gamma (6-Y)} \frac{(M^{Y-4}+G^{Y-4})^{2}}{(M^{Y-2}+G^{Y-2})(M^{Y-6}+G^{Y-6})} \\ &= \frac{(2-Y)(3-Y)}{(4-Y)(5-Y)} \frac{\rho ^{2Y-8}+1+2\rho ^{Y-4}}{\rho ^{2Y-8}+1+\rho ^{Y-2}+\rho ^{Y-6}} \\ & \le \frac{(2-Y)(3-Y)}{(4-Y)(5-Y)}, \end{aligned}$$

(A.3)

where the last step follows from $(2\rho ^{Y-4})/(\rho ^{Y-2}+\rho ^{Y-6})=(2\rho ^{2})/(\rho ^{4}+1)$ and the inequality $2z\le 1+z^{2}$ with $z=\rho ^{2}$. Here the right-hand side of (A.3) decreases monotonically from $3/5$ to 0 as $Y$ increases from 0 to 2, with $R_{4}=3/10$ if and only if $Y=0$, $\rho =1$. □

Proof of Lemma 8.1

(a) Continuity of $\varphi _{Y}$ is clear, as well as $\varphi _{Y}(1/2)=0$, $\varphi _{Y}(1)=1$. Also, by elementary calculus, one gets $f'_{Y}=h_{Y}k_{Y}/g_{Y}^{2}$, where

$$ k_{Y}(\pi ) = 2g_{Y}(\pi )h'_{Y}(\pi )-h_{Y}(\pi )g'_{Y}(\pi ) = \pi ^{P}+(1- \pi )^{P}+(3Q+1)\pi ^{P}(1-\pi )^{P}$$

with $P=(3Q-1)/2$. Here $g_{Y}(\pi )$ and $k_{Y}(\pi )$ are obviously strictly positive for $\pi \in [1/2,1]$, and $h_{Y}(\pi )$ is equally so for $\pi \in (1/2,1)$. This implies $f'_{Y}(\pi )>0$ for $\pi \in (1/2,1)$ and the strictly increasing property. That $\varphi _{Y}(\pi )\sim 1-\pi$ as $\pi \uparrow 1$ follows since then $g_{Y}(\pi )\sim 1$, $h_{Y}(\pi )\sim 1$, $k_{Y}(\pi )\sim 1$ and hence $f'_{Y}(\pi )\sim 1$.

(b) Let $L=L(\pi )=\ell (1-\pi )=(1-\pi )/\pi$ and $T=1/(2-Y)$, so that $L<1$ and $Q=1+2T$, $Q_{1}=1+T$. We can write

$$\begin{aligned} \varphi _{Y}(\pi ) = \frac{ (\pi \pi ^{T}-(1-\pi )(1-\pi )^{T} )^{2}}{\pi \pi ^{2T}+(1-\pi )(1-\pi )^{2T}} = \pi \frac{(1-L^{1+T})^{2}}{1+L^{1+2T}} \end{aligned}$$

(for the second expression, multiply both the numerator and denominator by $\pi ^{-2T}$). Since $L<1$, $L^{T}$ is a strictly decreasing function of $T$ and hence of $Y$, implying $\varphi _{Y}(\pi )$ to be strictly increasing in $Y$. Since $L<1$ and $T\to \infty$, we have $L^{T}\to 0$ for such a fixed $\pi$, giving $\varphi _{Y}(\pi )\to \pi$. □

Proof of Proposition 6.7

Parts (a) and (b) are direct corollaries of parts (a) resp. (b) of Theorem 1.2. For part (c), we use characteristic functions together with

$$\begin{aligned} M^{*} &= \sqrt{\frac{(2-Y)(3-Y)}{K}} = \sqrt{ \frac{R(3-Y)^{2}}{K(1-R)}}, \end{aligned}$$

(A.4)

$$\begin{aligned} \kappa ^{*}(s) &= \frac{{M^{*}}^{2}}{Y(Y-1)}\bigl((1-s/M^{*})^{Y}-1 \bigr)+s\frac{M^{*}}{Y-1}, \end{aligned}$$

(A.5)

as follows from Proposition 6.1 and $\kappa ^{*}_{2}=1$. Here (A.5) holds for $Y\ne 0,1$ and the final term is needed to ensure ${\kappa ^{*}}'(0)=0$. Now $2-Y=R/(1-R)$ and so (A.4) gives first that $Y\to 2$, $M^{*}\to 0$ and next that

$$\begin{aligned} & |(1-\mathrm {i}s/M^{*})^{Y-2} | \\ &= {M^{*}}^{2-Y}\bigl(1+{\mathrm {o}}(1)\bigr) = \exp \big((2-Y)\log M^{*} \big)\bigl(1+{\mathrm {o}}(1)\bigr) \\ &= \exp \bigg(\frac{R}{1-R}\bigl(\log R/2-\log K/2-\log (1-R)/2+ {\mathrm {o}}(1)\big)\bigg)\bigl(1+{\mathrm {o}}(1)\bigr) \\ & = \exp \big({\mathrm {o}}(1)\big)\bigl(1+{\mathrm {o}}(1)\bigr) = 1+{\mathrm {o}}(1). \end{aligned}$$

Here we used that $R\log K\to 0$ and $K\to \infty$ implies $R\to 0$ and hence $R\log R\to 0$. Hence by (A.5),

$$\begin{aligned} \kappa ^{*}(\mathrm {i}s) &= \frac{{M^{*}}^{2}}{Y(Y-1)}\Big((1-\mathrm {i}s/M^{*})^{2} \big(1+{\mathrm {o}}(1)\big)-1\Big)+\mathrm {i}s\frac{{M^{*}}}{Y-1} \\ &= \frac{{M^{*}}^{2}}{Y(Y-1)}(1-\mathrm {i}s/M^{*})^{2}{\mathrm {o}}(1)+ \frac{{M^{*}}^{2}}{Y(Y-1)}\bigl((1-\mathrm {i}s/M^{*})^{2}-1\bigr) + \mathrm {i}s\frac{{M^{*}}}{Y-1} \\ &= {\mathrm {o}}(1)+ \frac{{M^{*}}^{2}}{Y(Y-1)} (-s^{2}/{M^{*}}^{2}-2 \mathrm {i}s/M^{*} ) +\mathrm {i}s\frac{{M^{*}}}{Y-1} \\ &= {\mathrm {o}}(1)-\frac{s^{2}}{2+{\mathrm {o}}(1)}+\mathrm {i}s \frac{{M^{*}}}{Y-1}\bigg(1-\frac{2}{Y}\bigg) = -\frac{s^{2}}{2}+ {\mathrm {o}}(1). \end{aligned}$$

 □

Proof of Proposition 6.8

The gamma distribution of $X(1)$ corresponding to the asserted limit has cumulant generating function $-\kappa _{2}\gamma ^{2}\log (1-s/\gamma )$ for $s< M$; so it suffices to prove that $\kappa (s)$ has this asymptotic form. But $R\uparrow 2/3$ implies $Y\downarrow 0$ and $M\to \sqrt{6\kappa _{2}/\kappa _{4}}= \gamma$, and so by (6.3f),

$$\begin{aligned} \kappa (s) &= \frac{\kappa _{2}}{Y(Y-1)}M^{2-Y}\bigl((M-s)^{Y}-M^{Y} \bigr) \\ & = \frac{\kappa _{2}}{Y(Y-1)}M^{2}\Big(\exp \big(Y\log (1-s/M)\big)-1 \Big) \\ \vspace{-5mm} &\sim \frac{\kappa _{2}}{Y-1}\gamma ^{2}\log (1-s/M)\ \sim -\sigma ^{2} \gamma ^{2}\log (1-s/M). \end{aligned}$$

 □

Proof of Proposition 7.2

This is almost immediate from Proposition 6.7 and the positive and negative parts of a non-skewed CGMY process being identical. One just needs to notice that the $R$ of these is given by $R=(2-Y)/(3-Y)$, cf. (6.4), so that $(2-Y)/K\to \infty$ is equivalent to $R/K\to \infty$. Further, in $C$, one needs to replace $\kappa _{2}$ by $\kappa ^{+}_{2}=\kappa _{2}/2$. □

Proof of Theorem 8.3

(a) That $Y\uparrow Y_{\mathrm {max}}(R)$ is equivalent to $A\uparrow 1$ and hence by an easy continuity argument, we then have $\pi _{2}\uparrow 1$. This implies

$$\begin{aligned} \pi _{4}&=\frac{\pi _{2}^{Q}}{(1-\pi _{2})^{Q}+\pi _{2}^{Q}}\sim \frac{1}{0+1}=1, \\ \ 1-\pi _{4}&=\frac{(1-\pi _{2})^{Q}}{(1-\pi _{2})^{Q}+\pi _{2}^{Q}} \sim (1-\pi _{2})^{Q}={\mathrm {o}}(1-\pi _{2}). \end{aligned}$$

The expressions for $C,G,M$ then show that $G\to \infty$ and that $M$ and $C$ have the limits given by Proposition 6.1. This proves (a).

(b) First, $Y\to 0$ is equivalent to $A\to 3R/2$. Since $3R/2$ is an interior point of $(0,1)$, the limit $\pi _{2}$ of the solution to $\varphi _{Y}(\pi _{2})=A$ is indeed as asserted. The rest is then easy. □

Proof of Theorem 8.4

We establish (a) and (b) by showing that (d) $K(2-Y)\to 0$ implies $S^{+}\to 0$ and $S^{-}\to 0$. By Theorem 1.2(b), this gives that both $({X^{+}})^{*}$ and $({X^{-} })^{*}$ have Brownian limits. Hence so has $X^{*}$ as desired. Now

$$ K^{+}=\frac{\kappa _{4}^{+}}{({\kappa _{2}^{+}})^{2}}= \frac{\pi _{4}\kappa _{4}}{\pi _{2}^{2}\kappa _{2}^{2}}= \frac{\pi _{4}}{\pi _{2}^{2}}K,\qquad \text{and similarly} \qquad K^{-}= \frac{1-\pi _{4}}{(1-\pi _{2})^{2}}K. $$

(A.6)

Since $\pi _{2},\pi _{4}\in [1/2,1)$, this gives that $(S^{+})^{2}=K^{+}R^{+}=K^{+}(2-Y)/(3-Y)\to 0$ as desired. Similarly, $({S^{-}})^{2}=K^{-}(2-Y)/(3-Y)\to 0$ except when possibly $\pi _{2}\to 1$ along some subsequence. However, then ${X^{-}}$ can be ignored in the limit.

The proof of (c) is a similar application of (A.6), only using Proposition 6.7(c) instead of Theorem 1.2(b). □

Appendix B: NIG

The density of $X_{1}$ is

$$\frac{\alpha \delta }{\pi }\exp \bigg(\delta \sqrt{\alpha ^{2}-\beta ^{2}} +\beta (x-\mu )\bigg) \frac{K_{1} (\alpha \sqrt{\delta ^{2}+(x-\mu )^{2}} )}{\sqrt{\delta ^{2}+(x-\mu )^{2}}}, $$

which is called the $\text{NIG}(\alpha ,\beta ,\mu ,\delta )$ density; $\alpha$ is the tail heaviness of steepness, $\beta$ is the skewness, $\delta$ is the scale, and $\mu$ is the location. For the density of $X_{t}$, just replace $\delta$ by $\delta t$ and $\mu$ by $\mu t$. Numerically, we just used Matlab’s besselk routine for $K_{1}$. Scaling by $v$ changes the parameters to $\alpha v$, $\beta v$, $\delta /v$.

The cumulants are

$$ \kappa _{k} = \delta \frac{q_{k}(\beta )}{(\alpha ^{2}-\beta ^{2})^{k-1/2}},\qquad k\ge 2,$$

(B.1)

where the polynomials $q_{k}$ are given by the recurrence relation

$$ q_{k}(s) = (\alpha ^{2}-s^{2})q'_{k-1}(s)+(2k-3)sq_{k-1}(s)$$

starting from $q_{2}(s)=\alpha ^{2}$. In particular,

$$\begin{aligned} q_{3}(\beta ) &= 3\alpha ^{2}\beta ,\qquad q_{4}(\beta )=3\alpha ^{4}+12 \alpha ^{2}\beta ^{2}, \qquad q_{5}(\beta ) = 45\alpha ^{4}s+60 \alpha ^{2}\beta ^{3}, \\ q_{6}(\beta ) &= 45\alpha ^{6}+540\alpha ^{4}\beta ^{2}+360\alpha ^{2} \beta ^{4}. \end{aligned}$$

These expressions for the $\kappa _{k}$ with $k\le 4$ are classical for $k\le 4$, while for $k>4$, we refer to Asmussen and Bladt [4]. With $\rho =\beta ^{2}/\alpha ^{2}$, we get

$$R = \frac{q_{3}(\beta )^{2}}{q_{2}(\beta )q_{4}(\beta )} = \frac{3\rho}{1+4\rho}, \qquad R_{4} = \frac{q_{4}(\beta )^{2}}{q_{2}(\beta )q_{6}(\beta )} = \frac{(1+4\rho )^{2}}{5+60\rho +40\rho ^{2}}. $$

Letting $\rho$ vary from 0 to 1 shows that $R$ ranges from 0 to $3/5=0.6$. For $R_{4}$, the range is $[0.171,5/21)=[0.171,0.238)$.

Proposition B.1

Given values $\mathring {{\kappa }}_{1},\mathring {{\kappa }}_{2},\mathring {{\kappa }}_{3},\mathring {{\kappa }}_{4}$, an NIG process satisfying $\kappa _{k}=\mathring {{\kappa }}_{k}$ for $k=1,2,3,4$ exists if and only if $\mathring {{R}}=\mathring {{S}}^{2}/\mathring {{K}}\le 3/5$. In that case, the fitted parameters can be computed by first letting $\rho = \mathring {{R}}/(3-5\mathring {{R}})$ and then

$$\begin{aligned} \alpha = \frac{1}{1- \widehat {{\rho }}}\sqrt{ \frac{3\mathring {{\kappa }}_{2}(1+4\rho )}{\mathring {{\kappa }}_{4}}}, \qquad \beta ={\mathrm{sign}}( \mathring {{\kappa }}_{3}) \alpha \sqrt{\rho}, \\ \delta =\frac{1}{\alpha ^{2}}\mathring {{\kappa }}_{2}(\alpha ^{2}-\beta ^{2})^{3/2}, \qquad m=\mathring {{\kappa }}_{1}- \frac{\delta \beta}{\sqrt{\alpha ^{2}-\beta ^{2}}}. \end{aligned}$$

Note that related results are given in Eriksson et al. [18] and Ghysels and Wang [21].

Proof of Proposition B.1

With $\rho =\beta ^{2}/\alpha ^{2}$, we have

$$ R=\frac{3\rho /4}{\rho +1/4} = \frac{3}{4} \bigg(1-\frac{1}{4\rho +1} \bigg) $$

which increases monotonically from 0 to $3/5$ as $\rho$ varies from 0 to 1. We also get $\rho =R/(3-5R)$. The stated expression for $\alpha$ then follows from

$$ \frac{\kappa _{4}}{\kappa _{2}} = \frac{3(\alpha ^{2}+4\beta ^{2})}{(\alpha ^{2}-\beta ^{2})^{2}} = \frac{3(1+4\rho )}{\alpha ^{2}(1-\rho )^{2}}, $$

and those for $\beta$, $\delta$ from $\rho =\beta ^{2}/\alpha ^{2}$ resp. (B.1) with $k=2$. □

Appendix C: Meixner

Some basic references are Schoutens [49], [50, Chap. 5] and Mozzola and Muliere [36]. It is the special case $b^{+}=b^{-}$ of the generalised $z$-process in Grigelionis [23], for which $b$ is allowed to take different values $b^{+},b^{-}$ for $x>0$ resp. $x<0$. The cumulant function and the mean/variance/skewness/kurtosis are

$$\begin{aligned} \kappa (s) &= 2d\log \bigl(\cos (b/2)\bigr)-2d\log \big(\cos (as+b)/2 \big)+ms, \\ \kappa _{1}&=m+da\tan (b/2),\qquad \kappa _{2}=d \frac{a^{2}}{2\cos ^{2}(b/2)}, \\ S&=\frac{\sin b}{\sqrt{d(\cos b+1)}}=\frac{1}{\sqrt{d}}\sqrt{2}\sin (b/2), \qquad K=\frac{1}{d}\bigl(3-2\cos ^{2}(b/2)\bigr). \end{aligned}$$

Letting $t(s)=\tan ((as+b)/2) )$ and using that the derivative of $\tan x$ is $1+\tan ^{2} x$, one gets from $\kappa ^{(1)}(s)=dat(s)$ that $\kappa ^{(k)}(s)$ is a polynomial $p_{k}(t(s))$ of degree $k$ in $t(s)$, given by the recursion

$$ p_{k}(x) = \frac{a}{2}p'_{k-1}(x)(1+x^{2}), \qquad k\ge 2.$$

Thus the cumulants are $\kappa _{k}=p_{k}(\tan (b/2))$. In particular,

$$\begin{aligned} p_{2}(x)&= \frac{da^{2}}{2}(1+x^{2}), \qquad p_{3}(x)= \frac{da^{3}}{4}(2x+2x^{3}), \\ p_{4}(x)&= \frac{da^{4}}{8} (2+8x^{2}+6x^{4} ), \qquad p_{5}(x) = \frac{da^{5}}{16} (16x+40x^{3}+24x^{5} ), \\ p_{6}(x)&= \frac{da^{6}}{32} (16+136x^{2}+120x^{4}+120x^{6} ). \end{aligned}$$

From these formulas, we found numerically (letting $x^{2}=\tan ^{2}(b/2)$ vary in $[0,\infty )$) that the range of $R_{4}$ is $[0.240,0.340]$.

The density of $X_{1}$ is

$$\frac{(2\cos (b/2))^{2d}}{3a\pi \Gamma (2d)}\mathrm {e}^{b(x-m)/a} \big| \Gamma \big(d+\mathrm {i}(x-m)/a\big) \big|^{2}. $$

Numerically, the most obvious possibility is to write the absolute values of the gamma function $|\Gamma (d+\mathrm {i}y)|^{2}$ of a complex argument as $I_{1}^{2}+I_{2}^{2}$, where

$$ I_{1} = \int _{0}^{\infty }z^{d-1}\cos (y\log z)\mathrm {e}^{-z}\, \mathrm {d}z, \qquad I_{2} = \int _{0}^{\infty }z^{d-1}\sin (y\log z) \mathrm {e}^{-z}\,\mathrm {d}z, $$

and evaluate $I_{1},I_{2}$ by numerical integration. However, in some cases, Matlab’s integration routine failed to perform this task, possibly because of the highly oscillatory nature of the integrands. Instead, we then used simulation based on the representations $I_{1}=\Gamma (d)\mathbb{E}[\cos (y\log Z)]$, $I_{2}=\Gamma (d)\mathbb{E}[\sin (y\log Z)]$ with $Z$ gamma-distributed with form parameter $d$ and rate parameter 1.

For the density of $X_{t}$, replace $d$ by $dt$. Scaling by $v$ changes $a$ to $a/v$.

Proposition C.1

Given values $\mathring {{\kappa }}_{1},\ldots ,\mathring {{\kappa }}_{4}$, a Meixner process satisfying $\kappa _{k}=\mathring {{\kappa }}_{k}$ for $k=1,2,3,4$ exists if and only if $\mathring {{R}}<2/3$. In that case, the fitted parameters can be computed by first letting $q^{2}=(2-3\mathring {{R}})/(2(1-\mathring {{R}}))$ and then recursively defining

$$\begin{aligned} d&=2(1-q)^{2}/\mathring {{S}}^{2},\qquad b={\mathrm{sign}}(\mathring {{\kappa }}_{3})2\arcsin \Big(\sqrt{1-q^{2}}\Big), \\ a&=\sqrt{2\mathring {{\kappa }}_{2} q^{2}/d}, \qquad m=\mathring {{\kappa }}_{1}-da\tan (b/2). \end{aligned}$$

Proof

In terms of $q=\cos (b/2)$, we have $R=S^{2}/K=2(1-q^{2})/(3-q^{2})$, so we must have $q^{2}=(2-3R)/(2(1-R))$. The rest is then easy. □